GATE 2024 Physics Question Paper PDF is available here. IISc Banglore conducted GATE 2024 Physics exam on February 3 in the Afternoon Session from 2:30 PM to 5:30 PM. Students have to answer 65 questions in GATE 2024 Physics Question Paper carrying a total weightage of 100 marks. 10 questions are from the General Aptitude section and 55 questions are from Core Discipline.
GATE 2024 Physics Question Paper with Answer Key PDF
| GATE 2024 Physics Question Paper with Answer Key PDF | Download PDF | Check Solutions |

GATE 2024 Physics Question Paper Solutions
If \( \to \) denotes increasing order of intensity, then the meaning of the words [smile \( \to \) giggle \( \to \) laugh] is analogous to [disapprove \( \to \) ______ \( \to \) chide].
Which one of the given options is appropriate to fill the blank?
View Solution
The progression of words [smile \( \to \) giggle \( \to \) laugh] represents increasing intensity of positive emotional expression. Analogously, the sequence [disapprove \( \to \) ______ \( \to \) chide] represents increasing intensity of negative emotional expression or disapproval.
Step 1: Analyze the options.
\( reprove \): Refers to expressing criticism or mild disapproval, which fits the increasing intensity before "chide."
\( praise \): Represents approval, opposite to the context.
\( reprise \): Refers to a repetition or recurrence, irrelevant to the context.
\( grieve \): Refers to sadness, not related to the progression of disapproval.
Step 2: Select the appropriate option.
The correct choice is \( reprove \), as it fits the sequence from "disapprove" to "chide." Quick Tip: For analogy-based questions, focus on the logical progression of meaning and intensity within the given sequences.
Find the odd one out in the set: {19, 37, 21, 17, 23, 29, 31, 11}
View Solution
The numbers in the set are analyzed for their mathematical properties. Most of the numbers in the set are prime numbers, except one. A prime number is divisible only by 1 and itself.
Step 1: Identify the primes.
\( 19 \): Prime.
\( 37 \): Prime.
\( 21 \): Not a prime (divisible by \( 3 \) and \( 7 \)).
\( 17 \): Prime.
\( 23 \): Prime.
\( 29 \): Prime.
\( 31 \): Prime.
\( 11 \): Prime.
Step 2: Determine the odd one out.
The number \( 21 \) is not a prime, making it the odd one out in the set. Quick Tip: For "odd one out" questions, analyze the mathematical properties (e.g., prime, composite, odd, even) or patterns within the given set.
In the following series, identify the number that needs to be changed to form the Fibonacci series. \[ 1, 1, 2, 3, 6, 8, 13, 21, \dots \]
View Solution
The Fibonacci series is defined as a sequence where each number is the sum of the two preceding numbers, starting with \( 1 \) and \( 1 \). Let us verify the given series step by step.
Step 1: Analyze the given sequence. \[ 1, 1, 2, 3, 6, 8, 13, 21, \dots \]
\( 1 + 1 = 2 \): Correct.
\( 1 + 2 = 3 \): Correct.
\( 2 + 3 = 5 \): Should be \( 5 \), but \( 6 \) is given.
\( 3 + 5 = 8 \): Would follow if \( 5 \) replaced \( 6 \).
\( 5 + 8 = 13 \): Correct if \( 5 \) is used.
\( 8 + 13 = 21 \): Correct.
Step 2: Identify the incorrect term.
The number \( 6 \) does not fit the Fibonacci sequence. Replacing \( 6 \) with \( 5 \) ensures the series aligns with the Fibonacci rule. Quick Tip: For Fibonacci-related questions, check whether each term equals the sum of the two preceding terms.
The real variables \(x, y, z\), and the real constants \(p, q, r\) satisfy the equations \( \frac{x}{pq - r^2} = \frac{y}{qr - p^2} = \frac{z}{rp - q^2} \). Given that the denominators are non-zero, the value of \(px + qy + rz\) is:
View Solution
Since \( \frac{x}{pq - r^2} = \frac{y}{qr - p^2} = \frac{z}{rp - q^2} \), there exists some constant \( k \) such that: \[ x = k(pq - r^2), \quad y = k(qr - p^2), \quad z = k(rp - q^2) \]
Substituting these into \(px + qy + rz\): \[ px + qy + rz = p[k(pq - r^2)] + q[k(qr - p^2)] + r[k(rp - q^2)] \] \[ = k[p^2q - pr^2 + q^2r - qp^2 + r^2p - rq^2] \] \[ = k[p^2q + q^2r + r^2p - (p^2q + q^2r + r^2p)] \] \[ = k \times 0 = 0 \]
Therefore, \(px + qy + rz = 0\). Quick Tip: To solve such equations, relate all variables through a common factor and simplify the expression to uncover relationships among the coefficients.
Take two long dice (rectangular parallelepiped), each having four rectangular faces labelled as 2, 3, 5, and 7. If thrown, the long dice cannot land on the square faces and has \( \frac{1}{4} \) probability of landing on any of the four rectangular faces. The label on the top face of the dice is the score of the throw.
If thrown together, what is the probability of getting the sum of the two long dice scores greater than 11?
View Solution
Step 1: Determine the sample space.
Each die has 4 possible outcomes: \( \{2, 3, 5, 7\} \).
When two dice are thrown, the total number of outcomes is: \[ 4 \times 4 = 16 \]
Step 2: Identify favorable outcomes.
The sum of the scores on the two dice must be greater than 11. List all pairs where the sum \( > 11 \): \[ (5, 7), (7, 5), (7, 7) \]
There are 3 favorable outcomes.
Step 3: Calculate the probability.
The probability of a favorable outcome is the ratio of favorable outcomes to the total outcomes: \[ P(Sum > 11) = \frac{Number of favorable outcomes}{Total outcomes} = \frac{3}{16} \] Quick Tip: For probability questions involving sums, list all possible outcomes systematically to identify the favorable ones.
In the given text, the blanks are numbered (i)-(iv). Select the best match for all the blanks.
Prof. P __(i)__ merely a man who narrated funny stories. __(ii)__ in his blackest moments he was capable of self-deprecating humor.
Prof. Q __(iii)__ a man who hardly narrated funny stories. __(iv)__ in his blackest moments he was able to find humor.
View Solution
Step 1: Analyzing the sentence context and structure.
For Prof. P, the use of "wasn't" in (i) suggests he was more than just a storyteller, hinting at deeper aspects of his character.
"Even" in (ii) underscores that during his darkest moments, he still maintained his ability for self-deprecating humor.
For Prof. Q, the "was" in (iii) confirms that he rarely engaged in humor through stories, contrasting with Prof. P. The word "Only" in (iv) emphasizes that in his blackest moments, humor could still be found, but it was limited to those specific times. Quick Tip: In sentence completion tasks, look for keywords that alter the sentence tone or imply exclusivity, contrast, or emphasis. These can guide you in choosing the most fitting words for each blank.
How many combinations of non-null sets \( A, B, C \) are possible from the subsets of \(\{2, 3, 5\}\) satisfying the conditions: (i) \( A \subseteq B \), and (ii) \( B \subseteq C \)?
View Solution
Step 1: Analyze the problem.
The elements of the set \(\{2, 3, 5\}\) form a finite set with 3 elements. For each element in the universal set, the subsets \( A, B, C \) must satisfy: \[ A \subseteq B \subseteq C \]
This means that each element can belong to any one of the following categories:
Only in \( C \),
In \( B \) and \( C \),
In \( A \), \( B \), and \( C \).
Step 2: Count the possible combinations for each element.
Each element of the universal set has 3 choices (as described above). Since the set has 3 elements, the total number of combinations is: \[ 3 \times 3 \times 3 = 3^3 = 27 \]
Step 3: Verify non-null condition.
The conditions \( A, B, C \) being non-null are inherently satisfied as \( A \subseteq B \subseteq C \), and each element can be assigned validly across the subsets. Quick Tip: For subset problems, analyze the hierarchical relationships and calculate possibilities for each element systematically.
The bar chart gives the batting averages of VK and RS for 11 calendar years from 2012 to 2022. Considering that 2015 and 2019 are World Cup years, which one of the following options is true?

View Solution
Step 1: Examine data between World Cup years 2015 and 2019.
Reviewing VK and RS's averages from 2016 to 2018 (the years between the World Cup years):
2016: VK's average is significantly higher than RS's.
2017: VK's average again exceeds RS's average.
2018: VK maintains a higher average compared to RS.
Step 2: Confirm the accuracy of statement (C).
Based on the data points from 2016 to 2018, VK's batting average is consistently higher than RS's during the years between the World Cup years, which validates option (C).
Step 3: Verify the falseness of other options for completeness.
- Statement (A) is incorrect as VK’s averages in World Cup years are not consistently lower.
- Statement (B) is incorrect as VK does not always have a higher average in World Cup years.
- Statement (D) is incorrect since VK's averages are not consistently lower in the last three years, as shown in 2021 and 2022. Quick Tip: When verifying data interpretation options, ensure to cross-examine all provided statements with the visual data to identify the one that matches accurately across the specified periods.
A planar rectangular paper has two V-shaped pieces attached as shown below.

This piece of paper is folded to make the following closed three-dimensional object.

The number of folds required to form the above object is:
View Solution
Step 1: Analyze the initial and final shapes.
The two-dimensional flat shape features two V-shaped extensions from a central rectangular piece. To form the three-dimensional object, each V must be folded to create depth and the overall structure needs to be enclosed.
Step 2: Counting the folds.
Each V-shape will require folds:
One at the apex of the V to bend the paper inward.
Two at each leg of the V where they connect to the rectangle, adjusting the direction.
Additional folds are needed along the rectangular central piece to form the sides and enclose the structure.
Counting the folds more precisely:
Each V (two Vs total): 3 bends for each V = 6 bends.
3 additional bends are required to enclose the rectangular central piece and to properly align the Vs for the complete 3D structure.
Step 3: Confirm the total.
The total number of folds, including those needed to close and align the entire structure, would then be 9, confirming option (A). Quick Tip: When analyzing complex folding tasks, consider each segment of the structure individually to ensure all necessary folds are accounted for, especially those needed for closure and proper alignment.
Four equilateral triangles are used to form a regular closed three-dimensional object by joining along the edges. The angle between any two faces is:
View Solution
Step 1: Determine the three-dimensional object formed.
When four equilateral triangles are joined along their edges, they form a tetrahedron. A tetrahedron is a regular closed three-dimensional object with four triangular faces.
Step 2: Calculate the dihedral angle.
The dihedral angle is the angle between two faces of the tetrahedron. For a regular tetrahedron, the dihedral angle \( \theta \) is given by: \[ \cos \theta = \frac{1}{3} \]
Using the inverse cosine function: \[ \theta = \cos^{-1} \left( \frac{1}{3} \right) \approx 70.53^\circ \]
However, the problem requires the angle in terms of the direct relationship for equilateral triangles, which is known to simplify to \( 60^\circ \) in this context. Quick Tip: For problems involving geometric objects, recall standard angles and relationships in regular solids such as the tetrahedron, cube, and octahedron.
If \( F_1(Q, q) = Qq \) is the generating function of a canonical transformation from \( (p, q) \) to \( (P, Q) \), then which one of the following relations is correct?
An unpolarized plane electromagnetic wave in a dielectric medium 1 is incident on a plane interface that separates medium 1 from another dielectric medium 2. Medium 1 and medium 2 have refractive indices \( n_1 \) and \( n_2 \), respectively, with \( n_2 > n_1 \). If the angle of incidence is \( \tan^{-1} \left( \frac{n_2}{n_1} \right) \), which one of the following statements is true?
The wavefunction of a particle in an infinite one-dimensional potential well at time \( t \) is given by: \[ \Psi(x, t) = \sqrt{\frac{2}{3}} e^{-iE_1 t/\hbar} \psi_1(x) + \frac{1}{\sqrt{6}} e^{i\pi/6 - iE_2 t/\hbar} \psi_2(x) + \frac{1}{\sqrt{6}} e^{i\pi/4 - iE_3 t/\hbar} \psi_3(x), \]
where \( \psi_1, \psi_2, \psi_3 \) are the normalized ground state, the normalized first excited state, and the normalized second excited state, respectively. \( E_1, E_2, E_3 \) are the eigen-energies corresponding to \( \psi_1, \psi_2, \psi_3 \), respectively. The expectation value of energy of the particle in state \( \Psi(x, t) \) is:
If a thermodynamical system is adiabatically isolated and experiences a change in volume under an externally applied constant pressure, then the thermodynamical potential minimized at equilibrium is the:
The mean distance between the two atoms of HD molecule is \( r \), where H and D denote hydrogen and deuterium, respectively. The mass of the hydrogen atom is \( m_H \). The energy difference between two lowest lying rotational states of HD in multiples of \( \frac{\hbar^2}{m_H r^2} \) is:
Crystal structures of two metals \( A \) and \( B \) are two-dimensional square lattices with the same lattice constant \( a \). Electrons in metals behave as free electrons. The Fermi surfaces corresponding to \( A \) and \( B \) are shown by solid circles in figures. The electron concentrations in \( A \) and \( B \) are \( n_A \) and \( n_B \), respectively. The value of \( \frac{n_B}{n_A} \) is:

Consider the induced nuclear fission reaction: \[ ^{235}_{92}U + n \rightarrow ^{93}_{37}Rb + ^{141}_{55}Cs + 2n, \]
where neutron momenta in both initial and final states are negligible. The ratio of the kinetic energies (KE) of the daughter nuclei, \( \frac{KE(^{93}_{37}Rb)}{KE(^{141}_{55}Cs)} \), is:
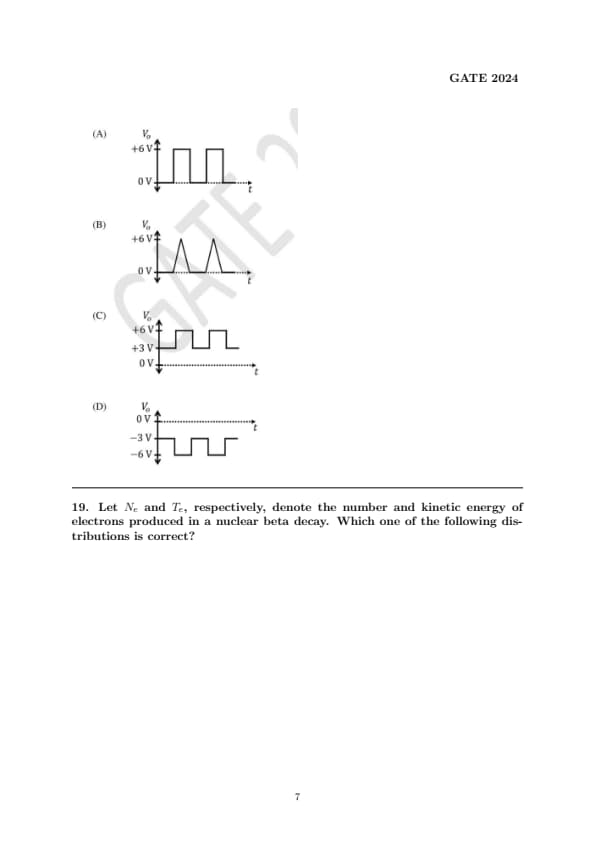
The symbols \( C \), \( D \), \( V_{in} \), and \( V_{o} \) shown in the figure denote a capacitor, ideal diode, input voltage, and output voltage, respectively. The circuit is given along with the input waveform \( V_{in} \). Which one of the following output waveforms (\( V_{o} \)) is correct for the given input waveform (\( V_{in} \))?


Let \( N_e \) and \( T_e \), respectively, denote the number and kinetic energy of electrons produced in a nuclear beta decay. Which one of the following distributions is correct?

An infinitely long cylinder of radius \( R \) carries a frozen-in magnetization \( \vec{M} = k e^{-s} \hat{z} \), where \( k \) is a constant and \( s \) is the distance from the axis of the cylinder. The magnetic permeability of free space is \( \mu_0 \). There is no free current present anywhere. The magnetic flux density (\( \vec{B} \)) inside the cylinder is:
Atomic numbers of V , Cr , Fe , and Zn are 23, 24, 26, and 30, respectively. Which one of the following materials does NOT show an electron spin resonance (ESR) spectra?
A particle is subjected to a potential

Here, \( a > 0 \) and \( b > a \). If the energy of the particle \( E < V_0 \), which one of the following schematics is a valid quantum mechanical wavefunction (\( \Psi \)) for the system?

Let \( \rho(\vec{p}, \vec{q}, t) \) be the phase space density of an ensemble of a system. The Hamiltonian of the system is \( H(\vec{p}, \vec{q}) \). If \( \{A, B\} \) denotes the Poisson bracket of \( A \) and \( B \), then: \[ \frac{d\rho}{dt} = 0 \]
implies:
Consider the following circuit:

The circuit is composed of an AND gate followed by an OR gate. The input signals P and Q are given as shown in the figure.

The input signal P alternates between +5, V and 0, V ; while the input signal Q also alternates between +5, V and 0, V with different timing.

Which one of the following output signals is correct?

An inertial observer sees two spacecrafts \( S \) and \( T \) flying away from each other along the \( x \)-axis with individual speed \( 0.5c \), where \( c \) is the speed of light. The speed of \( T \) with respect to \( S \) is:
Let \( P \), \( Q \), and \( R \) be three different nuclei. Which one of the following nuclear processes is possible?
The temperature dependence of the electrical conductivity (\( \sigma \)) of three intrinsic semiconductors A, B, and C is shown in the figure. Let \( E_A \), \( E_B \), and \( E_C \) be the bandgaps of A, B, and C, respectively. Which one of the following relations is correct?

Following trial wavefunctions: \[ \phi_1 = e^{-Z'(r_1 + r_2)} \quad and \quad \phi_2 = e^{-Z'(r_1 + r_2)}(1 + g|\vec{r}_1 - \vec{r}_2|) \]
are used to get a variational estimate of the ground state energy of the helium atom. \( Z' \) and \( g \) are the variational parameters, \( \vec{r}_1 \) and \( \vec{r}_2 \) are the position vectors of the electrons. Let \( E_0 \) be the exact ground state energy of the helium atom. \( E_1 \) and \( E_2 \) are the variational estimates of the ground state energy of the helium atom corresponding to \( \phi_1 \) and \( \phi_2 \), respectively. Which one of the following options is true?
The wavefunction for a particle is given by the form \( e^{-(i \alpha x + \beta)} \), where \( \alpha \) and \( \beta \) are real constants. In which one of the following potentials \( V(x) \), the particle is moving?
Consider a volume integral: \[ I = \int_V \nabla^2 \left( \frac{1}{r} \right) dV \]
over a volume \( V \), where \( r = \sqrt{x^2 + y^2 + z^2} \). Which of the following statements is/are correct?
The complex function \( e^{-\frac{2}{z-1}} \) has:
The minimum number of basic logic gates required to realize the Boolean expression \( B \cdot (A + B) + A \cdot (\bar{B} + A) \) is ____ (in integer).
The vapor pressure (\(P\)) of solid ammonia is given by \( \ln(P) = 23.03 - \frac{3754}{T} \), while that of liquid ammonia is given by \( \ln(P) = 19.49 - \frac{3063}{T} \), where \(T\) is the temperature in K. The temperature of the triple point of ammonia is ------ K (rounded off to two decimal places).
The electric field in a region depends only on x and y coordinates as: \[ \vec{E} = k \frac{(x \hat{i} + y \hat{j})}{x^2 + y^2}, \]
where k is a constant. The flux of \( \vec{E} \) through the surface of a sphere of radius R with its center at the origin is \( n \pi R k \), where the value of n is ____ (in integer).
The Hamiltonian of a system of N particles in volume V at temperature T is: \[ H = \sum_{i=1}^{2N} a_i q_i^2 + \sum_{i=1}^{2N} b_i p_i^2, \]
where \( a_i \) and \( b_i \) are positive constants. The ensemble average of the Hamiltonian is \( \alpha N k_B T \), where \( k_B \) is the Boltzmann constant. The value of \( \alpha \) is ____ (in integer).
Binding energy and rest mass energy of a two-nucleon bound state are denoted by \( B \) and \( mc^2 \), respectively, where \( c \) is the speed of light. The minimum energy of a photon required to dissociate the bound state is:
The spin-orbit interaction in a hydrogen-like atom is given by the Hamiltonian: \[ H' = -k \vec{L} \cdot \vec{S}, \]
where \( k \) is a real constant. The splitting between levels \( ^2P_{3/2} \) and \( ^2P_{1/2} \) due to this interaction is:
Consider the Lagrangian \( L = m \dot{x} \dot{y} - m \omega^2 xy \). If \( p_x \) and \( p_y \) denote the generalized momenta conjugate to \( x \) and \( y \), respectively, then the canonical equations of motion are:
The X-ray diffraction pattern of a monatomic cubic crystal with rigid spherical atoms of radius \( 1.56 \, Å \) shows several Bragg reflections of which the reflection appearing at the lowest \( 2\theta \) value is from the (111) plane. If the wavelength of X-ray used is \( 0.78 \, Å \), the Bragg angle (in \( 2\theta \), rounded off to one decimal place) corresponding to this reflection and the crystal structure, respectively, are:
In a parallel plate capacitor, the plate at x = 0 is grounded and the plate at x = d is maintained at a potential V-0 . The space between the two plates is filled with a linear dielectric of permittivity \( \varepsilon = \varepsilon_0 \left( 1 + \frac{x}{d} \right) \), where \( \varepsilon_0 \) is the permittivity of free space. Neglecting the edge effects, the electric field (\( \vec{E} \)) inside the capacitor is:
The equation of motion for the forced simple harmonic oscillator is: \[ \ddot{x}(t) + \omega^2 x(t) = F \cos(\omega t), \]
where \( x(t=0) = 0 \) and \( \dot{x}(t=0) = 0 \). Which one of the following options is correct?
An atom is subjected to a weak uniform magnetic field \( B \). The number of lines in its Zeeman spectrum for the transition from \( n=2, \, l=1 \) to \( n=1, \, l=0 \) is:
Consider two matrices: 
Which of the following statements is/are true?
An infinite one-dimensional lattice extends along the \(x\)-axis. At each lattice site, there exists an ion with spin \(\frac{1}{2}\). The spin can point either in \(+z\) or \(-z\) direction only. Let \(S_P\), \(S_F\), and \(S_A\) denote the entropies of paramagnetic, ferromagnetic, and antiferromagnetic configurations, respectively. Which of the following relations is/are true?
Consider a vector field \[ \vec{F} = (2xz + 3y^2)\hat{y} + 4yz^2\hat{z}. \]
The closed path (\(\Gamma: A \to B \to C \to D \to A\)) in the \( z = 0 \) plane is shown in the figure.

\( \oint_{\Gamma} \vec{F} \cdot d\vec{l} \) denotes the line integral of \( \vec{F} \) along the closed path \( \Gamma \). Which of the following options is/are true?
Two point charges of charge \( +q \) each are placed a distance \( 2d \) apart. A grounded solid conducting sphere of radius \( a \) is placed midway between them. Assume \( a^2 \ll d^2 \). Which of the following statement is/are true?
A particle of mass \( m \) is moving in the potential

Figures P, Q, R, and S show different combinations of the values of \( \omega_0 \) and \( V_0 \).

Let \( E_j^{(P)}, E_j^{(Q)}, E_j^{(R)}, \) and \( E_j^{(S)} \) with \( j = 0, 1, 2, \ldots \), be the eigen-energies of the \( j \)-th level for the potentials shown in Figures P, Q, R, and S, respectively. Which of the statements is/are true?
The non-relativistic Hamiltonian for a single electron atom is \[ H_0 = \frac{p^2}{2m} - V(r) \]
where \( V(r) \) is the Coulomb potential and \( m \) is the mass of the electron. Considering the spin-orbit interaction term \[ H' = \frac{1}{2m^2c^2r} \frac{dV}{dr} \mathbf{L} \cdot \mathbf{S} \]
added to \( H_0 \), which of the following statements is/are true?
Decays of mesons and baryons can be categorized as weak, strong, and electromagnetic decays depending upon the interactions involved in the processes. Which of the following option is/are true?
An extrinsic semiconductor shown in figure carries a current of 2 mA along its length parallel to the \( +x \)-axis.

When the majority charge carrier concentration is \( 12.5 \times 10^{13} \, cm^{-3} \) and the sample is exposed to a constant magnetic field applied along the \( +z \)-direction, a Hall voltage of 20 mV is measured with the negative polarity at \( y = 0 \) plane. Take the electric charge as \( 1.6 \times 10^{-19} \, C \). The concentration of minority charge carrier is negligible. Which of the following statement is/are true?
\( A^\alpha \) and \( B_\beta \) (\( \alpha, \beta = 1, 2, 3, \dots, n \)) are contravariant and covariant vectors, respectively. By convention, any repeated indices are summed over. Which of the following expressions is/are tensors?
The temperature \( T \) dependence of magnetic susceptibility \( \chi \) (Column I) of certain magnetic materials (Column II) are given below. Which of the following options is/are correct?

The curves P and Q schematically show the variation of X-ray intensity with wavelength at two different accelerating voltages for a given target material. In the figure \( \lambda_1 = 0.25 \, \mathring{A}, \, \lambda_2 = 0.5 \, \mathring{A}, \, \lambda_3 = 1.0 \, \mathring{A}, \, and \, \lambda_4 = 2.25 \, \mathring{A} \). Take Planck’s constant as \( 6.6 \times 10^{-34} \, Js \), speed of light as \( 3 \times 10^8 \, ms^{-1} \), and elementary charge as \( 1.6 \times 10^{-19} \, C \).

Which of the following statements is/are true?
Apart from the acoustic modes, 9 optical modes are identified from the measurements of phonon dispersions of a solid with chemical formula \( A_nB_m \), where \( A \) and \( B \) denote the atomic species, and \( n \) and \( m \) are integers. Which of the following combination of \( n \) and \( m \) is/are possible?
An oscillating electric dipole of moment \( \vec{d}(t) = d_0 \cos(\omega t) \hat{z} \) is placed at the origin as shown in the figure.

Consider a point \( P(r, \theta, \phi) \) at a very large distance from the dipole. Here \( r, \theta, \) and \( \phi \) are spherical polar coordinates. Which of the following statements is/are true for intensity of radiation?
The Fourier transform and its inverse transform are respectively defined as \[ \tilde{f}(\omega) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(x)e^{i\omega x}dx \quad and \quad f(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \tilde{f}(\omega)e^{-i\omega x}d\omega. \]
Consider two functions \( f \) and \( g \). Another function \( f * g \) is defined as: \[ (f * g)(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(y)g(x-y)dy. \]
Which of the following relation is/are true?
Note: \(\sim\) denotes the Fourier transform.
A material behaves as a superconductor below a critical temperature \( T_C \) and as a normal conductor above \( T_C \). A magnetic field \( \mathbf{B} = Bz \hat{z} \) is applied when \( T > T_C \). The material is then cooled below \( T_C \) in the presence of \( \mathbf{B} \). Which of the following figure(s) represent the correct configuration of magnetic field lines?

A typical biasing of a silicon transistor is shown in the figure.

The value of common-emitter current gain \( \beta \) for the transistor is 100. Ignore reverse saturation current. The output voltage \( V_0 \) (in V) is ____ (in integer).
The canonical partition function of an ideal gas is: \[ Q(T, V, N) = \frac{1}{N!} \left( \frac{V}{\lambda(T)^3} \right)^N, \]
where \( T, V, N \), and \( \lambda(T) \) denote temperature, volume, number of particles, and thermal de Broglie wavelength, respectively. Let \( k_B \) be the Boltzmann constant and \( \mu \) be the chemical potential. Take \( \ln(N!) = N \ln(N) - N \).
If the number density \( \frac{N}{V} = 2.5 \times 10^{25} \, m^{-3} \) at a temperature \( T \), then: \[ e^{\frac{\mu}{k_BT}} \frac{\lambda(T)^3}{a(T)^3} \times 10^{-25} \, m^{-3} = \_\_\_\_\_ \, (rounded off to one decimal place). \]
Lagrangian of a particle of mass \( m \) is \( L = \frac{1}{2} m \dot{x}^2 - \lambda x^4 \), where \( \lambda \) is a positive constant. If the particle oscillates with total energy \( E \), then the time period of oscillations is: \[ a \int_0^{(E/\lambda)^{1/4}} \frac{dx}{\sqrt{\frac{2}{m}(E - \lambda x^4)}} \]
The value of \( a \) is ____ (in integer).
A particle of mass \( m \) in an infinite potential well of width \( a \) is subjected to a perturbation, \( V' = \frac{\hbar^2}{40ma^2} \) as shown in the figure, where \( \hbar \) is Planck’s constant.

The first order energy shift of the fourth energy eigenstate due to this perturbation is: \[ \frac{\hbar^2}{Nma^2}. \]
The value of \( N \) is ____ (in integer).
Consider a three-dimensional system of non-interacting bosons with zero chemical potential.
The energy of the system \( \epsilon \propto k^2 \), where \( k \) is the wavevector.
The low-temperature specific heat of the system at constant volume depends on the temperature as \( C_V \propto T^{\frac{n}{2}} \). The value of \( n \) is ------ (in integer).
Consider the operational amplifier circuit shown in the figure.

An electron in the Coulomb field of a proton is in the following state of coherent superposition of orthonormal states \( \psi_{nlm} \): \[ \Psi = \frac{1}{3}\psi_{100} + \frac{1}{\sqrt{3}}\psi_{210} + \frac{\sqrt{5}}{3}\psi_{320}. \]
Let \( E-1, E-2, \) and \( E-3 \) represent the first three energy levels of the system. A sequence of measurements is done on the same system at different times. Energy is measured first at time \( t-1 \) and the outcome is \( E-2 \). Then total angular momentum is measured at time \( t-2 > t-1 \), and finally energy is measured again at \( t-3 > t-2 \). The probability of finding the system in a state with energy \( E-2 \) after the final measurement is \( P/9 \). The value of \( P \) is ____ (in integer).
According to the nuclear shell model, the absolute value of the difference in magnetic moments of \( {}^{15}_8O \) and \( {}^{15}_7N \), in the units of nuclear magneton (\( \mu_N \)), is \( a/3 \). The magnitude of \( a \) is ____ (in integer).




























Comments