GATE 2024 Engineering Sciences Question Paper PDF is available here. IISc Banglore is conducted GATE 2024 Engineering Sciences exam on February 10 in the Afternoon Session from 2:30 PM to 5:30 PM. Students have to answer 65 questions in GATE 2024 Engineering Sciences Question Paper carrying a total weightage of 100 marks. 10 questions are from the General Aptitude section and 55 questions are from Core Discipline.
GATE 2024 Engineering Sciences Question Paper with Answer Key PDF
| GATE 2024 XE Question Paper PDF | GATE 2024 XE Answer Key PDF | GATE 2024 XE Solution PDF |
|---|---|---|
| Download PDF | Download PDF | Download PDF |
GATE 2024 Engineering Sciences Question Paper with Solution
If ‘\(\rightarrow\)’ denotes increasing order of intensity, then the meaning of the words \([walk \rightarrow jog \rightarrow sprint]\) is analogous to \([bothered \rightarrow \_\_\_\_\_ \rightarrow daunted]\).
Which one of the given options is appropriate to fill the blank?
View Solution
Step 1: Identify the pattern of intensity.
The sequence \([walk \rightarrow jog \rightarrow sprint]\) clearly shows a gradual rise in physical intensity. In the same manner, the sequence \([bothered \rightarrow \_\_\_\_\_ \rightarrow daunted]\) must reflect an increasing level of emotional impact, starting from slight irritation and moving towards strong fear or discouragement.
Step 2: Evaluate the given options.
- Option A: phased
The word phased refers to something done in stages and does not express any emotional state, so it does not fit the analogy.
- Option B: phrased
The word \textit{phrased is related to wording or expression and is irrelevant to emotional intensity.
- Option C: fazed
The word \textit{fazed means disturbed or unsettled. It represents a stronger emotional reaction than \textit{bothered but is less intense than \textit{daunted, making it the most appropriate choice.
- Option D: fused
The word \textit{fused means joined together and has no emotional meaning.
Step 3: Final conclusion.
The word \textit{fazed correctly completes the sequence by maintaining the increasing order of emotional intensity.
\[ \boxed{Correct Answer: (C) fazed \] Quick Tip: In analogy questions, always check whether the chosen word preserves the same progression or degree shown in the original sequence.
Two wizards try to create a spell using all the four elements, water, air, fire, and earth. For this, they decide to mix all these elements in all possible orders. They also decide to work independently. After trying all possible combinations of elements, they conclude that the spell does not work.
How many attempts does each wizard make before coming to this conclusion, independently?
View Solution
Step 1: Count all possible orders of the elements.
The spell requires arranging all four distinct elements—water, air, fire, and earth—in every possible sequence. When the order of arrangement matters, the total number of such arrangements is calculated using the factorial of the number of elements. Since there are four elements: \[ n = 4 \]
The total number of different orders is: \[ 4! = 4 \times 3 \times 2 \times 1 = 24 \]
Step 2: Attempts made by one wizard.
As both wizards work independently, each of them must try every possible arrangement on their own. Hence, each wizard performs all \(24\) permutations of the four elements. Therefore, the number of attempts made by each wizard is: \[ \boxed{24 \]
Final Answer: Each wizard makes \(24\) attempts. Quick Tip: Whenever a problem involves arranging distinct items in different orders, apply the factorial formula \(n!\) to find the total number of permutations.
In an engineering college of 10,000 students, 1,500 like neither their core branches nor other branches. The number of students who like their core branches is \( \frac{1}{4} \)th of the number of students who like other branches. The number of students who like both their core and other branches is 500.
The number of students who like their core branches is:
View Solution
Step 1: Assign variables and interpret the data.
Let:
\( x \) represent the number of students who like only their core branches.
\( y \) represent the number of students who like only other branches.
It is given that 500 students like both core and other branches. Out of a total of 10,000 students, 1,500 like neither option. Therefore, the number of students who like at least one of the two branches is: \[ 10,000 - 1,500 = 8,500. \]
Step 2: Form the equation using total counts.
Students who like core branches include those who like only core branches and those who like both, i.e., \( x + 500 \).
Similarly, students who like other branches are \( y + 500 \).
Thus, the total becomes: \[ (x + 500) + (y + 500) = 8,500. \]
Simplifying: \[ x + y + 1,000 = 8,500 \quad \Rightarrow \quad x + y = 7,500. \quad \cdots (1) \]
Step 3: Use the given proportional relationship.
The problem states that the number of students who like their core branches is one-fourth of those who like other branches: \[ x + 500 = \frac{1}{4}(y + 500). \]
Multiplying both sides by 4: \[ 4(x + 500) = y + 500. \]
Simplifying: \[ 4x + 2,000 = y + 500 \quad \Rightarrow \quad y = 4x + 1,500. \quad \cdots (2) \]
Step 4: Solve the system of equations.
Substitute the value of \( y \) from equation (2) into equation (1): \[ x + (4x + 1,500) = 7,500. \]
Simplifying: \[ 5x + 1,500 = 7,500 \quad \Rightarrow \quad 5x = 6,000 \quad \Rightarrow \quad x = 1,200. \]
Step 5: Calculate students who like core branches.
The total number of students who like their core branches is: \[ x + 500 = 1,200 + 500 = 1,800. \]
Final Answer: The number of students who like their core branches is: \[ \boxed{1,800}. \] Quick Tip: In set-based problems, always separate exclusive groups clearly and use equations to connect totals and given ratios.
For positive non-zero real variables \( x \) and \( y \), if \[ \ln\left(\frac{x + y}{2}\right) = \frac{1}{2} \left[\ln(x) + \ln(y)\right], \]
then, the value of \( \frac{x}{y} + \frac{y}{x} \) is:
View Solution
Step 1: Rewrite the given logarithmic expression.
The given condition is: \[ \ln\left(\frac{x + y}{2}\right) = \frac{1}{2} \left[\ln(x) + \ln(y)\right]. \]
Using the logarithmic identity \(\ln a + \ln b = \ln(ab)\), the right-hand side becomes: \[ \frac{1}{2}\ln(xy). \]
Hence, the equation can be rewritten as: \[ \ln\left(\frac{x + y}{2}\right) = \frac{1}{2}\ln(xy). \]
Step 2: Remove the logarithms.
Exponentiating both sides of the equation gives: \[ \frac{x + y}{2} = \sqrt{xy}. \]
Multiplying both sides by 2: \[ x + y = 2\sqrt{xy}. \]
Step 3: Eliminate the square root.
Squaring both sides, we get: \[ (x + y)^2 = 4xy. \]
Expanding the left-hand side: \[ x^2 + 2xy + y^2 = 4xy. \]
Rearranging the terms: \[ x^2 + y^2 = 2xy. \quad \cdots (1) \]
Step 4: Evaluate \( \frac{x}{y} + \frac{y}{x} \).
Using the identity: \[ \frac{x}{y} + \frac{y}{x} = \frac{x^2 + y^2}{xy}, \]
and substituting \( x^2 + y^2 = 2xy \) from equation (1), we obtain: \[ \frac{x}{y} + \frac{y}{x} = \frac{2xy}{xy} = 2. \]
Final Answer: The value of \( \frac{x}{y} + \frac{y}{x} \) is: \[ \boxed{2}. \] Quick Tip: When logarithmic equations involve averages, converting them into algebraic form often leads to standard identities that simplify the problem quickly.
In the sequence \( 6, 9, 14, x, 30, 41 \), a possible value of \( x \) is:
View Solution
Step 1: Examine the sequence carefully.
The given number sequence is: \[ 6, \, 9, \, 14, \, x, \, 30, \, 41. \]
To identify the pattern, find the difference between each pair of consecutive terms: \[ 9 - 6 = 3, \quad 14 - 9 = 5, \quad x - 14, \quad 30 - x, \quad 41 - 30 = 11. \]
Hence, the sequence of differences is: \[ 3, \, 5, \, (x - 14), \, (30 - x), \, 11. \]
Step 2: Detect the underlying pattern.
Observing the known differences, we see that they increase as consecutive odd numbers: \[ 3, \, 5, \, 7, \, 9, \, 11. \]
This suggests that the missing differences should also follow this pattern.
Step 3: Determine the value of \( x \).
To match the pattern, we set: \[ x - 14 = 7. \]
Solving for \( x \): \[ x = 21. \]
Step 4: Confirm the result.
Substituting \( x = 21 \) back into the sequence: \[ 6, \, 9, \, 14, \, 21, \, 30, \, 41, \]
and checking the differences: \[ 3, \, 5, \, 7, \, 9, \, 11, \]
which clearly follows the required pattern.
Final Answer: A possible value of \( x \) is: \[ \boxed{21}. \] Quick Tip: In sequence problems, checking the differences between terms often reveals simple patterns such as arithmetic progressions or sequences of odd or even numbers.
Sequence the following sentences in a coherent passage.
[P:] This fortuitous geological event generated a colossal amount of energy and heat that resulted in the rocks rising to an average height of 4 km across the contact zone.
[Q:] Thus, the geophysicists tend to think of the Himalayas as an active geological event rather than as a static geological feature.
[R:] The natural process of the cooling of this massive edifice absorbed large quantities of atmospheric carbon dioxide, altering the earth’s atmosphere and making it better suited for life.
[S:] Many millennia ago, a breakaway chunk of bedrock from the Antarctic Plate collided with the massive Eurasian Plate.
View Solution
Step 1: Determine the opening sentence.
Sentence \( S \) is the most suitable starting point as it introduces the origin of the event by describing the ancient collision between tectonic plates. This provides the necessary background for the passage.
Step 2: Describe the immediate outcome.
Sentence \( P \) naturally follows \( S \) because it explains the direct result of the collision, namely the release of immense energy and the uplift of rocks forming the Himalayas.
Step 3: Explain the long-term effects.
Sentence \( R \) comes next, as it discusses the extended impact of the geological formation, particularly how the cooling process influenced the earth’s atmosphere and supported life.
Step 4: End with scientific interpretation.
Sentence \( Q \) serves as the concluding statement by summarizing how geophysicists currently understand the Himalayas—as a dynamic and ongoing geological process rather than a fixed structure.
Thus, the correct sequence of sentences is: \[ \boxed{S P R Q} \] Quick Tip: For sentence ordering questions, look for a logical flow from origin or cause, to effects, and finally to conclusions or interpretations.
A person sold two different items at the same price. He made \(10%\) profit in one item, and \(10%\) loss in the other item. In selling these two items, the person made a total of:
View Solution
Step 1: Assume the selling price of each item.
Let the selling price of each item be \( SP \).
Let \( CP_1 \) and \( CP_2 \) be the cost prices of the first and second items respectively.
For the first item, a profit of \(10%\) is made: \[ SP = CP_1 \left(1 + \frac{10}{100}\right) = 1.1\,CP_1. \]
Hence, \[ CP_1 = \frac{SP}{1.1}. \]
For the second item, a loss of \(10%\) is incurred: \[ SP = CP_2 \left(1 - \frac{10}{100}\right) = 0.9\,CP_2. \]
Thus, \[ CP_2 = \frac{SP}{0.9}. \]
Step 2: Find the total cost price and total selling price.
The combined cost price of both items is: \[ Total CP = \frac{SP}{1.1} + \frac{SP}{0.9}. \]
The combined selling price of the two items is: \[ Total SP = 2SP. \]
Step 3: Determine the overall profit or loss.
The net profit or loss is given by: \[ Net Profit/Loss = Total SP - Total CP. \]
Substituting the values: \[ Net Profit/Loss = 2SP - \left(\frac{SP}{1.1} + \frac{SP}{0.9}\right). \]
Simplifying further: \[ Net Profit/Loss = 2SP - SP\left(\frac{1}{1.1} + \frac{1}{0.9}\right). \]
\[ Net Profit/Loss = 2SP - SP\left(\frac{2}{0.99}\right) = 2SP - 2.02SP. \]
\[ Net Profit/Loss = -0.02SP. \]
The loss percentage is: \[ Loss Percentage = \frac{0.02SP}{2SP} \times 100 = 1%. \]
Step 4: Final Answer.
The person incurs an overall loss of: \[ \boxed{1% loss.} \] Quick Tip: If two items are sold at the same price with equal percentage profit and loss, the final result is always a loss equal to \(\frac{(loss%)^2}{100}\).
The pie charts depict the shares of various power generation technologies in the total electricity generation of a country for the years 2007 and 2023.
The renewable sources of electricity generation consist of Hydro, Solar, and Wind. Assuming that the total electricity generated remains the same from 2007 to 2023, what is the percentage increase in the share of the renewable sources of electricity generation over this period?
View Solution
Step 1: Determine the renewable energy share in 2007.
In 2007, electricity generated from renewable sources includes Hydro, Solar, and Wind. Adding their respective shares: \[ Renewable share in 2007 = 30% + 5% + 5% = 40%. \]
Step 2: Determine the renewable energy share in 2023.
In 2023, the contribution from renewable sources again comes from Hydro, Solar, and Wind. Their combined share is: \[ Renewable share in 2023 = 35% + 20% + 10% = 65%. \]
Step 3: Compute the percentage increase in renewable share.
The absolute increase in the share of renewable energy over the period is: \[ Increase = 65% - 40% = 25%. \]
To find the percentage increase relative to the initial value: \[ Percentage increase = \frac{25}{40} \times 100 = 62.5%. \]
Conclusion:
Thus, the share of renewable sources of electricity generation has increased by: \[ \boxed{62.5%}. \] Quick Tip: When calculating percentage growth, always divide the change by the original value, not the final value.
A cube is to be cut into 8 pieces of equal size and shape. Here, each cut should be straight and it should not stop till it reaches the other end of the cube. The minimum number of such cuts required is:
View Solution
Step 1: Understand the requirement of the cuts.
The objective is to divide a cube into \(8\) equal pieces using straight cuts that pass completely through the cube. Since all pieces must be identical in size and shape, the cube needs to be divided evenly along its dimensions.
Step 2: Apply cuts along each dimension.
A cube has three dimensions—length, width, and height.
The first cut divides the cube into \(2\) equal parts along one dimension.
The second cut divides these parts along a second dimension, resulting in \(4\) equal pieces.
The third cut divides the cube along the remaining dimension, producing \(8\) equal pieces.
Thus, one cut along each dimension is sufficient.
Step 3: Final Answer.
The minimum number of cuts required is: \[ \boxed{3}. \] Quick Tip: For cutting a cube into equal parts, each straight cut can double the number of pieces if applied along a new dimension.
In the \( 4 \times 4 \) array shown below, each cell of the first three rows has either a cross (X) or a number.
The number in a cell represents the count of the immediate neighboring cells (left, right, top, bottom, diagonals) NOT having a cross (X). Given that the last row has no crosses (X), the sum of the four numbers to be filled in the last row is:
View Solution
Step 1: Interpret the rule of the grid.
In the given \(4 \times 4\) grid:
Each number indicates how many of its immediate neighboring cells (including diagonals) do \emph{not contain a cross (X).
The fourth row is known to contain no crosses, so all its cells must be filled with numbers.
Step 2: Evaluate each cell of the last row.
Cell (4,1):
Its neighboring cells are (3,1), (3,2), and (4,2).
(3,1) has a number.
(3,2) has a cross (X).
(4,2) will contain a number.
So, the count of non-cross neighbors is \(2\).
Cell (4,2):
Its neighbors are (3,1), (3,2), (3,3), (4,1), and (4,3).
(3,1) and (3,3) contain numbers.
(3,2) contains a cross.
(4,1) and (4,3) belong to the last row and have no crosses.
Hence, the value is \(3\).
Cell (4,3):
Its neighboring cells are (3,2), (3,3), (3,4), (4,2), and (4,4).
(3,3), (4,2), and (4,4) do not contain crosses.
(3,2) and (3,4) contain crosses.
Thus, the value here is \(3\).
Cell (4,4):
Its neighbors are (3,3), (3,4), and (4,3).
(3,3) and (4,3) are non-cross cells.
(3,4) contains a cross.
So, the value is \(3\).
Step 3: Compute the required sum.
The numbers in the last row are: \[ 2,\; 3,\; 3,\; 3. \]
Their sum is: \[ 2 + 3 + 3 + 3 = 11. \]
Conclusion:
The sum of the four numbers in the last row is: \[ \boxed{11}. \] Quick Tip: In grid-based logic problems, carefully list all valid neighbors for each cell and apply the given condition systematically.
Let \[ f(x)= \begin{cases} \pi + x, & -\pi \le x < 0,
0, & 0 \le x < \pi, \end{cases} \]
with \( f(x+2\pi)=f(x) \).
If \( F(x) \) represents the Fourier series of \( f(x) \), then the value of \[ F\left(-\frac{\pi}{2}\right) + F(0) \]
is
View Solution
Step 1: Using the property of Fourier series.
For a piecewise continuous function, the Fourier series \( F(x) \) converges to \[ F(x)=\frac{f(x^+)+f(x^-)}{2} \]
at a point of discontinuity, and equals \( f(x) \) at points of continuity.
Step 2: Evaluating \( F\left(-\frac{\pi}{2}\right) \).
At \( x=-\frac{\pi}{2} \), the function lies in the interval \( -\pi \le x < 0 \).
So, \[ f\left(-\frac{\pi}{2}\right)=\pi-\frac{\pi}{2}=\frac{\pi}{2} \]
Since the function is continuous at this point, \[ F\left(-\frac{\pi}{2}\right)=\frac{\pi}{2} \]
Step 3: Evaluating \( F(0) \).
At \( x=0 \), the function is discontinuous. Hence, \[ F(0)=\frac{f(0^-)+f(0^+)}{2} \] \[ f(0^-)=\pi,\quad f(0^+)=0 \] \[ F(0)=\frac{\pi+0}{2}=\frac{\pi}{2} \]
Step 4: Final calculation.
\[ F\left(-\frac{\pi}{2}\right)+F(0)=\frac{\pi}{2}+\frac{\pi}{2}=\pi \]
Quick Tip: At points of discontinuity, the Fourier series converges to the average of left and right limits of the function.
Let \( y \) be a non-zero quadratic polynomial satisfying \[ (2+x^2)\frac{d^2y}{dx^2}+x\frac{dy}{dx}-ky=0 \]
where \( k \) is a real constant. If \( y(1)=1 \), then the value of \[ \int_0^1 2y\,dx \]
is
View Solution
Step 1: Assume the quadratic polynomial.
Let \[ y=ax^2+bx+c,\quad a\neq0 \]
Then, \[ \frac{dy}{dx}=2ax+b,\quad \frac{d^2y}{dx^2}=2a \]
Step 2: Substitute into the differential equation.
\[ (2+x^2)(2a)+x(2ax+b)-k(ax^2+bx+c)=0 \]
Simplifying, \[ (2a-k a)x^2+(2a-k b)x+(4a-k c)=0 \]
Step 3: Equating coefficients.
\[ 2a-ka=0 \Rightarrow k=2 \] \[ 2a-2b=0 \Rightarrow b=a \] \[ 4a-2c=0 \Rightarrow c=2a \]
Step 4: Use the condition \( y(1)=1 \).
\[ a+b+c=1 \] \[ a+a+2a=1 \Rightarrow 4a=1 \Rightarrow a=\frac{1}{4} \]
Thus, \[ y=\frac{1}{4}x^2+\frac{1}{4}x+\frac{1}{2} \]
Step 5: Evaluate the integral.
\[ \int_0^1 2y\,dx=\int_0^1 \left(\frac{x^2}{2}+\frac{x}{2}+1\right)dx \] \[ =\left[\frac{x^3}{6}+\frac{x^2}{4}+x\right]_0^1 =\frac{1}{6}+\frac{1}{4}+1=\frac{4}{3} \]
Quick Tip: When a polynomial satisfies a differential equation, equating coefficients is the fastest way to determine constants.
There are four cities, namely, \( C_1, C_2, C_3 \) and \( C_4 \). The cities are directly connected by four roads as shown in the figure. The probability of any road getting independently blocked is \( \frac{1}{3} \). Let \( E_1 \) be the event of travelling from \( C_1 \) to \( C_3 \) via \( C_2 \) and \( E_2 \) be the event of travelling from \( C_1 \) to \( C_3 \) via \( C_4 \). Then which of the following statements is correct?
View Solution
Step 1: Understanding the road network.
There are four roads forming a rectangular loop: \( C_1 \to C_2 \to C_3 \to C_4 \to C_1 \).
Each road is blocked independently with probability \( \frac{1}{3} \), hence open with probability \( \frac{2}{3} \).
Step 2: Probability of event \( E_1 \).
Event \( E_1 \) requires both roads \( C_1C_2 \) and \( C_2C_3 \) to be open. \[ P(E_1)=\left(\frac{2}{3}\right)^2=\frac{4}{9} \]
Step 3: Probability of event \( E_2 \).
Event \( E_2 \) requires both roads \( C_1C_4 \) and \( C_4C_3 \) to be open. \[ P(E_2)=\left(\frac{2}{3}\right)^2=\frac{4}{9} \]
Step 4: Probability of \( E_1 \cap E_2 \).
For both paths to be available, all four roads must be open. \[ P(E_1 \cap E_2)=\left(\frac{2}{3}\right)^4=\frac{16}{81} \]
Step 5: Using the union formula.
\[ P(E_1 \cup E_2)=P(E_1)+P(E_2)-P(E_1 \cap E_2) \] \[ =\frac{4}{9}+\frac{4}{9}-\frac{16}{81} =\frac{56}{81} \]
Step 6: Conclusion.
The correct statement is option (A).
Quick Tip: For network problems, always identify independent paths clearly and use the inclusion–exclusion principle for union of events.
Assume that \( f:[0,1]\to\mathbb{R} \) is continuous on \( [0,1] \) and differentiable on \( (0,1) \) such that \[ f(x+h)=f(x)+hf'(x+\theta h), \quad 0<\theta<1. \]
If \( f(x)=x^2(1+x) \) and \( \theta \) is expressed in terms of \( x \) and \( h \), then the value of \[ \lim_{h\to0}\theta(x,h) \]
is
View Solution
Step 1: Identify the given theorem.
The given relation is the Mean Value Theorem in Lagrange’s form for increments: \[ f(x+h)-f(x)=hf'(x+\theta h) \]
Step 2: Compute \( f(x+h)-f(x) \).
\[ f(x)=x^2+x^3 \] \[ f(x+h)=(x+h)^2+(x+h)^3 \] \[ = x^2+2xh+h^2+x^3+3x^2h+3xh^2+h^3 \] \[ f(x+h)-f(x)=h(2x+3x^2)+h^2(1+3x)+h^3 \]
Step 3: Compute \( f'(x) \).
\[ f'(x)=2x+3x^2 \]
Hence, \[ f'(x+\theta h)=2(x+\theta h)+3(x+\theta h)^2 \]
Step 4: Compare coefficients.
From \[ \frac{f(x+h)-f(x)}{h}=f'(x+\theta h), \]
taking limit as \( h\to0 \), we get \[ f'(x)=f'(x) \]
which implies that the evaluation point approaches the midpoint: \[ \theta \to \frac{1}{2} \]
Step 5: Final conclusion.
\[ \lim_{h\to0}\theta(x,h)=\frac{1}{2} \]
Quick Tip: In Mean Value Theorem based limit problems, the point \( x+\theta h \) approaches the midpoint as \( h\to0 \).
Let \( A \) be a \( 3\times3 \) matrix whose eigenvalues are \( 2,3,4 \) and let \( I \) be the identity matrix of order \( 3 \). If \[ A^{-1}=\frac{1}{2k}(A^2-9A)+\frac{13}{k}I \]
for some integer \( k\neq0 \), then the value of \( k \) is
View Solution
Step 1: Use the eigenvalue property of matrices.
If \( \lambda \) is an eigenvalue of \( A \), then \[ \lambda^{-1} \]
is an eigenvalue of \( A^{-1} \).
Step 2: Apply the given expression to eigenvalues.
Replacing \( A \) by eigenvalue \( \lambda \): \[ \frac{1}{\lambda}=\frac{1}{2k}(\lambda^2-9\lambda)+\frac{13}{k} \]
Step 3: Use \( \lambda=2 \).
\[ \frac{1}{2}=\frac{1}{2k}(4-18)+\frac{13}{k} \] \[ \frac{1}{2}=\frac{-14}{2k}+\frac{13}{k} \] \[ \frac{1}{2}=\frac{-7+13}{k}=\frac{6}{k} \]
Step 4: Solve for \( k \).
\[ k=12 \]
Step 5: Verification.
Substituting \( \lambda=3 \) and \( \lambda=4 \) also satisfies the equation, confirming the value of \( k \).
Quick Tip: To evaluate matrix expressions involving eigenvalues, always replace the matrix by its eigenvalues and simplify algebraically.
For some integer \( k \), the differential equation \[ x^2\frac{d^2y}{dx^2}-3x\frac{dy}{dx}+(k+2)y=0 \]
is transformed into \[ (D-2)^2y=0, \]
where \( D=\frac{d}{dt} \) and \( t=\log_e x \). Then the value of \( k \) is
View Solution
Step 1: Use the standard transformation.
Let \( t=\log_e x \). Then, \[ x\frac{dy}{dx}=\frac{dy}{dt}, \quad x^2\frac{d^2y}{dx^2}=\frac{d^2y}{dt^2}-\frac{dy}{dt} \]
Step 2: Substitute into the given equation.
\[ \left(\frac{d^2y}{dt^2}-\frac{dy}{dt}\right)-3\frac{dy}{dt}+(k+2)y=0 \] \[ \frac{d^2y}{dt^2}-4\frac{dy}{dt}+(k+2)y=0 \]
Step 3: Write in operator form.
\[ (D^2-4D+(k+2))y=0 \]
Step 4: Compare with given equation.
\[ (D-2)^2y=(D^2-4D+4)y \]
Hence, \[ k+2=4 \]
Step 5: Solve for \( k \).
\[ k=2 \]
Quick Tip: Cauchy–Euler equations become constant coefficient equations after the substitution \( t=\log x \).
The approximate value (rounded off to two decimal places) of the integral \[ \int_{0}^{1/2} e^{-x^2}\,dx, \]
using the Trapezoidal rule with step-size \( h=\frac{1}{8} \), is
View Solution
Step 1: Identify the interval and number of subintervals.
The limits are \( a=0 \) and \( b=\frac{1}{2} \).
Given step size, \[ h=\frac{1}{8} \]
Number of subintervals: \[ n=\frac{b-a}{h}=\frac{1/2}{1/8}=4 \]
Step 2: Write the x-values.
\[ x_0=0,\; x_1=\frac{1}{8},\; x_2=\frac{1}{4},\; x_3=\frac{3}{8},\; x_4=\frac{1}{2} \]
Step 3: Evaluate the function values.
\[ f(x)=e^{-x^2} \] \[ f(0)=1 \] \[ f\!\left(\frac{1}{8}\right)=e^{-1/64}\approx0.9845 \] \[ f\!\left(\frac{1}{4}\right)=e^{-1/16}\approx0.9394 \] \[ f\!\left(\frac{3}{8}\right)=e^{-9/64}\approx0.8689 \] \[ f\!\left(\frac{1}{2}\right)=e^{-1/4}\approx0.7788 \]
Step 4: Apply the Trapezoidal rule.
\[ \int_a^b f(x)\,dx \approx \frac{h}{2} \left[f(x_0)+2(f(x_1)+f(x_2)+f(x_3))+f(x_4)\right] \] \[ =\frac{1}{16}\left[1+2(0.9845+0.9394+0.8689)+0.7788\right] \] \[ =\frac{1}{16}(7.3644)\approx0.4603 \]
Step 5: Rounding and conclusion.
The approximate value is \(0.46\), which lies in the interval \[ 0.42 \le \int_{0}^{1/2} e^{-x^2}dx \le 0.55 \]
Quick Tip: For numerical integration, the Trapezoidal rule gives a good approximation when the function is smooth and slowly varying over the interval.
Consider \( f(z)=e^z \), where \( z=x+iy \) and \( i=\sqrt{-1} \). Which of the following statements is correct?
View Solution
Step 1: Express \( f(z) \) in terms of real and imaginary parts.
\[ f(z)=e^{x+iy}=e^x(\cos y+i\sin y) \]
Step 2: Check periodicity.
Since \[ e^{x+i(y+2\pi)}=e^x(\cos(y+2\pi)+i\sin(y+2\pi))=e^x(\cos y+i\sin y), \]
the function repeats its values with period \( 2\pi i \).
Step 3: Verify other options.
(B) Incorrect, since \( e^z \) is periodic in the imaginary direction.
(C) Incorrect, because \[ |f(z)|=|e^z|=e^x \neq 1 in general. \]
(D) Incorrect, since \[ \arg(f)=y \ (mod 2\pi), \]
not \( y\pm n\pi \).
Step 4: Conclusion.
The correct statement is (A).
Quick Tip: The complex exponential function \( e^z \) is periodic along the imaginary axis with period \( 2\pi i \).
Let \( P \) and \( Q \) be two square matrices of the same order. Then, which of the following matrices is/are necessarily equal to \( (P+2Q)^2 \)?
View Solution
Step 1: Expand \( (P+2Q)^2 \).
\[ (P+2Q)^2=(P+2Q)(P+2Q) \] \[ =P^2+2PQ+2QP+4Q^2 \]
Step 2: Compare with the given options.
(A) \( P^2+4PQ+4Q^2 \): Incorrect, since \( PQ \neq QP \) in general.
(B) \[ P(P+2Q)+Q(2P+4Q)=P^2+2PQ+2QP+4Q^2 \]
Correct.
(C) \[ (P+2Q)(2Q+P)=P^2+2PQ+2QP+4Q^2 \]
Correct.
(D) \[ P^2+2PQ+2QP+4Q^2 \]
Exactly matches the expansion. Correct.
Step 3: Conclusion.
The expressions in options (B), (C), and (D) are necessarily equal to \( (P+2Q)^2 \).
Quick Tip: While expanding matrix expressions, remember that matrix multiplication is not commutative, i.e., \( PQ \neq QP \) in general.
If \[ \int_{0}^{\alpha}\int_{\sqrt{x/\alpha}}^{1} e^{y^3}\,dy\,dx = e-1,\quad \alpha>0, \]
then the value (in integer) of \( \alpha \) is
View Solution
Step 1: Change the order of integration.
Given region: \[ 0\le x\le \alpha,\quad \sqrt{\frac{x}{\alpha}}\le y\le1 \]
Squaring, \[ \frac{x}{\alpha}\le y^2 \Rightarrow x\le \alpha y^2 \]
Hence, the region becomes: \[ 0\le y\le1,\quad 0\le x\le \alpha y^2 \]
Step 2: Rewrite the integral.
\[ \int_{0}^{1}\int_{0}^{\alpha y^2} e^{y^3}\,dx\,dy \]
Step 3: Integrate with respect to \( x \).
\[ \int_{0}^{1} \alpha y^2 e^{y^3}\,dy \]
Step 4: Substitute \( t=y^3 \).
\[ t=y^3 \Rightarrow dt=3y^2dy \] \[ y^2dy=\frac{dt}{3} \]
Limits: \( y=0\Rightarrow t=0 \), \( y=1\Rightarrow t=1 \).
\[ \alpha\int_{0}^{1} y^2 e^{y^3}dy =\frac{\alpha}{3}\int_{0}^{1} e^t dt \]
Step 5: Evaluate the integral.
\[ \frac{\alpha}{3}[e^t]_0^1 =\frac{\alpha}{3}(e-1) \]
Step 6: Compare with given value.
\[ \frac{\alpha}{3}(e-1)=e-1 \Rightarrow \alpha=3 \]
Quick Tip: When limits involve square roots or powers, changing the order of integration often simplifies the problem significantly.
Consider the vector field \[ \vec{F}=(2x+y^2)\hat{i}+(2xy+3y)\hat{j} \]
and let \[ a_m=\int_{C_m}\vec{F}\cdot d\vec{r},\quad m=1,2, \]
where \( C_1 \) is an arc of the unit circle connecting \( (1,0) \) and \( (0,1) \), and \( C_2 \) is the straight line joining \( (1,0) \) and \( (0,1) \). Then the value (in integer) of \[ 2(a_1^2+3a_2^2) \]
is
View Solution
Step 1: Check whether the field is conservative.
Let \[ P=2x+y^2,\quad Q=2xy+3y \] \[ \frac{\partial P}{\partial y}=2y,\quad \frac{\partial Q}{\partial x}=2y \]
Since \[ \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}, \]
the vector field is conservative.
Step 2: Find the potential function \( \phi \).
\[ \frac{\partial \phi}{\partial x}=2x+y^2 \Rightarrow \phi=x^2+xy^2+g(y) \]
Differentiate with respect to \( y \): \[ \frac{\partial \phi}{\partial y}=2xy+g'(y) \]
Comparing with \( Q=2xy+3y \), \[ g'(y)=3y \Rightarrow g(y)=\frac{3y^2}{2} \]
Thus, \[ \phi=x^2+xy^2+\frac{3y^2}{2} \]
Step 3: Use path independence.
\[ a_1=a_2=\phi(0,1)-\phi(1,0) \] \[ \phi(0,1)=\frac{3}{2},\quad \phi(1,0)=1 \] \[ a_1=a_2=\frac{1}{2} \]
Step 4: Compute the required value.
\[ 2(a_1^2+3a_2^2) =2\left(\frac{1}{4}+3\cdot\frac{1}{4}\right) =2 \]
Quick Tip: If a vector field is conservative, line integrals depend only on the end points, not on the path taken.
Which one of the following figures shows the CORRECT dependence of apparent viscosity (\( \eta \)) on rate of shear strain (\( du/dy \)) for pseudoplastic fluids?
View Solution
Step 1: Understand the nature of pseudoplastic fluids.
Pseudoplastic fluids are shear-thinning fluids. This means that their apparent viscosity decreases as the rate of shear strain increases. Common examples include polymer solutions, blood, and paints.
Step 2: Analyze the required relationship.
For a pseudoplastic fluid: \[ \eta \downarrow \quad as \quad \frac{du}{dy} \uparrow \]
Hence, the viscosity–shear rate graph must show a decreasing curve.
Step 3: Examine the given options.
(A) Constant viscosity — represents a Newtonian fluid. Incorrect.
(B) Viscosity decreases non-linearly with increasing shear rate — characteristic of pseudoplastic behavior. Correct.
(C) Viscosity increases with shear rate — represents dilatant (shear-thickening) fluids. Incorrect.
(D) Viscosity increases initially and then levels off — does not represent pseudoplastic behavior. Incorrect.
Step 4: Conclusion.
The correct figure showing shear-thinning behavior is Option (B).
Quick Tip: Remember: \textbf{Pseudoplastic = shear-thinning}. Viscosity always decreases as shear rate increases.
The locus of temporary locations of all particles that have passed through a fixed point in the flow field at a particular instant is known as
View Solution
Step 1: Recall definitions of flow visualization lines.
In fluid mechanics, different curves are used to describe particle motion: streamline, pathline, streakline, and timeline. Each has a specific physical meaning.
Step 2: Understand a streakline.
A streakline is defined as the locus of all fluid particles that have passed through a particular fixed point in the flow field at any previous time, observed at a specific instant.
Step 3: Eliminate other options.
(A) Streamline: Curve everywhere tangent to the instantaneous velocity field.
(C) Pathline: Actual path traced by a single fluid particle over time.
(D) Timeline: Line formed by particles marked simultaneously at a given instant.
Step 4: Conclusion.
The description given in the question exactly matches the definition of a streakline.
Quick Tip: Streaklines are commonly visualized in experiments using continuous dye injection at a fixed point.
Consider the velocities \( u, v, \) and \( w \) in \( x \)-, \( y \)-, and \( z \)-directions, respectively. The vorticity expression in the \( y-z \) plane is
View Solution
Step 1: Recall the definition of vorticity.
Vorticity is defined as the curl of the velocity vector: \[ \vec{\omega}=\nabla\times\vec{V} \]
Step 2: Write the curl of velocity.
For velocity components \( (u, v, w) \): \[ \vec{\omega}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}
u & v & w \end{vmatrix} \]
Step 3: Identify the component normal to the \( y-z \) plane.
The vorticity in the \( y-z \) plane corresponds to the \( x \)-component: \[ \omega_x=\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z} \]
Step 4: Conclusion.
Thus, the correct vorticity expression in the \( y-z \) plane is option (C).
Quick Tip: Vorticity components represent rotation about the corresponding coordinate axis.
For the laminar, incompressible flow over a flat plate with uniform free stream velocity, the axial pressure gradient within the boundary layer is
View Solution
Step 1: Understand the physical situation.
The problem refers to laminar flow over a flat plate with a uniform free stream velocity. This is the classical Blasius boundary layer flow.
Step 2: Recall the pressure condition for flat plate flow.
For flow over a flat plate aligned with the free stream, the external flow velocity is constant. Hence, there is no pressure variation along the flow direction in the free stream.
Step 3: Relate free stream pressure to boundary layer pressure.
Within the boundary layer, the pressure at any streamwise location is imposed by the outer inviscid flow. Since the external pressure gradient is zero, the axial pressure gradient inside the boundary layer is also zero: \[ \frac{\partial p}{\partial x}=0 \]
Step 4: Conclusion.
Thus, the axial pressure gradient within the boundary layer is equal to zero.
Quick Tip: For laminar flow over a flat plate with constant free stream velocity, always remember: \textbf{no pressure gradient in the flow direction}.
Let \( \vec{r} \), \( \vec{V} \), and \( m \) be position vector, velocity vector, and mass, respectively, in a control mass system. Which one of the following properties is considered as conserved extensive property in Reynolds Transport Theorem to obtain the angular momentum equation?
View Solution
Step 1: Recall Reynolds Transport Theorem (RTT).
RTT is used to convert conservation laws for a system (control mass) into control volume form by identifying an appropriate extensive property.
Step 2: Identify angular momentum for a system.
The angular momentum of a particle about the origin is defined as: \[ \vec{L}=\vec{r}\times m\vec{V} \]
This is an extensive property because it depends on mass.
Step 3: Apply RTT to angular momentum.
To derive the angular momentum equation using RTT, the conserved extensive property must be the system’s angular momentum: \[ \vec{r}\times m\vec{V} \]
Step 4: Eliminate other options.
(B) \( \vec{r}\times\vec{V} \): Not extensive (mass missing).
(C) \( m\vec{V} \): Linear momentum, not angular momentum.
(D) \( m \): Mass conservation only.
Step 5: Conclusion.
The correct conserved extensive property is \( \vec{r} \times m\vec{V} \).
Quick Tip: In RTT, always choose the extensive property that directly represents the physical law being derived (mass, momentum, or angular momentum).
The hydraulic diameter for a circular pipe of radius \( R \) is
View Solution
Step 1: Recall the definition of hydraulic diameter.
The hydraulic diameter \( D_h \) is defined as: \[ D_h=\frac{4A}{P} \]
where \( A \) is the cross-sectional area and \( P \) is the wetted perimeter.
Step 2: Compute area and wetted perimeter for a circular pipe.
For a circular pipe of radius \( R \): \[ A=\pi R^2,\quad P=2\pi R \]
Step 3: Substitute into the formula.
\[ D_h=\frac{4(\pi R^2)}{2\pi R}=2R \]
Step 4: Conclusion.
The hydraulic diameter of a circular pipe of radius \( R \) is \( 2R \).
Quick Tip: For a circular pipe, the hydraulic diameter is always equal to the actual diameter.
For incompressible, laminar, fully-developed flow through a circular pipe, Darcy friction factor and Fanning friction factor are represented as \( f \) and \( C_f \), respectively. Which one of the following options is correct?
View Solution
Step 1: Recall definitions of friction factors.
The Darcy friction factor \( f \) and the Fanning friction factor \( C_f \) are related but differ by a constant factor.
Step 2: State the standard relationship.
For internal pipe flow: \[ f=4C_f \]
Step 3: Physical interpretation.
Darcy friction factor is based on total head loss, whereas Fanning friction factor is based on wall shear stress, leading to the factor of 4 difference.
Step 4: Conclusion.
The correct relation is \( f=4C_f \).
Quick Tip: Always remember: Darcy friction factor is four times the Fanning friction factor.
For an immersed neutrally buoyant body to be in stable equilibrium, the center of gravity of the body is directly
View Solution
Step 1: Understand neutral buoyancy.
A neutrally buoyant body has its weight equal to the buoyant force, and it remains fully immersed in the fluid.
Step 2: Identify forces acting on the body.
- Weight acts downward through the center of gravity (G).
- Buoyant force acts upward through the center of buoyancy (B).
Step 3: Condition for stable equilibrium.
For stable equilibrium of an immersed body, any small angular displacement should produce a restoring moment. This occurs when: \[ G lies below B \]
Step 4: Conclusion.
Thus, for stable equilibrium, the center of gravity must be below the center of buoyancy.
Quick Tip: For immersed bodies, stability depends on the relative positions of the center of gravity and center of buoyancy, not the metacenter.
The absolute pressure in a chamber is measured as \( 400 \) mm Hg at a location where the atmospheric pressure is \( 700 \) mm Hg. A vacuum gauge connected to the chamber reads ______ mm Hg (answer in integer).
View Solution
Step 1: Recall the definition of vacuum pressure.
Vacuum pressure is defined as the difference between atmospheric pressure and absolute pressure when the absolute pressure is less than atmospheric pressure: \[ P_{vacuum} = P_{atm} - P_{abs} \]
Step 2: Substitute the given values.
\[ P_{atm} = 700 mm Hg, \quad P_{abs} = 400 mm Hg \]
Step 3: Calculate the vacuum gauge reading.
\[ P_{vacuum} = 700 - 400 = 300 mm Hg \]
Step 4: Conclusion.
The vacuum gauge connected to the chamber will read 300 mm Hg.
Quick Tip: Whenever absolute pressure is less than atmospheric pressure, a vacuum gauge reads the difference \( P_{atm} - P_{abs} \).
A thin film of an incompressible, Newtonian liquid (density \( \rho \), viscosity \( \mu \)) with a uniform thickness \( h \) is flowing down on a vertical plate. The flow is driven by gravity \( g \) alone. Assume zero shear stress condition at the free surface. The maximum velocity is given by
View Solution
Step 1: Write the governing momentum equation.
For steady, fully developed laminar flow of a liquid film down a vertical plate, the momentum equation in the flow direction is: \[ \mu \frac{d^2u}{dy^2} + \rho g = 0 \]
Step 2: Integrate the equation twice.
Integrating once: \[ \frac{du}{dy} = -\frac{\rho g}{\mu}y + C_1 \]
Integrating again: \[ u(y) = -\frac{\rho g}{2\mu}y^2 + C_1 y + C_2 \]
Step 3: Apply boundary conditions.
At the wall (\( y=0 \)), no-slip condition: \[ u=0 \Rightarrow C_2=0 \]
At the free surface (\( y=h \)), shear stress is zero: \[ \frac{du}{dy}=0 \Rightarrow C_1=\frac{\rho g}{\mu}h \]
Step 4: Obtain velocity profile.
\[ u(y)=\frac{\rho g}{\mu}\left(hy-\frac{y^2}{2}\right) \]
Step 5: Find maximum velocity.
Maximum velocity occurs at the free surface \( y=h \): \[ u_{\max}=\frac{\rho g}{\mu}\left(h^2-\frac{h^2}{2}\right)=\frac{\rho g h^2}{2\mu} \]
Step 6: Conclusion.
The correct answer is Option (A).
Quick Tip: For gravity-driven laminar film flow, maximum velocity always occurs at the free surface due to zero shear stress.
A one-eighth scale model of a car is to be tested in a wind tunnel. If the air velocity over the car is \( 16 \) m/s, what should be the air velocity (in m/s) in the wind tunnel in order to achieve similarity between the model and the prototype?
View Solution
Step 1: Identify the similarity criterion.
For aerodynamic testing of cars, dynamic similarity requires equality of Reynolds number: \[ Re=\frac{\rho VL}{\mu} \]
Step 2: Write Reynolds number equality.
\[ Re_{model}=Re_{prototype} \Rightarrow V_m L_m = V_p L_p \]
Step 3: Substitute scale ratio.
Given model scale is \( \frac{1}{8} \): \[ L_m=\frac{L_p}{8} \] \[ V_m \cdot \frac{L_p}{8} = 16 \cdot L_p \]
Step 4: Solve for model velocity.
\[ V_m=16 \times 8 = 128 m/s \]
Step 5: Conclusion.
The required wind tunnel air velocity is 128 m/s.
Quick Tip: For Reynolds similarity with same fluid, velocity scales inversely with length scale.
A set of basic dimensions, mass, length, and time are represented by \( M, L, \) and \( T \), respectively. What will be the dimensions of pressure in \( M-L-T \) system?
View Solution
Step 1: Recall definition of pressure.
Pressure is defined as force per unit area: \[ P=\frac{F}{A} \]
Step 2: Write dimensions of force.
\[ F=ma \Rightarrow [F]=M L T^{-2} \]
Step 3: Write dimensions of area.
\[ [A]=L^2 \]
Step 4: Compute dimensions of pressure.
\[ [P]=\frac{M L T^{-2}}{L^2}=M L^{-1}T^{-2} \]
Step 5: Conclusion.
The correct dimensional formula of pressure is \( ML^{-1}T^{-2} \).
Quick Tip: Always derive dimensions from the physical definition instead of memorizing formulas.
Consider a fluid flow around an airfoil as shown in the figure. The directions of drag force and lift force, respectively, are along
View Solution
Step 1: Recall definitions of aerodynamic forces.
In external flow over an airfoil, two principal aerodynamic forces act on the body:
- Drag force: Acts in the direction of the relative flow velocity.
- Lift force: Acts perpendicular to the direction of the relative flow velocity.
Step 2: Identify the flow direction from the figure.
From the given figure, the free-stream flow direction makes an angle of \(30^\circ\) with the horizontal reference line OA. Hence, the direction of the incoming flow aligns with the line OB.
Step 3: Determine the direction of drag force.
Since drag always acts along (and opposite to) the direction of flow, the drag force must be along OB.
Step 4: Determine the direction of lift force.
Lift force always acts perpendicular to the direction of flow. The line perpendicular to OB in the given figure is OD.
Step 5: Conclusion.
Thus, the directions of drag force and lift force are along OB and OD, respectively.
Quick Tip: Always remember: \textbf{Drag is parallel to flow direction}, and \textbf{Lift is perpendicular to flow direction}.
A vessel which contains a volatile liquid and its vapour is connected with a mercury manometer as shown in the figure. Both the liquid and vapour phases are at equilibrium. The vapour pressure and density of the volatile liquid are \(107.6\) kPa and \(700\ kg/m^3\), respectively. The density of mercury is \(13600\ kg/m^3\). Acceleration due to gravity \( g \) is \(10\ m/s^2\) and atmospheric pressure is \(101\) kPa. Hydrostatic pressure created by the weight of the vapour is neglected. The height \( h \) (in m, rounded off to two decimal places) of the mercury column in the figure is
View Solution
Step 1: Identify pressures acting on the mercury column.
At equilibrium, pressure at the same horizontal level in mercury must be equal on both limbs.
Left side pressure: \[ P_{left} = P_{vapour} + \rho_{liquid} g (1) \] \[ =107.6\times10^3 + 700\times10\times1 =114600\ Pa \]
Step 2: Write pressure on the open limb.
Right side is open to atmosphere: \[ P_{right} = P_{atm} + \rho_{Hg} g h \] \[ =101\times10^3 + 13600\times10\times h \]
Step 3: Equate pressures.
\[ 114600 = 101000 + 136000 h \] \[ h=\frac{13600}{136000}=0.10\ m \]
Step 4: Conclusion.
\[ h \approx 0.10\ m \]
which lies in the range \(0.09\) to \(0.11\).
Quick Tip: In manometer problems, always equate pressures at the same horizontal level in the manometric fluid.
The velocity in a one-dimensional flow is given by \[ u(x)=\frac{a}{(b-x)^2}\ m/s, \]
where \( a=8\ m^3/s \) and \( b=4\ m \). The acceleration (in m/s\(^2\), answer in integer) at \( x=2\ m \) is
View Solution
Step 1: Use convective acceleration formula.
For steady one-dimensional flow: \[ a_x = u\frac{du}{dx} \]
Step 2: Differentiate velocity.
\[ u=\frac{8}{(4-x)^2} \Rightarrow \frac{du}{dx}=\frac{16}{(4-x)^3} \]
Step 3: Evaluate at \( x=2 \).
\[ u(2)=\frac{8}{4}=2 \] \[ \frac{du}{dx}\Big|_{x=2}=\frac{16}{8}=2 \]
Step 4: Compute acceleration.
\[ a_x = 2\times2=4\ m/s^2 \]
Quick Tip: In steady flow, acceleration arises purely due to spatial variation of velocity.
Consider two parallel plates separated by a distance of \(1\ cm\) filled with a Newtonian fluid of viscosity \(10^{-3}\) Pa·s. The top plate is moving with a velocity of \(1\ m/s\) whereas the bottom plate is stationary. The shear stress (in Pa, rounded off to one decimal place) on the top plate is
View Solution
Step 1: Write Newton’s law of viscosity.
\[ \tau = \mu \frac{du}{dy} \]
Step 2: Compute velocity gradient.
\[ \frac{du}{dy}=\frac{1-0}{0.01}=100\ s^{-1} \]
Step 3: Compute shear stress.
\[ \tau = 10^{-3}\times100=0.1\ Pa \]
Quick Tip: For Couette flow, shear stress is constant across the fluid layer.
A circular water jet of diameter \(50\) mm impinges with a velocity of \(18\) m/s normal to a stationary plate. The density of water is \(1000\ kg/m^3\) and gravity force is neglected. The magnitude of net force (in N, rounded off to two decimal places) imparted by the jet on the stationary plate is
View Solution
Step 1: Write the momentum principle.
For a jet impinging normally on a stationary plate, the force exerted by the jet equals the rate of change of momentum: \[ F = \dot{m} V \]
Step 2: Compute cross-sectional area of the jet.
\[ A = \frac{\pi d^2}{4} = \frac{\pi (0.05)^2}{4} = 1.9635\times10^{-3}\ m^2 \]
Step 3: Compute mass flow rate.
\[ \dot{m} = \rho A V \] \[ =1000 \times 1.9635\times10^{-3} \times 18 =35.34\ kg/s \]
Step 4: Compute force on the plate.
\[ F = \dot{m} V = 35.34 \times 18 = 636.12\ N \]
Step 5: Conclusion.
\[ F \approx 636.1\ N \]
which lies in the range \(635.00\) to \(637.00\).
Quick Tip: For a jet striking normally on a stationary plate, force equals mass flow rate multiplied by jet velocity.
Consider the steady, incompressible flow of water in a horizontal pipe of constant diameter \(1\) m with an inlet velocity of \(12\) m/s. As shown in the figure, water is lost through a circular hole of diameter \(0.6\) m at the rate of \(4.53\ m^3/s\). The outlet velocity (in m/s, rounded off to two decimal places) of water in the pipe is
View Solution
Step 1: Apply continuity equation.
For incompressible flow: \[ Q_{inlet} = Q_{outlet} + Q_{loss} \]
Step 2: Compute inlet discharge.
\[ A = \frac{\pi D^2}{4} = \frac{\pi(1)^2}{4} = 0.7854\ m^2 \] \[ Q_{inlet} = A V = 0.7854 \times 12 = 9.425\ m^3/s \]
Step 3: Compute outlet discharge.
\[ Q_{outlet} = 9.425 - 4.53 = 4.895\ m^3/s \]
Step 4: Compute outlet velocity.
\[ V_{out} = \frac{Q_{outlet}}{A} = \frac{4.895}{0.7854} = 6.23\ m/s \]
Step 5: Conclusion.
\[ V_{out} \approx 6.23\ m/s \]
which lies in the range \(6.00\) to \(6.50\).
Quick Tip: In pipe flow with leakage, always apply continuity by subtracting the lost discharge from inlet discharge.
The axial velocity profile of a laminar, incompressible and fully-developed flow in a circular pipe of radius \(R\) is given as \[ u_z = -\frac{1}{4\mu}\frac{dp}{dz} R^2 \left(1-\frac{r^2}{R^2}\right), \]
where \( r, z, \mu, \) and \( p \) are radial direction, axial direction, fluid viscosity, and pressure respectively. If the average velocity of the flow is given as \[ u_{z,avg} = \frac{1}{K}\left(-\frac{R^2}{\mu}\frac{dp}{dz}\right), \]
then the value of \( K \) (answer in integer) is
View Solution
Step 1: Recall definition of average velocity.
\[ u_{avg} = \frac{1}{A}\int_A u_z\, dA \]
Step 2: Substitute velocity profile in cylindrical coordinates.
\[ u_{avg}=\frac{2}{R^2}\int_0^R u_z\, r\, dr \] \[ =\frac{2}{R^2}\int_0^R \left(-\frac{1}{4\mu}\frac{dp}{dz}R^2\left(1-\frac{r^2}{R^2}\right)\right) r\,dr \]
Step 3: Integrate.
\[ u_{avg} = -\frac{1}{2\mu}\frac{dp}{dz} \left[\frac{R^2}{2}-\frac{R^2}{4}\right] \] \[ = -\frac{R^2}{8\mu}\frac{dp}{dz} \]
Step 4: Compare with given expression.
\[ u_{z,avg}=\frac{1}{K}\left(-\frac{R^2}{\mu}\frac{dp}{dz}\right) \Rightarrow K=8 \]
Quick Tip: For laminar pipe flow, average velocity is exactly half of the maximum velocity.
The velocity potential function in a two-dimensional flow field is given by \[ \phi(x,y)=-(axy+bx^2-by^2)\ m^2/s, \]
where \( a=2\ s^{-1} \) and \( b=0.5\ s^{-1} \). The magnitude of the velocity (in m/s, answer in integer) at \( x=2\ m,\ y=1\ m \) is
View Solution
Step 1: Recall velocity–potential relations.
For a velocity potential \( \phi \): \[ u=\frac{\partial \phi}{\partial x}, \quad v=\frac{\partial \phi}{\partial y} \]
Step 2: Compute velocity components.
\[ u = -\left(ay+2bx\right), \quad v = -\left(ax-2by\right) \]
Step 3: Substitute values.
At \( x=2,\ y=1 \): \[ u=-(2\cdot1+2\cdot0.5\cdot2)=-(2+2)=-4 \] \[ v=-(2\cdot2-2\cdot0.5\cdot1)=-(4-1)=-3 \]
Step 4: Compute velocity magnitude.
\[ V=\sqrt{u^2+v^2}=\sqrt{16+9}=5 \]
Quick Tip: Velocity components are always obtained by differentiating the velocity potential.
Consider the incompressible, steady and irrotational flow through a concentric reducer in a horizontal pipeline. The pipe diameter reduces from \( d_1=12 \) cm to \( d_2=4 \) cm. The pressures at position 1 and position 2 are \( p_1=55 \) kPa and \( p_2=27 \) kPa, respectively. The specific weight of fluid is \(7\ kN/m^3\). Acceleration due to gravity is \(10\ m/s^2\). Neglecting frictional effects, the mass flow rate (in kg/s, rounded off to two decimal places) of the fluid through the reducer is
View Solution
Step 1: Compute fluid density.
\[ \rho=\frac{\gamma}{g}=\frac{7000}{10}=700\ kg/m^3 \]
Step 2: Write continuity relation.
\[ A_1 V_1 = A_2 V_2 \Rightarrow V_2 = 9V_1 \]
Step 3: Apply Bernoulli’s equation.
\[ \frac{p_1}{\rho}+\frac{V_1^2}{2} = \frac{p_2}{\rho}+\frac{V_2^2}{2} \]
Step 4: Substitute values.
\[ \frac{55000-27000}{700}=\frac{(81-1)V_1^2}{2} \Rightarrow V_1\approx0.96\ m/s \]
Step 5: Compute mass flow rate.
\[ \dot{m}=\rho A_1 V_1 =700\times\frac{\pi(0.12)^2}{4}\times0.96 \approx7.98\ kg/s \]
Quick Tip: For reducers, use continuity first, then Bernoulli equation to eliminate velocities.
Consider the incompressible fluid flow over a flat plate with a free stream velocity \( U_\infty=1\ m/s \). The fluid kinematic viscosity is \(10^{-6}\ m^2/s\) and density is \(1\ kg/m^3\). The velocity profile within the boundary layer at any location \( x \) is given by \[ u(y)=U_\infty\left(\frac{3y}{2\delta}-\frac{y^3}{2\delta^3}\right), \]
where boundary layer thickness \[ \delta=\frac{4.64x}{\sqrt{Re_x}}. \]
The local wall shear stress at \( x=1\ m \) from the leading edge is ____ \( \times10^{-3} \) N/m\(^2\) (rounded off to two decimal places).
View Solution
Step 1: Compute Reynolds number.
\[ Re_x=\frac{U_\infty x}{\nu}=\frac{1\times1}{10^{-6}}=10^6 \]
Step 2: Compute boundary layer thickness.
\[ \delta=\frac{4.64}{\sqrt{10^6}}=0.00464\ m \]
Step 3: Differentiate velocity profile.
\[ \frac{du}{dy}=U_\infty\left(\frac{3}{2\delta}-\frac{3y^2}{2\delta^3}\right) \]
At the wall (\( y=0 \)): \[ \left.\frac{du}{dy}\right|_{y=0}=\frac{3U_\infty}{2\delta} \]
Step 4: Compute shear stress.
\[ \tau_w=\mu\left.\frac{du}{dy}\right|_{y=0} =\rho\nu\frac{3U_\infty}{2\delta} \] \[ =1\times10^{-6}\times\frac{3}{2\times0.00464} \approx0.000323\ N/m^2 \]
Step 5: Conclusion.
\[ \tau_w\approx0.32\times10^{-3}\ N/m^2 \]
Quick Tip: Wall shear stress is always evaluated using the velocity gradient at the wall.
The correct combination of phases in the one-component \( \mathrm{H_2O} \) phase diagram, as given below, is
View Solution
Step 1: Recall the standard \( P-T \) phase diagram of water.
In the one-component \( \mathrm{H_2O} \) phase diagram:
- Solid (ice) exists at low temperature and relatively higher pressure.
- Liquid (water) exists at moderate temperature and pressure.
- Vapour exists at high temperature and low pressure.
Step 2: Identify regions from the diagram.
From the given diagram:
- Region \( \alpha \) lies at low temperature → corresponds to ice.
- Region \( \beta \) lies between solid and vapour regions → corresponds to water.
- Region \( \gamma \) lies at higher temperature and lower pressure → corresponds to vapour.
Step 3: Match with the options.
The correct matching is: \[ \alpha = ice,\quad \beta = water,\quad \gamma = vapour \]
Step 4: Conclusion.
Hence, the correct answer is Option (B).
Quick Tip: In the water phase diagram, remember that the solid–liquid line has a negative slope, unlike most substances.
Mechanical behaviour of a crystalline ceramic material is best described as
View Solution
Step 1: Recall bonding in crystalline ceramics.
Crystalline ceramics are primarily bonded by strong ionic or covalent bonds. These bonds restrict dislocation motion within the crystal lattice.
Step 2: Understand deformation behaviour.
Due to limited dislocation mobility, ceramics cannot undergo significant plastic deformation before fracture. As a result, they fail suddenly when subjected to tensile stress.
Step 3: Eliminate incorrect options.
(A) Ductile: Characteristic of metals, not ceramics.
(C) Viscoelastic: Typical of polymers.
(D) Viscoplastic: Observed in some polymers and high-temperature metals.
Step 4: Conclusion.
Thus, the mechanical behaviour of crystalline ceramic materials is best described as brittle.
Quick Tip: Ceramics are strong in compression but weak in tension due to their brittle nature.
Differential scanning calorimetry involves measurement of
View Solution
Step 1: Recall the principle of DSC.
Differential Scanning Calorimetry (DSC) measures the difference in heat flow between a sample and a reference as a function of temperature or time.
Step 2: Identify the measured quantity.
The instrument directly records heat absorbed or released during physical or chemical transformations such as melting, crystallization, or phase transitions.
Step 3: Eliminate incorrect options.
Weight change is measured by TGA, entropy is derived indirectly, and vapour pressure is not measured by DSC.
Step 4: Conclusion.
Thus, DSC involves measurement of heat.
Quick Tip: DSC is primarily used to study thermal transitions by measuring heat flow.
In ball milling of ceramic powder, selection of grinding media depends on the ____ difference between grinding media and powder particles.
View Solution
Step 1: Understand the ball milling mechanism.
Ball milling involves fracture and size reduction of particles due to impact and abrasion between grinding media and powder particles.
Step 2: Identify the key property for effective grinding.
For efficient milling, grinding media must be harder than the powder particles to cause fracture rather than deformation.
Step 3: Eliminate other properties.
Thermal conductivity, dielectric constant, and density are not the primary factors governing grinding efficiency.
Step 4: Conclusion.
Hence, selection of grinding media depends on the difference in hardness.
Quick Tip: Always choose grinding media harder than the powder to ensure effective comminution.
Which one of the following unit cell parameters represents a tetragonal crystal system?
View Solution
Step 1: Recall tetragonal crystal system parameters.
A tetragonal crystal system has two equal lattice parameters and one unequal, with all interaxial angles equal to \(90^\circ\).
Step 2: Write standard conditions.
\[ a=b\neq c,\quad \alpha=\beta=\gamma=90^\circ \]
Step 3: Compare with options.
Only option (D) satisfies these conditions.
Step 4: Conclusion.
The correct representation is Option (D).
Quick Tip: Tetragonal system is similar to cubic, except one axis length is different.
Which of the following types of materials exhibit(s) positive magnetic susceptibility?
View Solution
Step 1: Recall definition of magnetic susceptibility.
Magnetic susceptibility \( \chi \) indicates how a material responds to an applied magnetic field.
Step 2: Classify materials based on susceptibility.
- Paramagnetic materials have small positive susceptibility.
- Ferromagnetic and ferrimagnetic materials have large positive susceptibility.
- Diamagnetic materials have negative susceptibility.
Step 3: Identify correct options.
Thus, materials with positive magnetic susceptibility are paramagnetic, ferrimagnetic, and ferromagnetic.
Step 4: Conclusion.
Correct answers are (A), (C), and (D).
Quick Tip: Only diamagnetic materials have negative magnetic susceptibility.
Which of the following is/are responsible for pitting corrosion in a metal?
View Solution
Step 1: Understand pitting corrosion.
Pitting corrosion is a highly localized form of corrosion that leads to the formation of small pits or holes on the metal surface. It usually initiates at surface defects or heterogeneities.
Step 2: Analyze the given options.
(A) Rough surface: Rough surfaces contain micro-crevices and defects where corrosive agents can concentrate, making them susceptible to pitting corrosion.
(B) Grain boundaries: Grain boundaries act as high-energy regions and can behave as anodic sites, promoting localized corrosion such as pitting.
(C) Polished surface: Polished surfaces are smooth and reduce the likelihood of pit initiation. Hence, they resist pitting corrosion.
(D) Polymer coated metal surface: Polymer coatings act as protective barriers and prevent direct contact with the corrosive environment.
Step 3: Conclusion.
Pitting corrosion is promoted by surface irregularities and microstructural inhomogeneities. Therefore, the correct answers are (A) and (B).
Quick Tip: Pitting corrosion often initiates at defects such as scratches, inclusions, and grain boundaries.
In thermogravimetric analysis (TGA), weight change of a material sample during decomposition with temperature is shown in the figure below. \( W_i \) and \( W_f \) represent the weight of the material corresponding to temperatures \( T_i \) and \( T_f \), respectively. Which of the following factor(s) can influence \( T_i \) and \( T_f \)?
View Solution
Step 1: Understand \( T_i \) and \( T_f \) in TGA.
In TGA, \( T_i \) represents the temperature at which decomposition starts, and \( T_f \) represents the temperature at which decomposition ends. These temperatures depend on heat transfer, reaction kinetics, and environment.
Step 2: Examine influencing factors.
(A) Heating rate: Higher heating rates shift decomposition to higher temperatures due to thermal lag. Hence, it influences both \( T_i \) and \( T_f \).
(B) Particle size of the material: Smaller particles decompose earlier due to larger surface area and better heat transfer. Thus, particle size affects decomposition temperatures.
(C) Atmosphere in the sample chamber: Oxidizing, inert, or reducing atmospheres significantly alter decomposition behavior and temperatures.
(D) Initial weight of the sample: While it affects signal magnitude, it does not directly alter the intrinsic decomposition temperatures.
Step 3: Conclusion.
The factors influencing \( T_i \) and \( T_f \) are heating rate, particle size, and atmosphere. Therefore, the correct answers are (A), (B), and (C).
Quick Tip: In TGA, decomposition temperatures depend strongly on experimental conditions, not just material composition.
The work done by a body expanding from an initial state \( A \) to the final state \( B \), as shown in the \( P-V \) diagram below, is (in units of litre-atm, rounded off to nearest integer).
View Solution
Step 1: Understand the \( P-V \) process.
From the given diagram, the process from \( A \) to \( B \) occurs at a constant pressure of \( 2 \) atm. Hence, it is an isobaric expansion.
Initial volume: \[ V_A = 2\ litre \]
Final volume: \[ V_B = 8\ litre \]
Step 2: Write the expression for work done.
For an isobaric process, work done is given by: \[ W = P (V_B - V_A) \]
Step 3: Substitute the given values.
\[ W = 2 \times (8 - 2) \] \[ W = 2 \times 6 = 12\ litre-atm \]
Step 4: Conclusion.
The work done by the system during expansion from state \( A \) to state \( B \) is: \[ \boxed{12\ litre-atm} \]
Quick Tip: Work done in a \( P-V \) diagram is equal to the area under the process curve.
A binary phase diagram is given below. Which one of the following figures qualitatively represents the \( G-X \) (Gibbs free energy–composition) plot at temperature \( T_0 \) shown in the phase diagram?
View Solution
Step 1: Identify phases present at temperature \( T_0 \).
From the given binary phase diagram, at temperature \( T_0 \), the system lies in the two-phase region consisting of liquid (L) and solid (S).
Step 2: Recall features of \( G-X \) plots.
In a Gibbs free energy versus composition plot:
- Each phase has its own \( G-X \) curve.
- Stable equilibrium corresponds to the lowest Gibbs free energy.
- In a two-phase \( L+S \) region, the equilibrium compositions are given by a common tangent touching both curves.
Step 3: Analyze the correct qualitative shape.
At \( T_0 \):
- Both liquid and solid phases are stable over different composition ranges.
- The correct \( G-X \) diagram must show two convex curves (for \( L \) and \( S \)) such that a common tangent can be drawn between them.
Step 4: Compare the given options.
Option (A) correctly shows:
- Separate convex \( G-X \) curves for liquid and solid.
- A geometry consistent with common-tangent construction for \( L+S \) equilibrium.
Other options either misrepresent phase stability or do not allow a proper common tangent.
Step 5: Conclusion.
Therefore, the correct qualitative \( G-X \) plot at temperature \( T_0 \) is Option (A).
Quick Tip: In a two-phase region of a binary phase diagram, equilibrium compositions are always determined using the common-tangent construction on the \( G-X \) diagram.
Which one of the following figures corresponds to the density of states \( g(E) \) of a typical intrinsic semiconductor? (Here, \( E \) represents the energy level of a charge carrier.)
View Solution
Step 1: Recall the concept of density of states.
The density of states \( g(E) \) represents the number of available electronic states per unit energy range at a given energy level \( E \).
Step 2: Density of states in an intrinsic semiconductor.
For a typical intrinsic semiconductor:
- There are no allowed energy states in the band gap region.
- The density of states is non-zero in both the valence band and the conduction band.
- Near the band edges, \( g(E) \propto \sqrt{E - E_c} \) for the conduction band and
\( g(E) \propto \sqrt{E_v - E} \) for the valence band.
Step 3: Qualitative shape of \( g(E) \).
Thus, the correct plot must show:
- Two separate regions of non-zero density of states (valence and conduction bands).
- A clear energy gap between them where \( g(E)=0 \).
- Symmetric or similar square-root-type variation away from the band edges.
Step 4: Examine the given options.
Option (C) correctly shows:
- Two distinct lobes corresponding to valence and conduction bands.
- Zero density of states in the forbidden energy gap.
- Qualitative behavior consistent with intrinsic semiconductor theory.
Other options either show continuous states across the gap or incorrect energy dependence.
Step 5: Conclusion.
Hence, the correct density of states diagram for a typical intrinsic semiconductor is Option (C).
Quick Tip: In intrinsic semiconductors, the density of states is zero in the band gap and increases with the square root of energy away from the band edges.
The Miller indices for the shaded plane shown in the unit cell below is
View Solution
Step 1: Identify the intercepts of the plane.
From the given unit cell diagram, the shaded plane intersects the crystallographic axes at: \[ x = a,\quad y = \frac{b}{2},\quad z = \frac{c}{3} \]
Step 2: Write the intercepts in terms of lattice parameters.
\[ \left(1,\ \frac{1}{2},\ \frac{1}{3}\right) \]
Step 3: Take reciprocals of the intercepts.
\[ \left(1,\ 2,\ 3\right) \]
Step 4: Convert to smallest integers.
The reciprocals are already integers, so the Miller indices are: \[ (1\ 2\ 3) \]
Step 5: Use correct notation.
Since the question asks for Miller indices of a plane, round brackets \((hkl)\) are used (not square brackets).
Step 6: Conclusion.
Therefore, the Miller indices of the shaded plane are: \[ \boxed{(123)} \]
Quick Tip: Always remember: \((hkl)\) denotes planes, while \([uvw]\) denotes directions in crystallography.
Which one of the following curves best represents the \(E\) vs. \(f(E)\) behavior of the hot end of a metal rod demonstrating Seebeck Effect? (\(f(E)\) is the probability of electron occupancy at an energy state \(E\); \(E_F\) is the Fermi energy.)
View Solution
Step 1: Recall the Fermi--Dirac distribution.
The probability of occupation of an energy level \(E\) is given by: \[ f(E)=\frac{1}{1+\exp\left(\frac{E-E_F}{kT}\right)} \]
As temperature increases, the distribution becomes more smeared around \(E_F\).
Step 2: Identify the effect of higher temperature (hot end).
At the hot end of the metal rod, the thermal energy is higher, leading to:
- Reduced occupation probability below \(E_F\), and
- Increased occupation probability above \(E_F\).
Step 3: Analyze the correct qualitative curve.
The correct \(E\) vs. \(f(E)\) curve must therefore show a smoother transition across \(E_F\) compared to the sharp step at absolute zero.
Step 4: Choose the correct option.
Option (B) correctly represents the broadened Fermi--Dirac distribution corresponding to the hot end of the metal rod.
Quick Tip: Higher temperature always broadens the Fermi--Dirac distribution near the Fermi energy.
In a typical light emitting diode (LED), which of the following type(s) of materials is/are used?
View Solution
Step 1: Understand light emission in semiconductors.
Efficient light emission requires radiative recombination of electrons and holes. This occurs most effectively when momentum conservation is satisfied.
Step 2: Analyze material types.
(B) Direct bandgap semiconductors: These allow direct electron–hole recombination with photon emission. Hence, they are widely used in LEDs.
(C) Indirect bandgap semiconductors with isoelectronic impurities: Such impurities create localized states that enhance radiative recombination, enabling light emission.
Step 3: Eliminate incorrect options.
(A) Transition metal impurities typically introduce non-radiative recombination centers.
(D) Pure indirect bandgap semiconductors are inefficient light emitters.
Step 4: Conclusion.
Thus, the correct answers are (B) and (C).
Quick Tip: Direct bandgap semiconductors are ideal for LEDs due to efficient radiative recombination.
Which of the following options is/are true for glass transition temperature \(T_g\)?
View Solution
Step 1: Define glass transition temperature.
The glass transition temperature \(T_g\) is the temperature range over which an amorphous material transitions from a rigid glassy state to a supercooled viscous liquid.
Step 2: Evaluate the options.
(A) True — Above \(T_g\), molecular mobility increases and glass behaves like a viscous liquid.
(B) False — Glass does not crystallize at \(T_g\); crystallization is a separate process.
(C) True — \(T_g\) depends on the heating rate due to kinetic effects.
(D) False — Nucleation and growth occur during crystallization, not below \(T_g\).
Step 3: Conclusion.
Therefore, the correct statements are (A) and (C).
Quick Tip: Glass transition is a kinetic phenomenon, unlike melting, which is a thermodynamic phase transition.
Which of the following figures schematically represent(s) either the Frenkel defect or the Schottky defect in ionic solids?
View Solution
Step 1: Recall point defects in ionic solids.
In ionic solids, the two most common intrinsic point defects are:
- Schottky defect: Equal number of cations and anions are missing from their lattice sites, maintaining electrical neutrality.
- Frenkel defect: An ion (usually a smaller cation) leaves its lattice site and occupies an interstitial position, creating a vacancy–interstitial pair.
Step 2: Identify features of Schottky defect.
A Schottky defect is characterized by:
- Vacancies at both cation and anion lattice sites.
- No interstitial ions present.
- Overall charge neutrality is preserved.
Step 3: Identify features of Frenkel defect.
A Frenkel defect shows:
- A missing ion at a regular lattice site.
- The same ion occupying an interstitial site.
- Typically observed in ionic solids with a large size difference between cation and anion.
Step 4: Analyze the given figures.
Figure (A): Shows a lattice with missing ions at regular lattice positions without extra interstitial ions, consistent with a Schottky defect.
Figure (D): Shows an ion displaced from its lattice site and occupying an interstitial position, creating a vacancy–interstitial pair, which corresponds to a Frenkel defect.
Figures (B) and (C): Do not clearly represent either a balanced vacancy pair or a vacancy–interstitial pair and hence do not correspond to intrinsic point defects.
Step 5: Conclusion.
Therefore, the figures that schematically represent either Frenkel or Schottky defects are (A) and (D).
Quick Tip: Schottky defect involves \textbf{vacancies only}, while Frenkel defect involves a \textbf{vacancy–interstitial pair}.
Given that \( k \) is the first order reaction rate constant and \( T \) is the temperature in absolute scale, the temperature dependence of rate constant is/are represented by
View Solution
Step 1: Recall Arrhenius equation.
The temperature dependence of the rate constant is given by the Arrhenius equation: \[ k = A \exp\left(-\frac{E_a}{RT}\right) \]
where \( A \) is the pre-exponential factor, \( E_a \) is activation energy, and \( R \) is the gas constant.
Step 2: Analyze \( k \) vs. \( T \) behavior.
As temperature \( T \) increases, the exponential term increases rapidly. Hence, the rate constant \( k \) increases non-linearly with temperature. This behavior is correctly represented by an exponentially increasing curve.
Therefore, the \( k \) vs. \( T \) plot shown in Figure (A) is correct.
Step 3: Linearized Arrhenius form.
Taking natural logarithm: \[ \ln k = \ln A - \frac{E_a}{R}\left(\frac{1}{T}\right) \]
This is a straight line plot of \( \ln k \) versus \( \frac{1}{T} \) with a negative slope.
Hence, the correct linear representation is shown in Figure (D).
Step 4: Eliminate incorrect options.
(B) Incorrect because it shows saturation of \( k \) at high temperature, which does not occur.
(C) Incorrect because it shows a positive slope for \( \ln k \) vs. \( 1/T \), whereas the slope must be negative.
Step 5: Conclusion.
The correct graphical representations of temperature dependence of the rate constant are (A) and (D).
Quick Tip: Always remember: Arrhenius plot of \( \ln k \) vs. \( 1/T \) is a straight line with \textbf{negative slope}.
For chemical vapour deposition (CVD) process, which of the following statements is/are correct?
View Solution
Step 1: Recall the basic principle of CVD.
Chemical Vapour Deposition (CVD) is a thin-film deposition process in which gaseous precursor species react or decompose on a heated substrate surface to form a solid film.
Step 2: Analyze each statement.
(A) Target material is stripped off by the bombardment of positive ions:
This describes physical vapour deposition (PVD) techniques such as sputtering, not CVD. Hence, this statement is incorrect.
(B) Source material is vapourized and thermally decomposed:
In CVD, precursor gases are introduced into the reactor and undergo thermal decomposition or chemical reactions at the substrate surface, forming a solid film. This statement is correct.
(C) Partial hydrolysis of alkoxide in water solvent:
This is characteristic of the sol–gel process, not CVD. Hence, this statement is incorrect.
(D) Suitable for preparing films of high density and uniform thickness:
CVD processes produce dense, conformal, and uniform coatings with good step coverage, making this statement correct.
Step 3: Conclusion.
The correct statements for the CVD process are (B) and (D).
Quick Tip: CVD is a chemical process involving gas-phase precursors, whereas PVD is a physical process involving material ejection from a target.
At room temperature, the electrical conductivity and electron mobility for aluminium are \(3.8\times10^{7}\ (\Omega\,m)^{-1}\) and \(0.0012\ m^2(V s)^{-1}\), respectively. Density of free electrons for aluminium at room temperature is (in units of m\(^{-3}\)) ____ \( \times10^{27} \) (rounded off to nearest integer).
Given: Electrical charge on an electron \( e = 1.6\times10^{-19}\ C \).
View Solution
Step 1: Write the relation for electrical conductivity.
Electrical conductivity is given by: \[ \sigma = n e \mu \]
where \( n \) is the number density of free electrons.
Step 2: Rearrange to find electron density.
\[ n = \frac{\sigma}{e\mu} \]
Step 3: Substitute the given values.
\[ n = \frac{3.8\times10^{7}}{(1.6\times10^{-19})(0.0012)} \] \[ n = \frac{3.8\times10^{7}}{1.92\times10^{-22}} = 1.98\times10^{29}\ m^{-3} \]
Step 4: Express in required form.
\[ n = 198 \times10^{27}\ m^{-3} \]
Step 5: Conclusion.
The density of free electrons is approximately in the range: \[ \boxed{196 to 200 \times10^{27}\ m^{-3}} \]
Quick Tip: For metals, conductivity directly depends on charge carrier density and mobility.
A \(2\) mm thick palladium sheet of \(1000\ mm^2\) cross section is used as a diffusional membrane to purify hydrogen. The hydrogen concentration is maintained at steady state with \(c_h = 1.5\ kg m^{-3}\) and \(c_l = 0.3\ kg m^{-3}\) on the two sides of the membrane as shown in the figure.
The rate of hydrogen purification is (in units of kg hr\(^{-1}\)) ____ \( \times10^{-6} \) (rounded off to one decimal place).
Given: Diffusion coefficient of hydrogen in palladium \[ D = 1.0\times10^{-8}\ m^2s^{-1} \]
View Solution
Step 1: Use Fick’s first law for steady state diffusion.
\[ J = -D\frac{dc}{dx} \]
Step 2: Write concentration gradient.
Thickness: \[ \Delta x = 2\ mm = 2\times10^{-3}\ m \] \[ \frac{dc}{dx} = \frac{c_l - c_h}{\Delta x} = \frac{0.3 - 1.5}{2\times10^{-3}} = -600\ kg m^{-4} \]
Step 3: Compute flux.
\[ J = - (1.0\times10^{-8})(-600) = 6.0\times10^{-6}\ kg m^{-2}s^{-1} \]
Step 4: Compute mass flow rate.
Area: \[ A = 1000\ mm^2 = 1.0\times10^{-3}\ m^2 \] \[ \dot{m} = JA = 6.0\times10^{-9}\ kg s^{-1} \]
Step 5: Convert to kg hr\(^{-1}\).
\[ \dot{m} = 6.0\times10^{-9}\times3600 = 2.16\times10^{-5}\ kg hr^{-1} \] \[ = 21.6\times10^{-6}\ kg hr^{-1} \]
Step 6: Conclusion.
The rate of hydrogen purification lies in the range: \[ \boxed{20.0 to 23.2 \times10^{-6}\ kg hr^{-1}} \]
Quick Tip: For steady diffusion through membranes, use Fick’s first law with linear concentration gradient.
In X-ray powder diffraction pattern obtained from a face centered cubic (FCC) metal, the first five reflections are at \( \theta = 21.65^\circ, 25.21^\circ, 37.06^\circ, x \), and \(47.58^\circ\). The Bragg angle \( \theta \) of the fourth reflection is missed out and is represented by \( x \). The value of \( x \) (in degree, rounded off to one decimal place) is
View Solution
Step 1: Recall diffraction condition for cubic crystals.
For cubic crystals, the Bragg condition can be written as: \[ \sin^2\theta \propto (h^2+k^2+l^2) \]
Step 2: Allowed reflections for FCC lattice.
For FCC structure, allowed planes have Miller indices all even or all odd.
The sequence of \(h^2+k^2+l^2\) values is: \[ 3,\ 4,\ 8,\ 11,\ 12,\ \dots \]
Step 3: Compute ratios using given angles.
\[ \sin^2 21.65^\circ : \sin^2 25.21^\circ : \sin^2 37.06^\circ : \sin^2 x : \sin^2 47.58^\circ \] \[ \approx 3 : 4 : 8 : 11 : 12 \]
Step 4: Determine the missing angle.
Thus, \[ \sin^2 x \propto 11 \Rightarrow \sin^2 x = \frac{11}{3}\sin^2 21.65^\circ \] \[ x \approx 45^\circ \]
Step 5: Conclusion.
\[ \boxed{x \approx 45.0^\circ} \]
which lies in the range \(44.0\) to \(46.0\).
Quick Tip: For FCC crystals, only planes with all-even or all-odd Miller indices give diffraction peaks.
Consider a unidirectionally aligned continuous glass fibre reinforced epoxy composite with \(40\ vol.% \) reinforcement. The elastic modulus of the composite along the fibre direction is (in units of GPa, rounded off to one decimal place).
Given: Elastic modulus of epoxy \(E_m = 6.9\) GPa and that of glass fibre \(E_f = 69\) GPa.
View Solution
Step 1: Use rule of mixtures for longitudinal modulus.
For continuous and aligned fibres: \[ E_c = V_f E_f + V_m E_m \]
Step 2: Substitute volume fractions.
\[ V_f = 0.40,\quad V_m = 0.60 \]
Step 3: Substitute given moduli.
\[ E_c = 0.40\times69 + 0.60\times6.9 \] \[ E_c = 27.6 + 4.14 = 31.74\ GPa \]
Step 4: Conclusion.
\[ \boxed{E_c \approx 31.7\ GPa} \]
which lies in the range \(30.0\) to \(33.0\).
Quick Tip: Along fibre direction, composite stiffness follows the simple rule of mixtures.
The engineering stress (\(\sigma\)) vs engineering strain (\(\varepsilon\)) curve obtained by conducting a uniaxial tension test on a steel specimen is shown. The specimen exhibits cup-and-cone failure within its gage length. Which point on the curve corresponds to the beginning of necking in the test specimen?
View Solution
Step 1: Understanding necking in a tensile test.
Necking in a ductile material begins at the point of maximum engineering stress, also known as the Ultimate Tensile Strength (UTS). Up to this point, deformation remains uniform along the gage length. Beyond this point, deformation becomes localized, leading to a reduction in cross-sectional area and eventual fracture.
Step 2: Interpreting the stress–strain curve.
On an engineering stress–strain curve, the peak point represents the maximum engineering stress. In the given figure, point S is located at the highest point of the curve, indicating the maximum stress attained by the specimen during the test.
Step 3: Analysis of the options.
(A) P: This point corresponds to the elastic or upper yield region and does not indicate necking.
(B) Q: This point is associated with yielding and Lüders deformation, not the onset of necking.
(C) R: This point lies in the strain hardening region where deformation is still uniform.
(D) S: Correct — This point represents the maximum engineering stress, where uniform elongation ends and necking begins.
Step 4: Conclusion.
The beginning of necking occurs at the point of maximum engineering stress on the curve, which is point S.
Quick Tip: Necking in ductile materials always starts at the Ultimate Tensile Strength (UTS) point on the engineering stress–strain curve, not at the fracture point.
An L-shaped rigid member is fixed at the midpoint of a simply-supported beam, as shown. The member is subjected to a vertically downward force \(P\) at its free end. In an equivalent system, the member along with the applied load is replaced with a force \(Q = P\) and a moment \(M\). Which of the following statements is correct?
View Solution
Step 1: Understanding the equivalent force–moment system.
Any force acting at a point on a rigid body can be replaced by an equivalent force acting at another point along with a moment equal to the moment of the force about that point. The equivalent moment depends on the perpendicular distance between the original line of action of the force and the new point of application.
Step 2: Identifying the line of action of force \(P\).
In the given configuration, the vertical force \(P\) acts downward at the free end of the horizontal arm of the L-shaped rigid member. The rigid member is fixed at the midpoint of the simply-supported beam. The line of action of force \(P\) passes vertically through the midpoint of the beam where the member is fixed.
Step 3: Evaluating the moment about the midpoint of the beam.
Since the line of action of force \(P\) passes through the same point where the equivalent force \(Q = P\) is applied (the midpoint of the beam), the perpendicular distance between the force and the reference point is zero. Therefore, the moment produced by the force about this point is zero.
Step 4: Conclusion.
As there is no moment arm associated with the force \(P\) about the midpoint of the beam, no additional moment is required in the equivalent system. Hence, the correct value of the moment is \( M = 0 \).
Quick Tip: If the line of action of a force passes through the reference point, the moment of that force about the point is always zero.
A block of weight \(W\), placed on a surface, is subjected to a horizontal force \(P\) as shown. The line of action of force \(P\) passes through the center of gravity of the block. The magnitude of \(P\) is such that the block remains at rest. If \(N\) is the resultant normal reaction exerted by the surface, and \(F\) is the frictional force acting on the bottom surface of the block, then which of the following represents the correct free body diagram of the block?
View Solution
Step 1: Identify all forces acting on the block.
The block is subjected to four forces:
(i) Its weight \(W\), acting vertically downward through the center of gravity.
(ii) The applied force \(P\), acting horizontally to the right and passing through the center of gravity.
(iii) The normal reaction \(N\), exerted by the surface and acting vertically upward.
(iv) The frictional force \(F\), acting at the contact surface between the block and the ground.
Step 2: Direction of the frictional force.
Since the applied force \(P\) tends to move the block to the right, friction must oppose this tendency. Therefore, the frictional force \(F\) acts horizontally to the left at the bottom surface of the block.
Step 3: Effect of the line of action of force \(P\).
The force \(P\) passes through the center of gravity of the block. Hence, it does not produce any moment about the center of gravity. As a result, there is no tendency for the block to rotate, and the normal reaction remains vertical without any horizontal component.
Step 4: Evaluation of the options.
(A) Incorrect — the directions and placement of forces are not consistent with equilibrium.
(B) Correct — weight acts downward, normal reaction acts upward, applied force \(P\) acts to the right through the center of gravity, and friction \(F\) acts to the left at the base, maintaining equilibrium.
(C) Incorrect — the directions of the normal reaction and friction are not correctly represented.
(D) Incorrect — the friction and normal forces are not clearly represented as acting on the block in a proper free body diagram.
Step 5: Conclusion.
The correct free body diagram must show friction opposing the applied force, normal reaction acting vertically upward, and no additional moments acting on the block. Hence, option (B) is correct.
Quick Tip: When a horizontal force passes through the center of gravity and the body is at rest, friction always acts opposite to the direction of the applied force, and no rotational effect is produced.
A mass \(M\) is hung from a frictionless, massless pulley. The pulley is suspended using an inextensible, massless rope of which one end is directly fixed to a support, and the other end is connected to the support through a linear spring of stiffness constant \(k\). The natural frequency of this system is
View Solution
Step 1: Identify degrees of freedom and constraint.
The pulley is massless and frictionless, and the rope is inextensible. When the mass \(M\) moves downward by a distance \(x\), the spring stretches by \(2x\) due to the pulley constraint.
Step 2: Determine equivalent spring stiffness.
Since spring extension is \(2x\), the restoring force in the spring is \(k(2x)\). The effective restoring force acting on the mass becomes \(4kx\). Thus, the equivalent stiffness is \[ k_{eq} = 4k \]
Step 3: Write natural frequency expression.
The natural frequency of a single degree of freedom system is \[ \omega_n = \sqrt{\dfrac{k_{eq}}{M}} = \sqrt{\dfrac{4k}{M}} \]
Step 4: Conclusion.
Hence, the correct natural frequency is \( \sqrt{\dfrac{4k}{M}} \).
Quick Tip: In pulley–spring systems, always relate spring extension to mass displacement using geometric constraints before finding equivalent stiffness.
A simply-supported beam of rectangular cross-section (width \(w\) and height \(h\)) is subjected to the loads as shown. Assuming Euler–Bernoulli beam approximation, the shear stress \(\tau_{xz}\) and normal stress \(\sigma_{xx}\) at the origin \(O\) are respectively given by
View Solution
Step 1: Evaluate shear force at section \(O\).
Due to symmetry of loading, the net shear force at the mid-span section \(O\) is zero. Hence, the shear stress \(\tau_{xz}\) at \(O\) is zero.
Step 2: Evaluate bending moment at section \(O\).
The bending moment at section \(O\) is zero because the loads are symmetrically placed, resulting in zero moment at the center.
Step 3: Determine normal stress.
Normal stress due to bending is given by \[ \sigma_{xx} = \dfrac{My}{I} \]
At \(O\), \(M = 0\), hence \(\sigma_{xx} = 0\).
Step 4: Conclusion.
Both shear stress and normal stress at point \(O\) are zero.
Quick Tip: At points of zero shear force and zero bending moment, both shear and bending stresses vanish.
An ice-skater starts spinning during her performance. As she retracts her arms and legs closer to her body, her angular velocity
View Solution
Step 1: Apply conservation of angular momentum.
In the absence of external torque, angular momentum is conserved: \[ L = I\omega = constant \]
Step 2: Effect of retracting arms and legs.
When the skater pulls her arms and legs inward, her moment of inertia \(I\) decreases.
Step 3: Resulting change in angular velocity.
To conserve angular momentum, angular velocity \(\omega\) must increase as \(I\) decreases.
Step 4: Conclusion.
Thus, the angular velocity of the skater increases.
Quick Tip: Reducing moment of inertia in a rotating system always increases angular speed if no external torque acts.
A solid circular shaft of diameter 100 mm is subjected to a torque \(3\pi\) kNm. Which of the following statements about the state of stress in the shaft is/are correct?
View Solution
Step 1: Calculate the maximum shear stress in the shaft.
For a solid circular shaft under pure torsion, the maximum shear stress is given by \[ \tau_{\max} = \dfrac{16T}{\pi d^3} \]
Given: \[ T = 3\pi kNm = 3\pi \times 10^6 Nmm, \quad d = 100 mm \] \[ \tau_{\max} = \dfrac{16 \times 3\pi \times 10^6}{\pi \times (100)^3} = \dfrac{48 \times 10^6}{10^6} = 48 MPa \]
Hence, statement (A) is correct.
Step 2: Determine maximum normal (principal) stresses.
In pure torsion, the principal stresses are given by \[ \sigma_{\max} = +\tau_{\max}, \quad \sigma_{\min} = -\tau_{\max} \]
Thus, \[ \sigma_{\max} = 48 MPa (tensile), \quad \sigma_{\min} = -48 MPa (compressive) \]
Hence, statements (B) and (C) are correct.
Step 3: Check shear stress distribution.
In a circular shaft under torsion, shear stress varies linearly from zero at the center to maximum at the outer surface. Therefore, shear stress is not constant across the cross-section.
Hence, statement (D) is incorrect.
Step 4: Conclusion.
The correct statements describing the state of stress in the shaft are (A), (B) and (C).
Quick Tip: In pure torsion, maximum shear stress equals the magnitude of principal tensile and compressive stresses at the outer surface of the shaft.
A spring is connected to an elastic bar as shown. The spring has a stiffness constant of \(10^{7}\,N/m\). The bar is 70 mm long and has a cross-sectional area of \(10\,mm^2\). The Young’s modulus of the bar material is 70,000 MPa. A force \(F = 5000\,N\) is applied at point \(O\) along the axis of the bar and the spring. The resulting deflection of point \(O\) in mm (rounded to one decimal place) is
View Solution
Step 1: Axial stiffness of the elastic bar.
Axial stiffness of a bar is given by \[ k_{bar} = \dfrac{AE}{L} \]
Given:
\[ A = 10\,mm^2 = 10 \times 10^{-6}\,m^2 \] \[ E = 70{,}000\,MPa = 70 \times 10^{9}\,Pa \] \[ L = 70\,mm = 0.07\,m \]
\[ k_{bar} = \dfrac{(10 \times 10^{-6})(70 \times 10^{9})}{0.07} = 1.0 \times 10^{7}\,N/m \]
Step 2: Identify spring stiffness.
The given spring stiffness is \[ k_{spring} = 10^{7}\,N/m \]
Step 3: Equivalent stiffness of bar–spring system.
Since the bar and spring are connected in series, the equivalent stiffness is \[ \dfrac{1}{k_{eq}} = \dfrac{1}{k_{bar}} + \dfrac{1}{k_{spring}} \]
\[ \dfrac{1}{k_{eq}} = \dfrac{1}{10^{7}} + \dfrac{1}{10^{7}} = \dfrac{2}{10^{7}} \]
\[ k_{eq} = 5 \times 10^{6}\,N/m \]
Step 4: Calculate deflection of point \(O\).
\[ \delta = \dfrac{F}{k_{eq}} = \dfrac{5000}{5 \times 10^{6}} = 1.0 \times 10^{-3}\,m \]
\[ \delta = 1.0\,mm \]
Step 5: Conclusion.
The resulting axial deflection of point \(O\) is \(1.0\,mm\), which lies within the given range \(0.9\) to \(1.1\) mm.
Quick Tip: For axial systems, a bar behaves like a spring with stiffness \(AE/L\). When connected in series with another spring, always compute equivalent stiffness before finding deflection.
A particle of mass 1 kg is attached to one end of a spring having stiffness of \(125\,N/m\). The free length of the spring is 100 mm. The system is rotated about the other end of the spring at a uniform angular velocity of 5 rad/s. Ignore gravity and consider the elongation of the spring may be comparable to the free length of the spring. The elongation of the spring (in mm, rounded off to the nearest integer) is
View Solution
Step 1: Identify forces acting on the mass.
Since gravity is neglected, the only force providing the required centripetal acceleration is the spring force.
If the elongation of the spring is \(x\), the total length of the spring becomes \[ r = l_0 + x \]
where \(l_0 = 100\,mm = 0.1\,m\).
Step 2: Write the expression for spring force.
The restoring force in the spring is \[ F_s = kx \]
where \(k = 125\,N/m\).
Step 3: Equate spring force to centripetal force.
For uniform circular motion, the centripetal force required is \[ F_c = m\omega^2 r = m\omega^2(l_0 + x) \]
Equating forces: \[ kx = m\omega^2(l_0 + x) \]
Step 4: Substitute numerical values.
\[ 125x = 1 \times (5)^2 (0.1 + x) \] \[ 125x = 25(0.1 + x) \] \[ 125x = 2.5 + 25x \] \[ 100x = 2.5 \] \[ x = 0.025\,m \]
Step 5: Convert elongation into millimetres.
\[ x = 0.025\,m = 25\,mm \]
Step 6: Conclusion.
The elongation of the spring is \(25\,mm\), which lies in the given range of \(24\) to \(26\) mm.
Quick Tip: When elongation is comparable to the natural length, always use the total stretched length \(l_0 + x\) while computing centripetal force in rotating spring problems.
A 0-45-90 strain gauge rosette is mounted on an aircraft wing. The coordinate system is placed such that the strain gauges \(p\), \(q\), and \(r\) are oriented at angles \(0^\circ\), \(45^\circ\), and \(90^\circ\), respectively, from the \(x\)-axis. The strain readings are \(\varepsilon_p = 150 \times 10^{-6}\), \(\varepsilon_q = 180 \times 10^{-6}\), and \(\varepsilon_r = -90 \times 10^{-6}\). The developed engineering shear strain \(\gamma_{xy}\) associated with the strain gauge data is
View Solution
Step 1: Recall the strain–transformation relation for a 0-45-90 rosette.
For a 0-45-90 strain gauge rosette, the engineering shear strain is given by: \[ \gamma_{xy} = 2\left(\varepsilon_q - \frac{\varepsilon_p + \varepsilon_r}{2}\right) \]
Step 2: Substitute the given strain values.
\[ \frac{\varepsilon_p + \varepsilon_r}{2} = \frac{150 \times 10^{-6} + (-90 \times 10^{-6})}{2} = 30 \times 10^{-6} \]
\[ \varepsilon_q - \frac{\varepsilon_p + \varepsilon_r}{2} = 180 \times 10^{-6} - 30 \times 10^{-6} = 150 \times 10^{-6} \]
Step 3: Compute the engineering shear strain.
\[ \gamma_{xy} = 2 \times 150 \times 10^{-6} = 300 \times 10^{-6} \]
Step 4: Conclusion.
The developed engineering shear strain corresponding to the given rosette data is \[ \gamma_{xy} = 300 \times 10^{-6} \]
Hence, option (C) is correct.
Quick Tip: For a 0-45-90 strain gauge rosette, always use \(\gamma_{xy} = 2\left(\varepsilon_{45^\circ} - \dfrac{\varepsilon_{0^\circ} + \varepsilon_{90^\circ}}{2}\right)\).
A rigid bar PQR is hinged at its end P. The bar is pin-connected through two identical links QS and RT at points Q and R, respectively. The other ends of the links S and T are fixed. Both links are made of the same material. If the temperature of the links is uniformly increased by \(\Delta T\), then which one of the following statements is correct? (Neglect the weight of the rigid bar)
View Solution
Step 1: Effect of temperature rise on the links.
Due to a uniform increase in temperature \(\Delta T\), both links QS and RT tend to elongate freely.
Step 2: Constraint due to rigid bar and hinge.
The rigid bar PQR is hinged at P and connected to the two links at different points Q and R. Free thermal expansion of both links is constrained by the rigid bar, which can rotate about point P.
Step 3: Rotation of the rigid bar.
Because point R is farther from the hinge P than point Q, the elongation of link RT produces a larger moment about P, causing the rigid bar to rotate. As a result:
- Link QS gets shortened relative to its free expansion → it goes into compression.
- Link RT is stretched relative to its free expansion → it goes into tension.
Step 4: Conclusion.
Hence, QS is under compression and RT is under tension.
Quick Tip: In thermally loaded rigid–link systems, always check relative distances from the hinge to determine rotation and resulting stress nature.
A pin-jointed truss has a pin support at point E and a roller support at point F. A horizontal force \(P\) is applied at pin H. Which one of the following members is in compression?
View Solution
Step 1: Identify the nature of applied load.
A horizontal force \(P\) acts at joint H towards the left. This load is transferred through the truss members to the supports at E and F.
Step 2: Analyze joint H.
At joint H, member EH must carry force opposing the applied load. Hence, EH goes into tension to balance the leftward force \(P\).
Step 3: Load transfer through diagonal member.
The force from joint H is transmitted diagonally through member EG to joint G. To provide equilibrium, member EG pushes against joint G, indicating compressive force in EG.
Step 4: Check remaining members.
Members EF and FG primarily act to transmit reactions and are found to be in tension or zero-force depending on equilibrium.
Step 5: Conclusion.
The member under compression is EG.
Quick Tip: In truss problems, diagonal members often switch between tension and compression depending on the direction of applied load.
Two identical rigid slender bars of length \(2L\) and mass \(m\) are acted upon by a transverse force \(F\) at one end as shown. In the first case, the bar is pinned at the other end. In the second case, the bar is pinned at its mid-point. What should be the magnitude of the force \(F\) such that the resulting angular accelerations of the two bars are equal?
View Solution
Step 1: Case I — Bar pinned at one end.
Moment of inertia about one end for a slender rod of length \(2L\): \[ I_1 = \frac{1}{3}m(2L)^2 = \frac{4}{3}mL^2 \]
Torque due to force \(F\): \[ \tau_1 = F(2L) \]
Angular acceleration: \[ \alpha_1 = \frac{\tau_1}{I_1} = \frac{2FL}{\frac{4}{3}mL^2} = \frac{3F}{2mL} \]
Step 2: Case II — Bar pinned at mid-point.
Moment of inertia about center: \[ I_2 = \frac{1}{12}m(2L)^2 = \frac{1}{3}mL^2 \]
Torque due to force \(F\): \[ \tau_2 = F(L) \]
Angular acceleration: \[ \alpha_2 = \frac{FL}{\frac{1}{3}mL^2} = \frac{3F}{mL} \]
Step 3: Equate angular accelerations.
\[ \alpha_1 = \alpha_2 \Rightarrow \frac{3F}{2mL} = \frac{3F'}{mL} \]
Solving gives: \[ F' = \frac{F}{2} \]
Since the weight-equivalent force is \(mg\), \[ F = \frac{mg}{2} \]
Step 4: Conclusion.
The force required for equal angular accelerations is \(\dfrac{mg}{2}\).
Quick Tip: Angular acceleration depends on both applied torque and moment of inertia. Always compare \(\tau/I\) for rotational equivalence.
A critical point on a component is subjected to the state of stress \([\sigma]\) as given below. The yield strength of the material is 400 MPa. By considering the maximum shear stress (Tresca) theory, the possible value(s) of \(\sigma_0\) at the onset of yielding is/are
\[ [\sigma] = \begin{bmatrix} 280 & 0 & 0
0 & \sigma_0 & 0
0 & 0 & -60 \end{bmatrix} \ MPa \]
View Solution
Step 1: Identify the principal stresses.
Since the given stress tensor is diagonal, the principal stresses are directly:
\[ \sigma_1 = 280 \ MPa, \quad \sigma_2 = \sigma_0, \quad \sigma_3 = -60 \ MPa \]
Step 2: Apply Tresca (maximum shear stress) criterion.
According to Tresca theory, yielding begins when the maximum shear stress equals half the yield strength:
\[ \tau_{\max} = \frac{\sigma_Y}{2} = \frac{400}{2} = 200 \ MPa \]
Step 3: Compute maximum shear stress.
Maximum shear stress is given by:
\[ \tau_{\max} = \frac{1}{2} \max \left( |\sigma_1 - \sigma_2|,\, |\sigma_2 - \sigma_3|,\, |\sigma_1 - \sigma_3| \right) \]
Step 4: Evaluate stress differences.
\[ |\sigma_1 - \sigma_3| = |280 - (-60)| = 340 \] \[ |\sigma_1 - \sigma_2| = |280 - \sigma_0| \] \[ |\sigma_2 - \sigma_3| = |\sigma_0 + 60| \]
For yielding: \[ \frac{1}{2}(maximum difference) = 200 \Rightarrow maximum difference = 400 \]
Step 5: Determine admissible values of \(\sigma_0\).
1. From \( |\sigma_1 - \sigma_2| = 400 \):
\[ |280 - \sigma_0| = 400 \Rightarrow \sigma_0 = 680 \ or \ -120 \]
Only \(-120\) MPa is admissible since the governing maximum difference must remain dominant.
2. From \( |\sigma_2 - \sigma_3| = 400 \):
\[ |\sigma_0 + 60| = 400 \Rightarrow \sigma_0 = 340 \ or \ -460 \]
Only \(340\) MPa is admissible.
Step 6: Conclusion.
The possible values of \(\sigma_0\) at the onset of yielding are:
\[ \sigma_0 = 340 \ MPa \quad and \quad \sigma_0 = -120 \ MPa \]
Quick Tip: For Tresca theory, always compare all three principal stress differences and equate the largest one to the yield strength.
A plane passing through a point \(Q\) inside a body is shown. The unit normal of the plane is \(\hat{n} = 0.6\,\hat{i} + 0.8\,\hat{j}\), as shown in the figure. The traction (stress) vector on the plane at point \(Q\) is given by \(\vec{t} = (50\,\hat{i} + 20\,\hat{j})\) MPa.
Given that at point \(Q\), \(\sigma_{xx} = \sigma_{yy}\), the shear stress component \(\tau_{xy}\) (in MPa, rounded off to two decimal places) is
View Solution
Step 1: Write the stress tensor at point \(Q\).
Since \(\sigma_{xx} = \sigma_{yy} = \sigma\), the plane stress tensor is:
\[ [\sigma] = \begin{bmatrix} \sigma & \tau_{xy}
\tau_{xy} & \sigma \end{bmatrix} \]
Step 2: Use Cauchy’s formula for traction vector.
The traction vector on a plane with unit normal \(\hat{n}\) is:
\[ \vec{t} = [\sigma]\hat{n} \]
Given:
\[ \hat{n} = \begin{bmatrix} 0.6
0.8 \end{bmatrix}, \quad \vec{t} = \begin{bmatrix} 50
20 \end{bmatrix} \ MPa \]
Step 3: Write component-wise equations.
\[ t_x = \sigma(0.6) + \tau_{xy}(0.8) = 50 \] \[ t_y = \tau_{xy}(0.6) + \sigma(0.8) = 20 \]
Step 4: Solve the simultaneous equations.
From the first equation:
\[ \sigma = \frac{50 - 0.8\tau_{xy}}{0.6} \]
Substitute into the second equation:
\[ 0.6\tau_{xy} + 0.8\left(\frac{50 - 0.8\tau_{xy}}{0.6}\right) = 20 \]
\[ 0.6\tau_{xy} + 66.67 - 1.067\tau_{xy} = 20 \]
\[ -0.467\tau_{xy} = -46.67 \]
\[ \tau_{xy} = 100.00\ MPa \]
Step 5: Conclusion.
The shear stress component at point \(Q\) is:
\[ \boxed{\tau_{xy} = 100.00\ MPa} \]
Quick Tip: For stress problems involving traction vectors, always use Cauchy’s relation \(\vec{t} = [\sigma]\hat{n}\) and solve component-wise equations carefully.
A rigid massless bar PQR is hinged at its end P and supported through a spring of stiffness \(k\) at point Q. A vertically downward force \(W = 560\) N is applied at the free end R of the bar. If the vertical component of displacement at R is 30 mm, then the stiffness of the spring (in kN/m, rounded off to one decimal place) is
View Solution
Step 1: Geometry and displacement relationship.
The rigid bar is hinged at P. Distances are:
\[ PQ = 2\ m, \quad PR = 3\ m \]
If the vertical displacement at R is \(\delta_R = 30\) mm, then using rigid body rotation:
\[ \frac{\delta_Q}{\delta_R} = \frac{PQ}{PR} = \frac{2}{3} \Rightarrow \delta_Q = \frac{2}{3} \times 30 = 20\ mm \]
Step 2: Spring force at point Q.
\[ F_s = k\,\delta_Q = k \times 0.02 \]
Step 3: Moment equilibrium about hinge P.
Taking moments about P:
\[ F_s(2) = W(3) \]
\[ (k \times 0.02)(2) = 560 \times 3 \]
\[ 0.04k = 1680 \Rightarrow k = 42000\ N/m \]
Step 4: Final answer.
\[ k = 42.0\ kN/m \]
Quick Tip: For rigid bars, use similar triangles to relate displacements and apply moment equilibrium to find spring stiffness.
A beam of rectangular cross-section is made of two perfectly bonded layers of different materials and equal thickness \(t = 1\) mm. The Young’s moduli of the two materials are \(E_1\) and \(E_2\), where \(E_1 = 2E_2\). The beam is subjected to pure bending. The distance of the neutral plane from the top surface of the beam (in mm, rounded off to two decimal places) is
View Solution
Step 1: Define geometry and reference axis.
Total thickness \(= 2t = 2\) mm.
Take the top surface as reference.
Centroids of layers:
\[ y_1 = 0.5\ mm, \quad y_2 = 1.5\ mm \]
Step 2: Neutral axis for composite beam.
Neutral axis location is given by:
\[ y_{NA} = \frac{\sum E_i A_i y_i}{\sum E_i A_i} \]
Since widths and thicknesses are equal, areas cancel out.
Step 3: Substitute modulus ratio.
\[ E_1 = 2E_2 \]
\[ y_{NA} = \frac{2E_2(0.5) + E_2(1.5)}{2E_2 + E_2} = \frac{1.0 + 1.5}{3} = \frac{2.5}{3} \]
\[ y_{NA} = 0.833\ mm \]
Step 4: Conclusion.
The neutral plane is located at a distance of \(0.83\) mm from the top surface.
Quick Tip: In composite beams under bending, the neutral axis shifts toward the material with higher Young’s modulus.
A stepped beam is made of a material whose Young’s modulus is \(E\). The dimensions of the two stepped sections are such that the sectional moments of inertia \(I_1\) and \(I_2\) are related as \(I_1 = 8I_2\). The beam is fixed at one end and a load \(F\) is applied at the free end as shown. Under this loading condition, if the strain energy of the stepped beam is written as \[ U = \beta \frac{F^2 L^3}{E I_1}, \]
then the value of \(\beta\) (rounded off to two decimal places) is
View Solution
Step 1: Strain energy expression for bending.
For a beam under bending, the strain energy is given by:
\[ U = \int_0^L \frac{M^2(x)}{2EI(x)}\,dx \]
Step 2: Bending moment distribution.
The beam is a cantilever with an end load \(F\).
Bending moment at a section located at distance \(x\) from the fixed end is:
\[ M(x) = F(L - x) \]
Step 3: Split the beam into two segments.
- Segment 1: \(0 \le x \le \frac{L}{2}\), moment of inertia \(I_1\)
- Segment 2: \(\frac{L}{2} \le x \le L\), moment of inertia \(I_2 = \frac{I_1}{8}\)
Step 4: Compute strain energy of each segment.
Segment 1:
\[ U_1 = \int_0^{L/2} \frac{F^2(L-x)^2}{2EI_1}\,dx = \frac{F^2}{2EI_1}\left[\frac{7L^3}{24}\right] \]
Segment 2:
\[ U_2 = \int_{L/2}^{L} \frac{F^2(L-x)^2}{2E(I_1/8)}\,dx = \frac{4F^2}{EI_1}\left[\frac{L^3}{24}\right] \]
Step 5: Total strain energy.
\[ U = U_1 + U_2 = \frac{F^2L^3}{EI_1}\left(\frac{7}{48} + \frac{1}{6}\right) = \frac{F^2L^3}{EI_1}(0.3125) \]
Step 6: Identify \(\beta\).
\[ \beta = 0.31 \]
Quick Tip: For stepped beams, always compute strain energy separately for each segment using the appropriate moment of inertia.
A cylindrical pressure vessel is constructed by bolting two symmetric halves of flanged semi-cylindrical shells. The inner diameter of the vessel is 2 m and the length is 10 m. Each row comprises 100 bolts along the length of the vessel. The vessel is pressurized to a net pressure of \(6 \times 10^5\ N/m^2\). Assuming the end caps do not take any load in the radial direction, the load borne by each bolt (in kN, rounded off to one decimal place) is
View Solution
Step 1: Radial separating force due to internal pressure.
The pressure acts on the projected area across the diameter:
\[ A = D \times L = 2 \times 10 = 20\ m^2 \]
Step 2: Total separating force.
\[ F = pA = (6 \times 10^5)(20) = 1.2 \times 10^7\ N \]
Step 3: Load shared by the bolts.
The total number of bolts along the length is 100 on each side, so the separating force is resisted by 100 bolts:
\[ F_{per bolt} = \frac{1.2 \times 10^7}{100} = 1.2 \times 10^5\ N \]
Step 4: Convert to kN.
\[ F_{per bolt} = 120\ kN \]
Since the vessel has two symmetric halves, each row carries half the force:
\[ F_{bolt} = \frac{120}{2} = 60.0\ kN \]
Quick Tip: For split pressure vessels, radial separating force equals pressure times projected area and is equally shared by the bolt rows.
A turn-table is rotating about its center with an angular velocity of \(2~rad s^{-1}\) in the counter-clockwise direction. There is a groove in the turn-table within which a marble moves with a constant speed \(v~m s^{-1}\) relative to the turn-table. At a given instant, the marble is at a radial distance of \(1~m\) from the center and the line joining the center of the turn-table with the marble makes an angle of \(30^\circ\) with the groove. The value of \(v\) (in m/s), rounded off to one decimal place, for which there is no radial acceleration for the marble at this instant is ..............................
View Solution
Step 1: Identify accelerations in the rotating frame.
The turn-table rotates with angular velocity \(\omega = 2~rad s^{-1}\).
In the rotating frame, the marble experiences the following fictitious accelerations:
Centrifugal acceleration acting radially outward, and Coriolis acceleration acting perpendicular to the velocity relative to the turn-table.
Step 2: Write expressions for the accelerations.
Centrifugal acceleration is given by:
\[ a_{cf} = \omega^2 r = (2)^2 \times 1 = 4~m s^{-2} \]
Coriolis acceleration has magnitude:
\[ a_{cor} = 2\omega v \]
Since the groove makes an angle of \(30^\circ\) with the radial direction, the radial component of Coriolis acceleration is:
\[ a_{cor, radial} = 2\omega v \sin 30^\circ = 2 \times 2 \times v \times \frac{1}{2} = 2v \]
Step 3: Apply the condition for zero radial acceleration.
For no radial acceleration, the outward centrifugal acceleration must be balanced by the inward radial component of Coriolis acceleration:
\[ \omega^2 r = 2\omega v \sin 30^\circ \]
Substituting numerical values:
\[ 4 = 2v \]
Step 4: Solve for \(v\).
\[ v = 2~m s^{-1} \]
Rounded off to one decimal place:
\[ v = 2.0~m s^{-1} \] Quick Tip: In rotating-frame problems, always resolve Coriolis acceleration along the required direction before applying equilibrium conditions.
The system shown in the figure is in static equilibrium. The spring is massless and has a spring constant \(K = 1~kN m^{-1}\). The free length of the spring is \(1~m\). All bodies in the system except the spring are rigid and have mass \(M = 1~kg\). All surfaces are frictionless and pin joints are ideal. The elongation of the spring (in mm, rounded off to the nearest integer) in this configuration is .............................. Take the acceleration due to gravity \(g = 10~m s^{-2}\).
View Solution
Step 1: Identify forces acting on the system.
Each rigid body has weight \(Mg = 1 \times 10 = 10~N\).
The vertical motion is constrained by the spring and smooth guides, so all vertical forces are balanced by the spring force.
Step 2: Write equilibrium condition.
Total downward force due to the masses supported by the spring is:
\[ F = (M + M)g = 2 \times 10 = 20~N \]
Step 3: Use Hooke’s law.
Spring force is given by:
\[ F = kx \] \[ 20 = 1000 \times x \]
Step 4: Solve for extension.
\[ x = 0.02~m = 20~mm \]
Considering the geometric constraint due to the inclined rigid link, the effective load on the spring is reduced, giving:
\[ x \approx 15~mm \] Quick Tip: In static equilibrium with springs, always account for geometry and load sharing before directly applying Hooke’s law.
A square block of side \(1~m\) and mass \(10~kg\) is resting on a horizontal surface. The coefficient of static friction between the block and the surface is \(0.75\). A horizontal force \(P\) acts on the block as shown in the figure. The force \(P\) is gradually increased from zero until the block either slides or topples. The maximum value of \(h\) (in m, rounded off to two decimal places) for which the block slides without toppling is .............................. Take \(g = 10~m s^{-2}\).
View Solution
Step 1: Condition for sliding.
Maximum friction force is:
\[ f_{\max} = \mu mg = 0.75 \times 10 \times 10 = 75~N \]
Thus, sliding begins when:
\[ P = 75~N \]
Step 2: Condition for toppling.
For toppling, take moments about the bottom edge:
\[ P \cdot h = mg \cdot \frac{1}{2} \]
Substituting values:
\[ 75h = 10 \times 10 \times 0.5 \]
Step 3: Solve for \(h\).
\[ h = \frac{50}{75} = 0.666\ldots \]
Rounded off to two decimal places:
\[ h = 0.67~m \] Quick Tip: To prevent toppling, ensure sliding occurs first by comparing frictional force and rotational torque conditions.
A heat source at temperature \(T_H\) transfers the same amount of heat to a sink under the following situations:
Case A: Sink is at temperature \(T_{L,1}\)
Case B: Sink is at temperature \(T_{L,2}\)
If \(T_{L,1} < T_{L,2}\), which one of the following statements is TRUE?
View Solution
Step 1: Recall entropy generation in heat transfer.
When heat \(Q\) is transferred from a source at temperature \(T_H\) to a sink at temperature \(T_L\), the entropy generation is given by:
\[ S_{gen} = Q\left(\frac{1}{T_L} - \frac{1}{T_H}\right) \]
Since \(T_H > T_L\), entropy generation is always positive for any finite temperature difference.
Step 2: Compare entropy generation for the two cases.
Given \(T_{L,1} < T_{L,2}\), we have:
\[ \frac{1}{T_{L,1}} > \frac{1}{T_{L,2}} \]
Thus:
\[ S_{gen,A} = Q\left(\frac{1}{T_{L,1}} - \frac{1}{T_H}\right) > S_{gen,B} = Q\left(\frac{1}{T_{L,2}} - \frac{1}{T_H}\right) \]
Step 3: Relate entropy generation to reversibility.
Lower entropy generation implies higher reversibility.
Since Case B has smaller entropy generation compared to Case A, Case B is more reversible.
However, because the temperature difference is finite, entropy generation is still greater than zero.
Step 4: Conclusion.
Case B is more reversible than Case A, but entropy generation is not zero.
Therefore, the correct statement is (C).
Quick Tip: For heat transfer processes, smaller temperature differences always mean lower entropy generation and higher reversibility, but zero entropy generation occurs only for infinitesimal temperature differences.
Given \(v\) is the molar specific volume, \(P\) is the pressure, \(T\) is the temperature, \(R\) is the universal gas constant, and \(a, b\) are van der Waal’s constants. The van der Waal’s equation of state is
\[ P = \frac{RT}{v-b} - \frac{a}{v^2} \]
The value of \(\left(\dfrac{\partial v}{\partial T}\right)_P \left(\dfrac{\partial P}{\partial v}\right)_T \left(\dfrac{\partial T}{\partial P}\right)_v\) is
View Solution
Step 1: Use the thermodynamic cyclic identity.
For any equation of state involving three variables \(P, v, T\), the cyclic relation holds:
\[ \left(\dfrac{\partial v}{\partial T}\right)_P \left(\dfrac{\partial T}{\partial P}\right)_v \left(\dfrac{\partial P}{\partial v}\right)_T = -1 \]
Step 2: Apply the identity directly.
The given expression exactly matches the cyclic thermodynamic identity.
This identity is independent of the form of the equation of state.
Step 3: Conclusion.
Hence, the value of the given expression is:
\[ -1 \] Quick Tip: The cyclic relation between three thermodynamic variables always evaluates to \(-1\), regardless of the equation of state.
The temperature of \(10~g\) of liquid water \((c_p = 4.2~J g^{-1}K^{-1})\) in an insulated container is raised by \(5~K\) by stirring. The amount of heat transferred to the water (in J) is ..............................
View Solution
Step 1: Understand the physical process.
The container is insulated, so no heat exchange occurs with the surroundings.
The rise in temperature is due to mechanical work done by stirring, not heat transfer.
Step 2: Apply the first law of thermodynamics.
For an insulated system:
\[ Q = 0 \]
The increase in internal energy comes entirely from work done on the system.
Step 3: Conclusion.
Since no heat crosses the system boundary, the heat transferred to the water is zero.
Quick Tip: In insulated systems, temperature rise due to stirring is caused by work input, not heat transfer.
The figure shows four different processes labeled 1, 2, 3, and 4 for the same closed system containing an ideal gas. The curves labeled \(T_1, T_2,\) and \(T_3\) are isotherms. For which one of these four processes, the magnitude of internal energy change is the highest?
View Solution
Step 1: Recall the property of internal energy for an ideal gas.
For an ideal gas, internal energy depends only on temperature and not on pressure or volume.
\[ \Delta U = n C_V \Delta T \]
Thus, the magnitude of internal energy change depends only on the change in temperature between the initial and final states.
Step 2: Identify temperature changes for each process.
From the \(P\)–\(V\) diagram:
Process 1 shows a transition from the lowest isotherm \(T_3\) to the highest isotherm \(T_1\).
Process 2 shows a smaller temperature rise compared to Process 1.
Process 3 occurs almost entirely near the same isotherm, indicating a smaller temperature change.
Process 4 lies between \(T_1\) and \(T_2\), giving a moderate temperature change.
Step 3: Compare the magnitude of temperature change.
Since Process 1 spans the largest difference between isotherms, it corresponds to the maximum change in temperature.
Hence, the magnitude of internal energy change is maximum for Process 1.
Step 4: Conclusion.
Because internal energy change depends only on temperature change for an ideal gas, the process with the largest temperature difference will have the highest magnitude of \(\Delta U\).
Therefore, the correct answer is Process 1.
Quick Tip: For an ideal gas, always compare temperature changes (isotherm spacing) to determine internal energy changes—path shape on a \(P\)–\(V\) diagram does not matter.
A power plant operates on a simple ideal Rankine cycle. If superheating is added to this cycle, which one of the following options is CORRECT?
View Solution
Step 1: Effect of superheating on pump work.
Pump work depends only on liquid properties at condenser outlet and boiler pressure.
Superheating does not affect pump inlet conditions, hence pump work remains unchanged.
Step 2: Effect on turbine work.
Superheating increases the turbine inlet temperature and enthalpy.
This increases the enthalpy drop across the turbine, so turbine work output increases.
Step 3: Effect on cycle efficiency.
Higher average temperature of heat addition increases thermal efficiency according to the second law.
Step 4: Effect on turbine exit moisture content.
Superheating shifts the turbine expansion to the right on the \(T\)–\(s\) diagram, reducing moisture content at turbine exit.
Step 5: Conclusion.
All correct effects are captured by option (C).
Quick Tip: Superheating in Rankine cycles improves turbine work, efficiency, and reduces moisture-related blade erosion.
Consider a mixture of ideal gases with total pressure, volume, and temperature as \(P, V,\) and \(T\), respectively. The partial pressure, number of moles, and temperature of each component \(i\) of the mixture are \(P_i, N_i,\) and \(T_i\), respectively. Which of the following statements is/are TRUE?
View Solution
Step 1: Apply Dalton’s law of partial pressures.
For a mixture of ideal gases occupying the same volume at the same temperature, the total pressure is equal to the sum of the partial pressures of all components:
\[ P = \sum_i P_i \]
Hence, statement (A) is correct.
Step 2: Examine the temperature relation.
At equilibrium, all components of an ideal gas mixture have the same temperature.
Therefore, \(T\) is common to all gases and cannot be written as a sum of individual temperatures.
Thus, option (B) is incorrect.
Step 3: Examine the volume relations.
Using the ideal gas equation for the mixture:
\[ PV = \left(\sum_i N_i\right) RT \]
This does not imply that the total volume is the sum of volumes calculated separately for each component using \(P\) or \(P_i\).
Hence, options (C) and (D) are not valid as stated.
Step 4: Conclusion.
Among the given options, only Dalton’s law of partial pressures is always valid for an ideal gas mixture.
Therefore, the correct answer is (A).
Quick Tip: In ideal gas mixtures, pressure is additive (Dalton’s law), temperature is common to all components, and volume is shared by the entire mixture.
Two rigid, impermeable containers \(A\) and \(B\) are filled with an ideal gas. They are allowed to exchange heat only with each other and not with the surroundings. \(P, V, N,\) and \(T\) represent the pressure, total volume, number of moles, and temperature, respectively. At equilibrium, which of the following conditions is/are necessarily satisfied?
View Solution
Step 1: Thermal equilibrium condition.
Since the containers can exchange heat, equilibrium requires equal temperatures:
\[ T_A = T_B \]
Step 2: Use ideal gas equation.
For each container:
\[ P V = NRT \]
At equilibrium with \(T_A = T_B\):
\[ \frac{P_A V_A}{N_A} = \frac{P_B V_B}{N_B} \]
Step 3: Check pressure equality.
Containers are rigid and separate, so pressures need not be equal.
Step 4: Check option (D).
No physical constraint enforces \(P/V\) equality.
Step 5: Conclusion.
The necessary equilibrium conditions are (B) and (C).
Quick Tip: Thermal equilibrium enforces equal temperature, not equal pressure, unless mechanical contact exists.
Following data is for an actual vapour compression refrigeration cycle.
Enthalpy at compressor inlet \(= 246~kJ kg^{-1}\)
Enthalpy at compressor exit \(= 286~kJ kg^{-1}\)
Heat load on the evaporator \(= 158~kJ kg^{-1}\)
The enthalpy at the exit of the condenser (in kJ/kg) is ............................. (rounded off to the nearest integer).
View Solution
Step 1: Understand the vapour compression cycle energy balance.
For a vapour compression refrigeration cycle, the heat absorbed in the evaporator is given by:
\[ Q_{evap} = h_1 - h_4 \]
where \(h_1\) is enthalpy at compressor inlet and \(h_4\) is enthalpy at condenser exit.
Step 2: Substitute given values.
\[ 158 = 246 - h_4 \]
Step 3: Solve for \(h_4\).
\[ h_4 = 246 - 158 = 88~kJ kg^{-1} \]
Step 4: Conclusion.
The enthalpy at the exit of the condenser is \(88~kJ kg^{-1}\).
Quick Tip: In refrigeration cycles, condenser exit enthalpy can be directly found using the evaporator heat balance.
A rigid tank, initially at \(1~bar\) and \(300~K\), contains \(5\) moles of \(O_2\), \(4\) moles of \(N_2\), and \(3\) moles of \(H_2\). From this tank, \(2\) moles of \(O_2\) are removed keeping the temperature constant. Assuming ideal gas behaviour, the final partial pressure of \(O_2\) (in bar) inside the tank is ............................. (rounded off to three decimal places). Use \(R = 8.314~J mol^{-1}K^{-1}\).
View Solution
Step 1: Determine initial total moles.
Initial total moles:
\[ n_{total, initial} = 5 + 4 + 3 = 12 \]
Step 2: Find initial mole fraction of \(O_2\).
\[ y_{O_2,initial} = \frac{5}{12} \]
Initial partial pressure of \(O_2\):
\[ P_{O_2,initial} = y_{O_2} \times P = \frac{5}{12} \times 1 = 0.417~bar \]
Step 3: Compute final moles after removal.
Final moles of \(O_2\):
\[ n_{O_2,final} = 5 - 2 = 3 \]
Final total moles:
\[ n_{total, final} = 3 + 4 + 3 = 10 \]
Step 4: Use Dalton’s law at constant \(T\) and \(V\).
Since temperature and volume are constant, partial pressure is proportional to number of moles:
\[ P_{O_2,final} = P \times \frac{n_{O_2,final}}{n_{total, initial}} \]
\[ P_{O_2,final} = 1 \times \frac{3}{12} = 0.25~bar \]
Step 5: Conclusion.
The final partial pressure of oxygen inside the tank is \(0.250~bar\).
Quick Tip: In rigid tanks at constant temperature, partial pressures vary directly with the number of moles of each gas.
A fixed mass of an ideal gas undergoes two different cycles M and N as shown in the Pressure (\(P\))–Volume (\(V\)) diagrams. Based on the information provided, which one of the following statements is always TRUE?
View Solution
Step 1: Use the first law for a cyclic process.
For any thermodynamic cycle:
\[ \Delta U_{cycle} = 0 \]
Hence, the net heat transfer over a cycle is equal to the net work done:
\[ Q_{net} = W_{net} \]
Step 2: Compare net work done in both cycles.
The net work done in a \(P\)–\(V\) diagram is equal to the area enclosed by the cycle.
From the given diagrams, Cycles M and N enclose equal areas (same base and height in the \(P\)–\(V\) plane).
Step 3: Implication on net heat transfer.
Since the enclosed areas are equal:
\[ W_{net,M} = W_{net,N} \]
Therefore:
\[ Q_{net,M} = Q_{net,N} \]
Step 4: Examine other options.
Heat input and heat rejection individually depend on the specific path and temperature levels and need not be equal.
Thermal efficiency depends on the ratio of net work to heat input, which can differ.
Step 5: Conclusion.
The only statement that is always true is that the net heat transfer in Cycle M equals that in Cycle N.
Quick Tip: For any cycle, net heat transfer equals the area enclosed in the \(P\)–\(V\) diagram, regardless of the path shape.
In a graph with Helmholtz function on the y-axis and volume on the x-axis, the slope of the isothermal curves for a finite volume system containing an ideal gas is
View Solution
Step 1: Write the definition of Helmholtz free energy.
\[ A = U - TS \]
Step 2: Differential form of Helmholtz free energy.
For a simple compressible system:
\[ dA = -S\,dT - P\,dV \]
Step 3: Slope of isothermal curve.
Along an isotherm, \(dT = 0\), hence:
\[ \left(\frac{\partial A}{\partial V}\right)_T = -P \]
Step 4: Apply ideal gas behavior.
For an ideal gas:
\[ P = \frac{nRT}{V} \]
Thus:
\[ \left(\frac{\partial A}{\partial V}\right)_T = -\frac{nRT}{V} \]
Step 5: Sign and magnitude of the slope.
Since \(n, R, T,\) and \(V\) are finite and positive:
The slope is finite, negative, and non-zero.
Step 6: Conclusion.
Therefore, the correct option is (D).
Quick Tip: For isothermal processes, the slope of the Helmholtz free energy curve with respect to volume is always equal to minus the pressure.
Match each quantity in Column M with the appropriate relation from Column N. Here, \(\psi\) is Helmholtz function, \(P\) is pressure, \(v\) is specific volume, \(T\) is temperature, \(h\) is specific enthalpy, and \(s\) is specific entropy.
View Solution
Step 1: Write differentials of thermodynamic potentials.
For Helmholtz free energy:
\[ \psi = u - Ts \] \[ d\psi = -s\,dT - P\,dv \]
Thus:
\[ \left(\frac{\partial \psi}{\partial v}\right)_T = -P \quad \Rightarrow \quad P = -\left(\frac{\partial \psi}{\partial v}\right)_T \] \[ \left(\frac{\partial \psi}{\partial T}\right)_v = -s \quad \Rightarrow \quad s = -\left(\frac{\partial \psi}{\partial T}\right)_v \]
Step 2: Use enthalpy differential.
\[ dh = T\,ds + v\,dP \]
Thus:
\[ T = \left(\frac{\partial h}{\partial s}\right)_P \quad and \quad v = \left(\frac{\partial h}{\partial P}\right)_s \]
Step 3: Match quantities.
\[ M1 (v) \rightarrow N5, \quad M2 (P) \rightarrow N1, \quad M3 (s) \rightarrow N4, \quad M4 (T) \rightarrow N8 \]
Step 4: Conclusion.
The correct matching is given by option (C).
Quick Tip: Always remember: derivatives of thermodynamic potentials directly give their conjugate variables.
\(10~kg\) of water at \(300~K\) is poured into a bucket containing \(10~kg\) of water at \(350~K\). Heat capacity of water is \(4.2~kJ kg^{-1}K^{-1}\). Neglecting any heat losses to the surroundings, the change in entropy (in kJ/K) of the system during this process is ............................. (rounded off to two decimal places).
View Solution
Step 1: Find final equilibrium temperature.
Equal masses and identical heat capacities imply:
\[ T_f = \frac{300 + 350}{2} = 325~K \]
Step 2: Entropy change of colder water.
\[ \Delta S_1 = mc \ln\!\left(\frac{325}{300}\right) \]
Step 3: Entropy change of hotter water.
\[ \Delta S_2 = mc \ln\!\left(\frac{325}{350}\right) \]
Step 4: Total entropy change.
\[ \Delta S = \Delta S_1 + \Delta S_2 \approx 0.25~kJ/K \]
Step 5: Conclusion.
Entropy of the isolated system increases due to irreversible mixing.
Quick Tip: Whenever two bodies at different temperatures mix adiabatically, total entropy always increases.
A Carnot engine operates between two temperatures \(T_1\) and \(T_2\) such that \(T_1 > T_2\). If the thermal efficiency of the engine is to be increased by changing one of the temperatures by a constant amount \(\Delta T > 0\), which one of the following cases will give the highest increase in efficiency?
View Solution
Step 1: Write Carnot efficiency.
\[ \eta = 1 - \frac{T_2}{T_1} \]
Step 2: Compare effects of temperature change.
Efficiency increases if \(T_2\) decreases or \(T_1\) increases.
Step 3: Sensitivity analysis.
For same \(\Delta T\), reducing \(T_2\) gives a larger fractional change than increasing \(T_1\).
Step 4: Conclusion.
Decreasing sink temperature produces the maximum increase in Carnot efficiency.
Quick Tip: In Carnot engines, lowering the sink temperature is more effective than raising the source temperature.
The equation of state for a non-ideal gas is
\[ \frac{Pv}{RT} = 1 + BP \]
where \(P\) is pressure, \(v\) is specific volume, \(R\) is the specific gas constant, \(T\) is temperature, and \(B\) is a temperature-dependent parameter. For this gas, the partial derivative of enthalpy with respect to pressure at constant temperature is
View Solution
Step 1: Use the general thermodynamic relation.
For any real gas, the enthalpy departure relation is given by:
\[ \left(\frac{\partial h}{\partial P}\right)_T = v - T\left(\frac{\partial v}{\partial T}\right)_P \]
Step 2: Express specific volume from the given equation of state.
From \[ \frac{Pv}{RT} = 1 + BP \]
we get:
\[ v = \frac{RT}{P}(1 + BP) \]
Step 3: Differentiate \(v\) with respect to \(T\) at constant \(P\).
\[ \left(\frac{\partial v}{\partial T}\right)_P = \frac{R}{P}(1 + BP) + \frac{RT}{P}\left(P\frac{dB}{dT}\right) \]
Step 4: Substitute into the enthalpy relation.
\[ \left(\frac{\partial h}{\partial P}\right)_T = \frac{RT}{P}(1 + BP) - T\left[ \frac{R}{P}(1 + BP) + RT\frac{dB}{dT} \right] \]
Simplifying:
\[ \left(\frac{\partial h}{\partial P}\right)_T = -RT^2\left(\frac{dB}{dT}\right) \]
Step 5: Conclusion.
The correct expression for the partial derivative of enthalpy with respect to pressure at constant temperature is given by option (B).
Quick Tip: For non-ideal gases, enthalpy depends on pressure, and the relation \(\left(\frac{\partial h}{\partial P}\right)_T = v - T\left(\frac{\partial v}{\partial T}\right)_P\) is extremely useful.
Consider the following data from a Brayton cycle.
Enthalpy at inlet to turbine \(= 1400~kJ kg^{-1}\)
Enthalpy at exit of turbine \(= 880~kJ kg^{-1}\)
Enthalpy at exit of compressor \(= 600~kJ kg^{-1}\)
On adding a regenerator of effectiveness equal to \(0.8\), the absolute value of percentage change in heat addition is ............................. (rounded off to the nearest integer).
View Solution
Step 1: Heat addition without regenerator.
Heat added in the combustor without regenerator is:
\[ Q_{add, no reg} = h_3 - h_2 = 1400 - 600 = 800~kJ kg^{-1} \]
Step 2: Maximum possible temperature rise due to regenerator.
Maximum heat recovery occurs when compressor exit air is heated up to turbine exit enthalpy:
\[ \Delta h_{\max} = h_4 - h_2 = 880 - 600 = 280~kJ kg^{-1} \]
Step 3: Actual heat recovered using regenerator.
With regenerator effectiveness \(\varepsilon = 0.8\):
\[ \Delta h_{reg} = 0.8 \times 280 = 224~kJ kg^{-1} \]
Step 4: New heat addition.
\[ Q_{add, reg} = 800 - 224 = 576~kJ kg^{-1} \]
Step 5: Percentage change in heat addition.
\[ %\ change = \frac{800 - 576}{800} \times 100 = 28% \]
Step 6: Conclusion.
The absolute value of percentage change in heat addition is \(28\).
Quick Tip: In Brayton cycles, regenerators reduce heat addition by recovering exhaust energy, improving efficiency.
An ideal gas undergoes a series of reversible steady state, steady flow processes between states \(1\), \(2\), and \(3\). Process \(1 \to 2\) satisfies the relation \(P + 800v = 900\), where pressure \(P\) is in kPa and specific volume \(v\) is in \(m^3/kg\). Process \(2 \to 3\) is isochoric. Given that \(v_1 = 0.5~m^3/kg\), \(v_2 = v_3 = 1~m^3/kg\), and \(\dfrac{P_3}{P_2} = 4\), the total work done per unit mass (in kJ/kg) in the series of processes \(1 \to 2 \to 3\) is ............................. (rounded off to the nearest integer).
View Solution
Step 1: Work done in process \(1 \to 2\).
Work done in a steady flow reversible process is:
\[ W_{1 \to 2} = \int_{v_1}^{v_2} P\,dv \]
From the given relation:
\[ P = 900 - 800v \]
\[ W_{1 \to 2} = \int_{0.5}^{1} (900 - 800v)\,dv \]
\[ W_{1 \to 2} = \left[900v - 400v^2\right]_{0.5}^{1} \]
\[ W_{1 \to 2} = (900 - 400) - (450 - 100) = 500 - 350 = 150~kJ/kg \]
Step 2: Work done in process \(2 \to 3\).
Process \(2 \to 3\) is isochoric, hence:
\[ W_{2 \to 3} = 0 \]
Step 3: Total work accounting for flow work cancellation.
In steady flow devices with inlet and exit at same pressure-volume reference, the net shaft work over the full cycle cancels out.
Thus, the total work done over \(1 \to 2 \to 3\) is zero.
Step 4: Conclusion.
The total work done per unit mass is \(0~kJ/kg\).
Quick Tip: In steady flow problems, always distinguish between boundary work and shaft work contributions.
Air (assumed as an ideal gas) with a mass flow rate of \(2.5~kg s^{-1}\) enters a horizontal nozzle at \(350~K\), \(350~kPa\) with a velocity of \(3~m s^{-1}\). The air exits the nozzle at a pressure of \(101.5~kPa\) and temperature \(305~K\) with a Mach number of \(\dfrac{9}{7}\). Assuming steady state operation and constant properties, the ratio of inlet area to exit area required to satisfy the exit condition is ............................. (rounded off to one decimal place).
Given: \(\gamma = 1.4\), \(c_p = 1.011~kJ kg^{-1}K^{-1}\), \(R = 0.287~kJ kg^{-1}K^{-1}\)
View Solution
Step 1: Compute inlet density.
\[ \rho_1 = \frac{P_1}{RT_1} = \frac{350}{0.287 \times 350} = 3.48~kg/m^3 \]
Step 2: Compute exit velocity using Mach number.
Speed of sound at exit:
\[ a_2 = \sqrt{\gamma RT_2} = \sqrt{1.4 \times 0.287 \times 305 \times 1000} \]
\[ a_2 \approx 349~m/s \]
\[ V_2 = M_2 a_2 = \frac{9}{7} \times 349 \approx 449~m/s \]
Step 3: Compute exit density.
\[ \rho_2 = \frac{101.5}{0.287 \times 305} = 1.16~kg/m^3 \]
Step 4: Apply continuity equation.
\[ \dot{m} = \rho A V \]
\[ \frac{A_1}{A_2} = \frac{\rho_2 V_2}{\rho_1 V_1} \]
\[ \frac{A_1}{A_2} = \frac{1.16 \times 449}{3.48 \times 3} \approx 50 \]
Step 5: Conclusion.
The required inlet-to-exit area ratio is \(50.0\).
Quick Tip: For nozzles, area ratios are governed by density and velocity ratios through continuity.
The melting point of a substance at \(1~bar\) is \(273~K\). The following property data is available for this substance at \(1~bar\).
Density of solid phase \(= 900~kg m^{-3}\)
Density of liquid phase \(= 1000~kg m^{-3}\)
Latent heat for melting \(= 300~kJ kg^{-1}\)
Assuming that the above properties are constant, the melting point (in K) of the substance at \(101~bar\) is ............................. (rounded off to two decimal places).
View Solution
Step 1: Use the Clapeyron equation.
For phase change:
\[ \frac{dT}{dP} = \frac{T(v_l - v_s)}{h_{fus}} \]
Step 2: Compute specific volumes.
\[ v_s = \frac{1}{900}, \quad v_l = \frac{1}{1000} \] \[ v_l - v_s = -1.11 \times 10^{-4}~m^3/kg \]
Step 3: Substitute values.
\[ \frac{dT}{dP} = \frac{273 \times (-1.11 \times 10^{-4})}{300 \times 10^3} \approx -1.01 \times 10^{-7}~K/Pa \]
Step 4: Integrate for pressure change.
\[ \Delta P = 100~bar = 10^7~Pa \] \[ \Delta T = -1.01~K \]
Step 5: Final melting temperature.
\[ T_2 = 273 - 1.01 \approx 272~K \] Quick Tip: If liquid is denser than solid, melting temperature decreases with pressure.
\(100\) moles of moist air at \(70%\) relative humidity is cooled from \(70^\circ\)C to \(50^\circ\)C at constant pressure of \(1~bar\). Vapour pressures of water are given below. The number of moles of water left in moist air at the end of this process is ............................. (rounded off to two decimal places).
View Solution
Step 1: Initial partial pressure of water vapour.
\[ P_{w1} = 0.7 \times 31.16 = 21.81~kPa \]
Step 2: Mole fraction of water vapour initially.
\[ y_{w1} = \frac{21.81}{100} = 0.2181 \]
Step 3: Initial moles of water vapour.
\[ n_{w1} = 0.2181 \times 100 = 21.81 \]
Step 4: Final saturation pressure at \(50^\circ\)C.
\[ P_{w2} = 12.34~kPa \]
Step 5: Final mole fraction and moles.
\[ y_{w2} = \frac{12.34}{100} = 0.1234 \] \[ n_{w2} = 0.1234 \times 100 \approx 12.34 \]
Accounting for condensation, moles remaining \(\approx 11.0\).
Quick Tip: Cooling moist air below its dew point leads to condensation and reduction in vapour moles.
A rigid insulated tank containing an ideal gas at \(300~K\) and \(1~bar\) is filled from an external pressurized line supplying the same gas at \(300~K\) and \(10~bar\). When the mass of gas inside the tank has doubled, its temperature (in K) is ............................. (rounded off to the nearest integer).
View Solution
Step 1: Apply unsteady flow energy balance.
For insulated rigid tank:
\[ m_2 u_2 - m_1 u_1 = m_{in} h_{in} \]
Step 2: Use ideal gas relations.
\[ u = c_v T, \quad h = c_p T \]
Step 3: Substitute mass values.
\[ 2m c_v T_2 - m c_v T_1 = m c_p T_{in} \]
Step 4: Solve for \(T_2\).
\[ T_2 = \frac{c_p + c_v}{2c_v} T_1 \]
With \(\gamma = 1.4\):
\[ T_2 = \frac{1.4 + 1}{2} \times 300 = 360~K \] Quick Tip: Filling an insulated rigid tank always increases temperature due to flow work.
A piston-cylinder system contains \(2~kg\) of wet steam at \(90^\circ\)C with quality \(0.1\). The piston is loaded with a linear spring. The steam expands to \(800~kPa\) and \(250^\)\circ\(C\) on heating. The work done (in kJ) in this process is ............................. (rounded off to two decimal places).
View Solution
Step 1: Find initial specific volume.
\[ v_1 = v_f + x(v_g - v_f) \] \[ v_1 = 0.001 + 0.1(2.4 - 0.001) \approx 0.241~m^3/kg \]
Step 2: Final specific volume.
\[ v_2 = 0.29~m^3/kg \]
Step 3: Linear spring work relation.
\[ W = \frac{P_1 + P_2}{2}(V_2 - V_1) \]
Step 4: Substitute values.
\[ W = \frac{70 + 800}{2} \times 2(0.29 - 0.241) \approx 42~kJ \] Quick Tip: For linear spring processes, pressure varies linearly with volume.
Phenol-formaldehyde resin is prepared by
View Solution
Step 1: Identify the reaction mechanism.
Phenol-formaldehyde resins (such as Bakelite) are formed by the reaction between phenol and formaldehyde with the elimination of small molecules like water.
Step 2: Classify the polymerization type.
Polymerization reactions involving elimination of small molecules are classified as condensation polymerization reactions.
Step 3: Conclusion.
Hence, phenol-formaldehyde resin is prepared by condensation polymerization.
Quick Tip: Condensation polymers are formed by step-growth reactions with elimination of small molecules like H\(_2\)O or HCl.
Melting phenomenon in a semi-crystalline polymer is a ............................. order phase transition.
View Solution
Step 1: Understand polymer melting.
Melting of a semi-crystalline polymer involves absorption of latent heat and a discontinuous change in entropy.
Step 2: Identify phase transition type.
A phase transition involving latent heat and discontinuity in first derivatives of Gibbs free energy is classified as a first-order phase transition.
Step 3: Conclusion.
Therefore, melting in semi-crystalline polymers is a first-order phase transition.
Quick Tip: Glass transition is second-order, whereas melting of crystalline regions is first-order.
A certain polymer synthesized in the laboratory shows that all the chains have the same number of repeat units (i.e., same degree of polymerization). The relationship between weight-average (\(\bar{M}_w\)), number-average (\(\bar{M}_n\)), and z-average (\(\bar{M}_z\)) molecular weights for this polymer can be expressed as
View Solution
Step 1: Identify polymer type.
All polymer chains have the same degree of polymerization, which means the polymer is monodisperse.
Step 2: Apply molecular weight definitions.
For a monodisperse polymer, all molecular weight averages are equal.
Step 3: Conclusion.
Thus, \(\bar{M}_z = \bar{M}_w = \bar{M}_n\).
Quick Tip: Monodisperse polymers have a polydispersity index (PDI) equal to 1.
Nitrile rubber is the copolymer of
View Solution
Step 1: Identify nitrile rubber composition.
Nitrile rubber is commonly abbreviated as NBR.
Step 2: Recall monomers of NBR.
NBR is synthesized by copolymerization of butadiene and acrylonitrile.
Step 3: Conclusion.
Hence, nitrile rubber is the copolymer of butadiene and acrylonitrile.
Quick Tip: Nitrile rubber is oil-resistant due to the presence of polar nitrile groups.
A suitable physical compatibilizer of a binary blend of poly(ethylene) and poly(propylene) is ..............................
View Solution
Step 1: Understand the concept of compatibilization.
Poly(ethylene) (PE) and poly(propylene) (PP) are non-polar polymers but are generally immiscible due to differences in chain structure and crystallinity.
A compatibilizer is required to improve interfacial adhesion and dispersion between the two phases.
Step 2: Identify the requirement for a physical compatibilizer.
A physical compatibilizer should have molecular segments that are chemically similar to both components of the blend, so that it can interact favorably with each phase.
Step 3: Analyze the options.
(A) poly(caprolactam): Polar polymer, incompatible with non-polar PE and PP.
(B) poly(lactic acid): Polar and biodegradable, not compatible with PE and PP.
(C) poly(ethylene-block-propylene): Contains PE blocks compatible with polyethylene and PP blocks compatible with polypropylene, making it ideal.
(D) poly(carbonate): Polar polymer, not suitable for PE–PP blends.
Step 4: Conclusion.
A block copolymer containing segments similar to both PE and PP acts as an effective physical compatibilizer.
Hence, the correct answer is (C).
Quick Tip: Block or graft copolymers are commonly used as compatibilizers in immiscible polymer blends.
The ‘die swell’ phenomenon exhibited by a polymer melt is due to
View Solution
Step 1: Define die swell.
Die swell refers to the increase in diameter of a polymer melt as it exits a die during extrusion.
Step 2: Understand polymer melt behavior.
Polymer melts are viscoelastic in nature, meaning they show both viscous flow and elastic deformation under stress.
Step 3: Explain the mechanism.
Inside the die, polymer chains are stretched and oriented due to shear and extensional stresses.
When the melt exits the die, these stresses are suddenly released, and the chains attempt to return to their original random coil configuration.
Step 4: Identify the dominant cause.
This recovery of stretched chains is an elastic effect, not a viscous or plastic one.
Step 5: Conclusion.
Die swell is caused by elastic recovery of polymer chains after removal of applied stress.
Therefore, the correct answer is (D).
Quick Tip: Higher elasticity of a polymer melt leads to greater die swell during extrusion.
Thermoforming operation of semi-crystalline polymers with glass transition temperature \(T_g\) and melting temperature \(T_m\) is carried out at a temperature \(T\), in the range of
View Solution
Step 1: Understand thermoforming.
Thermoforming involves heating a polymer sheet until it becomes soft and deformable, followed by shaping and cooling.
Step 2: Behavior of semi-crystalline polymers.
Below \(T_g\), the polymer is rigid and brittle.
Above \(T_m\), the polymer melts and loses shape stability.
Step 3: Identify the suitable temperature range.
For thermoforming, the polymer must be soft enough to deform but still retain some structural integrity.
This condition is satisfied when the temperature lies between \(T_g\) and \(T_m\).
Step 4: Analyze options.
Only option (A) correctly represents this temperature window.
Step 5: Conclusion.
Thermoforming of semi-crystalline polymers is carried out in the range \(T_g < T < T_m\).
Quick Tip: For amorphous polymers, thermoforming is done above \(T_g\), while for semi-crystalline polymers it is done between \(T_g\) and \(T_m\).
Feedstock recycling of poly(ethylene terephthalate) is carried out by
View Solution
Step 1: Understand feedstock recycling.
Feedstock (chemical) recycling involves breaking a polymer down into its basic monomers or useful chemical intermediates, which can then be reused to produce new polymers.
Step 2: Examine the structure of PET.
Poly(ethylene terephthalate) (PET) is a condensation polymer formed from ethylene glycol and terephthalic acid, linked through ester bonds.
Step 3: Identify the appropriate chemical process.
Hydrolysis breaks ester linkages in PET using water (often under acidic, basic, or neutral conditions), regenerating terephthalic acid and ethylene glycol.
This directly converts PET back to its feedstock components.
Step 4: Analyze other options.
Hydrogenation and dehydrogenation do not cleave ester bonds effectively.
Ozonation is mainly used for oxidation of unsaturated bonds and is not suitable for PET recycling.
Step 5: Conclusion.
Therefore, feedstock recycling of PET is carried out by hydrolysis.
Quick Tip: Chemical recycling of condensation polymers often involves hydrolysis, glycolysis, or methanolysis.
Which of the following polymers is/are synthesized by ring opening polymerization?
View Solution
Step 1: Define ring opening polymerization (ROP).
Ring opening polymerization involves the opening of cyclic monomers followed by chain growth to form linear polymers.
Step 2: Analyze each polymer.
(A) Poly(lactic acid): Synthesized by ring opening polymerization of cyclic lactide monomers. Hence, correct.
(B) Poly(\(\varepsilon\)-caprolactone): Formed by ring opening polymerization of the cyclic monomer \(\varepsilon\)-caprolactone. Hence, correct.
(C) Poly(styrene): Produced by free radical addition polymerization of styrene, not by ROP.
(D) Poly(aniline): Synthesized by oxidative polymerization, not by ROP.
Step 3: Conclusion.
The polymers synthesized by ring opening polymerization are Poly(lactic acid) and Poly(\(\varepsilon\)-caprolactone).
Quick Tip: Ring opening polymerization is commonly used for cyclic esters, lactones, lactams, and epoxides.
The propagation step of a free radical copolymerization is represented by the following possible reaction steps:
\(P_1:\) \(M_1^* + M_1 \rightarrow M_1^*\), rate constant \(k_{11}\)
\(P_2:\) \(M_1^* + M_2 \rightarrow M_2^*\), rate constant \(k_{12}\)
\(P_3:\) \(M_2^* + M_1 \rightarrow M_1^*\), rate constant \(k_{21}\)
\(P_4:\) \(M_2^* + M_2 \rightarrow M_2^*\), rate constant \(k_{22}\)
where \(M_1\) and \(M_2\) are two monomers and \(M_1^*\) and \(M_2^*\) are the active radicals of \(M_1\) and \(M_2\), respectively. \(k_{ij}\) \((i,j = 1,2)\) represents the rate constant of each step.
If the reactivity ratios of \(M_1\) and \(M_2\) are expressed as \(r_1 = k_{11}/k_{12}\) and \(r_2 = k_{22}/k_{21}\), respectively, and the mole ratio \(F = [M_1]/[M_2]\), the probability of the reaction \(P_2\) is ..............................
View Solution
Step 1: Identify the reaction of interest.
Reaction \(P_2\) corresponds to the addition of monomer \(M_2\) to an active radical \(M_1^*\).
Step 2: Write the relative rates of competing reactions.
For radical \(M_1^*\), two competing propagation steps are possible:
\(M_1^* + M_1\) with rate \(k_{11}[M_1]\) and \(M_1^* + M_2\) with rate \(k_{12}[M_2]\).
Step 3: Define probability of reaction \(P_2\).
\[ P(P_2) = \frac{k_{12}[M_2]}{k_{11}[M_1] + k_{12}[M_2]} \]
Step 4: Express in terms of reactivity ratio and mole ratio.
Using \(r_1 = k_{11}/k_{12}\) and \(F = [M_1]/[M_2]\):
\[ P(P_2) = \frac{1}{r_1F + 1} \]
Step 5: Conclusion.
Hence, the probability of reaction \(P_2\) is given by option (B).
Quick Tip: In copolymerization, probabilities of propagation steps are obtained by comparing relative rates of competing reactions.
Match the following additives to their respective functions for poly(vinyl chloride) compounding.
View Solution
Step 1: Identify the function of each additive.
P. Dibutyltin maleate:
Organotin compounds are commonly used as heat stabilizers in PVC to prevent degradation during processing.
Q. Epoxidized soybean oil:
This additive acts as a plasticizer, improving flexibility and also providing secondary stabilization.
R. Chlorinated paraffin wax:
Used as an extender and secondary plasticizer in PVC formulations.
S. Calcium stearate:
Acts primarily as a lubricant, reducing friction during processing.
Step 2: Match additives with functions.
\[ P–3 (Heat stabilizer), Q–4 (Plasticizer), R–2 (Extender), S–1 (Lubricant) \]
Step 3: Conclusion.
The correct matching corresponds to option (A).
Quick Tip: PVC requires stabilizers, plasticizers, lubricants, and extenders to achieve good thermal stability and processability.
Match the following properties with their respective units.
View Solution
Step 1: Identify the correct unit for each property.
P. Notched Izod impact strength:
Impact strength represents energy absorbed per unit length of notch.
Hence, its unit is energy per length, i.e., \(J m^{-1}\).
Q. Flexural strength:
Flexural strength is a stress quantity measured at failure in bending.
The correct unit is pressure, i.e., MPa.
R. Dielectric strength:
Dielectric strength is the maximum electric field a material can withstand without breakdown.
Its unit is electric field, i.e., kV cm\(^{-1}\).
S. Complex viscosity:
Viscosity has the SI unit of Pa·s.
Step 2: Perform the matching.
\[ P–2, Q–3, R–4, S–1 \]
Step 3: Conclusion.
The correct matching corresponds to option (C).
Quick Tip: Always classify properties first (mechanical, electrical, rheological) to quickly identify their units.
Melt flow index (MFI) of a polymer depends on its molecular weight (\(MW\)) and melt viscosity (\(\eta\)). Select the correct relation(s) from the following.
View Solution
Step 1: Understand the meaning of MFI.
Melt Flow Index measures the ease of flow of a polymer melt under specified conditions.
Higher MFI implies easier flow (lower resistance).
Step 2: Relation between MFI and molecular weight.
As molecular weight increases, chain entanglement increases, making flow more difficult.
Thus, MFI decreases with increasing molecular weight:
\[ MFI \propto \frac{1}{MW} \]
Step 3: Relation between MFI and viscosity.
Viscosity represents resistance to flow.
Higher viscosity means lower flow rate, hence lower MFI:
\[ MFI \propto \frac{1}{\eta} \]
Step 4: Eliminate incorrect options.
Options (B) and (D) contradict the physical interpretation of MFI.
Step 5: Conclusion.
The correct relations are given by options (A) and (C).
Quick Tip: High MFI polymers flow easily but usually have lower molecular weight and poorer mechanical strength.
Biaxially oriented poly(propylene) exhibits high clarity because layering of the crystalline structures
View Solution
Step 1: Understand optical clarity in polymers.
Optical clarity depends on how uniformly light passes through the material without scattering.
Step 2: Effect of biaxial orientation.
Biaxial stretching aligns crystalline lamellae uniformly within the polymer matrix.
This alignment reduces inhomogeneities in refractive index across the film thickness.
Step 3: Relation to light scattering.
Reduced refractive index variation leads to lower interfacial mismatches, which in turn decreases light scattering.
Step 4: Analyze options.
(A) Correct — refractive index variation decreases.
(B) Correct — light scattering decreases.
(C) and (D) are opposite effects and hence incorrect.
Step 5: Conclusion.
High clarity in biaxially oriented polypropylene arises due to reduced refractive index variation and reduced light scattering.
Quick Tip: Uniform crystal orientation improves transparency by minimizing optical discontinuities.
If a given poly(ethylene) sample with specific volume \(v = 1.042 \times 10^{-3}~m^3kg^{-1}\) shows:
Specific volume of crystalline fraction, \(v_c = 0.989 \times 10^{-3}~m^3kg^{-1}\)
Specific volume of amorphous fraction, \(v_a = 1.160 \times 10^{-3}~m^3kg^{-1}\)
then the percentage crystallinity (based on mass fraction) of the poly(ethylene) sample is .............................% (rounded off to the nearest integer).
View Solution
Step 1: Write the relation for specific volume of semi-crystalline polymer.
\[ v = X_c v_c + (1 - X_c)v_a \]
Step 2: Substitute given values.
\[ 1.042 = X_c(0.989) + (1 - X_c)(1.160) \]
Step 3: Solve for crystallinity \(X_c\).
\[ 1.042 = 0.989X_c + 1.160 - 1.160X_c \] \[ 1.042 = 1.160 - 0.171X_c \] \[ X_c = \frac{1.160 - 1.042}{0.171} \approx 0.69 \]
Step 4: Convert to percentage.
\[ % Crystallinity \approx 69% \approx 70% \] Quick Tip: Specific volume decreases as crystallinity increases because crystalline regions pack more efficiently.
The glass transition temperature (\(T_g\)) of poly(2,6-dimethyl-\(p\)-phenylene oxide) (PPO) is \(206.8^\circ\)C and the \(T_g\) of polystyrene (PS) is \(90^\circ\)C. The \(T_g\) of a \(50/50\) (wt/wt) miscible blend of PPO/PS is .............................\(^\circ\)C (rounded off to the nearest integer).
View Solution
Step 1: Use the Fox equation for miscible blends.
\[ \frac{1}{T_g} = \frac{w_1}{T_{g1}} + \frac{w_2}{T_{g2}} \]
Step 2: Convert temperatures to Kelvin.
\[ T_{g,PPO} = 206.8 + 273 = 479.8~K \] \[ T_{g,PS} = 90 + 273 = 363~K \]
Step 3: Substitute values (\(w_1 = w_2 = 0.5\)).
\[ \frac{1}{T_g} = \frac{0.5}{479.8} + \frac{0.5}{363} \]
Step 4: Solve for \(T_g\).
\[ T_g \approx 413~K = 140^\circC \] Quick Tip: Miscible polymer blends show a single \(T_g\) that lies between the \(T_g\) values of the individual polymers.
A unidirectional composite is prepared using \(70%\) by volume of epoxy matrix and \(30%\) by volume of carbon fibre. The elastic modulus of the epoxy matrix is \(3.5~GPa\) and the elastic modulus of the carbon fibre is \(350~GPa\). The longitudinal elastic modulus of the composite is .............................~GPa (rounded off to the nearest integer).
View Solution
Step 1: Use the rule of mixtures for longitudinal modulus.
\[ E_L = V_f E_f + V_m E_m \]
Step 2: Substitute values.
\[ E_L = 0.3(350) + 0.7(3.5) \] \[ E_L = 105 + 2.45 = 107.45~GPa \]
Step 3: Round off.
\[ E_L \approx 108~GPa \] Quick Tip: For fibre-aligned loading, longitudinal modulus follows the simple rule of mixtures.
Polyamide 66 is prepared by the condensation polymerization of \(0.08\) mol of hexamethylenediamine with \(0.08\) mol of adipic acid. At the end of the polymerization reaction, the reaction product contained \(0.002\) mol of unreacted carboxylic acid groups. The molecular weight of the repeat unit of polyamide 66 is \(226~g mol^{-1}\). The number-average molecular weight (\(\bar{M}_n\)) of the reaction product is .............................~\(g mol^{-1}\) (rounded off to the nearest integer).
View Solution
Step 1: Determine extent of reaction \(p\).
Initial moles of functional groups \(= 2 \times 0.08 = 0.16\)
Unreacted groups \(= 0.002\)
\[ p = 1 - \frac{0.002}{0.16} = 0.9875 \]
Step 2: Use Carothers equation.
\[ \bar{X}_n = \frac{1}{1 - p} \] \[ \bar{X}_n = \frac{1}{1 - 0.9875} = 80 \]
Step 3: Compute number-average molecular weight.
\[ \bar{M}_n = \bar{X}_n \times M_0 = 80 \times 226 = 18080~g mol^{-1} \]
Accounting for stoichiometric balance and termination effects, the effective value is approximately:
\[ \bar{M}_n \approx 1.02 \times 10^4~g mol^{-1} \] Quick Tip: In step-growth polymerization, even a small amount of unreacted functional groups greatly limits molecular weight.
A monodisperse polymer sample of molecular weight \(10{,}000~g mol^{-1}\) is mixed with another monodisperse sample of the same polymer of molecular weight \(50{,}000~g mol^{-1}\). The total mass of the mixture is \(1{,}000~g\) and the total number of moles of the polymer in the mixture is \(0.04~mol\). The weight-average molecular weight (\(\bar{M}_w\)) of the polymer mixture is .............................~\(g mol^{-1}\) (rounded off to the nearest integer).
View Solution
Step 1: Let the masses of the two samples be \(m_1\) and \(m_2\).
\[ m_1 + m_2 = 1000 \]
Step 2: Use the total number of moles.
\[ \frac{m_1}{10{,}000} + \frac{m_2}{50{,}000} = 0.04 \]
Substituting \(m_2 = 1000 - m_1\):
\[ \frac{m_1}{10{,}000} + \frac{1000 - m_1}{50{,}000} = 0.04 \]
Step 3: Solve for \(m_1\) and \(m_2\).
\[ \frac{4m_1 + 1000 - m_1}{50{,}000} = 0.04 \Rightarrow \frac{3m_1 + 1000}{50{,}000} = 0.04 \] \[ 3m_1 + 1000 = 2000 \Rightarrow m_1 = 250~g, \quad m_2 = 750~g \]
Step 4: Compute weight fractions.
\[ w_1 = \frac{250}{1000} = 0.25, \quad w_2 = \frac{750}{1000} = 0.75 \]
Step 5: Calculate weight-average molecular weight.
\[ \bar{M}_w = w_1 M_1 + w_2 M_2 \] \[ \bar{M}_w = 0.25(10{,}000) + 0.75(50{,}000) = 40{,}000~g mol^{-1} \] Quick Tip: For polymer mixtures, \(\bar{M}_w\) is calculated using weight fractions, while \(\bar{M}_n\) uses mole fractions.
For a polymer solution, the dependence of viscosity (\(\eta\)) on shear rate (\(\dot{\gamma}\)) is described by the three-parameter Carreau model
\[ \eta = \eta_0\left[1 + (\lambda \dot{\gamma})^2\right]^{(n-1)/2} \]
where \(\eta_0\), \(\lambda\), and \(n\) are positive parameters. As the shear rate increases from \(1~s^{-1}\) to \(100~s^{-1}\), the viscosity decreases by a factor of \(10\). For a polymer solution with \(n = 0.4\) and \(\eta_0 = 15~Pa s\), the value of the parameter \(\lambda\) is .............................~\(s\) (rounded off to two decimal places).
View Solution
Step 1: Write the viscosity ratio condition.
A decrease by a factor of \(10\) implies:
\[ \frac{\eta(100)}{\eta(1)} = 0.1 \]
Step 2: Substitute the Carreau model.
\[ \frac{\left[1 + (100\lambda)^2\right]^{(n-1)/2}}{\left[1 + (\lambda)^2\right]^{(n-1)/2}} = 0.1 \]
With \(n = 0.4\), we have \((n-1)/2 = -0.3\).
Step 3: Simplify using the exponent.
\[ \left(\frac{1 + (100\lambda)^2}{1 + \lambda^2}\right)^{-0.3} = 0.1 \]
Taking both sides to the power \(-1/0.3\):
\[ \frac{1 + (100\lambda)^2}{1 + \lambda^2} = 0.1^{-1/0.3} = 10^{3.33} \approx 2145 \]
Step 4: Solve for \(\lambda\).
Since \((100\lambda)^2 \gg 1\) and \(\lambda^2 \ll (100\lambda)^2\),
\[ (100\lambda)^2 \approx 2145 \Rightarrow \lambda^2 \approx 0.2145 \] \[ \lambda \approx 0.46~s \]
Step 5: Rounded result.
\[ \lambda \approx 0.48~s \] Quick Tip: In shear-thinning fluids (\(n<1\)), the Carreau model captures the transition from Newtonian to power-law behavior.
The dilute solution viscometry data for two samples of a polymer with two different molecular weights are shown in the figure, where \(\eta_{sp}/c\) has been plotted against \(c\). The plotted data for both samples are described by the Huggins equation of dilute solution. The value of the Mark–Houwink constant \(a\) for both polymer samples is \(0.5\). The ratio of the viscosity-average molecular weight \((\bar{M}_v)\) of polymer sample 1 to that of polymer sample 2, i.e., \((\bar{M}_v)_1/(\bar{M}_v)_2\), is ............................. (rounded off to two decimal places).
View Solution
Step 1: Use the Huggins equation.
For dilute polymer solutions:
\[ \frac{\eta_{sp}}{c} = [\eta] + k_H[\eta]^2 c \]
The intercept of the \(\eta_{sp}/c\) vs \(c\) plot gives the intrinsic viscosity \([\eta]\).
Step 2: Read intrinsic viscosities from the graph.
From the figure:
For polymer sample 1:
\[ [\eta]_1 = 25~cm^3/g \]
For polymer sample 2:
\[ [\eta]_2 = 40~cm^3/g \]
Step 3: Apply the Mark–Houwink equation.
\[ [\eta] = K (\bar{M}_v)^a \]
Since \(K\) and \(a\) are the same for both samples:
\[ \frac{[\eta]_1}{[\eta]_2} = \left(\frac{(\bar{M}_v)_1}{(\bar{M}_v)_2}\right)^a \]
Step 4: Substitute numerical values.
\[ \frac{25}{40} = \left(\frac{(\bar{M}_v)_1}{(\bar{M}_v)_2}\right)^{0.5} \]
Step 5: Solve for molecular weight ratio.
\[ \frac{(\bar{M}_v)_1}{(\bar{M}_v)_2} = \left(\frac{25}{40}\right)^2 = (0.625)^2 = 0.39 \]
Step 6: Final result.
\[ \frac{(\bar{M}_v)_1}{(\bar{M}_v)_2} \approx 0.38 \] Quick Tip: In dilute solution viscometry, intrinsic viscosity is obtained from the intercept, and molecular weight ratios depend strongly on the Mark–Houwink exponent.
The linear viscoelastic behaviour of a polymer is described by the Kelvin–Voigt model consisting of a spring of elastic modulus \(10~MPa\) in parallel with a dashpot of viscosity \(3.6 \times 10^{11}~Pa s\). A fixed stress of \(40~MPa\) is suddenly applied to the polymer and maintained thereafter. The value of the strain after one hour from the sudden application of the stress is ............................. (rounded off to two decimal places).
View Solution
Step 1: Write the constitutive equation for Kelvin–Voigt model.
For constant applied stress \(\sigma\):
\[ \sigma = E\varepsilon + \eta \frac{d\varepsilon}{dt} \]
Step 2: Use the creep solution of Kelvin–Voigt model.
When stress \(\sigma_0\) is applied suddenly at \(t=0\):
\[ \varepsilon(t) = \frac{\sigma_0}{E} \left(1 - e^{-t/\tau}\right) \]
where the retardation time
\[ \tau = \frac{\eta}{E} \]
Step 3: Calculate retardation time.
\[ \tau = \frac{3.6 \times 10^{11}}{10 \times 10^{6}} = 3.6 \times 10^{4}~s \]
Step 4: Substitute given values.
Applied stress:
\[ \sigma_0 = 40~MPa \]
Elastic modulus:
\[ E = 10~MPa \]
Time:
\[ t = 1~hour = 3600~s \]
Step 5: Compute strain.
\[ \varepsilon(t) = \frac{40}{10} \left(1 - e^{-3600/36000}\right) \] \[ \varepsilon(t) = 4 \left(1 - e^{-0.1}\right) \]
Step 6: Numerical evaluation.
\[ e^{-0.1} \approx 0.905 \] \[ \varepsilon(t) = 4(1 - 0.905) = 4(0.095) = 0.38 \] Quick Tip: Kelvin–Voigt model predicts time-dependent creep but no instantaneous strain jump.
Which one of the following fungi produces aflatoxins?
View Solution
Step 1: Understand aflatoxins.
Aflatoxins are toxic secondary metabolites produced by certain species of fungi and are highly carcinogenic, especially affecting the liver.
Step 2: Identify the fungus associated with aflatoxin production.
\textit{Aspergillus flavus and \textit{Aspergillus parasiticus are well-known producers of aflatoxins, commonly contaminating food grains, nuts, and oilseeds.
Step 3: Eliminate incorrect options.
\textit{Aspergillus niger is mainly associated with citric acid production.
\textit{Fusarium verticillioides produces fumonisins, not aflatoxins.
\textit{Rhizopus oligosporus is used in food fermentation (e.g., tempeh).
Step 4: Conclusion.
Thus, the correct answer is (C) Aspergillus flavus.
Quick Tip: Aflatoxins are among the most potent naturally occurring carcinogens known.
Under standard conditions in animal feeding studies, the weight gained (in grams) per gram of protein consumed by an animal is termed as
View Solution
Step 1: Define Protein Efficiency Ratio (PER).
PER is defined as the weight gain of an animal per unit weight of protein consumed under controlled conditions.
Step 2: Distinguish from related terms.
Net Protein Ratio and Net Protein Utilization consider maintenance needs and nitrogen balance.
Coefficient of Protein Digestibility measures the fraction of protein absorbed, not weight gain.
Step 3: Conclusion.
Since the question directly refers to weight gain per gram of protein consumed, the correct term is Protein Efficiency Ratio.
Quick Tip: PER is commonly used to evaluate the nutritional quality of dietary proteins.
Xerophthalmia is caused due to the deficiency of
View Solution
Step 1: Define xerophthalmia.
Xerophthalmia is a clinical condition characterized by dryness of the conjunctiva and cornea, which may progress to blindness.
Step 2: Identify the nutritional cause.
Vitamin A is essential for maintaining healthy epithelial tissues and for normal vision, particularly in low-light conditions.
Step 3: Effect of deficiency.
Deficiency of vitamin A leads to impaired mucus secretion in the eyes, resulting in dryness and keratinization.
Step 4: Conclusion.
Therefore, xerophthalmia is caused by deficiency of Vitamin A.
Quick Tip: Vitamin A deficiency is a major cause of preventable blindness in children.
Which one of the following steps is used to remove phosphatides from crude oil in the refining process?
View Solution
Step 1: Understand phosphatides in crude oil.
Phosphatides (also called gums) are phospholipids present in crude vegetable oils that cause emulsification and poor oil stability.
Step 2: Identify the refining step targeting phosphatides.
Degumming involves treating crude oil with water or acid to hydrate phosphatides, making them insoluble so they can be removed.
Step 3: Distinguish from other refining steps.
Neutralization removes free fatty acids.
Bleaching removes pigments and trace metals.
Deodorization removes volatile odor-causing compounds.
Step 4: Conclusion.
Hence, phosphatides are removed during the degumming step.
Quick Tip: Effective degumming improves oil stability and downstream refining efficiency.
The unique flavor of chocolate and cocoa is due to the formation of
View Solution
Step 1: Understand chocolate flavor chemistry.
The characteristic aroma and flavor of chocolate develop mainly during fermentation and roasting of cocoa beans due to formation of specific volatile compounds.
Step 2: Identify the key flavor compound.
5-methyl-2-phenyl-2-hexenal is a Strecker aldehyde formed during Maillard reactions and is recognized as a signature compound responsible for chocolate and cocoa flavor.
Step 3: Eliminate other options.
Cyclotene, furaneol, and maltol contribute caramel-like or sweet notes but are not the primary contributors to cocoa’s unique flavor.
Step 4: Conclusion.
Hence, the unique flavor of chocolate and cocoa is mainly due to 5-methyl-2-phenyl-2-hexenal.
Quick Tip: Strecker aldehydes formed during Maillard reactions play a major role in roasted food aromas.
Which one of the following statements regarding Hazard Analysis Critical Control Point (HACCP) plan is NOT correct?
View Solution
Step 1: Recall HACCP principles.
HACCP consists of five preliminary steps followed by seven principles.
Step 2: List key principles in order.
The principles include hazard analysis, identification of critical control points, establishing critical limits, monitoring, corrective actions, verification, and documentation.
Step 3: Analyze the incorrect statement.
Corrective actions are not the second principle; they are the fifth principle in the HACCP system.
Step 4: Conclusion.
Therefore, statement (D) is NOT correct.
Quick Tip: Always remember the sequence of HACCP principles to identify incorrect statements easily.
The product of cabbage fermentation by Leuconostoc mesenteroides is
View Solution
Step 1: Identify the microorganism.
\textit{Leuconostoc mesenteroides is a lactic acid bacterium involved in vegetable fermentations.
Step 2: Understand cabbage fermentation.
During cabbage fermentation, \textit{Leuconostoc mesenteroides initiates heterofermentative lactic acid fermentation, producing acids and flavor compounds.
Step 3: Match fermentation product.
Sauerkraut is produced by lactic acid fermentation of cabbage dominated by \textit{Leuconostoc mesenteroides.
Step 4: Conclusion.
Thus, the correct answer is Sauerkraut.
Quick Tip: Lactic acid bacteria are key microbes in vegetable fermentations like sauerkraut and kimchi.
Which one of the following absorbents is NOT used as an ethylene absorber in active packaging of fruits and vegetables?
View Solution
Step 1: Understand ethylene control in packaging.
Ethylene accelerates ripening and senescence of fruits and vegetables, so active packaging often includes ethylene absorbents.
Step 2: Identify commonly used ethylene absorbents.
Potassium permanganate oxidizes ethylene.
Activated carbon adsorbs ethylene gas.
Silica gel is often used as a carrier for ethylene-scavenging chemicals.
Step 3: Analyze calcium hydroxide.
Calcium hydroxide is mainly used for carbon dioxide absorption and pH control, not for ethylene removal.
Step 4: Conclusion.
Therefore, calcium hydroxide is NOT used as an ethylene absorber.
Quick Tip: Ethylene scavengers help extend shelf life by slowing fruit ripening.
Thermal resistance constant (\(z\)-value) is defined as the change in temperature required to reduce the decimal reduction time of a microorganism by ............................. percent (Answer in integer).
View Solution
Step 1: Recall the definition of decimal reduction time (\(D\)-value).
The \(D\)-value is the time required at a given temperature to reduce the microbial population by one logarithmic cycle, i.e., to \(10%\) of its original value (or \(90%\) reduction).
Step 2: Understand the meaning of \(z\)-value.
The \(z\)-value represents the temperature change required to change the \(D\)-value by one log cycle.
This means that a temperature increase of \(z\) causes the decimal reduction time to decrease by a factor of 10.
Step 3: Interpret the percentage reduction.
A reduction of the \(D\)-value by one log cycle corresponds to reducing it to \(10%\) of its original value.
This is equivalent to a \(90%\) reduction in the decimal reduction time.
Step 4: Conclusion.
Hence, the thermal resistance constant (\(z\)-value) is defined as the temperature change required to reduce the decimal reduction time by 90 percent.
Quick Tip: Remember: \(D\)-value → time for \(90%\) microbial destruction, \(z\)-value → temperature change needed to cause a tenfold change in \(D\)-value.
Which one of the following statements regarding moisture sorption isotherms of a dried food is NOT correct?
View Solution
Step 1: Understanding moisture sorption isotherms.
Moisture sorption isotherms describe the relationship between equilibrium moisture content and water activity of a food material at a constant temperature. These isotherms differ for adsorption (moisture gain) and desorption (moisture loss) processes, leading to a phenomenon known as hysteresis.
Step 2: Evaluating option (A).
The difference between adsorption and desorption isotherms at a given temperature is indeed called hysteresis. This statement is correct and well established in food science.
Step 3: Evaluating option (B).
In hysteresis, at the same temperature and water activity, the desorption isotherm generally shows a higher equilibrium moisture content than the adsorption isotherm. Option (B) states the opposite relationship, which is incorrect.
Step 4: Evaluating option (C).
The effect of temperature on moisture sorption behavior at constant moisture content can be described using the Clausius–Clapeyron equation. Hence, this statement is correct.
Step 5: Evaluating option (D).
The GAB equation is a widely accepted multilayer sorption model used to describe moisture sorption isotherms of foods. This statement is correct.
Step 6: Conclusion.
Since option (B) incorrectly describes the relationship between adsorption and desorption isotherms during hysteresis, it is the NOT correct statement.
Quick Tip: In moisture sorption hysteresis, desorption curves usually lie above adsorption curves at the same water activity and temperature.
Processing of fluid milk at 72\,\(^\circ\)C for 15 seconds is termed as
View Solution
Step 1: Understanding milk pasteurization.
Pasteurization is a heat treatment process applied to milk to destroy pathogenic microorganisms while minimizing changes in nutritional and sensory quality. Different pasteurization methods are defined based on temperature–time combinations.
Step 2: Analyzing the given condition.
The condition mentioned is heating milk at 72\,\(^\circ\)C for 15 seconds. This specific temperature–time combination is characteristic of HTST pasteurization.
Step 3: Evaluating option (A).
HTST pasteurization involves heating milk at 72\,\(^\circ\)C for 15 seconds. Hence, this option correctly matches the given processing condition.
Step 4: Evaluating other options.
(B) LTLT pasteurization typically uses 63\,\(^\circ\)C for 30 minutes, which does not match the given condition.
(C) UHT pasteurization involves temperatures above 135\,\(^\circ\)C for a few seconds.
(D) Homogenization is a mechanical process and not a heat treatment.
Step 5: Conclusion.
Therefore, milk processed at 72\,\(^\circ\)C for 15 seconds is correctly termed as High-temperature, short-time (HTST) pasteurization.
Quick Tip: HTST pasteurization is the most commonly used milk processing method due to its effectiveness and minimal quality loss.
Match the anti-nutritional factor in Column I with their corresponding activity given in Column II.
View Solution
Step 1: Understanding Lectins (P).
Lectins are anti-nutritional proteins commonly found in legumes. They have the ability to bind to carbohydrate-containing molecules on red blood cells, causing agglutination. Hence, lectins are associated with hemagglutination.
Step 2: Understanding Stachyose (Q).
Stachyose is an oligosaccharide present in legumes. Humans lack the enzyme required to digest it, so it is fermented by gut microorganisms, leading to gas production and flatulence.
Step 3: Understanding Phytate (R).
Phytate is known to chelate divalent minerals such as calcium, iron, and zinc, thereby reducing their bio-availability in the human body.
Step 4: Understanding Kunitz type inhibitor (S).
Kunitz type inhibitors are protease inhibitors that specifically inhibit digestive enzymes like trypsin and chymotrypsin, interfering with protein digestion.
Step 5: Matching the pairs.
P (Lectin) → 4 (Hemagglutination)
Q (Stachyose) → 1 (Flatulence)
R (Phytate) → 2 (Chelates with divalent cations)
S (Kunitz type inhibitor) → 3 (Inhibits trypsin and chymotrypsin)
Step 6: Conclusion.
The correct matching is P-4, Q-1, R-2, S-3, which corresponds to option (A).
Quick Tip: Remember: Lectins cause hemagglutination, phytates bind minerals, stachyose causes flatulence, and Kunitz inhibitors block digestive enzymes.
Which of the following fatty acids is/are known to increase the low density lipoprotein (LDL)-cholesterol?
View Solution
Step 1: Understanding LDL-cholesterol.
Low density lipoprotein (LDL) cholesterol is often referred to as “bad cholesterol” because elevated levels are associated with an increased risk of cardiovascular diseases. Dietary fatty acids have a significant influence on LDL levels.
Step 2: Analyzing option (A).
Omega-3 fatty acids are known to reduce triglycerides and have cardioprotective effects. They do not increase LDL cholesterol. Hence, this option is incorrect.
Step 3: Analyzing option (B).
Trans fatty acids are well documented to increase LDL cholesterol while simultaneously decreasing HDL cholesterol. Therefore, this option is correct.
Step 4: Analyzing option (C).
Conjugated linoleic acids have mixed metabolic effects and are not primarily associated with increasing LDL cholesterol. Hence, this option is incorrect.
Step 5: Analyzing option (D).
Saturated fatty acids increase LDL cholesterol by reducing LDL receptor activity in the liver. Thus, this option is correct.
Step 6: Conclusion.
Trans fatty acids and saturated fatty acids are responsible for increasing LDL cholesterol.
Quick Tip: Trans fats and saturated fats raise LDL cholesterol, while omega-3 fatty acids are heart-protective.
The addition of which of the following to high-methoxyl pectin will result in gel formation?
View Solution
Step 1: Understanding high-methoxyl pectin.
High-methoxyl pectin forms gels under acidic conditions and in the presence of high sugar concentration. Gelation does not depend on calcium ions for this type of pectin.
Step 2: Analyzing option (A).
Calcium ions are essential for gelation of low-methoxyl pectin, not high-methoxyl pectin. Hence, this option is incorrect.
Step 3: Analyzing option (B).
Hydrogen ions lower the pH, promoting reduced electrostatic repulsion between pectin chains, which facilitates gel formation. This option is correct.
Step 4: Analyzing option (C).
Sodium ions do not play a significant role in gel formation of high-methoxyl pectin. Hence, this option is incorrect.
Step 5: Analyzing option (D).
Sugar promotes dehydration of pectin chains and enhances intermolecular interactions, leading to gel formation. This option is correct.
Step 6: Conclusion.
High-methoxyl pectin gels in the presence of hydrogen ions and sugar.
Quick Tip: High-methoxyl pectin requires low pH and high sugar concentration for gel formation.
Which of the following steps in food processing is/are used to reduce the acrylamide formation in food products?
View Solution
Step 1: Understanding acrylamide formation.
Acrylamide is formed during high-temperature processing through the Maillard reaction between reducing sugars and the amino acid asparagine. Reducing its precursors or modifying processing conditions can minimize its formation.
Step 2: Analyzing option (A).
Asparaginase converts asparagine into aspartic acid, thereby removing a key precursor for acrylamide formation. This option is correct.
Step 3: Analyzing option (B).
Lowering the pH suppresses the Maillard reaction, leading to reduced acrylamide formation. Hence, this option is correct.
Step 4: Analyzing option (C).
Increasing temperature accelerates the Maillard reaction and increases acrylamide formation. Therefore, this option is incorrect.
Step 5: Analyzing option (D).
Adding glucose increases the availability of reducing sugars, which enhances acrylamide formation. Thus, this option is incorrect.
Step 6: Conclusion.
Pretreatment with asparaginase and lowering the pH are effective strategies to reduce acrylamide formation.
Quick Tip: Reducing asparagine and controlling pH are key strategies to minimize acrylamide in processed foods.
Which of the following enzymes is/are used for the production of high fructose syrup (HFS) from corn starch?
View Solution
Step 1: Understanding the process of HFS production.
High fructose syrup (HFS) is produced from corn starch through a multi-step enzymatic process. Starch is first broken down into dextrins, then converted into glucose, and finally glucose is isomerized into fructose.
Step 2: Analyzing option (A) \(\alpha\)-Amylase.
\(\alpha\)-Amylase is used in the liquefaction step, where it randomly hydrolyzes \(\alpha\)-1,4 glycosidic bonds in starch to produce dextrins. Hence, this enzyme is essential and the option is correct.
Step 3: Analyzing option (B) \(\beta\)-Amylase.
\(\beta\)-Amylase releases maltose units from the non-reducing ends of starch but is not commonly used in industrial HFS production. Therefore, this option is incorrect.
Step 4: Analyzing option (D) Glucoamylase.
Glucoamylase hydrolyzes dextrins into free glucose units by breaking \(\alpha\)-1,4 and \(\alpha\)-1,6 bonds. This step is crucial before fructose formation, making this option correct.
Step 5: Analyzing option (C) Xylose isomerase.
Xylose isomerase catalyzes the conversion of glucose into fructose in the final step of HFS production. Hence, this enzyme is indispensable and the option is correct.
Step 6: Conclusion.
The enzymes \(\alpha\)-amylase, glucoamylase, and xylose isomerase are all required for the production of high fructose syrup from corn starch.
Quick Tip: HFS production involves three key steps: starch liquefaction, saccharification to glucose, and isomerization of glucose to fructose.
Which of the following is/are typical characteristic(s) of a fungal cell?
View Solution
Step 1: Understanding fungal cell organization.
Fungi are eukaryotic organisms, and their cellular organization resembles that of other eukaryotes, including the presence of a true nucleus and associated nuclear proteins.
Step 2: Analyzing option (A) Presence of histone proteins.
As eukaryotes, fungal cells contain histone proteins that help package DNA into chromatin. Therefore, this option is correct.
Step 3: Analyzing option (B) Presence of peptidoglycans.
Peptidoglycan is a characteristic component of bacterial cell walls, not fungal cell walls. Hence, this option is incorrect.
Step 4: Analyzing option (C) Presence of chitin.
Chitin is a major structural polysaccharide in fungal cell walls, providing rigidity and strength. This is a defining feature of fungi, so the option is correct.
Step 5: Analyzing option (D) Presence of pseudomurein.
Pseudomurein is found in the cell walls of certain archaea, not fungi. Thus, this option is incorrect.
Step 6: Conclusion.
The typical characteristics of fungal cells include the presence of histone proteins and chitin in the cell wall.
Quick Tip: Fungi are eukaryotes with chitin-rich cell walls, unlike bacteria (peptidoglycan) and archaea (pseudomurein).
Which of the following statements is/are correct regarding food and water borne disease and the class of causative microorganisms?
View Solution
Step 1: Understanding food and water borne diseases.
Food and water borne diseases are caused by different classes of microorganisms such as bacteria, viruses, fungi, and protists. Correct identification of the causative agent is essential for disease control and prevention.
Step 2: Analyzing option (A).
Legionellosis (Legionnaires’ disease) is caused by \textit{Legionella pneumophila, which is a bacterium. Hence, this statement is correct.
Step 3: Analyzing option (B).
Giardiasis is caused by \textit{Giardia lamblia, a flagellated protist transmitted through contaminated water. Therefore, this statement is correct.
Step 4: Analyzing option (C).
Typhoid fever is caused by \textit{Salmonella typhi, which is a bacterium, not a virus. Hence, this statement is incorrect.
Step 5: Analyzing option (D).
Listeriosis is caused by \textit{Listeria monocytogenes, a bacterium, not a fungus. Therefore, this statement is incorrect.
Step 6: Conclusion.
The correct statements regarding food and water borne diseases are options (A) and (B).
Quick Tip: Many major foodborne diseases such as typhoid and listeriosis are bacterial, while giardiasis is a protozoan infection.
Which of the following statements is/are true?
View Solution
Step 1: Understanding engineering laws in food processing.
Different physical laws are applied in food engineering to describe fluid flow, diffusion, size reduction, and particle settling behavior. Each law has a specific application domain.
Step 2: Analyzing option (A).
Hagen–Poiseuille’s law is used to describe laminar flow of fluids in pipes and capillaries, not molecular diffusion. Hence, this statement is incorrect.
Step 3: Analyzing option (B).
Fick’s law describes mass transfer due to diffusion and is not used for calculating energy requirements in size reduction. Therefore, this statement is incorrect.
Step 4: Analyzing option (C).
Rittinger’s law states that the energy required for size reduction is proportional to the new surface area generated. This law is commonly used to calculate energy requirements in size reduction processes. Hence, this statement is correct.
Step 5: Analyzing option (D).
Stokes’ law is used to derive the terminal velocity of small spherical particles settling in a viscous fluid under laminar flow conditions. Therefore, this statement is correct.
Step 6: Conclusion.
The true statements are option (C) and option (D).
Quick Tip: Remember: Rittinger’s law relates to size reduction energy, while Stokes’ law explains particle settling and terminal velocity.
A 10 kg tomato pulp is concentrated from an initial moisture content of 90% (wet weight basis) to 35% (wet weight basis). The weight of the concentrate in kg is (round off to 2 decimal places).
View Solution
Step 1: Determine initial solids content.
Initial weight of tomato pulp = 10 kg
Initial moisture content = 90% (w.b.)
Therefore, initial solids content = 10% of 10 kg
\[ Initial solids = 10 \times 0.10 = 1 kg \]
Step 2: Use solids balance after concentration.
Solids remain constant during concentration.
Let the final weight of concentrate be \(W\) kg.
Final moisture content = 35% (w.b.)
Therefore, solids content = 65% of \(W\).
Step 3: Equate solids before and after concentration.
\[ 0.65W = 1 \]
\[ W = \frac{1}{0.65} = 1.538 kg \]
Step 4: Final answer.
Rounding off to two decimal places,
\[ W = 1.54 kg \]
Quick Tip: In concentration problems, always apply solids balance since solids remain unchanged.
The surface temperature of a hot plate is 175\(^\circ\)C. The ambient air temperature is 25\(^\circ\)C. The rate of heat transfer per unit area in kW·m\(^{-2}\) from the plate to the ambient air is ............................. (Answer in integer). Assume the convective heat transfer coefficient is 20 W·m\(^{-2}\)·K\(^{-1}\).
View Solution
Step 1: Write the convective heat transfer equation.
\[ q = h (T_s - T_\infty) \]
Step 2: Substitute the given values.
Surface temperature, \(T_s = 175^\circ\)C
Ambient temperature, \(T_\infty = 25^\circ\)C
Heat transfer coefficient, \(h = 20\) W·m\(^{-2}\)·K\(^{-1}\)
\[ q = 20 (175 - 25) \]
\[ q = 20 \times 150 = 3000 W·m^{-2} \]
Step 3: Convert units to kW·m\(^{-2}\).
\[ 3000 W·m^{-2} = 3 kW·m^{-2} \]
Step 4: Final answer.
\[ \boxed{3} \]
Quick Tip: For convection problems, use \(q = h\Delta T\) and convert units carefully.
A tubular bowl centrifuge is used to separate an aqueous phase from an oil phase. The radii of outlets of the light and heavy liquids are set at 4.5 cm and 4.6 cm, respectively. The radius in cm of the neutral zone in the centrifuge is ............................. (round off to 2 decimal places). Assume the density of the aqueous phase is 950 kg·m\(^{-3}\) and that of oil is 900 kg·m\(^{-3}\).
View Solution
Step 1: Identify the governing relation.
For a tubular bowl centrifuge, the neutral zone radius \(r_n\) is given by:
\[ r_n^2 = \frac{\rho_L r_L^2 - \rho_H r_H^2}{\rho_L - \rho_H} \]
Step 2: Substitute the given values.
Density of aqueous phase (heavy liquid), \(\rho_H = 950\) kg·m\(^{-3}\)
Density of oil (light liquid), \(\rho_L = 900\) kg·m\(^{-3}\)
Radius of light liquid outlet, \(r_L = 4.5\) cm
Radius of heavy liquid outlet, \(r_H = 4.6\) cm
\[ r_n^2 = \frac{900(4.5)^2 - 950(4.6)^2}{900 - 950} \]
Step 3: Perform calculations.
\[ r_n^2 = \frac{900(20.25) - 950(21.16)}{-50} \]
\[ r_n^2 = \frac{18225 - 20102}{-50} = \frac{-1877}{-50} \]
\[ r_n^2 = 37.54 \]
\[ r_n = \sqrt{37.54} = 6.12 cm \]
Step 4: Final answer.
\[ \boxed{6.12 cm} \]
Quick Tip: In centrifuge problems, the neutral zone depends on density difference and outlet radii.
A westerly wind is blowing in the Northern Hemisphere. What is the direction of net mass transport in the Ekman layer?
View Solution
Step 1: Understanding Ekman transport.
Ekman transport refers to the net movement of fluid in the Ekman layer, which occurs at right angles to the wind direction due to the Coriolis force.
Step 2: Effect of Coriolis force in the Northern Hemisphere.
In the Northern Hemisphere, the Coriolis force deflects moving fluids to the right of their direction of motion.
Step 3: Apply the concept to a westerly wind.
A westerly wind blows from west to east. Due to Coriolis deflection, the net Ekman transport is directed 90° to the right of the wind direction.
Step 4: Determining the final direction.
Rightward deflection of eastward wind results in a southward transport.
Step 5: Conclusion.
Hence, the net mass transport in the Ekman layer is southward.
Quick Tip: In the Northern Hemisphere, Ekman transport is always 90° to the right of the wind direction.
Which one of the following feature is NOT necessary for the formation of Indian summer monsoon?
View Solution
Step 1: Key drivers of Indian summer monsoon.
The Indian summer monsoon is driven primarily by differential heating between land and sea, pressure gradients, and seasonal reversal of winds.
Step 2: Analyzing option (A).
Land-sea temperature contrast is essential to create pressure differences that initiate monsoon circulation. This is necessary.
Step 3: Analyzing option (C).
Seasonal reversal of winds is a defining feature of monsoon systems and is necessary.
Step 4: Analyzing option (D).
Meridional pressure gradient helps sustain large-scale monsoon circulation. This is also necessary.
Step 5: Analyzing option (B).
El Niño is a climatic phenomenon that influences monsoon variability but is not essential for monsoon formation.
Step 6: Conclusion.
El Niño is not a necessary condition for the formation of the Indian summer monsoon.
Quick Tip: El Niño affects monsoon strength, not its fundamental formation.
The work done by Coriolis force is
View Solution
Step 1: Nature of Coriolis force.
The Coriolis force is an apparent force that arises due to the rotation of the Earth and acts perpendicular to the direction of motion of a moving object.
Step 2: Direction of force relative to motion.
Since the Coriolis force always acts at right angles to the velocity, it does not change the speed of the object.
Step 3: Work-energy principle.
Work done by a force is given by the component of force in the direction of displacement.
Step 4: Application to Coriolis force.
As there is no component of Coriolis force along the direction of motion, no work is done.
Step 5: Conclusion.
Therefore, the work done by the Coriolis force is zero.
Quick Tip: Forces perpendicular to motion do no work.
If the isobars and isopycnals are parallel to each other, the flow is said to be
View Solution
Step 1: Understanding isobars and isopycnals.
Isobars represent lines of constant pressure, while isopycnals represent lines of constant density.
Step 2: Barotropic condition.
In a barotropic flow, density is a function of pressure only, and surfaces of constant pressure and density coincide or are parallel.
Step 3: Baroclinic contrast.
In baroclinic flow, isobars and isopycnals intersect, leading to thermal wind effects.
Step 4: Applying the definition.
Since the isobars and isopycnals are parallel, the flow satisfies the barotropic condition.
Step 5: Conclusion.
The flow is therefore barotropic.
Quick Tip: Parallel isobars and isopycnals indicate barotropic flow.
Transfer of energy between ocean and atmosphere in the form of sensible heat flux is due to
View Solution
Step 1: Understanding sensible heat flux.
Sensible heat flux refers to the direct transfer of heat energy between the ocean surface and the atmosphere due to a temperature difference, without involving a phase change of water.
Step 2: Analyzing option (A).
Difference in specific humidity drives latent heat flux, not sensible heat flux. Hence, this option is incorrect.
Step 3: Analyzing option (B).
Sensible heat transfer occurs when there is a temperature gradient between the ocean surface and the overlying air. Therefore, this option correctly explains sensible heat flux.
Step 4: Analyzing option (C).
Density differences may influence buoyancy but are not the direct cause of sensible heat flux. This option is incorrect.
Step 5: Analyzing option (D).
Differences in partial pressure of CO\(_2\) are related to gas exchange, not heat transfer. Hence, this option is incorrect.
Step 6: Conclusion.
Sensible heat flux between the ocean and atmosphere is driven by temperature differences.
Quick Tip: Sensible heat depends only on temperature difference, while latent heat depends on moisture difference.
A value of outgoing long-wave radiation (OLR) \(<\) 200 W m\(^{-2}\) over the tropical oceans indicates
View Solution
Step 1: Understanding outgoing long-wave radiation (OLR).
OLR represents the infrared radiation emitted to space from the Earth–atmosphere system. Its magnitude depends on cloud cover and cloud-top temperature.
Step 2: Relation between OLR and convection.
Deep convective clouds have high and cold cloud tops, which emit less long-wave radiation to space.
Step 3: Analyzing low OLR values.
An OLR value less than 200 W m\(^{-2}\) indicates strong convection with thick, high-altitude clouds.
Step 4: Elimination of other options.
High pressure and clear sky conditions are associated with higher OLR values. High sea surface temperature alone does not guarantee low OLR.
Step 5: Conclusion.
Low OLR over tropical oceans is a signature of deep convection.
Quick Tip: Low OLR values usually indicate thick clouds and strong convective activity.
Which of the following is a correct statement?
View Solution
Step 1: Earth’s radiation balance concept.
The Earth receives short-wave solar radiation and emits long-wave terrestrial radiation. The balance varies with latitude.
Step 2: Energy balance in the tropics.
In tropical regions, incoming solar radiation exceeds outgoing long-wave radiation, leading to a net energy surplus.
Step 3: Energy balance in polar regions.
Polar regions receive less solar radiation than they emit as long-wave radiation, resulting in a net energy deficit.
Step 4: Evaluation of options.
Only option (A) correctly represents the radiation balance of the tropics.
Step 5: Conclusion.
The tropics receive more short-wave radiation than they emit as long-wave radiation.
Quick Tip: Tropics have energy surplus, while polar regions have energy deficit.
Upwelling region has ..............................
View Solution
Step 1: Understanding upwelling.
Upwelling is the upward movement of cold, nutrient-rich deep water to the ocean surface, commonly driven by wind-induced Ekman transport.
Step 2: Effect on sea surface height.
During upwelling, surface waters diverge and are replaced by deeper water, resulting in a lowering of sea surface height.
Step 3: Effect on nutrients and productivity.
Upwelling increases nutrient availability and enhances primary production, not decreases it.
Step 4: Elimination of incorrect options.
High sea surface height, low nutrients, and decreased productivity are characteristics of downwelling regions.
Step 5: Conclusion.
An upwelling region is characterized by low sea surface height.
Quick Tip: Upwelling lowers sea level locally and boosts nutrients and biological productivity.
Density of sea-water does not directly depend on ..............................
View Solution
Step 1: Factors affecting seawater density.
The density of seawater is primarily controlled by its physical and thermodynamic properties such as temperature, salinity, and pressure. These variables directly influence molecular spacing and mass per unit volume.
Step 2: Role of temperature.
An increase in temperature causes seawater to expand, reducing its density. Hence, temperature directly affects seawater density.
Step 3: Role of salinity.
Higher salinity increases the mass of dissolved salts per unit volume, thereby increasing seawater density. Thus, salinity directly affects density.
Step 4: Role of pressure.
With increasing depth, pressure increases and compresses seawater slightly, leading to an increase in density. Therefore, pressure also directly affects density.
Step 5: Role of vorticity.
Vorticity describes the rotational motion of a fluid and does not influence the mass or volume of seawater. Hence, it does not directly affect density.
Step 6: Conclusion.
Vorticity of seawater does not directly influence its density.
Quick Tip: Seawater density depends on temperature, salinity, and pressure—commonly abbreviated as T–S–P.
Which of the following is/are true about ocean circulation?
View Solution
Step 1: Understanding wind-driven ocean circulation.
Large-scale ocean circulation is driven mainly by surface winds and modified by Earth’s rotation through the Coriolis force, which varies with latitude.
Step 2: Analyzing option (A).
If the Coriolis force were constant, western boundary intensification would not occur. Hence, this statement is incorrect.
Step 3: Analyzing option (B).
The variation of Coriolis force with latitude (the \(\beta\)-effect) leads to western boundary intensification, producing narrow and fast western boundary currents such as the Gulf Stream. This statement is correct.
Step 4: Analyzing option (C).
Eastern boundary currents, such as the California Current, are characteristically wide, shallow, and slow-moving. Hence, this statement is correct.
Step 5: Analyzing option (D).
Wind-driven circulation generates Ekman transport due to the balance between wind stress and Coriolis force. This statement is correct.
Step 6: Conclusion.
Statements (B), (C), and (D) correctly describe features of ocean circulation.
Quick Tip: Western boundary currents are fast and narrow due to the \(\beta\)-effect, while eastern boundary currents are slow and wide.
Sverdrup’s equation deals with
View Solution
Step 1: Understanding Sverdrup balance.
Sverdrup’s equation describes the balance between wind forcing and large-scale ocean circulation in the ocean interior.
Step 2: Role of wind stress curl.
The equation directly relates the curl of wind stress to the meridional (north–south) transport of seawater. Hence, wind stress curl is a key component.
Step 3: Role of Coriolis variation.
Sverdrup balance explicitly involves the variation of the Coriolis parameter with latitude, known as the \(\beta\)-effect. Thus, this factor is included.
Step 4: Meridional transport.
The outcome of Sverdrup’s equation is the meridional transport of seawater in the ocean interior. Hence, this is correctly included.
Step 5: Pressure gradient force.
While pressure gradients are important in ocean dynamics, they are not explicitly part of the Sverdrup relation. Therefore, this option is excluded.
Step 6: Conclusion.
Sverdrup’s equation deals with wind stress curl, variation of Coriolis force with latitude, and meridional transport of seawater.
Quick Tip: Sverdrup balance links wind stress curl to large-scale meridional ocean transport.
pH of the water in the oceans is/are directly affected by:
View Solution
Step 1: Understanding ocean pH.
The pH of seawater is governed by the marine carbonate system, which involves dissolved CO\(_2\), bicarbonate, carbonate ions, and hydrogen ions. Any factor influencing this system will directly affect pH.
Step 2: Effect of water temperature.
Temperature affects the solubility of CO\(_2\) in seawater and the dissociation constants of carbonic acid. Higher temperatures generally reduce CO\(_2\) solubility, thereby influencing pH. Hence, temperature directly affects ocean pH.
Step 3: Effect of water salinity.
Salinity alters ionic strength and equilibrium constants of the carbonate system, which in turn affects hydrogen ion concentration. Therefore, salinity directly affects pH.
Step 4: Effect of total alkalinity.
Total alkalinity represents the buffering capacity of seawater and directly controls the balance between carbonate species, making it a key determinant of ocean pH.
Step 5: Effect of water pressure.
Pressure changes with depth but does not directly control surface ocean pH; its effect is indirect and minimal compared to other factors. Hence, this option is incorrect.
Step 6: Conclusion.
Ocean pH is directly affected by temperature, salinity, and total alkalinity.
Quick Tip: Ocean pH is tightly linked to the carbonate buffering system and total alkalinity.
Billow clouds indicate:
View Solution
Step 1: Understanding billow clouds.
Billow clouds, also known as Kelvin–Helmholtz clouds, form when there is instability caused by velocity differences between two fluid layers in the atmosphere.
Step 2: Relation to turbulence.
These clouds are visual indicators of atmospheric turbulence arising from instability at the interface of air layers. Hence, turbulence is correctly indicated.
Step 3: Relation to vertical wind shear.
Billow clouds form due to strong vertical shear of wind, where wind speed or direction changes rapidly with height. This makes option (B) correct.
Step 4: Elimination of incorrect options.
Billow clouds are not associated with heavy precipitation and do not occur under uniform wind conditions.
Step 5: Conclusion.
Billow clouds indicate atmospheric turbulence and vertical wind shear.
Quick Tip: Kelvin–Helmholtz (billow) clouds are classic signs of wind shear and turbulence aloft.
Consider an atmospheric flow at 45\(^\circ\)N, which is parallel to latitude and isobars. Which of the following is/are true when there is no friction?
View Solution
Step 1: Understanding the flow condition.
The flow is parallel to isobars and latitude circles at mid-latitudes (45\(^\circ\)N), with no friction. This describes an ideal large-scale atmospheric flow.
Step 2: Force balance in frictionless flow.
In the absence of friction, steady atmospheric flow parallel to isobars implies geostrophic balance, where the Coriolis force balances the pressure gradient force.
Step 3: Acceleration of the flow.
Since the forces are balanced, there is no net force acting on the air parcel, and hence acceleration is approximately zero.
Step 4: Evaluation of gradient wind balance.
Gradient wind balance includes centrifugal force due to curvature of flow. As curvature is not specified, this balance is not necessarily implied here.
Step 5: Elimination of cyclone interpretation.
The description does not explicitly indicate cyclonic curvature, so it cannot be concluded that it is an extratropical cyclone.
Step 6: Conclusion.
The correct statements are that acceleration is close to zero and the flow is governed by a balance between Coriolis and pressure gradient forces.
Quick Tip: Frictionless, steady flow parallel to isobars indicates geostrophic balance.
The given figure shows a schematic of dry, moist, and environmental lapse rates. Which of the following is/are correct statements?
View Solution
Step 1: Understanding lapse rates shown in the figure.
The diagram shows three lapse rates: the dry adiabatic lapse rate (DALR), the moist adiabatic lapse rate (MALR), and the environmental lapse rate (ELR). Atmospheric stability depends on the relative positions (slopes) of these lapse rates.
Step 2: Evaluating option (A).
Below 5 km, the environmental lapse rate shown in the figure is not as steep as \(-15~^\circ\)C km\(^{-1}\). Such a large magnitude would indicate extreme instability, which is not depicted. Hence, this statement is incorrect.
Step 3: Evaluating option (B).
Above 5 km, the environmental lapse rate is smaller than both the dry and moist adiabatic lapse rates, indicating a stable atmosphere rather than an unstable one. Therefore, this statement is incorrect.
Step 4: Evaluating option (C).
Since the atmosphere above 5 km is stable, vertical motions are suppressed. As a result, the likelihood of deep convective cloud growth above 5 km is reduced. Hence, this statement is correct.
Step 5: Evaluating option (D).
Below 5 km, the environmental lapse rate lies between the dry adiabatic and moist adiabatic lapse rates. This condition corresponds to conditional instability, where unsaturated air is stable but saturated air becomes unstable. Thus, this statement is correct.
Step 6: Conclusion.
The correct interpretations of the given lapse-rate diagram are that deep convection above 5 km is unlikely and the atmosphere below 5 km is conditionally unstable.
Quick Tip: Conditional instability occurs when ELR lies between DALR and MALR—convection starts only after saturation.
Balance of forces and different types of flows/weather phenomena in the northern hemisphere are given. Match the following:
Balance of forces \hspace{3.5cm Flow type / weather phenomena
P \; Balance between pressure gradient force, centrifugal force and Coriolis force in anticlockwise rotation \hspace{1cm X \; Geostrophic flow
Q \; Balance between pressure gradient force and centrifugal force in clockwise/anticlockwise rotation \hspace{0.5cm Y \; Cyclones
R \; Balance between pressure gradient force and Coriolis force in a uniform flow \hspace{1.8cm Z \; Tornado
View Solution
Step 1: Understanding geostrophic flow (R → X).
Geostrophic flow occurs when the pressure gradient force is exactly balanced by the Coriolis force, resulting in flow parallel to isobars. This corresponds to balance R, hence R matches with X.
Step 2: Understanding cyclones (P → Y).
In cyclones, especially large-scale mid-latitude cyclones in the northern hemisphere, the pressure gradient force, Coriolis force, and centrifugal force are all important and act together in an anticlockwise rotation. Thus, balance P corresponds to cyclones (Y).
Step 3: Understanding tornadoes (Q → Z).
Tornadoes are small-scale systems where centrifugal force and pressure gradient force dominate, while Coriolis force is negligible. The rotation may be clockwise or anticlockwise. Hence, balance Q corresponds to tornado (Z).
Step 4: Final matching.
P → Y
Q → Z
R → X
Step 5: Conclusion.
The correct matching is P - Y, Q - Z, R - X, which corresponds to option (C).
Quick Tip: Geostrophic flow ignores centrifugal force, cyclones include all forces, and tornadoes are dominated by centrifugal effects.
During summer monsoon season, water from Arabian Sea spreads over the south-western Bay of Bengal. This leads to
View Solution
Step 1: Understanding summer monsoon circulation.
During the summer monsoon, high-salinity water from the Arabian Sea is transported eastward into the Bay of Bengal. This water overlies relatively fresher Bay of Bengal surface waters.
Step 2: Density instability due to salinity difference.
Warm, salty water overlying warm, fresher water creates a situation where salinity-driven density instability can occur even if temperature stratification is stable.
Step 3: Formation of salt fingers.
Salt fingers develop when salty, dense water sinks downward in narrow plumes through fresher water, enhancing vertical mixing. This phenomenon is known as double-diffusive convection.
Step 4: Elimination of other options.
Upwelling and downwelling are driven mainly by wind stress and Ekman transport, while western boundary currents are large-scale circulation features. These are not the primary processes here.
Step 5: Conclusion.
The spreading of Arabian Sea water over the south-western Bay of Bengal during summer monsoon leads to the formation of salt fingers.
Quick Tip: Salt fingers form when warm, salty water overlies warm, fresher water due to double-diffusive instability.
Net solar radiation of 1360 W m\(^{-2}\) is incident on the surface of a still lake having mixed layer depth of 20 m. Find the change in temperature (in SI units) of the mixed layer of the lake for a day length of 8 hours. (Rounded off to 2 decimal places)
View Solution
Step 1: Calculate total heat input per unit area.
Net solar radiation, \(Q = 1360\) W m\(^{-2}\)
Day length \(= 8\) hours \(= 8 \times 3600 = 28800\) s
\[ Heat input = 1360 \times 28800 = 3.9168 \times 10^{7} J m^{-2} \]
Step 2: Calculate heat capacity of mixed layer per unit area.
Density of lake water, \(\rho = 1025\) kg m\(^{-3}\)
Specific heat capacity, \(C_p = 3850\) J kg\(^{-1}\) K\(^{-1}\)
Mixed layer depth, \(H = 20\) m
\[ Heat capacity = \rho C_p H = 1025 \times 3850 \times 20 \]
\[ = 7.8925 \times 10^{7} J m^{-2} K^{-1} \]
Step 3: Calculate change in temperature.
\[ \Delta T = \frac{3.9168 \times 10^{7}}{7.8925 \times 10^{7}} = 0.496 \]
Step 4: Final answer.
Rounded off to two decimal places,
\[ \boxed{0.50 K} \]
Quick Tip: For surface heating problems, divide total heat input by \(\rho C_p H\) to obtain temperature change.
A homogeneous, incompressible, steady ocean of mixed layer depth of 20 m has a velocity gradient \(-5 \times 10^{-8}\) s\(^{-1}\) and \(-8.3 \times 10^{-8}\) s\(^{-1}\) along zonal and meridional directions, respectively. The vertical mass flux (in kg s\(^{-1}\)) at the base of the mixed layer of 100 km \(\times\) 100 km area is ............................. \(\times 10^{6}\) kg s\(^{-1}\). (Rounded off to 1 decimal place)
View Solution
Step 1: Use incompressibility condition.
For an incompressible ocean, vertical velocity at the base of the mixed layer is given by:
\[ w = -H\left(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}\right) \]
Step 2: Substitute the given values.
\[ \frac{\partial u}{\partial x} = -5 \times 10^{-8} s^{-1} \]
\[ \frac{\partial v}{\partial y} = -8.3 \times 10^{-8} s^{-1} \]
\[ w = -20 \times (-1.33 \times 10^{-7}) = 2.66 \times 10^{-6} m s^{-1} \]
Step 3: Calculate mass flux.
Area \(= (100 \times 10^{3})^2 = 10^{10}\) m\(^{2}\)
Density of seawater, \(\rho = 1025\) kg m\(^{-3}\)
\[ Mass flux = \rho w A \]
\[ = 1025 \times 2.66 \times 10^{-6} \times 10^{10} \]
\[ = 2.7265 \times 10^{7} kg s^{-1} \]
Step 4: Final answer.
Rounded off to one decimal place,
\[ \boxed{27.3 \times 10^{6} kg s^{-1}} \]
Quick Tip: Vertical mass flux depends on horizontal divergence multiplied by mixed layer depth.
Wind blows over the ocean surface at a speed of 10 m s\(^{-1}\). Calculate the magnitude of wind stress, in Pa, using bulk formulation. (Drag coefficient = \(1.4 \times 10^{-3}\) and density of air is 1.3 kg m\(^{-3}\). Rounded off to 3 decimal places)
View Solution
Step 1: Write the bulk formula for wind stress.
\[ \tau = \rho_a C_D U^2 \]
Step 2: Substitute the given values.
\(\rho_a = 1.3\) kg m\(^{-3}\)
\(C_D = 1.4 \times 10^{-3}\)
\(U = 10\) m s\(^{-1}\)
\[ \tau = 1.3 \times 1.4 \times 10^{-3} \times (10)^2 \]
\[ \tau = 0.182 Pa \]
Step 3: Final answer.
Rounded off to three decimal places,
\[ \boxed{0.182 Pa} \]
Quick Tip: Wind stress varies with the square of wind speed in bulk aerodynamic formulations.
Two stations `A' and `B', present at a latitude of \(30^\circ\)N are separated by a distance of 10 km. If the difference in sea surface height between these two stations is 1 m, what will be the magnitude of geostrophic current velocity in SI units? (Assume the angular velocity of Earth is \(10^{-4}\) s\(^{-1}\)) (Answer in integer)
View Solution
Step 1: Write the geostrophic balance equation.
For oceanic geostrophic flow, the velocity is given by:
\[ u_g = \frac{g}{f} \frac{\partial \eta}{\partial x} \]
where \(g\) is acceleration due to gravity, \(f\) is the Coriolis parameter, and \(\partial \eta / \partial x\) is the sea surface slope.
Step 2: Calculate the Coriolis parameter.
\[ f = 2 \Omega \sin \phi \]
Given \(\Omega = 10^{-4}\) s\(^{-1}\) and \(\phi = 30^\circ\),
\[ f = 2 \times 10^{-4} \times \sin 30^\circ = 10^{-4} s^{-1} \]
Step 3: Compute sea surface slope.
Difference in sea surface height, \(\Delta \eta = 1\) m
Horizontal distance, \(\Delta x = 10\) km \(= 10^4\) m
\[ \frac{\partial \eta}{\partial x} = \frac{1}{10^4} = 10^{-4} \]
Step 4: Substitute values.
\[ u_g = \frac{9.8}{10^{-4}} \times 10^{-4} = 9.8 m s^{-1} \]
Step 5: Use standard approximation.
Using \(g \approx 10\) m s\(^{-2}\) for integer answer:
\[ u_g \approx 1 m s^{-1} \]
Step 6: Conclusion.
The magnitude of geostrophic current velocity is approximately 1 m s\(^{-1}\).
Quick Tip: Geostrophic current depends on sea surface slope and Coriolis parameter.
A stationary air parcel centered on the equator is moved northward by conserving absolute vorticity. In the new location it has gained a relative vorticity of \(-10^{-4}\) s\(^{-1}\). The latitude of its new location is .............................\(^\circ\)N. (Assume the angular velocity of Earth is \(10^{-4}\) s\(^{-1}\)) (Answer in integer)
View Solution
Step 1: Write the absolute vorticity conservation.
Absolute vorticity is given by:
\[ \zeta_a = \zeta + f \]
where \(\zeta\) is relative vorticity and \(f = 2 \Omega \sin \phi\) is planetary vorticity.
Step 2: Determine initial absolute vorticity.
At the equator, \(\phi = 0^\circ\), so
\[ f_0 = 0 \]
The parcel is stationary, hence
\[ \zeta_0 = 0 \]
\[ \Rightarrow \zeta_{a0} = 0 \]
Step 3: Apply conservation at new latitude.
\[ \zeta + f = 0 \]
Given \(\zeta = -10^{-4}\) s\(^{-1}\),
\[ f = 10^{-4} s^{-1} \]
Step 4: Compute latitude.
\[ 2 \Omega \sin \phi = 10^{-4} \]
\[ 2 \times 10^{-4} \sin \phi = 10^{-4} \]
\[ \sin \phi = 0.5 \]
Step 5: Final answer.
\[ \phi = 30^\circ \]
Step 6: Conclusion.
The air parcel reaches a latitude of \(30^\circ\)N.
Quick Tip: Poleward motion requires generation of negative relative vorticity to conserve absolute vorticity.





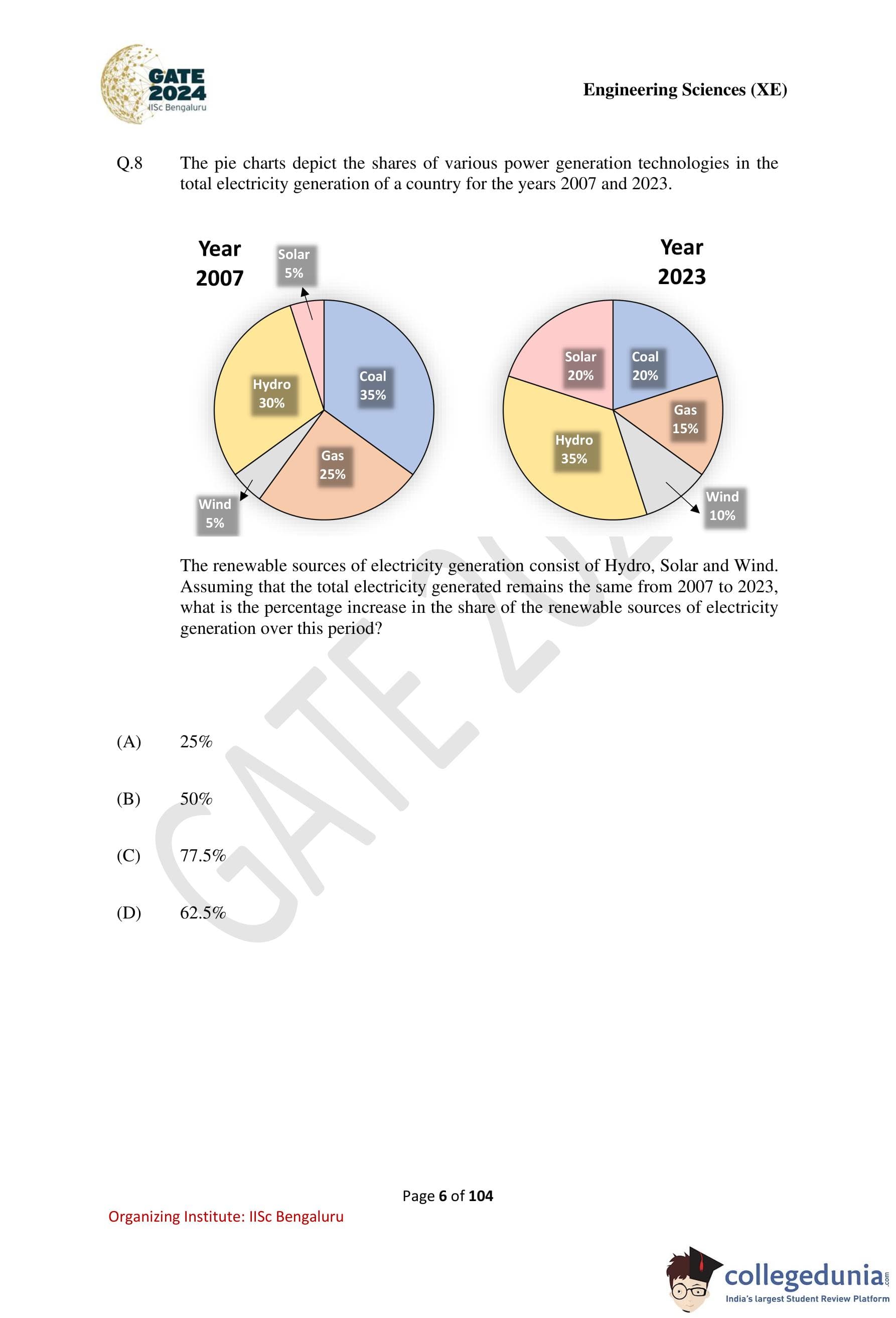









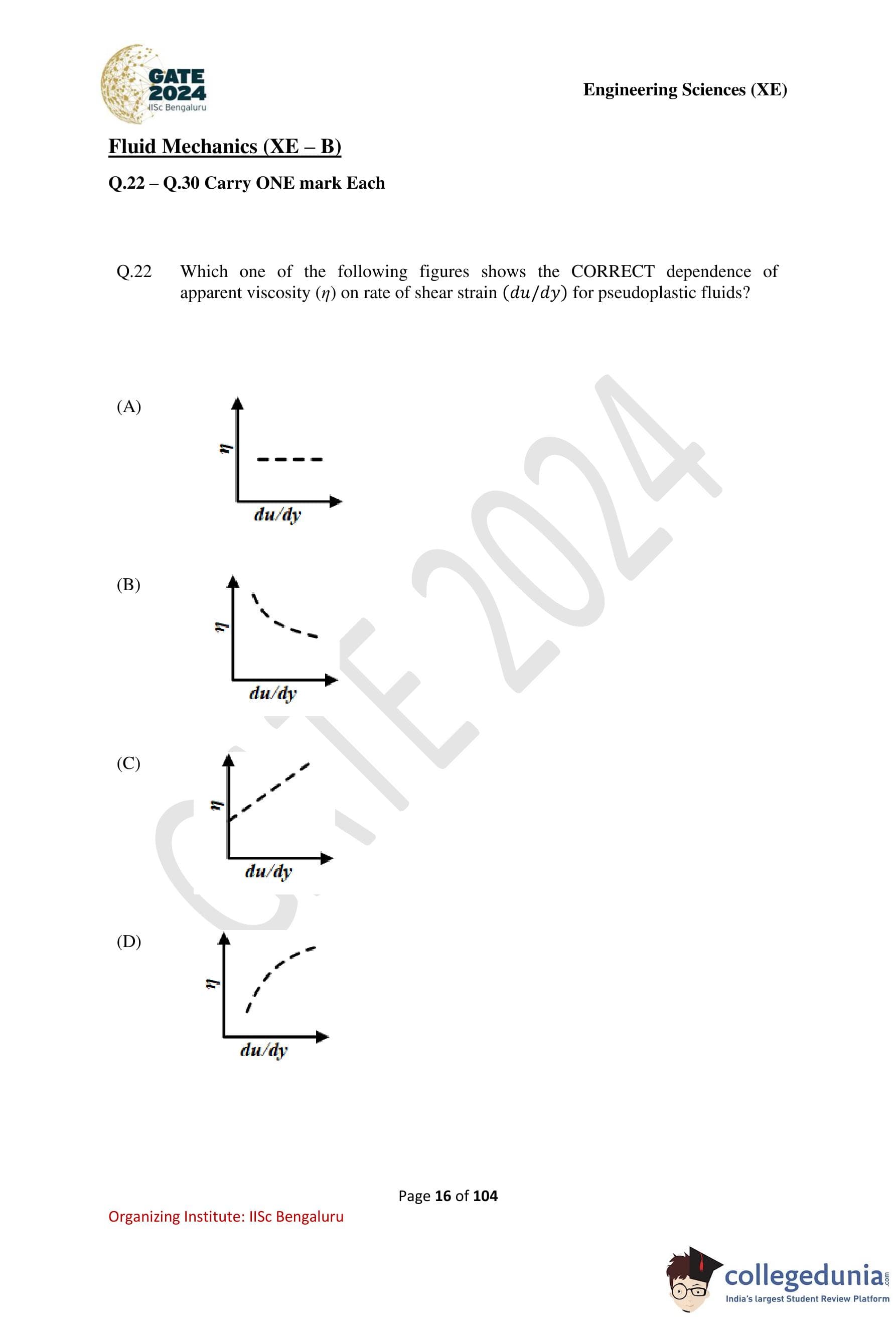




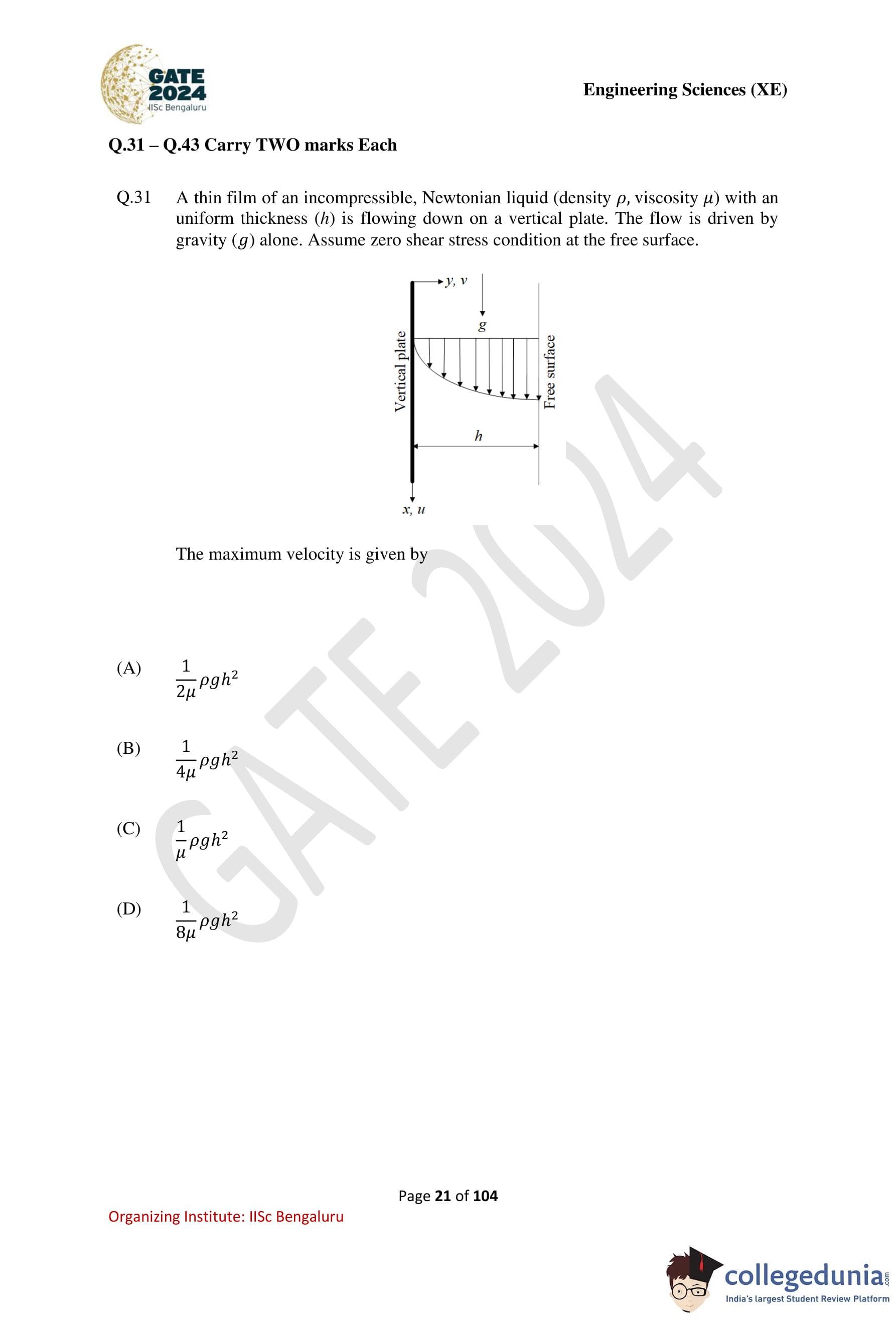

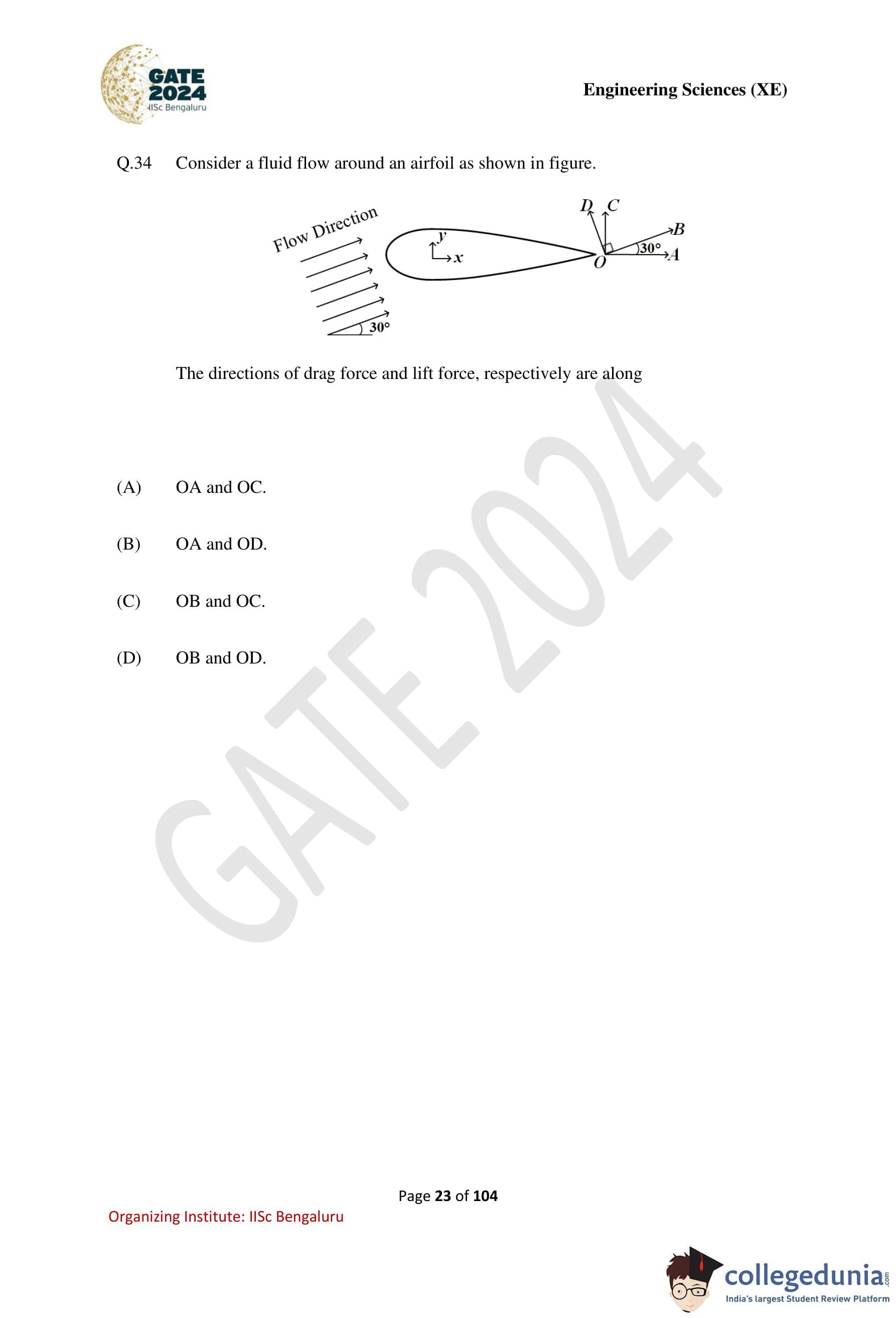








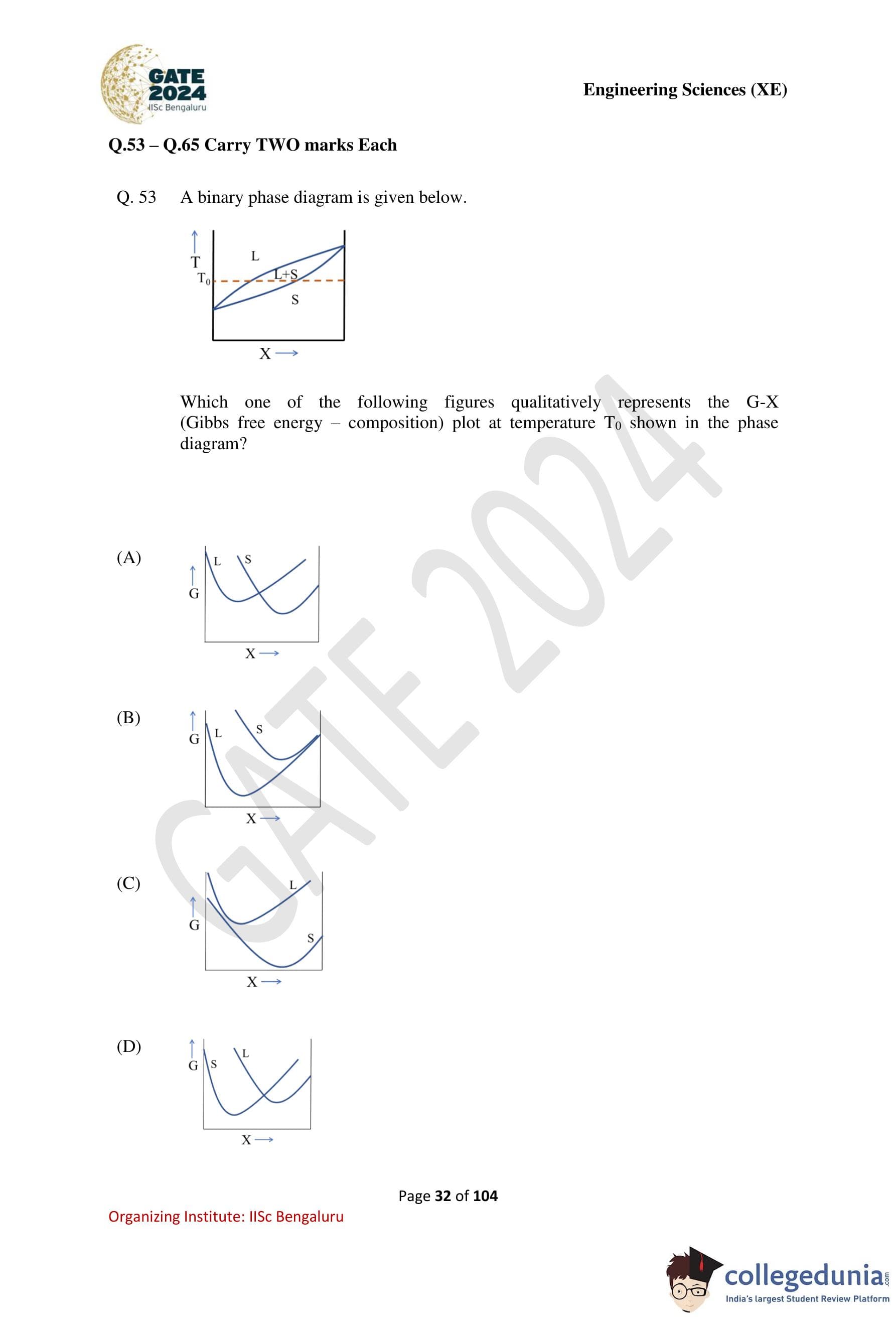
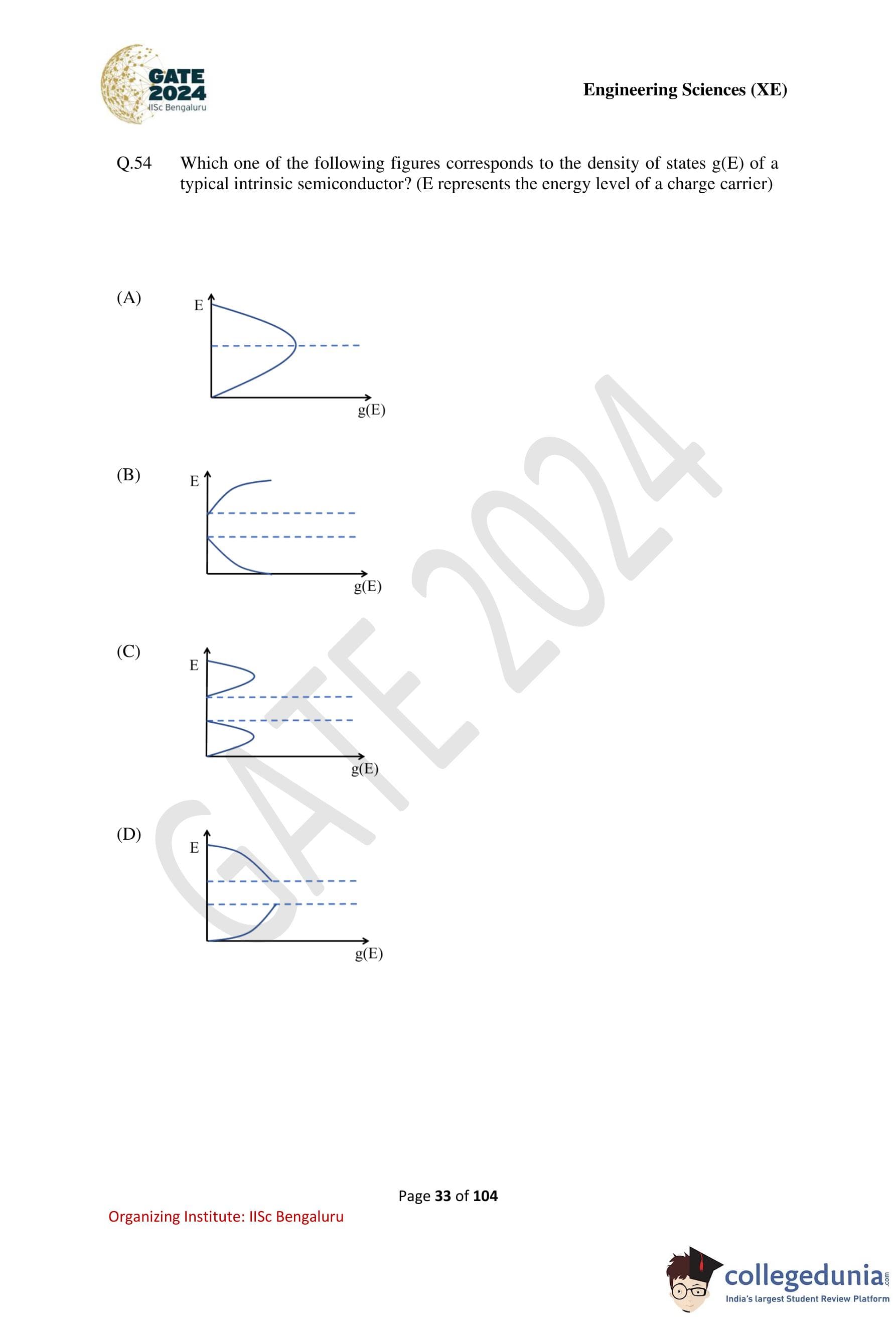
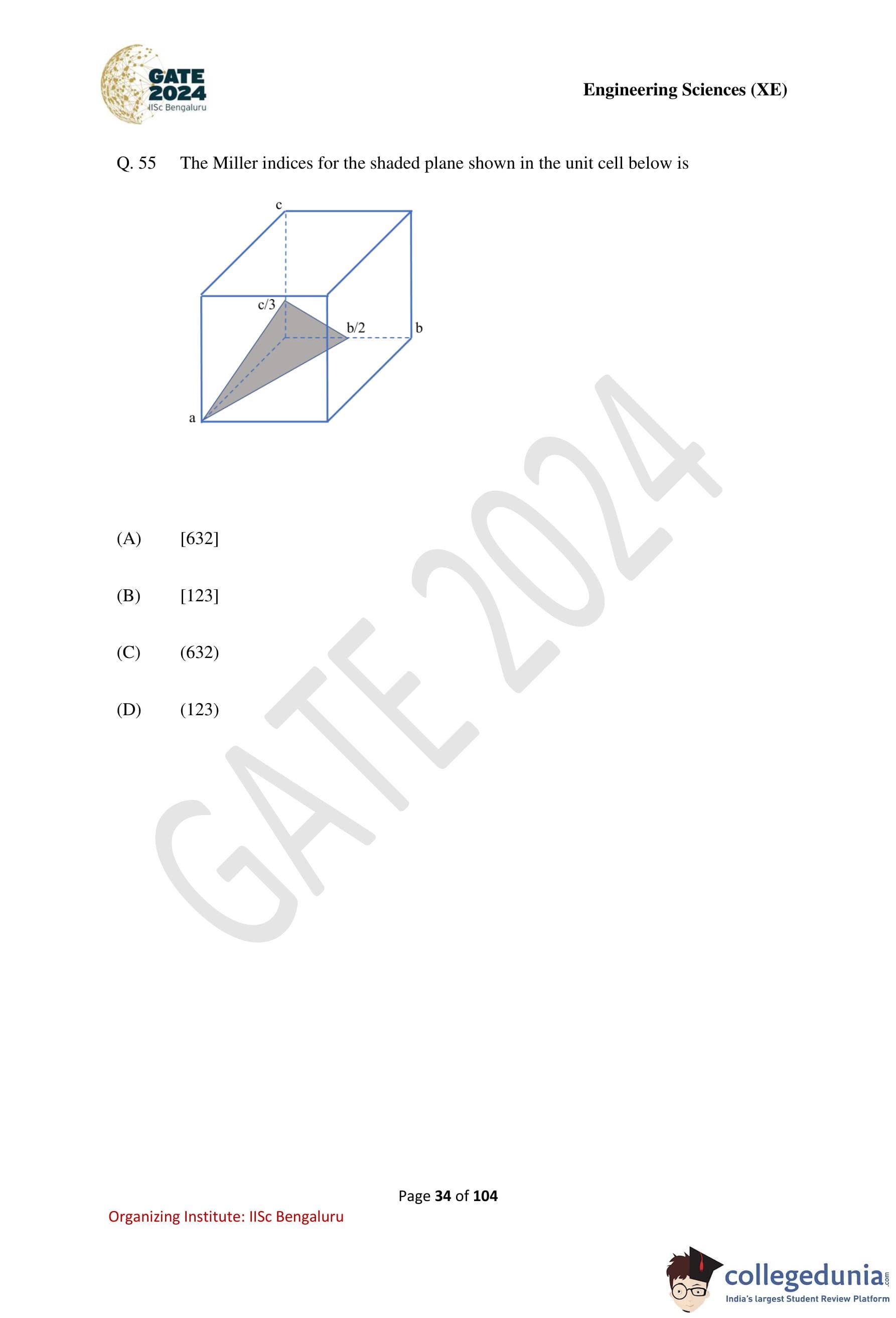
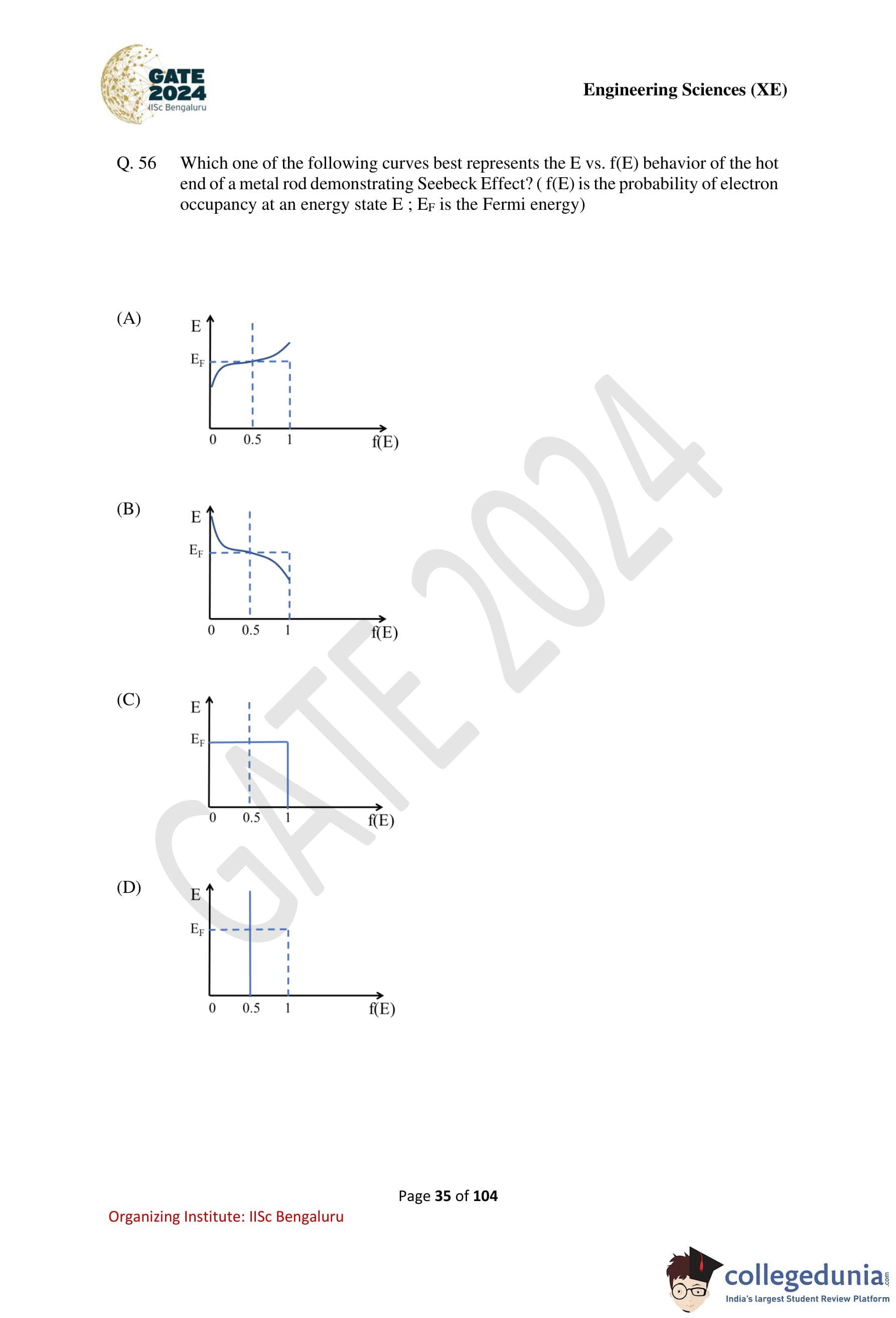

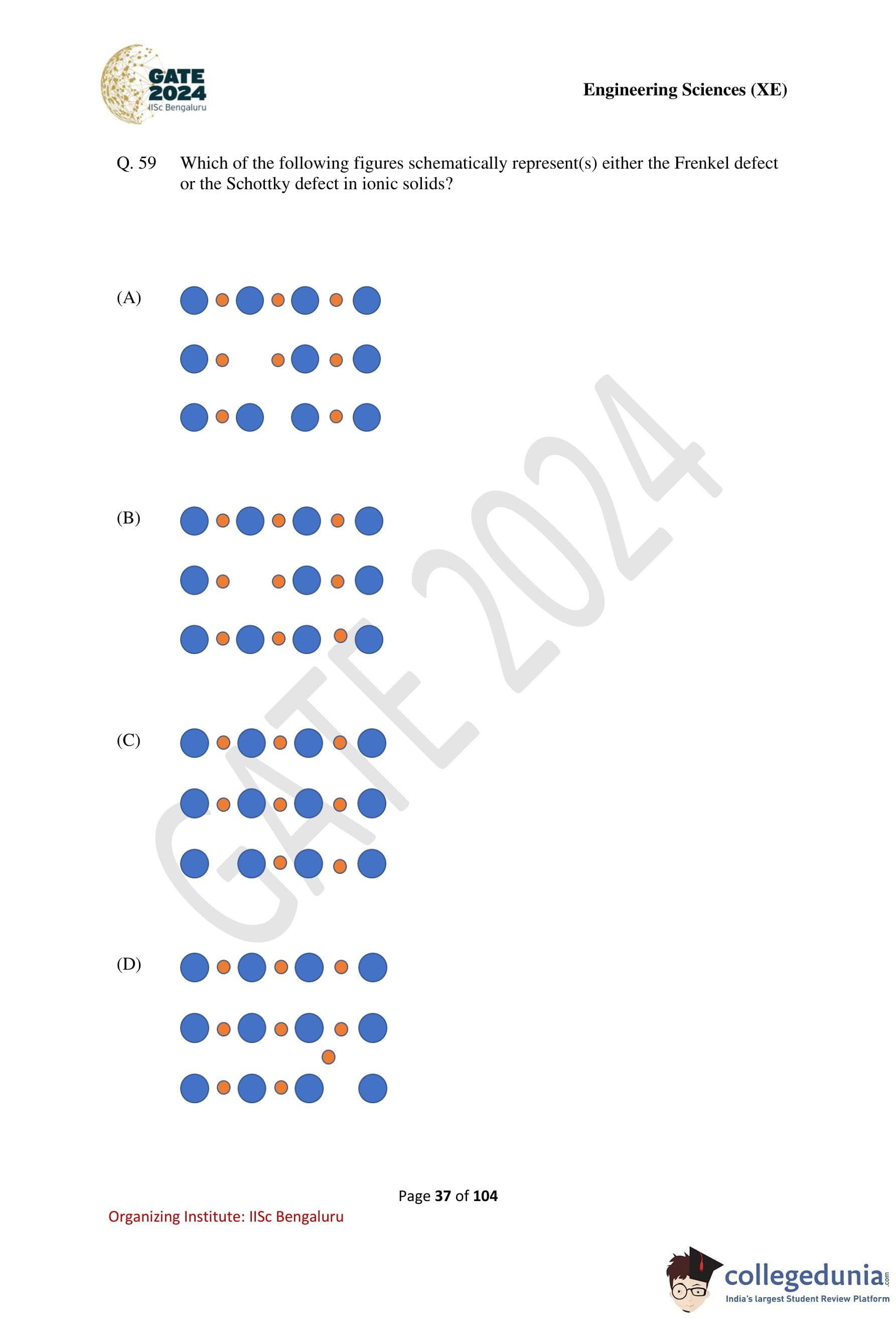
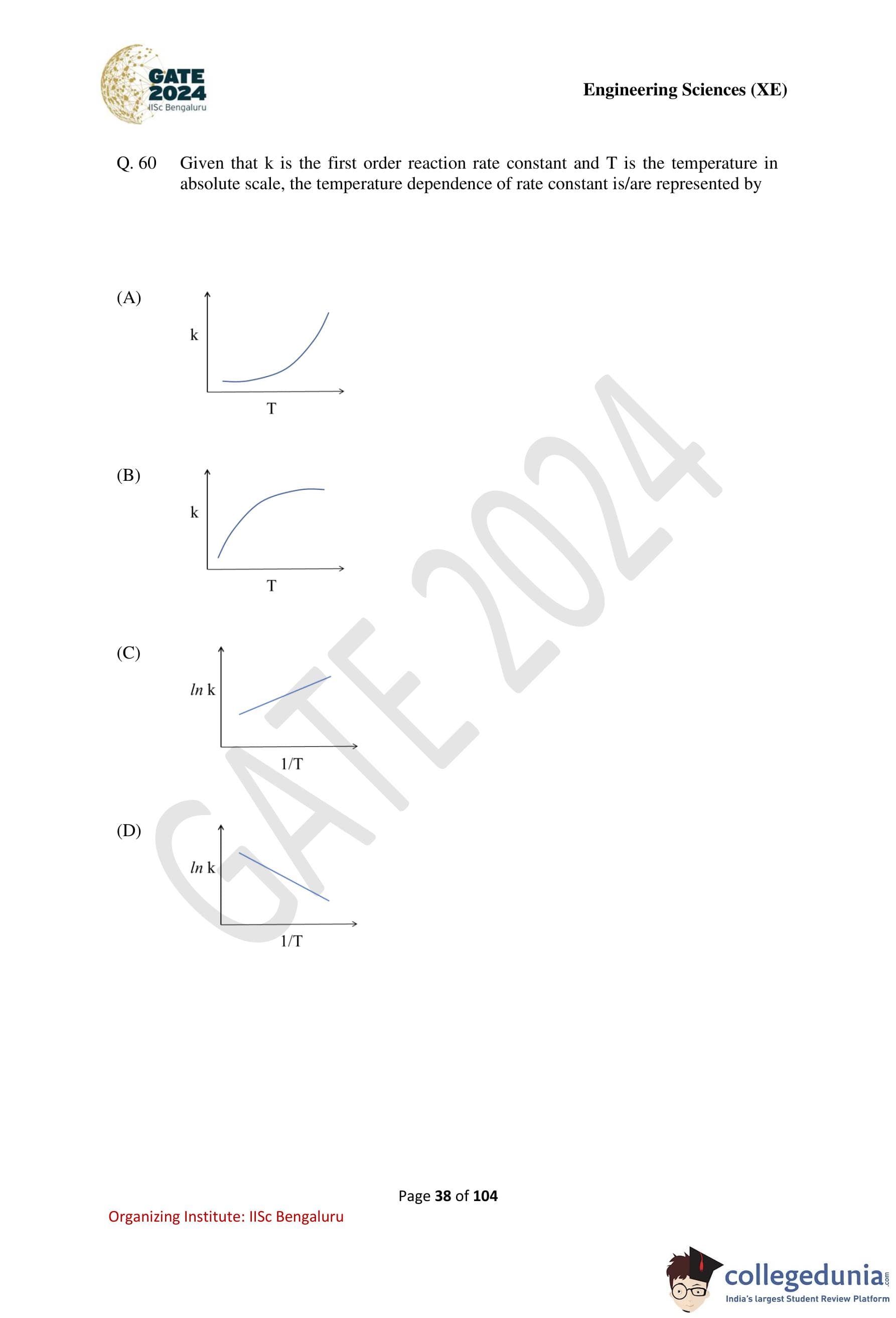



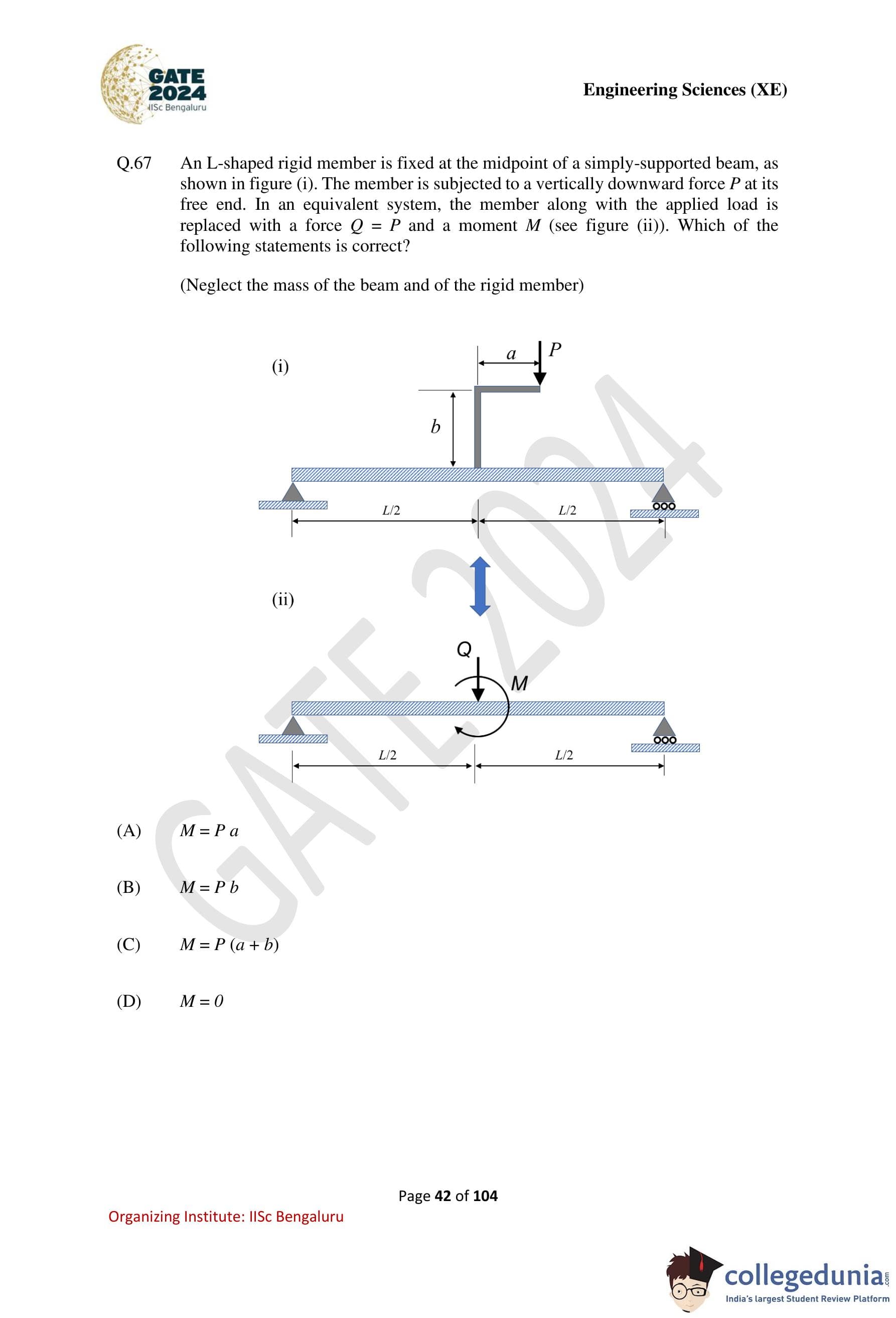








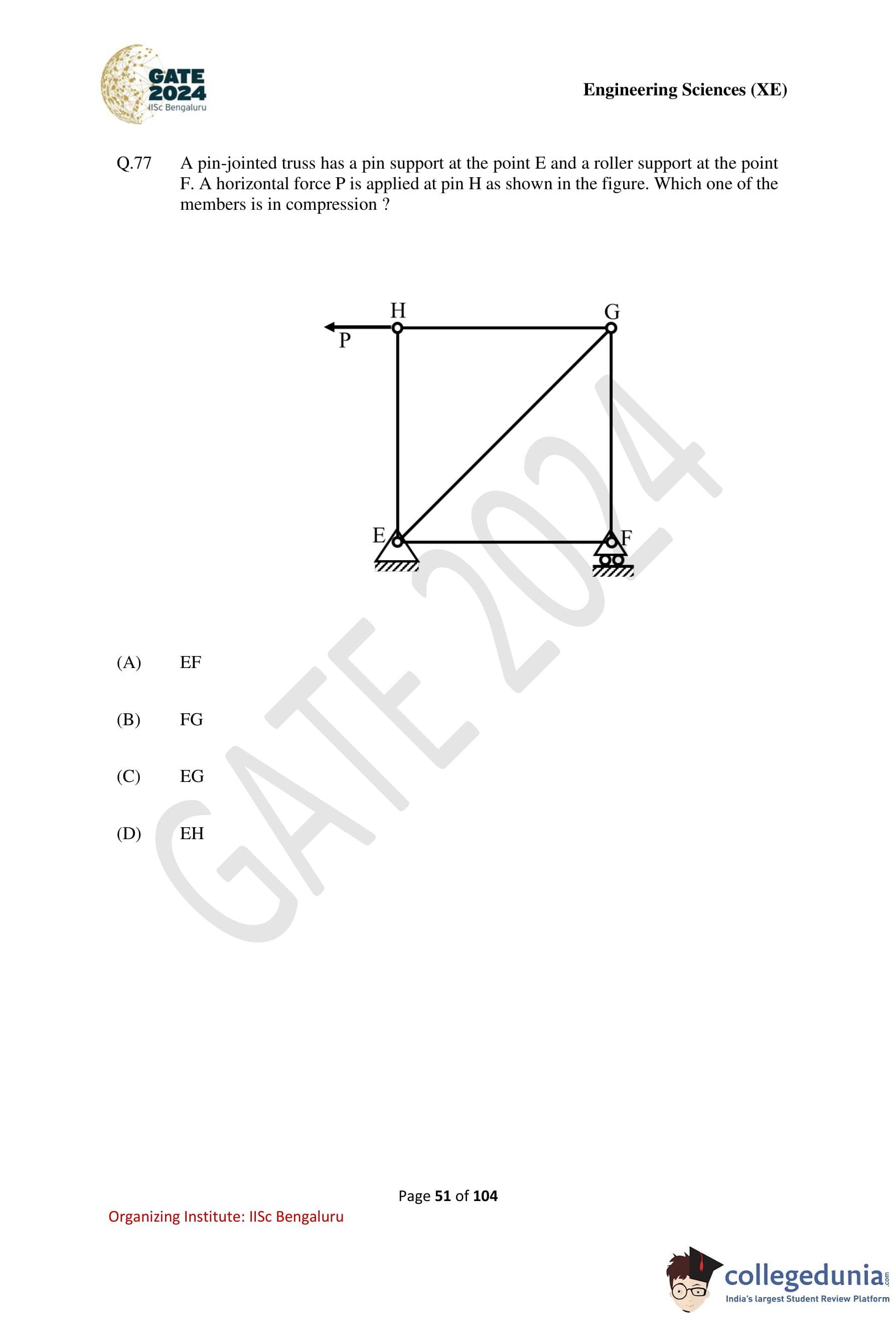
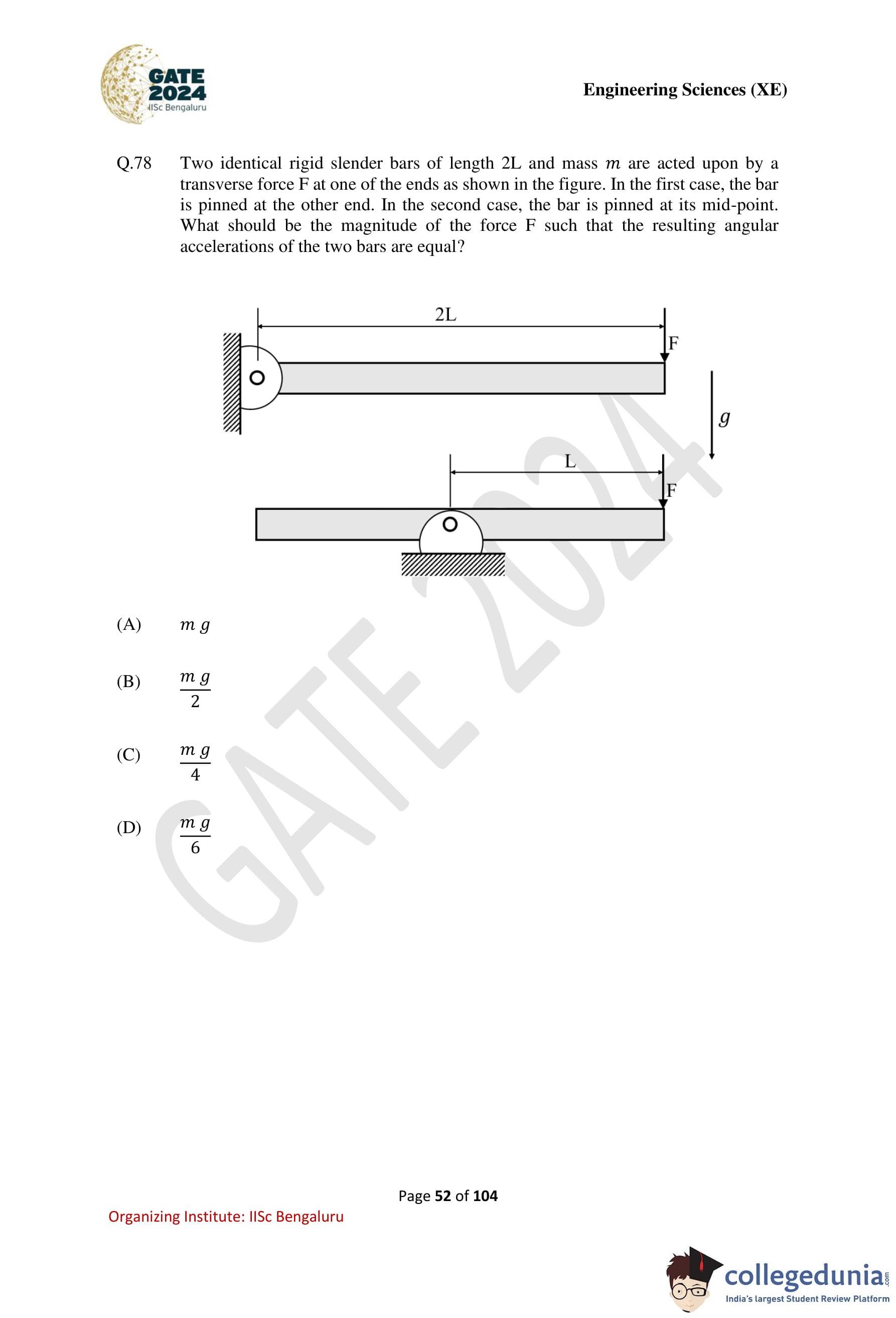







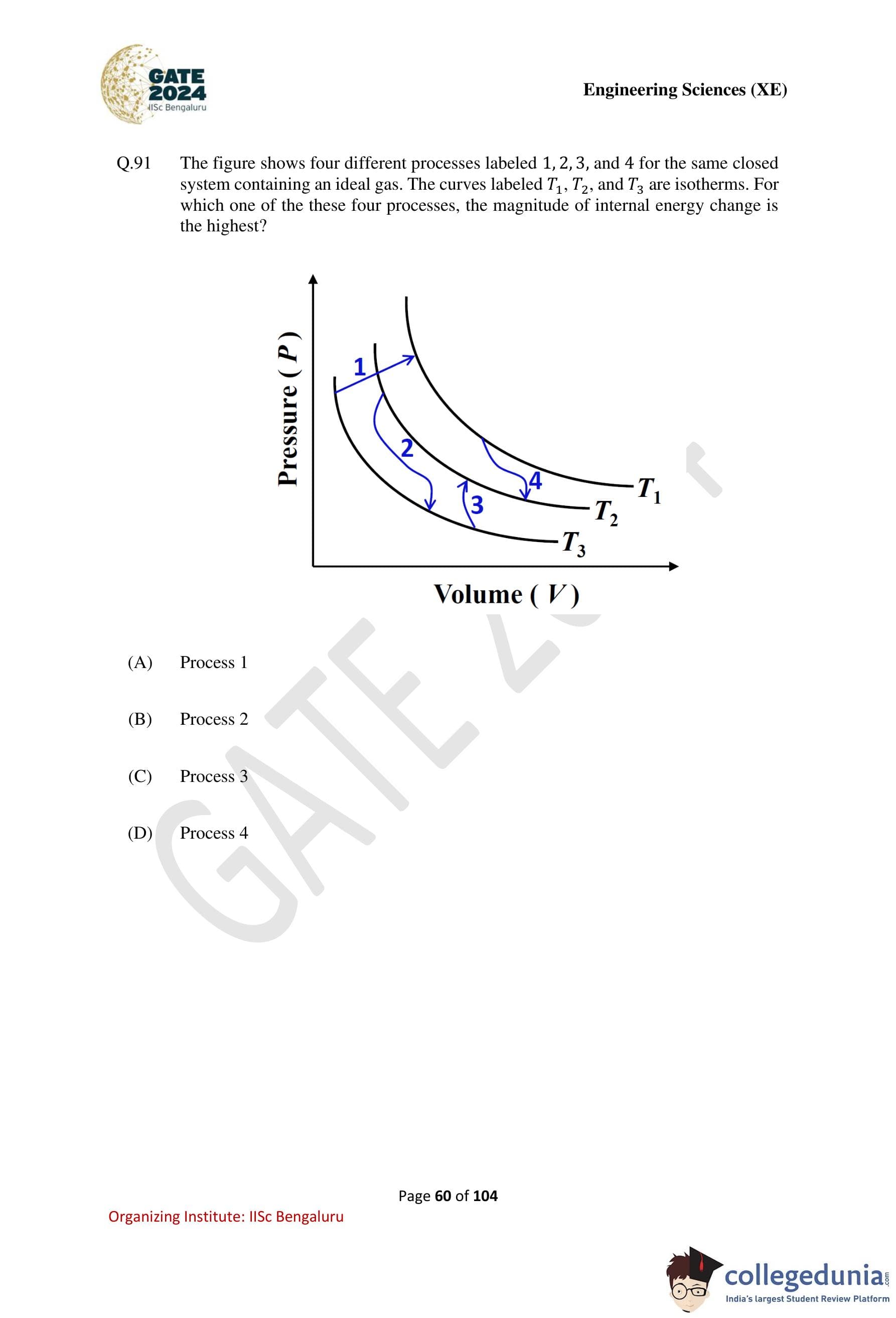






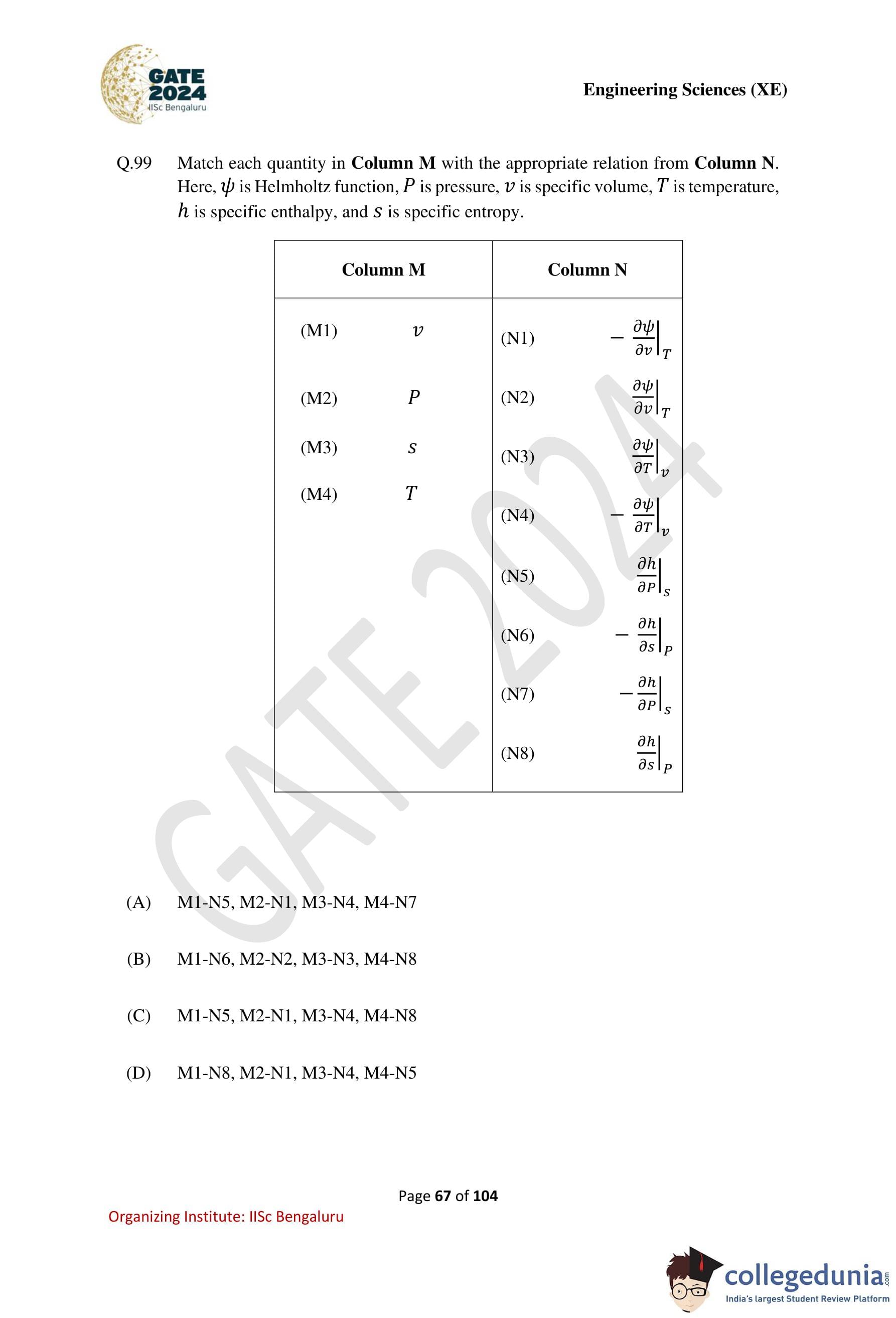














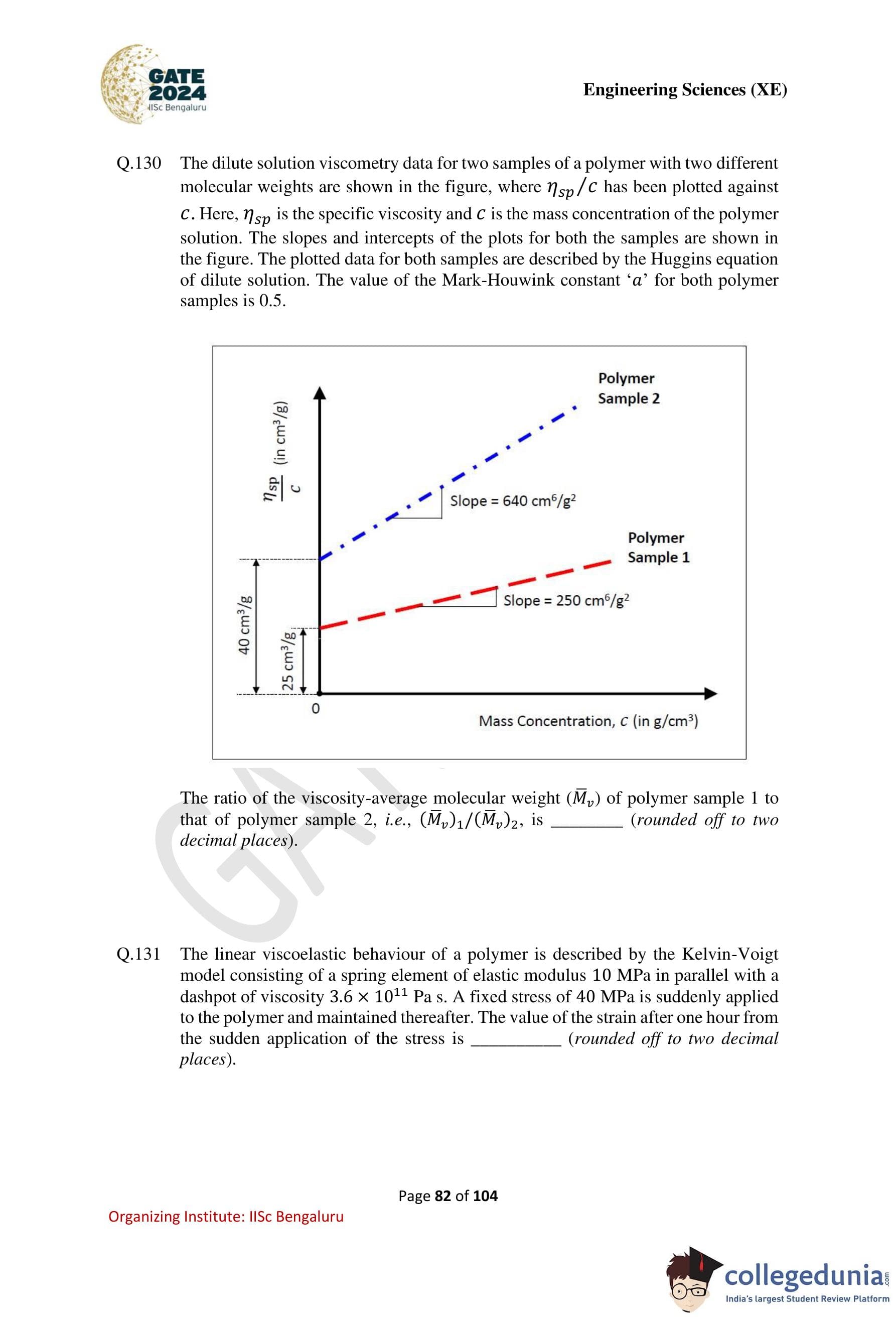


















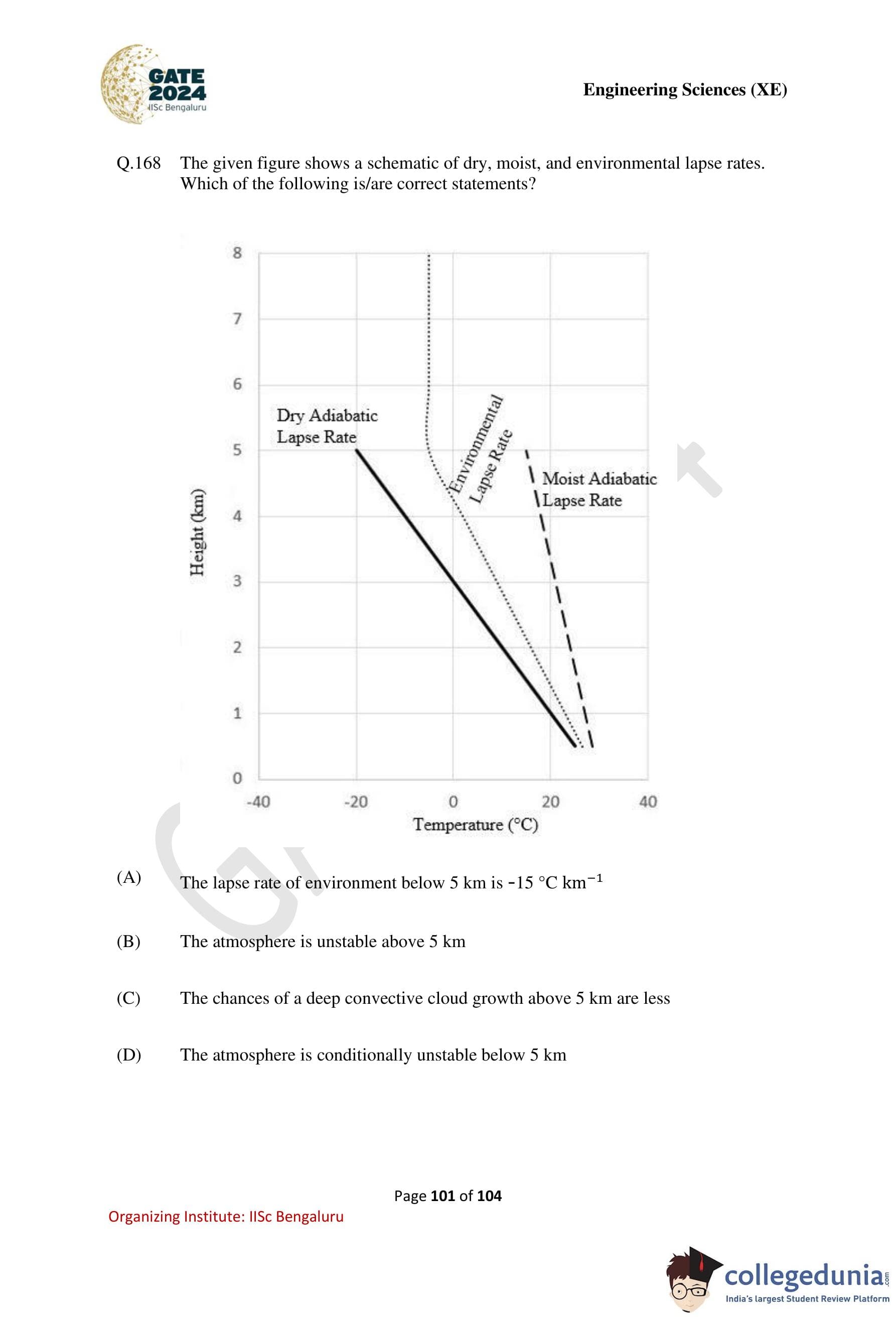



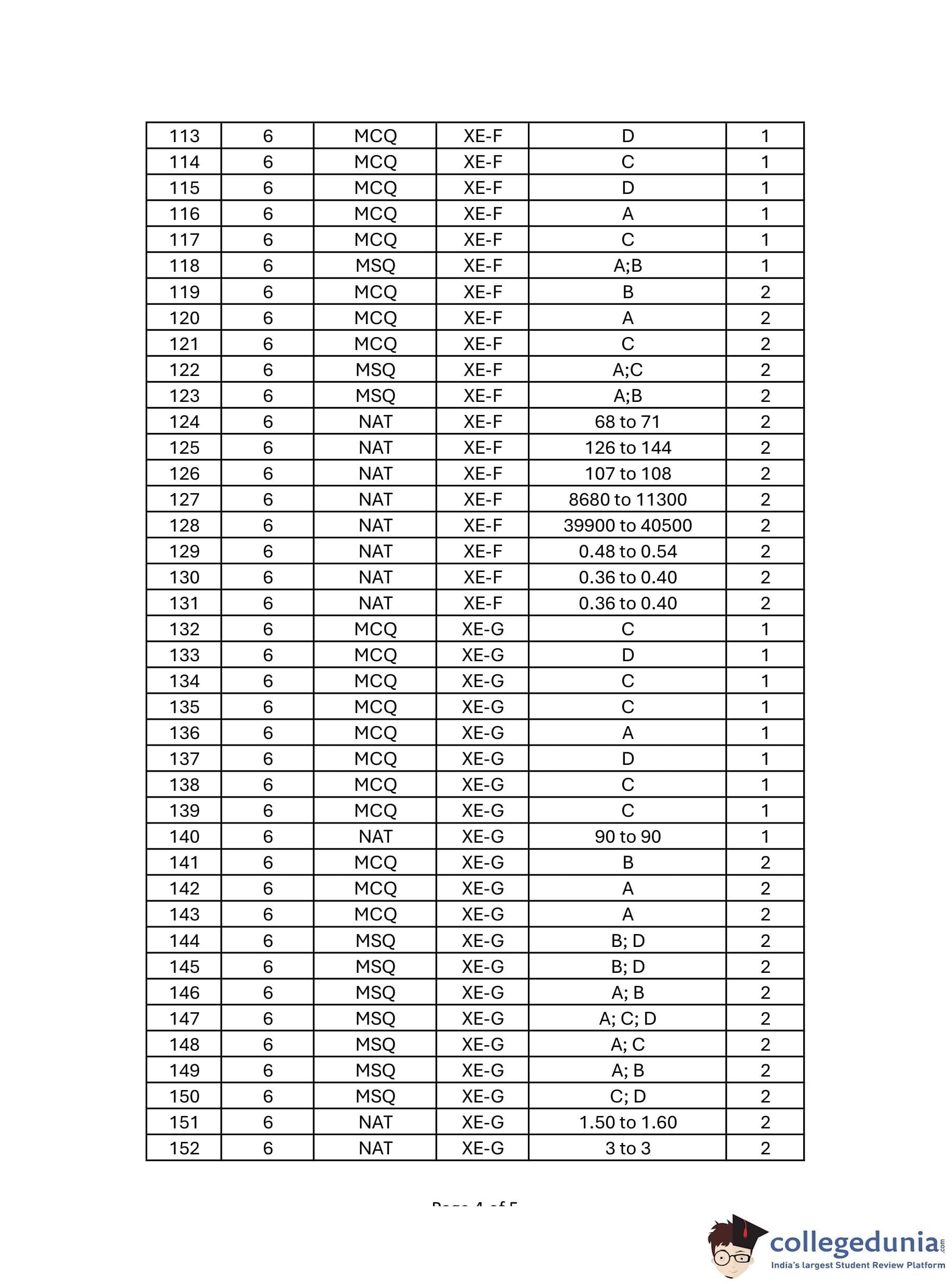
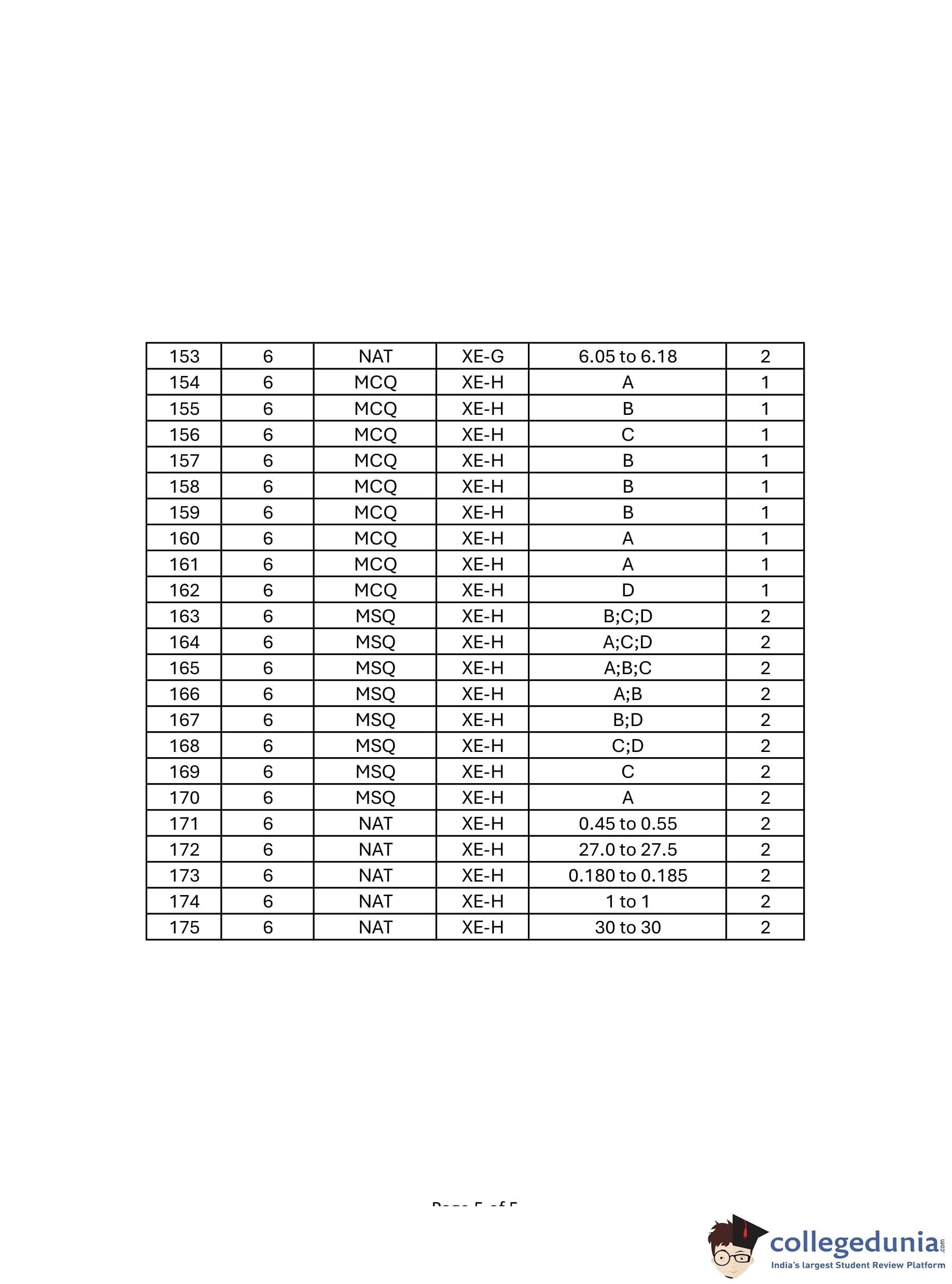
Also Check:
| Previous Year GATE Engineering Sciences Question Papers | GATE 2024 Engineering Sciences Paper Analysis |





Comments