GATE 2023 Physics (PH) Question Paper PDF is available here for download. IIT Kanpur conducted GATE 2023 Physics exam on February 11, 2023 in the Afternoon Session from 02:30 PM to 05:30 PM. Students have to answer 65 questions in GATE 2023 Physics Question Paper carrying a total weightage of 100 marks. 10 questions are from the General Aptitude section and 55 questions are from Core Discipline.
GATE 2023 Physics (PH) Question Paper with Solutions PDF
| GATE 2023 Physics (PH) Question Paper with Solutions PDF | Check Solutions |

“You are delaying the completion of the task. Send _________ contributions at the earliest.”
References : _________ : : Guidelines : Implement
(By word meaning)
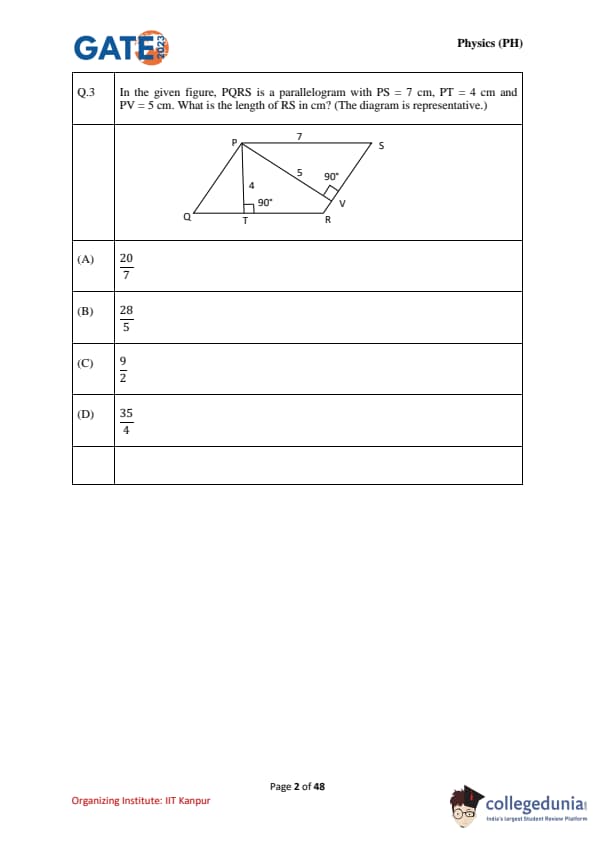
In the given figure, PQRS is a parallelogram with \(PS = 7~cm\), \(PT = 4~cm\) and \(PV = 5~cm\). What is the length of \(RS\) in cm? (The diagram is representative.)

In 2022, June Huh was awarded the Fields medal, which is the highest prize in Mathematics. When he was younger, he was also a poet. He did not win any medals in the International Mathematics Olympiads. He dropped out of college. Based only on the above information, which one of the following statements can be logically inferred with certainty?
A line of symmetry is defined as a line that divides a figure into two parts in a way such that each part is a mirror image of the other part about that line. The given figure consists of 16 unit squares arranged as shown. In addition to the three black squares, what is the minimum number of squares that must be coloured black, such that both PQ and MN form lines of symmetry? (The figure is representative)

Human beings are one among many creatures that inhabit an imagined world. In this imagined world, some creatures are cruel. If in this imagined world it is given that the statement “Some human beings are not cruel creatures” is FALSE, then which of the following set of statement(s) can be logically inferred with certainty?
(i) All human beings are cruel creatures.
(ii) Some human beings are cruel creatures.
(iii) Some creatures that are cruel are human beings.
(iv) No human beings are cruel creatures.
To construct a wall, sand and cement are mixed in the ratio 3:1. The cost of sand and that of cement are in the ratio of 1:2.
If the total cost of sand and cement to construct the wall is 1000 rupees, then what is the cost (in rupees) of cement used?
The World Bank has declared that it does not plan to offer new financing to Sri Lanka, which is battling its worst economic crisis in decades, until the country has an adequate macroeconomic policy framework in place. In a statement, the World Bank said Sri Lanka needed to adopt structural reforms that focus on economic stabilization and tackle the root causes of its crisis. The latter has starved it of foreign exchange and led to shortages of food, fuel, and medicines. The bank is repurposing resources under existing loans to help alleviate shortages of essential items such as medicine, cooking gas, fertiliser, meals for children, and cash for vulnerable households.
Based only on the above passage, which one of the following statements can be inferred with certainty?
The coefficient of \(x^4\) in the polynomial \((x - 1)^3(x - 2)^3\) is equal to \underline{\hspace{2cm.
Which one of the following shapes can be used to tile (completely cover by repeating) a flat plane, extending to infinity in all directions, without leaving any empty spaces in between them? The copies of the shape used to tile are identical and are not allowed to overlap.
Which one of the following entropy (S) - temperature (T) diagrams CORRECTLY represents the Carnot cycle abcda shown in the P-V diagram?

Which one of the following is a dimensionless constant?
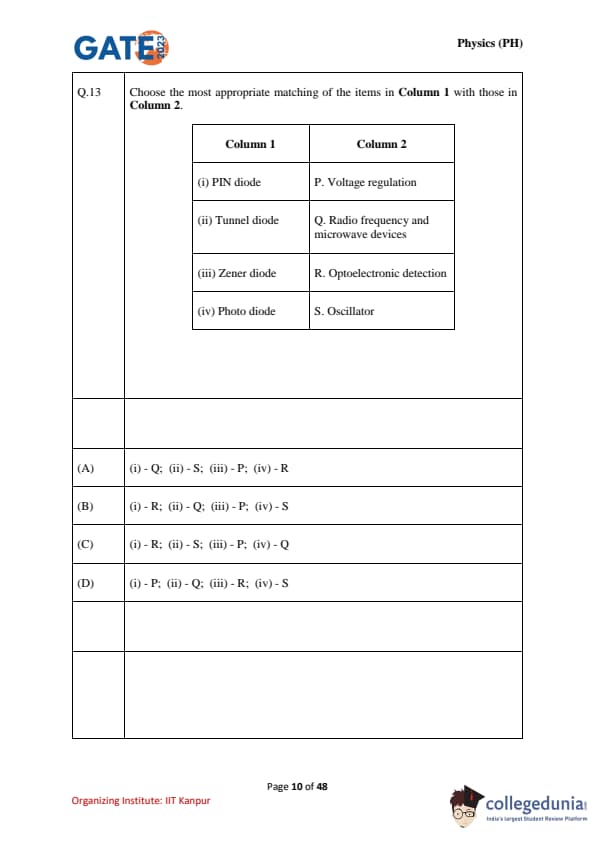
Choose the most appropriate matching of the items in Column 1 with those in Column 2.

The atomic number of an atom is 6. What is the spectroscopic notation of its ground state, according to Hund’s rules?
H is the Hamiltonian, \(\vec{L}\) the orbital angular momentum, and \(L_z\) is the z-component of \(\vec{L}\). The 1S state of the hydrogen atom in the non-relativistic formalism is an eigen function of which one of the following sets of operators?
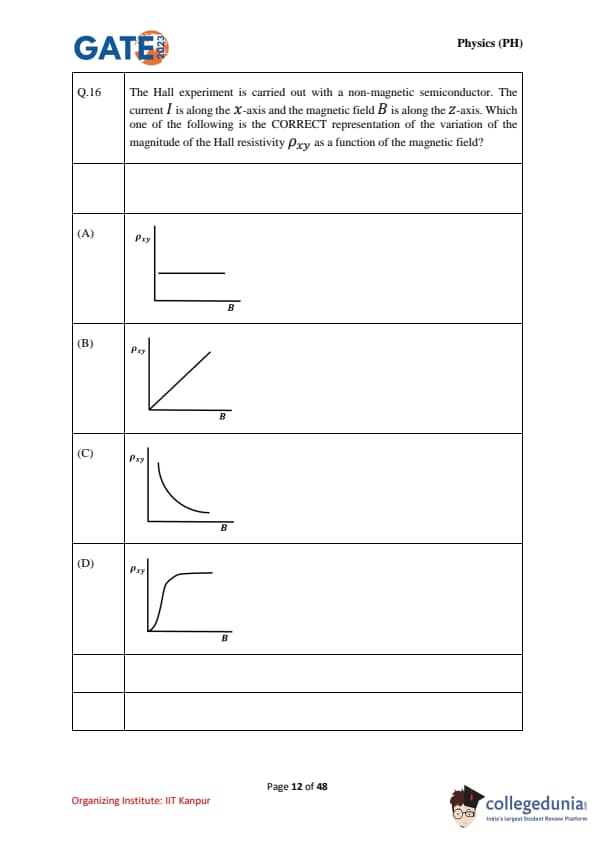
The Hall experiment is carried out with a non-magnetic semiconductor. The current \(I\) is along the X-axis and the magnetic field \(B\) is along the Z-axis. Which one of the following is the CORRECT representation of the variation of the magnitude of the Hall resistivity \(\rho_{xy}\) as a function of the magnetic field?

Consider a two-dimensional Cartesian coordinate system in which a rank 2 contravariant tensor is represented by the matrix \[ \begin{pmatrix} 0 & 1
1 & 0 \end{pmatrix} \]
The coordinate system is rotated anticlockwise by an acute angle \(\theta\) with the origin fixed. Which one of the following matrices represents the tensor in the new coordinate system?
A compound consists of three ions X, Y, and Z. The Z ions are arranged in an FCC arrangement. The X ions occupy \(\frac{1}{6}\) of the tetrahedral voids and the Y ions occupy \(\frac{1}{3}\) of the octahedral voids. Which one of the following is the CORRECT chemical formula of the compound?
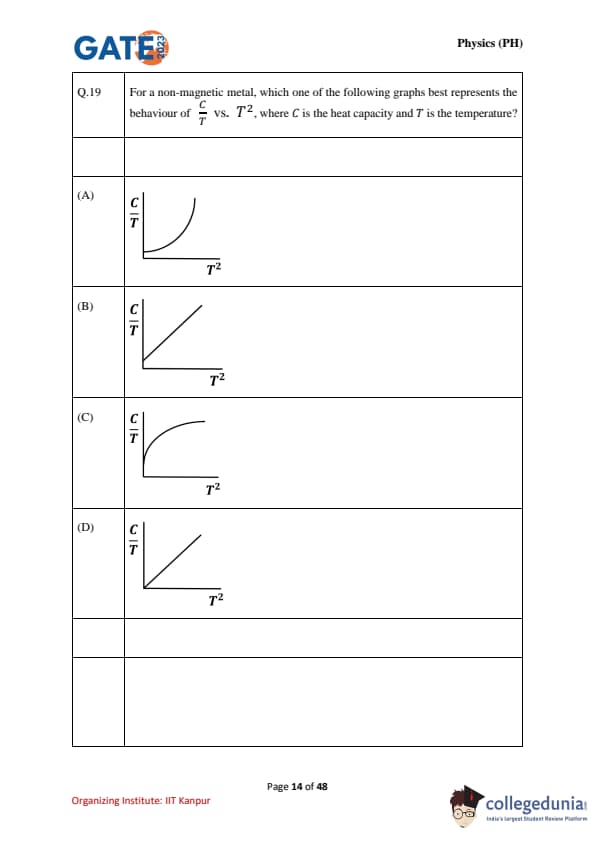
For a non-magnetic metal, which one of the following graphs best represents the behaviour of \(\frac{C}{T}\) vs. \(T^2\), where \(C\) is the heat capacity and \(T\) is the temperature?

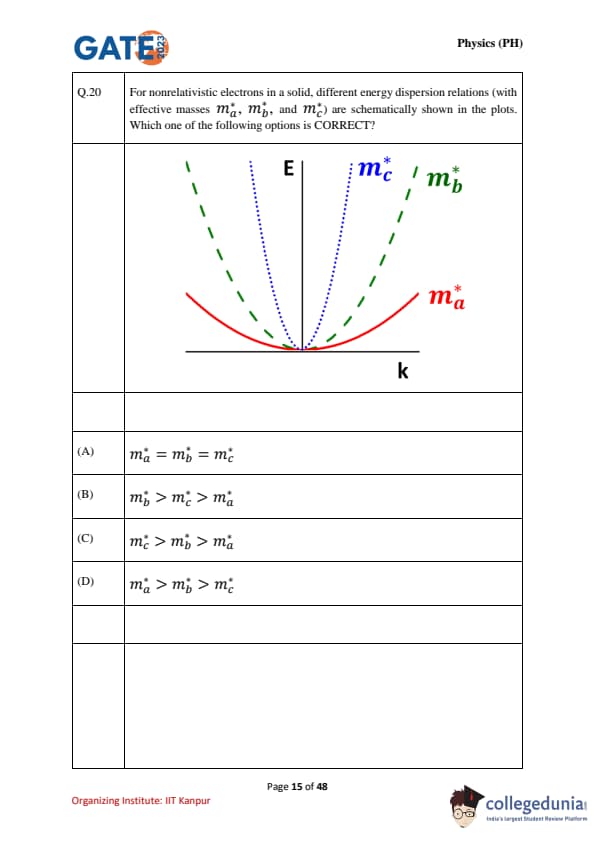
For nonrelativistic electrons in a solid, different energy dispersion relations with effective masses \(m_a^*, m_b^*, m_c^*\) are schematically shown in the plots. Which one of the following options is CORRECT?

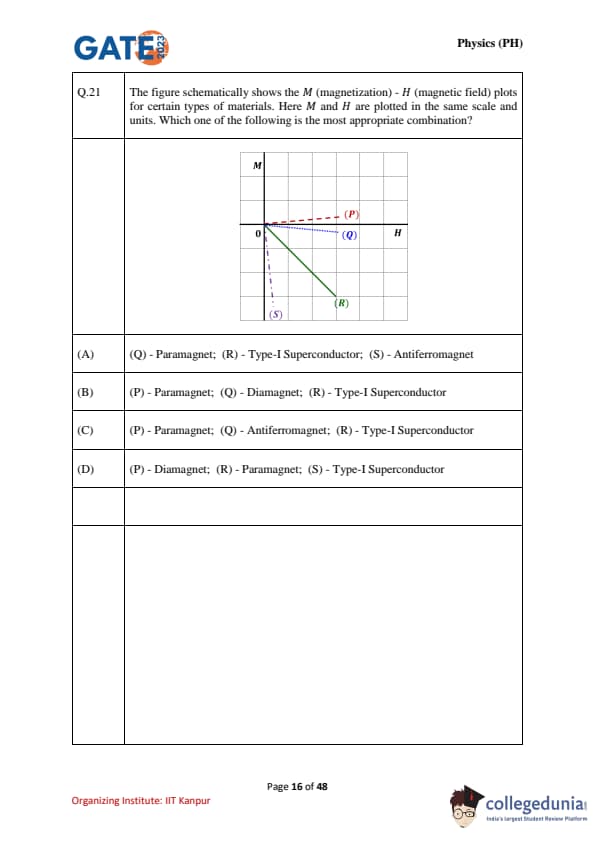
The figure schematically shows the M (magnetization) - H (magnetic field) plots for certain types of materials. Here M and H are plotted in the same scale and units. Which one of the following is the most appropriate combination?

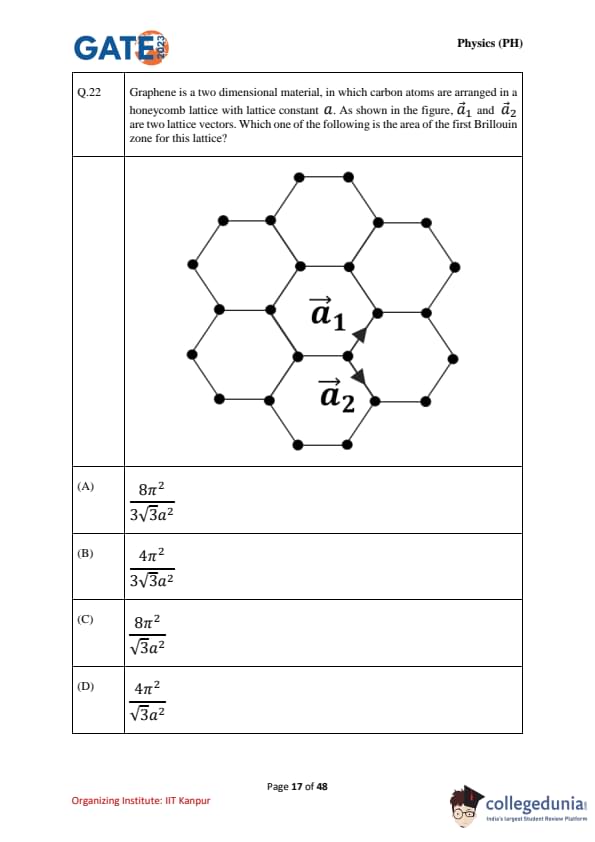
Graphene is a two-dimensional material, in which carbon atoms are arranged in a honeycomb lattice with lattice constant \(a\). As shown in the figure, \(\vec{a_1}\) and \(\vec{a_2}\) are two lattice vectors. Which one of the following is the area of the first Brillouin zone for this lattice?

A \(^{60}\)Co nucleus emits a \(\beta\)-particle and is converted to \(^{60}\)Ni\(^{*}\) with \(J^P = 4^+\), which in turn decays to the \(^{60}\)Ni ground state with \(J^P = 0^+\) by emitting two photons in succession, as shown in the figure. Which one of the following statements is CORRECT?

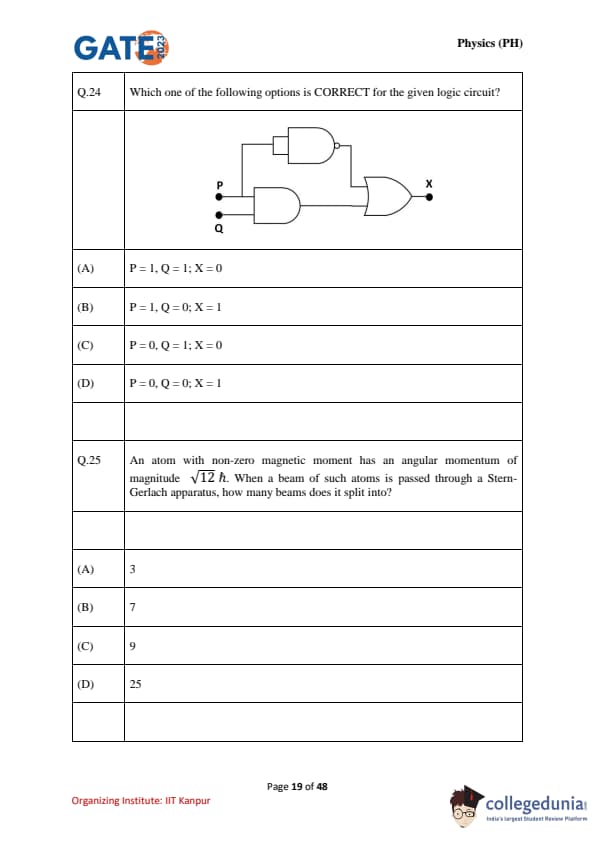
Which one of the following options is CORRECT for the given logic circuit?

An atom with non-zero magnetic moment has an angular momentum of magnitude \(\sqrt{12}\hbar\). When a beam of such atoms is passed through a Stern-Gerlach apparatus, how many beams does it split into?
A \(4 \times 4\) matrix \(M\) has the property \(M^{\dagger} = -M\) and \(M^4 = 1\), where \(1\) is the \(4 \times 4\) identity matrix. Which one of the following is the CORRECT set of eigenvalues of the matrix \(M\)?
The \(\Xi^{0*}\) particle is a member of the Baryon decuplet with isospin state \[ | I, I_3 \rangle = \left| \frac{1}{2}, \frac{1}{2} \right| \quad and strangeness quantum number \quad -2. \]
In the quark model, which one of the following is the flavour part of the \(\Xi^{0*}\) wavefunction?
Which of the following is/are the CORRECT option(s) for the Joule-Thomson effect?
The deuteron is a bound state of a neutron and a proton. Which of the following statements is/are CORRECT?
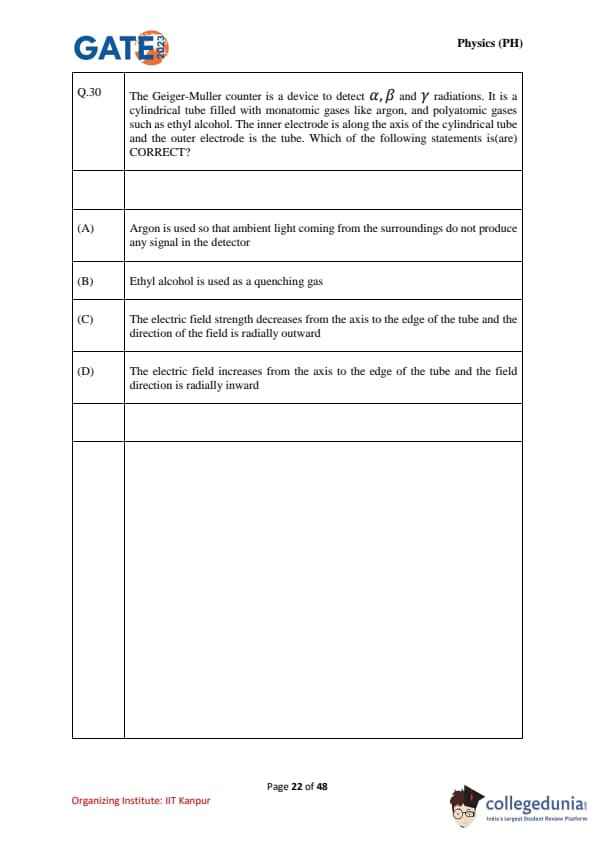
The Geiger-Muller counter is a device to detect \(\alpha\), \(\beta\), and \(\gamma\) radiations. It is a cylindrical tube filled with monatomic gases like argon, and polyatomic gases such as ethyl alcohol. The inner electrode is along the axis of the cylindrical tube and the outer electrode is the tube. Which of the following statements is/are CORRECT?
Consider an isolated magnetized sphere of radius \(R\) with a uniform magnetization \(\vec{M}\) along the positive \(z\) direction, with the north and south poles of the sphere lying on the \(z\) axis. It is given that the magnetic field inside the sphere is \(\vec{B} = \dfrac{2\mu_0}{3}\vec{M}\), where \(\mu_0\) is the permeability of vacuum. Which of the following statements is(are) CORRECT?
Which of the following options represent(s) linearly independent pair(s) of functions of a real variable \(x\)?
In the vector model of angular momentum applied to atoms, what is the minimum angle in degrees (in integer) made by the orbital angular momentum vector and the positive z axis for a \(2p\) electron?
For a transistor amplifier, the frequency response is such that the mid band voltage gain is 200. The cutoff frequencies are 20 Hz and 20 kHz. What is the ratio (rounded off to two decimal places) of the voltage gain at 10 Hz to that at 100 kHz?
An electric field as a function of radial coordinate \(r\) has the form \(\vec{E} = \alpha \dfrac{e^{-r^2}}{r} \hat{r}\), where \(\alpha\) is a constant. Assume that dimensions are appropriately taken care of. The electric flux through a sphere of radius \(\sqrt{2}\), centered at the origin, is \(\Phi\). What is the value of \(\dfrac{\Phi}{2\pi\alpha}\) (rounded off to two decimal places)?
It is given that the electronic ground state of a diatomic molecule \(X_2\) has even parity and the nuclear spin of \(X\) is 0. Which one of the following is the CORRECT statement with regard to the rotational Raman spectrum (\(J\) is the rotational quantum number) of this molecule?
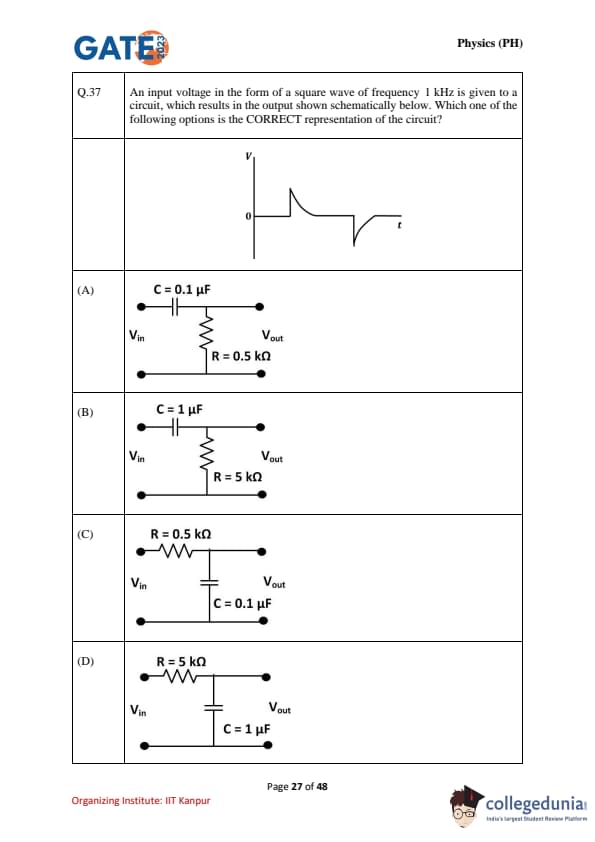
An input voltage in the form of a square wave of frequency 1 kHz is given to a circuit, which results in the output shown schematically below. Which one of the following options is the CORRECT representation of the circuit?

A simple harmonic oscillator with an angular frequency \(\omega\) is in thermal equilibrium with a reservoir at absolute temperature \(T\), with \(\omega = \frac{2\pi k_B T}{h}\). Which one of the following is the partition function of the system?
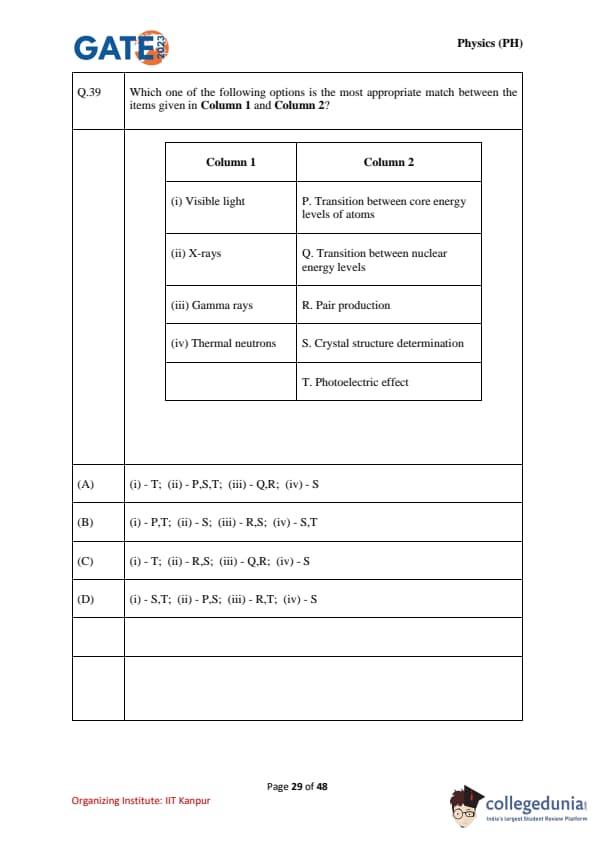
Which one of the following options is the most appropriate match between the items given in Column 1 and Column 2?

A rod \(PQ\) of proper length \(L\) lies along the \(X\)-axis and moves towards the positive \(X\)-direction with speed \(v = \frac{3c}{5}\) with respect to the ground (see figure), where \(c\) is the speed of light in vacuum. An observer on the ground measures the positions of \(P\) and \(Q\) at different times \(t_P\) and \(t_Q\) respectively in the ground frame, and finds the difference between them to be \(\frac{9L}{10}\). What is the value of \(t_Q - t_P\)?

A symmetric top has principal moments of inertia \(I_1 = I_2 = \dfrac{2\alpha}{3}\), \(I_3 = 2\alpha\) about a set of principal axes 1, 2, 3 respectively, passing through its center of mass, where \(\alpha\) is a positive constant. There is no force acting on the body and the angular speed of the body about the 3-axis is \(\omega_3 = \dfrac{1}{8}\) rad/s. With what angular frequency in rad/s does the angular velocity vector \(\vec{\omega_1}\) precess about the 3-axis?
A particle of mass \(m\) is free to move on a frictionless horizontal two-dimensional \((r, \theta)\) plane, and is acted upon by a force \(\vec{F} = -\dfrac{k}{r^3}\hat{r}\) with \(k\) being a positive constant. If \(p_r\) and \(p_\theta\) are the generalized momenta corresponding to \(r\) and \(\theta\) respectively, then what is the value of \(\dfrac{dp_r}{dt}\)?
Consider two real functions \[ U(x,y) = xy(x^2 - y^2), \] \[ V(x,y) = ax^4 + by^4 + cx^2y^2 + k, \]
where \(k\) is a real constant and \(a, b, c\) are real coefficients. If \(U(x, y) + i V(x, y)\) is analytic, then what is the value of \(a \times b \times c\)?
Young’s double slit experiment is performed using a beam of \(C_{60}\) (fullerene) molecules, each molecule being made up of 60 carbon atoms. When the slit separation is 50 nm, fringes are formed on a screen kept at a distance of 1 m from the slits. Now, the experiment is repeated with \(C_{70}\) molecules with a slit separation of 92.5 nm. The kinetic energies of both the beams are the same. The position of the 4\(^{th}\) bright fringe for \(C_{60}\) will correspond to the \(n^{th}\) bright fringe for \(C_{70}\). What is the value of \(n\) (rounded off to the nearest integer)?
A neutron beam with a wave vector \(\vec{k}\) and an energy 20.4 meV diffracts from a crystal with an outgoing wave vector \(\vec{k'}\). One of the diffraction peaks is observed for the reciprocal lattice vector \(\vec{G}\) of magnitude \(3.14\) \AA\(^{-1}\). What is the diffraction angle in degrees (rounded off to the nearest integer) that \(\vec{k}\) makes with the plane? (Use mass of neutron = \(1.67 \times 10^{-27}\) Kg)
In the first Brillouin zone of a rectangular lattice (lattice constants \(a = 6\) \AA\ and \(b = 4\) \AA), three incoming phonons with the same wave vector \(\langle 1.2\) \AA\(^{-1}, 0.6\) \AA\(^{-1}\rangle\) interact to give one phonon. Which one of the following is the CORRECT wave vector of the resulting phonon?
For a covalently bonded solid consisting of ions of mass \(m\), the binding potential can be assumed to be given by \[ U(r) = -\varepsilon \left( \frac{r}{r_0} \right) e^{-\frac{r}{r_0}}, \]
where \(\varepsilon\) and \(r_0\) are positive constants. What is the Einstein frequency of the solid in Hz?
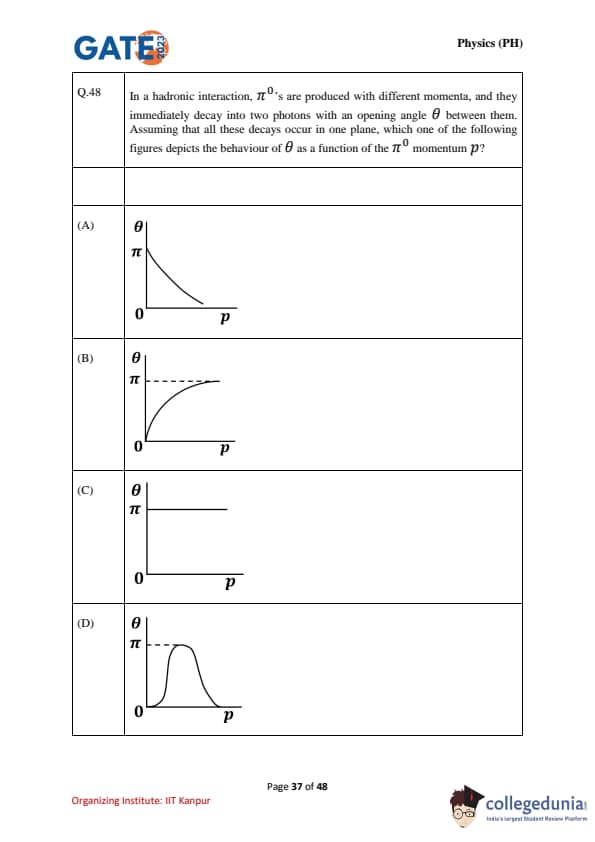
In a hadronic interaction, \(\pi^0\)'s are produced with different momenta, and they immediately decay into two photons with an opening angle \(\theta\) between them. Assuming that all these decays occur in one plane, which one of the following figures depicts the behaviour of \(\theta\) as a function of the \(\pi^0\) momentum \(p\)?

A particle has wavefunction \[ \psi(x, y, z) = N z e^{-\alpha(x^2 + y^2 + z^2)}, \]
where \(N\) is a normalization constant and \(\alpha\) is a positive constant. In this state, which one of the following options represents the eigenvalues of \(L^2\) and \(L_z\) respectively?
Some values of \(Y_\ell^m\) are: \[ Y_0^0 = \frac{1}{\sqrt{4\pi}}, \ Y_1^0 = \frac{\sqrt{3}}{\sqrt{4\pi}} \cos \theta, \ Y_1^{\pm 1} = \mp \frac{\sqrt{3}}{8\pi} \sin \theta e^{\pm i \phi} \]
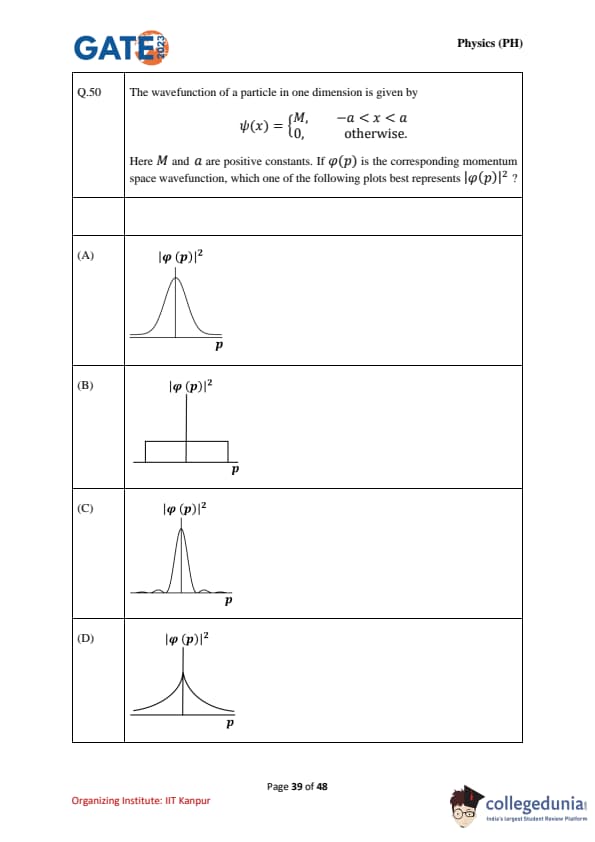
The wavefunction of a particle in one dimension is given by \[ \psi(x) = \begin{cases} M, & for \ -a < x < a,
0, & otherwise. \end{cases} \]
Here \(M\) and \(a\) are positive constants. If \(\varphi(p)\) is the corresponding momentum space wavefunction, which one of the following plots best represents \(|\varphi(p)|^2\)?

Consider a particle in a two dimensional infinite square well potential of side \(L\), with \(0 \leq x \leq L\) and \(0 \leq y \leq L\). The wavefunction of the particle is zero only along the line \(y = \dfrac{L}{2}\), apart from the boundaries of the well. If the energy of the particle in this state is \(E\), what is the energy of the ground state?
Consider two non-identical spin-\(\dfrac{1}{2}\) particles labelled 1 and 2 in the spin product state \(\left[\left|\dfrac{1}{2}, -\dfrac{1}{2}\right\rangle \left|\dfrac{1}{2}, \dfrac{1}{2}\right\rangle\right]\). The Hamiltonian of the system is \(H = \dfrac{4\lambda}{\hbar^2} \vec{S_1} \cdot \vec{S_2}\), where \(\vec{S_1}\) and \(\vec{S_2}\) are the spin operators of particles 1 and 2, respectively, and \(\lambda\) is a constant with appropriate dimensions. What is the expectation value of \(H\) in the above state?
A spin \(\dfrac{1}{2}\) particle is in a spin up state along the \(x\)-axis (with unit vector \(\hat{x}\)) and is denoted as \(\left|\dfrac{1}{2}, \dfrac{1}{2}\right\rangle_x\). What is the probability of finding the particle to be in a spin up state along the direction \(\hat{x'}\), which lies in the \(xy\)-plane and makes an angle \(\theta\) with respect to the positive \(x\)-axis, if such a measurement is made?
Different spectral lines of the Balmer series (transitions \(n \to 2\), with \(n\) being the principal quantum number) fall one at a time on a Young’s double slit apparatus. The separation between the slits is \(d\) and the screen is placed at a constant distance from the slits. What factor should \(d\) be multiplied by to maintain a constant fringe width for various lines, as \(n\) takes different allowed values?
Under parity and time reversal transformations, which of the following statements is(are) TRUE about the electric dipole moment \(\vec{p}\) and the magnetic dipole moment \(\mu\)?
Consider the complex function \[ f(z) = \dfrac{z^2 \sin z}{(z - \pi)^4}. \]
At \(z = \pi\), which of the following options is(are) CORRECT?
Consider the vector field \(\vec{V}\) consisting of the velocities of points on a thin horizontal disc of radius \(R = 2 \, m\), moving anticlockwise with uniform angular speed \(\omega = 2 \, rad/sec\) about an axis passing through its center. If \(V = |\vec{V}|\), then which of the following options is/are CORRECT? (In the options, \(\hat{r}\) and \(\hat{\theta}\) are unit vectors corresponding to the plane polar coordinates \(r\) and \(\theta\)).
A slow moving \(\pi^{-}\) particle is captured by a deuteron (\(d\)) and this reaction produces two neutrons (\(n\)) in the final state, i.e., \(\pi^{-} + d \to n + n\). Neutron and deuteron have even intrinsic parities, whereas \(\pi^{-}\) has odd intrinsic parity. \(L\) and \(S\) are the orbital and spin angular momenta, respectively of the system of two neutrons. Which of the following statements regarding the final two-neutron state is/are CORRECT?
Two independent electrostatic configurations are shown in the figure. Configuration (I) consists of an isolated point charge \(q = 1\ C\), and configuration (II) consists of another identical charge surrounded by a thick conducting shell of inner radius \(R_1 = 1\ m\) and outer radius \(R_2 = 2\ m\), with the charge being at the center of the shell.
\[ W_I = \frac{\epsilon_0}{2} \int E_I^2 dV \quad and \quad W_{II} = \frac{\epsilon_0}{2} \int E_{II}^2 dV, \]
where \(E_I\) and \(E_{II}\) are the magnitudes of the electric fields for configurations (I) and (II) respectively, \(\epsilon_0\) is the permittivity of vacuum, and the volume integrations are carried out over all space. If \[ \frac{8\pi}{\epsilon_0} |W_I - W_{II}| = \frac{1}{n}, \]
what is the value of the integer \(n\)?

In pion nucleon scattering, the pion and nucleon can combine to form a short-lived bound state called the \(\Delta\) particle (\(\pi + N \rightarrow \Delta\)). The masses of the pion, nucleon, and the \(\Delta\) particle are 140 MeV/\(c^2\), 938 MeV/\(c^2\), and 1230 MeV/\(c^2\), respectively. In the lab frame, where the nucleon is at rest, what is the minimum energy (in MeV/\(c^2\), rounded off to one decimal place) of the pion to produce the \(\Delta\) particle?
Consider an electromagnetic wave propagating in the \(z\)-direction in vacuum, with the magnetic field given by \(\vec{B} = \vec{B_0} e^{i(kz - \omega t)}\). If \(B_0 = 10^{-8}\) T, the average power passing through a circle of radius 1.0 m placed in the \(xy\) plane is \(P\) (in Watts). Using \(\epsilon_0 = 10^{-11} \dfrac{c^2}{N m^2}\), what is the value of \(\dfrac{10^3 P}{\pi}\) (rounded off to one decimal place)?
An \(\alpha\)-particle is emitted from the decay of Americium (Am) at rest, i.e., \(^{241}_{94}Am \rightarrow ^{237}_{92}U + \alpha\). The rest masses of \(^{241}_{94}Am\), \(^{237}_{92}U\) and \(\alpha\) are 224.544 GeV/c\(^2\), 220.811 GeV/c\(^2\) and 3.728 GeV/c\(^2\) respectively. What is the kinetic energy (in MeV/c\(^2\), rounded off to two decimal places) of the \(\alpha\)-particle?
Consider 6 identical, non-interacting, spin \(\dfrac{1}{2}\) atoms arranged on a crystal lattice at absolute temperature \(T\). The z-component of the magnetic moment of each of these atoms can be \(\pm \mu_B\). If \(P\) and \(Q\) are the probabilities of the net magnetic moment of the solid being \(2\mu_B\) and \(6\mu_B\) respectively, what is the value of \(\dfrac{P}{Q}\) (in integer)?
Two identical, non-interacting \(^4He_2\) atoms are distributed among 4 different non-degenerate energy levels. The probability that they occupy different energy levels is \(p\). Similarly, two \(^3He_2\) atoms are distributed among 4 different non-degenerate energy levels, and the probability that they occupy different levels is \(q\). What is the value of \(\dfrac{p}{q}\) (rounded off to one decimal place)?
Two identical bodies kept at temperatures 800 K and 200 K act as the hot and the cold reservoirs of an ideal heat engine, respectively. Assume that their heat capacity (\(C\)) in Joules/K is independent of temperature and that they do not undergo any phase change. Then, the maximum work that can be obtained from the heat engine is \(n \times C\) Joules. What is the value of \(n\) (in integer)?


































Also Check:
| Previous Year GATE Physics Question Papers | GATE 2023 Physics Paper Analysis |
| GATE Physics Exam Pattern | GATE Physics Syllabus |





Comments