GATE 2023 Naval Architecture and Marine Engineering (NM) Question Paper PDF is available here for download. IIT Kanpur conducted GATE 2023 Naval Architecture and Marine Engineering exam on February 11, 2023 in the Afternoon Session from 02:30 PM to 05:30 PM. Students have to answer 65 questions in GATE 2023 Naval Architecture and Marine Engineering Question Paper carrying a total weightage of 100 marks. 10 questions are from the General Aptitude section and 55 questions are from Engineering Mathematics and Core Discipline.
GATE 2023 Naval Architecture and Marine Engineering (NM) Question Paper with Solutions PDF
| GATE 2023 Naval Architecture and Marine Engineering Question Paper with Solutions | Check Solutions |

"You are delaying the completion of the task. Send _______________ contributions at the earliest."
References : _______________ :: Guidelines : Implement
(By word meaning)
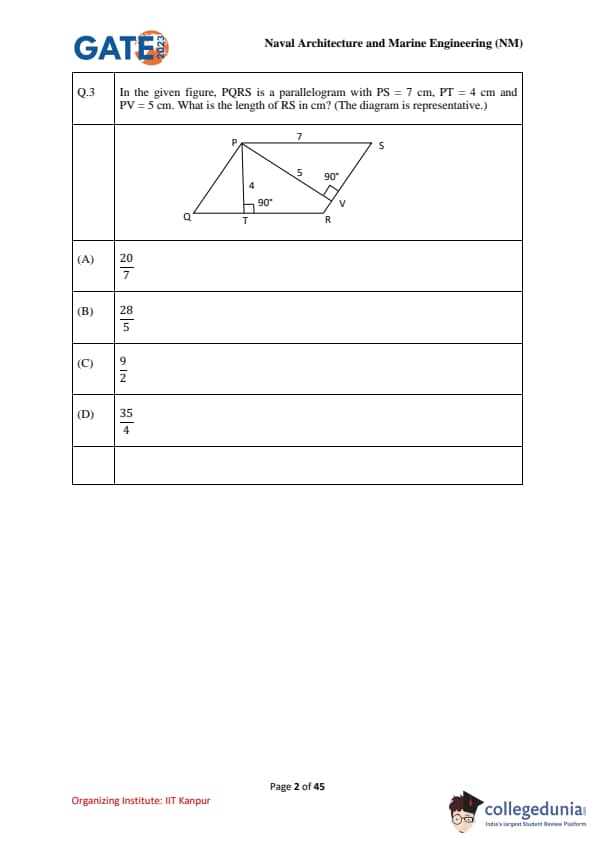
In the given figure, PQRS is a parallelogram with PS = 7 cm, PT = 4 cm and PV = 5 cm. What is the length of RS in cm? (The diagram is representative.)

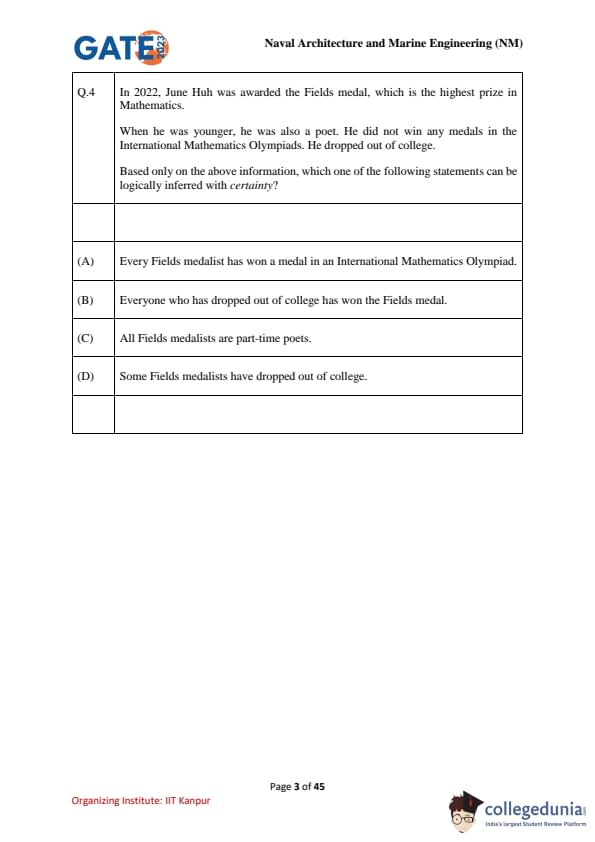
In 2022, June Huh was awarded the Fields medal, which is the highest prize in Mathematics.
When he was younger, he was also a poet. He did not win any medals in the International Mathematics Olympiads. He dropped out of college.
Based only on the above information, which one of the following statements can be logically inferred with certainty?
A line of symmetry is defined as a line that divides a figure into two parts in a way such that each part is a mirror image of the other part about that line.
The given figure consists of 16 unit squares arranged as shown. In addition to the three black squares, what is the minimum number of squares that must be coloured black, such that both PQ (anti-diagonal) and MN (main diagonal) form lines of symmetry? (The figure is representative)

Human beings are one among many creatures that inhabit an imagined world. In this imagined world, some creatures are cruel. If in this imagined world, it is given that the statement "Some human beings are not cruel creatures" is FALSE, then which of the following set of statement(s) can be logically inferred with certainty?
(i) All human beings are cruel creatures.
(ii) Some human beings are cruel creatures.
(iii) Some creatures that are cruel are human beings.
(iv) No human beings are cruel creatures.
To construct a wall, sand and cement are mixed in the ratio of 3:1. The cost of sand and that of cement are in the ratio of 1:2.
If the total cost of sand and cement to construct the wall is 1000 rupees, then what is the cost (in rupees) of cement used?
The World Bank has declared that it does not plan to offer new financing to Sri Lanka, which is battling its worst economic crisis in decades, until the country has an adequate macroeconomic policy framework in place. In a statement, the World Bank said Sri Lanka needed to adopt structural reforms that focus on economic stabilisation and tackle the root causes of its crisis. The latter has starved it of foreign exchange and led to shortages of food, fuel, and medicines. The bank is repurposing resources under existing loans to help alleviate shortages of essential items such as medicine, cooking gas, fertiliser, meals for children, and cash for vulnerable households.
Based only on the above passage, which one of the following statements can be inferred with certainty?
The coefficient of \(x^4\) in the polynomial \((x - 1)^3 (x - 2)^3\) is equal to _________.
Which one of the following shapes can be used to tile (completely cover by repeating) a flat plane, extending to infinity in all directions, without leaving any empty spaces in between them? The copies of the shape used to tile are identical and are not allowed to overlap.
Consider the function \( z = \tan^{-1}\left(\frac{y}{x}\right) \), where \( x = u \sin v \) and \( y = u \cos v \). The partial derivative, \( \frac{\partial z}{\partial v} \) is
Consider the function \( z = x^3 - 2x^2y + xy^2 + 1 \). The directional derivative of z at the point (1, 2) along the direction \( 3\hat{i} + 4\hat{j} \) is
The vapor quality of steam in the turbine of a Rankine cycle can be improved by employing
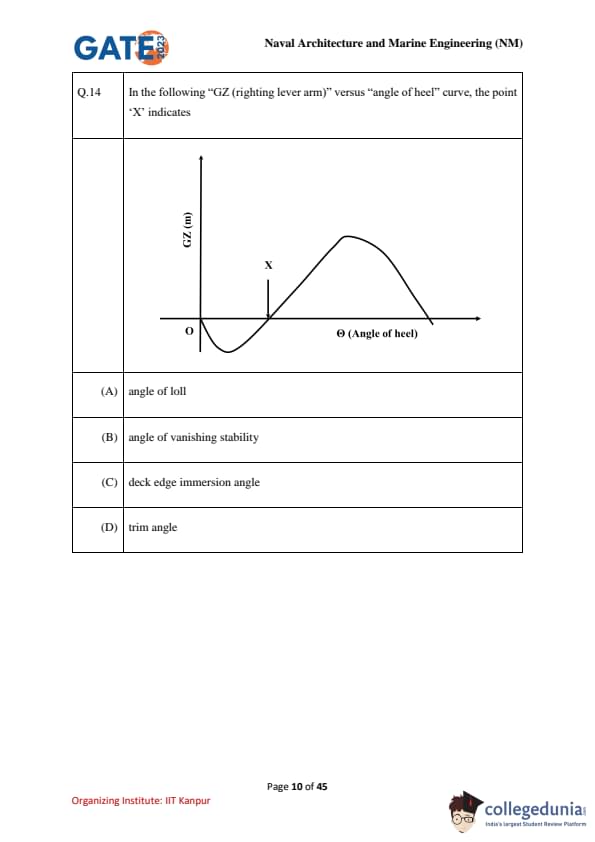
In the following "GZ (righting lever arm)" versus "angle of heel" curve, the point 'X' indicates

Comparing a catamaran (with a separation between demi-hulls) and a mono-hull craft of the same displacement and water plane area, the initial metacentric radius of the catamaran will be
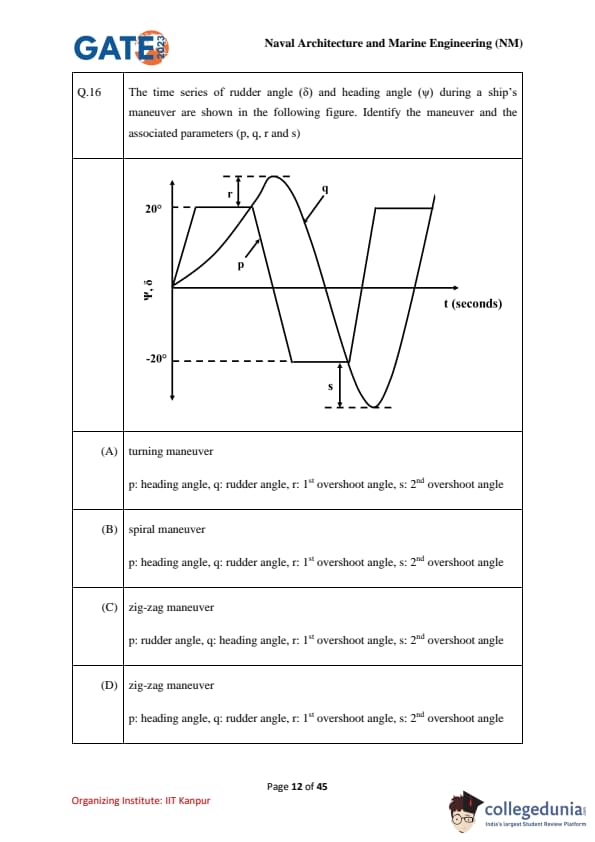
The time series of rudder angle (\(\delta\)) and heading angle (\(\psi\)) during a ship's maneuver are shown in the following figure. Identify the maneuver and the associated parameters (p, q, r and s)

A closed system undergoing a thermodynamic cycle consisting of two reversible isothermal and two reversible adiabatic processes is shown in the following figure. If \(\delta Q\) is the infinitesimal heat transfer and T is the instantaneous temperature, then the value of the contour integral \( \oint \frac{\delta Q}{T} \) is

In a marine steam power cycle employing regeneration, the feed water heater for waste heat recovery is placed after the
From the following, choose the offshore platform that can be used ONLY for offshore drilling purpose.
Which method among the following is based on the strain energy principle?
In dimensional analysis, according to Buckingham's \(\pi\)-theorem, if n is the total number of variables and m is the number of independent dimensions, then the maximum number of independent dimensionless \(\pi\)-groups will be
A submerged cylinder of diameter 1 m is rotating clockwise at 100 rpm, in a flow with a free stream velocity of 10 m/s. Assuming ideal flow, the number of stagnation points on the cylinder is
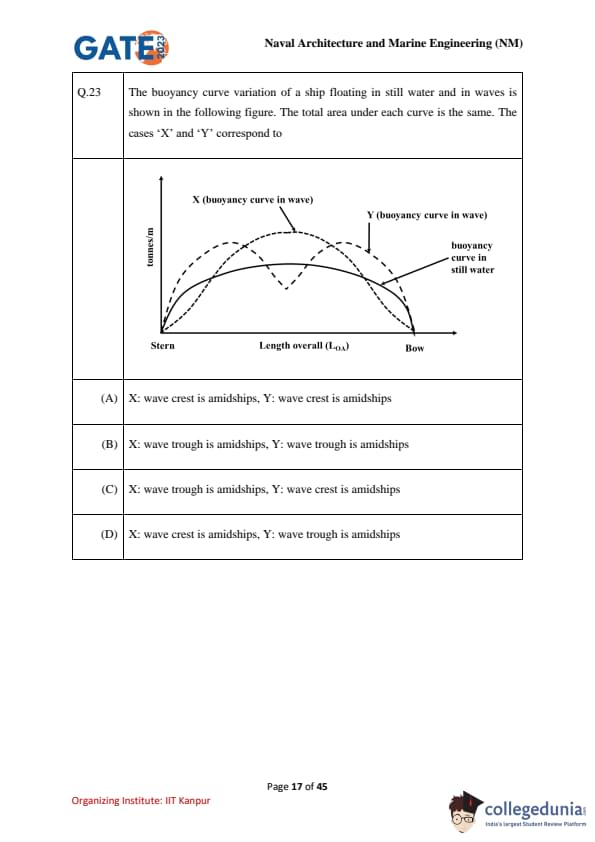
The buoyancy curve variation of a ship floating in still water and in waves is shown in the following figure. The total area under each curve is the same. The cases 'X' and 'Y' correspond to

Let X be any random variable and \( Y = -2X + 3 \). If E[Y] = 1 and E[Y\(^2\)] = 9, then which of the following are TRUE?
Consider the contour integral \( \oint_C \frac{dz}{z^4 + z^3 - 2z^2} \), along the curve \( |z| = 3 \) oriented in the counterclockwise direction. If Res[f, z\(_0\)] denotes the residue of f(z) at the point z\(_0\), then which of the following are TRUE?
A stationary ship has longitudinal symmetry. The surge, sway and heave motions are represented by indices 1-2-3, respectively and roll, pitch and yaw motions are represented by indices 4-5-6, respectively. Which of the following are TRUE about the added mass (\(A_{ij}\))?
The failure modes that may be observed in a riveted joint to fasten two plate members, subjected to shear load are
A rectangular barge is freely floating in a drydock as shown in the following figure. For longitudinal strength analysis which of the following are TRUE?

A ship of length 180 m has a displacement of 14400 tonnes and is floating on an even keel in sea water of density 1025 kg/m\(^3\). The trim changes by 0.18 m when a weight of 120 tonnes that is already onboard, is shifted 24 m forward. The longitudinal metacentric height is ____________ m.
A piezometer and a pitot tube measure the static and the total pressure of a fluid in a pipe flow respectively. The piezometer reads 100 kPa and the pitot tube shows 200 kPa. The density of the fluid is 1000 kg/m\(^3\). The velocity of the flow is ___________ m/s (round off to one decimal place)
A Carnot heat engine operates between two reservoirs of temperatures 900 \(^{\circ}\)C (T\(_H\)) and 30 \(^{\circ}\)C (T\(_L\)). If the heat transferred during one cycle to the engine from T\(_H\) is 150 kJ, then the energy rejected to T\(_L\) is ___________ kJ (round off to the nearest integer)
An oil tanker of breadth 20 m and having a displacement of 24000 tonnes in sea water (density of sea water = 1025 kg/m\(^3\)) is carrying oil of relative density 0.8 in 9 longitudinally distributed tanks which are all half-filled. Each longitudinal tank is 12 m long and 16 m wide. The apparent change in vertical center of gravity, due to the presence of oil in the tanks is ___________ m (round off to one decimal place)
For a regular sinusoidal wave propagating in deep water having wave height of 3.5 m and wave period of 9 s, the wave steepness is ___________ (round off to three decimal places)
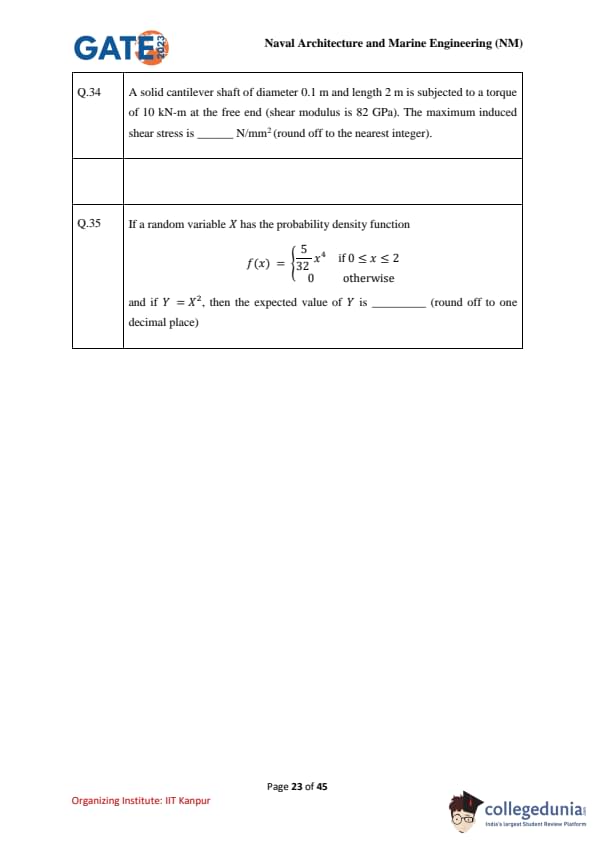
A solid cantilever shaft of diameter 0.1 m and length 2 m is subjected to a torque of 10 kN-m at the free end (shear modulus is 82 GPa). The maximum induced shear stress is ___________ N/mm\(^2\) (round off to the nearest integer).
If a random variable X has the probability density function \[ f(x) = \begin{cases} \frac{5}{32}x^4 & if 0 \le x \le 2
0 & otherwise \end{cases} \]
and if \( Y = X^2 \), then the expected value of Y is ___________ (round off to one decimal place)
The value of the surface integral \( \iint_S (x^2 \,dydz + y^2 \,dzdx + z^2 \,dxdy) \) over the surface of the cube given by \( 0 \le x \le 2, 0 \le y \le 2, 0 \le z \le 2 \), is
If the system of linear equations, \( x - ay - z = 0, ax - y - z = 0, x + y - z = 0 \), has infinite number of solutions, then the possible values of a are
Two 30 m long bilge keels of mass 40 tonnes each, are fitted at the turn of the bilge on port and starboard sides of a ship. The cross section of the bilge keel is shown in the following figure. Assume density of water = 1000 kg/m\(^3\). If the TPC (tonnes per centimeter) immersion of the ship is 50, then the change in the mean draft is ___________ cm

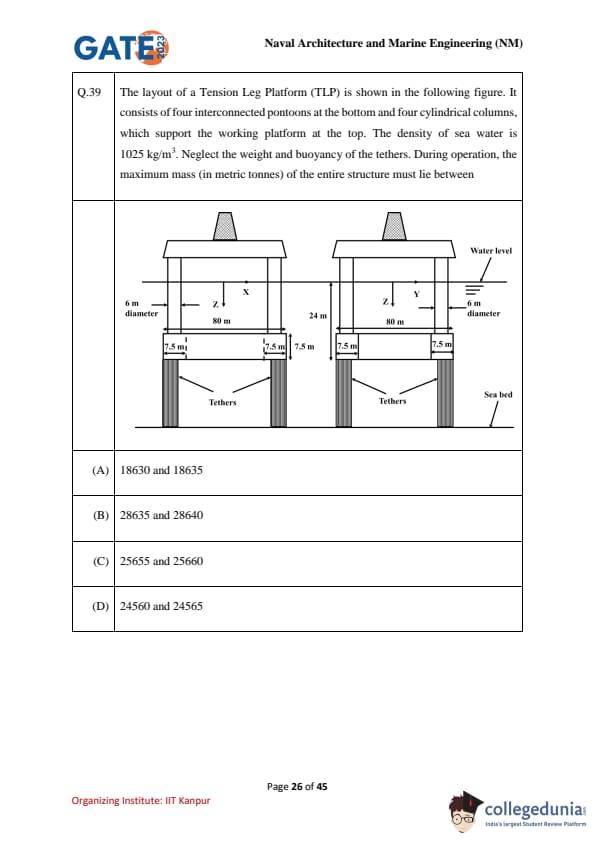
The layout of a Tension Leg Platform (TLP) is shown in the following figure. It consists of four interconnected pontoons at the bottom and four cylindrical columns, which support the working platform at the top. The density of sea water is 1025 kg/m\(^3\). Neglect the weight and buoyancy of the tethers. During operation, the maximum mass (in metric tonnes) of the entire structure must lie between

The trajectory of a model ship during a pure sway PMM test is shown below. The steady forward speed, u is 2.0 m/s. The maximum amplitude of sway motion, \(y_{Max}\) is 0.5 m and its period is 8 s. The magnitude of maximum drift angle, in degrees (round off to the nearest integer), and the magnitude of maximum sway acceleration, in m/s\(^2\) (round off to one decimal place), of the model respectively are

A ship of length 125 m has a design speed of 25 knots (1 knot = 0.5144 m/s). A 5.0 m long geometrically similar model with wetted surface area of 4 m\(^2\) has a coefficient of residuary resistance of \(1.346 \times 10^{-3}\) at the corresponding speed. The ship's residuary resistance in kN (in sea water of density 1025 kg/m\(^3\)), and the model speed in knots (round off to the nearest integer) respectively are
A fully filled water tank OABCD has a circular arc (AB) of radius 10 m at the bottom as shown in the following figure. The height BC is 10 m. The length OA and CD are 5 m and 15 m, respectively. The density of the water is \(\rho\) kg/m³ and the acceleration due to gravity is \(g\) m/s². The magnitude of the resultant hydrostatic force per unit width acting on AB in N/m lies between

The velocity vector of a 2D flow field is given by \(\vec{V} = 2y^2 \hat{i} + x^2t \hat{j}\).
The acceleration is
% Note: There's a typo in the OCR of the question (î twice) and options. The solution assumes the standard form V = uî + vĵ.
Water is flowing with a free stream velocity of 0.25 m/s around a submerged flat plate of 2 m length (in the direction of flow) and 1 m width. The local shear stress at a distance \(x\) from the leading edge of the plate is given by \[ \tau = \frac{0.332\rho u^2}{\sqrt{Re_x}} \]
where \(\rho = 1000\) kg/m³ is the density of the water, \(u\) is the free stream velocity and \(Re_x\) is the Reynolds number at \(x\). Assume that the flow is laminar, and the kinematic viscosity of water is \(10^{-6}\) m²/s. The drag force (in Newton) acting on one side of the plate lies between
For a 2D ideal flow, let \(\varphi\) be the velocity potential and \(\psi\) be the stream function. Which one of the following is TRUE?
A long body with elliptical cross section is held perpendicular to a 2D uniform steady flow field of horizontal velocity \(U_\infty\) as shown in the following figure. The heights of the control volume (bounded by the dashed lines) at the inlet and outlet are \(2h\) and \(4h\), respectively. The profile of the horizontal velocity far downstream is given by \(U(y) = \frac{U_\infty y}{2h}\). The density of the fluid is \(\rho\). The magnitude of the drag force per unit length acting on the body is

A 'T' section is welded to the flat bottom shell plate of a ship as shown in the following figure (bottom shell longitudinal). The neutral axis of the ship's midship section is 14 m above the bottom shell plate. The distance (X) of neutral axis of the 'T' section from the ship's neutral axis is ____________ m (round off to two decimal places)

A vertical frictionless piston-cylinder arrangement contains air of mass 1 kg. During a process, 50 J of heat is transferred from outside to the system such that the piston is raised slowly by 0.1 m from its initial equilibrium position. The mass of the piston is 1 kg, and the diameter is 0.1 m. Assume that g = 9.81 m/s², and Patm = 100 kPa. The change in internal energy of the air in J (round off to two decimal places) lies between

An insulated nozzle has an inlet cross-sectional area of 314 cm². Air flows through the nozzle with an inlet temperature of 300 K at a steady rate of 1.256 m³/s. The velocity at the exit is greater than that at the inlet by 210 m/s. Assume a constant \(C_p = 1.004\) kJ/kg-K. The temperature (in K) of air at the exit of the nozzle lies between
The heave natural frequencies of a Jacket structure, FPSO and a semi-submersible are \(\omega_J\), \(\omega_F\) and \(\omega_S\) respectively. Each one of them has a pay load capacity of 10000 tonnes. Which of the following is TRUE?
A simply supported beam with an overhang has experienced the bending moment as shown below. The corresponding concentrated load is

Let \(L = \begin{pmatrix} 3 & -1 & -1 & -1
-1 & 2 & -1 & 0
-1 & -1 & 3 & 0
-1 & 0 & -1 & 1 \end{pmatrix}\). Which of the following are TRUE?
For a given time varying load applied on a single degree of freedom system, the dynamic response amplitude is always less than the static response amplitude if
The stress field, \(\sigma_x = 4x^3 + 3x^2y + 5xy^2\) \(\sigma_y = -x^3 + 6x^2y - 7xy^2\) \(\tau_{xy} = -5x^2y - 3xy^2\)
would satisfy the strain compatibility condition if
If y(x) is the solution of the differential equation \[ (1+x^2)y'' - 2xy' = 0 \]
satisfying y(0) = 0 and y'(0) = 3, then y(1) equals ____________
For a ship of length L = 100 m, the distance between the bow and stern pressure system is 0.942L. Assume g = 10 m/s². The ship velocity corresponding to the prismatic hump of the wave making resistance curve is ____________ m/s (round off to one decimal place)
A vessel of 100 m length has a constant triangular cross-section with a depth of 12 m and breadth of 15 m as shown in following figure. The vessel has a vertical center of gravity (KG) = 6.675 m. The minimum draft (d), at which the vessel will become stable is ____________ m (round off to one decimal place)

For a marine screw propeller, the open water characteristics at J = 0.6 are \(K_T = 0.1336\) and \(10K_Q = 0.2010\). The open water propeller efficiency \(\eta_o\), is ____________ (round off to two decimal places)
Saturated liquid water (m = 1 kg) initially at 0.101 MPa and 100 °C is heated at constant pressure until the temperature increases to 500 °C. Assume a constant \(C_p\) of steam = 1.9 kJ/kg-K, and enthalpy of vaporization, \(h_{fg}\) = 2257 kJ/kg at 0.101 MPa. The change in entropy of the water is ____________ kJ/K (round off to two decimal places)
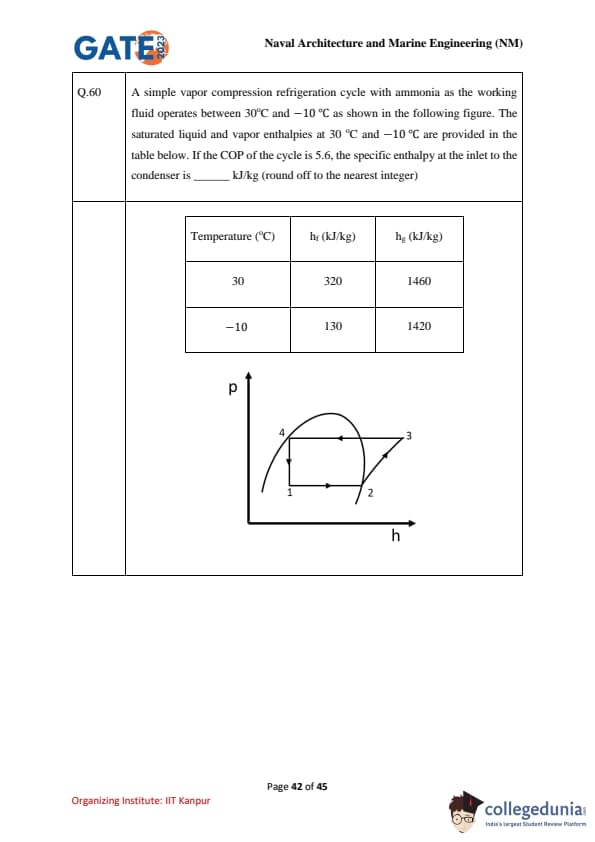
A simple vapor compression refrigeration cycle with ammonia as the working fluid operates between 30°C and -10 °C as shown in the following figure. The saturated liquid and vapor enthalpies at 30 °C and -10 °C are provided in the table below. If the COP of the cycle is 5.6, the specific enthalpy at the inlet to the condenser is ____________ kJ/kg (round off to the nearest integer)

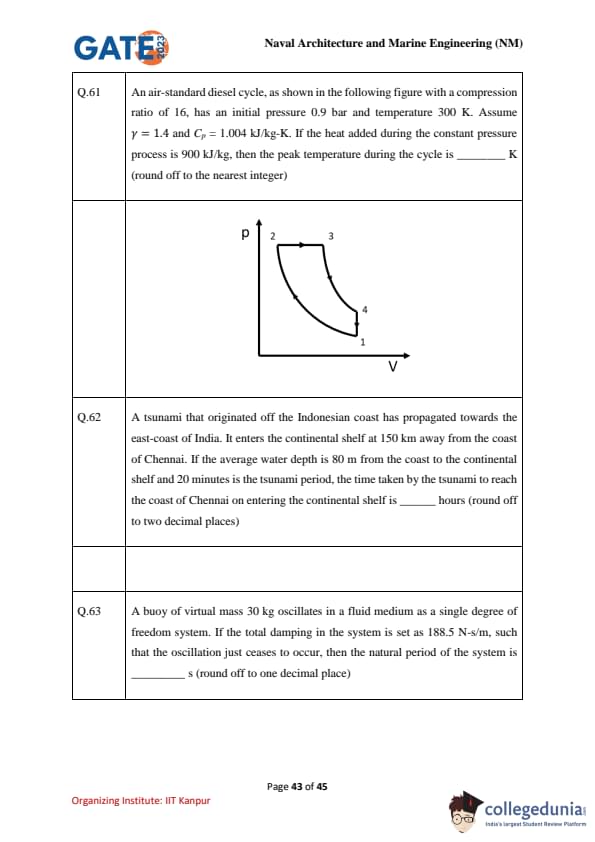
An air-standard diesel cycle, as shown in the following figure with a compression ratio of 16, has an initial pressure 0.9 bar and temperature 300 K. Assume \(\gamma = 1.4\) and \(C_p = 1.004\) kJ/kg-K. If the heat added during the constant pressure process is 900 kJ/kg, then the peak temperature during the cycle is ____________ K (round off to the nearest integer)

A tsunami that originated off the Indonesian coast has propagated towards the east-coast of India. It enters the continental shelf at 150 km away from the coast of Chennai. If the average water depth is 80 m from the coast to the continental shelf and 20 minutes is the tsunami period, the time taken by the tsunami to reach the coast of Chennai on entering the continental shelf is ____________ hours (round off to two decimal places)
A buoy of virtual mass 30 kg oscillates in a fluid medium as a single degree of freedom system. If the total damping in the system is set as 188.5 N-s/m, such that the oscillation just ceases to occur, then the natural period of the system is ____________ s (round off to one decimal place)
Consider a truss as shown in the following figure. The length of each member is 2 m. The area of cross section of each member is 100 \(mm^2\) and Young's modulus is \(2 x 10^5 N/mm^2\). The vertical deflection at C is ____________ mm (round off to one decimal place)

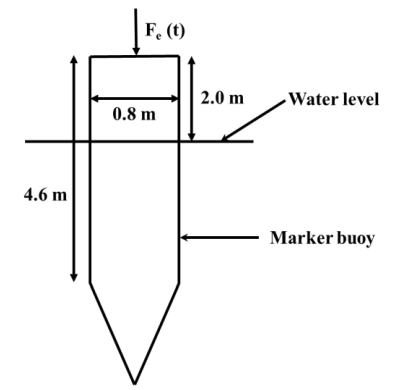
A marker buoy of mass 1500 kg floating in sea water of density 1025 kg/m³, consists of a cylinder and cone as shown in the following figure. The buoy is suitably ballasted to make it stable in the floating condition. The buoy is subjected to an external periodic excitation force in Newton, \(F_e(t) = 2000 \sin (1.25 t)\). Ignore damping effects and assume g = 9.81 m/s², added mass = 25% of the mass of the buoy. The maximum heave response amplitude of the buoy is ____________ m (round off to one decimal place)






































Also Check:
| Previous Year GATE Naval Architecture and Marine Engineering Question Papers | GATE 2023 Naval Architecture and Marine Engineering Paper Analysis |





Comments