GATE 2023 ECE Question Paper is available here for download. IIT Kanpur conducted GATE 2023 ECE paper on February 5, 2023 in the Afternoon Session from 02:30 PM to 05:30 PM. Students reported GATE 2023 ECE question paper to be easy to moderate with 4 MSQs, 16 NATs and 45 MCQs. The General Aptitude and Engineering Mathematics carried an equal weightage in GATE 2023 ECE paper with 15 marks each.
GATE 2023 ECE Question Paper with Solutions PDF
| GATE 2023 ECE Question Paper with Solutions | Check Solutions |
“I cannot support this proposal. My ______ will not permit it.”
Courts : ______ :: Parliament : Legislature (By word meaning)
What is the smallest number with distinct digits whose digits add up to 45?

In a class of 100 students,
(i) there are 30 students who neither like romantic movies nor comedy movies,
(ii) the number of students who like romantic movies is twice the number of students who like comedy movies, and
(iii) the number of students who like both romantic movies and comedy movies is 20.
How many students in the class like romantic movies?
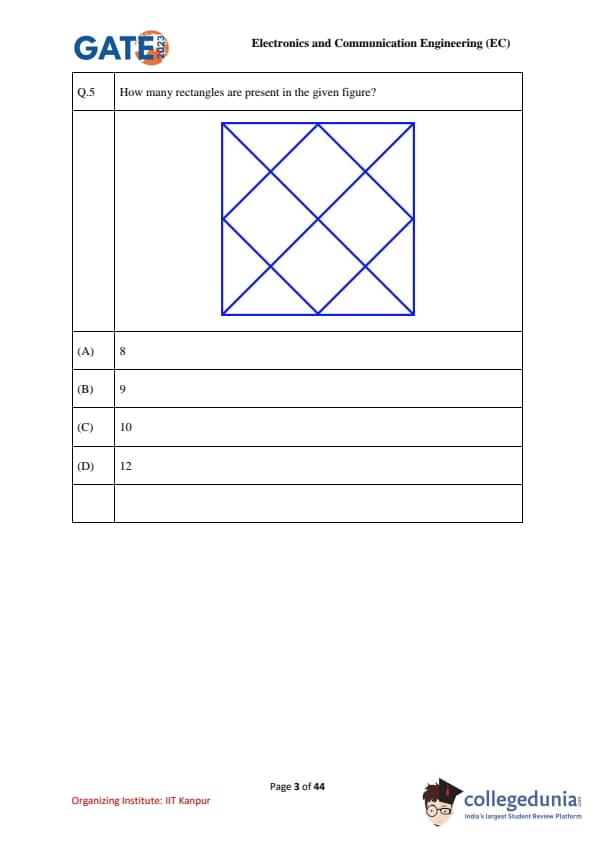
How many rectangles are present in the given figure?
Forestland is a planet inhabited by different kinds of creatures. Among other creatures, it is populated by animals all of whom are ferocious. There are also creatures that have claws, and some that do not. All creatures that have claws are ferocious.
Based only on the information provided above, which one of the following options can be logically inferred with certainty?
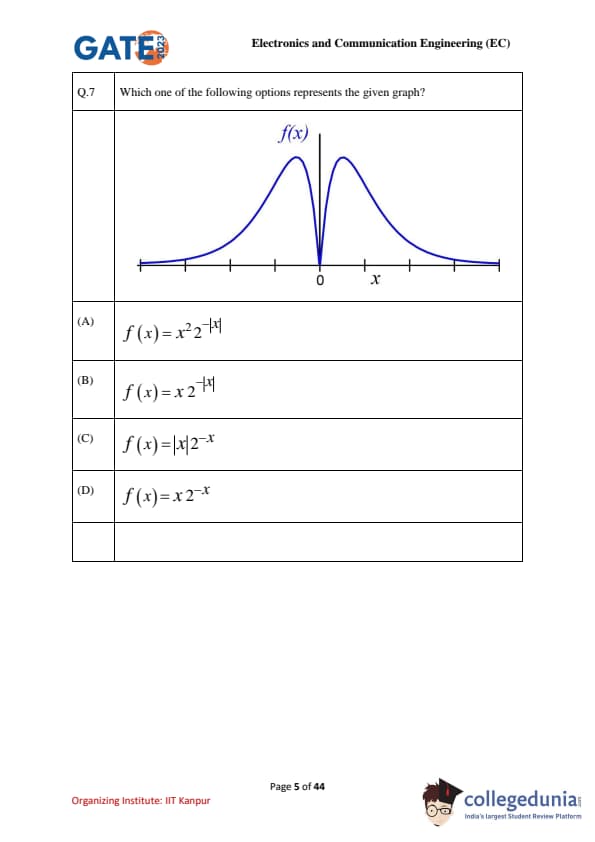
Which one of the following options represents the given graph?

Which one of the following options can be inferred from the given passage alone?
When I was a kid, I was partial to stories about other worlds and interplanetary travel. I used to imagine that I could just gaze off into space and be whisked to another planet.
Excerpt from The Truth about Stories by T. King]
Out of 1000 individuals in a town, 100 unidentified individuals are covid positive. Due to lack of adequate covid-testing kits, the health authorities of the town devised a strategy to identify these covid-positive individuals. The strategy is to:
(i) Collect saliva samples from all 1000 individuals and randomly group them into sets of 5.
(ii) Mix the samples within each set and test the mixed sample for covid.
(iii) If the test done in (ii) gives a negative result, then declare all the 5 individuals to be covid negative.
(iv) If the test done in (ii) gives a positive result, then all the 5 individuals are separately tested for covid.
Given this strategy, no more than _____ testing kits will be required to identify all the 100 covid positive individuals irrespective of how they are grouped.
A 100 cm \(\times\) 32 cm rectangular sheet is folded 5 times. Each time the sheet is folded, the long edge aligns with its opposite side. Eventually, the folded sheet is a rectangle of dimensions 100 cm \(\times\) 1 cm.
The total number of creases visible when the sheet is unfolded is ______.
Let \(\mathbf{v}_1=\begin{bmatrix}1
2
0\end{bmatrix}\) and \(\mathbf{v}_2=\begin{bmatrix}2
1
3\end{bmatrix}\) be two vectors. The value of the coefficient \(\alpha\) in the expression \(\mathbf{v}_1=\alpha\mathbf{v}_2+\mathbf{e}\), which minimizes the length of the error vector \(\mathbf{e}\), is
The rate of increase, of a scalar field \(f(x,y,z) = xyz\), in the direction \(v=(2,1,2)\) at a point \((0,2,1)\) is
Let \(w^4 = 16j\). Which of the following cannot be a value of \(w\)?
The value of the contour integral, \(\displaystyle \oint_{C}\left(\frac{z+2}{z^{2}+2z+2}\right)dz\), where the contour \(C\) is \(\left\{ z: \left| z+1-\tfrac{3}{2}j \right| = 1 \right\}\), taken in the counter clockwise direction, is
Let the sets of eigenvalues and eigenvectors of a matrix \(B\) be \(\{\lambda_k \mid 1 \le k \le n\}\) and \(\{\mathbf{v}_k \mid 1 \le k \le n\}\), respectively. For any invertible matrix \(P\), the sets of eigenvalues and eigenvectors of the matrix \(A\), where \(B=P^{-1}AP\), respectively, are
In a semiconductor, if the Fermi energy level lies in the conduction band, then the semiconductor is known as
For an intrinsic semiconductor at temperature \(T=0K\), which of the following statement is true?
A series RLC circuit has a quality factor \(Q\) of 1000 at a center frequency of \(10^{6}\) rad/s. The possible values of \(R\), \(L\) and \(C\) are
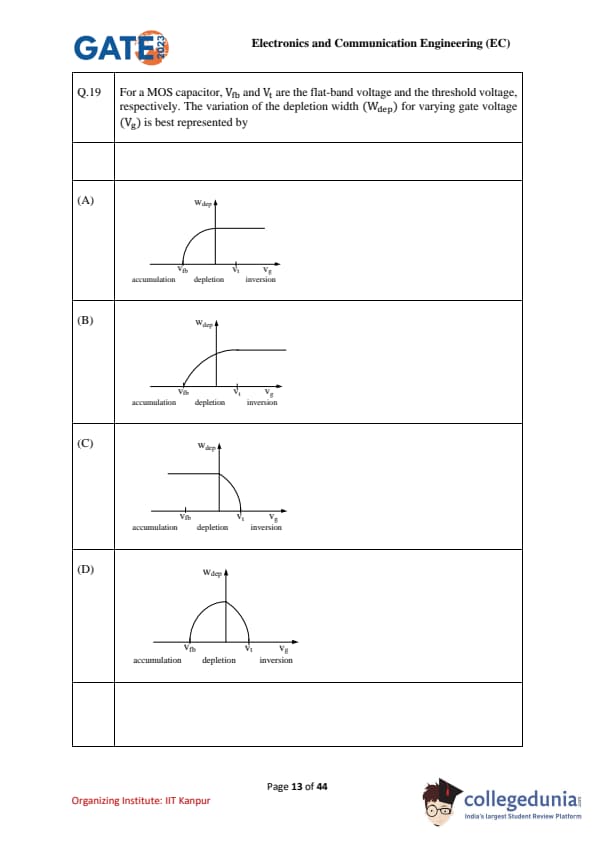
For a MOS capacitor, \(V_{fb}\) and \(V_t\) are the flat-band voltage and the threshold voltage, respectively. The variation of the depletion width (\(W_{dep}\)) for varying gate voltage (\(V_g\)) is best represented by

Consider a narrow band signal, propagating in a lossless dielectric medium \((\varepsilon_r = 4, \mu_r = 1)\), with phase velocity \(v_p\) and group velocity \(v_g\). Which of the following statement is true? (\(c\) is the velocity of light in vacuum.)
In the circuit shown below, \(V_1\) and \(V_2\) are bias voltages. Based on input and output impedances, the circuit behaves as a
A cascade of common-source amplifiers in a unity gain feedback configuration oscillates when
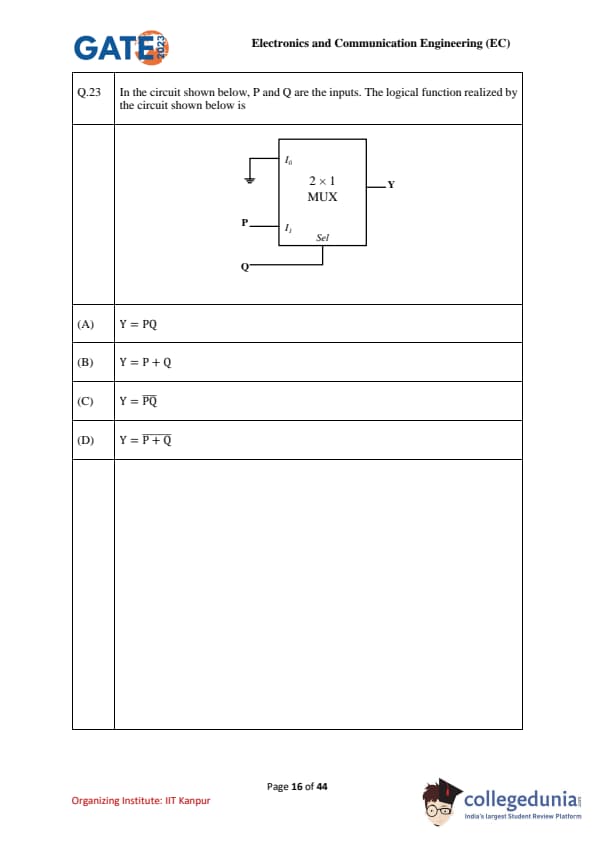
In the circuit shown below, P and Q are the inputs. The logical function realized by the circuit shown below is
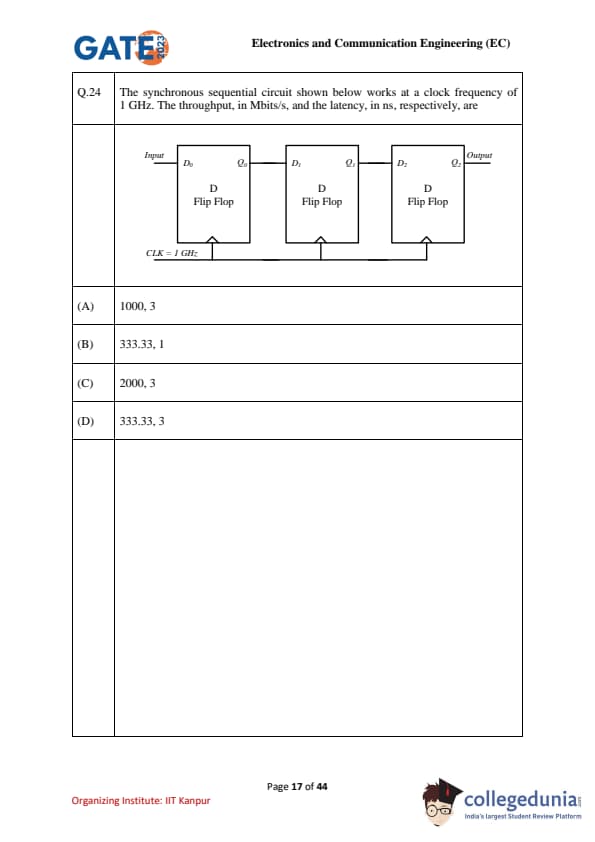
The synchronous sequential circuit shown below works at a clock frequency of 1 GHz. The throughput, in Mbits/s, and the latency, in ns, respectively, are
The open loop transfer function of a unity negative feedback system is \[ G(s) = \frac{k}{s(1+sT_1)(1+sT_2)}, \]
where \(k\), \(T_1\) and \(T_2\) are positive constants. The phase cross-over frequency, in rad/s, is
Consider a system with input x(t) and output y(t) = x(e^t). The system is
Let \(m(t)\) be a strictly band-limited signal with bandwidth \(B\) and energy \(E\). Assuming \(\omega_0=10B\), the energy in the signal \(m(t)\cos \omega_0 t\) is
The Fourier transform \(X(\omega)\) of \(x(t)=e^{-t^{2}}\) is
In the table shown below, match the signal type with its spectral characteristics.
\[ \begin{array}{|c|c|} \hline Signal type & Spectral characteristics
\hline (i) Continuous, aperiodic & (a) Continuous, aperiodic
(ii) Continuous, periodic & (b) Continuous, periodic
(iii) Discrete, aperiodic & (c) Discrete, aperiodic
(iv) Discrete, periodic & (d) Discrete, periodic
\hline \end{array} \]
For a real signal, which of the following is/are valid power spectral density/densities?
The signal-to-noise ratio (SNR) of an ADC with a full-scale sinusoidal input is given to be 61.96 dB. The resolution of the ADC is ______ bits (rounded off to the nearest integer).
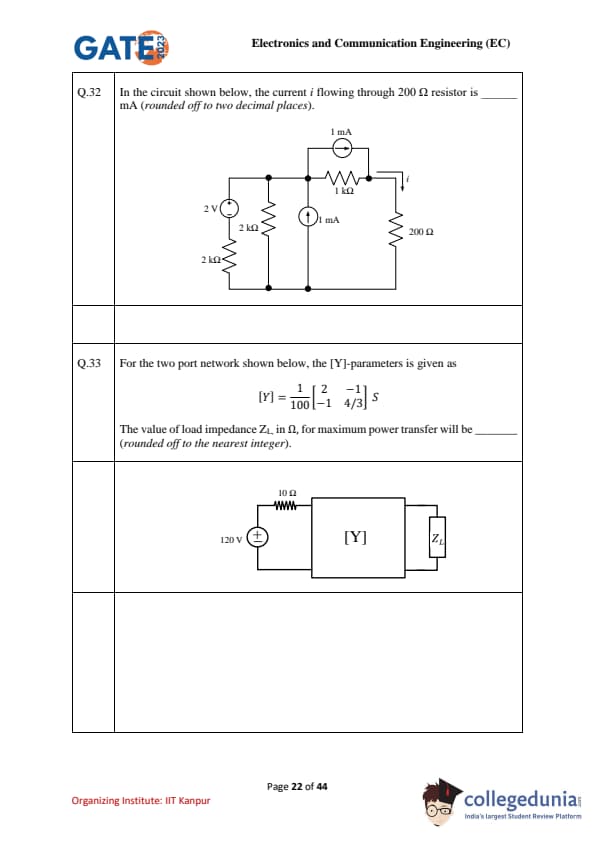
In the circuit shown below, the current \(i\) flowing through \(200\,\Omega\) resistor is _____ mA (rounded off to two decimal places).
For the two port network shown below, the [Y]-parameters is given as \(\displaystyle [Y]=\frac{1}{100}\begin{bmatrix}2 & -1
[-2pt]-1 & \frac{4}{3}\end{bmatrix}\ S\). The value of load impedance \(Z_L\), in \(\Omega\), for maximum power transfer will be (rounded off to the nearest integer).
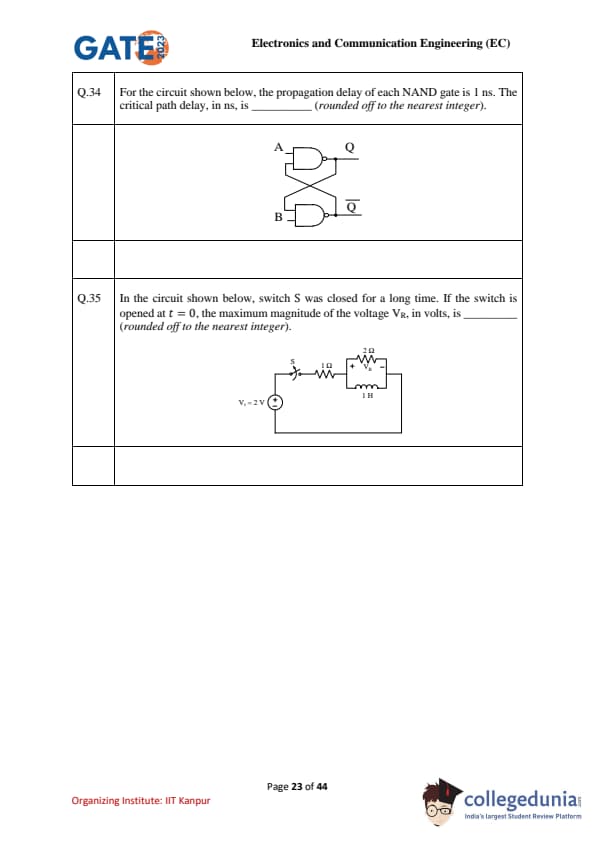
For the circuit shown below, the propagation delay of each NAND gate is 1 ns. The critical path delay, in ns, is ________ (rounded off to the nearest integer).
In the circuit shown below, switch S was closed for a long time. If the switch is opened at \(t=0\), the maximum magnitude of the voltage \(V_R\), in volts, is ________ (rounded off to the nearest integer).
A random variable \(X\), distributed normally as \(N(0,1)\), undergoes the transformation \(Y = h(X)\), given in the figure. The form of the probability density function of \(Y\) is
(In the options given below, \(a, b, c\) are non-zero constants and \(g(y)\) is a piece-wise continuous function)
The value of the line integral \(\displaystyle \int_{P}^{Q}\!\left(z^{2}\,dx+3y^{2}\,dy+2xz\,dz\right)\) along the straight line joining the points \(P(1,1,2)\) and \(Q(2,3,1)\) is
Let \(\mathbf{x}\) be an \(n \times 1\) real column vector with length \(l=\sqrt{\mathbf{x}^T\mathbf{x}}\). The trace of the matrix \(P=\mathbf{x}\mathbf{x}^T\) is
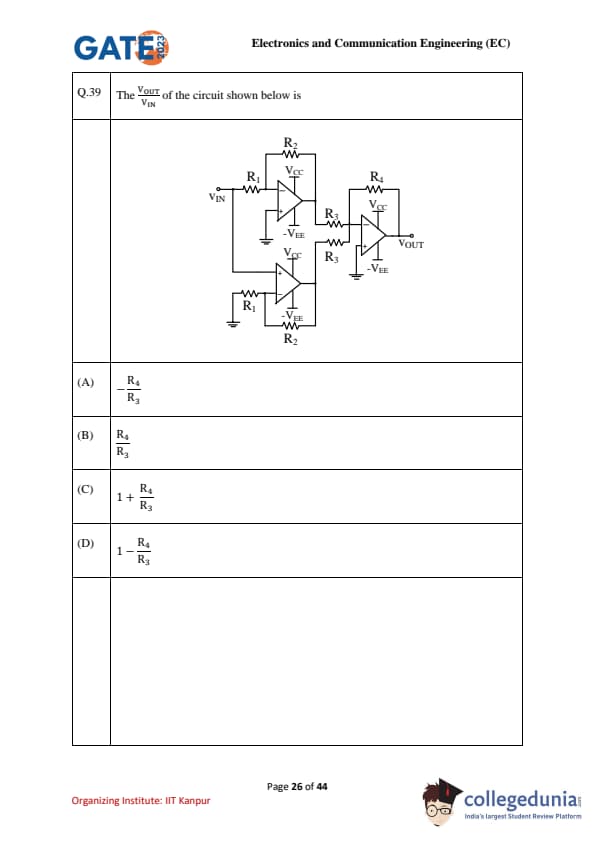
The \(\dfrac{V_{OUT}}{V_{IN}}\) of the circuit shown below is
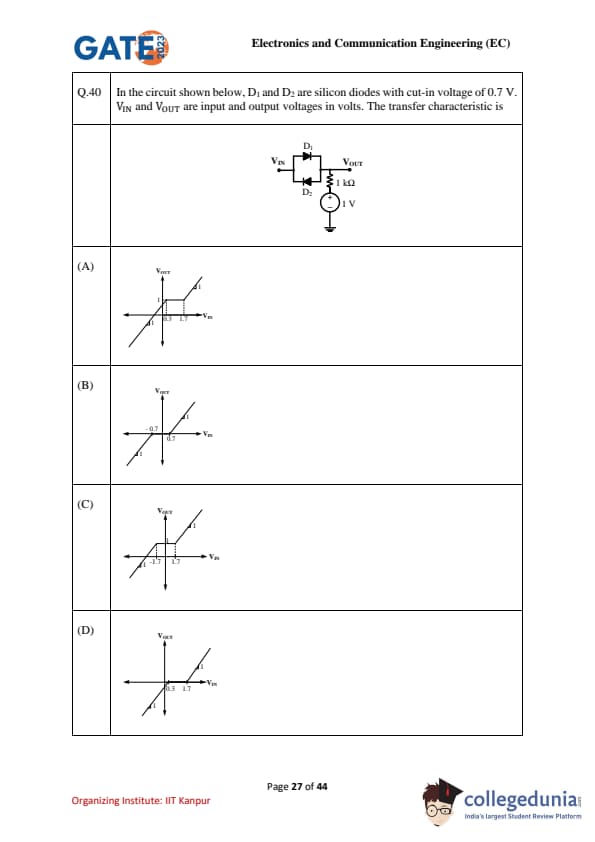
In the circuit shown below, \(D_1\) and \(D_2\) are silicon diodes with cut-in voltage of 0.7 V. \(V_{IN}\) and \(V_{OUT}\) are input and output voltages in volts. The transfer characteristic is
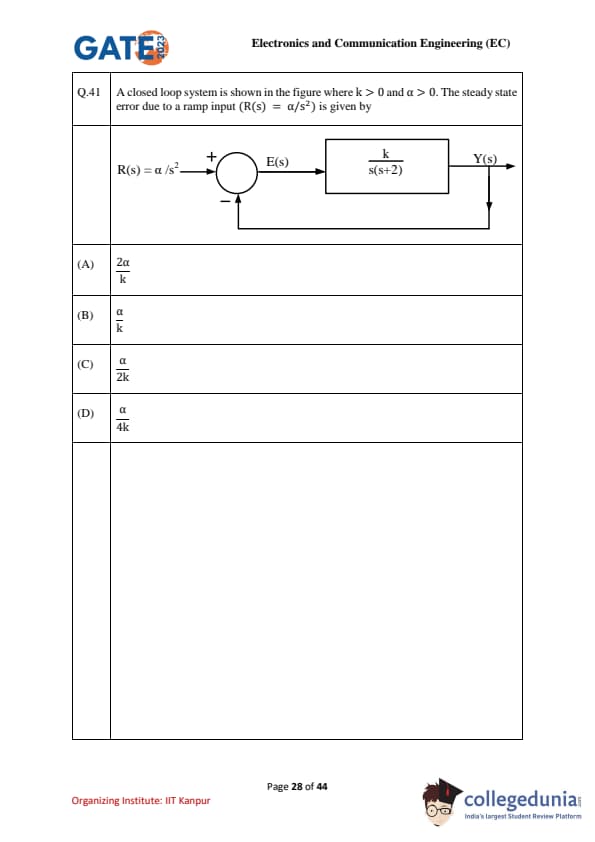
A closed loop system is shown in the figure where \(k>0\) and \(\alpha>0\). The steady state error due to a ramp input (\(R(s)=\alpha/s^{2}\)) is given by
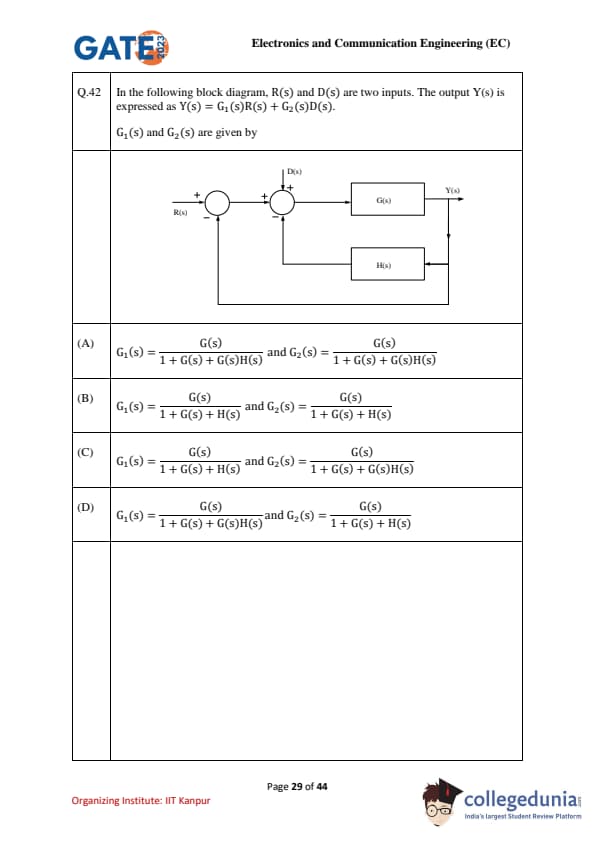
In the following block diagram, R(s) and D(s) are two inputs. The output Y(s) is expressed as Y(s) = G\(_1\)(s)R(s) + G\(_2\)(s)D(s).
G\(_1\)(s) and G\(_2\)(s) are given by
The state equation of a second order system is \(\dot{x}(t)=Ax(t)\), \(x(0)\) is the initial condition. Suppose \(\lambda_1\) and \(\lambda_2\) are two distinct eigenvalues of \(A\) and \(v_1\) and \(v_2\) are the corresponding eigenvectors. For constants \(\alpha_1\) and \(\alpha_2\), the solution, \(x(t)\), of the state equation is
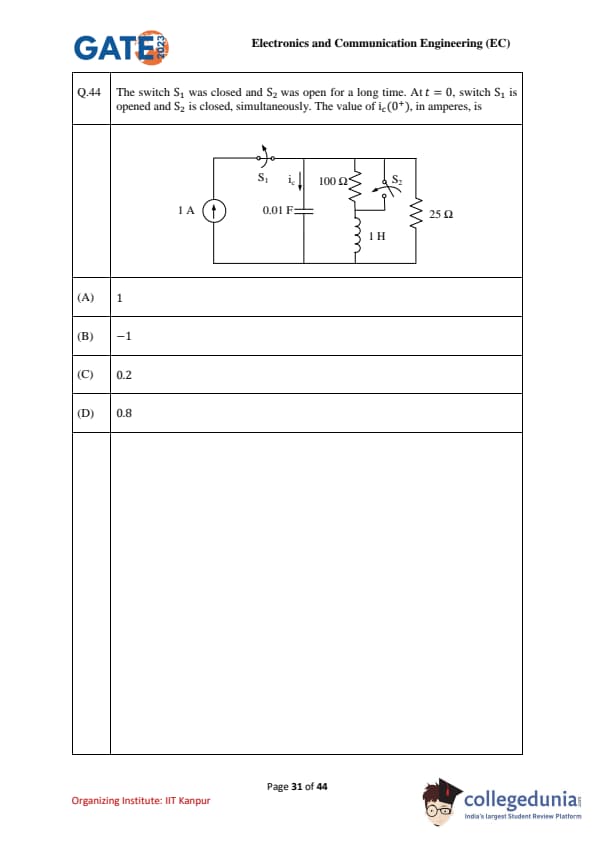
The switch \(S_1\) was closed and \(S_2\) was open for a long time. At \(t=0\), switch \(S_1\) is opened and \(S_2\) is closed, simultaneously. The value of \(i_c(0^+)\), in amperes, is
Let a frequency modulated (FM) signal \(x(t)=A\cos\!\big(\omega_c t+k_f\!\int_{-\infty}^{t}\! m(\lambda)\,d\lambda\big)\), where \(m(t)\) is a message signal of bandwidth \(W\). It is passed through a non-linear system with output \(y(t)=2x(t)+5\,(x(t))^{2}\). Let \(B_T\) denote the FM bandwidth. The minimum value of \(\omega_c\) required to recover \(x(t)\) from \(y(t)\) is
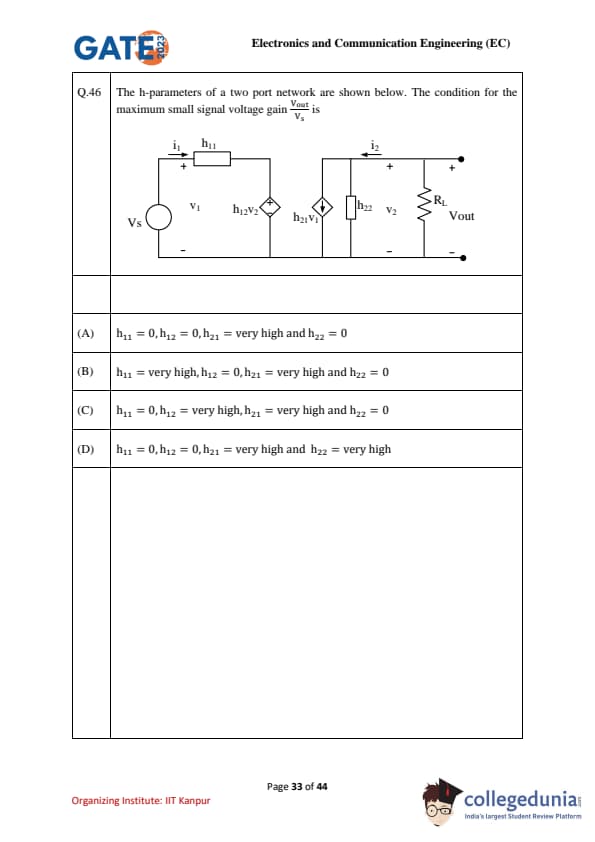
The h-parameters of a two port network are shown below. The condition for the maximum small signal voltage gain \(\dfrac{V_{out}}{V_s}\) is
Consider a discrete-time periodic signal with period \(N=5\). Let the discrete-time Fourier series (DTFS) representation be \(x[n]=\sum_{k=0}^{4} a_k e^{j\frac{2\pi kn}{5}}\), where \(a_0=1, a_1=3j, a_2=2j, a_3=-2j\) and \(a_4=-3j\). The value of the sum \(\sum_{n=0}^{4} x[n]\sin\frac{4\pi n}{5}\) is
Let an input \(x[n]\) having discrete-time Fourier transform \[ X(e^{j\Omega}) = 1 - e^{-j\Omega} + 2e^{-j3\Omega} \]
be passed through an LTI system whose frequency response is \[ H(e^{j\Omega}) = 1 - \tfrac12 e^{-j2\Omega}. \]
The output \(y[n]\) of the system is
Let \(x(t)=10\cos(10.5Wt)\) be passed through an LTI system having impulse response \(h(t)=\pi\!\left(\dfrac{\sin Wt}{\pi t}\right)^{\!2}\!\cos(10Wt)\). The output of the system is
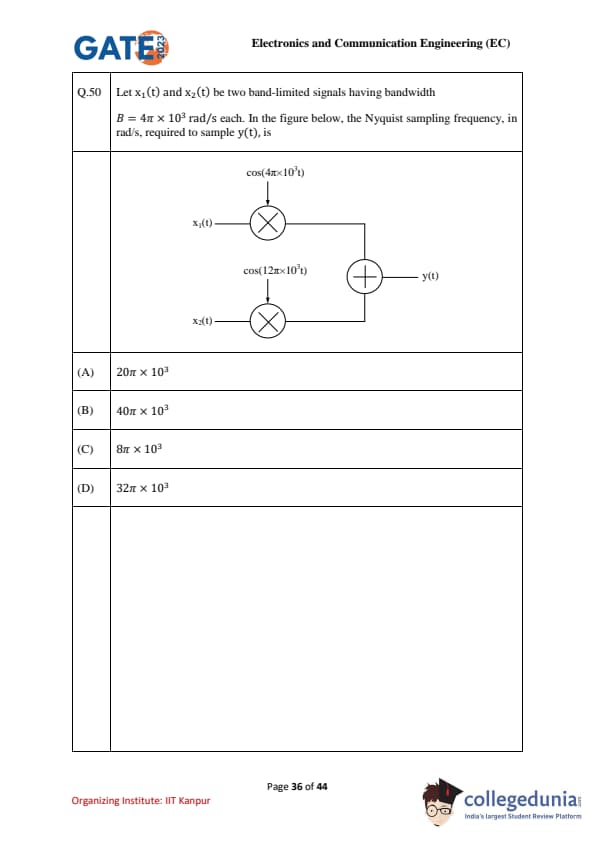
Let \(x_1(t)\) and \(x_2(t)\) be two band-limited signals having bandwidth \(B=4\pi\times 10^{3}\) rad/s each. In the figure below, the Nyquist sampling frequency, in rad/s, required to sample \(y(t)\), is
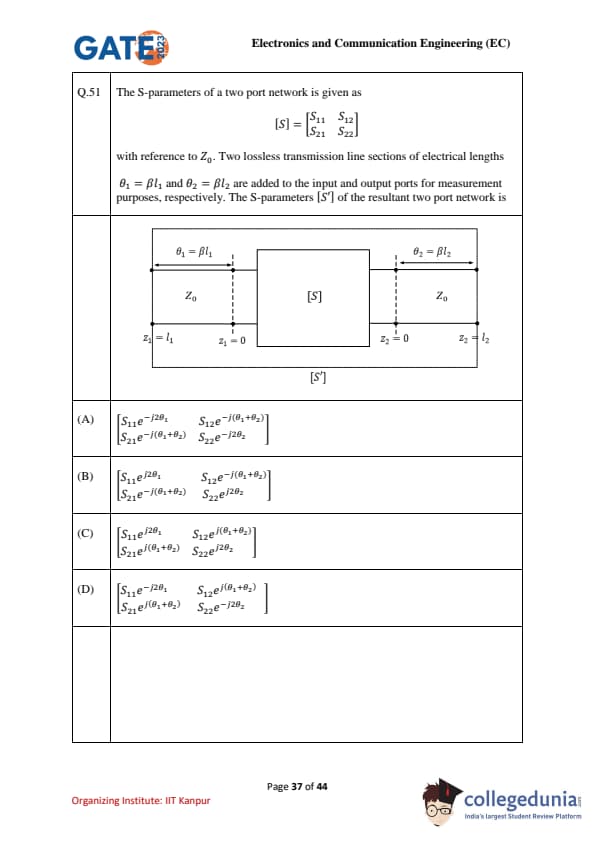
The S-parameters of a two port network is given as \[ [S]=\begin{bmatrix}S_{11}&S_{12}
[2pt] S_{21}&S_{22}\end{bmatrix} \]
with reference to \(Z_0\). Two lossless transmission line sections of electrical lengths \(\theta_1=\beta l_1\) and \(\theta_2=\beta l_2\) are added to the input and output ports for measurement purposes, respectively. The S-parameters \([S']\) of the resultant two port network is
The standing wave ratio on a \(50\ \Omega\) lossless transmission line terminated in an unknown load impedance is found to be \(2.0\). The distance between successive voltage minima is \(30\ cm\) and the first minimum is located at \(10\ cm\) from the load. \(Z_L\) can be replaced by an equivalent length \(l_m\) and terminating resistance \(R_m\) of the same line. The value of \(R_m\) and \(l_m\), respectively, are
The electric field of a plane electromagnetic wave is \[ \textbf{E}= \mathbf{a_x}\,C_{1x}\cos(\omega t-\beta z)+\mathbf{a_y}\,C_{1y}\cos(\omega t-\beta z+\theta)\ V/m. \]
Which of the following combination(s) will give rise to a left handed elliptically polarized (LHEP) wave?
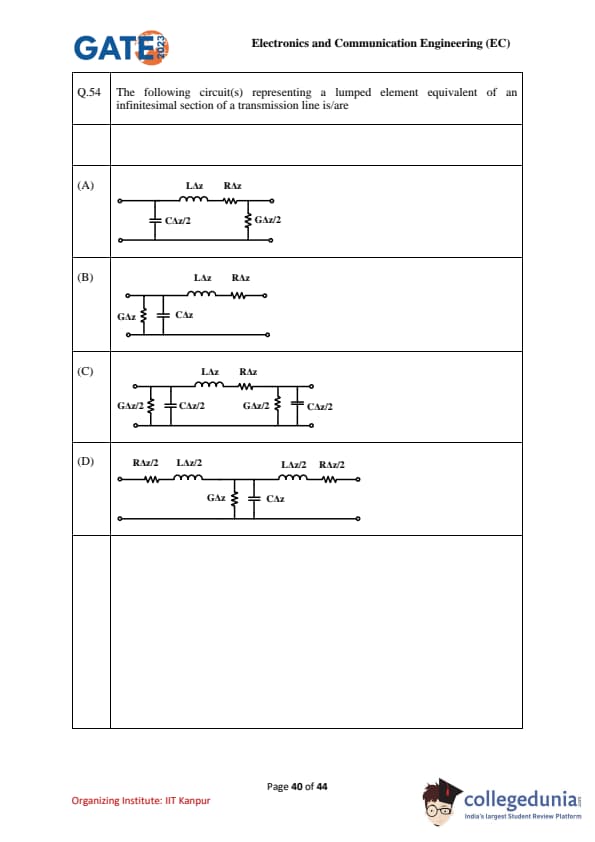
The following circuit(s) representing a lumped element equivalent of an infinitesimal section of a transmission line is/are
The value of the integral \(\displaystyle \iint_R xy\,dx\,dy\) over the region \(R\), given in the figure, is ______ (rounded off to the nearest integer).
In an extrinsic semiconductor, the hole concentration is given to be \(1.5n_i\) where \(n_i\) is the intrinsic carrier concentration of \(1\times10^{10}\ cm^{-3}\). The ratio of electron to hole mobility for equal hole and electron drift current is given as {\hspace{2cm (rounded off to two decimal places).
The asymptotic magnitude Bode plot of a minimum phase system is shown in the figure. The transfer function of the system is \(G(s)=\dfrac{k(s+z)^a}{s^b(s+p)^c}\), where \(k\), \(z\), \(p\), \(a\), \(b\) and \(c\) are positive constants. The value of \((a+b+c)\) is ______ (rounded off to the nearest integer).
Let \(x_1(t)=u(t+1.5)-u(t-1.5)\) and \(x_2(t)\) is shown in the figure below. For \(y(t)=x_1(t)\ast x_2(t)\), the \(\displaystyle \int_{-\infty}^{\infty}y(t)\,dt\) is ______________________ (rounded off to the nearest integer).
Let \(X(t)\) be a white Gaussian noise with power spectral density \(\dfrac{1}{2}\) W/Hz. If \(X(t)\) is input to an LTI system with impulse response \(e^{-t}u(t)\). The average power of the system output is ______ W (rounded off to two decimal places).
A transparent dielectric coating is applied to glass \((\varepsilon_r=4,\ \mu_r=1)\) to eliminate the reflection of red light \((\lambda_0=0.75~\mum)\). The minimum thickness of the dielectric coating, in \(\mu\)m, that can be used is {\hspace{2cm (rounded off to two decimal places).
In a semiconductor device, the Fermi-energy level is \(0.35\) eV above the valence band energy. The effective density of states in the valence band at \(T=300\) K is \(1\times10^{19}\ cm^{-3}\). The thermal equilibrium hole concentration in silicon at \(400\) K is __________ \(\times 10^{13}\ cm^{-3}\) (rounded off to two decimal places).
Given \(kT\) at \(300\) K is \(0.026\) eV.
A sample and hold circuit is implemented using a resistive switch and a capacitor with a time constant of 1 \(\mu\)s. The time for the sampling switch to stay closed to charge a capacitor adequately to a full scale voltage of 1 V with 12-bit accuracy is ____ \(\mu\)s (rounded off to two decimal places).
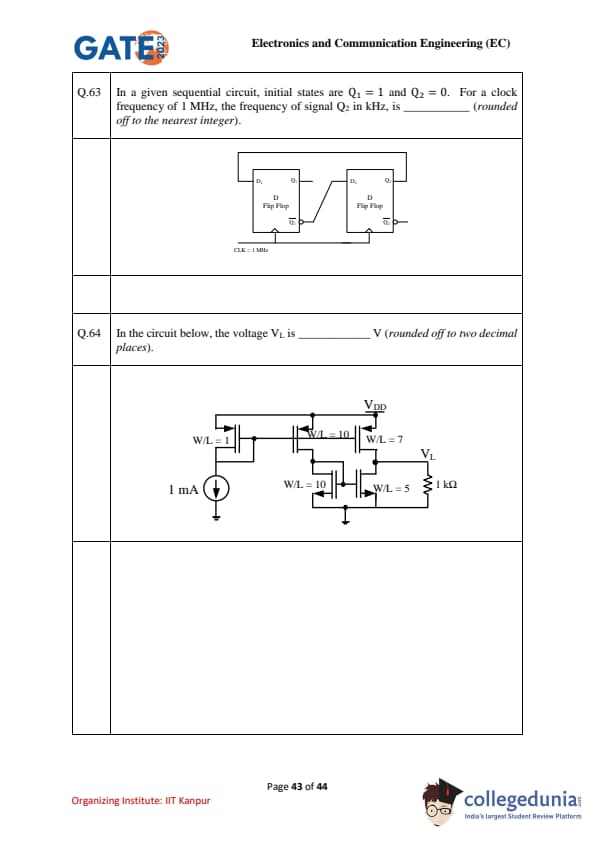
In a given sequential circuit, initial states are \(Q_1=1\) and \(Q_2=0\). For a clock frequency of 1 MHz, the frequency of signal \(Q_2\) in kHz, is _______ (rounded off to the nearest integer).
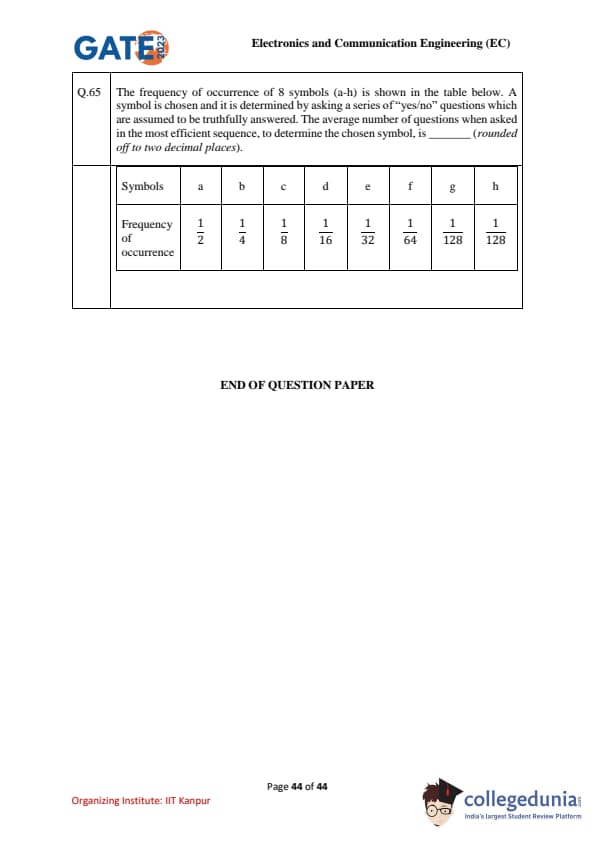
In the circuit below, the voltage \(V_L\) is _________ V (rounded off to two decimal places).

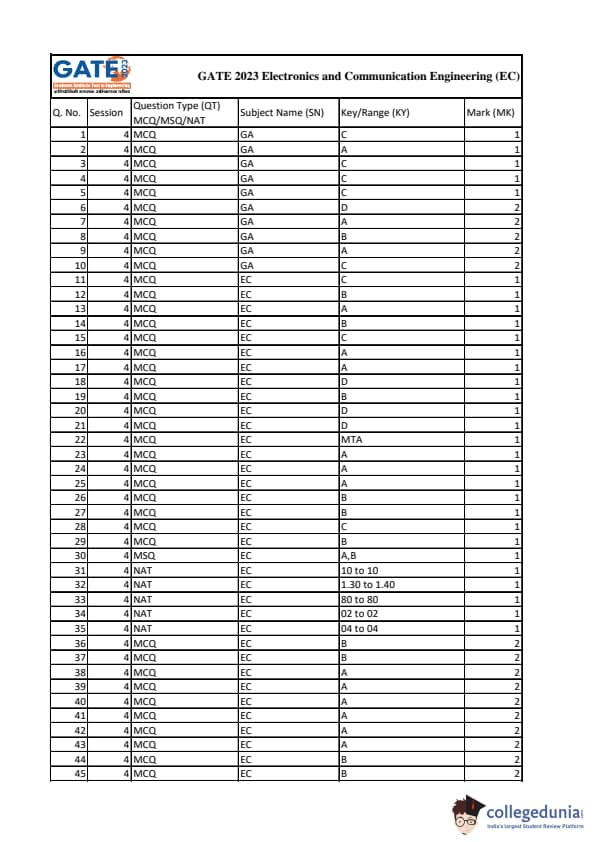
The frequency of occurrence of 8 symbols (a–h) is shown in the table below. A symbol is chosen and it is determined by asking a series of “yes/no” questions which are assumed to be truthfully answered. The average number of questions when asked in the most efficient sequence, to determine the chosen symbol, is ______ (rounded off to two decimal places).


























GATE 2023 ECE Paper Analysis
| Particulars | GATE EC Paper Analysis |
|---|---|
| Overall Difficulty Level | Easy to Moderate |
| Number of MCQs | 45 |
| Number of NATs | 16 |
| Number of MSQs | 4 |
GATE 2023 ECE Question Paper: Weightage of Topics
The table covers the subject-wise weightage in GATE 2023 ECE Question Paper.
| Subjects | Number of Questions | Total Marks | |
|---|---|---|---|
| 1 Mark | 2 Marks | ||
| Engineering Mathematics | 5 | 5 | 15 |
| General Aptitude | 5 | 5 | 15 |
| Control Systems | 1 | 3 | 7 |
| Digital Circuits | 4 | 2 | 8 |
| Electronic Devices | 3 | 2 | 7 |
| Signals Systems | 3 | 4 | 11 |
| Communication Systems | 2 | 4 | 10 |
| Analog Circuits | 2 | 3 | 8 |
| Network Theory | 4 | 2 | 8 |
| Electromagnetics | 1 | 5 | 11 |
| Total | 30 | 35 | 100 |
Also Check:



.jpg?h=35&w=35&mode=stretch)

Comments