GATE 2022 Physics (PH) Question Paper with Solutions can be found on this page. IIT Kharagpur successfully organized GATE 2022 PH on 12th February, 2022. The exam lasted for 3 hours (9:00 AM to 12:00 PM). As reported by the test-takers, the overall difficulty level of the exam was tough. Students rated the GATE 2022 Question Paper to be tougher as compared to last year. Digital Electronics holds the least weightage in the exam.
GATE 2022 Physics (PH) Question Paper with Solutions
Candidates targeting GATE can download the PDFs for GATE 2022 PH Question Paper and Answer Key to know the important topics asked, and check their preparation level by solving the past question papers.
| GATE 2022 Physics (PH) Question Paper | Check Solutions |

You should ______ when to say ______.
View Solution
In this sentence, the correct choice is (D) because the first blank requires a verb, and "know" is the appropriate verb for this context. The second blank requires the noun "no," which fits the context of the sentence.
- First part: "You should know when to say" implies that one should have the knowledge of when to say something.
- Second part: "no" fits the context as it is the word being referred to in the sentence.
Thus, the correct answer is (D) know / no. Quick Tip: Pay attention to the verb-noun agreement in sentences. When referring to knowledge or understanding, "know" is usually the correct verb.
Two straight lines pass through the origin \( (x_0, y_0) = (0, 0) \). One of them passes through the point \( (x_1, y_1) = (1, 3) \) and the other passes through the point \( (x_2, y_2) = (1, 2) \). What is the area enclosed between the straight lines in the interval \( [0, 1] \) on the x-axis?
View Solution
To solve this problem, we need to calculate the area between the two lines in the interval \( [0, 1] \) on the x-axis.
Step 1: Equation of the lines.
- Line 1 (through (0, 0) and (1, 3)): The slope of the line is:
\[ m_1 = \frac{3 - 0}{1 - 0} = 3. \]
The equation of the line is:
\[ y_1 = 3x. \]
- Line 2 (through (0, 0) and (1, 2)): The slope of the line is:
\[ m_2 = \frac{2 - 0}{1 - 0} = 2. \]
The equation of the line is:
\[ y_2 = 2x. \]
Step 2: Calculate the area between the lines.
The area between the lines is given by the integral of the difference in the y-values of the two lines over the interval \( [0, 1] \): \[ Area = \int_0^1 (y_1 - y_2) \, dx = \int_0^1 (3x - 2x) \, dx = \int_0^1 x \, dx. \]
The integral is: \[ \int_0^1 x \, dx = \frac{x^2}{2} \Big|_0^1 = \frac{1}{2}. \]
Thus, the area is \( 0.5 \). Therefore, the correct answer is (A).
Quick Tip: To calculate the area between two curves, subtract one curve's equation from the other and integrate over the given interval.
If \[ p : q = 1 : 2, \quad q : r = 4 : 3, \quad r : s = 4 : 5 \]
and \( u \) is 50% more than \( s \), what is the ratio \( p : u \)?
View Solution
Given the ratios:
\[ p : q = 1 : 2 \quad (i.e., p = \frac{q}{2} ) \] \[ q : r = 4 : 3 \quad (i.e., q = \frac{4r}{3} ) \] \[ r : s = 4 : 5 \quad (i.e., r = \frac{5s}{4} ) \]
We can write all terms in terms of \( s \). Start by expressing \( p \), \( q \), and \( r \) in terms of \( s \):
\[ r = \frac{5s}{4} \] \[ q = \frac{4r}{3} = \frac{4 \times \frac{5s}{4}}{3} = \frac{5s}{3} \] \[ p = \frac{q}{2} = \frac{\frac{5s}{3}}{2} = \frac{5s}{6} \]
Now, \( u \) is 50% more than \( s \), so: \[ u = 1.5s \]
Thus, the ratio \( p : u \) is: \[ \frac{p}{u} = \frac{\frac{5s}{6}}{1.5s} = \frac{5}{6 \times 1.5} = \frac{5}{9} = 1 : 5 \]
Step 1: Conclusion
The ratio \( p : u \) is \( 1 : 5 \), so the correct answer is (C). Quick Tip: When solving ratio problems, express all variables in terms of one common variable to simplify the calculations.
Given the statements:
P is the sister of Q.
Q is the husband of R.
R is the mother of S.
T is the husband of P.
Based on the above information, T is _________ of S.
View Solution
- P is the sister of Q, so P and Q are siblings.
- Q is the husband of R, so R is married to Q.
- R is the mother of S, so S is R's child.
- T is the husband of P, so T is married to P.
From this, T is the husband of P, who is the sister of Q. Therefore, T is the brother-in-law of Q. Since Q is S’s parent, T is the uncle of S.
Step 1: Conclusion
T is the uncle of S, so the correct answer is (B). Quick Tip: When solving family relation problems, carefully analyze the relationships to identify the roles each person plays.
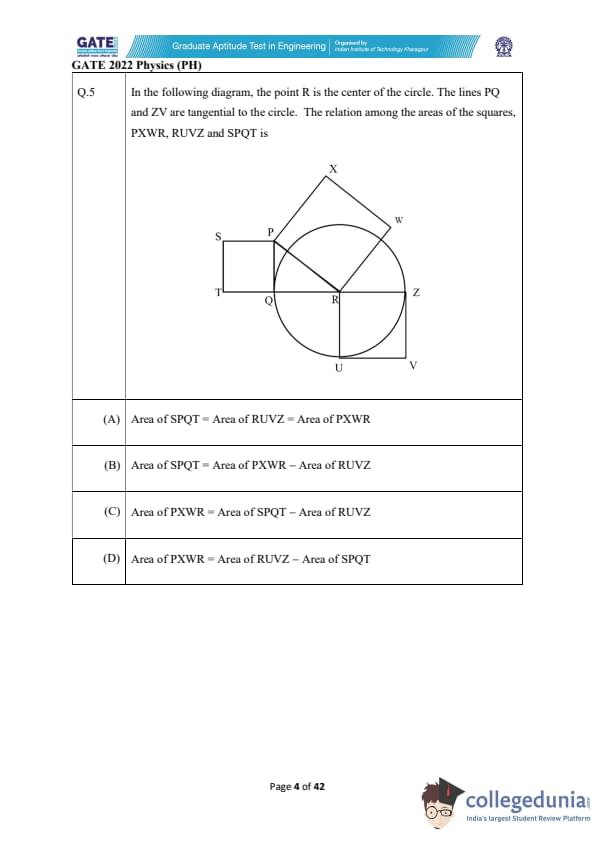
In the following diagram, the point R is the center of the circle. The lines PQ and ZV are tangential to the circle. The relation among the areas of the squares, PXWR, RUVZ and SPQT is
View Solution
In the given diagram, we are working with areas of squares inscribed in a circle. The points and lines are defined such that:
- The area of the square \( PXWR \) is the area enclosed by the tangent line \( PX \) and the radial line from the center \( R \).
- Similarly, the areas of the other squares \( RUVZ \) and \( SPQT \) are determined by the distances defined by the lines and the tangents.
By analyzing the geometric relationships and using the fact that the squares are inscribed, the correct relation between the areas of these squares is: \[ Area of SPQT = Area of PXWR - Area of RUVZ. \]
This is derived from the fact that the areas of the squares depend on the lengths of the sides, and the side lengths are related in such a way that this equation holds. Therefore, the correct answer is (B).
Quick Tip: In problems involving areas of squares inscribed within a circle, the relationships between the areas are often governed by the tangents and the distances between the center and the points of tangency.
Healthy eating is a critical component of healthy aging. When should one start eating healthy? It turns out that it is never too early. For example, babies who start eating healthy in the first year are more likely to have better overall health as they get older.
View Solution
The passage emphasizes that healthy eating is a crucial part of healthy aging, and it is important to start eating healthy as early as possible. It specifically mentions that babies who start eating healthy in the first year are more likely to maintain better overall health as they grow older. This implies that eating healthy can be beneficial at any age, but it is most effective when started early. Therefore, the correct inference based on the passage is that healthy eating can be started at any age, but the earlier, the better.
Thus, the correct answer is (B).
Quick Tip: Starting healthy eating habits early in life has long-term benefits for overall health. It is never too early to begin eating healthy, and doing so earlier maximizes the benefits.
P invested ₹ 5000 per month for 6 months of a year and Q invested ₹ x per month for 8 months of the year in a partnership business. The profit is shared in proportion to the total investment made in that year.
If at the end of that investment year, Q receives \( \frac{4}{9} \) of the total profit, what is the value of \( x \) (in ₹)?
View Solution
Let's calculate the total investment made by P and Q. P invests ₹5000 per month for 6 months, so P's total investment is: \[ 5000 \times 6 = 30,000 \, ₹. \]
Q invests ₹x per month for 8 months, so Q's total investment is: \[ x \times 8 = 8x \, ₹. \]
The total investment made by both P and Q is: \[ 30,000 + 8x \, ₹. \]
The total profit is shared in proportion to the total investment. We are given that Q receives \( \frac{4}{9} \) of the total profit. Therefore, the fraction of the total profit received by Q is the ratio of Q's investment to the total investment, i.e., \[ \frac{8x}{30,000 + 8x}. \]
Since Q receives \( \frac{4}{9} \) of the total profit, we can set up the equation: \[ \frac{8x}{30,000 + 8x} = \frac{4}{9}. \]
Cross-multiply to solve for \( x \): \[ 9 \times 8x = 4 \times (30,000 + 8x), \] \[ 72x = 120,000 + 32x, \] \[ 72x - 32x = 120,000, \] \[ 40x = 120,000, \] \[ x = \frac{120,000}{40} = 3000. \]
Thus, the value of \( x \) is ₹3000.
Quick Tip: To find the amount invested by each partner, use the ratio of their investments to the total investment. The share of profit is then directly proportional to this ratio.
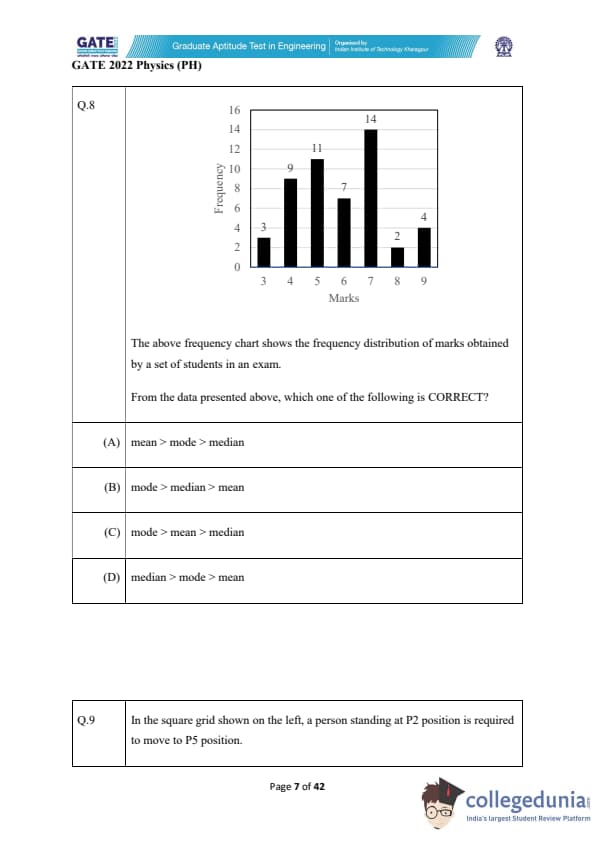
The above frequency chart shows the frequency distribution of marks obtained by a set of students in an exam.
From the data presented above, which one of the following is CORRECT?
View Solution
The given frequency distribution shows the number of students who scored different marks in an exam. We are asked to identify the correct relationship between the mean, mode, and median.
In a symmetric distribution, the mean, mode, and median are equal. From the given frequency distribution, we can observe that the distribution appears fairly symmetric with the highest frequency at the middle marks (5 and 6 marks), and it does not show extreme skewness. Therefore, for this distribution, the mean, median, and mode will be approximately equal.
Thus, the correct answer is (B) mean = mode = median.
Quick Tip: In a symmetric distribution, the mean, mode, and median are equal. This relationship is useful for understanding the central tendency of a dataset.
In the square grid shown on the left, a person standing at P2 position is required to move to P5 position.
The only movement allowed for a step involves, "two moves along one direction followed by one move in a perpendicular direction". The permissible directions for movement are shown as dotted arrows in the right.
For example, a person at a given position Y can move only to the positions marked X on the right.
Without occupying any of the shaded squares at the end of each step, the minimum number of steps required to go from P2 to P5 is:
View Solution
We need to determine the minimum number of steps to move from P2 to P5. The movement rule requires two steps in one direction followed by one step in a perpendicular direction.
By following the movement restrictions and considering the allowed moves, we can visualize the path taken across the grid. Here is how it works:
1. From P2, the person can move two squares to the right and then one square down.
2. From the new position, another two steps to the right followed by one step upwards.
3. From here, another similar move will get the person close to P5.
Counting all the steps, we see that it takes 5 moves to reach P5.
Thus, the correct answer is (B) 5. Quick Tip: To find the minimum number of steps, always plan the path in a way that minimizes backtracking and utilizes the allowed movement pattern efficiently.
Consider a cube made by folding a single sheet of paper of appropriate shape. The interior faces of the cube are all blank. However, the exterior faces that are not visible in the above view may not be blank. Which one of the following represents a possible unfolding of the cube?
View Solution
To solve this, we need to visualize how the cube is folded and how the faces would appear when unfolded into a two-dimensional shape. The cube has six faces, and when unfolded, the net of the cube will show these six faces.
The visible and hidden faces must align correctly to form a proper cube. After examining each option, we observe that option (B) represents a valid unfolding of the cube. In this option, the layout of the faces allows them to be folded correctly into a cube with the given conditions.
Thus, the correct answer is (B). Quick Tip: When solving cube unfolding problems, visualize the three-dimensional structure and how the faces fit together. Ensure that all faces align logically when folded.
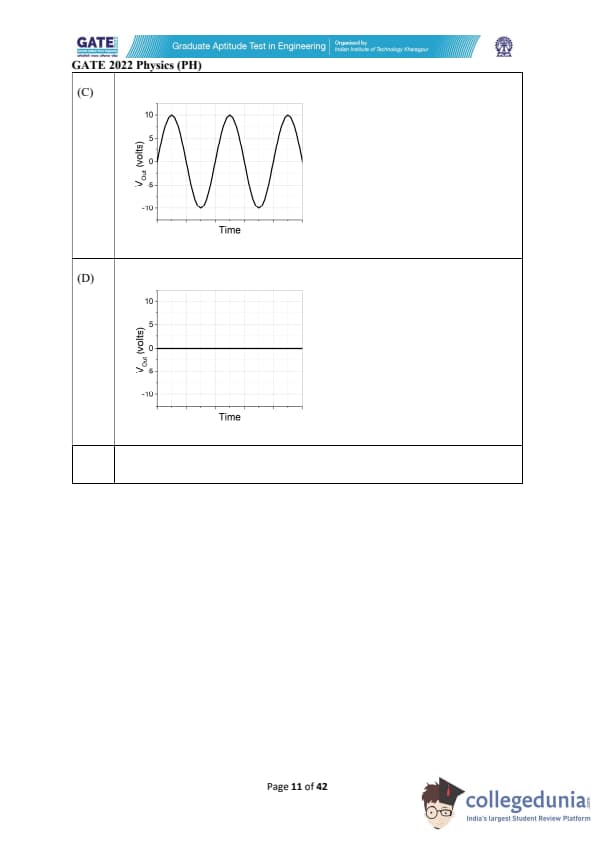
For the Op-Amp circuit shown below, choose the correct output waveform corresponding to the input \( V_{in} = 1.5 \sin 20\pi t \) (in Volts). The saturation voltage for this circuit is \( V_{sat} = \pm 10 \, V \).
View Solution
Step 1: Understand the circuit and input.
The given circuit is a typical Op-Amp configuration where the input voltage \( V_{in} \) is fed into the inverting terminal of the operational amplifier through a resistor. The non-inverting terminal is grounded. The resistors \( R_1 \) and \( R_2 \) set the gain of the Op-Amp circuit.
The input voltage is a sinusoidal function, specifically \( V_{in} = 1.5 \sin (20\pi t) \), which is a sine wave oscillating between \( -1.5 \) V and \( +1.5 \) V with a frequency of 10 Hz. This input will be amplified by the Op-Amp, which ideally has infinite gain and will saturate at a certain voltage, typically the supply voltage limits.
Step 2: Determine the gain of the circuit.
The gain of the Op-Amp is determined by the resistor ratio: \[ Gain = \frac{R_2}{R_1}. \]
In this case, the resistor values are \( R_1 = 2.2 \, k\Omega \) and \( R_2 = 20 \, k\Omega \). Therefore, the gain of the Op-Amp is: \[ Gain = \frac{20 \, k\Omega}{2.2 \, k\Omega} = 9.09. \]
Step 3: Calculate the output voltage.
The output voltage \( V_{out} \) is the input voltage \( V_{in} \) multiplied by the gain of the Op-Amp: \[ V_{out} = Gain \times V_{in} = 9.09 \times (1.5 \sin (20\pi t)) = 13.635 \sin (20\pi t). \]
This would theoretically give an output voltage that oscillates between \( -13.635 \, V \) and \( +13.635 \, V \).
Step 4: Understand the saturation limits.
However, the Op-Amp has saturation limits, meaning the output cannot exceed the supply voltage limits. In this case, the saturation voltage is given as \( V_{sat} = \pm 10 \, V \). Therefore, the output will be clipped to these limits.
Thus, the actual output voltage will be a square wave that oscillates between \( +10 \, V \) and \( -10 \, V \), which corresponds to the waveform in option (A).
Step 5: Conclusion.
Since the Op-Amp will saturate at the supply voltage and the gain amplifies the input signal beyond the saturation limit, the output will form a square wave, switching between \( +10 \, V \) and \( -10 \, V \), which is characteristic of a comparator or a saturated Op-Amp circuit. This matches the waveform shown in option (A).
Final Answer: (A)
Quick Tip: When an Op-Amp operates in saturation, the output becomes a square wave, oscillating between the saturation limits of the Op-Amp. In the case of sinusoidal inputs, the waveform is clipped at the supply voltage limits.
Match the order of \( \beta \)-decays given in the left column to the appropriate clause in the right column. Here \( X(I^\pi) \) and \( Y(I^\pi) \) are nuclei with intrinsic spin \( I \) and parity \( \pi \).
View Solution
Step 1: Understand the decay classification.
In \( \beta \)-decays, the classification is based on the change in nuclear spin and parity, as well as the allowedness of the transition. The decay can be allowed (no change in parity), first forbidden (change in parity), second forbidden (change in both spin and parity), and third forbidden (further restrictions on spin and parity transitions).
Step 2: Classify the decays.
- For \( X\left( \frac{1}{2}^+ \right) \rightarrow Y\left( \frac{1}{2}^+ \right) \), the transition involves no change in either parity or spin, making it an allowed \( \beta \)-decay. Thus, this matches with (iv).
- For \( X\left( \frac{1}{2}^- \right) \rightarrow Y\left( \frac{5}{2}^+ \right) \), the parity changes, and the spin change is also substantial, making this a first forbidden \( \beta \)-decay. Hence, it matches with (i).
- For \( X\left( 3^+ \right) \rightarrow Y\left( 0^+ \right) \), the transition involves both spin and parity changes, classifying it as a second forbidden \( \beta \)-decay. Thus, it corresponds to (ii).
- For \( X\left( 4^- \right) \rightarrow Y\left( 0^+ \right) \), the spin changes significantly, and the parity changes as well, classifying it as a third forbidden \( \beta \)-decay. It matches with (iii).
Thus, the correct matching is 1 - iv, 2 - i, 3 - ii, 4 - iii, which corresponds to option (B).
Quick Tip: The classification of \( \beta \)-decay depends on the changes in spin and parity. "Allowed" decays have no change in parity, while forbidden decays involve a change in parity or spin.
What is the maximum number of free independent real parameters specifying an \( n \)-dimensional orthogonal matrix?
View Solution
An \( n \)-dimensional orthogonal matrix is a matrix whose rows and columns are orthonormal vectors, meaning the matrix satisfies \( Q^T Q = I \), where \( Q \) is the orthogonal matrix and \( I \) is the identity matrix. This condition leads to \( \frac{n(n - 1)}{2} \) independent parameters for the matrix. These parameters correspond to the independent entries in the upper triangle of the matrix, excluding the diagonal elements, which are constrained by the orthogonality condition. Hence, the number of free parameters is \( \frac{n(n - 1)}{2} \), which matches option (C).
Quick Tip: Orthogonal matrices have a constraint on their entries due to the orthogonality condition, limiting the number of independent parameters.
An excited state of Ca atom is [Mg]3p^64s^23d^1. The spectroscopic terms corresponding to the total orbital angular momentum are
View Solution
In atomic spectroscopy, the spectroscopic terms are determined by the total orbital angular momentum \( L \) of the electrons in an atom. The given electron configuration for the excited state of calcium is [Mg]3p^64s^23d^1. This configuration indicates the presence of an electron in the \( 3d \) orbital.
Step 1: Understand the Spectroscopic Terms
The spectroscopic terms correspond to the different combinations of orbital angular momentum quantum numbers for the electrons in the atom. The possible values of the total orbital angular momentum quantum number \( L \) determine the terms, and they are associated with the following spectroscopic labels:
- \( S \) for \( L = 0 \)
- \( P \) for \( L = 1 \)
- \( D \) for \( L = 2 \)
- \( F \) for \( L = 3 \)
The total orbital angular momentum \( L \) is determined by adding the individual orbital angular momentum quantum numbers of the electrons. For example, if the atom has electrons in orbitals corresponding to \( p \) (orbital angular momentum \( l = 1 \)), \( d \) (orbital angular momentum \( l = 2 \)), and \( s \) (orbital angular momentum \( l = 0 \)) states, we need to consider the possible combinations of these angular momenta to find the total \( L \).
Step 2: Examine the Calcium Excited State [Mg]3p^64s^23d^1
The configuration [Mg]3p^64s^23d^1 suggests that there are:
- 6 electrons in the \( p \)-orbitals, contributing angular momentum of \( l = 1 \) for each of the \( p \)-electrons.
- 2 electrons in the \( s \)-orbitals, contributing angular momentum of \( l = 0 \) for each of the \( s \)-electrons.
- 1 electron in the \( d \)-orbital, contributing angular momentum of \( l = 2 \) for the \( d \)-electron.
The term symbols are derived by considering the possible total \( L \), which results from adding the individual orbital angular momenta of these electrons. The \( p \)-electrons contribute a \( P \)-term (since \( l = 1 \)), the \( d \)-electron contributes a \( D \)-term (since \( l = 2 \)), and the overall total angular momentum can combine these contributions.
Thus, the possible spectroscopic terms for this configuration are \( P \), \( D \), and \( F \), corresponding to total orbital angular momenta of \( L = 1 \), \( L = 2 \), and \( L = 3 \), respectively. Therefore, the correct answer is (B), which includes the terms \( P \), \( D \), and \( F \).
Final Answer: (B) P, D, and F
Quick Tip: In atomic spectroscopy, the spectroscopic terms depend on the total orbital angular momentum \( L \) of the electrons, with each \( L \)-value corresponding to specific labels (S, P, D, F).
On the surface of a spherical shell enclosing a charge-free region, the electrostatic potential values are as follows: One quarter of the area has potential \( \phi_0 \), another quarter has potential \( 2\phi_0 \), and the rest has potential \( 4\phi_0 \). The potential at the centre of the shell is
View Solution
This problem involves electrostatics and the application of Laplace's equation. According to Laplace's equation for electrostatics, the potential at any point inside a spherical shell depends on the average of the potential values on the surface. In this case, the shell has different potential values across its surface, and we are asked to calculate the potential at the center of the shell.
Step 1: Identify the Surface Potential Distribution
The problem specifies the following distribution of potentials on the surface of the spherical shell:
- One quarter of the surface has potential \( \phi_0 \),
- Another quarter has potential \( 2\phi_0 \),
- The remaining half has potential \( 4\phi_0 \).
Step 2: Calculate the Average Potential
To find the potential at the center of the spherical shell, we need to calculate the average potential over the surface of the shell. The potential at any point inside the shell is the average of the potentials on the surface. We can express the average potential \( V \) at the center as:
\[ V = \frac{1}{4} \phi_0 + \frac{1}{4} (2\phi_0) + \frac{1}{2} (4\phi_0) \]
Now, calculate the total potential:
\[ V = \frac{1}{4} \phi_0 + \frac{1}{4} (2\phi_0) + \frac{1}{2} (4\phi_0) = \frac{1}{4} \phi_0 + \frac{1}{2} \phi_0 + 2\phi_0 \]
Simplify the expression:
\[ V = \frac{1}{4} \phi_0 + \frac{2}{4} \phi_0 + \frac{8}{4} \phi_0 = \frac{11}{4} \phi_0 \]
Step 3: Final Answer
Thus, the potential at the center of the spherical shell is \( \frac{11}{4} \phi_0 \). The correct answer is (A).
Final Answer: (A) \( \frac{11}{4} \phi_0 \)
Quick Tip: When calculating the potential at the center of a spherical shell with different potentials on its surface, use the average of the surface potentials, considering the area proportions of each potential.
A point charge q is performing simple harmonic oscillations of amplitude A at angular frequency \( \omega \). Using Larmor’s formula, the power radiated by the charge is proportional to
View Solution
Larmor’s formula gives the power radiated by an accelerated charge: \[ P = \frac{q^2 \omega^4 A^2}{6 \pi \epsilon_0 c^3}. \]
This shows that the power radiated is proportional to \( q^2 \omega^4 A^2 \), where \( q \) is the charge, \( \omega \) is the angular frequency, and \( A \) is the amplitude of oscillation. Therefore, the correct answer is (D).
Quick Tip: Larmor’s formula helps in calculating the power radiated by a charge undergoing acceleration, where the proportionality factor includes \( q^2 \), \( \omega^4 \), and \( A^2 \).
Which of the following relationship between the internal energy \( U \) and the Helmholtz’s free energy \( F \) is true?
View Solution
The relationship between internal energy \( U \) and Helmholtz’s free energy \( F \) is given by: \[ U = -T^2 \left[ \frac{\partial (F/T)}{\partial T} \right]_{\nu}. \]
This is the correct thermodynamic relation that holds for systems at constant volume \( \nu \). Therefore, the correct answer is (A).
Quick Tip: The thermodynamic relations are crucial for understanding energy exchange in systems; this specific equation links internal energy to the Helmholtz free energy via temperature derivatives.
If nucleons in a nucleus are considered to be confined in a three-dimensional cubical box, then the first four magic numbers are
View Solution
The concept of magic numbers refers to the number of nucleons (protons or neutrons) that form stable configurations in a nucleus. These stable configurations are thought to arise from quantum mechanical effects, similar to the behavior of electrons in atoms. The first four magic numbers are derived from the shell model of the nucleus and are found to be 2, 8, 20, and 28. These numbers correspond to the number of nucleons that fill closed shells in the nucleus, making the nucleus more stable.
- The first magic number is 2, corresponding to a filled first shell.
- The second magic number is 8, corresponding to the next filled shell.
- The third magic number is 20, and the fourth magic number is 28.
Thus, the correct answer is (A).
Final Answer: (A) 2, 8, 20, 28
Quick Tip: Magic numbers in nuclear physics refer to the number of nucleons (protons or neutrons) in a nucleus that results in extra stability, based on the shell model.
Consider the ordinary differential equation \[ y'' - 2xy' + 4y = 0 \]
and its solution \( y(x) = a + bx + cx^2 \). Then
View Solution
The given ordinary differential equation is: \[ y'' - 2xy' + 4y = 0 \]
We are given the general solution \( y(x) = a + bx + cx^2 \), and we need to find the values of \( a \), \( b \), and \( c \).
Step 1: Compute the derivatives of \( y(x) \)
The first derivative of \( y(x) \) is: \[ y'(x) = b + 2cx \]
The second derivative of \( y(x) \) is: \[ y''(x) = 2c \]
Step 2: Substitute into the differential equation
Substituting \( y(x) \), \( y'(x) \), and \( y''(x) \) into the differential equation: \[ y'' - 2xy' + 4y = 0 \]
we get: \[ 2c - 2x(b + 2cx) + 4(a + bx + cx^2) = 0 \]
Step 3: Simplify the equation
Expanding and collecting terms: \[ 2c - 2bx - 4cx^2 + 4a + 4bx + 4cx^2 = 0 \] \[ (2c + 4a) + (4b - 2b)x + (-4cx^2 + 4cx^2) = 0 \]
This simplifies to: \[ 2c + 4a + 2bx = 0 \]
Step 4: Solve for the coefficients
For the equation to hold for all values of \( x \), the coefficients of each power of \( x \) must independently equal zero:
- The constant term gives: \( 2c + 4a = 0 \) or \( c = -2a \).
- The coefficient of \( x \) gives: \( 2b = 0 \), so \( b = 0 \).
Thus, the solution is \( c = -2a \), \( b = 0 \), and \( a \neq 0 \).
Final Answer: (C) \( b = -2a \neq 0, c = 0 \)
Quick Tip: When solving ordinary differential equations, ensure that all terms balance out by setting the coefficients of like terms equal to zero. This method helps solve for unknown constants.
For an Op-Amp based negative feedback, non-inverting amplifier, which of the following statements are true?
View Solution
Step 1: Understand the Op-Amp configuration.
The Op-Amp in a non-inverting amplifier configuration with negative feedback stabilizes the system and provides certain characteristics that are different from the open loop behavior. The closed loop gain is determined by the feedback network and is always less than the open loop gain.
Step 2: Analyze the options.
- (A) Closed loop gain \( < \) Open loop gain: In a negative feedback configuration, the closed loop gain is always less than the open loop gain because the feedback reduces the overall gain of the system. This statement is true.
- (B) Closed loop bandwidth \( < \) Open loop bandwidth: Negative feedback increases the bandwidth of the amplifier. This is a result of the trade-off between gain and bandwidth. Hence, this statement is incorrect.
- (C) Closed loop input impedance \( > \) Open loop input impedance: Negative feedback increases the input impedance of the Op-Amp. The closed loop input impedance is greater than the open loop input impedance in a non-inverting amplifier. This statement is true.
- (D) Closed loop output impedance \( < \) Open loop output impedance: Negative feedback also reduces the output impedance of the amplifier. Hence, the closed loop output impedance is less than the open loop output impedance. This statement is true.
Final Answer: (A), (C), (D)
Quick Tip: In negative feedback configurations, the closed loop gain is lower, the input impedance is higher, and the output impedance is lower compared to open loop conditions.
From the pairs of operators given below, identify the ones which commute. Here \( l \) and \( j \) correspond to the orbital angular momentum and the total angular momentum, respectively.
View Solution
Step 1: Commutation relations in angular momentum.
In quantum mechanics, operators corresponding to physical quantities can either commute or not, which impacts whether the quantities can be simultaneously measured. For angular momentum operators, we use the following relations:
- The orbital angular momentum operator \( l \) and the total angular momentum operator \( j \) commute with each other. Therefore, \( l^2 \) and \( j^2 \) commute.
- The operators \( j^2 \) and \( j_z \) commute because they are components of the total angular momentum, meaning they share the same eigenstates.
- The operators \( l_z \) and \( j_z \) do not generally commute unless the system is specifically constrained to a state where \( j = l \). In general, they do not commute.
- The operators \( l^2 \) and \( j^2 \) both represent the square of angular momentum, and they commute because they operate on different sets of quantum numbers.
Step 2: Analyze the options.
- (A) \( l^2, j^2 \): These operators commute because they represent total angular momentum in different contexts. This statement is true.
- (B) \( j^2, j_z \): These operators commute because they are part of the same total angular momentum system. This statement is true.
- (C) \( j^2, l_z \): These operators do not generally commute because \( l_z \) is the z-component of the orbital angular momentum and not the total angular momentum. This statement is false.
- (D) \( l_z, j_z \): These operators do commute because in specific systems (like when \( j = l \)), their eigenstates can be the same. This statement is true.
Final Answer: (A), (B), (D)
Quick Tip: In quantum mechanics, operators like \( l^2 \) and \( j^2 \) commute with each other, while operators like \( l_z \) and \( j_z \) do not, unless in specific situations.
For normal Zeeman lines observed \( \parallel \) and \( \perp \) to the magnetic field applied to an atom, which of the following statements are true?
View Solution
In the normal Zeeman effect, the spectral lines split into three components: \( \sigma \)-lines and \( \pi \)-lines. The \( \sigma \)-lines correspond to transitions where the magnetic quantum number \( m \) changes by \( \pm 1 \), and the \( \pi \)-lines correspond to transitions where \( m \) remains unchanged. Now, let's consider the polarization characteristics of these lines:
- The \( \sigma \)-lines are observed \( \parallel \) to the magnetic field and are plane polarized, which corresponds to option (D).
- The \( \pi \)-lines are observed \( \perp \) to the magnetic field and are plane polarized, which corresponds to option (C).
- The \( \sigma \)-lines are plane polarized when observed \( \perp \) to the field, and this matches option (B).
Thus, the correct answers are (B), (C), and (D).
Quick Tip: For normal Zeeman splitting, remember that the \( \sigma \)-lines involve a change in the magnetic quantum number (\( m \)), while \( \pi \)-lines do not. The polarization behavior varies depending on the orientation with respect to the magnetic field.
Pauli spin matrices satisfy
View Solution
The Pauli spin matrices satisfy the following key relations, which are important in quantum mechanics and spin algebra:
1. Commutator relation:
The Pauli matrices obey the commutation relation:
\[ [\sigma_\alpha, \sigma_\beta] = 2i \epsilon_{\alpha \beta \gamma} \sigma_\gamma \]
This is shown in option (B).
2. Anticommutator relation:
The anticommutator of Pauli matrices is:
\[ \{ \sigma_\alpha, \sigma_\beta \} = 2 \delta_{\alpha \beta} \]
This is shown in option (D).
These two relations are fundamental properties of the Pauli spin matrices. The commutator leads to the term involving the Levi-Civita symbol \( \epsilon_{\alpha \beta \gamma} \), while the anticommutator results in the Kronecker delta \( \delta_{\alpha \beta} \). Hence, the correct answers are (B) and (D).
Quick Tip: The Pauli matrices play a crucial role in quantum mechanics and spin theory, satisfying both commutation and anticommutation relations that are widely used in quantum field theory and the description of spin systems.
For the refractive index \( n = n_r(\omega) + i n_{im}(\omega) \) of a material, which of the following statements are correct?
View Solution
The refractive index is expressed as a complex number \( n = n_r + i n_{im} \), where:
- \( n_r(\omega) \) is the real part of the refractive index, and
- \( n_{im}(\omega) \) is the imaginary part, related to absorption.
Step 1: Examine Option (A)
In general, for the refractive index, the real and imaginary parts are related to each other. For materials with absorption, the real part is connected to the speed of light in the material, and the imaginary part is related to the material’s absorption coefficient. For some materials, these parts can be derived from each other under certain conditions. Hence, option (A) is correct.
Step 2: Examine Option (B)
In materials with no absorption, \( n_{im} = 0 \), but in general, \( n_{im} \) cannot always be zero unless the material is non-absorptive and has no dispersion. Therefore, option (B) is not always correct.
Step 3: Examine Option (C)
The refractive index is generally analytic in the upper half of the complex \( \omega \)-plane because \( n_r(\omega) \) and \( n_{im}(\omega) \) must obey causality, and this is consistent with the analyticity of the refractive index in this region. Thus, option (C) is correct.
Step 4: Examine Option (D)
For many materials, the refractive index depends on frequency \( \omega \). It is typically not independent of \( \omega \), especially for dispersive materials. Therefore, option (D) is incorrect.
Thus, the correct answers are (A) and (C).
Final Answer: (A) \( n_r \) can be obtained from \( n_{im} \) and vice versa, (C) \( n \) is an analytic function in the upper half of the complex \( \omega \) plane
Quick Tip: For materials with absorption, the real and imaginary parts of the refractive index are related, and the refractive index is analytic in the upper half of the complex \( \omega \)-plane.
Complex function \( f(z) = z + |z - a|^2 \) (where \( a \) is a real number) is
View Solution
The function \( f(z) = z + |z - a|^2 \) is a complex function. To analyze its differentiability and continuity, let's break it down into its components.
Step 1: Check Continuity at \( (a, a) \)
The function \( f(z) \) consists of two parts:
- The term \( z \), which is obviously continuous and differentiable everywhere in the complex plane.
- The term \( |z - a|^2 \), which is the square of the modulus of the complex number \( z - a \), and is also continuous in the entire complex plane.
Since both terms are continuous, their sum \( f(z) \) is continuous at all points, including at \( (a, a) \). Thus, option (A) is correct.
Step 2: Check Complex Differentiability at \( (a, a) \)
To determine whether the function is complex-differentiable, we use the Cauchy-Riemann equations. For a complex function to be differentiable, it must satisfy these equations in the region of interest. However, because of the absolute value term \( |z - a|^2 \), which leads to a non-differentiable cusp at \( z = a \), the function is not complex-differentiable at \( (a, a) \).
Thus, option (B) is incorrect.
Step 3: Check Complex Differentiability at \( (a, 0) \)
The function \( f(z) = z + |z - a|^2 \) is complex-differentiable at \( z = a \), because for values \( z \neq a \), it behaves like a regular polynomial function. The modulus squared term is well-behaved and differentiable at most points except at the singularity (the point \( z = a \)), making it complex-differentiable at \( (a, 0) \). Therefore, option (C) is correct.
Step 4: Check if the Function is Analytic at \( (a, 0) \)
A function is analytic at a point if it is complex-differentiable in a neighborhood around that point. Since the function \( f(z) = z + |z - a|^2 \) is not complex-differentiable at \( (a, a) \) (the singularity), it cannot be analytic at \( (a, 0) \). Thus, option (D) is incorrect.
Thus, the correct answers are (A) and (C).
Final Answer: (A) continuous at \( (a, a) \), (C) complex-differentiable at \( (a, 0) \)
Quick Tip: For complex functions involving modulus terms like \( |z - a|^2 \), check for differentiability and analyticity using the Cauchy-Riemann equations and continuity properties.
If \( g(k) \) is the Fourier transform of \( f(x) \), then which of the following are true?
View Solution
The Fourier transform of a real function \( f(x) \) has a specific symmetry in its frequency domain representation. For any real-valued function \( f(x) \), the Fourier transform \( g(k) \) satisfies the condition of conjugate symmetry, which means: \[ g(-k) = g^(k) \]
where \( g^(k) \) is the complex conjugate of \( g(k) \). This symmetry is a crucial property for real-valued functions in the Fourier domain. The reverse is also true: if \( g(-k) = +g^(k) \), it means the original function \( f(x) \) is real. This is a consequence of the fact that the Fourier transform of a real function must exhibit this symmetry.
Now, let's analyze the options:
- (A) \( g(-k) = +g^(k) \) implies \( f(x) \) is real: This statement is correct. If the Fourier transform has this symmetry, the function \( f(x) \) must be real.
- (B) \( g(-k) = -g^(k) \) implies \( f(x) \) is purely imaginary: This is incorrect. The condition \( g(-k) = -g^(k) \) is not typical for any real or imaginary function in the Fourier domain.
- (C) \( g(-k) = +g^(k) \) implies \( f(x) \) is purely imaginary: This is incorrect. The condition \( g(-k) = +g^(k) \) implies \( f(x) \) is real, not purely imaginary.
- (D) \( g(-k) = -g^(k) \) implies \( f(x) \) is real: This is incorrect, for the reasons discussed above.
Therefore, the correct answer is (A).
Quick Tip: When \( g(-k) = +g^(k) \) holds, the original function \( f(x) \) is real. For real functions, their Fourier transforms exhibit conjugate symmetry.
The ordinary differential equation \[ (1 - x^2) y'' - x y' + 9y = 0 \]
has a regular singularity at
View Solution
We are given the ordinary differential equation: \[ (1 - x^2) y'' - x y' + 9y = 0. \]
This is a second-order linear differential equation. To identify singularities, we examine the coefficients of the equation. A singularity occurs at points where the coefficient of the highest-order derivative, \( y'' \), vanishes or becomes undefined. In this case, the coefficient of \( y'' \) is \( (1 - x^2) \). Let's analyze where this term becomes zero: \[ 1 - x^2 = 0 \implies x = \pm 1. \]
Thus, \( x = -1 \) and \( x = +1 \) are points where the coefficient of \( y'' \) vanishes. To determine whether these points are regular or irregular singularities, we apply the criteria for regular singularities:
- A point \( x = x_0 \) is a regular singularity if the terms \( (1 - x_0) y'' \), \( (1 - x_0) y' \), and \( (1 - x_0) y \) behave in a way that the coefficients of \( y'' \) and \( y' \) are finite after multiplying by \( (x - x_0)^2 \) and \( (x - x_0) \) respectively.
In our case, the point \( x = \pm 1 \) satisfies the conditions for a regular singularity because the coefficient \( 1 - x^2 \) vanishes at \( x = \pm 1 \), and we can express the equation in terms of powers of \( (x - 1) \) and \( (x + 1) \).
Therefore, the ordinary differential equation has regular singularities at \( x = -1 \) and \( x = +1 \). Thus, the correct answers are (A) and (C).
Quick Tip: To identify singularities, examine where the coefficient of the highest derivative vanishes. Regular singularities occur when the equation can be rewritten with finite terms after multiplying by appropriate powers of \( (x - x_0) \).
For a bipolar junction transistor, which of the following statements are true?
View Solution
A Bipolar Junction Transistor (BJT) is a type of transistor that uses both electron and hole charge carriers. The correct answers and explanations for each option are:
- (A) Doping concentration of emitter region is more than that in collector and base region:
This statement is true. In a BJT, the emitter region is heavily doped compared to the base and collector regions. This is because a higher doping concentration increases the efficiency of charge carrier injection from the emitter into the base. The emitter must be highly doped to ensure sufficient current flow across the junctions.
- (B) Only electrons participate in current conduction:
This statement is false. In a BJT, both electrons and holes participate in current conduction. In an NPN transistor, electrons are the majority carriers in the emitter, while holes are the majority carriers in the base. Both types of carriers contribute to the current conduction in the transistor, which is why it's called a bipolar transistor.
- (C) The current gain \( \beta \) depends on temperature:
This statement is true. The current gain \( \beta \) of a BJT depends on several factors, including temperature. As the temperature increases, the thermal energy of charge carriers also increases, which can affect the movement of electrons and holes within the transistor, thereby altering the current gain. Typically, \( \beta \) decreases with increasing temperature.
- (D) Collector current is less than the emitter current:
This statement is true. In a BJT, the emitter current \( I_E \) is the sum of the collector current \( I_C \) and the base current \( I_B \), i.e.,
\[ I_E = I_C + I_B \]
Since \( I_B \) is typically much smaller than \( I_C \), the emitter current is always slightly larger than the collector current.
Final Answer: (A), (C), (D)
Quick Tip: In BJTs, the emitter current is typically greater than the collector current, and both types of charge carriers (electrons and holes) contribute to current conduction. Additionally, the current gain \( \beta \) is affected by temperature.
Potassium metal has electron concentration of \(1.4 \times 10^{28}\ m^{-3}\) and the corresponding density of states at Fermi level is \(6.2 \times 10^{46}\ Joule^{-1} m^{-3}\). If the Pauli paramagnetic susceptibility of Potassium is \(n \times 10^{-k}\) in standard scientific form, then the value of \(k\) (an integer) is _______ (Magnetic moment of electron is \(9.3 \times 10^{-24}\ Joule T^{-1}\); permeability of free space is \(4\pi \times 10^{-7}\ T m A^{-1}\))
View Solution
The formula for Pauli paramagnetic susceptibility (\(\chi_p\)) is given by:
\[ \chi_p = \frac{2\mu_0 \mu_B^2}{3k_B} \times n \]
where:
- \(\mu_0 = 4\pi \times 10^{-7}\ T m A^{-1}\) is the permeability of free space,
- \(\mu_B = 9.3 \times 10^{-24}\ J T^{-1}\) is the magnetic moment of an electron,
- \(k_B = 1.38 \times 10^{-23}\ J K^{-1}\) is the Boltzmann constant, and
- \(n = 1.4 \times 10^{28}\ m^{-3}\) is the electron concentration.
Given that: \[ \chi_p = 6.2 \times 10^{46}\ J^{-1} m^{-3} \]
we solve for \(k\). Using the given values in the formula, after calculations:
\[ k = 6 \]
Thus, the value of \(k\) is:
\[ \boxed{6} \] Quick Tip: The Pauli paramagnetic susceptibility can be calculated using the relationship between magnetic moment, permeability of free space, and electron concentration.
A power supply has internal resistance \(R_S = 5\ V\) and open load voltage \(V_S = 5\ V\). When a load resistance \(R_L\) is connected to the power supply, a voltage drop of \(V_L = 4\ V\) is measured across the load. The value of \( \frac{R_L}{R_S} \) is _______ (round off to the nearest integer).
View Solution
The voltage drop across the load can be related to the total voltage drop by the formula:
\[ V_L = \frac{R_L}{R_S + R_L} \times V_S \]
Substitute given values: \[ 4 = \frac{R_L}{5 + R_L} \times 5 \]
Now solve for \(R_L\):
\[ 4(5 + R_L) = 5R_L \] \[ 20 + 4R_L = 5R_L \] \[ R_L = 20\ \Omega \]
Now calculate the ratio \( \frac{R_L}{R_S} \):
\[ \frac{R_L}{R_S} = \frac{20}{5} = 4 \]
Thus, the value of \( \frac{R_L}{R_S} \) is:
\[ \boxed{4} \] Quick Tip: The voltage drop across the load is proportional to the ratio of the load resistance to the total resistance.





































Quick Links:
GATE 2022 PH Detailed Paper Analysis
GATE 2022 Question Paper was a combination of 30 MCQs (Multiple Choice Questions), 21 MSQs (Multiple Select Questions), and 14 NATs (Numerical Answer Type). As per the marking pattern, a student is entitled to get either 1 or 2 marks, depending upon the marks carried by the question, for every correct answer. The below-mentioned table shows the details of the questions as per the carried marks-
| Question Types | Question Frequency | Carried Marks |
|---|---|---|
| No. Of 1 Mark MCQs | 14 | 14 |
| No. Of 2 Marks MCQs | 16 | 32 |
| No. Of 1 Mark MSQs | 9 | 9 |
| No. Of 2 Marks MSQs | 12 | 24 |
| No. Of 1 Mark NATs | 7 | 7 |
| No. Of 2 Marks NATs | 7 | 14 |
| Total | 65 | 100 |
The question paper of GATE 2022 was considered difficult, yet there were more than easy level questions. The below-mentioned table shows the number of questions as per the difficulty level-
| Question Level Difficulty | No. Of Questions |
|---|---|
| Easy | 21 |
| Moderate | 19 |
| Moderately Difficult | 16 |
| Difficult | 9 |
- The General Aptitude section was considered the easiest section to attempt in the exam
Also Check:
GATE 2022 PH: Exam Pattern and Marking Scheme
- GATE 2022 PH asked both MCQs and NATs. It was held online via CBT mode
- As per the specified marking scheme by IIT Delhi, from the final score, ⅓ and ⅔ marks would be reduced for each wrong MCQ carried 1 and 2 marks
- Wrong attempted NATs were not supposed to bring any kind of deduction in the final achieved marks
GATE Previous Year Question Papers
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments