GATE 2022 Geomatics Engineering (GE) Question Paper with Solutions PDFs are available for download. GATE GE (Geomatics Engineering) was a newly introduced paper. GATE 2022 GE was successfully conducted on February 13, 2022, by IIT Kharagpur. The exam commenced at 2:30 PM and concluded at 5:30 PM. Since it was the first session of GATE GE, students found it difficult to rate the question paper in terms of overall difficulty level.
GATE 2022 Geomatics Engineering (GE) Question Paper with Solutions
Candidates targeting GATE can download the PDFs for GATE 2022 GE Question Paper and Solution to know the important topics asked, and check their preparation level by solving the past question papers.
| GATE 2022 Geomatics Engineering (GE) Question Paper | Check Solutions |

Writing too many things on the \hspace{2cm} while teaching could make the students get \hspace{2cm}.
Which one of the following is a representation (not to scale and in bold) of all values of \( x \) satisfying the inequality \( 2 - 5x \leq \frac{-6x - 5}{3} \) on the real number line?

If \( f(x) = 2 \ln(\sqrt{e^x}) \), what is the area bounded by \( f(x) \) for the interval \([0, 2]\) on the x-axis?
A person was born on the fifth Monday of February in a particular year.
Which one of the following statements is correct based on the above information?
Which one of the groups given below can be assembled to get the shape that is shown above using each piece only once without overlapping with each other? (rotation and translation operations may be used).


Fish belonging to species S in the deep sea have skins that are extremely black (ultra-black skin). This helps them not only to avoid predators but also sneakily attack their prey. However, having this extra layer of black pigment results in lower collagen on their skin, making their skin more fragile.
For the past \( m \) days, the average daily production at a company was 100 units per day.
If today’s production of 180 units changes the average to 110 units per day, what is the value of \( m \)?
Consider the following functions for non-zero positive integers, \( p \) and \( q \):
\[ f(p, q) = p \times p \times p \times \cdots \times p = p^q \quad ; \quad f(p, 1) = p \] \[ g(p, q) = ppppp\cdots (up to q terms) \quad ; \quad g(p, 1) = p \]
Which one of the following options is correct based on the above?
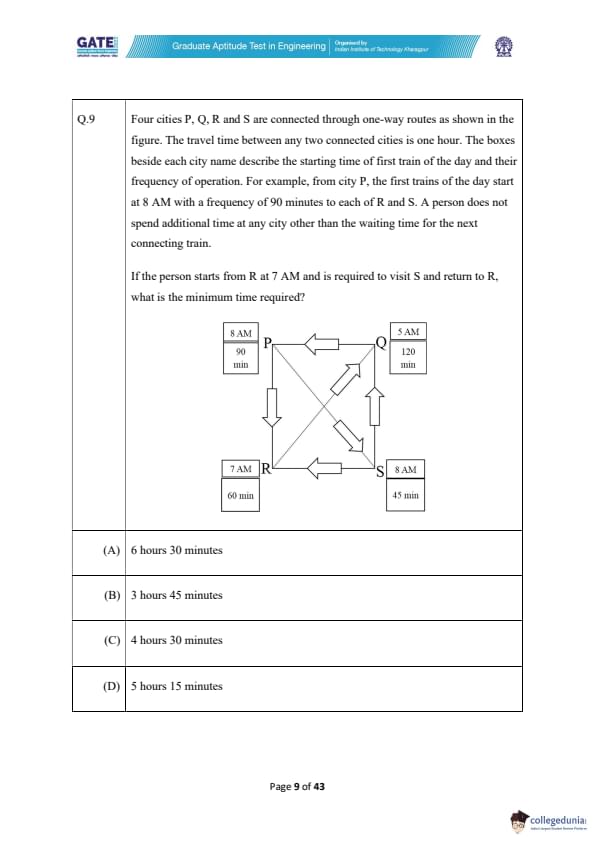
Four cities P, Q, R, and S are connected through one-way routes as shown in the figure. The travel time between any two connected cities is one hour. The boxes beside each city name describe the starting time of the first train of the day and their frequency of operation. For example, from city P, the first trains of the day start at 8 AM with a frequency of 90 minutes to each of R and S. A person does not spend additional time at any city other than the waiting time for the next connecting train.
If the person starts from R at 7 AM and is required to visit S and return to R, what is the minimum time required?

Equal sized circular regions are shaded in a square sheet of paper of 1 cm side length. Two cases, case M and case N, are considered as shown in the figures below. In the case M, four circles are shaded in the square sheet and in the case N, nine circles are shaded in the square sheet as shown.
What is the ratio of the areas of unshaded regions of case M to that of case N?

Most probable value of a quantity
Two surveyors, P and Q measured a 20 m distance six times each, as given below (in m):
Surveyor P: 19.97, 20.02, 20.04, 19.98, 19.96, 20.03
Surveyor Q: 20.05, 20.07, 20.05, 20.06, 20.07, 20.07
On the basis of accuracy and precision of the measured values, choose the CORRECT statement.
Identify the error, which has all the following characteristics:
(i) Caused by observer’s misunderstanding and carelessness
(ii) Reading an angle counter-clockwise, but recording it as clockwise angle
(iii) Sighting the wrong target
(iv) Poor judgment by the observer
Electromagnetic Spectrum can be broadly divided as (in order of increasing wavelength)
The relationship between wavelength (\( \lambda \)), frequency (\( \nu \)), and velocity (\( c \)) of electromagnetic wave is
Spectral signature of an object in a satellite image does NOT depend on the
Component of GPS signal that gets deciphered by all types of GPS receivers is
For 3D-positioning, Global Navigational Satellite System (GNSS) requires a minimum of _________ satellites.
Basic objective of NAVSTAR GPS is to provide services for
A satellite image with 6-bit radiometric resolution has _________ gray levels.
Thermal Infrared images are provided by
Which of the following gets mitigated in DGPS positioning?
In GIS database, which type of attribute may be used to represent area?
What is attribute uncertainty?
In GIS, _____ triangulation is a proximal method that satisfies the requirement that a circle drawn through the three nodes of a triangle contains no other node.
In GIS, reclassification is performed to
For the following observation equation \[ 2\alpha = 124^\circ 52' 22'' \quad weight 4, \]
the weight of \( \left( \frac{\alpha{3 \right) \text{ is _________ (in integer).
Following observation equations are obtained in a survey task.
\[ x + y = 3
2x + y = 6
x + 2y = 4 \]
Using least square method, the most probable values of x and y will be
The internal angles P, Q, R of a triangle are observed in degree minute second (° ' "). The angles along with their probable errors are given below.
P = 40° 30' 01'' ± 02'', Q = 60° 00' 02'' ± 03'', R = 79° 30' 05'' ± 04''
The corrected values of the angles P, Q and R are
How many number of cells of a 30 m spatial resolution DEM would be required to cover a 1:50,000 topographic map of Survey of India, assuming that 1 minute = 1.85 km?
Choose the CORRECT statement(s)
Choose the CORRECT statement(s) in case of visual image interpretation.
The spatial resolution of a satellite image \( P \) is 80 m and another satellite image \( Q \) is 20 m; each of 512 \(\times\) 512 pixel size. Choose the CORRECT option(s).
Which statement(s) is/are CORRECT for Hyperspectral images?
Satellite-Based NAVSTAR GPS Augmentation System(s) is/are
Identify the CORRECT statement(s)
Identify the CORRECT statement(s).
During GPS Surveying, initialization of rover receiver is required for
Centroid of a polygon is
The area of a buffer of 50 m around a proposed 1 km straight road segment to restrict any future construction is _________ sq. m. (in integer).
(Take the value of \(\pi = 3.14\))
The Degree of Accuracy of a traverse having error of closure of 0.5 m and perimeter of 100 m is _________ (round off to 3 decimal places).
Using the following regression equations, the correlation coefficient between two survey quantities x and y will be _________ (round off to 2 decimal places).
\[ 2x - 5y + 98 = 0 \] \[ 6x - 7y + 114 = 0 \]
If population variance is 14.8, sample variance is 15.4 and the number of degrees of freedom is 10, then Chi-square value is _________ (round off to 2 decimal places).
Height of a station determined by Global Navigational Satellite System (GNSS) is 284.097 m and the geoid height of the station is –30.052 m. The elevation of the station is _________ m (round off to 3 decimal places).
Number of cells required to cover an area of 9 sq. km of ASTER-GDEM are _________ (in integer).
If a 1:50,000 scale map is digitized to an accuracy of ± 0.5 mm, the level of error that might be expected in ground is ± _________ m (in integer).
The main principle of Surveying is to work from
The type of survey carried out to define the property boundaries for transfer of land property is called
Departure of a line of a traverse is obtained by multiplying its length by the _________ of the reduced bearing of the line.
The multiplying constant of a Tacheometer, where \( f \) is the focal length and \( i \) is the distance between the stadia hairs, is
The camera axis of an aerial camera is defined as
Bowditch rule for adjusting a closed traverse of perimeter ‘l’ is based on the assumption that the probable error is proportional to
Select the INCORRECT statement:
A topographic map prepared by Survey of India covers 1 degree by 1 degree area on a single map. The minimum ground distance which can be represented on this map is _________ m (round off to 2 decimal places).
In a closed traverse, the sum of the latitudes is 1.39 m and the sum of the departures is 2.17 m. The Length and Whole Circle Bearing of the closing error are
In surveying, an odometer is used for measuring
Choose the CORRECT statement(s).
Choose the CORRECT statement(s).
A map projection is
Face Left and Face Right observations using a vernier theodolite will eliminate
The parallax of a point ‘a’ on a pair of successive overlapping photographs is 73.22 mm and the micrometer reading of a parallax bar of point ‘a’ is 12.10 mm. Similarly, the micrometer reading of the parallax bar of point ‘b’ is 9.65 mm, then the parallax of the point ‘b’ is _________ mm (round off to 2 decimal places).
The scale of an aerial photograph is 5 mm = 100 m. The size of the photograph is 23 cm × 23 cm. If the longitudinal overlap is 65% and sidelap is 20%, the number of photographs required to cover an area of 12.5 km × 8 km is _________ (in integer).
An instrument is set up at a station P and the angle of depression to a vane, 1.20 m above the foot of the staff held at Q is 5°. The horizontal distance PQ is observed to be 300 m. The R.L. of point Q is _________ m (round off to 3 decimal places). Given that the staff reading at a BM (Elevation 436.050 m) is 2.865 m.
A staff is held vertical at a distance of 100 m and 300 m, respectively. Observations are taken with a Tacheometer and staff intercepts, with the telescope kept horizontal, are 0.990 m and 3.000 m, respectively. The theodolite is set over a station having a RL of 950.500 m and the height of instrument is 1.425 m. The multiplicative constant of the Tacheometer is _________ (round off to 2 decimal places).
Survey of India topographic sheet is 53G/12. At this scale, the number of toposheets that would cover a land area equivalent to 4 degree by 4 degree is _________ (in integer).
The correlation coefficient between two bands of remote sensing data that would yield good classification is
In a covariance matrix, the main diagonal shows the _________ of each band.
Choose the INCORRECT statement about image segmentation in digital image processing.
When the histogram of an image is non-Gaussian in nature, the type of linear contrast enhancement preferred to be used is
Spinning of the Earth, as viewed from the North pole, appears to be from
In case of Principal Component Analysis (PCA), the variance of a single variable expresses the spread of its values about the
Select the CORRECT sequence for supervised classification of satellite image.
(i) Classification
(ii) Training
(iii) Accuracy assessment
(iv) Radiometric/geometric correction
The sum of all the values of a normalized histogram is equal to _________ (in integer).
In a Landsat-8 scene, digital number (DN) values of a pixel in band-4, band-5 and band-10 are 80, 100 and 30, respectively. What would be the NDVI value for the same pixel (round off to 3 decimal places)?
For a given set of radiance values, which amongst the following is/are unitless?
Identify the CORRECT statement(s).
Choose the CORRECT statement(s).
Match the CORRECT option(s) for the types of filters given in (I), (II), (III), and (IV) with their kernels given in (P), (Q), (R), and (S).

Band ratio in satellite images interpretation is applied to
The decorrelation stretch enhances colour differences and removes inter-band _________.
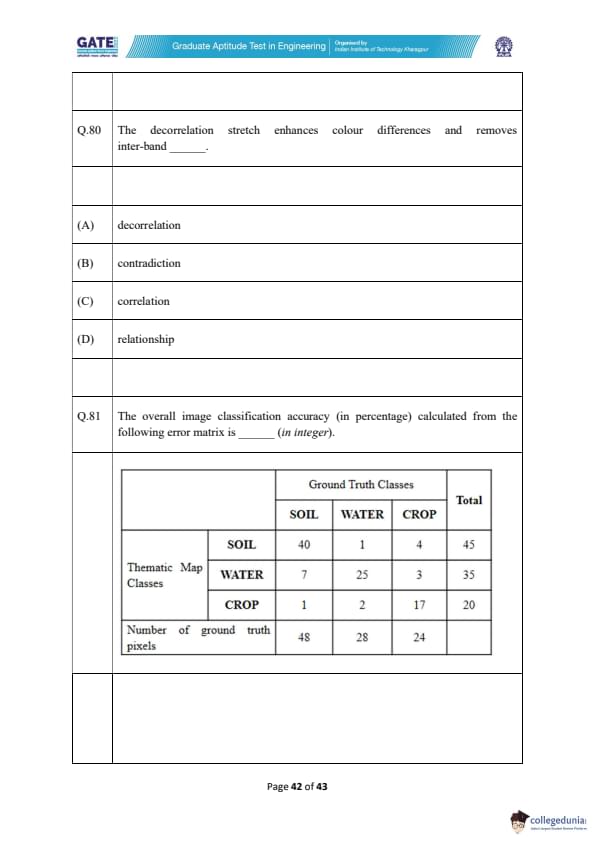
The overall image classification accuracy (in percentage) calculated from the following error matrix is _________ (in integer).

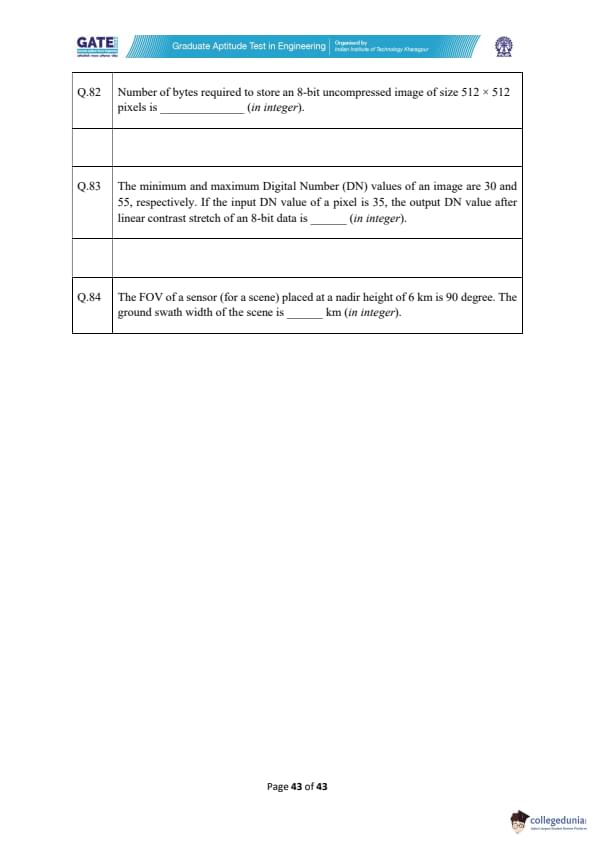
Number of bytes required to store an 8-bit uncompressed image of size 512 × 512 pixels is _________ (in integer).
The minimum and maximum Digital Number (DN) values of an image are 30 and 55, respectively. If the input DN value of a pixel is 35, the output DN value after linear contrast stretch of an 8-bit data is _________ (in integer).
The FOV of a sensor (for a scene) placed at a nadir height of 6 km is 90 degree. The ground swath width of the scene is _________ km (in integer).






































Quick Links:
GATE 2022 GE Detailed Paper Analysis
Likewise any other GATE exam, GATE GE 2022 question paper also comprised 65 questions. GATE 2022 GE question paper was distributed in two sections i.e. Part A and Part B.
- Part A contained 10 General Aptitude questions that were mandatory to attempt.
- Part B was related to core GE based questions that were further distributed between Sections i.e. Section A and Section B.
- Candidates opting for GE could also choose any of the papers from Civil Engineering (CE), Geology and Geophysics (GG), Environmental Science and Engineering (ES), and Mining Engineering (MN).
- A total of 55 questions were listed in Part B of GATE 2022 GE. Some of the listed concept based questions were based on the following topics:
- Finding number of images - photogrammetry
- Thermal infrared images
- Question on Tacheometry
- Principle of surveying, Bowditch Relationship
Also Check:
GATE 2022 GE: Exam Pattern and Marking Scheme
- GATE 2022 GE asked both MCQs and NATs. It was held online via CBT mode
- As per the specified marking scheme by IIT Delhi, from the final score, ⅓ and ⅔ marks would be reduced for each wrong MCQ carried 1 and 2 marks
- Wrong attempted NATs were not supposed to bring any kind of deduction in the final achieved marks
GATE Previous Year Question Papers
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments