GATE 2022 Environmental Science and Engineering (ES) Question Paper with Solutions was successfully concluded on 6th February, 2022 by IIT Kharagpur. The overall difficulty level was rated moderate. Although students reviewed the question paper tougher as compared to last year. The question paper had three sections General Aptitude, Engineering Mathematics, and Environmental Science based questions. Maximum weightage was carried by ES based questions.
GATE 2022 Environmental Science and Engineering (ES) Question Paper with Solutions
Candidates targeting GATE can download the PDFs for GATE 2022 ES Question Paper and ASolutions to know the important topics asked, and check their preparation level by solving the past question papers.
| GATE 2022 Environmental Science and Engineering (ES) Question Paper | Check Solutions |

Mr. X speaks _____ Japanese _____ Chinese.
A sum of money is to be distributed among P, Q, R, and S in the proportion 5 : 2 : 4 : 3, respectively.
If R gets ₹1000 more than S, what is the share of Q (in ₹)?
A trapezium has vertices marked as P, Q, R, and S (in that order anticlockwise). The side PQ is parallel to side SR. Further, it is given that, PQ = 11 cm, QR = 4 cm, RS = 6 cm, and SP = 3 cm. What is the shortest distance between PQ and SR (in cm)?
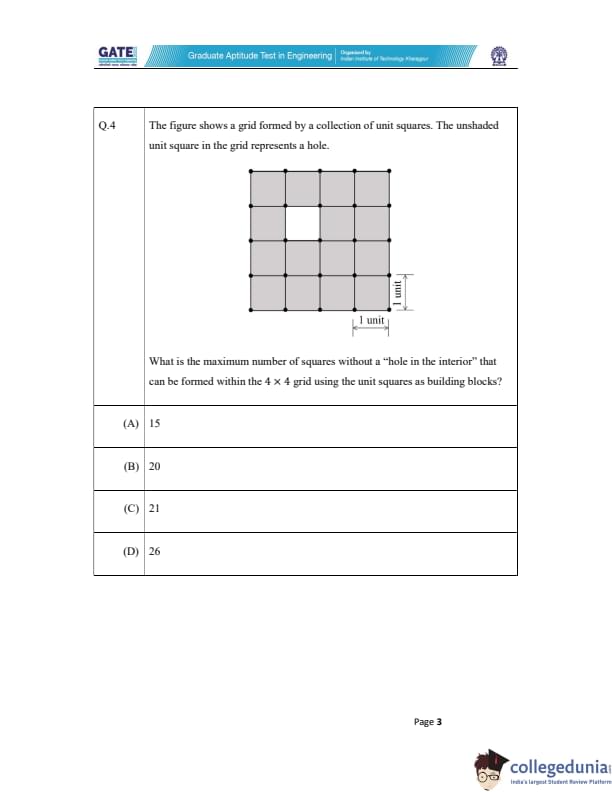
The figure shows a grid formed by a collection of unit squares. The unshaded unit square in the grid represents a hole. What is the maximum number of squares without a "hole in the interior" that can be formed within the 4 \(\times\) 4 grid using the unit squares as building blocks?

An art gallery engages a security guard to ensure that the items displayed are protected. The diagram below represents the plan of the gallery where the boundary walls are opaque. The location the security guard posted is identified such that all the inner space (shaded region in the plan) of the gallery is within the line of sight of the security guard.
If the security guard does not move around the posted location and has a 360° view, which one of the following correctly represents the set of ALL possible locations among the locations P, Q, R and S, where the security guard can be posted to watch over the entire inner space of the gallery?

Mosquitoes pose a threat to human health. Controlling mosquitoes using chemicals may have undesired consequences. In Florida, authorities have used genetically modified mosquitoes to control the overall mosquito population. It remains to be seen if this novel approach has unforeseen consequences.
Which one of the following is the correct logical inference based on the information in the above passage?
Consider the following inequalities.
(i) 2x - 1 \(>\) 7
(ii) 2x - 9 \(<\)1
Which one of the following expressions below satisfies the above two inequalities?
Four points \( P(0, 1), Q(0, -3), R(-2, -1), \) and \( S(2, -1) \) represent the vertices of a quadrilateral. What is the area enclosed by the quadrilateral?
In a class of five students P, Q, R, S and T, only one student is known to have copied in the exam. The disciplinary committee has investigated the situation and recorded the statements from the students as given below.
Statement of P: R has copied in the exam.
Statement of Q: S has copied in the exam.
Statement of R: P did not copy in the exam.
Statement of S: Only one of us is telling the truth.
Statement of T: R is telling the truth.
The investigating team had authentic information that S never lies.
Based on the information given above, the person who has copied in the exam is:
Consider the following square with the four corners and the center marked as P, Q, R, S and T respectively.
Let X, Y, and Z represent the following operations:
X: rotation of the square by 180 degree with respect to the S-Q axis.
Y: rotation of the square by 180 degree with respect to the P-R axis.
Z: rotation of the square by 90 degree clockwise with respect to the axis perpendicular, going into the screen and passing through the point T.
Consider the following three distinct sequences of operation (which are applied in the left to right order).
(1) XYZ
(2) XY
(3) ZZZZ
Which one of the following statements is correct as per the information provided above?

A student reported following arsenic concentrations in water samples:

Which one of the following is a correct statement about arsenic concentration distribution?
X is normally distributed with the following data (25.8, 36.6, 26.3, 21.8, 27.2). Select the correct statement about X (\(t_{crit,\ \alpha=0.05,4}=2.132\)):
Assuming \(s > 0\), the Laplace transform for \(f(x) = \sin(ax)\) is
Given \(P\) is an \(m\times n\) matrix, \(Q\) is an \(n\times l\) matrix, and \(R\) and \(S\) are \(n\times n\) matrices. Consider:
Relationship 1: \quad \((PQ)^T = Q^T P^T\)
Relationship 2: \quad \((RS)^{-1} = S^{-1} R^{-1}\)
Which one of the following is correct?
Specific conductance is used in water analysis to indirectly estimate dissolved solids. The measurements used in the method account for
Ten litres of the sample was filtered through a membrane filter and the filter was transferred to solid agar media which supports growth of coliform organisms. After incubation at 37°C for 48 hours, the agar plates showed an average of 64 colonies per plate. What was the average concentration of coliform organisms (in CFU/ml) in the original water sample?
Reverse Transcriptase Polymerase Chain Reaction is an analytical procedure used in detection of pathogenic microorganisms. Which one of the following statements is NOT correct in this context?
Consider the following statements:
Statement 1: Goodrich method for reservoir routing is based on hydrologic flood routing method.
Statement 2: Muskingum method for channel routing is based on hydraulic flood routing method.
Which one of the following is correct?
The correct order of hydraulic conductivity for the geologic formations is
Centrifugal pumps with suction pipe (shown by solid arrow) and delivery pipe (shown by dotted arrow) are shown in the figures. Choose the option that gives the correct connection.

Carbon dioxide is used in recarbonation process. A solution has 1 mole/L supersaturated calcium carbonate. Estimated amount of carbon dioxide (in grams) needed to completely convert calcium carbonate to calcium ions in 1 litre solution is _____.
A river water sample has pH of 4 and suspended solids concentration of 100 mg/L. If alum is chosen as a coagulant, what will be the coagulation mechanism?
Which one of the following is most commonly used raw material in flue gas desulfurization units?
Leachate generated from a legacy municipal solid waste dumping site has to be collected and managed carefully. Which statement is correct for treatment of such leachate?
Which one of the following statements is correct regarding Global warming?
In context of ecosystems, which one of the following is NOT a correct statement?
Which one of the following statements correctly defines the concept of ‘Extended Producer’s Responsibility’?
If \(G\) represents Gibbs free energy, select the correct statement(s).
For effluents generated by a molasses-based distillery and wood-based pulp and paper industry, which of the following statement(s) is/are NOT correct?
PM\(_{2.5}\) concentrations in ambient air can be measured using
Biodegradable wastes like vegetable peelings from kitchen are usually processed by composting techniques. Which of the following option(s) regarding the processing of biodegradable wastes is/are correct?
As per ‘Hazardous and Other Wastes (Management and Transboundary Movement) Rules, 2016’ of Govt. of India, the import of hazardous and other wastes from any country shall NOT be permitted for which of the following option(s)?
The Ministry of Environment, Forest and Climate Change (MoEF\&CC), Govt. of India has published the Environment Impact Assessment (EIA) draft Notification 2020, intended to replace the existing EIA Notification 2006 under the Environment (Protection) Act, 1986. Which of the following is/are the key change(s) from existing regulation?
\[ \lim_{x\to 0} \frac{\sqrt{1+x}-1}{x} \]
is ______ (rounded off to one decimal place).
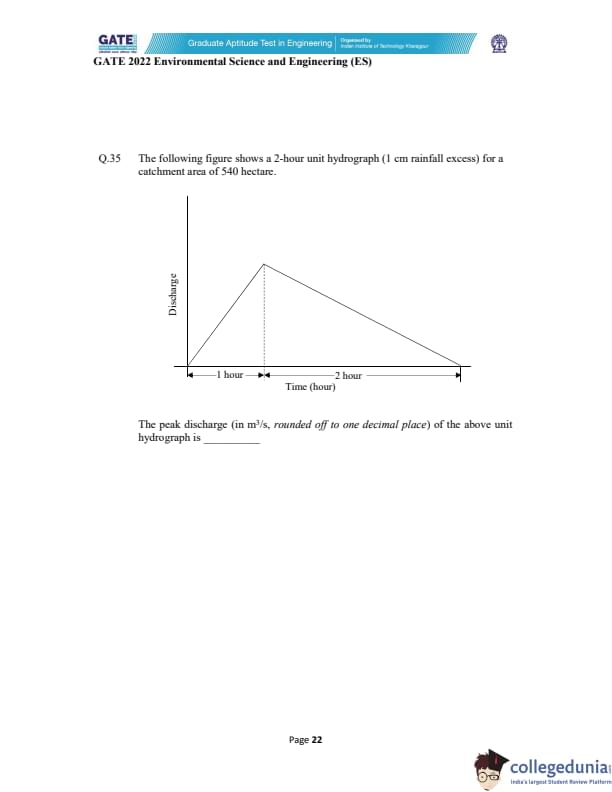
The following figure shows a 2-hour unit hydrograph (1 cm rainfall excess) for a catchment area of 540 hectare.
Find the peak discharge (in m\(^3\)/s, rounded to one decimal place).

Given, \(y = f(x)\); \(\dfrac{d^2 y}{dx^2} + 4y = 0\); \(y(0) = 0\); \(\dfrac{dy}{dx}(0) = 1\). The problem is a/an
Eigenvalues of the matrix \(\begin{bmatrix} 0 & 1
-2 & 3 \end{bmatrix}\) are
For an exponentially growing microbial culture, the specific growth rate \((\mu)\) is related to its doubling time \((t_d)\) by which one of the following relations?
A microbial culture with a specific growth rate of \(\mu_1\) (per hour) is being grown in a continuous reactor at steady state with hydraulic retention time (HRT) of 24 hours. The reactor is subjected to a perturbation by reducing the HRT to 12 hours. The reactor recovers and comes to a new steady state with a specific growth rate of \(\mu_2\). Which one of the following statements is correct?
Which one of the following statements is NOT correct with respect to a batch reactor?
A bag filter is used for removal of particulate matter having a range of sizes. The correct sequence of air filtration mechanisms for their removal, in order of decreasing size, is
A relatively calm room has background sound power level (SPL) of 30 decibels (dB). A television and a radio with SPL of 80 dB and 70 dB, respectively, started operating simultaneously in this room. Given the reference sound power is \(10^{-12}\) Watts, what will be the resulting SPL in the room, assuming all the sources operate independently?
During night, in troposphere, which of the following is/are NOT correct?
A typical plasmid-free bacterial cell having a single chromosome consists of \(\sim 55%\) protein, \(\sim 3%\) DNA and \(\sim 21%\) RNA (percent of dry weight). Assuming there are 2500 different types of protein molecules (with at least one copy number) being expressed in a bacterial cell at any given time, which of the following statements is/are NOT correct with respect to the number of intracellular DNA, RNA and protein molecules?
Average values of the re-aeration rate constant for river X and Y are 0.92 day\(^{-1}\) and 1.12 day\(^{-1}\) respectively. Average de-oxygenation rate constants are 0.23 day\(^{-1}\) and 0.35 day\(^{-1}\) for the same rivers. Which of the following statement(s) is/are correct?
Which of the following statement(s) is/are NOT correct while comparing continuously stirred tank reactor (CSTR) and plug flow reactor (PFR)?
According to the National Ambient Air Quality Standards (CPCB, Govt. of India, 2009), which of the following statement(s) is/are correct?
Consider the figure shown below for three different cases.
Which of the following statement(s) is/are correct for surface level emissions, given the environmental temperature?

As per the Solid Waste Management Rules of 2016 (Govt. of India), which of the following statement(s) is/are correct?
Carbon cycle, nitrogen cycle and phosphorus cycle play important roles in ecosystems. Which of the following statement(s) is/are NOT correct about the phosphorus cycle?
Which of the following statement(s) is/are correct regarding National Green Tribunal (NGT) of India?
The area of the region (rounded off to one decimal place) enclosed between the curves \(y = x\) and \(y = 3\sqrt{x}\) and between the lines \(x = 0\) and \(x = 1\) is ______ units.
An individual has four different email accounts. 60% of emails come into his corporate account,
30% come into his gmail account and the remaining 10% are equally divided into his yahoo and zoho accounts.
Only 1% of the emails in his corporate accounts are spam, whereas corresponding percentages for gmail, yahoo and zoho accounts are 2%, 3% and 3%, respectively. Assuming that the same spam filter is used in all the four email accounts, the probability (in percentage, rounded off to one decimal place) of having a randomly selected email as spam is ______.
A solution has 0.001 mole/L zinc ions with pH = 6.
The solubility product of zinc hydroxide is \[ K_{sp} = 8 \times 10^{-18}\ (mol/L)^{3}. \]
Ignoring activity corrections, find the ratio (rounded to two decimals) of the reaction quotient to the solubility product.
The Henry’s law constant of CO\(_2\) is \(3.4 \times 10^{-2}\) M/atm at 25\(^\circ\)C.
Dissolved CO\(_2\) undergoes:
CO\(_2 \cdot\)H\(_2\)O \(\rightleftharpoons\) H\(^+\) + HCO\(_3^-\) \quad (\(K_1 = 4.3 \times 10^{-7}\) M)
HCO\(_3^- \rightleftharpoons\) H\(^+\) + CO\(_3^{2-}\) \quad (\(K_2 = 4.7 \times 10^{-11}\) M)
If ambient CO\(_2\) concentration is 300 ppm, the total dissolved CO\(_2\) (in \(\mu\)M, rounded off to one decimal place) is _____.
An isolated 3-hour storm occurred over a catchment.
Given the \(\phi\)–index and rainfall data, compute the total rainfall excess
(rounded off to one decimal place).

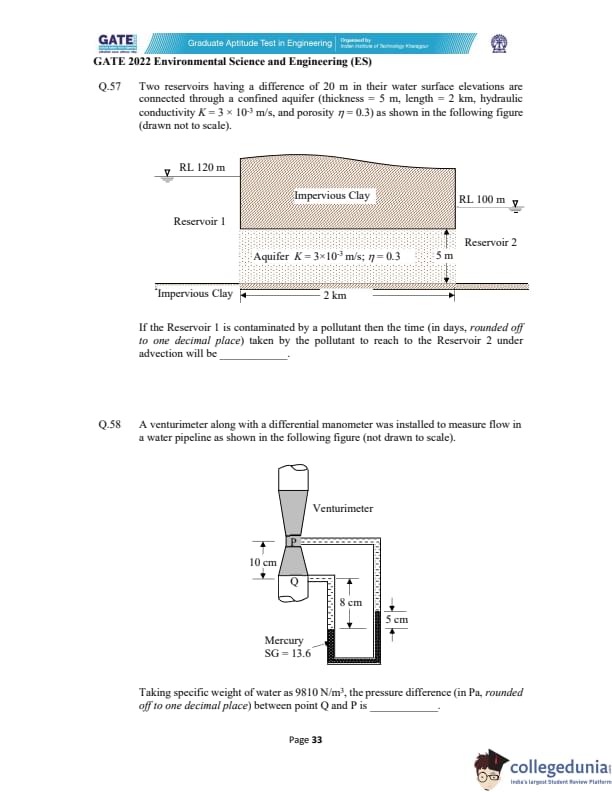
Two reservoirs differ by 20 m in water levels and are connected through a confined aquifer
(thickness = 5 m, length = 2 km, hydraulic conductivity \(K = 3\times10^{-3}\) m/s,
porosity \(\eta = 0.3\)). If Reservoir 1 is contaminated, the time (in days, rounded off to one decimal place)
taken by the pollutant to reach Reservoir 2 by advection is _____.

A venturimeter with a differential manometer is installed to measure flow in a water pipeline.
Taking water specific weight = 9810 N/m\(^3\), compute the pressure difference (in Pa,
rounded off to one decimal place) between points Q and P.

Two reservoirs differ by 10 m in water surface elevation and are connected by a 50 m long,
10 cm diameter pipeline (friction factor \(f = 0.02\)).
If the last 25 m is replaced with a 20 cm diameter pipe of the same material,
the increase in discharge (in %, rounded to one decimal place) is:
Find the depth of flow (in m, rounded to two decimals)
in a hydraulically efficient rectangular channel (\(n = 1/80\))
carrying 64 m\(^3\)/s at slope \(S = 0.01\).
Clean water is passed through a bed of uniform spherical sand at a filtration velocity of 0.002 m/s.
Sand grains are 0.4 mm diameter, specific gravity 2.65, bed depth = 0.67 m, porosity \(\eta = 0.35\).
Water density = 998.2 kg/m\(^3\), viscosity = \(1.002\times10^{-3}\) Pa·s.
Friction factor: \[ f = 1.75 + \frac{150(1-\eta)}{Re}, \]
where \(Re\) is Reynolds number.
The headloss (in m, rounded off to three decimal places) using the Carman–Kozeny equation is _____.
A sewage treatment plant (capacity 10 MLD) treats wastewater using an aerobic biological process.
Inlet BOD = 100 mg/L, outlet BOD = 30 mg/L. Microbial yield = 0.5 g VSS/g BOD removed.
At 80% plant capacity, the sludge production rate (in kg/day, rounded off to one decimal place) is _____.
A centrifuge processes 1000 L/h of water containing 2 g/L suspended solids.
The thickened slurry leaving the centrifuge has 20 g per 100 mL of solids.
If the centrifuge has 99% solids-separation efficiency,
find the flow rate (in L/h, rounded to one decimal place) of the supernatant stream.
A ground level source emits 1000 g/day of SO\(_2\). Wind speed = 2 m/s.
Dispersion coefficients at 1000 m downwind are given.
Estimate the ground-level SO\(_2\) concentration (in \(\mu\)g/m\(^3\), rounded off to two decimals)
at 1000 m at the plume centerline.

The figure shows heat inflow and outflow for a waste-to-energy plant furnace.
Assume:
(i) total heat loss = 3% of heat released from waste,
(ii) sensible heat of waste is negligible,
(iii) complete burning of waste.

Given waste feed rate = 70 kg/h, air heat input = 300 kcal/h,
flue gas = 90000 kcal/h, ash = 10000 kcal/h.
Find the heat content of waste (kcal/kg), rounded to one decimal place.
































Also Check:
Quick Links:
GATE 2022 ES Detailed Paper Analysis
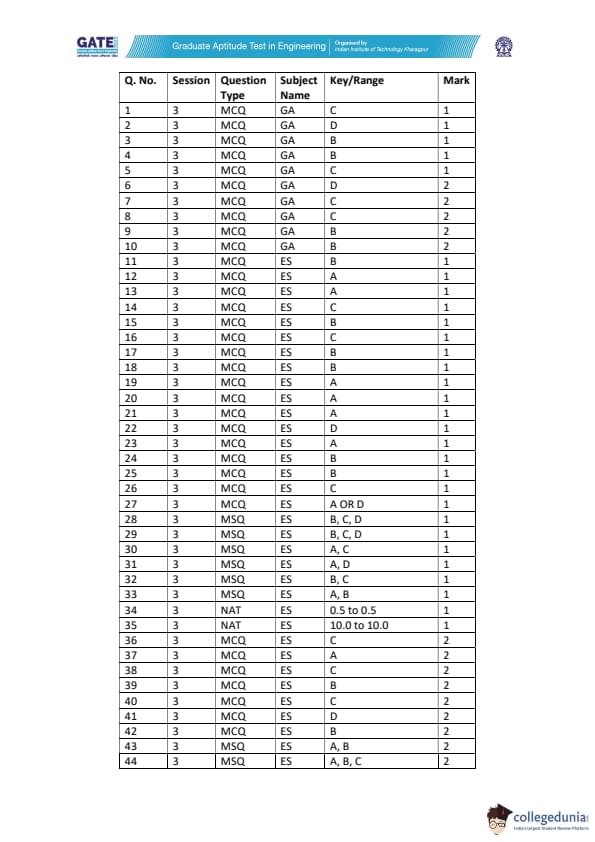
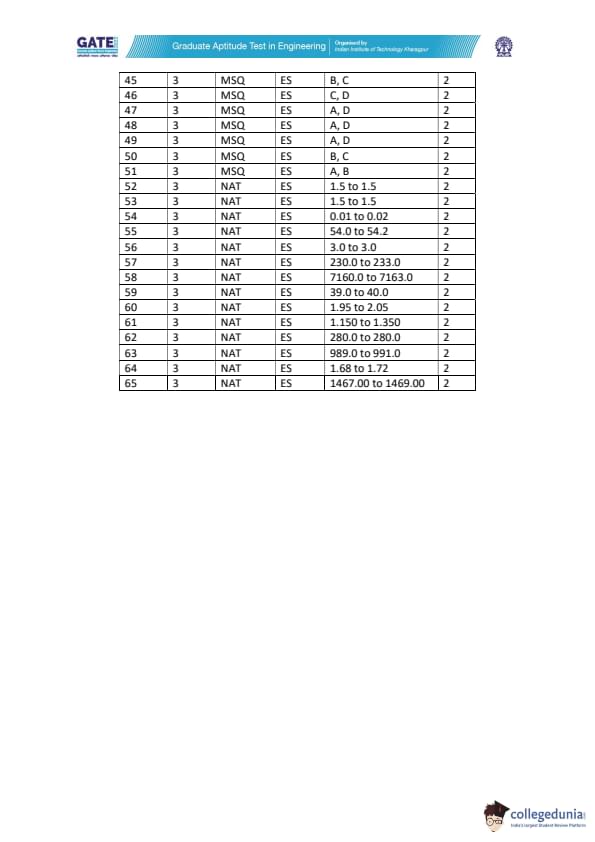
A total of 65 questions listed in GATE 2022 ES that were related to 10 sections. Follow the below-mentioned table in order to get details of the appeared questions as per the sections-
| Topics/Sections | No. Of Questions Carried |
|---|---|
| General Aptitude | 10 |
| Engineering Mathematics | 10 |
| Environmental Chemistry | 5 |
| Air and Noise Pollution | 6 |
| Environmental Microbiology | 5 |
| Water & Wastewater Treatment and Management | 8 |
| Global Issues | 4 |
| Environmental Management and Sustainable Development | 5 |
| Water Resources and Environmental Hydraulics | 4 |
| Water & Wastewater Treatment and Management | 8 |
| Total | 65 |
- The question paper carried more theory based questions, along with a few tricky questions
- The General Aptitude and Mathematics section was rated comparatively easy
GATE 2022 ES Question Types and Question Frequency
The appeared questions were in three forms i.e. MCQs (Multiple Choice Questions), NATs (Numerical Answer Type), and MSQs (Multiple Select Questions). More number of MSQs made the paper difficult to attemp. Candidates can go through the below-mentioned table to see the total number of MCQs, MSQs and NATs in GATE 2022 ES Question Paper-
| Question Types | Question Frequency |
|---|---|
| No. Of MCQs | 33 |
| No. Of MSQs | 14 |
| No. Of NATs | 18 |
| Total | 65 |
Also Check:
GATE 2022 ES: Exam Pattern and Marking Scheme
- GATE 2022 ES asked both MCQs and NATs. It was held online via CBT mode
- As per the specified marking scheme by IIT Delhi, from the final score, ⅓ and ⅔ marks would be reduced for each wrong MCQ carried 1 and 2 marks
- Wrong attempted NATs were not supposed to bring any kind of deduction in the final achieved marks
GATE Previous Year Question Papers
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments