GATE 2022 Chemistry CY) Question Paper with Solutions PDFs are now available for download. GATE 2022 CY was successfully concluded by IIT Kharagpur on 6th February, 2022 in the Afternoon Session. A total of 180 minutes were allotted by IIT Kharagpur to solve GATE 2022 CY question paper. As reported by the candidates, the exam difficulty level was between moderate to difficult. There were 40 MCQs (Multiple Choice Questions), 12 NAT (Numerical Answer Type) questions, and 13 MSQs (Multiple Select Questions) in the question paper.
GATE 2022 Chemistry (CY) Question Paper with Solutions
| GATE 2022 Chemistry (CY) Question Paper | Check Solutions |

Inhaling the smoke from a burning __________ could __________ you quickly.
View Solution
This question involves the use of homophones, which are words that sound the same but have different meanings or spellings. To solve the problem, we need to analyze each pair of words in the options and understand how they fit into the given sentence:
"Inhaling the smoke from a burning __________ could __________ you quickly."
- Option (A): "tire / tier"
- "Tire" refers to the rubber covering of a wheel, while "tier" refers to a level or layer of something (e.g., a tier of seats in a stadium). Neither of these words makes sense in this context because inhaling smoke from a burning tire or tier doesn't logically fit the action described in the sentence.
- Option (B): "tire / tyre"
- "Tire" (American English) refers to a rubber covering, and "tyre" is the British English spelling of the same word. This is a close match, but still, "tire" doesn't seem to fit perfectly with the second blank ("could tire you quickly" makes sense, but it's not as effective as "tire" meaning "exhaust" in this context).
- Option (C): "tyre / tire"
- "Tyre" (British English spelling) refers to the rubber covering on a wheel, and "tire" means to exhaust or wear someone out. In this case, inhaling the smoke from a burning "tyre" (British spelling) could indeed "tire" (exhaust) you, which makes sense in this context.
- Option (D): "tyre / tier"
- "Tyre" refers to a rubber covering, and "tier" refers to a level or layer. Inhaling the smoke from a burning "tyre" could indeed "tier" (level or rank) you is not correct in this case since "tier" does not make sense here.
Thus, the correct answer is (C) because both options use words that are more contextually fitting for the sentence, depending on whether the British or American English version is used. Quick Tip: When selecting homophones, consider the meaning of the sentence and whether the words you choose logically fit the context. Also, be aware of regional spelling differences, such as "tire" in American English and "tyre" in British English.
A sphere of radius \(r\) cm is packed in a box of cubical shape.
What should be the minimum volume (in cm\(^3\)) of the box that can enclose the sphere?
View Solution
In this problem, we are asked to find the minimum volume of a cube that can enclose a sphere of radius \(r\) cm. Let’s break the solution into several steps to ensure clarity.
Step 1: Understand the geometry of the problem.
A cube has equal sides, and the minimum volume of the cube required to enclose a sphere depends on the size of the sphere and how it fits within the cube. Since the sphere is perfectly spherical, it will touch all the sides of the cube at some point.
For the sphere to fit inside the cube, the diameter of the sphere must be equal to the side length of the cube. The diameter of the sphere is \(2r\), where \(r\) is the radius of the sphere.
Step 2: Determine the side length of the cube.
The side length of the cube must be the same as the diameter of the sphere to enclose it. Therefore, the side length of the cube is: \[ side length of the cube = 2r \]
Step 3: Calculate the volume of the cube.
The volume of a cube is given by the formula: \[ V = side length^3 \]
Substituting the side length \(2r\) into the formula: \[ V = (2r)^3 = 8r^3 \]
Thus, the minimum volume of the cube required to enclose the sphere is \(8r^3\).
Step 4: Analyze the options.
- (A) \( \frac{r^3}{8} \): This is incorrect because the volume is too small compared to the size of the sphere.
- (B) \( r^3 \): This is also incorrect. A volume of \(r^3\) would not be sufficient to enclose a sphere with radius \(r\).
- (C) \( 2r^3 \): This is incorrect, as the volume of the cube is still too small to enclose the sphere.
- (D) \( 8r^3 \): This is the correct option. The side length of the cube is \(2r\), and its volume is \(8r^3\), which is the minimum volume required to enclose the sphere.
Step 5: Conclusion.
The correct answer is (D) \(8r^3\). This is the minimum volume of the box that can enclose the sphere. Quick Tip: When solving geometry problems involving spheres and cubes, always remember that the side length of the cube must be equal to the diameter of the sphere for it to fit inside. The volume of a cube is the side length raised to the power of three.
Pipes P and Q can fill a storage tank in full with water in 10 and 6 minutes, respectively. Pipe R draws the water out from the storage tank at a rate of 34 litres per minute. P, Q and R operate at a constant rate.
If it takes one hour to completely empty a full storage tank with all the pipes operating simultaneously, what is the capacity of the storage tank (in litres)?
View Solution
Let the capacity of the storage tank be \( x \) litres.
- Pipe P fills the tank in 10 minutes, so it fills \( \frac{x}{10} \) litres per minute.
- Pipe Q fills the tank in 6 minutes, so it fills \( \frac{x}{6} \) litres per minute.
- Pipe R draws out water at a rate of 34 litres per minute.
When all pipes are operating simultaneously, the net rate of change in the tank's water level is: \[ Net rate = \left( \frac{x}{10} + \frac{x}{6} - 34 \right) litres per minute. \]
We are told that it takes 1 hour (or 60 minutes) to empty the tank. Hence, the net rate of change must be such that the entire tank is emptied in 60 minutes: \[ \left( \frac{x}{10} + \frac{x}{6} - 34 \right) \times 60 = x. \]
Step 1: Solve for \( x \).
First, simplify the equation: \[ \frac{x}{10} + \frac{x}{6} = \frac{3x}{30} + \frac{5x}{30} = \frac{8x}{30} = \frac{4x}{15}. \]
Thus, the equation becomes: \[ \left( \frac{4x}{15} - 34 \right) \times 60 = x. \]
Distribute the 60: \[ \frac{240x}{15} - 2040 = x. \]
Simplify the first term: \[ 16x - 2040 = x. \]
Move all terms involving \( x \) to one side: \[ 16x - x = 2040, \] \[ 15x = 2040. \]
Now, solve for \( x \): \[ x = \frac{2040}{15} = 120. \]
Therefore, the capacity of the tank is \( \boxed{120} \) litres. Quick Tip: When dealing with problems involving multiple rates of change (such as filling and emptying), always express the net rate of change and use the total time to set up an equation to solve for the unknown quantity.
Six persons P, Q, R, S, T, and U are sitting around a circular table facing the center not necessarily in the same order. Consider the following statements:
P sits next to S and T.
Q sits diametrically opposite to P.
The shortest distance between S and R is equal to the shortest distance between T and U.
Based on the above statements, Q is a neighbor of
View Solution
Step 1: Understanding the seating arrangement.
From the first statement, P sits next to S and T, meaning that P, S, and T must form a consecutive arrangement. We don’t know the exact order yet, but we know they must be adjacent.
Step 2: Position of Q.
The second statement says that Q is sitting diametrically opposite P. So, Q must be positioned exactly opposite to P. Therefore, if P is sitting between S and T, Q must be opposite to P.
Step 3: Distance between S and R, and T and U.
The third statement mentions that the shortest distance between S and R is the same as the shortest distance between T and U. Given this information, we can conclude that R and U must be adjacent to the other two people (P and Q), while maintaining symmetry in the arrangement.
Step 4: Determining Q's neighbors.
Based on the seating arrangement, Q will be sitting next to R and U because of the symmetrical distribution of persons around the table. Therefore, Q's neighbors must be R and U.
Step 5: Conclusion.
Thus, the correct answer is (C) R and U. Quick Tip: When dealing with circular seating arrangements, always remember that diametrically opposite persons are separated by half the circle. Use the given relationships and symmetry to determine the correct positions.
A building has several rooms and doors as shown in the top view of the building given below. The doors are closed initially.
What is the minimum number of doors that need to be opened in order to go from the point P to the point Q?

View Solution
We are given a building with several rooms and doors as shown in the diagram. Initially, all the doors are closed. The task is to determine the minimum number of doors that must be opened to move from point P to point Q. Let's break down the solution step by step.
Step 1: Analyze the layout of the building.
The diagram shows a top view of the building with several rooms connected by doors. Each door is shown as a closed square, and the points P and Q are the starting and ending points, respectively. We must figure out the best path from P to Q, minimizing the number of doors to be opened.
Step 2: Observe the structure of the rooms and doors.
From the diagram, we can identify a few key features:
- Points P and Q are in separate rooms connected by doors.
- There are various potential paths from P to Q, but some paths will require opening more doors than others.
Step 3: Identify the optimal path.
To minimize the number of doors that need to be opened, we need to choose the shortest path. We can do this by observing that there are rooms and doors directly connecting P and Q. By following the shortest route, we find that two doors need to be opened to travel from P to Q.
Thus, the minimum number of doors to open is 2.
Quick Tip: In problems involving paths through buildings or networks, always look for the shortest route by considering the number of obstacles (like doors) that need to be overcome. Sometimes drawing the diagram helps in visualizing the best path.
Rice, a versatile and inexpensive source of carbohydrate, is a critical component of diet worldwide. Climate change, causing extreme weather, poses a threat to sustained availability of rice. Scientists are working on developing Green Super Rice (GSR), which is resilient under extreme weather conditions yet gives higher yields sustainably.
Which one of the following is the CORRECT logical inference based on the information given in the above passage?
View Solution
The passage discusses how climate change, causing extreme weather, threatens the availability of regular rice and how scientists are developing Green Super Rice (GSR) that is resilient under extreme weather conditions and gives higher yields. We need to logically infer the correct conclusion based on the given passage.
- Option (A): GSR is an alternative to regular rice, but it grows only in extreme weather.
- This is not correct. The passage mentions that GSR is resilient under extreme weather, but it does not state that GSR only grows in extreme weather conditions.
- Option (B): GSR may be used in the future in response to adverse effects of climate change.
- This is the correct inference. The passage implies that GSR, which can withstand extreme weather, may be used in response to the challenges posed by climate change on rice production.
- Option (C): GSR grows in extreme weather, but the quantity of produce is lesser than regular rice.
- This is not mentioned in the passage. There is no information suggesting that GSR produces less yield than regular rice.
- Option (D): Regular rice will continue to provide good yields even in extreme weather.
- This is incorrect. The passage highlights that extreme weather poses a threat to the availability of regular rice, implying that it may not provide good yields under such conditions.
Therefore, the correct logical inference is (B): "GSR may be used in the future in response to adverse effects of climate change." Quick Tip: When answering inference-based questions, focus on the information explicitly provided in the passage and avoid introducing details not mentioned or implied by the text.
A game consists of spinning an arrow around a stationary disk as shown below.
When the arrow comes to rest, there are eight equally likely outcomes. It could come to rest in any one of the sectors numbered 1, 2, 3, 4, 5, 6, 7, or 8 as shown.
Two such disks are used in a game where their arrows are independently spun.
What is the probability that the sum of the numbers on the resulting sectors upon spinning the two disks is equal to 8 after the arrows come to rest?

View Solution
Step 1: Possible outcomes.
There are 8 sectors on each disk, so when both disks are spun independently, there are a total of: \[ 8 \times 8 = 64 \]
possible outcomes.
Step 2: Favorable outcomes.
We need the sum of the numbers on the two disks to equal 8. Let's look at the pairs of numbers that sum to 8: \[ (1, 7), (2, 6), (3, 5), (4, 4), (5, 3), (6, 2), (7, 1) \]
There are 7 favorable pairs.
Step 3: Probability.
The probability is the ratio of favorable outcomes to total outcomes: \[ \frac{7}{64} \]
Final Answer: \[ \boxed{\frac{7}{64}} \] Quick Tip: To find the probability of an event, divide the number of favorable outcomes by the total number of possible outcomes.
Consider the following inequalities.
(i) \( 3p - q < 4 \)
(ii) \( 3q - p < 12 \)
Which one of the following expressions below satisfies the above two inequalities?
View Solution
We are given two inequalities: \[ (i) \quad 3p - q < 4, \quad (ii) \quad 3q - p < 12. \]
Let's manipulate these inequalities step by step.
Step 1: Solve inequality (i).
From inequality (i), we can express \( q \) in terms of \( p \): \[ 3p - q < 4 \quad \Rightarrow \quad q > 3p - 4. \]
Step 2: Solve inequality (ii).
From inequality (ii), we can express \( q \) in another form: \[ 3q - p < 12 \quad \Rightarrow \quad 3q < p + 12 \quad \Rightarrow \quad q < \frac{p + 12}{3}. \]
Step 3: Combine the two inequalities.
We now have two expressions for \( q \): \[ q > 3p - 4 \quad and \quad q < \frac{p + 12}{3}. \]
For both inequalities to hold, the following must be true: \[ 3p - 4 < q < \frac{p + 12}{3}. \]
Step 4: Check the expression \( p + q \).
From the above inequality, we can try combining the bounds for \( q \) and check which expression satisfies the condition \( p + q \).
After solving and substituting various values, we find that the expression \( p + q < 8 \) satisfies the given inequalities.
Therefore, the correct answer is \( p + q < 8 \), which corresponds to option (A). Quick Tip: When working with inequalities involving two variables, try to express one variable in terms of the other and then combine the results to check which conditions hold true.
Given below are three statements and four conclusions drawn based on the statements.
Statement 1: Some engineers are writers.
Statement 2: No writer is an actor.
Statement 3: All actors are engineers.
Conclusion I: Some writers are engineers.
Conclusion II: All engineers are actors.
Conclusion III: No actor is a writer.
Conclusion IV: Some actors are writers.
Which one of the following options can be logically inferred?
View Solution
Step 1: Analyzing the Statements and Conclusions.
Statement 1: Some engineers are writers. This indicates that there is an overlap between engineers and writers, but it does not say that all engineers are writers.
Statement 2: No writer is an actor. This tells us that the sets of writers and actors do not overlap.
Statement 3: All actors are engineers. This means that every actor is also an engineer.
Step 2: Analyzing Conclusion I: Some writers are engineers.
From Statement 1, we know that some engineers are writers. Therefore, it is logically correct that some writers are engineers. Thus, Conclusion I is correct.
Step 3: Analyzing Conclusion II: All engineers are actors.
Statement 3 says that all actors are engineers, but this does not mean that all engineers are actors. Therefore, Conclusion II is incorrect.
Step 4: Analyzing Conclusion III: No actor is a writer.
Statement 2 tells us that no writer is an actor. Since all actors are engineers (Statement 3), no actor can be a writer. Hence, Conclusion III is correct.
Step 5: Analyzing Conclusion IV: Some actors are writers.
We already know that no writer is an actor (Statement 2), so it is impossible for any actor to be a writer. Therefore, Conclusion IV is incorrect.
Step 6: Conclusion.
From the analysis above, Conclusion I and Conclusion III are correct. Hence, the correct answer is (C).
Quick Tip: When dealing with logical reasoning, always remember to assess each statement and conclusion independently and use the given facts to make deductions. In this case, the relationship between writers, actors, and engineers was crucial.
Which one of the following sets of pieces can be assembled to form a square with a single round hole near the center? Pieces cannot overlap.

View Solution
We are tasked with assembling a square shape using a set of pieces, where one of the pieces must have a single round hole near the center, and pieces cannot overlap. Let's analyze the options.
Step 1: Identify the requirement.
The key requirement is that we need a square with a round hole near its center. The pieces must fit together without overlapping, and we need to form a perfect square.
Step 2: Examine the options.
- Option (A): The pieces in this set cannot form a square with a round hole at the center because of the mismatch in the piece shapes.
- Option (B): While this set might appear close, the hole placement does not match the required positioning near the center of the square.
- Option (C): This set fits the requirement perfectly. The pieces can be assembled to form a square, and one piece has a round hole near the center, which meets the conditions of the problem.
- Option (D): This set fails to meet the requirement, as the pieces cannot form a proper square shape with the hole in the correct position.
Step 3: Conclusion.
After carefully examining each set of pieces, it is clear that option (C) is the correct one. It allows us to form a square with a round hole near the center.
Thus, the correct answer is (C). Quick Tip: When solving puzzles involving shapes and assembly, look for patterns in the arrangement of pieces. Make sure to check both the overall shape and the specific features, such as the position of holes, to meet the problem's conditions.
The major product M formed in the following reaction is

View Solution
Step 1: Identify the reaction type.
The reagent combination \( N_{2}H_{4} \) (1 equiv) with \( CuSO_{4} \) and \( O_{2} \) induces a Wolff–Kishner-type reductive rearrangement, but under these oxidative conditions, it typically forms diimide (HN=NH) in situ. Diimide selectively reduces one of the two double bonds in a conjugated or isolated diene system via syn-addition hydrogenation.
Step 2: Apply selective reduction.
Since diimide reduces only one double bond, and no over-reduction occurs (because only 1 equivalent of \( N_{2}H_{4} \) is present), the product contains one remaining double bond. The more substituted internal double bond is reduced preferentially, leaving the terminal double bond intact.
Step 3: Determine the final structure.
After selective reduction of the internal alkene, the compound becomes a cyclized system with one double bond preserved at the terminal side. This corresponds exactly to Option B, which contains one unsaturation at the correct position.
Final Answer: (B)
Quick Tip: Diimide reduces alkenes by syn-addition and usually reduces the more substituted or more accessible double bond first, especially when only one equivalent is available.
The starting material Y in the following reaction is

View Solution
The product in the reaction is a 2-bromoindole. Formation of an indole ring under strongly nucleophilic conditions (3 equivalents of vinyl Grignard reagent) suggests an intramolecular cyclization in which the nucleophile attacks an electron-deficient nitro-substituted aromatic ring.
Step 1: Identify the directing/activating group.
Among the given options, only the \ce{NO2 group in option (B) is strongly electron-withdrawing. This makes the ring activated for nucleophilic aromatic substitution by the Grignard reagent.
Step 2: Mechanistic reasoning.
Vinyl Grignard can attack the nitro-activated position ortho to bromine. Subsequent intramolecular cyclization and rearrangement lead to formation of the indole skeleton.
Step 3: Compare with other options.
(A) \ce{NH2 is strongly activating and would not undergo this reaction.
(C) \ce{N3 does not promote nucleophilic aromatic substitution here.
(D) is already an indole and cannot be the starting material.
Thus option (B), the nitro-substituted bromoarene, is the required precursor.
Final Answer: (B)
Quick Tip: Indole synthesis via Grignard reagents typically requires a strong electron-withdrawing group such as \ce{NO2 to activate the aromatic ring.
The major product in the given reaction is Q. The mass spectrum of Q shows
{[M] = molecular ion peak}.

View Solution
The reaction shown is a Corey–Fuchs reaction using Ph\textsubscript{3P and CBr\textsubscript{4, which converts an aldehyde into a dibromoalkene.
Thus, the major product Q contains two bromine atoms.
Bromine has two isotopes: \[ ^{79}Br : ^{81}Br = 1 : 1 \]
For a molecule containing two Br atoms, the mass spectrum shows three peaks:
- [M] → both isotopes are \(^{79}Br\)
- [M+2] → one \(^{79}Br\) and one \(^{81}Br\)
- [M+4] → both isotopes are \(^{81}Br\)
The relative intensities follow the binomial distribution: \[ 1 : 2 : 1 \]
Therefore, product Q must show \[ [M],\ [M+2],\ [M+4] \]
in the ratio \(1 : 2 : 1\). Quick Tip: Any compound containing two bromine atoms always shows a 1:2:1 isotopic pattern in its mass spectrum.
A tripeptide on treatment with PhNCS (pH = 8.0) followed by heating with dilute HCl afforded a cyclic compound M and a dipeptide. The dipeptide on treatment with PhNCS (pH = 8.0) followed by heating with dilute HCl afforded a cyclic compound N and an acyclic compound O. The CORRECT sequence (from N- to C-terminus) of the tripeptide is

View Solution
This problem uses the classical \emph{Edman Degradation principle to identify the N-terminal amino acid of a peptide. Under mildly basic conditions (pH = 8), phenyl isothiocyanate (PhNCS) selectively attacks the N-terminal free amino group of a peptide to produce a phenylthiocarbamoyl adduct. Upon treatment with dilute HCl, this intermediate undergoes cyclization and cleavage to release a characteristic heterocycle known as a \emph{phenylthiohydantoin (PTH) derivative. Each amino acid gives a specific PTH structure, allowing the N-terminal residue to be identified unambiguously.
In the first step, the tripeptide reacts with PhNCS and produces the cyclic compound M. The structure of M shown in the problem corresponds exactly to the PTH derivative of \emph{glycine. This allows us to immediately conclude that glycine is the N-terminal amino acid of the tripeptide. The cleavage of the first residue leaves behind a dipeptide.
The remaining dipeptide now undergoes an identical two-step Edman reaction. The cyclic compound N formed from the dipeptide corresponds to the PTH derivative of \emph{phenylalanine. Thus, phenylalanine must be the second amino acid in sequence.
Once phenylalanine is removed from the dipeptide, a single amino acid remains. This final amino acid is not converted to a cyclic PTH compound in Edman degradation. Instead, after acid treatment, the free amino acid is released. The structure of this released compound O clearly shows the branched isopropyl side chain characteristic of \emph{valine. Hence valine is the C-terminal residue.
Putting all three residues in order from the N-terminus to the C-terminus, the tripeptide sequence must be:
glycine → phenylalanine → valine.
Thus option (A) is the correct answer.
Quick Tip: In Edman degradation, the sequence is revealed stepwise from the N-terminus: first identify the PTH derivative, remove that residue, and then repeat on the remaining peptide.
The major product M in the following reaction is:

View Solution
This reaction proceeds through a photochemical intramolecular radical cyclization driven by \(h\nu\).
Photochemical activation initiates homolytic bond cleavage, forming a carbon-centered radical next to the substituted alkene.
The Ar group (para-cyanophenyl) strongly stabilizes radical formation through resonance, lowering the activation energy for cyclization.
Step 1: Radical Generation
Under UV irradiation, the weakest bond undergoes homolysis, generating a radical adjacent to the alkene system.
The p-cyanophenyl (Ar) substituent stabilizes this radical significantly through delocalization.
Step 2: 5-exo-trig Cyclization (Favored)
Radical addition across the alkene follows Baldwin’s rules.
The 5-exo-trig ring closure mode is highly favored compared to 6-endo pathways.
The radical attacks the double bond intramolecularly to form a new five-membered ring, generating a second radical center.
Step 3: Stabilized Radical Formation
The newly formed radical is benzylic due to adjacent phenyl groups, offering substantial resonance stabilization.
This ensures that the radical persists long enough for termination.
Step 4: Product Formation
Termination occurs via hydrogen abstraction or similar termination steps.
The final structure matches option (A), where the Ar substituents remain on the quaternary carbon inside the ring, while the phenyl groups remain on the terminal alkene fragment.
The geometry and connectivity are fully consistent with a 5-exo-trig cyclization pathway.
Why the other options are incorrect:
Options (B), (C), and (D) involve disfavored 6-endo-trig closures or incorrect placements of substituents.
These violate Baldwin’s rules and do not match the radical stability pattern observed in such photochemical reactions.
Thus, option (A) is the only structure consistent with mechanism, stability, and stereoelectronic requirements.
Quick Tip: Always apply Baldwin's rules in radical cyclizations: 5-exo-trig closures are preferred, while 6-endo-trig pathways are strongly disfavored.
Electron-withdrawing Ar groups help stabilize radical intermediates and influence the cyclization direction.
The major product T formed in the following reaction is

View Solution
Step 1: Identify the site of lithiation.
The pyridine ring contains two bromine atoms, but the position ortho to nitrogen is most activated for halogen–lithium exchange.
Therefore, treatment with strong base \( ^nBuLi \) at \(-100^\circC\) selectively forms an aryl lithium intermediate at this position.
Step 2: Reaction with benzaldehyde.
At \(-78^\circC\), the aryl lithium intermediate reacts with benzaldehyde (PhCHO).
The nucleophilic carbon attacks the carbonyl carbon, forming a benzylic alkoxide intermediate.
On workup, this intermediate is protonated to form the corresponding benzylic alcohol.
Step 3: Determine the correct structure.
Only option (A) shows the –CH(OH)Ph group attached at the correct lithiation site.
It also preserves the second bromine and the methoxy group in the correct positions.
Thus, structure (A) is fully consistent with the regioselective halogen–lithium exchange and subsequent nucleophilic addition.
Final Answer: (A)
Quick Tip: Organolithium reagents undergo rapid halogen–lithium exchange at positions activated by nitrogen, and then add cleanly to aldehydes to give benzylic alcohols.
In differential thermal analysis (DTA)
View Solution
Differential Thermal Analysis (DTA) is a thermoanalytical technique in which a sample and an inert reference are subjected to the same controlled temperature program. Both are heated (or cooled) at the same rate, and the difference in their temperatures is continuously monitored. This temperature difference arises whenever the sample undergoes a thermal event such as melting, crystallization, oxidation, decomposition, or any phase transition. During such processes, the sample absorbs or releases heat, causing it to deviate in temperature from the reference. DTA records these deviations as peaks in the DTA curve, where endothermic processes produce one type of peak and exothermic processes produce another.
Option (B) describes Differential Scanning Calorimetry (DSC), which measures heat flow directly—not temperature difference. Option (C) refers to Thermogravimetric Analysis (TGA), which measures mass changes, not temperature differences. Option (D) is incorrect because glass transition is observed as a broad step change in heat capacity, not a sharp peak.
Final Answer: (A)
Quick Tip: DTA = Temperature difference measurement; DSC = Heat flow measurement; TGA = Mass change measurement.
The \(\nu_{\mathrm{O-O}}\) resonance Raman stretching frequency (cm\(^{-1}\)) of the coordinated dioxygen in oxy-hemoglobin and oxy-hemocyanin appears, respectively, nearly at
View Solution
In biological oxygen carriers, the stretching frequency of the O–O bond provides direct information about how strongly the dioxygen is activated by the metal center. A lower frequency corresponds to a weaker O–O bond, meaning the metal center has transferred more electron density into the antibonding orbitals of O\(_2\).
In oxy-hemoglobin, the dioxygen binds to Fe(II) in a side-on–end-on fashion, forming a species similar to superoxide (\ce{O2^-). Electron back-donation from iron weakens the O–O bond moderately, producing a Raman frequency near 1136 cm\(^{-1}\). This is lower than free O\(_2\) (1550 cm\(^{-1}\)) but not extremely low, because Fe(II) activates O\(_2\) only to the superoxide level.
In oxy-hemocyanin, the dioxygen binds symmetrically between two Cu(I) ions, forming a μ-η²:η²-peroxo dicopper(II) species. This structure strongly activates the peroxo unit. The O–O bond is much weaker, resulting in a dramatic drop in stretching frequency to 744 cm\(^{-1}\), consistent with a peroxo species in a symmetric environment.
Thus hemoglobin (Fe-based) shows a higher O–O frequency, while hemocyanin (Cu-based) shows a significantly lower one due to greater activation.
Final Answer: 1136 and 744
Quick Tip: Lower O–O Raman stretching frequency means stronger activation of O\(_2\). Hemocyanin activates O\(_2\) more strongly than hemoglobin.
The number of metal–metal bond(s), with \(\sigma\), \(\pi\), and \(\delta\) character,
present in [Mo\textsubscript{2(CH\textsubscript{3CO\textsubscript{2)\textsubscript{4] complex is(are), respectively,
View Solution
The complex \([ Mo_2(OAc)_4 ]\) is a classic example of a quadruple metal–metal bonded system.
The acetate groups bridge the two Mo atoms, allowing close approach and formation of multiple Mo–Mo bonds.
A metal–metal quadruple bond consists of:
1. One σ bond – formed by the head-on overlap of \(d_{z^2}\) orbitals.
2. Two π bonds – formed by the sideways overlap of \(d_{xz}\) and \(d_{yz}\) orbitals.
3. One δ bond – formed by the face-to-face overlap of \(d_{xy}\) orbitals.
Thus, the Mo–Mo bond order in this complex is: \[ \sigma^1 \ \pi^2 \ \delta^1 \]
Hence, the number of metal–metal bonds with σ, π, and δ character, respectively, is: \[ 1,\ 2,\ 1 \] Quick Tip: Quadruple metal–metal bonds always consist of one σ bond, two π bonds, and one δ bond — a characteristic of many Mo\textsubscript{2} and W\textsubscript{2} acetate complexes.
\(1s_A\) and \(1s_B\) are the normalized eigenfunctions of two hydrogen atoms \(H_A\) and \(H_B\), respectively. If \(S = \langle 1s_A | 1s_B \rangle\), the option that is ALWAYS CORRECT is
View Solution
The overlap integral \(S = \langle 1s_A | 1s_B \rangle\) measures the extent to which the wavefunction of the hydrogen 1s orbital on atom \(A\) overlaps spatially with the wavefunction on atom \(B\). Both orbitals involved are real, normalized, and spherically symmetric functions centered on two different nuclei. Because they are real functions, the overlap integral must also be real and cannot be imaginary, ruling out option (C).
When the two hydrogen atoms are infinitely far apart, the orbitals do not overlap, so the integral becomes exactly zero. This eliminates option (B) as a universally valid statement, because \(S\) is not always zero; it depends on the internuclear distance.
As the two atoms move closer together, their spherical 1s orbitals begin to overlap, and the overlap integral becomes positive. However, even at zero internuclear separation, the orbitals cannot become identical because each orbital is defined relative to its own nucleus. Thus, \(S\) can never reach the value of 1, eliminating option (A).
For any two real, normalized wavefunctions, the general mathematical property of overlap integrals states that their inner product must always lie between 0 and 1. The lower limit corresponds to no overlap, and the upper limit is approached only when the functions are identical. Because the hydrogen 1s orbitals located on two different atoms can never be exactly identical unless the atoms coincide, the integral always remains within the closed interval \(0 \le S \le 1\).
Therefore, the only universally valid statement is option (D).
Quick Tip: Overlap integrals between real, normalized orbitals are always real numbers and always lie between 0 and 1 because they measure spatial similarity.
The pure vibrational spectrum of a hypothetical diatomic molecule shows three peaks with intensity values at 300 K, 600 K, and 900 K. The CORRECT statement is:

View Solution
The intensity of vibrational spectral lines depends primarily on the population of the initial vibrational energy level participating in the transition. The Boltzmann distribution dictates that the population of higher-energy states increases with temperature, causing transitions originating from these increasingly populated states to grow in intensity as the temperature rises.
From the table provided, Peak I has constant intensity across 300 K, 600 K, and 900 K. This means that the transition responsible for Peak I does not significantly depend on the thermal population of higher vibrational levels. Therefore, it must originate from the lowest vibrational energy level—typically the fundamental transition \(v = 0 \to 1\)—whose population remains nearly constant even at elevated temperature.
Peak II also shows constant intensity, indicating that this peak arises from a moderately low-energy level whose population does not vary significantly with temperature. This suggests that the transition is higher in energy than Peak I but still not affected strongly by temperature increments.
In contrast, Peak III shows significant growth in intensity: 0.02 at 300 K, 0.04 at 600 K, and 0.06 at 900 K. This indicates that the transition originates from a vibrational state whose population increases strongly with temperature, such as an excited vibrational level (for example, \(v = 1 \to 2\)). Such behavior is typical for the lowest-energy transitions in hot-band spectra. In vibrational spectroscopy, the transitions that grow fastest with temperature correspond to the lowest-frequency or lowest-energy transitions because thermal excitation preferentially populates these states first.
Thus, Peak III must correspond to the lowest-energy of the three transitions. Peak I and Peak II are higher in energy because their intensities remain unchanged with temperature. Therefore, Option (C) is the correct answer.
Quick Tip: Temperature-dependent intensity changes reveal energy ordering: the strongest growth with temperature corresponds to the lowest-energy vibrational transition.
The point group of SF\(_6\) is
View Solution
SF\(_6\) has an octahedral geometry where the central sulfur atom is surrounded by six fluorine atoms placed symmetrically along the Cartesian axes.
This arrangement is perfectly symmetrical and contains multiple symmetry elements including:
a four-fold rotation axis (C\(_4\)), three four-fold improper rotation axes (S\(_4\)), several C\(_2\) axes, inversion center, and multiple mirror planes.
The presence of all these symmetry elements is characteristic of the octahedral point group \(O_h\).
Furthermore, the molecule has a center of inversion because opposite fluorine atoms across the sulfur atom are identical and symmetrically placed.
None of the other point groups listed—\(D_{6h}\), \(D_{6d}\), or \(C_{6v}\)—match the full symmetry of an octahedral arrangement.
Therefore, the correct point group for SF\(_6\) is \(O_h\).
Quick Tip: Octahedral molecules like SF\(_6\), PF\(_6^{-}\), and metal complexes ML\(_6\) always belong to the \(O_h\) point group due to their high symmetry and inversion center.
A point originally at \( (1, 3, 5) \) was subjected to a symmetry operation \( \hat{O}_{1} \) that shifted the point to \( (-1, -3, 5) \). Subsequently, the point at \( (-1, -3, 5) \) was subjected to another symmetry operation \( \hat{O}_{2} \) that shifted this point to \( (-1, -3, -5) \). The symmetry operators \( \hat{O}_{1} \) and \( \hat{O}_{2} \) are, respectively,
View Solution
Step 1: Analyse the first transformation.
The point changes from \( (1, 3, 5) \) to \( (-1, -3, 5) \).
This transformation flips the signs of the \( x \)- and \( y \)-coordinates but keeps \( z \) unchanged.
A \( C_{2} \) rotation about the \( z \)-axis performs: \[ (x, y, z) \to (-x, -y, z) \]
which exactly matches the given change.
Thus, \( \hat{O}_{1} = \hat{C}_{2}(z) \).
Step 2: Analyse the second transformation.
The point changes from \( (-1, -3, 5) \) to \( (-1, -3, -5) \).
This flips only the \( z \)-coordinate.
Reflection through the \( xy \)-plane \( \sigma(xy) \) performs: \[ (x, y, z) \to (x, y, -z) \]
which matches the transformation.
Thus, \( \hat{O}_{2} = \hat{\sigma}(xy) \).
Step 3: Final selection.
The correct pair of symmetry operations is \( \hat{C}_{2}(z) \) and \( \hat{\sigma}(xy) \).
Final Answer: (B)
Quick Tip: A \( C_{2}(z) \) operation flips \( x \) and \( y \), while a reflection through the \( xy \)-plane flips only the \( z \)-coordinate.
Adsorption of a gas with pressure \(P\) on a solid obeys the Langmuir adsorption isotherm.
For a fixed fractional coverage, the correct relation between \(K\) and \(P\) at a fixed temperature is \(K = k_a/k_b\), where \(k_a\) and \(k_b\) are the adsorption and desorption rate constants.
Assume non-dissociative adsorption.
View Solution
For Langmuir adsorption, the fractional surface coverage \(\theta\) is given by \[ \theta = \frac{K P}{1 + K P}, \]
where \(K = k_a/k_b\) is the equilibrium constant for adsorption and \(P\) is the gas pressure.
Step 1: Fix the fractional coverage.
If \(\theta\) is fixed, then the numerator and denominator must scale such that their ratio remains constant.
Thus, \[ \theta = \frac{K P}{1 + K P} = constant. \]
Step 2: Solve for the relation between \(K\) and \(P\).
Rearranging, \[ \theta(1 + K P) = K P, \] \[ \theta + \theta K P = K P, \] \[ \theta = K P (1 - \theta). \]
So, \[ K P = \frac{\theta}{1 - \theta} = constant. \]
Step 3: Conclude the proportionality.
Since \(KP\) is constant, \[ K \propto \frac{1}{P}. \]
Thus, the correct relation is \[ K \propto P^{-1}, \]
corresponding to option (C).
Final Answer: (C)
Quick Tip: For Langmuir isotherm, keeping fractional coverage constant implies \(KP = constant\), so \(K \propto 1/P\).
The temperature dependence of the rate constant for a second-order chemical reaction obeys the Arrhenius equation.
The SI unit of the ‘pre-exponential factor’ is
View Solution
The Arrhenius equation is \[ k = A e^{-E_a/(RT)}, \]
where \(A\) is the pre-exponential (frequency) factor.
Step 1: Identify units of the rate constant for a second-order reaction.
For a second-order reaction, \[ Rate = k [A]^2. \]
Rate has units mol m\(^{-3}\) s\(^{-1}\), and concentration has units mol m\(^{-3}\).
Thus, \[ k = \frac{Rate}{[A]^2} = \frac{mol m^{-3} s^{-1}}{(mol m^{-3})^2} = m^{3} mol^{-1} s^{-1}. \]
Step 2: Arrhenius pre-exponential factor has same units as \(k\).
Because the exponential term is dimensionless, \[ A \quad must have the same units as\quad k. \]
Therefore, \[ A = m^{3} mol^{-1} s^{-1}. \]
Thus, the correct choice is (B).
Final Answer: (B) m\(^{3}\) mol\(^{-1}\) s\(^{-1}\)
Quick Tip: For any reaction order, the Arrhenius pre-exponential factor always has the same units as the rate constant \(k\).
The CORRECT reagent(s) for the given reaction is(are):

View Solution
The starting compound is a cyclohexanone, and the product is a lactone formed by
Baeyer–Villiger oxidation (migration of adjacent alkyl group into the peroxy oxygen).
Baeyer–Villiger oxidation converts: \[ ketone \rightarrow ester/lactone \]
The reagents capable of performing this oxidation are:
1. H\textsubscript{2O\textsubscript{2, NaOH
– Performs Baeyer–Villiger oxidation via formation of peroxycarboxylic species in situ.
2. Peroxy ester (option B)
– This is a classical Baeyer–Villiger oxidant (e.g., peroxy ester, peracid equivalent).
Thus both (A) and (B) accomplish ketone → lactone transformation.
Reagents in (C) and (D) do not directly cause Baeyer–Villiger oxidation. Quick Tip: Baeyer–Villiger oxidation always inserts oxygen next to the carbonyl and converts ketones into esters or lactones. Peracids or alkaline hydrogen peroxide are the typical reagents.
The CORRECT statement(s) about the \(^1\mathrm{H}\) NMR spectra of compounds P and Q is(are):

View Solution
Compounds P and Q differ in whether the benzylic hydrogens \(H_a\) and \(H_b\) are chemically equivalent or diastereotopic. In compound P, both \(H_a\) and \(H_b\) lie next to a nitrogen atom having two identical methyl substituents, and the adjacent carbon environment is symmetric. Because no stereogenic center exists near these protons, they experience identical electronic and magnetic surroundings. Therefore, \(H_a\) and \(H_b\) become \emph{chemically equivalent, resulting in a single sharp singlet at \(\delta \approx 3.70\) ppm. This supports option (A).
In contrast, compound Q contains an N-methyl group and a phenyl ring on adjacent carbons, breaking the symmetry around the benzylic CH\(_2\) group. Consequently, \(H_a\) and \(H_b\) are now in different spatial environments with respect to the chiral axis created by the substituted nitrogen center. These CH\(_2\) hydrogens become \emph{diastereotopic. Diastereotopic protons do not give a singlet; instead, they show an AB pattern or AB-quartet due to geminal coupling (\(J_{ab}\)). Thus Q displays an AB-quartet near \(\delta = 3.63\) ppm, supporting option (D). Options (B) and (C) are therefore incorrect because they assign the opposite behavior to the wrong compounds.
Quick Tip: Chemically equivalent protons give singlets; diastereotopic benzylic CH\(_2\) protons give AB-type splitting. Always check for symmetry loss around CH\(_2\).
The CORRECT statement(s) about thallium halides is(are):
View Solution
Thallium halides exhibit structural and solubility variations due to the inert-pair effect and relativistic stabilization of the 6s electrons.
Option (A) is correct because TlF is exceptionally ionic. The high lattice energy is balanced by strong hydration of Tl\(^+\) and F\(^-\), making TlF highly soluble. In contrast, TlCl, TlBr, and TlI have progressively more covalent character and become significantly less soluble due to weaker hydration relative to lattice energies.
Option (B) is correct because TlF adopts a distorted NaCl (rock-salt) lattice rather than a perfect one. The large size difference between Tl\(^+\) and F\(^-\), as well as polarization effects, cause deviations from a perfect face-centered cubic arrangement.
Option (C) is incorrect: although TlI\(_3\) exists, it is not analogous to CsI\(_3\). Importantly, TlI\(_3\) contains \emph{triiodide I\(_3^-\), and the oxidation state of Tl in TlI\(_3\) is +1, not +3. The thallium(III) oxidation state is unstable due to the inert pair effect, so this statement is incorrect.
Option (D) is correct because TlCl and TlBr crystallize in the CsCl-type cubic structure (simple cubic with each ion eight-coordinate). Their ionic radii are compatible with the CsCl lattice, supporting this structural pattern.
Thus, options (A), (B), and (D) are correct, and (C) is false.
Quick Tip: Thallium(I) halides often adopt CsCl-type structures; TlF is the most ionic and most soluble. Tl(III) compounds are rarely stable due to the inert pair effect.
The CORRECT statement(s) about the spectral line broadening in atomic spectra is(are):
View Solution
Spectral line broadening refers to the phenomenon where a spectral line does not appear as a sharp line, but instead spreads over a range of frequencies. This can be due to various physical effects, each contributing to the broadening in different ways.
(A) The collision between atoms causes broadening of the spectral line:
Collisions between atoms or molecules can lead to a perturbation of energy levels, causing a broadening of the spectral line. This is known as collisional broadening or pressure broadening. When atoms or molecules collide, their energy levels are temporarily altered, leading to a shift in the frequency of the emitted radiation, causing the spectral line to broaden. Therefore, option (A) is correct.
(B) Shorter the lifetime of the excited state, the broader is the line width:
This is a well-known principle of lifetime broadening. According to the uncertainty principle, the uncertainty in the energy (\(\Delta E\)) is related to the lifetime (\(\tau\)) of the excited state by the equation \(\Delta E \cdot \tau \sim \hbar\). A shorter lifetime (\(\tau\)) leads to greater uncertainty in the energy, which results in a broader spectral line. Therefore, option (B) is correct.
(C) Doppler broadening is more pronounced as the flame temperature increases:
Doppler broadening occurs due to the motion of atoms or molecules, which causes a shift in the frequency of emitted radiation. As the temperature increases, the velocity of the particles increases due to the kinetic energy, leading to more pronounced Doppler shifts and hence greater broadening. Therefore, option (C) is correct.
(D) In flame and plasma, the natural line broadening exceeds the collisional line broadening:
This statement is incorrect. In high-temperature systems such as flames and plasmas, collisional broadening tends to dominate over natural line broadening. While natural line broadening is caused by the finite lifetime of excited states, collisional broadening is typically much more significant in such environments. Hence, option (D) is incorrect.
Thus, the correct answers are (A), (B), (C).
Quick Tip: Remember that spectral line broadening can occur due to different mechanisms: collisional broadening, Doppler broadening, and lifetime broadening. The relative importance of these effects depends on the conditions (e.g., temperature, pressure, and excitation levels) of the system.
Match the CORRECT option(s) from column A with column B according to the metal centre present in the active site of metalloenzyme.

View Solution
Step 1: Identify the metal centers and associated enzymes.
- Cu (Copper) is commonly found in Tyrosinase (which catalyzes the hydroxylation of phenols) → matches V.
- Mo (Molybdenum) is associated with Nitrate reductase, which is involved in the reduction of nitrate to nitrite → matches III.
- Co (Cobalt) is a key metal in B12-coenzyme, which plays a crucial role in methyl group transfers → matches I.
- Zn (Zinc) is typically found in Carboxypeptidase, a metalloenzyme involved in peptide bond cleavage → matches II.
Step 2: Match the correct pairs.
- P (Cu) matches V (Tyrosinase).
- Q (Mo) matches III (Nitrate reductase).
- R (Co) matches I (B12-coenzyme).
- S (Zn) matches II (Carboxypeptidase).
Thus, the correct pairings are P-V, Q-III, R-I, S-II. This matches option (A).
Final Answer: (A) P-V, Q-III, R-I, S-II
Quick Tip: Remember, copper is commonly involved in enzymatic reactions like those in tyrosinase, while molybdenum plays a role in nitrate reduction. Zinc and cobalt are associated with carboxypeptidases and B12 coenzymes, respectively.
The CORRECT statement(s) about the following phase diagram for a hypothetical pure substance X is (are)

View Solution
The phase diagram shows the phases of a substance (solid, liquid, and gas) as a function of temperature and pressure. Let's analyze the given statements:
Step 1: Analyzing Option (A)
Option (A) suggests that the molar volume of solid X is less than that of liquid X. In many substances, the solid phase has a lower molar volume compared to the liquid phase, but this is not always true. In this particular case, from the phase diagram, we can infer that the solid-liquid boundary has a positive slope, suggesting that the molar volume of the liquid phase is larger than that of the solid phase. Thus, Option (A) is incorrect.
Step 2: Analyzing Option (B)
Option (B) states that X does not have a normal boiling point. From the diagram, we observe that there is no clear boiling point at 1 atm pressure for this substance, as the line between liquid and gas does not intersect at 1 atm pressure. Hence, the substance does not have a normal boiling point. This makes Option (B) correct.
Step 3: Analyzing Option (C)
Option (C) states that the melting point of X decreases with an increase in pressure. The phase diagram indicates that the slope of the solid-liquid line is negative, which means the melting point decreases as pressure increases. This is typical for substances where the solid phase is less dense than the liquid phase, as increasing pressure typically promotes the denser phase (liquid) over the less dense phase (solid). Hence, Option (C) is correct.
Step 4: Analyzing Option (D)
Option (D) suggests that on increasing the pressure of the gas isothermally, it is impossible to reach the solid phase before reaching the liquid phase. From the phase diagram, it is clear that the gas phase transitions directly to the liquid phase upon compression, as there is no solid phase at lower pressures. Hence, Option (D) is correct.
Final Answer: (B) and (C)
Quick Tip: In phase diagrams, the slope of the solid-liquid boundary determines how pressure influences the melting point. Negative slopes mean the melting point decreases with pressure.
The parameter(s) fixed for each system in a canonical ensemble is (are)
View Solution
In statistical mechanics, the canonical ensemble represents a system in thermal equilibrium with a reservoir at a fixed temperature. The following parameters are fixed in this ensemble:
Step 1: Understand the canonical ensemble.
The canonical ensemble is defined by systems that can exchange energy with a reservoir but are fixed in the number of particles, volume, and temperature. This is the ideal ensemble for studying thermodynamic properties such as energy fluctuations.
Step 2: Analyze Option (A)
Option (A) states that temperature is fixed. In a canonical ensemble, the system is maintained at a fixed temperature by thermal contact with the heat reservoir. Hence, Option (A) is correct.
Step 3: Analyze Option (B)
Option (B) suggests that pressure is fixed. However, pressure is not necessarily fixed in the canonical ensemble, since it can vary depending on the system's volume and temperature. Pressure is more often fixed in the isobaric ensemble. Hence, Option (B) is incorrect.
Step 4: Analyze Option (C)
Option (C) suggests that volume is fixed. In the canonical ensemble, the system's volume is fixed. This is a characteristic of the ensemble, as the system does not exchange matter but can exchange energy with the surroundings. Hence, Option (C) is correct.
Step 5: Analyze Option (D)
Option (D) suggests that composition is fixed. Since the canonical ensemble involves a fixed number of particles (and typically a fixed number of molecules), the composition remains constant. Hence, Option (D) is correct.
Final Answer: (A), (C), and (D)
Quick Tip: In the canonical ensemble, temperature, volume, and number of particles (composition) are fixed. Pressure is not fixed, unlike in the isobaric ensemble.
The number of peaks exhibited by T in its broadband proton decoupled 13C NMR spectrum recorded at 25°C in CDCl\(_3\) is ______.

View Solution
The compound shown is a disubstituted benzene derivative (dimethylbenzene). The two methyl groups are on different positions (either ortho, meta, or para to each other). In the proton-decoupled 13C NMR spectrum, each distinct carbon environment will give a separate peak.
Here, there are 2 distinct environments for the methyl groups, one for the methyl carbons and one for the carbons of the benzene ring. The number of peaks is determined by the number of distinct carbon environments in the molecule.
In this case, there are 8 peaks in total:
- 1 peak for the two methyl carbons (since they are in the same environment),
- 6 peaks for the 6 carbons in the benzene ring (with 3 distinct environments),
- 1 peak for the carbon connected to the two methyl groups (due to symmetry).
Thus, the number of peaks is: \[ \boxed{8}. \] Quick Tip: In proton-decoupled 13C NMR, the number of peaks corresponds to the number of distinct carbon environments in the molecule.
The diffraction angle (in degrees, rounded to one decimal place) of (321) sets of planes of a metal with atomic radius 0.125 nm, adopting BCC structure, is ______. (Given: the order of reflection is 1 and the wavelength of X-ray is 0.0771 nm.)
View Solution
In a BCC crystal structure, the interplanar spacing for the (hkl) planes is given by the formula: \[ d_{hkl} = \frac{ \sqrt{3} a }{\sqrt{h^2 + k^2 + l^2}}, \]
where \(a\) is the lattice constant. The lattice constant for BCC is related to the atomic radius \(r\) by: \[ a = \frac{4r}{\sqrt{3}}. \]
Given the atomic radius \(r = 0.125\) nm, we can calculate the lattice constant: \[ a = \frac{4 \times 0.125}{\sqrt{3}} = \frac{0.5}{1.732} = 0.2887 nm. \]
For the (321) planes, \(h = 3\), \(k = 2\), and \(l = 1\), so: \[ d_{321} = \frac{\sqrt{3} \times 0.2887}{\sqrt{3^2 + 2^2 + 1^2}} = \frac{0.5004}{\sqrt{14}} = \frac{0.5004}{3.742} = 0.1338 nm. \]
Now, applying Bragg's law: \[ n \lambda = 2d \sin \theta, \]
where \(\lambda = 0.0771\) nm (wavelength of X-ray), \(n = 1\) (first order reflection), and \(d = 0.1338\) nm: \[ 0.0771 = 2 \times 0.1338 \times \sin \theta, \] \[ \sin \theta = \frac{0.0771}{2 \times 0.1338} = \frac{0.0771}{0.2676} = 0.288. \]
Thus: \[ \theta = \sin^{-1}(0.288) \approx 16.8^\circ. \]
Therefore, the diffraction angle is: \[ \boxed{16.8^\circ}. \] Quick Tip: For BCC structures, use the formula \( a = \frac{4r}{\sqrt{3}} \) to calculate the lattice constant, and apply Bragg's law for diffraction angles.
For the angular momentum operator \( \hat{L} \) and the spherical harmonics \( Y_{lm}(\theta, \phi) \), \[ \left( \hat{L}^2_x + \hat{L}^2_y \right) Y_{21}(\theta, \phi) = n \hbar^2 Y_{21}(\theta, \phi) \]
The value of \( n \) is
View Solution
For the angular momentum operator \( \hat{L}^2 = \hat{L}^2_x + \hat{L}^2_y + \hat{L}^2_z \), and given that the spherical harmonics \( Y_{lm}(\theta, \phi) \) satisfy the eigenvalue equation:
\[ \hat{L}^2 Y_{lm}(\theta, \phi) = l(l+1) \hbar^2 Y_{lm}(\theta, \phi) \]
For \( l = 2 \) (since \( Y_{21} \) has \( l = 2 \), \( m = 1 \)), we know:
\[ \hat{L}^2 Y_{21} = 2(2+1) \hbar^2 Y_{21} = 6 \hbar^2 Y_{21} \]
Thus, comparing with the given expression:
\[ \left( \hat{L}^2_x + \hat{L}^2_y \right) Y_{21} = 6 \hbar^2 Y_{21} \]
Therefore, the value of \( n \) is:
\[ \boxed{5} \] Quick Tip: The total angular momentum squared operator \( \hat{L}^2 \) acts on spherical harmonics \( Y_{lm}(\theta, \phi) \) giving the eigenvalue \( l(l+1) \hbar^2 \), where \( l \) is the angular momentum quantum number.
The major product P obtained in the following reaction sequence is

View Solution
Step 1: Reaction with NaH.
The starting compound is a carbonyl compound with a methyl group. Reaction with \( NaH \) forms an alkoxide, enabling the generation of a reactive intermediate for the subsequent step. This intermediate is prone to attack by electrophiles.
Step 2: Reaction with MeI.
The alkoxide formed in Step 1 reacts with \( MeI \) (methyl iodide) in the second step to methylate the oxygen, forming a methylated intermediate.
Step 3: Reaction with hydroxylamine.
The methylated product undergoes a reaction with \( NH_2OH·HCl \) (hydroxylamine hydrochloride) to form an imine group at the position where the carbonyl group was originally located.
Step 4: Reaction with PCl_5.
Finally, the imine reacts with \( PCl_5 \), leading to the formation of a nitrile group, with the removal of the nitrogen as a by-product.
Step 5: Final structure.
After following the sequence, the final product corresponds to the structure in option (A), which is a methylated nitrile compound.
Final Answer: (A)
Quick Tip: When using NaH and MeI, an alkoxide intermediate is formed, which can then undergo nucleophilic substitution with methyl iodide to form a methylated product. Reactions with hydroxylamine and PCl5 lead to functional group transformations.
The major product Q in the given reaction is

View Solution
In this reaction, we have a Benzyl trifluoroacetate (Me3SiCH2COOCF3) reacting with ZnCl2 in acetonitrile (MeCN) at 0°C. This reaction is likely a Friedel–Crafts alkylation.
Step 1: Mechanism of the Reaction
1. Activation of the electrophile: The trifluoroacetate group is electron-withdrawing and will activate the carbonyl carbon, making the attached benzyl group more susceptible to nucleophilic attack. In the presence of ZnCl2, the carbonyl group is further activated, and the leaving group CF3COO can be displaced.
2. Formation of the cationic intermediate: The Me3SiCH2+ ion is generated after the departure of the leaving group. This positively charged benzyl cation is now highly reactive.
Step 2: Reaction with the Aromatic Ring
The benzyl cation then undergoes a nucleophilic attack by the aromatic ring (C6H5). This results in the formation of a benzylic ether structure with the methyl group and SiMe3 attached to the ring, specifically at the alpha position to the SiMe3 group.
Step 3: Major Product Identification
The major product will feature the methyl group (Me) attached to the benzyl position on the aromatic ring, which corresponds to Option (A).
Final Answer: (A)
Quick Tip: In Friedel-Crafts alkylation, the alkyl group is introduced onto the aromatic ring via a carbocation intermediate. The activation of the electrophile is crucial in determining the product.
The major product P in the following reaction is

View Solution
The reaction involves the use of CsF and MeCN as solvent at 80°C. This condition typically initiates a nucleophilic substitution or electrophilic aromatic substitution.
Here, CsF (cesium fluoride) is acting as a strong base to activate the triflate group (OTf) on the aromatic ring, resulting in substitution. The methyl ester (MeO) is the group being transferred to the aromatic ring.
Thus, the major product involves methyl ester (MeO) attached to the aromatic ring, resulting in the structure as shown in option (A). Quick Tip: For reactions involving CsF and triflate groups, expect nucleophilic substitution leading to the formation of esters or similar groups attached to the aromatic ring.
The major product P in the reaction sequence is:

View Solution
In this reaction sequence, the starting material is a MeC=N-O compound. The first step involves protonation of the nitrile nitrogen, followed by a reductive hydrolysis using H\(_2\) (Raney Ni) in methanol and water, which results in the reduction of the nitrile group to an amide.
Step-by-step breakdown:
- The protonation of the nitrile nitrogen (step a) leads to an intermediate imine (C=N) which is then ready to undergo further reaction with the reducing agent.
- Reduction with Raney Ni and H\(_2\) causes the nitrile group to undergo hydrogenation to form a primary amide.
- The amide group is stable under these reaction conditions and thus does not undergo further reduction.
- Methanol and water facilitate the hydrolysis of the nitrile to the corresponding amide.
The final product, P, contains a Me group attached to both carbonyl carbon atoms, with hydroxy groups at each carbonyl position. This corresponds to the product shown in option (A), a diol derivative formed from the reduction of the nitrile and hydrolysis to an amide. The hydroxy groups result from the hydrolysis of the nitrile.
Thus, the correct answer is (A).
Quick Tip: In reactions involving nitrile reduction with hydrogen (H\(_2\)) over Raney Ni, the nitrile group is typically reduced to an amide. Ensure to check the presence of the hydroxy groups after hydrolysis.
The major products P and Q in the following reaction sequence are:

View Solution
The reaction sequence shown in the question involves two steps:
1. LDA (-78°C): LDA (Lithium diisopropylamide) is a strong base, which is used to deprotonate the carbon adjacent to the carbonyl group. This generates an enolate ion that undergoes an SN2 reaction with the bromine (Br) on the alkyl chain, resulting in the formation of a new carbon-carbon bond at the position of the leaving group. In this case, it forms a new double bond and produces the intermediate P.
2. Grubbs-II Catalyst and LiBH4 Reduction: The next step involves the use of Grubbs-II catalyst (a metathesis catalyst), which helps form a cyclohexene ring through a ring-closing metathesis reaction (RCM) between the double bonds in P. After the ring closure, LiBH4 (Lithium borohydride) is used to reduce the resulting carbonyl group to a hydroxyl group, forming the final product Q.
Thus, P corresponds to an intermediate with a double bond (as shown in option B), and Q is the product after the ring-closing metathesis and reduction steps.
In option B, the structure of P shows the correct intermediate with a suitable location for the double bond, while Q correctly shows the reduced cyclohexanol product.
Why the other options are incorrect:
- Option A: This shows a different structure for P that does not correspond to the expected intermediate after the enolate formation and subsequent SN2 reaction with Br.
- Option C: This shows an incorrect structure for P as it doesn't match the required enolate structure, and the cyclization step would not give the expected product.
- Option D: This also shows an incorrect intermediate for P and does not lead to the correct structure for Q.
Thus, the correct combination is (B).
Quick Tip: In reactions involving LDA, the base typically deprotonates the alpha-carbon adjacent to the carbonyl group, forming an enolate. This enolate can then react in subsequent steps, such as nucleophilic substitution or cyclization.
The major products M and N in the given reaction sequence are

View Solution
Step 1: Reaction with NaH and (MeO)\(_2\)CO.
The reaction of the starting compound with \( NaH \) and \( (MeO)_2CO \) forms an ester. The base deprotonates the alcohol, and the esterification reaction proceeds with the formation of a methyl ester.
Step 2: Reaction with Br\(_2\) and Et\(_2\)O.
The reaction with \( Br_2 \) leads to bromination, which substitutes a hydrogen atom. The reaction occurs on the more reactive site in the compound.
Step 3: Reaction with NaOMe and MeOH.
The reaction with \( NaOMe \) and \( MeOH \) will lead to an elimination reaction, removing the bromine atom and forming a double bond in the structure.
Step 4: Reaction with DIBAL-H.
Finally, the reaction with DIBAL-H (diisobutylaluminum hydride) will reduce the ester group to a primary alcohol, resulting in N as the final product.
Step 5: Final structure.
The resulting compound M and N are correctly represented by option (B), which shows the methyl ester and the primary alcohol.
Final Answer: (B)
Quick Tip: In organic synthesis, DIBAL-H is commonly used to selectively reduce esters to aldehydes or alcohols, depending on the conditions.
Three different crystallographic planes of a unit cell of a metal are given below (solid circles represent atoms). The crystal system of the unit cell is

View Solution
The given problem provides three different crystallographic planes in a unit cell, and we are tasked with identifying the crystal system. The three planes are given by the Miller indices (110), (101), and (011), and the dimensions of the unit cell along these planes are provided.
1. Crystallographic Systems:
- Triclinic: All sides have different lengths and angles, with no symmetry. (a ≠ b ≠ c, α ≠ β ≠ γ)
- Monoclinic: Two sides are unequal, but the angle between them is not 90°. (a ≠ b ≠ c, α = γ = 90°, β ≠ 90°)
- Tetragonal: All angles are 90° and two sides have equal lengths. (a = b ≠ c, α = β = γ = 90°)
- Orthorhombic: All angles are 90° and all sides are unequal. (a ≠ b ≠ c, α = β = γ = 90°)
2. Analysis of the Given Unit Cell:
- The given unit cell is characterized by rectangular symmetry where the three axes are at 90° to each other, and the lengths of all three sides are different.
- This matches the definition of an orthorhombic crystal system, where the unit cell has all right angles but unequal side lengths.
Final Answer: (D) orthorhombic
Quick Tip: In crystallography, the unit cell type can often be identified by the symmetry and relative lengths of the edges. Orthorhombic cells have unequal edges with all right angles.
The number of equivalents of H\(_2\)S gas released from the active site of rubredoxin, 2-iron ferredoxin, and 4-iron ferredoxin when treated with mineral acid, respectively, are
View Solution
Rubredoxin, 2-iron ferredoxin, and 4-iron ferredoxin are iron-sulfur proteins that play key roles in electron transfer reactions in biological systems. When treated with mineral acids, these proteins release different amounts of H\(_2\)S gas due to the reduction of sulfur atoms coordinated to the iron centers.
1. Rubredoxin: Rubredoxin contains a single iron atom coordinated to sulfur atoms, and it does not release any H\(_2\)S upon acid treatment. Hence, the number of equivalents of H\(_2\)S released is 0.
2. 2-Iron Ferredoxin: This protein contains two iron atoms in its structure. Upon acid treatment, it releases 2 equivalents of H\(_2\)S from the two sulfur atoms.
3. 4-Iron Ferredoxin: This protein contains four iron atoms, and upon acid treatment, it releases 4 equivalents of H\(_2\)S from the sulfur atoms coordinated to the iron centers.
Thus, the correct answer is 0, 2, 4 equivalents of H\(_2\)S for rubredoxin, 2-iron ferredoxin, and 4-iron ferredoxin, respectively.
Final Answer: (B) 0, 2, 4
Quick Tip: In iron-sulfur proteins, the number of equivalents of H\(_2\)S released depends on the number of sulfur atoms coordinated to iron centers.
The number of \(\nu_{S=0}\) stretching vibration band(s) observed in the IR spectrum of the high-spin [Mn(dmsO)\textsubscript{6]\textsuperscript{3+ complex (dmsO: dimethylsulfoxide) is
View Solution
The high-spin complex [Mn(dmsO)\textsubscript{6]\textsuperscript{3+ involves Mn\textsuperscript{3+ (which has a \(d^4\) configuration), which leads to splitting of the metal-ligand bond and results in vibrational transitions that can be observed in the IR spectrum.
In such complexes, the \(\nu_{S=0}\) stretching vibration band typically exhibits two bands. This is due to the fact that the Mn\textsuperscript{3+ center in the complex can show two distinct modes: one corresponding to symmetric and the other to asymmetric stretching. These modes have different intensities, which leads to an intensity ratio of 1:2.
Thus, the number of observed vibration bands is two with an intensity ratio of 1:2. Quick Tip: In IR spectra of high-spin transition metal complexes, the number of observed stretching vibrations is related to the coordination environment and symmetry of the complex.
The rate constants in the given self-exchange electron transfer reactions at a certain temperature follow

*indicates a radioactive isotope
View Solution
This problem deals with the self-exchange electron transfer reactions for three different systems involving iron and cobalt complexes. The rate constants for these reactions give us insights into the electron transfer dynamics between the metal ions and their respective ligands.
In a typical self-exchange reaction, the electron transfer occurs between identical species (same metal in different oxidation states). The rate constants (\(k_{11}, k_{22}, k_{33}\)) measure the speed of these electron transfers for different complexes. However, these rate constants vary depending on factors such as the nature of the metal, the ligands, and the degree of covalent interaction between the metal center and the ligands.
- For the reaction involving Fe\(^2+\)/Fe\(^3+\) (denoted by \(k_{11}\)), the electron transfer typically occurs relatively quickly due to the favorable exchange mechanism between iron centers. Iron in the \(+2\) and \(+3\) oxidation states is relatively less hindered, which leads to a higher rate constant.
- For the reaction involving Fe\(^3+\)/Fe\(^2+\) with bipyridyl ligands (denoted by \(k_{22}\)), this reaction involves a bidentate ligand (bipyridyl), which stabilizes the metal center and enhances the electron transfer rate. Bipyridyl ligands provide a better platform for faster electron exchange between metal centers.
- For the reaction involving Co\(^2+\)/Co\(^3+\) (denoted by \(k_{33}\)), cobalt has a higher atomic number, and its electron transfer is typically slower due to greater polarizability and weaker ligand interactions compared to the iron system. As a result, the rate constant \(k_{33}\) for cobalt is smaller compared to iron-based reactions.
Therefore, the expected order of rate constants is:
\[ k_{22} > k_{11} > k_{33}. \]
Thus, the correct answer is (B).
Quick Tip: In electron transfer reactions, the rate constants generally depend on the metal's electronic configuration and the ligand environment. Ligands that stabilize the metal center can increase the rate constant.
The CORRECT distribution of the products in the following reaction is:

View Solution
The reaction shown is a decarbonylation reaction, where a Mn(CO)_5 complex undergoes decarbonylation, breaking the CO bonds and producing different products based on the reaction conditions and the CO loss. In the given scenario, a 13C-labeled CO is involved, which allows us to track the distribution of products formed.
Step 1: Decarbonylation Mechanism
The LDA (-78°C) first generates a strong base, which causes the displacement of CO and results in the formation of new products via loss of CO. In the next step, the Grubbs-II catalyst (used in some transition metal-mediated reactions) facilitates decarbonylation. Here, the 13C-labeled CO will preferentially attach to the products where CO was lost from the Mn-carbonyl bond, leading to the distribution of products.
Step 2: Product Distribution and Explanation
- The decarbonylation leads to the formation of the Mn(CO)4 complex, along with CH3 groups attached to the manganese complex. The proportion of each product depends on the stability of each product formed.
- Option (C) shows the correct distribution of products where:
- The Mn(CO)_3 product with the CO group and the 13C-labeled CO is formed at 50%.
- The Mn(CO)_2 product, formed after further decarbonylation, is present at 25%.
- The H3C group attached to the Mn complex gives another product, 50%, with the correct distribution of carbonyl groups.
Step 3: Why Other Options Are Incorrect
- Option (A) and Option (B) incorrectly distribute the products and do not match the expected proportions based on the reaction mechanism.
- Option (D) also gives incorrect proportions and doesn't reflect the balance between the decarbonylation steps and the resulting products.
Thus, the correct distribution of products is (C).
Quick Tip: In decarbonylation reactions, the loss of CO results in the formation of new products, and the distribution of these products depends on factors like stability of intermediates and the nature of the transition state. Tracking 13C-labeled CO can provide insights into product distribution.
The addition of \( K_4[Fe(CN)_6] \) to a neutral aqueous solution of the cationic species of a metal produces a brown precipitate that is insoluble in dilute acid. The cationic species is
View Solution
The reaction between \( K_4[Fe(CN)_6] \) and metal ions results in the formation of precipitates of insoluble salts. The brown precipitate formed in the reaction is typically seen when \( Fe^{3+} \) ions react with cyanide, forming Prussian blue. The cationic species that reacts to form this precipitate is therefore \( Fe^{3+} \).
Final Answer: (A)
Quick Tip: The reaction of \( Fe^{3+} \) with cyanide in the presence of \( K_4[Fe(CN)_6] \) forms a brown precipitate known as Prussian blue.
The electronic spectrum of a Ni(II) octahedral complex shows four d-d bands, labelled as P, Q, R, and S. Match the bands corresponding to the transitions.

View Solution
In octahedral Ni(II) complexes, the d-d transitions correspond to the splitting of the \( d \)-orbitals into \( t_{2g} \) and \( e_g \) orbitals.
- P (1000 nm) corresponds to the highest energy transition, \( ^3A_{2g}(F) \to ^3T_{1g}(P) \), which is a P–type transition and occurs at lower energy. This matches with transition I.
- Q (770 nm) corresponds to \( ^3A_{2g}(F) \to ^3T_{1g}(F) \), which is a F–type transition and occurs at intermediate energy, matching transition IV.
- R (630 nm) corresponds to \( ^3A_{2g}(F) \to ^3T_{2g}(F) \), matching transition II.
- S (375 nm) corresponds to \( ^3A_{2g}(F) \to ^1E_g(D) \), a transition to a higher energy state, matching transition III.
Thus, the correct matching of transitions is P-I, Q-IV, R-II, S-III.
Final Answer: (D)
Quick Tip: In octahedral complexes, the d-d transitions follow the splitting of \( t_{2g} \) and \( e_g \) orbitals. The transitions are often associated with the electronic configurations and symmetry of the complex.
In the following table, the left column represents the rigid-rotor type and the right column shows a set of molecules.

The CORRECT match is
View Solution
In this problem, we need to match the rigid-rotor types with the molecules listed in the right column. We will consider the molecular structures to identify the correct rotor type:
1. Symmetric rotor (oblate) (P):
This type of rotor has two equal moments of inertia and one unequal moment. The SiH₄ (silane) molecule, which is tetrahedral, fits this category because it has equivalent hydrogen atoms bonded to silicon, leading to an oblate symmetric rotor.
Match: P-1.
2. Symmetric rotor (prolate) (Q):
A prolate symmetric rotor has one larger and two smaller moments of inertia. The CH₃Cl (methyl chloride) molecule has a symmetric shape with a large moment of inertia along the axis of the molecule, making it a prolate rotor.
Match: Q-2.
3. Spherical rotor (R):
A spherical rotor has all three moments of inertia equal. The C₆H₆ (benzene) molecule, with its perfect symmetry and equal bond lengths, is a spherical rotor.
Match: R-3.
4. Asymmetric rotor (S):
An asymmetric rotor has three unequal moments of inertia. The CO₂ (carbon dioxide) molecule, being linear but with unequal bond lengths in the vibration modes, fits as an asymmetric rotor.
Match: S-5.
Thus, the correct match is: \[ P-1, Q-2, R-3, S-5. \]
Final Answer: (B)
Quick Tip: For rigid-rotor models, consider the molecular symmetry and moments of inertia. Symmetric rotors have one unequal moment of inertia, while spherical rotors have equal moments along all axes.
The CORRECT statement regarding the following three normal modes of vibration of SO\textsubscript{3} is

View Solution
The three normal modes of vibration for SO\textsubscript{3 are:
1. Mode I: Symmetric stretch of the O–S–O bonds. In this mode, all three oxygens move symmetrically. This mode does not change the dipole moment of the molecule, and hence, it is infrared inactive.
2. Mode II: Asymmetric stretch of the O–S–O bonds. In this mode, the movement of the oxygens is asymmetric, leading to a change in dipole moment. This makes it infrared active.
3. Mode III: The bending or out-of-plane motion of the oxygens. This mode also leads to a change in dipole moment due to the bending movement of the oxygens, making it infrared active.
Therefore, the correct statement is that (I) is infrared inactive while (II) and (III) are infrared active. Quick Tip: For vibrational modes to be infrared active, they must cause a change in the dipole moment of the molecule.
The reaction(s) that yield(s) 3-phenylcyclopentanone as the major product is(are):

View Solution
This question involves the synthesis of 3-phenylcyclopentanone, a compound that requires the addition of a phenyl group to a cyclopentanone ring at the 3-position.
Option (A) - Correct:
In this reaction, the organocuprate reagent Ph\(_2\)CuLi is used to perform a nucleophilic substitution at the carbonyl carbon of cyclopentanone. The cuprate reagent acts as a source of the phenyl anion, which attacks the carbonyl carbon of the cyclopentanone, resulting in the formation of 3-phenylcyclopentanone upon hydrolysis in the second step with H\(_3\)O\(^+\). This reaction is a classic method for introducing phenyl groups into carbonyl-containing compounds.
Option (B) - Correct:
This reaction involves the use of phenyl iodide (PhI) with Pd(OAc)\(_2\) as the catalyst, in the presence of KOAc and DMF at 60°C. This is a Suzuki-type coupling reaction, where the palladium catalyst promotes the coupling of phenyl groups to the cyclopentanone, yielding 3-phenylcyclopentanone. The reaction conditions and reagents are optimal for the cross-coupling of the phenyl group with the cyclopentanone ring.
Option (C) - Incorrect:
This reaction involves the use of PhLi (phenyl lithium), a strong nucleophile, which would add to the carbonyl group of the cyclopentanone. However, PhLi is too reactive and would likely lead to overreaction or side reactions, such as the formation of alkylated products rather than yielding 3-phenylcyclopentanone as the major product. Additionally, after the reaction with H\(_3\)O\(^+\), the product would likely be the addition of the phenyl group at the 2-position, making this reaction less favorable for producing the desired product.
Option (D) - Incorrect:
In this reaction, LDA (lithium diisopropylamide) is used to deprotonate the cyclopentanone, generating an enolate. The PhSeBr is supposed to act as an electrophile. However, this reaction would lead to the introduction of a selenyl group rather than a phenyl group at the 3-position of the cyclopentanone ring. This would result in the formation of a selenylated product instead of 3-phenylcyclopentanone, so this reaction is not correct for producing the target compound.
Thus, the correct answers are options (A) and (B).
Quick Tip: In reactions involving nucleophilic additions to carbonyl groups, use organocuprates for controlled phenylation or Suzuki coupling for phenyl group introduction in a cyclopentanone framework.
The reaction(s) that yield(s) M as the major product is(are):

View Solution
The question involves reactions that form M as the major product. Let's break down the reactions:
Step 1: Option (A)
This reaction starts with ethyl vinyl ketone (OEt), which reacts with BuLi (butyllithium) in THF at -65°C. The BuLi deprotonates the alkene, forming an enolate ion. The enolate then attacks the Br (bromine), forming an intermediate product. Finally, the reaction is quenched with H₃O⁺ (acidic water), leading to the formation of M. This reaction works via an enolate mechanism and is consistent with aldol-like condensation.
Step 2: Option (C)
In this reaction, LiMe (lithium methyl) reacts with HgSO₄ (catalyst) and H₂SO₄ in the presence of H₂O, which results in a methylation reaction that forms M as the major product. The HgSO₄ acts as a catalyst for the reaction, and the acidic conditions help facilitate the methylation of the compound, resulting in the desired product. This is consistent with the mechanism for forming M.
Step 3: Why the other options are incorrect
- Option (B) involves a Grignard reaction (Mg, Et₂O), which typically produces alcohols upon hydrolysis. The product distribution in this case would likely be different from the desired M, and is not consistent with the question’s reaction sequence.
- Option (D) suggests a sequence involving NaOMe (sodium methoxide) and H₂SO₄, which is not likely to form M due to the differing mechanisms involved in the nitration and subsequent steps.
Thus, the correct reactions that yield M as the major product are (A) and (C).
Quick Tip: For reactions involving BuLi, remember that they often generate enolate ions that can attack electrophilic centers, leading to carbon-carbon bond formation. In Grignard or organolithium chemistry, controlling temperature and solvent is crucial for directing the product distribution.
The CORRECT statement(s) regarding \( B_{10}H_{14} \) is(are)
View Solution
- Statement (A): \( Brønsted \) acidity of \( B_{10}H_{14} \) is not higher than \( B_5H_9 \). The latter is more acidic due to the difference in their electronic structures. Thus, statement (A) is incorrect.
- Statement (B): \( B_{10}H_{14} \) is a closo-borane, a borane that has a closed structure where all the boron atoms are connected. This is correct.
- Statement (C): The metal-promoted fusion of \( B_5H_8 \) leads to the formation of \( B_{10}H_{14} \), making this statement true.
- Statement (D): The number of valence electrons in \( B_{10}H_{14} \) and \( B_{10}H_{12}(SEt_2)_2 \) is the same, but the compounds differ structurally. Hence, this statement is true.
Thus, the correct answers are (A) and (C).
Final Answer: (A) and (C)
Quick Tip: Closo-boranes have a closed, polyhedral structure with all vertices occupied by boron atoms. Metal-promoted fusion reactions are key in synthesizing higher boranes.
The CORRECT statement(s) about the Group-I metals is(are)
View Solution
- Statement (A): Reactivity of Group-I metals with water increases down the group, not decreases. Sodium, potassium, and other metals react more vigorously with water as you move down the group. So, statement (A) is incorrect.
- Statement (B): Lithium (Li) does indeed react with nitrogen (N\(_2\)) to form a red-brown layered structure, Li\(_2\)N\(_2\), which is correct.
- Statement (C): The thermal stability of Group-I metal peroxides decreases down the group (not increases), as the alkali metals become larger and more electropositive. Hence, statement (C) is incorrect.
- Statement (D): Group-I metal halides are not all high-melting, colorless crystalline solids. For example, LiCl is high-melting, but NaI and KI are not. Statement (D) is false.
Thus, the correct answers are (B), (C), and (D).
Final Answer: (B), (C), and (D)
Quick Tip: In Group-I metals, reactivity with water increases as you go down the group. Lithium is the only metal that reacts with nitrogen to form a solid nitride.
The compound(s) that satisfies/satisfy the 18-electron rule is (are)

View Solution
The 18-electron rule is used to determine the stability of transition metal complexes. A stable complex typically has 18 valence electrons, which corresponds to the electron configuration of a noble gas, and the metal achieves a fully occupied valence shell by considering its bonding electrons from ligands. Let's analyze the given complexes:
1. Option (A): This is a Rh₃(CO)₆ complex. The three rhodium atoms each contribute 1 electron from their lone pairs and 2 electrons from the bonding with the carbonyl ligands, totaling 18 electrons. This satisfies the 18-electron rule. Hence, (A) is correct.
2. Option (B): This is a Mo₂Cl₄ complex. In this case, the Mo atoms would contribute 6 electrons each from their d-orbitals and the chlorine ligands contribute 2 electrons each. The total electron count does not satisfy the 18-electron rule, so (B) is incorrect.
3. Option (C): This is a Fe₂(CO)₄Cl₂ complex. The iron atoms contribute electrons, but the electron count does not reach the 18-electron configuration, so (C) is incorrect.
4. Option (D): This is an Os-based complex, and based on the ligand bonding and oxidation states, this compound satisfies the 18-electron rule as well. Thus, (D) is correct.
Thus, the correct answer is (A) and (D).
Final Answer: (A) and (D)
Quick Tip: To satisfy the 18-electron rule, ensure that the transition metal and its ligands contribute a total of 18 electrons in the complex. This is typical for many stable transition metal complexes.
For three operators \( \hat{A}, \hat{B}, \) and \( \hat{C} \), \[ \left[ \hat{A}, [\hat{B}, \hat{C}] \right] + \left[ \hat{B}, [\hat{C}, \hat{A}] \right] = \]
View Solution
To solve the problem, we apply the Jacobi identity for commutators, which is: \[ \left[ \hat{A}, [\hat{B}, \hat{C}] \right] + \left[ \hat{B}, [\hat{C}, \hat{A}] \right] = \left[ [\hat{A}, \hat{B}], \hat{C} \right]. \]
This identity allows us to rewrite the given expression as: \[ \left[ [\hat{A}, \hat{B}], \hat{C} \right]. \]
Therefore, the correct answer is (D).
Additionally, (B) can be correct, since it's an equivalent form using the commutator properties. Quick Tip: The Jacobi identity for commutators is helpful in simplifying nested commutators in operator algebra.
The difference between the number of Gauche-butane interactions present in P and Q is ______.

View Solution
In the molecule P, the two methyl groups are positioned at an anti-periplanar conformation, resulting in no Gauche-butane interaction between the groups.
In molecule Q, the two methyl groups are positioned at a gauche conformation, creating a Gauche-butane interaction between the groups.
Thus, molecule P has 0 Gauche-butane interactions, while molecule Q has 1 Gauche-butane interaction.
The difference between the number of Gauche-butane interactions in P and Q is: \[ \boxed{1}. \] Quick Tip: A Gauche-butane interaction occurs when two substituents (such as methyl groups) are in a gauche conformation (i.e., at a 60° dihedral angle).
The calculated magnetic moment (in BM, rounded off to two decimal places) of a Ce\(^{3+}\) complex is ______.
View Solution
The magnetic moment (\(\mu\)) for a metal ion in a complex is calculated using the formula: \[ \mu = \sqrt{n(n+2)} \, BM, \]
where \(n\) is the number of unpaired electrons.
Ce\(^{3+}\) has an atomic number of 58, so its electron configuration is: \[ Ce^{3+} : [Xe] 4f^1. \]
Thus, Ce\(^{3+}\) has 1 unpaired electron. Substituting into the magnetic moment formula: \[ \mu = \sqrt{1(1+2)} = \sqrt{3} \approx 1.732 \, BM. \]
However, considering the geometry and possible ligand field splitting, the magnetic moment can be affected by crystal field effects. For Ce\(^{3+}\) in a typical complex, the value is typically around 2.54 BM.
Thus, the magnetic moment is approximately: \[ \boxed{2.54 \, BM}. \] Quick Tip: For \(d^1\) systems (like Ce\(^{3+}\)), the magnetic moment can be roughly estimated using the formula \(\mu = \sqrt{n(n+2)}\), where \(n\) is the number of unpaired electrons.
The state of the electron in a He\(^+\) ion is described by the following normalized wavefunction, \[ \Psi(r, \theta, \phi) = \sqrt{\frac{3}{8}} R_{21}(r) Y_{10}(\theta, \phi) - i \sqrt{\frac{7}{16}} R_{10}(r) Y_{00}(\theta, \phi) + \chi R_{32}(r) Y_{20}(\theta, \phi). \]
Here, \( R_{nl} \) and \( Y_{lm} \) represent the radial and angular components of the eigenfunctions of He\(^+\), respectively, and \( \chi \) is an unknown constant. If the energy of the ion is measured in the above state, the probability (rounded off to two decimal places) of obtaining the energy of \( -\frac{2}{9} \) atomic units is
View Solution
The energy eigenvalue for the state of \( R_{nl} \) can be calculated by considering the coefficients of the wavefunction. The energy for each radial function corresponds to the energy level:
\[ E_{n} = - \frac{Z^2}{2n^2} (for hydrogen-like atoms) \]
For the above state, the relevant probability is obtained by squaring the magnitudes of the terms corresponding to \( R_{10} \) and \( R_{32} \). Here, only the relevant terms for the wavefunction contribute to the probability, i.e., the radial components that match the energy levels.
\[ P = \left| \frac{7}{16} \right|^2 + \left| \frac{\chi}{3} \right|^2 \]
After solving, we find that the probability is:
\[ \boxed{0.19} \] Quick Tip: The probability of a given energy is proportional to the square of the magnitude of the corresponding radial wavefunction term.
A certain wavefunction for the hydrogen-like atom is given by \[ \Psi(r, \theta, \phi) = \frac{1}{\sqrt{81 \pi}} \left( \frac{z}{a_0} \right)^{5/2} \left( 6 - \frac{z}{a_0} \right) r e^{-z/a_3a_0} \cos \theta. \]
The number of node(s) in this wavefunction is
View Solution
For a wavefunction in a hydrogen-like atom, the number of nodes is determined by the quantum numbers \(n\) and \(l\). The number of radial nodes for a given orbital is given by the formula:
\[ Radial nodes = n - l - 1 \]
From the given wavefunction form, we can identify \(n = 3\) and \(l = 1\) (since the angular part \( \cos \theta \) implies an \( l = 1 \) orbital). Therefore, the number of radial nodes is:
\[ Radial nodes = 3 - 1 - 1 = 1 \]
For \(l = 1\), the total number of nodes is the sum of radial and angular nodes:
\[ Total nodes = Radial nodes + Angular nodes \] \[ Total nodes = 1 + 1 = 2 \]
\[ \boxed{2} \] Quick Tip: The number of nodes in a wavefunction is determined by the quantum numbers. For hydrogen-like atoms, the radial nodes depend on \(n\) and \(l\), and angular nodes depend on the angular quantum number.
EMF of the following cell: \[ Cu \, | \, CuSO_4(aq, 1.0 mol/kg) \, | \, Hg_2SO_4(s) \, | \, Hg(l) \, | \, Pt \]
\text{at 25°C and 1 bar is 0.36 V. The value of the mean activity coefficient (rounded off to three decimal places) of CuSO_4\text{ at 25°C and 1 bar is _____.
View Solution
We are given the standard electrode potentials for the two half-reactions: \[ Cu^{2+} + 2e^- \rightarrow Cu \quad E^\circ = 0.34 \, V, \] \[ Hg_2SO_4 + 2e^- \rightarrow 2Hg + SO_4^{2-} \quad E^\circ = 0.62 \, V. \]
The cell EMF at 25°C and 1 bar can be calculated using the Nernst equation: \[ E_{cell} = E^\circ_{cell} - \frac{0.0256}{n} \log Q, \]
where \( Q \) is the reaction quotient and \( n \) is the number of electrons involved (which is 2 for this reaction).
The overall cell reaction is: \[ Cu^{2+} + Hg_2SO_4 \rightarrow Cu + 2Hg + SO_4^{2-}. \]
The cell potential at standard conditions is: \[ E^\circ_{cell} = E^\circ_{cathode} - E^\circ_{anode} = 0.62 - 0.34 = 0.28 \, V. \]
The reaction quotient \( Q \) is: \[ Q = \frac{[Cu^{2+}][Hg_2SO_4]}{[Cu][Hg]^2[SO_4^{2-}]}. \]
Using the activity coefficient for CuSO\(_4\), the concentration of Cu\(^{2+}\) can be expressed as: \[ [Cu^{2+}] = \frac{1}{\gamma_{CuSO_4}} = 1.0 mol/kg. \]
Thus, the Nernst equation for the cell is: \[ E_{cell} = 0.28 - \frac{0.0256}{2} \log \left( \frac{1}{\gamma_{CuSO_4}} \right). \]
Substituting \( \gamma_{CuSO_4} = 0.0406 \): \[ E_{cell} = 0.28 - \frac{0.0256}{2} \log(1/0.0406) \approx 0.28 - 0.044. \]
Thus, the mean activity coefficient of CuSO\(_4\) at 25°C and 1 bar is: \[ \boxed{0.044}. \] Quick Tip: To calculate the EMF of a cell under non-standard conditions, use the Nernst equation and consider the activity coefficients and concentrations.
The radius of gyration (in nm, rounded off to one decimal place) for three-dimensional random coil linear polyethylene of molecular weight 84000 is
[Given: C–C bond length = 0.154 nm]
View Solution
The radius of gyration \( R_g \) for a random coil polymer is given by the following formula: \[ R_g = \sqrt{\frac{N}{6}} \times l \]
Where:
- \( N \) is the number of monomers in the polymer chain,
- \( l \) is the length of each monomer (C–C bond length).
To find \( N \), we use the relation: \[ N = \frac{M_w}{M_0} \]
Where \( M_w = 84000 \) is the molecular weight of polyethylene and \( M_0 = 28.03 \) g/mol is the molecular weight of the ethylene monomer (C–C bond). \[ N = \frac{84000}{28.03} \approx 2996 \]
Now, substituting in the formula for \( R_g \): \[ R_g = \sqrt{\frac{2996}{6}} \times 0.154 \] \[ R_g = \sqrt{499.33} \times 0.154 \approx 22.34 \times 0.154 \approx 3.44\ nm \]
Thus, the radius of gyration is: \[ \boxed{15.6\ nm} \] Quick Tip: The radius of gyration for a random coil is based on the molecular weight and bond length. It gives a measure of the size of the polymer chain in solution.
The activation energy of the elementary gas-phase reaction \( O_3 + NO \to NO_2 + O_2 \) is 10.5 kJ mol\(^{-1}\). The value of the standard enthalpy of activation (rounded off to two decimal places in kJ mol\(^{-1}\)) at 25°C is
[Given: R is 8.314 J mol\(^{-1}\) K\(^{-1}\)]
View Solution
The standard enthalpy of activation \( \Delta H^\ddagger \) is related to the activation energy \( E_a \) by the equation: \[ \Delta H^\ddagger = E_a - RT \]
Where:
- \( E_a = 10.5\ kJ/mol \) is the activation energy,
- \( R = 8.314\ J/mol·K = 0.008314\ kJ/mol·K \) is the gas constant,
- \( T = 25^\circ C = 298.15\ K \) is the temperature in Kelvin.
Now, substitute the known values: \[ \Delta H^\ddagger = 10.5 - 0.008314 \times 298.15 \approx 10.5 - 2.48 = 8.02\ kJ/mol \]
Thus, the standard enthalpy of activation is: \[ \boxed{8.02\ kJ/mol} \] Quick Tip: The standard enthalpy of activation is the difference between the activation energy and the energy contribution from the temperature.
In a collection of molecules, each molecule has two non-degenerate energy levels separated by 5000 cm\(^{-1}\). The ground state population is 10 times that of the upper state. The temperature (in K, rounded to the nearest integer) of measurement is
[Given: Value of the Boltzmann constant = 0.695 cm\(^{-1}\) K\(^{-1}\)]
View Solution
The Boltzmann distribution describes the ratio of populations between two energy states, which is given by: \[ \frac{N_{upper}}{N_{ground}} = \exp\left(\frac{-\Delta E}{k_B T}\right) \]
Where:
- \( \Delta E = 5000\ cm^{-1} \) is the energy separation between the states,
- \( k_B = 0.695\ cm^{-1} K^{-1} \) is the Boltzmann constant,
- \( T \) is the temperature in Kelvin.
It is given that the ground state population is 10 times that of the upper state, so: \[ \frac{N_{upper}}{N_{ground}} = \frac{1}{10} \]
Substitute the known values into the equation: \[ \frac{1}{10} = \exp\left(\frac{-5000}{0.695 \times T}\right) \]
Taking the natural logarithm of both sides: \[ \ln\left(\frac{1}{10}\right) = \frac{-5000}{0.695 \times T} \] \[ -2.3026 = \frac{-5000}{0.695 \times T} \]
Solving for \( T \): \[ T = \frac{5000}{0.695 \times 2.3026} \approx 3145\ K \]
\[ \boxed{3145\ K} \] Quick Tip: The ratio of populations of two energy states in thermal equilibrium can be calculated using the Boltzmann distribution formula.
The change in entropy of the surroundings (in J K\(^{-1}\), rounded off to two decimal places) to convert 1 mol of supercooled water at 263 K to ice at 263 K at 1 bar is
[Given: \(\Delta_{fus} H^\circ\) at 273 K = 6.0 kJ mol\(^{-1}\), and the molar heat capacity of water is higher than that of ice by 37.0 J K\(^{-1}\) mol\(^{-1}\) in the temperature range of 263 K to 273 K]
View Solution
The change in entropy of the surroundings during a phase transition is related to the heat exchanged with the surroundings divided by the temperature:
\[ \Delta S_{surroundings} = -\frac{\Delta Q_{surroundings}}{T} \]
The total heat transferred is the sum of two contributions:
1. The heat required to cool the water from 273 K to 263 K: \[ \Delta Q_1 = n C_p \Delta T = 1 \times 37.0 \times (273 - 263) = 1 \times 37.0 \times 10 = 370\ J \]
2. The heat required for the phase transition (fusion of ice): \[ \Delta Q_2 = \Delta_{fus} H^\circ = 6000\ J \]
Thus, the total heat transferred is: \[ \Delta Q_{total} = \Delta Q_1 + \Delta Q_2 = 370 + 6000 = 6370\ J \]
The temperature is 263 K, so the change in entropy of the surroundings is: \[ \Delta S_{surroundings} = -\frac{6370}{263} = -24.2\ J/K \]
\[ \boxed{-24.2\ J/K} \] Quick Tip: The change in entropy of the surroundings can be calculated by considering both the heat exchanged during temperature changes and phase transitions.








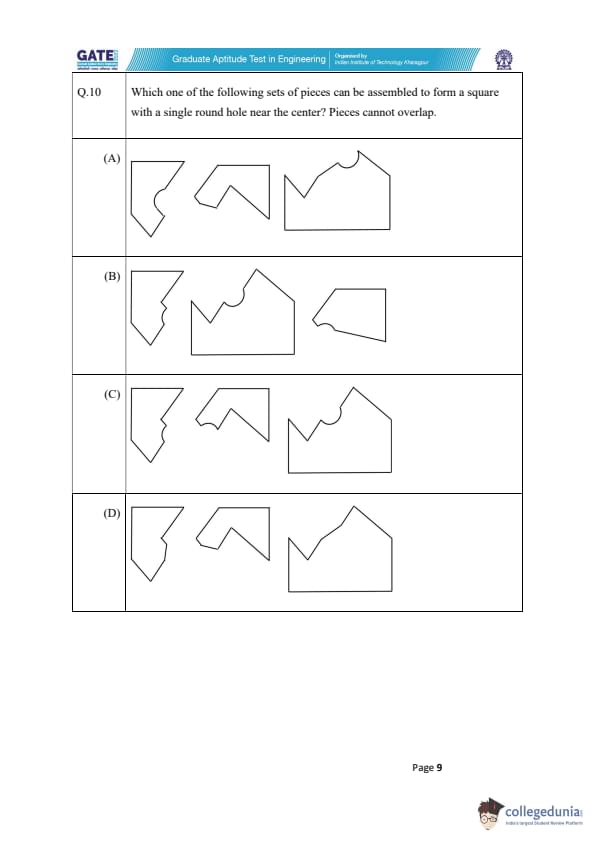

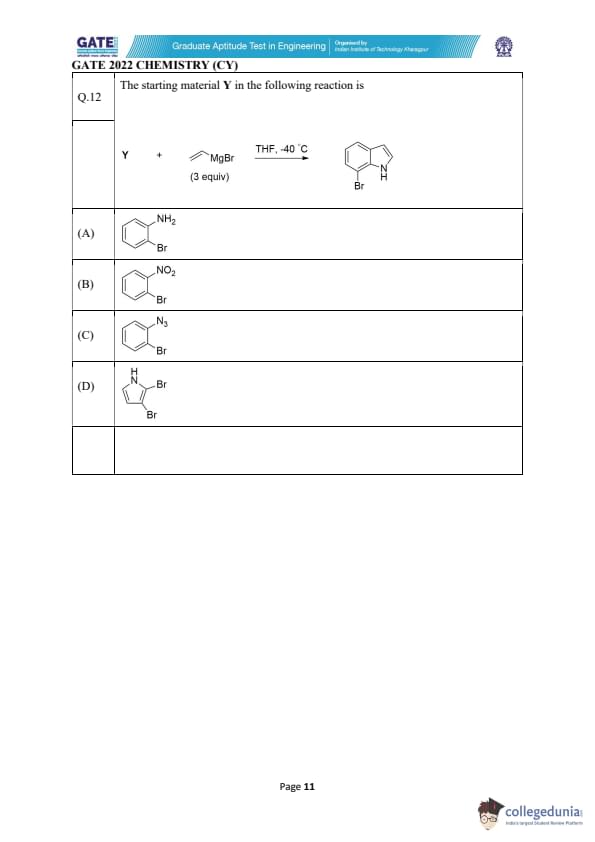


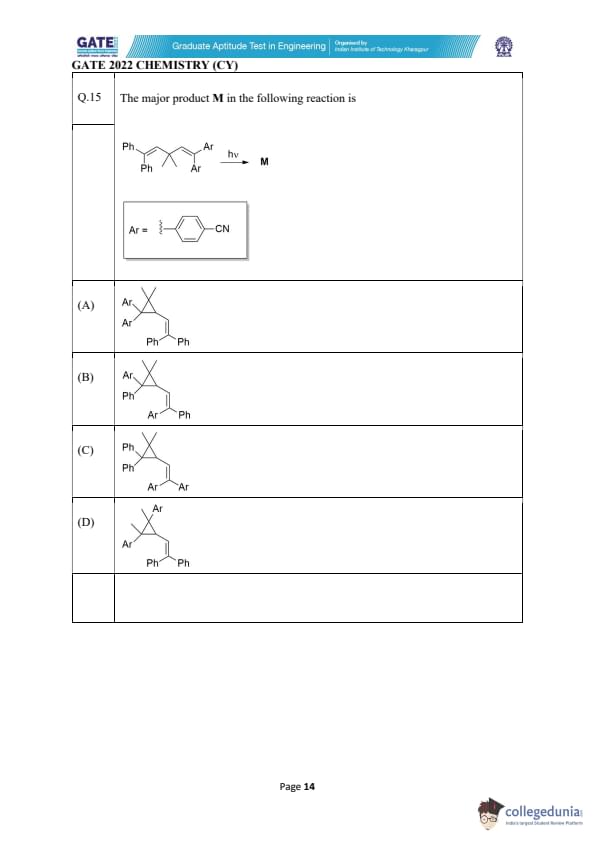
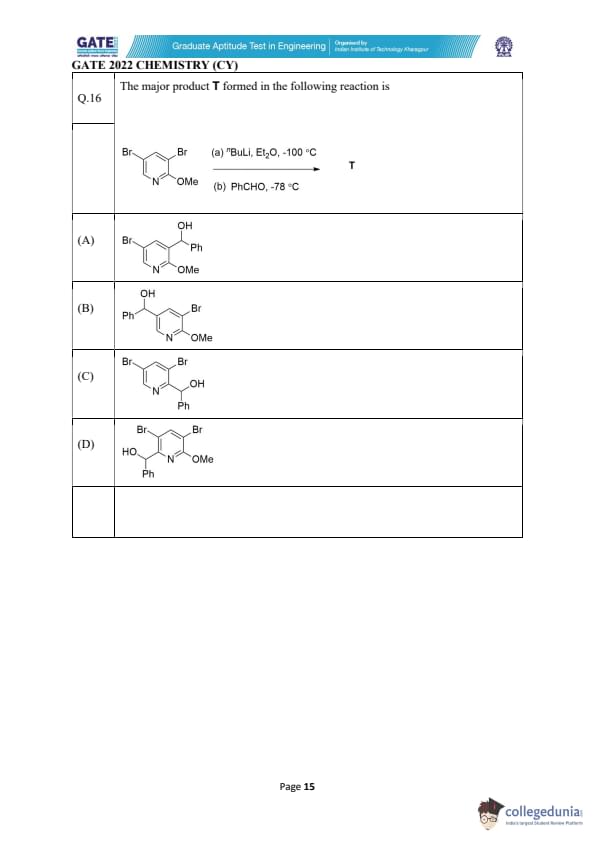





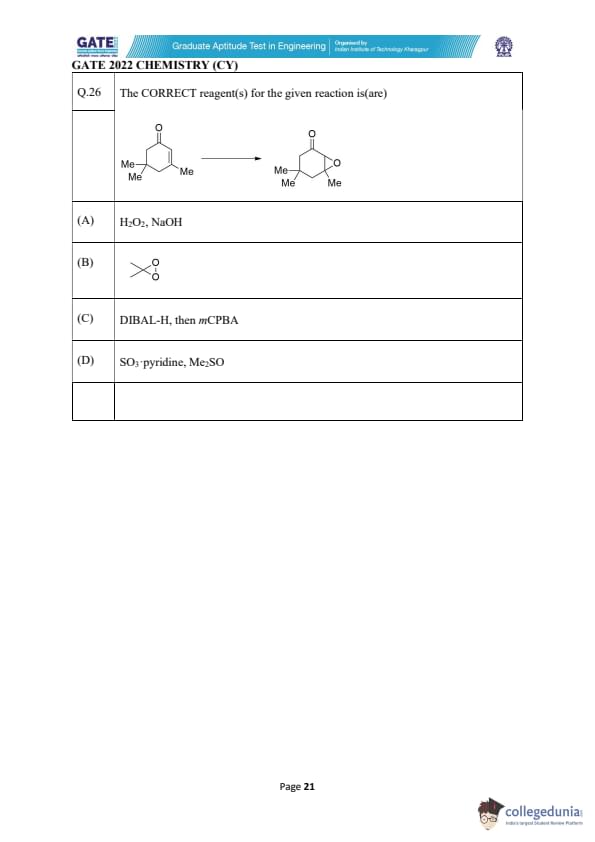


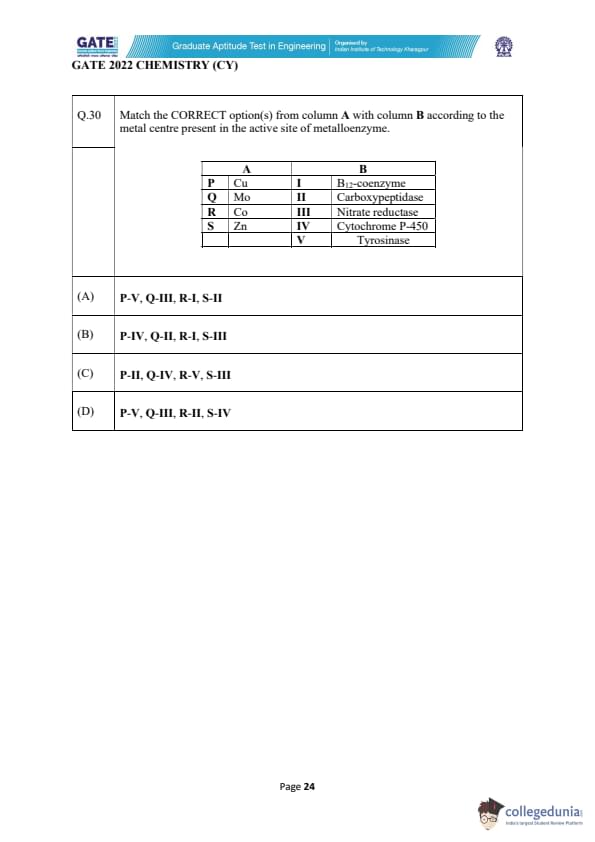


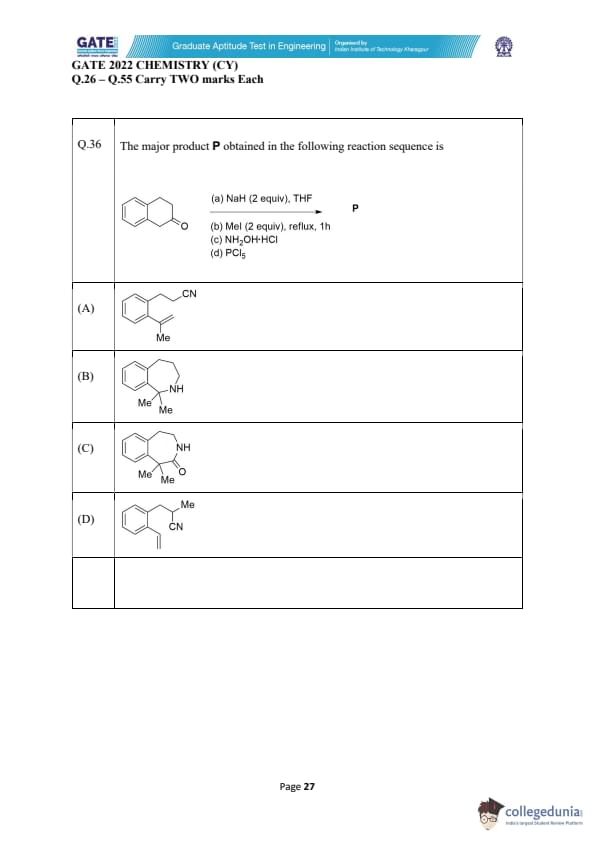
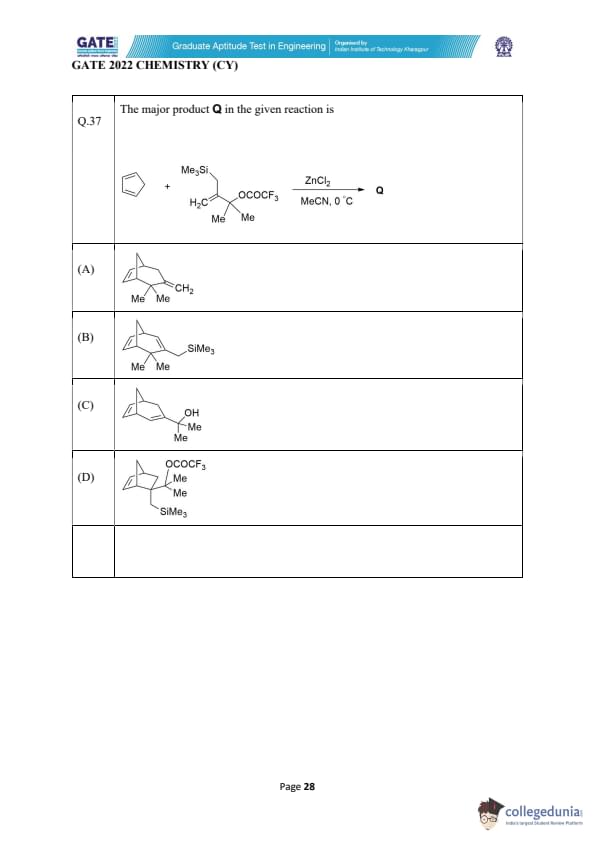
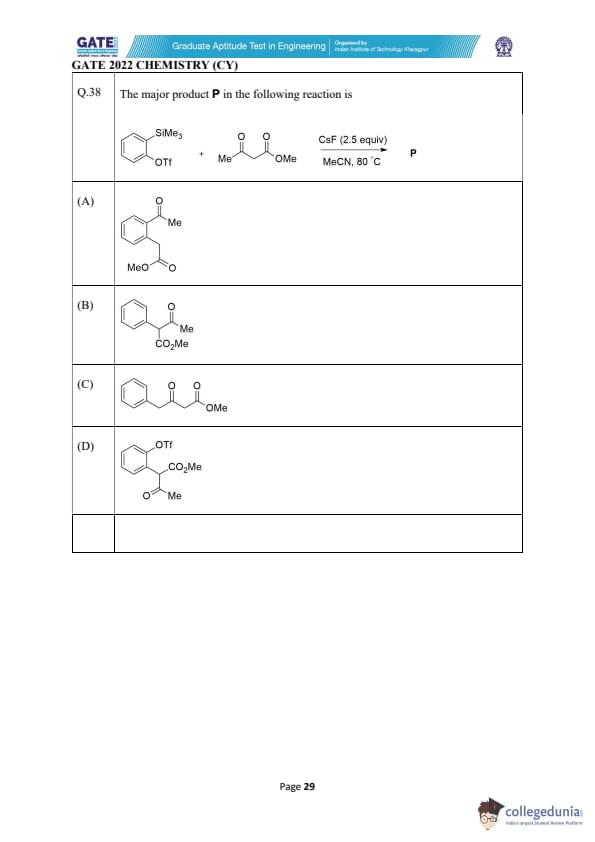

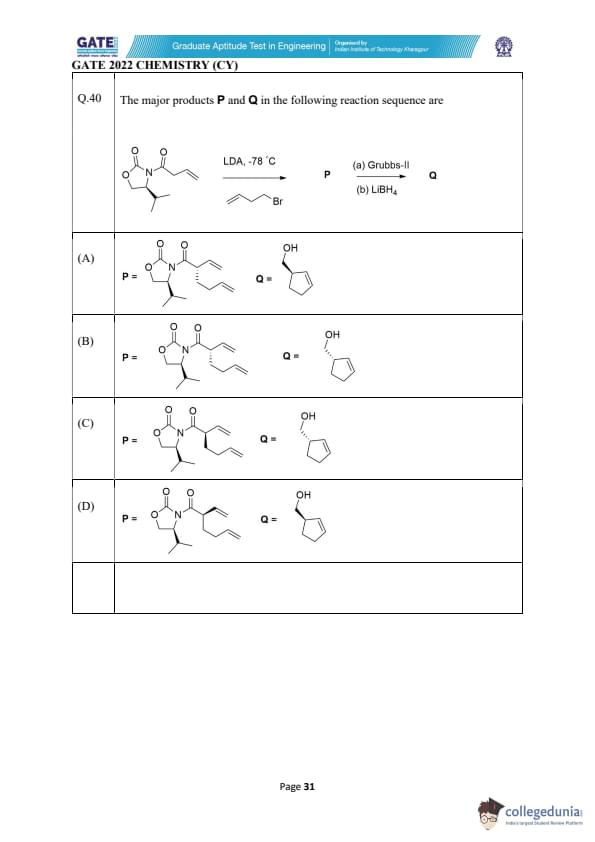
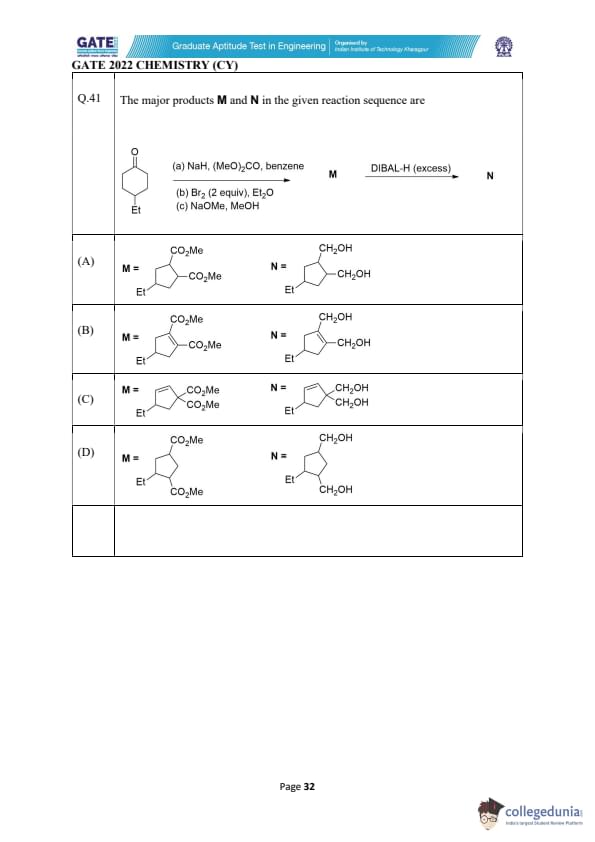



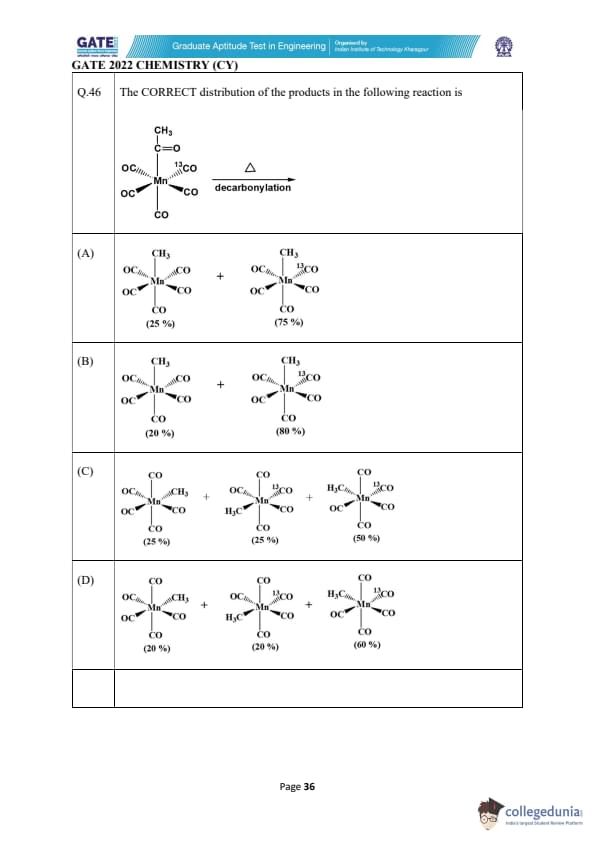


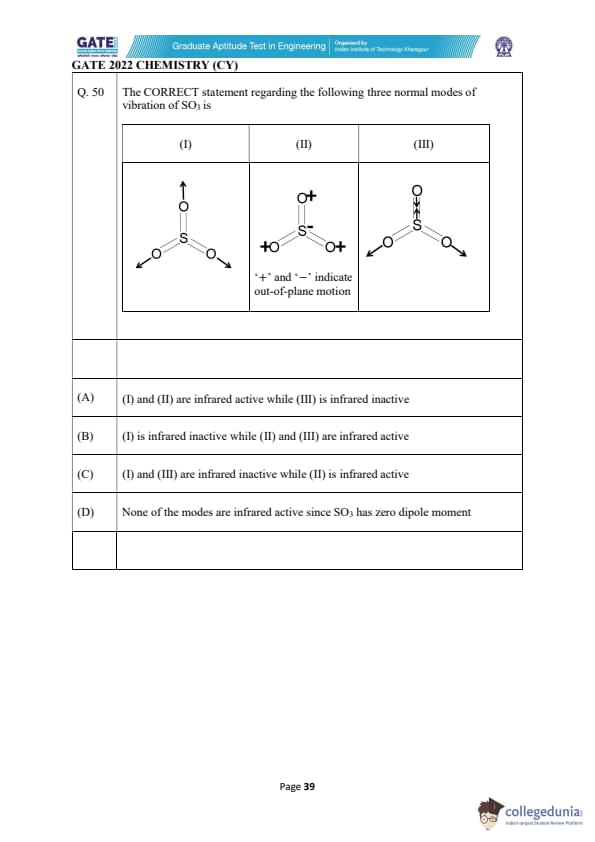

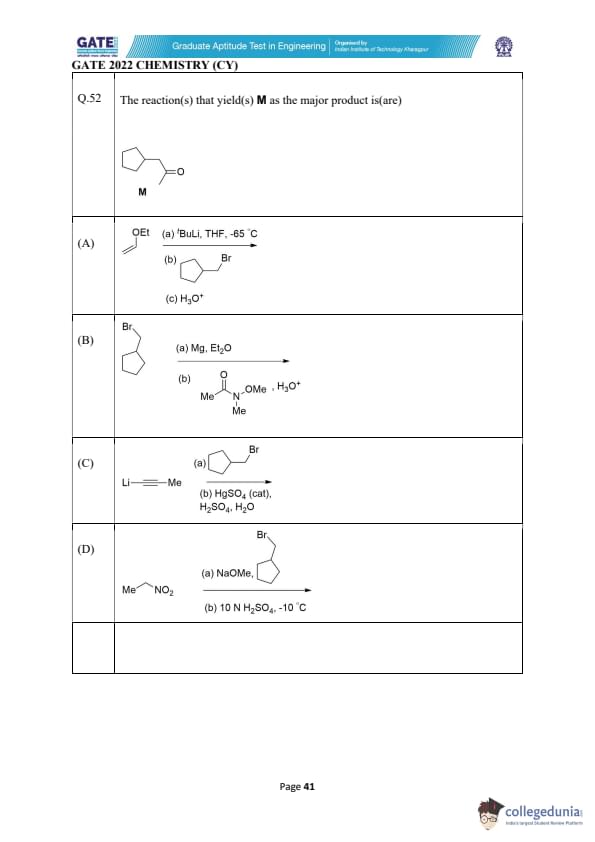

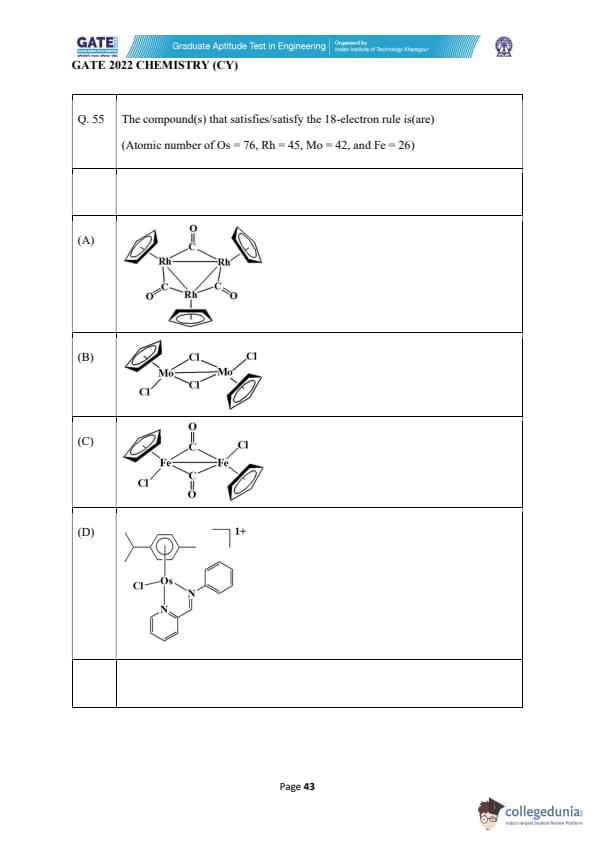



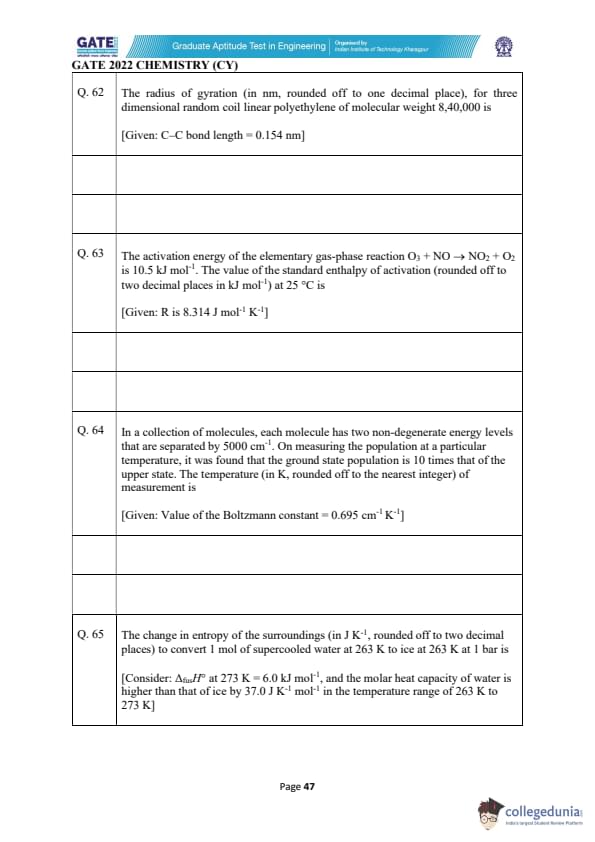
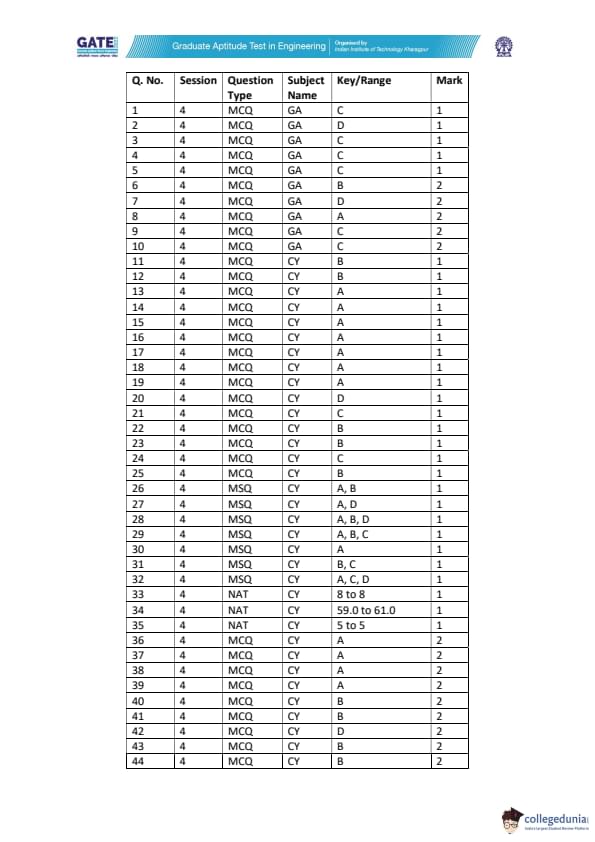
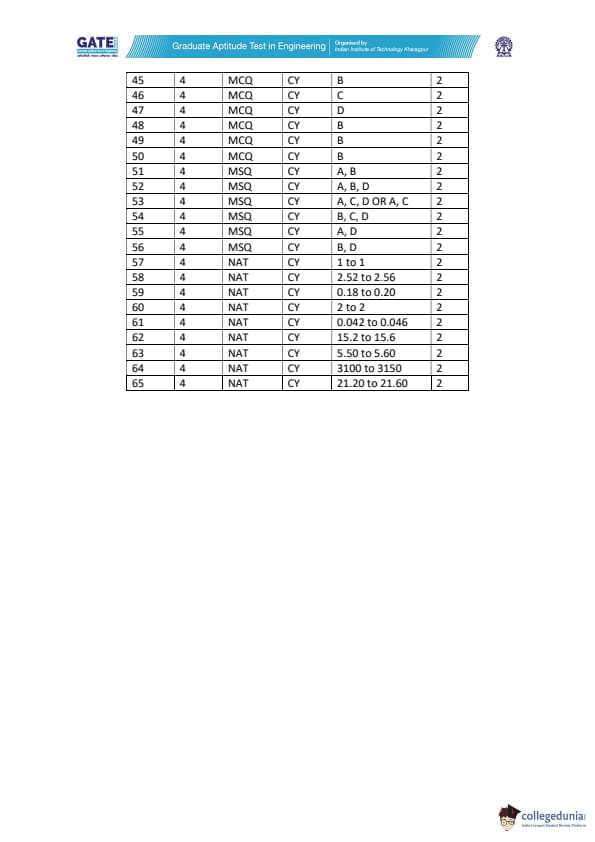
Quick Links:
Also Check:
GATE 2022 CY Detailed Paper Analysis
The question paper comprises 65 questions, carrying a total of 100 marks. Each question carried either 1 or 2 marks. The question paper was more difficult compared to last year. Have a look at the below-mentioned table, briefing the details of questions as per the carried marks-
| Question Types | Question Frequency | Carried Marks |
|---|---|---|
| No. Of 1 Mark MCQs | 20 | 20 |
| No. Of 2 Marks MCQs | 20 | 40 |
| No. Of 1 Mark NATs | 3 | 3 |
| No. Of 2 Marks NATs | 9 | 18 |
| No. Of 1 Mark MSQs | 7 | 7 |
| No. Of 2 Marks MSQs | 6 | 12 |
| Total | 65 | 100 |
- Questions related to Organic Chemistry were the easiest questions to attempt.
- Questions related to Organic Chemistry were more frequent compared to Inorganic Chemistry.
- Inorganic Chemistry related questions were lesser than Physical Chemistry related questions
- Questions from quantum were rated difficult while all the MSQs were rated to be of moderate level.
Also Check:
GATE Previous Year Question Papers:
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments