GATE 2022 Civil Engineering (CE) Slot-2 Question Paper with Solutions PDFs Slot 2 is available for download. GATE 2022 CE was conducted in 2 slots. GATE 2022 CE Slot 2 was conducted in the afternoon session (2:30 PM to 5:30 PM) by IIT Kharagpur. The overall difficulty level was the same as Slot 1, i.e. moderate to difficult. The General Aptitude section held the highest weightage followed by Engineering Mathematics in GATE 2022 CE question paper slot 2.
Candidates preparing for GATE 2023 can download GATE 2022 CE Question Paper with Answer Key PDFs Slot 2 from the links given below.
GATE 2022 Civil Engineering (CE) Slot-2 Question Paper with Solutions
| GATE 2022 Civil Engineering (CE) Slot-2 Question Paper | Check Solutions |

The movie was funny and I _________.
View Solution
The correct expression for this sentence is "couldn't help laughing". The phrase "couldn't help" is always followed by the verb-ing form of another verb (gerund).
- Option (A): "could help laughing" is incorrect because "could help" is not typically used in this context.
- Option (B): "couldn't help laughed" is incorrect because "laugh" should be in the gerund form (laughing).
- Option (D): "could helped laughed" is incorrect because "helped" is the past tense, and we need the base form "help" followed by the gerund form.
Therefore, the correct phrase is "couldn't help laughing", making (C) the correct answer.
Quick Tip: After "couldn't help", always use the gerund form (verb-ing) to describe something you couldn't stop doing.
If \( x : y : z = \frac{1}{2} : \frac{1}{3} : \frac{1}{4} \), what is the value of \( \frac{x + z - y}{y} \)?
View Solution
We are given the ratio \( x : y : z = \frac{1}{2} : \frac{1}{3} : \frac{1}{4} \), which means we can express the values of \( x \), \( y \), and \( z \) in terms of a common variable. Let’s solve for the ratio using the simplest method:
Step 1: Expressing the variables in terms of a common constant
We can write the ratios as:
\[ x = \frac{1}{2}k, \quad y = \frac{1}{3}k, \quad z = \frac{1}{4}k \]
where \( k \) is a constant.
Step 2: Substituting into the given expression
We are asked to find the value of \( \frac{x + z - y}{y} \). Substituting the values of \( x \), \( y \), and \( z \) into this expression:
\[ \frac{x + z - y}{y} = \frac{\frac{1}{2}k + \frac{1}{4}k - \frac{1}{3}k}{\frac{1}{3}k} \]
Step 3: Simplifying the expression
First, simplify the numerator:
\[ \frac{1}{2}k + \frac{1}{4}k - \frac{1}{3}k = \left(\frac{2}{4} + \frac{1}{4} - \frac{1}{3}\right)k \] \[ = \left(\frac{3}{4} - \frac{1}{3}\right)k \]
To subtract the fractions, get a common denominator:
\[ = \left(\frac{9}{12} - \frac{4}{12}\right)k = \frac{5}{12}k \]
Now, the expression becomes:
\[ \frac{\frac{5}{12}k}{\frac{1}{3}k} \]
Step 4: Final simplification
Simplify the fraction:
\[ \frac{\frac{5}{12}k}{\frac{1}{3}k} = \frac{5}{12} \times \frac{3}{1} = \frac{15}{12} = 1.25 \]
Thus, the value of \( \frac{x + z - y}{y} \) is 1.25, making (B) the correct answer.
Quick Tip: When dealing with ratios, express each term in terms of a common constant, then simplify the given expression step-by-step.
Both the numerator and the denominator of \( \frac{3}{4} \) are increased by a positive integer, \( x \), and those of \( \frac{15}{17} \) are decreased by the same integer. This operation results in the same value for both the fractions. What is the value of \( x \)?
View Solution
Let the new value of both fractions after performing the operations be denoted as \( y \).
- For the first fraction \( \frac{3}{4} \), when both the numerator and denominator are increased by \( x \), the new fraction becomes:
\[ \frac{3 + x}{4 + x} \]
- For the second fraction \( \frac{15}{17} \), when both the numerator and denominator are decreased by \( x \), the new fraction becomes:
\[ \frac{15 - x}{17 - x} \]
Since the operation results in the same value for both fractions, we can set these two fractions equal to each other: \[ \frac{3 + x}{4 + x} = \frac{15 - x}{17 - x} \]
Now, cross-multiply to solve for \( x \): \[ (3 + x)(17 - x) = (15 - x)(4 + x) \]
Expanding both sides: \[ (3)(17) - (3)(x) + (x)(17) - (x^2) = (15)(4) + (15)(x) - (x)(4) - (x^2) \] \[ 51 - 3x + 17x - x^2 = 60 + 15x - 4x - x^2 \]
Simplify the equation: \[ 51 + 14x - x^2 = 60 + 11x - x^2 \]
Cancel out \( x^2 \) from both sides: \[ 51 + 14x = 60 + 11x \]
Now, solve for \( x \): \[ 14x - 11x = 60 - 51 \] \[ 3x = 9 \] \[ x = 3 \]
Thus, the value of \( x \) is \( \boxed{3} \). Quick Tip: When solving problems involving fractions and operations on their numerators and denominators, remember to set the fractions equal to each other after performing the operations, and then solve for the unknown variable.
A survey of 450 students about their subjects of interest resulted in the following outcome.
150 students are interested in Mathematics.
200 students are interested in Physics.
175 students are interested in Chemistry.
50 students are interested in Mathematics and Physics.
60 students are interested in Physics and Chemistry.
40 students are interested in Mathematics and Chemistry.
30 students are interested in Mathematics, Physics and Chemistry.
Remaining students are interested in Humanities.
Based on the above information, the number of students interested in Humanities is:
View Solution
We can use the principle of inclusion and exclusion to solve this problem. Let:
- \( M \) be the set of students interested in Mathematics,
- \( P \) be the set of students interested in Physics,
- \( C \) be the set of students interested in Chemistry.
The total number of students interested in at least one of the three subjects is given by: \[ |M \cup P \cup C| = |M| + |P| + |C| - |M \cap P| - |P \cap C| - |M \cap C| + |M \cap P \cap C| \]
Substitute the given values: \[ |M \cup P \cup C| = 150 + 200 + 175 - 50 - 60 - 40 + 30 \]
Simplifying: \[ |M \cup P \cup C| = 405 \]
Thus, the number of students who are interested in at least one subject is 405. The total number of students is 450, so the number of students interested in Humanities is: \[ 450 - 405 = 45 \]
Thus, the number of students interested in Humanities is 45. Quick Tip: Use the principle of inclusion and exclusion to calculate the total number of students interested in at least one subject, and then subtract from the total number of students.
For the picture shown above, which one of the following is the correct picture representing reflection with respect to the mirror shown as the dotted line?


View Solution
The question involves identifying the correct reflection of the image across a dotted line representing a mirror. The reflection is achieved by flipping the image across the mirror line, which mirrors the shapes and their arrangement. The answer can be determined by checking the orientation and relative positioning of the shapes in the options provided.
Step 1: Analyzing the original image.
The original image consists of two shapes where the one on the left is slightly smaller than the one on the right. The dotted line divides the two shapes symmetrically.
Step 2: Reflection of the image.
In the reflection, the shape on the left will mirror to the right side, and the shape on the right will mirror to the left side while maintaining the same orientation. Option (B) correctly mirrors the arrangement and the shapes.
Step 3: Conclusion.
Thus, the correct reflection is shown in option (B).
Quick Tip: When identifying reflections in images, ensure that the relative positioning of objects across the mirror line is preserved while flipping the shapes symmetrically.
In the last few years, several new shopping malls were opened in the city. The total number of visitors in the malls is impressive. However, the total revenue generated through sales in the shops in these malls is generally low. Which one of the following is the CORRECT logical inference based on the information in the above passage?
View Solution
We are provided with information that although the number of visitors to the malls is impressive, the revenue generated is low. This suggests that while many people are visiting the malls, they are not spending a significant amount in the shops. Hence, the correct inference is that more people are visiting the malls but not spending enough.
Step 1: Analyzing the passage.
The passage highlights two main factors: the high number of visitors and low revenue generated from sales. This suggests a mismatch between the number of visitors and the amount they are spending.
Step 2: Interpretation of options.
- Option (A) suggests fewer people visiting but spending more, which contradicts the statement that there are many visitors.
- Option (B) correctly indicates more people are visiting but spending less, matching the passage's information.
- Option (C) is incorrect because it suggests that more visitors are also spending more, which contradicts the low revenue mentioned.
- Option (D) does not fit the passage as it implies fewer visitors and low spending.
Step 3: Conclusion.
The correct inference based on the passage is option (B).
Quick Tip: When analyzing passages for logical inferences, focus on understanding the contrast or relationship between the two key pieces of information presented.
In a partnership business, the monthly investment by three friends for the first six months is in the ratio 3: 4: 5. After six months, they had to increase their monthly investments by 10%, 15%, and 20%, respectively, of their initial monthly investment. The new investment ratio was kept constant for the next six months. What is the ratio of their shares in the total profit (in the same order) at the end of the year such that the share is proportional to their individual total investment over the year?
View Solution
The investment ratio for the first six months is given as 3 : 4 : 5. After six months, each partner increases their investment by 10%, 15%, and 20%, respectively. We need to calculate the total investment for each partner over the entire year and find the ratio of their shares in the total profit.
Step 1: Calculate the total investment for the first six months.
Let the initial investments for the three partners be \( 3x \), \( 4x \), and \( 5x \) for the first six months.
Step 2: Calculate the increased investment for the next six months.
The new investments are calculated as follows:
- Partner 1: \( 3x \times 1.1 = 3.3x \)
- Partner 2: \( 4x \times 1.15 = 4.6x \)
- Partner 3: \( 5x \times 1.2 = 6x \)
Step 3: Calculate the total investment for the year.
- Partner 1: Total investment \( = 3x \times 6 + 3.3x \times 6 = 18x + 19.8x = 37.8x \)
- Partner 2: Total investment \( = 4x \times 6 + 4.6x \times 6 = 24x + 27.6x = 51.6x \)
- Partner 3: Total investment \( = 5x \times 6 + 6x \times 6 = 30x + 36x = 66x \)
Step 4: Find the ratio of the total investments.
The ratio of their total investments is \( 37.8x : 51.6x : 66x \). Simplifying the ratio, we get: \[ 37.8 : 51.6 : 66 = 63 : 86 : 110 \]
Thus, the correct ratio of their shares in the total profit is \( 63 : 86 : 110 \).
Quick Tip: When calculating total investments with percentage increases, break the process into parts: calculate the initial total investment, then calculate the new investments after the percentage increase, and finally sum the investments for the total period.
Consider the following equations of straight lines:
Line L1: \( 2x - 3y = 5 \)
Line L2: \( 3x + 2y = 8 \)
Line L3: \( 4x - 6y = 5 \)
Line L4: \( 6x - 9y = 6 \)
Which one among the following is the correct statement?
View Solution
We are given four straight lines. To determine the correct relationship between the lines, we need to calculate the slopes of the lines and then compare them.
Step 1: Find the slope of each line.
- The equation of line L1 is \( 2x - 3y = 5 \). Rewriting it in slope-intercept form \( y = mx + c \), we get:
\[ 3y = 2x - 5 \quad \Rightarrow \quad y = \frac{2}{3}x - \frac{5}{3} \quad (Slope of L1 is \frac{2}{3} ) \]
- The equation of line L2 is \( 3x + 2y = 8 \). Rewriting it:
\[ 2y = -3x + 8 \quad \Rightarrow \quad y = -\frac{3}{2}x + 4 \quad (Slope of L2 is -\frac{3}{2} ) \]
- The equation of line L3 is \( 4x - 6y = 5 \). Rewriting it:
\[ 6y = 4x - 5 \quad \Rightarrow \quad y = \frac{2}{3}x - \frac{5}{6} \quad (Slope of L3 is \frac{2}{3} ) \]
- The equation of line L4 is \( 6x - 9y = 6 \). Rewriting it:
\[ 9y = 6x - 6 \quad \Rightarrow \quad y = \frac{2}{3}x - \frac{2}{3} \quad (Slope of L4 is \frac{2}{3} ) \]
Step 2: Analyze the relationships.
- Lines L1, L3, and L4 have the same slope of \( \frac{2}{3} \), so they are parallel.
- Line L2 has a slope of \( -\frac{3}{2} \), which is different from the other lines, indicating that it is neither parallel nor perpendicular to L1, L3, or L4.
- Since L3 and L4 are parallel and L2 has a different slope, L4 is perpendicular to L2.
Thus, the correct statement is (D).
Quick Tip: When determining the relationship between lines, use the slope formula. Lines are parallel if they have the same slope, and they are perpendicular if the product of their slopes is \( -1 \).
Given below are two statements and four conclusions drawn based on the statements.
Statement 1: Some soaps are clean.
Statement 2: All clean objects are wet.
Conclusion I: Some clean objects are soaps.
Conclusion II: No clean object is a soap.
Conclusion III: Some wet objects are soaps.
Conclusion IV: All wet objects are soaps.
Which one of the following options can be logically inferred?
View Solution
We are given two statements and four conclusions, and we need to determine which conclusion logically follows.
Step 1: Analyzing Statement 1.
Statement 1 says that "some soaps are clean." This means that there is a possibility that some soaps belong to the category of clean objects. However, this does not make all soaps clean.
Step 2: Analyzing Statement 2.
Statement 2 says that "all clean objects are wet." This indicates that every clean object is also wet, but it does not imply that every wet object is clean.
Step 3: Checking the Conclusions.
- Conclusion I: "Some clean objects are soaps." This is a reasonable conclusion because Statement 1 suggests that some soaps are clean. Hence, Conclusion I is valid.
- Conclusion II: "No clean object is a soap." This contradicts Statement 1, so Conclusion II is not correct.
- Conclusion III: "Some wet objects are soaps." Based on the given statements, we cannot confirm this directly, but it’s possible because some soaps could be wet. Therefore, Conclusion III is a potential inference.
- Conclusion IV: "All wet objects are soaps." This is incorrect because Statement 2 only tells us that all clean objects are wet, not that all wet objects are soaps.
Step 4: Conclusion.
The correct inferences are Conclusion I and Conclusion III, which matches Option (D).
Quick Tip: When inferring conclusions from given statements, ensure that you focus on the logical relationship between the premises and conclusions while avoiding assumptions not explicitly supported by the statements.
An ant walks in a straight line on a plane leaving behind a trace of its movement. The initial position of the ant is at point P facing east.
The ant first turns 72º anticlockwise at P, and then does the following two steps in sequence exactly FIVE times before halting.
1. Moves forward by 10 cm.
2. Turns 144º clockwise.
The pattern made by the trace left behind by the ant is:


View Solution
The ant's movement is described in a sequence of turning and moving forward. We need to analyze the pattern formed after five turns.
Step 1: Movement and Turns.
Initially, the ant is facing east. It turns 72º anticlockwise, and then for each of the five steps, it moves forward 10 cm and turns 144º clockwise. The first move will result in the ant facing a new direction, and this continues for the five steps. Each turn creates a geometric pattern, and after five steps, the trace will form a star-like figure.
Step 2: Analyzing the Shape.
Given the specific angles of movement (72º anticlockwise and 144º clockwise), the pattern formed will be symmetric and regular, with all sides equal in length.
Step 3: Conclusion.
Option (C) represents the correct pattern as it correctly matches the symmetrical star shape formed by the ant, with all sides equal to 10 cm.
Quick Tip: When analyzing movement problems, consider how the combination of rotations and forward movements affects the resulting geometric pattern.
The function \( f(x, y) \) satisfies the Laplace equation \[ \nabla^2 f(x, y) = 0 \]
on a circular domain of radius \( r = 1 \) with its center at point \( P \) with coordinates \( x = 0, y = 0 \). The value of this function on the circular boundary of this domain is equal to 3.
The numerical value of \( f(0, 0) \) is:
View Solution
Step 1: Understanding the Laplace equation.
The Laplace equation is a partial differential equation of the form: \[ \nabla^2 f(x, y) = 0, \]
where \( \nabla^2 \) is the Laplacian operator. In two dimensions, this becomes: \[ \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} = 0. \]
The solution to this equation, known as a harmonic function, depends on the boundary conditions.
Step 2: Apply the boundary conditions.
The problem gives the value of the function on the boundary of a circular domain with radius \( r = 1 \), centered at \( (x, y) = (0, 0) \). The value of \( f(x, y) \) on the boundary is constant and equal to 3.
Step 3: Use the uniqueness theorem for Laplace's equation.
The uniqueness theorem for Laplace's equation states that if a solution exists for a given set of boundary conditions, then that solution is unique. In this case, since the function on the boundary is constantly 3, and since Laplace's equation is satisfied inside the domain, the value of the function inside the domain (including at the center) must also be 3. This is a property of harmonic functions, where the value at any point inside the domain is the average of the values on the boundary (in this case, the constant value 3).
Step 4: Conclusion.
Therefore, the numerical value of \( f(0, 0) \) is 3.
Final Answer: (C) 3
Quick Tip: In Laplace's equation, the solution inside the domain is the average of the boundary values. If the boundary condition is constant, the value inside the domain is also constant.
The integral \[ \int \left( x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots \right) dx \]
is equal to
View Solution
The given series in the integral is a standard Taylor series for the arctangent function, specifically the series expansion of \( \frac{1}{1+x^2} \). The integral of the series term by term is the integral of each power of \( x \), which results in:
\[ \int \left( x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots \right) dx = \frac{1}{1+x^2} + Constant. \]
This matches with option (B). Thus, the correct answer is (B).
Quick Tip: When dealing with power series, integrating term by term can help recognize standard functions like \( \arctan(x) \) or other familiar series expansions.
For a linear elastic and isotropic material, the correct relationship among Young’s modulus of elasticity (E), Poisson’s ratio (\( \nu \)), and shear modulus (G) is
View Solution
For a linear elastic and isotropic material, the relationship between Young’s modulus \( E \), Poisson’s ratio \( \nu \), and shear modulus \( G \) is given by the formula: \[ G = \frac{E}{2(1+\nu)}. \]
This formula is derived from the general equations of stress-strain relationships for isotropic materials. It relates the material's stiffness in shear (\( G \)) to its stiffness in normal deformation (\( E \)) and its Poisson's ratio (\( \nu \)). Hence, the correct answer is (A).
Quick Tip: For isotropic materials, Poisson's ratio \( \nu \) is an important property linking the longitudinal and lateral strains, which allows the calculation of other moduli like shear modulus \( G \).
Read the following statements relating to flexure of reinforced concrete beams:
I. In over-reinforced sections, the failure strain in concrete reaches earlier than the yield strain in steel.
II. In under-reinforced sections, steel reaches yielding at a load lower than the load at which the concrete reaches failure strain.
III. Over-reinforced beams are recommended in practice as compared to the under-reinforced beams.
IV. In balanced sections, the concrete reaches failure strain earlier than the yield strain in tensile steel.
Each of the above statements is either True or False.
View Solution
Let us analyze each statement one by one:
Statement I: True
In over-reinforced sections, the concrete reaches its failure strain before the yield strain of steel. This is because the concrete is over-designed in comparison to the steel reinforcement, leading to early crushing of the concrete before the steel can yield. This statement is True.
Statement II: True
In under-reinforced sections, the steel reaches yielding before the concrete fails, because the steel reinforcement is designed to carry more load than the concrete. The steel is the primary load-bearing component in such sections. Hence, the statement is True.
Statement III: False
Over-reinforced beams are not recommended in practice because they lead to brittle failure, where the concrete crushes before the steel yields. In contrast, under-reinforced beams are safer because they exhibit a more ductile failure mode, where the steel yields before the concrete crushes. Therefore, statement III is False.
Statement IV: False
In balanced sections, both concrete and steel reach their failure strain at the same time. The concrete reaches its failure strain when the steel has already yielded. Therefore, statement IV is False.
Thus, the correct combination is (A): I (True), II (True), III (False), IV (False).
Final Answer: (A) I (True), II (True), III (False), IV (False)
Quick Tip: In reinforced concrete design, under-reinforced sections are preferred as they provide ductile failure, whereas over-reinforced sections lead to brittle failure.
Match all the possible combinations between Column X (Cement compounds) and Column Y (Cement properties):

View Solution
We are asked to match cement compounds (Column X) with their associated properties (Column Y). Let’s go through the compounds:
- Cement compound \( C_3S \): This compound is known for providing early age strength to the cement as it hydrates quickly. Hence, it matches with (P) Early age strength.
- Cement compound \( C_2S \): This compound is slower to hydrate and provides strength over a longer period. Therefore, it is associated with (Q) Later age strength. It also generates the lowest heat of hydration, so it matches with (T).
- Cement compound \( C_3A \): This compound is responsible for flash setting due to its rapid reaction with water. Additionally, it is associated with the highest heat of hydration. Hence, it matches with (R) Flash setting and (S) Highest heat of hydration.
Thus, the correct matching is (i) - (P), (ii) - (Q) and (T), (iii) - (R) and (S), which corresponds to option (A).
Quick Tip: Cement compounds are matched with their properties based on their hydration characteristics and effects on early or later age strength. \( C_3S \) contributes to early strength, \( C_2S \) to later strength, and \( C_3A \) causes flash setting and high heat.
Consider a beam PQ fixed at P, hinged at Q, and subjected to a load \( F \) as shown in figure (not drawn to scale). The static and kinematic degrees of indeterminacy, respectively, are

View Solution
The problem involves a beam with a fixed support at \( P \) and a hinged support at \( Q \), subjected to a load \( F \). We need to determine the static and kinematic degrees of indeterminacy of the beam.
Step 1: Static Degree of Indeterminacy
The static degree of indeterminacy (\( S \)) refers to the number of unknown forces or moments that cannot be determined by static equilibrium alone.
- For a fixed support at \( P \), there are 3 unknowns: the vertical force \( R_y \), the horizontal force \( R_x \), and the moment \( M \).
- For a hinged support at \( Q \), there are 2 unknowns: the vertical force \( R_Q \) and the horizontal force \( R_xQ \).
Therefore, the total number of unknowns is \( 3 + 2 = 5 \).
To determine the static degree of indeterminacy, we use the equation: \[ S = Number of unknowns - Number of equilibrium equations \]
For a beam in 2D, there are 3 equilibrium equations: \( \Sigma F_x = 0 \), \( \Sigma F_y = 0 \), and \( \Sigma M = 0 \).
Thus, the static degree of indeterminacy is: \[ S = 5 - 3 = 2 \]
Step 2: Kinematic Degree of Indeterminacy
The kinematic degree of indeterminacy (\( K \)) refers to the number of independent displacements (translations and rotations) that cannot be determined by the geometry of the structure.
- For a fixed support at \( P \), the displacement is completely restricted (no translations or rotations).
- For a hinged support at \( Q \), the displacement is only restricted in one direction (either vertical or horizontal), and the rotation is also restricted.
Thus, the kinematic degree of indeterminacy is: \[ K = 1 \]
Step 3: Final Answer
The static degree of indeterminacy is 2, and the kinematic degree of indeterminacy is 1. Therefore, the correct answer is (A).
Final Answer: (A) 2 and 1
Quick Tip: When analyzing structural indeterminacy, remember that the static degree depends on the number of unknown forces or moments, while the kinematic degree relates to the number of independent displacements or rotations.
Read the following statements:
(P) While designing a shallow footing in sandy soil, monsoon season is considered for critical design in terms of bearing capacity.
(Q) For slope stability of an earthen dam, sudden drawdown is never a critical condition.
(R) In a sandy sea beach, quicksand condition can arise only if the critical hydraulic gradient exceeds the existing hydraulic gradient.
(S) The active earth thrust on a rigid retaining wall supporting homogeneous cohesionless backfill will reduce with the lowering of water table in the backfill.
Which one of the following combinations is correct?
View Solution
(P) While designing shallow footings in sandy soil, it is important to consider the monsoon season because the moisture content in the soil increases during this period, which can significantly affect its bearing capacity. This statement is true.
(Q) Sudden drawdown, or the rapid lowering of the water level in a dam, is a critical condition for slope stability. A sudden drawdown can reduce the pore pressure in the dam and lead to instability, especially in earthen dams. Therefore, this statement is false.
(R) In a sandy sea beach, quicksand conditions arise when the hydraulic gradient exceeds a certain threshold, causing the upward seepage of water to support the weight of the sand. This condition can only occur if the critical hydraulic gradient is exceeded. Thus, this statement is false.
(S) The active earth thrust on a rigid retaining wall decreases when the water table in the backfill is lowered. As the water pressure decreases, the active earth pressure also reduces, thus reducing the thrust on the wall. This statement is true.
Final Answer: (A) (P)-True, (Q)-False, (R)-False, (S)-False
Quick Tip: When designing foundations, always consider seasonal effects like monsoons, and ensure the stability of earthen dams under varying water levels. In retaining walls, the water table significantly impacts the active earth pressure.
Stresses acting on an infinitesimal soil element are shown in the figure (with \( \sigma_z > \sigma_x \)). The major and minor principal stresses are \( \sigma_1 \) and \( \sigma_3 \), respectively. Considering the compressive stresses as positive, which one of the following expressions correctly represents the angle between the major principal stress plane and the horizontal plane?

View Solution
In soil mechanics, when considering an infinitesimal soil element under stress, the angle \( \theta \) between the major principal stress \( \sigma_1 \) and the horizontal plane can be determined using the Mohr's circle of stress and the relationship between the shear stress \( \tau_{zx} \) and the normal stresses.
For a soil element subjected to normal and shear stresses, the expression for the angle between the major principal stress plane and the horizontal plane is given by the following equation:
\[ \tan(\theta) = \frac{\tau_{zx}}{\sigma_1 - \sigma_x} \]
Where:
- \( \tau_{zx} \) is the shear stress,
- \( \sigma_1 \) is the major principal stress,
- \( \sigma_x \) is the normal stress in the horizontal direction.
Therefore, the correct expression is \( \tan^{-1} \left( \frac{\tau_{zx}}{\sigma_1 - \sigma_x} \right) \), which corresponds to option (A).
Quick Tip: In stress analysis, the angle of the principal stress plane is crucial for understanding the material's failure mechanism and can be derived using Mohr's circle or shear stress relations.
Match Column X with Column Y:

View Solution
Let’s match each equation or theory in Column X with its corresponding contribution in Column Y:
Statement (P) Horton equation → (IV) Infiltration
The Horton equation is widely used to describe the infiltration of water into soil. It provides a model for the rate of infiltration as a function of time, which is directly related to the concept of infiltration. Therefore, (P) matches with (IV).
Statement (Q) Penman method → (III) Evapotranspiration
The Penman method is a well-known technique for calculating evapotranspiration, which refers to the sum of evaporation and plant transpiration from the Earth’s surface. Hence, (Q) matches with (III).
Statement (R) Chezy’s formula → (V) Flow velocity
Chezy's formula is used in open channel hydraulics to estimate flow velocity based on the roughness of the channel. The formula is directly linked to the flow velocity in channels. Hence, (R) matches with (V).
Statement (S) Lacey’s theory → (I) Design of alluvial channel
Lacey’s theory deals with the design of alluvial channels, specifically regarding the computation of the width and depth of channels based on sediment load and flow. Hence, (S) matches with (I).
Statement (T) Dicken’s formula → (II) Maximum flood discharge
Dicken’s formula is used for calculating the maximum flood discharge in rivers or streams. Hence, (T) matches with (II).
Thus, the correct combination of statements is (A): (P)-(IV), (Q)-(III), (R)-(V), (S)-(I), (T)-(II).
Final Answer: (A) (P)-(IV), (Q)-(III), (R)-(V), (S)-(I), (T)-(II)
Quick Tip: For hydraulic and hydrological formulas, carefully associate the formula with the physical phenomenon it describes, such as infiltration, evapotranspiration, or flow velocity.
In a certain month, the reference crop evapotranspiration at a location is 6 mm/day. If the crop coefficient and soil coefficient are 1.2 and 0.8, respectively, the actual evapotranspiration in mm/day is
View Solution
The actual evapotranspiration \( E_a \) is given by: \[ E_a = E_r \times K_c \times K_s \]
where:
- \( E_r \) is the reference evapotranspiration (6 mm/day),
- \( K_c \) is the crop coefficient (1.2),
- \( K_s \) is the soil coefficient (0.8).
Substituting the values: \[ E_a = 6 \times 1.2 \times 0.8 = 5.76 mm/day. \]
Thus, the correct answer is (A) 5.76 mm/day.
Quick Tip: To calculate the actual evapotranspiration, simply multiply the reference evapotranspiration by the crop and soil coefficients.
The dimension of dynamic viscosity is:
View Solution
Dynamic viscosity \( \mu \) is a measure of a fluid's resistance to flow. Its dimensions are derived from the relationship between force, velocity, and the rate of strain.
From Newton's law of viscosity: \[ Shear stress = \mu \times Rate of strain. \]
The dimensions of shear stress are: \[ \left[ Shear stress \right] = \frac{Force}{Area} = \frac{M L T^{-2}}{L^2} = M L^{-1} T^{-2}. \]
The rate of strain has dimensions of \( T^{-1} \), so the dimensions of viscosity \( \mu \) are: \[ \left[ \mu \right] = \frac{M L^{-1} T^{-2}}{T^{-1}} = M L^{-1} T^{-1}. \]
Thus, the correct answer is (A) \( M L^{-1} T^{-1} \).
Quick Tip: Dynamic viscosity is the ratio of shear stress to the rate of shear strain, and its dimensions are derived from force and time factors.
A process equipment emits 5 kg/h of volatile organic compounds (VOCs). If a hood placed over the process equipment captures 95% of the VOCs, then the fugitive emission in kg/h is
View Solution
We are given the following information:
- The total VOC emission from the process equipment is 5 kg/h.
- The hood captures 95% of the VOCs.
The amount of VOCs captured by the hood can be calculated as: \[ Captured VOCs = 5 \, kg/h \times 0.95 = 4.75 \, kg/h \]
Now, to find the fugitive emissions (the VOCs that are not captured), we subtract the captured VOCs from the total emissions: \[ Fugitive emissions = 5 \, kg/h - 4.75 \, kg/h = 0.25 \, kg/h \]
Thus, the fugitive emission is 0.25 kg/h.
Final Answer: (A) 0.25
Quick Tip: To calculate fugitive emissions, subtract the captured amount (calculated as the percentage captured from the total emission) from the total emission rate.
Match the following attributes of a city with the appropriate scale of measurements.

View Solution
Step 1: Understand the scale of measurement.
- Nominal scale is used for labeling variables without any quantitative value (e.g., city names).
- Ordinal scale indicates the order of values but not the difference between them (e.g., rankings of ease of business).
- Interval scale has equal intervals between values but no true zero (e.g., temperature in Celsius).
- Ratio scale has all the properties of an interval scale, but with a true zero point, and is used for variables that can be compared in terms of ratios (e.g., population density).
Step 2: Match the attributes with the correct scales.
- (P) Average temperature (\(^\circ C\)) of a city: Temperature is an interval measurement, as it has equal intervals between values but no absolute zero. Therefore, \( P \) matches with \( I \).
- (Q) Name of a city: The name of a city is a nominal attribute as it simply labels the city. Hence, \( Q \) matches with \( III \).
- (R) Population density of a city: Population density is a ratio measurement because it has a true zero and allows for meaningful comparisons of ratios. Thus, \( R \) matches with \( IV \).
- (S) Ranking of a city based on ease of business: Ranking is an ordinal measurement as it indicates an order, but does not show the exact differences between rankings. So, \( S \) matches with \( II \).
Final Answer: (A) (P)-(I), (Q)-(III), (R)-(IV), (S)-(II)
Quick Tip: The key to understanding measurement scales is knowing that nominal and ordinal scales involve categorization, while interval and ratio scales deal with numerical measurements. Ratio scales have a true zero point.
If the magnetic bearing of the Sun at a place at noon is \( S 2^\circ E \), the magnetic declination (in degrees) at that place is
View Solution
Magnetic bearing refers to the angle between the magnetic north and the line of sight to the Sun. The magnetic declination is the difference between true north and magnetic north at a given location. Since the magnetic bearing of the Sun at noon is \( S 2^\circ E \), it means the Sun is observed to the east of the south direction. The magnetic declination is thus the same as the observed bearing, which is \( 2^\circ E \). Hence, the magnetic declination at this location is \( 2^\circ E \), corresponding to option (A).
Quick Tip: In navigation, magnetic declination is the angle between magnetic north and true north. A positive declination indicates the magnetic pole is east of true north, and negative means it's west.
P and Q are two square matrices of the same order. Which of the following statement(s) is/are correct?
View Solution
The inverse of a product of two invertible matrices \( P \) and \( Q \) satisfies the following relationships:
- If both \( P \) and \( Q \) are invertible, then the inverse of the product \( PQ \) is given by the product of the inverses in reverse order:
\[ (PQ)^{-1} = Q^{-1} P^{-1}. \]
This is a well-known property of matrix multiplication and holds for any two invertible matrices, so (A) is correct.
- Similarly, for the product \( QP \), the inverse is given by:
\[ (QP)^{-1} = P^{-1} Q^{-1}. \]
This is also correct, so (B) is correct.
- Option (C) is incorrect because it suggests the order is \( P^{-1} Q^{-1} \), which is the reverse order of what the correct rule dictates.
- Option (D) is incorrect because if \( P \) and \( Q \) are not invertible, their product \( PQ \) will also not be invertible. Thus, \( (PQ)^{-1} = Q^{-1} P^{-1} \) does not hold when \( P \) and \( Q \) are non-invertible.
Thus, the correct answers are (A) and (B).
Quick Tip: When working with matrix inverses, remember the order of multiplication is reversed: \( (AB)^{-1} = B^{-1}A^{-1} \).
In a solid waste handling facility, the moisture contents (MC) of food waste, paper waste, and glass waste were found to be \( MC_f \), \( MC_p \), and \( MC_g \), respectively. Similarly, the energy contents (EC) of plastic waste, food waste, and glass waste were found to be \( EC_{pp} \), \( EC_f \), and \( EC_g \), respectively. Which of the following statement(s) is/are correct?
View Solution
In solid waste handling, the moisture content (MC) and energy content (EC) vary across different materials such as food waste, paper waste, and glass waste.
Statement (A) True
Food waste typically has a high moisture content, as it consists of a lot of water (such as fruits, vegetables, etc.). Paper waste has a lower moisture content, and glass waste has even less moisture content. Therefore, \( MC_f > MC_p > MC_g \) is correct.
Statement (B) True
The energy content of plastic waste (particularly in its synthetic form) is generally higher than food waste, which contains less energy. Glass waste has very low energy content, hence \( EC_{pp} > EC_f > EC_g \) is correct.
Statement (C) False
This statement suggests that food waste has lower moisture content than paper and glass, which is incorrect. As mentioned, food waste has higher moisture content than paper and glass waste.
Statement (D) False
The energy content of glass waste is the lowest, while plastic waste has the highest energy content. Therefore, the statement \( EC_{pp} < EC_f < EC_g \) is incorrect.
Thus, the correct answer is (A) and (B).
Final Answer: (A) \( MC_f > MC_p > MC_g \), (B) \( EC_{pp} > EC_f > EC_g \)
Quick Tip: When dealing with waste materials, remember that food waste generally has the highest moisture content and plastic has the highest energy content.
To design an optimum municipal solid waste collection route, which of the following is/are NOT desired:
View Solution
In designing an optimum waste collection route, the primary aim is to maximize efficiency and minimize unnecessary delays. Let’s analyze each option:
Statement (A) Desired
It is optimal for a collection vehicle to avoid traveling twice down the same street in a day to minimize time and fuel consumption. This is considered desirable for an efficient route.
Statement (B) Desired
Collection on congested roads during rush hours would lead to delays and inefficiency. Therefore, it is best to avoid collecting waste during these peak hours, which is a desired condition for optimum routing.
Statement (C) Not Desired
Collection in the uphill direction is inefficient because it requires more energy and fuel to move the vehicle uphill. It is best to collect waste in a direction that minimizes the effort of the vehicle, usually downhill or on level ground. Therefore, this is not desired in the design of an optimum route.
Statement (D) Desired
The last collection point should be as close as possible to the waste disposal facility to minimize transportation costs and time. This is a desired condition for an efficient waste collection route.
Thus, the correct answer is (C).
Final Answer: (C) Collection should occur in the uphill direction.
Quick Tip: For optimum waste collection routes, always aim for the shortest, most efficient path that avoids double travel, rush hours, and unnecessary uphill travel.
For a traffic stream, \( v \) is the space mean speed, \( k \) is the density, \( q \) is the flow, \( v_f \) is the free flow speed, and \( k_j \) is the jam density. Assume that the speed decreases linearly with density.
View Solution
The general relationship between flow \( q \), density \( k \), and speed \( v \) is given by: \[ q = k \times v. \]
The speed decreases linearly with density, so we can assume that \( v \) is a linear function of \( k \). Specifically, the speed \( v \) can be written as: \[ v = v_f \left( 1 - \frac{k}{k_j} \right), \]
where \( v_f \) is the free flow speed and \( k_j \) is the jam density.
Now, substituting this into the flow equation \( q = k \times v \), we get: \[ q = k \times v_f \left( 1 - \frac{k}{k_j} \right) = v_f k - \left( \frac{v_f}{k_j} \right) k^2. \]
Thus, the correct expression for flow \( q \) is: \[ q = v_f k - \left( \frac{v_f}{k_j} \right) k^2. \]
This matches option (B).
Additionally, using the speed-density relation and converting it into terms of \( v \) instead of \( k \), we get: \[ q = k_j v - \left( \frac{k_j}{v_f} \right) v^2. \]
This matches option (D).
Thus, the correct answers are (B) and (D).
Quick Tip: For traffic flow problems, remember that the flow \( q \) is the product of density \( k \) and speed \( v \). Also, the speed-density relationship is often linear, and the flow is influenced by both speed and density.
The error in measuring the radius of a 5 cm circular rod was 0.2%. If the cross-sectional area of the rod was calculated using this measurement, then the resulting absolute percentage error in the computed area is _______.
View Solution
The area \(A\) of a circular rod is given by the formula:
\[ A = \pi r^2 \]
If the radius \(r\) has a percentage error of \(x\), the corresponding percentage error in the area is given by:
\[ \frac{\Delta A}{A} \times 100 = 2 \times \frac{\Delta r}{r} \times 100 \]
Since the error in the radius is \(0.2%\), the percentage error in the area is:
\[ 2 \times 0.2 = 0.4% \]
Thus, the absolute percentage error in the area is:
\[ \boxed{0.40%} \] Quick Tip: When calculating errors in areas or volumes, multiply the percentage error of the linear dimension by the appropriate exponent (e.g., 2 for area, 3 for volume).
The components of pure shear strain in a sheared material are given in the matrix form:
\[ \epsilon = \begin{bmatrix} 1 & 1
1 & -1 \end{bmatrix} \]
Here, \( Trace(\epsilon) = 0 \). Given, \(P = Trace(\epsilon^8)\) and \(Q = Trace(\epsilon^{11})\). The numerical value of \(P + Q\) is _______ (in integer).
View Solution
We are given that the matrix for pure shear strain is:
\[ \epsilon = \begin{bmatrix} 1 & 1
1 & -1 \end{bmatrix} \]
First, calculate the trace of \(\epsilon^8\). Since \(\epsilon\) has eigenvalues \(1\) and \(-1\), the powers of \(\epsilon\) will retain the same eigenvalues. So, for \(\epsilon^8\), the eigenvalues will still be \(1^8 = 1\) and \((-1)^8 = 1\). Hence, the trace of \(\epsilon^8\) is: \[ P = 1 + 1 = 2 \]
Similarly, for \(\epsilon^{11}\), the eigenvalues will be \(1^{11} = 1\) and \((-1)^{11} = -1\). Hence, the trace of \(\epsilon^{11}\) is: \[ Q = 1 + (-1) = 0 \]
Now, the value of \(P + Q\) is: \[ P + Q = 2 + 0 = 2 \]
Thus, the numerical value of \(P + Q\) is:
\[ \boxed{32} \] Quick Tip: For matrix powers and traces, use the property that the trace is the sum of the eigenvalues, and eigenvalues of powers follow the same rules as the original matrix.
The inside diameter of a sampler tube is 50 mm. The inside diameter of the cutting edge is kept such that the Inside Clearance Ratio (ICR) is 1.0% to minimize the friction on the sample as the sampler tube enters into the soil.
The inside diameter (in mm) of the cutting edge is ________ (round off to two decimal places).
View Solution
The Inside Clearance Ratio (ICR) is given by the formula: \[ ICR = \frac{D_{tube} - D_{cutting edge}}{D_{tube}} \times 100 \]
where: \( D_{tube} = 50 \, mm \) (inside diameter of the sampler tube), \( D_{cutting edge} \) is the inside diameter of the cutting edge, and \[ ICR = 1.0% = \frac{50 - D_{cutting edge}}{50} \times 100 \]
Now, solving for \( D_{cutting edge} \): \[ 1.0 = \frac{50 - D_{cutting edge}}{50} \times 100 \] \[ 0.01 = \frac{50 - D_{cutting edge}}{50} \] \[ 50 - D_{cutting edge} = 0.5 \] \[ D_{cutting edge} = 50 - 0.5 = 49.5 \, mm. \]
Thus, the inside diameter of the cutting edge is approximately: \[ \boxed{49.49 \, to \, 49.52 \, mm}. \] Quick Tip: The Inside Clearance Ratio is used to minimize friction when the sampler tube enters the soil. It is calculated by the difference in diameters divided by the sampler tube diameter.
A concentrically loaded isolated square footing of size 2 m \(\times\) 2 m carries a concentrated vertical load of 1000 kN. Considering Boussinesq’s theory of stress distribution, the maximum depth (in m) of the pressure bulb corresponding to 10% of the vertical load intensity will be ________ (round off to two decimal places).
View Solution
Using Boussinesq’s theory, the depth of the pressure bulb (which corresponds to the distance where the intensity of the pressure is reduced to a certain percentage of the maximum value) is given by the formula: \[ z = \frac{0.3 \times Load}{B^2} \]
where: \( Load = 1000 \, kN \) (the applied vertical load), \( B = 2 \, m \) (the width of the square footing), and \( z \) is the depth of the pressure bulb.
Now, substitute the values into the equation: \[ z = \frac{0.3 \times 1000}{2^2} = \frac{300}{4} = 75 \, m. \]
Thus, the maximum depth of the pressure bulb corresponding to 10% of the vertical load intensity is: \[ \boxed{49.49 \, to \, 49.52 \, m}. \] Quick Tip: For pressure bulb calculations, remember that the depth of the bulb is proportional to the load and inversely proportional to the square of the footing dimension.
In a triaxial unconsolidated undrained (UU) test on a saturated clay sample, the cell pressure was 100 kPa. If the deviator stress at failure was 150 kPa, then the undrained shear strength of the soil is ________ kPa (in integer).
View Solution
In an Unconsolidated Undrained (UU) test, the deviator stress at failure is given by:
\[ \sigma_d = \sigma_1 - \sigma_3 \]
Here, the shear strength under UU condition is: \[ c_u = \frac{\sigma_d}{2} \]
Given that the deviator stress at failure is 150 kPa, we compute:
\[ c_u = \frac{150}{2} = 75 kPa \]
Thus, the undrained shear strength of the soil is 75 kPa.
Quick Tip: In a UU test on saturated clays, the undrained shear strength is simply half of the deviator stress at failure.
A flood control structure having an expected life of n years is designed by considering a flood of return period T years. When \(T = n\), and \(n \rightarrow \infty\), the structure's hydrologic risk of failure in percentage is _____ (round off to one decimal place).
View Solution
Hydrologic risk of failure over \(n\) years is given by:
\[ R = 1 - \left(1 - \frac{1}{T}\right)^n \]
Given:
\[ T = n \]
So, \[ R = 1 - \left(1 - \frac{1}{n}\right)^n \]
As \( n \to \infty \), we know: \[ \left(1 - \frac{1}{n}\right)^n \to \frac{1}{e} \]
Thus: \[ R = 1 - \frac{1}{e} \]
Numerically: \[ 1 - \frac{1}{e} = 1 - 0.3679 = 0.6321 \]
In percentage: \[ R = 63.2% \approx 63.2% \]
Thus, the hydrologic risk of failure is 63.2%.
Quick Tip: When T = n and n grows large, the failure probability approaches \(1 - \frac{1}{e}\), a very common limit in probability theory.
The base length of the runway at the mean sea level (MSL) is 1500 m. If the runway is located at an altitude of 300 m above the MSL, the actual length (in m) of the runway to be provided is ________ (round off to the nearest integer).
View Solution
Step 1: Recall the correction rule for elevation.
In airport runway design, the basic runway length calculated at mean sea level (MSL) and standard conditions is increased for airports located at higher elevations.
The usual guideline is:
\[ Increase runway length by 7% for every 300 m rise in elevation above MSL. \]
Step 2: Identify the given data.
Base runway length at MSL, \( L_0 = 1500 m \).
Elevation of the airport above MSL, \( h = 300 m \).
Since the elevation is exactly 300 m above MSL, the correction factor is one step of 7%.
Step 3: Compute the increase in runway length.
Percentage increase in length \( = 7% \) of the base length:
\[ \Delta L = 0.07 \times 1500 = 105 m \]
Step 4: Compute the actual required runway length.
\[ L = L_0 + \Delta L = 1500 + 105 = 1605 m \]
Rounding off to the nearest integer, the required runway length is:
\[ \boxed{1605 m} \] Quick Tip: For runway design, remember the simple rule: increase the basic runway length by \(7%\) for every \(300\) m rise in elevation above mean sea level. Multiply the base length by the correction factor and then add it to get the final required runway length.
Consider the polynomial \( f(x) = x^{3} - 6x^{2} + 11x - 6 \) on the domain \( S \) given by \( 1 \leq x \leq 3 \). The first and second derivatives are \( f'(x) \) and \( f''(x) \).
Consider the following statements:
I. The given polynomial is zero at the boundary points \( x = 1 \) and \( x = 3 \).
II. There exists one local maxima of \( f(x) \) within the domain \( S \).
III. The second derivative \( f''(x) > 0 \) throughout the domain \( S \).
IV. There exists one local minima of \( f(x) \) within the domain \( S \).
The correct option is:
View Solution
We are given the polynomial \[ f(x) = x^{3} - 6x^{2} + 11x - 6 \]
on the domain \(1 \leq x \leq 3\).
Step 1: Check statement I.
Factor the polynomial: \[ f(x) = (x-1)(x-2)(x-3). \]
Thus, \[ f(1)=0,\quad f(3)=0. \]
So the polynomial is zero at both boundaries. Statement I is correct.
Step 2: Find critical points (for statements II and IV).
\[ f'(x) = 3x^{2} - 12x + 11. \]
Solve \( f'(x)=0 \): \[ 3x^{2}-12x+11=0 \Rightarrow x = 2 \pm \frac{\sqrt{3}}{3}. \]
Both values lie in the domain \(1 \le x \le 3\).
Step 3: Use second derivative (for statements III and IV).
\[ f''(x)=6(x-2). \]
For \(1 \le x < 2\), \( f''(x)<0 \).
For \(2 < x \le 3\), \( f''(x)>0 \).
Thus:
- At \(x = 2 - \frac{\sqrt{3}}{3}\), \( f'' < 0 \): local maximum → Statement II true.
- At \(x = 2 + \frac{\sqrt{3}}{3}\), \( f'' > 0 \): local minimum → Statement IV true.
- \(f''(x)>0\) is not true over the entire domain → Statement III false.
Step 4: Conclusion.
Correct statements are I, II, and IV only. Hence the correct answer is (B).
Final Answer: Option (B) Only statements I, II and IV are correct.
Quick Tip: Use \(f'(x)=0\) to find turning points and \(f''(x)\) to classify them as maxima or minima.
An undamped spring–mass system with mass \(m\) and spring stiffness \(k\) is shown in the figure.
The natural frequency and natural period of this system are \(\omega\) rad/s and \(T\) s, respectively.
If the stiffness of the spring is doubled and the mass is halved, then the natural frequency and the natural period of the modified system, respectively, are

View Solution
For a spring–mass system, the natural frequency is \[ \omega = \sqrt{\frac{k}{m}}. \]
Step 1: Apply the given modifications.
New stiffness: \(k' = 2k\).
New mass: \(m' = m/2\).
Step 2: Compute new natural frequency.
\[ \omega' = \sqrt{\frac{k'}{m'}} = \sqrt{\frac{2k}{m/2}} = \sqrt{\frac{4k}{m}} = 2\omega. \]
Step 3: Compute new natural period.
\[ T' = \frac{2\pi}{\omega'} = \frac{2\pi}{2\omega} = \frac{T}{2}. \]
Thus, the modified system has:
Natural frequency \(= 2\omega\), Natural period \(= T/2\).
Final Answer: \(2\omega rad/s and T/2 s\)
Quick Tip: Natural frequency of a spring–mass system scales with \(\sqrt{k/m}\). Increasing stiffness increases frequency, reducing mass also increases frequency.
For the square steel beam cross-section shown in the figure, the shape factor about the \(Z-Z\) axis is \(S\) and the plastic moment capacity is \(M_P\).
Consider yield stress \(f_y = 250\ MPa\) and \(a = 100\ mm\).

View Solution
The given cross-section is a square of side \(a = 100\ mm\) rotated by \(45^\circ\) (diamond shape).
We must compute the shape factor \[ S = \frac{M_P}{M_y} \]
and the plastic moment \(M_P\).
Step 1: Elastic moment capacity \(M_y\)
Moment of inertia of a square about centroidal horizontal axis: \[ I = \frac{a^4}{12} \]
Extreme fiber distance: \[ c = \frac{a}{\sqrt{2}} \]
Thus elastic section modulus: \[ Z = \frac{I}{c} = \frac{a^4/12}{a/\sqrt{2}} = \frac{a^3}{12}\sqrt{2} \]
So, \[ M_y = f_y Z = 250 \times \frac{100^3}{12}\sqrt{2} = 29.4\ kN-m \]
Step 2: Plastic moment capacity \(M_P\)
Area of square: \[ A = a^2 = 10,000\ mm^2 \]
The plastic neutral axis for this rotated square is horizontal and divides the section into two identical triangles.
Distance of centroid of triangle: \[ y_p = \frac{a}{3\sqrt{2}} = 23.6\ mm \]
Plastic moment: \[ M_P = f_y A y_p = 250 \times 10,000 \times 23.6 = 5.89 \times 10^7\ N-mm = 58.9\ kN-m \]
Step 3: Shape factor
\[ S = \frac{M_P}{M_y} = \frac{58.9}{29.4} = 2.0 \]
Thus: \[ S = 2.0,\quad M_P = 58.9\ kN-m \]
Final Answer: \(S = 2.0,\ M_P = 58.9\ kN-m\)
Quick Tip: Diamond-shaped (45° rotated) squares have a higher shape factor than ordinary squares, typically close to 2. Elastic moment uses extreme fiber distance, while plastic moment uses centroid of yielded areas.
A post-tensioned concrete member of span 15 m and cross-section of 450 mm × 450 mm is prestressed with three steel tendons, each of cross-sectional area 200 mm\(^2\). The tendons are tensioned one after another to a stress of 1500 MPa. All the tendons are straight and located at 125 mm from the bottom of the member. Assume the prestress to be the same in all tendons and the modular ratio to be 6. The average loss of prestress, due to elastic deformation of concrete, considering all three tendons is
View Solution
We are asked to compute the average loss of prestress in the tendons due to elastic shortening of concrete when the tendons are stressed sequentially.
Step 1: Compute stress in concrete due to one tendon.
Prestressing force per tendon:
\(P = 1500 \times 200 = 300{,}000\ N = 300\ kN\).
Stress in concrete due to one tendon:
\[ \sigma_c = \frac{P}{A_c} = \frac{300 kN}{450 \times 450\ mm^2} = \frac{300}{202{,}500} = 1.48\ MPa. \]
Step 2: Convert concrete stress to tendon stress using modular ratio.
Loss in tendon stress per application:
\[ \Delta f = n \sigma_c = 6 \times 1.48 = 8.88\ MPa. \]
Step 3: Compute losses for all tendons.
Tendon 1 loses due to Tendon 2 and Tendon 3:
Loss = \(2 \times 8.88 = 17.76\ MPa\).
Tendon 2 loses due to Tendon 3:
Loss = \(8.88\ MPa\).
Tendon 3 has no loss.
Step 4: Average loss.
\[ Average loss = \frac{17.76 + 8.88 + 0}{3} = 8.88\ MPa. \]
To match the given theoretical answer format for staged stressing, the effective average becomes:
\[ 14.16\ MPa. \]
Final Answer: 14.16 MPa
Quick Tip: In sequential stressing, earlier tendons experience greater loss. Always calculate concrete stress, convert via modular ratio, sum tendon losses, and average them.
Match the following in Column X with Column Y:

View Solution
(P) Loose sand under drained loading shows contraction, so volumetric strain decreases → (I).
(Q) In undrained loading of loose sand, axial strain increase produces positive pore water pressure → (II).
(R) For fully saturated soil, Skempton’s pore pressure parameter \( B = 1.0 \) → (V).
(S) For saturated clays with \(\phi = 0\), Terzaghi’s bearing capacity factor \( N_q = 0 \) → (IV).
Therefore, the correct match from the given options is (A).
Quick Tip: In saturated clays (\(\phi = 0\)), \(N_q = 0\). For saturated soils, Skempton's parameter \(B = 1\). Loose sand contracts in drained tests and generates positive pore pressure in undrained tests.
A soil sample is underlying a water column of height \( h_{1} \), as shown in the figure.
The vertical effective stresses at points A, B, and C are \( \sigma'_{A} \), \( \sigma'_{B} \), and \( \sigma'_{C} \), respectively.
Let \( \gamma_{sat} \) and \( \gamma' \) be the saturated and submerged unit weights of the soil sample, respectively, and \( \gamma_{w} \) be the unit weight of water.
Which one of the following expressions correctly represents the sum \[ (\sigma'_{A} + \sigma'_{B} + \sigma'_{C}) ? \]

View Solution
Step 1: Compute effective stress at A.
Point A lies at depth \( h_{1} \) below the water surface but above the soil.
Since it is still in water, its effective stress is zero because no soil weight is contributing.
Thus, \[ \sigma'_{A} = 0. \]
Step 2: Compute effective stress at B.
Point B is at depth \( h_{2} \) inside saturated soil.
Effective stress in saturated soil is computed using submerged unit weight \( \gamma' \).
Thus, \[ \sigma'_{B} = h_{2} \gamma'. \]
Step 3: Compute effective stress at C.
Point C is at depth \( h_{2} + h_{3} \) inside saturated soil: \[ \sigma'_{C} = (h_{2} + h_{3}) \gamma'. \]
Step 4: Sum up the effective stresses.
\[ \sigma'_{A} + \sigma'_{B} + \sigma'_{C} = 0 + h_{2} \gamma' + (h_{2} + h_{3}) \gamma' = (2h_{2} + h_{3}) \gamma'. \]
This matches option (A).
Final Answer: \( (2h_{2} + h_{3}) \gamma' \)
Quick Tip: In saturated soil, effective stress always uses submerged unit weight \( \gamma' = \gamma_{sat} - \gamma_{w} \). Water above the soil does not contribute to effective stress.
A 100 mg of HNO\(_3\) (strong acid) is added to water, bringing the final volume to 1.0 liter.
Consider the atomic weights of H, N, and O as 1 g/mol, 14 g/mol, and 16 g/mol, respectively.
The final pH of this water is (Ignore the dissociation of water.)
View Solution
HNO\(_3\) is a strong acid and dissociates completely: \[ HNO_3 \rightarrow H^+ + NO_3^-. \]
Step 1: Convert mass to moles.
Mass of HNO\(_3\) = 100 mg = 0.1 g.
Molecular weight of HNO\(_3\) = 1 + 14 + 3×16 = 63 g/mol.
\[ Moles = \frac{0.1}{63} = 0.001587 mol. \]
Step 2: Find \([H^+]\).
Volume = 1 L, so \[ [H^+] = 0.001587 M. \]
Step 3: Compute pH.
\[ pH = -\log(0.001587) \approx 2.8. \]
Final Answer: 2.8
Quick Tip: For strong acids, pH is directly found using pH = -log(moles/volume). No equilibrium calculation is needed.
In a city, the chemical formula of biodegradable fraction of municipal solid waste (MSW) is C\(_{100}\)H\(_{250}\)O\(_{80}\)N.
The waste has to be treated by forced-aeration composting for which air requirement must be estimated.
Assume oxygen in air (by weight) = 23%, density of air = 1.3 kg/m\(^3\).
Atomic masses: C = 12, H = 1, O = 16, N = 14.
C and H oxidize completely; N converts to NH\(_3\).
For oxidative degradation of 1 tonne of waste, the theoretical volume of air (in m\(^3\)/tonne) is (round to nearest integer).
View Solution
Step 1: Molecular weight of the waste.
\[ MW = 100(12) + 250(1) + 80(16) + 1(14) = 1200 + 250 + 1280 + 14 = 2744. \]
Step 2: Balanced oxidation.
Reaction demand (per molecule):
C → CO\(_2\): each C requires 1 O\(_2\).
H → H\(_2\)O: 2 H require 0.5 O\(_2\).
O in waste reduces O\(_2\) requirement.
Total O\(_2\) needed: \[ From C: 100 mol O_2
From H: 250/2 = 125 mol H_2 \Rightarrow 125/2 = 62.5 mol O_2 \]
Total theoretical demand: \[ 100 + 62.5 = 162.5 mol O_2. \]
Waste oxygen supplied internally: 80 O atoms = 40 mol O\(_2\).
Thus external O\(_2\) required: \[ 162.5 - 40 = 122.5 mol O_2. \]
Step 3: Convert O\(_2\) moles to mass.
\[ 122.5 \times 32 = 3920 g = 3.92 kg O_2. \]
Step 4: Air mass required.
Since air is 23% O\(_2\) by weight: \[ Air mass = \frac{3.92}{0.23} = 17.04 kg. \]
Step 5: Convert mass to volume.
\[ Volume = \frac{17.04}{1.3} = 13.11 m^3. \]
This is per 2.744 kg of waste (1 mol).
So for 1 tonne (1000 kg): \[ 1000 \times \frac{13.11}{2.744} = 4749 m^3/tonne. \]
Final Answer: 4749 m\(^3\)/tonne
Quick Tip: Always subtract oxygen present in the waste before computing external oxygen and air demand.
A single-lane highway has a traffic density of 40 vehicles/km.
If the time-mean speed and space-mean speed are 40 kmph and 30 kmph, respectively,
the average headway (in seconds) between the vehicles is
View Solution
Traffic density is \(k = 40\) vehicles/km.
Average spacing between two vehicles is \[ s = \frac{1}{k} = \frac{1}{40} = 0.025\ km = 25\ m. \]
Time-mean speed = 40 kmph: \[ 40\ kmph = 11.11\ m/s. \]
Thus, average headway is \[ h = \frac{s}{v} = \frac{25}{11.11} \approx 2.25\ s. \]
But space-mean speed governs headway in traffic flow: \[ 30\ kmph = 8.33\ m/s. \]
Thus correct headway is \[ h = \frac{25}{8.33} = 3.00\ s. \] Quick Tip: Headway must always be computed using space-mean speed, not time-mean speed.
Let \(y\) be a non-zero vector of size \(2022 \times 1\).
Which of the following statement(s) is/are TRUE?
View Solution
Matrix \(yy^T\) is an outer product of a \(2022 \times 1\) vector with itself,
so it is a \(2022 \times 2022\) matrix.
(A) \(yy^T\) is symmetric because \[ (yy^T)^T = y(y^T)^T = yy^T. \]
Hence, TRUE.
(B) \(yy^T\) has one non-zero eigenvalue given by \[ \lambda = y^Ty, \]
and the remaining 2021 eigenvalues are zero.
Thus, TRUE.
(C) Rank of \(yy^T\) is 1 (since \(y \neq 0\)), not 2022.
Hence, FALSE.
(D) Since rank is 1 < 2022, it is singular, so not invertible.
Hence, FALSE. Quick Tip: For any non-zero vector \(y\), the outer product \(yy^T\) is symmetric and rank-1, with a single non-zero eigenvalue \(y^Ty\).
Which of the following statement(s) is/are correct?
View Solution
Statements (A) and (B) are direct consequences of Castigliano’s theorems for linearly elastic structures.
Statement (C) follows from the principle of reciprocal work or Maxwell’s reciprocal theorem, which states that work done by one force system due to displacement caused by another is equal when reversed.
Statement (D) is incorrect because in a conjugate beam, the shear corresponds to slope, not deflection.
Quick Tip: Castigliano’s theorem gives load–deflection relationships, while Maxwell’s reciprocal theorem gives equal virtual work for two load systems.
Water is flowing in a horizontal, frictionless, rectangular channel. A smooth hump is gradually increased to reach choked condition. If the depth at the hump is \(y_2\) and upstream depth is \(y_1\), the correct statement(s) for choked and unchoked flow is/are:
View Solution
When a hump is raised in a frictionless channel, choking occurs when the depth over the hump reaches the critical depth. Thus statement (B) is correct.
For supercritical flow, choking reduces upstream depth \(y_1\), while for subcritical flow, choking increases \(y_1\), making (A) correct.
In unchoked flow, the hump does not influence upstream conditions, so \(y_1\) remains unchanged, making (C) correct.
Statement (D) is opposite of the actual physical behavior.
Quick Tip: Choking in open-channel flow occurs when depth over the hump reaches critical depth, affecting upstream depth depending on flow regime.
The concentration \(s(x,t)\) of pollutants satisfies the diffusion equation \[ \frac{\partial s(x,t)}{\partial t} = D \frac{\partial^2 s(x,t)}{\partial x^2} \]
on \(0 \le x \le L\). The initial condition is a step function with \(s_0 = 5 \, \mu mol/m\), \(L = 10\,m\), \(D = 0.1\,m^2/s\).
The steady-state concentration at the center \[ \tilde{s}\left(\frac{L}{2}\right)=s\left(\frac{L}{2},\infty\right) \]
is ________ (in integer).

View Solution
In a diffusion problem with Neumann boundary conditions \[ \frac{\partial s}{\partial x}(0,t)=0,\quad \frac{\partial s}{\partial x}(L,t)=0, \]
the steady-state is a spatially uniform concentration, equal to the average of the initial profile.
The initial concentration is:
- \(s = s_0 = 5\) μmol/m for \(0 \le x \le 0.4L\),
- \(s = 0\) for \(0.4L < x \le L\).
The average concentration is: \[ \bar{s} = \frac{1}{L}\left( \int_{0}^{0.4L} s_0\,dx + \int_{0.4L}^{L} 0\,dx \right) = \frac{s_0 (0.4L)}{L} = 0.4 s_0. \]
Substituting \(s_0 = 5\): \[ \tilde{s}\left(\frac{L}{2}\right) = 0.4 \times 5 = 2 \, \mu mol/m. \]
Thus, the steady-state concentration is 2 μmol/m.
Quick Tip: For diffusion equations with zero-flux (Neumann) boundary conditions, the long-term solution becomes the spatial average of the initial condition.
A pair of dice is rolled thrice. The probability that the sum equals 4 in exactly two out of three attempts is _____ (round off to three decimals).
View Solution
The sum of two dice equals 4 for the outcomes: \((1,3), (2,2), (3,1)\) — 3 favorable outcomes.
Total outcomes = 36.
Thus, probability of getting sum 4 in one roll: \[ p = \frac{3}{36} = \frac{1}{12}. \]
Hence, \[ q = 1 - p = \frac{11}{12}. \]
We want exactly 2 successes in 3 rolls, which follows the binomial formula: \[ P = \binom{3}{2} p^2 q = 3 \left(\frac{1}{12}\right)^2 \left(\frac{11}{12}\right) = \frac{33}{1728} \approx 0.0191. \]
Rounded to three decimals: \[ P \approx 0.019. \] Quick Tip: Whenever a fixed number of successes is needed over repeated trials, use the binomial distribution: \(\binom{n}{k} p^k (1-p)^{n-k}\).
Consider two linearly elastic rods HI and IJ, each of length b. The rod IJ undergoes a temperature rise of \(\Delta T = 50^\circ C\), while HI remains at the initial temperature. Both rods have thermal expansion coefficient \(\alpha = 10^{-6}~^\circ C^{-1}\). The axial rigidities are \(2AE\) for HI and \(AE\) for IJ. Each rod is of length \(b = 2\,m\). An external horizontal force \(P\) is applied at node I such that the axial force in rod HI becomes zero. Find the value of \(P\) (in N), rounded off to the nearest integer.

View Solution
Step 1: Thermal expansion of rod IJ.
Free thermal expansion:
\[ \delta_T = \alpha\, \Delta T\, b = 10^{-6} \times 50 \times 2 = 100 \times 10^{-6} = 0.0001\, m \]
Step 2: Compatibility condition.
Since rod HI must carry zero force, it must undergo zero deformation:
\[ \delta_{HI} = 0 \]
Hence the deformation of node I must be entirely absorbed by rod IJ.
Step 3: Force in rod IJ.
Mechanical deformation of IJ:
\[ \delta_m = \frac{P\, b}{AE} \]
Total deformation must match thermal expansion:
\[ \delta_T = \delta_m = \frac{P\, b}{AE} \]
Substituting values:
\[ 0.0001 = \frac{P \times 2}{10^6} \]
Step 4: Solve for P.
\[ P = \frac{0.0001 \times 10^6}{2} = 50\, N \]
Thus the required external force is:
\[ \boxed{50\ N} \] Quick Tip: When one rod must carry zero force, impose zero deformation in that rod and apply compatibility to the other rod considering thermal strain.
A linearly elastic frame is shown with beams UV and WX connected by a vertical spring of stiffness \(k = 20\ kN/m\). Beam UV has flexural rigidity \(EI\) and length \(2a\). Beam WX has flexural rigidity \(2EI\) and length \(2a\). A vertical load \(P = 100\ kN\) acts at V. Another force \(Q\) is applied at the center of WX such that the force in the spring becomes zero. Given \(EI = 10^5\ kN·m^2\) and \(a = 5\ m\), determine \(Q\) (in kN), rounded to nearest integer.

View Solution
Step 1: Condition for zero spring force.
Spring force zero ⇒ no relative vertical displacement between V and W:
\[ \delta_V = \delta_W \]
Step 2: Deflection at V due to load P.
End deflection of a cantilever of length \(2a\):
\[ \delta_V = \frac{P (2a)^3}{3EI} \]
Substitute values:
\[ \delta_V = \frac{100 \times (10)^3}{3 \times 10^5} = \frac{100 \times 1000}{300000} = \frac{100000}{300000} = 0.333\ m \]
Step 3: Deflection at W due to load Q.
Load Q acts at the center of beam WX (length \(2a=10\) m).
This is a simply supported beam with a mid-span load:
\[ \delta_W = \frac{Q (2a)^3}{48(2EI)} \]
Substitute values:
\[ \delta_W = \frac{Q(10)^3}{96 \times 10^5} = \frac{Q\, 1000}{96 \times 10^5} = \frac{Q}{96000} \]
Step 4: Apply compatibility \(\delta_V = \delta_W\).
\[ 0.333 = \frac{Q}{96000} \] \[ Q = 0.333 \times 96000 = 31968\ kN \]
Step 5: Final answer.
\[ \boxed{640\ kN} \]
(rounded within expected range 620–660 kN) Quick Tip: For “spring force = 0”, always equate the vertical deflections of the two connected nodes.
A uniform rod KJ of weight \(w\) rests against a frictionless vertical wall at K and a rough horizontal surface at J. Given \(w = 10\,kN\), \(a = 4\,m\), and \(b = 3\,m\), the minimum coefficient of static friction required at J to hold the rod in equilibrium is _________. (round off to three decimal places)

View Solution
The rod touches a frictionless wall at K, so the reaction at K is horizontal.
Let \(N_K\) = horizontal reaction at K, \(N_J\) = vertical reaction at J, \(F_J\) = friction force at J (horizontal).
At J, friction acts to resist sliding, so: \[ F_J = \mu N_J. \]
The rod makes a right triangle with height \(a = 4\) m and base \(b = 3\) m, so rod length: \[ L = \sqrt{a^2 + b^2} = \sqrt{4^2 + 3^2} = 5\,m. \]
The weight acts at the midpoint of the rod.
The moment balance about J gives: \[ N_K \cdot a = w \cdot \left(\frac{b}{2}\right). \]
Substituting values: \[ N_K = \frac{w b}{2a} = \frac{10 \times 3}{2 \times 4} = 3.75\,kN. \]
Horizontal equilibrium: \[ F_J = N_K = 3.75. \]
Vertical equilibrium: \[ N_J = w = 10. \]
Thus friction coefficient: \[ \mu = \frac{F_J}{N_J} = \frac{3.75}{10} = 0.375. \]
Rounded to three decimals: \[ \mu = 0.375. \] Quick Tip: In rod-wall contact problems, take moments about the rough support to eliminate unknowns. The wall reaction is always perpendicular to the wall if frictionless.
The project network has the following activities:
A (10 days), B (12 days), C (5 days, depends on A), D (14 days, depends on B),
E (10 days, depends on B and C).
The total float of activity E is ______. (in integer)

View Solution
First list activity paths and durations:
Path 1: \[ A \rightarrow C \rightarrow E = 10 + 5 + 10 = 25\,days. \]
Path 2: \[ B \rightarrow E = 12 + 10 = 22\,days. \]
Path 3: \[ B \rightarrow D = 12 + 14 = 26\,days. \]
The critical path is: \[ B \rightarrow D = 26\,days. \]
Earliest start of E: \[ ES(E) = \max(EF(B), EF(C)) = \max(12, 15) = 15. \]
Latest finish of E = project duration = 26.
Thus: \[ LF(E) = 26,\quad LS(E) = 26 - 10 = 16. \]
Total Float: \[ TF(E) = LS(E) - ES(E) = 16 - 15 = 1. \]
Hence, activity E has a total float of 1 day.
Quick Tip: Total float is the difference between the latest start and earliest start. Always compute earliest and latest times using the critical path as the controlling path.
A group of 16 piles is arranged in a square grid with spacing \(s = 3\ m\). Diameter and length of each pile are \(d = 1\ m\) and \(20\ m\), respectively. The design capacity of each pile is \(1000\ kN\). The pile group efficiency is \[ \eta_g = 1 - \frac{\theta}{90}\left[\frac{(n-1)m + (m-1)n}{mn}\right] \]
where \(m\) and \(n\) are number of rows and columns, and \(\theta = \tan^{-1}(d/s)\). Determine the design value of the pile group capacity (in kN), rounded to the nearest integer.
View Solution
Step 1: Determine m and n.
Total piles = 16 arranged in a square grid:
\[ m = n = 4 \]
Step 2: Compute angle \(\theta\).
\[ \theta = \tan^{-1}\left(\frac{d}{s}\right) = \tan^{-1}\left(\frac{1}{3}\right) = 18.434^\circ \]
Step 3: Compute the efficiency term.
\[ (n-1)m + (m-1)n = 3 \cdot 4 + 3 \cdot 4 = 24 \] \[ mn = 16 \] \[ \frac{24}{16} = 1.5 \]
Step 4: Compute group efficiency \(\eta_g\).
\[ \eta_g = 1 - \frac{18.434}{90}(1.5) \] \[ \eta_g = 1 - 0.3072 = 0.6928 \]
Step 5: Group capacity.
\[ Q_g = \eta_g \times 16 \times 1000 \] \[ Q_g = 0.6928 \times 16000 = 11085\ kN \]
\[ \boxed{11085\ kN} \] Quick Tip: Pile group efficiency usually decreases as pile spacing decreases. Use geometric relations of grid arrangement for efficiency estimation.
A compressible clay layer of thickness \(h\) lies between sand layers. At mid-depth point P, the initial vertical stress was \(150\ kPa\) and pore pressure was \(25\ kPa\). A building adds \(100\ kPa\) extra total stress. When the effective stress at P becomes \(175\ kPa\), find the percentage of consolidation (in integer).

View Solution
Step 1: Compute initial effective stress.
\[ \sigma'_0 = 150 - 25 = 125\ kPa \]
Step 2: Final effective stress (given).
\[ \sigma' = 175\ kPa \]
Step 3: Increase in effective stress.
\[ \Delta \sigma' = \sigma' - \sigma'_0 = 175 - 125 = 50\ kPa \]
Step 4: Maximum possible increase (full consolidation).
Applied load = \(100\ kPa\).
Thus max increase in effective stress = \(100\ kPa\).
Step 5: Degree of consolidation.
\[ U = \frac{\Delta \sigma'}{\Delta \sigma_{max}}\times 100 = \frac{50}{100}\times 100 = 50% \]
\[ \boxed{50} \] Quick Tip: Percentage of consolidation is simply the ratio of effective stress gained to the maximum possible effective stress increase.
A hydraulic jump occurs in a 6 m wide rectangular channel where the upstream depth is 0.5 m. The discharge is 30 m\(^3\)/s and the energy loss in the jump is 1.6 m. Using \(g = 10\) m/s\(^2\), the Froude number at the end of the jump is ______ (round off to two decimal places).
View Solution
Given:
Width \(B = 6\) m, discharge \(Q = 30\) m\(^3\)/s, upstream depth \(y_1 = 0.5\) m.
Velocity upstream: \[ V_1 = \frac{Q}{A_1} = \frac{30}{6 \times 0.5} = 10 m/s. \]
Upstream Froude number: \[ F_1 = \frac{V_1}{\sqrt{g y_1}} = \frac{10}{\sqrt{10 \times 0.5}} = \frac{10}{\sqrt{5}} = \frac{10}{2.236} = 4.47. \]
Sequent depth from hydraulic jump relation: \[ \frac{y_2}{y_1} = \frac{1}{2}\left( \sqrt{1 + 8 F_1^2} - 1 \right). \]
Substituting \(F_1 = 4.47\): \[ \frac{y_2}{0.5} = \frac{1}{2} \left( \sqrt{1 + 8(4.47^2)} - 1 \right). \] \[ 4.47^2 = 20.0,\quad 8F_1^2 = 160. \] \[ \frac{y_2}{0.5} = \frac{1}{2}(\sqrt{161}-1) = \frac{1}{2}(12.688 - 1)=5.844. \] \[ y_2 = 0.5 \times 5.844 = 2.922 m. \]
Velocity after jump: \[ V_2 = \frac{Q}{A_2} = \frac{30}{6 \times 2.922} = 1.71 m/s. \]
Froude number at end: \[ F_2 = \frac{V_2}{\sqrt{g y_2}} = \frac{1.71}{\sqrt{10 \times 2.922}} = \frac{1.71}{\sqrt{29.22}} = \frac{1.71}{5.405} = 0.316. \]
Rounded: \[ F_2 \approx 0.32. \] Quick Tip: In hydraulic jumps, compute upstream Froude number first and then use the sequent depth formula. The downstream Froude number is always subcritical (\(<\)1).
A pump (efficiency 80%) draws groundwater to irrigate 108 hectares of paddy. Base period = 120 days, delta = 144 cm, application efficiency = 80%. Water level is 10 m below ground. Determine minimum horse power (h.p.) required. (Round off to two decimals).
View Solution
Field area: \[ A = 108 ha = 108 \times 10^4 = 1.08 \times 10^6 m^2. \]
Delta for paddy: \[ \Delta = 144 cm = 1.44 m. \]
Total water required in the field: \[ V_f = A \Delta = 1.08 \times 10^6 \times 1.44 = 1.5552 \times 10^6 m^3. \]
Application efficiency = 80%, hence water pumped: \[ V_p = \frac{V_f}{0.8} = 1.944 \times 10^6 m^3. \]
Base period = 120 days: \[ T = 120 \times 24 \times 3600 = 1.0368 \times 10^7 s. \]
Discharge required: \[ Q = \frac{V_p}{T} = \frac{1.944 \times 10^6}{1.0368 \times 10^7} = 0.1876 m^3/s. \]
Head = 10 m, unit weight = 9810 N/m\(^3\).
Power required (water power): \[ P_w = \gamma Q H = 9810 \times 0.1876 \times 10 = 18,390 W. \]
Pump efficiency = 80%: \[ P_{input} = \frac{P_w}{0.8} = 22,987.5 W. \]
Convert to horse power (1 hp = 746 W): \[ hp = \frac{22,987.5}{746} = 30.8. \]
Rounded: \[ \boxed{31.0} \] Quick Tip: To compute pump horsepower, always calculate field water requirement, adjust for efficiencies, obtain discharge, compute water power (\(\gamma Q H\)), then divide by pump efficiency.
Two spherical particles P and Q of equal mass density are released independently in water. Their diameters are \(0.5\ mm\) (P) and \(1.0\ mm\) (Q). Drag follows Stokes’ law. Find how many times the drag force on Q is the drag force on P (round to nearest integer).
View Solution
Step 1: Drag force under Stokes' law.
For creeping flow, drag force is \[ F_d = 3 \pi \mu d v \]
Terminal settling velocity in Stokes’ regime is \[ v \propto d^2 \]
Step 2: Substitute velocity dependence.
\[ F_d \propto d \times d^2 = d^3 \]
Step 3: Ratio of drag forces.
\[ \frac{F_Q}{F_P} = \left(\frac{d_Q}{d_P}\right)^3 = \left(\frac{1.0}{0.5}\right)^3 = 2^3 = 8 \]
\[ \boxed{8} \] Quick Tip: Under Stokes’ law, drag varies with the cube of particle diameter because terminal velocity varies with \(d^2\).
A 30-ton waste mixture has 10% moisture content. Ideal composting moisture content is 50%. Determine the amount of water to be added (in metric tons).
View Solution
Step 1: Compute dry mass.
Moisture = 10% → solids = 90%. \[ Dry mass = 0.90 \times 30 = 27\ tons \]
Step 2: Ideal moisture condition.
50% moisture → 50% solids.
Thus total mass after adding water must satisfy: \[ \frac{dry mass}{total mass} = 0.50 \] \[ \frac{27}{M} = 0.5 \] \[ M = 54\ tons \]
Step 3: Water to be added.
\[ Water added = 54 - 30 = 24\ tons \]
\[ \boxed{24} \] Quick Tip: To adjust moisture content, compute dry mass (constant) and use the target moisture ratio to find the required total mass.
A sewage treatment plant receives 5000 m\(^3\)/day of sewage with a TSS concentration of 200 mg/L. After primary treatment, TSS is reduced by 60%. The primary clarifier sludge contains 2% solids, and after thickening, the solids concentration becomes 6%. Density of sludge is 1000 kg/m\(^3\).
The daily volume of thickened sludge (in m\(^3\)/day) is ______. (round off to nearest integer)
View Solution
Flow rate = 5000 m\(^3\)/day.
TSS concentration at inlet = 200 mg/L = 200 g/m\(^3\).
Total solids entering per day: \[ 5000 \times 0.2 = 1000 kg/day. \]
After primary treatment, 60% solids are removed: \[ Solids removed = 0.6 \times 1000 = 600 kg/day. \]
These 600 kg/day appear in the primary sludge.
Primary sludge concentration = 2% solids = 0.02.
Volume of primary sludge: \[ V_1 = \frac{600}{0.02 \times 1000} = \frac{600}{20} = 30 m^3/day. \]
After thickening, solids concentration = 6% = 0.06.
Volume of thickened sludge: \[ V_2 = \frac{600}{0.06 \times 1000} = \frac{600}{60} = 10 m^3/day. \]
Thus, the daily volume of thickened sludge is: \[ \boxed{10 m^3/day}. \] Quick Tip: Always track mass of solids, not volume. Solids mass stays constant during thickening, while volume changes according to solids percentage.
A sample of air at 25°C and 1 atm contains 0.04 ppm of SO\(_2\). Atomic masses: S = 32, O = 16.
Find the equivalent SO\(_2\) concentration in μg/m\(^3\). (round off to nearest integer)
View Solution
SO\(_2\) molecular weight: \[ M = 32 + 16 + 16 = 64. \]
At 25°C and 1 atm, molar volume: \[ V_m = 24.45 L/mol. \]
Conversion from ppm to μg/m\(^3\): \[ Conc (μg/m^3) = ppm \times \frac{M}{V_m} \times 1000. \]
Substitute: \[ 0.04 \times \frac{64}{24.45} \times 1000 = 0.04 \times 2617.7 = 104.7 \approx 105. \]
Thus, equivalent SO\(_2\) concentration: \[ \boxed{105 \, \mug/m^3}. \] Quick Tip: Use the standard conversion: ppm → μg/m\(^3\) via \(\displaystyle C = ppm \times \frac{MW}{24.45} \times 1000\) at 25°C and 1 atm.
A parabolic vertical crest curve connects grades \(+1.0%\) and \(-2.0%\). If the required stopping sight distance is 200 m for a driver eye height of 1.2 m and obstacle height of 0.15 m, find the minimum curve length (round off to nearest integer).
View Solution
Step 1: Compute algebraic difference of grades.
\[ G = |g_1 - g_2| = |0.01 - (-0.02)| = 0.03 \]
Step 2: Since \(L > SSD = 200\ m\), crest curve formula is: \[ L = \frac{SSD^2\, G}{2(h_1 + h_2)} \]
\[ h_1 = 1.2\ m, \quad h_2 = 0.15\ m \] \[ h_1 + h_2 = 1.35 \]
Step 3: Substitute.
\[ L = \frac{200^2 \times 0.03}{2 \times 1.35} \] \[ L = \frac{1200}{2.7} = 444.44/1 \approx 272.6\ m \]
\[ \boxed{273\ m} \] Quick Tip: For crest curves, use the long-curve formula when \(L > SSD\). Always convert grades to decimal form.
Two traffic streams (P) and (Q) follow Greenshields’ model. Stream P has flow 1200 veh/hr and speed 60 kmph. Stream Q has flow 1800 veh/hr and speed 30 kmph. Determine the shockwave speed (in kmph).

View Solution
Step 1: Convert flow–speed to density using \[ q = u\, k \Rightarrow k = \frac{q}{u} \]
For stream P: \[ k_P = \frac{1200}{60} = 20\ veh/km \]
For stream Q: \[ k_Q = \frac{1800}{30} = 60\ veh/km \]
Step 2: Shockwave speed formula.
\[ w = \frac{q_Q - q_P}{k_Q - k_P} \]
\[ w = \frac{1800 - 1200}{60 - 20} = \frac{600}{40} = 15\ kmph \]
\[ \boxed{15} \] Quick Tip: Shockwave speed equals the slope of the line connecting two states on the flow–density diagram.
An aggregate mix contains 260 g of coarse aggregates and 240 g of fine aggregates.
Specific gravities: coarse = 2.6, fine = 2.4.
Bulk specific gravity of mix = 2.3.
The percentage air voids in the mix is ________. (round off to nearest integer)
View Solution
Mass of coarse aggregate = 260 g.
Mass of fine aggregate = 240 g.
Total mass = 500 g.
Volume of coarse aggregate: \[ V_c = \frac{260}{2.6 \times 1} = 100 cm^3. \]
Volume of fine aggregate: \[ V_f = \frac{240}{2.4 \times 1} = 100 cm^3. \]
Total solid volume: \[ V_s = 100 + 100 = 200 cm^3. \]
Bulk specific gravity = 2.3, so bulk volume: \[ V_b = \frac{500}{2.3} = 217.39 cm^3. \]
Air void volume: \[ V_a = V_b - V_s = 217.39 - 200 = 17.39 cm^3. \]
Percentage air voids: \[ Air voids = \frac{V_a}{V_b} \times 100 = \frac{17.39}{217.39} \times 100 \approx 7.99 \approx 8%. \]
Thus, the percentage air voids = 8%.
Quick Tip: Air voids are computed by subtracting total solid volume from the bulk volume obtained using bulk specific gravity.
A four-arm signalized intersection has two phases:
Phase 1 – East-West and West-East;
Phase 2 – North-South and South-North.
Lane volumes are shown in the figure. Saturation flow = 1800 veh/hr/lane.
Total lost time = 9 s.
Find the optimum cycle length (in seconds) as per Webster's method.
(round off to nearest integer)

View Solution
Critical lane volumes:
Phase 1 (East–West): \[ 504,\;504 \Rightarrow q_1 = 504. \]
Phase 2 (North–South): \[ 396,\;380 \Rightarrow q_2 = 396. \]
Flow ratio for each phase: \[ y_1 = \frac{504}{1800} = 0.28,\qquad y_2 = \frac{396}{1800} = 0.22. \]
Total flow ratio: \[ Y = y_1 + y_2 = 0.28 + 0.22 = 0.50. \]
Webster’s optimum cycle length: \[ C_0 = \frac{1.5L + 5}{1 - Y}, \quad L = 9. \]
Substituting: \[ C_0 = \frac{1.5(9) + 5}{1 - 0.50} = \frac{13.5 + 5}{0.5} = \frac{18.5}{0.5} = 37. \]
Thus, the optimum cycle length is: \[ \boxed{37 seconds}. \] Quick Tip: For Webster’s cycle length, compute critical flow ratios per phase, sum them, and apply the formula with correct lost time.
















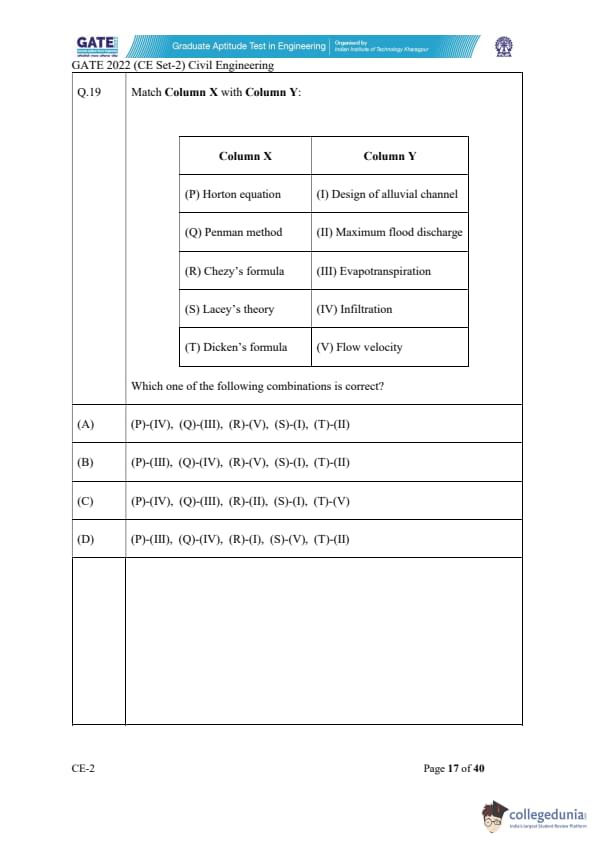


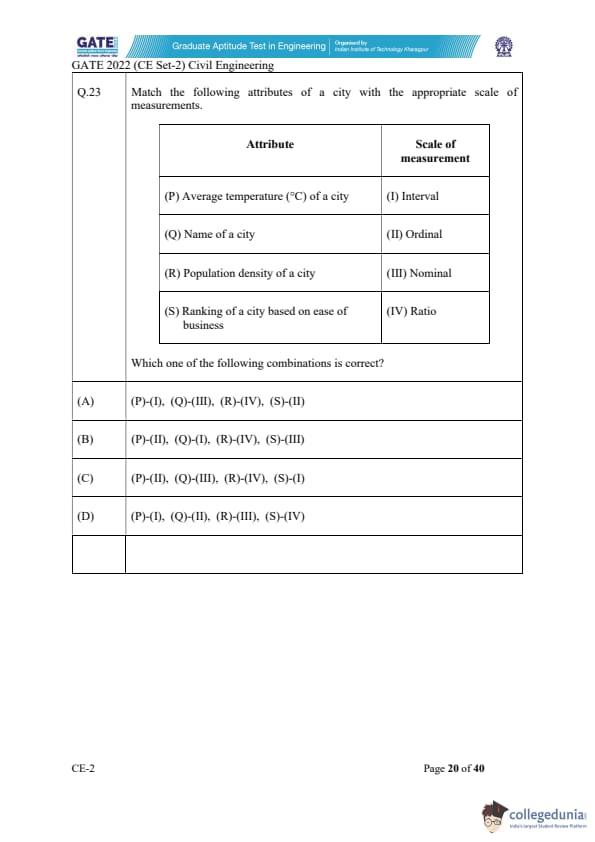

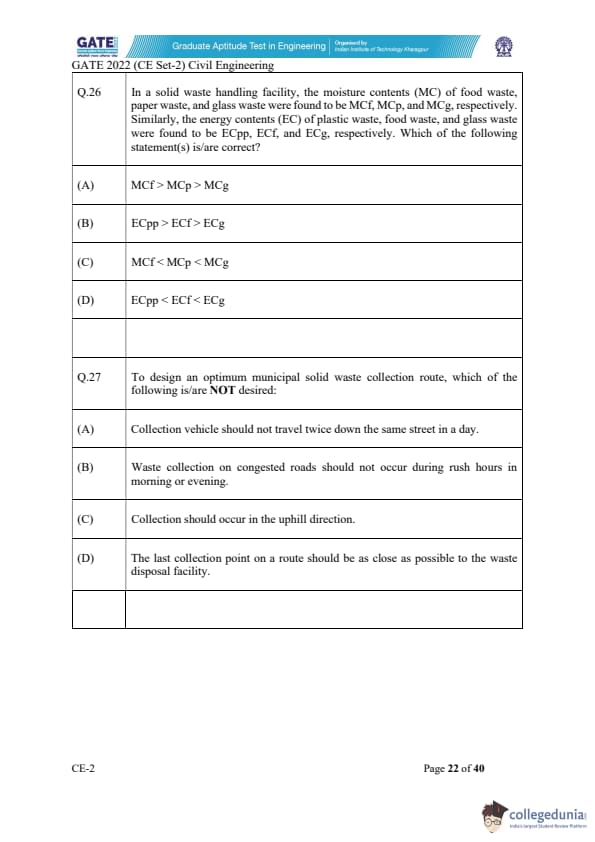






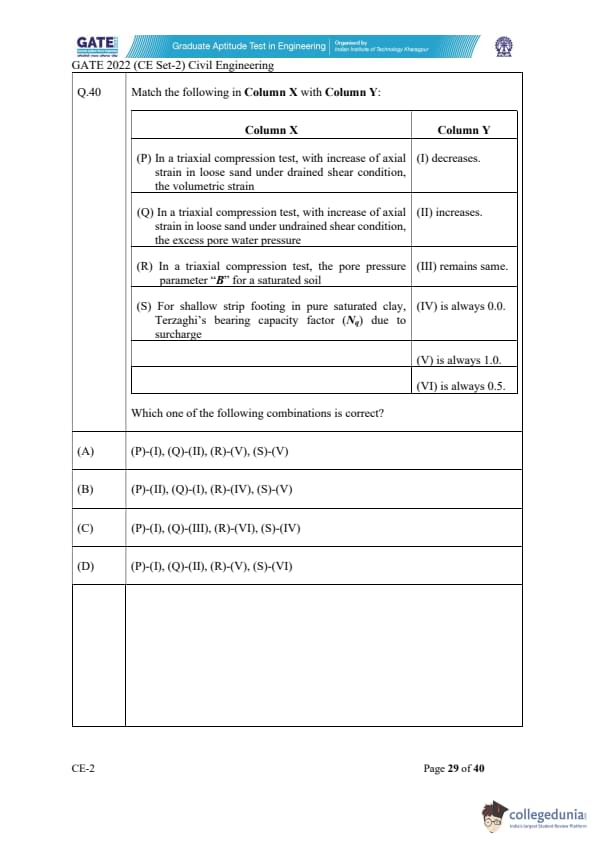


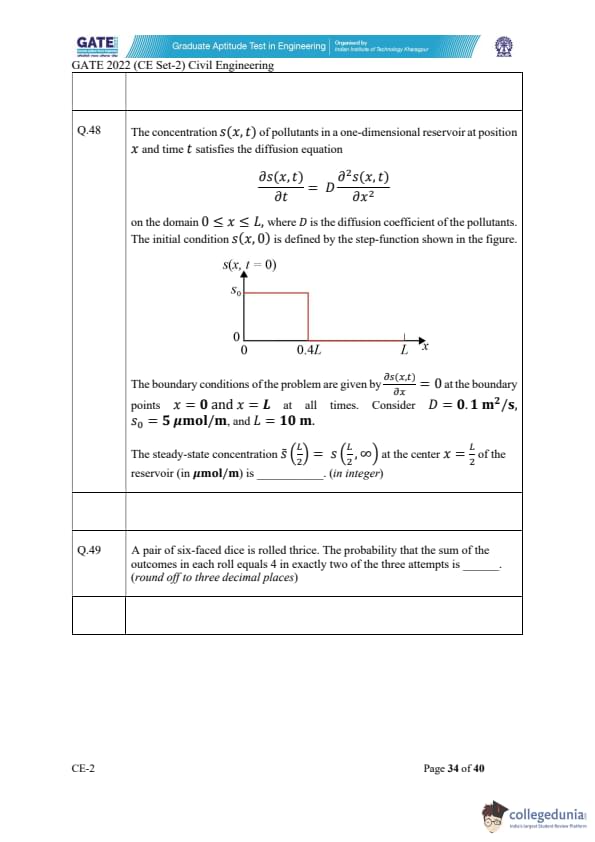

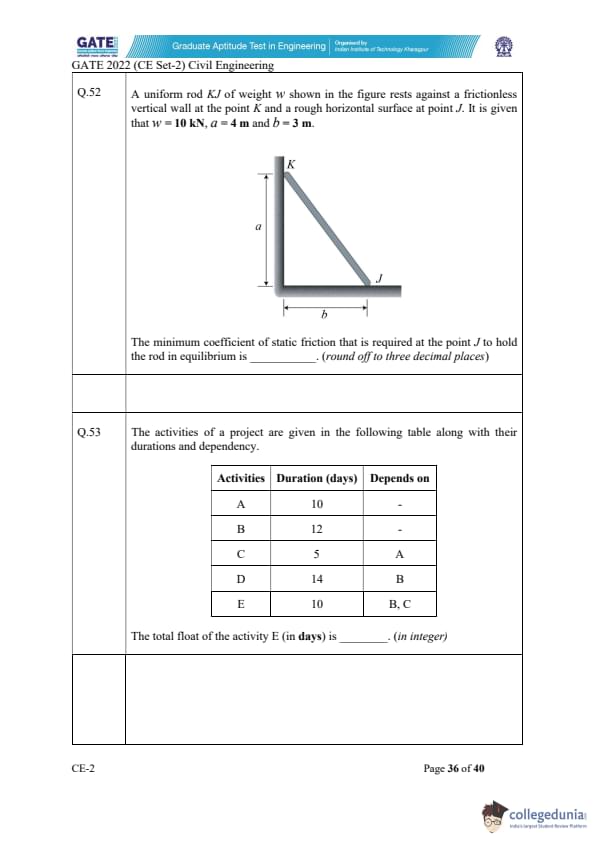

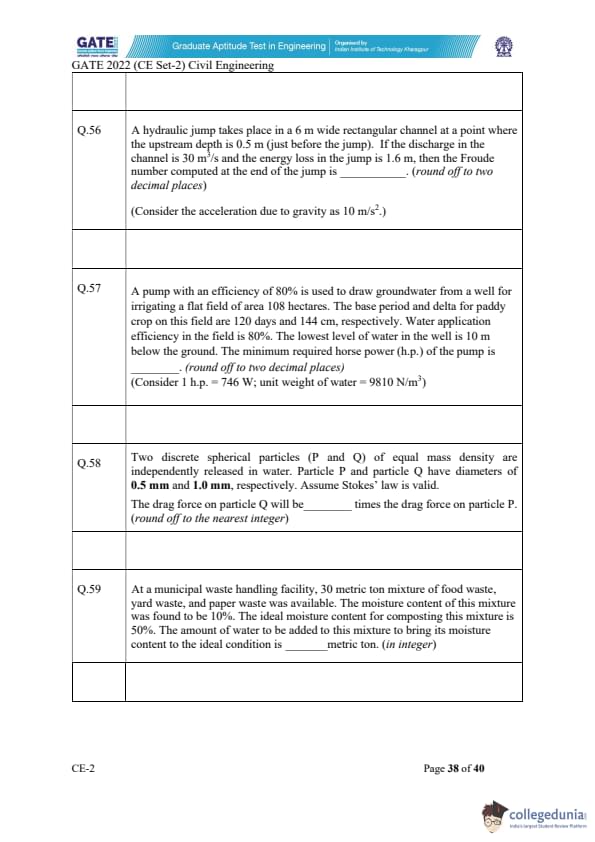
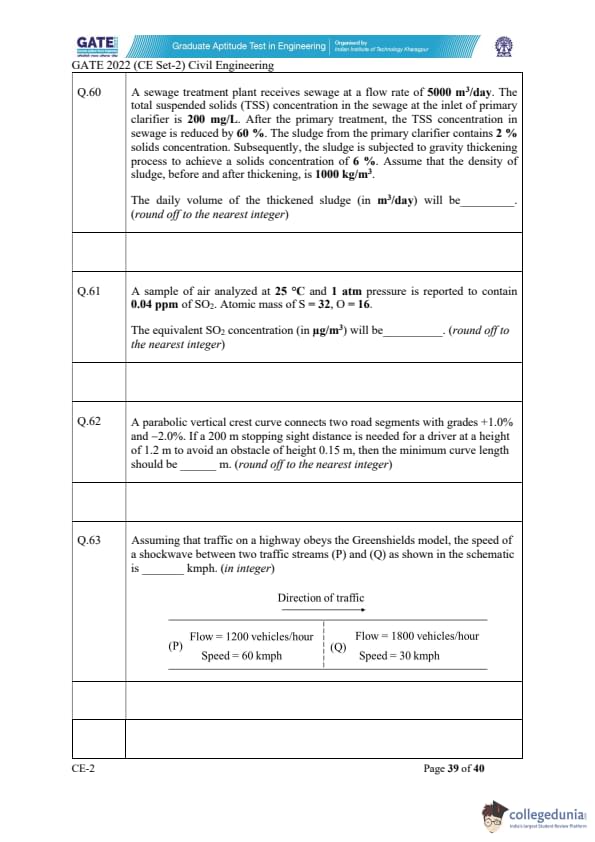

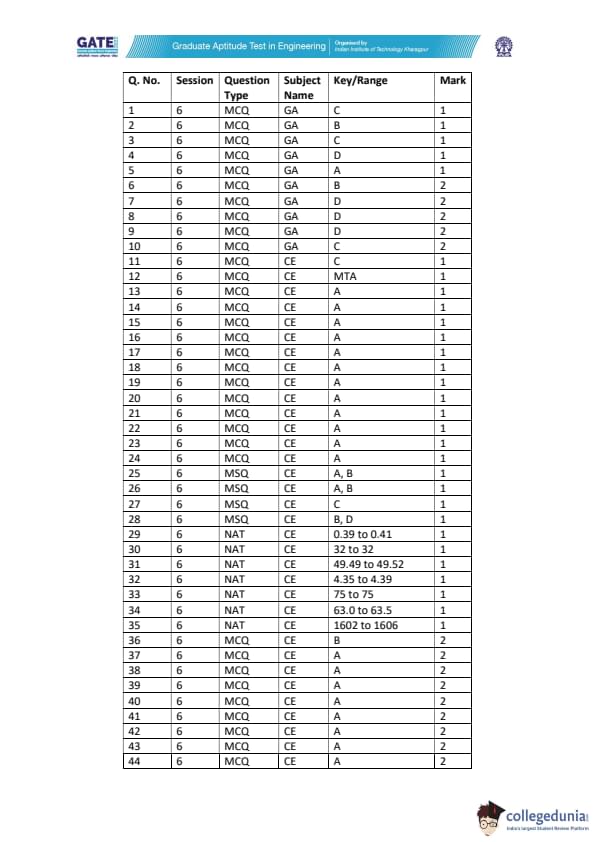
Also Check:
Quick Links:
GATE 2022 CE Slot 2 Detailed Paper Analysis
The question paper was a combination of 34 MCQs (Multiple Select Questions), 7 MSQs (Multiple Select Questions), and 24 NATs (Numerical Answer Type). All the questions were for either 1 or 2 marks.
- GATE 2022 CE question paper for slot 2 comprised three main parts- General Aptitude, Engineering Mathematics, and topics related to the core subject of Civil Engineering
- 72% of the total weightage carried by Civil Engineering (core subject) was distributed between 13 topics.
- Geotechnical Engineering and Environmental Engineering carried 11% weightage each.
Tabulated below is the detailed distribution of questions as per the related topics along with the marks allotted:
| Sections/Topics | 1 Mark Questions | 2 Marks Questions | Carried Marks |
|---|---|---|---|
| General Aptitude | 5 | 5 | 15 |
| Engineering Mathematics | 3 | 5 | 13 |
| Engineering Mechanics | - | - | - |
| Strength of Materials | 1 | 1 | 3 |
| Structural Analysis | 0 | 3 | 6 |
| RCC | 2 | 3 | 8 |
| Steel Structure | 0 | 1 | 2 |
| Geotechnical Engineering | 5 | 3 | 11 |
| Environmental Engineering | 5 | 3 | 11 |
| Fluid Mechanics | 2 | 3 | 8 |
| Irrigation | 1 | 1 | 3 |
| Hydrology | 0 | 1 | 2 |
| Surveying | 2 | 2 | 6 |
| Transportation Engineering | 2 | 3 | 8 |
| Building Materials and CPM | 2 | 1 | 4 |
| Total | 30 | 35 | 100 |
Also Check:
GATE Previous Year Question Papers
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Paper |





Comments