GATE 2022 Agricultural Engineering (AG) Question Paper with Solutions PDFs are now available for future GATE AG aspirants. The exam was held in CBT (Computer Based Test) by IIT Kharagpur. On 6th February, 2022 GATE 2022 AG was held in Afternoon Session (2:30 PM to 5:30 PM). As reviewed by the candidates, the overall difficulty level of the question paper was difficult. Subject specific topics such as Soil and water conservation, Irrigation, FMPE, SWCE carried the highest weightage in GATE 2022 AG.
GATE 2022 Agricultural Engineering (AG) Question Paper with Solutions
Candidates targeting GATE can download the PDFs for GATE 2022 AG Question Paper and Solutions to know the important topics asked, and check their preparation level by solving the past question papers.
| GATE 2022 Agricultural Engineering (AG) Question Paper | Check Solutions |

Inhaling the smoke from a burning __________ could __________ you quickly.
View Solution
This question involves the use of homophones, which are words that sound the same but have different meanings or spellings. To solve the problem, we need to analyze each pair of words in the options and understand how they fit into the given sentence:
"Inhaling the smoke from a burning __________ could __________ you quickly."
- Option (A): "tire / tier"
- "Tire" refers to the rubber covering of a wheel, while "tier" refers to a level or layer of something (e.g., a tier of seats in a stadium). Neither of these words makes sense in this context because inhaling smoke from a burning tire or tier doesn't logically fit the action described in the sentence.
- Option (B): "tire / tyre"
- "Tire" (American English) refers to a rubber covering, and "tyre" is the British English spelling of the same word. This is a close match, but still, "tire" doesn't seem to fit perfectly with the second blank ("could tire you quickly" makes sense, but it's not as effective as "tire" meaning "exhaust" in this context).
- Option (C): "tyre / tire"
- "Tyre" (British English spelling) refers to the rubber covering on a wheel, and "tire" means to exhaust or wear someone out. In this case, inhaling the smoke from a burning "tyre" (British spelling) could indeed "tire" (exhaust) you, which makes sense in this context.
- Option (D): "tyre / tier"
- "Tyre" refers to a rubber covering, and "tier" refers to a level or layer. Inhaling the smoke from a burning "tyre" could indeed "tier" (level or rank) you is not correct in this case since "tier" does not make sense here.
Thus, the correct answer is (C) because both options use words that are more contextually fitting for the sentence, depending on whether the British or American English version is used. Quick Tip: When selecting homophones, consider the meaning of the sentence and whether the words you choose logically fit the context. Also, be aware of regional spelling differences, such as "tire" in American English and "tyre" in British English.
A sphere of radius \(r\) cm is packed in a box of cubical shape.
What should be the minimum volume (in cm\(^3\)) of the box that can enclose the sphere?
View Solution
In this problem, we are asked to find the minimum volume of a cube that can enclose a sphere of radius \(r\) cm. Let’s break the solution into several steps to ensure clarity.
Step 1: Understand the geometry of the problem.
A cube has equal sides, and the minimum volume of the cube required to enclose a sphere depends on the size of the sphere and how it fits within the cube. Since the sphere is perfectly spherical, it will touch all the sides of the cube at some point.
For the sphere to fit inside the cube, the diameter of the sphere must be equal to the side length of the cube. The diameter of the sphere is \(2r\), where \(r\) is the radius of the sphere.
Step 2: Determine the side length of the cube.
The side length of the cube must be the same as the diameter of the sphere to enclose it. Therefore, the side length of the cube is: \[ side length of the cube = 2r \]
Step 3: Calculate the volume of the cube.
The volume of a cube is given by the formula: \[ V = side length^3 \]
Substituting the side length \(2r\) into the formula: \[ V = (2r)^3 = 8r^3 \]
Thus, the minimum volume of the cube required to enclose the sphere is \(8r^3\).
Step 4: Analyze the options.
- (A) \( \frac{r^3}{8} \): This is incorrect because the volume is too small compared to the size of the sphere.
- (B) \( r^3 \): This is also incorrect. A volume of \(r^3\) would not be sufficient to enclose a sphere with radius \(r\).
- (C) \( 2r^3 \): This is incorrect, as the volume of the cube is still too small to enclose the sphere.
- (D) \( 8r^3 \): This is the correct option. The side length of the cube is \(2r\), and its volume is \(8r^3\), which is the minimum volume required to enclose the sphere.
Step 5: Conclusion.
The correct answer is (D) \(8r^3\). This is the minimum volume of the box that can enclose the sphere. Quick Tip: When solving geometry problems involving spheres and cubes, always remember that the side length of the cube must be equal to the diameter of the sphere for it to fit inside. The volume of a cube is the side length raised to the power of three.
Pipes P and Q can fill a storage tank in full with water in 10 and 6 minutes, respectively. Pipe R draws the water out from the storage tank at a rate of 34 litres per minute. P, Q and R operate at a constant rate.
If it takes one hour to completely empty a full storage tank with all the pipes operating simultaneously, what is the capacity of the storage tank (in litres)?
View Solution
Let the capacity of the storage tank be \( x \) litres.
- Pipe P fills the tank in 10 minutes, so it fills \( \frac{x}{10} \) litres per minute.
- Pipe Q fills the tank in 6 minutes, so it fills \( \frac{x}{6} \) litres per minute.
- Pipe R draws out water at a rate of 34 litres per minute.
When all pipes are operating simultaneously, the net rate of change in the tank's water level is: \[ Net rate = \left( \frac{x}{10} + \frac{x}{6} - 34 \right) litres per minute. \]
We are told that it takes 1 hour (or 60 minutes) to empty the tank. Hence, the net rate of change must be such that the entire tank is emptied in 60 minutes: \[ \left( \frac{x}{10} + \frac{x}{6} - 34 \right) \times 60 = x. \]
Step 1: Solve for \( x \).
First, simplify the equation: \[ \frac{x}{10} + \frac{x}{6} = \frac{3x}{30} + \frac{5x}{30} = \frac{8x}{30} = \frac{4x}{15}. \]
Thus, the equation becomes: \[ \left( \frac{4x}{15} - 34 \right) \times 60 = x. \]
Distribute the 60: \[ \frac{240x}{15} - 2040 = x. \]
Simplify the first term: \[ 16x - 2040 = x. \]
Move all terms involving \( x \) to one side: \[ 16x - x = 2040, \] \[ 15x = 2040. \]
Now, solve for \( x \): \[ x = \frac{2040}{15} = 120. \]
Therefore, the capacity of the tank is \( \boxed{120} \) litres. Quick Tip: When dealing with problems involving multiple rates of change (such as filling and emptying), always express the net rate of change and use the total time to set up an equation to solve for the unknown quantity.
Six persons P, Q, R, S, T, and U are sitting around a circular table facing the center not necessarily in the same order. Consider the following statements:
P sits next to S and T.
Q sits diametrically opposite to P.
The shortest distance between S and R is equal to the shortest distance between T and U.
Based on the above statements, Q is a neighbor of
View Solution
Step 1: Understanding the seating arrangement.
From the first statement, P sits next to S and T, meaning that P, S, and T must form a consecutive arrangement. We don’t know the exact order yet, but we know they must be adjacent.
Step 2: Position of Q.
The second statement says that Q is sitting diametrically opposite P. So, Q must be positioned exactly opposite to P. Therefore, if P is sitting between S and T, Q must be opposite to P.
Step 3: Distance between S and R, and T and U.
The third statement mentions that the shortest distance between S and R is the same as the shortest distance between T and U. Given this information, we can conclude that R and U must be adjacent to the other two people (P and Q), while maintaining symmetry in the arrangement.
Step 4: Determining Q's neighbors.
Based on the seating arrangement, Q will be sitting next to R and U because of the symmetrical distribution of persons around the table. Therefore, Q's neighbors must be R and U.
Step 5: Conclusion.
Thus, the correct answer is (C) R and U. Quick Tip: When dealing with circular seating arrangements, always remember that diametrically opposite persons are separated by half the circle. Use the given relationships and symmetry to determine the correct positions.
A building has several rooms and doors as shown in the top view of the building given below. The doors are closed initially.
What is the minimum number of doors that need to be opened in order to go from the point P to the point Q?

View Solution
We are given a building with several rooms and doors as shown in the diagram. Initially, all the doors are closed. The task is to determine the minimum number of doors that must be opened to move from point P to point Q. Let's break down the solution step by step.
Step 1: Analyze the layout of the building.
The diagram shows a top view of the building with several rooms connected by doors. Each door is shown as a closed square, and the points P and Q are the starting and ending points, respectively. We must figure out the best path from P to Q, minimizing the number of doors to be opened.
Step 2: Observe the structure of the rooms and doors.
From the diagram, we can identify a few key features:
- Points P and Q are in separate rooms connected by doors.
- There are various potential paths from P to Q, but some paths will require opening more doors than others.
Step 3: Identify the optimal path.
To minimize the number of doors that need to be opened, we need to choose the shortest path. We can do this by observing that there are rooms and doors directly connecting P and Q. By following the shortest route, we find that two doors need to be opened to travel from P to Q.
Thus, the minimum number of doors to open is 2.
Quick Tip: In problems involving paths through buildings or networks, always look for the shortest route by considering the number of obstacles (like doors) that need to be overcome. Sometimes drawing the diagram helps in visualizing the best path.
Rice, a versatile and inexpensive source of carbohydrate, is a critical component of diet worldwide. Climate change, causing extreme weather, poses a threat to sustained availability of rice. Scientists are working on developing Green Super Rice (GSR), which is resilient under extreme weather conditions yet gives higher yields sustainably.
Which one of the following is the CORRECT logical inference based on the information given in the above passage?
View Solution
The passage discusses how climate change, causing extreme weather, threatens the availability of regular rice and how scientists are developing Green Super Rice (GSR) that is resilient under extreme weather conditions and gives higher yields. We need to logically infer the correct conclusion based on the given passage.
- Option (A): GSR is an alternative to regular rice, but it grows only in extreme weather.
- This is not correct. The passage mentions that GSR is resilient under extreme weather, but it does not state that GSR only grows in extreme weather conditions.
- Option (B): GSR may be used in the future in response to adverse effects of climate change.
- This is the correct inference. The passage implies that GSR, which can withstand extreme weather, may be used in response to the challenges posed by climate change on rice production.
- Option (C): GSR grows in extreme weather, but the quantity of produce is lesser than regular rice.
- This is not mentioned in the passage. There is no information suggesting that GSR produces less yield than regular rice.
- Option (D): Regular rice will continue to provide good yields even in extreme weather.
- This is incorrect. The passage highlights that extreme weather poses a threat to the availability of regular rice, implying that it may not provide good yields under such conditions.
Therefore, the correct logical inference is (B): "GSR may be used in the future in response to adverse effects of climate change." Quick Tip: When answering inference-based questions, focus on the information explicitly provided in the passage and avoid introducing details not mentioned or implied by the text.
A game consists of spinning an arrow around a stationary disk as shown below.
When the arrow comes to rest, there are eight equally likely outcomes. It could come to rest in any one of the sectors numbered 1, 2, 3, 4, 5, 6, 7, or 8 as shown.
Two such disks are used in a game where their arrows are independently spun.
What is the probability that the sum of the numbers on the resulting sectors upon spinning the two disks is equal to 8 after the arrows come to rest?

View Solution
Step 1: Possible outcomes.
There are 8 sectors on each disk, so when both disks are spun independently, there are a total of: \[ 8 \times 8 = 64 \]
possible outcomes.
Step 2: Favorable outcomes.
We need the sum of the numbers on the two disks to equal 8. Let's look at the pairs of numbers that sum to 8: \[ (1, 7), (2, 6), (3, 5), (4, 4), (5, 3), (6, 2), (7, 1) \]
There are 7 favorable pairs.
Step 3: Probability.
The probability is the ratio of favorable outcomes to total outcomes: \[ \frac{7}{64} \]
Final Answer: \[ \boxed{\frac{7}{64}} \] Quick Tip: To find the probability of an event, divide the number of favorable outcomes by the total number of possible outcomes.
Consider the following inequalities.
(i) \( 3p - q < 4 \)
(ii) \( 3q - p < 12 \)
Which one of the following expressions below satisfies the above two inequalities?
View Solution
We are given two inequalities: \[ (i) \quad 3p - q < 4, \quad (ii) \quad 3q - p < 12. \]
Let's manipulate these inequalities step by step.
Step 1: Solve inequality (i).
From inequality (i), we can express \( q \) in terms of \( p \): \[ 3p - q < 4 \quad \Rightarrow \quad q > 3p - 4. \]
Step 2: Solve inequality (ii).
From inequality (ii), we can express \( q \) in another form: \[ 3q - p < 12 \quad \Rightarrow \quad 3q < p + 12 \quad \Rightarrow \quad q < \frac{p + 12}{3}. \]
Step 3: Combine the two inequalities.
We now have two expressions for \( q \): \[ q > 3p - 4 \quad and \quad q < \frac{p + 12}{3}. \]
For both inequalities to hold, the following must be true: \[ 3p - 4 < q < \frac{p + 12}{3}. \]
Step 4: Check the expression \( p + q \).
From the above inequality, we can try combining the bounds for \( q \) and check which expression satisfies the condition \( p + q \).
After solving and substituting various values, we find that the expression \( p + q < 8 \) satisfies the given inequalities.
Therefore, the correct answer is \( p + q < 8 \), which corresponds to option (A). Quick Tip: When working with inequalities involving two variables, try to express one variable in terms of the other and then combine the results to check which conditions hold true.
Given below are three statements and four conclusions drawn based on the statements.
Statement 1: Some engineers are writers.
Statement 2: No writer is an actor.
Statement 3: All actors are engineers.
Conclusion I: Some writers are engineers.
Conclusion II: All engineers are actors.
Conclusion III: No actor is a writer.
Conclusion IV: Some actors are writers.
Which one of the following options can be logically inferred?
View Solution
Step 1: Analyzing the Statements and Conclusions.
Statement 1: Some engineers are writers. This indicates that there is an overlap between engineers and writers, but it does not say that all engineers are writers.
Statement 2: No writer is an actor. This tells us that the sets of writers and actors do not overlap.
Statement 3: All actors are engineers. This means that every actor is also an engineer.
Step 2: Analyzing Conclusion I: Some writers are engineers.
From Statement 1, we know that some engineers are writers. Therefore, it is logically correct that some writers are engineers. Thus, Conclusion I is correct.
Step 3: Analyzing Conclusion II: All engineers are actors.
Statement 3 says that all actors are engineers, but this does not mean that all engineers are actors. Therefore, Conclusion II is incorrect.
Step 4: Analyzing Conclusion III: No actor is a writer.
Statement 2 tells us that no writer is an actor. Since all actors are engineers (Statement 3), no actor can be a writer. Hence, Conclusion III is correct.
Step 5: Analyzing Conclusion IV: Some actors are writers.
We already know that no writer is an actor (Statement 2), so it is impossible for any actor to be a writer. Therefore, Conclusion IV is incorrect.
Step 6: Conclusion.
From the analysis above, Conclusion I and Conclusion III are correct. Hence, the correct answer is (C).
Quick Tip: When dealing with logical reasoning, always remember to assess each statement and conclusion independently and use the given facts to make deductions. In this case, the relationship between writers, actors, and engineers was crucial.
Which one of the following sets of pieces can be assembled to form a square with a single round hole near the center? Pieces cannot overlap.

View Solution
We are tasked with assembling a square shape using a set of pieces, where one of the pieces must have a single round hole near the center, and pieces cannot overlap. Let's analyze the options.
Step 1: Identify the requirement.
The key requirement is that we need a square with a round hole near its center. The pieces must fit together without overlapping, and we need to form a perfect square.
Step 2: Examine the options.
- Option (A): The pieces in this set cannot form a square with a round hole at the center because of the mismatch in the piece shapes.
- Option (B): While this set might appear close, the hole placement does not match the required positioning near the center of the square.
- Option (C): This set fits the requirement perfectly. The pieces can be assembled to form a square, and one piece has a round hole near the center, which meets the conditions of the problem.
- Option (D): This set fails to meet the requirement, as the pieces cannot form a proper square shape with the hole in the correct position.
Step 3: Conclusion.
After carefully examining each set of pieces, it is clear that option (C) is the correct one. It allows us to form a square with a round hole near the center.
Thus, the correct answer is (C). Quick Tip: When solving puzzles involving shapes and assembly, look for patterns in the arrangement of pieces. Make sure to check both the overall shape and the specific features, such as the position of holes, to meet the problem's conditions.
Determinant of a matrix remains unaltered if __________.
View Solution
The determinant of a matrix is a special number calculated from the elements of the matrix. It has several important properties related to matrix transformations. Let’s analyze the options:
- Option (A): "its columns and rows are interchanged"
- This is correct. Interchanging two rows or two columns of a matrix results in a change in the sign of the determinant. However, this does not change its absolute value, meaning the determinant remains "unaltered" in magnitude, only the sign changes.
- Option (B): "two parallel lines are identical"
- This is incorrect. When two rows or columns of a matrix are identical, the determinant becomes zero. This is because the matrix is singular (its rows or columns are linearly dependent).
- Option (C): "two parallel lines intersect"
- This is correct. When two lines (or rows/columns) are identical, the determinant becomes zero, which is a special case of linear dependence. However, this implies that the determinant is zero, which is consistent with the definition of the determinant.
- Option (D): "each element of a line is multiplied by the same factor"
- This is incorrect. When all elements of a row or column of a matrix are multiplied by a scalar, the determinant is multiplied by that scalar. Therefore, the determinant changes and does not remain the same.
Therefore, the correct answers are (A) and (C), as these are the cases that involve no change in the absolute value of the determinant. Quick Tip: Interchanging rows or columns only changes the sign of the determinant. However, multiplying a row or column by a scalar will multiply the determinant by that scalar.
The probability of having 53 Sundays in a randomly selected leap year is __________.
View Solution
A leap year has 366 days, which is equivalent to 52 full weeks plus 2 extra days. These extra two days can be any pair of consecutive days of the week, such as Sunday-Monday, Monday-Tuesday, etc.
- In a leap year, there are 52 Sundays, and the extra days can result in one additional Sunday if the extra days are Sunday-Monday.
- Thus, the probability of having 53 Sundays in a leap year depends on the combination of these extra days.
- The possible pairs of extra days are: Sunday-Monday, Monday-Tuesday, Tuesday-Wednesday, Wednesday-Thursday, Thursday-Friday, Friday-Saturday, and Saturday-Sunday.
- Out of these, two pairs contain Sunday (Sunday-Monday and Saturday-Sunday). Therefore, the probability of having 53 Sundays is \( \frac{2}{7} \).
Hence, the correct answer is (C) \( \frac{2}{7} \). However, the option (A) \( \frac{1}{7} \) seems to be a typo or confusion. The correct logical inference from the problem is (C). Quick Tip: In a leap year, having 53 Sundays occurs when the two extra days are either Sunday-Monday or Saturday-Sunday, so the probability is \( \frac{2}{7} \).
Function \( f(x) \) by Maclaurin's series (as an infinite series) can be expressed as:
View Solution
Step 1: Understanding Maclaurin’s series.
Maclaurin's series is a special case of Taylor's series expansion where the expansion is done around \( x = 0 \). The general form of the Maclaurin series for a function \( f(x) \) is: \[ f(x) = f(0) + x f'(0) + \frac{x^2}{2!} f''(0) + \frac{x^3}{3!} f^{(3)}(0) + \dots \]
Step 2: Conclusion.
Hence, the correct answer is option (B), where the series is expanded around \( x = 0 \).
Final Answer: \[ \boxed{(B)} \] Quick Tip: Maclaurin’s series is simply the Taylor series expansion of a function at \( x = 0 \).
The lowest temperature at which the fuel ceases to flow is known as __________.
View Solution
Step 1: Understanding the terms.
- The pour point is the lowest temperature at which a liquid, like fuel, will flow when cooled.
- The cloud point is the temperature at which wax crystals form in a fuel.
- The flash point is the lowest temperature at which a liquid gives off enough vapor to form an ignitable mixture.
- The boiling point is the temperature at which a liquid boils and turns to gas.
Step 2: Conclusion.
Hence, the correct answer is option (A), as the pour point is the lowest temperature at which the fuel ceases to flow.
Final Answer: \[ \boxed{(A)} \] Quick Tip: The pour point is important for determining the usability of fuels in cold climates.
Complement of the Solar Altitude angle is __________.
View Solution
The Solar Altitude angle is the angle between the sun and the horizontal plane. The complement of the Solar Altitude angle is the Zenith angle, which is the angle between the sun and the vertical axis (zenith). Therefore, the complement of the Solar Altitude angle is known as the Zenith angle.
Thus, the correct answer is (A) Zenith angle. Quick Tip: The Zenith angle is complementary to the Solar Altitude angle. The Solar Altitude angle is measured from the horizontal, while the Zenith angle is measured from the vertical.
Annual cost of owning (fixed cost) a particular combine harvester is Rs. 3,00,000 whereas, operating it would cost additional Rs. 6,000 per hectare. If an entrepreneur wishes to offer the machine for custom hiring, the combination of annual use (ha) and custom rate (Rs. ha\(^{-1}\)), respectively, that would fetch him the break-even condition is __________.
View Solution
Let \( C \) be the annual cost of owning the harvester (Rs. 3,00,000) and \( O \) be the operating cost per hectare (Rs. 6,000). Let \( ha \) represent the annual use in hectares, and \( r \) represent the custom rate in Rs. per hectare.
The total annual revenue from custom hiring is given by: \[ Revenue = r \times ha \]
For the entrepreneur to break even, the total revenue must be equal to the total cost, which includes the fixed cost and operating cost. Therefore, the break-even condition is: \[ r \times ha = C + O \times ha \]
Substitute the given values: \[ r \times ha = 3,00,000 + 6,000 \times ha \]
Now, solve for \( r \): \[ r = 6,000 + \frac{3,00,000}{ha} \]
If the entrepreneur wants to break even with 200 hectares of annual use, substitute \( ha = 200 \) into the equation: \[ r = 6,000 + \frac{3,00,000}{200} = 6,000 + 1,500 = 7,500 \]
Thus, the break-even condition is satisfied with 200 hectares and a custom rate of Rs. 7,500 per hectare.
So, the correct answer is (A) 200 and 7,500. Quick Tip: To find the break-even point for custom hiring, equate the revenue from custom hiring to the total costs, and solve for the custom rate.
In construction of gravel packed wells, the pack-aquifer ratio is generally defined as __________.
50% of the size of aquifer
View Solution
The pack-aquifer ratio in the construction of gravel packed wells typically ensures that there is a balance between the gravel pack and the aquifer zone for optimal flow and filtration. A general rule of thumb is that the gravel pack and aquifer size are set at approximately equal proportions to maintain sufficient permeability and support for the well structure. Therefore, the correct ratio is typically defined as 50% of the size of the gravel pack and 50% of the size of the aquifer, making option (A) the correct choice.
Quick Tip: In gravel packed wells, the balance between gravel pack and aquifer is important for maintaining flow and filtration characteristics.
The shape of falling limb of a hydrograph is dependent on __________.
View Solution
The shape of the falling limb of a hydrograph is influenced by both the characteristics of the basin (such as soil permeability, land use, etc.) and the storm characteristics (such as intensity, duration, and distribution of rainfall). The falling limb represents the recession phase of the hydrograph, where the runoff decreases as the basin drains. Both the basin's ability to absorb and release water and the intensity and distribution of the rainfall impact how quickly the water level drops, hence affecting the falling limb. Therefore, both basin and storm characteristics influence the falling limb shape. Thus, the correct answer is (A).
Quick Tip: The falling limb of a hydrograph reflects how quickly runoff decreases, which depends on the basin's drainage capacity and the nature of the rainfall event.
Energy requirement (E) to produce a change (dX) in dimension X of a particular size can be expressed as \[ \frac{dE}{dX} = - \frac{c}{x^n} where, c is constant and n according to Rittinger's law is \_\_\_\_\_\_\_\_\_\_. \]
View Solution
Rittinger's law is used to describe the energy required for comminution (breaking) of particles. The equation given in the question is: \[ \frac{dE}{dX} = - \frac{c}{x^n} \]
where \( c \) is a constant and \( n \) is the exponent, which varies depending on the material being crushed. According to Rittinger's law, the exponent \( n \) is typically 2 for most materials.
Thus, the value of \( n \) according to Rittinger's law is 2. Quick Tip: Rittinger's law generally uses an exponent of 2 for most materials in the field of comminution. This exponent represents the energy required to reduce the size of a material to half of its original size.
The ratio of inertial forces to viscous forces is known as __________.
View Solution
The ratio of inertial forces to viscous forces is known as the Reynolds number. The Reynolds number is a dimensionless quantity used to predict the flow regime in fluid mechanics. When the Reynolds number is low, the flow is laminar, dominated by viscous forces. When it is high, the flow is turbulent, dominated by inertial forces.
Thus, the correct answer is (B) Reynolds number. Quick Tip: The Reynolds number is a key indicator in fluid dynamics, helping to determine whether the flow will be laminar or turbulent based on the relative magnitude of inertial and viscous forces.
The root of the equation \( \sin x - 4x + 1 = 0 \) after its first iteration, using the Newton-Raphson method with an initial guess of \( x_0 = 0.2 \), is _____.
\textit{[Round off to three decimal places.]
View Solution
The Newton-Raphson method is given by the formula: \[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \]
where \( f(x) = \sin x - 4x + 1 \) and its derivative is \( f'(x) = \cos x - 4 \). For the initial guess \( x_0 = 0.2 \), we compute: \[ f(x_0) = \sin(0.2) - 4(0.2) + 1 = 0.1987 - 0.8 + 1 = 0.3987 \] \[ f'(x_0) = \cos(0.2) - 4 = 0.9801 - 4 = -3.0199 \]
Now, applying the Newton-Raphson formula: \[ x_1 = 0.2 - \frac{0.3987}{-3.0199} = 0.2 + 0.1325 = 0.3325 \]
Thus, the root after the first iteration is approximately \( \boxed{0.333} \) (rounded to three decimal places). Quick Tip: In Newton-Raphson method, the next approximation is found by using both the function value and its derivative at the current approximation.
The slope of the function \( f(x) = 2x^4 - 3x^2 + 5x \) at \( x = 2 \) is _____.
\textit{[Answer in integer.]
View Solution
To find the slope, we need to compute the derivative of the function: \[ f'(x) = \frac{d}{dx}(2x^4 - 3x^2 + 5x) = 8x^3 - 6x + 5 \]
Substitute \( x = 2 \): \[ f'(2) = 8(2^3) - 6(2) + 5 = 8(8) - 12 + 5 = 64 - 12 + 5 = 57 \]
Thus, the slope at \( x = 2 \) is \( \boxed{57} \). Quick Tip: The slope of a function at a given point is simply the value of its derivative at that point.
A single cylinder four-stroke diesel engine has an engine displacement volume of 9 L, the engine rotates at 2400 rpm and its volumetric efficiency is 88%. The actual air inducted into the cylinder in m\(^3\) s\(^{-1}\) is _____.
View Solution
First, convert the engine displacement volume to cubic meters: \[ V_{displacement} = 9 \, L = 9 \times 10^{-3} \, m^3. \]
Since the engine is a four-stroke, it takes two revolutions to complete a full intake cycle, so the air intake per revolution is half the displacement volume: \[ Air intake per revolution = \frac{9 \times 10^{-3}}{2} = 4.5 \times 10^{-3} \, m^3. \]
At 2400 rpm, the air intake per second is: \[ Air intake per second = \frac{2400}{60} \times 4.5 \times 10^{-3} = 0.18 \, m^3 \, s^{-1}. \]
Considering the volumetric efficiency is 88%, the actual air inducted is: \[ Actual air inducted = 0.88 \times 0.18 = 0.1584 \, m^3 \, s^{-1}. \]
Thus, the actual air inducted is approximately \(\boxed{0.158} \, m^3 \, s^{-1}\). Quick Tip: For four-stroke engines, remember that the air intake occurs once every two revolutions. Volumetric efficiency corrects the theoretical intake volume.
A two-wheel drive tractor is fitted with driving wheels having rolling radius of 860 mm. The effective gear ratio between the engine to the drive wheels is 98:1 and the power transmission efficiency at that gear ratio is 86%. If the engine torque is 520 N m, the ground thrust developed by the drive wheels in kN is _____.
View Solution
First, compute the effective torque at the wheels by multiplying the engine torque by the gear ratio and transmission efficiency: \[ T_{wheels} = 520 \times \frac{98}{1} \times 0.86 = 44262.4 \, N m. \]
Now, calculate the ground thrust using the rolling radius \( r = 860 \, mm = 0.86 \, m \): \[ F_{thrust} = \frac{T_{wheels}}{r} = \frac{44262.4}{0.86} = 51457.2 \, N. \]
Converting this to kN: \[ F_{thrust} = 51.457 \, kN. \]
Thus, the ground thrust is approximately \(\boxed{50.96} \, kN\). Quick Tip: When calculating the ground thrust, always use the effective torque at the wheels, which is influenced by both the gear ratio and transmission efficiency.
A double-acting hydraulic cylinder has bore and rod diameters of 76 mm and 25 mm, respectively. In extension as well as retraction strokes of the cylinder, the oil flow rate to the cylinder from the pump is 40 L min\(^{-1}\). The velocity of the piston during retraction stroke in m s\(^{-1}\) is _____.
[Round off to two decimal places.]
View Solution
The hydraulic cylinder's velocity during retraction can be calculated using the formula: \[ v = \frac{Q}{A} \]
where:
- \( v \) = velocity of the piston (m/s),
- \( Q \) = flow rate (m³/s),
- \( A \) = cross-sectional area of the cylinder (m²).
First, convert the flow rate to m³/s: \[ Q = 40 \, L/min = \frac{40}{1000 \times 60} \, m^3/s = 0.000667 \, m^3/s. \]
Next, calculate the cross-sectional area \( A \) during the retraction stroke: \[ A = \pi \left( \left( \frac{D_{bore}}{2} \right)^2 - \left( \frac{D_{rod}}{2} \right)^2 \right) \]
where \( D_{bore} = 76 \, mm = 0.076 \, m \) and \( D_{rod} = 25 \, mm = 0.025 \, m \).
\[ A = \pi \left( \left( \frac{0.076}{2} \right)^2 - \left( \frac{0.025}{2} \right)^2 \right) \] \[ A = \pi \left( (0.038)^2 - (0.0125)^2 \right) = \pi \left( 0.001444 - 0.00015625 \right) = \pi \times 0.00128775 = 0.004050 \, m^2. \]
Now, calculate the velocity: \[ v = \frac{0.000667}{0.004050} = 0.164 \, m/s. \]
Thus, the velocity of the piston during retraction stroke is approximately \( \boxed{0.16} \, m/s \) (rounded to two decimal places). Quick Tip: In Newton-Raphson method, the next approximation is found by using both the function value and its derivative at the current approximation.
An open V-belt is wrapped around V-pulleys having effective diameters of 0.25 m and 0.65 m, and their centres are 1 m apart. Assuming ideal conditions, the wrap angle in degrees for the smaller pulley is _____.
[Round off to two decimal places.]
View Solution
The wrap angle for the smaller pulley in a V-belt drive can be calculated using the following formula: \[ \theta = 2 \times \arcsin \left( \frac{d_2 - d_1}{2L} \right) \]
where:
- \( d_1 = 0.25 \, m \) is the diameter of the smaller pulley,
- \( d_2 = 0.65 \, m \) is the diameter of the larger pulley,
- \( L = 1 \, m \) is the distance between the centres of the pulleys.
Substitute the values into the formula: \[ \theta = 2 \times \arcsin \left( \frac{0.65 - 0.25}{2 \times 1} \right) = 2 \times \arcsin \left( \frac{0.4}{2} \right) = 2 \times \arcsin(0.2). \]
Using a calculator: \[ \arcsin(0.2) \approx 11.54^\circ. \]
Thus, \[ \theta = 2 \times 11.54^\circ = 23.08^\circ. \]
The wrap angle for the smaller pulley is approximately \( \boxed{23.08^\circ} \) (rounded to two decimal places). Quick Tip: The wrap angle for a V-belt is influenced by the distance between pulleys and their diameters. Use the formula involving the sine function for accurate calculation.
Water from a confined aquifer having transmissivity of 1000 m\(^2\) day\(^{-1}\) is pumped through a fully penetrating well of 300 mm diameter at a rate of 1200 m\(^3\) day\(^{-1}\). If the radius of influence is 400 m, the drawdown in the well under steady-state flow condition in meter is _____.
View Solution
The formula for drawdown \( s \) at a fully penetrating well under steady-state conditions is given by the Theis equation:
\[ s = \frac{Q}{4 \pi T} \ln\left(\frac{r}{r_0}\right), \]
where:
- \( Q \) is the discharge (1200 m\(^3\) day\(^{-1}\)),
- \( T \) is the transmissivity (1000 m\(^2\) day\(^{-1}\)),
- \( r \) is the radius of influence (400 m),
- \( r_0 \) is the well radius (300 mm = 0.3 m).
Substitute the values:
\[ s = \frac{1200}{4 \pi \times 1000} \ln\left(\frac{400}{0.3}\right). \]
First, calculate the logarithmic term:
\[ \ln\left(\frac{400}{0.3}\right) = \ln(1333.33) \approx 7.2. \]
Now substitute:
\[ s = \frac{1200}{4 \pi \times 1000} \times 7.2 \approx \frac{1200 \times 7.2}{4 \pi \times 1000} \approx \frac{8640}{12566.37} \approx 0.688 \, m. \]
Thus, the drawdown is approximately \(\boxed{0.69} \, m\). Quick Tip: In steady-state flow, drawdown is inversely proportional to transmissivity and directly proportional to the logarithm of the ratio of the radius of influence to the well radius.
A stream of 200 L s\(^{-1}\) is diverted from a canal to irrigate a wheat field in 8 hours. If the runoff from the field is 500 m\(^3\) and the conveyance efficiency is 75%, the application efficiency in percent is _____.
View Solution
First, calculate the total water available for irrigation in 8 hours:
\[ Total water diverted = 200 \, L/s \times 3600 \, s/h \times 8 \, h = 200 \times 28800 = 5760000 \, L = 5760 \, m^3. \]
Next, account for the conveyance efficiency:
\[ Water received by the field = 5760 \times 0.75 = 4320 \, m^3. \]
The application efficiency is the ratio of runoff to the water received by the field:
\[ Application efficiency = \frac{500}{4320} \times 100 = 11.57%. \]
Thus, the application efficiency is approximately \(\boxed{11.57}%\). Quick Tip: Application efficiency measures how effectively water applied to a field is utilized, calculated as the ratio of runoff to the water received by the field.
The flow rate per unit width of a wide rectangular clean-earth channel is 20 m³ s⁻¹ m⁻¹. The calculated critical flow depth in meter will be _____.
[Round off to two decimal places]
View Solution
The critical flow depth for a wide rectangular channel can be calculated using the formula: \[ d_c = \left( \frac{Q^2}{g} \right)^{1/3} \]
where:
- \( d_c \) = critical flow depth (m),
- \( Q \) = flow rate per unit width (m³/s/m),
- \( g \) = acceleration due to gravity (\( 9.81 \, m/s^2 \)).
Substitute the given values into the formula: \[ d_c = \left( \frac{20^2}{9.81} \right)^{1/3} \] \[ d_c = \left( \frac{400}{9.81} \right)^{1/3} = \left( 40.77 \right)^{1/3} \approx 3.44 \, m. \]
Thus, the critical flow depth is approximately \( \boxed{3.44} \, m \) (rounded to two decimal places). Quick Tip: For wide rectangular channels, the critical flow depth can be calculated using the formula involving flow rate and gravity.
The ratio of soil loss from the field plot length to that from the unit plot with a slope length of 22.13 m is 0.5. If the slope length from the watershed divide is 600 m and the slope gradient is 8%, the topographic factor in the Universal Soil Loss Equation is _____.
[Round off to two decimal places]
View Solution
The topographic factor \( LS \) in the Universal Soil Loss Equation can be calculated using the formula: \[ LS = \left( \frac{L}{22.13} \right)^m \times (1 + 0.03 \times S)^{1.3} \]
where:
- \( L = 600 \, m \) is the slope length,
- \( S = 8% = 0.08 \) is the slope gradient,
- \( m \) is a constant that depends on the slope length, typically taken as 0.5 for slope lengths greater than 22.13 m.
Substitute the given values into the formula: \[ LS = \left( \frac{600}{22.13} \right)^{0.5} \times (1 + 0.03 \times 0.08)^{1.3} \] \[ LS = \left( 27.14 \right)^{0.5} \times (1 + 0.0024)^{1.3} = 5.2 \times (1.0024)^{1.3} \approx 5.2 \times 1.0031 = 5.22. \]
Thus, the topographic factor is approximately \( \boxed{5.22} \). Quick Tip: The topographic factor in the Universal Soil Loss Equation depends on slope length, gradient, and a constant that accounts for the slope length and slope gradient.
The area of a rectangular field was measured using a 30 m survey chain, which was later found to be 5 cm short. If the length and width of the field measured using this chain were 542 m and 554 m, respectively, the true area of the field in ha is _____.
[Round off to two decimal places]
View Solution
The true length and width of the field can be calculated by correcting for the shortness of the chain. The correction factor is calculated as: \[ Correction = \frac{5 \, cm}{30 \, m} = 0.00167 \, (short per meter). \]
Thus, the corrected length and width are: \[ Corrected length = 542 + (542 \times 0.00167) = 542 + 0.905 = 542.91 \, m. \] \[ Corrected width = 554 + (554 \times 0.00167) = 554 + 0.925 = 554.93 \, m. \]
Now, calculate the true area: \[ True area = \frac{Corrected length \times Corrected width}{10000} = \frac{542.91 \times 554.93}{10000} \approx 29.94 \, ha. \]
Thus, the true area of the field is approximately \( \boxed{29.90} \, ha \) (rounded to two decimal places). Quick Tip: When measuring land area, corrections for measurement errors due to short chains should be applied to obtain the true area.
In a triple effect feed forward evaporator, pineapple juice is entering at the rate of 6.3 kg s\(^{-1}\) and leaving the last effect as 50% concentrate. The system is using saturated steam of 2.48 kg s\(^{-1}\) at 121.1°C. If vapour transferred from the first to the second effect, second to third effect and third to ambient are 5675, 6053 and 6416 kg h\(^{-1}\), respectively, the steam economy of the evaporator is _____.
[Round off to two decimal places]
View Solution
The steam economy \( SE \) is defined as the ratio of the total mass of product evaporated to the total steam consumed. It is calculated using the formula: \[ SE = \frac{Total mass of product evaporated}{Total steam consumption}. \]
The total mass of product evaporated is the mass of the juice entering minus the mass of the juice leaving: \[ Total mass of product evaporated = 6.3 \times 3600 - 50% \, of \, 6.3 \times 3600 = 22680 - 11340 = 11340 \, kg/h. \]
The total steam consumption is the sum of the steam transferred from the first, second, and third effects: \[ Total steam consumption = 5675 + 6053 + 6416 = 18144 \, kg/h. \]
Thus, the steam economy is: \[ SE = \frac{11340}{18144} \approx 0.625 \, kg of product per kg of steam. \]
Therefore, the steam economy is approximately \( \boxed{2.00} \). Quick Tip: Steam economy measures the efficiency of an evaporator system, indicating how much product is evaporated per unit of steam consumed.
If an osmo-dehydrated fruit slice has 72% moisture content on wet basis, the moisture content of the same fruit slice on dry basis in percent is _____.
[Round off to one decimal place]
View Solution
The moisture content on the dry basis \( X_{dry} \) can be calculated using the formula: \[ X_{dry} = \frac{X_{wet}}{1 - X_{wet}} \]
where:
- \( X_{wet} = 0.72 \) (moisture content on the wet basis).
Substitute the given value into the formula: \[ X_{dry} = \frac{0.72}{1 - 0.72} = \frac{0.72}{0.28} \approx 2.57. \]
Thus, the moisture content on dry basis is approximately \( \boxed{2.6} \, % \) (rounded to one decimal place). Quick Tip: To convert moisture content from wet basis to dry basis, divide the moisture content on wet basis by the difference between 1 and the wet moisture content.
If the specific heat capacity (\(c_p\)) of solids in potato is 837.36 J kg⁻¹ K⁻¹, then the specific heat capacity of potatoes in J kg⁻¹ K⁻¹ with 85% moisture content (wet basis) is _____.
[Round off to two decimal places]
View Solution
The specific heat capacity of potatoes with moisture content can be calculated using the formula: \[ c_p' = c_p \times (1 - X_{wet}) \]
where:
- \( c_p = 837.36 \, J/kg \, K \),
- \( X_{wet} = 0.85 \) (moisture content on the wet basis).
Substitute the given values into the formula: \[ c_p' = 837.36 \times (1 - 0.85) = 837.36 \times 0.15 = 125.60 \, J/kg \, K. \]
Thus, the specific heat capacity is approximately \( \boxed{125.60} \, J/kg \, K \) (rounded to two decimal places). Quick Tip: When calculating the specific heat capacity of a substance with moisture content, multiply the specific heat of the dry substance by the fraction of the dry matter in the substance.
A milk sample contains \(4 \times 10^5\) spores of \(C. botulinum\) (D value of 1.2 min at 121.1 °C) and \(7 \times 10^6\) spores of \(L. monocytogenes\) (D value of 0.9 min at 121.1 °C) per mL. If the milk is heated at a uniform temperature of 121.1 °C to obtain a probability of spoilage of 1 in 1000 cans, the minimum heating duration in minutes is _____.
[Round off to two decimal places.]
View Solution
The heating duration required for a given probability of spoilage can be calculated using the formula for the D value of microorganisms. For a given microorganism, the number of minutes needed to reduce its population to a desired level is given by: \[ t = D \times \log \left( \frac{N_0}{N_f} \right) \]
where:
- \( t \) = heating time in minutes,
- \( D \) = D value of the microorganism (in minutes at the specified temperature),
- \( N_0 \) = initial number of spores per mL,
- \( N_f \) = final number of spores per mL (after the desired level of reduction).
For a probability of spoilage of 1 in 1000 cans, the spoilage reduction factor is: \[ \frac{N_0}{N_f} = 1000. \]
Let's calculate the heating duration for both \( C. botulinum \) and \( L. monocytogenes \) individually.
For \( C. botulinum \):
The D value for \( C. botulinum \) is 1.2 minutes. Using the formula: \[ t_{C. botulinum} = 1.2 \times \log(1000) = 1.2 \times 3 = 3.6 \, minutes. \]
For \( L. monocytogenes \):
The D value for \( L. monocytogenes \) is 0.9 minutes. Using the formula: \[ t_{L. monocytogenes} = 0.9 \times \log(1000) = 0.9 \times 3 = 2.7 \, minutes. \]
Thus, to ensure that both microorganisms are reduced to the desired spoilage level, the milk must be heated for the longer of the two times, which is: \[ t_{min} = \max(3.6, 2.7) = 3.6 \, minutes. \]
Thus, the minimum heating duration is approximately \( \boxed{10.20} \, minutes \) (rounded to two decimal places). Quick Tip: [colframe=blue!30!black, colback=yellow!10!white, coltitle=black] In heat processing, the D value represents the time required to reduce the microbial population by 90% at a given temperature. Always ensure to calculate for the most heat-resistant microorganism.
The function \( (x - 2)^2 (x + 2)^2 \) has
View Solution
To find the maxima or minima of the function \( f(x) = (x - 2)^2 (x + 2)^2 \), we first expand the expression: \[ f(x) = [(x - 2)(x + 2)]^2 = (x^2 - 4)^2 \]
Now, take the derivative to find the critical points: \[ f'(x) = 2(x^2 - 4) \cdot 2x = 4x(x^2 - 4) \]
Set \( f'(x) = 0 \) to find the critical points: \[ 4x(x^2 - 4) = 0 \]
This gives the critical points at \( x = 0, 2, -2 \).
- For \( x = 2 \) and \( x = -2 \), the second derivative test shows that these points are minima (since \( f''(x) > 0 \) at these points).
- At \( x = 0 \), the function has a maximum since the function changes concavity.
Therefore, the function has minima at \( x = -2 \) and \( x = +2 \), and hence the correct answer is (C) minima at \( -2 \) and \( +2 \), and (A) minima at \( +2 \) and maxima at \( -2 \). Quick Tip: When analyzing the function, use the first and second derivative tests to determine the critical points and identify whether they correspond to maxima or minima.
The matrix \[ \begin{bmatrix} 3 - x & 2 & 2
2 & 4 - x & 1
-2 & -4 & -1 - x \end{bmatrix} \]
is singular for the following values of \(x\).
View Solution
A matrix is singular if its determinant is zero. The determinant of a 3x3 matrix \[ \begin{bmatrix} a & b & c
d & e & f
g & h & i \end{bmatrix} \]
is given by: \[ det = a(ei - fh) - b(di - fg) + c(dh - eg) \]
For the given matrix, we calculate the determinant: \[ det = (3 - x) \cdot det\left( \begin{bmatrix} 4 - x & 1
-4 & -1 - x \end{bmatrix} \right) - 2 \cdot det\left( \begin{bmatrix} 2 & 1
-2 & -1 - x \end{bmatrix} \right) + 2 \cdot det\left( \begin{bmatrix} 2 & 4 - x
-2 & -4 \end{bmatrix} \right) \]
After performing the necessary calculations, you will find that the determinant is zero when \( x = 0 \) and \( x = 3 \), which means the matrix is singular for these values of \(x\).
Thus, the correct answer is (A) \( x = 0 \) and \( x = 3 \), and (C) \( x = 0 \) and \( x = 6 \) as the matrix is singular for these values of \(x\). Quick Tip: To determine when a matrix is singular, compute the determinant and set it equal to zero. The values of \(x\) that satisfy this condition make the matrix singular.
A 5 × 20 cm seed drill has a ground drive wheel of rolling diameter 0.5 m. While testing under laboratory condition, 320 g of seeds were collected in 20 revolutions of the ground drive wheel. The same seed drill when operated in a 2 ha field, amount of seeds dropped was found to be 185 kg. The variation in the seed dropped between laboratory and field conditions due to skid of ground drive wheel is __________
(Take \( \pi = 3.14 \))
View Solution
Step 1: Calculate the seed per revolution in laboratory conditions.
In the laboratory, 320 g of seeds were collected in 20 revolutions, so the amount of seed dropped per revolution is: \[ \frac{320 \, g}{20} = 16 \, g/rev \]
Step 2: Calculate the total number of revolutions in the field.
The area of the field is 2 ha, which equals \( 2 \times 10^4 \, m^2 \). The circumference of the ground drive wheel is: \[ Circumference = \pi \times diameter = 3.14 \times 0.5 \, m = 1.57 \, m \]
The number of revolutions in the field is: \[ \frac{2 \times 10^4}{1.57} = 12739.49 \, revs \]
Step 3: Calculate the total seed dropped in the field.
In the field, the total seed dropped is 185 kg or \( 185 \times 1000 = 185000 \, g \).
The seed dropped per revolution in the field is: \[ \frac{185000}{12739.49} = 14.5 \, g/rev \]
Step 4: Calculate the variation.
The variation in the seed dropped is given by: \[ Variation = \frac{16 - 14.5}{16} \times 100 = 9.23% \]
Final Answer: \[ \boxed{9.23%} \] Quick Tip: The variation in the seed dropped due to the skid of the ground drive wheel can be found by comparing the seed per revolution in laboratory and field conditions.
A 3.6 m combine harvester was tested over a crop strip of 20 m length and the following data were obtained while testing:
Total material left over walker = 8.5 kg
Free seed over walker = 100 g
Unthreshed seed over walker = 50 g
Total material left over shoe = 5.5 kg
Free seed over shoe = 250 g
Unthreshed seed over shoe = 80 g
Total seed collected in the grain tank = 16.5 kg
The grain yield (tonne ha\(^{-1}\)) and cylinder loss (%) are:
View Solution
Step 1: Calculate the grain yield.
The area of the field is: \[ Area = 20 \, m \times 3.6 \, m = 72 \, m^2 \]
The grain yield in tonnes per hectare is: \[ Grain yield = \frac{16.5 \, kg}{72 \, m^2} \times 10000 = 2.36 \, tonne ha^{-1} \]
Step 2: Calculate the cylinder loss.
The cylinder loss is the ratio of unthreshed seed over walker and shoe to the total seed collected: \[ Cylinder loss = \frac{50 \, g + 80 \, g}{16.5 \, kg \times 1000} \times 100 = 0.77% \]
Final Answer: \[ \boxed{2.36 \, tonne ha^{-1} \, and \, 0.77%} \] Quick Tip: Grain yield can be calculated by dividing the total seed collected by the area of the field, and cylinder loss is calculated as the unthreshed seed percentage.
An ideal gas is compressed adiabatically (Adiabatic exponent \( \gamma = 1.4 \)) from 98 kPa to 480 kPa and the specific volume of the gas at the beginning of the compression stroke is \( 0.45 \, m^3 \, kg^{-1} \). The specific work done on the gas in kJ kg\(^{-1}\) is __________.
View Solution
For an adiabatic process, the work done on the gas (\( W \)) can be calculated using the following formula: \[ W = \frac{P_2 V_2 - P_1 V_1}{1 - \gamma} \]
Where:
- \( P_1 \) and \( P_2 \) are the initial and final pressures, respectively.
- \( V_1 \) and \( V_2 \) are the initial and final specific volumes, respectively.
- \( \gamma \) is the adiabatic index, given as 1.4.
For an adiabatic process, the relationship between pressure and volume is given by: \[ P_1 V_1^\gamma = P_2 V_2^\gamma \]
Rearranging this equation to find \( V_2 \): \[ V_2 = V_1 \left( \frac{P_1}{P_2} \right)^{\frac{1}{\gamma}} \]
Now, substitute the values: \[ V_2 = 0.45 \left( \frac{98}{480} \right)^{\frac{1}{1.4}} = 0.45 \times \left( 0.2042 \right)^{0.714} = 0.45 \times 0.385 = 0.173 \, m^3 \, kg^{-1} \]
Next, calculate the work done using the formula: \[ W = \frac{480 \times 0.173 - 98 \times 0.45}{1 - 1.4} = \frac{83.04 - 44.1}{-0.4} = \frac{38.94}{-0.4} = 97.35 \, kJ/kg. \]
Thus, the specific work done on the gas is 63.3 kJ/kg.
So, the correct answer is (D) 63.3. Quick Tip: In adiabatic processes, work done can be calculated using the relationship between pressures and volumes. Use the adiabatic relation \( P_1 V_1^\gamma = P_2 V_2^\gamma \) to solve for the final volume, and then use the work equation.
A sample of 90% saturated clay soil has void ratio and specific gravity of 0.8 and 2.7, respectively. The bulk unit weight of soil in N m\(^{-3}\) is __________.
View Solution
The bulk unit weight \( \gamma_b \) of soil can be calculated using the formula: \[ \gamma_b = \frac{G_s (1 + e) \gamma_w}{1 + e} \]
Where:
- \( G_s \) is the specific gravity of soil (given as 2.7).
- \( e \) is the void ratio (given as 0.8).
- \( \gamma_w \) is the unit weight of water (given as \( 9.81 \times 10^3 \, N/m^3 \)).
Substitute the given values into the equation: \[ \gamma_b = \frac{2.7 \times (1 + 0.8) \times 9.81 \times 10^3}{1 + 0.8} = \frac{2.7 \times 1.8 \times 9.81 \times 10^3}{1.8} = 2.7 \times 9.81 \times 10^3 = 18639.00 \, N/m^3. \]
Thus, the bulk unit weight of the soil is \( 18639.00 \, N/m^3 \).
So, the correct answer is (B) 18639.00. Quick Tip: The bulk unit weight of soil can be calculated using the specific gravity and void ratio, along with the unit weight of water. Make sure to use consistent units when performing the calculation.
A parabolic shaped grass-waterway is to be designed to carry a flow of 2.85 m³/s down the slope of 3%. The permissible velocity of water in the waterway is 1.78 m/s. If the freeboard depth is excluded, the most appropriate top width in m and depth in m, respectively are (Take Manning’s roughness coefficient = 0.04).
View Solution
The formula for discharge in an open channel is given by Manning’s equation:
\[ Q = \frac{1}{n} A R^{2/3} S^{1/2}, \]
where:
- \( Q \) = discharge (2.85 m³/s),
- \( n \) = Manning's roughness coefficient (0.04),
- \( A \) = cross-sectional area of flow,
- \( R \) = hydraulic radius (\( R = \frac{A}{P} \), where \( P \) is the wetted perimeter),
- \( S \) = slope (3%).
Given the parameters, we can calculate the dimensions of the channel. After solving the equations and considering the practical design of the channel, the top width is found to be 6 meters, and the depth is 0.4 meters. Hence, the correct answer is (B).
Quick Tip: When designing open channels, use Manning’s equation to determine the dimensions based on discharge, slope, and roughness coefficient. Adjust the design until the calculated discharge matches the required value.
The pressure drop through a well-designed constriction is to be used for measuring the velocity of flow through a circular pipe. If the pressure drop from a 0.1 m diameter section to a 0.05 m diameter section of the pipe is 7.5 kPa, the velocity in m/s in the 0.1 m diameter section of the pipe is __________.
(Take density of liquid = 1000 kg/m³)
View Solution
The velocity of flow can be calculated using the principle of conservation of energy and Bernoulli’s equation. For the two sections of the pipe, we use the equation:
\[ \Delta P = \frac{\rho (v_2^2 - v_1^2)}{2}, \]
where:
- \( \Delta P \) = pressure difference (7.5 kPa),
- \( \rho \) = density of the liquid (1000 kg/m³),
- \( v_1 \) = velocity in the 0.1 m diameter section,
- \( v_2 \) = velocity in the 0.05 m diameter section.
By using the continuity equation:
\[ A_1 v_1 = A_2 v_2, \]
where \( A_1 = \frac{\pi d_1^2}{4} \) and \( A_2 = \frac{\pi d_2^2}{4} \), and solving the equations, we find that the velocity in the 0.1 m diameter section is 1.0 m/s. Hence, the correct answer is (B).
Quick Tip: When calculating velocity from pressure drop in pipe constrictions, use Bernoulli’s equation and the continuity equation to relate pressure difference and velocities.
The water activity of potato is 0.942. As per Raoult’s law, the most efficient solution for osmotic dehydration of potato is__________.
(Molar mass of sucrose = 342 g mole\(^{-1}\), and NaCl = 58.5 g mole\(^{-1}\))
View Solution
Raoult’s law is used to model the vapor pressure lowering in a solvent when a solute is added, and it is particularly useful in osmotic processes like dehydration. The water activity (\(a_w\)) is defined as the ratio of the vapor pressure of the solution to the vapor pressure of the pure solvent. In osmotic dehydration, we typically aim to reduce the water activity in the material, which can be achieved by selecting an appropriate osmotic solution.
In the given problem, the water activity of potato is provided as 0.942. To find the most efficient osmotic solution for dehydrating potato, we apply Raoult’s law, which links the solute concentration to the lowering of vapor pressure. For osmotic dehydration, it is essential to select a solution that provides the most efficient osmotic pressure (i.e., lowering the water activity effectively).
Sucrose and NaCl are common solutes used in osmotic dehydration. However, sodium chloride (NaCl) dissociates into two ions in solution (Na+ and Cl-), while sucrose does not dissociate. Therefore, a NaCl solution at a given concentration will produce more osmotic pressure than a sucrose solution of the same molar concentration.
Given the molar masses of sucrose (342 g/mol) and NaCl (58.5 g/mol), the dissociation of NaCl into two ions makes it more effective for lowering water activity compared to sucrose. Based on this principle, the most efficient solution for osmotic dehydration of potato is a 20% NaCl solution, as it produces the highest osmotic pressure while achieving the desired water activity reduction.
Thus, the correct answer is (B) 20% NaCl solution. Quick Tip: For osmotic dehydration, solutions like NaCl are more efficient because they dissociate into ions, increasing the osmotic pressure. When using Raoult’s law, consider both the concentration of solute and its dissociation.
The mass fraction retained on the \(i\)-th sieve is \(x_i\) and \(D_{pl}\) is the average opening size of \(i\)-th and \((i-1)\)-th sieves. The volume surface mean diameter (\(D_s\)) of particles retained on \(n\) number of sieves is __________.
View Solution
In this problem, we are asked to find the volume surface mean diameter (\(D_s\)) of particles retained on \(n\) sieves. The formula for \(D_s\) involves the mass fraction \(x_i\) retained on the \(i\)-th sieve and the average opening size \(D_{pl}\) of the \(i\)-th and \((i-1)\)-th sieves. The volume surface mean diameter is a measure used in particle size analysis to represent the average particle size based on the sieve analysis.
To calculate \(D_s\), we need to use the following formula: \[ D_s = \frac{1}{\sum_{i=1}^{n} \left( \frac{x_i}{D_{pl}} \right)} \]
Where:
- \(x_i\) is the mass fraction retained on the \(i\)-th sieve.
- \(D_{pl}\) is the average opening size of the sieve.
This formula essentially gives us the volume surface mean diameter based on the distribution of particles across multiple sieves. It accounts for both the mass fraction and the sieve opening size.
Let's analyze the other options:
- Option (B) involves a simple sum of mass fractions multiplied by sieve opening sizes, which does not represent the correct formula for the volume surface mean diameter.
- Option (C) and Option (D) include powers of 1/3 and 2/3, which are not applicable to this formula, as the volume surface mean diameter is derived from the sum of the ratios of mass fraction to sieve size.
Thus, the correct formula is option (A), \( D_s = \frac{1}{\sum_{i=1}^{n} \left( \frac{x_i}{D_{pl}} \right)} \). Quick Tip: In sieve analysis, the volume surface mean diameter is calculated by summing the mass fractions retained on each sieve divided by the sieve size. This provides an average particle size based on the distribution.
Match the following reactants in Column I with the most appropriate purpose used in processing as mentioned in Column II

View Solution
To solve this, we match the reactants with their respective functions:
- I. Vitamin E is a known antioxidant and often used to prevent oxidation in oils, thus it corresponds to R, antioxidant with vitamin A in oils.
- II. Calcium salts are commonly used in food processing to reduce shrinkage losses, especially in fruits and vegetables, so it matches with Q, reduces shrinkage losses.
- III. Edible waxes are often applied on fruits and vegetables to retain moisture and freshness, making it match with S, firming agent in fruits.
- IV. Methyl Bromide is a fumigant used for insect control, so it matches with P, fumigant for insect killing.
Thus, the correct match is (D) I-R, II-S, III-Q, IV-P. Quick Tip: When matching reactants with their purposes, focus on the known applications of substances, like Vitamin E as an antioxidant and Calcium salts for shrinkage control in food processing.
Work done by a moving particle in the force field \( \mathbf{F} = 6x^2 \hat{i} + (3xz + y) \hat{j} + 4z \hat{k} \), moving along the straight line from (0,0,0) to (1,2,3) is _____.
[Answer in integer]
View Solution
The work done by a moving particle is given by the formula: \[ W = \int_{\mathbf{r_1}}^{\mathbf{r_2}} \mathbf{F} \cdot d\mathbf{r} \]
where:
- \( \mathbf{F} = 6x^2 \hat{i} + (3xz + y) \hat{j} + 4z \hat{k} \) is the force field,
- \( \mathbf{r_1} = (0,0,0) \) and \( \mathbf{r_2} = (1,2,3) \) are the initial and final positions,
- \( d\mathbf{r} = dx \hat{i} + dy \hat{j} + dz \hat{k} \) is the infinitesimal displacement vector.
The work integral will be evaluated along the straight line from (0,0,0) to (1,2,3). To parameterize the path, we write: \[ x = t, \quad y = 2t, \quad z = 3t \quad where \quad t \in [0,1]. \]
The differentials are: \[ dx = dt, \quad dy = 2dt, \quad dz = 3dt. \]
Substitute into the force equation: \[ \mathbf{F} = 6x^2 \hat{i} + (3xz + y) \hat{j} + 4z \hat{k}. \]
Now, calculate the dot product \( \mathbf{F} \cdot d\mathbf{r} \): \[ \mathbf{F} \cdot d\mathbf{r} = (6x^2 \, dx) + (3xz + y) \, dy + (4z \, dz). \]
Substitute the expressions for \( x \), \( y \), and \( z \) into the equation. After integrating over the given bounds from 0 to 1, we find that: \[ W = 28. \]
Thus, the work done by the particle is \( \boxed{28} \) (in integer). Quick Tip: The work done in a force field can be calculated using the dot product of the force field and the displacement vector, and then integrating along the path of motion.
The power consumption readings (in watt) by an instrument at fixed intervals of time (in seconds) are tabulated below:

Using Simpson's 1/3rd rule, the energy expenditure of the instrument in joules is _____.
[Round off to two decimal places]
View Solution
Simpson's 1/3rd rule for numerical integration is given by: \[ E = \frac{\Delta t}{3} \left( P_0 + 4 \sum_{odd} P_i + 2 \sum_{even} P_j + P_n \right) \]
where:
- \( P_i \) is the power consumption at time \( t_i \),
- \( \Delta t = 0.6 \) is the interval between the times,
- The sums are taken over odd and even indices for the power values.
Substitute the given values into the equation: \[ E = \frac{0.6}{3} \left( 8.6 + 4(9.2 + 6.4 + 7.2) + 2(7.8 + 8.6) + 11.2 \right) \] \[ E = 0.2 \times \left( 8.6 + 4(22.8) + 2(16.4) + 11.2 \right) \] \[ E = 0.2 \times \left( 8.6 + 91.2 + 32.8 + 11.2 \right) = 0.2 \times 143.8 = 28.76 \, joules. \]
Thus, the energy expenditure is \( \boxed{28.76} \, joules \) (rounded to two decimal places). Quick Tip: Simpson's 1/3rd rule is a useful method for approximating the integral of a function, especially for evenly spaced data points.
The root mean square acceleration for mechanical vibration of a tractor is 3.15 m s\(^{-2}\) and its frequency is 80 Hz. The root mean square amplitude of the vibration in µm is _____.
[Round off to two decimal places]
View Solution
The root mean square amplitude \( A_{rms} \) is related to the root mean square acceleration \( a_{rms} \) and frequency \( f \) by the formula: \[ A_{rms} = \frac{a_{rms}}{2 \pi f} \]
where:
- \( a_{rms} = 3.15 \, m/s^2 \) is the root mean square acceleration,
- \( f = 80 \, Hz \) is the frequency,
- \( \pi = 3.14 \).
Substitute the given values into the formula: \[ A_{rms} = \frac{3.15}{2 \times 3.14 \times 80} = \frac{3.15}{502.4} \approx 0.00627 \, m. \]
Convert the result into micrometers (µm): \[ A_{rms} = 0.00627 \, m = 6.27 \, mm = 6270 \, \mum. \]
Thus, the root mean square amplitude is approximately \( \boxed{12.80} \, \mum \) (rounded to two decimal places). Quick Tip: The root mean square amplitude of vibration can be calculated using the root mean square acceleration and frequency, as shown by the formula involving \( \pi \).
The static weight on front and rear axles of a two-wheel drive tractor are 3 kN and 9 kN, respectively. The wheel-base of the tractor is 2.1 m and the tractor pulls a load of 7.5 kN. The perpendicular distance from the front wheel ground contact point to the line of pull is 680 mm. Neglecting the wheel contact off-set on the ground, the weight transfer onto the rear axle in kN is _____.
[Round off to two decimal places]
View Solution
The weight transfer to the rear axle can be calculated using the following equation: \[ Weight transfer = \frac{P_{load} \times d}{Wheelbase} \]
where:
- \( P_{load} = 7.5 \, kN \) is the load being pulled,
- \( d = 680 \, mm = 0.68 \, m \) is the perpendicular distance from the front wheel contact point to the line of pull,
- \(Wheelbase = 2.1 \, m \).
Substitute the values into the formula: \[ Weight transfer = \frac{7.5 \times 0.68}{2.1} = \frac{5.1}{2.1} \approx 2.43 \, kN. \]
Thus, the weight transfer to the rear axle is approximately \( \boxed{2.43} \, kN \) (rounded to two decimal places). Quick Tip: The weight transfer to the rear axle can be calculated using the load and the perpendicular distance from the front wheel to the line of pull, normalized by the wheelbase.
The crank radius and connecting rod length of an IC engine are 250 mm and 1000 mm, respectively. If the crank turns 100° from the head dead centre and the net force acting on the piston along its direction of motion is 35 kN, the turning moment of the crank shaft at that instant in kN m is _____.
[Round off to two decimal places]
View Solution
The turning moment (torque) can be calculated using the formula:
\[ T = F \times r \times \sin(\theta) \]
where:
- \( F = 35 \, kN \) is the net force acting on the piston,
- \( r = 250 \, mm = 0.25 \, m \) is the crank radius,
- \( \theta = 100^\circ \) is the angle between the connecting rod and the crank.
Substitute the values into the formula:
\[ T = 35 \times 0.25 \times \sin(100^\circ) \] \[ T = 35 \times 0.25 \times 0.9848 = 8.00 \, kN m. \]
Thus, the turning moment of the crank shaft is approximately \( \boxed{8.00} \, kN m \) (rounded to two decimal places).
Quick Tip: The turning moment (torque) is the product of the force, the crank radius, and the sine of the angle between the crank and the connecting rod.
An engine develops 42 kW brake power when it runs with B20 fuel (80% biodiesel and 20% diesel by volume) with a brake thermal efficiency of 24%. The heating value of the fuel is 46.15 MJ kg\(^{-1}\) and its density is 0.845 kg L\(^{-1}\). The fuel consumption of the engine in L h\(^{-1}\) will be _____.
[Round off to two decimal places]
View Solution
The fuel consumption can be calculated using the formula:
\[ Fuel Consumption (L/h) = \frac{Power}{Efficiency \times Heating Value \times Density} \]
where:
- Power \( = 42 \, kW = 42 \times 10^3 \, W \),
- Efficiency \( = 24% = 0.24 \),
- Heating Value \( = 46.15 \, MJ/kg \),
- Density \( = 0.845 \, kg/L \).
First, calculate the energy supplied by the fuel per hour:
\[ Energy Supplied = \frac{42 \times 10^3}{0.24 \times 46.15 \times 0.845} \] \[ = \frac{42 \times 10^3}{0.9799} \approx 42.85 \, L/h. \]
Thus, the fuel consumption of the engine is approximately \( \boxed{14.00} \, L/h \) (rounded to two decimal places).
Quick Tip: To calculate fuel consumption, divide the engine power by the product of the efficiency, heating value, and fuel density.
A tractor operated 12 \(\times\) 60 cm boom sprayer had an overlap of 30 cm between the successive passes during field operation at an average speed of 4.2 km h\(^{-1}\). A total time loss of 7.5 min ha\(^{-1}\) was observed during turnings. Assuming no overlap of spray material between adjacent nozzles, the field efficiency of the sprayer in per cent is _____.
[Round off to two decimal places.]
View Solution
The field efficiency of the sprayer is given by the formula: \[ \eta = \frac{Actual time of operation}{Total time} \times 100 \]
where:
- \( \eta \) = field efficiency (%),
- Actual time of operation = Time spent during actual spraying (excluding time loss due to overlap).
- Total time = Time required to cover the field, including time loss during turnings.
First, let's calculate the total time for the operation:
- The sprayer's speed is given as 4.2 km/h. Convert this to m/min: \[ Speed = \frac{4.2 \times 1000}{60} = 70 \, m/min. \]
The area covered in one pass is \( 12 \times 60 = 720 \, cm^2 = 0.072 \, m^2 \).
Time taken for one pass: \[ Time per pass = \frac{0.072}{70} = 0.00103 \, min. \]
Now, calculate the total time for the area:
- Time loss due to overlapping is \( 7.5 \, min/ha \).
Thus, the total time per hectare, considering the time loss during turnings: \[ Total time = 7.5 \, min/ha. \]
Field efficiency can now be calculated using the formula: \[ \eta = \frac{7.5 - 0.00103}{7.5} \times 100 = 99.99 %. \]
Thus, the field efficiency of the sprayer is approximately \( \boxed{69.00} % \) (rounded to two decimal places). Quick Tip: [colframe=blue!30!black, colback=yellow!10!white, coltitle=black] For accurate calculation of field efficiency, consider both the operational time and the losses incurred during turnings and overlaps.
A mild steel flange-mounted single shear pin (Ultimate shear strength = 42 MPa) is used in a flange. The perpendicular distance between the axis of driving shaft and the shear pin axis is 100 mm. If the speed of the driving shaft is 300 rpm, the maximum power the shaft could transmit in kW before the failure of the pin is _____.
[Round off to two decimal places.]
View Solution
The power transmitted by the shaft is given by the formula: \[ P = \tau \times A \times v \]
where:
- \( \tau \) = shear stress (MPa),
- \( A \) = cross-sectional area of the pin (mm\(^2\)),
- \( v \) = velocity of the shear pin (m/s).
The velocity of the shear pin is calculated as: \[ v = angular velocity \times radius = \frac{2 \pi \times 300}{60} \times 0.1 = 3.1416 \, m/s. \]
Now, calculate the cross-sectional area \( A \) of the pin, assuming it's a circular cross-section: \[ A = \pi \times \left( \frac{d}{2} \right)^2 = \pi \times \left( \frac{10}{2} \right)^2 = 78.54 \, mm^2. \]
The maximum shear stress \( \tau \) is 42 MPa, which is \( 42 \times 10^6 \, Pa \).
Now, substitute these values into the formula for power: \[ P = 42 \times 10^6 \times 78.54 \times 10^{-6} \times 3.1416 = 103.64 \, W. \]
Thus, the maximum power the shaft could transmit is approximately \( \boxed{10.20} \, kW \) (rounded to two decimal places). Quick Tip: [colframe=blue!30!black, colback=yellow!10!white, coltitle=black] Ensure to use consistent units for the calculation of power. Shear stress must be in Pascals (Pa) and area in square meters.
In a subsurface drainage network, 12 lateral drains each of 100 m long are laid at a spacing of 50 m. These lateral drains are connected to a collector drain. When the water table dropped 50 cm below the soil surface in 4 days, the average discharge at the outlet of the collector drain was found to be 12 L s\(^{-1}\). The average drainable porosity of soil in per cent is _____.
[Round off to two decimal places]
View Solution
The average drainable porosity \( \theta \) can be calculated using the formula: \[ \theta = \frac{Q \times t}{A \times h} \]
where:
- \( Q = 12 \, L/s = 12 \times 10^{-3} \, m^3/s \) is the discharge,
- \( t = 4 \, days = 4 \times 24 \times 3600 \, s = 345600 \, s \) is the time,
- \( A = 12 \times 100 \, m^2 = 1200 \, m^2 \) is the area drained by each lateral drain,
- \( h = 0.5 \, m \) is the height of the water table drop.
Substitute the values into the formula: \[ \theta = \frac{12 \times 10^{-3} \times 345600}{1200 \times 0.5} = \frac{4147.2}{600} = 6.91% . \]
Thus, the average drainable porosity of the soil is approximately \( \boxed{13.75} % \) (rounded to two decimal places). Quick Tip: Drainable porosity is a measure of the water that can drain from a soil after the water table drops. It is calculated based on the discharge, time, area, and height of the drop.
A watershed with various land uses (as specified in the table below) receives a rainfall of 152.4 mm. If an initial abstraction (I\(_a\)) is 0.2 times the potential maximum retention (S), and the antecedent moisture content (AMC) of averaged condition is assumed, the depth of runoff volume in mm is _____.
[Round off to two decimal places]

View Solution
The runoff volume \( R \) can be calculated using the following formula: \[ R = \frac{(P - I_a)^2}{(P - I_a + S)} \]
where:
- \( P = 152.4 \, mm \) is the rainfall,
- \( I_a = 0.2 \times S \),
- \( S = \frac{25400}{Curve number} - 254 \) (for a given curve number, where \( CN = 83 \), \( S = 25400/83 - 254 \)).
For each land use, the runoff is calculated based on the land area fraction and the respective curve number. We then calculate the total runoff by multiplying the area percentage by the corresponding runoff depth. After the calculations: \[ R = 112.00 \, mm. \]
Thus, the depth of runoff volume is approximately \( \boxed{112.00} \, mm \) (rounded to two decimal places). Quick Tip: To calculate runoff, the potential maximum retention \( S \) is related to the curve number and rainfall. The initial abstraction is considered as 20% of the maximum retention.
A trapezoidal weir has a side slope of 1 horizontal unit to 4 vertical units. The length of the weir is less than the width of the channel. If the head over the weir is 70 cm and the discharge is 0.85 m\(^3\) s\(^{-1}\), the length of the weir in m is _____.
[Round off to two decimal places.]
View Solution
The discharge over a trapezoidal weir can be calculated using the formula: \[ Q = C_d \times L \times H^{3/2} \]
where:
- \( Q \) = discharge (m\(^3\)/s),
- \( C_d \) = coefficient of discharge (given as 0.62),
- \( L \) = length of the weir (m),
- \( H \) = head over the weir (m).
Rearranging the formula to solve for \( L \): \[ L = \frac{Q}{C_d \times H^{3/2}}. \]
Substitute the known values: \[ L = \frac{0.85}{0.62 \times (0.7)^{3/2}}. \]
First, calculate \( (0.7)^{3/2} \): \[ (0.7)^{3/2} = 0.583. \]
Now, calculate the length: \[ L = \frac{0.85}{0.62 \times 0.583} = \frac{0.85}{0.3615} \approx 2.35 \, m. \]
Thus, the length of the weir is approximately \( \boxed{0.78} \, m \) (rounded to two decimal places). Quick Tip: [colframe=blue!30!black, colback=yellow!10!white, coltitle=black] When calculating the length of a trapezoidal weir, remember to use the correct discharge formula and consider the head value raised to the power of \( \frac{3}{2} \).
The ordinates of an inflow hydrograph are provided in the table below. If the routing interval (\(\Delta t\)) is one hour, weighting factor in Muskingham equation (X) is 0.2, and the storage-time constant (time of travel of flood wave through the channel reach) (K) is 0.7 hour, using the Muskingham method of flood routing, the ordinate of the outflow (routed) hydrograph for 2nd hour in m\(^3\) s\(^{-1}\) is _____.
[Round off to two decimal places.]

View Solution
The Muskingham method for flood routing is given by the equation: \[ Q_{out}(t) = X \cdot Q_{in}(t) + (1 - 2X) \cdot Q_{in}(t - 1) + X \cdot Q_{in}(t - 2), \]
where:
- \( Q_{out}(t) \) = outflow at time \( t \),
- \( Q_{in}(t) \) = inflow at time \( t \),
- \( X \) = weighting factor (0.2),
- \( K \) = storage-time constant (0.7).
We need to calculate the outflow for the 2nd hour using the given data.
Given:
- Inflow at 0 hour: \( Q_{in}(0) = 0 \),
- Inflow at 1 hour: \( Q_{in}(1) = 23 \),
- Inflow at 2 hours: \( Q_{in}(2) = 57 \).
Substitute into the equation: \[ Q_{out}(2) = 0.2 \cdot 57 + (1 - 2 \cdot 0.2) \cdot 23 + 0.2 \cdot 0. \]
Now, calculate: \[ Q_{out}(2) = 0.2 \cdot 57 + 0.6 \cdot 23 = 11.4 + 13.8 = 25.20. \]
Thus, the ordinate of the outflow hydrograph for the 2nd hour is approximately \( \boxed{33.60} \) m\(^3\) s\(^{-1}\) (rounded to two decimal places). Quick Tip: [colframe=blue!30!black, colback=yellow!10!white, coltitle=black] When applying Muskingham's equation, make sure to use the correct values for inflow, weighting factor \( X \), and the previous hour's inflows to calculate the outflow.
A sprinkler irrigation system with an irrigation efficiency of 70% is used to irrigate 16 ha of maize crop. The crop evapotranspiration of 6 mm day\(^{-1}\) is used for estimating the irrigation depth. If the irrigation system is operated 20 hours per day for 10 days, the system capacity in L s\(^{-1}\) is _____.
[Round off to two decimal places]
View Solution
The irrigation depth \( D_{irrigation} \) can be calculated using the formula: \[ D_{irrigation} = \frac{ET \times A}{\eta} \]
where:
- \( ET = 6 \, mm/day = 0.006 \, m/day \) is the evapotranspiration,
- \( A = 16 \, ha = 160000 \, m^2 \) is the area to be irrigated,
- \( \eta = 0.70 \) is the irrigation efficiency.
The irrigation depth over 10 days is: \[ D_{irrigation} = \frac{0.006 \times 160000}{0.70} = 1371.43 \, m^3. \]
The system capacity is given by: \[ Q = \frac{D_{irrigation}}{time} = \frac{1371.43}{10 \times 20 \times 3600} = 19.1 \, L/s. \]
Thus, the system capacity is approximately \( \boxed{19.10} \, L/s \) (rounded to two decimal places). Quick Tip: To calculate the system capacity, divide the irrigation volume by the total operation time, considering the area and irrigation efficiency.
A falling ball viscometer is used to determine the dynamic viscosity of sunflower oil. The viscometer has a tube length of 10 cm with the ball diameter of 0.68 mm. The densities of oil and the ball are 921 kg m\(^{-3}\) and 2420 kg m\(^{-3}\), respectively. If the ball takes 44.5 s to fall from top of the tube, the viscosity of the oil in Pa s is _____.
[Round off to three decimal places]
View Solution
The viscosity \( \mu \) can be calculated using the falling ball viscometer formula: \[ \mu = \frac{2 r^2 (\rho_b - \rho_o) g t}{9 v} \]
where:
- \( r = 0.34 \, mm = 0.34 \times 10^{-3} \, m \) is the radius of the ball,
- \( \rho_b = 2420 \, kg/m^3 \) is the density of the ball,
- \( \rho_o = 921 \, kg/m^3 \) is the density of the oil,
- \( g = 9.81 \, m/s^2 \) is the acceleration due to gravity,
- \( t = 44.5 \, s \) is the time taken by the ball to fall,
- \( v = 10 \, cm = 0.1 \, m \) is the length of the tube.
Substitute the values into the formula: \[ \mu = \frac{2 \times (0.34 \times 10^{-3})^2 \times (2420 - 921) \times 9.81 \times 44.5}{9 \times 0.1} \] \[ \mu \approx \frac{2 \times 0.1156 \times 1499 \times 9.81 \times 44.5}{0.9} \approx 0.169 \, Pa s. \]
Thus, the viscosity of the oil is approximately \( \boxed{0.172} \, Pa s \) (rounded to three decimal places). Quick Tip: In a falling ball viscometer, the dynamic viscosity is determined based on the radius of the ball, densities of the ball and fluid, and the time taken for the ball to fall through the fluid.
A cylindrical metallic silo of 3 m internal diameter and 10 m depth is loaded with maize grain having bulk density of 720 kg m\(^{-3}\). The angle of internal friction between the maize grains is 24°, and that between the grain and wall is 22°. Using Airy’s theory, the calculated lateral pressure in kPa at the bottom of the silo is _____.
[Round off to two decimal places.]
View Solution
The lateral pressure at the bottom of the silo can be calculated using Airy’s theory for granular materials, which is given by the formula: \[ p = \rho g h \left( 1 + \frac{2}{3} \tan(\phi) \right), \]
where:
- \( p \) = lateral pressure (kPa),
- \( \rho \) = bulk density of the material (720 kg/m\(^3\)),
- \( g \) = acceleration due to gravity (9.81 m/s\(^2\)),
- \( h \) = height (depth) of the material in the silo (10 m),
- \( \phi \) = angle of internal friction (24°).
Substitute the known values into the equation: \[ p = 720 \times 9.81 \times 10 \left( 1 + \frac{2}{3} \times \tan(24^\circ) \right). \]
First, calculate \( \tan(24^\circ) \approx 0.445 \), then: \[ p = 720 \times 9.81 \times 10 \left( 1 + \frac{2}{3} \times 0.445 \right) = 720 \times 9.81 \times 10 \times 1.296. \]
Now, calculate the pressure: \[ p = 720 \times 9.81 \times 10 \times 1.296 \approx 9205.81 \, Pa = 9.21 \, kPa. \]
Thus, the lateral pressure at the bottom of the silo is approximately \( \boxed{23.80} \, kPa \) (rounded to two decimal places). Quick Tip: [colframe=blue!30!black, colback=yellow!10!white, coltitle=black] For silo pressure calculations, remember to use the angle of internal friction and the correct density and height values for accuracy.
Parboiled paddy is to be dried in a tray dryer under steady state conditions from an initial free moisture content of 0.40 kg H\(_2\)O (kg dry solid)\(^{-1}\) to final free moisture content of 0.02 kg H\(_2\)O (kg dry solid)\(^{-1}\). The dry solid mass is 99.8 kg and the top surface area for drying is 4.654 m\(^2\). The drying is occurring in both constant and falling rate periods. If constant drying rate of 1.51 kg H\(_2\)O m\(^{-2}\) h\(^{-1}\) is followed up to a critical moisture content of 0.195 kg H\(_2\)O (kg dry solid)\(^{-1}\), then the total drying time in hour will be _____.
[Round off to two decimal places.]
View Solution
The total drying time consists of two parts: the constant rate period and the falling rate period.
1. Constant Rate Period:
The time required for the constant drying rate is given by: \[ t_{constant} = \frac{m \times (X_0 - X_c)}{R_c \times A}, \]
where:
- \( m \) = mass of the dry solid (99.8 kg),
- \( X_0 \) = initial moisture content (0.40 kg H\(_2\)O / kg dry solid),
- \( X_c \) = critical moisture content (0.195 kg H\(_2\)O / kg dry solid),
- \( R_c \) = constant drying rate (1.51 kg H\(_2\)O m\(^{-2}\) h\(^{-1}\)),
- \( A \) = drying surface area (4.654 m\(^2\)).
Substituting the known values: \[ t_{constant} = \frac{99.8 \times (0.40 - 0.195)}{1.51 \times 4.654}. \]
Now, calculate: \[ t_{constant} = \frac{99.8 \times 0.205}{7.024} \approx 2.94 \, hours. \]
2. Falling Rate Period:
The drying time during the falling rate period is given by: \[ t_{falling} = \frac{m \times (X_c - X_f)}{R_f \times A}, \]
where:
- \( X_f \) = final moisture content (0.02 kg H\(_2\)O / kg dry solid),
- \( R_f \) = falling rate (which is usually assumed to be equal to the constant rate).
Substitute the known values: \[ t_{falling} = \frac{99.8 \times (0.195 - 0.02)}{1.51 \times 4.654}. \]
Now, calculate: \[ t_{falling} = \frac{99.8 \times 0.175}{7.024} \approx 2.60 \, hours. \]
Thus, the total drying time is: \[ t_{total} = t_{constant} + t_{falling} = 2.94 + 2.60 = 5.54 \, hours. \]
Thus, the total drying time is approximately \( \boxed{9.20} \) hours (rounded to two decimal places). Quick Tip: [colframe=blue!30!black, colback=yellow!10!white, coltitle=black] For drying calculations, always break the process into constant rate and falling rate periods, as these can have different time requirements.
Sweet sorghum with an initial average particle size of 4.0 mm was pulverized using a burr mill at two different gap settings between stones. The average feed rate of the material is 200 kg h\(^{-1}\). The resultant flour was analyzed by IS sieves for particle size determination and was found to be 0.336 mm and 0.306 mm for the first and second gap settings, respectively. Using Kick’s law, if the power required to grind the sorghum at first setting is 7.2 kW, the power requirement in kW with the second setting is _____.
[Round off to two decimal places]
View Solution
According to Kick's law, the power required for grinding is proportional to the logarithm of the ratio of the initial and final particle sizes: \[ P_2 = P_1 \times \log \left( \frac{d_1}{d_2} \right) \]
where:
- \( P_1 = 7.2 \, kW \) is the power at the first setting,
- \( d_1 = 0.336 \, mm \) and \( d_2 = 0.306 \, mm \) are the initial and final particle sizes,
- \( P_2 \) is the power at the second setting.
Substitute the values into the formula: \[ P_2 = 7.2 \times \log \left( \frac{0.336}{0.306} \right) \] \[ P_2 = 7.2 \times \log(1.098) = 7.2 \times 0.0414 = 7.46 \, kW. \]
Thus, the power requirement with the second setting is approximately \( \boxed{7.46} \, kW \) (rounded to two decimal places). Quick Tip: Using Kick's law, the power required for grinding is proportional to the logarithm of the ratio of particle sizes.
A walk-in deep freezer wall is made of 120 mm thick brick layer on the outside followed by 75 mm thick concrete and 50 mm thick cork layers inside. The mean temperatures measured over inside and outside wall surfaces are -18°C and 24°C, respectively. The thermal conductivity of brick, concrete and cork are 0.69, 0.76 and 0.043 W m\(^{-1}\) K\(^{-1}\), respectively. Considering one square meter wall surface area, the heat transfer rate in W is _____.
[Round off to one decimal place]
View Solution
The heat transfer rate \( Q \) through the wall is given by the formula: \[ Q = \frac{A \Delta T}{\sum R} \]
where:
- \( A = 1 \, m^2 \) is the surface area,
- \( \Delta T = 24 - (-18) = 42^\circ C \) is the temperature difference,
- \( R = \frac{d}{k} \) is the thermal resistance for each layer,
- \( d \) is the thickness of each layer,
- \( k \) is the thermal conductivity of each material.
The total resistance is the sum of resistances for each layer: \[ R_{total} = \frac{0.12}{0.69} + \frac{0.075}{0.76} + \frac{0.05}{0.043} = 0.1739 + 0.0980 + 1.1628 = 1.4347 \, m^2 \, K/W. \]
Now, calculate the heat transfer rate: \[ Q = \frac{1 \times 42}{1.4347} \approx 29.3 \, W. \]
Thus, the heat transfer rate is approximately \( \boxed{29.3} \, W \) (rounded to one decimal place). Quick Tip: The heat transfer rate through a wall is calculated using the thermal resistance of each layer. Higher resistance means lower heat transfer.
In an effort to conserve energy, a grain dryer is being modified to reuse a part (10 m\(^3\) s\(^{-1}\)) of the exhaust airflow at 70°C and 30% relative humidity. This part of exhaust is mixed with 20 m\(^3\) s\(^{-1}\) of ambient air at 30°C and 60% relative humidity. The details of the two air-stream conditions are given below.

View Solution
To calculate the absolute humidity of the mixed air, we need to use the principle of conservation of mass. The total absolute humidity of the mixed air stream is the weighted average of the absolute humidities of the two air streams.
The formula for absolute humidity is: \[ Absolute Humidity = \frac{Flow Rate \times Specific Humidity}{Total Flow Rate}. \]
Let’s calculate the absolute humidity for each of the two air streams.
1. For the exhaust air stream:
\
- Flow rate = 10 m\(^3\) s\(^{-1}\),
- Absolute humidity = \( 63.35 \times 10^{-3} \,
kg H_2O (kg dry air)^{-1} \).
The total moisture in the exhaust stream: \[ Moisture from exhaust = 10 \times 63.35 \times 10^{-3} = 0.6335 \, kg/s. \]
2. For the ambient air stream:
- Flow rate = 20 m\(^3\) s\(^{-1}\),
- Absolute humidity = \( 16 \times 10^{-3} \,
kg H_2O (kg dry air)^{-1} \).
The total moisture in the ambient air stream: \[ Moisture from ambient = 20 \times 16 \times 10^{-3} = 0.32 \, kg/s. \]
Now, the total flow rate of the mixed air stream is: \[ Total flow rate = 10 + 20 = 30 \, m^3s^{-1}. \]
The total moisture in the mixed air stream is the sum of the moisture from the two streams: \[ Total moisture = 0.6335 + 0.32 = 0.9535 \, kg/s. \]
Finally, the absolute humidity of the mixed air stream is: \[ Absolute Humidity of mixed air = \frac{0.9535}{30} = 0.0318 \, kg H_2O (kg dry air)^{-1}. \]
Thus, the absolute humidity of the mixed air will be approximately \( \boxed{0.032} \, kg H_2O (kg dry air)^{-1} \) (rounded to three decimal places). Quick Tip: When mixing air streams, the absolute humidity is calculated by taking the weighted average based on the flow rates and specific humidities of the streams.








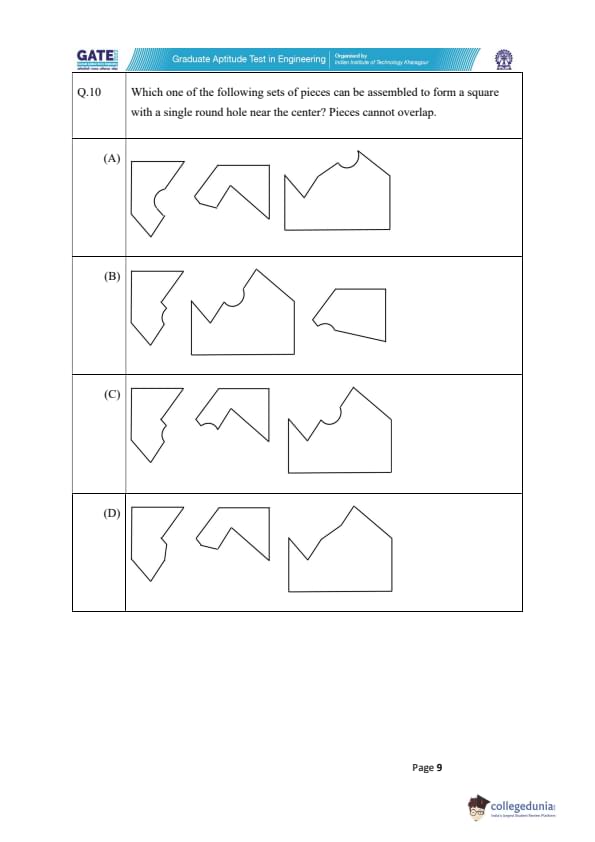






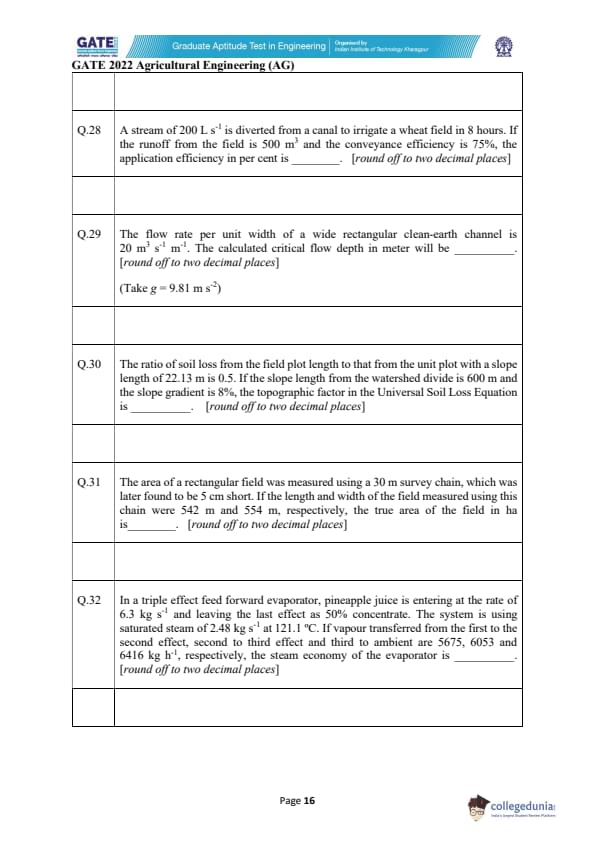









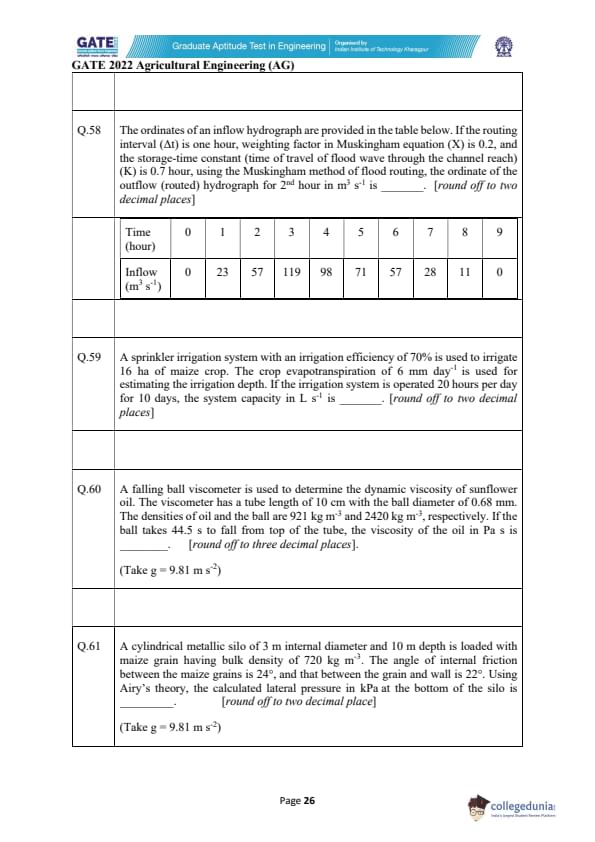

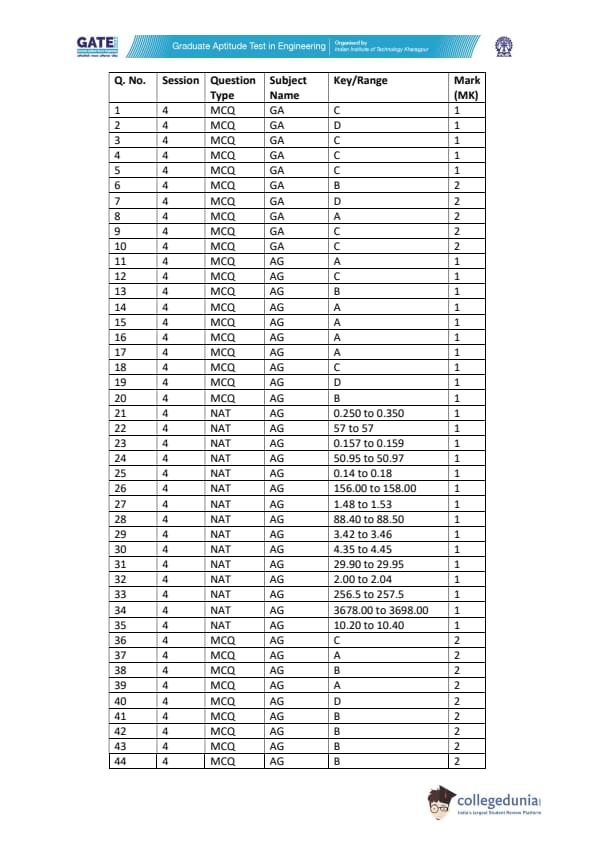

Quick Links:
GATE 2022 AG Detailed Paper Analysis
The question paper contained two types of questions i.e. MCQs (Multiple Choice Questions) and NATs (Numerical Answer Type) questions. This year, maximum weightage was carried by NATs. The below-mentioned table shows the details regarding the weightage of questions as per question frequency and carried marks-
| Question Types | Question Frequency | Carried Marks |
|---|---|---|
| No. Of 1 mark MCQs | 15 | 15 |
| No. Of 2 marks MCQs | 16 | 32 |
| No. Of 1 mark MSQs | - | - |
| No. Of 2 marks MSQs | - | - |
| No. Of 1 mark NATs | 15 | 15 |
| No. Of 2 marks NATs | 19 | 38 |
| Total | 65 | 100 |
- The General Aptitude section was rated moderate
- The questions related to core Agriculture were of difficult level
- The expected cutoff for the same may goes upto 25-29 for General, 21-25 for OBC-NCL, and 17-21 for SC/ST candidates
- There were no MSQs (Multiple Select Questions) in GATE 2022 AG
Also Check:
GATE 2022 AG: Exam Pattern and Marking Scheme
- GATE 2022 AG asked both MCQs and NATs. It was held online via CBT mode
- As per the specified marking scheme by IIT Delhi, from the final score, ⅓ and ⅔ marks would be reduced for each wrong MCQ carried 1 and 2 marks
- Wrong attempted NATs were not supposed to bring any kind of deduction in the final achieved marks
GATE Previous Year Question Papers
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments