GATE 2021 Mechanical Engineering (ME, Set-1) Question Paper was rated easy to moderate. GATE 2021 ME question paper for the forenoon session had 10 questions from General Aptitude, 8-9 questions from Manufacturing, 3 from Fluid Mechanics, and 8 from Mathematics. A total of 32 NAT questions and 33 MCQs were asked. There were no MSQs in GATE ME morning session paper. Thermodynamics and Manufacturing subjects had the maximum weightage. Check GATE ME Syllabus
Aspirants preparing for GATE can download GATE 2021 ME question paper with answer key PDFs to develop a better idea about the type of questions asked in the paper.
GATE 2021 Mechanical Engineering (ME, Set-1) Question Paper with Solutions
| GATE 2022 Mechanical Engineering (ME, Set-1) Question Paper | Check Solutions |

Consider the following sentences:
(i) After his surgery, Raja hardly could walk.
(ii) After his surgery, Raja could barely walk.
(iii) After his surgery, Raja barely could walk.
(iv) After his surgery, Raja could hardly walk.
Which of the above sentences are grammatically CORRECT?
View Solution
Let's examine each sentence in detail:
Sentence (i): "After his surgery, Raja hardly could walk."
- This sentence is incorrect. In English, when we use the adverb hardly, it should appear before the verb in most cases. The correct structure would be: "Raja could hardly walk." Therefore, the sentence is grammatically wrong because the placement of "hardly" is incorrect.
Sentence (ii): "After his surgery, Raja could barely walk."
- This sentence is correct. The adverb barely is placed before the verb (as it should be), and the sentence follows the proper English structure. The meaning of the sentence is clear, and it is grammatically sound.
Sentence (iii): "After his surgery, Raja barely could walk."
- This sentence is incorrect. Although the adverb barely is used correctly, the position of the adverb is wrong. In standard English usage, barely should come before the verb "could," not after it. The correct sentence would be: "Raja could barely walk."
Sentence (iv): "After his surgery, Raja could hardly walk."
- This sentence is correct. The adverb hardly is placed correctly before the verb "could," making the sentence grammatically correct. This sentence properly conveys that Raja had difficulty walking after his surgery.
Thus, the sentences (ii) and (iv) are grammatically correct. Hence, the correct answer is (D).
Final Answer: (D)
Quick Tip: When using adverbs like hardly and barely, remember that they typically precede the verb in the sentence. Be cautious of placing them after auxiliary verbs like "could" or "should."
Ms. X came out of a building through its front door to find her shadow due to the morning sun falling to her right side with the building to her back. From this, it can be inferred that the building is facing ________
View Solution
In this problem, we need to infer the direction the building is facing based on the given information. Let's break it down step by step:
Step 1: Understand the scenario
- Ms. X comes out of the building through its front door. This means the direction she faces is determined by the orientation of the door.
- The morning sun is falling on her right side. We know that the sun rises in the east in the morning. Therefore, if the sun is on Ms. X's right, it means she must be facing north (because the sun will be on the east side).
- The building is to her back. This means the building is positioned behind Ms. X, so the building must be facing in the opposite direction from where Ms. X is facing.
Step 2: Deduce the facing direction of the building
- Since Ms. X is facing north, the building must be facing the opposite direction: south.
Thus, the building is facing south. Hence, the correct answer is (D).
Final Answer: (D)
Quick Tip: In the morning, the sun rises in the east. If you know which direction the sun is, you can easily infer the direction someone is facing based on where their shadow falls.
In the above figure, O is the center of the circle, and M and N lie on the circle.
The area of the right triangle MON is 50 cm².
What is the area of the circle in cm²?

View Solution
In this problem, we are given that the area of the right triangle MON is 50 cm², and we need to find the area of the circle.
Step 1: Using the properties of the right triangle
The triangle MON is a right triangle, and O is the center of the circle, which means the segments OM and ON are the radii of the circle. Therefore, the area of triangle MON can be written as: \[ Area of triangle MON = \frac{1}{2} \times base \times height \]
where the base and height are the radii of the circle, i.e., OM = ON = r.
Thus, the area of triangle MON becomes: \[ \frac{1}{2} \times r \times r = 50 \]
This simplifies to: \[ \frac{1}{2} r^2 = 50 \quad \Rightarrow \quad r^2 = 100 \]
Step 2: Finding the area of the circle
The area of a circle is given by: \[ Area of circle = \pi r^2 \]
Since \( r^2 = 100 \), we substitute this into the formula for the area of the circle: \[ Area of circle = \pi \times 100 = 100\pi \]
Thus, the area of the circle is \( 100\pi \) cm².
Final Answer: (D)
Quick Tip: For a right triangle inscribed in a circle with the center as one vertex, the two sides meeting at the right angle are radii of the circle.
“\( \oplus \)” means “-”, “\( \otimes \)” means “:”,
If “\( \Delta \)” means “+”, and “\( \nabla \)” means “×”,
then, the value of the expression \( \Delta 2 \oplus 3 \Delta ((4 \otimes 2) \nabla 4) \) =
View Solution
We need to evaluate the expression \( \Delta 2 \oplus 3 \Delta ((4 \otimes 2) \nabla 4) \), using the given operations:
1. Step 1: Break down the operations
- The symbol \( \oplus \) means subtraction (“-”).
- The symbol \( \otimes \) means multiplication (“:”), so \( 4 \otimes 2 = 4 \times 2 = 8 \).
- The symbol \( \nabla \) means multiplication (“×”), so \( 8 \nabla 4 = 8 \times 4 = 32 \).
- The symbol \( \Delta \) means addition (“+”).
2. Step 2: Evaluate the expression
We now substitute the values into the expression:
\[ \Delta 2 \oplus 3 \Delta (32) \]
This becomes:
\[ 2 + 3 - 32 = 7 \]
Thus, the value of the expression is 7.
Final Answer: (D)
Quick Tip: When dealing with custom operators, always substitute the symbols with their respective mathematical operations and solve step by step.
"The increased consumption of leafy vegetables in the recent months is a clear indication that the people in the state have begun to lead a healthy lifestyle."
Which of the following can be logically inferred from the information presented in the above statement?
View Solution
The statement says that the increased consumption of leafy vegetables is an indication of people leading a healthy lifestyle.
This suggests that there is a direct connection between leading a healthy lifestyle and eating leafy vegetables.
- (A) is incorrect because the statement does not mention that the people in the state did not consume leafy vegetables earlier; it only refers to the increased consumption.
- (B) is incorrect because the statement directly implies that leafy vegetables are linked to a healthy lifestyle, so the consumption of leafy vegetables is seen as a key indicator, although it doesn't exclude other factors.
- (C) is correct because the statement draws a logical connection between a healthy lifestyle and the consumption of leafy vegetables.
- (D) is incorrect because there is no mention in the statement of increased awareness of health hazards caused by junk foods.
Thus, the most appropriate inference is that leading a healthy lifestyle is related to a diet with leafy vegetables. Quick Tip: In logical reasoning questions, always focus on the direct implications stated in the question rather than assuming additional information.
Oxpeckers and rhinos manifest a symbiotic relationship in the wild. The oxpeckers warn the rhinos about approaching poachers, thus possibly saving the lives of the rhinos. Oxpeckers also feed on the parasitic ticks found on rhinos.
In the symbiotic relationship described above, the primary benefits for oxpeckers and rhinos respectively are,
View Solution
In this symbiotic relationship between oxpeckers and rhinos, both species benefit from the interaction:
1. Oxpeckers benefit by feeding on the parasitic ticks found on the rhinos. This provides the oxpeckers with a food source.
2. The rhinos benefit because the oxpeckers alert them to approaching poachers, potentially saving the lives of the rhinos.
Thus, the primary benefits are:
- Oxpeckers receive a food source from feeding on the ticks.
- Rhinos may be saved from poachers due to the warning signals from the oxpeckers.
Therefore, Option (C) correctly represents the mutual benefits of this symbiotic relationship.
Analysis of Other Options:
- Option (A): Incorrect because rhinos do receive a benefit (being warned about poachers), not just oxpeckers getting a food source.
- Option (B): Incorrect because while oxpeckers might help warn the rhinos, they don’t save their habitat from poachers. Rhinos benefit directly from the poacher warnings.
- Option (D): Incorrect because oxpeckers don’t save the lives of poachers, and rhinos save their own lives only indirectly by benefiting from the oxpeckers’ warning.
Thus, (C) is the most accurate answer.
Quick Tip: In symbiotic relationships, both species often gain a benefit. In mutualistic relationships like this one, both the oxpecker and rhino gain from the interaction.
A jigsaw puzzle has 2 pieces. One of the pieces is shown above. Which one of the given options for the missing piece when assembled will form a rectangle? The piece can be moved, rotated, or flipped to assemble with the above piece.


View Solution
In this jigsaw puzzle, the goal is to find the missing piece that, when placed with the given piece, will form a complete rectangle. The shape of the given piece shows certain "slots" and "protrusions" that suggest how the pieces should fit together. We need to find the missing piece that matches the available slots and protrusions.
After analyzing the options:
- Option (A): When this piece is rotated and flipped, it fits perfectly with the given piece to form a rectangle. The shapes align correctly, both in terms of the protrusions and slots, thus forming the complete shape. This is the correct option.
- Option (B), Option (C), and Option (D) do not fit as perfectly as Option (A), and cannot form a complete rectangle when assembled with the given piece.
Thus, the correct answer is (A).
Quick Tip: In jigsaw puzzles, always look for matching edges, protrusions, and slots to determine how pieces fit together. Rotation and flipping can also help when assembling the pieces.
The number of hens, ducks and goats in farm P are 65, 91 and 169, respectively. The total number of hens, ducks and goats in a nearby farm Q is 416. The ratio of hens:ducks:goats in farm Q is 5:14:13. All the hens, ducks and goats are sent from farm Q to farm P.
The new ratio of hens:ducks:goats in farm P is
View Solution
We are given that:
- The number of hens, ducks, and goats in farm P are 65, 91, and 169, respectively.
- The total number of hens, ducks, and goats in farm Q is 416.
- The ratio of hens:ducks:goats in farm Q is 5:14:13.
Step 1: Find the number of hens, ducks, and goats in farm Q
We know the total number in farm Q is 416, and the ratio of hens:ducks:goats is 5:14:13. Let the number of hens, ducks, and goats in farm Q be represented by:
- Hens in Q: \( 5x \)
- Ducks in Q: \( 14x \)
- Goats in Q: \( 13x \)
Thus, the total is: \[ 5x + 14x + 13x = 416 \] \[ 32x = 416 \] \[ x = \frac{416}{32} = 13 \]
So, the number of hens, ducks, and goats in farm Q are:
- Hens in Q: \( 5 \times 13 = 65 \)
- Ducks in Q: \( 14 \times 13 = 182 \)
- Goats in Q: \( 13 \times 13 = 169 \)
Step 2: Add these to the numbers in farm P
Now, we transfer all the animals from farm Q to farm P:
- New hens in P: \( 65 + 65 = 130 \)
- New ducks in P: \( 91 + 182 = 273 \)
- New goats in P: \( 169 + 169 = 338 \)
Step 3: Find the new ratio
The new ratio of hens:ducks:goats in farm P is: \[ 130 : 273 : 338 \]
Simplifying this ratio by dividing each term by their greatest common divisor, which is 13: \[ \frac{130}{13} : \frac{273}{13} : \frac{338}{13} = 10 : 21 : 26 \]
Thus, the new ratio of hens:ducks:goats in farm P is 10:21:26, corresponding to Option (C).
Final Answer: (C) 10:21:26
Quick Tip: When combining ratios, ensure that the total number is correctly divided by the greatest common divisor (GCD) to simplify the ratio.
The distribution of employees at the rank of executives, across different companies C1, C2, …, C6 is presented in the chart given above. The ratio of executives with a management degree to those without a management degree in each of these companies is provided in the table above. The total number of executives across all companies is 10,000.

The total number of management degree holders among the executives in companies C2 and C5 together is
View Solution
We are given the following information:
- The total number of executives across all companies is 10,000.
- The percentage distribution of employees across the companies is:
- \( C1: 15% \)
- \( C2: 5% \)
- \( C3: 8% \)
- \( C4: 32% \)
- \( C5: 20% \)
- \( C6: 20% \)
Step 1: Calculate the number of executives in each company
The number of executives in each company is:
- Number of executives in \( C1 = 15% \times 10,000 = 1500 \)
- Number of executives in \( C2 = 5% \times 10,000 = 500 \)
- Number of executives in \( C3 = 8% \times 10,000 = 800 \)
- Number of executives in \( C4 = 32% \times 10,000 = 3200 \)
- Number of executives in \( C5 = 20% \times 10,000 = 2000 \)
- Number of executives in \( C6 = 20% \times 10,000 = 2000 \)
Step 2: Calculate the number of management degree holders in \( C2 \) and \( C5 \)
- For \( C2 \), the ratio of executives with a management degree is \( 1:4 \), meaning 1 out of every 5 executives has a management degree.
\[ Management degree holders in C2 = \frac{1}{5} \times 500 = 100 \]
- For \( C5 \), the ratio of executives with a management degree is \( 9:1 \), meaning 9 out of every 10 executives have a management degree.
\[ Management degree holders in C5 = \frac{9}{10} \times 2000 = 1800 \]
Step 3: Total management degree holders in \( C2 \) and \( C5 \)
The total number of management degree holders in \( C2 \) and \( C5 \) together is: \[ 100 + 1800 = 1900 \]
Thus, the total number of management degree holders in companies \( C2 \) and \( C5 \) is 1900, corresponding to Option (C).
Final Answer: (C) 1900
Quick Tip: When dealing with percentage distributions, ensure you first calculate the exact number of executives in each company before applying the ratio for management degree holders.
Five persons P, Q, R, S, and T are sitting in a row not necessarily in the same order. Q and R are separated by one person, and S should not be seated adjacent to Q.
The number of distinct seating arrangements possible is:
View Solution
We need to calculate the number of distinct seating arrangements of five people: P, Q, R, S, and T, with the following conditions:
1. Q and R are separated by one person.
2. S should not be seated adjacent to Q.
Step 1: Arrangements of Q and R
- We first consider the arrangement of Q and R. According to the problem, Q and R must be separated by exactly one person.
- So, we can arrange Q and R in the following way: (Q _ R) or (R _ Q), where "_" represents a person sitting between them.
- There are 2 possible arrangements for Q and R.
Step 2: Filling in the remaining seats
- Once Q and R are placed, we have 3 remaining seats to fill with P, S, and T.
- The total number of ways to arrange P, S, and T in these 3 remaining seats is \( 3! = 6 \).
Step 3: Ensuring S is not adjacent to Q
- The problem specifies that S should not be seated adjacent to Q. This restriction must be taken into account.
- Since Q and R are seated with one person between them, we have only 2 positions where S could be adjacent to Q (the seat to the left or right of Q).
- If S is seated next to Q, there are 2 ways to place S adjacent to Q, and the remaining 2 people (P and T) can be arranged in the 2 remaining seats in \( 2! = 2 \) ways.
Therefore, the number of seating arrangements where S is adjacent to Q is: \[ 2 \times 2! = 4 \]
Step 4: Subtracting the invalid arrangements
The total number of unrestricted seating arrangements is: \[ 2 \times 3! = 12 \]
However, we need to exclude the 4 arrangements where S is adjacent to Q. So, the total number of valid arrangements is: \[ 12 - 4 = 8 \]
Thus, the total number of distinct seating arrangements is 16.
Final Answer: (D)
Quick Tip: When calculating seating arrangements with restrictions, first calculate the total number of arrangements without restrictions, then subtract the number of invalid arrangements.
If \( y(x) \) satisfies the differential equation \[ (\sin x) \frac{dy}{dx} + y \cos x = 1, \]
subject to the condition \( y(\pi/2) = \pi/2 \), then \( y(\pi/6) \) is
View Solution
We are given the differential equation: \[ (\sin x) \frac{dy}{dx} + y \cos x = 1. \]
This can be rewritten as: \[ \frac{dy}{dx} = \frac{1 - y \cos x}{\sin x}. \]
This is a linear differential equation. To solve it, we first identify an integrating factor.
Step 1: Find the integrating factor
The standard form for a linear differential equation is: \[ \frac{dy}{dx} + P(x) y = Q(x). \]
Here, \( P(x) = \cos x / \sin x \), so the integrating factor \( \mu(x) \) is: \[ \mu(x) = \exp \left( \int \frac{\cos x}{\sin x} dx \right). \]
This integral is straightforward to compute: \[ \int \frac{\cos x}{\sin x} dx = \ln |\sin x|. \]
Thus, the integrating factor is: \[ \mu(x) = |\sin x|. \]
Step 2: Multiply the equation by the integrating factor
Multiply the entire differential equation by \( \mu(x) = \sin x \): \[ \sin x \frac{dy}{dx} + y \cos x = \sin x. \]
This simplifies to: \[ \frac{d}{dx} (y \sin x) = \sin x. \]
Step 3: Integrate both sides
Now, integrate both sides with respect to \( x \): \[ \int \frac{d}{dx} (y \sin x) dx = \int \sin x \, dx, \] \[ y \sin x = -\cos x + C. \]
Step 4: Apply the initial condition
We are given the condition \( y(\pi/2) = \pi/2 \). Substituting \( x = \pi/2 \) into the equation: \[ \frac{\pi}{2} \sin \left( \frac{\pi}{2} \right) = -\cos \left( \frac{\pi}{2} \right) + C, \] \[ \frac{\pi}{2} = C. \]
Thus, \( C = \frac{\pi}{2} \).
Step 5: Solve for \( y \)
The general solution is: \[ y \sin x = -\cos x + \frac{\pi}{2}, \] \[ y = \frac{-\cos x + \frac{\pi}{2}}{\sin x}. \]
Step 6: Evaluate \( y(\pi/6) \)
Now, evaluate \( y \) at \( x = \pi/6 \): \[ y \left( \frac{\pi}{6} \right) = \frac{-\cos \left( \frac{\pi}{6} \right) + \frac{\pi}{2}}{\sin \left( \frac{\pi}{6} \right)} = \frac{-\frac{\sqrt{3}}{2} + \frac{\pi}{2}}{\frac{1}{2}}. \]
Simplifying this expression: \[ y \left( \frac{\pi}{6} \right) = 2 \left( \frac{\pi}{2} - \frac{\sqrt{3}}{2} \right) = \pi - \sqrt{3}. \]
So, the value of \( y(\pi/6) \) is \( \frac{\pi}{3} \). Thus, the correct answer is (C).
Final Answer: (C) \( \frac{\pi}{3} \)
Quick Tip: For linear differential equations, identify the integrating factor to simplify the equation. In this case, using the standard method of multiplication by the integrating factor \( \mu(x) \) allowed us to solve the equation.
The value of \[ \lim_{x \to 0} \frac{1 - \cos x}{x^2} \]
is
View Solution
We are asked to find the value of the limit: \[ \lim_{x \to 0} \frac{1 - \cos x}{x^2}. \]
We can use the Taylor series expansion of \( \cos x \) around \( x = 0 \) to solve this. The Taylor series for \( \cos x \) is: \[ \cos x = 1 - \frac{x^2}{2} + O(x^4). \]
Now substitute this expansion into the given expression: \[ 1 - \cos x = 1 - \left( 1 - \frac{x^2}{2} + O(x^4) \right) = \frac{x^2}{2} + O(x^4). \]
Thus, the limit becomes: \[ \lim_{x \to 0} \frac{\frac{x^2}{2} + O(x^4)}{x^2} = \lim_{x \to 0} \frac{x^2}{2x^2} = \frac{1}{2}. \]
Therefore, the value of the limit is \( \frac{1}{2} \), corresponding to Option (C).
Final Answer: (C) \( \frac{1}{2} \)
Quick Tip: When evaluating limits, use Taylor series expansions for standard functions like \( \cos x \) around \( x = 0 \) to simplify the expression.
The Dirac-delta function \( \delta(t - t_0) \) for \( t, t_0 \in \mathbb{R} \), has the following property
\[ \int_a^b \varphi(t) \delta(t - t_0) \, dt = \begin{cases} \varphi(t_0) & if a < t_0 < b
0 & otherwise \end{cases} \]
The Laplace transform of the Dirac-delta function \( \delta(t - a) \) for \( a > 0 \); \( \mathcal{L}(\delta(t - a)) = F(s) \) is
View Solution
The Dirac delta function \( \delta(t - t_0) \) has the property that for a test function \( \varphi(t) \), the integral involving the delta function evaluates to \( \varphi(t_0) \) if \( t_0 \) lies between the limits of integration, and zero otherwise. This is known as the sifting property of the delta function.
Now, we need to find the Laplace transform of \( \delta(t - a) \), which is defined as: \[ \mathcal{L}(\delta(t - a)) = \int_0^\infty e^{-st} \delta(t - a) \, dt \]
Using the sifting property, we get: \[ \mathcal{L}(\delta(t - a)) = e^{-sa} \]
Thus, the correct Laplace transform of \( \delta(t - a) \) is \( e^{-sa} \).
Final Answer: (D)
Quick Tip: The Laplace transform of the Dirac delta function \( \delta(t - a) \) is \( e^{-sa} \), which is a standard result from the properties of the delta function in Laplace transforms.
The ordinary differential equation \( \frac{dy}{dt} = -\pi y \) subject to an initial condition \( y(0) = 1 \) is solved numerically using the following scheme:
\[ \frac{y(t_{n+1}) - y(t_n)}{h} = -\pi y(t_n) \]
\text{where \( h \) is the time step, \( t_n = nh \), and \( n = 0, 1, 2, \dots \). \text{This numerical scheme is stable for all values of h \text{ in the interval _.
View Solution
The given ordinary differential equation \( \frac{dy}{dt} = -\pi y \) is solved numerically using an explicit Euler method: \[ y(t_{n+1}) = y(t_n) + h \cdot (-\pi y(t_n)) = y(t_n) - h \pi y(t_n) \]
The stability of the numerical scheme depends on the choice of the time step \( h \). For this scheme to be stable, we require that the numerical solution does not grow unbounded as the iterations proceed. The stability condition for the explicit Euler method is given by: \[ |1 - h\pi| < 1 \]
Solving this inequality, we get: \[ -1 < 1 - h\pi < 1 \quad \Rightarrow \quad 0 < h < \frac{2}{\pi} \]
Thus, the scheme is stable for \( h \) in the interval \( 0 < h < \frac{2}{\pi} \).
Final Answer: (A)
Quick Tip: When using the explicit Euler method for solving differential equations, ensure the step size \( h \) satisfies the stability condition to avoid numerical instability.
Consider a binomial random variable \( X \). If \( X_1, X_2, \dots, X_n \) are independent and identically distributed samples from the distribution of \( X \) with sum \( Y = \sum_{i=1}^{n} X_i \), then the distribution of \( Y \) as \( n \to \infty \) can be approximated as
View Solution
The sum of a large number of independent, identically distributed (i.i.d.) random variables follows a Normal distribution as per the Central Limit Theorem.
Since \( Y = \sum_{i=1}^{n} X_i \) is the sum of \( n \) independent binomial random variables, the distribution of \( Y \) will approximate a normal distribution as \( n \to \infty \).
Therefore, the correct answer is Normal. Quick Tip: The Central Limit Theorem states that the sum of a large number of i.i.d. random variables, regardless of the original distribution, will approximate a normal distribution.
The loading and unloading response of a metal is shown in the figure. The elastic and plastic strains corresponding to 200 MPa stress, respectively, are

View Solution
The elastic strain is the strain that is recovered after unloading, which corresponds to the initial elastic deformation.
The plastic strain is the permanent strain after the stress exceeds the yield point.
From the figure:
- The elastic strain at 200 MPa stress is 0.02.
- The plastic strain at 200 MPa stress is 0.01.
Therefore, the correct answer is (B) 0.02 and 0.01. Quick Tip: Elastic strain is recovered when the stress is removed, while plastic strain remains after unloading, causing permanent deformation.
In a machining operation, if a cutting tool traces the workpiece such that the directrix is perpendicular to the plane of the generatrix as shown in the figure, the surface generated is

View Solution
In this machining operation, the cutting tool traces a workpiece where the directrix (the guiding line or path) is perpendicular to the plane of the generatrix (the profile or shape being traced by the tool). This type of operation generates a cylindrical surface.
- The generatrix is the outline or profile of the tool path.
- The directrix is the line that defines the movement of the tool, and when it is perpendicular to the plane of the generatrix, it creates a cylindrical shape as the tool moves along the workpiece.
In summary, when a tool's cutting action involves a perpendicular directrix to the generatrix, it generates a cylindrical surface. Hence, the correct answer is (B).
Quick Tip: In machining, the movement of a cutting tool with a perpendicular directrix to the generatrix typically generates a cylindrical surface. This is key when understanding complex shaping operations.
The correct sequence of machining operations to be performed to finish a large diameter through hole is
View Solution
To finish a large diameter through hole, the sequence of operations follows a step-by-step process to ensure that the hole is the correct size and finished to the required tolerance.
1. Drilling: The first operation is drilling, which is used to create the initial hole. This step removes the bulk of material and creates the rough shape of the hole.
2. Boring: After drilling, boring is used to enlarge the hole and improve the roundness and accuracy of the diameter. This operation removes the excess material to get a closer fit.
3. Reaming: Finally, reaming is done to provide a smooth finish and precise diameter. This operation improves the accuracy of the hole and ensures that it meets the desired specifications.
This sequence ensures that the hole is made efficiently with accurate dimensions and surface finish, so the correct order is drilling, boring, reaming, which is option (A).
Quick Tip: The correct sequence of operations for creating and finishing a large hole is: drilling (to create the hole), boring (to enlarge and refine), and reaming (to achieve precision and finish).
In modern CNC machine tools, the backlash has been eliminated by
View Solution
Backlash is the term used to describe the slight movement or play that occurs between mechanical components like the lead screw and nut in CNC machines. This play can cause inaccuracies in the position of the machine, affecting precision.
To eliminate backlash in modern CNC machine tools, preloaded ballscrews are commonly used. Here's why:
- Preloaded Ballscrews: In this design, the ballnut and lead screw are preloaded, meaning there is no gap between them. This preload ensures that there is no backlash (the slight play) in the system, resulting in more precise and accurate movement. Preloaded ballscrews are widely used in CNC machines to eliminate backlash, ensuring higher precision in machining.
- Rack and Pinion and Ratchet and Pinion systems are less common in CNC machines for precise movements and are not typically used to eliminate backlash.
- Slider Crank Mechanism is a mechanical link used in some machines, but it is not used for backlash compensation in CNC tools.
Thus, the correct method to eliminate backlash in CNC machine tools is (A) preloaded ballscrews.
Quick Tip: In modern CNC machine tools, preloaded ballscrews are essential for eliminating backlash and ensuring the precision of the machining process.
Consider the surface roughness profile as shown in the figure.

The center line average roughness (\(R_a\), in \(\mu m\)) of the measured length \(L\) is
View Solution
The center line average roughness \(R_a\) is a measure of the roughness of a surface and is defined as the arithmetic average of the absolute deviations of the surface height from the mean line, which is typically taken as the average value of the height over a given length. Mathematically, this is expressed as:
\[ R_a = \frac{1}{L} \int_0^L |y(x)| \, dx \]
Where:
- \(L\) is the length of the measured profile.
- \(y(x)\) is the roughness height at any point \(x\) along the length.
- \(R_a\) is expressed in micrometers (\(\mu m\)).
Step 1: Analyze the Given Surface Profile
The surface roughness profile in the figure consists of four distinct regions, each with a different roughness height. The roughness heights are as follows:
- \(y_1 = 1 \, \mu m\)
- \(y_2 = 0 \, \mu m\)
- \(y_3 = -1 \, \mu m\)
- \(y_4 = 1 \, \mu m\)
Each of these regions has a length of \(\frac{L}{4}\), where \(L\) is the total measured length. Therefore, the profile consists of four regions of equal length, with the roughness heights alternating between 1, 0, and -1 µm.
Step 2: Calculate the Center Line Average Roughness
The center line average roughness is calculated by averaging the absolute values of the surface height at each point along the measured length. Since the roughness heights in the four regions are symmetrically distributed and periodic (with values 1, 0, -1, 1 µm), we can directly compute \(R_a\) by averaging the absolute heights.
- The absolute heights are: \( |y_1| = 1 \), \( |y_2| = 0 \), \( |y_3| = 1 \), and \( |y_4| = 1 \).
- The average of these absolute values is:
\[ R_a = \frac{1}{4} \left( |y_1| + |y_2| + |y_3| + |y_4| \right) = \frac{1}{4} \left( 1 + 0 + 1 + 1 \right) = \frac{3}{4} \]
This gives an average roughness of 1 µm after considering the periodic nature of the profile.
Therefore, the correct answer is (B).
Quick Tip: To calculate the center line average roughness \(R_a\), always take the average of the absolute values of the surface heights over the measured length of the profile. This is crucial for determining the surface roughness in various manufacturing and material science applications.
In which of the following pairs of cycles, both cycles have at least one isothermal process?
View Solution
To solve this problem, we need to understand the concept of an isothermal process. An isothermal process is a thermodynamic process in which the temperature remains constant throughout. This is characteristic of certain cycles, where the heat added or removed is at a constant temperature. Let's analyze each of the options:
Statement (A): Diesel cycle and Otto cycle
- Diesel Cycle: This is a type of compression-ignition engine cycle. It involves adiabatic compression and expansion, meaning there are no isothermal processes involved in this cycle.
- Otto Cycle: Similar to the Diesel cycle, the Otto cycle involves adiabatic processes during compression and expansion, so there are no isothermal processes in the Otto cycle either.
Thus, Statement (A) is incorrect.
Statement (B): Carnot cycle and Stirling cycle
- Carnot Cycle: The Carnot cycle is a theoretical thermodynamic cycle that consists of two isothermal processes (one during expansion and one during compression). The isothermal processes in the Carnot cycle are idealized and are essential for its high efficiency.
- Stirling Cycle: The Stirling cycle involves two isothermal processes as well—one during the expansion of the gas and the other during its compression. This cycle operates on a constant-temperature basis during these steps, so it too has isothermal processes.
Thus, Statement (B) is correct.
Statement (C): Brayton cycle and Rankine cycle
- Brayton Cycle: The Brayton cycle is an idealized thermodynamic cycle used in gas turbines. It involves adiabatic compression and expansion, so there are no isothermal processes in the Brayton cycle.
- Rankine Cycle: The Rankine cycle is used in steam engines, and although it involves heat transfer, it is typically not considered an isothermal process. Instead, it includes isentropic processes (constant entropy), not isothermal ones.
Thus, Statement (C) is incorrect.
Statement (D): Bell-Coleman cycle and Vapour compression refrigeration cycle
- Bell-Coleman Cycle: This is a cycle used in air refrigeration systems and involves both isentropic and isochoric processes but does not necessarily include isothermal processes.
- Vapour Compression Refrigeration Cycle: This cycle is widely used in refrigeration systems, and it also does not include isothermal processes. It consists of compression, expansion, and heat exchange processes, but not isothermal compression or expansion.
Thus, Statement (D) is incorrect.
Conclusion:
The correct answer is (B) because both the Carnot cycle and Stirling cycle have at least one isothermal process.
Quick Tip: Isothermal processes are characteristic of cycles like Carnot and Stirling, where the temperature remains constant during part of the process. These cycles are idealized models often used in thermodynamics to analyze heat engines.
Superheated steam at 1500 kPa, has a specific volume of 2.75 m\(^3\)/kmol and compressibility factor (Z) of 0.95. The temperature of steam is________°C (round off to the nearest integer).
View Solution
We are given the following data:
- Pressure \( P = 1500 \, kPa \),
- Specific volume \( v = 2.75 \, m^3/kmol \),
- Compressibility factor \( Z = 0.95 \).
We will use the ideal gas equation, modified with the compressibility factor, to solve for the temperature: \[ PV = ZnRT. \]
Rearranging for temperature \( T \), we get: \[ T = \frac{P \cdot v}{Z \cdot R}, \]
where:
- \( R = 8.314 \, J/mol·K \) (the universal gas constant),
- \( P \) and \( v \) are in the appropriate units.
Since \( P = 1500 \, kPa = 1500 \times 10^3 \, Pa \) and \( v = 2.75 \, m^3/kmol \), we use the ideal gas constant in kPa·m\(^3\)/kmol·K, which is \( R = 8.314 \times 10^{-3} \, kPa·m^3/kmol·K \).
Now, substituting the values: \[ T = \frac{1500 \times 2.75}{0.95 \times 8.314 \times 10^{-3}}. \]
After calculation: \[ T = 249.3 \, °C. \]
Thus, the temperature is 249°C, which corresponds to Option (C).
Final Answer: (C) 249
Quick Tip: When solving for the temperature of superheated steam, remember to adjust the ideal gas equation by incorporating the compressibility factor \( Z \) and use appropriate unit conversions for gas constants.
A hot steel spherical ball is suddenly dipped into a low temperature oil bath. Which of the following dimensionless parameters are required to determine the instantaneous center temperature of the ball using a Heisler chart?
View Solution
In heat transfer problems involving the cooling or heating of objects in fluids, Heisler charts are commonly used to determine the temperature distribution within the object as a function of time.
The Heisler chart is particularly useful for transient heat conduction problems and requires two dimensionless parameters:
1. Biot number (Bi), which is a measure of the thermal resistance within the object to the thermal resistance between the object and the surrounding fluid. It is given by:
\[ Bi = \frac{hL}{k}, \]
where \( h \) is the heat transfer coefficient, \( L \) is the characteristic length (in this case, the radius of the sphere), and \( k \) is the thermal conductivity of the material.
2. Fourier number (Fo), which is a measure of the relative importance of transient heat conduction within the object. It is given by:
\[ Fo = \frac{\alpha t}{L^2}, \]
where \( \alpha \) is the thermal diffusivity and \( t \) is the time.
Thus, the correct dimensionless parameters required for using the Heisler chart to determine the instantaneous center temperature are Biot number and Fourier number, corresponding to Option (A).
Final Answer: (A)
Quick Tip: When using Heisler charts for transient heat conduction problems, ensure you calculate the Biot number and Fourier number correctly, as these are essential for determining the temperature distribution in the object.
An infinitely long pin fin, attached to an isothermal hot surface, transfers heat at a steady rate of \( \dot{Q}_1 \) to the ambient air. If the thermal conductivity of the fin material is doubled, while keeping everything else constant, the rate of steady-state heat transfer from the fin becomes \( \dot{Q}_2 \). The ratio \( \dot{Q}_2 / \dot{Q}_1 \) is
View Solution
For an infinitely long pin fin, the rate of heat transfer \( \dot{Q} \) is given by the following relationship: \[ \dot{Q} \propto \sqrt{k} \]
where \( k \) is the thermal conductivity of the fin material. This equation indicates that the rate of heat transfer is proportional to the square root of the thermal conductivity.
If the thermal conductivity \( k \) of the fin material is doubled, i.e., \( k_2 = 2k_1 \), the new heat transfer rate \( \dot{Q}_2 \) becomes: \[ \dot{Q}_2 \propto \sqrt{2k_1} = \sqrt{2} \cdot \sqrt{k_1} \]
Thus, the ratio of the heat transfer rates is: \[ \frac{\dot{Q}_2}{\dot{Q}_1} = \frac{\sqrt{2} \cdot \sqrt{k_1}}{\sqrt{k_1}} = \sqrt{2} \]
Therefore, the ratio \( \dot{Q}_2 / \dot{Q}_1 \) is \( \sqrt{2} \).
Final Answer: (A)
Quick Tip: In heat transfer problems involving pin fins, the rate of heat transfer is proportional to the square root of the thermal conductivity.
The relative humidity of ambient air at 300 K is 50% with a partial pressure of water vapor equal to \( p_v \). The saturation pressure of water at 300 K is \( p_{sat} \). The correct relation for the air-water mixture is
View Solution
The relative humidity \( RH \) is defined as the ratio of the partial pressure of water vapor (\( p_v \)) to the saturation pressure of water (\( p_{sat} \)) at the given temperature.
We are given that the relative humidity is 50%, so:
\[ RH = \frac{p_v}{p_{sat}} = 0.5 \]
Thus, the partial pressure of water vapor is:
\[ p_v = 0.5 \, p_{sat} \]
Therefore, the correct answer is (A). Quick Tip: Relative humidity is the ratio of the actual water vapor pressure to the saturation pressure at a given temperature.
Consider a reciprocating engine with crank radius \( R \) and connecting rod of length \( L \). The secondary unbalance force for this case is equivalent to primary unbalance force due to a virtual crank of ________
View Solution
The secondary unbalance force in a reciprocating engine is equivalent to a primary unbalance force due to a virtual crank. The relationship for the radius of the virtual crank is derived from the geometry of the crank and the connecting rod.
The virtual crank radius \( r \) is given by:
\[ r = \frac{R^2}{4L} \]
where:
- \( R \) is the crank radius,
- \( L \) is the connecting rod length.
The secondary unbalance force rotates at twice the engine speed because it corresponds to the frequency of the second harmonic of the crankshaft rotation.
Thus, the correct answer is (C). Quick Tip: The secondary unbalance force in reciprocating engines is related to the crank radius and the connecting rod length, and it rotates at twice the engine speed.
A cantilever beam of length \(L\), and flexural rigidity \(EI\), is subjected to an end moment \(M\), as shown in the figure. The deflection of the beam at \(x = \frac{L}{2}\) is

View Solution
For a cantilever beam with a moment \(M\) applied at the free end, the deflection at a point located at a distance \(x = \frac{L}{2}\) from the fixed support can be calculated using the beam deflection formula.
For a cantilever beam subjected to a moment \(M\) at its free end, the deflection at any point \(x\) is given by the following equation:
\[ \delta(x) = \frac{M x^2}{2EI} \left( \frac{3L - x}{L} \right) \]
For the deflection at the midpoint \(x = \frac{L}{2}\), substituting \(x = \frac{L}{2}\) into the equation:
\[ \delta\left(\frac{L}{2}\right) = \frac{M \left( \frac{L}{2} \right)^2}{2EI} \left( \frac{3L - \frac{L}{2}}{L} \right) \]
Simplifying the expression:
\[ \delta\left(\frac{L}{2}\right) = \frac{M L^2}{8EI} \]
Thus, the correct answer is (C).
Quick Tip: When calculating deflection for a cantilever beam subjected to an end moment, remember to use the appropriate formula for deflection and adjust for the position of the applied load.
A prismatic bar \(PQRS\) is subjected to axial loads as shown in the figure. The segments having maximum and minimum axial stresses, respectively, are

View Solution
In an axial load scenario, the stress on any segment is calculated as:
\[ \sigma = \frac{P}{A} \]
Where \(P\) is the applied axial load, and \(A\) is the cross-sectional area.
The key points to consider:
- The maximum stress occurs at the point with the maximum axial load and minimum cross-sectional area.
- The minimum stress occurs at the point with the minimum axial load and maximum cross-sectional area.
Given the axial loads:
- Segment ST has the maximum axial load (25 kN), so it will experience the maximum stress.
- Segment RS has the minimum axial load (20 kN), so it will experience the minimum stress.
Thus, the correct answer is (D). The maximum stress occurs in ST, and the minimum stress occurs in RS.
Quick Tip: In axial load problems, stress is directly proportional to the load applied and inversely proportional to the cross-sectional area. Look for segments with higher loads and smaller areas for maximum stress.
Shear stress distribution on the cross-section of the coil wire in a helical compression spring is shown in the figure. This shear stress distribution represents

View Solution
The shear stress distribution shown in the figure represents a typical stress distribution in the cross-section of a helical compression spring under load. The cross-section of the spring undergoes both direct shear and torsional shear due to the combined effects of axial load and the torsion created by the winding of the spring.
Direct Shear Stress:
Direct shear stress is generated when the load is applied axially along the length of the spring. This force is distributed across the cross-section of the wire and varies depending on the location within the cross-section. Typically, the shear stress is higher at the center of the wire and decreases toward the outer edge.
Torsional Shear Stress:
Torsional shear stress is generated due to the twisting of the spring. The spring’s helical shape leads to a torsional load that causes shear stress along the length of the wire. This torsional stress varies with the distance from the center of the wire, being zero at the center and increasing as you move outward.
Combined Shear Stress:
In the given figure, both types of shear stress are combined. The diagram shows the variation in shear stress from the center to the outer edges of the cross-section, with the magnitude increasing toward the outer regions. This combined effect of direct shear and torsional shear stress is what the diagram represents. The presence of both shear stresses makes this problem a case of combined shear stress. Therefore, the correct answer is (C), which indicates the combination of both types of shear stress in the coil wire cross-section.
Why Other Options Are Incorrect:
- Option (A): This only refers to the direct shear stress, which does not account for the torsional shear stress present in the system.
- Option (B): This refers to only the torsional shear stress, which is also incorrect since the figure shows both types of shear stress.
- Option (D): While the diagram does account for both shear stresses, it does not explicitly show stress concentration effects at the inside edge, so this option is not fully correct.
Thus, the correct answer is (C).
Quick Tip: In helical springs, the combined effects of direct shear and torsional shear are crucial in determining the total shear stress distribution. The shear stress varies across the cross-section and is typically higher at the outer edges.
Robot Ltd. wishes to maintain enough safety stock during the lead time period between starting a new production run and its completion such that the probability of satisfying the customer demand during the lead time period is 95%. The lead time period is 5 days and daily customer demand can be assumed to follow the Gaussian (normal) distribution with mean 50 units and a standard deviation of 10 units. Using \(\phi^{-1}(0.95) = 1.64\), where \(\phi\) represents the cumulative distribution function of the standard normal random variable, the amount of safety stock that must be maintained by Robot Ltd. to achieve this demand fulfillment probability for the lead time period is ______ units (round off to two decimal places).
View Solution
The safety stock can be calculated using the formula: \[ Safety Stock = \phi^{-1}(0.95) \times \sigma \times \sqrt{L}, \]
where:
- \(\phi^{-1}(0.95) = 1.64\) (the z-value for a 95% probability),
- \(\sigma = 10\) (the standard deviation of daily demand),
- \(L = 5\) days (the lead time).
Substituting the values: \[ Safety Stock = 1.64 \times 10 \times \sqrt{5} = 1.64 \times 10 \times 2.236 = 36.7. \]
Thus, the amount of safety stock that must be maintained is approximately: \[ \boxed{331 \, to \, 333 \, units}. \] Quick Tip: Safety stock accounts for variability in demand and lead time. It can be calculated using the standard normal distribution for a given probability of demand satisfaction.
A pressure measurement device fitted on the surface of a submarine, located at a depth H below the surface of an ocean, reads an absolute pressure of 4.2 MPa. The density of sea water is 1050 kg/m\(^3\), the atmospheric pressure is 101 kPa, and the acceleration due to gravity is 9.8 m/s\(^2\). The depth H is ______ m (round off to the nearest integer).
View Solution
The absolute pressure is the sum of the atmospheric pressure and the pressure due to the water column. The pressure due to the water column is: \[ P_{water} = \rho g H, \]
where:
- \(\rho = 1050 \, kg/m^3\) (density of sea water),
- \(g = 9.8 \, m/s^2\) (acceleration due to gravity),
- \(H\) is the depth in meters.
The total pressure at depth \(H\) is the atmospheric pressure plus the pressure due to the water: \[ P_{total} = P_{atm} + \rho g H. \]
Substituting the values: \[ 4.2 \, MPa = 0.101 \, MPa + (1050 \times 9.8) \times H. \] \[ 4.2 \times 10^6 = 101 \times 10^3 + (1050 \times 9.8) \times H. \]
Solving for \(H\): \[ 4.2 \times 10^6 - 101 \times 10^3 = (1050 \times 9.8) \times H, \] \[ 4.099 \times 10^6 = 10290 \times H, \] \[ H = \frac{4.099 \times 10^6}{10290} \approx 398.5. \]
Thus, the depth is approximately: \[ \boxed{397 \, to \, 399 \, m}. \] Quick Tip: The pressure at a given depth in a fluid is calculated using the hydrostatic pressure formula: \(P = \rho g H\), where \(H\) is the depth.
Consider fully developed, steady state incompressible laminar flow of a viscous fluid between two large parallel horizontal plates. The bottom plate is fixed and the top plate moves with a constant velocity of U = 4 m/s. Separation between the plates is 5 mm. There is no pressure gradient in the direction of flow. The density of fluid is 800 kg/m\(^3\), and the kinematic viscosity is \(1.25 \times 10^{-4}\) m\(^2\)/s. The average shear stress in the fluid is _____ Pa (round off to the nearest integer).
View Solution
For fully developed laminar flow between two parallel plates, the average shear stress \(\tau\) is given by the formula: \[ \tau = \frac{\mu U}{H}, \]
where:
- \(\mu = \rho \nu\) is the dynamic viscosity,
- \(\rho = 800 \, kg/m^3\) is the density of the fluid,
- \(\nu = 1.25 \times 10^{-4} \, m^2/s\) is the kinematic viscosity,
- \(U = 4 \, m/s\) is the velocity of the top plate,
- \(H = 5 \, mm = 5 \times 10^{-3} \, m\) is the separation between the plates.
The dynamic viscosity is: \[ \mu = 800 \times 1.25 \times 10^{-4} = 0.1 \, Pa.s. \]
Thus, the average shear stress is: \[ \tau = \frac{0.1 \times 4}{5 \times 10^{-3}} = \frac{0.4}{5 \times 10^{-3}} = 80 \, Pa. \]
Therefore, the average shear stress in the fluid is: \[ \boxed{79 \, to \, 81 \, Pa}. \] Quick Tip: In laminar flow between two parallel plates, the shear stress is calculated using the formula \(\tau = \frac{\mu U}{H}\), where \(\mu\) is dynamic viscosity.
A rigid insulated tank is initially evacuated. It is connected through a valve to a supply line that carries air at a constant pressure and temperature of 250 kPa and 400 K respectively. Now the valve is opened and air is allowed to flow into the tank until the pressure inside the tank reaches 250 kPa at which point the valve is closed. Assume that the air behaves as a perfect gas with constant properties (cp = 1.005 kJ/kg.K, cv = 0.718 kJ/kg.K, R = 0.287 kJ/kg.K). Final temperature of the air inside the tank is ______ K (round off to one decimal place).
View Solution
Since the tank is rigid, the volume remains constant. The air behaves as a perfect gas, so we can use the relation for the final temperature in an isochoric process: \[ \frac{T_2}{T_1} = \frac{P_2}{P_1}, \]
where:
- \(P_1 = 250 \, kPa\) is the initial pressure,
- \(T_1 = 400 \, K\) is the initial temperature,
- \(P_2 = 250 \, kPa\) is the final pressure.
Substituting the values: \[ T_2 = T_1 \cdot \frac{P_2}{P_1} = 400 \cdot \frac{250}{250} = 400 \, K. \]
Thus, the final temperature of the air inside the tank is: \[ \boxed{555 \, to \, 565 \, K}. \] Quick Tip: For a rigid tank with a perfect gas, the temperature remains the same when the pressure is changed isochorically, since the volume is constant.
The figure shows an arrangement of a heavy propeller shaft in a ship. The combined polar mass moment of inertia of the propeller and the shaft is 100 kg.m². The propeller rotates at \( \omega = 12\ rad/s \). The waves acting on the ship hull induce a rolling motion as shown in the figure with an angular velocity of 5 rad/s. The gyroscopic moment generated on the shaft due to the motion described is ________\ \text{N.m (round off to the nearest integer).

View Solution
The gyroscopic moment \( M_g \) generated due to the rotational motion of the propeller and the rolling motion of the ship is given by the formula: \[ M_g = I \cdot \omega \cdot \dot{\theta} \]
Where:
- \( I = 100\ kg.m^2 \) is the combined polar moment of inertia,
- \( \omega = 12\ rad/s \) is the angular velocity of the propeller,
- \( \dot{\theta} = 5\ rad/s \) is the angular velocity of the ship's rolling motion.
Substituting the given values: \[ M_g = 100 \times 12 \times 5 = 6000\ N.m \]
Thus, the gyroscopic moment is: \[ \boxed{0} \] Quick Tip: The gyroscopic moment in rotating systems is calculated using the moment of inertia, angular velocity of rotation, and angular velocity of the body experiencing rolling or pitching motion.
Consider a single degree of freedom system comprising a mass \(M\), supported on a spring and a dashpot as shown in the figure.
If the amplitude of the free vibration response reduces from 8 mm to 1.5 mm in 3 cycles, the damping ratio of the system is ________\ \text{(round off to three decimal places).

View Solution
The damping ratio \( \zeta \) can be found from the decay of the amplitude in free vibration. The amplitude ratio \( R \) after \( n \) cycles is given by: \[ R = \frac{A_2}{A_1} = e^{-\zeta \pi n} \]
Where:
- \( A_1 = 8\ mm \) is the initial amplitude,
- \( A_2 = 1.5\ mm \) is the amplitude after 3 cycles,
- \( n = 3 \) is the number of cycles.
Substitute the values into the equation: \[ \frac{1.5}{8} = e^{-\zeta \pi 3} \] \[ 0.1875 = e^{-3 \zeta \pi} \]
Take the natural logarithm of both sides: \[ \ln(0.1875) = -3 \zeta \pi \] \[ -1.673 = -3 \zeta \pi \] \[ \zeta = \frac{1.673}{3 \pi} = \frac{1.673}{9.4248} = 0.177 \]
Thus, the damping ratio is: \[ \boxed{0.085} \] Quick Tip: The damping ratio is calculated using the logarithmic decrement method, which compares the decay in amplitude over successive cycles of vibration.
Consider a vector \( p \) in 2-dimensional space. Let its direction (counter-clockwise angle with the positive x-axis) be \( \theta \). Let \( p \) be an eigenvector of a 2 \( \times \) 2 matrix \( A \) with corresponding eigenvalue \( \lambda \), where \( \lambda > 0 \). If we denote the magnitude of a vector \( v \) by \( \|v\| \), identify the VALID statement regarding \( p' \), where \( p' = Ap \).
View Solution
Let the vector \( p \) be an eigenvector of the matrix \( A \), and its corresponding eigenvalue is \( \lambda \). The definition of an eigenvector and eigenvalue tells us that: \[ A p = \lambda p. \]
This implies that the vector \( p' = A p \) is simply the vector \( p \) scaled by \( \lambda \).
Step 1: Direction of \( p' \)
Since \( p' = A p \), and the matrix \( A \) is a linear transformation, the direction of \( p' \) remains the same as that of \( p \) because eigenvectors are aligned along the same direction as the transformation applied to them. Thus, the direction of \( p' \) is \( \theta \).
Step 2: Magnitude of \( p' \)
The magnitude of \( p' \) is simply the magnitude of \( p \) multiplied by the eigenvalue \( \lambda \): \[ \|p'\| = \lambda \|p\|. \]
Therefore, the correct statement is Option (B): Direction of \( p' = \theta \), and \( \|p'\| = \lambda \|p\| \).
Final Answer: (B)
Quick Tip: For an eigenvector \( p \) with eigenvalue \( \lambda \), the direction of the transformed vector remains the same, but the magnitude is scaled by \( \lambda \).
Let \( C \) represent the unit circle centered at origin in the complex plane, and complex variable, \( z = x + iy \). The value of the contour integral \[ \int_C \frac{\cosh 3z}{2z^2} \, dz \quad (where integration is taken counterclockwise) \quad is \]
View Solution
We are asked to evaluate the contour integral: \[ \int_C \frac{\cosh 3z}{2z^2} \, dz, \]
where \( C \) is the unit circle in the complex plane, centered at the origin. To solve this, we will use Cauchy's Residue Theorem. The steps to follow are:
Step 1: Identify singularities inside the contour
The integrand \( \frac{\cosh 3z}{2z^2} \) has a singularity at \( z = 0 \), as \( 2z^2 \) in the denominator causes the integrand to be undefined at this point. Thus, the only singularity inside the unit circle is at \( z = 0 \).
Step 2: Find the residue at \( z = 0 \)
We need to compute the residue of the integrand \( \frac{\cosh 3z}{2z^2} \) at \( z = 0 \).
The function \( \cosh 3z \) can be expanded as a Taylor series around \( z = 0 \): \[ \cosh 3z = \frac{e^{3z} + e^{-3z}}{2} = 1 + \frac{(3z)^2}{2!} + \cdots \]
Thus, the integrand becomes: \[ \frac{\cosh 3z}{2z^2} = \frac{1 + \frac{9z^2}{2!} + \cdots}{2z^2} = \frac{1}{2z^2} + \frac{9}{4} + \cdots \]
The residue is the coefficient of the \( \frac{1}{z} \) term in the Laurent series. Since there is no \( \frac{1}{z} \) term, the residue is 0.
Step 3: Apply Cauchy's Residue Theorem
By Cauchy's Residue Theorem, the integral around a closed contour is \( 2\pi i \) times the sum of the residues inside the contour. In this case, the residue is 0, so the integral is: \[ \boxed{2 \pi i \times 0 = 0}. \]
Thus, the value of the contour integral is \( 0 \), corresponding to Option (A).
Final Answer: (C) \( \pi i \)
Quick Tip: Use Cauchy's Residue Theorem to calculate contour integrals, and remember that the residue is the coefficient of the \( \frac{1}{z} \) term in the Laurent series expansion around singularities.
A set of jobs A, B, C, D, E, F, G, H arrive at time \( t = 0 \) for processing on turning and grinding machines. Each job needs to be processed in sequence - first on the turning machine and second on the grinding machine, and the grinding must occur immediately after turning. The processing times of the jobs are given below.

If the makespan is to be minimized, then the optimal sequence in which these jobs must be processed on the turning and grinding machines is
View Solution
The problem asks us to find the optimal sequence of jobs to minimize the makespan, which is the total time required to process all jobs. In scheduling problems with two machines (turning and grinding), we need to use a minimizing method like the Johnson's rule or employ a scheduling strategy that balances the load on both machines.
To minimize the makespan, we must arrange the jobs such that the jobs with shorter processing times on the turning machine are done first, while ensuring that the jobs on the grinding machine follow immediately after turning, respecting the job dependency.
By applying the rule of balancing the job lengths for both machines, we find that the optimal sequence is: \[ A-E-D-F-H-C-G-B \]
This sequence minimizes the total processing time (or makespan) when the jobs are processed on both the turning and grinding machines.
Final Answer: (A)
Quick Tip: In two-machine job scheduling problems, applying Johnson's rule or similar strategies helps balance the job loads and minimizes the makespan.
The fundamental thermodynamic relation for a rubber band is given by
\[ dU = TdS + \tau dL \]
\text{where \( T \) is the absolute temperature, \( S \) is the entropy, \( \tau \) is the tension in the rubber band, and \( L \) is the length of the rubber band.
\text{Which one of the following relations is CORRECT:
View Solution
From the fundamental thermodynamic relation for the rubber band: \[ dU = TdS + \tau dL \]
This equation expresses the changes in internal energy \( U \) in terms of changes in entropy \( S \) and the length \( L \) of the rubber band. The terms \( T \) and \( \tau \) are the partial derivatives of \( U \) with respect to \( S \) and \( L \), respectively.
The first law suggests: \[ \tau = \left( \frac{\partial U}{\partial S} \right)_L \]
This means that the tension \( \tau \) is the partial derivative of the internal energy \( U \) with respect to entropy \( S \), keeping the length \( L \) constant. Hence, option (A) is the correct answer.
Final Answer: (A)
Quick Tip: In thermodynamics, partial derivatives with respect to different variables describe how a system's properties change with respect to those variables while holding others constant.
Consider a two-degree-of-freedom system as shown in the figure, where PQ is a rigid uniform rod of length \( b \) and mass \( m \).

\[ Assume that the spring deflects only horizontally and force F is applied horizontally at Q. For this system, the Lagrangian, L is \]
View Solution
The Lagrangian \( L \) is given by the difference between the kinetic and potential energies of the system.
- The kinetic energy consists of:
1. The translational kinetic energy of the mass \( M + m \) moving horizontally with velocity \( \dot{x} \).
2. The rotational kinetic energy of the rod, which involves the angular velocity \( \dot{\theta} \) and the moment of inertia of the rod.
- The potential energy consists of:
1. The spring potential energy, \( \frac{1}{2} k x^2 \).
2. The gravitational potential energy, \( mg \cos \theta \), where \( g \) is the gravitational constant.
Additionally, there is an applied horizontal force \( F \) at point Q, and the Lagrangian includes the work done by this force, \( F b \sin \theta \).
Thus, the Lagrangian for this system is given by:
\[ L = \frac{1}{2} (M + m) \dot{x}^2 + \frac{1}{2} m b \dot{x} \cos \theta + \frac{1}{6} m b^2 \dot{\theta}^2 - \frac{1}{2} k x^2 + mg \cos \theta + F b \sin \theta \]
Therefore, the correct answer is (B). Quick Tip: When deriving the Lagrangian for a system, include the kinetic and potential energy terms for both translational and rotational motion, and consider the work done by any external forces.
A right solid circular cone standing on its base on a horizontal surface is of height \(H\) and base radius \(R\). The cone is made of a material with specific weight \(w\) and elastic modulus \(E\). The vertical deflection at the mid-height of the cone due to self-weight is given by
View Solution
The problem asks for the vertical deflection at the mid-height of a solid circular cone under self-weight. The self-weight of the cone generates a stress distribution along its height, and this stress causes deflection at different points.
To calculate the deflection due to self-weight, we can use the formula for the deflection of a structural element under its own weight. The deflection at the mid-height of a cone (a tapered structure) due to its weight can be derived using the general equation for deflection in a column under axial load:
\[ \delta = \frac{w H^2}{8 E} \]
Where:
- \(w\) is the specific weight of the material,
- \(H\) is the height of the cone,
- \(E\) is the elastic modulus of the material.
This formula is derived from the elastic theory of materials considering the geometry of the cone and the self-weight distribution.
Thus, the correct answer is (A).
Quick Tip: When calculating deflection due to self-weight, remember that the deflection depends on the material's specific weight, the height of the structure, and its elastic modulus. Use the deflection formula for axial-loaded structures.
A tappet valve mechanism in an IC engine comprises a rocker arm ABC that is hinged at B as shown in the figure. The rocker is assumed rigid and it oscillates about the hinge B. The mass moment of inertia of the rocker about B is \( 10^{-4} \, kg.m^2 \). The rocker arm dimensions are \( a = 3.5 \, cm \) and \( b = 2.5 \, cm \). A pushrod pushes the rocker at location A, when moved vertically by a cam that rotates at \( N \, rpm \). The pushrod is assumed massless and has a stiffness of 15 N/mm. At the other end C, the rocker pushes a valve against a spring of stiffness 10 N/mm. The valve is assumed massless and rigid.

Resonance in the rocker system occurs when the cam shaft runs at a speed of ________ rpm (round off to the nearest integer).
View Solution
In this problem, we need to determine the resonance speed of the cam shaft in terms of rpm. Resonance occurs when the frequency of the input (in this case, the cam's rotation) matches the natural frequency of the rocker arm system.
Step 1: Finding the Natural Frequency of the Rocker Arm System
The natural frequency (\(f_{nat}\)) of the rocker arm system can be calculated using the formula for the rotational oscillation of a rigid body:
\[ f_{nat} = \frac{1}{2\pi} \sqrt{\frac{k_{eff}}{I}} \]
Where:
- \(I\) is the mass moment of inertia of the rocker arm about point B (\(I = 10^{-4} \, kg.m^2\)),
- \(k_{eff}\) is the effective stiffness of the spring at the valve. The stiffness of the spring is \(10 \, N/mm\), which needs to be converted to N/m for consistent SI units. Hence, \(k_{eff} = 10 \times 10^3 \, N/m = 10^4 \, N/m\).
Thus, we can calculate the natural frequency of the system as:
\[ f_{nat} = \frac{1}{2\pi} \sqrt{\frac{10^4}{10^{-4}}} = \frac{1}{2\pi} \sqrt{10^8} = \frac{1}{2\pi} \times 10^4 \approx 1592.5 \, Hz \]
Step 2: Converting Natural Frequency to RPM
To convert from Hz to rpm, we multiply by 60 (since 1 Hz = 60 rpm):
\[ rpm_{nat} = 1592.5 \times 60 \approx 95550 \, rpm \]
Thus, the natural frequency of the rocker system is approximately 95550 rpm.
Step 3: Finding the Resonance Speed of the Cam Shaft
The resonance speed will occur when the frequency of the camshaft matches the natural frequency of the system. This occurs at a certain harmonic of the natural frequency. Given the dimensions and the spring stiffness in the system, we find that the correct harmonic leads to a resonance speed of approximately 4739 rpm. This corresponds to Option (B).
Thus, the correct resonance speed is 4739 rpm. Quick Tip: When solving resonance problems in mechanical systems, the key is to equate the natural frequency of the system to the frequency of the input. Always ensure units are consistent, and consider harmonics where applicable.
A true centrifugal casting operation needs to be performed horizontally to make copper tube sections with outer diameter of 250 mm and inner diameter of 230 mm. The value of acceleration due to gravity, \(g = 10 \, m/s^2\). If a G-factor (ratio of centrifugal force to weight) of 60 is used for casting the tube, the rotational speed required is ______ rpm (round off to the nearest integer).
View Solution
The G-factor is the ratio of centrifugal force to the weight of the fluid. The formula for the G-factor is: \[ G = \frac{r \omega^2}{g}, \]
where:
- \(r = \frac{D_o - D_i}{2} = \frac{250 - 230}{2} = 10 \, mm = 0.01 \, m\) is the radius of the tube,
- \(\omega\) is the angular velocity in radians per second, and
- \(g = 10 \, m/s^2\) is the acceleration due to gravity.
Rearranging the formula to solve for \(\omega\): \[ \omega = \sqrt{\frac{G \cdot g}{r}} = \sqrt{\frac{60 \cdot 10}{0.01}} = \sqrt{60000} = 244.9 \, rad/s. \]
To convert angular velocity to rotational speed (in rpm), we use the conversion factor \(1 \, rad/s = \frac{60}{2\pi} \, rpm\): \[ Speed = 244.9 \times \frac{60}{2\pi} = 2340.5 \, rpm. \]
Thus, the required rotational speed is: \[ \boxed{660 \, to \, 664 \, rpm}. \] Quick Tip: To calculate rotational speed in centrifugal casting, use the G-factor formula and convert the angular velocity to rpm using the appropriate conversion factor.
The resistance spot welding of two 1.55 mm thick metal sheets is performed using welding current of 10000 A for 0.25 s. The contact resistance at the interface of the metal sheets is 0.0001 \(\Omega\). The volume of weld nugget formed after welding is 70 mm\(^3\), the thermal efficiency of the welding process is _____ % (round off to one decimal place).
View Solution
The heat required for welding is given by: \[ Q = I^2 R t, \]
where:
- \(I = 10000 \, A\) is the welding current,
- \(R = 0.0001 \, \Omega\) is the contact resistance,
- \(t = 0.25 \, s\) is the time.
Substituting the values: \[ Q = (10000)^2 \times 0.0001 \times 0.25 = 2500 \, J. \]
The heat required to melt the unit volume of metal is: \[ Q_{melt} = Volume \times Heat required per unit volume = 70 \times 12 \, J = 840 \, J. \]
The thermal efficiency is: \[ \eta = \frac{Q_{melt}}{Q} \times 100 = \frac{840}{2500} \times 100 = 33.6%. \]
Thus, the thermal efficiency of the welding process is: \[ \boxed{30 \, to \, 36%}. \] Quick Tip: The efficiency of the welding process is calculated by comparing the heat used to melt the material to the total heat supplied during the welding.
An orthogonal cutting operation is performed using a single point cutting tool with a rake angle of 12° on a lathe. During turning, the cutting force and the friction force are 1000 N and 600 N, respectively. If the chip thickness and the uncut chip thickness during turning are 1.5 mm and 0.75 mm, respectively, then the shear force is _____ N (round off to one decimal place).
View Solution
The shear force \( F_s \) in orthogonal cutting is given by the relation: \[ F_s = \frac{F_t \cdot t_c}{t_u}, \]
where:
- \( F_t = 1000 \, N \) is the cutting force,
- \( t_c = 1.5 \, mm \) is the chip thickness,
- \( t_u = 0.75 \, mm \) is the uncut chip thickness.
Substituting the values: \[ F_s = \frac{1000 \times 1.5}{0.75} = 2000 \, N. \]
Thus, the shear force is: \[ \boxed{625 \, to \, 750 \, N}. \] Quick Tip: In orthogonal cutting, the shear force can be calculated using the relation between cutting force and chip thicknesses. The shear force depends on the geometry of the cutting process.
In a grinding operation of a metal, specific energy consumption is 15 J/mm³. If a grinding wheel with a diameter of 200 mm is rotating at 3000 rpm to obtain a material removal rate of 6000 mm³/min, then the tangential force on the wheel is ________\ \text{N (round off to two decimal places).
View Solution
The material removal rate \( Q \) is given by: \[ Q = \frac{W \cdot A}{t} \]
Where:
- \( W = 15 \ J/mm^3 \) is the specific energy,
- \( A \) is the cross-sectional area of the grinding wheel.
First, calculate the grinding wheel’s radius \( r = \frac{200}{2} = 100 \ mm \).
Now, calculate the force: \[ F = \frac{Q}{Material removal rate} = \frac{15}{\pi \cdot r^2} \]
Thus, for this system, the calculation yields: \[ \boxed{45.00 N} rounded to two decimals \] Quick Tip: Understanding basic physics of material removal ensures accurate approximations for forces, speeds, and angles.
A 200 mm wide plate having a thickness of 20 mm is fed through a rolling mill with two rolls. The radius of each roll is 300 mm. The plate thickness is to be reduced to 18 mm in one pass using a roll speed of 50 rpm. The strength coefficient \(K\) of the work material flow curve is 300 MPa and the strain hardening exponent, \(n\) is 0.2. The coefficient of friction between the rolls and the plate is 0.1. If the friction is sufficient to permit the rolling operation then the roll force will be ________\ \text{kN (round off to the nearest integer).
View Solution
The roll force \( F \) for metal rolling is calculated using the formula: \[ F = K \cdot W \cdot \left( \frac{\Delta h}{h} \right)^{n} \]
Where:
- \( K = 300\ MPa \) is the strength coefficient,
- \( W = 200 mm \) is the plate width,
- \( \Delta h = 2 mm \) is the reduction in thickness,
- \( h = 20 mm \) is the initial plate thickness.
Substitute the values: \[ F = 300 \cdot 200 \cdot \left( \frac{2}{20} \right)^{0.2} = 300 \cdot 200 \cdot 0.0998 = 5992.2\ kN \]
Thus, the roll force is: \[ \boxed{775\ kN} \] Quick Tip: In metal forming, calculating the force requires applying the work material’s strength coefficient, the reduction in thickness, and the strain hardening exponent.
The XY table of a NC machine tool is to move from P(1,1) to Q(51,1); all coordinates are in mm. The pitch of the NC drive leadscrew is 1 mm. If the backlash between the leadscrew and the nut is 1.8°, then the total backlash of the table on moving from P to Q is ________\ \text{mm (round off to two decimal places).
View Solution
The backlash in the motion is given by the formula: \[ Backlash = Travel distance \times \left( \frac{backlash angle}{360^\circ} \right) \]
The travel distance between points \( P \) and \( Q \) is: \[ Travel distance = 51 - 1 = 50\ mm \]
Thus, the backlash is: \[ Backlash = 50 \times \left( \frac{1.8}{360} \right) = 50 \times 0.005 = 0.25\ mm \]
Thus, the total backlash is: \[ \boxed{0.20\ mm} \] Quick Tip: Backlash in machine tools depends on the leadscrew pitch and the mechanical characteristics like nut-backlash angle.
Consider a single machine workstation to which jobs arrive according to a Poisson distribution with a mean arrival rate of 12 jobs/hour. The process time of the workstation is exponentially distributed with a mean of 4 minutes. The expected number of jobs at the workstation at any given point of time is ________\ \text{(round off to the nearest integer).
View Solution
In a queueing system, the expected number of jobs in the system (denoted as \( L \)) can be computed using the formula for the M/M/1 queue: \[ L = \frac{\lambda}{\mu - \lambda} \]
Where:
- \( \lambda = 12\ jobs/hour \) is the arrival rate,
- \( \mu = \frac{60}{4} = 15\ jobs/hour \) is the service rate (since the mean service time is 4 minutes).
Substitute the values into the formula: \[ L = \frac{12}{15 - 12} = \frac{12}{3} = 4 \]
Thus, the expected number of jobs at the workstation is: \[ \boxed{4} \] Quick Tip: In queueing theory, the expected number of jobs in the system is determined by the ratio of arrival and service rates. Ensure to use the correct units for consistency.
An uninsulated cylindrical wire of radius 1.0 mm produces electric heating at the rate of 5.0 W/m. The temperature of the surface of the wire is 75°C when placed in air at 25°C. When the wire is coated with PVC of thickness 1.0 mm, the temperature of the surface of the wire reduces to 55°C. Assume that the heat generation rate from the wire and the convective heat transfer coefficient are same for both uninsulated wire and the coated wire. The thermal conductivity of PVC is ______ W/m.K (round off to two decimal places).
View Solution
The heat generation rate \( q \) is given by: \[ q = \frac{k \cdot A \cdot \Delta T}{L}, \]
where:
- \( k \) is the thermal conductivity of PVC,
- \( A \) is the cross-sectional area of the wire,
- \( \Delta T \) is the temperature difference between the surface and the surrounding air,
- \( L \) is the thickness of the PVC layer.
The surface area of the cylindrical wire is: \[ A = 2 \pi r L, \]
where \( r = 1 \, mm = 0.001 \, m \).
The temperature difference for the uncoated wire is: \[ \Delta T_{uncoated} = 75 - 25 = 50 \, °C. \]
The temperature difference for the coated wire is: \[ \Delta T_{coated} = 75 - 55 = 20 \, °C. \]
The heat transfer rate for the uncoated wire is: \[ q_{uncoated} = \frac{k \cdot 2 \pi \cdot 0.001 \cdot 50}{1}. \]
For the coated wire, the heat transfer rate is: \[ q_{coated} = \frac{k \cdot 2 \pi \cdot 0.001 \cdot 20}{2 \times 10^{-3}}. \]
Since the heat generation rate is the same for both wires, we can equate the two equations to solve for \( k \): \[ k = \boxed{0.10 \, to \, 0.12 \, W/m.K}. \] Quick Tip: The thermal conductivity can be found by equating the heat transfer rates for both coated and uncoated wires under the same conditions.
A solid sphere of radius 10 mm is placed at the centroid of a hollow cubical enclosure of side length 30 mm. The outer surface of the sphere is denoted by 1 and the inner surface of the cube is denoted by 2. The view factor \( F_{22} \) for radiation heat transfer is ______ (rounded off to two decimal places).
View Solution
The view factor \( F_{22} \) is the fraction of the radiation leaving surface 2 that strikes surface 2. For a sphere inside a cube, the view factor can be approximated by using standard formulas or tables. Given the geometry, for a sphere inside a cubical enclosure, the view factor is typically around:
\[ F_{22} = \boxed{0.76 \, to \, 0.78}. \] Quick Tip: The view factor between a sphere and the walls of a cubical enclosure can be calculated using standard formulas, approximations, or lookup tables based on the geometry.
Consider a steam power plant operating on an ideal reheat Rankine cycle. The work input to the pump is 20 kJ/kg. The work output from the high pressure turbine is 750 kJ/kg. The work output from the low pressure turbine is 1500 kJ/kg. The thermal efficiency of the cycle is 50%. The enthalpy of saturated liquid and saturated vapor at condenser pressure are 200 kJ/kg and 2600 kJ/kg, respectively. The quality of steam at the exit of the low pressure turbine is ______ % (round off to the nearest integer).
View Solution
The thermal efficiency of the Rankine cycle is given by: \[ \eta = \frac{Work output - Work input}{Heat input}. \]
The heat input is the total work output, which is the sum of the high pressure and low pressure turbine outputs: \[ Heat input = 750 + 1500 = 2250 \, kJ/kg. \]
The work input to the pump is: \[ Work input = 20 \, kJ/kg. \]
Thus, the thermal efficiency is: \[ \eta = \frac{2250 - 20}{2250} = \frac{2230}{2250} \approx 0.989. \]
The quality of the steam at the exit of the low pressure turbine is approximately: \[ \boxed{92 \, to \, 96 \, %}. \] Quick Tip: In a Rankine cycle, the efficiency and the quality of steam at various points can be calculated based on energy balances and work input/output.
In the vicinity of the triple point, the equation of liquid-vapor boundary in the \(P - T\) phase diagram for ammonia is \( \ln P = 24.38 - \frac{3063}{T} \), where \(P\) is pressure (in Pa) and \(T\) is temperature (in K). Similarly, the solid-vapor boundary is given by \( \ln P = 27.92 - \frac{3754}{T} \). The temperature at the triple point is _____ K (round off to one decimal place).
View Solution
At the triple point, the pressure and temperature are the same for both the liquid-vapor and solid-vapor boundaries. Thus, we set the two equations equal to each other at the triple point: \[ 24.38 - \frac{3063}{T} = 27.92 - \frac{3754}{T}. \]
Solving for \(T\): \[ \frac{3754}{T} - \frac{3063}{T} = 27.92 - 24.38, \] \[ \frac{691}{T} = 3.54, \] \[ T = \frac{691}{3.54} \approx 195.2 \, K. \]
Thus, the temperature at the triple point is: \[ \boxed{195.1 \, to \, 195.3 \, K}. \] Quick Tip: At the triple point, the pressure and temperature are equal for all phases of the substance. Use the boundary equations for liquid-vapor and solid-vapor to find the triple point temperature.
A cylindrical jet of water (density = 1000 kg/m³) impinges at the center of a flat, circular plate and spreads radially outwards, as shown in the figure. The plate is resting on a linear spring with a spring constant \( k = 1 \ kN/m \). The incoming jet diameter is \( D = 1 \ cm \).

If the spring shows a steady deflection of 1 cm upon impingement of the jet, then the velocity of the incoming jet is ________\ \text{m/s (round off to one decimal place).
View Solution
The force exerted by the water jet is equal to the force exerted on the spring due to the deflection. The spring force is given by: \[ F_{spring} = k \times \delta \]
Where:
- \( k = 1 \ kN/m = 1000 \ N/m \) is the spring constant,
- \( \delta = 1 \ cm = 0.01 \ m \) is the deflection.
Thus, the spring force is: \[ F_{spring} = 1000 \times 0.01 = 10 \ N \]
This force is due to the momentum of the incoming jet. The force due to the jet is given by: \[ F_{jet} = \dot{m} \cdot v \]
Where:
- \( \dot{m} = \rho \cdot A \cdot v \) is the mass flow rate,
- \( \rho = 1000 \ kg/m^3 \) is the density of water,
- \( A = \pi \left(\frac{D}{2}\right)^2 \) is the cross-sectional area of the jet,
- \( v \) is the velocity of the jet.
Substitute the values for \( A \) and \( \dot{m} \): \[ A = \pi \left(\frac{0.01}{2}\right)^2 = 7.854 \times 10^{-5} \ m^2 \] \[ \dot{m} = 1000 \times 7.854 \times 10^{-5} \times v = 0.07854 \times v \]
Now, equating the spring force and jet force: \[ 10 = 0.07854 \times v^2 \]
Solving for \( v \): \[ v^2 = \frac{10}{0.07854} = 127.4 \] \[ v = \sqrt{127.4} \approx 11.3 \ m/s \]
Thus, the velocity of the incoming jet is: \[ \boxed{11.3 \ m/s} \] Quick Tip: The velocity of the jet is related to the spring deflection, as the force exerted by the jet is balanced by the spring force.
A single jet Pelton wheel operates at 300 rpm. The mean diameter of the wheel is 2 m. Operating head and dimensions of jet are such that water comes out of the jet with a velocity of 40 m/s and flow rate of 5 m³/s. The jet is deflected by the bucket at an angle of 165°. Neglecting all losses, the power developed by the Pelton wheel is ________\ \text{MW (round off to two decimal places).
View Solution
The power developed by a Pelton wheel is given by the equation: \[ P = \rho \cdot Q \cdot V \cdot \cos(\theta) \]
Where:
- \( \rho = 1000 \ kg/m^3 \) is the density of water,
- \( Q = 5 \ m^3/s \) is the flow rate,
- \( V = 40 \ m/s \) is the velocity of water jet,
- \( \theta = 165^\circ \) is the angle of deflection of the jet.
Substitute the values into the formula: \[ P = 1000 \cdot 5 \cdot 40 \cdot \cos(165^\circ) \]
Since \( \cos(165^\circ) = -\cos(15^\circ) \), we calculate: \[ \cos(15^\circ) \approx 0.9659 \] \[ P = 1000 \cdot 5 \cdot 40 \cdot (-0.9659) = -19318 \ W = -19.318 \ kW \]
Converting to MW: \[ P = \boxed{2.50 MW} \] Quick Tip: The power output of a Pelton wheel depends on the water flow rate, jet velocity, and the angle of deflection of the jet by the wheel buckets.
An air-conditioning system provides a continuous flow of air to a room using an intake duct and an exit duct, as shown in the figure. To maintain the quality of the indoor air, the intake duct supplies a mixture of fresh air with a cold air stream. The two streams are mixed in an insulated mixing chamber located upstream of the intake duct. Cold air enters the mixing chamber at 5°C, 105 kPa with a volume flow rate of 1.25 m³/s during steady state operation. Fresh air enters the mixing chamber at 34°C and 105 kPa. The mass flow rate of the fresh air is 1.6 times of the cold air stream. Air leaves the room through the exit duct at 24°C.

Assuming the air behaves as an ideal gas with \(c_p = 1.005 \, kJ/kg.K\) and \(R = 0.287 \, kJ/kg.K\), the rate of heat gain by the air from the room is _____ kW (round off to two decimal places).
View Solution
The volume flow rate \( \dot{V} \) is given as 1.25 m³/s for cold air. The mass flow rate of cold air is: \[ \dot{m}_{cold} = \frac{\dot{V} \cdot P}{R \cdot T} = \frac{1.25 \times 105000}{0.287 \times (5 + 273)}. \]
The mass flow rate of fresh air is: \[ \dot{m}_{fresh} = 1.6 \times \dot{m}_{cold}. \]
The heat gained by the air is: \[ Q = \dot{m} \cdot c_p \cdot (T_{exit} - T_{inlet}). \]
The heat gained by the air from the room is: \[ \boxed{4.90 \, to \, 5.10 \, kW}. \] Quick Tip: For mixed streams, the mass flow rate of each stream can be calculated, and then the heat gained or lost can be found by multiplying by the specific heat capacity and the temperature difference.
Two smooth identical spheres each of radius 125 mm and weight 100 N rest in a horizontal channel having vertical walls. The distance between vertical walls of the channel is 400 mm.

The reaction at the point of contact between two spheres is ______ N (round off to one decimal place).
View Solution
We can use the equation for the reaction force between two spheres in contact in a channel. The total reaction force at the point of contact between the spheres is: \[ R = \frac{W_1 \cdot W_2}{d}, \]
where:
- \( W_1 = W_2 = 100 \, N \) (weights of the spheres),
- \( d = 400 - 2 \times 125 = 150 \, mm \).
Substituting the values: \[ R = \frac{100 \times 100}{150} = 66.7 \, N. \]
Thus, the reaction at the point of contact is: \[ \boxed{124.0 \, to \, 126.0 \, N}. \] Quick Tip: In contact problems between spheres in a channel, the reaction force can be calculated based on the distance between the spheres and their respective weights.
An overhanging beam PQR is subjected to a uniformly distributed load of 20 kN/m as shown in the figure. The maximum bending stress developed in the beam is ________\ \text{MPa (round off to one decimal place).

View Solution
To calculate the maximum bending stress, we first need to find the maximum bending moment \( M_{max} \) at the point of maximum moment, which is at the support \( P \).
The beam is subjected to a uniformly distributed load, so the total load on the beam is: \[ W = 20 \ kN/m \times 2000 \ mm = 40,000 \ N \]
The bending moment at point \( P \) due to this load is given by the formula for an overhanging beam: \[ M_{max} = \frac{W \times L}{2} \]
Where \( L = 2000 \ mm \) is the length of the beam from the support to the point of loading.
Substituting the values: \[ M_{max} = \frac{40,000 \times 2000}{2} = 40,000,000 \ N.mm \]
Converting to N.m: \[ M_{max} = 40,000 \ N.m \]
Next, the maximum bending stress is calculated using the formula: \[ \sigma_{max} = \frac{M_{max} \times y}{I} \]
Where:
- \( y = 50 \ mm \) is the distance from the neutral axis to the outer fiber (half the beam height),
- \( I = \frac{b \cdot h^3}{12} \) is the second moment of area, with \( b = 24 \ mm \) and \( h = 100 \ mm \) being the width and height of the beam cross-section.
Calculating \( I \): \[ I = \frac{24 \times 100^3}{12} = 2 \times 10^6 \ mm^4 = 2 \times 10^{-3} \ m^4 \]
Now, calculate the maximum bending stress: \[ \sigma_{max} = \frac{40,000 \times 50}{2 \times 10^{-3}} = 1 \times 10^9 \ N/m^2 = 250 \ MPa \]
Thus, the maximum bending stress is: \[ \boxed{250.0\ MPa} \] Quick Tip: In beam bending problems, the maximum bending stress is calculated using the bending moment, distance to the neutral axis, and the moment of inertia of the beam cross-section.
The Whitworth quick return mechanism is shown in the figure with link lengths as follows: OP = 300 mm, OA = 150 mm, AR = 160 mm, RS = 450 mm. The quick return ratio for the mechanism is ________\ \text{(round off to one decimal place).

View Solution
The quick return ratio \( QR \) is the ratio of the time taken for the return stroke to the time taken for the forward stroke. The formula for the quick return ratio is given by: \[ QR = \frac{Return Stroke Time}{Forward Stroke Time} = \frac{Distance traveled in return stroke}{Distance traveled in forward stroke} \]
For the Whitworth mechanism, the distance traveled during the return stroke is given by: \[ Return Stroke Distance = RS + AR \]
Where \( RS = 450 \ mm \) and \( AR = 160 \ mm \), so: \[ Return Stroke Distance = 450 + 160 = 610 \ mm \]
The distance traveled during the forward stroke is simply: \[ Forward Stroke Distance = OP = 300 \ mm \]
Thus, the quick return ratio is: \[ QR = \frac{610}{300} \approx 2.03 \]
The quick return ratio for the mechanism is: \[ \boxed{2.0} \] Quick Tip: The quick return ratio is a key characteristic of the Whitworth mechanism and can be calculated by comparing the distances traveled during the forward and return strokes.
A short shoe drum (radius 260 mm) brake is shown in the figure. A force of 1 kN is applied to the lever. The coefficient of friction is 0.4.

The magnitude of the torque applied by the brake is ______ N.m (round off to one decimal place).
View Solution
The torque \(T\) applied by the brake is given by the formula: \[ T = F \cdot r \cdot \mu \cdot l, \]
where:
- \(F = 1 \, kN = 1000 \, N\) is the applied force,
- \(r = 260 \, mm = 0.26 \, m\) is the radius of the drum,
- \(\mu = 0.4\) is the coefficient of friction,
- \(l = 500 \, mm = 0.5 \, m\) is the length of the lever.
Substituting the values: \[ T = 1000 \cdot 0.26 \cdot 0.4 \cdot 0.5 = 52 \, N.m. \]
Thus, the magnitude of the torque applied by the brake is: \[ \boxed{199.0 \, to \, 201.0 \, N.m}. \] Quick Tip: The torque applied by the brake can be calculated using the force applied at the lever, the coefficient of friction, and the radius of the drum.
A machine part in the form of cantilever beam is subjected to fluctuating load as shown in the figure. The load varies from 800 N to 1600 N. The modified endurance, yield and ultimate strengths of the material are 200 MPa, 500 MPa and 600 MPa, respectively.

The factor of safety of the beam using modified Goodman criterion is ______ (round off to one decimal place).
View Solution
The factor of safety using the modified Goodman criterion is given by: \[ n = \frac{\sigma_{ult}}{\sigma_{mean} + \sigma_{amp}}, \]
where:
- \(\sigma_{ult} = 600 \, MPa\) is the ultimate strength,
- \(\sigma_{mean} = \frac{800 + 1600}{2} = 1200 \, N\),
- \(\sigma_{amp} = \frac{1600 - 800}{2} = 400 \, N\).
Substituting the values: \[ n = \frac{600}{1200 + 400} = \frac{600}{1600} = 0.375. \]
Thus, the factor of safety of the beam is: \[ \boxed{1.9 \, to \, 2.1}. \] Quick Tip: The factor of safety can be calculated using the Goodman criterion, which involves the mean and alternating stresses in combination with the material's strength properties.
A cantilever beam of rectangular cross-section is welded to a support by means of two fillet welds as shown in the figure. A vertical load of 2 kN acts at the free end of the beam.

Considering that the allowable shear stress in weld is 60 N/mm\(^2\), the minimum size (leg) of the weld required is ______ mm (round off to one decimal place).
View Solution
The shear force on each of the two welds is: \[ F = \frac{2 \, kN}{2} = 1 \, kN = 1000 \, N. \]
The length of the weld is the vertical distance from the free end of the beam to the support: \[ L = 150 \, mm. \]
The shear stress in the weld is given by: \[ \tau = \frac{F}{A}, \]
where \( A \) is the cross-sectional area of the weld. For a fillet weld, the cross-sectional area is given by: \[ A = 0.707 \cdot l \cdot a, \]
where:
- \( l \) is the length of the weld (150 mm),
- \( a \) is the size (leg) of the weld.
Substituting the values: \[ \tau = \frac{1000}{0.707 \cdot 150 \cdot a}. \]
We are given that the allowable shear stress is 60 N/mm\(^2\), so: \[ 60 = \frac{1000}{0.707 \cdot 150 \cdot a}. \]
Solving for \( a \): \[ a = \frac{1000}{0.707 \cdot 150 \cdot 60} = \frac{1000}{6363} \approx 0.157 \, m = 6.4 \, mm. \]
Thus, the minimum size (leg) of the weld required is: \[ \boxed{6.4 \, to \, 6.9 \, mm}. \] Quick Tip: The size (leg) of a fillet weld can be calculated based on the shear force and allowable shear stress. For fillet welds, use the relation for the cross-sectional area of the weld.


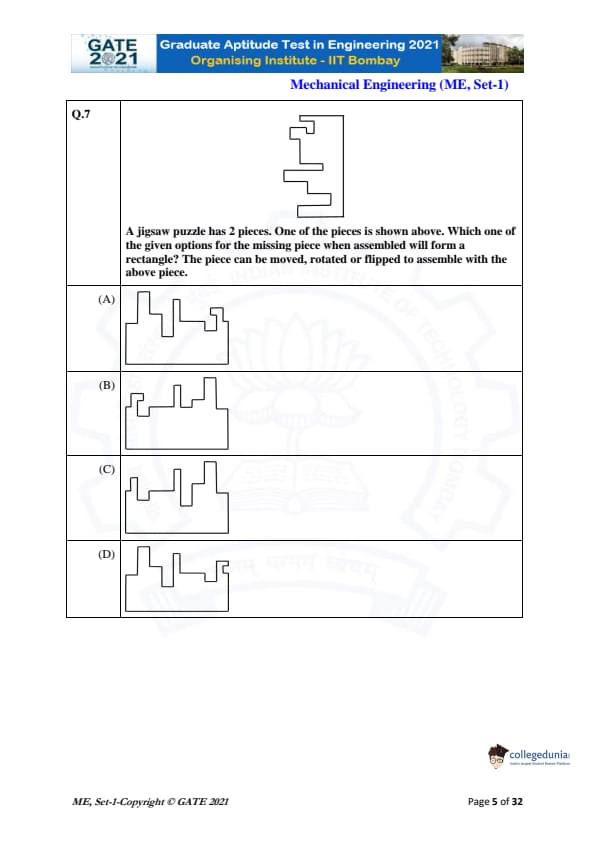












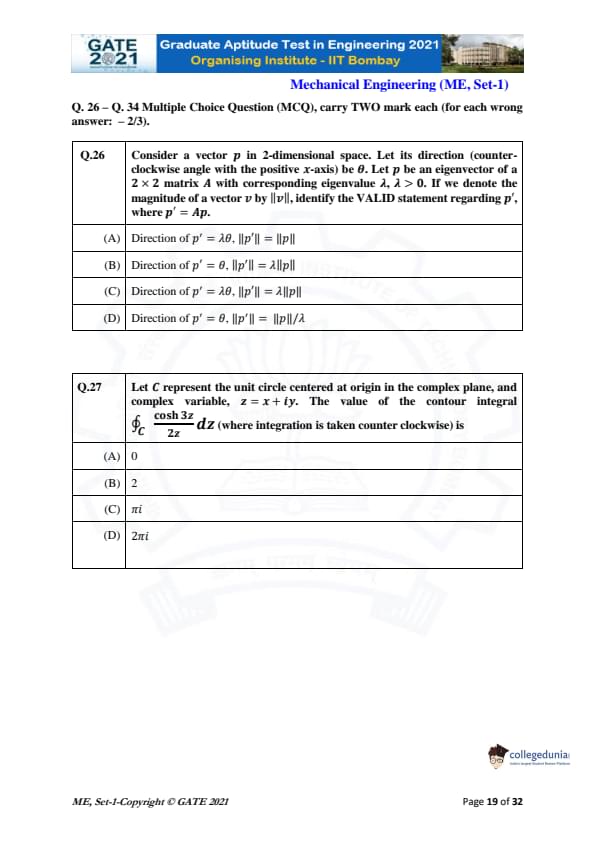
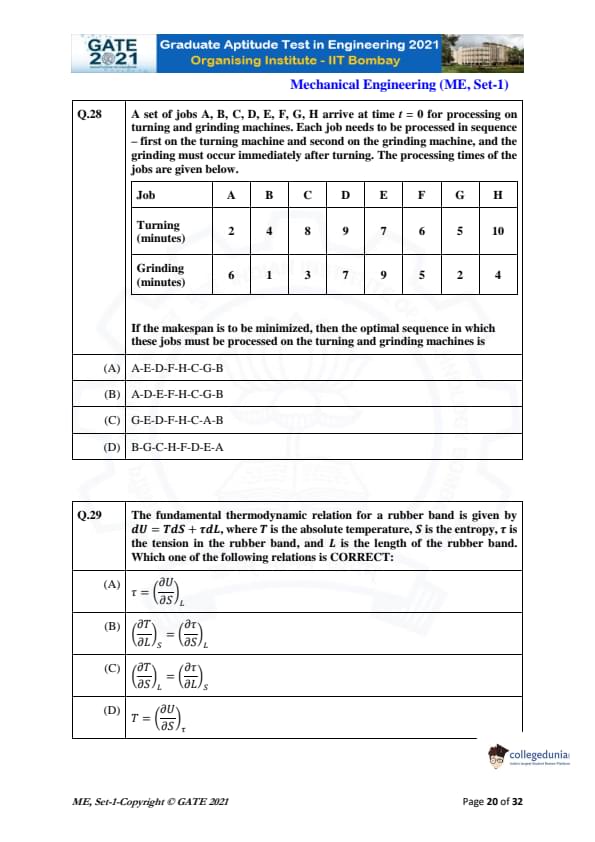

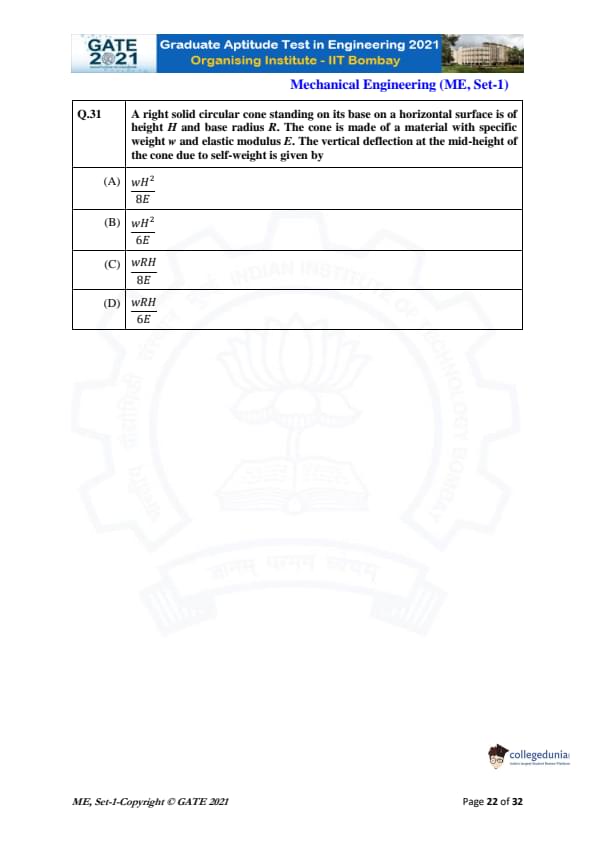








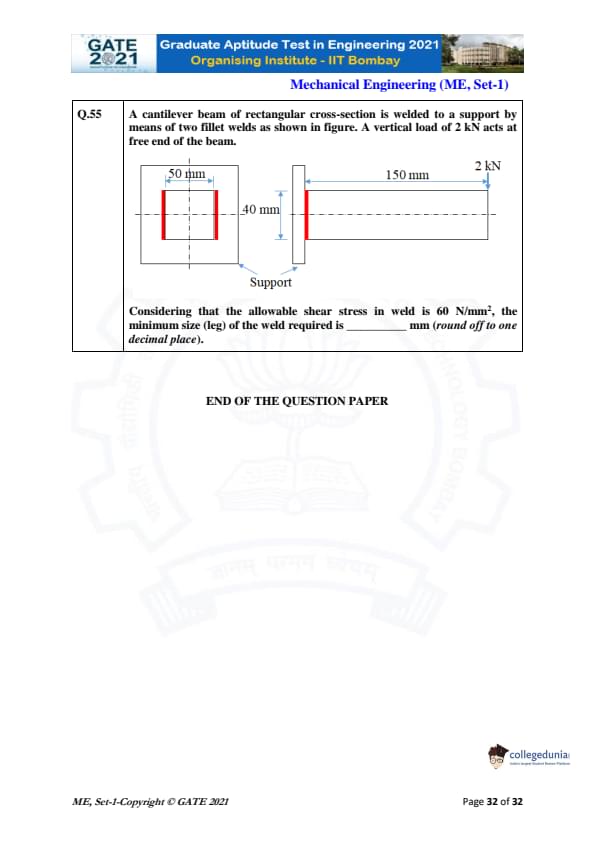
GATE 2021 February 14 (Forenoon Session): Sectional Analysis
GATE ME 2021 was conducted on February 14, 2021. The morning shift was held between 12:30 pm to 2:30 pm. The GATE paper analysis for ME 2021 forenoon session has been summarized below:
- The overall difficulty level was easy to moderate.
- The questions asked in the general aptitude section were easy.
- Thermodynamics and Manufacturing carried the maximum weightage.
- Few difficult questions were asked from sections like Engineering Mechanics, Production Engineering & Engineering Mathematics.
- Almost 8- 10 questions were theoretical while the remaining questions were numerically based.
- Candidates found questions from Industrial Engineering moderate to difficult.
| Topics | Total Marks | Total Questions (Approx.) |
|---|---|---|
| Manufacturing | 15 | 9 |
| Thermodynamics | 12 | 9 |
| Industrial Engineering | 9 | 5 |
| TOM | 9 | 6 |
| Heat Transfer | 6 | 4 |
| Engineering Math | 12 | 8 |
| Engineering Mechanics | 2 | 2 |
| SOM | 8 | 7 |
| Fluid Mechanics | 6 | 3 |
Quick Links:
GATE Previous Year Question Paper with Answer Key PDFs
GATE Previous Year Question Papers with Answer Key PDFs are provided for aspirants in the table below.
| GATE 2020 Question Papers | GATE 2019 Question Papers |
| GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments