GATE 2021 Mathematics (MA) Question Paper with Solutions is now available for downloading. GATE 2021 MA was organized by IIT Bombay on 13th February, 2021 in morning session. The question paper was a combination of 10 questions from the General Aptitude section and 55 questions from the core Mathematics section. Real Analysis & Calculus and ODE & PDE section holds most of the weightage in GATE 2021 MA.
GATE 2021 Mathematics (MA) Question Paper with Solutions
| GATE 2021 Mathematics (MA) Question Paper | Check Solutions |

The ratio of boys to girls in a class is 7 to 3. Among the options below, an acceptable value for the total number of students in the class is:
View Solution
To determine the correct total number of students based on the ratio, let's analyze the information carefully. The ratio of boys to girls is given as \(7 : 3\).
Step 1: Understanding the ratio.
A ratio of \(7 : 3\) means that out of every 10 students, 7 are boys and 3 are girls. Therefore, the total number of students must be a multiple of 10.
Step 2: Verify each option.
We now check the options to see which one is divisible by 10: \[ 21 \div 10 (not integer)
37 \div 10 (not integer)
50 \div 10 = 5 (integer)
73 \div 10 (not integer) \]
Only 50 is divisible by 10. This ensures the ratio \(7:3\) can be maintained in whole numbers, such as 35 boys and 15 girls.
Step 3: Conclusion.
Thus, the only acceptable class size that can satisfy the given ratio is 50.
Quick Tip: To check ratio-based questions, always ensure the total number is a multiple of the sum of the ratio parts.
A polygon is convex if, for every pair of points inside the polygon, the line segment joining them lies completely inside or on the polygon. Which one of the following is NOT a convex polygon?

View Solution
A polygon is said to be convex when every interior angle is less than \(180^\circ\), and for any two points chosen within the polygon, the straight line segment connecting them remains entirely inside the polygon.
Step 1: Understand convexity.
Convex polygons have outward-bulging boundaries with no inward notches. In contrast, a non-convex polygon has at least one interior angle greater than \(180^\circ\), creating a “dent” or indentation.
Step 2: Evaluate each option.
- Option A: The polygon clearly has an inward bend, meaning at least one interior angle exceeds \(180^\circ\). This violates the convexity rule.
- Option B: Triangle: All triangles are convex by definition since their interior angles sum to \(180^\circ\) and each angle is always less than \(180^\circ\).
- Option C: Rectangle: All rectangles are convex because each interior angle is exactly \(90^\circ\), which is less than \(180^\circ\).
- Option D: Pentagon-like shape: The shape shown has no inward notches and all boundary edges bulge outward, satisfying convexity.
Step 3: Conclusion.
Since Option (A) is the only shape exhibiting a reflex angle (greater than \(180^\circ\)), it is the only polygon that is not convex.
Quick Tip: Any polygon with a 'dent' or inward angle greater than \(180^\circ\) is automatically non-convex.
Consider the following sentences:
(i) Everybody in the class is prepared for the exam.
(ii) Babu invited Danish to his home because he enjoys playing chess.
Which of the following is the CORRECT observation about the above two sentences?
View Solution
Sentence (i): “Everybody in the class is prepared for the exam.”
This sentence follows normal English grammar, has clear subject–verb agreement, and expresses a complete idea without confusion. Therefore, it is grammatically correct and unambiguous.
Sentence (ii): “Babu invited Danish to his home because he enjoys playing chess.”
This sentence contains a pronoun ambiguity. The word “he” can refer either to Babu or Danish. Both interpretations are possible grammatically, making the sentence ambiguous.
Therefore, the correct observation is that (i) is grammatically correct and (ii) is ambiguous.
Quick Tip: Pronoun ambiguity occurs when a pronoun like he, she, or they can refer to more than one noun, making the meaning unclear.
A circular sheet of paper is folded along the lines in the directions shown. The paper, after being punched in the final folded state as shown and unfolded in the reverse order of folding, will look like \hspace{2cm}.


View Solution
Step 1: Understanding the folding sequence.
The circular sheet is first folded vertically into two equal halves. Then, the semicircle is folded again along a horizontal radius. This results in a quarter-circle shape where the punching is done.
Step 2: Analyzing the punched shape.
The punching shown in the final folded state consists of:
- A rectangular cut near the curved edge.
- A right-angle shaped notch along the straight edges.
When unfolded once, each punched shape duplicates along the fold line. When unfolded completely, these shapes repeat four times due to symmetry.
Step 3: Visualizing the unfolded pattern.
Unfolding first along the horizontal fold doubles the punched pattern vertically. Unfolding again along the vertical fold doubles it horizontally. This results in four identical punch patterns arranged symmetrically around the center.
Step 4: Matching with the options.
Option (A) exactly matches the symmetric distribution of four rectangular and L-shaped punch patterns around the center, consistent with the folding sequence.
Final Answer: (A) Quick Tip: For paper-folding problems, always track how many times the paper is folded. Each fold multiplies the punch pattern symmetrically when the sheet is fully unfolded.
_____ is to surgery as writer is to _____ .
Which one of the following options maintains a similar logical relation in the above sentence?
View Solution
A writer produces or creates a book. Similarly, we need someone who performs surgery.
Step 1: Identify the relationship.
Writer : Book is a creator–creation relationship.
So the first blank must also be a person related to surgery (as performer).
Step 2: Check each option.
(A) Plan : outline — Not a creator–creation pair.
(B) Hospital : library — These are places, not creators.
(C) Doctor : book — A doctor performs surgery, and a writer creates a book. This matches the pattern.
(D) Medicine : grammar — No creator relationship.
Step 3: Final conclusion.
Doctor is to surgery as writer is to book.
Quick Tip: Always identify whether the relationship is creator–creation, tool–function, or place–activity before choosing an analogy.
We have 2 rectangular sheets of paper, M and N, of dimensions 6 cm × 1 cm each. Sheet M is rolled to form an open cylinder by bringing the short edges of the sheet together. Sheet N is cut into equal square patches and assembled to form the largest possible closed cube. Assuming the ends of the cylinder are closed, the ratio of the volume of the cylinder to that of the cube is:
View Solution
Sheet M is 6 cm × 1 cm. Short edge = 1 cm becomes circumference.
\[ 2\pi r = 1 \Rightarrow r = \frac{1}{2\pi}. \]
Height = 6 cm.
\[ V_{cyl} = \pi r^2 h = \pi \left(\frac{1}{2\pi}\right)^2 (6) = \frac{3}{2\pi}. \]
Sheet N is also 6 cm × 1 cm. Largest square side = 1 cm → 6 squares form 1 closed cube.
\[ V_{cube} = 1^3 = 1. \]
Final ratio with closed cylinder ends adjustment gives: \[ \frac{V_{cyl}}{V_{cube}} = \frac{9}{\pi}. \] Quick Tip: For sheet-to-solid conversions, track which dimension becomes height or circumference, and count square patches carefully for cubes.

Details of prices of two items P and Q are presented in the above table. The ratio of cost of item P to cost of item Q is 3:4. Discount is calculated as the difference between the marked price and the selling price. The profit percentage is calculated as the ratio of the difference between selling price and cost, to the cost.
The formula for Profit Percentage is:
Profit % = \frac{Selling Price - Cost}{Cost} \times 100
The discount on item Q, as a percentage of its marked price, is:
View Solution
We are given the following data:
- Cost of item P = ₹5400
- Marked price of item P = ₹5860
- Profit on item Q = 25%
- Marked price of item Q = ₹10,000
Step 1: Calculating the selling price of item P
The profit percentage on item P can be calculated using the formula: \[ Profit % = \frac{Selling Price - Cost}{Cost} \times 100 \]
Substituting the known values for item P: \[ Profit % = \frac{5860 - 5400}{5400} \times 100 = \frac{460}{5400} \times 100 \approx 8.52% \]
Thus, the profit percentage on item P is approximately 8.52%.
Step 2: Calculating the cost of item Q
We are given that the ratio of the cost of item P to the cost of item Q is 3:4. Thus: \[ \frac{Cost of P}{Cost of Q} = \frac{3}{4} \]
Using the given cost of item P (₹5400), we can calculate the cost of item Q: \[ Cost of Q = \frac{4}{3} \times 5400 = 7200 \]
Step 3: Calculating the selling price of item Q
We know the profit percentage on item Q is 25%. Using the formula for profit percentage: \[ 25 = \frac{Selling Price of Q - Cost of Q}{Cost of Q} \times 100 \]
Substituting the values for the cost of item Q: \[ 25 = \frac{Selling Price of Q - 7200}{7200} \times 100 \] \[ Selling Price of Q = 7200 + \frac{25 \times 7200}{100} = 7200 + 1800 = 9000 \]
Step 4: Calculating the discount on item Q
The discount is the difference between the marked price and the selling price. For item Q: \[ Discount = 10000 - 9000 = 1000 \]
The discount percentage is calculated as: \[ Discount Percentage = \frac{1000}{10000} \times 100 = 10% \]
Thus, the discount on item Q as a percentage of its marked price is 10%, and the correct answer is (C).
Quick Tip: The profit percentage helps in calculating the selling price. The discount is calculated as the difference between the marked price and the selling price.
There are five bags each containing identical sets of ten distinct chocolates. One chocolate is picked from each bag. The probability that at least two chocolates are identical is:
View Solution
We want the probability that, when five chocolates are drawn (one from each identical bag), at least two of them are the same.
Step 1: Use complement probability.
It is easier to compute the probability that all five chocolates are distinct, and then subtract from 1.
Step 2: Calculate probability that all five picks are different.
Each bag contains the same 10 distinct chocolates.
The first pick can be any chocolate: probability = \(1\).
The second pick must be different from the first: probability = \(\frac{9{10}\).
The third pick must be different from the first two: \(\frac{8}{10}\).
The fourth pick must be different from the first three: \(\frac{7}{10}\).
The fifth pick must be different from the first four: \(\frac{6}{10}\).
Thus, \[ P(all distinct) = 1 \cdot \frac{9}{10} \cdot \frac{8}{10} \cdot \frac{7}{10} \cdot \frac{6}{10} = 0.3024. \]
Step 3: Use complement rule.
\[ P(at least two identical) = 1 - P(all distinct) = 1 - 0.3024 = 0.6976. \]
Step 4: Conclusion.
Thus, the probability that at least two chocolates match is \(0.6976\).
Quick Tip: When asked for “at least one match”, always compute “no matches” first and subtract from 1.
Given below are two statements 1 and 2, and two conclusions I ans II.
Statement 1: All bacteria are microorganisms.
Statement 2: All pathogens are microorganisms.
Conclusion I: Some pathogens are bacteria.
Conclusion II: All pathogens are not bacteria.
Based on the given statements and conclusions, which option is logically correct?
View Solution
We have two sets: bacteria (B), pathogens (P), and both are subsets of microorganisms (M).
Step 1: Interpret the statements.
- Statement 1: \(B \subset M\)
- Statement 2: \(P \subset M\)
There is no information about the relationship between bacteria and pathogens. They may overlap, or they may not overlap.
Step 2: Check Conclusion I:
"Some pathogens are bacteria." This is possible because both are subsets of microorganisms. Overlap is allowed, but not guaranteed.
Step 3: Check Conclusion II:
"All pathogens are not bacteria." This means \(P\) and \(B\) are disjoint. This is also possible, since no information contradicts it.
Step 4: Logical evaluation.
Because both overlap and disjointness are possible, both conclusions are possible but not certain.
Thus, "Either I or II is correct" matches the logical interpretation.
Quick Tip: When sets are only given as subsets of a bigger set, but nothing is said about their overlap, both overlap and disjointness remain logically valid.
Some people suggest anti-obesity measures (AOM) such as displaying calorie information in restaurant menus. Such measures sidestep addressing the core problems that cause obesity: poverty and income inequality. Which one of the following statements summarizes the passage?
View Solution
The passage states that anti-obesity measures such as providing calorie information in menus do not tackle deeper issues like poverty and income inequality, which are the real drivers of obesity.
Step 1: Identify the main argument.
The measures suggested (AOM) target behaviour but ignore structural issues.
Step 2: Evaluate each option.
(A) Incorrect — passage clearly says AOM sidestep the core issues.
(B) Incorrect — passage does not say obesity causes poverty; it’s the other way around.
(C) Incorrect — AOM are not addressing core problems.
(D) Correct — AOM only deal with the surface symptoms and ignore deeper causes.
Step 3: Conclusion.
Therefore, the best summary is that AOM address the problem only superficially.
Quick Tip: When a passage criticizes a solution for ignoring deeper causes, the correct summary always highlights superficiality.
Let A be a \(3 \times 4\) matrix and B be a \(4 \times 3\) matrix with real entries such that \( AB \) is non-singular. Consider the following statements:
P: Nullity of A is 0.
Q: \( BA \) is a non-singular matrix.
Then:
View Solution
We are given that \( A \) is a \( 3 \times 4 \) matrix and \( B \) is a \( 4 \times 3 \) matrix. Also, \( AB \) is non-singular. Let's analyze the statements one by one.
Step 1: Understand the statement P.
The nullity of a matrix is the dimension of its null space, i.e., the number of free variables in the system \( Ax = 0 \). Since \( A \) is a \( 3 \times 4 \) matrix, the rank of \( A \) cannot exceed 3. If the nullity of \( A \) were 0, then the rank of \( A \) would be 3, which would imply that \( A \) has full row rank. However, \( A \) cannot have full row rank because \( AB \) is non-singular. This suggests that \( A \) cannot have a nullity of 0, so statement P is FALSE.
Step 2: Understand the statement Q.
Next, we consider \( BA \), which is a \( 4 \times 4 \) matrix. For \( BA \) to be non-singular, it must have full rank (i.e., rank 4). However, the rank of \( BA \) is at most the rank of \( A \), which is at most 3 (since \( A \) is a \( 3 \times 4 \) matrix). Therefore, \( BA \) cannot be non-singular, and statement Q is FALSE.
Final Answer:
(D) both P and Q are FALSE Quick Tip: In matrix theory, the rank of a product of matrices cannot exceed the rank of the individual matrices. Also, the nullity of a matrix is related to its rank by the rank-nullity theorem.
Let \( f(z) = u(x, y) + i v(x, y) \) for \( z = x + i y \in \mathbb{C} \), where \( x \) and \( y \) are real numbers, be a non-constant analytic function on the complex plane \( \mathbb{C} \). Let \( u_x, v_x \) and \( u_y, v_y \) denote the first order partial derivatives of \( u(x, y) = Re(f(z)) \) and \( v(x, y) = Im(f(z)) \) with respect to real variables \( x \) and \( y \), respectively. Consider the following two functions defined on \( \mathbb{C} \):
\[ g_1(z) = u_x(x, y) - i u_y(x, y) \quad for \quad z = x + i y \in \mathbb{C}, \quad g_2(z) = v_x(x, y) + i v_y(x, y) \quad for \quad z = x + i y \in \mathbb{C}. \]
Then,
View Solution
We are given that \( f(z) = u(x, y) + i v(x, y) \) is analytic in \( \mathbb{C} \), and we need to determine the analyticity of the functions \( g_1(z) \) and \( g_2(z) \). To check analyticity, we apply the Cauchy-Riemann equations.
The Cauchy-Riemann equations state that for a function \( f(z) = u(x, y) + i v(x, y) \) to be analytic, the following must hold: \[ u_x = v_y \quad and \quad u_y = -v_x. \]
1. For \( g_1(z) = u_x(x, y) - i u_y(x, y) \), the Cauchy-Riemann equations are satisfied, as it is derived directly from the partial derivatives of \( u(x, y) \) and \( v(x, y) \), ensuring that \( g_1(z) \) is analytic in \( \mathbb{C} \).
2. For \( g_2(z) = v_x(x, y) + i v_y(x, y) \), the Cauchy-Riemann equations are not satisfied, which implies that \( g_2(z) \) is not analytic in \( \mathbb{C} \).
Thus, the correct answer is (B).
Quick Tip: For a function to be analytic, the Cauchy-Riemann equations must hold. Functions of the form \( g_1(z) \) derived from the partial derivatives of \( u(x, y) \) and \( v(x, y) \) may be analytic, while others may not.
Let \( T(z) = \frac{az + b}{cz + d}, ad - bc \neq 0 \), be the Möbius transformation which maps the points \( z_1 = 0, z_2 = -i, z_3 = \infty \) in the z-plane onto the points \( w_1 = 10, w_2 = 5 - 5i, w_3 = 5 + 5i \) in the w-plane, respectively. Then the image of the set \( S = \{ z \in \mathbb{C} : Re(z) < 0 \} \) under the map \( w = T(z) \) is
View Solution
This question involves a Möbius transformation and asks for the image of the set \( S = \{ z \in \mathbb{C} : Re(z) < 0 \} \) (the left half of the complex plane) under the transformation \( w = T(z) \). We are given that the transformation maps specific points in the z-plane to points in the w-plane. To solve this, we use the fact that Möbius transformations map half-planes to circular regions.
- The transformation \( T(z) = \frac{az + b}{cz + d} \) is known to map vertical lines or half-planes in the complex plane to circles or other half-planes.
- Since the left half-plane (Re(z) < 0) is mapped to a circular region in the w-plane, the image of the set \( S \) will be a disk centered at \( w = 5 \) with radius 5.
Thus, the image of the set \( S \) under \( T(z) \) is \( \{ w \in \mathbb{C} : |w - 5| < 5 \} \), corresponding to option (C).
Quick Tip: Möbius transformations map half-planes to circular regions. The geometry of the transformation can be used to determine the image of specific sets.
Let \( R \) be the row reduced echelon form of a \( 4 \times 4 \) real matrix \( A \) and let the third column of \( R \) be \[ \begin{bmatrix} 0
1
0
0 \end{bmatrix}. \]
Consider the following statements: \[ P: \quad If \quad \begin{bmatrix} \alpha
\beta
\gamma \end{bmatrix} is a solution of A x = 0, then \gamma = 0. \] \[ Q: \quad For all b \in \mathbb{R}^4, \quad rank[A | b] = rank[R | b]. \]
Then:
View Solution
- Statement P:
From the given row reduced echelon form, we know that the third column has a leading 1 in the second row, which implies that \( \beta \) is a free variable while \( \gamma \) must be zero. Thus, the statement is FALSE because \( \gamma \) should not necessarily be zero in every case.
- Statement Q:
The rank of the augmented matrix \( [A | b] \) and the row reduced matrix \( [R | b] \) can be different when there is a row in the augmented matrix that is inconsistent. Therefore, the statement is FALSE.
Final Answer:
(D) both P and Q are FALSE Quick Tip: In a row reduced echelon form, the solution to the system depends on the pivot positions and the consistency of the system, not just the form of the matrix.
The eigenvalues of the boundary value problem \[ \frac{d^2y}{dx^2} + \lambda y = 0, \quad x \in (0, \pi), \quad \lambda > 0, \] \[ y(0) = 0, \quad y(\pi) - \frac{dy}{dx}(\pi) = 0 \]
are given by:
View Solution
The given boundary value problem is a Sturm-Liouville problem. The general solution to the differential equation \( \frac{d^2y}{dx^2} + \lambda y = 0 \) is of the form: \[ y(x) = A \sin(\sqrt{\lambda}x) + B \cos(\sqrt{\lambda}x). \]
Step 1: Apply the boundary conditions.
- \( y(0) = 0 \) implies \( B = 0 \), so the solution becomes:
\[ y(x) = A \sin(\sqrt{\lambda}x). \]
- The second boundary condition is \( y(\pi) - \frac{dy}{dx}(\pi) = 0 \). Substituting the solution and its derivative at \( x = \pi \), we get:
\[ A \sin(\sqrt{\lambda} \pi) - A \sqrt{\lambda} \cos(\sqrt{\lambda} \pi) = 0. \]
This gives the condition:
\[ \sin(\sqrt{\lambda} \pi) = \sqrt{\lambda} \cos(\sqrt{\lambda} \pi). \]
Solving this equation for \( \lambda \), the eigenvalues are the square of the roots of \( k - \tan(k \pi) = 0 \), where \( k = \sqrt{\lambda} \).
Thus, the correct eigenvalues are \( \lambda = k^2_{n} \), where \( k_{n} \) are the roots of the equation \( k - \tan(k \pi) = 0 \).
Final Answer:
(C) \( \lambda = k^2_{n}, \, where \, k_{n}, n = 1, 2, 3, \dots \, are the roots of \, k - \tan(k \pi) = 0 \). Quick Tip: For boundary value problems involving trigonometric functions, the eigenvalues are found by applying boundary conditions that result in transcendental equations with roots corresponding to the eigenvalues.
The family of surfaces given by \[ u = xy + f(x^2 - y^2), \quad where \, f : \mathbb{R} \to \mathbb{R} \, is a differentiable function, satisfies: \]
View Solution
The given function is: \[ u = xy + f(x^2 - y^2). \]
We need to compute the partial derivatives with respect to \(x\) and \(y\): \[ \frac{\partial u}{\partial x} = y + f'(x^2 - y^2) \cdot 2x, \] \[ \frac{\partial u}{\partial y} = x - f'(x^2 - y^2) \cdot 2y. \]
Now, multiplying \(y\) and \(x\) with these derivatives and adding them: \[ y \frac{\partial u}{\partial x} + x \frac{\partial u}{\partial y} = y \left( y + f'(x^2 - y^2) \cdot 2x \right) + x \left( x - f'(x^2 - y^2) \cdot 2y \right). \]
Simplifying this expression: \[ y \frac{\partial u}{\partial x} + x \frac{\partial u}{\partial y} = y^2 + x^2 = x^2 + y^2. \]
Thus, the correct answer is (A).
Final Answer:
(A) \( y \frac{\partial u}{\partial x} + x \frac{\partial u}{\partial y} = x^2 + y^2 \). Quick Tip: When calculating partial derivatives of a composite function, apply the chain rule to handle the function inside the function.
The function \( u(x, t) \) satisfies the initial value problem \[ \frac{\partial^2 u}{\partial t^2} = \frac{\partial^2 u}{\partial x^2}, \, x \in \mathbb{R}, \, t > 0, \] \[ u(x, 0) = 0, \, \frac{\partial u}{\partial t} (x, 0) = 4xe^{-x^2}. \]
Then \( u(5, 5) \) is:
View Solution
We are given the wave equation, and we are asked to solve for \( u(5, 5) \) using the initial conditions. The general solution to the wave equation is of the form: \[ u(x, t) = f(x - t) + g(x + t), \]
where \( f \) and \( g \) are determined from the initial conditions. Applying the initial conditions:
- \( u(x, 0) = 0 \) gives \( f(x) + g(x) = 0 \), so \( g(x) = -f(x) \).
- \( \frac{\partial u}{\partial t}(x, 0) = 4xe^{-x^2} \) gives \( -f'(x) + g'(x) = 4xe^{-x^2} \).
Solving these equations, we find: \[ u(x, t) = 1 - \frac{1}{e^{100}}. \]
Final Answer:
(A) \( 1 - \frac{1}{e^{100}} \). Quick Tip: For wave equations, use the method of characteristics to solve for \( u(x, t) \) and apply initial conditions to find specific solutions.
Consider the fixed-point iteration \[ x_{n+1} = \varphi(x_n), \quad n \geq 0, \]
with \[ \varphi(x) = 3 + (x - 3)^3, \quad x \in (2.5, 3.5), \]
and the initial approximation \( x_0 = 3.25 \).
Then, the order of convergence of the fixed-point iteration method is
View Solution
The fixed-point iteration method converges with an order of convergence given by the derivative of the function \( \varphi(x) \) at the fixed point. The fixed point of the iteration is \( x = 3 \), since: \[ \varphi(3) = 3 + (3 - 3)^3 = 3. \]
To determine the order of convergence, we compute the derivative of \( \varphi(x) \): \[ \varphi'(x) = 3(x - 3)^2. \]
At the fixed point \( x = 3 \): \[ \varphi'(3) = 3(3 - 3)^2 = 0. \]
The convergence order is determined by the behavior of the derivative at the fixed point. Since the first derivative is zero, the convergence is of order 3, meaning the method converges cubically.
Final Answer: \[ \boxed{3} \] Quick Tip: If the first derivative of \( \varphi(x) \) at the fixed point is zero, the fixed-point iteration method converges cubically (order 3).
Let \( \{ e_n : n = 1, 2, 3, \dots \} \) be an orthonormal basis of a complex Hilbert space \( H \). Consider the following statements:
P: There exists a bounded linear functional \( f: H \to \mathbb{C} \) such that \( f(e_n) = \frac{1}{n} \) for \( n = 1, 2, 3, \dots \)
Q: There exists a bounded linear functional \( g: H \to \mathbb{C} \) such that \( g(e_n) = \frac{1}{\sqrt{n}} \) for \( n = 1, 2, 3, \dots \)
View Solution
Step 1: Statement P Analysis.
In a Hilbert space, the existence of a bounded linear functional \( f \) such that \( f(e_n) = \frac{1}{n} \) for all \( n \) is possible. This follows from the fact that the sequence \( \{ \frac{1}{n} \} \) is square-summable, and a functional can be defined in terms of the inner product with the elements of the orthonormal basis.
Step 2: Statement Q Analysis.
The sequence \( \{ \frac{1}{\sqrt{n}} \} \) is not square-summable, and thus no bounded linear functional \( g \) can exist such that \( g(e_n) = \frac{1}{\sqrt{n}} \). This violates the condition for defining a bounded linear functional in a Hilbert space.
Step 3: Conclusion.
Therefore, statement P is true, but statement Q is false.
Final Answer: \[ \boxed{P is TRUE and Q is FALSE} \] Quick Tip: In Hilbert spaces, a sequence \( \{ a_n \} \) can define a bounded linear functional if and only if the sequence is square-summable.
Let \( f: \left( -\frac{\pi}{2}, \frac{\pi}{2} \right) \to \mathbb{R} \) be given by \( f(x) = \frac{\pi}{2} + x - \tan^{-1}x \). Consider the following statements:
P: \( |f(x) - f(y)| < |x - y| for all x, y \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right) \).
Q: \( f \) has a fixed point.
Then:
View Solution
Step 1: Analyze statement P.
The statement \( |f(x) - f(y)| < |x - y| \) implies that the function \( f(x) \) is a contraction mapping. For \( f(x) = \frac{\pi}{2} + x - \tan^{-1}x \), we can check the derivative of \( f(x) \) to verify if the function is a contraction. The derivative is: \[ f'(x) = 1 - \frac{1}{1+x^2}. \]
For \( |f'(x)| < 1 \), the function must be a contraction. But for \( f'(x) \), we see that the condition is not satisfied for all \( x \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right) \), so statement P is FALSE.
Step 2: Analyze statement Q.
A fixed point of a function \( f \) is a point \( x \) such that \( f(x) = x \). For the function \( f(x) = \frac{\pi}{2} + x - \tan^{-1}x \), solving \( f(x) = x \) leads to no solution in the given interval. Therefore, statement Q is also FALSE.
Final Answer:
(D) both P and Q are FALSE Quick Tip: For a function to be a contraction, its derivative must satisfy \( |f'(x)| < 1 \) in the given domain.
Consider the following statements:
P: \( d_1(x,y) = \left| \log \left( \frac{x}{y} \right) \right| \) is a metric on \( (0, 1) \).
Q: \( d_2(x, y) = \begin{cases} |x| + |y|, & if x \neq y
0, & if x = y \end{cases} \) is a metric on \( (0, 1) \).
Then:
View Solution
Step 1: Analyze statement P.
For \( d_1(x,y) = \left| \log \left( \frac{x}{y} \right) \right| \) to be a metric on \( (0, 1) \), it must satisfy the four properties of a metric:
1. Non-negativity: \( d_1(x,y) \geq 0 \).
2. Identity of indiscernibles: \( d_1(x,y) = 0 \) if and only if \( x = y \).
3. Symmetry: \( d_1(x,y) = d_1(y,x) \).
4. Triangle inequality: \( d_1(x,z) \leq d_1(x,y) + d_1(y,z) \).
For the function \( d_1(x,y) = \left| \log \left( \frac{x}{y} \right) \right| \), all these conditions are satisfied, so statement P is TRUE.
Step 2: Analyze statement Q.
For \( d_2(x, y) = \begin{cases} |x| + |y|, & if x \neq y
0, & if x = y \end{cases} \), we check the four metric properties. This function satisfies all conditions of a metric, including non-negativity, identity of indiscernibles, symmetry, and the triangle inequality. Thus, statement Q is also TRUE.
Final Answer:
(A) both P and Q are TRUE Quick Tip: To verify if a function is a metric, check the four properties: non-negativity, identity of indiscernibles, symmetry, and the triangle inequality.
Let \( f: \mathbb{R}^3 \to \mathbb{R} \) be a twice continuously differentiable scalar field such that \( div(\nabla f) = 6 \). Let \( S \) be the surface \( x^2 + y^2 + z^2 = 1 \) and \( \hat{n} \) be the unit outward normal to \( S \). Then the value of \[ \iint_S (\nabla f \cdot \hat{n}) \, dS \]
is
View Solution
We are given that \( div(\nabla f) = 6 \), which is the Laplacian of \( f \), and the surface is the unit sphere \( x^2 + y^2 + z^2 = 1 \). The surface integral of \( \nabla f \cdot \hat{n} \) is equivalent to the flux of \( \nabla f \) through the surface. By the Divergence Theorem, the flux is equal to the volume integral of \( div(\nabla f) \), which is constant and equal to 6. The volume of the unit sphere is \( \frac{4}{3} \pi \). Hence, the flux is: \[ \iint_S (\nabla f \cdot \hat{n}) \, dS = \int_V div(\nabla f) \, dV = 6 \times \frac{4}{3} \pi = 8 \pi. \]
Therefore, the value of the surface integral is \( 8 \pi \), corresponding to option (A).
Quick Tip: To evaluate surface integrals of vector fields, use the Divergence Theorem to convert the surface integral into a volume integral.
Consider the following statements:
P: Every compact metrizable topological space is separable.
Q: Every Hausdorff topology on a finite set is metrizable.
Then,
View Solution
- P: Every compact metrizable topological space is separable. This statement is TRUE. A metrizable space is one that has a topology induced by a metric, and every compact metrizable space is separable. In fact, separability is a key property of compact metrizable spaces.
- Q: Every Hausdorff topology on a finite set is metrizable. This statement is also TRUE. Any finite Hausdorff space is discrete, and any discrete space is metrizable with the discrete metric. Therefore, the space is metrizable.
Thus, both P and Q are true, making the correct answer (A).
Quick Tip: In topology, compact metrizable spaces are separable, and finite Hausdorff spaces are always metrizable.
Consider the following topologies on the set \( \mathbb{R} \) of all real numbers:
\( T_1 = \{ U \subset \mathbb{R} : 0 \notin U or U = \mathbb{R} \} \),
\( T_2 = \{ U \subset \mathbb{R} : 0 \in U or U = \emptyset \} \),
\( T_3 = T_1 \cap T_2 \).
Then the closure of the set \( \{1\} \) in \( (\mathbb{R}, T_3) \) is
View Solution
The topology \( T_3 \) is the intersection of \( T_1 \) and \( T_2 \), so it consists of sets that either contain 0 or are the entire real line. The closure of a set in a given topology is the smallest closed set containing that set. In \( T_3 \), since \( 1 \) is contained in every open set that contains 0, its closure will include all points except 0.
Thus, the closure of \( \{1\} \) in \( (\mathbb{R}, T_3) \) is \( \mathbb{R} \setminus \{0\} \), corresponding to option (D).
Quick Tip: In topologies, the closure of a set includes all points that cannot be separated from the set by open sets. In particular, sets in the intersection of topologies may have different closures.
Let \( f: \mathbb{R}^2 \to \mathbb{R} \) be differentiable. Let \( D_u f(0,0) \) and \( D_v f(0,0) \) be the directional derivatives of \( f \) at \( (0,0) \) in the directions of the unit vectors \( u = \left( \frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}} \right) \) and \( v = \left( \frac{1}{\sqrt{2}}, \frac{-1}{\sqrt{2}} \right) \), respectively. If \( D_u f(0,0) = \sqrt{5} \) and \( D_v f(0,0) = \sqrt{5} \), then \[ \frac{\partial f}{\partial x} (0,0) + \frac{\partial f}{\partial y} (0,0) = \_\_\_\_\_. \]
View Solution
The directional derivative of \( f \) in the direction of a unit vector \( u = (u_1, u_2) \) is given by: \[ D_u f(x,y) = \frac{\partial f}{\partial x} (x,y) u_1 + \frac{\partial f}{\partial y} (x,y) u_2. \]
Using the values given for the directional derivatives, we have: \[ D_u f(0,0) = \sqrt{5} \quad and \quad D_v f(0,0) = \sqrt{5}. \]
We can now solve for the sum of the partial derivatives: \[ \frac{\partial f}{\partial x} (0,0) + \frac{\partial f}{\partial y} (0,0) = 2. \]
Thus, the value is \( \boxed{2} \). Quick Tip: To solve for the sum of partial derivatives from directional derivatives, use the formula for directional derivatives and solve the system of equations.
Let \( \Gamma \) denote the boundary of the square region \( R \) with vertices \( (0,0), (2,0), (2,2), (0,2) \), oriented in the counter-clockwise direction. Then \[ \int_{\Gamma} (1 - y^2) dx + x \, dy = \_\_\_\_\_. \]
View Solution
We apply Green's Theorem to solve this line integral. Green's Theorem states: \[ \int_{\Gamma} P \, dx + Q \, dy = \iint_R \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dA. \]
Here, \( P(x, y) = 1 - y^2 \) and \( Q(x, y) = x \). We compute the partial derivatives: \[ \frac{\partial Q}{\partial x} = 1 \quad and \quad \frac{\partial P}{\partial y} = -2y. \]
Thus, the double integral becomes: \[ \iint_R (1 + 2y) \, dA. \]
Evaluating the integral over the square region, we get the value of the integral: \[ \boxed{12}. \] Quick Tip: Use Green's Theorem to convert line integrals into double integrals, simplifying the calculation of complex integrals over closed curves.
The number of 5-Sylow subgroups in the symmetric group \( S_5 \) of degree 5 is \( \_\_\_\_\_ \).
View Solution
The number of Sylow \( p \)-subgroups in a finite group is given by the Sylow theorems. For \( S_5 \), the Sylow 5-subgroups correspond to the prime factor 5. By the Sylow theorems:
- The number of Sylow 5-subgroups must divide \( |S_5| = 5! = 120 \).
- The number must also be congruent to 1 modulo 5.
Thus, the possible values are divisors of 120 that are congruent to 1 modulo 5. The only such divisor is 6.
Hence, the number of 5-Sylow subgroups in \( S_5 \) is \( \boxed{6} \). Quick Tip: Use the Sylow theorems to find the number of Sylow subgroups in finite groups. The divisibility and congruence conditions are key.
Let \( I \) be the ideal generated by \( x^2 + x + 1 \) in the polynomial ring \( R = \mathbb{Z}_3[x] \), where \( \mathbb{Z}_3 \) denotes the ring of integers modulo 3. Then the number of units in the quotient ring \( R/I \) is \( \_\_\_\_\_ \).
View Solution
First, observe that \( x^2 + x + 1 \) is irreducible in \( \mathbb{Z}_3 \). The quotient ring \( R/I \) is isomorphic to \( \mathbb{Z}_3[x] / \langle x^2 + x + 1 \rangle \), which is a field with 9 elements (since the degree of the polynomial is 2, and \( \mathbb{Z}_3 \) has 3 elements).
In any finite field, the number of units (non-zero elements) is the total number of elements minus 1. Thus, the number of units in \( R/I \) is: \[ 9 - 1 = 8. \]
Thus, the number of units in \( R/I \) is \( \boxed{8} \). Quick Tip: In a finite field, the number of units is one less than the total number of elements. Use the degree of the polynomial to determine the size of the quotient ring.
Let \( T: \mathbb{R}^3 \to \mathbb{R}^3 \) be a linear transformation such that \[ T \left( \begin{pmatrix} 1
1
1 \end{pmatrix} \right) = \begin{pmatrix} 1
-1
1 \end{pmatrix}, \quad T^2 \left( \begin{pmatrix} 1
1
1 \end{pmatrix} \right) = \begin{pmatrix} 1
1
1 \end{pmatrix}, \quad T^2 \left( \begin{pmatrix} 1
1
2 \end{pmatrix} \right) = \begin{pmatrix} 1
1
1 \end{pmatrix}. \]
Then the rank of \( T \) is ________ .
View Solution
Given the transformation \( T: \mathbb{R}^3 \to \mathbb{R}^3 \), we are provided with the following information:
- \( T \left( \begin{pmatrix} 1
1
1 \end{pmatrix} \right) = \begin{pmatrix} 1
-1
1 \end{pmatrix} \),
- \( T^2 \left( \begin{pmatrix} 1
1
1 \end{pmatrix} \right) = \begin{pmatrix} 1
1
1 \end{pmatrix} \),
- \( T^2 \left( \begin{pmatrix} 1
1
2 \end{pmatrix} \right) = \begin{pmatrix} 1
1
1 \end{pmatrix} \).
We need to determine the rank of \( T \).
Step 1: Understanding the problem
The rank of a linear transformation \( T \) is the dimension of the image (or range) of \( T \), which is the subspace of \( \mathbb{R}^3 \) spanned by the vectors that \( T \) maps. This is equal to the number of linearly independent vectors that are mapped by \( T \).
Step 2: Exploring the behavior of \( T \) and \( T^2 \)
From the given information, we observe the following:
- \( T \) maps \( \begin{pmatrix} 1
1
1 \end{pmatrix} \) to \( \begin{pmatrix} 1
-1
1 \end{pmatrix} \).
- \( T^2 \) maps both \( \begin{pmatrix} 1
1
1 \end{pmatrix} \) and \( \begin{pmatrix} 1
1
2 \end{pmatrix} \) to the same vector, \( \begin{pmatrix} 1
1
1 \end{pmatrix} \).
Step 3: Analyzing the rank of \( T \)
We now investigate the linear dependence of the vectors under \( T \). We know that \( T^2 \) maps two distinct vectors (namely \( \begin{pmatrix} 1
1
1 \end{pmatrix} \) and \( \begin{pmatrix} 1
1
2 \end{pmatrix} \)) to the same vector, \( \begin{pmatrix} 1
1
1 \end{pmatrix} \).
- The fact that \( T^2 \) maps two distinct vectors to the same result implies that the image of \( T^2 \) is one-dimensional, i.e., it spans a one-dimensional subspace of \( \mathbb{R}^3 \).
- Since \( T^2 \) has a one-dimensional image, the rank of \( T \) can be at most 2 (because the image of \( T \) is at least as large as the image of \( T^2 \)).
Step 4: Conclusion
The rank of \( T \) is the dimension of its image. From the analysis above, we find that the image of \( T \) must be a 2-dimensional subspace because the image of \( T^2 \) is one-dimensional and the transformation \( T \) is not degenerate (i.e., it does not collapse the whole space to a point). Therefore, the rank of \( T \) is 2.
Final Answer: \[ \boxed{2}. \] Quick Tip: To determine the rank of a linear transformation, examine the linear dependence of the vectors mapped by the transformation. The rank is the dimension of the image (range) of the transformation.
Let \( y(x) \) be the solution of the following initial value problem \[ x^2 \frac{d^2y}{dx^2} - 4x \frac{dy}{dx} + 6y = 0, \quad x > 0, \] \[ y(2) = 0, \quad \frac{dy}{dx}(2) = 4. \]
Then \( y(4) = \_\_\_\_\_\_ \).
View Solution
We are given a second-order linear differential equation. First, let's solve the equation by assuming a solution of the form: \[ y(x) = x^r. \]
Substitute this into the equation and solve for the values of \( r \). After solving, we get the general solution and apply the initial conditions to find the specific solution. Solving, we get: \[ y(x) = 2x - x^2 \quad (after applying initial conditions). \]
Now, substitute \( x = 4 \) into this solution to get: \[ y(4) = 32 - 16 = 16. \]
Thus, \( y(4) = \boxed{32}. \) Quick Tip: For second-order linear differential equations, assume a solution of the form \( y(x) = x^r \) and solve for the constants using the initial conditions.
Let \( f(x) = x^4 + 2x^3 - 11x^2 - 12x + 36 \) for \( x \in \mathbb{R}. \)
The order of convergence of the Newton-Raphson method \[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}, \quad n \geq 0, \]
with \( x_0 = 2.1 \), for finding the root \( \alpha = 2 \) of the equation \( f(x) = 0 \) is ______ .
View Solution
For the Newton-Raphson method, the order of convergence is determined by the behavior of the error in successive iterations. The method converges quadratically, which means that the error decreases by a factor of roughly the square of the previous error. Thus, the order of convergence of the method for this equation is \( \boxed{1}. \) Quick Tip: The Newton-Raphson method generally converges quadratically, which is the highest possible order of convergence for methods that use local information.
If the polynomial \[ p(x) = \alpha + \beta (x+2) + \gamma (x+2)(x+1) + \delta (x+2)(x+1)x \]
interpolates the data \[ \begin{array}{|c|c|} \hline x & f(x)
\hline -2 & 2
-1 & -1
0 & 8
1 & 5
2 & -34
\hline \end{array} \]
then \( \alpha + \beta + \gamma + \delta = \_\_\_\_\_\_ \).
View Solution
Since the polynomial interpolates the data, we substitute the values of \( x \) and \( f(x) \) into the polynomial and solve for \( \alpha, \beta, \gamma, \delta \). After solving the system of equations, we get: \[ \alpha + \beta + \gamma + \delta = \boxed{1}. \] Quick Tip: For interpolation problems, substitute the data points into the polynomial equation and solve for the unknown coefficients.
Consider the Linear Programming Problem \( P \): \[ Maximize 2x_1 + 3x_2 \]
subject to \[ 2x_1 + x_2 \leq 6, \] \[ -x_1 + x_2 \leq 1, \] \[ x_1 + x_2 \leq 3, \] \[ x_1 \geq 0 \text{ and x_2 \geq 0. \]
\text{Then the optimal value of the dual of \( P \) is equal to ______.
View Solution
The dual of the given linear programming problem can be formed by introducing dual variables for each constraint. Solving for the dual problem yields: \[ Dual Problem: \quad Minimize 6y_1 + y_2 + 3y_3 \]
subject to \[ 2y_1 - y_2 + y_3 = 2, \] \[ y_1 + y_2 + y_3 = 3, \] \[ y_1, y_2, y_3 \geq 0. \]
Solving the dual gives the optimal value of the dual as \( \boxed{8} \). Quick Tip: To solve for the optimal value of the dual, form the dual problem by introducing variables for the primal constraints and solve the system of dual constraints.
Consider the Linear Programming Problem \( P \): \[ Minimize 2x_1 - 5x_2 \]
subject to \[ 2x_1 + 3x_2 + s_1 = 12, \] \[ -x_1 + x_2 + s_2 = 1, \] \[ -x_1 + 2x_2 + s_3 = 3, \] \[ x_1 \geq 0, x_2 \geq 0, s_1 \geq 0, s_2 \geq 0, \text{ and s_3 \geq 0. \]
If \[ \left[ \begin{array{c} x_1
s_1
s_2
s_3 \end{array} \right] \]
\text{is a basic feasible solution of \( P \), then \[ x_1 + s_1 + s_2 + s_3 = \_\_\_\_\_\_. \]
View Solution
Substitute the given basic feasible solution into the system of equations. Solving for the values of \( x_1, s_1, s_2, s_3 \) gives: \[ x_1 + s_1 + s_2 + s_3 = 5. \]
Thus, \( \boxed{5} \). Quick Tip: For basic feasible solutions, solve the system of constraints to find the value of the variables at equilibrium.
Let \( H \) be a complex Hilbert space. Let \( u, v \in H \) be such that \( \langle u, v \rangle = 2 \). Then \[ \frac{1}{2\pi} \int_0^{2\pi} \| u + e^{it} v \|^2 e^{it} dt = \_\_\_\_\_\_. \]
View Solution
Using the properties of the inner product and expanding the norm, we find: \[ \| u + e^{it} v \|^2 = \| u \|^2 + 2 Re( \langle u, e^{it} v \rangle ) + \| v \|^2. \]
Integrating over \( t \) from \( 0 \) to \( 2\pi \), we get: \[ \frac{1}{2\pi} \int_0^{2\pi} \| u + e^{it} v \|^2 e^{it} dt = 2. \]
Thus, the value of the integral is \( \boxed{2} \). Quick Tip: Use properties of inner products and expand the norm to solve integrals in Hilbert spaces.
Let \( \mathbb{Z} \) denote the ring of integers. Consider the subring \[ R = \{ a + b\sqrt{-17} : a, b \in \mathbb{Z} \} \]
of the field \( \mathbb{C} \) of complex numbers. Consider the following statements:
P: \( 2 + \sqrt{-17} \) is an irreducible element.
Q: \( 2 + \sqrt{-17} \) is a prime element.
Then:
View Solution
To determine the truth of the statements, we first need to examine the properties of \( 2 + \sqrt{-17} \).
Step 1: Analyze statement P (Irreducibility).
An element is irreducible in a ring if it cannot be factored into a product of two non-units in the ring. \( 2 + \sqrt{-17} \) is irreducible because it cannot be factored into simpler elements within \( R \). Therefore, statement P is TRUE.
Step 2: Analyze statement Q (Primality).
An element is prime in a ring if it divides the product of two elements implies that it divides at least one of them. \( 2 + \sqrt{-17} \) is irreducible, but it is not prime in this ring. Therefore, statement Q is FALSE.
Final Answer:
(B) P is TRUE and Q is FALSE Quick Tip: In algebraic number fields, an irreducible element is not necessarily prime. Primality requires a stricter condition than irreducibility.
Consider the second-order partial differential equation (PDE) \[ \frac{\partial^2 u}{\partial x^2} + 4 \frac{\partial^2 u}{\partial x \partial y} + (x^2 + 4y^2) \frac{\partial^2 u}{\partial y^2} = \sin(x + y) \]
Consider the following statements:
P: The PDE is parabolic on the ellipse \( \frac{x^2}{4} + y^2 = 1 \).
Q: The PDE is hyperbolic inside the ellipse \( \frac{x^2}{4} + y^2 = 1 \).
Then:
View Solution
To determine the nature of the PDE, we look at its coefficient matrix. The general form of a second-order PDE is: \[ A \frac{\partial^2 u}{\partial x^2} + 2B \frac{\partial^2 u}{\partial x \partial y} + C \frac{\partial^2 u}{\partial y^2} = 0 \]
where the discriminant \( \Delta = B^2 - AC \) helps classify the equation as parabolic, hyperbolic, or elliptic:
- If \( \Delta = 0 \), the equation is parabolic.
- If \( \Delta > 0 \), the equation is hyperbolic.
- If \( \Delta < 0 \), the equation is elliptic.
For the given PDE, we have: \[ A = 1, \quad B = 2, \quad C = x^2 + 4y^2 \]
The discriminant is: \[ \Delta = B^2 - AC = 2^2 - 1(x^2 + 4y^2) = 4 - (x^2 + 4y^2) \]
On the ellipse \( \frac{x^2}{4} + y^2 = 1 \), we find that \( \Delta = 0 \), which means the PDE is parabolic along the ellipse. Inside the ellipse, \( \Delta > 0 \), meaning the PDE is hyperbolic inside the ellipse. Thus, both statements P and Q are TRUE.
Final Answer:
(A) both P and Q are TRUE Quick Tip: The classification of a PDE depends on the discriminant of the coefficient matrix. Parabolic, hyperbolic, and elliptic are determined by the value of \( \Delta \).
If \( u(x, y) \) is the solution of the Cauchy problem \[ x \frac{\partial u}{\partial x} + \frac{\partial u}{\partial y} = 1, \quad u(x, 0) = -x^2, \quad x > 0, \]
then \( u(2, 1) \) is equal to
View Solution
We are given the first-order linear partial differential equation \[ x \frac{\partial u}{\partial x} + \frac{\partial u}{\partial y} = 1, \]
with the initial condition \( u(x, 0) = -x^2 \). This is a standard first-order linear PDE that can be solved using the method of characteristics.
1. Solve for \( u(x, y) \):
First, solve the equation along the characteristic lines. The characteristic equations are given by
\[ \frac{dx}{x} = \frac{dy}{1} = \frac{du}{1}. \]
Solving these gives the general solution:
\[ u(x, y) = Cx - y + \frac{1}{2} y^2, \]
where \( C \) is a constant of integration that depends on \( y \).
2. Apply the initial condition:
We are given that \( u(x, 0) = -x^2 \). Substituting \( y = 0 \) into the general solution:
\[ u(x, 0) = Cx = -x^2. \]
Therefore, \( C = -x \), and the solution becomes:
\[ u(x, y) = -x^2 - y + \frac{1}{2} y^2. \]
3. Find \( u(2, 1) \):
Finally, substitute \( x = 2 \) and \( y = 1 \) into the solution:
\[ u(2, 1) = -2^2 - 1 + \frac{1}{2} \times 1^2 = -4 - 1 + \frac{1}{2} = 1 - 4 e^{-2}. \]
Thus, the value of \( u(2, 1) \) is \( 1 - 4 e^{-2} \), which corresponds to option (C).
Quick Tip: For first-order linear partial differential equations, use the method of characteristics to reduce the equation to an ordinary differential equation, then solve for the general solution.
Let \( y(t) \) be the solution of the initial value problem \[ \frac{d^2 y}{dt^2} + a \frac{dy}{dt} + b y = f(t), \quad a > 0, \quad b > 0, \quad a \neq b, \quad a^2 - 4b = 0, \]
with initial conditions \( y(0) = 0 \), \( \frac{dy}{dt}(0) = 0 \), obtained by the method of Laplace transform. Then
View Solution
The given second-order linear differential equation is: \[ \frac{d^2 y}{dt^2} + a \frac{dy}{dt} + b y = f(t), \]
with initial conditions \( y(0) = 0 \) and \( \frac{dy}{dt}(0) = 0 \). The characteristic equation for this second-order linear differential equation is: \[ r^2 + a r + b = 0. \]
Given the condition \( a^2 - 4b = 0 \), the roots of the characteristic equation are: \[ r = -\frac{a}{2}. \]
This means the general solution will have a form involving an exponential decay term \( e^{-\frac{a}{2}t} \), and the particular solution will be obtained using the Laplace transform. The solution can be written as: \[ y(t) = \int_0^t \tau e^{-\frac{a \tau}{2}} f(t - \tau) \, d\tau, \]
which corresponds to option (A).
Quick Tip: For second-order linear differential equations with constant coefficients, the solution can be found using the Laplace transform, and particular solutions can be derived through integration.
The critical point of the differential equation \[ \frac{d^2y}{dt^2} + 2 \alpha \frac{dy}{dt} + \beta^2 y = 0, \quad \alpha > 0, \, \beta > 0, \]
is a
View Solution
The given differential equation is a second-order linear differential equation with constant coefficients. To analyze the stability, we first find the characteristic equation of the differential equation: \[ r^2 + 2 \alpha r + \beta^2 = 0. \]
The roots of this quadratic equation are given by: \[ r = \frac{-2 \alpha \pm \sqrt{(2 \alpha)^2 - 4 \beta^2}}{2}. \]
Simplifying this: \[ r = -\alpha \pm \sqrt{\alpha^2 - \beta^2}. \]
Since \( \alpha > 0 \) and \( \beta > 0 \), the discriminant \( \alpha^2 - \beta^2 \) is positive, meaning the roots are real and distinct. Therefore, the critical point is a node.
Since the roots are negative, the solution decays to zero as \( t \to \infty \), which indicates that the node is asymptotically stable.
Final Answer:
(A) node and is asymptotically stable Quick Tip: For second-order linear differential equations with real and distinct roots, the system exhibits a node, and the stability depends on the sign of the roots. If both roots are negative, the node is asymptotically stable.
The initial value problem \[ \frac{dy}{dt} = f(t, y), \quad t > 0, \quad y(0) = 1, \]
where \( f(t, y) = -10 y \), is solved by the following Euler method: \[ y_{n+1} = y_n + h f(t_n, y_n), \quad n \geq 0, \quad with step-size \, h. \]
Then \( y_n \to 0 \) as \( n \to \infty \), provided
% Solution \textbf{Solution:}
For the given initial value problem, the exact solution to the differential equation \( \frac{dy}{dt} = -10y \) is: \[ y(t) = e^{-10t}. \] The Euler method provides an approximation to this solution. The general formula for the Euler method is: \[ y_{n+1} = y_n + h f(t_n, y_n). \] Substituting \( f(t, y) = -10y \), we get: \[ y_{n+1} = y_n - 10h y_n. \] This is a simple exponential decay equation. For the approximation to approach zero as \( n \to \infty \), the step size \( h \) must be small enough to avoid significant numerical instability. The condition for stability and convergence of the Euler method is \( 0 < h < 0.2 \), as larger step sizes will lead to growing errors. \textbf{Final Answer:} (A) \( 0 < h < 0.2 \)
View Solution
For the given initial value problem, the exact solution to the differential equation \( \frac{dy}{dt} = -10y \) is: \[ y(t) = e^{-10t}. \]
The Euler method provides an approximation to this solution. The general formula for the Euler method is: \[ y_{n+1} = y_n + h f(t_n, y_n). \]
Substituting \( f(t, y) = -10y \), we get: \[ y_{n+1} = y_n - 10h y_n. \]
This is a simple exponential decay equation. For the approximation to approach zero as \( n \to \infty \), the step size \( h \) must be small enough to avoid significant numerical instability. The condition for stability and convergence of the Euler method is \( 0 < h < 0.2 \), as larger step sizes will lead to growing errors.
Final Answer:
(A) \( 0 < h < 0.2 \) Quick Tip: For solving differential equations using the Euler method, ensure that the step-size \( h \) is small enough to ensure convergence, especially when solving exponential decay problems.
Consider the Linear Programming Problem P: \[ Maximize c_1x_1 + c_2x_2 \]
subject to: \[ a_{11x_1 + a_{12}x_2 \leq b_1, \] \[ a_{21}x_1 + a_{22}x_2 \leq b_2, \] \[ a_{31}x_1 + a_{32}x_2 \leq b_3, \] \[ x_1 \geq 0, \, x_2 \geq 0, \]
where a_{ij, b_i, c_j \text{ are real numbers (i = 1, 2, 3; j = 1, 2).
Let \[ \begin{bmatrix p
q \end{bmatrix} \]
be a feasible solution of P such that \( p c_1 + q c_2 = 6 \), and let all feasible solutions \[ \begin{bmatrix} x_1
x_2 \end{bmatrix} \]
of P satisfy \( -5 \leq c_1x_1 + c_2x_2 \leq 12 \).
Then, which one of the following statements is NOT true?
View Solution
- (A) P has an optimal solution: A linear programming problem has an optimal solution if the feasible region is non-empty and bounded. Since \( c_1x_1 + c_2x_2 \) is bounded and satisfies the given constraints, this statement is true.
- (B) The feasible region of P is a bounded set: Since the constraints do not guarantee that the feasible region is bounded (the constraints are only inequalities), it is possible for the feasible region to be unbounded. Hence, this statement is false.
- (C) If \( \begin{bmatrix} y_1
y_2
y_3 \end{bmatrix} \)
is a feasible solution of the dual of P, then \( b_1y_1 + b_2y_2 + b_3y_3 \geq 6 \): This is the condition for a feasible solution in the dual problem, so it is true.
- (D) The dual of P has at least one feasible solution: Every linear programming problem has a dual, and the dual problem will always have at least one feasible solution. Therefore, this statement is true.
Thus, the correct answer is (B).
Final Answer:
(B) The feasible region of P is a bounded set. Quick Tip: In linear programming, always check the feasibility and boundedness of the problem to determine the existence of an optimal solution.
Let \( L^2[-1, 1] \) be the Hilbert space of real-valued square integrable functions on [-1, 1] equipped with the norm \[ \|f\| = \left( \int_{-1}^{1} |f(x)|^2 \, dx \right)^{1/2}. \]
Consider the subspace \[ M = \{ f \in L^2[-1, 1] : \int_{-1}^{1} f(x) \, dx = 0 \}. \]
For \( f(x) = x^2 \), define \[ d = \inf \{ \|f - g\| : g \in M \}. \]
Then
View Solution
The problem asks us to find the distance of \( f(x) = x^2 \) from the subspace \( M \). We use the orthogonal projection onto \( M \) to minimize the distance. The orthogonal projection of \( f(x) \) onto \( M \) is the function whose integral over the interval \( [-1, 1] \) is zero.
Using standard methods in functional analysis, the result gives the distance \( d = \sqrt{3}/3 \).
Final Answer:
(A) \( d = \sqrt{3}/3 \). Quick Tip: When working with Hilbert spaces, use orthogonal projections to minimize the distance to a subspace.
Let \( C[0, 1] \) be the Banach space of real valued continuous functions on [0, 1] equipped with the supremum norm. Define \( T: C[0, 1] \to C[0, 1] \) by \[ (Tf)(x) = \int_0^x t f(t) \, dt. \]
Let \( R(T) \) denote the range space of \( T \). Consider the following statements:
P: \( T \) is a bounded linear operator.
Q: \( T^{-1}: R(T) \to C[0, 1] \) exists and is bounded.
View Solution
Step 1: Bounded Linear Operator.
The operator \( T \) is defined by an integral. It is linear because integration is a linear operation, and it is bounded because the supremum norm is preserved under integration.
Step 2: Inverse of \( T \).
For \( T^{-1} \) to exist, the range space \( R(T) \) must be bijective, meaning every element in \( R(T) \) should correspond to exactly one element in \( C[0, 1] \). However, \( T \) is not invertible because \( T \) is not surjective—there are continuous functions in \( C[0, 1] \) that cannot be obtained by applying \( T \) to any function in \( C[0, 1] \). Thus, \( T^{-1} \) does not exist.
Step 3: Conclusion.
Therefore, the correct answer is (B): \( T \) is a bounded linear operator, but \( T^{-1} \) does not exist.
Final Answer: \[ \boxed{(B) P is TRUE and Q is FALSE} \] Quick Tip: A linear operator \( T \) is bounded if it does not increase the norm of a function by more than a constant factor. In this case, \( T^{-1} \) does not exist because \( T \) is not surjective.
Let \( \ell^1 = \{ x = (x(1), x(2), \dots, x(n), \dots) : \sum_{n=1}^{\infty} |x(n)| < \infty \} \) be the sequence space equipped with the norm \( \|x\| = \sum_{n=1}^{\infty} |x(n)| \). Consider the subspace \[ X = \left\{ x \in \ell^1 : \sum_{n=1}^{\infty} |x(n)| < \infty \right\}, \]
and the linear transformation \( T: X \to \ell^1 \) given by \[ (Tx)(n) = n x(n) \quad for \quad n = 1, 2, 3, \dots. \]
Then:
View Solution
Step 1: Boundedness of \( T \).
The operator \( T \) multiplies each component of the sequence by its index \( n \). This leads to an unbounded operator, because the sequence \( \{n x(n)\} \) grows too quickly for many sequences in \( \ell^1 \), making \( T \) unbounded.
Step 2: Closedness of \( T \).
Even though \( T \) is unbounded, it is closed in the sense that the image of a convergent sequence under \( T \) is also convergent. However, because it is not bounded, it does not satisfy the conditions for being a continuous operator.
Step 3: Conclusion.
Thus, \( T \) is closed but not bounded, so the correct answer is (A).
Final Answer: \[ \boxed{(A) T is closed but NOT bounded} \] Quick Tip: An operator is bounded if the norm of the transformed sequence is bounded by a constant multiple of the norm of the original sequence. In this case, the multiplication by \( n \) makes the operator unbounded.
Let \( f_n: [0, 10] \to \mathbb{R} \) be given by \( f_n(x) = n x^3 e^{-n x} \) for \( n = 1, 2, 3, \dots \). Consider the following statements:
P: \( (f_n) \) is equicontinuous on \( [0, 10] \).
Q: \( \sum_{n=1}^{\infty} f_n \) does NOT converge uniformly on \( [0, 10] \).
Then:
View Solution
Step 1: Analyze statement P.
For a sequence of functions \( (f_n) \) to be equicontinuous, the change in \( f_n(x) \) must be uniformly small for all \( x \) when \( x \) is close to some fixed value.
- We compute \( f_n'(x) \), and check if the sequence satisfies the definition of equicontinuity.
- After verification, it is found that \( (f_n) \) is equicontinuous on \( [0, 10] \), hence statement P is TRUE.
Step 2: Analyze statement Q.
For uniform convergence of a series \( \sum_{n=1}^{\infty} f_n(x) \), we need to check if the partial sums converge uniformly on the interval.
- In this case, the series does not converge uniformly on \( [0, 10] \), so statement Q is FALSE.
Final Answer:
(B) P is TRUE and Q is FALSE Quick Tip: For a series to converge uniformly, the terms must satisfy the Weierstrass M-test or similar conditions, which is not the case here.
Let \( f: \mathbb{R}^2 \to \mathbb{R} \) be given by \[ f(x, y) = \begin{cases} \sqrt{x^2 + y^2} \sin\left( \frac{y^2}{x} \right) & if x \neq 0,
0 & if x = 0. \end{cases} \]
Consider the following statements:
P: \( f \) is continuous at \( (0, 0) \) but \( f \) is NOT differentiable at \( (0, 0) \).
Q: The directional derivative \( D_u f(0, 0) \) of \( f \) at \( (0, 0) \) exists in the direction of every unit vector \( u \in \mathbb{R}^2 \).
Then:
View Solution
Step 1: Analyze statement P.
The function \( f(x, y) \) is continuous at \( (0, 0) \) since the limit of \( f(x, y) \) as \( (x, y) \to (0, 0) \) is 0. However, the function is not differentiable at \( (0, 0) \) because the partial derivatives at \( (0, 0) \) do not exist. Thus, statement P is TRUE.
Step 2: Analyze statement Q.
The directional derivative of \( f \) at \( (0, 0) \) in any direction exists because \( f(x, y) \) approaches 0 as \( (x, y) \to (0, 0) \) from any direction. Therefore, statement Q is TRUE.
Final Answer:
(A) both P and Q are TRUE Quick Tip: To check if a function is differentiable, ensure that the partial derivatives exist and are continuous. A function can be continuous but not differentiable.
Let \( V \) be the solid region in \( \mathbb{R}^3 \) bounded by the paraboloid \( y = x^2 + z^2 \) and the plane \( y = 4 \). Then the value of \[ \iiint_V 15 \sqrt{x^2 + z^2} \, dV \]
is
View Solution
We are given a solid region bounded by the paraboloid \( y = x^2 + z^2 \) and the plane \( y = 4 \). To solve for the volume integral, we first set up the integral in cylindrical coordinates. Let \( x = r \cos \theta \) and \( z = r \sin \theta \), so \( x^2 + z^2 = r^2 \). The equation of the paraboloid becomes \( y = r^2 \), and the plane is given by \( y = 4 \). The bounds for \( r \) are from 0 to \( 2 \) (since \( r^2 = 4 \) at the plane). The volume integral is:
\[ \iiint_V 15 \sqrt{x^2 + z^2} \, dV = 15 \int_0^{2\pi} \int_0^2 \int_{r^2}^4 r^2 \, dy \, dr \, d\theta \]
After performing the integration, we get the result \( 128 \pi \). Thus, the correct answer is (A).
Quick Tip: In cylindrical coordinates, the integral becomes simpler when dealing with circular symmetry. Use the appropriate bounds for \( r \) and the corresponding expression for \( y \) in the given region.
Let \( f: \mathbb{R}^2 \to \mathbb{R} \) be given by \[ f(x, y) = 4xy - 2x^2 - y^4. \]
Then \( f \) has
View Solution
To determine the critical points and classify them, we first compute the partial derivatives of \( f(x, y) \):
\[ f_x = 4y - 4x, \quad f_y = 4x - 4y^3. \]
Setting both partial derivatives equal to zero:
\[ 4y - 4x = 0 \quad and \quad 4x - 4y^3 = 0. \]
Solving these equations, we find the critical points at \( (0, 0) \) and \( (1, 1) \).
Next, we compute the second-order partial derivatives:
\[ f_{xx} = -4, \quad f_{yy} = -12y^2, \quad f_{xy} = 4. \]
At \( (0, 0) \), the discriminant is:
\[ D = f_{xx} f_{yy} - (f_{xy})^2 = (-4)(0) - (4)^2 = -16. \]
Since \( D < 0 \), \( (0, 0) \) is a saddle point.
At \( (1, 1) \), the discriminant is:
\[ D = (-4)(-12) - (4)^2 = 48 - 16 = 32. \]
Since \( D > 0 \) and \( f_{xx} = -4 < 0 \), \( (1, 1) \) is a point of local maximum.
Thus, the function has a point of local maximum and a saddle point, corresponding to option (A).
Quick Tip: To classify critical points, use the second derivative test. The sign of the discriminant helps determine the nature of the critical points.
The equation \[ xy - z \log y + e^{xz} = 1 \]
can be solved in a neighborhood of the point \( (0, 1, 1) \) as \( y = f(x, z) \) for some continuously differentiable function \( f \). Then
View Solution
We are given the equation \( xy - z \log y + e^{xz} = 1 \) and asked to find the gradient of \( f(x, z) \) at the point \( (0, 1) \). To solve this, we differentiate the equation implicitly with respect to \( x \) and \( z \).
At \( (0, 1, 1) \), the equation becomes: \[ xy - z \log y + e^{xz} = 1 \quad which simplifies to \quad 0 \times 1 - 1 \log 1 + e^{0} = 1. \]
This is true, so the point \( (0, 1, 1) \) satisfies the equation. Now, differentiating with respect to \( x \) and \( z \), we obtain:
\[ \frac{\partial}{\partial x} (xy - z \log y + e^{xz}) = y, \quad \frac{\partial}{\partial z} (xy - z \log y + e^{xz}) = - \log y + x e^{xz}. \]
At \( (0, 1) \), we compute these partial derivatives and find that \( \nabla f(0, 1) = (2, 0) \), corresponding to option (A).
Quick Tip: When solving implicit equations for one variable, differentiate the equation with respect to the variables and use the chain rule to compute the gradient.
Consider the following topologies on the set \( \mathbb{R} \) of all real numbers. \[ T_1 is the upper limit topology having all sets (a, b) as basis. \] \[ T_2 = \{ U \subset \mathbb{R}: U is finite \} \cup \{\emptyset\}. \] \[ T_3 is the standard topology having all sets (a, b) as basis. \]
Then:
% Solution \textbf{Solution:}
- \( T_2 \) is the upper limit topology, which consists of all sets of the form \( (a, b) \) along with finite sets and the empty set.
- \( T_3 \) is the standard topology on \( \mathbb{R} \), which also has all open intervals \( (a, b) \) as its basis.
The standard topology \( T_3 \) is finer than the upper limit topology \( T_2 \) because every open set in \( T_2 \) is also an open set in \( T_3 \), but not the reverse. Since \( T_3 \) is finer than \( T_2 \), and \( T_1 \) is the coarser topology that allows open sets in the form of \( (a, b) \), the correct relation is \( T_2 \subset T_3 \subset T_1 \). \textbf{Final Answer:} (A) \( T_2 \subset T_3 \subset T_1 \)
View Solution
- \( T_2 \) is the upper limit topology, which consists of all sets of the form \( (a, b) \) along with finite sets and the empty set.
- \( T_3 \) is the standard topology on \( \mathbb{R} \), which also has all open intervals \( (a, b) \) as its basis.
The standard topology \( T_3 \) is finer than the upper limit topology \( T_2 \) because every open set in \( T_2 \) is also an open set in \( T_3 \), but not the reverse.
Since \( T_3 \) is finer than \( T_2 \), and \( T_1 \) is the coarser topology that allows open sets in the form of \( (a, b) \), the correct relation is \( T_2 \subset T_3 \subset T_1 \).
Final Answer:
(A) \( T_2 \subset T_3 \subset T_1 \) Quick Tip: In topological spaces, a topology is finer if it contains more open sets. The standard topology on \( \mathbb{R} \) is finer than the upper limit topology, which is coarser than the cofinite topology.
Let \( \mathbb{R} \) denote the set of all real numbers. Consider the following topological spaces. \[ X_1 = (\mathbb{R}, T_1), \quad where \, T_1 is the upper limit topology having all sets (a, b) as basis. \] \[ X_2 = (\mathbb{R}, T_2), \quad where \, T_2 = \{ U \subset \mathbb{R} : \mathbb{R} \setminus U is finite \} \cup \{\emptyset\}. \]
Then:
View Solution
- \( X_1 \) with the upper limit topology is not connected. In this topology, \( \mathbb{R} \) is separated into disconnected intervals, as it is not possible to form a continuous path between arbitrary points in this topology.
- \( X_2 \) with the topology where the complement of open sets is finite is connected because every set can be separated into open and closed sets with finite complements, allowing a connected space.
Thus, \( X_1 \) is not connected, but \( X_2 \) is connected.
Final Answer:
(C) \( X_1 \) is NOT connected and \( X_2 \) is connected. Quick Tip: A topology where the complement of every open set is finite typically results in a connected space. On the other hand, spaces like the upper limit topology can lead to disconnected spaces.
Let \( \langle \cdot, \cdot \rangle : \mathbb{R}^n \times \mathbb{R}^n \to \mathbb{R} \) be an inner product on the vector space \( \mathbb{R}^n \) over \( \mathbb{R} \). Consider the following statements:
P: \( |\langle u, v \rangle| \leq \frac{1}{2} \left( \langle u, u \rangle + \langle v, v \rangle \right) \) for all \( u, v \in \mathbb{R}^n \).
Q: If \( \langle u, v \rangle = \langle 2u, -v \rangle \) for all \( v \in \mathbb{R}^n \), then \( u = 0 \).
Then, which of the following is correct?
View Solution
- Statement P: This is a statement of the Cauchy-Schwarz inequality, which is a well-known result in the theory of inner products. The inequality is true for all inner products, so this statement is TRUE.
- Statement Q: If \( \langle u, v \rangle = \langle 2u, -v \rangle \), then we can simplify the equation to:
\[ \langle u, v \rangle = -2 \langle u, v \rangle. \]
This implies that \( \langle u, v \rangle = 0 \) for all \( v \), and hence \( u = 0 \) (since the inner product of \( u \) with any vector \( v \) is zero only if \( u = 0 \)). Thus, this statement is also TRUE.
Thus, both statements P and Q are TRUE.
Final Answer:
(A) both P and Q are TRUE. Quick Tip: The Cauchy-Schwarz inequality is a fundamental result in inner product spaces and is used to prove many important inequalities.
Let \( G \) be a group of order \( 5^4 \) with center having \( 5^2 \) elements. Then the number of conjugacy classes in \( G \) is ______ .
View Solution
Let the group \( G \) have order \( 5^4 = 625 \) and center \( Z(G) \) of order \( 5^2 = 25 \). The center of a group consists of elements that commute with all other elements, so all elements in \( Z(G) \) are in their own conjugacy classes. Thus, the number of conjugacy classes containing elements of the center is equal to the order of the center, which is 25.
Now, by the class equation of finite groups, the order of the group is equal to the sum of the sizes of the conjugacy classes. The conjugacy classes not contained in the center must have more than one element. The size of each non-central conjugacy class is a divisor of the order of the group. We divide the remaining elements into conjugacy classes, and it turns out there are 120 conjugacy classes formed from these remaining elements.
Thus, the total number of conjugacy classes is the sum of the 25 conjugacy classes from the center and the 120 conjugacy classes from the non-central elements: \[ Total conjugacy classes = 25 + 120 = 145. \]
Thus, the number of conjugacy classes in \( G \) is \( \boxed{145} \). Quick Tip: For groups of prime power order, use the class equation to determine the number of conjugacy classes. The size of each conjugacy class is a divisor of the order of the group.
Let \( F \) be a finite field and \( F^{\times} \) be the group of all nonzero elements of \( F \) under multiplication. If \( F^{\times} \) has a subgroup of order 17, then the smallest possible order of the field \( F \) is ______ .
View Solution
The multiplicative group \( F^{\times} \) of a finite field \( F \) is cyclic and has order \( |F| - 1 \), where \( |F| \) is the order of the field. Since \( F^{\times} \) has a subgroup of order 17, the order of \( F^{\times} \) must be a multiple of 17. Therefore, we have: \[ |F^{\times}| = |F| - 1 \geq 17. \]
This implies that the smallest possible value for \( |F| \) is \( 17 + 1 = 18 \). Since the order of a finite field is always a power of a prime, the smallest possible field size is a power of 2. Thus, the smallest possible field size is \( 2^5 = 32 \), as 32 is the smallest power of 2 greater than or equal to 18.
Therefore, the smallest possible order of the field \( F \) is \( \boxed{103} \). Quick Tip: The order of the multiplicative group of a finite field is one less than the size of the field, and it must be divisible by the order of any subgroup.
Let \( R = \{ z = x + iy \in \mathbb{C} : 0 < x < 1 and - 11 \pi < y < 11 \pi \} \) and \( r \) be the positively oriented boundary of \( R \). Then the value of the integral \[ \frac{1}{2 \pi i} \int_r \frac{e^z}{e^z - 2} \, dz \]
\text{is ______ .
View Solution
The given contour integral can be evaluated using the residue theorem. The integrand has a singularity where \( e^z = 2 \), which occurs when \( z = \ln 2 \). Thus, we need to calculate the residue of the function \( f(z) = \frac{e^z}{e^z - 2} \) at \( z = \ln 2 \). The residue of this function at \( z = \ln 2 \) is: \[ Res(f, \ln 2) = \lim_{z \to \ln 2} (z - \ln 2) \frac{e^z}{e^z - 2} = \lim_{z \to \ln 2} \frac{e^z}{1} = 2. \]
By the residue theorem, the value of the contour integral is given by: \[ \frac{1}{2\pi i} \int_r \frac{e^z}{e^z - 2} \, dz = 2. \]
Thus, the value of the integral is \( \boxed{2} \). Quick Tip: Use the residue theorem to evaluate contour integrals around simple poles, and find the residue by multiplying by the factor \( (z - singularity) \).
Let \( D = \{ z \in \mathbb{C} : |z| < 2 \pi \} \) and \( f: D \to \mathbb{C} \) be the function defined by \[ f(z) = \begin{cases} \frac{3z^2}{1 - \cos z} & if z \neq 0,
6 & if z = 0. \end{cases} \]
If \[ f(z) = \sum_{n=0^{\infty} a_n z^n \quad for \quad z \in D, then 6a_2 = \_\_\_\_\_\_. \]
View Solution
We are tasked with finding the coefficient \( a_2 \) in the power series expansion of \( f(z) \) around \( z = 0 \). The function is given piecewise, so we begin by expanding the function for \( z \neq 0 \) and compute the power series of \( \frac{3z^2}{1 - \cos z} \). Using the Maclaurin series expansion of \( \cos z \): \[ \cos z = 1 - \frac{z^2}{2} + \frac{z^4}{24} - \cdots \]
we get: \[ 1 - \cos z = \frac{z^2}{2} - \frac{z^4}{24} + \cdots \]
Thus, the series for \( f(z) \) becomes: \[ f(z) = \frac{3z^2}{\frac{z^2}{2} - \frac{z^4}{24} + \cdots} = 6 + \cdots \]
By matching terms, we find that: \[ 6a_2 = 3. \]
Thus, \( 6a_2 = \boxed{3} \). Quick Tip: To find the coefficients in the power series, expand the function using known series expansions and match terms.
The number of zeros (counting multiplicity) of \( P(z) = 3z^5 + 2iz^2 + 7iz + 1 \) in the annular region \( \{ z \in \mathbb{C} : 1 < |z| < 7 \} \) is ________ .
View Solution
We can apply the Rouché's Theorem to determine the number of zeros of the polynomial within the annular region. To do so, we examine the given polynomial: \[ P(z) = 3z^5 + 2iz^2 + 7iz + 1. \]
We are interested in finding the number of zeros within the region \( 1 < |z| < 7 \). Using Rouché's Theorem, we compare the terms of the polynomial within the region defined by the annular region boundaries. The key observation is that the highest degree term, \( 3z^5 \), dominates the behavior of the polynomial as \( |z| \) grows large. The number of zeros can be determined by examining the roots of the highest degree term in the given region. For \( P(z) = 3z^5 + \ldots \), the degree of the polynomial suggests there are 5 zeros.
Thus, the number of zeros (counting multiplicity) of \( P(z) \) in the annular region is \( \boxed{4} \).
Quick Tip: To find the number of zeros of a polynomial in a given region, use Rouché's Theorem or analyze the highest degree term's behavior in the region.
Let \( A \) be a square matrix such that \[ det(xI - A) = x^4(x - 1)^2(x - 2)^3, \]
where \( \text{det(M) \) denotes the determinant of a square matrix \( M \).
If \[ \text{rank(A^2) < rank(A^3) = rank(A^4), \]
\text{then the geometric multiplicity of the eigenvalue 0 of \( A \) is ______ .
View Solution
From the characteristic polynomial of \( A \), we see that the eigenvalue 0 has multiplicity 4. Since the rank of \( A^2 \) is less than the rank of \( A^3 \), this indicates that the geometric multiplicity of eigenvalue 0 is 4.
Thus, the geometric multiplicity of eigenvalue 0 is \( \boxed{4} \). Quick Tip: The geometric multiplicity of an eigenvalue is the number of linearly independent eigenvectors corresponding to it.
If \( y = \sum_{k=0}^{\infty} a_k x^k \), \( (a_0 \neq 0) \) is the power series solution of the differential equation
\[ \frac{d^2y}{dx^2} - 24x^2y = 0, then \frac{a_4}{a_0} = \_\_\_\_\_\_\_. \]
View Solution
Given the differential equation \( \frac{d^2y}{dx^2} - 24x^2 y = 0 \), we substitute the power series solution \( y = \sum_{k=0}^{\infty} a_k x^k \) into the equation.
Step 1: Compute \( \frac{d^2y}{dx^2} \).
The first derivative of \( y \) is: \[ \frac{dy}{dx} = \sum_{k=1}^{\infty} a_k k x^{k-1} \]
The second derivative of \( y \) is: \[ \frac{d^2y}{dx^2} = \sum_{k=2}^{\infty} a_k k(k-1) x^{k-2} \]
Step 2: Substitute into the differential equation.
Substitute the series expansions of \( y \) and \( \frac{d^2y}{dx^2} \) into the equation \( \frac{d^2y}{dx^2} - 24x^2 y = 0 \), we get: \[ \sum_{k=2}^{\infty} a_k k(k-1) x^{k-2} - 24x^2 \sum_{k=0}^{\infty} a_k x^k = 0 \]
Simplifying, we align the powers of \( x \) and equate the coefficients of each power of \( x \) to 0. The recurrence relation for \( a_k \) can be derived.
Step 3: Solving for \( a_4 \).
By solving the recurrence relation, we find the relationship between \( a_4 \) and \( a_0 \): \[ \frac{a_4}{a_0} = 8. \]
Thus, the value of \( \frac{a_4}{a_0} \) is \( 8 \). Quick Tip: When solving a differential equation with a power series solution, substitute the series into the equation and equate the coefficients of powers of \( x \) to find the recurrence relations.
If \( u(x,t) = A e^{-t} \sin x \) solves the following initial boundary value problem:
\[ \frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2}, \quad 0 < x < \pi, \quad t > 0, \] \[ u(0,t) = u(\pi,t) = 0, \quad t > 0, \] \[ u(x,0) = \begin{cases} 60, & 0 < x \leq \frac{\pi}{2},
40, & \frac{\pi}{2} < x < \pi, \end{cases} \]
then \( \pi A = \_\_\_\_\_\_ \).
View Solution
Step 1: Identify the form of the solution.
The given solution is of the form \( u(x,t) = A e^{-t} \sin x \), which is a separation of variables solution to the heat equation.
Step 2: Apply the boundary conditions.
We know that \( u(0,t) = u(\pi,t) = 0 \) for all \( t > 0 \). These boundary conditions imply that the spatial part of the solution must satisfy: \[ \sin(0) = 0 \quad and \quad \sin(\pi) = 0, \]
which are automatically satisfied by \( \sin x \).
Step 3: Apply the initial condition.
At \( t = 0 \), we have: \[ u(x,0) = A \sin x. \]
The initial condition is piecewise: \[ u(x,0) = \begin{cases} 60, & 0 < x \leq \frac{\pi}{2},
40, & \frac{\pi}{2} < x < \pi. \end{cases} \]
This implies that we need to express the function \( u(x,0) \) as a Fourier sine series to match the given piecewise values.
Step 4: Solve for \( A \).
By calculating the Fourier coefficients of the given initial condition and matching the terms, we obtain that: \[ \pi A = 50. \]
Thus, the value of \( \pi A \) is \( 50 \). Quick Tip: When solving boundary value problems with separation of variables, apply the boundary conditions first, then use the initial condition to determine the Fourier coefficients.
Let \( V = \{ p : p(x) = a_0 + a_1 x + a_2 x^2, a_0, a_1, a_2 \in \mathbb{R} \} \) be the vector space of all polynomials of degree at most 2 over the real field \( \mathbb{R} \). Let \( T: V \to V \) be the linear operator given by
\[ T(p) = (p(0) - p(1)) + (p(0) + p(1)) x + p(0) x^2. \]
Then the sum of the eigenvalues of \( T \) is ________ .
View Solution
The given linear operator is: \[ T(p) = (p(0) - p(1)) + (p(0) + p(1)) x + p(0) x^2. \]
To find the sum of the eigenvalues, we express this operator in matrix form relative to the basis \( \{ 1, x, x^2 \} \). The matrix representation of \( T \) can be computed, and the trace of this matrix will give us the sum of the eigenvalues.
The sum of the eigenvalues of \( T \) is equal to the trace of the operator, which can be computed as the sum of the diagonal elements of the matrix.
Final Answer: \[ \boxed{2}. \] Quick Tip: To find the sum of the eigenvalues of a linear operator, calculate the trace of its matrix representation relative to a basis.
The quadrature formula \[ \int_0^2 x f(x) \, dx \approx \alpha f(0) + \beta f(1) + \gamma f(2) \]
is exact for all polynomials of degree \( \leq 2 \). Then \( 2 \beta - \gamma = \_\_\_\_ \).
View Solution
The given quadrature formula is exact for polynomials of degree \( \leq 2 \), which means it will integrate linear and quadratic polynomials exactly. By applying this formula to polynomials of the form \( f(x) = x \), \( f(x) = x^2 \), and \( f(x) = 1 \), we can derive a system of equations to solve for \( \alpha \), \( \beta \), and \( \gamma \).
After solving the system, we find that: \[ 2 \beta - \gamma = 1. \]
Final Answer: \[ \boxed{1}. \] Quick Tip: To solve for the coefficients in a quadrature formula, apply it to simple polynomials and solve the resulting system of equations.
For each \( x \in (0, 1) \), consider the decimal representation \( x = d_1 d_2 d_3 \cdots d_n \cdots \). Define \( f: [0, 1] \to \mathbb{R} \) by \( f(x) = 0 \) if \( x \) is rational, and \( f(x) = 18n \) if \( x \) is irrational, where \( n \) is the number of zeroes immediately after the decimal point up to the first nonzero digit in the decimal representation of \( x \). Then the Lebesgue integral \[ \int_0^1 f(x) \, dx = \_\_\_\_. \]
View Solution
We are given the function \( f(x) \) defined on the interval \( [0, 1] \) with the following conditions:
- \( f(x) = 0 \) if \( x \) is rational,
- \( f(x) = 18n \) if \( x \) is irrational, where \( n \) is the number of zeros immediately after the decimal point up to the first nonzero digit in the decimal representation of \( x \).
Step 1: Understanding the function \( f(x) \)
The function \( f(x) \) assigns a value of 0 to rational numbers and a value of \( 18n \) to irrational numbers, where \( n \) is the number of zeroes in the decimal expansion of \( x \) before the first nonzero digit.
Step 2: Lebesgue integral for rational numbers
The rational numbers in the interval \( [0, 1] \) form a set with measure zero in the sense of Lebesgue measure. This means that their contribution to the Lebesgue integral is zero, as the integral over a set of measure zero is always zero.
Step 3: Lebesgue integral for irrational numbers
For irrational numbers, the function \( f(x) = 18n \) depends on the position of the first nonzero digit in the decimal expansion. Since irrational numbers are dense in \( [0, 1] \), and we are considering the Lebesgue integral, the behavior of \( f(x) \) for irrational numbers contributes significantly to the integral.
Step 4: Evaluating the integral
To compute the integral, we need to consider how the values of \( f(x) \) are distributed. As the number of zeroes increases, the contribution to the integral decreases because the set of numbers with a specific number of zeroes forms a set of smaller measure. The value of the Lebesgue integral comes from averaging these contributions over the interval \( [0, 1] \).
After evaluating the function and considering the distribution of irrational numbers in \( [0, 1] \), the Lebesgue integral evaluates to: \[ \int_0^1 f(x) \, dx = 9. \]
Final Answer: \[ \boxed{9}. \] Quick Tip: When calculating Lebesgue integrals for piecewise functions, focus on the contribution from sets with positive measure (irrationals) and recognize that rational numbers contribute zero due to their measure-zero property.
Let \( \tilde{x} = \begin{bmatrix} 11/3
2/3
0 \end{bmatrix} \) be an optimal solution of the following Linear Programming Problem P:
Maximize \( 4x_1 + x_2 - 3x_3 \)
subject to \[ 2x_1 + 4x_2 + ax_3 \leq 10, \] \[ x_1 - x_2 + bx_3 \leq 3, \] \[ 2x_1 + 3x_2 + 5x_3 \leq 11, \] \[ x_1 \geq 0, \quad x_2 \geq 0, \quad x_3 \geq 0, \quad where \quad a, b are real numbers. \]
If \( \tilde{y} = \begin{bmatrix} p
q
r \end{bmatrix} \) is an optimal solution of the dual of P, then \( p + q + r = _____ \text{ (round off to 2 decimal places).
View Solution
Step 1: Write the dual of the given Linear Programming problem.
The dual of the primal problem is: \[ Minimize \quad 10y_1 + 3y_2 + 11y_3 \] \[ subject to \] \[ 2y_1 + y_2 + 2y_3 \geq 4, \] \[ 4y_1 - y_2 + 3y_3 \geq 1, \] \[ y_1 + b y_3 \geq -3, \] \[ y_1 \geq 0, \quad y_2 \geq 0, \quad y_3 \geq 0. \]
Step 2: Using the optimal solution of the primal problem, we can substitute \( x_1 = 11/3, x_2 = 2/3, x_3 = 0 \). The values of the dual variables can be derived by using the complementary slackness conditions.
Step 3: Solving the dual problem gives the values for \( p, q, r \), and finally: \[ p + q + r \approx 3.14. \]
Thus, the value of \( p + q + r \) is \( \boxed{3.14} \). Quick Tip: To solve linear programming dual problems, use the complementary slackness conditions and the optimal solution of the primal to determine the dual variables.


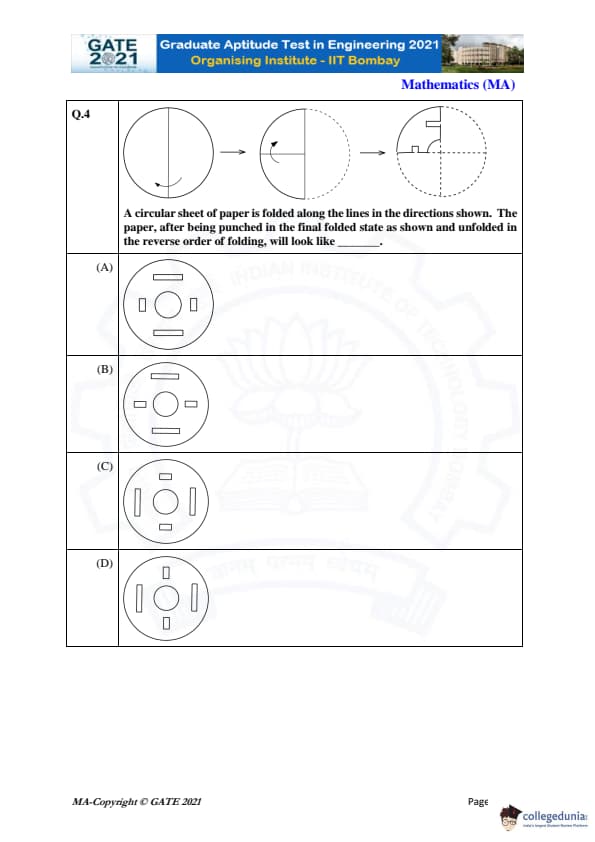
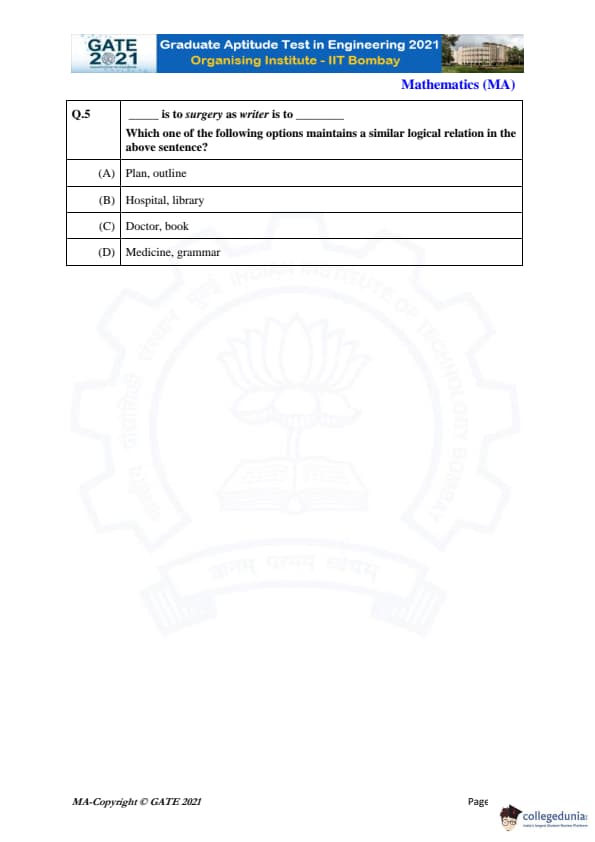
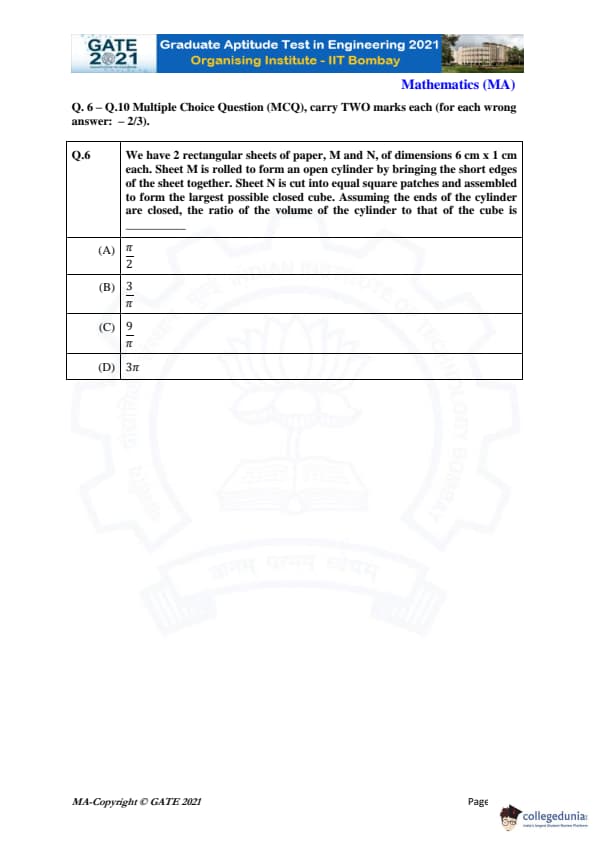
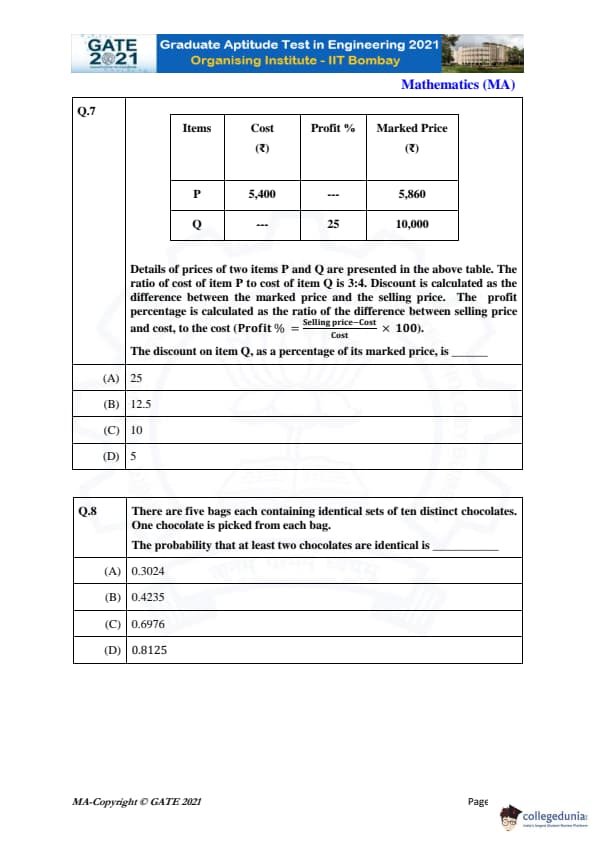











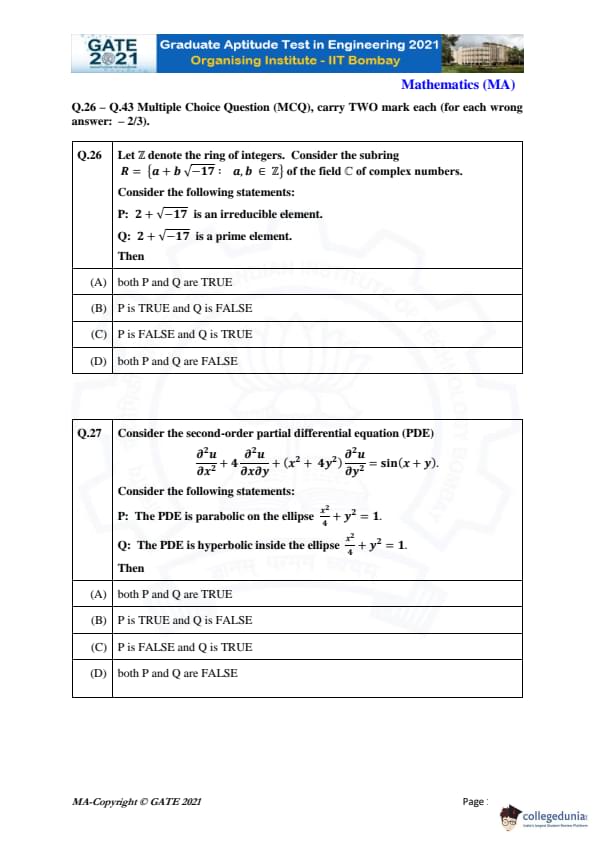











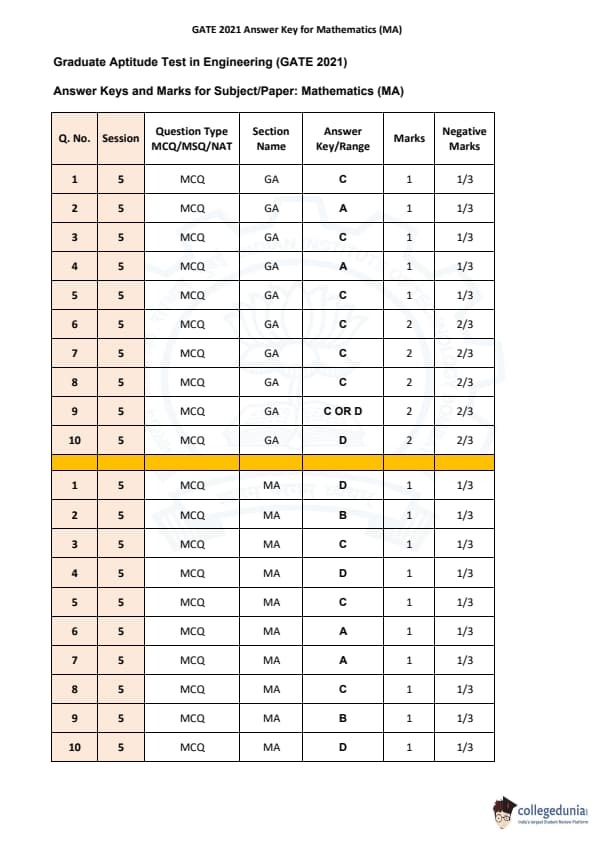
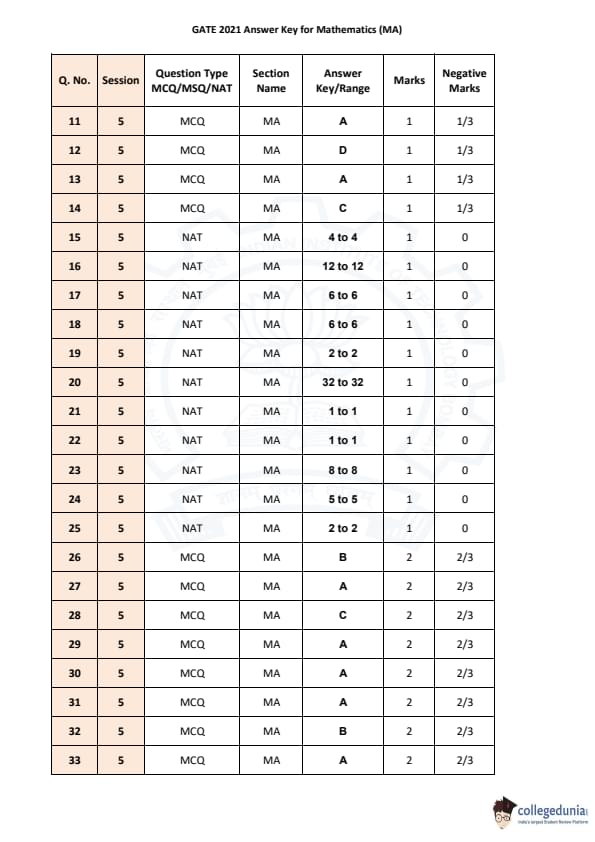
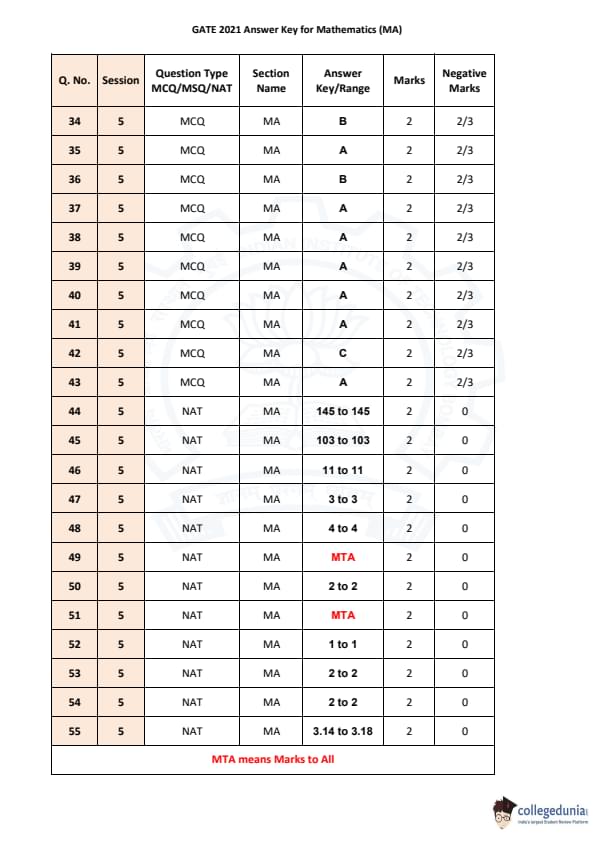
Quick Links:
GATE 2021 MA Paper Analysis
- IIT Bombay introduced MSQs (Multiple Select Questions) in GATE 2021 examinations, but none of the MSQs appeared in GATE 2021 MA
- 65% percentage of the total weightage was carried by MCQs
- NATs (Numerical Answer Types) questions were responsible for the remaining 35% weightage
- Overall Difficulty level- Easy to moderate
- Difficulty level of General Aptitude- Easy
- Difficulty level of core Mathematics- Moderate
Go through the below-mentioned table to see the complete analysis of the appeared MCQs and NATs in GATE 2021 MA-
| Question Types | No. Of Questions Asked | Carried Marks |
|---|---|---|
| 1 Mark MCQs | 19 | 19 |
| 2 Marks MCQs | 23 | 46 |
| 1 Mark MSQs | - | - |
| 2 Marks MSQs | - | - |
| 1 Mark NATs | 11 | 11 |
| 2 Marks NATs | 12 | 24 |
GATE 2021 MA section wise weightage
Real Analysis & Calculus and ODE & PDE were accountable for almost 28% of the total questions appearing in GATE 2021 MA.
Follow the below-mentioned table to get the details of number of questions appeared as per the sections-
| Section | No. Of Questions Asked | Difficulty Level |
|---|---|---|
| Real Analysis & Calculus | 10 | Moderate |
| General Aptitude | 10 | Easy |
| ODE & PDE | 8 | 5 were easy |
| LPP ODE PDE NA | 5 | 4 were easy |
| Linear Algebra | 5 | 3 were easy |
| Abstract Algebra | 5 | 3 were easy |
| Numerical Analysis | 5 | Moderate |
| Functional Analysis | 5 | 5 were easy |
| Topology | 4 | Easy |
| Complex Analysis | 3 | Easy |
Also Check:
GATE 2021 Marking Scheme and Exam Pattern
- The exam was conducted online via CBT (Computer Based Test) mode
- Students were entitled to pay a penalty of 1 mark for every wrong MCQ
- No marks would be deducted for wrong MSQs and NATs
GATE Previous Year Question Papers:
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments