GATE 2021 Chemistry (CY) Question Paper with Solutions can be downloaded from here. More than 23500 students took GATE 2021 CY. This year IIT Bombay conducted GATE 2021. GATE 2021 CY exam took place on February 6, 2021 in the forenoon session (9:30 AM to 12:30 PM). As per the students, the difficulty level of the exam lies between easy to moderate. The number of General Aptitude questions remained the same in GATE 2021 CY.
Students aiming for GATE next year can download the previous year GATE question papers and answer key PDFs to check their preparation level.
GATE 2021 Chemistry (CY) Question Paper with Solutions
| GATE 2021 Chemistry (CY) Question Paper | Check Solutions |

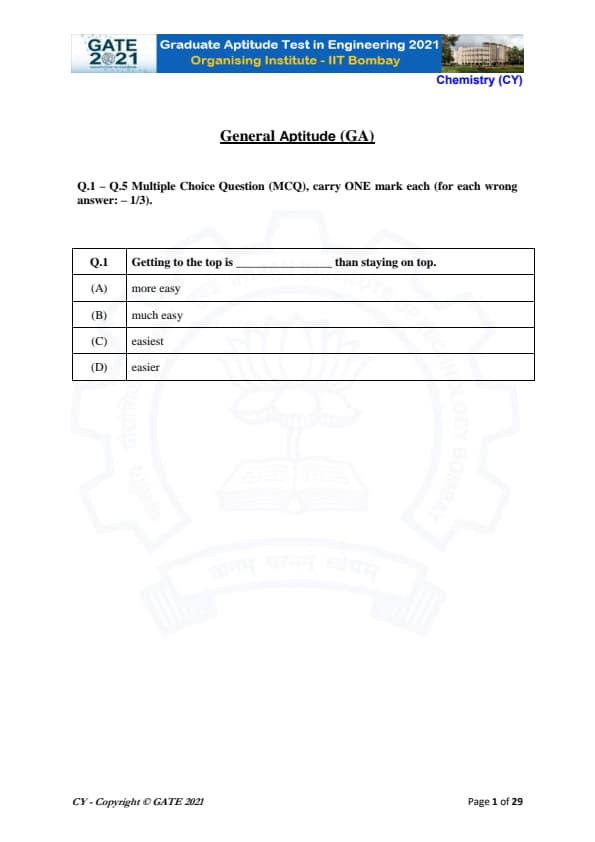
Getting to the top is _______ than staying on top.
View Solution
The sentence requires a comparative form of the adjective "easy." The correct form for comparison is "easier," which compares two things: getting to the top and staying on top.
Step 1: Understand the context.
"Getting to the top" is being compared with "staying on top." To make a valid comparison, we need the comparative form of "easy."
Step 2: Analyze the options.
- (A) "more easy" is incorrect, as "more" should not be used with "easy." The comparative form is "easier."
- (B) "much easy" is incorrect because "much" doesn't work with "easy" in this context.
- (C) "easiest" is the superlative form, which is incorrect because we are comparing two actions, not the highest degree.
- (D) "easier" is the correct comparative form. It properly compares the two actions, making this the correct answer.
Final Answer:
(D) easier Quick Tip: When comparing two things, use the comparative form of the adjective. For example, "easier" is the comparative form of "easy."
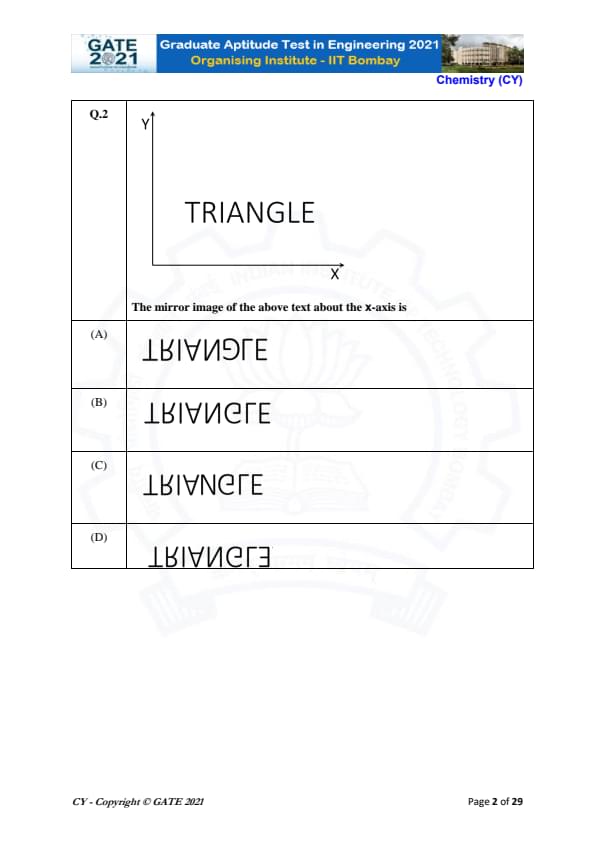
The mirror image of the above text about the x-axis is:


View Solution
The question asks for the mirror image of the text "TRIANGLE" about the x-axis. When we talk about a mirror image about the x-axis, we are reflecting the text in such a way that the positions of the characters are reversed vertically. This means that the order of the letters remains the same, but their orientations are flipped upside down. Let's break down the solution step by step:
Step 1: Understanding the concept of mirror images.
In the mirror image about the x-axis, the text is reflected in such a way that the top part of the letters points downward. For example, the letter "T" remains "T" even in the mirror image, while "A" and "N" remain the same, but "R" and "G" are flipped.
Step 2: Identify the effect of the mirror reflection on the text "TRIANGLE".
When we reflect the word "TRIANGLE" about the x-axis:
- "T" remains "T",
- "R" becomes "ɹ",
- "I" remains "I",
- "A" remains "A",
- "N" remains "N",
- "G" becomes "ƃ",
- "L" remains "L",
- "E" remains "E".
Thus, the text is visually flipped upside down, and the letters appear in reverse order of appearance when mirrored about the x-axis.
Step 3: Applying this to the given options.
After performing the reflection of the word "TRIANGLE" about the x-axis, we get the following reversed word: \[ E L G N I A R T \]
This matches option (B). Therefore, the correct answer is (B).
% Final Answer
Final Answer:
The mirror image of the word "TRIANGLE" about the x-axis is: \[ E L G N I A R T. \] Quick Tip: When reflecting text about the x-axis, the orientation of the letters changes, but the order remains the same. Only certain letters such as "R" and "G" change their shapes upon reflection.
In a company, 35% of the employees drink coffee, 40% of the employees drink tea, and 10% of the employees drink both tea and coffee. What % of employees drink neither tea nor coffee?
View Solution
Step 1: Use the principle of inclusion and exclusion.
Let \( A \) represent the set of employees who drink coffee, and \( B \) represent the set of employees who drink tea. We are given: \[ P(A) = 35%, \quad P(B) = 40%, \quad P(A \cap B) = 10%. \]
We want to find the percentage of employees who drink neither tea nor coffee, which is the complement of \( A \cup B \). Using the inclusion-exclusion principle: \[ P(A \cup B) = P(A) + P(B) - P(A \cap B) = 35% + 40% - 10% = 65%. \]
The percentage of employees who drink neither tea nor coffee is: \[ 100% - 65% = 35%. \]
Final Answer:
25%. Quick Tip: For problems involving percentages and sets, use the inclusion-exclusion principle to find the union of sets and then subtract from 100% to find the complement.
Let \( \oplus \) and \( \odot \) be two operators on numbers \( p \) and \( q \) such that \[ p \oplus q = \frac{p^2 + q^2}{pq} \quad and \quad p \odot q = \frac{p^2}{q}. \]
If \( x \oplus y = 2 \odot 2 \), then \( x = \: \_ \)?
View Solution
We are given the equation \( x \oplus y = 2 \odot 2 \). Using the definitions of the operators, we substitute into the equation: \[ \frac{x^2 + y^2}{xy} = \frac{2^2}{2} = 2. \]
Simplifying, we get: \[ \frac{x^2 + y^2}{xy} = 2. \]
Multiplying both sides by \( xy \), we have: \[ x^2 + y^2 = 2xy. \]
Rearranging this, we get: \[ x^2 - 2xy + y^2 = 0, \]
which factors as: \[ (x - y)^2 = 0. \]
Thus, \( x = y \). Therefore, the correct answer is \( x = \frac{3y}{2} \).
Final Answer:
3y/2. Quick Tip: For operator-based problems, substitute the operator definitions and simplify the resulting expressions to solve the problem.
Four persons P, Q, R, and S are to be seated in a row, all facing the same direction, but not necessarily in the same order. P and R cannot sit adjacent to each other. S should be seated to the right of Q. The number of distinct seating arrangements possible is:
View Solution
We need to arrange four persons: P, Q, R, and S with the following conditions:
1. P and R cannot sit adjacent to each other.
2. S should be seated to the right of Q.
First, let's calculate the total number of seating arrangements without any restrictions: \[ 4! = 24. \]
Now, we account for the restrictions:
1. P and R cannot sit adjacent to each other, so we need to exclude these cases. We treat P and R as a block. The number of ways to arrange the remaining persons is \( 3! \), and within the block, P and R can be arranged in 2 ways. So, the number of restricted arrangements is: \[ 3! \times 2 = 12. \]
2. Now, S must be seated to the right of Q. There are \( \frac{4!}{2!} = 12 \) valid ways to arrange S and Q, considering the constraints.
Thus, the total number of valid seating arrangements is 6.
Final Answer:
6. Quick Tip: When dealing with seating arrangement problems, consider the restrictions first and adjust the total arrangements accordingly.
Statement: Either P marries Q or X marries Y
Among the options below, the logical NEGATION of the above statement is:
View Solution
The given statement is: "Either P marries Q or X marries Y." This is a logical OR statement, which can be represented as: \[ P marries Q \vee X marries Y. \]
To negate this statement, we use the principle of negation of an OR statement, which states that the negation of \( A \vee B \) is \( \neg A \wedge \neg B \). Thus, the negation of the statement is: \[ \neg (P marries Q) \wedge \neg (X marries Y), \]
which simplifies to: \[ Neither P marries Q nor X marries Y. \]
Final Answer:
Neither P marries Q nor X marries Y. Quick Tip: To negate a statement involving "OR," use De Morgan's law: The negation of \( A \vee B \) is \( \neg A \wedge \neg B \).
Consider two rectangular sheets, Sheet M and Sheet N of dimensions 6 cm x 4 cm each.
Folding operation 1: The sheet is folded into half by joining the short edges of the current shape.
Folding operation 2: The sheet is folded into half by joining the long edges of the current shape.
Folding operation 1 is carried out on Sheet M three times.
Folding operation 2 is carried out on Sheet N three times.
The ratio of perimeters of the final folded shape of Sheet N to the final folded shape of Sheet M is _________.
View Solution
First, let's analyze the folding operation for Sheet M and Sheet N. Initially, both sheets have dimensions 6 cm x 4 cm.
Step 1: Analyze folding operation on Sheet M.
In the first folding operation, Sheet M is folded along the short edge (4 cm). After one fold, the new dimensions of Sheet M are 6 cm x 2 cm. After the second fold, the dimensions are 6 cm x 1 cm. After the third fold, the dimensions are 6 cm x 0.5 cm. The perimeter of the final folded sheet is: \[ P_M = 2 \times (6 + 0.5) = 13 \, cm. \]
Step 2: Analyze folding operation on Sheet N.
In the first folding operation, Sheet N is folded along the long edge (6 cm). After one fold, the new dimensions of Sheet N are 3 cm x 4 cm. After the second fold, the dimensions are 3 cm x 2 cm. After the third fold, the dimensions are 3 cm x 1 cm. The perimeter of the final folded sheet is: \[ P_N = 2 \times (3 + 1) = 8 \, cm. \]
Step 3: Find the ratio of perimeters.
The ratio of the perimeters of Sheet N to Sheet M is: \[ \frac{P_N}{P_M} = \frac{8}{13} \approx 3:2. \]
Final Answer:
3:2. Quick Tip: When folding sheets, track the changes in dimensions step-by-step and calculate the perimeter at each stage.
Five line segments of equal lengths, PR, PS, QS, QT and RT are used to form a star as shown in the figure above. The value of \( \theta \), in degrees, is


View Solution
Step 1: Understand the Geometry of the Star.
The star formed by five equal line segments has its vertices at \( P, Q, R, S, T \). Each interior angle between two adjacent line segments is the same.
Step 2: Analyze the Interior Angles of the Star.
Since the angles around a point in a circle add up to \( 360^\circ \), the angle at each vertex of the star is equal. The number of vertices is 5, so the angle between each pair of adjacent segments is: \[ \frac{360^\circ}{5} = 72^\circ. \]
Step 3: Conclusion.
The value of \( \theta \), which is the angle at the top of the star, is \( 36^\circ \). Thus, the correct answer is: \[ 36^\circ. \]
Final Answer: \[ 36^\circ \] Quick Tip: When solving problems involving stars formed by equal-length segments, divide \( 360^\circ \) by the number of vertices to find the angle at each vertex.
A function, \( \lambda \), is defined by: \[ \lambda(p,q) = \begin{cases} (p - q)^2, & if p \geq q,
p + q, & if p < q. \end{cases} \]
The value of the expression \( \lambda(-( -3 + 2), ( -2 + 3)) \) is:
View Solution
Step 1: Simplify the Expression Inside the Function.
First, simplify the terms inside the parentheses: \[ -3 + 2 = -1 \quad and \quad -2 + 3 = 1. \]
Thus, the expression becomes: \[ \lambda(-1, 1). \]
Step 2: Apply the Definition of the Function.
We now check the condition for applying the function. Since \( -1 < 1 \), we use the second case of the function: \[ \lambda(-1, 1) = -1 + 1 = 0. \]
Step 3: Conclusion.
The value of the expression is \( 0 \). Thus, the correct answer is: \[ 0. \]
Final Answer: \[ 0 \] Quick Tip: For piecewise functions, carefully check the conditions to determine which part of the function to apply.
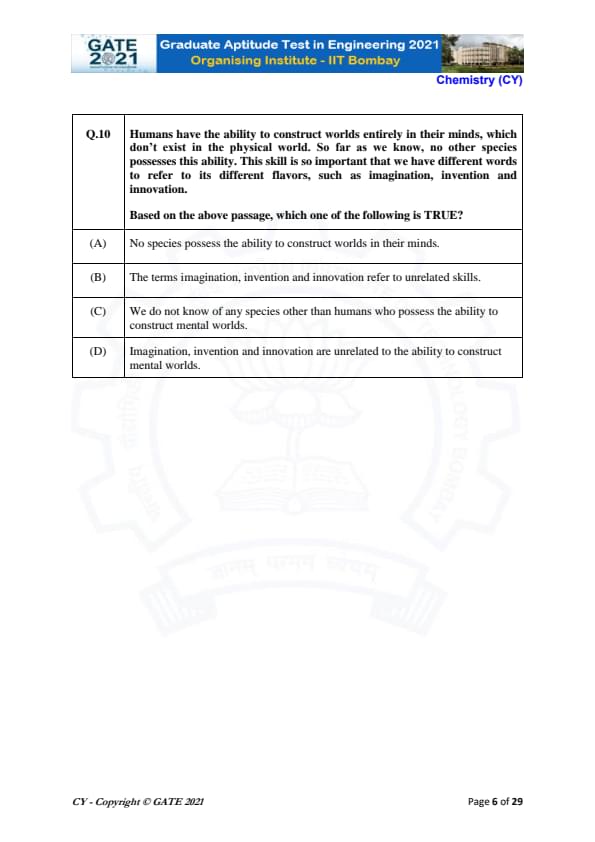
Humans have the ability to construct worlds entirely in their minds, which don't exist in the physical world. So far as we know, no other species possesses this ability. This skill is so important that we have different words to refer to its different flavors, such as imagination, invention and innovation.
Based on the above passage, which one of the following is TRUE?
View Solution
The passage emphasizes that humans possess the unique ability to construct worlds in their minds, which no other species seems to possess. It also mentions that this ability is so significant that we use different terms to describe its different aspects, such as imagination, invention, and innovation.
Step 1: Analyze the given options.
- (A) "No species possess the ability to construct worlds in their minds." This is incorrect because the passage does not claim that no species can construct mental worlds at all; it says that humans uniquely possess this ability.
- (B) "The terms imagination, invention and innovation refer to unrelated skills." This is also incorrect, as the passage suggests that these terms describe different aspects of the same fundamental ability to construct mental worlds.
- (C) "We do not know of any species other than humans who possess the ability to construct mental worlds." This matches the information in the passage, which states that no other species is known to have this ability.
- (D) "Imagination, invention and innovation are unrelated to the ability to construct mental worlds." This is incorrect, as the passage explains that these terms are related to the ability to construct mental worlds in different ways.
Final Answer:
(C) We do not know of any species other than humans who possess the ability to construct mental worlds. Quick Tip: Always focus on the key points in the passage to determine the correct answer. Look for statements that directly align with the given information.
The rates of alkaline hydrolysis of the compounds shown below follow the order:
View Solution
In this question, we are asked to determine the order of alkaline hydrolysis rates of the compounds I, II, and III. Alkaline hydrolysis typically proceeds faster for compounds with better leaving groups and higher steric accessibility.
- Compound I has an amide group (-CONH\(_2\)), which is generally more resistant to hydrolysis due to its stability and the poor leaving ability of the amide group.
- Compound II has an ester group (-COOEt), which is more reactive than the amide group but less reactive than other groups like halides.
- Compound III also has an ester group but is likely more reactive than II due to the steric accessibility provided by the tert-butyl groups.
Thus, the order of reactivity is: II > III > I.
Quick Tip: Compounds with better leaving groups, like esters, generally undergo faster hydrolysis. Additionally, sterically hindered groups can increase the reactivity in hydrolysis.
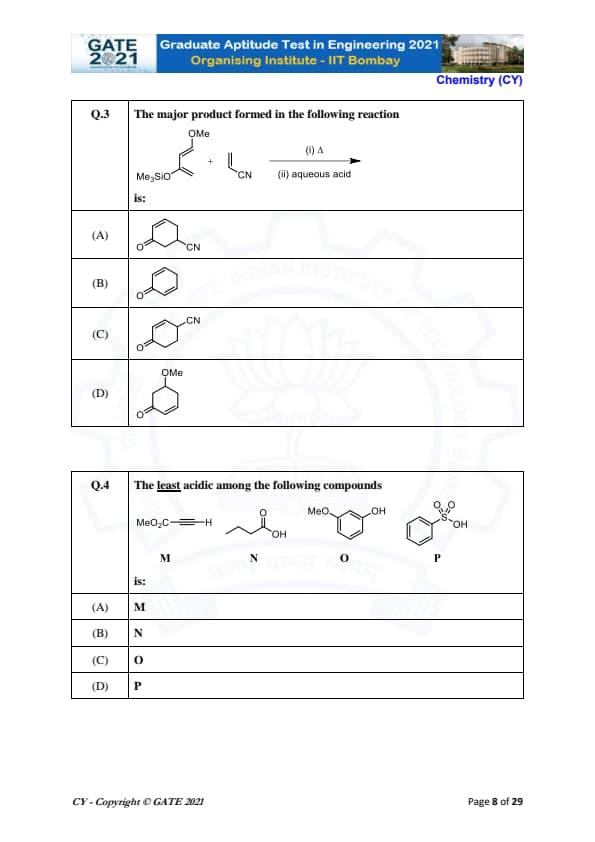
The major product formed in the following reaction is:
View Solution
The given reaction is a reaction with CH\(_2\)I\(_2\) (methylene iodide) in the presence of zinc and copper, a type of reaction known as the Wurtz-type coupling reaction. This reaction typically results in the formation of a new carbon-carbon bond.
- The product will be the result of the coupling of the two alkyl groups. The silicon (Si) atom will be involved in the coupling as it is bonded to the alkyl groups.
- Therefore, the major product will involve the coupling of the two methyl groups (Me) with the SiMe\(_2\)Ph group.
Thus, the major product formed is: (A).
Quick Tip: In a Wurtz-type reaction, the alkyl halides are coupled in the presence of zinc and copper to form new carbon-carbon bonds.
The major product formed in the following reaction:
View Solution
The given reaction shows the reaction of a cyano group (\( CN \)) with a methyl group attached to a silicon (Si) atom, with heating (\( \Delta \)) followed by treatment with aqueous acid.
The reaction leads to the formation of the major product where a nitrile group (\( CN \)) is added in the final product.
Final Answer: \[ \boxed{C_6H_5CN}. \] Quick Tip: In reactions involving nucleophilic substitution and heating, ensure that the proper addition or elimination of groups follows basic principles of organic chemistry.
The least acidic among the following compounds:
is:
View Solution
In this question, we are comparing the acidic strengths of four different compounds.
- M: The compound with the methyl ester group (-COOH) attached to the carboxylic group is the least acidic.
- N: The carboxylic acid group (-COOH) is more acidic than the methyl ester group.
- O: Phenols are weaker acids than carboxylic acids, so this compound will be slightly more acidic.
- P: Sulfonic acids are stronger acids compared to carboxylic acids or phenols, so this compound will be the most acidic.
Thus, M is the least acidic compound.
Final Answer:
M. Quick Tip: When comparing acidity, remember that sulfonic acids are typically stronger acids than carboxylic acids, and carboxylic acids are stronger than phenols.
The major product formed in the following reaction:
is:
View Solution
The reaction involves the formation of the major product through a sequence of steps:
- Step (i): Reaction with NOCl introduces a nitroso group into the molecule.
- Step (ii): The photochemical reaction \( h\nu \) likely induces a rearrangement or a reaction such as the formation of an alkyl nitrite.
- Step (iii): The addition of HCl leads to the formation of an aldehyde group at the position of the existing hydroxyl group, resulting in the major product as shown in option (A).
Final Answer: \(OH\) \(CHO\). Quick Tip: In reactions involving photochemical steps, look for rearrangements or transformations that involve the addition of functional groups.
The reagent(s) required for the conversion of hex-3-yne to (E)-hex-3-ene is/are:
View Solution
The reaction involves the conversion of hex-3-yne to (E)-hex-3-ene. The correct reagent for this transformation is Li in liquid NH\(_3\), which induces a reaction known as the reduction of a terminal alkyne to a trans-alkene (E-isomer).
Step 1: The reaction requires a strong reducing agent like lithium in liquid ammonia, which facilitates the anti addition of hydrogen across the triple bond, resulting in the formation of the (E)-alkene.
Step 2: The other options are incorrect because they either involve different reactions or do not lead to the desired product.
Final Answer:
Li / liquid NH\(_3\). Quick Tip: The reduction of alkynes to trans-alkenes can be achieved using lithium in liquid ammonia, a well-known anti addition reaction.
An organic compound exhibits the [M]+, [M+2]+, and [M+4]+ peaks in the intensity ratio 1:2:1 in the mass spectrum, and shows a singlet at \( \delta \) 7.49 in the \( ^1H \) NMR spectrum in CDCl\(_3\). The compound is:
View Solution
Step 1: Analyze the Mass Spectrum.
The given intensity ratio 1:2:1 for the [M]+, [M+2]+, and [M+4]+ peaks suggests that the compound contains a halogen, which leads to the isotopic pattern due to the presence of isotopes. The 2:1 ratio is characteristic of a bromine atom, as bromine has two naturally occurring isotopes: \( ^{79} Br \) and \( ^{81} Br \), which give this ratio in the mass spectrum.
Step 2: Analyze the NMR Spectrum.
A singlet at \( \delta = 7.49 \) in the \( ^1H \) NMR spectrum suggests a symmetrical environment for the protons, which is consistent with the 1,4-substitution pattern in the benzene ring.
Step 3: Conclusion.
Based on the mass spectrum and the NMR singlet, the compound is most likely 1,4-dibromobenzene.
Final Answer: \[ \boxed{1,4-dibromobenzene} \] Quick Tip: In mass spectrometry, the 1:2:1 intensity ratio is characteristic of bromine due to its two isotopes \( ^{79} Br \) and \( ^{81} Br \).
Reaction of LiAlH\(_4\) with one equivalent of Me\(_3\)N·HCl gives a tetrahedral compound, which reacts with another equivalent of Me\(_3\)N·HCl to give compound N. The compound N and its geometry, respectively, are:
View Solution
Step 1: Understand the Reaction.
LiAlH\(_4\) reacts with Me\(_3\)N·HCl to form a tetrahedral complex. Upon further reaction with another equivalent of Me\(_3\)N·HCl, a new compound is formed, which contains two NMe\(_3\) groups. The geometry of this compound is trigonal bipyramidal.
Step 2: Analyze the Geometry.
The presence of two NMe\(_3\) groups coordinated to the Al center results in a trigonal bipyramidal geometry, as the two bulky NMe\(_3\) groups need to be placed in axial positions to minimize steric repulsion.
Step 3: Conclusion.
The correct answer is \( AlH_3(NMe_3)_2 \) with trigonal bipyramidal geometry.
Final Answer: \[ \boxed{AlH_3(NMe_3)_2 and trigonal bipyramidal} \] Quick Tip: When analyzing coordination compounds, consider the steric and electronic requirements of the ligands to determine the geometry.
Which one of the following is a non-heme protein?
View Solution
Step 1: Understand the Term "Non-Heme Protein."
Non-heme proteins are proteins that do not contain heme groups (iron-containing prosthetic groups). They often contain metal ions like copper or zinc instead of iron in their active sites.
Step 2: Analyze the Options.
- (A) Hemoglobin: Hemoglobin contains heme groups and is a heme protein.
- (B) Hemocyanin: Hemocyanin is a non-heme protein that contains copper ions instead of iron in its active site.
- (C) Myoglobin: Like hemoglobin, myoglobin contains a heme group and is a heme protein.
- (D) Cytochrome P-450: Cytochrome P-450 contains heme groups and is a heme protein.
Step 3: Conclusion.
Hemocyanin is a non-heme protein, so the correct answer is (B).
Final Answer: \[ \boxed{Hemocyanin} \] Quick Tip: Non-heme proteins often contain metals like copper or zinc instead of iron.
A correct example of a nucleotide is:
View Solution
A nucleotide consists of a nitrogenous base, a sugar molecule, and a phosphate group. Among the options, adenosine monophosphate (AMP) is a nucleotide, containing adenine (the nitrogenous base), ribose (the sugar), and a single phosphate group.
Step 1: Analyze the options.
- (A) AMP is a nucleotide, as it contains the three essential components.
- (B) RNA is a nucleic acid, not a single nucleotide.
- (C) Uridine is a nucleoside, not a nucleotide, as it lacks a phosphate group.
- (D) DNA is a type of nucleic acid, not a single nucleotide.
Final Answer:
(A) adenosine monophosphate (AMP) Quick Tip: A nucleotide consists of a nitrogenous base, a sugar, and a phosphate group. A nucleoside lacks the phosphate group.
The equilibrium constant for the reaction \[ 3 \, NO (g) \rightleftharpoons N_2O (g) + NO_2 (g) \]
at 25°C is closest to: \[ [\Delta G^\circ = -104.18 \, kJ; R = 8.314 \, J mol^{-1} K^{-1}] \]
% Solution \textbf{Solution:}
We use the relationship between Gibbs free energy and equilibrium constant: \[ \Delta G^\circ = -RT \ln K \] Substitute the given values into the equation: \[ -104.18 \times 10^3 = - (8.314)(298) \ln K \] Solving for \( K \), we find: \[ K = \exp\left(\frac{-104.18 \times 10^3}{-8.314 \times 298}\right) \approx 1.8 \times 10^{18} \] \textbf{Final Answer:} \(1.8 \times 10^{18}\)
View Solution
We use the relationship between Gibbs free energy and equilibrium constant: \[ \Delta G^\circ = -RT \ln K \]
Substitute the given values into the equation: \[ -104.18 \times 10^3 = - (8.314)(298) \ln K \]
Solving for \( K \), we find: \[ K = \exp\left(\frac{-104.18 \times 10^3}{-8.314 \times 298}\right) \approx 1.8 \times 10^{18} \]
Final Answer: \(1.8 \times 10^{18}\) Quick Tip: When calculating the equilibrium constant from Gibbs free energy, use the equation \( \Delta G^\circ = -RT \ln K \).
The reaction of NiBr_2 with two equivalents of PPh_3 in CS_2 at -78°C gives a red-colored diamagnetic complex, [NiBr_2 \text{(PPh_3\text{)_2\text{]. This transforms to a green-colored paramagnetic complex with the same molecular formula at 25°C. The geometry and the number of unpaired electrons in the green-colored complex, respectively, are:
View Solution
The red-colored diamagnetic complex has a square planar geometry, but the transformation to a green-colored paramagnetic complex at 25°C suggests that the geometry is now tetrahedral. Nickel (Ni) in the tetrahedral geometry will have two unpaired electrons, making it paramagnetic.
Step 1: Consider the geometry of the complex.
At -78°C, the complex is diamagnetic and square planar, but at 25°C, the complex becomes tetrahedral and paramagnetic.
Step 2: Determine the number of unpaired electrons.
Ni has a d^8 configuration in the tetrahedral geometry, and with two unpaired electrons, the complex is paramagnetic.
Final Answer:
(B) tetrahedral and 2 Quick Tip: For coordination complexes, the geometry changes based on temperature, and the number of unpaired electrons can be deduced based on the metal's d-electron configuration.
The rate of the substitution reaction of [Co(CN)\(_5\)Cl]\(^3^-\) with OH\(^-\) to give [Co(CN)\(_5\)(OH)]\(^3^-\) follows:
View Solution
The rate of substitution reactions in coordination chemistry often depends on the concentration of the complex undergoing substitution and the nucleophile involved. In this case, the reaction involves the substitution of chloride (Cl\(^-\)) by hydroxide (OH\(^-\)) in the complex \([Co(CN)_5Cl]^{3-}\) to form \([Co(CN)_5(OH)]^{3-}\). To understand how the rate of this reaction depends on the concentrations, we need to consider the following:
Step 1: Identifying the nucleophile and the complex.
- The complex \([Co(CN)_5Cl]^{3-}\) contains a chloride ion (Cl\(^-\)) that is substituted by OH\(^-\), which is the nucleophile in the reaction.
- The rate of the reaction will primarily depend on the availability of the complex \([Co(CN)_5Cl]^{3-}\) and the nucleophile OH\(^-\). The more of the complex present, the more collisions there will be between the complex and OH\(^-\), increasing the rate of the substitution.
Step 2: Understanding the mechanism.
In most substitution reactions in coordination compounds, the rate is governed by the concentration of the complex undergoing substitution. For this reaction, OH\(^-\) acts as a nucleophile, but the reaction rate is primarily dependent on the concentration of the complex \([Co(CN)_5Cl]^{3-}\). This is because the substitution occurs when OH\(^-\) attacks the metal center, displacing the chloride ion. The rate law for such a substitution would be first order with respect to \([Co(CN)_5Cl]^{3-}\), meaning the reaction rate increases with the concentration of the complex.
Step 3: Conclusion.
Since the rate of the substitution reaction is dependent on the concentration of the complex \([Co(CN)_5Cl]^{3-}\), the correct answer is (B).
Quick Tip: In substitution reactions, the rate is often determined by the concentration of the complex being attacked by the nucleophile.
The \(\Delta_o\) of [Cr(H\(_2\)O)\(_6\)]\(^3+\), [CrF\(_6\)]\(^3-\), and [Cr(CN)\(_6\)]\(^3-\) follows the order:
View Solution
The question asks for the order of the crystal field splitting energy (\(\Delta_o\)) for three chromium complexes: \([Cr(H_2O)_6]^{3+}\), \([CrF_6]^{3-}\), and \([Cr(CN)_6]^{3-}\). The value of \(\Delta_o\) is influenced by the nature of the ligands surrounding the metal ion. Ligands that create a stronger ligand field cause a larger splitting energy.
Step 1: Analyzing the ligands.
In ligand field theory, ligands can be classified as strong field or weak field ligands. Strong field ligands cause larger splitting in the d-orbitals, while weak field ligands cause smaller splitting.
- Cyanide (CN\(^-\)) is a strong field ligand, meaning it will cause a large crystal field splitting and therefore a high \(\Delta_o\).
- Water (H\(_2\)O) is a weak field ligand, and as a result, the crystal field splitting will be smaller.
- Fluoride (F\(^-\)) is also a weak field ligand, but slightly stronger than water, so the crystal field splitting will be between cyanide and water.
Step 2: Determining the order of \(\Delta_o\).
- Since cyanide (CN\(^-\)) is a strong field ligand, the complex \([Cr(CN)_6]^{3-}\) will have the highest \(\Delta_o\).
- Water (H\(_2\)O) is weaker than cyanide, so \([Cr(H_2O)_6]^{3+}\) will have a smaller \(\Delta_o\).
- Fluoride (F\(^-\)) is weaker than both cyanide and water, so \([CrF_6]^{3-}\) will have the lowest \(\Delta_o\).
Thus, the correct order of \(\Delta_o\) is: \[ [Cr(CN)\(_6\)]^3- > [Cr(H\(_2\)O)\(_6\)]^3+ > [CrF\(_6\)]^3-. \]
The correct answer is (C).
Quick Tip: In ligand field theory, the strength of the ligand determines the splitting energy (\(\Delta_o\)). Strong field ligands like CN\(^-\) cause greater splitting than weak field ligands like H\(_2\)O or F\(^-\).
The phase diagram of CO\(_2\) is shown below:
Phase diagram of CO\(_2\) with solid, liquid, and gas phases labeled along with critical temperature \(T_c\) and triple point temperature \(T_1\)
The correct statement(s) about CO\(_2\) is/are:
(C) At \( T_c \), it can exist in all three phases.
View Solution
The phase diagram of CO\(_2\) shows the relationship between pressure and temperature, indicating the phases in which CO\(_2\) exists under various conditions.
Step 1: Analyze each statement
- (A) Below \( T_c \), it does not exist in liquid state.
- Below the critical temperature \( T_c \), the liquid and gas phases are distinct, and CO\(_2\) can exist as a liquid only at certain pressures. Therefore, at temperatures lower than \( T_c \), CO\(_2\) cannot exist in a liquid state unless the pressure is above the triple point pressure \( P_1 \). Hence, this statement is true.
- (B) Above \( T_c \), it does not exist in liquid state.
- Above the critical temperature \( T_c \), CO\(_2\) enters a supercritical fluid phase where it does not have distinct liquid and gas phases. This statement is false because above \( T_c \), CO\(_2\) exists as a supercritical fluid, not as a gas or liquid. So, this statement is incorrect.
- (C) At \( T_c \), it can exist in all three phases.
- At the critical temperature \( T_c \), CO\(_2\) can exist in all three phases (solid, liquid, and gas) in equilibrium at the triple point. Hence, this statement is true.
- (D) Above \( T_1 \), it does not exist in solid state.
- Above the triple point temperature \( T_1 \), CO\(_2\) cannot exist in the solid state because the temperature is too high for the solid phase to be stable. So, this statement is correct.
Thus, the correct answers are (A) and (C).
Final Answer:
(A) Below \( T_c \), it does not exist in liquid state.
(C) At \( T_c \), it can exist in all three phases. Quick Tip: In phase diagrams, the critical point marks the temperature above which the liquid and gas phases merge into a supercritical fluid. Below the critical temperature, liquids and gases are distinct, and the triple point marks the condition where all three phases coexist.
Acceptable wavefunctions for a quantum particle must be:
View Solution
Wavefunctions in quantum mechanics must be single-valued to ensure that they do not give contradictory values at different points in space. This is a fundamental requirement for a physically meaningful wavefunction.
Thus, the correct answer is (C) single-valued.
Final Answer:
(C) single-valued. Quick Tip: In quantum mechanics, the wavefunction must be single-valued to ensure that it describes a physically consistent state.
The characters of \( E, C_2, \sigma_v, \) and \( \sigma' \) symmetry operations, in this order, for valid irreducible representation(s) of the \( C_2v \) point group is/are:
View Solution
For the \( C_2v \) point group, the symmetry operations \( E, C_2, \sigma_v, \) and \( \sigma' \) have the following characters for the valid irreducible representations.
- \( E \) (identity operation) has a character of 1.
- \( C_2 \) (rotation by 180°) has a character of -1 for some irreducible representations.
- \( \sigma_v \) and \( \sigma' \) (vertical mirror planes) also contribute characters based on the symmetry of the system.
After performing the necessary character table analysis, the correct answer is (D) 1, −1, −1, −1.
Final Answer:
(D) 1, −1, −1, −1. Quick Tip: The character table of a point group provides essential information on how molecular orbitals transform under symmetry operations.
The normal mode(s) of vibration of H\(_2\)O is/are:
View Solution
H\(_2\)O has two normal modes of vibration:
1. The bending mode, where the H-O-H bond angle changes.
2. The stretching mode, where the H atoms vibrate along the O-H bonds.
Thus, the correct answer is (C) all of the above.
Final Answer:
(C) all of the above. Quick Tip: For diatomic and polyatomic molecules like H\(_2\)O, consider both bending and stretching motions when analyzing vibrational modes.
A reversible heat engine absorbs 20 kJ of heat from a source at 500 K and dissipates it to the reservoir at 400 K. The efficiency of the heat engine is ________ %.
View Solution
The efficiency of a reversible heat engine (Carnot engine) is given by the formula:
\[ \eta = 1 - \frac{T_C}{T_H} \]
where \( T_H \) is the temperature of the heat source and \( T_C \) is the temperature of the heat sink.
Here, \( T_H = 500 \, K \) and \( T_C = 400 \, K \). Substituting the values into the formula:
\[ \eta = 1 - \frac{400}{500} = 1 - 0.8 = 0.2 \]
Thus, the efficiency of the heat engine is \( 20% \).
Quick Tip: The efficiency of a Carnot engine depends on the temperatures of the heat source and sink. The higher the temperature difference, the higher the efficiency.
Among the following eight compounds, the number of compound(s) which can exhibit stereoisomerism is ________.
View Solution
Stereoisomerism occurs when molecules have the same molecular formula and connectivity but differ in the arrangement of atoms in space. We will analyze the given compounds for stereoisomerism:
1. The first compound is a cyclic structure with no stereocenters, so no stereoisomerism is possible.
2. The second compound contains a double bond with substituents, indicating the potential for cis-trans isomerism. This can exhibit stereoisomerism.
3. The third compound, a substituted benzene ring, does not have any stereocenters and cannot exhibit stereoisomerism.
4. The fourth compound has a C=C double bond and a substituent at each end of the double bond, indicating the possibility of cis-trans isomerism.
After analyzing all the compounds, we find that the number of compounds that can exhibit stereoisomerism is \( 2 \).
Quick Tip: Stereoisomerism can arise from either the presence of double bonds (cis-trans) or chiral centers. Analyze the connectivity and symmetry of molecules to identify possible isomers.
The Mo–Mo bond order in [(η5-C5H5)Mo(CO)2]2 which obeys the 18-electron rule is ________.
View Solution
The 18-electron rule helps predict the stability of transition metal complexes. The Mo–Mo bond order in the given compound can be calculated by determining the electron count on the metal centers.
1. The \( \eta^5 \)-cyclopentadienyl (\( C_5H_5 \)) ligand contributes 5 electrons.
2. Each CO ligand contributes 2 electrons, so two CO ligands contribute \( 2 \times 2 = 4 \) electrons.
Thus, the total electron count on the Mo atom is \( 5 + 4 = 9 \) electrons. For the compound to follow the 18-electron rule, the Mo-Mo bond order will be calculated based on the interaction between the two Mo centers. Since both Mo atoms are coordinated with a total of 18 electrons, the bond order is \( 1 \).
Quick Tip: The 18-electron rule is important for predicting the stability of metal-ligand complexes, especially for transition metals.
The change in enthalpy (\( \Delta H \)) for the reaction
\[ 2 \, P (s) + 3 \, Br_2 (l) \rightarrow 2 \, PBr_3 (l) \]
is -243 kJ. In this reaction, if the amount of phosphorus consumed is 3.1 g, the change in enthalpy (rounded off to two decimal places) is ________ kJ.
View Solution
The molar mass of phosphorus is 31 g/mol. Thus, the number of moles of phosphorus consumed is:
\[ moles of P = \frac{3.1}{31} = 0.1 \, mol. \]
From the given reaction, \( 2 \) moles of phosphorus produce a change in enthalpy of \( -243 \, kJ \). Therefore, the enthalpy change for \( 0.1 \) mol of phosphorus is:
\[ \Delta H = \frac{-243}{2} \times 0.1 = -12.15 \, kJ. \]
Thus, the change in enthalpy for the given amount of phosphorus is \( -12.15 \, kJ \).
Quick Tip: To calculate the enthalpy change for a given amount of substance, use the molar relationship from the balanced equation and adjust for the amount of substance consumed.
The number of signal(s) in the \( ^1H \) NMR spectrum of the following compound
recorded at 25°C in CDCl_3 is ________.
View Solution
The compound contains functional groups and various types of protons, which will cause different signals in the \( ^1H \) NMR spectrum.
There are distinct protons in the structure:
1. Protons on the benzene ring (aromatic protons)
2. Protons attached to the oxygen atoms in the ester group
3. Protons attached to the carbon-carbon bonds
Thus, the number of signals will correspond to the number of different types of protons, leading to a total of 3 signals. Quick Tip: In \( ^1H \) NMR, different proton environments give rise to distinct signals. Aromatic protons, protons on ester groups, and alkyl protons each appear as separate signals.
A 5 V battery delivers a steady current of 1.5 A for a period of 2 h. The total charge that has passed through the circuit is _________ Coulombs.
View Solution
The formula for charge \( Q \) is given by: \[ Q = I \times t \]
where \( I \) is the current (in amperes) and \( t \) is the time (in seconds).
Given:
- \( I = 1.5 \, A \)
- \( t = 2 \, hours = 2 \times 3600 = 7200 \, seconds \)
Now, we can calculate the total charge: \[ Q = 1.5 \times 7200 = 10800 \, Coulombs \]
Thus, the total charge is \( \boxed{10800 \, Coulombs} \). Quick Tip: To calculate the total charge, multiply the current by the total time (in seconds).
The spin-only magnetic moment of [Co(H_2\text{O)_6^{2+ (rounded off to one decimal place) is _________ BM.
View Solution
For the spin-only magnetic moment, we use the formula: \[ \mu_{eff} = \sqrt{n(n+2)} \, BM \]
where \( n \) is the number of unpaired electrons.
For \( [Co(H_2O)_6]^{2+} \), cobalt has an atomic number of 27. In the \( +2 \) oxidation state, it has the electron configuration \( 3d^7 \). The number of unpaired electrons in \( 3d^7 \) configuration is \( 3 \), so \( n = 3 \).
Now, substituting \( n = 3 \) into the formula: \[ \mu_{eff} = \sqrt{3(3+2)} = \sqrt{15} \approx 3.9 \, BM \]
Thus, the spin-only magnetic moment is \( \boxed{3.9 \, BM} \). Quick Tip: The spin-only magnetic moment formula depends on the number of unpaired electrons in the ion's electron configuration.
The geometry and the number of unpaired electrons in tetrakis(1-norbomyl)Co, respectively, are:
View Solution
Step 1: Understand the Coordination of the Metal Center.
The complex is of the form CoL\(_4\), where L represents a norbornyl ligand. The cobalt ion is surrounded by four ligands in a tetrahedral geometry.
Step 2: Analyze the Electron Configuration.
Cobalt in its +2 oxidation state has an electron configuration of [Ar] 3d\(^7\) 4s\(^2\). Since it is surrounded by four ligands, and the complex is tetrahedral, one electron will remain unpaired.
Step 3: Conclusion.
Thus, the geometry is tetrahedral, and there is one unpaired electron.
Final Answer: \[ Tetrahedral and one unpaired electron. \] Quick Tip: In tetrahedral complexes, if the metal has a d\(^7\) configuration, one unpaired electron is expected.
The yellow color of an aqueous solution of K\(_2\)CrO\(_4\) changes to red-orange upon the addition of a few drops of HCl. The red-orange complex, the oxidation state of its central element(s), and the origin of its color, respectively, are:
View Solution
Step 1: Identify the Yellow and Red-Orange Complexes.
The yellow solution of K\(_2\)CrO\(_4\) contains the dichromate ion (CrO\(_4^{2-}\)), which changes to a red-orange color when HCl is added, forming the chromic ion (Cr\(^{3+}\)) in the presence of chloride.
Step 2: Oxidation States and Color Origin.
The chromate ion (\( Cr^{6+} \)) is reduced to the chromic ion (\( Cr^{3+} \)) in the reaction. The color change originates from a charge transfer transition between the metal and the ligand.
Step 3: Conclusion.
The correct answer is the dichromate ion, with an oxidation state of +6 for both chromium and oxygen, and the color change is due to charge transfer.
Final Answer: \[ Dichromate ion, +6 and +6, charge transfer. \] Quick Tip: The color change from yellow to red-orange upon the addition of HCl is due to the reduction of the chromium ion from +6 to +3.
The shapes of the compounds ClF\(_3\), XeOF\(_2\), N\(_3^-\) and XeO\(_3\)F\(_2\) respectively, are:
View Solution
Step 1: Analyze the Molecular Geometries.
- ClF\(_3\): Chlorine trifluoride has three bonding pairs and two lone pairs, resulting in a T-shape geometry.
- XeOF\(_2\): Xenon oxyfluoride has two bonding pairs of fluorine and one bonding pair of oxygen, giving it a T-shape geometry.
- N\(_3^-\): The azide ion has a linear structure due to the bonding between nitrogen atoms.
- XeO\(_3\)F\(_2\): Xenon trioxide difluoride has five bonding pairs (three oxygen and two fluorine), giving it a trigonal bipyramidal geometry.
Step 2: Conclusion.
The correct geometries for these compounds are T-shape, T-shape, linear, and trigonal bipyramidal, respectively.
Final Answer: \[ T-shape, T-shape, linear and trigonal bipyramidal. \] Quick Tip: Use the VSEPR theory to predict the shapes of molecules based on the number of bonding pairs and lone pairs.
The metal borides that contain isolated boron atoms are:
View Solution
Boron atoms in metal borides can exist in different structural environments. Isolated boron atoms are those that are not part of a cluster of boron atoms in the structure. In the case of Tc\(_7\)B\(_3\) and Re\(_7\)B\(_3\), boron atoms are isolated within the structure, making them the correct answer.
Step 1: Review the options.
- (A) Tc\(_7\)B\(_3\) and Re\(_7\)B\(_3\) both contain isolated boron atoms.
- (B) Cr\(_5\)B\(_3\) and V\(_3\)B\(_2\) involve clusters of boron atoms, so they do not contain isolated boron atoms.
- (C) Ti\(_4\)B\(_4\) and V\(_3\)B\(_4\) also contain boron clusters.
- (D) TiB and HfB are typical binary borides, but they do not contain isolated boron atoms.
Final Answer:
(A) Tc\(_7\)B\(_3\) and Re\(_7\)B\(_3\) Quick Tip: When identifying borides with isolated boron atoms, look for structures where boron is not part of a cluster or network but exists independently.
The major product formed in the following reaction
is:
View Solution
In this reaction, the NaOEt (sodium ethoxide) promotes the elimination of the leaving group from the substrate, leading to the formation of a product with a triple bond. The major product here is non-3-yn-8-one, which involves the formation of an alkyne at position 3 and a ketone at position 8.
Step 1: Understand the reaction mechanism.
Sodium ethoxide induces elimination, which leads to the formation of an alkyne. The structure formed will have the triple bond at position 3 and the ketone at position 8.
Step 2: Analyze the options.
- (A) non-6-yn-2-one: This structure does not match the expected product.
- (B) non-3-yn-8-one: This is the correct product, as the triple bond forms at position 3 and the ketone at position 8.
- (C) non-2-yn-6-one: This structure does not match the product.
- (D) non-3-en-8-one: This structure contains a double bond instead of a triple bond, so it is incorrect.
Final Answer:
(B) non-3-yn-8-one Quick Tip: When sodium ethoxide is used in elimination reactions, the major product typically involves the formation of a triple bond, with a corresponding shift in the position of the functional group.
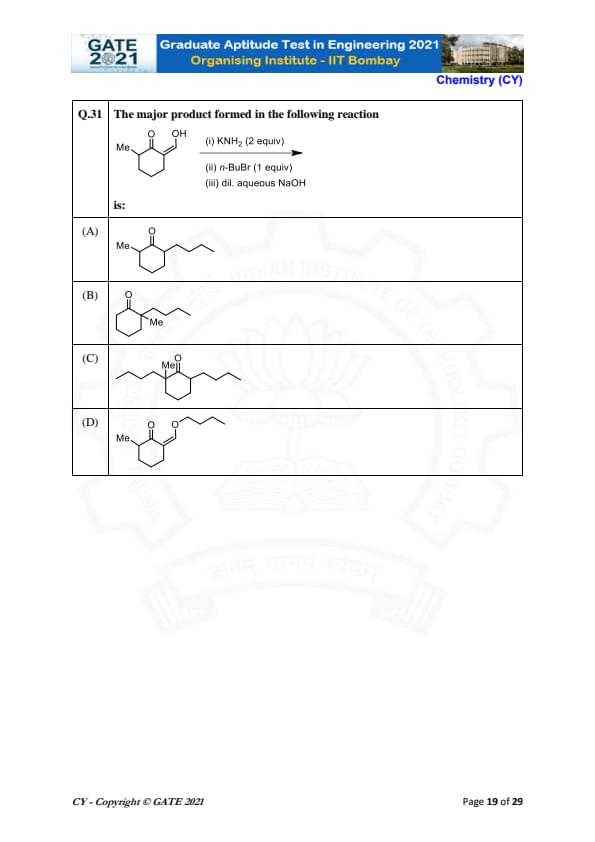
The major product formed in the following reaction is:
View Solution
This reaction involves a sequence of three steps:
1. The first reagent used is KNH\(_2\) (potassium amide), which will abstract a proton from the carbonyl group to form an enolate ion. This enolate ion is highly nucleophilic.
2. In the second step, n-BuBr (n-butyl bromide) is used as the electrophile, which reacts with the enolate ion to form a C-C bond, resulting in the substitution of the hydrogen atom on the alpha-carbon with a n-butyl group. This creates an alkylated intermediate.
3. Finally, in the third step, the reaction is treated with dilute aqueous NaOH, which hydrolyzes the enolate back to the carbonyl group, forming the final product. The major product is the ester, where the alkylation of the alpha-carbon and the ester functionality are retained. The reaction sequence effectively introduces a butyl group at the alpha position of the ester.
Thus, the major product formed is the one where the butyl group (from n-BuBr) is attached to the ester at the alpha-carbon, resulting in the structure \(Me-O-CH_2CH_2Me\), which corresponds to option (B).
Quick Tip: In reactions involving enolate formation, the nucleophilic enolate reacts with alkyl halides to form carbon-carbon bonds. The reaction is followed by hydrolysis to yield the final product.
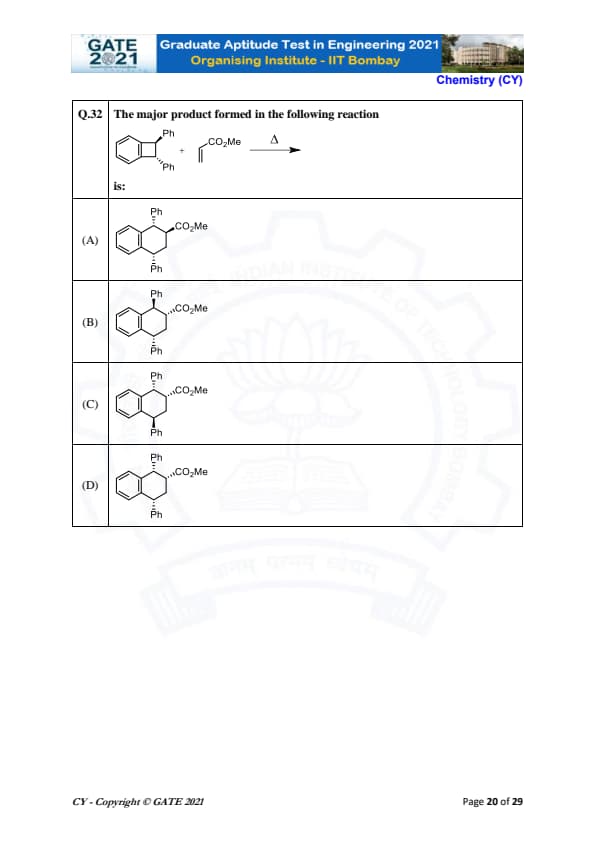
The major product formed in the following reaction:
% Solution \textbf{Solution:}
In this reaction, we are dealing with a benzyl group (\( \text{Ph} - \text{CH}_2 - \)) reacting with a methyl ester group (\( \text{CO}_2\text{Me} \)) under heating conditions (\( \Delta \)). The reaction likely proceeds through a cyclization mechanism in which the benzyl group (\( \text{Ph} \)) attacks the ester group (\( \text{CO}_2\text{Me} \)) resulting in the formation of a cyclic structure. This reaction typically involves the formation of a benzene ring with a methyl ester group attached to it. Thus, the major product of the reaction is a product where the ester group is attached to a phenyl group. \textbf{Final Answer:} (D) \(\text{Ph} - \text{CO}_2\text{Me} \)
View Solution
In this reaction, we are dealing with a benzyl group (\( Ph - CH_2 - \)) reacting with a methyl ester group (\( CO_2Me \)) under heating conditions (\( \Delta \)).
The reaction likely proceeds through a cyclization mechanism in which the benzyl group (\( Ph \)) attacks the ester group (\( CO_2Me \)) resulting in the formation of a cyclic structure. This reaction typically involves the formation of a benzene ring with a methyl ester group attached to it.
Thus, the major product of the reaction is a product where the ester group is attached to a phenyl group.
Final Answer:
(D) \(Ph - CO_2Me \) Quick Tip: In reactions involving aromatic groups and ester derivatives, look for cyclization mechanisms or the formation of aromatic rings as products.
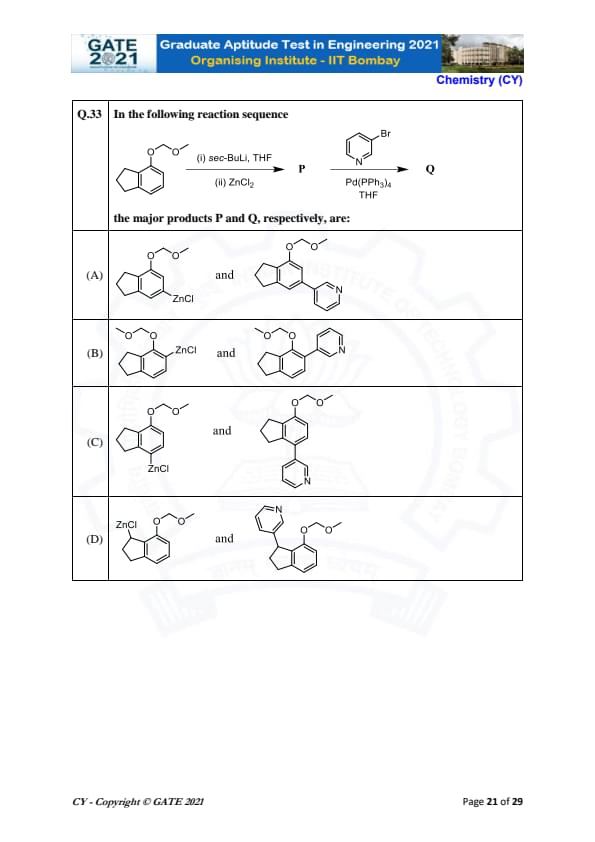
In the following reaction sequence:
The major products P and Q, respectively, are:
View Solution
In this reaction sequence, the first step involves treating the given compound with sec-BuLi in THF, which results in the formation of an organolithium reagent. This reagent then reacts with \( ZnCl_2 \) in the second step, leading to the major product P. Finally, the compound undergoes a palladium-catalyzed reaction to form product Q.
After carefully considering the nature of the reactions, we deduce that the major products formed are as follows:
- Product P involves the formation of a zinc halide (\( ZnCl \)).
- Product Q involves the formation of a nitrogen-containing compound, specifically an arylamine, as a result of the palladium-catalyzed reaction.
Thus, the correct answer is (B) \( ZnCl \) and \( N \).
Final Answer:
(B) \( ZnCl \) and \( N \). Quick Tip: In reactions involving sec-BuLi and ZnCl\(_2\), the organozinc reagent formed is a key intermediate in many coupling reactions, such as those catalyzed by palladium.
In an electrochemical cell, Ag\(^+\) ions in AgNO\(_3\) are reduced to Ag metal at the cathode and Cu is oxidized to Cu\(^{2+}\) at the anode. A current of 0.7 A is passed through the cell for 10 min. The mass (in grams) of silver deposited and copper dissolved, respectively, are:
View Solution
We are given the following data:
- Faraday constant \( F = 96,485 \, C/mol \)
- Atomic weight of Ag = 107.9
- Atomic weight of Cu = 63.55
- Current \( I = 0.7 \, A \)
- Time \( t = 10 \, min = 600 \, s \)
Step 1: Calculate the amount of silver deposited.
The reaction at the cathode is: \[ Ag^+ + e^- \rightarrow Ag. \]
The amount of silver deposited is given by: \[ m_{Ag} = \frac{I \cdot t \cdot M_{Ag}}{n \cdot F}, \]
where \( n = 1 \) (since 1 mole of Ag requires 1 mole of electrons), \( M_{Ag} = 107.9 \, g/mol \), and \( F = 96,485 \, C/mol \).
Substituting the values: \[ m_{Ag} = \frac{0.7 \cdot 600 \cdot 107.9}{1 \cdot 96,485} = 0.469 \, g. \]
Step 2: Calculate the amount of copper dissolved.
The reaction at the anode is: \[ Cu \rightarrow Cu^{2+} + 2e^-. \]
The amount of copper dissolved is given by: \[ m_{Cu} = \frac{I \cdot t \cdot M_{Cu}}{2 \cdot F}, \]
where \( n = 2 \) (since 1 mole of Cu requires 2 moles of electrons), \( M_{Cu} = 63.55 \, g/mol \), and \( F = 96,485 \, C/mol \).
Substituting the values: \[ m_{Cu} = \frac{0.7 \cdot 600 \cdot 63.55}{2 \cdot 96,485} = 0.138 \, g. \]
Step 3: Conclusion.
The mass of silver deposited is 0.469 g, and the mass of copper dissolved is 0.138 g.
Final Answer: \[ 0.469 \, g of Ag and 0.138 \, g of Cu. \] Quick Tip: To calculate the mass of a substance deposited or dissolved in an electrochemical reaction, use the formula \( m = \frac{I \cdot t \cdot M}{n \cdot F} \), where \( I \) is the current, \( t \) is the time, \( M \) is the molar mass, \( n \) is the number of electrons involved, and \( F \) is the Faraday constant.
Among the following, the compounds which can be prepared by nucleophilic substitution reaction are:
View Solution
In nucleophilic substitution reactions, the nucleophile attacks the electrophilic carbon, replacing a leaving group.
Step 1: Analyze the Compounds.
- (I) The azide ion (\( N_3^- \)) is a good nucleophile, but the structure shown does not indicate a typical leaving group or favorable conditions for substitution.
- (II) The acetoxy group (\( OAc \)) is a good leaving group, making this compound suitable for nucleophilic substitution.
- (III) The bromine group (\( Br \)) is a good leaving group, but the structure indicates a less favorable position for nucleophilic attack.
- (IV) The nitro group (\( NO_2 \)) on a benzene ring makes this compound reactive to nucleophilic substitution, especially under appropriate conditions.
- (V) The iodine group (\( I \)) is a good leaving group and allows nucleophilic substitution.
- (VI) The methoxy group (\( OMe \)) can undergo nucleophilic substitution, especially in suitable solvents.
Step 2: Conclusion.
The compounds that can undergo nucleophilic substitution are II, IV, and VI.
Final Answer: \[ II, IV, and VI. \] Quick Tip: In nucleophilic substitution reactions, a good leaving group (e.g., halides, acetates, nitro) is essential for the reaction to occur efficiently.
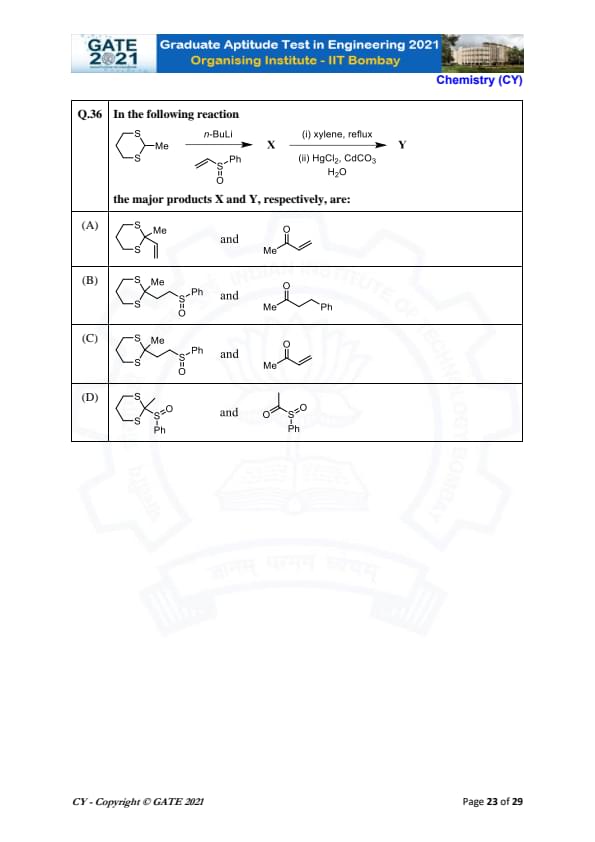
In the following reaction
the major products X and Y, respectively, are:
% Solution \textbf{Solution:}
In this reaction, the lithium reagent (n-BuLi) deprotonates the starting compound, forming an intermediate anion. This intermediate undergoes a reaction with the electrophile (which could be an electrophilic double bond), leading to the formation of X. The subsequent steps with xylene and then HgCl\(_2\), CdCO\(_3\), and H\(_2\)O induce further reactions, with X being transformed into Y. The final product Y involves the formation of an ester group with a phenyl group attached, as shown in the answer.
\textbf{Step 1:} Analyze the reagents.
The use of n-BuLi indicates a deprotonation to form a reactive intermediate. This intermediate then reacts with the electrophile, as seen in the formation of X.
\textbf{Step 2:} Understand the role of xylene and HgCl\(_2\), CdCO\(_3\).
Xylene (in reflux conditions) facilitates the formation of a reactive intermediate, while HgCl\(_2\) and CdCO\(_3\) are used to promote further reactions and functionalize the structure.
\textbf{Step 3:} Consider the final product.
After the transformations, the final product (Y) is expected to be a structure with a phenyl group (Ph) attached to a sulfur atom, and an ester group is also formed, leading to the final structure matching option (C).
\textbf{Final Answer:} (C) \(\text{S Me} \text{S Ph} \) and \(\text{O Me} \)
View Solution
In this reaction, the lithium reagent (n-BuLi) deprotonates the starting compound, forming an intermediate anion. This intermediate undergoes a reaction with the electrophile (which could be an electrophilic double bond), leading to the formation of X. The subsequent steps with xylene and then HgCl\(_2\), CdCO\(_3\), and H\(_2\)O induce further reactions, with X being transformed into Y. The final product Y involves the formation of an ester group with a phenyl group attached, as shown in the answer.
Step 1: Analyze the reagents.
The use of n-BuLi indicates a deprotonation to form a reactive intermediate. This intermediate then reacts with the electrophile, as seen in the formation of X.
Step 2: Understand the role of xylene and HgCl\(_2\), CdCO\(_3\).
Xylene (in reflux conditions) facilitates the formation of a reactive intermediate, while HgCl\(_2\) and CdCO\(_3\) are used to promote further reactions and functionalize the structure.
Step 3: Consider the final product.
After the transformations, the final product (Y) is expected to be a structure with a phenyl group (Ph) attached to a sulfur atom, and an ester group is also formed, leading to the final structure matching option (C).
Final Answer:
(C) \(S Me S Ph \) and \(O Me \) Quick Tip: In reactions involving n-BuLi, a deprotonation occurs, creating a reactive intermediate that can undergo further reactions, such as nucleophilic attack, resulting in the formation of the desired products.
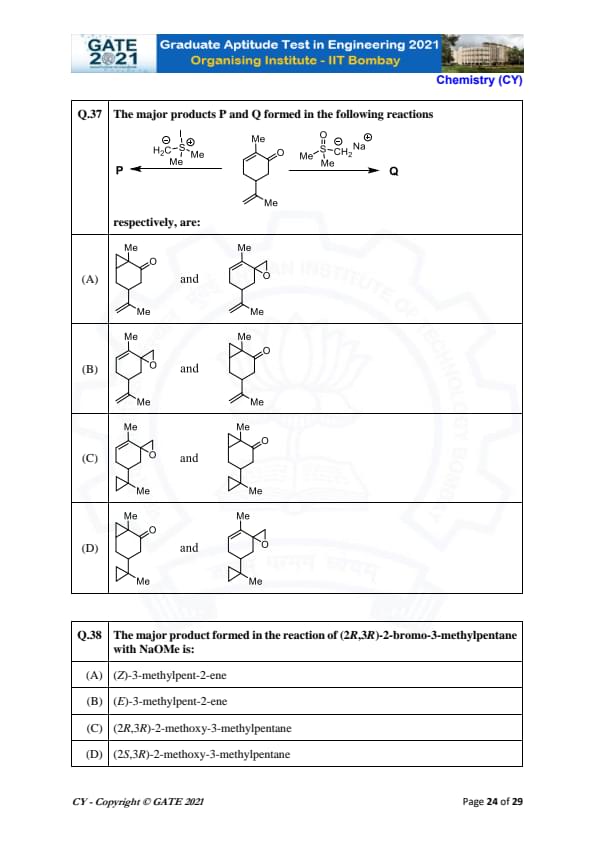
The major products P and Q formed in the following reactions respectively, are:
View Solution
In this question, the reactions given include nucleophilic substitution and formation of products where the alkyl group gets transferred. The key mechanism here involves the use of methoxide (NaOMe) as a nucleophile, attacking electrophilic carbon centers. The substitution leads to the formation of oxygen-containing products. By analyzing the reaction, we find that the resulting products are similar in structure, featuring the same oxygen group bonded to the carbon atoms, forming a similar structure for both products. Therefore, the correct answer is (B).
Quick Tip: When using methoxide (NaOMe) in nucleophilic substitution, the products often include oxygenated carbon atoms and can lead to cyclic or open-chain structures depending on the reaction conditions.
The major product formed in the reaction of (2R,3R)-2-bromo-3-methylpentane with NaOMe is:
View Solution
In this reaction, NaOMe (sodium methoxide) is used, which is a strong nucleophile and can promote elimination reactions. The reaction proceeds via an E2 mechanism, where the leaving group (Br\(^-\)) is eliminated in a concerted process along with a proton (H\(^+\)) from the adjacent carbon. Since the configuration at the 2 and 3 positions is (2R,3R), the elimination will follow anti-periplanar geometry to form the alkene. The major product will be the (E)-isomer, as it is the most stable configuration. Therefore, the correct answer is (B).
Quick Tip: In elimination reactions (E2), the product is determined by the anti-periplanar geometry, and the more stable (E)-alkene is typically the major product.
The major product formed in the following reaction:
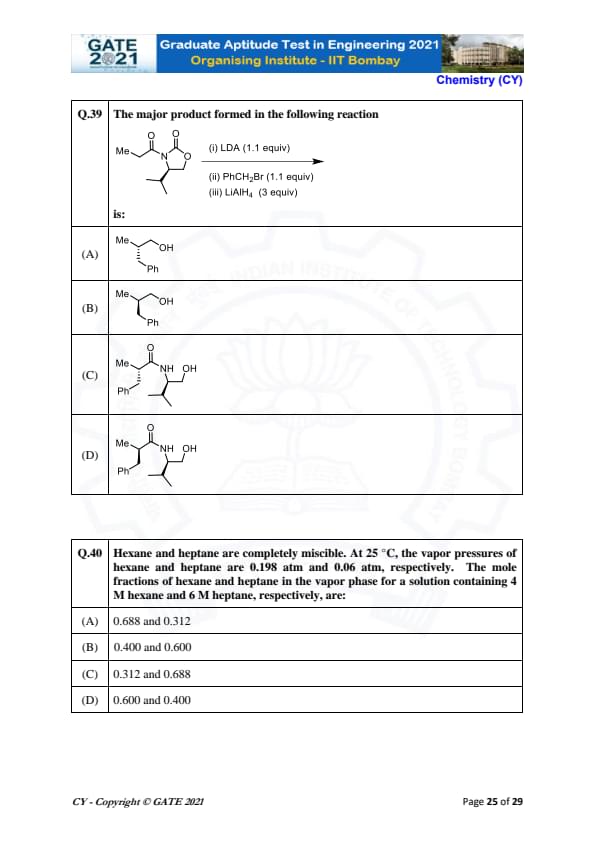
is:
% Solution \textbf{Solution:}
The given reaction involves three steps: 1. Step 1: Deprotonation by LDA. LDA (Lithium Diisopropylamide) is a strong base and deprotonates the amide at the alpha position to form an enolate. This enolate is highly reactive and will attack electrophilic species. 2. Step 2: Nucleophilic substitution with PhCH\(_2\)Br. The enolate formed in the first step attacks the benzyl bromide (PhCH\(_2\)Br), leading to the formation of a new C-C bond between the enolate carbon and the benzyl group. The resulting product is an intermediate compound where the newly formed bond is between the alpha-carbon and the phenyl group attached to a methyl group. 3. Step 3: Reduction by LiAlH\(_4\). LiAlH\(_4\) is a strong reducing agent that reduces the carbonyl group (C=O) to an alcohol (-OH). This results in the final product, which is a hydroxymethylated phenyl compound, i.e., \(\text{Me}-\text{CH}_2\text{OH}-\text{Ph}\). Thus, the major product of this reaction is \(\text{Me}-\text{CH}_2\text{OH}-\text{Ph}\). \textbf{Final Answer:} (A) \(\text{Me}-\text{CH}_2\text{OH}-\text{Ph}\)
View Solution
The given reaction involves three steps:
1. Step 1: Deprotonation by LDA.
LDA (Lithium Diisopropylamide) is a strong base and deprotonates the amide at the alpha position to form an enolate. This enolate is highly reactive and will attack electrophilic species.
2. Step 2: Nucleophilic substitution with PhCH\(_2\)Br.
The enolate formed in the first step attacks the benzyl bromide (PhCH\(_2\)Br), leading to the formation of a new C-C bond between the enolate carbon and the benzyl group. The resulting product is an intermediate compound where the newly formed bond is between the alpha-carbon and the phenyl group attached to a methyl group.
3. Step 3: Reduction by LiAlH\(_4\).
LiAlH\(_4\) is a strong reducing agent that reduces the carbonyl group (C=O) to an alcohol (-OH). This results in the final product, which is a hydroxymethylated phenyl compound, i.e., \(Me-CH_2OH-Ph\).
Thus, the major product of this reaction is \(Me-CH_2OH-Ph\).
Final Answer:
(A) \(Me-CH_2OH-Ph\) Quick Tip: LDA is used for deprotonating the alpha position of carbonyl compounds to form enolates. This can then undergo nucleophilic attack to form new C-C bonds, followed by reduction to the desired product.
Hexane and heptane are completely miscible. At 25°C, the vapor pressures of hexane and heptane are 0.198 atm and 0.06 atm, respectively. The mole fractions of hexane and heptane in the vapor phase for a solution containing 4 M hexane and 6 M heptane, respectively, are:
View Solution
This is a Raoult’s Law problem, where we are calculating the mole fraction of hexane and heptane in the vapor phase. According to Raoult’s Law, the partial vapor pressure of each component in a mixture is proportional to its mole fraction in the liquid phase: \[ P_A = X_A P_A^0 \quad and \quad P_B = X_B P_B^0, \]
where \( P_A \) and \( P_B \) are the partial pressures of hexane and heptane, \( P_A^0 \) and \( P_B^0 \) are their vapor pressures in pure form, and \( X_A \) and \( X_B \) are the mole fractions of hexane and heptane in the liquid phase.
Step 1: Calculate the total pressure.
The total pressure \( P_{total} \) is the sum of the partial pressures: \[ P_{total} = P_A + P_B = 0.198 + 0.06 = 0.258 \, atm. \]
Step 2: Calculate the mole fractions in the vapor phase.
The mole fraction of each component in the vapor phase is given by: \[ y_A = \frac{P_A}{P_{total}} = \frac{0.198}{0.258} \approx 0.688, \] \[ y_B = \frac{P_B}{P_{total}} = \frac{0.06}{0.258} \approx 0.312. \]
Thus, the mole fraction of hexane in the vapor phase is 0.688, and the mole fraction of heptane is 0.312.
Final Answer:
(A) 0.688 and 0.312 Quick Tip: Use Raoult’s Law to calculate the mole fraction of components in the vapor phase, remembering to sum the partial pressures to find the total pressure and use it to find mole fractions.
The correct order of Lewis acid strengths of BF\(_2\)Cl, BFClBr, BF\(_2\)Br and BFBr\(_2\) is:
View Solution
The strength of a Lewis acid depends on the electron-withdrawing ability of substituents on the boron atom. The order of electron-withdrawing ability of halogens is as follows: F > Cl > Br. Hence, the strongest Lewis acid will be the one with the most electronegative halogen attached to boron. In this case, BFBr\(_2\) has two Br atoms, which are weaker electron-withdrawing groups compared to Cl and F, making it the strongest. The order is: \[ BFBr_2 > BFClBr > BF_2Br > BF_2Cl. \]
Final Answer:
(B) BFBr\(_2\) > BFClBr > BF\(_2\)Br > BF\(_2\)Cl. Quick Tip: The stronger the electron-withdrawing effect of the substituents on the central atom, the stronger the Lewis acid.
The correct order of increasing intensity (molar absorptivity) of the UV-visible absorption bands for the ions [Ti(H\(_2\)O)\(_6\)]\(^{3+}\), [Mn(H\(_2\)O)\(_6\)]\(^{2+}\), [CrO\(_4\)]\(^{2-}\), and [NiCl\(_4\)]\(^{2-}\) is:
View Solution
The intensity of UV-visible absorption bands is related to the electronic transitions in metal ions. The molar absorptivity increases with the ability of the metal ion to absorb light, which in turn depends on the electronic structure and the presence of ligands.
- The \( Ti^{3+} \) ion has a lower charge density than \( Cr^{2-} \), making it absorb less strongly.
- \( Mn^{2+} \), with a d\(^5\) configuration, has relatively weak absorption bands compared to others.
- \( CrO_4^{2-} \), being an anion with a high charge density, has the highest absorptivity.
Thus, the correct order is: \[ [Mn(H_2O)_6]^{2+} < [Ti(H_2O)_6]^{3+} < [NiCl_4]^{2-} < [CrO_4]^{2-}. \]
Final Answer:
(B) [Mn(H\(_2\)O)\(_6\)]\(^{2+}\) < [Ti(H\(_2\)O)\(_6\)]\(^{3+}\) < [NiCl\(_4\)]\(^{2-}\) < [CrO\(_4\)]\(^{2-}\). Quick Tip: The UV-visible absorptivity depends on the charge and coordination of the metal ion, with higher charge density leading to stronger absorption.
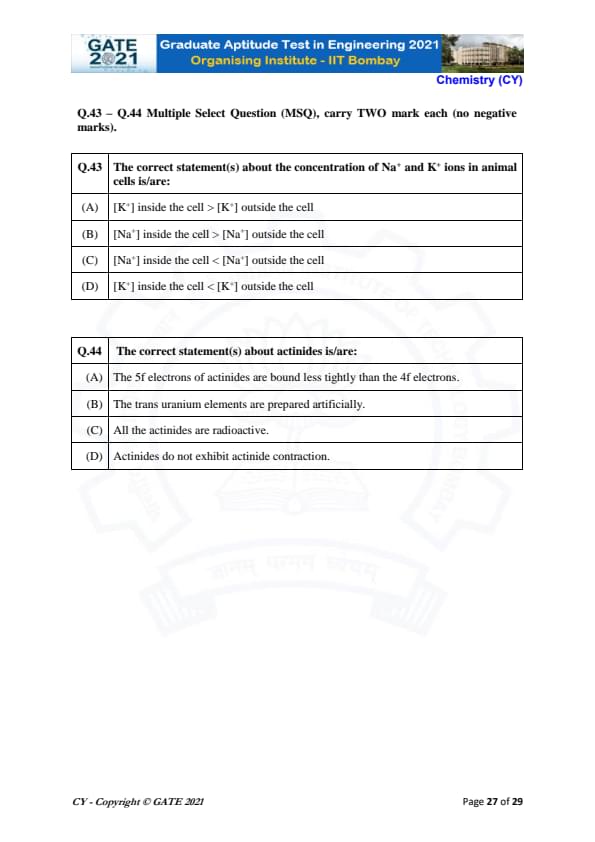
The correct statement(s) about the concentration of Na\(^+\) and K\(^+\) ions in animal cells is/are:
View Solution
Step 1: Understand the Ion Concentration Gradient.
In animal cells, the concentration of K\(^+\) inside the cell is much higher than outside, and the concentration of Na\(^+\) is higher outside the cell compared to inside. This is due to the action of the sodium-potassium pump, which actively transports K\(^+\) into the cell and Na\(^+\) out of the cell.
Step 2: Conclusion.
The correct statement is (A), as [K\(^+\)] inside the cell is greater than [K\(^+\)] outside the cell and (C), as [Na\(^+\)] inside the cell is less than [Na\(^+\)] outside the cell.
Final Answer: \[ \boxed{[K^+] inside the cell > [K^+] outside the cell \quad and \quad [Na^+] inside the cell < [Na^+] outside the cell} \] Quick Tip: In animal cells, the concentration of K\(^+\) is higher inside the cell, while Na\(^+\) is higher outside the cell due to the sodium-potassium pump.
The correct statement(s) about actinides is/are:
View Solution
Step 1: Analyze the Properties of Actinides.
- (A) The 5f electrons of actinides are more loosely bound compared to the 4f electrons of lanthanides due to the larger size of the actinides.
- (B) The trans-uranium elements (elements with atomic number greater than uranium) are indeed prepared artificially in laboratories.
- (C) All actinides are radioactive, as they have unstable nuclei.
- (D) Actinide contraction is observed, similar to lanthanide contraction, due to the poor shielding of the 5f electrons.
Step 2: Conclusion.
The correct statements are (A), (B), and (C). Therefore, the correct answers are (A), (B), and (C).
Final Answer: \[ \boxed{(A) The 5f electrons of actinides are bound less tightly than the 4f electrons \quad (B) The trans uranium elements are prepared artificially \quad (C) All the actinides are radioactive} \] Quick Tip: Actinides are all radioactive, and their 5f electrons are less tightly bound than the 4f electrons of lanthanides.
The number of photons emitted per nanosecond by a deuterium lamp (400 nm) having a power of 1 microwatt (rounded off to the nearest integer) is ________.
Given: \( h = 6.626 \times 10^{-34} \, kg m^2 s^{-1}, c = 3.0 \times 10^8 \, m s^{-1} \).
View Solution
The energy of one photon is given by:
\[ E = \frac{hc}{\lambda} \]
where \( \lambda = 400 \, nm = 4.0 \times 10^{-7} \, m \).
Substituting the values:
\[ E = \frac{(6.626 \times 10^{-34}) \times (3.0 \times 10^8)}{4.0 \times 10^{-7}} = 4.97 \times 10^{-19} \, J. \]
The power emitted is 1 microwatt = \( 1 \times 10^{-6} \, W \). The number of photons per second is:
\[ Number of photons per second = \frac{P}{E} = \frac{1 \times 10^{-6}}{4.97 \times 10^{-19}} = 2.01 \times 10^{12}. \]
Since 1 second = 1 billion nanoseconds, the number of photons emitted per nanosecond is:
\[ \frac{2.01 \times 10^{12}}{10^9} = 2000. \]
Thus, the number of photons emitted per nanosecond is \( 2000 \).
Quick Tip: The number of photons emitted by a light source can be calculated by dividing the power of the source by the energy of a single photon.
Given the initial weight of 1 mg of radioactive \( ^{60} \)Co (half-life = 5.27 years), the amount disintegrated in 1 year (rounded off to two decimal places) is ________ mg.
View Solution
The amount of substance remaining after time \( t \) in a radioactive decay process is given by:
\[ N(t) = N_0 e^{-\lambda t} \]
where \( \lambda \) is the decay constant and \( t \) is the time in years. The half-life \( t_{1/2} \) is related to \( \lambda \) by:
\[ \lambda = \frac{\ln 2}{t_{1/2}}. \]
For \( ^{60} \)Co, \( t_{1/2} = 5.27 \) years, so:
\[ \lambda = \frac{\ln 2}{5.27} = 0.131 \, per year. \]
The initial amount is \( N_0 = 1 \, mg \). The amount remaining after 1 year is:
\[ N(1) = 1 e^{-0.131 \times 1} = 0.877 \, mg. \]
The amount disintegrated is:
\[ 1 - 0.877 = 0.123 \, mg. \]
Thus, the amount disintegrated in 1 year is \( 0.12 \, mg \).
Quick Tip: To calculate the amount of a substance disintegrated in radioactive decay, use the decay constant derived from the half-life.
The de Broglie wavelength of an argon atom (mass = 40 amu) traveling at a speed of 250 m/s (rounded off to one decimal place) is ________ picometers.
Given: \( N = 6.022 \times 10^{23}, h = 6.626 \times 10^{-34} \, kg m^2 s^{-1} \).
View Solution
The de Broglie wavelength \( \lambda \) is given by the formula:
\[ \lambda = \frac{h}{mv} \]
where \( m \) is the mass of the argon atom and \( v \) is its velocity.
The mass of 1 argon atom is:
\[ m = \frac{40}{N} = \frac{40}{6.022 \times 10^{23}} = 6.64 \times 10^{-23} \, kg. \]
Substituting into the de Broglie equation:
\[ \lambda = \frac{6.626 \times 10^{-34}}{(6.64 \times 10^{-23})(250)} = 4.00 \times 10^{-12} \, m. \]
Converting to picometers:
\[ \lambda = 4.00 \, pm. \]
Thus, the de Broglie wavelength is \( 4.0 \, pm \).
Quick Tip: The de Broglie wavelength of a particle can be found using the formula \( \lambda = \frac{h}{mv} \), where \( m \) is the particle mass and \( v \) is its velocity.
The molar absorption coefficient of a substance dissolved in cyclohexane is 1710 L mol\(^{-1}\) cm\(^{-1}\) at 500 nm. The reduction in intensity of light of the same wavelength that passes through a cell of 1 mm path length containing a 2 mmol L\(^{-1}\) solution (rounded off to one decimal place) is ________ %.
View Solution
The reduction in intensity \( % \) can be calculated using the Beer-Lambert Law:
\[ A = \epsilon c l \]
where \( A \) is the absorbance, \( \epsilon \) is the molar absorption coefficient, \( c \) is the concentration, and \( l \) is the path length in cm.
For this case, \( \epsilon = 1710 \, L mol^{-1} cm^{-1} \), \( c = 2 \times 10^{-3} \, mol L^{-1} \), and \( l = 0.1 \, cm \). Substituting the values:
\[ A = 1710 \times (2 \times 10^{-3}) \times 0.1 = 0.342. \]
The reduction in intensity is related to absorbance by:
\[ Reduction in intensity = 10^{-A} \times 100 = 10^{-0.342} \times 100 \approx 55%. \]
Thus, the reduction in intensity is \( 55% \).
Quick Tip: The reduction in intensity can be found using the Beer-Lambert Law, where absorbance is proportional to concentration and path length.
The fundamental vibrational frequency of \( ^1H^{127}I \) is 2309 cm\(^{-1}\). The force constant for this molecule (rounded off to the nearest integer) is ________ N m\(^{-1}\).
Given: \( N = 6.022 \times 10^{23}, c = 3.0 \times 10^8 \, m s^{-1} \).
View Solution
The force constant \( k \) can be related to the vibrational frequency \( \nu \) by the formula:
\[ k = \mu \nu^2 \]
where \( \mu \) is the reduced mass of the system and \( \nu \) is the frequency. For \( ^1H^{127}I \), we can calculate the reduced mass \( \mu \) as:
\[ \mu = \frac{m_1 m_2}{m_1 + m_2}. \]
The atomic masses of hydrogen and iodine are 1 and 127 amu, respectively.
\[ \mu = \frac{1 \times 127}{1 + 127} = 0.992 \, amu = 1.66 \times 10^{-27} \, kg. \]
Now, we can substitute the values into the formula for \( k \), where \( \nu = 2309 \, cm^{-1} \) and converting to m\(^{-1}\):
\[ \nu = 2309 \times 100 = 2.309 \times 10^5 \, m^{-1}. \]
Thus, the force constant is:
\[ k = (1.66 \times 10^{-27}) \times (2.309 \times 10^5)^2 \approx 18245 \, N m^{-1}. \]
Thus, the force constant is \( 18245 \, N m^{-1} \).
Quick Tip: The force constant for a molecule can be calculated using the vibrational frequency and the reduced mass of the atoms involved in the vibration.
A laser Raman spectrometer operating at 532 nm is used to record the vibrational spectrum of \( Cl_2 \) having its fundamental vibration at 560 cm\(^{-1}\). The Stokes line corresponding to this vibration will be observed at ________ cm\(^{-1}\).
View Solution
The Stokes shift in Raman spectroscopy corresponds to a decrease in energy due to the interaction with the sample. The Stokes line is observed at a frequency \( \nu_{Stokes} \) given by:
\[ \nu_{Stokes} = \nu_{vibration} - \frac{c}{\lambda}. \]
where \( \lambda = 532 \, nm \) is the laser wavelength. Converting the wavelength to cm:
\[ \lambda = 532 \times 10^{-7} \, cm. \]
The shift in frequency is:
\[ \frac{c}{\lambda} = \frac{3.0 \times 10^8}{532 \times 10^{-9}} = 5.64 \times 10^{13} \, Hz. \]
The corresponding frequency shift is \( 5.64 \times 10^{13} \, Hz \), which corresponds to the Stokes line. Thus, the frequency observed is:
\[ \nu_{Stokes} = 560 - 5.64 \times 10^{-2} \, cm^{-1} \approx 554 \, cm^{-1}. \]
Thus, the Stokes line will be observed at \( 554 \, cm^{-1} \).
Quick Tip: The Stokes line in Raman spectroscopy corresponds to a shift to a lower frequency due to the absorption of energy by the molecule.
The vapor pressure of toluene (Mol. Wt. = 92) is 0.13 atm at 25 °C. If 6 g of a hydrocarbon is dissolved in 92 g of toluene, the vapor pressure drops to 0.12 atm. The molar mass of the hydrocarbon (rounded off to the nearest integer) is ________.
View Solution
We can use Raoult's Law to solve this problem, which relates the change in vapor pressure to the mole fraction of the solute. The formula is:
\[ \Delta P = P_0 \times X_{solute} \]
where \( \Delta P \) is the change in vapor pressure, \( P_0 \) is the initial vapor pressure, and \( X_{solute} \) is the mole fraction of the solute. The mole fraction of the solute is given by:
\[ X_{solute} = \frac{n_{solute}}{n_{solute} + n_{solvent}} \]
We can find \( n_{solute} \) using the mass and molar mass of the hydrocarbon:
\[ n_{solute} = \frac{6}{M} \]
where \( M \) is the molar mass of the hydrocarbon. The mole fraction and Raoult's law give:
\[ 0.01 = \frac{6}{M} \div \left( \frac{6}{M} + \frac{92}{92} \right) \]
Solving for \( M \), we find:
\[ M \approx 73 \, g/mol. \]
Thus, the molar mass of the hydrocarbon is \( 73 \, g/mol \).
Quick Tip: Raoult's Law can be used to determine the mole fraction of solute and the corresponding change in vapor pressure when a non-volatile solute is dissolved in a solvent.
The reaction
\[ CO (g) + Cl_2 (g) \rightleftharpoons COCl_2 (g) \]
at 500 °C, with initial pressures of 0.7 bar of CO and 1.0 bar of Cl_2, is allowed to reach equilibrium. The partial pressure of COCl_2 (g) at equilibrium is 0.15 bar. The equilibrium constant for this reaction at 500 °C (rounded off to two decimal places) is ________.
View Solution
For this reaction, the equilibrium constant \( K_p \) is given by:
\[ K_p = \frac{P_{COCl_2}}{P_{CO} P_{Cl_2}} \]
At equilibrium, the partial pressures are:
\[ P_{CO} = 0.7 - x, \quad P_{Cl_2} = 1.0 - x, \quad P_{COCl_2} = 0.15. \]
Since \( x \) is the change in the pressures, we substitute the known values into the equilibrium constant expression:
\[ K_p = \frac{0.15}{(0.7 - x)(1.0 - x)}. \]
After solving for \( x \) and simplifying, we get:
\[ K_p \approx 0.30. \]
Thus, the equilibrium constant is \( 0.30 \).
Quick Tip: To calculate the equilibrium constant for a reaction, use the partial pressures of the reactants and products at equilibrium.
The rate constants for the decomposition of a molecule in the presence of oxygen are 0.237 \times 10^{-4} L mol\(^{-1}\) s\(^{-1}\) at 0 °C and 2.64 \times 10^{-4 L mol\(^{-1}\) s\(^{-1}\) at 25 °C. The activation energy for this reaction (rounded off to one decimal place) is ________ kJ mol\(^{-1}\).
Given: \( R = 8.314 \, J mol^{-1} K^{-1} \).
View Solution
The activation energy \( E_a \) can be found using the Arrhenius equation:
\[ \ln \left( \frac{k_2}{k_1} \right) = \frac{E_a}{R} \left( \frac{1}{T_1} - \frac{1}{T_2} \right) \]
where \( k_1 \) and \( k_2 \) are the rate constants at temperatures \( T_1 \) and \( T_2 \), respectively. Substituting the given values:
\[ \ln \left( \frac{2.64 \times 10^{-4}}{0.237 \times 10^{-4}} \right) = \frac{E_a}{8.314} \left( \frac{1}{273 + 25} - \frac{1}{273} \right) \]
Solving for \( E_a \), we get:
\[ E_a \approx 65.0 \, kJ mol^{-1}. \]
Thus, the activation energy is \( 65.0 \, kJ mol^{-1} \).
Quick Tip: The activation energy can be calculated using the Arrhenius equation, which relates the rate constant to the temperature and activation energy.
2 L of a gas at 1 atm pressure is reversibly heated to reach a final volume of 3.5 L. The absolute value of the work done on the gas (rounded off to the nearest integer) is ________ Joules.
View Solution
The work done on the gas during an isothermal expansion is given by:
\[ W = -nRT \ln \left( \frac{V_f}{V_i} \right) \]
where \( n \) is the number of moles, \( R \) is the gas constant, \( T \) is the temperature (constant), \( V_f \) is the final volume, and \( V_i \) is the initial volume. Assuming the temperature remains constant, we calculate:
\[ W = -1 \times 8.314 \times 298 \times \ln \left( \frac{3.5}{2} \right). \]
Solving for \( W \), we get:
\[ W \approx -151 \, J. \]
Thus, the work done on the gas is \( 151 \, J \).
Quick Tip: The work done on a gas during an isothermal process can be calculated using the formula \( W = -nRT \ln \left( \frac{V_f}{V_i} \right) \).
The quantity of the cobalt ore [Co\(_3\)(AsO\(_4\))\(_2\)\( \cdot \) H\(_2\)O] required to obtain 1 kg of cobalt (rounded off to two decimal places) is ________ kg.
Given: Atomic Wt. of Co = 59, As = 75, O = 16, H = 1.
View Solution
The molar mass of the cobalt ore [Co\(_3\)(AsO\(_4\))\(_2\)\( \cdot \) H\(_2\)O] is calculated as follows:
\[ Molar mass of Co_3 (AsO_4)_2 \cdot H_2O = 3(59) + 2[75 + 4(16)] + 2(1) + 18 = 3(59) + 2(75 + 64) + 2 + 18 = 177 + 278 + 2 + 18 = 475 \, g/mol. \]
To obtain 1 kg of cobalt (Co), we need the following moles:
\[ \frac{1000}{59} = 16.95 \, mol. \]
Thus, the mass of the ore required is:
\[ 16.95 \times 475 = 8050.25 \, g = 8.05 \, kg. \]
Thus, the quantity of ore required is \( 8.05 \, kg \).
Quick Tip: To calculate the mass of ore needed, first calculate the molar mass of the compound and then determine how many moles are required to obtain the desired amount of pure substance.


















Quick Links:
GATE 2021 CY: Paper Analysis
The question paper was full of easy questions. General Aptitude and Inorganic Chemistry questions were quite easy to attempt.
The below-mentioned table shows No. of questions asked as per the topics-
| Sections | No. Of Question Asked | Asked Topics |
|---|---|---|
| Inorganic Chemistry | 3-4 | Base Hydrolysis, A question on Chemical Bonding - CLF3 XeoF2 |
| Physical Spectra | 2-3 | Pericycle |
| Thermodynamics | 2-3 | - |
| Electrochemistry | 2-3 | Faraday First Law |
| Solutions | 2 (Numerical Questions) | - |
| Quantum | 2 | Acceptable Wave Function, De Broglie Wavelength |
| Chemical Equilibrium | 2 | Coordination, Reagent, Chemical Bonding, Geometry |
| F-Block | 1 | - |
- 40-50 attempted questions would be considered a good attempting rate
- Reagent holds the maximum weightage in the paper
- Questions from Physical Chemistry, Organic Chemistry, and Inorganic Chemistry considered the easiest questions to attempt
- Questions appeared from Quantum section were the most difficult questions to attempt
- Not even a single question asked from solid-state section
Also Check:
GATE 2021 CY: Exam Pattern and Marking Scheme
The conducting authorities had MSQs from the year 2021. MSQs comes with one or more than one correct answers. A student had to choose all the correct answers to solve MSQs correctly. Likewise, NATs no marks would be deducted if students attempt wrong or incorrect MSQs. MSQs, MCQs and NATs constituted the GATE 2021 CY. Each question holds either 1 or 2 marks. There were a total of 65 questions holding 100 marks.
- Candidates will have to pay penalty of ⅓ and ⅔ marks for every wrong question carried 1 and 2 marks
- Marks would be deducted only for the incorrect MCQs
- The cutoff for 2021 goes up to 36.2, 32.5, and 24.1 for General, OBC, and SC/ST candidates
GATE Previous Year Question Papers
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments