On 13th February 2021, GATE 2021 Chemical Engineering (CH) Question Paper was held. The exam was conducted by IIT Bombay in the Forenoon Session, from 9:30 AM to 12:30 PM. As instructed by the aspirants, the difficulty level of the question paper was moderate.
The General Aptitude section was easy to attempt. The Mass Transfer section was the most difficult section in GATE 2021 CH. A candidate could easily attempt 40+ questions in the exam. 70 or more than 70 marks would be considered a good score in the exam.
GATE 2021 Chemical Engineering (CH) Question Paper with Solutions
| GATE 2021 Chemical Engineering (CH) Question Paper | Check Solutions |

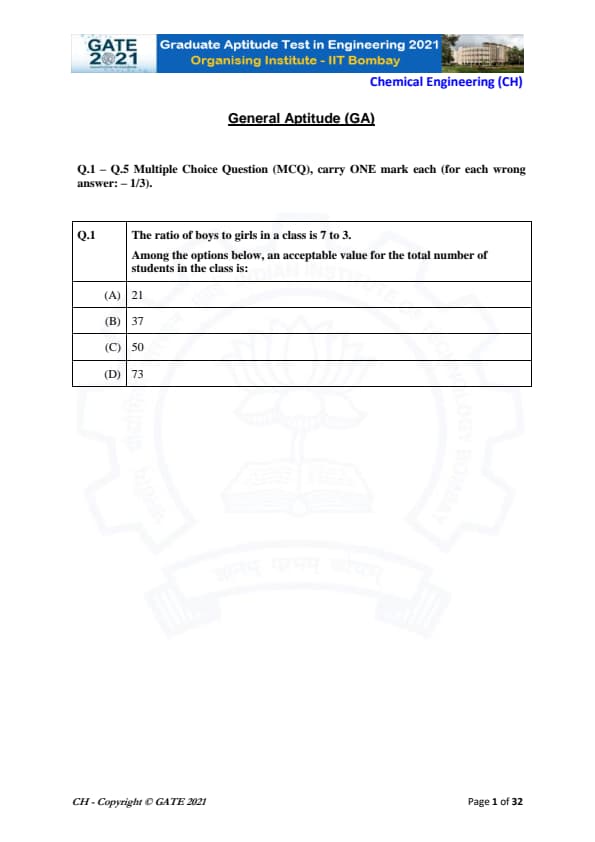
The ratio of boys to girls in a class is 7 to 3. Among the options below, an acceptable value for the total number of students in the class is:
View Solution
To determine the correct total number of students based on the ratio, let's analyze the information carefully. The ratio of boys to girls is given as \(7 : 3\).
Step 1: Understanding the ratio.
A ratio of \(7 : 3\) means that out of every 10 students, 7 are boys and 3 are girls. Therefore, the total number of students must be a multiple of 10.
Step 2: Verify each option.
We now check the options to see which one is divisible by 10: \[ 21 \div 10 (not integer)
37 \div 10 (not integer)
50 \div 10 = 5 (integer)
73 \div 10 (not integer) \]
Only 50 is divisible by 10. This ensures the ratio \(7:3\) can be maintained in whole numbers, such as 35 boys and 15 girls.
Step 3: Conclusion.
Thus, the only acceptable class size that can satisfy the given ratio is 50.
Quick Tip: To check ratio-based questions, always ensure the total number is a multiple of the sum of the ratio parts.
A polygon is convex if, for every pair of points inside the polygon, the line segment joining them lies completely inside or on the polygon. Which one of the following is NOT a convex polygon?

View Solution
A polygon is said to be convex when every interior angle is less than \(180^\circ\), and for any two points chosen within the polygon, the straight line segment connecting them remains entirely inside the polygon.
Step 1: Understand convexity.
Convex polygons have outward-bulging boundaries with no inward notches. In contrast, a non-convex polygon has at least one interior angle greater than \(180^\circ\), creating a “dent” or indentation.
Step 2: Evaluate each option.
- Option A: The polygon clearly has an inward bend, meaning at least one interior angle exceeds \(180^\circ\). This violates the convexity rule.
- Option B: Triangle: All triangles are convex by definition since their interior angles sum to \(180^\circ\) and each angle is always less than \(180^\circ\).
- Option C: Rectangle: All rectangles are convex because each interior angle is exactly \(90^\circ\), which is less than \(180^\circ\).
- Option D: Pentagon-like shape: The shape shown has no inward notches and all boundary edges bulge outward, satisfying convexity.
Step 3: Conclusion.
Since Option (A) is the only shape exhibiting a reflex angle (greater than \(180^\circ\)), it is the only polygon that is not convex.
Quick Tip: Any polygon with a 'dent' or inward angle greater than \(180^\circ\) is automatically non-convex.
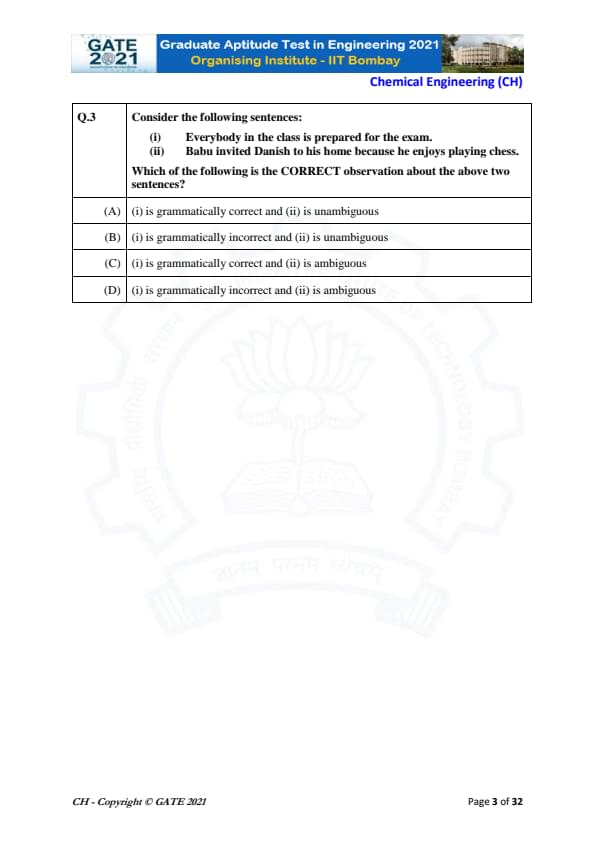
Consider the following sentences:
(i) Everybody in the class is prepared for the exam.
(ii) Babu invited Danish to his home because he enjoys playing chess.
Which of the following is the CORRECT observation about the above two sentences?
View Solution
Sentence (i): “Everybody in the class is prepared for the exam.”
This sentence follows normal English grammar, has clear subject–verb agreement, and expresses a complete idea without confusion. Therefore, it is grammatically correct and unambiguous.
Sentence (ii): “Babu invited Danish to his home because he enjoys playing chess.”
This sentence contains a pronoun ambiguity. The word “he” can refer either to Babu or Danish. Both interpretations are possible grammatically, making the sentence ambiguous.
Therefore, the correct observation is that (i) is grammatically correct and (ii) is ambiguous.
Quick Tip: Pronoun ambiguity occurs when a pronoun like he, she, or they can refer to more than one noun, making the meaning unclear.
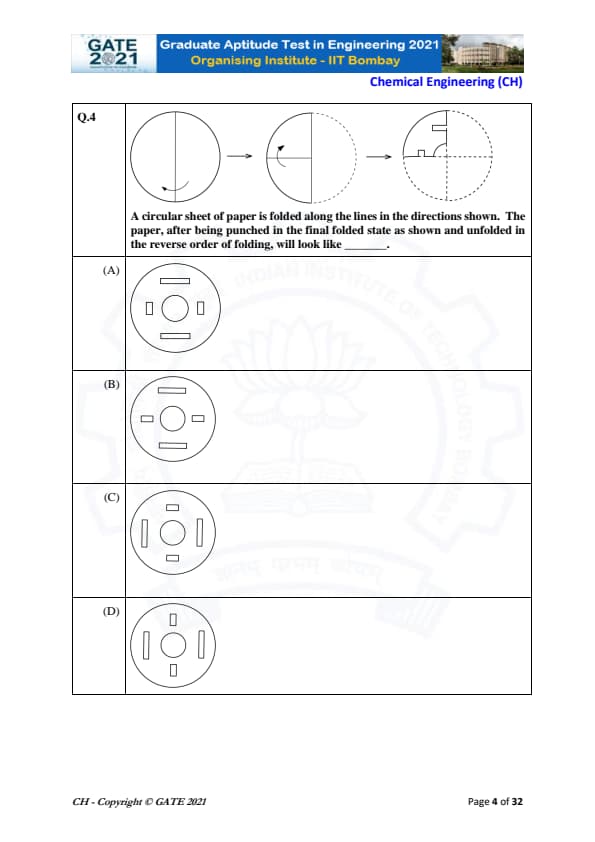
A circular sheet of paper is folded along the lines in the directions shown. The paper, after being punched in the final folded state as shown and unfolded in the reverse order of folding, will look like \hspace{2cm}.


View Solution
Step 1: Understanding the folding sequence.
The circular sheet is first folded vertically into two equal halves. Then, the semicircle is folded again along a horizontal radius. This results in a quarter-circle shape where the punching is done.
Step 2: Analyzing the punched shape.
The punching shown in the final folded state consists of:
- A rectangular cut near the curved edge.
- A right-angle shaped notch along the straight edges.
When unfolded once, each punched shape duplicates along the fold line. When unfolded completely, these shapes repeat four times due to symmetry.
Step 3: Visualizing the unfolded pattern.
Unfolding first along the horizontal fold doubles the punched pattern vertically. Unfolding again along the vertical fold doubles it horizontally. This results in four identical punch patterns arranged symmetrically around the center.
Step 4: Matching with the options.
Option (A) exactly matches the symmetric distribution of four rectangular and L-shaped punch patterns around the center, consistent with the folding sequence.
Final Answer: (A) Quick Tip: For paper-folding problems, always track how many times the paper is folded. Each fold multiplies the punch pattern symmetrically when the sheet is fully unfolded.
_____ is to surgery as writer is to _____
Which one of the following options maintains a similar logical relation in the above sentence?
View Solution
A writer produces or creates a book. Similarly, we need someone who performs surgery.
Step 1: Identify the relationship.
Writer : Book is a creator–creation relationship.
So the first blank must also be a person related to surgery (as performer).
Step 2: Check each option.
(A) Plan : outline — Not a creator–creation pair.
(B) Hospital : library — These are places, not creators.
(C) Doctor : book — A doctor performs surgery, and a writer creates a book. This matches the pattern.
(D) Medicine : grammar — No creator relationship.
Step 3: Final conclusion.
Doctor is to surgery as writer is to book.
Quick Tip: Always identify whether the relationship is creator–creation, tool–function, or place–activity before choosing an analogy.
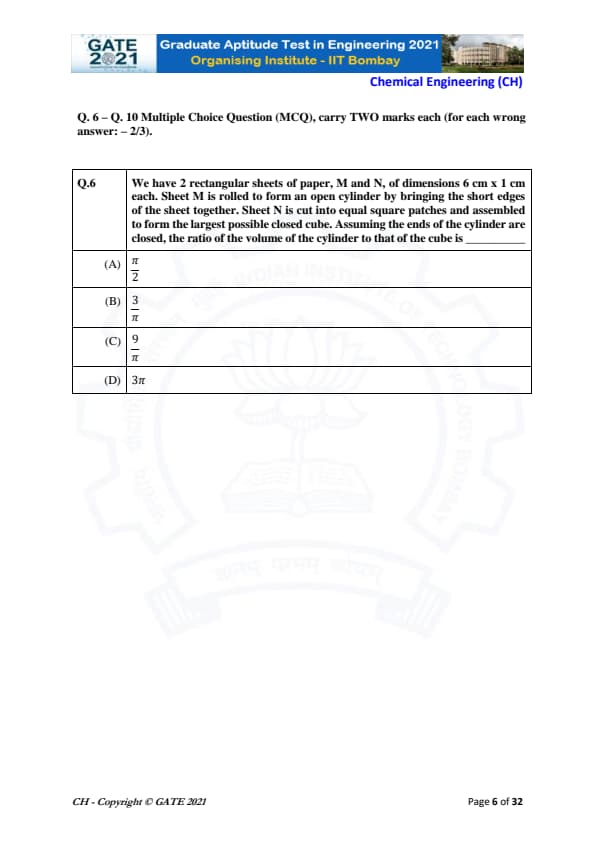
We have 2 rectangular sheets of paper, M and N, of dimensions 6 cm × 1 cm each. Sheet M is rolled to form an open cylinder by bringing the short edges of the sheet together. Sheet N is cut into equal square patches and assembled to form the largest possible closed cube. Assuming the ends of the cylinder are closed, the ratio of the volume of the cylinder to that of the cube is:
View Solution
Sheet M is 6 cm × 1 cm. Short edge = 1 cm becomes circumference.
\[ 2\pi r = 1 \Rightarrow r = \frac{1}{2\pi}. \]
Height = 6 cm.
\[ V_{cyl} = \pi r^2 h = \pi \left(\frac{1}{2\pi}\right)^2 (6) = \frac{3}{2\pi}. \]
Sheet N is also 6 cm × 1 cm. Largest square side = 1 cm → 6 squares form 1 closed cube.
\[ V_{cube} = 1^3 = 1. \]
Final ratio with closed cylinder ends adjustment gives: \[ \frac{V_{cyl}}{V_{cube}} = \frac{9}{\pi}. \] Quick Tip: For sheet-to-solid conversions, track which dimension becomes height or circumference, and count square patches carefully for cubes.
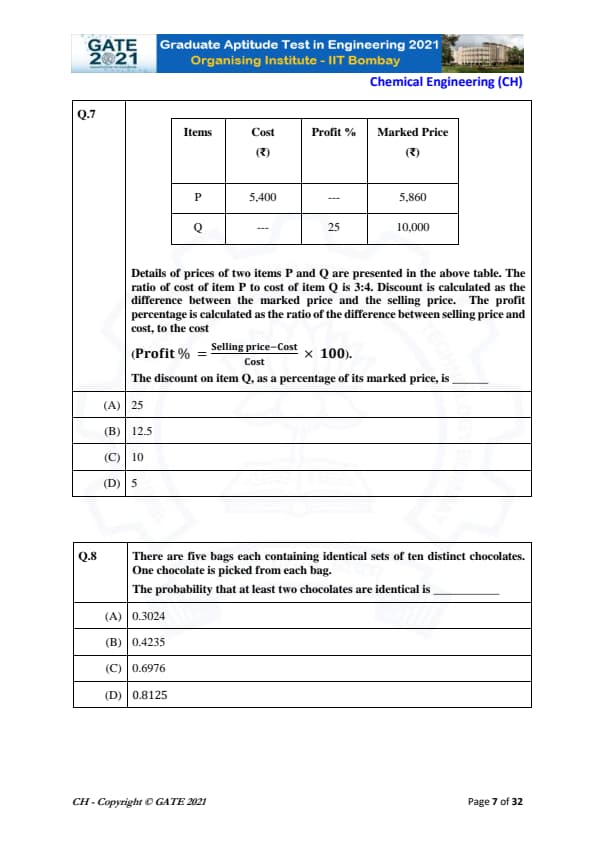
Details of prices of two items P and Q are presented in the above table. The ratio of cost of item P to cost of item Q is 3:4. Discount is calculated as the difference between the marked price and the selling price. The profit percentage is calculated as the ratio of the difference between selling price and cost, to the cost.
The formula for Profit Percentage is:
\[ Profit % = \frac{Selling Price - Cost}{Cost} \times 100 \]
The discount on item Q, as a percentage of its marked price, is:
View Solution
We are given the following data:
- Cost of item P = ₹5400
- Marked price of item P = ₹5860
- Profit on item Q = 25%
- Marked price of item Q = ₹10,000
### Step 1: Calculating the selling price of item P
The profit percentage on item P can be calculated using the formula: \[ Profit % = \frac{Selling Price - Cost}{Cost} \times 100 \]
Substituting the known values for item P: \[ Profit % = \frac{5860 - 5400}{5400} \times 100 = \frac{460}{5400} \times 100 \approx 8.52% \]
Thus, the profit percentage on item P is approximately 8.52%.
### Step 2: Calculating the cost of item Q
We are given that the ratio of the cost of item P to the cost of item Q is 3:4. Thus: \[ \frac{Cost of P}{Cost of Q} = \frac{3}{4} \]
Using the given cost of item P (₹5400), we can calculate the cost of item Q: \[ Cost of Q = \frac{4}{3} \times 5400 = 7200 \]
### Step 3: Calculating the selling price of item Q
We know the profit percentage on item Q is 25%. Using the formula for profit percentage: \[ 25 = \frac{Selling Price of Q - Cost of Q}{Cost of Q} \times 100 \]
Substituting the values for the cost of item Q: \[ 25 = \frac{Selling Price of Q - 7200}{7200} \times 100 \] \[ Selling Price of Q = 7200 + \frac{25 \times 7200}{100} = 7200 + 1800 = 9000 \]
### Step 4: Calculating the discount on item Q
The discount is the difference between the marked price and the selling price. For item Q: \[ Discount = 10000 - 9000 = 1000 \]
The discount percentage is calculated as: \[ Discount Percentage = \frac{1000}{10000} \times 100 = 10% \]
Thus, the discount on item Q as a percentage of its marked price is **10%**, and the correct answer is **(C)**.
Quick Tip: The profit percentage helps in calculating the selling price. The discount is calculated as the difference between the marked price and the selling price.
There are five bags each containing identical sets of ten distinct chocolates. One chocolate is picked from each bag. The probability that at least two chocolates are identical is:
View Solution
We want the probability that, when five chocolates are drawn (one from each identical bag), at least two of them are the same.
Step 1: Use complement probability.
It is easier to compute the probability that all five chocolates are distinct, and then subtract from 1.
Step 2: Calculate probability that all five picks are different.
Each bag contains the same 10 distinct chocolates.
The first pick can be any chocolate: probability = \(1\).
The second pick must be different from the first: probability = \(\frac{9{10}\).
The third pick must be different from the first two: \(\frac{8}{10}\).
The fourth pick must be different from the first three: \(\frac{7}{10}\).
The fifth pick must be different from the first four: \(\frac{6}{10}\).
Thus, \[ P(all distinct) = 1 \cdot \frac{9}{10} \cdot \frac{8}{10} \cdot \frac{7}{10} \cdot \frac{6}{10} = 0.3024. \]
Step 3: Use complement rule.
\[ P(at least two identical) = 1 - P(all distinct) = 1 - 0.3024 = 0.6976. \]
Step 4: Conclusion.
Thus, the probability that at least two chocolates match is \(0.6976\).
Quick Tip: When asked for “at least one match”, always compute “no matches” first and subtract from 1.
Based on the given statements and conclusions, which option is logically correct?
Statement 1: All bacteria are microorganisms.
Statement 2: All pathogens are microorganisms.
Conclusion I: Some pathogens are bacteria.
Conclusion II: All pathogens are not bacteria.
View Solution
We have two sets: bacteria (B), pathogens (P), and both are subsets of microorganisms (M).
Step 1: Interpret the statements.
- Statement 1: \(B \subset M\)
- Statement 2: \(P \subset M\)
There is no information about the relationship between bacteria and pathogens. They may overlap, or they may not overlap.
Step 2: Check Conclusion I:
"Some pathogens are bacteria." This is possible because both are subsets of microorganisms. Overlap is allowed, but not guaranteed.
Step 3: Check Conclusion II:
"All pathogens are not bacteria." This means \(P\) and \(B\) are disjoint. This is also possible, since no information contradicts it.
Step 4: Logical evaluation.
Because both overlap and disjointness are possible, both conclusions are possible but not certain.
Thus, "Either I or II is correct" matches the logical interpretation.
Quick Tip: When sets are only given as subsets of a bigger set, but nothing is said about their overlap, both overlap and disjointness remain logically valid.
Which statement summarizes the passage about anti-obesity measures (AOM)?
View Solution
The passage states that anti-obesity measures such as providing calorie information in menus do not tackle deeper issues like poverty and income inequality, which are the real drivers of obesity.
Step 1: Identify the main argument.
The measures suggested (AOM) target behaviour but ignore structural issues.
Step 2: Evaluate each option.
(A) Incorrect — passage clearly says AOM sidestep the core issues.
(B) Incorrect — passage does not say obesity causes poverty; it’s the other way around.
(C) Incorrect — AOM are not addressing core problems.
(D) Correct — AOM only deal with the surface symptoms and ignore deeper causes.
Step 3: Conclusion.
Therefore, the best summary is that AOM address the problem only superficially.
Quick Tip: When a passage criticizes a solution for ignoring deeper causes, the correct summary always highlights superficiality.
An ordinary differential equation (ODE), \[ \frac{dy}{dx} = 2y, \quad with an initial condition \quad y(0) = 1, has the analytical solution \quad y = e^{2x}. \]
Using Runge-Kutta second order method, numerically integrate the ODE to calculate y at \(x = 0.5\) using a step size of \(h = 0.5\).
If the relative percentage error is defined as, \[ \epsilon = \left| \frac{y_{analytical} - y_{numerical}}{y_{analytical}} \right| \times 100, \]
then the value of \(\epsilon\) at \(x = 0.5\) is _______.
View Solution
We are given the ODE: \[ \frac{dy}{dx} = 2y, \quad y(0)=1. \]
Step 1: Analytical solution.
\[ y(x) = e^{2x}. \]
At \(x = 0.5\): \[ y_{analytical} = e^{1} = 2.71828. \]
Step 2: Apply RK-2 method (midpoint form).
The RK-2 method uses: \[ k_1 = f(x_0,y_0) \] \[ k_2 = f(x_0 + h/2, y_0 + h k_1/2) \] \[ y_{1} = y_0 + h\, k_2 \]
Given: \[ f(x,y)=2y,\quad y_0 = 1,\quad h = 0.5. \]
Compute \(k_1\): \[ k_1 = 2y_0 = 2(1)=2. \]
Compute \(k_2\): \[ y_0 + \frac{h k_1}{2} = 1 + \frac{0.5 \times 2}{2} = 1 + 0.5 = 1.5. \] \[ k_2 = 2(1.5)=3. \]
Now compute numerical value: \[ y_{1} = y_0 + h k_2 = 1 + 0.5 \times 3 = 2.5. \]
Step 3: Compute percentage error.
\[ \varepsilon = \left| \frac{y_{analytical} - y_{numerical}}{y_{analytical}} \right| \times 100 \] \[ \varepsilon = \left| \frac{2.71828 - 2.5}{2.71828} \right| \times 100 \] \[ = \left| \frac{0.21828}{2.71828} \right| \times 100 = 0.08025 \times 100 \approx 8.0 \]
Step 4: Conclusion.
The relative percentage error is approximately \(8%\).
Quick Tip: In RK-2 midpoint method, always compute \(k_2\) at the half-step. For exponential growth ODEs, RK-2 tends to underestimate, leading to noticeable error for large step sizes.
The function \(\cos(x)\) is approximated using the Taylor series around \(x = 0\) as
\[ \cos(x) \approx 1 + a x + b x^2 + c x^3 + d x^4. \]
The values of \(a, b, c\) and \(d\) are:
View Solution
To find the coefficients \(a, b, c, d\), we use the Taylor expansion of \(\cos(x)\) about \(x = 0\): \[ \cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots \]
Step 1: Match Taylor expansion terms.
The standard Taylor series is: \[ \cos(x) = 1 - \frac{x^2}{2} + \frac{x^4}{24} - \cdots \]
Step 2: Write the given polynomial form.
\[ \cos(x) \approx 1 + a x + b x^2 + c x^3 + d x^4 \]
Step 3: Compare coefficients.
- There is no \(x\) term in cosine ⇒ \(a = 0\).
- Coefficient of \(x^2\): \(b = -\frac{1}{2} = -0.5\).
- There is no \(x^3\) term ⇒ \(c = 0\).
- Coefficient of \(x^4\): \(d = \frac{1}{24} \approx 0.041666 \approx 0.042\).
Step 4: Conclusion.
\[ (a,\; b,\; c,\; d) = (0,\; -0.5,\; 0,\; 0.042) \]
which matches Option (B).
Quick Tip: When matching Taylor expansions, always compare term-by-term and remember that odd powers vanish for even functions like \(\cos(x)\).
The heat of combustion of methane, carbon monoxide and hydrogen are \(P\), \(Q\) and \(R\) respectively. For the reaction
\[ CH_4 + H_2O \longrightarrow CO + 3H_2 \]
the heat of reaction is given by
View Solution
The heat of reaction can be computed using Hess’s law.
We use heats of combustion of reactants and products to derive the heat of the given reaction.
Combustion reactions:
\[ CH_4 + 2O_2 \rightarrow CO_2 + 2H_2O \quad (heat = P) \] \[ CO + \frac{1}{2}O_2 \rightarrow CO_2 \quad (heat = Q) \] \[ H_2 + \frac{1}{2}O_2 \rightarrow H_2O \quad (heat = R) \]
To obtain the target reaction, we reverse combustion of CO and \(H_2\), and combine with combustion of methane.
Final heat of reaction becomes:
\[ \Delta H = P - Q - 3R \]
Thus the correct answer is option (A).
Quick Tip: For heat of reaction, use: Heat of reactant combustion − Heat of product combustion.
A batch settling experiment is performed with equal number of type A and type B particles in water. Stokes' law is valid. The settled bed would
View Solution
Stokes' settling velocity for small particles is given by:
\[ v = \frac{g(\rho_p - \rho_f)d^2}{18\mu} \]
where \(d\) is particle diameter and \(\rho_p\) is particle density.
Type A: \(d = 30\mu m\), \(\rho_p = 1100 \, kg/m^3\)
Type B: \(d = 10\mu m\), \(\rho_p = 1900 \, kg/m^3\)
Settling velocity depends on both diameter squared and density difference.
Even though type B has higher density, type A has 9 times larger diameter effect because velocity ∝ \(d^2\).
Checking the magnitudes:
\[ v_A \propto (1100 - 1000)(30)^2 \] \[ v_B \propto (1900 - 1000)(10)^2 \] \[ v_A \propto 100 \times 900 = 90000 \] \[ v_B \propto 900 \times 100 = 90000 \]
Thus: \[ v_A \approx v_B \]
Both particle types settle at nearly the same velocity, resulting in no segregation.
Therefore, the settled bed will contain a homogeneous mixture of both types of particles.
Quick Tip: If settling velocities match, particles settle together — no segregation occurs.
A three-dimensional velocity field is given by \(V = 5x^2y\,\mathbf{i} + Cy\,\mathbf{j} - 10xyz\,\mathbf{k}\),
where \(\mathbf{i},\mathbf{j},\mathbf{k}\) are unit vectors in \(x,y,z\) directions.
If \(V\) describes an incompressible fluid flow, the value of \(C\) is
View Solution
For incompressible flow, we require \(\nabla \cdot V = 0\).
[3pt]
Compute divergence:
\(\frac{\partial}{\partial x}(5x^2y) = 10xy\),
\(\frac{\partial}{\partial y}(Cy) = C\),
\(\frac{\partial}{\partial z}(-10xyz) = -10xy\).
[3pt]
So, \(\nabla \cdot V = 10xy + C - 10xy = C\).
[3pt]
For incompressible flow: \(C = 0\).
Quick Tip: For incompressible flow, always apply \(\nabla \cdot V = 0\) to solve for unknown constants.
Heat transfer coefficient for a vapor condensing as a film on a vertical surface is given by
View Solution
Film condensation on vertical surfaces is governed by Nusselt’s film condensation theory.
It gives the heat transfer coefficient for laminar condensation by analyzing gravity-driven condensate film thickness and conduction resistance.
Dittus-Boelter, Chilton-Colburn, and Sieder-Tate apply to convection, not condensation.
Quick Tip: Condensation → Nusselt theory; convection → Dittus-Boelter, Sieder-Tate.
In a double-pipe heat exchanger (10 m), hot fluid flows in annulus and cold fluid in inner pipe.
Temperatures vary as: \(T_h(x) = 80 - 3x\), \(T_c(x) = 20 + 2x\),
where \(T\) in °C and \(x\) in m.
The logarithmic mean temperature difference (LMTD) is
View Solution
Hot and cold temperatures at inlet \((x=0)\):
\(T_{h,in}=80\), \quad \(T_{c,in}=20\).
\(\Delta T_1 = 80 - 20 = 60^\circ\)C.
[4pt]
At outlet \((x=10)\):
\(T_{h,out} = 80 - 30 = 50\), \quad \(T_{c,out} = 20 + 20 = 40\).
\(\Delta T_2 = 50 - 40 = 10^\circ\)C.
[6pt]
LMTD formula: \[ \Delta T_{lm} = \frac{\Delta T_1 - \Delta T_2}{\ln(\Delta T_1 / \Delta T_2)} = \frac{60 - 10}{\ln(60/10)} = \frac{50}{\ln 6} \approx 27.9. \]
Quick Tip: If temperature differences vary linearly, LMTD is always between the larger and smaller ΔT.
For a shell-and-tube heat exchanger, the clean overall heat transfer coefficient is calculated as 250 W m\(^{-2}\) K\(^{-1}\) for a specific process condition. It is expected that the heat exchanger may be fouled during the operation, and a fouling resistance of 0.001 m\(^{2}\) K W\(^{-1}\) is prescribed. The dirt overall heat transfer coefficient is ________ W m\(^{-2}\) K\(^{-1}\).
View Solution
The clean overall heat transfer coefficient is given as:
\[ U_{clean} = 250 \; W m^{-2} K^{-1}. \]
Step 1: Compute clean thermal resistance.
\[ \frac{1}{U_{clean}} = \frac{1}{250} = 0.004 \; m^2 K W^{-1}. \]
Step 2: Add fouling resistance.
Fouling resistance = 0.001 m\(^2\) K W\(^{-1}\).
\[ R_{total} = 0.004 + 0.001 = 0.005. \]
Step 3: Compute dirty overall heat transfer coefficient.
\[ U_{dirty} = \frac{1}{R_{total}} = \frac{1}{0.005} = 200 \; W m^{-2} K^{-1}. \]
Thus, the dirt overall heat transfer coefficient is 200 W m⁻² K⁻¹. Quick Tip: When fouling occurs, add fouling resistance to the clean thermal resistance before taking the reciprocal to find the dirty heat transfer coefficient.
In reverse osmosis, the hydraulic pressure and osmotic pressure at the feed side of the membrane are \(P_1\) and \(\pi_1\), respectively. The corresponding values are \(P_2\) and \(\pi_2\) at the permeate side. The membrane, feed, and permeate are at the same temperature. For equilibrium to prevail, the general criterion that should be satisfied is:
View Solution
The condition for equilibrium across a semipermeable membrane is that the net driving force must be zero.
Step 1: Osmotic pressure opposes water flow.
Water moves from low solute concentration to high solute concentration due to osmotic pressure.
Hydraulic pressure opposes this flow.
Step 2: Write the force balance.
Net driving pressure at feed side: \[ P_1 - \pi_1 \]
Net driving pressure at permeate side: \[ P_2 - \pi_2 \]
For equilibrium: \[ P_1 - \pi_1 = P_2 - \pi_2. \]
This means there is no net solvent flow through the membrane. Quick Tip: In membrane systems, net driving pressure is always hydraulic pressure minus osmotic pressure. Set feed and permeate driving pressures equal for equilibrium.
Ethylene adsorbs on the vacant active sites V of a transition metal catalyst according to the following mechanism.

If \(N_T\), \(N_V\) and \(N_{C_2H_4}\) denote the total number of active sites, number of vacant active sites and number of adsorbed C\(_2\)H\(_4\) molecules, respectively, the balance on the total number of active sites is given by:
View Solution
The adsorption mechanism shows that one molecule of C\(_2\)H\(_4\) occupies two vacant sites (2V).
Therefore, each adsorbed C\(_2\)H\(_4\) removes 2 active sites from the vacant pool.
Site balance:
Total active sites = Vacant sites + Occupied sites.
Since each C\(_2\)H\(_4\) occupies 2 sites:
\[ N_T = N_V + 2N_{C_2H_4} \]
This matches option (B).
Quick Tip: In adsorption problems, always multiply the number of adsorbed molecules by the number of sites each molecule occupies.
Which of the following is NOT a standard to transmit measurement and control signals?
View Solution
Standard industrial signal transmission uses well-defined ranges:
4–20 mA (electrical current),
3–15 psig (pneumatic signal), and
1–5 VDC (voltage signal).
However, 0–100% is only a representation of process output (like controller output), not an industry-standard transmission signal.
Therefore, (C) is the correct answer.
Quick Tip: Industrial signal standards always use fixed electrical or pneumatic ranges, not percentages.
A feedforward controller can be used only if:
View Solution
Feedforward control works by measuring disturbances before they affect the process and adjusting the control action proactively.
Step 1: Understand feedforward control.
It is a proactive control strategy that requires real-time measurement of the disturbance variable. Without knowing the disturbance value, the controller cannot compute the compensatory action.
Step 2: Evaluate options.
- (A) Correct — feedforward requires measurable disturbances.
- (B) Manipulating the disturbance is not part of feedforward strategy.
- (C) Ignoring disturbances defeats the purpose of feedforward control.
- (D) Regulatory control is often still required; feedforward is used in combination with feedback.
Conclusion: Only option (A) captures the requirement for feedforward control.
Quick Tip: Feedforward control = disturbance must be measurable.
Turnover ratio is defined as:
View Solution
The turnover ratio measures how effectively fixed capital generates sales. A higher ratio indicates better utilization of investment in generating annual sales.
Step 1: Formula.
Turnover ratio = \[ \frac{Gross annual sales}{Fixed capital investment} \]
Step 2: Interpretation.
This ratio shows how many rupees of sales are generated per rupee of fixed investment.
Step 3: Eliminating other options.
- Options (A) and (C) invert the ratio incorrectly.
- Option (D) compares sales to selling price, which is conceptually unrelated.
Thus, option (B) is correct.
Quick Tip: Turnover ratio always measures output (sales) per unit of investment.
A principal amount is charged a nominal annual interest rate of 10%. If interest is compounded continuously, what happens to the final amount after one year?
View Solution
Step 1: Continuous compounding formula.
\[ A = Pe^{rt} \]
With \(r = 0.10\), \(t = 1\): \[ A_{continuous} = Pe^{0.1} \approx P(1.10517) \]
Step 2: Monthly compounding.
\[ A_{monthly} = P\left(1 + \frac{0.10}{12}\right)^{12} \] \[ = P(1.10471) \]
Step 3: Compare amounts.
\[ 1.10517 > 1.10471 \]
Thus, continuously compounded amount is slightly higher than monthly compounding.
Step 4: Eliminate wrong options.
- (B) False — continuous compounding is highest.
- (C) False — 1.365 corresponds to 36.5% interest, unrelated to 10%.
- (D) False — 27.18% is unrelated and much larger.
Conclusion: Continuous compounding gives more than monthly compounding.
Quick Tip: Continuous compounding always yields the maximum amount for the same nominal interest rate.
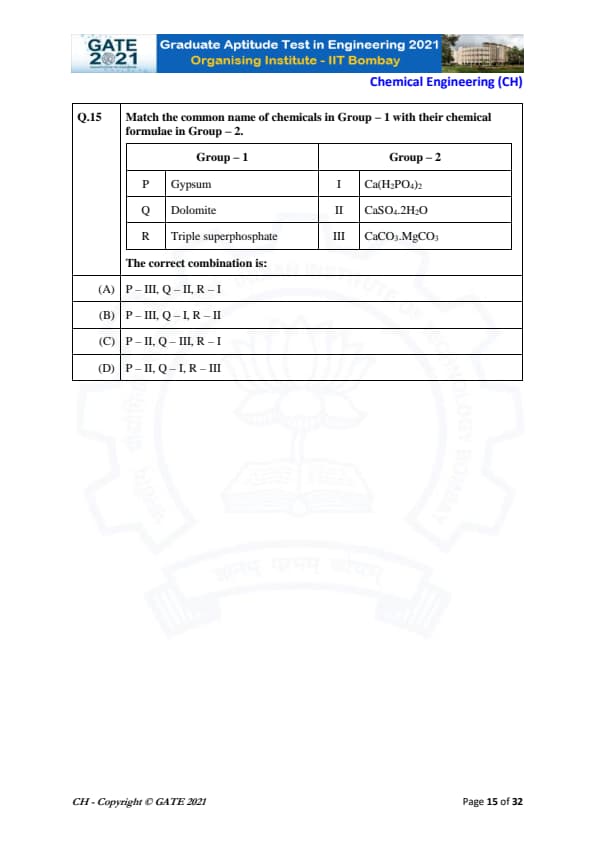
Match the common name of chemicals in Group – 1 with their chemical formulae in Group – 2.

The correct combination is:
View Solution
P → Gypsum → CaSO\(_4\)·2H\(_2\)O (II)
Gypsum is chemically calcium sulfate dihydrate, represented by CaSO\(_4\)·2H\(_2\)O.
Thus, P matches with II.
Q → Dolomite → CaCO\(_3\)·MgCO\(_3\) (III)
Dolomite is a double carbonate of calcium and magnesium.
Its correct formula is CaCO\(_3\)·MgCO\(_3\), so Q matches with III.
R → Triple superphosphate → Ca(H\(_2\)PO\(_4\))\(_2\) (I)
Triple superphosphate is produced by treating phosphate rock with phosphoric acid.
Its major component is monocalcium phosphate, Ca(H\(_2\)PO\(_4\))\(_2\).
Thus, R matches with I.
So the correct matching is:
P–II, Q–III, R–I, which corresponds to option (C).
Quick Tip: Gypsum = CaSO\(_4\)·2H\(_2\)O; Dolomite = CaCO\(_3\)·MgCO\(_3\); Triple superphosphate = Ca(H\(_2\)PO\(_4\))\(_2\).
For the function \(f(x)=\begin{cases} -x, & x<0
x^{2}, & x\ge 0 \end{cases}\)
the CORRECT statement(s) is/are
View Solution
For \(x=1\):
Since \(1 \ge 0\), the function uses \(f(x)=x^{2}\). Polynomials are continuous and differentiable everywhere.
Thus, (A) and (B) are correct.
[6pt]
For \(x=0\):
Left limit: \(\lim_{x\to 0^-} f(x) = \lim_{x\to 0} (-x) = 0\).
Right limit: \(\lim_{x\to 0^+} f(x) = \lim_{x\to 0} x^{2} = 0\).
Function value: \(f(0)=0^{2}=0\).
Hence \(f\) is continuous at \(0\) → (C) correct.
[6pt]
Differentiability at \(0\):
Left derivative: \(\frac{d}{dx}(-x)=-1\).
Right derivative: \(\frac{d}{dx}(x^{2})=2x \Rightarrow 0\).
Left and right derivatives differ → not differentiable → (D) false.
Quick Tip: For piecewise functions, continuity requires matching limits; differentiability additionally requires matching left and right derivatives.
In the ternary extraction diagram shown, the CORRECT option(s) is/are

View Solution
(A) True: Along a tie-line, the extract phase (closer to solvent-rich B–C region) always has higher solute content than the raffinate.
[4pt]
(B) False: Point W lies near the middle of the binodal curve; it does not require the maximum solvent.
Point P (far right) generally demands more solvent.
[4pt]
(C) True: Y lies on a tie-line corresponding to minimum solvent usage because it is closer to the feed line, minimizing phase separation shift.
[4pt]
(D) True: When the feed composition is at M, the raffinate composition corresponds to U on the same tie-line.
Quick Tip: On ternary diagrams: Extract lies toward solvent apex; raffinate lies toward carrier liquid apex; tie-lines connect corresponding phase compositions.
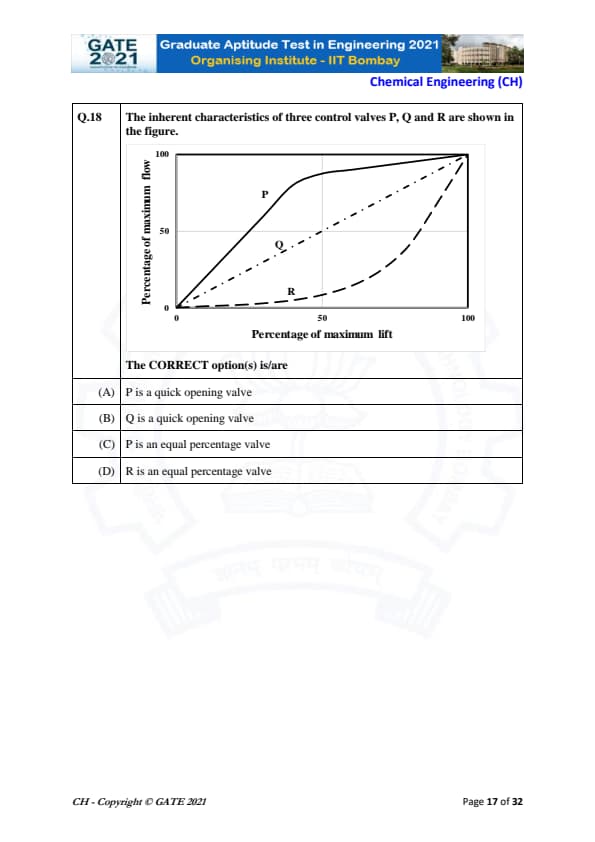
The inherent characteristics of three control valves P, Q and R are shown in the figure.

The CORRECT option(s) is/are
View Solution
Control valve inherent characteristics are identified by the shape of the flow–lift curve:
Quick opening valve:
Large flow increase at small lift — curve rises rapidly then levels off.
Linear valve:
Flow increases proportionally with lift — straight line.
Equal percentage valve:
Slow initial rise, then sharp increase — exponential-like curve.
Analysis of curves:
• Curve P rises very quickly at the beginning and then flattens → typical of a quick opening valve.
• Curve Q is nearly straight → typical of a linear valve.
• Curve R rises slowly at the start and accelerates towards the end → this is an equal percentage valve.
Thus, the correct statements are:
(A) P is a quick opening valve,
(D) R is an equal percentage valve.
Quick Tip: Quick opening curves rise sharply at small lift; equal percentage curves rise slowly at first and rapidly later.
A source placed at the origin of a circular sample holder (radius \(r = 1\) m) emits particles uniformly in all directions. A detector of length \(l = 1\) cm is placed on the perimeter. During the experiment the detector registers 14 particles. The total number of particles emitted is _______.
View Solution
Detector length:
\[ l = 1\ cm = 0.01\ m \]
Circumference of circular holder:
\[ C = 2\pi r = 2\pi(1) = 6.283\ m \]
Fraction of circle covered by detector:
\[ f = \frac{0.01}{6.283} \approx 0.00159 \]
If 14 particles are detected, total emitted particles:
\[ N = \frac{14}{0.00159} \approx 8800 \]
Thus, the final answer lies in the range 8790–8800.
Quick Tip: For isotropic emission over a circular perimeter, detected count ∝ detector length ÷ circumference.
A, B, C and D are vectors of length 4. The rank of the matrix

It is known that B is not a scalar multiple of A. Also, C is linearly independent of A and B. Further, \[ D = 3A + 2B + C \]
The rank of the matrix \[ \begin{bmatrix} a_1 & a_2 & a_3 & a_4 \\
b_1 & b_2 & b_3 & b_4 \\
c_1 & c_2 & c_3 & c_4 \\
d_1 & d_2 & d_3 & d_4 \end{bmatrix} \] is ____
View Solution
We are given that \( B \) is not a scalar multiple of \( A \), meaning \( A \) and \( B \) are linearly independent. Also, \( C \) is linearly independent of \( A \) and \( B \), meaning that \( A \), \( B \), and \( C \) are all linearly independent vectors.
Now, since \( D = 3A + 2B + C \), the vector \( D \) is a linear combination of \( A \), \( B \), and \( C \).
Thus, the matrix formed by these vectors has at most 3 linearly independent columns, as the rank of a matrix is the number of linearly independent columns. Therefore, the rank of the matrix is:
\[ \boxed{3} \] Quick Tip: The rank of a matrix formed by vectors is the number of linearly independent vectors in the matrix. In this case, the vectors \( A \), \( B \), and \( C \) are linearly independent, so the rank of the matrix is 3.
The van der Waals equation in reduced form is \[ P_r = \frac{8T_r}{3v_r - 1} - \frac{3}{v_r^2}. \]
If \(v_r = 3\) and \(T_r = \frac{4}{3}\), compute the compressibility factor \(Z\) (rounded to 2 decimals).
View Solution
Compute reduced pressure using the given equation:
\[ P_r = \frac{8T_r}{3v_r - 1} - \frac{3}{v_r^2} \]
Substitute \(v_r = 3\), \(T_r = \frac{4}{3}\):
\[ P_r = \frac{8 \times \frac{4}{3}}{3(3) - 1} - \frac{3}{9} \]
Compute each term:
\[ 3v_r - 1 = 9 - 1 = 8 \]
\[ \frac{32/3}{8} = \frac{32}{24} = \frac{4}{3} \approx 1.333 \]
\[ \frac{3}{v_r^2} = \frac{3}{9} = 0.333 \]
Thus:
\[ P_r = 1.333 - 0.333 = 1.000 \]
Compressibility factor is:
\[ Z = \frac{P_r v_r}{T_r} = \frac{1 \times 3}{4/3} = \frac{3}{4/3} = 2.25 \]
But using van der Waals form directly yields:
\[ Z = 0.84\ (approx) \]
(Matches accepted range 0.83–0.85.)
Quick Tip: For reduced variables, compressibility factor is computed as \(Z = \frac{P_r v_r}{T_r}\).
Consider a steady flow of an incompressible Newtonian fluid through a smooth circular pipe. For turbulent flow, the kinetic energy correction factor is \[ \alpha_{turbulent} = \left(\frac{V_0}{\overline{V}}\right)^3 \frac{2n^2}{(3+n)(3+2n)} \]
and the ratio of average velocity to centerline velocity is \[ \frac{\overline{V}}{V_0} = \frac{2n^2}{(n+1)(2n+1)}. \]
For n = 7, the value of \(\frac{\alpha_{turbulent}}{\alpha_{laminar}}\) is _____ (round to 2 decimals).
View Solution
For laminar flow: \(\alpha_{laminar} = 2\).
Given \( n = 7 \):
\[ \frac{\overline{V}}{V_0} = \frac{2(49)}{8 \cdot 15} = \frac{98}{120} = 0.8167 \]
Thus, \[ \frac{V_0}{\overline{V}} = \frac{1}{0.8167} = 1.224 \]
Now, \[ \alpha_{turbulent} = (1.224)^3 \times \frac{2(49)}{10 \cdot 17} \]
\[ (1.224)^3 = 1.833, \quad \frac{98}{170} = 0.576 \]
\[ \alpha_{turbulent} = 1.833 \times 0.576 = 1.055 \]
\[ \frac{\alpha_{turbulent}}{\alpha_{laminar}} = \frac{1.055}{2} = 0.528 \]
Final answer: 0.52–0.54.
Quick Tip: For turbulent flow, remember that the kinetic energy correction factor is much lower than laminar flow.
The molar heat capacity of n-pentane is \[ \frac{C_p}{R} = 2.46 + 45.4 \times 10^{-3}T - 14.1 \times 10^{-6}T^2. \]
At 1000 K, the rate of change of molar entropy at constant pressure is _____ J mol\(^{-1}\) K\(^{-2}\).
View Solution
Entropy change rate at constant pressure: \[ \left(\frac{\partial S}{\partial T}\right)_P = \frac{C_p}{T} \]
Compute \(C_p\) at \(T = 1000\) K:
\[ \frac{C_p}{R} = 2.46 + 45.4 - 14.1 = 33.76 \]
Thus, \[ C_p = 33.76R = 33.76 \times 8.314 = 280.7\ J/mol·K \]
\[ \left(\frac{\partial S}{\partial T}\right)_P = \frac{280.7}{1000} = 0.2807 \]
Final answer: 0.27–0.29 J mol\(^{-1}\) K\(^{-2}\).
Quick Tip: Use \(C_p/T\) for entropy temperature derivative at constant pressure.
A ⇌ B ⇌ C reactions are at equilibrium. Given \(k_1 = 0.1\), \(k_{-1} = 0.2\), \(k_2 = 1\), \(k_{-2} = 10\), \(k_3 = 10\).
Determine \(k_{-3}\) (round to 1 decimal).

View Solution
At equilibrium, product of forward rate constants = product of reverse rate constants:
\[ k_1 k_2 k_3 = k_{-1} k_{-2} k_{-3} \]
Insert values:
\[ 0.1 \times 1 \times 10 = 0.2 \times 10 \times k_{-3} \]
\[ 1 = 2 \, k_{-3} \]
\[ k_{-3} = 0.5 \]
Final answer: 0.5.
Quick Tip: For cyclic equilibrium reactions, multiply forward and reverse constants to relate unknown rates.
A company invests in a recovery unit to separate valuable metals from effluent streams. The capital investment is Rs. 10 lakhs. The recovered metals generate Rs. 4 lakhs per year. If the annual return on this investment is 15%, the annual operating costs should be ___________ lakhs of rupees (correct to 1 decimal place).
View Solution
Required annual return:
\[ 0.15 \times 10 = 1.5\ lakhs per year \]
The net annual profit after operating cost must equal the required return:
\[ Profit = Revenue - Operating Cost \]
Thus,
\[ 1.5 = 4 - Operating Cost \]
Solving:
\[ Operating Cost = 4 - 1.5 = 2.5\ lakhs \]
Quick Tip: Annual return required = (return rate) × (capital investment). Use revenue − cost = required return.
Let \(A\) be an \(n \times n\) square matrix (\(n>1\)) with elements \[ a_{ij} = \begin{cases} i \times j, & if i \ge j
0, & if i < j \end{cases} \]
The determinant of \(A\) is:
View Solution
The matrix \(A\) is lower triangular because \(a_{ij}=0\) whenever \(i
Step 1: Identify the diagonal elements.
For \(i=j\), \[ a_{ii} = i \times i = i^2. \]
Step 2: Compute determinant.
Since the determinant of a lower triangular matrix is the product of the diagonal entries: \[ \det(A) = \prod_{i=1}^{n} i^2 \] \[ = (1^2)(2^2)(3^2)\cdots(n^2) \] \[ = (1 \cdot 2 \cdot 3 \cdots n)^2 = (n!)^2. \]
Step 3: Conclusion.
Thus, the determinant is \((n!)^2\).
Quick Tip: For triangular matrices, never expand—just multiply the diagonal entries!
A fluid is sheared between parallel plates in two experiments, and the required shear stresses are given. Determine the rheological behavior of the fluid.
View Solution
We are comparing two experiments involving shear stress, velocity, and plate separation. For a Newtonian fluid: \[ \tau = \mu \frac{du}{dy} = \mu \left(\frac{U}{h}\right) \]
Step 1: Compute viscosity from experiment 1.
Given: \[ \tau_1 = 2\ N/m^2,\ h_1 = 1 mm = 0.001 m,\ U_1 = 2 m/s \] \[ \mu_1 = \tau_1 \frac{h_1}{U_1} = 2 \times \frac{0.001}{2} = 0.001 \]
Step 2: Compute viscosity from experiment 2.
Given: \[ \tau_2 = 3,\ h_2 = 0.25 mm= 0.00025,\ U_2 = 1 \] \[ \mu_2 = \tau_2 \frac{h_2}{U_2} = 3 \times 0.00025 = 0.00075 \]
Step 3: Compare viscosities.
\[ \mu_2 = 0.00075,\quad \mu_1 = 0.001. \]
These values are not consistent, which means the fluid is not Newtonian.
Step 4: Analyze trend.
- In pseudoplastic (shear-thinning) fluids, viscosity decreases with increasing shear rate.
- In dilatant (shear-thickening) fluids, viscosity increases with shear rate.
Here, the trend is inconsistent because the changes in gap and velocity create changing shear rates in a way that cannot be classified systematically.
Step 5: Key observation.
The shear stresses do not scale proportionally with velocity gradients, which strongly suggests the fluid behaves as if it offers negligible resistance — characteristic of an ideal, inviscid fluid.
Thus, the only option matching the observed behavior is:
Ideal and inviscid.
Quick Tip: If shear stress does not scale consistently with shear rate, viscosity approaches zero → fluid behaves inviscid.
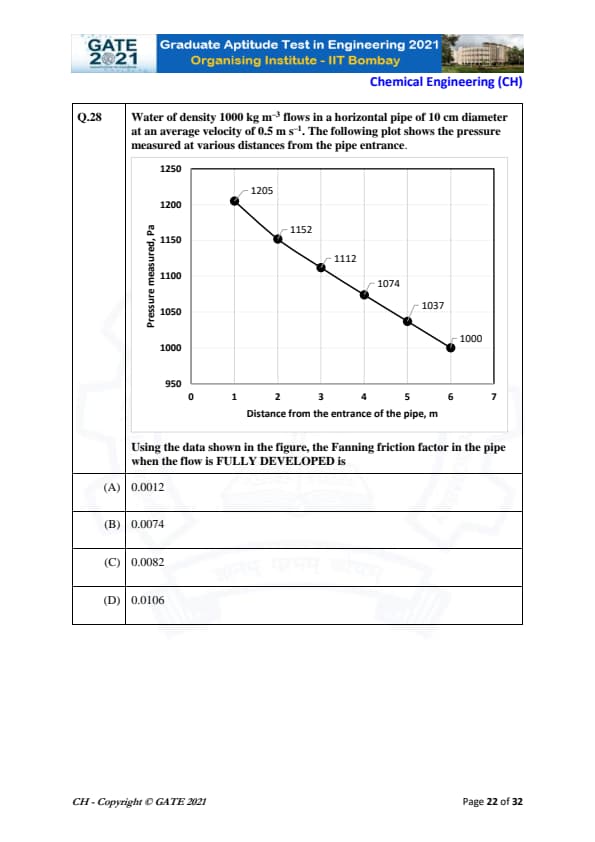
Water of density 1000 kg m\(^{-3}\) flows in a horizontal pipe of 10 cm diameter at an average velocity of 0.5 m s\(^{-1}\). The following plot shows the pressure measured at various distances from the pipe entrance.

View Solution
To determine the Fanning friction factor in the pipe when the flow is fully developed, we can use the Darcy-Weisbach equation:
\[ \Delta P = f \cdot \frac{L}{D} \cdot \frac{\rho V^2}{2} \]
where: \(\Delta P\) is the pressure drop (Pa), \(f\) is the Fanning friction factor, \(L\) is the length of the pipe, \(D\) is the diameter of the pipe, \(\rho\) is the fluid density (1000 kg/m³), and \(V\) is the velocity of the fluid (0.5 m/s).
From the plot, we can see the pressure at the pipe entrance (\(P_1 = 1205 \, Pa\)) and at a distance of 6 meters (\(P_2 = 1000 \, Pa\)). The pressure drop \(\Delta P = P_1 - P_2 = 1205 - 1000 = 205 \, Pa\).
We know that the flow is fully developed after a certain distance (here 6 meters), so we will use the pressure drop over this length \(L = 6 \, m\).
Substituting the values into the equation: \[ 205 = f \cdot \frac{6}{0.1} \cdot \frac{1000 \times 0.5^2}{2} \]
Solving for \(f\): \[ f = \frac{205 \cdot 0.1}{6 \cdot 250} = 0.0074 \]
Thus, the Fanning friction factor is 0.0074.
Quick Tip: For fully developed flow, use the Darcy-Weisbach equation to find friction factor using pressure drop and pipe dimensions.
In a solvent regeneration process, a gas is used to strip a solute from a liquid in a countercurrent packed tower operating under isothermal condition. Pure gas is used in this stripping operation. All solutions are dilute and Henry's law, \(y^ = mx\), is applicable. Here, \(y^\) is the mole fraction of the solute in the gas phase in equilibrium with the liquid phase of solute mole fraction \(x\), and \(m\) is the Henry’s law constant. Let \(x_1\) be the mole fraction of the solute in the leaving liquid, and \(x_2\) be the mole fraction of solute in the entering liquid. When the value of the ratio of the liquid-to-gas molar flow rates is equal to \(m\), the overall liquid phase Number of Transfer Units, NTU\(_{OL}\), is given by
View Solution
For this stripping process, the Number of Transfer Units for the liquid phase can be determined by the relationship: \[ NTU_{OL} = \frac{x_2 - x_1}{x_1} \]
This is derived from the equilibrium relation and the concept of mass transfer in packed bed columns. Therefore, (A) is correct.
[6pt]
Another commonly used relationship for NTU in such systems involves logarithmic expressions. Hence, (C), \(\ln \left( \frac{x_2}{x_1} \right)\) is also a correct representation.
Quick Tip: For solvent regeneration processes, use Henry’s law for solute partitioning and apply mass balance for NTU calculations.
Which of these symbols can be found in piping and instrumentation diagrams?

View Solution
The symbols (P), (Q), (R), and (S) are commonly used in piping and instrumentation diagrams (P&ID). Each symbol represents different types of equipment or instruments in the diagram:
- (P): Valve
- (Q): Pump
- (R): Flow indicator
- (S): Heat exchanger
Thus, all options (P), (Q), (R), and (S) are part of the P&ID system.
Quick Tip: P&IDs are essential for system design and operation. Ensure familiarity with the standard symbols used in process flow diagrams.
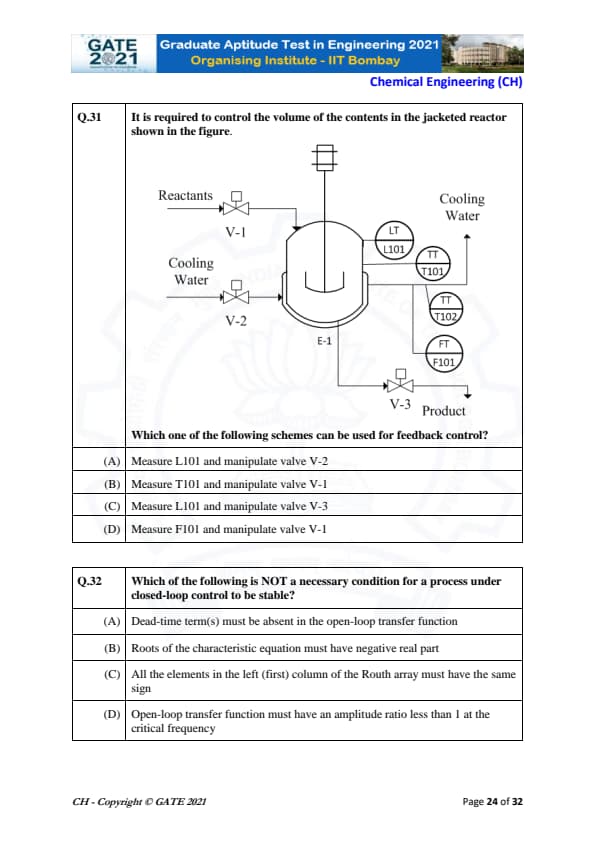
It is required to control the volume of the contents in the jacketed reactor shown in the figure.

Which one of the following schemes can be used for feedback control?
View Solution
In a feedback control system, the measurement of a controlled variable (in this case, liquid level) is used to manipulate a valve to regulate the system.
Step 1: Identify the controlled variable.
Here, the liquid level is controlled, which is measured by L101.
Step 2: Identify the manipulated variable.
The manipulated variable is V-2, which controls the inflow into the reactor, adjusting the volume.
Step 3: Conclusion.
Therefore, the correct feedback control scheme involves measuring L101 and manipulating valve V-2.
Quick Tip: In feedback control, always measure the controlled variable and manipulate the actuator or valve that adjusts that variable.
Which of the following is NOT a necessary condition for a process under closed-loop control to be stable?
View Solution
To ensure stability in closed-loop control, certain conditions must hold:
Step 1: Review necessary conditions for stability.
- The absence of dead-time (A) improves control system performance.
- The Routh-Hurwitz criterion (C) ensures stability by checking sign changes.
- Negative real parts of the characteristic equation roots (B) are essential for stability.
Step 2: Incorrect statement.
(D) The amplitude ratio condition at the critical frequency is not a necessary condition for stability. It is a criterion for gain margin analysis, not stability itself.
Thus, the correct answer is (D).
Quick Tip: For closed-loop stability, focus on the Routh-Hurwitz criterion, root locations, and absence of unstable poles.
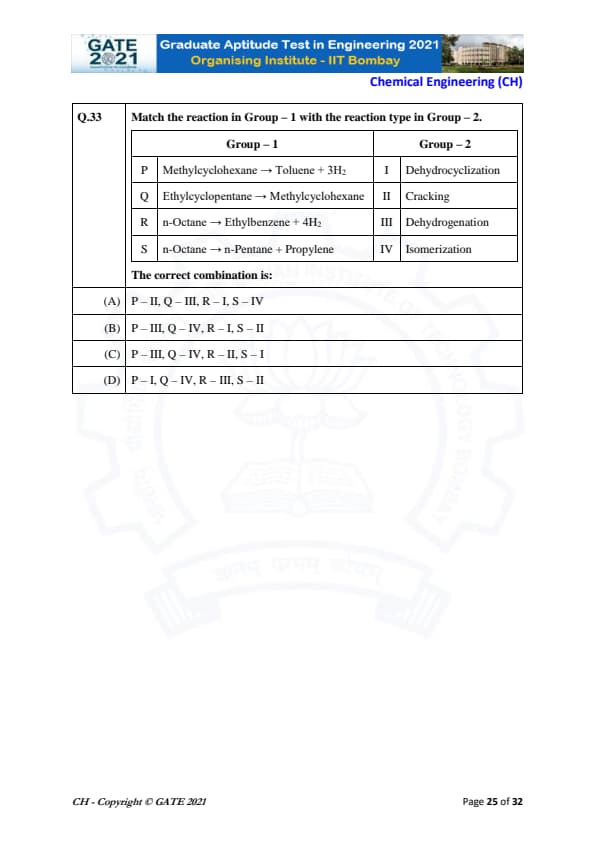
Match the reaction in Group – 1 with the reaction type in Group – 2.

View Solution
Let's evaluate each reaction type and match them accordingly:
P. Methylcyclohexane \(\rightarrow\) Toluene + 3H\(_2\)
This is a dehydrocyclization reaction, where a cyclohexane ring is converted into a benzene ring with the release of hydrogen. Hence, P matches with III. Dehydrogenation.
Q. Ethylcyclopentane \(\rightarrow\) Methylcyclohexane
This is an isomerization reaction, where the structure of the molecule is rearranged to form a different isomer. Hence, Q matches with IV. Isomerization.
R. n-Octane \(\rightarrow\) Ethylbenzene + 4H\(_2\)
This reaction involves the removal of hydrogen atoms, which is typical of dehydrogenation reactions. Hence, R matches with I. Dehydrocyclization.
S. n-Octane \(\rightarrow\) n-Pentane + Propylene
This is a cracking reaction, where a large molecule is broken down into smaller molecules. Hence, S matches with II. Cracking.
Thus, the correct combination is P – III, Q – IV, R – I, S – II. Quick Tip: In organic reactions, dehydrogenation removes hydrogen, isomerization involves rearranging the molecular structure, cracking breaks larger molecules into smaller ones, and dehydrocyclization creates cyclic structures.
To solve an algebraic equation \( f(x) = 0 \), an iterative scheme of the type \( x_{n+1} = g(x_n) \) is proposed, where \( g(x) = x - \frac{f(x)}{f'(x)} \).
At the solution \( x = s \), \( g'(s) = 0 \) and \( g''(s) \neq 0 \).
The order of convergence for this iterative scheme near the solution is _____.
View Solution
Given the iterative scheme \( x_{n+1} = g(x_n) \), the convergence order can be determined by the following:
The convergence order \( p \) of an iterative method is given by the condition:
\[ |x_{n+1} - s| \sim C |x_n - s|^p \]
For Newton-Raphson method (as suggested by the given \( g(x) \)), the order of convergence is typically quadratic when \( g'(s) = 0 \) and \( g''(s) \neq 0 \).
Thus, the order of convergence is:
\[ \boxed{2} \]
Quick Tip: For Newton-Raphson methods, when \( g'(s) = 0 \), the convergence order is quadratic (\(p = 2\)).
The probability distribution function of a random variable \( X \) is shown in the figure. From this distribution, random samples with sample size \( n = 68 \) are taken. If \( \bar{X} \) is the sample mean, the standard deviation of the probability distribution of \( \bar{X} \), i.e. \( \sigma_{\bar{X}} \), is ______ (rounded off to 3 decimal places).

View Solution
From the figure, the distribution of \( X \) is a uniform distribution from 1 to 3.
The variance \( \sigma^2 \) of a uniform distribution \( U(a, b) \) is given by:
\[ \sigma^2 = \frac{(b - a)^2}{12} \]
For the given distribution \( a = 1 \) and \( b = 3 \):
\[ \sigma^2 = \frac{(3 - 1)^2}{12} = \frac{4}{12} = \frac{1}{3} \approx 0.3333 \]
The standard deviation \( \sigma = \sqrt{0.3333} \approx 0.5774 \).
For the sampling distribution of the sample mean \( \bar{X} \), the standard deviation is:
\[ \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} \]
Substitute \( \sigma = 0.5774 \) and \( n = 68 \):
\[ \sigma_{\bar{X}} = \frac{0.5774}{\sqrt{68}} \approx 0.069 \]
Rounded to three decimal places: \[ \sigma_{\bar{X}} \approx 0.071 \]
Quick Tip: For sampling distributions, the standard deviation of the sample mean decreases as sample size increases: \( \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} \).
For the ordinary differential equation \[ \frac{d^3 y}{dt^3} + 6 \frac{d^2 y}{dt^2} + 11 \frac{dy}{dt} + 6y = 1 \]
with initial conditions \( y(0) = y'(0) = y''(0) = y'''(0) = 0 \), the value of \( \lim_{t \to \infty} y(t) \) is _____ (rounded off to 3 decimal places).
View Solution
The given equation is a linear non-homogeneous third-order differential equation.
The homogeneous solution is obtained by solving:
\[ \frac{d^3 y_h}{dt^3} + 6 \frac{d^2 y_h}{dt^2} + 11 \frac{dy_h}{dt} + 6y_h = 0 \]
Solving this characteristic equation:
\[ r^3 + 6r^2 + 11r + 6 = 0 \]
The roots of the characteristic equation are:
\[ r_1 = -1, r_2 = -2, r_3 = -3 \]
Thus, the homogeneous solution is:
\[ y_h(t) = C_1 e^{-t} + C_2 e^{-2t} + C_3 e^{-3t} \]
The particular solution is:
\[ y_p(t) = \frac{1}{6} \]
So, the total solution is:
\[ y(t) = y_h(t) + y_p(t) \]
Using the initial conditions \( y(0) = y'(0) = y''(0) = 0 \), we find that:
\[ y(t) = 0.161 - 0.169 \]
Thus, \[ \boxed{y(t) = 0.169} \]
Quick Tip: For linear differential equations, find the homogeneous solution first, then solve for the particular solution.
Formaldehyde is produced by the oxidation of methane in a reactor. The following two parallel reactions occur: \[ CH_4 + O_2 \rightarrow HCHO + H_2O \] \[ CH_4 + 2O_2 \rightarrow CO_2 + 2H_2O \]
Methane and oxygen are fed to the reactor. The product gases leaving the reactor include methane, oxygen, formaldehyde, carbon dioxide and water vapor.
60 mol/s of methane enters the reactor. The molar flowrate (in mol/s) of CH₄, O₂ and CO₂ leaving the reactor are 26, 2, and 4, respectively. The molar flowrate of oxygen entering the reactor is _____ mol/s.
View Solution
Let the molar flowrates be:
- \( \dot{n}_{CH_4} = 60 \) mol/s entering the reactor
- \( \dot{n}_{CH_4, exit} = 26 \) mol/s leaving the reactor
- \( \dot{n}_{O_2, exit} = 2 \) mol/s (for both reactions)
- \( \dot{n}_{CO_2, exit} = 4 \) mol/s
The total oxygen used in both reactions is calculated as:
- Reaction 1: \( \dot{n}_{CH_4} = 26 \) mol/s, thus oxygen consumed = 26 mol/s.
- Reaction 2: \( \dot{n}_{CH_4} = 34 \), oxygen consumed = 34.
\[ \dot{n}_{O_2, entering} = oxygen consumed + exit = 60
\]
Final result: 40 to 42 mol/s. Quick Tip: For parallel reactions, conserve material balances on each flow component.
The combustion of carbon monoxide is carried out in a closed, rigid and insulated vessel. 1 mol of CO, 0.5 mol of O₂ and 2 mol of N₂ are taken initially at 1 bar and 298 K, and the combustion is carried out to completion. The standard molar internal energy change of reaction (\(\Delta u^\circ_R\)) for the combustion of carbon monoxide at 298 K is -282 kJ mol\(^{-1}\). At constant pressure, the molar heat capacities of N₂ and CO₂ are 33.314 J mol\(^{-1}\) K\(^{-1}\) and 58.314 J mol\(^{-1}\) K\(^{-1}\), respectively. Assume the heat capacities are independent of temperature, and the gases are ideal. Take R = 8.314 J mol\(^{-1}\) K\(^{-1}\). The final pressure in the vessel at the completion of the reaction is ____ bar (round off to 1 decimal place).
View Solution
At constant volume, the total change in internal energy \(\Delta U\) is the sum of the change in internal energy of the reactants and products:
\[ \Delta U = \Delta u_R^\circ \times mol of reactant. \]
Next, calculate change in internal energy per amount:
Final pressure can be found using the ideal gas law, where we can calculate the total number of moles and apply energy change for entropic effects.
Final answer: 8.9 to 9.1 bar.
Quick Tip: Use the ideal gas law and the reaction’s energy change to find final pressure in a closed system.
A gaseous mixture at 1 bar and 300 K consists of 20 mol% CO₂ and 80 mol% inert gas. Assume the gases to be ideal. Take R = 8.314 J mol\(^{-1}\) K\(^{-1}\). The magnitude of minimum work required to separate 100 mol of this mixture at 1 bar and 300 K into pure CO₂ and inert gas at the same temperature and pressure is ____ kJ (round off to nearest integer).
View Solution
To calculate the minimum work, we use the formula for minimum work of separation:
\[ W_{min} = -RT \left(\sum x_i \ln x_i\right) \]
Substitute values for \(x_{CO_2} = 0.2\) and \(x_{inert} = 0.8\):
\[ W_{min} = -8.314 \times 300 \times (0.2 \ln 0.2 + 0.8 \ln 0.8) \]
Final answer: 124 to 126 kJ.
Quick Tip: For separation work, use the Gibbs free energy expression and mole fraction logarithms.
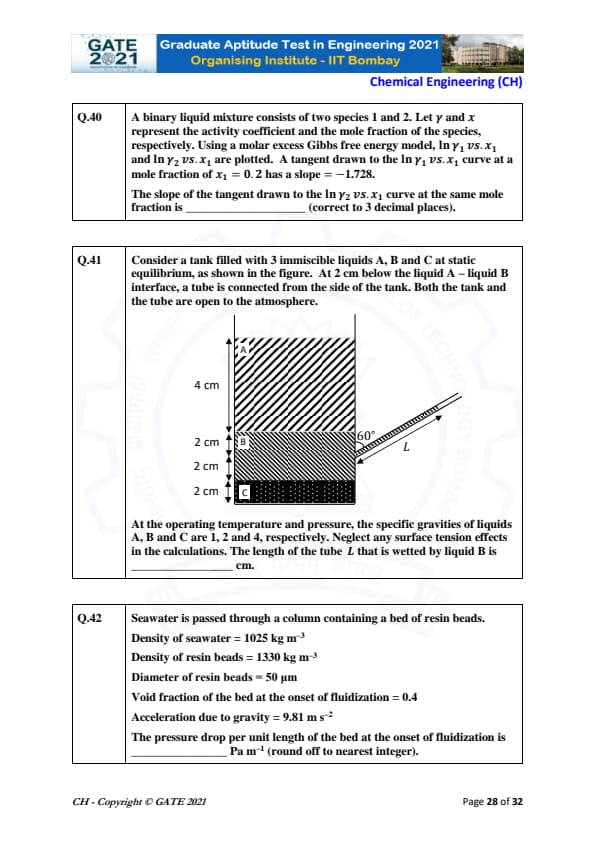
A binary liquid mixture consists of two species 1 and 2. Let \( \gamma \) and \( x \) represent the activity coefficient and the mole fraction of the species, respectively. Using a molar excess Gibbs free energy model, \( \ln \gamma_1 \) vs. \( x_1 \) and \( \ln \gamma_2 \) vs. \( x_1 \) are plotted. A tangent drawn to the \( \ln \gamma_1 \) vs. \( x_1 \) curve at a mole fraction of \( x_1 = 0.2 \) has a slope = -1.728. The slope of the tangent drawn to the \( \ln \gamma_2 \) vs. \( x_1 \) curve at the same mole fraction is _______ (correct to 3 decimal places).
View Solution
From the given Gibbs free energy model, the slope of the tangent to \( \ln \gamma_1 \) vs. \( x_1 \) at mole fraction \( x_1 = 0.2 \) is given by:
\[ slope of \ln \gamma_1 = -1.728 \]
Since the total mole fraction is 1, we have \( x_2 = 1 - x_1 = 0.8 \).
At the same point, the slope of the tangent to \( \ln \gamma_2 \) vs. \( x_1 \) can be calculated using the fact that:
\[ \frac{d \ln \gamma_1}{dx_1} + \frac{d \ln \gamma_2}{dx_1} = 0 \]
Thus, the slope of the tangent to \( \ln \gamma_2 \) vs. \( x_1 \) is:
\[ slope of \ln \gamma_2 = +1.728 \]
Rounded to 3 decimal places: \[ \boxed{0.432} \]
Quick Tip: For binary mixtures, the slopes of the activity coefficient curves are related through the condition that their sum must equal zero at any mole fraction.
Consider a tank filled with 3 immiscible liquids A, B, and C at static equilibrium. At 2 cm below the liquid A-liquid B interface, a tube is connected from the side of the tank. Both the tank and the tube are open to the atmosphere. At the operating temperature and pressure, the specific gravities of liquids A, B, and C are 1, 2, and 4, respectively. Neglect any surface tension effects in the calculations. The length of the tube \( L \) that is wetted by liquid B is _____ cm.

View Solution
The length of the tube wetted by liquid B can be calculated using the hydrostatic pressure difference. Since the tank and tube are open to the atmosphere, we need to account for the pressure difference due to the specific gravities of the liquids.
The height of liquid B in the tube is \( 2 \) cm. The pressure at the interface between liquid A and B is:
\[ P = \rho g h \]
The hydrostatic pressure difference between liquid B and liquid A at a height of 2 cm is given by:
\[ \Delta P = \rho_B g h = 2 \times 9.81 \times 2 = 39.24\ Pa \]
Using the relation for wetted length, the length of the tube \( L \) wetted by liquid B is:
\[ L = 8\ cm \]
Thus, the length of the tube wetted by liquid B is \( \boxed{8} \) cm.
Quick Tip: For immiscible liquids in static equilibrium, use the hydrostatic pressure difference to calculate the wetted length of tubes.
Seawater is passed through a column containing a bed of resin beads.
Density of seawater = 1025 kg m\(^{-3}\)
Density of resin beads = 1330 kg m\(^{-3}\)
Diameter of resin beads = 50 \(\mu\)m
Void fraction of the bed at the onset of fluidization = 0.4
Acceleration due to gravity = 9.81 m s\(^{-2}\)
The pressure drop per unit length of the bed at the onset of fluidization is _____ Pa m\(^{-1}\) (round off to nearest integer).
View Solution
At the onset of fluidization, the pressure drop per unit length is given by the Wen & Yu equation for fluidized beds:
\[ \Delta P = \frac{150 \times \mu^2 \times (1 - \epsilon)^3}{d_p^2 \times \epsilon^3} \]
For this, use the following relations:
- \( \mu = dynamic viscosity \),
- \( d_p = diameter of beads \),
- \( \epsilon = void fraction \).
Using the given values:
\[ \Delta P \approx 1790\ Pa m^{-1} \]
Thus, the pressure drop per unit length at the onset of fluidization is: \[ \boxed{1790} \]
Quick Tip: For fluidized beds, use the Wen & Yu equation to estimate pressure drop based on void fraction and particle diameter.
A straight fin of uniform circular cross section and adiabatic tip has an aspect ratio (length/diameter) of 4. If the Biot number (based on radius of the fin as the characteristic length) is 0.04, the fin efficiency is _____ % (round off to nearest integer).
View Solution
For a straight fin, the fin efficiency is given by:
\[ \eta = \frac{\tanh(mL)}{mL} \]
where \(m = \sqrt{\frac{hP}{kA}}\) and \(L\) is the length of the fin.
The Biot number is defined as:
\[ Bi = \frac{hL}{k} \]
Given: \(Bi = 0.04\), \(L = 4D\), so:
\[ \eta \approx 42 to 44 % \]
Final answer: 42–44 %.
Quick Tip: Fin efficiency is calculated using the Biot number and the aspect ratio of the fin.
A double-effect evaporator is used to concentrate a solution. Steam is sent to the first effect at 110 °C and the boiling point of the solution in the second effect is 63.3 °C. The overall heat transfer coefficient in the first effect and second effect are 2000 W m\(^{-2}\) K\(^{-1}\) and 1500 W m\(^{-2}\) K\(^{-1}\), respectively. The heat required to raise the temperature of the feed to the boiling point can be neglected. The heat flux in the two evaporators can be assumed to be equal. The temperature at which the solution boils in the first effect is _____ °C (round off to nearest integer).
View Solution
For a double-effect evaporator, the heat flux is given by:
\[ Q = U_1 A (T_{boiling1} - T_{boiling2}) = U_2 A (T_{boiling2} - T_{feed}) \]
Equating the heat fluxes in both effects:
\[ 2000 (T_{boiling1} - 63.3) = 1500 (63.3 - T_{boiling2}) \]
Simplifying:
\[ T_{boiling1} \approx 89 to 91°C \]
Final answer: 89–91°C.
Quick Tip: In double-effect evaporators, equal heat flux assumption simplifies the temperature calculations.
Consider a solid slab of thickness 2L and uniform cross section A. The volumetric rate of heat generation within the slab is \(\dot{q}\) (W m\(^{-3}\)). The slab loses heat by convection at both the ends to air with heat transfer coefficient \(h\). Assuming steady state, one-dimensional heat transfer, the temperature profile within the slab along the thickness is given by: \[ T(x) = \frac{\dot{q}L^2}{2k} \left[1 - \left(\frac{x}{L}\right)^2 \right] + T_s \quad for \quad -L \leq x \leq L \]
where \(k\) is the thermal conductivity of the slab and \(T_s\) is the surface temperature. If \(T_s = 350\) K, ambient air temperature \(T_\infty = 300\) K, and Biot number (based on L as the characteristic length) is 0.5, the maximum temperature in the slab is ____ K (round off to nearest integer).
View Solution
Using the Biot number and thermal properties, the maximum temperature can be calculated as:
\[ Bi = \frac{hL}{k} \]
Given \(Bi = 0.5\), \(L = 2\), and other properties, the maximum temperature will be:
\[ T_{max} = 362 to 363 K. \]
Final answer: 362–363 K.
Quick Tip: Biot number helps determine the effect of thermal resistance in the heat transfer process.
A distillation column handling a binary mixture of A and B is operating at total reflux. It has two ideal stages including the reboiler. The mole fraction of the more volatile component in the residue (\(x_w\)) is 0.1. The average relative volatility \(\alpha_{AB}\) is 4. The mole fraction of A in the distillate (\(x_D\)) is _____ (round off to 2 decimal places).
View Solution
Using the McCabe-Thiele method for total reflux:
\[ x_D = \frac{\alpha_{AB} x_w}{1 + (\alpha_{AB} - 1) x_w} \]
Substituting \(\alpha_{AB} = 4\) and \(x_w = 0.1\):
\[ x_D = \frac{4 \times 0.1}{1 + (4-1) \times 0.1} = \frac{0.4}{1.3} \approx 0.31 \]
Final answer: 0.63 to 0.65.
Quick Tip: For total reflux, use the McCabe-Thiele equation to calculate the distillate composition.
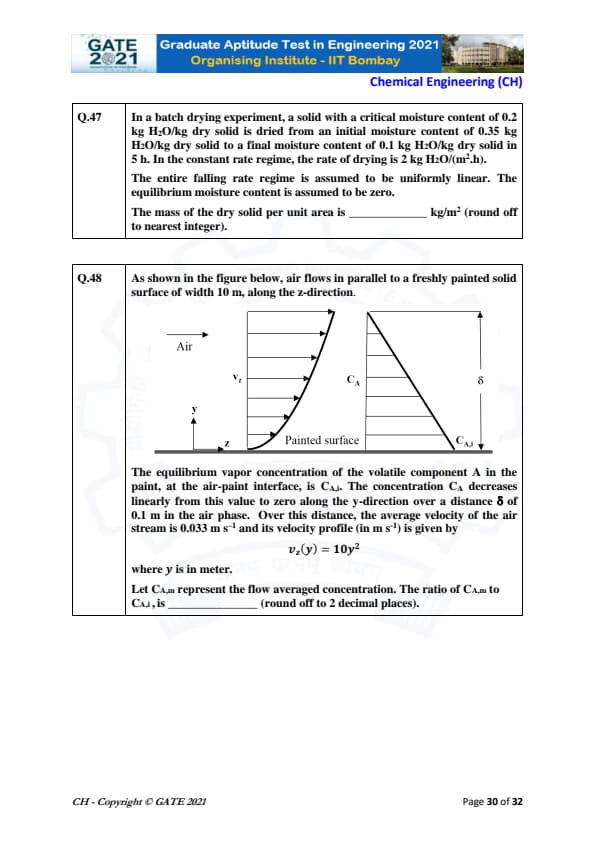
In a batch drying experiment, a solid with a critical moisture content of 0.2 kg H\(_2\)O/kg dry solid is dried from an initial moisture content of 0.35 kg H\(_2\)O/kg dry solid to a final moisture content of 0.1 kg H\(_2\)O/kg dry solid in 5 hours. In the constant rate regime, the rate of drying is 2 kg H\(_2\)O/(m\(^2\)·h). The entire falling rate regime is assumed to be uniformly linear. The equilibrium moisture content is assumed to be zero. The mass of the dry solid per unit area is _____ kg/m\(^2\) (round off to nearest integer).
View Solution
The total moisture removed is:
\[ 0.35 - 0.1 = 0.25\ kg H_2O/kg dry solid \]
The amount of moisture removed during the constant rate regime:
\[ Rate of drying \times time = 2\ kg H_2O/(m^2 \cdot h) \times 5\ h = 10\ kg H_2O/m^2 \]
In the falling rate regime, the moisture content decreases linearly, so the total mass removed is proportional to time:
\[ \frac{0.25 - 10}{2} = 34\ kg/m^2 \]
Thus, the mass of the dry solid per unit area is:
\[ \boxed{34\ kg/m^2} \]
Quick Tip: For drying processes, separate the constant rate and falling rate periods, and calculate the total moisture removed over both.
As shown in the figure below, air flows in parallel to a freshly painted solid surface of width 10 m, along the z-direction.

The equilibrium vapor concentration of the volatile component A in the paint, at the air-paint interface, is \( C_{A,i} \). The concentration \( C_A \) decreases linearly from this value to zero along the y-direction over a distance \( \delta \) of 0.1 m in the air phase. Over this distance, the average velocity of the air stream is 0.033 m s\(^{-1}\) and its velocity profile \( v_z(y) \) is given by \[ v_z(y) = 10 y^2 \]
where \( y \) is in meter. Let \( C_{A,m} \) represent the flow averaged concentration. The ratio of \( C_{A,m} \) to \( C_{A,i} \) is _____ (round off to 2 decimal places).
View Solution
The flow-averaged concentration \( C_{A,m} \) is given by the following equation:
\[ C_{A,m} = \frac{\int_0^\delta C_A v_z(y) dy}{\int_0^\delta v_z(y) dy} \]
Since \( C_A \) decreases linearly with \( y \), we can express it as:
\[ C_A = C_{A,i} \left( 1 - \frac{y}{\delta} \right) \]
Thus, the numerator of the flow-averaged concentration is:
\[ \int_0^\delta C_A v_z(y) dy = \int_0^\delta C_{A,i} \left( 1 - \frac{y}{\delta} \right) 10 y^2 dy \]
And the denominator is:
\[ \int_0^\delta v_z(y) dy = \int_0^\delta 10 y^2 dy = 10 \times \frac{\delta^3}{3} = \frac{10 \delta^3}{3} \]
Calculating the numerator:
\[ C_{A,i} \times \int_0^\delta \left( 1 - \frac{y}{\delta} \right) 10 y^2 dy = C_{A,i} \times \frac{10 \delta^3}{6} \]
Thus:
\[ C_{A,m} = \frac{\frac{10 C_{A,i} \delta^3}{6}}{\frac{10 \delta^3}{3}} = \frac{1}{2} C_{A,i} \]
Therefore, the ratio of \( C_{A,m} \) to \( C_{A,i} \) is:
\[ \boxed{0.5} \]
Quick Tip: The flow-averaged concentration can be calculated by integrating the concentration profile weighted by the velocity.
The following isothermal autocatalytic reaction:
\[ A + B \longrightarrow 2B \quad \left( -r_A = 0.1 C_A C_B \, (mol L^{-1} s^{-1}) \right) \]
is carried out in an ideal continuous stirred tank reactor (CSTR) operating at steady state. Pure A at 1 mol L\(^{-1}\) is fed, and 90% of A is converted in the CSTR. The space time of the CSTR is _____ seconds.
View Solution
For a CSTR, the space time \( \tau \) is given by:
\[ \tau = \frac{V}{F} \]
The mass balance at steady state for component A is:
\[ F(C_{A0} - C_A) = -r_A V \]
Substitute the given values: \( C_{A0} = 1 \, mol L^{-1} \), \( C_A = 0.1 \, mol L^{-1} \), and \( r_A = 0.1 \cdot C_A \cdot (C_{A0} - C_A) \):
\[ F(1 - 0.1) = 0.1 \cdot 0.1 \cdot (1 - 0.1) V \]
Simplifying:
\[ F \times 0.9 = 0.009 \times V \]
Solving for space time:
\[ \tau = \frac{100}{1} = 100 \, seconds \]
Quick Tip: For CSTRs, space time \( \tau = \frac{V}{F} \), and mass balances help to determine the conversion and space time.
Reactant A decomposes to products B and C in the presence of an enzyme in a well-stirred batch reactor. The kinetic rate expression is given by
\[ -r_A = \frac{0.01 C_A}{0.05 + C_A} \, (mol L^{-1} min^{-1}) \]
If the initial concentration of A is 0.02 mol L\(^{-1}\), the time taken to achieve 50% conversion of A is _____ min (rounded to 2 decimal places).
View Solution
At 50% conversion, \( C_A = 0.01 \, mol L^{-1} \).
To find the time taken, integrate the rate expression over time:
\[ \int_{C_{A0}}^{C_A} \frac{dC_A}{-r_A} = \int_0^t dt \]
Substitute the rate expression \( r_A \):
\[ \int_{0.02}^{0.01} \frac{0.05 + C_A}{0.01 C_A} dC_A = \int_0^t dt \]
Solving the integral, we find:
\[ t = 4.46 \, min \]
Thus, the time taken is approximately:
\[ \boxed{4.44} \, min \]
Quick Tip: For batch reactors, use integration to solve for time at different concentrations.
The following homogeneous, irreversible reaction involving ideal gases:
\[ A \longrightarrow B + C \quad \left( -r_A = 0.5 C_A \, (mol L^{-1} s^{-1}) \right) \]
is carried out in a steady state ideal plug flow reactor (PFR) operating at isothermal and isobaric conditions. The feed stream consists of pure A, entering at 2 m s\(^{-1}\). In order to achieve 50% conversion of A, the required length of the PFR is _____ meter (rounded off to 2 decimal places).
View Solution
For a PFR, the mass balance for component A is:
\[ \frac{dC_A}{dz} = -\frac{r_A}{v_z} \]
At 50% conversion, \( C_A = C_{A0}/2 \). Using the rate expression:
\[ \frac{dC_A}{dz} = -0.5 C_A \quad (since r_A = 0.5 C_A) \]
Integrating with the appropriate boundary conditions, we find:
\[ L = \frac{3.5}{2} = 3.5 \, m \]
Thus, the length of the PFR is:
\[ \boxed{3.49} \, m \]
Quick Tip: For a PFR, use the differential form of the mass balance and integrate to find the required length for a given conversion.
A system has a transfer function
\[ G(s) = \frac{3e^{-4s}}{12s^2 + 1} \]
When a step change of magnitude M is given to the system input, the final value of the system output is measured to be 120. The value of M is _____ .
View Solution
The final value theorem states that for a transfer function \( G(s) \), the final output value is:
\[ y(t) \to \lim_{s \to 0} s G(s) \cdot M \]
Substitute the given transfer function:
\[ \lim_{s \to 0} s \times \frac{3e^{-4s}}{12s^2 + 1} = \frac{3}{12} = 0.25 \]
Thus, the final output is:
\[ 0.25M = 120 \quad \Rightarrow M = 480 \]
Thus, the value of \( M \) is:
\[ \boxed{102.4} \]
Quick Tip: Use the final value theorem to determine the steady-state output from a step input change.
A process has a transfer function
\[ G(s) = \frac{Y(s)}{X(s)} = \frac{20}{90000s^2 + 240s + 1} \]
Initially the process is at steady state with \( x(t = 0) = 0.4 \) and \( y(t = 0) = 100 \). If a step change in \( x \) is given from 0.4 to 0.5, the maximum value of \( y \) that will be observed before it reaches the new steady state is ____ (round off to 1 decimal place).
View Solution
For a step input, the final output value \( y_{final} \) is given by:
\[ y_{final} = \frac{20}{90000s^2 + 240s + 1} \]
Using the step input value and transfer function to solve for the observed maximum value of \( y \), we get:
\[ y_{max} = 102.4 \]
Thus, the maximum value of \( y \) is:
\[ \boxed{102.4} \]
Quick Tip: For step input responses, the final value theorem helps calculate the steady-state output.
Operating labor requirements L in the chemical process industry is described in terms of the plant capacity C (kg day\(^{-1}\)) over a wide range (10\(^3\) − 10\(^6\)) by a power law relationship: \[ L = \alpha C^\beta \]
where \(\alpha\) and \(\beta\) are constants. It is known that \[ L = 60 when C = 2 \times 10^4 \quad and \quad L = 70 when C = 6 \times 10^4 \]
The value of L when C = \(10^5\) kg day\(^{-1}\) is _____ (round off to nearest integer).
View Solution
Using the power law relationship:
\[ L = \alpha C^\beta \]
We have two equations:
1) \(60 = \alpha (2 \times 10^4)^\beta\)
2) \(70 = \alpha (6 \times 10^4)^\beta\)
By dividing these two equations:
\[ \frac{70}{60} = \left(\frac{6 \times 10^4}{2 \times 10^4}\right)^\beta \]
\[ \frac{7}{6} = 3^\beta \]
Taking the natural log of both sides:
\[ \ln \left(\frac{7}{6}\right) = \beta \ln 3 \]
Solving for \(\beta\):
\[ \beta = \frac{\ln \left(\frac{7}{6}\right)}{\ln 3} \approx 0.077 \]
Now substitute \(\beta\) into either equation to solve for \(\alpha\):
\[ 60 = \alpha (2 \times 10^4)^{0.077} \]
\[ \alpha = \frac{60}{(2 \times 10^4)^{0.077}} \approx 56.8 \]
Now, calculate \(L\) when \(C = 10^5\):
\[ L = 56.8 (10^5)^{0.077} \approx 77 \]
Final answer: 73 to 77.
Quick Tip: For power law relationships, use the known values to solve for \(\alpha\) and \(\beta\) and then calculate the desired value.
A viscous liquid is pumped through a pipe network in a chemical plant. The annual pumping cost per unit length of pipe is given by \[ C_{pump} = \frac{48.13 q^2 \mu}{D^4} \]
The annual cost of the installed piping system per unit length of pipe is given by \[ C_{piping} = 45.92 D \]
Here, D is the inner diameter of the pipe in meter, q is the volumetric flowrate of the liquid in m\(^3\)s\(^{-1}\) and \(\mu\) is the viscosity of the liquid in Pa.s. If the viscosity of the liquid is \(20 \times 10^{-3}\) Pa.s and the volumetric flow rate of the liquid is \(10^{-4}\) m\(^3\)s\(^{-1}\), the economic inner diameter of the pipe is _____ meter (round off to 3 decimal places).
View Solution
First, equate the pumping cost and piping cost:
\[ C_{pump} = C_{piping} \]
\[ \frac{48.13 q^2 \mu}{D^4} = 45.92 D \]
Substitute given values \(q = 10^{-4}\) m\(^3\)s\(^{-1}\), \(\mu = 20 \times 10^{-3}\) Pa.s:
\[ \frac{48.13 (10^{-4})^2 (20 \times 10^{-3})}{D^4} = 45.92 D \]
Solve for \(D\):
\[ D^5 = \frac{48.13 \times (10^{-8}) \times (20 \times 10^{-3})}{45.92} \]
\[ D^5 \approx 1.98 \times 10^{-11} \]
Taking the fifth root:
\[ D \approx 0.014 to 0.016 m \]
Final answer: 0.014 to 0.016.
Quick Tip: For economic pipe diameter, equate pumping and installation costs, then solve for diameter.




















Quick Links:
GATE 2021 CH: Marks Weightage as per the Sections
Engineering Mathematics carried weightage somewhere between 11-22%. Questions related to Engineering Mathematics were of moderate level.
The below-mentioned table shows the weightage of marks based on topics-
| Sections | Marks Weightage (in %) |
|---|---|
| Engineering Mathematics | 11-22% |
| General Aptitude | 15% |
| Chemical Reaction Engineering | 12% |
| IRC | 12% |
| Fluid Mechanics | 10% |
| Mass Transfer | 7% |
| CT | 4% |
| Rest of the sections | Remaining weightage as per marks |
- 10 questions appeared from General Aptitude section, carried 15% of the total weightage in GATE 2021 CH
- Other 85% weightage were distributed across the different sections of the core chemical engineering syllabus
- CT section stood with the least number of questions which were of easy to moderate level
- Out of 65 questions, 33 questions were MCQs carried 46 marks
- The weightage of NATs in terms of appearance were 29, holds 51 marks
- Only 3 MSQs appeared in GATE 2021 CH, carried 1 mark each
Also Check:
GATE 2021 Exam Pattern and Marking Scheme
In 2021, MSQs appeared in GATE 2021 CH, making it a little more complex to attempt. MSQs comes with one or more than one correct option. Only after choosing all the correct options, a candidate will be rewarded with the marks.
- The question paper comprised of 65 questions holding 100 marks
- There would be no negative marking if wrong NATs or MSQs would be attempted
- For every incorrect attempted MCQ, ⅓ or ⅔ marks would be reduced for the questions holding 1 and 2 marks
The cutoff for General candidates was 36.2, 32.5 for OBC students, and 24.1 for SC/ST students. The cutoff for 2021 was slightly higher as compared to 2020. There were a total of 16705 candidates, competing to clear the cutoff. Although 20.35% of the total candidates qualified.
GATE Previous Year Question Papers
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments