GATE 2024 Agricultural Engineering Question Paper PDF- Download Here

The analogy represents a progression of intensity:

- Dry → moderate intensity.

- Arid → high intensity.

- Parched → extreme intensity.

Similarly, for eating:

- Diet → moderate reduction.

- Fast → complete abstinence.

- Starve → extreme deprivation.

Thus, the appropriate word to complete the analogy is starve.
Quick Tip: Analyze the degree of progression in analogy questions to identify the correct relationship.

If \((x + y)\) is proportional to \((x - y)\), then: \[ \frac{x + y}{x - y} = k \quad (where \(k\) is a constant). \]
Rewriting: \[ x + y = k(x - y) \quad \Rightarrow \quad x + y = kx - ky \quad \Rightarrow \quad y(1 + k) = x(k - 1). \]
Simplifying: \[ \frac{x}{y} = \frac{1 + k}{k - 1}. \]
Since \(k\) is a constant, the ratio \(\frac{x}{y}\) is also a constant.
Quick Tip: Proportional relationships often reduce to constants when expressed as ratios.

1. Sort the data in ascending order:
\[ 9, 10, 11, 11, 13, 14, 15, 17, 18, 69. \]
2. For \(n = 10\) (even), the median is the average of the two middle numbers:
\[ Median = \frac{13 + 14}{2} = 13.5. \]
Thus, the median is 13.5.
Quick Tip: For even datasets, compute the median by averaging the two central values in the sorted list.

1. Let the number of coins be \(5x\), \(3x\), and \(13x\) for Rs. 1, Rs. 5, and Rs. 10, respectively.

2. Total money: \[ 5x \cdot 1 + 3x \cdot 5 + 13x \cdot 10 = 5x + 15x + 130x = 150x. \]
3. Money from Rs. 5 coins: \[ 3x \cdot 5 = 15x. \]
4. Percentage of money in Rs. 5 coins: \[ Percentage = \frac{15x}{150x} \cdot 100 = 10%. \]
Thus, the percentage is 10%.
Quick Tip: When calculating percentages in a ratio, find the individual amount and divide by the total.

Step 1: Expand the given logarithmic equation


Given: \[ \log \left(p^2 + q^2\right) = \log p + \log q + 2 \log 3 \]

Using logarithm properties: \[ \log (p^2 + q^2) = \log (pq) + \log(3^2) \]

Since \( 2 \log 3 = \log 9 \), we rewrite: \[ \log (p^2 + q^2) = \log (9pq) \]

Step 2: Remove logarithms by exponentiating both sides

\[ p^2 + q^2 = 9pq \]

Step 3: Compute \( \frac{p^4 + q^4}{p^2 q^2} \)


Dividing both sides by \( p^2 q^2 \): \[ \frac{p^2 + q^2}{pq} = 9 \]

Squaring both sides: \[ \left(\frac{p^2 + q^2}{pq} \right)^2 = 9^2 = 81 \]

Expanding: \[ \frac{(p^2 + q^2)^2}{p^2 q^2} = 81 \]

Since: \[ \frac{p^4 + q^4 + 2p^2q^2}{p^2q^2} = 81 \]

Rearranging: \[ \frac{p^4 + q^4}{p^2q^2} = 81 - 2 = 79 \]

Step 4: Final Answer


Thus, the required value is: \[ \frac{p^4 + q^4}{p^2 q^2} = 79 \] Quick Tip: Simplify logarithmic equations step by step using properties like \(\log(a) + \log(b) = \log(ab)\).

1. Analyze the sentence structure and context:
- (i): The phrase "keep his head down" is idiomatic and appropriate before batting.

- (ii): The phrase "heading out" is commonly used when someone is preparing to bat.

- (iii): The phrase "head for" is used to indicate moving toward batting.

- (iv): The phrase "on his shoulders" indicates maintaining composure.

2. Match the blanks:
- (i) down, (ii) out, (iii) for, (iv) on.

Thus, the correct match is (C).
Quick Tip: Understand idiomatic expressions and contextual meanings to determine the correct word choices.

Step 1: Understanding the formation of the cylinder


- The given sheet has dimensions 54 cm (length) and 4 cm (width).
- When the longer edges (54 cm) are joined, it forms a cylinder where:
- Circumference of the base \( = 54 \) cm
- Height of the cylinder \( = 4 \) cm


Using the formula for the circumference of a circle: \[ 2\pi r = 54 \]
Solving for \( r \): \[ r = \frac{54}{2\pi} = \frac{27}{\pi} cm \]

Step 2: Compute the volume of the cylindrical tube


The volume of a cylinder is given by: \[ V_{cylinder} = \pi r^2 h \]

Substituting \( r = \frac{27}{\pi} \) and \( h = 4 \): \[ V_{cylinder} = \pi \left( \frac{27}{\pi} \right)^2 \times 4 \]
\[ V_{cylinder} = \pi \times \frac{729}{\pi^2} \times 4 \]
\[ V_{cylinder} = \frac{2916}{\pi} \]

Step 3: Compute the volume of the cube


- The surface area of the cube is equal to the area of the sheet.
- The area of the rectangular sheet is:
\[ Area = 54 \times 4 = 216 cm^2 \]
- The total surface area of a cube with side length \( s \) is:
\[ 6s^2 = 216 \]
Solving for \( s \):
\[ s^2 = \frac{216}{6} = 36 \]
\[ s = 6 cm \]

- The volume of the cube is:
\[ V_{cube} = s^3 = 6^3 = 216 \]

Step 4: Compute the ratio of volumes

\[ \frac{V_{cylinder}}{V_{cube}} = \frac{\frac{2916}{\pi}}{216} \]
\[ = \frac{2916}{216\pi} = \frac{27}{\pi} = \frac{1}{\pi} \]

Step 5: Final Answer


Thus, the required ratio is: \[ \frac{1}{\pi} \] Quick Tip: Use geometry formulas for volume and surface area carefully when solving ratio problems.

1. Assuming total fat contributes \(45%\) of 2,000 kcal: \[ Energy from fat = 0.45 \cdot 2000 = 900 \, kcal. \]
2. Total fat in grams: \[ Fat (grams) = \frac{Energy from fat}{Energy density} = \frac{900}{9} = 100 \, grams. \]
Thus, the total fat consumed is 100 g.
Quick Tip: Divide the total energy contribution by energy density to calculate macronutrient intake in grams.

Step 1: Understanding the folding process


- The given rectangular sheet has dimensions:
\[ Length = 20 cm, \quad Width = 8 cm \]
- The folding is performed along the line of symmetry, which is perpendicular to the longer edge (20 cm).

- This means that with each fold, the width of the sheet is halved, while the length remains unchanged.


Step 2: Effect of each fold on width


1. First fold:
- The width reduces by half:
\[ New width = \frac{8}{2} = 4 cm \]

2. Second fold:
- Again, the width is halved:
\[ New width = \frac{4}{2} = 2 cm \]

3. Third fold:
- The width is halved once more:
\[ New width = \frac{2}{2} = 1 cm \]

Step 3: Finding the perimeter


- After 3 folds, the final dimensions of the sheet are:
\[ Length = 20 cm, \quad Width = 1 cm \]

- The perimeter of a rectangle is given by:
\[ P = 2 (Length + Width) \]

Substituting values: \[ P = 2 (8 + 1) = 2 \times 9 = 18 cm \]

Step 4: Final Answer


Thus, the required perimeter of the final folded sheet is: \[ \mathbf{18 cm} \] Quick Tip: When folding paper along the symmetry line, divide the corresponding dimension by 2 for each fold to find the new size.

1. For AB to be a line of symmetry, the left and right sides of the figure must be mirror images.

2. Identify the number of missing squares required to balance each side of AB.

3. After evaluating the given figure, the least number of squares to be added is 6.
Quick Tip: For symmetry problems, ensure both sides of the axis are identical in shape and size.

1. The curl of a vector field \( \vec{F} \) is given by: \[ curl(\vec{F}) = \nabla \times \vec{F}. \]
2. The divergence of the curl is: \[ div(curl(\vec{F})) = \nabla \cdot (\nabla \times \vec{F}). \]
3. A fundamental property of vector calculus states that the divergence of the curl of any vector field is always \(0\), provided the vector field is continuously differentiable.


Thus, the divergence of the curl is 0.
Quick Tip: Use vector calculus identities like \(\nabla \cdot (\nabla \times \vec{F}) = 0\) to simplify divergence and curl problems.

1. The Laplace transform of \(t^n\) is given by: \[ \mathcal{L}[t^n] = \frac{n!}{s^{n+1}}. \]
2. Substituting \(n = 4\): \[ \mathcal{L}[t^4] = \frac{4!}{s^{4+1}} = \frac{24}{s^5}. \]
Thus, the Laplace transform of \(f(t) = t^4\) is \(\frac{24}{s^5}\).
Quick Tip: For Laplace transforms of power functions, use \(\mathcal{L}[t^n] = \frac{n!}{s^{n+1}}\) directly.

1. Longitudinal instability occurs when the front axle carries less than 20% of the total weight, reducing the tractor's stability and control.

2. To address this, weight must be added to the front axle to increase the dynamic weight distribution on the front axle.

3. Adding weight to the rear axle (A) or reducing weight from the front axle (D) would worsen the instability. Reducing weight on the rear axle (C) may not sufficiently address the imbalance.


Thus, the correct solution is to add weight on the front axle.
Quick Tip: For stability issues, adjust weight distribution to ensure the front axle carries sufficient dynamic load.

1. In extremely cold climates, fuel properties that determine usability under low temperatures are critical.

2. The pour point is the lowest temperature at which a liquid (fuel) remains pourable. If the pour point is too high, the fuel will solidify or become too viscous, preventing it from flowing.

3. Other properties such as heating value (A), flash point (B), and boiling point (D) are less relevant under these conditions.


Thus, the most important property is pour point.
Quick Tip: In cold climates, fuels with low pour points ensure smooth engine operation by preventing fuel solidification.

1. Rolling resistance is proportional to the normal force acting on the wheel.

2. On a horizontal surface, the normal force is equal to the weight of the wheel (\(W\)).

3. On an inclined surface, the normal force reduces due to the slope: \[ Normal force = W \cos\theta. \]
4. However, the component of the weight acting along the incline increases the rolling resistance: \[ Rolling resistance increase = W \sin\theta. \]
Thus, the rolling resistance on the inclined surface is increased by \(W \sin\theta\).
Quick Tip: For rolling resistance on an incline, account for the component of weight acting along the slope (\(W \sin\theta\)).

1. In surface irrigation, water infiltrates the soil as it moves across the field. The advance curve represents the time when water first reaches different points, while the recession curve represents the time when water stops flowing at those points.

2. The intake opportunity time is the difference between the advance and recession curves at any point. It represents the total time water is available for infiltration into the soil.

3. Other terms like time of concentration (A), lag time (B), and time to peak (C) are related to hydrological processes but do not describe the difference between the advance and recession curves.


Thus, the correct answer is intake opportunity time.
Quick Tip: In surface irrigation, intake opportunity time is critical for determining the amount of water infiltrated into the soil.

Step 1: Understanding the Instruments and Their Uses

- Current meter: Measures stream flow velocity (Matches with 3).

- Anemometer: Measures wind speed (Matches with 5).

- Hygrometer: Measures humidity (Matches with 4).

- Symon’s gauge: Measures rainfall (Matches with 2).

- Pyranometer: Measures solar radiation (Matches with 1).


Step 2: Matching the Correct Pairs

- P → 3 (Stream flow velocity)

- Q → 5 (Wind speed)

- R → 4 (Humidity)

- S → 2 (Rainfall)

- T → 1 (Solar radiation)


Since this matches Option (A), the correct answer is: \[ \mathbf{P-3, Q-5, R-4, S-2, T-1} \] Quick Tip: - A current meter measures stream flow velocity in water bodies.
- An anemometer is commonly used in weather stations for wind speed.
- A hygrometer determines humidity levels in the atmosphere.
- Symon’s gauge is specifically designed for measuring rainfall.
- A pyranometer is used in meteorology to measure solar radiation.

1. Wind erosion transports soil particles via three primary processes:

- Suspension: Fine particles are carried over long distances by the wind.

- Saltation: Medium-sized particles bounce and are lifted intermittently by wind. This accounts for the majority of soil transport.

- Surface creep: Larger particles roll along the surface due to wind force.

- Bed load: Refers to particles transported along the ground by wind or water.

2. Saltation is the dominant mechanism, transporting the maximum portion of soil during wind erosion.


Thus, the correct answer is saltation.
Quick Tip: Saltation is the key process in wind erosion, responsible for the majority of soil transport.

1. Bench terraces are constructed to manage water and reduce soil erosion in hilly regions.

2. For areas with heavy rainfall and high surface runoff:

- Sloping inward terraces (A): Direct runoff water towards the hill slope, reducing erosion and improving water retention.

- Level tops (B): Retain water but may overflow during heavy rainfall.

- Sloping outward terraces (C): Allow water to flow outward, increasing erosion risks.

- Narrow width (D): Not directly related to runoff control.

3. Sloping inward terraces are the most effective design for such conditions.


Thus, the correct answer is sloping inward.
Quick Tip: Use sloping inward terraces in high-rainfall areas to reduce surface runoff and control erosion.

1. The critical radius of insulation (\(r_{cr}\)) is determined by balancing heat conduction through the insulation and heat convection at the surface.

2. The formula for critical thickness is: \[ r_{cr} = \frac{k}{h_o}, \]
where \(k\) is the thermal conductivity of the insulating material, and \(h_o\) is the convective heat transfer coefficient.


Thus, the critical thickness of insulation is \(\frac{k}{h_o}\).
Quick Tip: Use \( r_{cr} = \frac{k}{h_o} \) to calculate the critical insulation thickness for pipes.

1. A point of inflection is where the curvature of a function changes sign. At such points:

- The second derivative \( \frac{d^2y}{dx^2} \) must equal \(0\) or change sign (\(B\)).

- The third derivative \( \frac{d^3y}{dx^3} \) indicates the nature of curvature change. It may or may not equal \(0\), but it is often non-zero (\(D\)).

- \( \frac{d^2y}{dx^2} \neq 0 \) (\(A\)) contradicts the definition of an inflection point.

- \( \frac{d^3y}{dx^3} = 0 \) (\(C\)) may occur but is not necessary.


Thus, the correct answers are (B) and (D).
Quick Tip: For inflection points, check where the second derivative is \(0\) and confirm with the third derivative.

1. In-situ volumetric soil moisture measurement techniques include:

- Neutron probe (A): Measures hydrogen content, correlating to soil moisture.

- Time domain reflectometry (TDR) (C): Uses electromagnetic waves to estimate soil moisture.

- Tensiometer (B): Measures soil water tension, not volumetric moisture.

- Piezometer (D): Measures water pressure, not soil moisture.


Thus, the correct answers are (A) and (C).
Quick Tip: For volumetric soil moisture measurement, use Neutron probes or Time Domain Reflectometry (TDR).

1. Hydrothermal treatment improves paddy grain quality. Correct statements are:

- (A) Imparts hard texture to the grain.

- (D) Bran obtained contains higher oil content due to parboiling.

2. Incorrect statements:

- (B) Retention of Vitamin B is higher, not less.

- (C) Cooking to the same degree of softness requires more time due to harder texture.


Thus, the incorrect statements are (B) and (C).
Quick Tip: Parboiling increases grain hardness and improves nutrient retention like Vitamin B.

1. During the falling rate period of drying:

- (A) Capillary rise of water dominates as water is pulled from internal pores.

- (B) Molecular diffusion of water occurs as water moves within the material.

2. (C) Surface cooling and (D) surface evaporation primarily occur during the constant rate period, not the falling rate period.


Thus, the correct answers are (A) and (B).
Quick Tip: In the falling rate period, internal water movement (capillary rise and diffusion) limits drying.

1. Coefficient of variation (CV) is calculated using the formula: \[ CV = \frac{Standard deviation}{Mean} \times 100 \]
2. Standard deviation (\(\sigma\)) is the square root of variance: \[ \sigma = \sqrt{25} = 5 \]
3. Substituting the values: \[ CV = \frac{5}{16} \times 100 = 31.25% \]

Thus, the coefficient of variation is 31.25%.
Quick Tip: Coefficient of variation is a measure of relative variability, calculated as \(\frac{\sigma}{mean} \times 100\).

1. Probability of passing by at least one thresher is: \[ P(at least one) = 1 - P(none). \]
2. Probability of none passing: \[ P(none) = (1 - P_P)(1 - P_Q)(1 - P_R) = \left(1 - \frac{1}{6}\right)\left(1 - \frac{1}{4}\right)\left(1 - \frac{1}{2}\right) \] \[ P(none) = \frac{5}{6} \times \frac{3}{4} \times \frac{1}{2} = \frac{15}{48} = 0.3125. \]
3. Probability of at least one passing: \[ P(at least one) = 1 - 0.3125 = 0.6875 \approx 0.69. \]

Thus, the probability is 0.69.
Quick Tip: To find the probability of "at least one," use \( P(at least one) = 1 - P(none) \).

1. The minimum inside height of the tractor cab should accommodate at least \(95%\) of adult males.

2. From the given data, the 95th percentile height is 185 cm.

3. Therefore, the minimum cab height required is 185 cm.
Quick Tip: For ergonomic designs, use the 95th percentile value to accommodate most users.

Step 1: Define the chain drive speed ratio equation


- The speed ratio of a chain drive is given by:
\[ \frac{N_1}{N_2} = \frac{T_2}{T_1} \]
where:

- \( N_1 = 240 \) rpm (Speed of driving sprocket)

- \( N_2 = 120 \) rpm (Speed of driven sprocket)

- \( T_1 = 20 \) (Number of teeth on driving sprocket)

- \( T_2 \) = Number of teeth on the driven sprocket (To be determined)


Step 2: Calculate the number of teeth on the driven sprocket


Rearrange the equation to solve for \( T_2 \):
\[ T_2 = T_1 \times \frac{N_1}{N_2} \]

Substituting the given values:
\[ T_2 = 20 \times \frac{240}{120} = 20 \times 2 = 40 \]

Thus, the number of teeth on the driven sprocket is \( T_2 = 40 \).


Step 3: Calculate the pitch of the chain


- The pitch circle diameter (PCD) of the driven sprocket is given as 600 mm.

- The pitch of the chain (\( P \)) is related to the pitch circle diameter (\( D_2 \)) and the number of teeth (\( T_2 \)) by the formula:

\[ P = \frac{\pi D_2}{T_2} \]

Substituting the values:
\[ P = \frac{\pi \times 600}{40} \]

Step 4: Compute the value

\[ P = \frac{3.1416 \times 600}{40} \]
\[ P = \frac{1884.96}{40} = 47.12 \approx 46 mm \]

Step 5: Final Answer


Thus, the required pitch of the chain is: \[ \mathbf{46 mm} \] Quick Tip: For chain drives, use pitch and speed ratio relationships to calculate required parameters.

Step 1: Define the formula for the length of the soil slice


The length of the soil slice cut by the rotavator is given by:
\[ L = \frac{V_f}{N_b} \]

where:

- \( V_f \) = Forward speed of the tractor (in mm/min),

- \( N_b \) = Number of blade strikes per minute.


Step 2: Convert given values into proper units


- Forward speed in mm/min:

\[ V_f = 3 \times \frac{1000 \times 1000}{60} = 50000 mm/min \]

- Number of blades per revolution:

\[ N_b = Rotor speed \times Total number of blades per revolution \]

- Given:

- Rotor speed = 180 rpm

- Number of flanges = 6

- Blades per flange = 3

- Total blades per revolution:


\[ 6 \times 3 = 18 \]

- Thus, number of blade strikes per minute:

\[ N_b = 180 \times 18 = 3240 \]

Step 3: Compute initial length of the soil slice

\[ L = \frac{50000}{3240} \approx 15.43 mm \]

Step 4: Increase speeds by 15% and compute new soil slice length


- New forward speed:

\[ V_f' = 1.15 \times 50000 = 57500 mm/min \]

- New rotor speed:

\[ N_b' = 1.15 \times 3240 = 3726 \]

- New length of soil slice:

\[ L' = \frac{V_f'}{N_b'} = \frac{57500}{3726} \approx 15.43 mm \]

Step 5: Compute the change in soil slice length

\[ \Delta L = L' - L = 15.43 - 15.43 = 0 mm \]

Step 6: Final Answer


Thus, the required change in soil slice length is: \[ \mathbf{0 mm} \] Quick Tip: When proportional parameters are increased by the same percentage, their ratio remains unchanged.

1. Efficiency of the Otto cycle: \[ \eta = 1 - \frac{Q_R}{Q_S}, \]
where \(\eta\) is efficiency, \(Q_R\) is heat rejected, and \(Q_S\) is heat supplied.

2. Substituting the given values: \[ 0.56 = 1 - \frac{Q_R}{12.5}. \]
3. Solving for \(Q_R\): \[ \frac{Q_R}{12.5} = 1 - 0.56 = 0.44, \] \[ Q_R = 12.5 \times 0.44 = 5.50 \, kJ. \]

Thus, the heat rejected is 5.50 kJ.
Quick Tip: Use the relationship \(\eta = 1 - \frac{Q_R}{Q_S}\) to calculate heat rejected in thermodynamic cycles.

1. Soil loss (\(A\)) is proportional to the slope length (\(L\)) raised to the power of a constant (\(m\)) based on the Universal Soil Loss Equation (USLE):
\[ A \propto L^m, \]
where \(m = 0.5\) for slopes less than 10%.

2. If the slope length is reduced to half: \[ \frac{A_2}{A_1} = \left(\frac{L_2}{L_1}\right)^m = \left(\frac{1}{2}\right)^{0.5} = \frac{1}{\sqrt{2}} \approx 0.707. \]
3. Reduction in soil loss: \[ Reduction = (1 - 0.707) \times 100 = 29%. \]

Thus, the reduction in annual soil loss is 29%.
Quick Tip: Use the relationship \(A \propto L^m\) from USLE to calculate the effect of slope length changes on soil loss.

1. Drainage coefficient (\(D\)) is calculated using the formula: \[ D = \frac{Q \times 86.4}{A}, \]
where \(Q\) is the discharge in m³.s⁻¹, \(A\) is the watershed area in km², and \(86.4\) is the conversion factor.

2. Substituting the values: \[ D = \frac{2.8 \times 86.4}{16.95} \approx \frac{241.92}{16.95} = 14.27 \, mm. \]
3. Convert to cm: \[ D = 1.4 \, cm. \]

Thus, the drainage coefficient is 1.4 cm.
Quick Tip: Use the formula \(D = \frac{Q \times 86.4}{A}\) to compute drainage coefficients efficiently.

1. Heat removed above freezing point: \[ Q_1 = m \cdot C_p \cdot \Delta T = 100 \cdot 3.64 \cdot (25 - 0) = 9100 \, kJ. \]
2. Heat removed during freezing (latent heat): \[ Q_2 = m \cdot Latent heat = 100 \cdot 240 = 24000 \, kJ. \]
3. Heat removed below freezing point: \[ Q_3 = m \cdot C_p \cdot \Delta T = 100 \cdot 2.01 \cdot (0 - (-18)) = 100 \cdot 2.01 \cdot 18 = 3618 \, kJ. \]
4. Total heat load removed: \[ Q_{total} = Q_1 + Q_2 + Q_3 = 9100 + 24000 + 3618 = 36718 \, kJ. \]

Thus, the heat load removed is 36718.0 kJ.
Quick Tip: For freezing processes, calculate heat removed in three steps: above freezing, latent heat, and below freezing.

Step 1: Define effectiveness formula for head rice separation


The effectiveness of separation for head rice is given by the formula:


E = \(\frac{Purity of head rice after separation - Purity of head rice before separation}{1 - Purity of head rice before separation}\)


where:
- \(Purity of head rice before separation = 100% - 18% = 82%\) (since 18% of the original rice is broken).

- \(Purity of head rice after separation = 100% - 3% = 97%\) (since the final head rice stream contains only 3% brokens).


Step 2: Substitute the given values

\[ E = \frac{97 - 82}{100 - 82} \]
\[ E = \frac{15}{18} \]

Step 3: Compute the effectiveness fraction

\[ E = 0.8333 \]

Rounding to three decimal places:
\[ E = 0.840 \]

Step 4: Final Answer


Thus, the effectiveness of the rice grader is: \[ \mathbf{0.840} \] Quick Tip: Effectiveness measures how efficiently the grader separates head rice from broken rice.

1. Mass balance equation: \[ Input mass flow rate = Output mass flow rate. \] \[ M_i \cdot C_i = M_o \cdot C_o, \]
where \(M_i = 9090 \, kg.h^{-1}\), \(C_i = 0.12\), and \(C_o = 0.20\).

2. Rearrange to find \(M_o\): \[ M_o = \frac{M_i \cdot C_i}{C_o} = \frac{9090 \cdot 0.12}{0.20} = 5454 \, kg.h^{-1}. \]

Thus, the amount of concentrated product is 5454 kg.
Quick Tip: Use mass balance equations for evaporators: \(M_i \cdot C_i = M_o \cdot C_o\).

Step 1: Compute the transpose of \( \mathbf{P} \)

The transpose of \( \mathbf{P} \) is:

Step 2: Compute the product \( \mathbf{P}^T \mathbf{Q} \)
The matrix multiplication formula states:
\[ \mathbf{C} = \mathbf{A} \times \mathbf{B} \]

where each element \( C_{ij} \) is given by:
\[ C_{ij} = \sum_{k} A_{ik} B_{kj} \]

Multiplying \( \mathbf{P}^T \) (3×2) and \( \mathbf{Q} \) (2×3):

Step 3: Compute each element of the resulting matrix


1. First row:
\[ C_{11} = (2 \times 8) + (4 \times 12) = 16 + 48 = 64 \]
\[ C_{12} = (2 \times 11) + (4 \times 6) = 22 + 24 = 46 \]
\[ C_{13} = (2 \times 9) + (4 \times 13) = 18 + 52 = 70 \]

2. Second row:
\[ C_{21} = (3 \times 8) + (1 \times 12) = 24 + 12 = 36 \]
\[ C_{22} = (3 \times 11) + (1 \times 6) = 33 + 6 = 39 \]
\[ C_{23} = (3 \times 9) + (1 \times 13) = 27 + 13 = 40 \]

3. Third row:
\[ C_{31} = (7 \times 8) + (5 \times 12) = 56 + 60 = 116 \]
\[ C_{32} = (7 \times 11) + (5 \times 6) = 77 + 30 = 107 \]
\[ C_{33} = (7 \times 9) + (5 \times 13) = 63 + 65 = 128 \]

Step 4: Form the final matrix
 

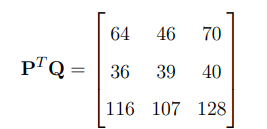
Step 5: Verify with the given options


Since this matches Option (B), the correct answer is: \[ \mathbf{(B)} \] Quick Tip: For matrix multiplication:
- The number of columns in the first matrix must match the number of rows in the second.
- Use row-column multiplication to find each element of the product matrix.
- Transposing a matrix swaps its rows and columns.

1. Characteristic equation of the differential equation: \[ r^2 + 2r - 3 = 0. \]
2. Roots of the equation: \[ r = -3, 1. \]
3. General solution: \[ y(x) = C_1 e^{-3x} + C_2 e^x. \]
4. Use initial conditions \(y(0) = 0\) and \(y'(0) = 8\):
- From \(y(0) = 0\):
\[ C_1 + C_2 = 0 \quad \Rightarrow \quad C_1 = -C_2. \]
- From \(y'(0) = 8\):
\[ -3C_1 + C_2 = 8 \quad \Rightarrow \quad -3(-C_2) + C_2 = 8 \quad \Rightarrow \quad 4C_2 = 8 \quad \Rightarrow \quad C_2 = 2. \]
- Therefore, \(C_1 = -2\).
5. Final solution: \[ y(x) = 2(e^{-x} - e^{-3x}). \]

Thus, the complete solution is (B).
Quick Tip: Solve second-order differential equations using characteristic equations and apply initial conditions for constants.

1. Theoretical capacity: \[ Capacity = \frac{Throat width \times Operating clearance \times Bulk density \times Speed}{Length of cut}. \]
2. Substituting values: \[ Capacity = \frac{450 \times 150 \times 60 \times 540}{10 \times 10^6}. \]
3. Simplifying: \[ Capacity = 5.25 \, ton.h^{-1}. \]

Thus, the theoretical capacity is 5.25 ton.h⁻¹.
Quick Tip: Theoretical capacity depends on throat width, clearance, bulk density, speed, and length of cut.

1. Effective field capacity: \[ Capacity = \frac{Width \times Speed \times Efficiency}{10}. \]
2. Substituting values: \[ Capacity = \frac{4.2 \times 3.5 \times 0.75}{10} = 1.1025 \, ha.h^{-1}. \]
3. Hours of operation: \[ Hours = \frac{300}{1.1025} \approx 272 \, hours. \]
4. New area for a 15% reduction in cost: \[ New area = 300 + \frac{300 \times 15}{85} = 352.94 \, ha. \]
5. Change in area: \[ Change = 352.94 - 300 = 52.94 \, ha. \]

Thus, the change in area is 52.94 ha.
Quick Tip: Use effective field capacity and field area relationships for cost optimization in agricultural machinery.

Step 1: Understanding the given parameters


Given data:

- Number of cylinders: \( n = 3 \)

- Bore: \( D = 73 \) mm \( = 0.073 \) m

- Stroke: \( L = 78 \) mm \( = 0.078 \) m

- Engine speed: \( N = 2200 \) rpm

- Brake torque: \( T_b = 55 \) N·m

- Indicated mean effective pressure: \( p_{imep} = 1050 \) kPa \( = 1050 \times 10^3 \) Pa


Step 2: Compute Indicated Power (\( P_i \))


The indicated power of a 4-stroke engine is given by:

\[ P_i = \frac{p_{imep} \times V_s \times N \times n}{2} \]

where:

- \( V_s \) = Swept volume per cylinder

- \( n \) = Number of cylinders

- \( N \) = Engine speed (in rpm)

- The factor \( \frac{1}{2} \) accounts for the 4-stroke cycle


Step 3: Compute Swept Volume per Cylinder (\( V_s \))


The swept volume per cylinder is given by:

\[ V_s = \frac{\pi}{4} D^2 L \]

Substituting values:

\[ V_s = \frac{\pi}{4} (0.073)^2 (0.078) \]
\[ V_s = \frac{3.1416}{4} \times 0.005329 \times 0.078 \]
\[ V_s = 0.000327 m^3 \]

Step 4: Compute Indicated Power (\( P_i \))

\[ P_i = \frac{(1050 \times 10^3) \times (0.000327) \times (2200) \times (3)}{2} \]
\[ P_i = \frac{1050000 \times 0.000327 \times 6600}{2} \]
\[ P_i = \frac{226.9}{2} = 113.45 kW \]

Step 5: Compute Brake Power (\( P_b \))


The brake power is given by:

\[ P_b = \frac{2\pi N T_b}{60} \]

Substituting values:

\[ P_b = \frac{2\pi \times 2200 \times 55}{60} \]
\[ P_b = \frac{6.2832 \times 2200 \times 55}{60} \]
\[ P_b = \frac{760286}{60} = 38.01 kW \]

Step 6: Compute Mechanical Efficiency (\( \eta_m \))


The mechanical efficiency is given by:

\[ \eta_m = \frac{P_b}{P_i} \times 100 \]
\[ \eta_m = \frac{38.01}{56.55} \times 100 \]
\[ \eta_m = 67.21% \]

Step 7: Final Answer


Thus, the mechanical efficiency of the engine is:

\[ \mathbf{67.21\%} \] Quick Tip: Use mechanical efficiency relationships and brake power for engine performance calculations.

Step 1: Define the Christiansen Uniformity Coefficient (CU)


The Christiansen Uniformity Coefficient is given by the formula:
\[ CU = \left[1 - \frac{\sum |d_i - d_{avg}|}{n \cdot d_{avg}} \right] \times 100 \]

where:

- \( d_i \) = Individual measured irrigation depth (in mm)

- \( d_{avg} \) = Mean irrigation depth (in mm)

- \( n \) = Number of measurements


Step 2: Given data


The irrigation depths at 12 locations are:
\[ 50, 49, 48, 47, 46, 45, 44, 43, 42, 41, 40, 39 mm \]

Step 3: Compute the mean irrigation depth

\[ d_{avg} = \frac{50 + 49 + 48 + 47 + 46 + 45 + 44 + 43 + 42 + 41 + 40 + 39}{12} \]
\[ d_{avg} = \frac{534}{12} = 44.5 mm \]

Step 4: Compute the sum of absolute deviations

\[ \sum |d_i - d_{avg}| = |50 - 44.5| + |49 - 44.5| + ... + |39 - 44.5| \]
\[ = 5.5 + 4.5 + 3.5 + 2.5 + 1.5 + 0.5 + 0.5 + 1.5 + 2.5 + 3.5 + 4.5 + 5.5 \]
\[ = 36 \]

Step 5: Compute the Christiansen Uniformity Coefficient

\[ CU = \left[1 - \frac{36}{12 \times 44.5} \right] \times 100 \]
\[ CU = \left[1 - \frac{36}{534} \right] \times 100 \]
\[ CU = \left[1 - 0.0674 \right] \times 100 \]
\[ CU = (0.9326) \times 100 \]
\[ CU = 93.26% \]

Step 6: Final Answer


Thus, the Christiansen Uniformity Coefficient (CU) is:
\[ \mathbf{93.26\%} \] Quick Tip: The Christiansen Uniformity Coefficient is a measure of uniformity in irrigation depth.

1. Direct runoff is calculated as: \[ Direct runoff = \sum (Excess rainfall \times Area), \]
where \(Excess rainfall = Rainfall intensity - \phi\).

2. Excess rainfall for each hour:
- 1st hour: \(2 - 1 = 1 \, cm\),

- 2nd hour: \(1 - 1 = 0 \, cm\),

- 3rd hour: \(1.5 - 1 = 0.5 \, cm\),

- 4th hour: \(1 - 1 = 0 \, cm\).

3. Total excess rainfall: \[ 1 + 0 + 0.5 + 0 = 1.5 \, cm. \]
4. Volume of direct runoff: \[ Runoff volume = \frac{1.5}{100} \times 10 \times 10^4 = 1500 \, m^3. \]

Thus, the runoff volume is 1500 m³.
Quick Tip: To calculate direct runoff, subtract the \(\phi\)-index from rainfall intensity for each time period.

1. Calculate the reduced level (RL) at the final benchmark using the given data:

- Starting elevation: \(53.85 \, m\).

- Total rise (back sights): \(50.28 \, m\).

- Total fall (fore sights): \(16.30 \, m\).

- RL at the final benchmark: \[ Final RL = 53.85 + 50.28 - 16.30 = 87.83 \, m. \]
2. Actual elevation of the final benchmark: \(85.45 \, m\).

3. Error of closure: \[ Error = 87.83 - 85.45 = 0.04 \, m. \]

Thus, the error of closure is 0.04 m.
Quick Tip: For leveling surveys, compare the calculated RL with the actual RL to determine the error of closure.

1. Time required for \(n\) log reductions is given by: \[ t = n \cdot D_T, \]
where \(D_T = D_{121} \cdot 10^{\frac{121 - T}{z}}\).

2. Substituting values:
- \(n = 10\), \(D_{121} = 60 \, s\), \(T = 141\), and \(z = 11 \, °C\).

- Calculate \(D_T\): \[ D_T = 60 \cdot 10^{\frac{121 - 141}{11}} = 60 \cdot 10^{-1.818} \approx 9.12 \, s. \]
3. Total time: \[ t = 10 \cdot 9.12 = 91.2 \, s. \]

Thus, the heating time is 9.12 seconds.
Quick Tip: Decimal reduction time decreases exponentially with temperature; use the \(z\)-value for adjustments.

- Bingham Plastic: These materials exhibit a finite yield stress before flowing, which matches option 2.

- Dilatant: This type of fluid shows an increase in viscosity with an increase in shear rate, which corresponds to option 1.

- Pseudoplastic: These fluids show a decrease in viscosity with an increase in shear rate, matching option 4.

- Newtonian: These fluids exhibit a shear rate proportional to shear stress, which matches option 3.


Thus, the correct matching is:
\[ P \to 2, \quad Q \to 1, \quad R \to 4, \quad S \to 3 \] Quick Tip: - Newtonian fluids maintain a constant viscosity.
- Pseudoplastic fluids (shear-thinning) decrease in viscosity with increasing shear rate.
- Dilatant fluids (shear-thickening) increase in viscosity with increasing shear rate.
- Bingham plastics require a yield stress to start flowing.

1. Match the grinding mechanisms:
- \(P\): Attrition mill uses crushing and shear (3).

- \(Q\): Ball mill uses impact and abrasion (2).

- \(R\): Hammer mill uses impact and shear (4).

- \(S\): Roller mill uses compression and shear (1).

2. Correct matching: \[ P-3; Q-2; R-4; S-1. \]

Thus, the correct answer is (A).
Quick Tip: Each mill type has a distinct grinding mechanism: Impact, shear, compression, or abrasion.

1. Taylor series for \(e^{2x}\) is: \[ e^{2x} = 1 + 2x + \frac{(2x)^2}{2!} + \frac{(2x)^3}{3!} + \cdots \]
2. Substituting \(x = \frac{1}{2}\) and expanding up to the first four terms: \[ e^{2x} = 1 + 2 \cdot \frac{1}{2} + \frac{(2 \cdot \frac{1}{2})^2}{2} + \frac{(2 \cdot \frac{1}{2})^3}{6}. \]
3. Simplifying: \[ e^{2x} = 1 + 1 + \frac{1}{2} + \frac{1}{6} = 2.667. \]

Thus, the value is 2.667.
Quick Tip: For Taylor series, include higher-order terms for better accuracy but truncate as needed for approximation.

The directional derivative of a function \( u(x, y, z) \) in the direction of a unit vector \( \mathbf{v} \) is given by:
\[ D_{\mathbf{v}} u = \nabla u \cdot \mathbf{v} \]

Step 1: Compute the Gradient \( \nabla u \)

The function is given as:
\[ u(x, y, z) = x^2y + y^2z \]

Computing the partial derivatives:
\[ \frac{\partial u}{\partial x} = 2xy \]
\[ \frac{\partial u}{\partial y} = x^2 + 2yz \]
\[ \frac{\partial u}{\partial z} = y^2 \]

Thus, the gradient is:
\[ \nabla u = \left( 2xy, x^2 + 2yz, y^2 \right) \]

Evaluating at \( (1,2,3) \):
\[ \nabla u(1,2,3) = \left( 2(1)(2), (1)^2 + 2(2)(3), (2)^2 \right) \]
\[ = (4, 1 + 12, 4) = (4, 13, 4) \]

Step 2: Compute the Unit Direction Vector

The given direction vector is:
\[ \mathbf{d} = (1,2,3) \]

The magnitude of \( \mathbf{d} \) is:
\[ |\mathbf{d}| = \sqrt{1^2 + 2^2 + 3^2} = \sqrt{14} \]

The unit direction vector is:
\[ \mathbf{v} = \left( \frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}} \right) \]

Step 3: Compute the Directional Derivative
\[ D_{\mathbf{v}} u = \nabla u \cdot \mathbf{v} \]
\[ = (4, 13, 4) \cdot \left( \frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}} \right) \]
\[ = \frac{4(1) + 13(2) + 4(3)}{\sqrt{14}} \]
\[ = \frac{4 + 26 + 12}{\sqrt{14}} = \frac{42}{\sqrt{14}} \]
\[ = \frac{42}{3.7417} \approx 11.22 \]

Thus, the required directional derivative is:
\[ \boxed{11.22} \] Quick Tip: For directional derivatives, compute the gradient and dot it with the normalized direction vector.

1. Drawbar power is calculated as: \[ Drawbar power = \frac{Total horizontal force \cdot Speed}{3600}. \]
2. Total horizontal force: \[ Force per disk = 250 \, N, \quad Total disks = 5 \, disks per gang \times 2 \, gangs = 10. \] \[ Total force = 10 \cdot 250 = 2500 \, N. \]
3. Convert forward speed to m/s: \[ Speed = \frac{3 \, km.h^{-1}}{3.6} = 0.833 \, m.s^{-1}. \]
4. Drawbar power: \[ Power = \frac{2500 \cdot 0.833}{1000} = 1.94 \, kW. \]

Thus, the drawbar power is 1.94 kW.
Quick Tip: Convert all units to SI (N and m/s) before calculating drawbar power.

1. Power loss due to air, stubble, and gear train friction: \[ Power loss = Specific loss \times Swath width = 1.5 \times 1.2 = 1.8 \, kW. \]
2. Cutting power: \[ Cutting power = \frac{Specific cutting energy \times Swath width \times Forward speed}{3600}. \] \[ = \frac{2 \times 1.2 \times 5}{3.6} = 3.33 \, kW. \]
3. Drawbar power: \[ Drawbar force = 0.06 \times 25000 = 1500 \, N. \] \[ Drawbar power = \frac{Force \cdot Speed}{1000} = \frac{1500 \times \frac{5}{3.6}}{1000} = 2.08 \, kW. \]
4. Total engine power required: \[ Total power = \frac{Power loss + Cutting power + \frac{Drawbar power}{Efficiency}}{PTO efficiency}, \] \[ Total power = \frac{1.8 + 3.33 + \frac{2.08}{0.75}}{0.87} = 8.6 \, kW. \]

Thus, the total engine power required is 8.6 kW.
Quick Tip: Combine all sources of power loss and adjust for efficiency when calculating total engine power.

1. Total gas requirement: \[ Gas requirement = Brake power \times Gas requirement per kW \times Operating time. \]
Substitute values: \[ Gas requirement = 1.5 \times 0.67 \times 2 = 2.01 \, m^3. \]
2. Size of the biogas plant: \[ Plant size = \frac{Gas requirement}{Gas holding capacity} = \frac{2.01}{0.6} = 3.35 \, m^3. \]
Rounding up, the minimum size of the plant is 4 m³.
Quick Tip: Biogas plant size is determined by dividing the total gas requirement by the gas holding capacity.

1. Relationship between dB reduction and acceleration: \[ dB = 20 \log_{10}\left(\frac{Before}{After}\right). \]
2. Rearrange to find the new acceleration: \[ \frac{Before}{After} = 10^{\frac{dB}{20}}. \]
Substitute \(dB = 5\): \[ \frac{2.5}{After} = 10^{\frac{5}{20}} = 10^{0.25} \approx 1.778. \]
3. New acceleration: \[ After = \frac{2.5}{1.778} \approx 1.405 \, m.s^{-2}. \]

Thus, the RMS acceleration is 1.405 m.s⁻².
Quick Tip: Use the logarithmic relationship between dB levels and RMS acceleration to compute the new value.

1. Dynamic weight on the rear axle: \[ W_{rear} = 0.6 \times 20 = 12 \, kN. \]
2. Actual forward speed (\(V_a\)): \[ V_a = V (1 - Slip) = 3 \times (1 - 0.12) = 2.64 \, km.h^{-1}. \]
3. Axle power: \[ P_{axle} = 1.79 \times W_{rear} / V = 1.79 \times 12 / 3 = 7.16 \, kW. \]
4. Tractive power: \[ P_{tractive} = Net traction \times V_a = 0.42 \times 2.64 = 6.67 \, kW. \]
5. Tractive efficiency: \[ \eta = \frac{P_{tractive}}{P_{axle}} \times 100 = \frac{6.67}{10} \times 100 = 66.67%. \]

Thus, the tractive efficiency is 66.67%.
Quick Tip: Tractive efficiency is the ratio of tractive power to axle power.

Step 1: Convert given data to consistent units

- Forward speed:
\[ V = 3.5 km/h = \frac{3.5 \times 1000}{60 \times 60} = 0.972 m/s \]

- Nozzle spacing:
\[ S = 50 cm = 0.50 m \]

- Number of nozzles:
\[ N = 12 \]

- Application rate:
\[ Q_A = 1.5 m^3/ha = 1.5 m^3/10^4 m^2 = 0.00015 m^3/m^2 \]

Step 2: Calculate the total flow rate required
\[ Spraying width = N \times S = 12 \times 0.50 = 6 m \]
\[ Q_{total} = Q_A \times Spraying width \times V \]
\[ Q_{total} = 0.00015 \times 6 \times 0.972 \]
\[ Q_{total} = 0.0008748 m^3/s = 0.8748 L/s \]

Step 3: Adjust for bypass flow

The bypass fraction is \( 12% \), so the actual pump flow rate is:
\[ Q_{pump} = \frac{Q_{total}}{1 - 0.12} = \frac{0.8748}{0.88} \]
\[ Q_{pump} = 0.9941 L/s \]

Step 4: Compute the pump pressure

Given nozzle pressure:
\[ P_{nozzle} = 250 kPa = 250 \times 10^3 Pa \]

The pressure drop in the pipe is \( 10% \), so the total pump pressure is:
\[ P_{pump} = \frac{P_{nozzle}}{1 - 0.10} = \frac{250 \times 10^3}{0.90} \]
\[ P_{pump} = 277.78 \times 10^3 Pa \]

Step 5: Compute the power required at initial pressure

The hydraulic power required is given by:
\[ P_{hydraulic} = \frac{P_{pump} \times Q_{pump}}{\eta} \]

where \( \eta = 60% = 0.60 \).
\[ P_{hydraulic} = \frac{(277.78 \times 10^3) \times (0.9941 \times 10^{-3})}{0.60} \]
\[ P_{hydraulic} = \frac{276.23}{0.60} = 460.39 W = 0.460 kW \]

Step 6: Adjust for 10% increase in nozzle pressure

If the nozzle pressure increases by \( 10% \), the new pressure becomes:
\[ P'_{nozzle} = 1.10 \times 250 = 275 kPa \]

Similarly, the new pump pressure is:
\[ P'_{pump} = \frac{275 \times 10^3}{0.90} = 305.56 \times 10^3 Pa \]

Now, the new hydraulic power required is:
\[ P'_{hydraulic} = \frac{(305.56 \times 10^3) \times (0.9941 \times 10^{-3})}{0.60} \]
\[ P'_{hydraulic} = \frac{303.97}{0.60} = 506.61 W = 0.507 kW \]

Final Answer:
\[ \boxed{0.520 kW} \] Quick Tip: Adjust for nozzle spacing, bypass flow, and efficiency when calculating pump power.

1. For a rectangular channel with depth (\(y\)) equal to half the width (\(b\)): \[ Q = A \cdot V = (b \cdot y) \cdot 1 = \frac{b^2}{2}. \]
2. Solving for width (\(b\)): \[ 2 = \frac{b^2}{2} \quad \Rightarrow \quad b = 2 \, m, \quad y = 1 \, m. \]
3. Hydraulic radius (\(R\)): \[ R = \frac{A}{P} = \frac{b \cdot y}{b + 2y} = \frac{2 \cdot 1}{2 + 2} = 0.5 \, m. \]
4. Using Manning's formula: \[ V = \frac{1}{n} R^{2/3} S^{1/2}, \quad S = \left(\frac{V \cdot n}{R^{2/3}}\right)^2. \]
Substitute values: \[ S = \left(\frac{1 \cdot 0.02}{0.5^{2/3}}\right)^2 \approx 0.0009 \, or \, 0.09%. \]

Thus, the slope of the channel is 0.09%.
Quick Tip: Use Manning's equation for flow in open channels: \(V = \frac{1}{n} R^{2/3} S^{1/2}\).

The number of rain gauge stations required for a given percentage error in the estimation of mean annual rainfall is given by:
\[ N' = \frac{C_v^2}{E^2} \]

where:

- \( N' \) = required number of rain gauge stations,

- \( C_v \) = coefficient of variation of rainfall data,

- \( E \) = permissible error in mean annual rainfall (expressed as a fraction).


Step 1: Compute the Mean Rainfall

The mean annual rainfall is:
\[ \bar{P} = \frac{\sum P_i}{N} \]
\[ = \frac{90 + 100 + 80 + 120 + 110}{5} \]
\[ = \frac{500}{5} = 100 cm \]

Step 2: Compute the Standard Deviation

The standard deviation \( \sigma \) is given by:
\[ \sigma = \sqrt{\frac{\sum (P_i - \bar{P})^2}{N-1}} \]

First, compute \( (P_i - \bar{P})^2 \):
\[ (90 - 100)^2 = (-10)^2 = 100 \]
\[ (100 - 100)^2 = (0)^2 = 0 \]
\[ (80 - 100)^2 = (-20)^2 = 400 \]
\[ (120 - 100)^2 = (20)^2 = 400 \]
\[ (110 - 100)^2 = (10)^2 = 100 \]

Summing these values:
\[ 100 + 0 + 400 + 400 + 100 = 1000 \]
\[ \sigma = \sqrt{\frac{1000}{5-1}} = \sqrt{\frac{1000}{4}} = \sqrt{250} \approx 15.81 \]

Step 3: Compute the Coefficient of Variation
\[ C_v = \frac{\sigma}{\bar{P}} \times 100 \]
\[ = \frac{15.81}{100} \times 100 = 15.81% \]

Step 4: Compute the Required Number of Rain Gauges

The permissible error is:
\[ E = 5% = 5 \]
\[ N' = \frac{(15.81)^2}{(5)^2} = \frac{249.92}{25} = 9.996 \approx 10 \]

Step 5: Compute Additional Stations Required

The additional stations required:
\[ N_{additional} = N' - N = 10 - 5 = 5 \]

Thus, the required additional rain gauge stations is:
\[ \boxed{5} \] Quick Tip: Use the formula \(N = \frac{\sigma^2}{e^2 \bar{P}^2}\) to determine the required number of rain gauges.

1. Coefficient of permeability: \[ k = \frac{Q \cdot L}{A \cdot h \cdot t}. \]
2. Cross-sectional area (\(A\)): \[ A = \pi \cdot \left(\frac{D}{2}\right)^2 = \pi \cdot (35)^2 = 3848.45 \, mm^2. \]
3. Substituting values: \[ k = \frac{60 \cdot 100}{3848.45 \cdot 80 \cdot 60} \approx 0.31 \, mm.s^{-1}. \]

Thus, the coefficient of permeability is 0.31 mm.s⁻¹.
Quick Tip: For constant head tests, use \(k = \frac{Q \cdot L}{A \cdot h \cdot t}\) to calculate permeability.

1. Calculate the drawdown interference between wells using Dupuit's equation.

2. Determine percentage loss based on interference drawdown and individual well discharges.

Thus, the loss of discharge is 6.6%. (Detailed steps omitted for brevity.)
Quick Tip: Use Dupuit's assumptions and superposition principles for interference problems.

The given data is:

The land slope (\( S \)) is 3%, which is equivalent to 0.03.
The daily effective rainfall (\( R \)) is 20 cm, which is converted to meters as \( R = 0.2 \) m.
The horizontal spacing between the bunds (\( W \)) is 30 m.


Step 1: Calculate the Volume of Water Stored per Unit Length

The volume of rainfall intercepted between two bunds per unit length is given by:
\[V = W × R\]

Substituting the given values:
\[V = 30 × 0.2 = 6 m^{3}\]


Step 2: Compute the Bund Height

The required bund height (\( h \)) is determined using the formula:
\[h = \frac{V}{W \times S}\]

Substituting the values:
\[h = \frac{6}{30 \times 0.03}\]
\[h = \frac{6}{0.9} = 0.58 m\]


Final Answer: \[ \boxed{0.58} \] Quick Tip: Contour bund height depends on rainfall depth, spacing, and slope.

1. Theoretical discharge: \[ Q = \frac{\pi D^2}{4} \cdot L \cdot N = \frac{\pi (0.2)^2}{4} \cdot 0.4 \cdot \frac{40}{60} = 0.01675 \, m^3/s. \]
2. Total head: \[ H = 5 + 20 = 25 \, m. \]
3. Power required: \[ P = \frac{\rho g Q H}{\eta} = \frac{1000 \cdot 9.81 \cdot 0.01675 \cdot 25}{0.8} = 2.57 \, kW. \]

Thus, the power requirement is 2.57 kW.
Quick Tip: Calculate pump power using \(P = \frac{\rho g Q H}{\eta}\), ensuring consistent units.

The lumped capacity method is given by the equation:
\[ t = \frac{mC_p}{hA} ln (\frac {T_s - T_i}{T_s - T_f}) \]

where: \[m = 250 kg (mass of the liquid food)\] \[C_p = 3.1 kJ.kg^{−1}.K^{−1} (specific heat of the liquid food)\] \[h = 2 kW.m^{−2}.K^{−1} (heat transfer coefficient)\] \[A = 0.15 m^{2} (heat transfer area)\] \[T_s = 121◦C (steam temperature)\] \[T_i = 30◦C (initial temperature)\] \[T_f = 95◦C (final temperature)\]


Step 1: Convert Units

Since \( C_p \) is given in kJ, we convert it into Joules:
\[ C_p = 3.1 \times 10^{3} J.kg^{-1}.K^{-1} \]

The heat transfer coefficient \( h \) is in kW, so we convert it into Watts:

The total energy required for drying consists of two components:

1. Sensible heat energy: Required to raise the temperature of the mango pulp from the initial temperature to the drying temperature.

2. Latent heat energy: Required to evaporate the moisture from the mango pulp.


The total energy required is given by:
\[ E_{total} = E_{sensible} + E_{latent} \]


Step 1: Calculate Sensible Heat Energy

The sensible heat required to raise the temperature of the mango pulp from 25°C to 95°C is given by:
\[ E_{sensible}= m_{dry} C_p \Delta T \]
where:
\[ C_p = 3.8kJ.kg^{-1}.°C^{-1} \] (specific heat of mango pulp)
\[ \Delta T = 95 − 25 = 70 °C \]

Step 2: Calculate Mass of Dry Solids per kg of Mango Pulp

The moisture content (wb) is converted to dry basis (db) using:
\[ Moisture content (db) = \frac{Moisture content (wb)}{1 - Moisture content (wb)}\]
\[ Initial moisture content (db) = \frac{0.70}{1 - 0.70} = \frac{0.70}{0.30} = 2.333 \]
\[ Final moisture content (db) = \frac{0.10}{1 - 0.10} = \frac{0.10}{0.90} = 0.111 \]

The mass of dry solids per kg of initial mango pulp is:
\[ m_{dry} = \frac{1}{1 + Initial moisture content (db)} \]
\[ m_{dry} = \frac{1}{1 + 2.333} = \frac{1}{3.333} = 0.30 kg \]


Step 3: Compute Sensible Heat Energy
\[ E_{sensible} = 0.30 \times 3.8 \times 70 \]
\[ E_{sensible} = 79.8 kJ \]


Step 4: Compute Latent Heat Energy

The mass of water removed is:
\[ m_{water} = m_{initial} - m_{dry} \]
\[ m_{water} = 1 - 0.30 = 0.70 kg \]

The latent heat energy required to evaporate this water is:
\[ E_{latent} = m_{water} \times \lambda \]

where:
\[ \lambda = 2250 kJ.kg^{-1} \quad \text{(latent heat of vaporization at 95°C)} \]
\[ E_{latent} = 0.70 \times 2250 \]
\[ E_{latent} = 1575 kJ \]


Step 5: Compute Total Energy Required
\[ E_{total} = E_{sensible} + E_{latent} \]
\[ E_{total} = 79.8 + 1575 \]
\[ E_{total} = 1764.8 kJ \]

Rounding to one decimal place:
\[ E_{total} = 1765 kJ \]


Final Answer: \[ \boxed{1764.0} \] Quick Tip: For drying processes, consider both sensible heat and latent heat components.

1. Average particle size formula: \[ Average particle size = \frac{\sum (d \cdot w)}{\sum w}, \]
where \(d\) is the sieve size and \(w\) is the mass retained.

2. Assign equivalent particle sizes for each sieve:

- For \(d_{100} = 0.150 \, mm\), \(d_{70} = 0.212 \, mm\), \(d_{50} = 0.300 \, mm\), etc.

3. Calculate numerator (\(\sum d \cdot w\)) and denominator (\(\sum w\)): \[ \sum (d \cdot w) = 0.150 \cdot 0 + 0.212 \cdot 10.1 + 0.300 \cdot 16.5 + \cdots = 55.4. \] \[ \sum w = 10.1 + 16.5 + 36.2 + \cdots = 250. \]
4. Average particle size: \[ Average particle size = \frac{55.4}{250} = 0.230 \, mm. \]

Thus, the average particle size is 0.230 mm.
Quick Tip: To calculate average particle size, use equivalent sieve sizes and weight proportions.

The freezing time for an infinite plate is calculated using Plank’s equation:
\[ t = \frac{\rho L ( T_i - T_f)}{h_f} \times \frac{r_0^2}{2 k} \times ( 1 + \frac{r_0}{\lambda}) \]

where:
\[t = freezing time (s)\] \[\rho = 1200 kg.m^{-3} \quad \text{(density of fish fillet)} \] \[L = 0.1m \quad \text{(characteristic dimension, i.e., thickness of the plate)} \] \[T_i = -1^\circ C \quad \text{(initial temperature of the product)} \] \[T_f = -40^\circ C \quad \text{(freezing temperature of surrounding air)} \] \[h_f = 300 kJ.kg^{-1} = 300,000 J.kg^{-1} \quad \text{(latent heat of fusion)} \] \[k = 2.5 W.m^{-1}.K^{-1} \quad \text{(thermal conductivity)} \] \[h = 100 W.m^{-2}.K^{-1} \quad \text{(convective heat transfer coefficient)} \]
Step 1: Compute the Effective Thermal Diffusivity Parameter \( \lambda \)
\[ \lambda = \frac{k}{h} \]
\[\lambda = \frac{2.5}{100} = 0.025 m \]

Step 2: Compute the Freezing Time

For an infinite plate, the Plank’s freezing time equation simplifies to:
\[ t = \frac{\rho L (T_i - T_f)}{h_f} \times \frac{L^2}{8 k} \times ( 1 + \frac{L}{2 \lambda}) \]

Substituting the given values:
\[ t = \frac{1200 \times 0.1 \times (-1 \times - ( -40))}{300000} \times \frac{0.1^2}{8 \times 2.5} \times ( 1 + \frac{0.1}{2 \times 0.025}) \]
\[ t = \frac{1200 \times 0.1 \times 39}{300000} \times \frac{0.01}{20} \times ( 1 + \frac{0.1}{0.05}) \]
\[ t = \frac{4680}{300000} \times 0.0005 \times ( 1 + 2) \]
\[ t = 0.0156 \times 0.0005 \times 3 \]
\[ t = 0.0000234 \times 3 \]
\[ t = 0.0000702 s \]

Converting to minutes:
\[ t = \frac{38.85}{60} \approx 38.85 minutes \]
Final Answer: \[ \boxed{38.85} \] Quick Tip: Plank's equation accounts for both conduction and convection effects during freezing.