GATE 2023 Statistics (ST) Question Paper PDF with Answer Key and Solutions PDF(Available)- Download Here

“I have not yet decided what I will do this evening; I _________ visit a friend.”

• (A) mite
• (B) would
• (C) might
• (D) didn’t

Eject : Insert :: Advance : ______ (By word meaning)

• (A) Advent
• (B) Progress
• (C) Retreat
• (D) Loan

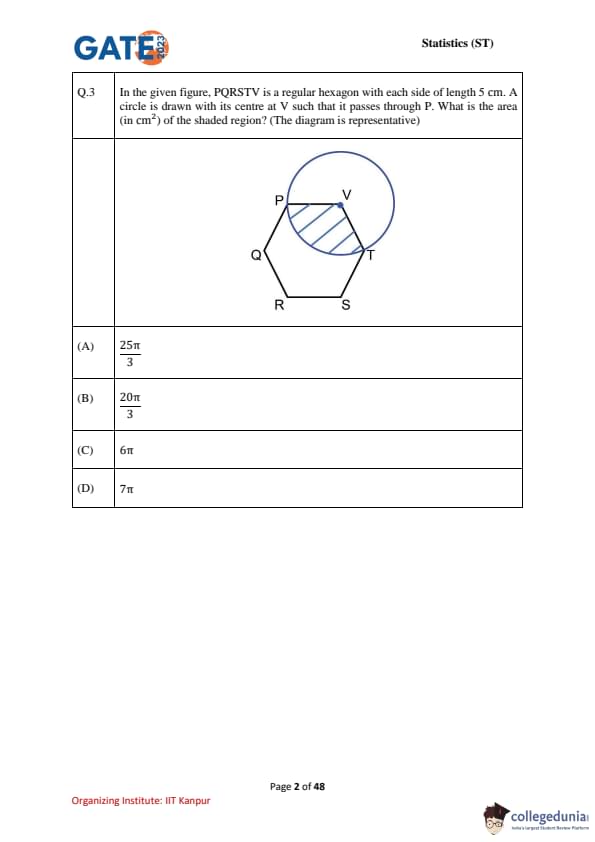
In the given figure, PQRSTV is a regular hexagon with each side of length 5 cm. A circle is drawn with its centre at V such that it passes through P. What is the area (in cm\(^2\)) of the shaded region? (The diagram is representative)

• (A) \(\dfrac{25\pi}{3}\)
• (B) \(\dfrac{20\pi}{3}\)
• (C) \(6\pi\)
• (D) \(7\pi\)

A duck named Donald Duck says “All ducks always lie.” Based only on the information above, which one of the following statements can be logically inferred with certainty?

• (A) Donald Duck always lies.
• (B) Donald Duck always tells the truth.
• (C) Donald Duck’s statement is true.
• (D) Donald Duck’s statement is false.

A line of symmetry is defined as a line that divides a figure into two parts in a way such that each part is a mirror image of the other part about that line. The figure below consists of 20 unit squares arranged as shown. In addition to the given black squares, up to 5 more may be coloured black. Which one among the following options depicts the minimum number of boxes that must be coloured black to achieve two lines of symmetry? (The figure is representative)

• (A) d
• (B) c, d, i
• (C) c, i
• (D) c, d, i, f, g

Based only on the truth of the statement ‘Some humans are intelligent’, which one of the following options can be logically inferred with certainty?

• (A) No human is intelligent.
• (B) All humans are intelligent.
• (C) Some non-humans are intelligent.
• (D) Some intelligent beings are humans.

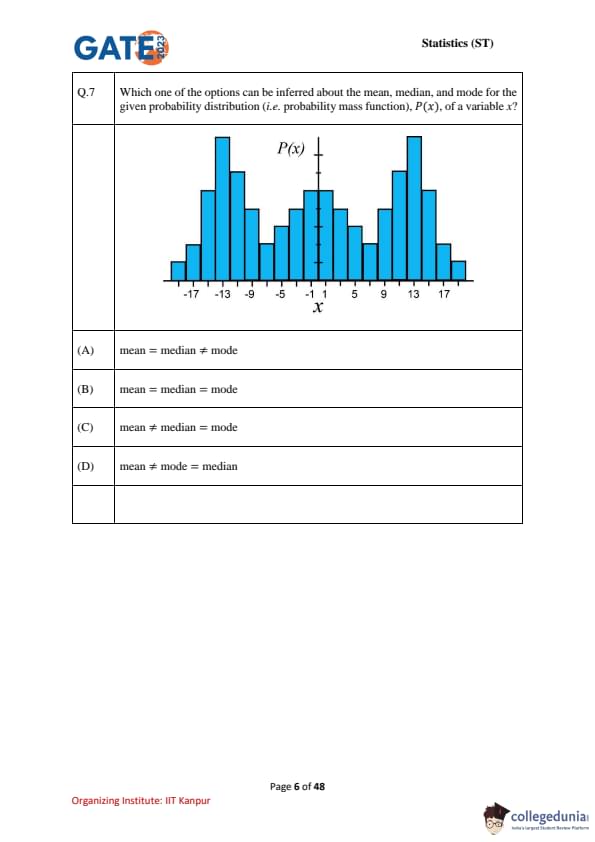
Which one of the options can be inferred about the mean, median, and mode for the given probability distribution (i.e. probability mass function), \(P(x)\), of a variable \(x\)?

• (A) mean = median \(\neq\) mode
• (B) mean = median = mode
• (C) mean \(\neq\) median = mode
• (D) mean \(\neq\) mode = median

The James Webb telescope, recently launched in space, is giving humankind unprecedented access to the depths of time by imaging very old stars formed almost 13 billion years ago. Astrophysicists and cosmologists believe that this odyssey in space may even shed light on the existence of dark matter. Dark matter is supposed to interact only via the gravitational interaction and not through the electromagnetic-, the weak- or the strong-interaction. This may justify the epithet “dark” in dark matter.

Based on the above paragraph, which one of the following statements is FALSE?

• (A) No other telescope has captured images of stars older than those captured by the James Webb telescope.
• (B) People other than astrophysicists and cosmologists may also believe in the existence of dark matter.
• (C) The James Webb telescope could be of use in the research on dark matter.
• (D) If dark matter was known to interact via the strong-interaction, then the epithet “dark” would be justified.

Let \(a = 30!\), \(b = 50!\), and \(c = 100!\). Consider the following numbers: \(\log_a c\), \(\log_c a\), \(\log_b a\), \(\log_a b\)

Which one of the following inequalities is CORRECT?

• (A) \(\log_a c < \log_a b < \log_b a < \log_a c\)
• (B) \(\log_c a < \log_a b < \log_b a < \log_b c\)
• (C) \(\log_c a < \log_a b < \log_a c < \log_b a\)
• (D) \(\log_b a < \log_c a < \log_a b < \log_a c\)

A square of side length 4 cm is given. The boundary of the shaded region is defined by one semi-circle on the top and two circular arcs at the bottom, each of radius 2 cm, as shown. The area of the shaded region is ______ cm\(^2\).

• (A) 8
• (B) 4
• (C) 12
• (D) 10

The area of the region bounded by the parabola \( x = -y^2 \) and the line \( y = x + 2 \) equals

• (A) \( \frac{3}{2} \)
• (B) \( \frac{7}{2} \)
• (C) \( \frac{9}{2} \)
• (D) 9

Let \( A \) be a \( 3 \times 3 \) real matrix having eigenvalues \( 1, 0, \) and \( -1 \). If \( B = A^2 + 2A + I_3 \), where \( I_3 \) is the \( 3 \times 3 \) identity matrix, then which one of the following statements is true?

• (A) \( B^3 - 5B^2 + 4B = 0 \)
• (B) \( B^3 - 5B^2 - 4B = 0 \)
• (C) \( B^3 + 5B^2 - 4B = 0 \)
• (D) \( B^3 + 5B^2 + 4B = 0 \)

Consider the following statements.

(I) Let A and B be two n \times n real matrices. If B is invertible, then rank(BA) = rank(A).

(II) Let A be an n \times n real matrix. If A^2x = b has a solution for every b \in \mathbb{R^n, then Ax = b also has a solution for every b \in \mathbb{R^n.

Which of the above statements is/are true?

• (A) Only (I)
• (B) Only (II)
• (C) Both (I) and (II)
• (D) Neither (I) nor (II)

Consider the probability space \((\Omega, \mathcal{G}, P)\), where \(\Omega = [0,2]\) and \(\mathcal{G} = \{\emptyset, \Omega, [0,1], (1,2]\}\). Let \(X\) and \(Y\) be two functions on \(\Omega\) defined as
\[ X(\omega) = \begin{cases} 1 & if \omega \in [0,1]
2 & if \omega \in (1,2] \end{cases} \]

and
\[ Y(\omega) = \begin{cases} 2 & if \omega \in [0,1.5]
3 & if \omega \in (1.5,2] \end{cases} \]

Then which one of the following statements is true?

• (A) \(X\) is a random variable with respect to \(\mathcal{G}\), but \(Y\) is not a random variable with respect to \(\mathcal{G}\)
• (B) \(Y\) is a random variable with respect to \(\mathcal{G}\), but \(X\) is not a random variable with respect to \(\mathcal{G}\)
• (C) Neither \(X\) nor \(Y\) is a random variable with respect to \(\mathcal{G}\)
• (D) Both \(X\) and \(Y\) are random variables with respect to \(\mathcal{G}\)

Let \( \Phi(\cdot) \) denote the cumulative distribution function of a standard normal random variable. If the random variable \( X \) has the cumulative distribution function \[ F(x) = \begin{cases} \Phi(x) & if x < -1,
\Phi(x + 1) & if x \geq -1, \end{cases} \]
then which one of the following statements is true?

• (A) \( P(X \leq -1) = \frac{1}{2} \)
• (B) \( P(X = -1) = \frac{1}{2} \)
• (C) \( P(X < -1) = \frac{1}{2} \)
• (D) \( P(X \leq 0) = \frac{1}{2} \)

Let \( X \) be a random variable with probability density function \[ f(x) = \begin{cases} \alpha \lambda x^{\alpha - 1} e^{-\lambda x^\alpha} & if x > 0
0 & otherwise \end{cases} \]
where \( \alpha > 0 \) and \( \lambda > 0 \). If the median of \( X \) is 1 and the third quantile is 2, then \( (\alpha, \lambda) \) equals:

• (A) \( (1, \log_e 2) \)
• (B) \( (1, 1) \)
• (C) \( (2, \log_e 2) \)
• (D) \( (1, \log_e 3) \)

Let \( X \) be a random variable having Poisson distribution with mean \( \lambda > 0 \). Then \( E \left( \frac{1}{X+1} \mid X > 0 \right) \) equals:

• (A) \( \frac{1 - e^{-\lambda} - \lambda e^{-\lambda}}{\lambda (1 - e^{-\lambda})} \)
• (B) \( \frac{1 - e^{-\lambda}}{\lambda} \)
• (C) \( \frac{1 - e^{-\lambda} - \lambda e^{-\lambda}}{\lambda} \)
• (D) \( \frac{1 - e^{-\lambda}}{\lambda + 1} \)

Suppose that \( X \) has the probability density function \[ f(x) = \begin{cases} \frac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha-1} e^{-\lambda x} & if x > 0
0 & otherwise, \end{cases} \]
where \( \alpha > 0 \) and \( \lambda > 0 \). Which one of the following statements is NOT true?

• (A) \( E(X) \) exists for all \( \alpha > 0 \) and \( \lambda > 0 \)
• (B) Variance of \( X \) exists for all \( \alpha > 0 \) and \( \lambda > 0 \)
• (C) \( E\left(\frac{1}{X}\right) \) exists for all \( \alpha > 0 \) and \( \lambda > 0 \)
• (D) \( E(\log(1 + X)) \) exists for all \( \alpha > 0 \) and \( \lambda > 0 \)

Let \( (X, Y) \) have joint probability density function \[ f(x, y) = \begin{cases} 8xy & if 0 < x < y < 1
0 & otherwise. \end{cases} \]
If \( E(X | Y = y_0) = \frac{1{2} \), then \( y_0 equals \)

• (A) \( \frac{3}{4} \)
• (B) \( \frac{1}{2} \)
• (C) \( \frac{1}{3} \)
• (D) \( \frac{2}{3} \)

Suppose that there are 5 boxes, each containing 3 blue pens, 1 red pen and 2 black pens. One pen is drawn at random from each of these 5 boxes. If the random variable X_1 denotes the total number of blue pens drawn and the random variable X_2 denotes the total number of red pens drawn, then P(X_1 = 2, X_2 = 1) equals:

• (A) \( \frac{5}{36} \)
• (B) \( \frac{5}{18} \)
• (C) \( \frac{5}{12} \)
• (D) \( \frac{5}{9} \)

Let \( \{X_n\}_{n \geq 1} \) and \( \{Y_n\}_{n \geq 1} \) be two sequences of random variables and \( X \) and \( Y \) be two random variables, all of them defined on the same probability space. Which one of the following statements is true?

• (A) If \( \{X_n\}_{n \geq 1} \) converges in distribution to a real constant \( c \), then \( \{X_n\}_{n \geq 1} \) converges in probability to \( c \)
• (B) If \( \{X_n\}_{n \geq 1} \) converges in probability to \( X \), then \( \{X_n\}_{n \geq 1} \) converges in 3rd mean to \( X \)
• (C) If \( \{X_n\}_{n \geq 1} \) converges in distribution to \( X \) and \( \{Y_n\}_{n \geq 1} \) converges in distribution to \( Y \), then \( \{X_n + Y_n\}_{n \geq 1} \) converges in distribution to \( X + Y \)
• (D) If \( E(X_n) \) converges to \( E(X) \), then \( \{X_n\}_{n \geq 1} \) converges in 1st mean to \( X \)

Let \( X \) be a random variable with probability density function \[ f(x; \lambda) = \begin{cases} \frac{1}{\lambda} e^{- \frac{x}{\lambda}} & if x > 0
0 & otherwise \end{cases} \]
where \( \lambda > 0 \) is an unknown parameter. Let \( Y_1, Y_2, \ldots, Y_n \) be a random sample of size \( n \) from a population having the same distribution as \( X^2 \). If \( \overline{Y} = \frac{1}{n} \sum_{i=1}^{n} Y_i \), then which one of the following statements is true?

• (A) \( \sqrt{\overline{Y}/2} \) is a method of moments estimator of \( \lambda \)
• (B) \( \sqrt{\overline{Y}} \) is a method of moments estimator of \( \lambda \)
• (C) \( \frac{1}{2} \sqrt{\overline{Y}} \) is a method of moments estimator of \( \lambda \)
• (D) \( 2 \sqrt{\overline{Y}} \) is a method of moments estimator of \( \lambda \)

Let X_1, X_2, \dots, X_n be a random sample of size n (\geq 2) from a population having probability density function \[ f(x; \theta) = \left\{ \begin{array{ll} \frac{2}{\theta} \left( -\log_e x \right)^2 e^{-\left( \frac{\log_e x}{\theta} \right)^2} & if 0 < x < 1
0 & otherwise \end{array} \right. \]
where \( \theta > 0 \) is an unknown parameter. Then which one of the following statements is true?

• (A) \( \frac{1}{n} \sum_{i=1}^{n} (\log_e X_i)^2 \) is the maximum likelihood estimator of \( \theta \)
• (B) \( \frac{1}{n-1} \sum_{i=1}^{n} (\log_e X_i) \) is the maximum likelihood estimator of \( \theta \)
• (C) \( \frac{1}{n} \sum_{i=1}^{n} \log_e X_i \) is the maximum likelihood estimator of \( \theta \)
• (D) \( \frac{1}{n-1} \sum_{i=1}^{n} \log_e X_i \) is the maximum likelihood estimator of \( \theta \)

Let \( X_1, X_2, \dots, X_n \) be a random sample of size \( n \) from a population having uniform distribution over the interval \( \left( \frac{1}{3}, \theta \right) \), where \( \theta > \frac{1}{3} \) is an unknown parameter. If \( Y = \max \{ X_1, X_2, \dots, X_n \} \), then which one of the following statements is true?

• (A) \( \left( \frac{n+1}{n} \right) (Y - \frac{1}{3}) + \frac{1}{3} \) is an unbiased estimator of \( \theta \)
• (B) \( \left( \frac{n}{n+1} \right) (Y - \frac{1}{3}) + \frac{1}{3} \) is an unbiased estimator of \( \theta \)
• (C) \( \left( \frac{n+1}{n} \right) (Y + \frac{1}{3}) - \frac{1}{3} \) is an unbiased estimator of \( \theta \)
• (D) \( Y \) is an unbiased estimator of \( \theta \)

Suppose that \( X_1, X_2, \dots, X_n, Y_1, Y_2, \dots, Y_n \) are independent and identically distributed random vectors each having \( N_p(\mu, \Sigma) \) distribution, where \( \Sigma \) is non-singular, \( p > 1 \) and \( n > 1 \). If \( \overline{X} = \frac{1}{n} \sum_{i=1}^n X_i \) and \( \overline{Y} = \frac{1}{n} \sum_{i=1}^n Y_i \), then which one of the following statements is true?

• (A) There exists \( c > 0 \) such that \( c (\overline{X} - \mu)^T \Sigma^{-1} (\overline{X} - \mu) \) has \( \chi^2 \)-distribution with \( p \) degrees of freedom
• (B) There exists \( c > 0 \) such that \( c (\overline{X} - \mu)^T \Sigma^{-1} (\overline{X} - \overline{Y}) \) has \( \chi^2 \)-distribution with \( (p - 1) \) degrees of freedom
• (C) There exists \( c > 0 \) such that \( c \sum_{i=1}^n (X_i - \overline{X})^T \Sigma^{-1} (X_i - \overline{X}) \) has \( \chi^2 \)-distribution with \( p \) degrees of freedom
• (D) There exists \( c > 0 \) such that \( c \sum_{i=1}^n (X_i - Y_i - \overline{X} + \overline{Y})^T \Sigma^{-1} (X_i - Y_i - \overline{X} + \overline{Y}) \) has \( \chi^2 \)-distribution with \( p \) degrees of freedom

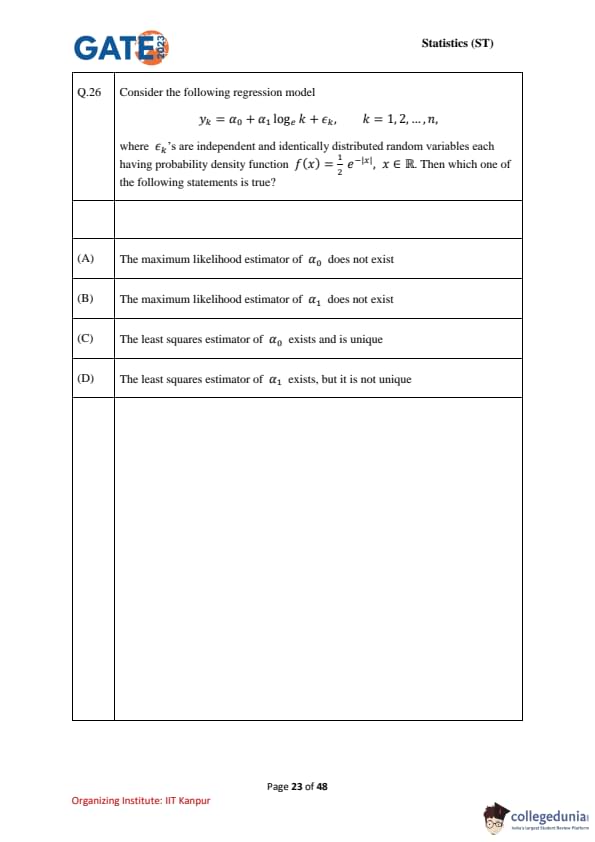
Consider the following regression model \[ y_k = \alpha_0 + \alpha_1 \log k + \epsilon_k, \quad k = 1, 2, \dots, n, \]
where \( \epsilon_k are independent and identically distributed random variables each having probability density function \ f(x) = \frac{1{2 e^{-|x|, \ x \in \mathbb{R. Then which one of the following statements is true?

• (A) The maximum likelihood estimator of \( \alpha_0 \) does not exist
• (B) The maximum likelihood estimator of \( \alpha_1 \) does not exist
• (C) The least squares estimator of \( \alpha_0 \) exists and is unique
• (D) The least squares estimator of \( \alpha_1 \) exists, but it is not unique

Suppose that \(X_1, X_2, \dots, X_n\) are independent and identically distributed random variables each having probability density function \(f(\cdot)\) and median \(\theta\). We want to test \[ H_0: \theta = \theta_0 \quad against \quad H_1: \theta > \theta_0. \]
Consider a test that rejects \(H_0\) if \(S > c\) for some \(c\) depending on the size of the test, where \(S\) is the cardinality of the set \(\{i: X_i > \theta_0, 1 \leq i \leq n\}\). Then which one of the following statements is true?

• (A) Under \(H_0\), the distribution of \(S\) depends on \(f(\cdot)\)
• (B) Under \(H_1\), the distribution of \(S\) does not depend on \(f(\cdot)\)
• (C) The power function depends on \(\theta\)
• (D) The power function does not depend on \(\theta\)

Suppose that \(x\) is an observed sample of size 1 from a population with probability density function \(f(\cdot)\). Based on \(x\), consider testing \[ H_0: f(y) = \frac{1}{\sqrt{2\pi}} e^{-y^2/2}, \quad y \in \mathbb{R} \quad against \quad H_1: f(y) = \frac{1}{2} e^{-|y|}, \quad y \in \mathbb{R}. \]
Then which one of the following statements is true?

• (A) The most powerful test rejects \(H_0\) if \(|x| > c\) for some \(c > 0\)
• (B) The most powerful test rejects \(H_0\) if \(|x| < c\) for some \(c > 0\)
• (C) The most powerful test rejects \(H_0\) if \(| |x| - 1 | > c\) for some \(c > 0\)
• (D) The most powerful test rejects \(H_0\) if \(| |x| - 1 | < c\) for some \(c > 0\)

Let \( f: \mathbb{R}^2 \rightarrow \mathbb{R} \) be defined by \( f(x, y) = xy \). Then the maximum value (rounded off to two decimal places) of \( f \) on the ellipse \( x^2 + 2y^2 = 1 \) equals ________.

Let \( A \) be a \( 2 \times 2 \) real matrix such that \( AB = BA \) for all \( 2 \times 2 \) real matrices \( B \). If the trace of \( A \) equals 5, then the determinant of \( A \) (rounded off to two decimal places) equals ________.

Two defective bulbs are present in a set of five bulbs. To remove the two defective bulbs, the bulbs are chosen randomly one by one and tested. If \( X \) denotes the minimum number of bulbs that must be tested to find out the two defective bulbs, then \( P(X = 3) \) (rounded off to two decimal places) equals:

• (A) 0.28 to 0.32
• (B) 0.15 to 0.20
• (C) 0.35 to 0.40
• (D) 0.45 to 0.50

Let \( \{X_n\}_{n \geq 1} \) be a sequence of independent and identically distributed random variables, each having mean 4 and variance 9. If \( Y_n = \frac{1}{n} \sum_{i=1}^{n} X_i \) for \( n \geq 1 \), then \[ \lim_{n \to \infty} E \left[ \left( \frac{Y_n - 4}{\sqrt{n}} \right)^2 \right] (in integer) equals: \]

• (A) 0
• (B) 4
• (C) 9
• (D) 1

Let \{W_t\_{t \geq 0 be a standard Brownian motion. Then E(W_4^2 | W_2 = 2) (in integer) equals:

Let \{X_n\_{n \geq 1 be a Markov chain with state space \{1, 2, 3\ and transition probability matrix \[ P = \begin{bmatrix \frac{1}{2} & \frac{1}{4} & \frac{1}{4}
\frac{1}{3} & \frac{1}{3} & \frac{1}{3}
0 & \frac{1}{2} & \frac{1}{2} \end{bmatrix} \]
Then P(X_2 = 1 | X_1 = 1, X_3 = 2) (rounded off to two decimal places) equals:

Suppose that \( (X_1, X_2, X_3) \) has a \( N_3(\mu, \Sigma) \) distribution with \[ \mu = \begin{pmatrix} 0
0 \end{pmatrix} \quad and \quad \Sigma = \begin{pmatrix} 2 & 2 & 1
2 & 5 & 1
1 & 1 & 1 \end{pmatrix}. \]
Given that \( \Phi(-0.5) = 0.3085 \), where \( \Phi(\cdot) \) denotes the cumulative distribution function of a standard normal random variable, \[ P\left( (X_1 - 2X_2 + 2X_3)^2 < \frac{7{2} \right) \quad (rounded off to two decimal places) equals \_\_\_\_\_\_\_\_ \]

Let \( A \) be an \( n \times n \) real matrix. Consider the following statements.

(I) If \( A \) is symmetric, then there exists \( c \geq 0 \) such that \( A + c I_n \) is symmetric and positive definite, where \( I_n \) is the \( n \times n \) identity matrix.

(II) If \( A \) is symmetric and positive definite, then there exists a symmetric and positive definite matrix \( B \) such that \( A = B^2 \).

Which of the above statements is/are true?

• (A) Only (I)
• (B) Only (II)
• (C) Both (I) and (II)
• (D) Neither (I) nor (II)

Let \(X\) be a random variable with probability density function \[ f(x) = \begin{cases} \frac{1}{x^2} & if x \geq 1,
0 & otherwise. \end{cases} \]
If \(Y = \log X\), then \(P(Y < 1 \mid Y < 2)\) equals

• (A) \(\frac{e}{1 + e}\)
• (B) \(\frac{e - 1}{e + 1}\)
• (C) \(\frac{1}{1 + e}\)
• (D) \(\frac{1}{e - 1}\)

Let \(\{N(t)\}_{t \geq 0}\) be a Poisson process with rate 1. Consider the following statements.


[(I)] \(P(N(3) = 3 \mid N(5) = 5) = \binom{5}{3} \left(\frac{3}{5}\right)^3 \left(\frac{2}{5}\right)^2\).
[(II)] If \(S_5\) denotes the time of occurrence of the 5th event for the above Poisson process, then \(E(S_5 \mid N(5) = 3) = 7\).


Which of the above statements is/are true?

• (A) Only (I)
• (B) Only (II)
• (C) Both (I) and (II)
• (D) Neither (I) nor (II)

Let \( X_1, X_2, \dots, X_n \) be a random sample of size \( n \) from a population having probability density function \[ f(x; \mu) = \begin{cases} e^{-(x-\mu)} & if \mu \leq x < \infty
0 & otherwise \end{cases} \]
where \( \mu \in \mathbb{R} \) is an unknown parameter. If \( \hat{M} \) is the maximum likelihood estimator of the median of \( X_1 \), then which one of the following statements is true?

• (A) \( P(\hat{M} \leq 2) = 1 - e^{-n(1 - \log 2)} if \mu = 1 \)
• (B) \( P(\hat{M} \leq 1) = 1 - e^{-n \log 2} if \mu = 1 \)
• (C) \( P(\hat{M} \leq 3) = 1 - e^{-n(1 - \log 2)} if \mu = 1 \)
• (D) \( P(\hat{M} \leq 4) = 1 - e^{-n(2 \log e 2 - 1)} if \mu = 1 \)

Let \( X_1, X_2, \dots, X_{10} \) be a random sample of size 10 from a population having \( N(0, \theta^2) \) distribution, where \( \theta > 0 \) is an unknown parameter.
Let \( T = \frac{1}{10} \sum_{i=1}^{10} X_i^2 \). If the mean square error of \( cT \) (for \( c > 0 \)), as an estimator of \( \theta^2 \), is minimized at \( c = c_0 \), then the value of \( c_0 \) equals

• (A) \( \frac{5}{6} \)
• (B) \( \frac{2}{3} \)
• (C) \( \frac{3}{5} \)
• (D) \( \frac{1}{2} \)

Suppose that \( X_1, X_2, \dots, X_{10} \) are independent and identically distributed random vectors each having \( N_2(\mu, \Sigma) \) distribution, where \( \Sigma \) is non-singular. If \[ U = \frac{1}{1 + (\bar{X} - \mu)^T \Sigma^{-1} (\bar{X} - \mu)} \]
where \( \bar{X = \frac{1}{10} \sum_{i=1}^{10} X_i \), then the value of \[ \log_e P(U \leq \frac{1}{2}) equals: \]

• (A) -5
• (B) -10
• (C) -2
• (D) -1

Suppose that \( (X, Y) \) has joint probability mass function \[ P(X = 0, Y = 0) = P(X = 1, Y = 1) = \theta, \quad P(X = 1, Y = 0) = P(X = 0, Y = 1) = \frac{1}{2} - \theta, \]
where \( 0 \leq \theta \leq \frac{1{2} \) is an unknown parameter. Consider testing \( H_0 : \theta = \frac{1}{4} \) against \( H_1 : \theta = \frac{1}{3} \), based on a random sample \[ \{ (X_1, Y_1), (X_2, Y_2), \dots, (X_n, Y_n) \} \]
from the above probability mass function. Let \( M \) be the cardinality of the set \[ \{ i : X_i = Y_i, 1 \leq i \leq n \, \]
If \( m \) is the observed value of \( M \), then which one of the following statements is true?

• (A) The likelihood ratio test rejects \( H_0 \) if \( m > c \) for some \( c \)
• (B) The likelihood ratio test rejects \( H_0 \) if \( m < c \) for some \( c \)
• (C) The likelihood ratio test rejects \( H_0 \) if \( c_1 < m < c_2 \) for some \( c_1 \) and \( c_2 \)
• (D) The likelihood ratio test rejects \( H_0 \) if \( m < c_1 \) or \( m > c_2 \) for some \( c_1 \) and \( c_2 \)

Let g(x) = f(x) + f(2 - x) for all x \in [0, 2], where f : [0, 2] \to \mathbb{R is continuous on [0, 2] and twice differentiable on (0, 2). If g' denotes the first derivative of g and f'' denotes the second derivative of f, then which of the following statements is NOT true?

• (A) There exists \( c \in (0, 2) \) such that \( g'(c) = 0 \)
• (B) If \( f'' > 0 \) on \( (0, 2) \), then \( g \) is strictly decreasing on \( (0, 1) \)
• (C) If \( f'' < 0 \) on \( (0, 2) \), then \( g \) is strictly increasing on \( (1, 2) \)
• (D) If \( f'' = 0 \) on \( (0, 2) \), then \( g \) is a constant function

For any subset \( U \) of \( \mathbb{R}^n \), let \( L(U) \) denote the span of \( U \). For any two subsets \( T \) and \( S \) of \( \mathbb{R}^n \), which one of the following statements is NOT true?

• (A) If \( T \) is a proper subset of \( S \), then \( L(T) \) is a proper subset of \( L(S) \)
• (B) \( L(L(S)) = L(S) \)
• (C) \( L(T \cup S) = \{ u + v : u \in L(T), v \in L(S) \} \)
• (D) If \( \alpha, \beta \) and \( \gamma \) are three vectors in \( \mathbb{R}^n \) such that \( \alpha + 2\beta + 3\gamma = 0 \), then \( L(\{ \alpha, \beta \}) = L(\{ \beta, \gamma \}) \)

Let \( f \) be a continuous function from \( [0, 1] \) to the set of all real numbers. Then which one of the following statements is NOT true?

• (A) For any sequence \( \{x_n\}_{n \geq 1} \) in \( [0, 1] \), \( \sum_{n=1}^{\infty} \frac{f(x_n)}{n^2} \) is absolutely convergent
• (B) If \( |f(x)| = 1 \) for all \( x \in [0, 1] \), then \( \left| \int_0^1 f(x) dx \right| = 1 \)
• (C) If \( \{x_n\}_{n \geq 1} \) is a sequence in \( [0, 1] \) such that \( \{f(x_n)\}_{n \geq 1} \) is convergent, then \( \{x_n\}_{n \geq 1} \) is convergent
• (D) If \( f \) is also monotonically increasing, then the image of \( f \) is given by \( [f(0), f(1)] \)

Let \( X \) be a random variable with cumulative distribution function \[ F(x) = \begin{cases} 0 & if x < -1
\frac{1}{4}(x + 1) & if -1 \leq x < 0
\frac{1}{4}(x + 3) & if 0 \leq x < 1
1 & if x \geq 1 \end{cases} \]
Which one of the following statements is true?

• (A) \( \lim_{n \to \infty} P\left( -\frac{1}{2} + \frac{1}{n} < X < -1 - \frac{1}{n} \right) = \frac{5}{8} \)
• (B) \( \lim_{n \to \infty} P\left( -\frac{1}{2} - \frac{1}{n} < X < 1 - \frac{1}{n} \right) = \frac{5}{8} \)
• (C) \( \lim_{n \to \infty} P\left( X = -\frac{1}{n} \right) = \frac{1}{2} \)
• (D) \( P(X = 0) = \frac{1}{3} \)

Let \((X, Y)\) have joint probability mass function \[ p(x, y) = \begin{cases} \frac{c}{2x + y + 2} & if x = 0, 1, 2, \dots; \, y = 0, 1, 2, \dots; \, x \neq y,
0 & otherwise. \end{cases} \]
Then which one of the following statements is true?

• (A) \(c = \frac{1}{2}\)
• (B) \(c = \frac{1}{4}\)
• (C) \(c > 1\)
• (D) \(X\) and \(Y\) are independent

Let \(X_1, X_2, \dots, X_{10}\) be a random sample of size 10 from a \(N_3(\mu, \Sigma)\) distribution, where \(\mu\) and non-singular \(\Sigma\) are unknown parameters. If \[ \overline{X_1} = \frac{1}{5} \sum_{i=1}^{5} X_i, \quad \overline{X_2} = \frac{1}{5} \sum_{i=6}^{10} X_i, \] \[ S_1 = \frac{1}{4} \sum_{i=1}^{5} (X_i - \overline{X_1})(X_i - \overline{X_1})^T, \quad S_2 = \frac{1}{4} \sum_{i=6}^{10} (X_i - \overline{X_2})(X_i - \overline{X_2})^T, \]
then which one of the following statements is NOT true?

• (A) \(\frac{5}{6} (\overline{X_1} - \mu)^T S_1^{-1} (\overline{X_1} - \mu)\) follows an \(F\)-distribution with 3 and 2 degrees of freedom.
• (B) \(\frac{6}{5} (\overline{X_1} - \mu)^T S_1^{-1} (\overline{X_1} - \mu)\) follows an \(F\)-distribution with 2 and 3 degrees of freedom.
• (C) \(4(S_1 + S_2)\) follows a Wishart distribution of order 3 with 8 degrees of freedom.
• (D) \(5(S_1 + S_2)\) follows a Wishart distribution of order 3 with 10 degrees of freedom.

Which of the following sets is/are countable?

• (A) The set of all functions from \( \{1, 2, 3, \dots, 10\} \) to the set of all rational numbers
• (B) The set of all functions from the set of all natural numbers to \( \{0, 1\} \)
• (C) The set of all integer-valued sequences with only finitely many non-zero terms
• (D) The set of all integer-valued sequences converging to 1

For a given real number \( a \), let \( a^+ = \max\{a, 0\} \) and \( a^- = \max\{-a, 0\} \). If \( \{x_n\}_{n \geq 1} \) is a sequence of real numbers, then which of the following statements is/are true?

• (A) If \( \{x_n\}_{n \geq 1} \) converges, then both \( \{x_n^+\}_{n \geq 1} \) and \( \{x_n^-\}_{n \geq 1} \) converge
• (B) If \( \{x_n\}_{n \geq 1} \) converges to 0, then both \( \{x_n^+\}_{n \geq 1} \) and \( \{x_n^-\}_{n \geq 1} \) converge to 0
• (C) If both \( \{x_n^+\}_{n \geq 1} \) and \( \{x_n^-\}_{n \geq 1} \) converge, then \( \{x_n\}_{n \geq 1} \) converges
• (D) If \( \{x_n^2\}_{n \geq 1} \) converges, then both \( \{x_n^+\}_{n \geq 1} \) and \( \{x_n^-\}_{n \geq 1} \) converge

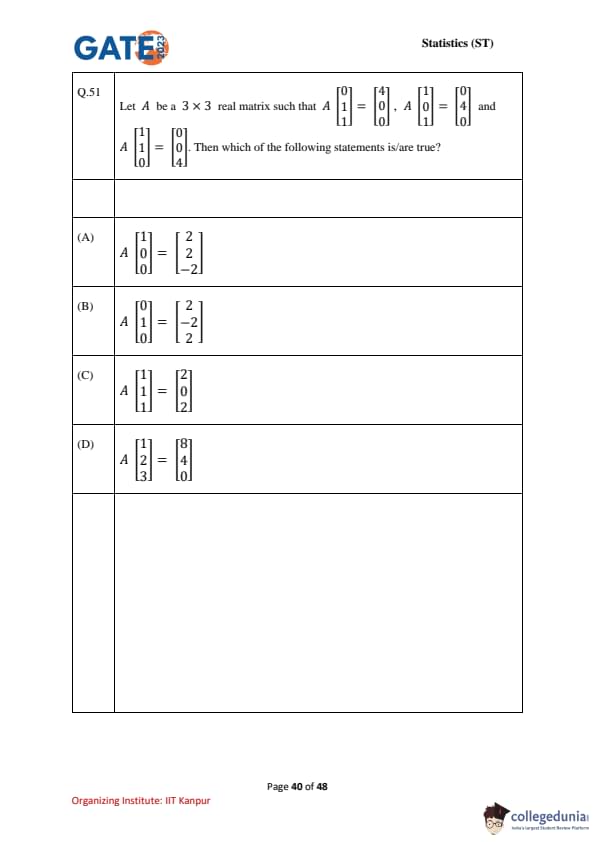
Let \( A \) be a \( 3 \times 3 \) real matrix such that \[ A \begin{bmatrix} 1
1
0 \end{bmatrix} = \begin{bmatrix} 0
4
0 \end{bmatrix}, \quad A \begin{bmatrix} 0
1
1 \end{bmatrix} = \begin{bmatrix} 4
0
0 \end{bmatrix}, \quad A \begin{bmatrix} 1
0
1 \end{bmatrix} = \begin{bmatrix} 0
0
4 \end{bmatrix}. \]
Then which of the following statements is/are true?

• (A) \( A \begin{bmatrix} 1
  0
  0 \end{bmatrix} = \begin{bmatrix} 2
  2
  -2 \end{bmatrix} \)
• (B) \( A \begin{bmatrix} 0
  1
  0 \end{bmatrix} = \begin{bmatrix} 2
  -2
  2 \end{bmatrix} \)
• (C) \( A \begin{bmatrix} 1
  1
  1 \end{bmatrix} = \begin{bmatrix} 2
  0
  2 \end{bmatrix} \)
• (D) \( A \begin{bmatrix} 1
  2
  3 \end{bmatrix} = \begin{bmatrix} 8
  4
  0 \end{bmatrix} \)

Let \( X \) be a positive valued continuous random variable with finite mean. If \( Y = \lfloor X \rfloor \), the largest integer less than or equal to \( X \), then which of the following statements is/are true?

• (A) \( P(Y \leq u) \leq P(X \leq u) \) for all \( u \geq 0 \)
• (B) \( P(Y \geq u) \leq P(X \geq u) \) for all \( u \geq 0 \)
• (C) \( E(Y) < E(X) \)
• (D) \( E(X) > E(Y) \)

Let X be a random variable with probability density function \[ f(x) = \begin{cases e^{-x} & if x \geq 0
0 & otherwise \end{cases} \]
For \( a < b \), if \( U(a, b) \) denotes the uniform distribution over the interval \( (a, b) \), then which of the following statements is/are true?

• (A) \( e^{-X} \) follows \( U(-1, 0) \) distribution
• (B) \( 1 - e^{-X} \) follows \( U(0, 2) \) distribution
• (C) \( 2e^{-X} - 1 \) follows \( U(-1, 1) \) distribution
• (D) The probability mass function of \( Y = [X] \) is \( P(Y = k) = (1 - e^{-1}) e^{-k} for k = 0, 1, 2, \dots \), where \( [X] \) denotes the largest integer not exceeding \( X \)

Suppose that X is a discrete random variable with the following probability mass function: \[ P(X = 0) = \frac{1{2}(1 + e^{-1}), \quad P(X = k) = \frac{e^{-1}}{2 k!} for k = 1, 2, 3, \dots \]
Which of the following statements is/are true?

• (A) \( E(X) = 1 \)
• (B) \( E(X) < 1 \)
• (C) \( E(X | X > 0) < \frac{1}{2} \)
• (D) \( E(X | X > 0) > \frac{1}{2} \)

Suppose that \( U \) and \( V \) are two independent and identically distributed random variables each having probability density function \[ f(x) = \begin{cases} \lambda^2 x e^{-\lambda x} & if x > 0
0 & otherwise, \end{cases} \]
where \( \lambda > 0 \). Which of the following statements is/are true?

• (A) The distribution of \( U - V \) is symmetric about 0
• (B) The distribution of \( UV \) does not depend on \( \lambda \)
• (C) The distribution of \( \frac{U}{V} \) does not depend on \( \lambda \)
• (D) The distribution of \( \frac{U}{V} \) is symmetric about 1

Let \( (X, Y) \) have joint probability mass function \[ p(x, y) = \begin{cases} \frac{e^{-2}}{x! (y - x)!} & if x = 0, 1, 2, \dots, y; \, y = 0, 1, 2, \dots
0 & otherwise. \end{cases} \]
Then which of the following statements is/are true?

• (A) \( E(X | Y = 4) = 2 \)
• (B) The moment generating function of \( Y \) is \( e^2 (e^{v-1}) \) for all \( v \in \mathbb{R} \)
• (C) \( E(X) = 2 \)
• (D) The joint moment generating function of \( (X, Y) \) is \( e^{-2} (1 + e^u) e^v \) for all \( (u, v) \in \mathbb{R}^2 \)

Let \(\{X_n\}_{n \geq 1}\) be a sequence of independent and identically distributed random variables with mean 0 and variance 1, all of them defined on the same probability space. For \(n = 1, 2, 3, \dots\), let \[ Y_n = \frac{1}{n} \left( X_1 X_2 + X_3 X_4 + \dots + X_{2n-1} X_{2n} \right). \]
Then which one of the following statements is/are true?

• (A) \(\{ \sqrt{n} Y_n \}_{n \geq 1}\) converges in distribution to a standard normal random variable.
• (B) \(\{ Y_n \}_{n \geq 1}\) converges in 2nd mean to 0.
• (C) \(\{ Y_n + \frac{1}{n} \}_{n \geq 1}\) converges in probability to 0.
• (D) \(\{ X_n \}_{n \geq 1}\) converges almost surely to 0.

Consider the following regression model \[ y_t = \alpha_0 + \alpha_1 t + \alpha_2 t^2 + \epsilon_t, \quad t = 1, 2, \dots, 100, \]
where \(\alpha_0, \alpha_1, \alpha_2\) are unknown parameters and \(\epsilon_t\)'s are independent and identically distributed random variables each having \(N(\mu, 1)\) distribution with \(\mu \in \mathbb{R}\) unknown. Then which one of the following statements is/are true?

• (A) There exists an unbiased estimator of \(\alpha_1\).
• (B) There exists an unbiased estimator of \(\alpha_2\).
• (C) There exists an unbiased estimator of \(\alpha_0\).
• (D) There exists an unbiased estimator of \(\mu\).

Consider the orthonormal set \[ v_1 = \begin{bmatrix} \frac{1}{\sqrt{3}}
\frac{1}{\sqrt{3}}
\frac{1}{\sqrt{3}} \end{bmatrix}, v_2 = \begin{bmatrix} \frac{1}{\sqrt{6}}
\frac{2}{\sqrt{6}}
\frac{1}{\sqrt{6}} \end{bmatrix}, v_3 = \begin{bmatrix} \frac{1}{\sqrt{2}}
0
\frac{1}{\sqrt{2}} \end{bmatrix} \]
with respect to the standard inner product on \( \mathbb{R}^3 \). If \( u = \begin{bmatrix} a
b
c \end{bmatrix} \) is the vector such that inner products of \( u \) with \( v_1, v_2 \) and \( v_3 \) are 1, 2 and 3, respectively, then \( a^2 + b^2 + c^2 \) (in integer) equals ________.

Consider the probability space \( (\Omega, \mathcal{G}, P) \), where \( \Omega = \{1, 2, 3, 4\} \), \[ \mathcal{G} = \{\emptyset, \Omega, \{4\}, \{2, 3\}, \{1, 4\}, \{1, 2, 3\}, \{2, 3, 4\}\}, \]
and \( P(\{1\}) = \frac{1}{4} \). Let \( X \) be the random variable defined on the above probability space as \[ X(1) = 1, X(2) = X(3) = 2, X(4) = 3. \]
If \( P(X \leq 2) = \frac{3}{4} \), then \( P(\{1, 4\}) \) (rounded off to two decimal places) equals ________.

Let \( \{ X_n \}_{n \geq 1} \) be a sequence of independent and identically distributed random variables each having probability density function \[ f(x) = \begin{cases} e^{-x} & if x > 0
0 & otherwise \end{cases} \]
For \( n \geq 1 \), let \[ Y_n = |X_{2n - X_{2n-1}|. \]
If \[ \bar{Y_n = \frac{1}{n} \sum_{i=1}^{n} Y_i \quad for \quad n \geq 1 \]
and \[ \left\{ \sqrt{n \left( e^{-\bar{Y}_n} - e^{-1} \right) \right\}_{n \geq 1} converges in distribution to a normal random variable with mean 0 and variance \sigma^2, then \sigma^2 (rounded off to two decimal places) equals: \]

Consider a birth-death process on the state space \( \{ 0, 1, 2, 3 \} \). The birth rates are given by \( \lambda_0 = 1, \lambda_1 = 1, \lambda_2 = 2, \lambda_3 = 0 \). The death rates are given by \( \mu_0 = 0, \mu_1 = 1, \mu_2 = 1, \mu_3 = 1 \). If \( [\pi_0, \pi_1, \pi_2, \pi_3] \) is the unique stationary distribution, then \( \pi_0 + 2\pi_1 + 3\pi_2 + 4\pi_3 \) (rounded off to two decimal places) equals:

Let \( \{-1, -\frac{1}{2}, 1, \frac{5}{2}, 3\} \) be a realization of a random sample of size 5 from a population having \( N \left(\frac{1}{2}, \sigma^2 \right) \) distribution, where \( \sigma > 0 \) is an unknown parameter. Let \( T \) be an unbiased estimator of \( \sigma^2 \) whose variance attains the Cramer-Rao lower bound. Then based on the above data, the realized value of \( T \) (rounded off to two decimal places) equals ______________.

Let X be a random sample of size 1 from a population with cumulative distribution function \[ F(x) = \begin{cases} 0 & if x < 0
1 - (1 - x)^\theta & if 0 \leq x < 1
1 & if x \geq 1 \end{cases} \]
where \( \theta > 0 \) is an unknown parameter. To test \( H_0 : \theta = 1 \) against \( H_1 : \theta = 2 \), consider using the critical region \( \{ x \in \mathbb{R} : x < 0.5 \} \). If \( \alpha \) and \( \beta \) denote the level and power of the test, respectively, then \( \alpha + \beta \) (rounded off to two decimal places) equals:

Let \( \{0.13, 0.12, 0.78, 0.51\} \) be a realization of a random sample of size 4 from a population with cumulative distribution function \( F(\cdot) \). Consider testing \( H_0: F = F_0 \) against \( H_1: F \neq F_0 \), where \[ F_0(x) = \begin{cases} 0 & if x < 0,
x & if 0 \leq x < 1,
1 & if x \geq 1. \end{cases} \]
Let \( D \) denote the Kolmogorov-Smirnov test statistic. If \( P(D > 0.669) = 0.01 under H_0 and \psi = \begin{cases} 1 & if H_0 is accepted at level 0.01,
0 & otherwise, \end{cases} \] then based on the given data, the observed value of \( D + \psi \) (rounded off to two decimal places) equals ________