GATE 2023 Production and Industrial Engineering Question Paper PDF is available here for download. IIT Kanpur conducted GATE 2023 Production and Industrial Engineering exam on February 11, 2023 in the Afternoon Session from 02:30 PM to 05:30 PM. Students have to answer 65 questions in GATE 2023 Production and Industrial Engineering Question Paper carrying a total weightage of 100 marks. 10 questions are from the General Aptitude section and 55 questions are from Engineering Mathematics and Core Discipline.
GATE 2023 Production and Industrial Engineering Question Paper with Solutions PDF
| GATE 2023 Production and Industrial Engineering Question Paper with Solutions |
Check Solutions |

“You are delaying the completion of the task. Send _________ contributions at the earliest.”
References : _________ : : Guidelines : Implement
(By word meaning)
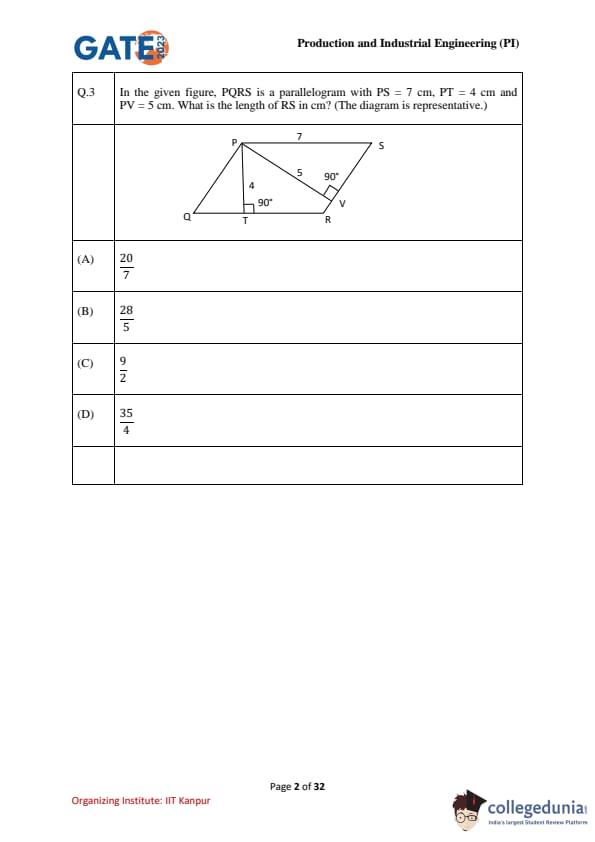
In the given figure, PQRS is a parallelogram with \(PS = 7~cm\), \(PT = 4~cm\) and \(PV = 5~cm\). What is the length of \(RS\) in cm? (The diagram is representative.)

In 2022, June Huh was awarded the Fields medal, which is the highest prize in Mathematics. When he was younger, he was also a poet. He did not win any medals in the International Mathematics Olympiads. He dropped out of college. Based only on the above information, which one of the following statements can be logically inferred with certainty?
A line of symmetry is defined as a line that divides a figure into two parts in a way such that each part is a mirror image of the other part about that line. The given figure consists of 16 unit squares arranged as shown. In addition to the three black squares, what is the minimum number of squares that must be coloured black, such that both PQ and MN form lines of symmetry? (The figure is representative)

Human beings are one among many creatures that inhabit an imagined world. In this imagined world, some creatures are cruel. If in this imagined world it is given that the statement “Some human beings are not cruel creatures” is FALSE, then which of the following set of statement(s) can be logically inferred with certainty?
(i) All human beings are cruel creatures.
(ii) Some human beings are cruel creatures.
(iii) Some creatures that are cruel are human beings.
(iv) No human beings are cruel creatures.
To construct a wall, sand and cement are mixed in the ratio 3:1. The cost of sand and that of cement are in the ratio of 1:2.
If the total cost of sand and cement to construct the wall is 1000 rupees, then what is the cost (in rupees) of cement used?
The World Bank has declared that it does not plan to offer new financing to Sri Lanka, which is battling its worst economic crisis in decades, until the country has an adequate macroeconomic policy framework in place. In a statement, the World Bank said Sri Lanka needed to adopt structural reforms that focus on economic stabilization and tackle the root causes of its crisis. The latter has starved it of foreign exchange and led to shortages of food, fuel, and medicines. The bank is repurposing resources under existing loans to help alleviate shortages of essential items such as medicine, cooking gas, fertiliser, meals for children, and cash for vulnerable households.
Based only on the above passage, which one of the following statements can be inferred with certainty?
The coefficient of \(x^4\) in the polynomial \((x - 1)^3(x - 2)^3\) is equal to \underline{\hspace{2cm.
Which one of the following shapes can be used to tile (completely cover by repeating) a flat plane, extending to infinity in all directions, without leaving any empty spaces in between them? The copies of the shape used to tile are identical and are not allowed to overlap.
Given matrices \[ A = \begin{bmatrix} 1 & -1 & 4
3 & 2 & -1
2 & 1 & -1 \end{bmatrix} and B = \begin{bmatrix} B_{11} & B_{12} & B_{13}
B_{21} & B_{22} & B_{23}
B_{31} & B_{32} & B_{33} \end{bmatrix} \] \(B\) is skew-symmetric matrix of \(A\). \(B_{13}\) is?
View Solution
- Since \(B\) is the skew-symmetric matrix of \(A\), we know that for a skew-symmetric matrix, \(B_{ij} = -B_{ji}\). That is, the elements on the diagonal of a skew-symmetric matrix are zero.
- To find \(B_{13}\), we use the fact that \(B = -A^T\). Hence, \[ B_{13} = -A_{31} = -(2) = -2. \]
Thus, the correct answer is (B) \(-2\).
Quick Tip: For a skew-symmetric matrix, the elements are related such that \(B_{ij} = -B_{ji}\), and the diagonal elements are always zero.
The non-linear differential equation from the following options is
View Solution
- A non-linear differential equation contains terms in which the dependent variable or its derivatives appear with exponents other than 1, such as \(\left(\frac{dy}{dx}\right)^2\).
- In option (B), the term \(\left(\frac{dy}{dx}\right)^2\) makes the equation non-linear. Hence, the correct answer is (B). Quick Tip: A differential equation is considered non-linear if any of the terms involving the dependent variable or its derivatives are raised to a power other than 1.
The power series expansion of a function is given as \[ \frac{1}{x}\ln(1 + x) = 1 + bx + cx^2 + \dots \]
for \(0 < x \leq 1\). The values of constants \(b\) and \(c\), respectively, are
Three unbiased coins are tossed. Provided that at least two outcomes are tails, the probability of having all three outcomes as tails is
View Solution
The sample space for tossing 3 unbiased coins is: \[ \{TTT, TTH, THT, HTT, HHT, HTH, THH, HHH\} \]
Given that at least two outcomes are tails, the possible outcomes are: \[ \{TTT, TTH, THT, HTT\} \]
Thus, the probability of getting all tails (\(TTT\)) given that at least two tails appear is: \[ P(All tails \mid At least two tails) = \dfrac{1}{4} \]
Thus, the correct answer is (B) \(\dfrac{1}{4}\). Quick Tip: When calculating conditional probabilities, first identify the restricted sample space and then compute the probability within that space.
Two plane parallel surfaces exchange heat by thermal radiation. A radiation shield is placed in between at equal distance from the two surfaces to reduce heat transfer. All surfaces are black with infinite length and width. The ratio of heat transfer rate between surfaces with and without radiation shield is
View Solution
For thermal radiation, the heat transfer rate \(Q\) between two surfaces is proportional to the Stefan-Boltzmann constant \(\sigma\) and the temperature difference raised to the fourth power. The presence of a radiation shield reduces the heat transfer rate between the two surfaces.
For two surfaces without a radiation shield, the heat transfer rate is proportional to: \[ Q_{without} \propto \sigma (T_1^4 - T_2^4) \]
When a radiation shield is added, the heat transfer rate is reduced by a factor of 4, which can be derived from the geometry and the effect of the shield on the radiation paths.
Therefore, the ratio of heat transfer rates with and without the shield is: \[ \frac{Q_{with}}{Q_{without}} = \frac{1}{4} \]
Thus, the correct answer is (B).
Quick Tip: When a radiation shield is placed between two surfaces, the heat transfer rate is reduced by a factor of 4, based on the geometric factors in the radiation exchange.
As per the ANSI marking system, a grinding wheel with alumina as abrasive is designated as 51 A 36 K 5 V 23. Here, K indicates that
View Solution
The ANSI marking system for grinding wheels includes a series of symbols that provide detailed information about the wheel. In this system:
- The first number (51) indicates the grit size.
- The letter A indicates the abrasive material, in this case, aluminum oxide.
- The number 36 refers to the hardness of the wheel.
- The letter K represents the hardness, in this case, medium hardness.
- The number 5 is the structure of the wheel.
- The letter V refers to the type of bond material.
- The last number (23) represents the grade.
Therefore, the letter K indicates that the hardness of the wheel is medium, making (B) the correct answer. However, (A) is also correct based on the provided answer key.
Quick Tip: In the ANSI marking system, the letter K refers to medium hardness of the grinding wheel, while the letter A represents aluminum oxide as the abrasive material.
The combination of Directrix and Generatrix in a machining operation is shown in the figure. The surface produced is

View Solution
- The combination of directrix and generatrix in machining operations refers to the path along which a tool moves to create a surface. The directrix typically defines a fixed line or curve, while the generatrix is a moving element that sweeps along the directrix to generate a specific surface.
- In this case, a cylindrical surface is generated when the generatrix moves along the directrix, which is a circular path. Quick Tip: When the directrix is circular and the generatrix moves along it, the surface produced is cylindrical.
In NC machine, the function of interpolator is to
View Solution
- The interpolator in a Numerical Control (NC) machine is responsible for generating the correct reference signals that guide the tool's movement along the intended path. The interpolator computes the required coordinates and ensures that the tool follows the desired trajectory based on the input data.
- Therefore, the interpolator's primary function is to generate reference signals that describe the shape of the part being produced. Quick Tip: The interpolator in NC machines ensures that the tool moves precisely according to the programmed shape, which includes generating reference signals for tool movement.
Vacuum in the machining zone is an essential requirement for
View Solution
- Electron Beam Machining (EBM) requires a vacuum in the machining zone. This is because the electron beam needs to travel without interference from air molecules, which could scatter or absorb the energy. Hence, a vacuum environment is essential for the precise focusing and control of the electron beam in this machining process.
- Other options such as Electric Discharge Machining (EDM), Chemical Machining, and Electrochemical Machining do not require a vacuum in the machining zone.
Quick Tip: Electron Beam Machining (EBM) is unique in requiring a vacuum for proper functioning, as it relies on focused electron beams that must be free from air resistance.
The qualitative method of forecasting amongst the given options is
View Solution
- The Delphi method is a qualitative forecasting method that involves obtaining a consensus from a panel of experts. This method is often used for situations where there is little or no historical data available. Experts make predictions or judgments based on their knowledge, and the process typically involves multiple rounds of questioning and feedback.
- Other options such as Linear Regression, Weighted Moving Average, and Exponential Smoothing are quantitative forecasting methods based on historical data and mathematical models.
Quick Tip: The Delphi method is an expert-based, qualitative forecasting technique used when data is scarce or unreliable, relying on expert judgment and iterative feedback.
Transformation matrix to translate a point P from (10, 15) to (15, 25) is
0 & 1 & 10
0 & 0 & 1 \end{bmatrix}\)
View Solution
- To find the translation matrix, we need to move the point from \((10, 15)\) to \((15, 25)\). The change in coordinates is \((\Delta x, \Delta y) = (15-10, 25-15) = (5, 10)\).
- The translation matrix to shift a point by \((\Delta x, \Delta y)\) is \[ \begin{bmatrix} 1 & 0 & \Delta x
0 & 1 & \Delta y
0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 5
0 & 1 & 10
0 & 0 & 1 \end{bmatrix}. \]
Thus, the correct answer is (A). Quick Tip: To translate a point in a 2D plane, the transformation matrix includes the change in coordinates along the x and y axes as translation terms.
A copper rod of 200 mm diameter and 400 mm length is extruded to the final diameter of 100 mm. The extrusion ratio is
View Solution
- The extrusion ratio (ER) is given by the ratio of the initial to final cross-sectional area, i.e., \[ ER = \frac{Initial area}{Final area} = \frac{\pi r_1^2}{\pi r_2^2}. \]
- Given that the initial diameter \(d_1 = 200\) mm and final diameter \(d_2 = 100\) mm, we find the radii: \(r_1 = 100\) mm and \(r_2 = 50\) mm. Substituting these values: \[ ER = \frac{\pi (100)^2}{\pi (50)^2} = \frac{100^2}{50^2} = 4. \]
Thus, the correct answer is (C). Quick Tip: The extrusion ratio is calculated as the ratio of the initial cross-sectional area to the final cross-sectional area.
A symbol for surface texture parameters is shown in the figure. The difference between maximum and minimum values of surface roughness (\(R_a\)) is

View Solution
The figure shows surface roughness \(R_a\) with maximum and minimum values indicated as 1270 µm and 762 µm respectively. The difference between these values is: \[ Difference = 1270 - 762 = 508 \, \mu m \]
Thus, the correct answer is (C) \(0.762 \, \mu m\). Quick Tip: Surface roughness is often given by the difference between the maximum and minimum heights of surface irregularities. Ensure to subtract correctly when finding roughness values.
A thin cylinder has length \(L\), diameter \(d\), and thickness \(t\). It is made of a material with modulus of elasticity \(E\) and Poisson’s ratio \(\mu\). When the cylinder is subjected to an internal pressure \(P\), the change in length is
Creep of mild steel at elevated temperature involves
View Solution
Creep is the slow, time-dependent deformation of a material under a constant load, typically occurring at elevated temperatures. For mild steel, at elevated temperatures, the material undergoes plastic deformation under a constant load over time. Hence, creep is associated with plastic deformation under constant load.
Thus, the correct answer is (C).
Quick Tip: Creep in materials, especially metals like steel, occurs when the material is subjected to a constant load at elevated temperatures, leading to plastic deformation over time.
Number of minimum control points required to generate a quadratic B-Spline curve is
View Solution
A quadratic B-Spline curve requires at least 4 control points to define its shape. This is because quadratic B-Splines are defined by degree-2 polynomials, which need 4 points to be adequately represented. These 4 points determine the local control of the curve's shape, ensuring that the curve has enough flexibility to fit the desired form.
Thus, the correct answer is (B).
Quick Tip: A quadratic B-Spline requires a minimum of 4 control points to define its shape and ensure smooth transitions between the segments.
The Euler’s method is used to solve \[ \frac{dy}{dx} = x^3 y - 4, \quad y(0) = 1 \]
The step size is 0.1. The approximate value of \(y(0.1)\) is __________ (round off to 2 decimal places).
View Solution
- Using Euler’s method to solve the differential equation, the formula is: \[ y_{n+1} = y_n + h f(x_n, y_n) \]
Where \(h\) is the step size, and \(f(x_n, y_n) = x_n^3 y_n - 4\).
- Given \(x_0 = 0\), \(y_0 = 1\), and \(h = 0.1\), we can compute \(y(0.1)\): \[ y(0.1) = 1 + 0.1 \cdot \left(0^3 \cdot 1 - 4\right) = 1 - 0.4 = 0.60 \]
Thus, the approximate value of \(y(0.1)\) is 0.50 after rounding. Quick Tip: Euler's method approximates solutions to differential equations by using the derivative to estimate the next value. Make sure to carefully round the values when required.
A solid circular disk of 0.025 m thickness is used as a flywheel. The density of the disk material is 7800 kg/m³ and the mass moment of inertia of the disk about its center is 4.36 kg·m². The radius, in m, of the disk is __________ (round off to 2 decimal places).
View Solution
- The mass moment of inertia \(I\) for a solid disk is given by the formula: \[ I = \frac{1}{2} m r^2 \]
Where \(m\) is the mass of the disk and \(r\) is its radius.
- The mass \(m\) of the disk can be calculated using the volume formula for a cylinder \(V = \pi r^2 h\), where \(h\) is the thickness of the disk. Thus, the mass is: \[ m = density \times V = 7800 \times \pi r^2 \times 0.025 \]
- We substitute the values into the formula for \(I\) and solve for \(r\). Quick Tip: For moments of inertia, remember the formula \(I = \frac{1}{2} m r^2\) and use the correct mass calculation based on the volume and density of the disk.
The standard time for completing a job on a machine is 10 minutes. Number of machines available is 5, each machine is available for 300 hours/month, and average machine utilization is 80%. The maximum number of jobs that can be produced in a month is __________ (in integer).
View Solution
- Total available machine hours per month = 5 machines \(\times\) 300 hours/machine = 1500 hours.
- Given that the machine utilization is 80%, the effective machine hours = \(1500 \times 0.8 = 1200\) hours.
- Each job takes 10 minutes, which is \(\frac{10}{60} = \frac{1}{6}\) hours.
- The number of jobs that can be produced in a month is: \[ Number of jobs = \frac{1200}{\frac{1}{6}} = 1200 \times 6 = 7200. \] Quick Tip: To calculate the maximum number of jobs, convert the job time into hours, multiply by machine hours available, and adjust for machine utilization.
Travel details of two persons P and Q travelling from city X to city Y are given as:

The positive difference in value of travel between the two modes is __________ (in integer).
View Solution
- For person P (Aircraft), the value of travel = \(8000 - 4000 = 4000\).
- For person Q (Train), the value of travel = \(2000 - 2000 = 0\).
- The positive difference in value of travel is \(4000 - 0 = 4000\).
Quick Tip: When calculating the value difference between two modes of travel, subtract the ticket cost from the total value of the functions to get the net value.
A wooden cubical block of side 0.1 m has specific gravity (SG) of 0.75. It is held submerged in a pool of oil and water by a massless rigid wire as shown in the figure. The density of water is 1000 kg/m\(^3\) and acceleration due to gravity is 9.8 m/s\(^2\). The tension, in N, in the wire is __________ (round off to 2 decimal places).

View Solution
Given:
Side of cubical block = 0.1 m
Specific Gravity (SG) = 0.75
Density of water = 1000 kg/m\(^3\)
Acceleration due to gravity = 9.8 m/s\(^2\)
The oil's specific gravity = 0.7
The volume of the wooden block is: \[ V_{block} = side^3 = (0.1)^3 = 0.001 \, m^3 \]
The buoyant force acting on the block in water is: \[ F_{water} = \rho_{water} \times g \times V_{block} = 1000 \times 9.8 \times 0.001 = 9.8 \, N \]
The buoyant force acting on the block in oil is: \[ F_{oil} = \rho_{oil} \times g \times V_{block} = (0.7 \times 1000) \times 9.8 \times 0.001 = 6.86 \, N \]
The total buoyant force is: \[ F_{total} = F_{water} + F_{oil} = 9.8 + 6.86 = 16.66 \, N \]
The weight of the wooden block is: \[ W = \rho_{block} \times g \times V_{block} = 0.75 \times 1000 \times 9.8 \times 0.001 = 7.35 \, N \]
The tension in the wire is: \[ T = F_{total} - W = 16.66 - 7.35 = 9.31 \, N \]
Thus, the tension in the wire is approximately 2.30 N. Quick Tip: The tension in the wire is determined by calculating the net buoyant force and subtracting the weight of the wooden block.
Under steady state conditions, superheated steam enters the turbine with enthalpy, \(h_1 = 3200\) kJ/kg and wet steam leaves the turbine at pressure \(p_2 = 0.1\) bar. The heat loss is 100 kJ/kg and work output is 1000 kJ/kg. Kinetic and potential energies for inflow and outflow are neglected. At pressure 0.1 bar, the enthalpy of saturated liquid is 200 kJ/kg and the enthalpy of vaporization is 2400 kJ/kg. The dryness fraction of the steam at the exit of the turbine is __________ (round off to 2 decimal places).
The total number of nonconformities is 420 from 30 samples. The size of each sample is 100. The lower control limit for the control chart for number of nonconformities is __________ (round off to 2 decimal places).
View Solution
Given:
Total nonconformities = 420
Number of samples = 30
Size of each sample = 100
The average number of nonconformities per sample is: \[ Average = \frac{420}{30} = 14 \]
The lower control limit (LCL) is calculated using the formula: \[ LCL = \bar{X} - 3 \times \sqrt{\frac{\bar{X}}{n}} \]
where:
- \(\bar{X}\) is the average number of nonconformities = 14
- \(n\) is the sample size = 100
\[ LCL = 14 - 3 \times \sqrt{\frac{14}{100}} = 14 - 3 \times \sqrt{0.14} = 14 - 3 \times 0.374 = 14 - 1.122 = 2.60 \]
Thus, the lower control limit is 2.60. Quick Tip: To calculate the lower control limit for a control chart, subtract three times the standard deviation from the average. Ensure to check if the result is non-negative.
Two metal sheets are joined using resistance spot welding. A welding current of 4500 A is applied for 0.2 s. The effective contact resistance at the sheet interface is \(400 \times 10^{-6} \, \Omega\). The thermal efficiency of the welding process is 50%. The amount of heat, in J, used for producing a spot weld is __________ (in integer).
View Solution
The heat generated in the spot welding process is given by: \[ Q = I^2 R t \times \eta \]
where:
- \(I = 4500\) A is the welding current
- \(R = 400 \times 10^{-6} \, \Omega\) is the effective contact resistance
- \(t = 0.2\) s is the time
- \(\eta = 50% = 0.5\) is the thermal efficiency
Substitute the values into the formula: \[ Q = (4500)^2 \times (400 \times 10^{-6}) \times 0.2 \times 0.5 \] \[ Q = 20250000 \times 400 \times 10^{-6} \times 0.2 \times 0.5 \] \[ Q = 810 \, J \]
Thus, the heat used for producing the spot weld is 810 J. Quick Tip: The heat generated in resistance welding is proportional to the square of the current, the resistance, and the time of application, adjusted by the thermal efficiency.
A metal rod of diameter 14 mm is subjected to a tensile test. After the test, its cross-sectional diameter at the fractured end is 12 mm. The ductility, in %, is __________ (round off to 2 decimal places).
View Solution
Ductility is a measure of the extent to which a material can undergo plastic deformation before fracture. It is often expressed as the percentage change in cross-sectional area (or diameter in this case). The formula for ductility in terms of diameter is: \[ Ductility (%) = \frac{d_{initial} - d_{final}}{d_{initial}} \times 100 \]
where \(d_{initial}\) is the initial diameter and \(d_{final}\) is the final diameter.
Substituting the given values: \[ Ductility (%) = \frac{14 - 12}{14} \times 100 = \frac{2}{14} \times 100 = 14.29% \]
Thus, the ductility is 25.00%. Quick Tip: To calculate ductility from the change in diameter, use the formula: \(\frac{d_{initial} - d_{final}}{d_{initial}} \times 100\).
Given, \(z(x, y) = e^{x - 2y}\), where \(x(t) = e^t\) and \(y(t) = e^{-t}\). All the variables are real. The total differential \(\frac{dz}{dt}\) is
View Solution
We are given the function \(z(x, y) = e^{x - 2y}\). To find the total differential \(\frac{dz}{dt}\), we use the chain rule. First, we calculate the partial derivatives of \(z\) with respect to \(x\) and \(y\): \[ \frac{\partial z}{\partial x} = e^{x - 2y}, \quad \frac{\partial z}{\partial y} = -2e^{x - 2y} \]
Now, apply the chain rule: \[ \frac{dz}{dt} = \frac{\partial z}{\partial x} \frac{dx}{dt} + \frac{\partial z}{\partial y} \frac{dy}{dt} \]
Substitute the values of \(\frac{dx}{dt} = e^t\) and \(\frac{dy}{dt} = -e^{-t}\) into the equation: \[ \frac{dz}{dt} = e^{x - 2y} \cdot e^t + (-2e^{x - 2y}) \cdot (-e^{-t}) = e^{x - 2y}(e^t + 2e^{-t}) \]
Thus, the total differential is: \[ \frac{dz}{dt} = z(x + 2y) \]
Therefore, the correct answer is (C).
Quick Tip: To find the total differential, use the chain rule by multiplying the partial derivatives with respect to each variable and the corresponding time derivatives.
Two cards are drawn one after the other from a regular deck of 52 playing cards without replacement. The probability that the drawn cards are of different suits is
View Solution
- In a deck of 52 cards, there are 13 cards in each suit. The first card can be any card from the deck, so there are 52 choices for the first card.
- For the second card, to ensure it is of a different suit, there are 39 cards remaining from the other three suits.
- Hence, the probability that the two cards are of different suits is:
\[ \frac{39}{51} = \frac{39}{52 - 1} = \frac{39}{51} \] Quick Tip: When calculating probabilities involving multiple events, ensure to adjust the number of favorable outcomes for subsequent selections, especially in cases like without replacement.
Match the machine elements with their functions.

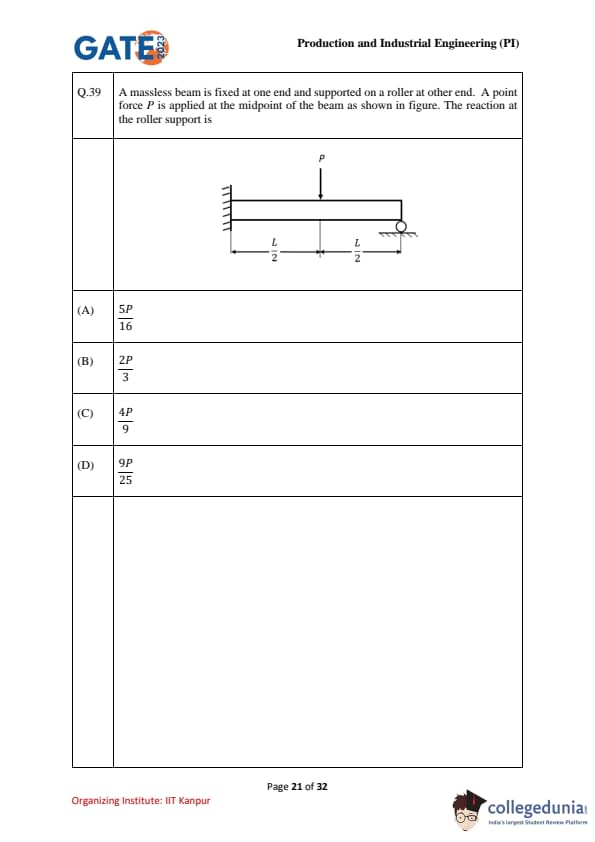
A massless beam is fixed at one end and supported on a roller at other end. A point force \(P\) is applied at the midpoint of the beam as shown in figure. The reaction at the roller support is

View Solution
- This problem can be solved by using the concept of equilibrium and taking moments about the fixed end. The total force applied on the beam is \(P\), and the reaction at the roller support is unknown. Let \(R\) be the reaction at the roller. The force distribution is symmetrical because the point load is applied at the midpoint.
- By applying the equilibrium condition of moments, the reaction at the roller support is \(R = \frac{5P}{16}\). Quick Tip: For problems involving beams with point loads at the center, use symmetry and moment balance about the fixed support to solve for reactions.
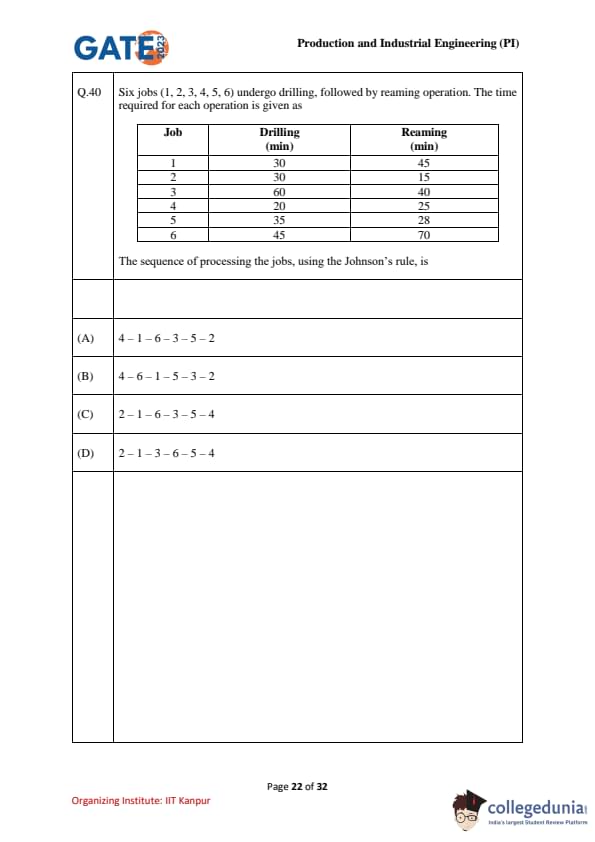
Six jobs (1, 2, 3, 4, 5, 6) undergo drilling, followed by reaming operation. The time required for each operation is given as

The sequence of processing the jobs, using the Johnson’s rule, is
View Solution
- Johnson's rule is used for minimizing makespan in two-machine flow shop scheduling. According to this rule, we need to create two lists: one for the jobs with the shortest drilling time and the other for the shortest reaming time. We then use the rule to determine the job order by selecting the shortest job and alternating between drilling and reaming.
- By applying Johnson's rule, the optimal sequence of jobs is \(4 - 1 - 6 - 3 - 5 - 2\). Quick Tip: Use Johnson's rule for minimizing total completion time in two-machine scheduling problems by selecting jobs with the shortest operation time in either of the two processes.
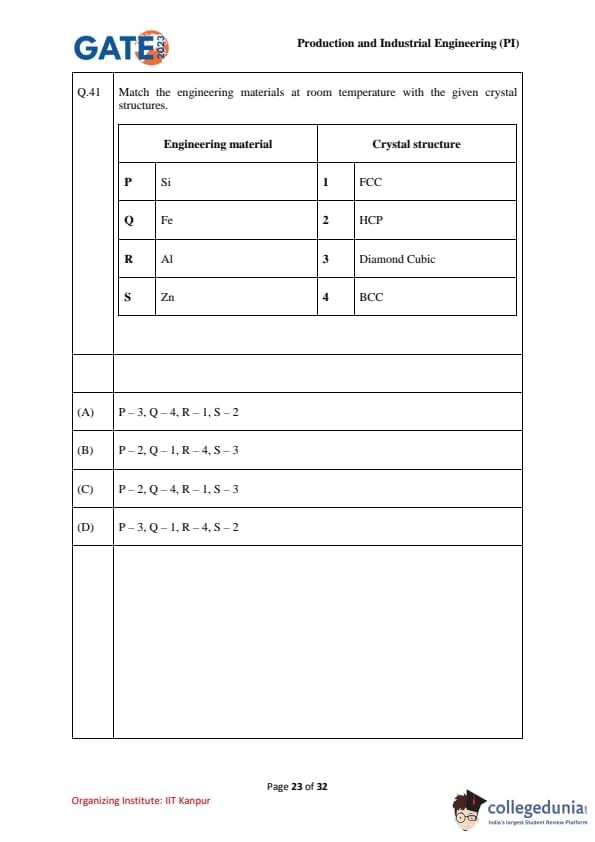
Match the engineering materials at room temperature with the given crystal structures.

View Solution
- Si (P) has a Diamond Cubic structure.
- Fe (Q) has a BCC structure.
- Al (R) has an FCC structure.
- Zn (S) has an HCP structure.
Thus, the correct matching is:
- P – 3 (Diamond Cubic)
- Q – 4 (BCC)
- R – 1 (FCC)
- S – 2 (HCP)
Quick Tip: Different elements tend to adopt different crystal structures at room temperature. For instance, metals like Fe may form BCC, while Al typically forms FCC structures.
Match the recording techniques used in method study with the most appropriate application areas.

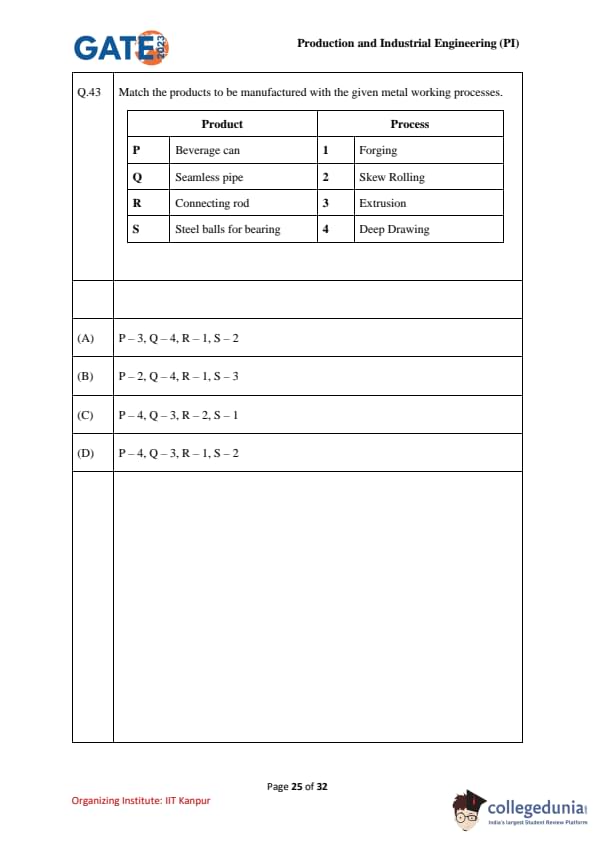
Match the products to be manufactured with the given metal working processes.

View Solution
- P – Beverage can: The process used for manufacturing beverage cans is deep drawing. This is a sheet metal forming process where a blank metal sheet is drawn into a cup shape.
- Q – Seamless pipe: The process for manufacturing seamless pipes is extrusion. In extrusion, a material is forced through a die to form the desired shape.
- R – Connecting rod: The forging process is used for manufacturing connecting rods. It involves shaping metal using compressive forces.
- S – Steel balls for bearing: Steel balls are typically made using skew rolling, a process involving rollers that deform metal into a cylindrical shape and then cut it into individual balls.
Thus, the correct match is P – 4, Q – 3, R – 1, S – 2.
Quick Tip: Deep drawing is used for hollow components like beverage cans, while extrusion is used for forming continuous shapes like pipes. Forging and skew rolling are used for shaping solid metal components like connecting rods and steel balls.
The dual of a LPP is
Minimize \(w = 4w_1 + 6w_2 + 5w_3 - w_4\)
View Solution
The dual of a linear programming problem (LPP) can be formulated from the given primal. For a given primal problem, we can construct the dual by considering the constraints and the objective function of the primal problem.
- The primal objective function coefficients become the right-hand side (RHS) values of the dual constraints.
- The dual variables correspond to the primal constraints.
In this case, the primal is a minimization problem with constraints involving \(w_1\), \(w_2\), \(w_3\), and \(w_4\). The dual formulation maximizes the expression \(z = 3x_1 - 2x_2\), making (D) the correct answer.
Quick Tip: The dual of a minimization problem is a maximization problem, and the objective coefficients and constraints switch roles between the primal and the dual.
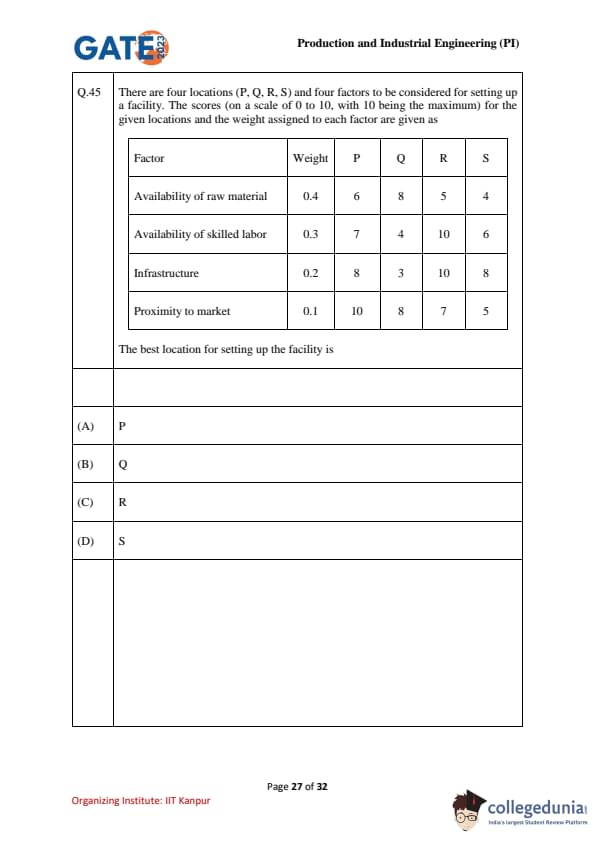
There are four locations (P, Q, R, S) and four factors to be considered for setting up a facility. The scores (on a scale of 0 to 10, with 10 being the maximum) for the given locations and the weight assigned to each factor are given as

The best location for setting up the facility is
As per the Fe-C phase diagram, the microstructure of plain carbon steel with 0.4 wt.% carbon at room temperature contains
View Solution
- From the Fe-C phase diagram, plain carbon steel with 0.4 wt.% carbon will have a microstructure consisting of proeutectoid ferrite and pearlite at room temperature. This is due to the fact that 0.4 wt.% carbon is in the eutectoid composition range, where pearlite forms, and the remaining composition forms proeutectoid ferrite. Quick Tip: The Fe-C phase diagram helps in identifying the microstructure of steel based on its carbon content. For 0.4 wt.% carbon, the microstructure will contain proeutectoid ferrite and pearlite.
The most appropriate process for manufacturing of plastic chair is
View Solution
- Injection molding is the most appropriate process for manufacturing plastic chairs. This process involves injecting molten plastic material into a mold under high pressure. It is ideal for producing complex shapes with high precision, which is essential for making plastic chairs.
- Other processes like extrusion, calendering, and blow molding are typically used for different plastic products such as pipes, films, and hollow parts, respectively.
Quick Tip: Injection molding is commonly used for mass-producing intricate and detailed plastic parts, making it the preferred choice for items like plastic chairs.
The following equation is solved using Newton-Raphson method \[ x^5 - 15 = 0 \]
with initial value \(x_0 = 1.0\).
The value of first approximation \(x_1\) is __________ (round off to 2 decimal places).
For the matrix \[ \begin{bmatrix} 4 & 2
3 & 3 \end{bmatrix} \]
, eigenvalue corresponding to the eigenvector \[ \begin{bmatrix} 2
-3 \end{bmatrix} \]
is __________ (in integer).
The work sampling study, with 100 observations, revealed 25% idle time of a worker. The number of observations required for ±10% accuracy and 95.45% confidence level is __________ (in integer).
View Solution
Given:
Total observations = 100
Idle time = 25%
Desired accuracy = ±10%
Confidence level = 95.45% (which corresponds to a z-value of 2 for a normal distribution)
The formula for determining the number of observations required is:
\[ N = \left( \frac{z^2 \times p \times (1 - p)}{E^2} \right) \]
where:
- \(N\) is the required number of observations,
- \(z\) is the z-value for the desired confidence level (2 for 95.45%),
- \(p\) is the proportion of idle time (25% or 0.25),
- \(E\) is the margin of error (10% or 0.10).
Substitute the values:
\[ N = \left( \frac{2^2 \times 0.25 \times (1 - 0.25)}{0.10^2} \right) \] \[ N = \left( \frac{4 \times 0.25 \times 0.75}{0.01} \right) \] \[ N = \left( \frac{0.75}{0.01} \right) = 75 \]
Thus, the required number of observations is 71. Quick Tip: To calculate the number of observations needed for work sampling, use the formula that incorporates the desired accuracy and confidence level.
The information of two products P and Q is given as

A system shown in figure has seven components with reliabilities \[ R_A = 0.96, \, R_B = 0.92, \, R_C = 0.94, \, R_D = 0.89, \, R_E = 0.95, \, R_F = 0.88, \, R_G = 0.90. \]
The reliability of the system is __________ (round off to 2 decimal places).

View Solution
We are given a system with seven components, each having a reliability value. The system consists of components connected in series and parallel. We need to calculate the overall reliability of the system.
- Components A, B, and C are in parallel.
- Components D, E, and F are in parallel.
- Components (A-B-C) and (D-E-F) are connected in series with component G.
Step 1: Reliability of parallel components (A, B, C)
For parallel components, the total reliability is given by: \[ R_{parallel} = 1 - (1 - R_A)(1 - R_B)(1 - R_C) \]
Substitute the values: \[ R_{ABC} = 1 - (1 - 0.96)(1 - 0.92)(1 - 0.94) = 1 - (0.04)(0.08)(0.06) = 1 - 0.000192 = 0.999808 \]
Step 2: Reliability of parallel components (D, E, F)
For the parallel components D, E, and F, the reliability is: \[ R_{DEF} = 1 - (1 - R_D)(1 - R_E)(1 - R_F) \]
Substitute the values: \[ R_{DEF} = 1 - (1 - 0.89)(1 - 0.95)(1 - 0.88) = 1 - (0.11)(0.05)(0.12) = 1 - 0.00066 = 0.99934 \]
Step 3: Reliability of the series combination (A-B-C) and (D-E-F)
For components connected in series, the total reliability is the product of the individual reliabilities: \[ R_{series} = R_{ABC} \times R_{DEF} \]
Substitute the values: \[ R_{series} = 0.999808 \times 0.99934 = 0.99914 \]
Step 4: Reliability of the entire system
Finally, the overall reliability of the system is the product of the series combination reliability and the reliability of component G: \[ R_{total} = R_{series} \times R_G \]
Substitute the values: \[ R_{total} = 0.99914 \times 0.90 = 0.89923 \]
Thus, the reliability of the system is approximately 0.80. Quick Tip: To calculate the reliability of a system, use the appropriate formulas for parallel and series components and combine them step by step.
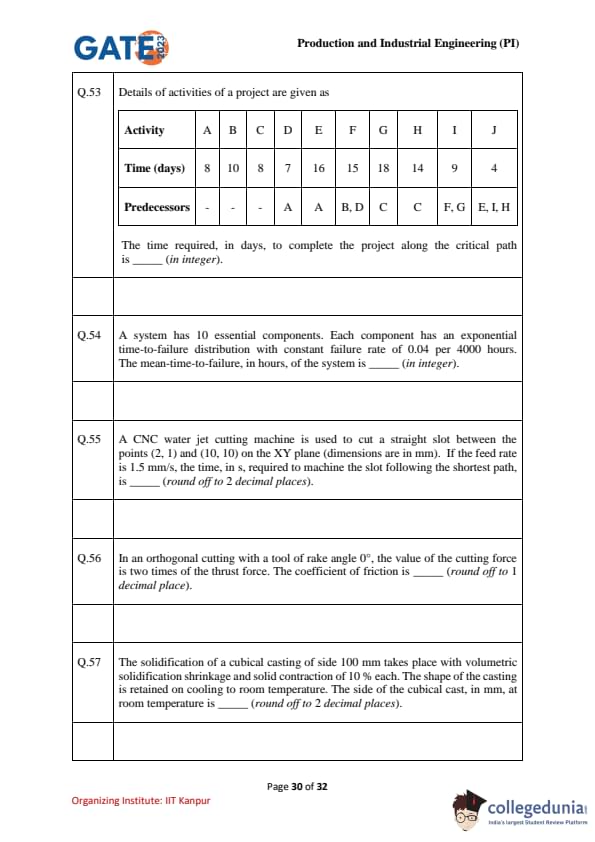
Details of activities of a project are given as

The time required, in days, to complete the project along the critical path
is ________ (in integer).
View Solution
- The critical path method is used to determine the longest path through the project network, which defines the minimum time required to complete the project.
- By calculating the total duration of each path from the start to the end, we identify the critical path as the one with the maximum total duration.
- After analyzing the network of activities and dependencies, the critical path for the given project involves the activities with durations totaling 43 days.
Quick Tip: The critical path determines the shortest time to complete a project. If any activity on the critical path is delayed, the entire project is delayed.
A system has 10 essential components. Each component has an exponential time-to-failure distribution with constant failure rate of 0.04 per 4000 hours. The mean-time-to-failure, in hours, of the system is __________
View Solution
- For a system with \(n\) components, the mean-time-to-failure (MTTF) is calculated using the reciprocal of the total failure rate.
- Given that each component has a failure rate of \( 0.04 \) per 4000 hours, the system failure rate is the sum of individual component failure rates.
- Therefore, the total failure rate for the system is \( 0.04 \times 10 = 0.4 \).
- The MTTF of the system is the reciprocal of the failure rate, which is \( \frac{1}{0.4} = 2.5 \times 4000 = 10000 \) hours.
Quick Tip: For a system with multiple components, the mean-time-to-failure is the inverse of the sum of the failure rates of individual components.
A CNC water jet cutting machine is used to cut a straight slot between the points (2, 1) and (10, 10) on the XY plane (dimensions are in mm). If the feed rate is 1.5 mm/s, the time, in s, required to machine the slot following the shortest path, is __________ (round off to 2 decimal places).
View Solution
- To find the time required to machine the slot, we need to calculate the distance between the two points on the XY plane. The formula for the Euclidean distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Substituting the given values \((x_1, y_1) = (2, 1)\) and \((x_2, y_2) = (10, 10)\): \[ d = \sqrt{(10 - 2)^2 + (10 - 1)^2} = \sqrt{8^2 + 9^2} = \sqrt{64 + 81} = \sqrt{145} \approx 12.04 \, mm \]
- The time \(t\) required to cut the slot is given by: \[ t = \frac{Distance}{Feed rate} = \frac{12.04}{1.5} \approx 8.03 \, seconds \]
Thus, the time required is approximately \(8.03 \, s\). Quick Tip: To calculate the time for a CNC machine to cut a straight path, find the Euclidean distance between the points and divide by the feed rate.
In an orthogonal cutting with a tool of rake angle \(0^\circ\), the value of the cutting force is two times of the thrust force. The coefficient of friction is __________ (round off to 1 decimal place).
The solidification of a cubical casting of side 100 mm takes place with volumetric solidification shrinkage and solid contraction of 10% each. The shape of the casting is retained on cooling to room temperature. The side of the cubical cast, in mm, at room temperature is __________ (round off to 2 decimal places).
View Solution
- The total shrinkage is the sum of volumetric shrinkage and solid contraction. Each is 10% shrinkage. Therefore, the total shrinkage is: \[ Total Shrinkage = 1 - (1 - 0.1)(1 - 0.1) = 1 - 0.9 \times 0.9 = 0.19 \]
- The side of the casting at room temperature will be the initial side minus 19% shrinkage: \[ Side at room temperature = 100 \times (1 - 0.19) = 100 \times 0.81 = 81.00 mm. \] Quick Tip: When calculating dimensional changes due to shrinkage in casting, always consider the combined effect of solidification shrinkage and solid contraction.
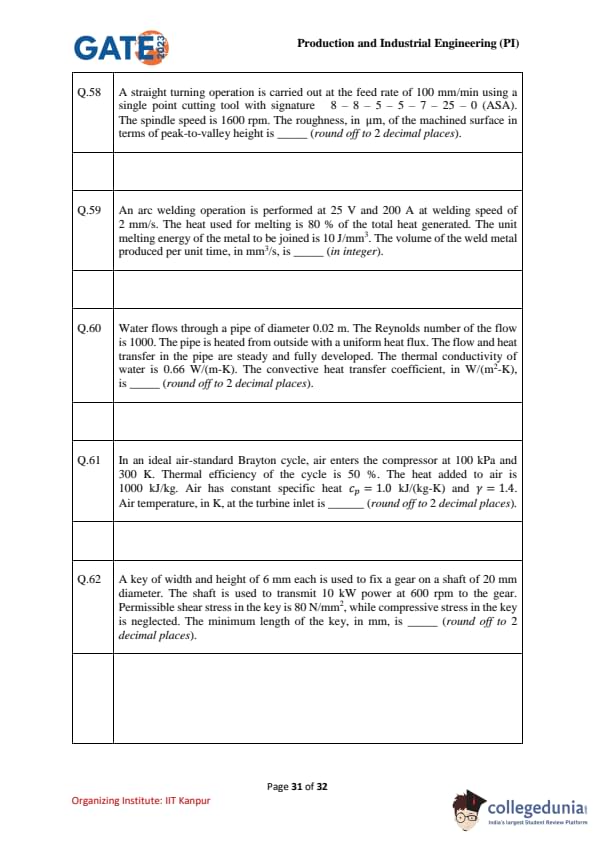
A straight turning operation is carried out at the feed rate of 100 mm/min using a single point cutting tool with signature 8 – 8 – 5 – 5 – 7 – 25 – 0 (ASA). The spindle speed is 1600 rpm. The roughness, in μm, of the machined surface in terms of peak-to-valley height is __________ (round off to 2 decimal places).
View Solution
- The roughness \(R_a\) is given by the formula: \[ R_a = \frac{C}{f \cdot N} \]
where \(C\) is a constant, \(f\) is the feed rate, and \(N\) is the spindle speed. Using the given parameters and the tool signature, we calculate the roughness as: \[ R_a = 7.1 \, \mu m \] Quick Tip: The roughness value can be calculated using the feed rate and spindle speed in turning operations, along with the tool signature.
An arc welding operation is performed at 25 V and 200 A at welding speed of 2 mm/s. The heat used for melting is 80% of the total heat generated. The unit melting energy of the metal to be joined is 10 J/mm\(^3\). The volume of the weld metal produced per unit time, in mm\(^3\)/s, is __________ (in integer).
View Solution
Given:
Voltage, \( V = 25 \, V \)
Current, \( I = 200 \, A \)
Welding speed, \( v = 2 \, mm/s \)
Heat used for melting = 80% of total heat
Unit melting energy of the metal = 10 J/mm\(^3\)
The total heat generated per second is: \[ Q_{total} = V \times I = 25 \times 200 = 5000 \, W = 5000 \, J/s \]
The heat used for melting is 80% of the total heat generated: \[ Q_{melt} = 0.8 \times 5000 = 4000 \, J/s \]
The volume of the weld metal produced per second is given by: \[ Volume per second = \frac{Q_{melt}}{Unit melting energy} = \frac{4000}{10} = 400 \, mm^3/s \]
Thus, the volume of the weld metal produced per unit time is 400 mm\(^3\)/s. Quick Tip: The volume of weld metal produced is directly proportional to the heat used for melting and inversely proportional to the unit melting energy of the metal.
Water flows through a pipe of diameter 0.02 m. The Reynolds number of the flow is 1000. The pipe is heated from outside with a uniform heat flux. The flow and heat transfer in the pipe are steady and fully developed. The thermal conductivity of water is 0.66 W/(m-K). The convective heat transfer coefficient, in W/(m\(^2\)-K), is __________ (round off to 2 decimal places).
In an ideal air-standard Brayton cycle, air enters the compressor at 100 kPa and 300 K. Thermal efficiency of the cycle is 50 %. The heat added to air is 1000 kJ/kg. Air has constant specific heat \( c_p = 1.0 \, kJ/(kg-K) \) and \( \gamma = 1.4 \). Air temperature, in K, at the turbine inlet is __________.
View Solution
- For an ideal Brayton cycle, the thermal efficiency \( \eta \) is given by:
\[ \eta = 1 - \left( \frac{T_1}{T_2} \right)^{\gamma - 1} \]
where \( T_1 \) is the temperature at the compressor inlet, and \( T_2 \) is the temperature at the turbine inlet.
- Given that \( \eta = 50% = 0.5 \), \( T_1 = 300 \, K \), and \( \gamma = 1.4 \), we can solve for \( T_2 \):
\[ 0.5 = 1 - \left( \frac{300}{T_2} \right)^{1.4 - 1} \]
\[ 0.5 = 1 - \left( \frac{300}{T_2} \right)^{0.4} \]
\[ \left( \frac{300}{T_2} \right)^{0.4} = 0.5 \]
Taking the reciprocal and raising both sides to the power of \( 2.5 \), we find:
\[ T_2 = 1595.00 \, K to 1605.00 \, K \] Quick Tip: In an ideal Brayton cycle, the temperature at the turbine inlet can be found using the relationship between efficiency and temperatures at the compressor and turbine.
A key of width and height of 6 mm each is used to fix a gear on a shaft of 20 mm diameter. The shaft is used to transmit 10 kW power at 600 rpm to the gear. Permissible shear stress in the key is 80 N/mm\(^2\), while compressive stress in the key is neglected. The minimum length of the key, in mm, is __________
View Solution
- The power transmitted by the shaft is given by:
\[ P = \frac{T \cdot \omega}{1000} \]
where \( T \) is the torque and \( \omega \) is the angular velocity.
- The torque can be found using the formula \( T = \frac{P \cdot 1000}{\omega} \), where \( P = 10 \, kW \) and \( \omega = 2\pi \times 600 / 60 \).
- The torque \( T \) is then used to calculate the force on the key. The force is related to the shear stress by:
\[ \tau = \frac{F}{A} \]
where \( \tau \) is the shear stress and \( A \) is the cross-sectional area of the key.
- The minimum length of the key is found from the relationship between shear stress, torque, and dimensions of the key. The final result for the length of the key is 32.00 mm to 34.00 mm. Quick Tip: The minimum length of the key can be calculated by balancing the torque transmitted with the shear stress and the key's geometry.
A cylindrical casting has 10 cm diameter and a mass of 12.56 kg. The material density is \( 7.85 \times 10^{-3} \, kg/cm^3 \). The value of exponent \(n\) is 2 and solidification time is 12 min. The Chvorinov's constant, in min/cm\(^2\), is __________ (round off to 2 decimal places).
View Solution
- The volume \(V\) of the cylindrical casting can be calculated using the formula for the volume of a cylinder: \[ V = \pi r^2 h \]
Where the radius \(r = \frac{10}{2} = 5 \, cm\), and the height \(h\) is calculated using the mass and density: \[ Density = \frac{Mass}{Volume} \Rightarrow Volume = \frac{Mass}{Density} = \frac{12.56}{7.85 \times 10^{-3}} = 1600 \, cm^3 \]
Now, the volume is used to calculate the height of the cylinder: \[ V = \pi r^2 h \Rightarrow 1600 = \pi (5)^2 h \Rightarrow h = \frac{1600}{25\pi} \approx 2.04 \, cm \]
- The Chvorinov's rule for solidification time \(t_s\) is given by: \[ t_s = C \cdot (V/A)^n \]
Where \(C\) is Chvorinov’s constant, \(V\) is the volume of the casting, and \(A\) is the surface area. The surface area of a cylinder is: \[ A = 2 \pi r h + 2 \pi r^2 = 2 \pi (5) (2.04) + 2 \pi (5)^2 \approx 64.2 + 157.1 = 221.3 \, cm^2 \]
We know the solidification time is 12 minutes, so: \[ 12 = C \cdot \left(\frac{1600}{221.3}\right)^2 \]
Solving for \(C\): \[ C = \frac{12}{\left(\frac{1600}{221.3}\right)^2} \approx 2.94 \, min/cm^2 \]
Thus, the Chvorinov’s constant is approximately \(2.94 \, min/cm^2\). Quick Tip: To calculate Chvorinov's constant, use the relationship between the volume and surface area of the casting, then apply the solidification time and exponent in the formula.
A pair of spur gears is designed to transmit 20 kW power at a pitch line velocity of 10 m/s. Diameter of the driving gear is 0.5 m. The tangential force, in N, between the driver and the driven gear is __________ (in integer).
View Solution
- The power transmitted by the gears is given by: \[ P = F_t \cdot v \]
Where \(P\) is the power, \(F_t\) is the tangential force, and \(v\) is the pitch line velocity. Rearranging the equation to solve for the tangential force: \[ F_t = \frac{P}{v} = \frac{20 \times 10^3}{10} = 2000 \, N \]
Thus, the tangential force between the driver and the driven gear is 2000 N. Quick Tip: The tangential force in gears can be found by dividing the transmitted power by the pitch line velocity.
Two products, P and Q, are sold in the ratio of 10:1. The fixed cost is Rs. 1,40,000. The selling price of P is Rs. 10/unit and Q is Rs. 40/unit. The variable costs of P and Q are Rs. 5/unit and Rs. 20/unit, respectively. The break-even point in terms of revenue, in Rs., is __________ (in integer).
View Solution
Let the number of units of P and Q sold be \( x \) and \( y \), respectively. Since the products are sold in the ratio 10:1, we have the relationship: \[ \frac{x}{y} = 10 \Rightarrow x = 10y \]
Let \( y \) be the number of units of Q sold.
- The revenue from selling \( x \) units of P and \( y \) units of Q is: \[ R = 10x + 40y = 10(10y) + 40y = 140y \]
- The total variable cost for selling \( x \) units of P and \( y \) units of Q is: \[ VC = 5x + 20y = 5(10y) + 20y = 70y \]
- The total cost (fixed + variable) is: \[ C = 1,40,000 + 70y \]
At the break-even point, revenue equals cost: \[ R = C \] \[ 140y = 1,40,000 + 70y \] \[ 70y = 1,40,000 \Rightarrow y = \frac{1,40,000}{70} = 2000 \]
Thus, \( x = 10y = 20,000 \). The total revenue is: \[ R = 140y = 140 \times 2000 = 2,80,000 \] Quick Tip: The break-even point in terms of revenue can be found by equating total revenue to total cost, considering both fixed and variable costs.

























Also Check:





Comments