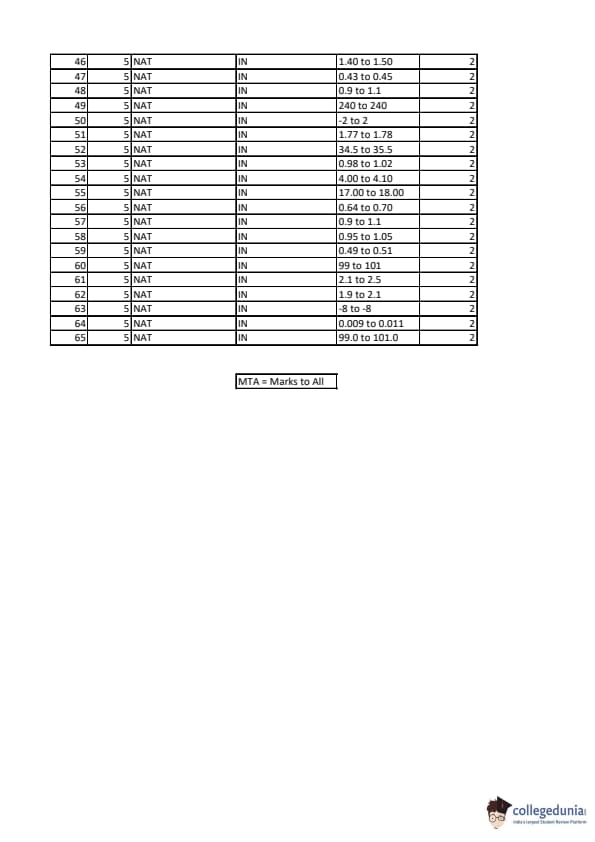
GATE 2023 Instrumentation Engineering (IN) Question Paper PDF is now available here for download. IIT Kanpur conducted GATE 2023 Instrumentation Engineering (IN) exam on February 11, 2023 in the Forenoon Session from 09:30 AM to 12:30 PM. Students have to answer 65 questions in GATE 2023 Instrumentation Engineering Question Paper carrying a total weightage of 100 marks. 10 questions are from the General Aptitude section and 55 questions are from Engineering Mathematics and Core Discipline.
GATE 2023 Instrumentation Engineering (IN) Question Paper with Solutions PDF
| GATE 2023 Instrumentation Engineering Question Paper with Solutions | Check Solutions |

The village was nestled in a green spot, ______ the ocean and the hills.
View Solution
1) Understanding the context:
The sentence talks about a village being located between two geographical features: the ocean and the hills. The preposition “between” is used to indicate the position of the village relative to two other objects, hence making it the most suitable choice.
2) Analysis of the options:
(A) through: This suggests movement across a space or location, which is incorrect in this context. \emph{“Nestled through the ocean and the hills” does not convey the correct meaning.
(B) in: This would indicate the village is located inside the space of both the ocean and hills, but this is not the intended meaning in the sentence.
(C) at: This is used for specifying exact locations but doesn’t convey the idea of being between two things.
(D) between: Correct choice. It indicates that the village is situated in the middle of the two features — the ocean and the hills.
\[ \boxed{The correct answer is (D) between.} \] Quick Tip: - \textbf{Through} indicates motion or passage. - \textbf{In} suggests being inside an area or a space. - \textbf{At} refers to a specific point or location. - \textbf{Between} refers to a position that is located in the middle of two objects.
Disagree : Protest : : Agree : ______ (By word meaning)
View Solution
1) Identifying word relationship:
The given pair “Disagree : Protest” suggests a relationship where protest is an act in response to disagreement. We need a similar relationship for “Agree,” where the corresponding action is associated with agreement.
2) Analysis of the options:
(A) Refuse: This is a negative response, but it doesn’t match the context of “agree.”
(B) Pretext: This means a false reason given for an action, which is unrelated to the context of agreement.
(C) Recommend: This is a fitting choice. When one agrees, they often make a recommendation.
(D) Refute: Refuting means disproving or denying something, which does not logically follow from agreeing.
\[ \boxed{The correct answer is (C) Recommend.} \] Quick Tip: - \textbf{Disagree} is often followed by \textbf{Protest}. - \textbf{Agree} is commonly followed by \textbf{Recommend}.
A ‘frabjous’ number is defined as a 3 digit number with all digits odd, and no two adjacent digits being the same. For example, 137 is a frabjous number, while 133 is not. How many such frabjous numbers exist?
View Solution
The problem defines a 'frabjous' number as a 3-digit number in which all digits are odd, and no two adjacent digits are the same. The possible odd digits are 1, 3, 5, 7, and 9. We will calculate the total number of such 3-digit frabjous numbers by considering the following conditions:
- For the first digit: Since the number is a 3-digit number, the first digit can be any of the 5 odd digits: \{1, 3, 5, 7, 9\. So, there are 5 choices for the first digit.
- For the second digit: The second digit must also be odd, but it cannot be the same as the first digit. Hence, there are only 4 choices for the second digit because one odd digit is already taken by the first digit.
- For the third digit: The third digit also needs to be odd, and it cannot be the same as the second digit. So, there are again 4 choices for the third digit.
Thus, the total number of frabjous numbers is the product of the number of choices for each digit:
\[ 5 \times 4 \times 4 = 80 \]
Therefore, the total number of frabjous numbers is \( 80 \). Quick Tip: When calculating the number of valid combinations for restricted problems, remember to reduce the available choices for each subsequent selection. Here, we reduced the choices for the second and third digits to avoid repetition of adjacent digits.
Which one among the following statements must be TRUE about the mean and the median of the scores of all candidates appearing for GATE 2023?
In the given diagram, ovals are marked at different heights (h) of a hill. Which one of the following options P, Q, R, and S depicts the top view of the hill?
Residency is a famous housing complex with many well-established individuals among its residents. A recent survey conducted among the residents of the complex revealed that all of those residents who are well established in their respective fields happen to be academicians. The survey also revealed that most of these academicians are authors of some best-selling books. Based only on the information provided above, which one of the following statements can be logically inferred with certainty?
Ankita has to climb 5 stairs starting at the ground, while respecting the following rules:
1. At any stage, Ankita can move either one or two stairs up.
2. At any stage, Ankita cannot move to a lower step.
Let \(F(N)\) denote the number of possible ways in which Ankita can reach the \(N^{th}\) stair. For example, \(F(1) = 1\), \(F(2) = 2\), \(F(3) = 3\). The value of \(F(5)\) is _______.
The information contained in DNA is used to synthesize proteins that are necessary for the functioning of life. DNA is composed of four nucleotides: Adenine (A), Thymine (T), Cytosine (C), and Guanine (G). The information contained in DNA can then be thought of as a sequence of these four nucleotides: A, T, C, and G. DNA has coding and non-coding regions. Coding regions—where the sequence of these nucleotides are read in groups of three to produce individual amino acids—constitute only about 2% of human DNA. For example, the triplet of nucleotides CCG codes for the amino acid glycine, while the triplet GGA codes for the amino acid proline. Multiple amino acids are then assembled to form a protein.
Based only on the information provided above, which of the following statements can be logically inferred with certainty?
(i) The majority of human DNA has no role in the synthesis of proteins.
(ii) The function of about 98% of human DNA is not understood.
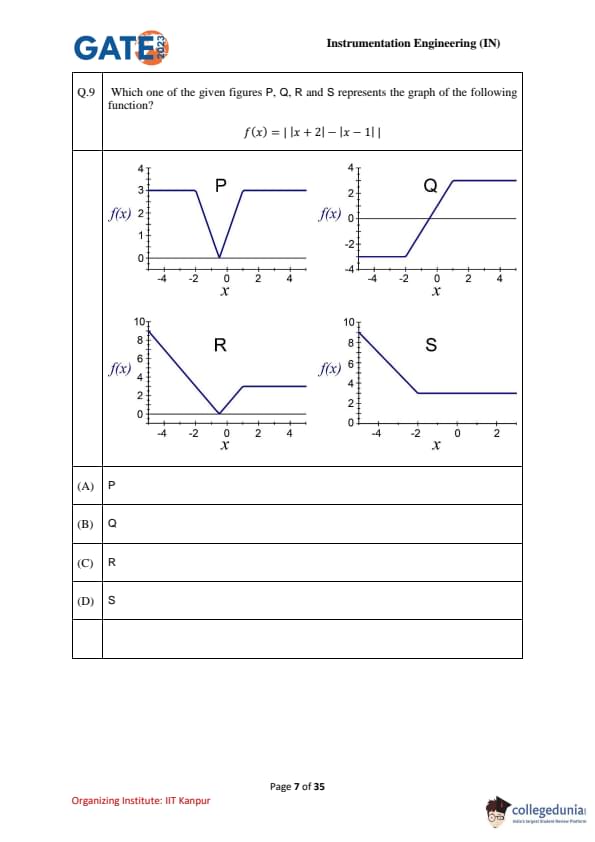
Which one of the given figures P, Q, R, and S represents the graph of the following function? \[ f(x) = |x + 2| - |x - 1| \]
An opaque cylinder (shown below) is suspended in the path of a parallel beam of light, such that its shadow is cast on a screen oriented perpendicular to the direction of the light beam. The cylinder can be reoriented in any direction within the light beam. Under these conditions, which one of the shadows P, Q, R, and S is NOT possible?
View Solution
We are given an opaque cylinder suspended in the path of a parallel beam of light, and the task is to analyze which shadow cannot be formed based on the cylinder's reorientation.
1) Shadow Formation:
When a cylindrical object is in the path of light, the shadow produced depends on the orientation of the cylinder.
- When the cylinder is oriented with its axis perpendicular to the direction of the light, it will cast a circular shadow.
- When the cylinder is reoriented with its axis at an angle to the light, the shadow may become elliptical.
- A shadow like \( S \) (which appears highly distorted) is not physically possible as it would require an impossible angle or distortion of light.
2) Conclusion:
The shadow in option \( S \) cannot be produced by the cylinder under the given conditions. Therefore, the correct answer is option (D).
\[ \boxed{The correct answer is (D) S.} \] Quick Tip: - Shadows of cylindrical objects can be circular or elliptical depending on the angle of light.
- Unusual or impossible shadows result from incorrect assumptions about the object's positioning or light angles.
Choose solution set \(S\) corresponding to the system of two equations \[ x-2y+z=0,\qquad x-z=0 \]
(Note: \(\mathbb{R}\) denotes the set of real numbers).
Inductance of a coil is measured as \(10\,mH\) using an LCR meter at \(10\,kHz\), when no objects are near the coil. If a pure copper sheet is brought near the coil, the same LCR meter will read _________.
Which of the following flow meters offers the lowest resistance to the flow?
Pair the quantities (p) to (s) with the measuring devices (i) to (iv).

Capacitance \(C\) of a parallel-plate structure is calculated as \(20~pF\) using \(C=\dfrac{\varepsilon_0\varepsilon_r A}{d}\). The value is then measured using an ideal LCR meter (no cable-capacitance error). Which reading is likely to be correct?
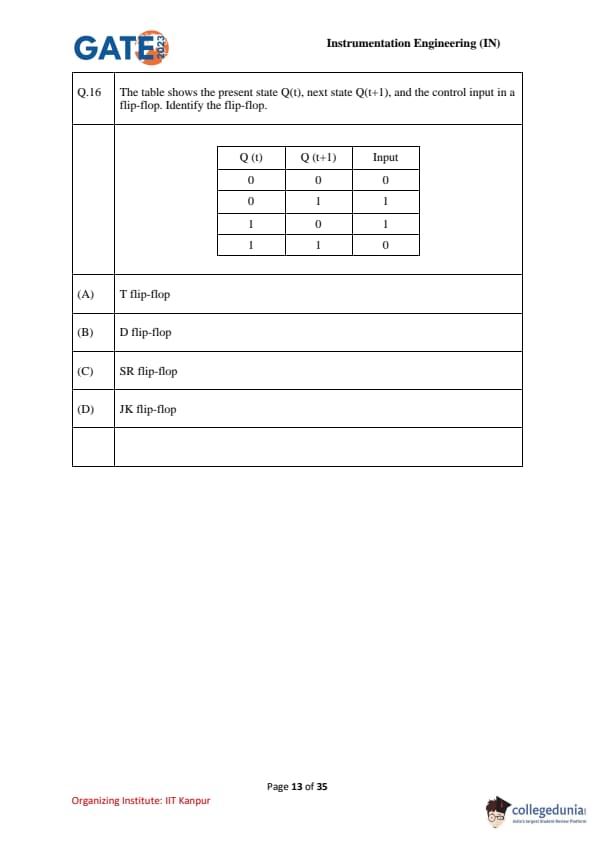
The table shows the present state \(Q(t)\), next state \(Q(t{+}1)\), and a single control input for a flip-flop. Identify the flip-flop.

Match the Exclusive-OR (XOR) operations (i)–(iv) with the results (p)–(s), where \(X\) is a Boolean input.

A light emitting diode (LED) emits light when it is _______________ biased. A photodiode provides maximum sensitivity to light when it is _______________ biased.
\(F(z)=\dfrac{1}{1-z}\), when expanded as a power series around \(z=2\), would result in \(F(z)=\sum_{k=0}^{\infty} a_k (z-2)^k\) with ROC \(|z-2|<1\). The coefficients \(a_k,\;k\ge 0\), are given by the expression ________.
The solution \(x(t)\), \(t\ge 0\), to \(\ddot{x}=-k\dot{x}\) (\(k>0\)) with \(x(0)=1\) and \(\dot{x}(0)=0\) is:
A system has the transfer function \(\dfrac{Y(s)}{X(s)}=\dfrac{s-\pi}{s+\pi}\). Let \(u(t)\) be the unit–step function. The input \(x(t)\) that results in a steady–state output \(y(t)=\sin(\pi t)\) is _____.
Choose the fastest logic family among the following:
What is \(\lim_{x \to 0} f(x)\), where \(f(x) = x \sin \frac{1}{x}\)?
The number of zeros of the polynomial \(P(s) = s^3 + 2s^2 + 5s + 80\) in the right-half plane is _____.
The number of times the Nyquist plot of \(G(s)H(s)=\dfrac{1}{2}\,\dfrac{(s-1)(s-2)}{(s+1)(s+2)}\) encircles the origin is _______________
The op-amp (ideal except \(I_b=1\,nA\) input bias current and \(V_{\!os}=10\,\muV\) input offset) is the inverting amplifier with \(R_{in}=1~k\Omega\) and \(R_f=100~k\Omega\). Find the worst-case output offset voltage \((\pm~\muV)\) (rounded to the nearest integer).

The force per unit length between two infinitely long parallel conductors, with a gap of 2 cm between them, is 10 \(\mu\)N/m. When the gap is doubled, the force per unit length will be _______________ \(\mu\)N/m (rounded off to one decimal place).
Consider the discrete-time signal \(x[n]=u[-n+5]-u[n+3]\), where \(u[n]=\begin{cases}1,&n\ge 0
0,&n<0\end{cases}\). The smallest \(n\) for which \(x[n]=0\) is _______________
Let \(y(t)=x(4t)\), where \(x(t)\) is a continuous–time periodic signal with fundamental period \(100~s\). The fundamental period of \(y(t)\) is _______________ s (rounded off to the nearest integer).
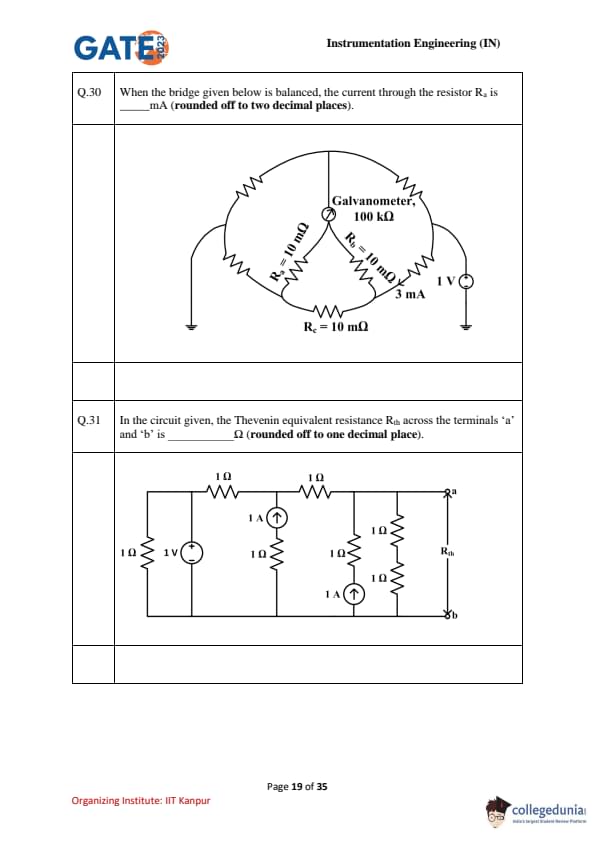
When the bridge shown is balanced, the current through the resistor \(R_a\) is _______________ mA (rounded off to two decimal places). The bridge has \(R_a=R_b=R_c=10~\mathrm{m\Omega\) and the detector (galvanometer) is ideal/open at balance; the source is \(1~V\).

In the circuit shown, the Thevenin equivalent resistance \(R_{th}\) across the terminals ‘a’ and ‘b’ is ______ \(\Omega\) (rounded off to one decimal place).

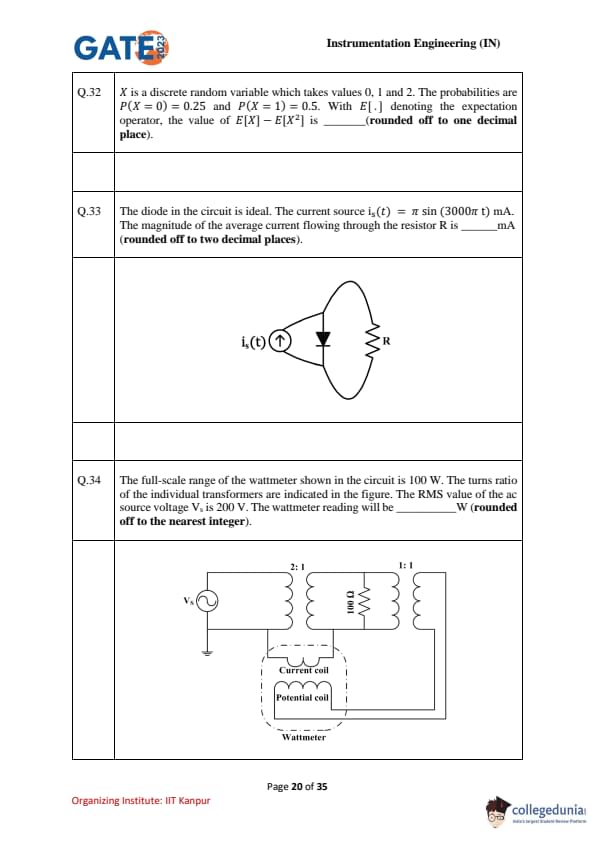
\(X\) is a discrete random variable taking values \(0,1,2\) with \(P(X=0)=0.25\), \(P(X=1)=0.5\), and \(P(X=2)=0.25\). With \(E[\cdot]\) denoting expectation, compute \(E[X]-E[X^2]\) (rounded off to one decimal place).
The diode in the circuit is ideal. The current source \(i_s(t)=\pi\sin(3000\pi t)\) mA. The magnitude of the average current flowing through the resistor \(R\) is _____ mA (rounded off to two decimal places).

The full-scale range of the wattmeter shown is 100 W. The turns ratios are as indicated. The RMS source voltage is \(V_s=200\) V. The wattmeter reading will be _____ W (rounded off to the nearest integer).

The no-load steady-state output voltage of a DC shunt generator is 200 V when it is driven in the clockwise direction at its rated speed. If the same machine is driven at the rated speed but in the opposite direction, the steady-state output voltage will be _______________ V (rounded off to the nearest integer).
The impulse response of an LTI system is \(h(t)=\delta(t)+0.5\,\delta(t-4)\). If the input is \(x(t)=\cos\!\left(\frac{7\pi}{4}t\right)\), the output is _______________
The Laplace transform of the continuous-time signal \(x(t)=e^{-3t}\,u(t-5)\) is _______________ where \(u(t)\) is the unit step.
In a p–i–n photodiode, a pulse with \(8\times10^{12}\) incident photons at \(\lambda_0=1.55\,\mu\)m yields \(4\times10^{12}\) electrons collected. The quantum efficiency at this wavelength is _______________
Let \(f(z)=j\,\dfrac{1-z}{1+z}\), where \(z\) is complex and \(j=\sqrt{-1}\). The inverse function \(f^{-1}(z)\) maps the \emph{real axis to the _______________
The simplified form of the Boolean function \(F(W,X,Y,Z)=\Sigma(4,5,10,11,12,13,14,15)\) with the minimum number of terms and literals is _______________
For the given digital circuit, \(A=B=1\). Assume that AND, OR, and NOT gates have propagation delays of \(10\) ns, \(10\) ns, and \(5\) ns respectively (wires have zero delay). Given that \(C=1\) at turn–on, the frequency of steady–state oscillation of the output \(Y\) is _____.

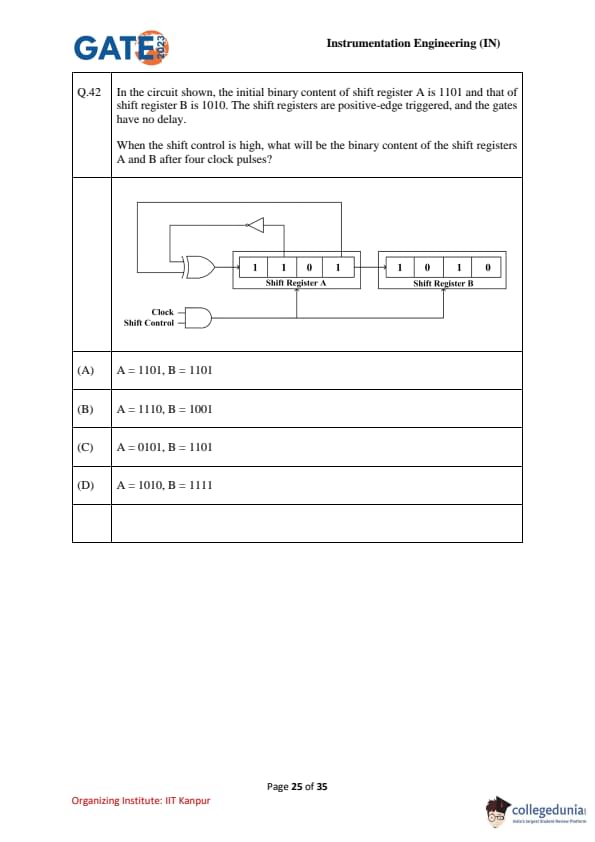
In the circuit shown, the initial binary content of shift register A is \(1101\) and that of shift register B is \(1010\). The shift registers are positive–edge triggered, and the gates have no delay. When the shift control is high, what will be the binary content of the shift registers A and B after four clock pulses?

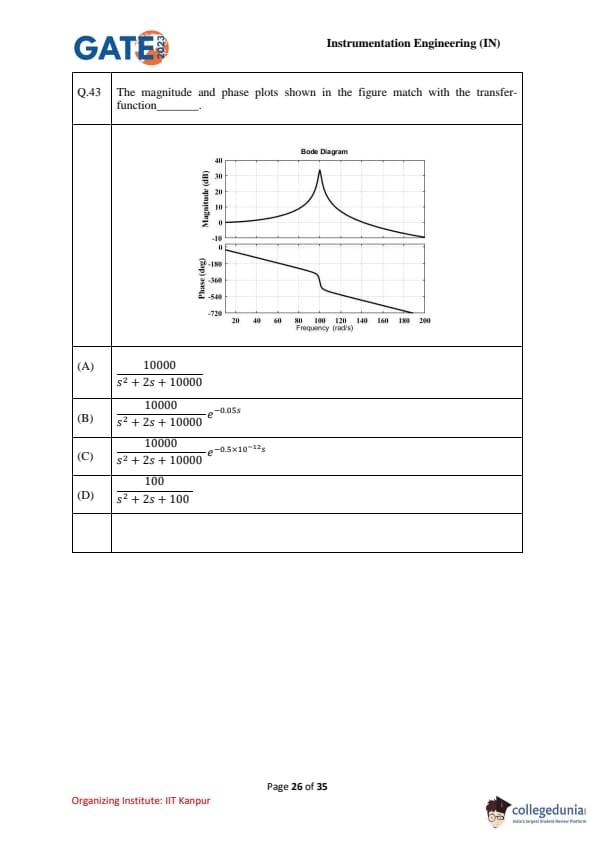
The magnitude and phase plots shown in the figure match with the transfer-function ______.

A continuous real-valued signal \(x(t)\) has finite positive energy and \(x(t)=0,\ \forall\,t<0\). From the list below, select ALL signals whose continuous-time Fourier transform is purely imaginary.
A silica-glass fiber has a core refractive index of 1.47 and a cladding refractive index of 1.44. If the cladding is completely stripped out and the core is dipped in water of refractive index 1.33, the numerical aperture (rounded to three decimal places) is _______________.
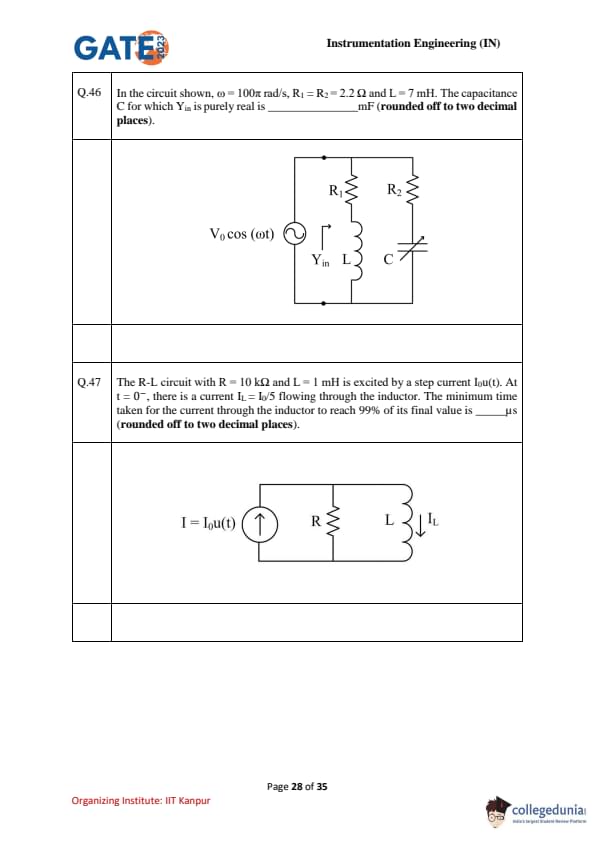
In the circuit shown, \(\omega=100\pi\ rad/s\), \(R_1=R_2=2.2~\Omega\), and \(L=7~mH\). The capacitance \(C\) for which \(Y_{in}\) is purely real is _______________ mF (rounded to two decimal places).

The R–L circuit with \(R=10\,k\Omega\) and \(L=1\,mH\) is excited by a step current \(I_0u(t)\). At \(t=0^-\), the inductor current is \(i_L=I_0/5\). The minimum time for \(i_L(t)\) to reach \(99%\) of its final value is _______________ \(\mu\)s (round off to two decimal places).

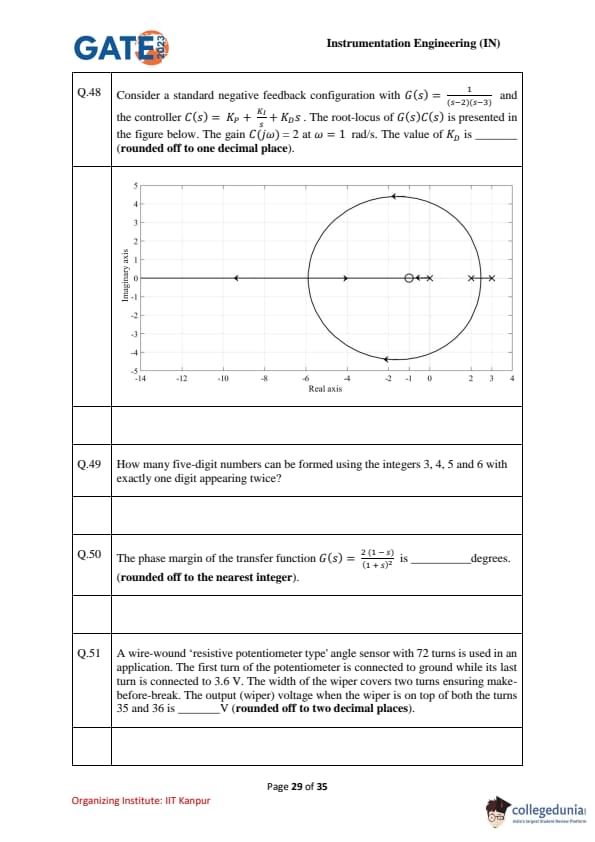
Consider a standard negative-feedback loop with \(G(s)=\dfrac{1}{(s-2)(s-3)}\) and a PID controller \(C(s)=K_P+\dfrac{K_I}{s}+K_Ds\). The root-locus of \(G(s)C(s)\) (shown) has a double zero at \(s=-1\). The gain \(|C(j\omega)|=2\) at \(\omega=1\) rad/s. The value of \(K_D\) is _______________ (round off to one decimal place).

How many five-digit numbers can be formed using the integers 3, 4, 5 and 6 with exactly one digit appearing twice?
The phase margin of the transfer function \(G(s)=\dfrac{2(1-s)}{(1+s)^2}\) is _______________ degrees (rounded off to the nearest integer).
A wire-wound `resistive potentiometer type' angle sensor with 72 turns is used. The first turn is connected to ground and the last turn to 3.6 V. The wiper width covers two turns ensuring make-before-break. The output (wiper) voltage when the wiper is on top of both turns 35 and 36 is (rounded off to two decimal places).
An ideal LVDT shows \(2\,V_{RMS}\) from each secondary at zero displacement. One secondary has a phase deviation of \(1^\circ\) from the expected \(180^\circ\) opposition; otherwise the LVDT is ideal. If the differential output sensitivity is \(1\ mV(RMS)/\mum\), the output for zero displacement is (rounded off to one decimal place) \(\mu\)m.
Five measurements are made using a weighing machine, and the readings are 80 kg, 79 kg, 81 kg, 79 kg and 81 kg. The sample standard deviation of the measurement is ___________ kg (rounded off to two decimal places).
Four strain gauges \(R_A, R_B, R_C, R_D\) (nominal \(R\)) are in a bridge. Under force: \(R_A\) and \(R_D\) increase by \(\Delta R\), \(R_B\) and \(R_C\) decrease by \(\Delta R\). A potentiometer of total resistance \(R_v\) is connected as shown to rebalance the bridge. If \(R=100~\Omega\) and \(\Delta R=1~\Omega\), the minimum \(R_v\) required to balance the bridge is _____ \(\Omega\) (rounded off to two decimal places).

Two inductors (4 H with current \(i_1(t)=1\sin(200\pi t)\,mA\) and 5 H with \(i_2(t)=2\sin(200\pi t)\,mA\)) are mutually coupled with coupling coefficient \(k=0.6\). Currents enter the dotted ends. Find the \emph{peak energy stored in the coupled system (in \(\mu\)J).

In the nMOS feedback amplifier (capacitors act as shorts at the signal frequency): \(V_{DD}=5\,V\), \(R_D=1~k\Omega\), \(R_S=1~k\Omega\), \(R_1=200~k\Omega\), \(R_2=300~k\Omega\). Given \(\mu_n C_{ox}=1~mA/V^2\), \(W/L=2\), \(V_T=1~V\), and the DC drain voltage is \(4~V\). Find \(V_{\mathrm{out}}/V_{\mathrm{in}}\) (magnitude).

Consider the real-valued function \( g(x)=\max\{(x-2)^2,\,-2x+7\}\), \(x\in(-\infty,\infty)\). The minimum value attained by \(g(x)\) is _______________ (rounded off to one decimal place).
Short-circuit test on a single-phase transformer at 1 kHz gives: wattmeter \(P=8\) W, primary current \(I=2\) A, primary voltage \(V=6\) V. Assume negligible no-load loss/current and linear core. With the secondary shorted, the primary is now fed from a \(2\) V\(_{\mathrm{RMS}}\), 1 kHz source in series with a capacitor of value \( \dfrac{1}{2\pi\sqrt{5}} \) mF. The primary RMS current is _______________ A (rounded off to two decimals).
The op-amps are ideal. Inputs: \(V_{S1}=3+0.10\sin(300t)\,V\) and \(V_{S2}=-2+0.11\sin(300t)\,V\). Find the \emph{average value of \(V_0\) (rounded to two decimals).

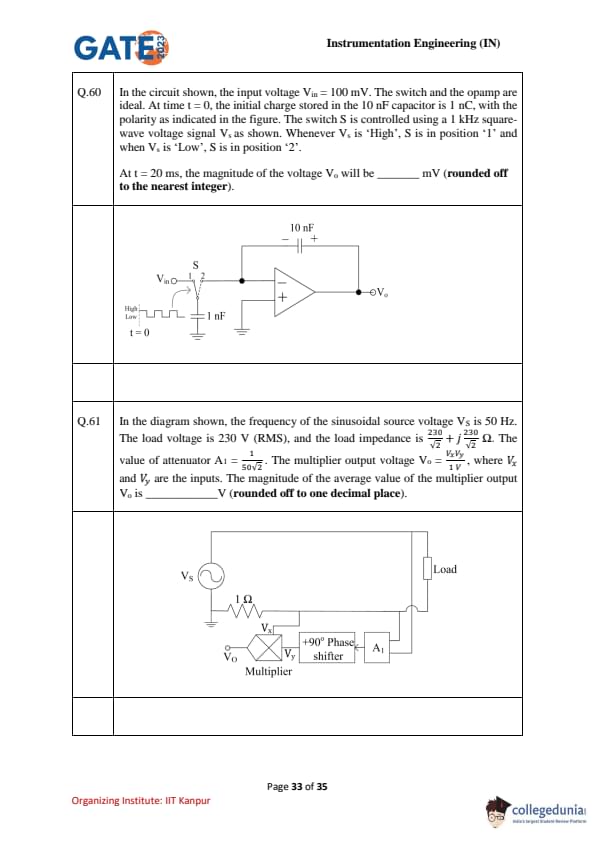
In the circuit, \(V_{in}=100\) mV. The \(10\) nF feedback capacitor initially stores \(1\) nC with the shown polarity (\(+\) at the op-amp output). The switch \(S\) toggles with a \(1\) kHz square wave (\(1\) ms period): position ‘1’ when High, ‘2’ when Low. Find \(|V_0|\) at \(t=20\) ms (nearest integer, in mV).

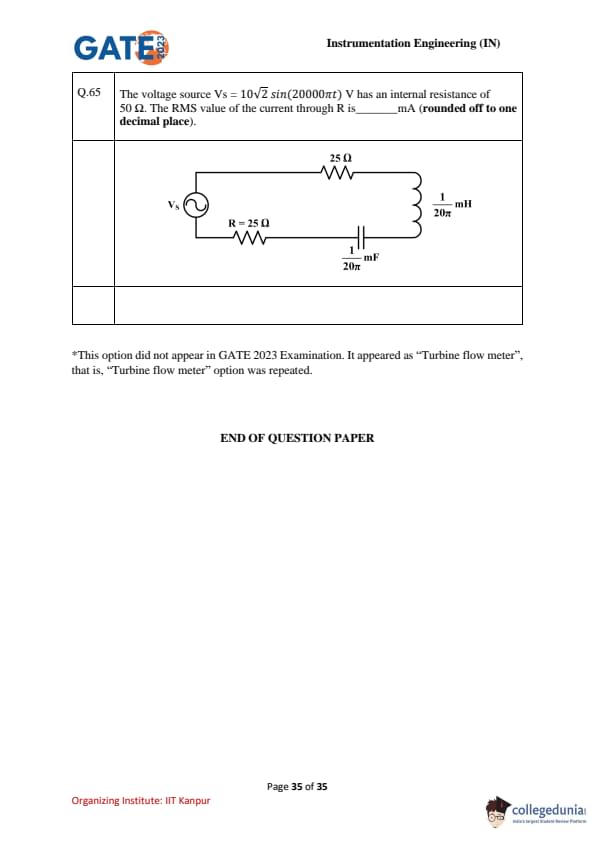
In the diagram, \(f=50\) Hz. The load voltage is \(230\) V (rms) and the load impedance is \(\frac{230}{\sqrt{2}}+j\frac{230}{\sqrt{2}}~\Omega\). The attenuator has \(A_1=\dfrac{1}{50\sqrt{2}}\). The multiplier output is \(v_o=\dfrac{v_x v_y}{1~V}\). Find the \emph{magnitude of the average value of \(v_o\) (rounded to one decimal place).

In the op-amp circuit (ideal op-amp), find \(V_o\) (rounded to one decimal place).

The rank of the matrix \(A\) given below is one. The ratio \(\dfrac{\alpha}{\beta}\) is ______ (rounded off to the nearest integer).
\[ A = \begin{bmatrix} 1 & 4
-3 & \alpha
\beta & 6 \end{bmatrix} \]
A 1.999 V True RMS 3-1/2 digit multimeter has an accuracy of \(\pm0.1 %\) of reading \(\pm 2\) digits. It is used to measure 100 A (RMS) current through a line using a 100:5 ratio Class-1 CT with burden \(0.1~\Omega \pm0.5%\). The worst-case absolute error in the multimeter output is _____ V (rounded off to three decimal places).
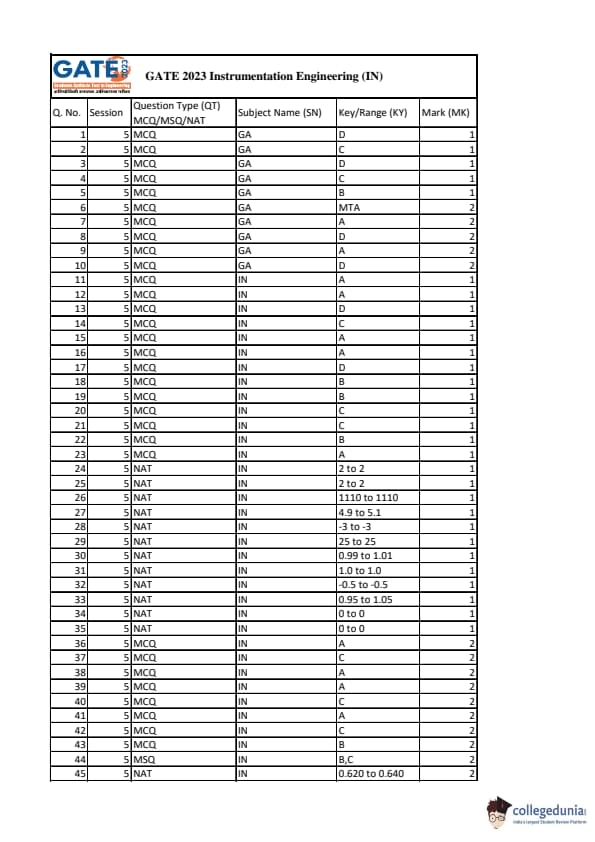
The voltage source \(v_s=10\sqrt{2}\sin(20000\pi t)\) V has an internal resistance of \(50~\Omega\). Find the RMS current through the \(R=25~\Omega\) resistor (rounded to one decimal place).


























GATE 2023 IN Paper Analysis
| Particulars | Details |
|---|---|
| Overall Difficulty Level | Moderate |
| Number of MCQs | 31 |
| Number of MSQs | 1 |
| Number of NATs | 33 |
Also Check:




Comments