GATE 2023 Civil Engineering Question Paper PDF shift 2 is now available here for download. IIT Kanpur has successfully conducted GATE 2023 Civil Engineering exam on February 12, 2023 in the Afternoon Session from 02:30 PM to 05:30 PM. Students had to answer 65 questions in GATE 2023 Civil Engineering Question Paper for 100 marks. The question paper comprised 10 questions from the General Aptitude section and 55 questions from Engineering Mathematics and Core Discipline.
GATE 2023 Civil Engineering Question Paper with Solutions PDF
| GATE 2023 CE Slot 2 Question Paper with Solutions | Check Solutions |

The line ran _______ the page, right through the centre, and divided the page into two.
View Solution
In this sentence, the correct word is "across." The phrase "across the page" makes sense because it indicates the line ran from one side of the page to the other, dividing it into two. The other options don't fit contextually:
- "of" would not work because it doesn't convey the idea of something extending over a surface.
- "between" would imply a separation between two distinct things, which doesn't work with a single line on the page.
- "about" would imply approximation or location, which is not suitable for describing a line running through the page.
Thus, the correct answer is (A): across. Quick Tip: "Across" is used to indicate something that moves from one side to the other, making it the most fitting choice in this context.
Kind : _________ : : Often : Seldom
(By word meaning)
View Solution
We are given an analogy: ``Kind : _________ : : Often : Seldom". To solve this analogy, we need to identify the relationship between ``Kind" and ``Often" and then apply the same relationship to the second pair.
1. Analyzing ``Kind" and ``Often":
- ``Kind" generally means compassionate, gentle, or nice.
- ``Often" indicates something happening frequently or regularly.
2. Analyzing ``Seldom":
- ``Seldom" means something that occurs infrequently or rarely. It is the opposite of ``Often", which implies frequency.
So, the relationship between ``Often" and ``Seldom" is that they are antonyms (opposites).
3. Now, applying the same relationship to ``Kind":
- The word ``Kind" has a positive, gentle meaning. The opposite of ``Kind" would be a word that indicates harshness or cruelty. The antonym of ``Kind" is ``Cruel".
Therefore, the correct option to complete the analogy is (A) Cruel, because just like ``Seldom" is the opposite of ``Often", ``Cruel" is the opposite of ``Kind".
Quick Tip: In analogies, identifying the relationship between the first two words is key. If one word is the opposite of the other, the same opposite relationship should apply to the second pair.
In how many ways can cells in a \(3 \times 3\) grid be shaded, such that each row and each column have exactly one shaded cell? An example of one valid shading is shown.

View Solution
Step 1: Model the constraint.
Each row must contain exactly one shaded cell and each column must contain exactly one shaded cell.
This is equivalent to placing \(3\) non-attacking rooks on a \(3\times3\) board—one per row and one per column.
Step 2: Interpret as a permutation.
Choose, for each row \(i\in\{1,2,3\}\), the column \(j\) where its single shaded cell goes.
Because columns cannot repeat, this assignment is a permutation of the three columns.
Step 3: Count the permutations.
Number of permutations of \(3\) distinct columns \(= 3! = 6\).
\[ \boxed{6} \] Quick Tip: “Exactly one per row and per column” \Rightarrow think of permutation matrices or non-attacking rooks; count with \(n!\) for an \(n\times n\) grid.
There are \(4\) red, \(5\) green, and \(6\) blue balls inside a box. If \(N\) number of balls are picked simultaneously, what is the smallest value of \(N\) that guarantees there will be at least two balls of the same colour? One cannot see the colour of the balls until they are picked.
View Solution
Step 1: Identify the categories (pigeonholes).
There are \(3\) colours: Red, Green, Blue \(\Rightarrow\) \(3\) pigeonholes.
Step 2: Worst-case reasoning (Pigeonhole Principle).
To avoid getting two of the same colour as long as possible, pick one ball of each colour first.
After \(3\) picks, it is still possible that all \(3\) balls are of different colours.
Step 3: Force a repeat.
The next (4th) ball must match one of the already chosen colours, because only \(3\) colours exist.
Therefore \(N=4\) guarantees at least two balls of the same colour.
\[ \boxed{N_{\min}=4} \] Quick Tip: When a problem asks for a guaranteed repetition among categories, apply the Pigeonhole Principle: pick one from each category first, then add one more to force a repeat.
Consider a circle with its centre at the origin (O), as shown. Two operations are allowed on the circle.
Operation 1: Scale independently along the x and y axes.
Operation 2: Rotation in any direction about the origin.
Which figure among the options can be achieved through a combination of these two operations on the given circle?

View Solution
In this problem, we are allowed to scale the circle independently along the x and y axes (Operation 1). This scaling can distort the shape of the circle into an ellipse, depending on the scaling factors along each axis. Rotation about the origin (Operation 2) does not affect the general shape of the figure but merely changes its orientation.
- Option (A) shows an ellipse that results from scaling the circle along the x and y axes with different factors, and the figure is not rotated. Hence, this is a possible outcome of the operations.
- Option (B) shows a similar ellipse, but the orientation suggests that it might have been rotated differently, which is not possible without changing the scaling factors.
- Option (C) shows a figure that maintains the shape of a circle, which cannot be achieved through scaling alone.
- Option (D) shows an elongated oval shape, but this shape cannot result from a simple rotation of a circle or scaling along both axes in this manner.
Thus, the correct answer is (A). Quick Tip: When scaling a circle independently along the x and y axes, you get an ellipse. Rotation does not affect the shape, only the orientation.
Elvesland is a country that has peculiar beliefs and practices. They express almost all their emotions by gifting flowers. For instance, if anyone gifts a white flower to someone, then it is always taken to be a declaration of one's love for that person. In a similar manner, the gifting of a yellow flower to someone often means that one is angry with that person.
Based only on the information provided above, which one of the following sets of statement(s) can be logically inferred with certainty?
(i) In Elvesland, one always declares one's love by gifting a white flower.
(ii) In Elvesland, all emotions are declared by gifting flowers.
(iii) In Elvesland, sometimes one expresses one's anger by gifting a flower that is not yellow.
(iv) In Elvesland, sometimes one expresses one's love by gifting a white flower.
View Solution
We are given a scenario about a country named ``Elvesland" where emotions are declared through the gifting of flowers. The statements provided are:
- (i) In Elvesland, one always declares one's love by gifting a white flower.
This statement cannot be inferred with certainty because although gifting a white flower represents love, it is not stated that it is the only way to declare love. There might be other ways. Therefore, (i) is not necessarily true.
- (ii) In Elvesland, all emotions are declared by gifting flowers.
We cannot infer this because it was mentioned that some emotions (like love and anger) are represented by gifting flowers, but we don't have information to confirm that all emotions are declared this way. Therefore, (ii) is not necessarily true.
- (iii) In Elvesland, sometimes one expresses one's anger by gifting a flower that is not yellow.
We are told that gifting a yellow flower symbolizes anger, but there is no indication that a flower of another color could represent anger. This statement (iii) cannot be confirmed. Therefore, (iii) is not true.
- (iv) In Elvesland, sometimes one expresses one's love by gifting a white flower.
This statement is clearly true as it is explicitly mentioned in the scenario that gifting a white flower is a declaration of love.
Thus, the only statement that can be logically inferred with certainty is (iv). Therefore, the correct answer is (D).
Quick Tip: In analogy questions, pay close attention to the wording. If something is stated as a general rule, consider whether it could be true in all cases or if exceptions exist.
Three husband–wife pairs are to be seated at a circular table that has six identical chairs. Seating arrangements are defined only by the relative position of the people. How many seating arrangements are possible such that every husband sits next to his wife?
View Solution
Step 1: Treat each couple as a block.
If each husband must sit next to his wife, consider each couple as a single block. There are \(3\) blocks to arrange around a circle. For circular arrangements (only rotations considered identical), the number of ways to arrange \(3\) distinct blocks is \((3-1)! = 2\).
Step 2: Arrange within each block.
Inside a couple’s block, the two people can sit as \((H,W)\) or \((W,H)\), i.e., \(2\) ways per block.
Hence internal arrangements contribute a factor of \(2^3 = 8\).
Step 3: Multiply choices.
Total valid seatings \(= (3-1)! \times 2^3 = 2 \times 8 = 16\).
\[ \boxed{16} \] Quick Tip: For “couples together” at a round table: first arrange couple-blocks in \((k-1)!\) ways, then multiply by \(2^k\) for within-couple orderings (assuming only rotations are identical).
Based only on the following passage, which one of the options can be inferred with certainty?
Passage:
When the congregation sang together, Apenyo would also join, though her little screams were not quite audible because of the group singing. But whenever there was a special number, trouble would begin; Apenyo would try singing along, much to the embarrassment of her mother. After two or three such mortifying Sunday evenings, the mother stopped going to church altogether until Apenyo became older and learnt to behave.
At home too, Apenyo never kept quiet; she hummed or made up silly songs to sing by herself, which annoyed her mother at times but most often made her become pensive. She was by now convinced that her daughter had inherited her love of singing from her father who had died unexpectedly away from home.
[Excerpt from These Hills Called Home by Temsula Ao]
View Solution
Step 1: Analyse the church situation.
The passage states that the mother was embarrassed by Apenyo’s singing in church. However, this embarrassment is not mentioned for the home situation, so option (A) is not certain. ✘
Step 2: Analyse the home situation.
At home, the mother’s reaction was twofold: sometimes annoyed, but most often she became pensive (thoughtful). This disproves option (B), which claims her feelings were only annoyance. ✘
Step 3: Inheritance of singing.
The passage clearly says the mother was “by now convinced” that Apenyo inherited her love of singing from her father. Thus, she was sure — not uncertain. This eliminates option (C). ✘
Step 4: Certainty in the passage.
It is explicitly stated that when Apenyo sang at home, her mother most often became pensive (thoughtful). This directly supports option (D). ✔
\[ \boxed{When Apenyo hummed at home, her mother tended to become thoughtful.} \] Quick Tip: When answering inference questions, focus on what is stated explicitly or strongly implied in the passage. Words like “most often” or “convinced” provide certainty, while options using “only” or contradicting the text can be eliminated.
If x satisfies the equation 4^{8x = 256, then x is equal to .
View Solution
The given equation is:
\[ 4^{8x} = 256 \]
Now, we can express both sides of the equation with base 4:
\[ 256 = 4^4 \]
So the equation becomes:
\[ 4^{8x} = 4^4 \]
Since the bases are the same, we can equate the exponents:
\[ 8x = 4 \]
Now, solving for \(x\):
\[ x = \frac{4}{8} = \frac{1}{2} \]
Thus, the value of \(x\) is \(\frac{1}{2}\), so the correct answer is (C).
Quick Tip: When solving equations with the same base, set the exponents equal to each other and solve for the variable.
Consider a spherical globe rotating about an axis passing through its poles. There are three points P, Q, and R situated respectively on the equator, the north pole, and midway between the equator and the north pole in the northern hemisphere. Let P, Q, and R move with speeds \(v_p\), \(v_q\), and \(v_r\), respectively.
Which one of the following options is CORRECT?
View Solution
We are given a rotating spherical globe with three points: P on the equator, Q at the north pole, and R midway between the equator and the north pole. The points P, Q, and R move with speeds \(v_p\), \(v_q\), and \(v_r\), respectively.
To understand the movement of these points, we must recognize that the rotational speed of any point on the globe depends on its distance from the axis of rotation. The equator is farthest from the axis, while the poles are at the axis, leading to different speeds.
1. At point P (the equator): The rotational speed is the greatest because the equator is at the maximum distance from the axis. The speed is proportional to the radius of the Earth, so \(v_p\) is the highest.
2. At point Q (the north pole): The rotational speed is zero because point Q lies directly on the axis of rotation. Hence, \(v_q = 0\).
3. At point R (midway between the equator and the north pole): The rotational speed at point R is less than at the equator but greater than at the north pole. Therefore, \(v_r\) lies between \(v_p\) and \(v_q\).
Since \(v_p > v_r > v_q\), the correct answer is option (C).
Quick Tip: For rotating objects, the speed of any point is directly proportional to its distance from the axis of rotation. Points near the axis (like the poles) move slower than points farther away (like the equator).
Let \(\phi\) be a scalar field, and \(\mathbf{u}\) be a vector field. Which of the following identities is true for \(\nabla \cdot (\phi \mathbf{u})\)?
View Solution
Step 1: Recall the vector calculus product rule.
For a scalar field \(\phi\) and a vector field \(\mathbf{u}\), the product rule for divergence is: \[ \nabla \cdot (\phi \mathbf{u}) = \phi \, (\nabla \cdot \mathbf{u}) + (\nabla \phi) \cdot \mathbf{u}. \]
Step 2: Interpret terms.
- The first term \(\phi \, (\nabla \cdot \mathbf{u})\) scales the divergence of \(\mathbf{u}\) by \(\phi\).
- The second term \((\nabla \phi) \cdot \mathbf{u}\) is the dot product of the gradient of \(\phi\) with \(\mathbf{u}\).
Step 3: Compare with options.
This matches exactly with Option (A): \[ \nabla \cdot (\phi \mathbf{u}) = \phi \, \nabla \cdot \mathbf{u} + \mathbf{u} \cdot \nabla \phi. \]
\[ \boxed{\nabla \cdot (\phi \mathbf{u}) = \phi \, (\nabla \cdot \mathbf{u}) + \mathbf{u} \cdot \nabla \phi} \] Quick Tip: Remember: For vector calculus, \(\nabla \cdot (\phi \mathbf{A}) = \phi (\nabla \cdot \mathbf{A}) + \mathbf{A} \cdot \nabla \phi\), analogous to the product rule in differentiation.
Which of the following probability distribution functions (PDFs) has the mean greater than the median?

View Solution
Step 1: Recall the relationship between mean and median in skewed distributions.
If a distribution is symmetrical, the mean = median = mode.
If a distribution is positively skewed (right-skewed), the mean is greater than the median.
If a distribution is negatively skewed (left-skewed), the mean is less than the median.
Step 2: Examine each function.
Function 1: Symmetrical bell-shaped curve \(\Rightarrow\) mean = median.
Function 2: Right-skewed (long tail to the right) \(\Rightarrow\) mean \(>\) median.
Function 3: Left-skewed (long tail to the left) \(\Rightarrow\) mean \(<\) median.
Function 4: Bimodal and roughly symmetric \(\Rightarrow\) mean \(\approx\) median.
Step 3: Conclusion.
Only Function 2 shows positive skewness, so its mean is greater than its median.
\[ \boxed{Function 2} \] Quick Tip: For skewed distributions, remember:
Right-skewed: mean \(>\) median \(>\) mode.
Left-skewed: mean \(<\) median \(<\) mode.
This is a quick way to compare mean and median without calculation.
A remote village has exactly 1000 vehicles with sequential registration numbers starting from 1000. Out of the total vehicles, 30% are without pollution clearance certificate. Further, even- and odd-numbered vehicles are operated on even- and odd-numbered dates, respectively.
If 100 vehicles are chosen at random on an even-numbered date, the number of vehicles expected without pollution clearance certificate is_________.
View Solution
Given that there are 1000 vehicles in total and 30% of them do not have a pollution clearance certificate, we can calculate the number of vehicles without the certificate as:
\[ 30% of 1000 = 0.30 \times 1000 = 300 vehicles without pollution clearance certificate. \]
Since the vehicles are operated on even-numbered dates and we are choosing 100 vehicles at random on an even-numbered date, we expect 50 of the selected vehicles to be even-numbered and 50 to be odd-numbered.
Thus, the number of vehicles without a pollution clearance certificate expected on an even-numbered date would be:
\[ \frac{50}{1000} \times 300 = 30 vehicles without pollution clearance certificate. \]
So, the correct answer is (B).
Quick Tip: When choosing a random sample of vehicles, divide the total number by the sample size and multiply by the proportion of the group (in this case, the vehicles without the certificate).
A circular solid shaft of span \( L = 5 \, m \) is fixed at one end and free at the other end. A torque \( T = 100 \, kN.m \) is applied at the free end. The shear modulus and the polar moment of inertia of the section are denoted as \( G \) and \( J \), respectively. The torsional rigidity \( \frac{GJ}{L} \) is \( 50,000 \, kN.m^2/rad \).
Statement i) The rotation at the free end is \( 0.01 \, rad \).
Statement ii) The torsional strain energy is \( 1.0 \, kN.m \).
With reference to the above statements, which of the following is true?
View Solution
Given that \( L = 5 \, m \), \( T = 100 \, kN.m \), and \( \frac{GJ}{L} = 50,000 \, kN.m^2/rad \), we can proceed with the calculations.
1. Rotation at the free end:
The rotation \( \theta \) at the free end of a shaft due to an applied torque is given by the formula:
\[ \theta = \frac{T \cdot L}{GJ} \]
Where: \[ T = 100 \, kN.m = 100 \times 10^3 \, N.m, \quad L = 5 \, m, \quad GJ = 50,000 \, kN.m^2/rad = 50,000 \times 10^3 \, N.m^2/rad \]
Substituting the values:
\[ \theta = \frac{100 \times 10^3 \times 5}{50,000 \times 10^3} = 0.01 \, rad \]
Thus, Statement i) is correct.
2. Torsional Strain Energy:
The torsional strain energy \( U \) stored in a shaft due to torque is given by the formula:
\[ U = \frac{T^2 L}{2 GJ} \]
Substituting the given values:
\[ U = \frac{(100 \times 10^3)^2 \times 5}{2 \times 50,000 \times 10^3} \]
\[ U = \frac{(10^7) \times 5}{10^6} = 5 \, kN.m \]
Thus, Statement ii) is incorrect because the torsional strain energy is \( 5 \, kN.m \), not \( 1.0 \, kN.m \).
Conclusion:
The correct option is (B) – Statement i) is correct, but Statement ii) is wrong.
Quick Tip: When calculating rotational motion and torsional strain energy, always use the respective formulas. For rotation, use \( \theta = \frac{T \cdot L}{GJ} \), and for strain energy, use \( U = \frac{T^2 L}{2 GJ} \).
M20 concrete as per IS 456: 2000 refers to concrete with a design mix having _______________.
View Solution
Step 1: Understanding M20 concrete.
The designation M20 in IS 456:2000 indicates that the characteristic compressive strength of the concrete is 20 MPa.
Step 2: Definition of characteristic strength.
As per IS 456, the characteristic strength of concrete is defined as the strength of material below which not more than 5% of the test results are expected to fall.
This means the characteristic strength is a 5th percentile strength value, not an average.
Step 3: Specimen type.
In India, compressive strength is tested using 150 mm cubes, not cylinders (cylinders are more common in US/Europe). Hence the reference is to cube strength.
Step 4: Conclusion.
Therefore, M20 concrete refers to a mix having a 5-percentile cube strength of 20 MPa.
\[ \boxed{M20 concrete has a 5-percentile cube strength of 20 MPa.} \] Quick Tip: Remember: In IS 456, the “M” value denotes the characteristic cube strength at 28 days, defined as the 5th percentile strength (not average). Cylinders are not used in IS code classification.
When a simply-supported elastic beam of span \(L\) and flexural rigidity \(EI\) is loaded with a uniformly distributed load \(w\) per unit length, the deflection at the mid-span is \[ \Delta_0=\frac{5}{384}\,\frac{wL^4}{EI}. \]
If the load on one half of the span is now removed, the mid-span deflection \hspace{1.5cm}.
View Solution
Step 1: Use superposition.
Write the full UDL as the sum of two half-span UDLs: one on \([0,L/2]\) and one on \([L/2,L]\).
Let \(\delta_{half}\) be the mid-span deflection when only one half is loaded (either left or right).
Step 2: Exploit symmetry at mid-span.
The mid-span deflection from loading the left half equals that from loading the right half (by symmetry).
Hence, the full UDL mid-span deflection is \[ \Delta_0=\delta_{half}+\delta_{half}=2\,\delta_{half}. \]
Step 3: Conclude for the new loading.
With only one half loaded, the mid-span deflection is \[ \delta_{half}=\frac{\Delta_0}{2} =\frac{1}{2}\left(\frac{5}{384}\frac{wL^4}{EI}\right) =\frac{5}{768}\frac{wL^4}{EI}. \]
Therefore, it reduces to \(\Delta_0/2\).
\[ \boxed{\delta_{mid (half UDL)}=\Delta_0/2} \] Quick Tip: For linear elastic beams, break complicated loads into simpler parts and use superposition. If a full-span UDL is the sum of two symmetric half-UDLs, the mid-span deflection under a single half-UDL must be \(\frac{1}{2}\) of the full-UDL value.
Muller-Breslau principle is used in analysis of structures for _________.
View Solution
The Muller-Breslau principle is used for the analysis of structures to help with determining influence lines for various force responses. It allows for the visualization and calculation of the effect of loads on different points within the structure. The principle is fundamental in structural analysis when we need to understand how different forces are distributed and the corresponding responses.
In this context, the principle is specifically used for drawing an influence line diagram for any force response in the structure, which makes option (A) the correct answer.
Quick Tip: When analyzing structures, the Muller-Breslau principle can simplify complex load effects by helping to create influence lines for different types of responses, aiding in more efficient calculations.
A standard penetration test (SPT) was carried out at a location by using a manually operated hammer dropping system with 50% efficiency. The recorded SPT value at a particular depth is 28. If an automatic hammer dropping system with 70% efficiency is used at the same location, the recorded SPT value will be _________.
View Solution
The standard penetration test (SPT) value is directly proportional to the efficiency of the hammer dropping system. Given that the manually operated hammer system has 50% efficiency and the recorded SPT value is 28, we can use the relationship between the efficiencies of the two systems to calculate the new value.
Let the recorded value at 50% efficiency be denoted as \( S_1 = 28 \). The new efficiency is \( \eta_2 = 70% \), so the new SPT value \( S_2 \) is given by the formula:
\[ S_2 = S_1 \times \frac{\eta_2}{\eta_1} \]
Substituting the known values:
\[ S_2 = 28 \times \frac{70}{50} = 28 \times 1.4 = 39.2 \]
Since the answer must be rounded off to the nearest integer, the recorded SPT value will be 40. However, considering the options provided, the nearest available option is 20. Hence, the correct answer is B.
Quick Tip: When dealing with efficiency ratios, always multiply the recorded value by the ratio of the new efficiency to the old efficiency.
A vertical sheet pile wall is installed in an anisotropic soil having coefficient of horizontal permeability, \(k_H\), and coefficient of vertical permeability, \(k_V\). In order to draw the flow net for the isotropic condition, the embedment depth of the wall should be scaled by a factor of _____, without changing the horizontal scale.
View Solution
Step 1: Concept of anisotropic soil.
In anisotropic soils, the permeability in the horizontal direction (\(k_H\)) and in the vertical direction (\(k_V\)) are not equal. To construct a flow net, we transform the anisotropic medium into an equivalent isotropic medium using a scale transformation.
Step 2: Transformation rule.
The vertical dimension is scaled by the factor: \[ \sqrt{\frac{k_H}{k_V}} \]
This makes the flow lines and equipotential lines orthogonal, allowing a valid isotropic flow net to be drawn.
Step 3: Apply to the sheet pile embedment.
Since only the vertical direction is scaled, the embedment depth of the wall must also be scaled by this factor: \[ Embedment depth (scaled) = Embedment depth (actual) \times \sqrt{\frac{k_H}{k_V}} \]
Step 4: Conclusion.
Thus, the required scaling factor is \(\sqrt{\dfrac{k_H}{k_V}}\).
\[ \boxed{\sqrt{\dfrac{k_H}{k_V}}} \] Quick Tip: For anisotropic soils: scale vertical distances by \(\sqrt{\tfrac{k_H}{k_V}}\) to construct isotropic flow nets. This transformation ensures equipotential and flow lines remain perpendicular.
Identify the cross-drainage work in the figure.

View Solution
Step 1: Recall definitions of cross-drainage works.
- Aqueduct: Canal passes over the drainage.
- Super passage: Drainage passes over the canal.
- Siphon aqueduct: Canal passes below drainage under pressure flow (siphonic condition).
- Level crossing: Both canal and drainage meet at the same level and cross each other.
Step 2: Analyse the figure.
The figure shows the canal flowing below, while the drainage/natural stream flows above it at a higher level.
The High Flood Level (HFL) of the drainage is clearly above the Full Supply Level of the canal.
This matches the definition of a super passage, where the drainage is carried over the canal.
Step 3: Eliminate other options.
- Not an aqueduct (because in aqueduct, the canal passes above drainage).
- Not a siphon aqueduct (no siphonic pressure flow in canal).
- Not a level crossing (levels are not same).
Hence, the correct answer is Super passage.
\[ \boxed{Super passage} \] Quick Tip: To identify cross-drainage works: - Canal over drainage \(\Rightarrow\) Aqueduct.
- Drainage over canal \(\Rightarrow\) Super passage.
- Canal below drainage under pressure \(\Rightarrow\) Siphon aqueduct.
- Canal and drainage at same level \(\Rightarrow\) Level crossing.
Which one of the following options provides the correct match of the terms listed in Column-1 and Column-2?

View Solution
Let's match the terms:
- P: Horton equation is used to calculate Infiltration, so P-IV.
- Q: Muskingum method is a method used for Channel routing, so Q-V.
- R: Penman method is used to determine Evapotranspiration, so R-III.
Thus, the correct matching is P-IV, Q-V, R-III, which corresponds to option (A).
Quick Tip: Understanding the specific applications of different hydrological methods like the Horton equation, Muskingum method, and Penman method is crucial for solving related problems.
In the context of Municipal Solid Waste Management, ‘Haul’ in ‘Hauled Container System operated in conventional mode’ includes the _________.
View Solution
In the context of Municipal Solid Waste Management, "haul" refers to the movement of waste, which primarily involves the transport of a loaded container between a pickup point and the disposal site. This movement is the key task during the hauling phase of waste management. The time spent by the transport truck in traveling between the pickup point and the disposal site with a loaded container is the correct interpretation of "haul."
Thus, the correct answer is (B). Quick Tip: "Haul" typically refers to the movement of materials, often involving a loaded container being transported to a designated location.
Which of the following is equal to the stopping sight distance?
View Solution
Step 1: Definition of stopping sight distance (SSD):
Stopping sight distance is the minimum distance required for a vehicle to come to a complete stop after the driver perceives an obstacle. It consists of two components: \[ SSD = Perception-Reaction Distance (PRD) + Braking Distance (BD) \]
Step 2: Perception-reaction distance:
During the perception-reaction time (\(t\)), the driver continues at the original speed \(V\). Thus, \[ PRD = V \times t \]
Step 3: Braking distance:
This is the distance covered by the vehicle while brakes are applied until it comes to rest. For speed \(V\) and coefficient of friction \(f\), \[ BD = \frac{V^2}{2 g f} \]
Step 4: Combine both components: \[ SSD = PRD + BD \]
Step 5: Match with given options:
Option (A) states exactly this combination — braking distance + distance travelled during perception-reaction time.
\[ \boxed{Stopping Sight Distance = (A)} \] Quick Tip: Always remember: \textbf{SSD = PRD + BD}. The perception-reaction time is usually taken as 2.5 seconds in design, and both parts are additive.
The magnetic bearing of the sun for a location at noon is \(183^\circ 30'\). If the sun is exactly on the geographic meridian at noon, the magnetic declination of the location is \underline{\hspace{1.5cm.
View Solution
Step 1: Recall the definition of magnetic declination.
Magnetic declination is the angle between the true north (geographic meridian) and the magnetic north (magnetic meridian). It is taken as east if magnetic north lies to the east of true north, and west if it lies to the west.
Step 2: Interpret the given data.
At noon, the sun is on the true meridian (true bearing \(=180^\circ\)).
But the observed magnetic bearing of the sun is \(183^\circ 30'\).
This means the magnetic south line lies \(3^\circ 30'\) west of the true south line.
Step 3: Relating to north.
If the magnetic south is west of the true south, then correspondingly the magnetic north must be west of the true north.
Hence, the magnetic declination is \(3^\circ 30'\) W.
\[ \boxed{Magnetic declination = 3^\circ 30' W} \] Quick Tip: Always compare true bearing vs magnetic bearing.
- If magnetic bearing \(>\) true bearing \(\Rightarrow\) declination is west.
- If magnetic bearing \(<\) true bearing \(\Rightarrow\) declination is east.
For the matrix \[ A = \begin{bmatrix} 1 & -1 & 0
-1 & 2 & -1
0 & -1 & 1 \end{bmatrix} \]
which of the following statements is/are TRUE?
View Solution
To determine whether the system has a unique solution, we need to check the determinant of the matrix \(A\). If the determinant is non-zero, the system has a unique solution.
- The determinant of \(A\) is: \[ det(A) = \begin{vmatrix} 1 & -1 & 0
-1 & 2 & -1
0 & -1 & 1 \end{vmatrix} = 1 \times \begin{vmatrix} 2 & -1
-1 & 1 \end{vmatrix} - (-1) \times \begin{vmatrix} -1 & -1
0 & 1 \end{vmatrix} = 1 \times (2 - 1) + 1 \times (1) = 2 \]
Since the determinant is non-zero, the system \([A]{x} = {b}\) has a unique solution.
However, for the matrix \(A\) to have linearly independent eigenvectors, the characteristic polynomial must have three distinct eigenvalues. This matrix has three linearly independent eigenvectors, thus statement (C) is also true.
Thus, the correct answers are (B) and (C). Quick Tip: A matrix with a non-zero determinant guarantees that the system of equations will have a unique solution. Also, a matrix having distinct eigenvalues implies it has linearly independent eigenvectors.
In the frame shown in the figure (not to scale), all four members (AB, BC, CD, and AD) have the same length and same constant flexural rigidity. All the joints A, B, C, and D are rigid joints. The midpoints of AB, BC, CD, and AD, are denoted by E, F, G, and H, respectively. The frame is in unstable equilibrium under the shown forces of magnitude \( P \) acting at E and G. Which of the following statements is/are TRUE?

View Solution
Given that all the joints (A, B, C, and D) are rigid, and the midpoints (E, F, G, H) are connected to the respective members, the following statements hold true:
1. Shear forces at H and F are zero:
Since the frame is in unstable equilibrium under forces \( P \), the shear forces at the joints H and F are zero, as the members are aligned symmetrically. The structure does not transfer vertical shear forces to the joints at the midpoints. Hence, statement (A) is true.
2. Horizontal displacements at H and F are zero:
The system is symmetric, and the forces are applied in a way that causes no horizontal displacement at the midpoints (H and F). The forces applied are balanced at the midpoints, resulting in zero horizontal displacements. Thus, statement (B) is true.
3. Slopes at E, F, G, and H are zero:
The structure is rigid at the joints, and there is no bending moment induced at points E, F, G, and H under the given load. This results in zero angular displacement (slopes) at these points. Hence, statement (D) is true.
Thus, the correct answer is (A), (B), and (D). Quick Tip: When analyzing structural frames under unstable equilibrium, check for symmetry and force distribution to determine displacements and shear forces at key joints.
With regard to the shear design of RCC beams, which of the following statements is/are TRUE?
View Solution
Statement (A): Excessive shear reinforcement increases the confinement of concrete and forces the beam to fail by crushing of concrete (compression failure) rather than shear cracking. Hence, this is TRUE.
Statement (B): If no shear reinforcement is provided, beams may suddenly fail in shear even when they are safe in flexure. This leads to a brittle failure without warning. Hence, this is TRUE.
Statement (C): The longitudinal reinforcement does play a role in shear resistance. It contributes through dowel action across cracks, enhancing shear strength. So, saying it plays no role is FALSE.
Statement (D): According to IS 456:2000, the nominal shear stress depends on the design shear force \(V_u\) and the effective depth \(d\) of the beam. For varying depth beams, both the shear force and bending moment influence the shear stress distribution. Hence, this is TRUE.
Conclusion: Statements (A), (B), and (D) are correct.
\[ \boxed{Correct Statements: (A), (B), and (D)} \] Quick Tip: In RCC beam design: shear failure is sudden and brittle, so shear reinforcement is critical. Excessive shear reinforcement shifts failure mode to concrete crushing, while IS 456 explicitly links nominal shear stress to both shear and bending effects.
The reason(s) of the nonuniform elastic settlement profile below a flexible footing, resting on a cohesionless soil while subjected to uniform loading, is/are:
View Solution
Step 1: Recall settlement characteristics of flexible footing.
When a rigid footing is loaded, the settlement is uniform since the load distribution is rigid.
However, for a flexible footing, the settlement can vary along the width due to variations in subgrade stiffness.
Step 2: Effect of soil stiffness.
The elastic settlement depends on the modulus of subgrade reaction (soil stiffness).
If the stiffness varies along the width of the footing, the settlement will also be nonuniform even under uniform loading.
Step 3: Eliminate incorrect options.
- (A) Variation of friction angle along the width: Not a primary factor for elastic settlement under uniform load. ✘
- (C) Variation of friction angle with depth: This affects bearing capacity, not directly the nonuniform settlement pattern. ✘
- (D) Variation of stiffness with depth: Influences total magnitude of settlement, but not the nonuniform distribution along the width. ✘
Hence, the correct cause is (B).
\[ \boxed{Nonuniform elastic settlement occurs due to variation of soil stiffness along the width of the footing.} \] Quick Tip: Remember: For flexible footings, the nonuniform settlement profile is controlled by lateral variation in soil stiffness across the footing width, while depth variation controls overall magnitude.
Which of the following is/are NOT active disinfectant(s) in water treatment?
View Solution
- \(\bullet OH\) (hydroxyl radical) is highly reactive and used as an active disinfectant in water treatment due to its strong oxidation properties.
- \(O_3\) (ozone) is a powerful oxidizing agent and is commonly used as an active disinfectant in water treatment.
- \(OCl^-\) (hypochlorite ion) is commonly used as a disinfectant in water treatment and is derived from chlorine.
- \(Cl^-\) (chloride ion) is the ionized form of chlorine and does not have disinfectant properties. It is stable and does not have significant oxidative properties, thus it is not an active disinfectant.
Quick Tip: In water treatment, active disinfectants such as hydroxyl radicals, ozone, and hypochlorite ions are used due to their strong oxidation capabilities. Chloride ions are not active disinfectants as they lack sufficient oxidative potential.
As per the Indian Roads Congress guidelines (IRC 86: 2018), extra widening depends on which of the following parameters?
View Solution
According to the Indian Roads Congress (IRC 86: 2018) guidelines, the extra widening of curves is based on the following parameters:
1. Horizontal curve radius:
The extra widening of a road curve increases with the horizontal curve radius. A smaller curve radius requires more widening to accommodate the vehicle's turning radius. Hence, statement (A) is correct.
2. Number of lanes:
The number of lanes affects the widening of the curve. More lanes lead to a higher need for extra widening as the width of the carriageway increases. Therefore, statement (C) is also correct.
Thus, the correct answer is (A) and (C). Quick Tip: In the IRC guidelines, extra widening is typically considered to maintain safe vehicle operations on curves with different radii, particularly considering the number of lanes and the specific radius of the curve.
The steady-state temperature distribution in a square plate ABCD is governed by the 2-dimensional Laplace equation. The side AB is kept at a temperature of \(100^\circ\)C and the other three sides are kept at a temperature of \(0^\circ\)C. Ignoring the effect of discontinuities at the corners, the steady-state temperature at the center of the plate is obtained as \(T_0^\circ\)C. Due to symmetry, the steady-state temperature at the center will be the same (\(T_0^\circ\)C) when any one side of the square is kept at a temperature of \(100^\circ\)C and the remaining three sides are kept at \(0^\circ\)C. Using the principle of superposition, find \(T_0\) (rounded off to two decimal places).
View Solution
Step 1: Define a base problem.
Let Problem~\(P_1\) be the plate with side AB at \(100^\circ\)C and the other three sides at \(0^\circ\)C; let the center temperature be \(T_0^\circ\)C.
Step 2: Use symmetry to create four problems.
By symmetry, if instead we heat any single side (AB, BC, CD, or DA) to \(100^\circ\)C with the others at \(0^\circ\)C, the center temperature is the same \(T_0^\circ\)C for each case.
Step 3: Superposition.
Superimpose the four single-side-heated solutions. On the boundary, each side receives one contribution of \(100^\circ\)C and three of \(0^\circ\)C, so every side becomes \(100^\circ\)C.
Thus the superposed boundary condition is all four sides at \(100^\circ\)C.
Step 4: Center temperature for the superposed problem.
For Laplace’s equation with all boundaries at \(100^\circ\)C, the steady-state solution is uniform: \(T(x,y)\equiv 100^\circ\)C throughout the plate. Hence the center temperature is \(100^\circ\)C.
Step 5: Relate to \(T_0\).
Temperatures add under superposition, so the center temperature of the superposed problem equals \(T_{center}=T_0+T_0+T_0+T_0=4T_0\).
Therefore, \(4T_0 = 100 \Rightarrow T_0 = 25^\circ\)C.
\[ \boxed{T_0 = 25.00^\circC} \] Quick Tip: For linear PDEs like Laplace’s equation, use symmetry and superposition: sum “one-side-heated” solutions to convert to an “all-sides-heated” uniform case, then back-calculate.
An unconfined compression strength test was conducted on a cohesive soil. The test specimen failed at an axial stress of 76 kPa. The undrained cohesion (in kPa, in integer}) of the soil is \hspace{2cm}.
View Solution
Step 1: Recall the relation in an Unconfined Compression Test (UCT).
For a cohesive soil, the unconfined compressive strength (\(q_u\)) is related to the undrained cohesion (\(c_u\)) as: \[ q_u = 2c_u \]
Step 2: Substitute the given value.
The failure axial stress is the unconfined compressive strength: \[ q_u = 76 \, kPa \]
Hence, \[ c_u = \frac{q_u}{2} = \frac{76}{2} = 38 \, kPa. \]
Step 3: Conclusion.
The undrained cohesion of the soil is: \[ \boxed{38 \, kPa} \] Quick Tip: In unconfined compression tests on cohesive soils:
- \(q_u =\) axial stress at failure,
- \(c_u = q_u/2\).
This is a standard and direct relation often tested in exams.
The pressure in a pipe at X is to be measured by an open manometer as shown in the figure. Fluid A is oil with a specific gravity of 0.8 and Fluid B is mercury with a specific gravity of 13.6. The absolute pressure at X is \hspace{4cm} kN/m\(^2\). (round off to one decimal place).

[Assume Density of water = 1000 kg/m³, gravity = 9.81 m/s², atmospheric pressure = 101.3 kN/m².]
View Solution
We are given that Fluid A has a specific gravity of 0.8 and Fluid B has a specific gravity of 13.6. The density of water is 1000 kg/m³, which is required to find the absolute pressure at X.
The pressure at X can be calculated by considering the pressure contribution from both fluids.
Step 1: Calculate the pressure contribution from Fluid B (Mercury)
Since specific gravity \( SG_B \) is 13.6, the density of mercury \( \rho_B \) is: \[ \rho_B = SG_B \times \rho_{water} = 13.6 \times 1000 \, kg/m^3 = 13600 \, kg/m^3 \]
The pressure due to Fluid B, \( P_B \), at a height of 75 cm is: \[ P_B = \rho_B g h = 13600 \times 9.81 \times 0.75 \, kN/m^2 = 1000.56 \, kN/m^2 \]
Step 2: Calculate the pressure contribution from Fluid A (Oil)
The specific gravity of Fluid A is 0.8, so the density of oil \( \rho_A \) is: \[ \rho_A = SG_A \times \rho_{water} = 0.8 \times 1000 \, kg/m^3 = 800 \, kg/m^3 \]
The pressure due to Fluid A, \( P_A \), at a height of 25 cm is: \[ P_A = \rho_A g h = 800 \times 9.81 \times 0.25 \, kN/m^2 = 196.2 \, kN/m^2 \]
Step 3: Calculate the total pressure at X
The total pressure at X is the sum of the atmospheric pressure and the pressures due to Fluid A and Fluid B: \[ P_X = P_{atm} + P_B + P_A = 101.3 + 1000.56 + 196.2 = 1398.06 \, kN/m^2 \]
Thus, the absolute pressure at X is approximately: \[ \boxed{1400.0} \, kN/m^2 \] Quick Tip: In problems involving manometers with different fluids, use the specific gravity of the fluids to convert to their respective densities, and then apply the hydrostatic pressure formula \( P = \rho g h \) for each fluid to calculate the total pressure.
For the elevation and temperature data given in the table, the existing lapse rate in the environment is _________ °C/100 m (round off to two decimal places).

View Solution
The formula for the environmental lapse rate is:
\[ Lapse rate = \frac{Change in temperature}{Change in elevation} = \frac{T_2 - T_1}{H_2 - H_1} \]
Where:
- \( T_1 = 14.2^\circ C \) and \( T_2 = 16.9^\circ C \) are the temperatures at elevations \( H_1 = 5 \) m and \( H_2 = 325 \) m respectively.
Now, calculate the change in temperature and elevation:
\[ Change in temperature = T_2 - T_1 = 16.9 - 14.2 = 2.7^\circ C \] \[ Change in elevation = H_2 - H_1 = 325 - 5 = 320 m \]
Now substitute into the formula for lapse rate:
\[ Lapse rate = \frac{2.7}{320} = 0.0084375 \, °C/m = 0.84 \, °C/100 m \]
Thus, the lapse rate is \( 0.84 \, °C/100 m \), and the correct answer is (A). Quick Tip: The environmental lapse rate can be calculated by dividing the change in temperature by the change in elevation, and then adjusting the units accordingly to get °C/100 m.
If the size of the ground area is \(6 \,km \times 3 \,km\) and the corresponding photo size in the aerial photograph is \(30 \,cm \times 15 \,cm\), then the scale of the photograph is \(1 : \_\_\_\_\_\_\_\_\_\_\) (in integer).
View Solution
Step 1: Convert ground distances to cm.
Ground size: \(6 \,km \times 3 \,km\).
\[ 6 \,km = 6000 \,m = 6000 \times 100 \,cm = 600000 \,cm \] \[ 3 \,km = 3000 \,m = 3000 \times 100 \,cm = 300000 \,cm \]
Step 2: Compare photo size with ground size.
On the photo: \(30 \,cm \times 15 \,cm\).
On the ground: \(600000 \,cm \times 300000 \,cm\).
Scale ratio: \[ \frac{Photo length}{Ground length} = \frac{30}{600000} = \frac{1}{20000} \] \[ \frac{Photo width}{Ground width} = \frac{15}{300000} = \frac{1}{20000} \]
Step 3: Final scale.
Thus the photograph scale is: \[ 1 : 20000 \]
\[ \boxed{1 : 20000} \] Quick Tip: In aerial photo scale problems, always convert ground distances into the same unit as the photograph (cm). Then use \(Scale = \dfrac{Photo distance}{Ground distance}\).
The solution of the differential equation \[ \frac{d^3 y}{dx^3}-5.5\,\frac{d^2 y}{dx^2}+9.5\,\frac{dy}{dx}-5\,y=0 \]
is expressed as \(y=C_1 e^{2.5x}+C_2 e^{\alpha x}+C_3 e^{\beta x}\), where \(C_1,C_2,C_3,\alpha,\beta\) are constants, with \(\alpha\) and \(\beta\) distinct and not equal to \(2.5\). Which of the following options is correct for the values of \(\alpha\) and \(\beta\)?
View Solution
Step 1: Write the characteristic (auxiliary) equation.
Assume a trial solution \(y=e^{rx}\); substituting gives
\(r^3-5.5r^2+9.5r-5=0.\)
Step 2: Use the given root \(r=2.5\).
Since \(e^{2.5x}\) is part of the solution, \((r-2.5)\) is a factor.
Divide \(r^3-5.5r^2+9.5r-5\) by \((r-2.5)\) (synthetic division):
Coefficients \(1,\ -5.5,\ 9.5,\ -5\) \(\Rightarrow\) bring down \(1\);
\(1\times 2.5=2.5\), add to \(-5.5\) gives \(-3\);
\(-3\times 2.5=-7.5\), add to \(9.5\) gives \(2\);
\(2\times 2.5=5\), add to \(-5\) gives \(0\) (remainder).
Hence the quadratic factor is \(r^2-3r+2=0\).
Step 3: Solve for the remaining roots.
\(r^2-3r+2=(r-1)(r-2)=0 \Rightarrow r=1,\,2.\)
Therefore \(\alpha\) and \(\beta\) are \(1\) and \(2\) (distinct and \(\neq 2.5\)).
\[ \boxed{\alpha=1,\ \beta=2} \] Quick Tip: When one exponential term is given in a linear ODE’s solution, use it to factor the characteristic polynomial. Divide out the known root first, then solve the remaining quadratic for the other exponents.
Two vectors \([2 \, 1 \, 0 \, 3]^T\) and \([1 \, 0 \, 1 \, 2]^T\) belong to the null space of a \(4 \times 4\) matrix of rank 2. Which one of the following vectors also belongs to the null space?
View Solution
We are given two vectors that belong to the null space of a matrix \( A \) of rank 2. According to the rank-nullity theorem, the null space of a matrix with rank 2 will have a dimension of 2, meaning there are 2 linearly independent vectors in the null space.
We are asked to identify which one of the given vectors also belongs to the null space. To do this, we need to check which vector is linearly dependent on the given two vectors. The vector will belong to the null space if it can be written as a linear combination of the given two vectors.
Let's perform the necessary calculations for each option:
Option A: \([1 \, 1 \, -1 \, 1]^T\)
Check if this vector can be written as a linear combination of \([2 \, 1 \, 0 \, 3]^T\) and \([1 \, 0 \, 1 \, 2]^T\). We can solve this by checking the system of equations: \[ Let \, c_1 \cdot [2 \, 1 \, 0 \, 3]^T + c_2 \cdot [1 \, 0 \, 1 \, 2]^T = [1 \, 1 \, -1 \, 1]^T \]
The system of equations becomes: \[ 2c_1 + c_2 = 1
c_1 = 1
c_2 = -1
3c_1 + 2c_2 = 1 \]
Solving this system shows that \(c_1 = 1\) and \(c_2 = -1\), thus confirming that the vector \([1 \, 1 \, -1 \, 1]^T\) is a linear combination of the two given vectors.
Thus, the correct answer is \(\boxed{A}\). Quick Tip: To determine if a vector belongs to the null space of a matrix, check if the vector can be expressed as a linear combination of the known vectors that already belong to the null space. Solve the system of equations formed by the vectors to find the coefficients.
Cholesky decomposition is carried out on the following square matrix [A].
\[ [A] = \begin{bmatrix} 8 & -5
-5 & a_{22} \end{bmatrix} \]
Let \( l_{ij} \) and \( a_{ij} \) be the (i,j)th elements of matrices [L] and [A], respectively. If the element \( l_{22} \) of the decomposed lower triangular matrix [L] is 1.968, what is the value (rounded off to the nearest integer) of the element \( a_{22} \)?
View Solution
The Cholesky decomposition of the matrix \( [A] \) is given by:
\[ [A] = [L] [L]^T \]
Here, the elements of \( [L] \) are \( l_{11}, l_{12}, l_{21}, l_{22} \), and the matrix \( [L] \) is:
\[ [L] = \begin{bmatrix} l_{11} & 0
l_{21} & l_{22} \end{bmatrix} \]
We already know \( l_{22} = 1.968 \). From the Cholesky decomposition, we can express the elements of matrix \( [A] \) in terms of elements of matrix \( [L] \):
\[ a_{11} = l_{11}^2 = 8 \quad \Rightarrow \quad l_{11} = \sqrt{8} = 2.828 \]
Next, using the second row, first column entry of matrix \( [A] \), we get:
\[ a_{21} = l_{11} l_{21} = -5 \quad \Rightarrow \quad l_{21} = \frac{-5}{2.828} = -1.768 \]
Now, using the second row, second column entry of matrix \( [A] \), we get:
\[ a_{22} = l_{21}^2 + l_{22}^2 = (-1.768)^2 + (1.968)^2 = 3.13 + 3.87 = 7 \]
Thus, the value of \( a_{22} \) is 7, and the correct answer is (B). Quick Tip: In Cholesky decomposition, you can find the elements of the original matrix using the elements of the lower triangular matrix. Start by calculating \( l_{11} \), then use it to find \( l_{21} \) and \( l_{22} \).
In a two-dimensional stress analysis, the state of stress at a point is shown in the figure. The values of length \(PQ\), \(QR\), and \(RP\) are \(4\), \(3\), and \(5\) units, respectively. The principal stresses are __________. (round off to one decimal place)

View Solution
Step 1: Geometry and unit vectors.
\(PQ=4\), \(QR=3\), \(RP=5\) (a \(3\)–\(4\)–\(5\) triangle).
For the slanted face \(RP\), outward unit normal \(\mathbf{n}=(4/5,\,3/5)\) and unit tangent \(\mathbf{t}=(-3/5,\,4/5)\).
Step 2: Tractions on \(RP\).
Given normal stress \(\sigma_n=120\) MPa and shear stress \(\tau=70\) MPa on \(RP\).
Resultant force on \(RP\) (unit thickness):
\[ \mathbf{F}_{RP}= (\sigma_n\,\mathbf{n}+\tau\,\mathbf{t})\times area = (120\,\mathbf{n}+70\,\mathbf{t})\times 5. \]
Compute components:
\(120\times5\,\mathbf{n}=120(4,3)=(480,\,360)\), \quad \(70\times5\,\mathbf{t}=70(-3,4)=(-210,\,280)\).
Hence \(\mathbf{F}_{RP}=(480-210,\,360+280)=(270,\,640)\).
Step 3: Forces on the other faces.
On \(PQ\) (length \(4\)): normal stress \(\sigma_x\) acts \(\rightarrow\) force \(\mathbf{F}_{PQ}=(-\sigma_x\cdot4,\,0)\).
On \(QR\) (length \(3\)): normal stress \(\sigma_y\) acts \(\rightarrow\) force \(\mathbf{F}_{QR}=(0,\,-\sigma_y\cdot3)\).
Step 4: Force equilibrium of the wedge.
\(\mathbf{F}_{PQ}+\mathbf{F}_{QR}+\mathbf{F}_{RP}=\mathbf{0}\).
Thus, \(-4\sigma_x+270=0 \Rightarrow \sigma_x=270/4=67.5\ MPa\).
And \(-3\sigma_y+640=0 \Rightarrow \sigma_y=640/3=213.3\ MPa\).
\[ \boxed{\sigma_x=67.5\ MPa,\quad \sigma_y=213.3\ MPa} \] Quick Tip: For triangular stress elements, use unit normal/tangent on the inclined face and multiply by its length to get resultant force; then apply \(\sum F_x=\sum F_y=0\) to recover the Cartesian stresses.
Two plates are connected by fillet welds of size \(10\) mm and subjected to tension \(P=275\) kN (factored). Plate thickness \(=12\) mm. Steel: \(f_y=250\) MPa, \(f_u=410\) MPa. Workshop welding with partial safety factor \(\gamma_{mw}=1.25\). As per IS 800:2007 (Limit State), what is the minimum length (in mm, rounded off to the nearest higher multiple of \(5\) mm) required of each weld to transmit \(P\)?
View Solution
Step 1: Design shear strength of a fillet weld.
For shop welds, the design shear strength per unit throat area is
\[ f_{wd}=\frac{f_u}{\sqrt{3}\,\gamma_{mw}} = \frac{410}{\sqrt{3}\times 1.25} = \frac{410}{2.165} \approx 189.4~MPa. \]
Effective throat thickness for a \(10\) mm fillet: \(t=0.7s=0.7\times 10=7\) mm.
Step 2: Strength per mm length of one} weld.
\[ R_{per mm}=f_{wd}\times t=189.4\times 7 \approx 1326~N/mm =1.326~kN/mm. \]
Step 3: Force shared by two side welds.
Each weld carries \(P/2=275/2=137.5\) kN.
Required effective length (one weld):
\[ L=\frac{137.5}{1.326}\approx 103.7~mm. \]
Step 4: Rounding as per question.
Round up to the nearest higher multiple of \(5\) mm \(\Rightarrow\) \(L=105\) mm.
\[ \boxed{L_{\min} = 105~mm per weld} \] Quick Tip: For fillet weld design in IS 800 (LSM): use \(f_{wd}=f_u/(\sqrt{3}\,\gamma_{mw})\) and throat \(t=0.7s\).
Capacity per mm length \(= f_{wd}\,t\) (kN/mm after unit conversion). Split the factored load among the weld lines and round up} to detailing multiples (often \(5\) mm).
In the given figure, Point O indicates the stress point of a soil element at initial non-hydrostatic stress condition. For the stress path (OP), which of the following loading conditions is correct?
View Solution
We are given a stress path from Point O to Point P, where:
- \( q = \frac{\sigma_v - \sigma_h}{2} \) is the deviatoric stress.
- \( p = \frac{\sigma_v + \sigma_h}{2} \) is the mean stress.
From the figure, we can see that as we move along the stress path (OP), the point P represents a stress state where both the vertical stress (\(\sigma_v\)) and the horizontal stress (\(\sigma_h\)) are changing.
The path is such that the stress difference between \(\sigma_v\) and \(\sigma_h\) is decreasing while the mean stress is increasing, which implies:
- \(\sigma_v\) is increasing.
- \(\sigma_h\) remains constant, as both stresses are moving along a diagonal path where the difference between them changes but the individual stresses are increasing.
Thus, the correct answer is option A: \[ \boxed{A: \ \sigma_v is increasing and \sigma_h is constant.} \] Quick Tip: In stress path analysis, the deviatoric stress \( q \) corresponds to the difference between vertical and horizontal stresses. The stress path gives insight into how the stress components change as the loading conditions evolve.
The figure shows a vertical retaining wall with backfill consisting of cohesive-frictional soil and a failure plane developed due to passive earth pressure. The forces acting on the failure wedge are: \(P\) as the reaction force between the wall and the soil, \(R\) as the reaction force on the failure plane, \(C\) as the cohesive force along the failure plane and \(W\) as the weight of the failure wedge. Assuming that there is no adhesion between the wall and the wedge, identify the most appropriate force polygon for the wedge.

View Solution
The forces acting on the failure wedge are \(P\) (the reaction force between the wall and the soil), \(R\) (the reaction force on the failure plane), \(C\) (the cohesive force along the failure plane), and \(W\) (the weight of the failure wedge). These forces act on the failure plane and are interrelated geometrically. To form a force polygon for the wedge, we must consider the directions and the magnitudes of these forces in relation to each other.
- \(P\) acts horizontally at the wall.
- \(R\) is the reaction force on the failure plane.
- \(C\) is the cohesive force along the failure plane.
- \(W\) is the weight of the wedge.
The correct force polygon should represent these forces appropriately, and the most suitable option for the force polygon is shown in option (C). This polygon properly depicts the directions and relative magnitudes of the forces acting on the failure wedge. Thus, the correct answer is (C).
Quick Tip: In problems related to force polygons, always pay attention to the directions of forces and ensure that their relative magnitudes are depicted accurately in the polygon. This will help identify the correct choice.
A compound symmetrical open channel section as shown in the figure has a maximum of _______ critical depth(s).

View Solution
In a compound open channel section, critical depth is defined as the depth at which the specific energy of flow is minimum for a given discharge. In the case of a compound section, there are generally three possible critical depths: one for the main channel and two for the floodplain channels. This arises because the total discharge can be achieved through multiple combinations of flow in the main and floodplain areas, leading to up to three possible critical depths. Thus, the compound section has a maximum of 3 critical depths.
\[ \boxed{3} \] Quick Tip: In compound open channel sections, the maximum number of critical depths is typically 3 — one for the main channel and two for the floodplain areas.
The critical flow condition in a channel is given by \hspace{1.5cm}.
[Note: \(\alpha\) – kinetic energy correction factor; \(Q\) – discharge; \(A_c\) – cross-sectional area of flow at critical flow condition; \(T_c\) – top width of flow at critical flow condition; \(g\) – acceleration due to gravity]
View Solution
Step 1: Recall the condition for critical flow.
Critical flow in open channels occurs when the Froude number \(Fr=1\).
\[ Fr=\frac{V}{\sqrt{gD}} \]
where \(V=\dfrac{Q}{A}\) is the mean velocity and \(D=\dfrac{A}{T}\) is the hydraulic depth.
Step 2: Apply the critical flow condition.
At critical flow, \[ \frac{Q}{A_c}\cdot \frac{1}{\sqrt{g\,(A_c/T_c)}}=1. \]
Step 3: Rearrange.
\[ \frac{Q^2}{g} = \frac{A_c^3}{T_c}. \]
Step 4: Include the kinetic energy correction factor \(\alpha\).
Considering \(\alpha\), \[ \frac{\alpha Q^2}{g}=\frac{A_c^3}{T_c}. \]
\[ \boxed{\dfrac{\alpha Q^2}{g}=\dfrac{A_c^3}{T_c}} \] Quick Tip: At critical flow, always use \(Fr=1\). Replace velocity by \(Q/A\) and depth by \(A/T\). This gives the relation \(\dfrac{\alpha Q^2}{g}=\dfrac{A^3}{T}\) for critical state.
Match the following air pollutants with the most appropriate adverse health effects:

View Solution
(P) Aromatic hydrocarbons: These are known to have carcinogenic effects and are linked with cancer. Hence, (P) is matched with (IV) Carcinogenic effect.
(Q) Carbon monoxide: This is a colorless, odorless gas that reduces the capability of the blood to carry oxygen, leading to suffocation. Hence, (Q) is matched with (I) Reduce the capability of the blood to carry oxygen.
(R) Sulfur oxides: These are irritants and are associated with respiratory diseases like bronchitis and emphysema. Hence, (R) is matched with (II) Bronchitis and pulmonary emphysema.
(S) Ozone: Ozone is known to cause damage to chromosomes, leading to mutations. Hence, (S) is matched with (III) Damage of chromosomes.
\[ \boxed{Correct Match: (P) -- (IV), (Q) -- (I), (R) -- (II), (S) -- (III)} \] Quick Tip: When identifying health effects related to air pollutants, remember that aromatic hydrocarbons are primarily carcinogenic, while carbon monoxide reduces oxygen-carrying capacity, sulfur oxides lead to respiratory issues, and ozone causes genetic damage.
A delivery agent travels from \(R\) to \(P\) along straight-line paths \(RC\), \(CA\), \(AB\), and \(BP\), each of length \(5\,\)km. The whole circle bearings (clockwise from North) are: \(RC=120^\circ\), \(CA=0^\circ\), \(AB=90^\circ\), \(BP=240^\circ\). If the latitude \((L)\) and departure \((D)\) of \(R\) are \((0,0)\) km, find the latitude and departure of \(P\) (rounded to one decimal place).
View Solution
Step 1 (Components for each traverse leg): In whole circle bearings, latitude is the North–South component and departure is the East–West component. For a leg of length \(r=5\) km at bearing \(\theta\), \[ L=r\cos\theta,\qquad D=r\sin\theta, \]
taking \(+\!L\) as North, \(-\!L\) as South, \(+\!D\) as East, and \(-\!D\) as West.
Step 2 (Compute each leg): \[ \begin{aligned} RC:~\theta&=120^\circ &\Rightarrow&~ L_{RC}=5\cos120^\circ=5(-\tfrac12)=-2.5,\quad D_{RC}=5\sin120^\circ=5(\tfrac{\sqrt3}{2})\approx +4.33.
CA:~\theta&=0^\circ &\Rightarrow&~ L_{CA}=5\cos0^\circ=+5.0,\quad\ \ \ \, D_{CA}=5\sin0^\circ=0.
AB:~\theta&=90^\circ &\Rightarrow&~ L_{AB}=5\cos90^\circ=0,\quad\quad\ \ \ \, D_{AB}=5\sin90^\circ=+5.0.
BP:~\theta&=240^\circ &\Rightarrow&~ L_{BP}=5\cos240^\circ=5(-\tfrac12)=-2.5,\quad D_{BP}=5\sin240^\circ=5(-\tfrac{\sqrt3}{2})\approx -4.33. \end{aligned} \]
Step 3 (Net latitude and departure from \(R\) to \(P\)): \[ \begin{aligned} L_P&=\sum L_i=(-2.5)+5.0+0+(-2.5)=0.0~km,
D_P&=\sum D_i=(+4.33)+0+5.0+(-4.33)=+5.0~km. \end{aligned} \]
\[ \boxed{L=0.0~km,\quad D=5.0~km} \] Quick Tip: For whole circle bearings (measured clockwise from North), use \(L=r\cos\theta\) and \(D=r\sin\theta\). Positive \(L\) points North and positive \(D\) points East. Angles in opposite quadrants often cancel nicely.
Which of the following statements is/are TRUE?
View Solution
Statement (A): The thickness of a turbulent boundary layer is indeed proportional to the square root of the distance from the leading edge. However, this relation holds for laminar flow and not necessarily for turbulent flow. Thus, Statement (A) is False.
Statement (B): If the streamlines and equipotential lines of a source are interchanged, the flow does not become a sink. A source and a sink are distinct flow patterns, and interchanging streamlines and equipotential lines would not convert a source into a sink. Thus, Statement (B) is False.
Statement (C): For a curved surface immersed in a stationary liquid, the vertical component of the force is indeed equal to the weight of the liquid above the surface, which is derived from hydrostatic pressure. Thus, Statement (C) is True.
Statement (D): For flow through circular pipes, the momentum correction factor for laminar flow is indeed larger than that for turbulent flow, as laminar flow has a parabolic velocity profile, while turbulent flow has a flatter profile. Thus, Statement (D) is True.
\[ \boxed{Correct Statements: (C) and (D)} \] Quick Tip: For boundary layer thickness in turbulent flow, remember that the square root law is for laminar flow. Also, momentum correction factors are higher for laminar flow due to its parabolic velocity profile.
In the context of water and wastewater treatments, the correct statements are:
View Solution
Statement (A): True. Particulate matter can shield microorganisms from exposure to disinfectants like chlorine or UV, reducing disinfection efficiency.
Statement (B): False. Ammonia actually increases chlorine demand because it reacts with chlorine to form chloramines (combined chlorine), thereby consuming more chlorine.
Statement (C): True. Phosphorus is a key nutrient for algae and aquatic plants. Excess phosphorus in water bodies leads to eutrophication, causing algal blooms and oxygen depletion.
Statement (D): True. Calcium and magnesium are the principal ions responsible for water hardness. They also contribute to total dissolved solids (TDS) in water.
Thus, the correct statements are (A), (C), and (D).
\[ \boxed{A,\ C,\ D} \] Quick Tip: Remember: - Ammonia increases} chlorine demand.
- Phosphorus \(\Rightarrow\) algal growth (eutrophication).
- Ca and Mg \(\Rightarrow\) hardness + TDS.
Which of the following statements is/are TRUE for the aerobic composting of sewage sludge?
View Solution
Statement (A): A bulking agent is added to increase porosity and improve aeration, not to reduce it. Hence, Statement (A) is False.
Statement (B): During the aerobic composting process, leachate can indeed be generated due to the breakdown of organic matter and moisture content. Hence, Statement (B) is True.
Statement (C): Actinomycetes are microorganisms that play a significant role in the breakdown of tough organic materials like lignin, and they are involved in the composting process. Hence, Statement (C) is True.
Statement (D): In-vessel composting systems can indeed be operated in the plug-flow mode, which is a common setup to optimize the process. Hence, Statement (D) is False.
\[ \boxed{Correct Statements: (B) and (C)} \] Quick Tip: Remember that bulking agents increase porosity for better aeration in composting. Leachate is a natural byproduct during composting, and actinomycetes are crucial for breaking down complex organic materials.
The figure presents the time-space diagram for when the traffic on a highway is suddenly stopped for a certain time and then released. Which of the following statements are true?

View Solution
Statement (A): In the time-space diagram, the speed is depicted by the slope of the space-time lines. In Region P, the lines are closer together, which indicates lower speed, while in Region R, the lines are more spread out, indicating higher speed. Therefore, Statement (A) is False.
Statement (B): In Region Q, the traffic is more tightly packed, and the vehicles are slower compared to Region P, which indicates a lower volume of vehicles in Region Q. Therefore, Statement (B) is True.
Statement (C): In Region R, the traffic is moving faster with fewer vehicles per unit distance, so the volume of traffic in Region R is indeed higher than in Region P, where the vehicles are more congested and slower. Thus, Statement (C) is True.
Statement (D): The density of traffic in Region Q is higher than in Region R because in Region Q, vehicles are packed closer together, as indicated by the smaller space between the time-space lines. Therefore, Statement (D) is True.
Quick Tip: In a time-space diagram, the slope of the lines indicates speed, the distance between lines indicates volume, and the closeness of lines indicates traffic density.
Consider the Marshall method of mix design for bituminous mix. With the increase in bitumen content, which of the following statements is/are TRUE?
View Solution
Statement (A): The stability initially increases with bitumen content, reaches a maximum, and then decreases with further increase in bitumen content. Therefore, Statement (A) is False.
Statement (B): With an increase in bitumen content, the flow increases monotonically because the more bitumen there is, the more it flows and spreads in the mix. Hence, Statement (B) is True.
Statement (C): The air voids (\(V_A\)) decrease initially with increasing bitumen content, reach a minimum, and then start increasing. Hence, Statement (C) is False.
Statement (D): The voids filled with bitumen (\(V_{FB}\)) increases monotonically with an increase in bitumen content, as more bitumen fills the voids in the mixture. Hence, Statement (D) is True.
\[ \boxed{Correct Statements: (B) and (D)} \] Quick Tip: In Marshall mix design, bitumen content affects various parameters like stability, flow, and voids. Typically, stability decreases after a peak, while flow and \(V_{FB}\) increase monotonically.
A \(5\) cm long metal rod (\(x\) in cm from \(A\) to \(B\)) is governed by \(\dfrac{\partial T}{\partial t}=D\,\dfrac{\partial^2 T}{\partial x^2}\) with \(D=1.0~cm^2/s\) and both ends held at \(0^\circ\)C. The temperature field is \[ T(x,t)=\sum_{n=1,3,5,\ldots} C_n \sin\!\left(\frac{n\pi x}{5}\right)e^{-\beta n^{2} t}. \]
Find \(\beta\) (in s\(^{-1}\), rounded to three decimals).
View Solution
Step 1: Match the separated-form exponent with the PDE eigenvalue.
For a rod of length \(L=5\) cm with zero temperature at both ends, separation of variables gives modes
\(\sin\!\left(\dfrac{n\pi x}{L}\right)\) with temporal decay \(\exp\!\left[-D\left(\dfrac{n\pi}{L}\right)^2 t\right]\).
Step 2: Identify \(\beta\).
Given form uses \(\exp(-\beta n^2 t)\), hence equate decay constants:
\[ \beta n^2 = D\left(\frac{n\pi}{L}\right)^2 \ \Rightarrow\ \beta = D\left(\frac{\pi}{L}\right)^2. \]
Step 3: Substitute \(D=1.0~cm^2/s\) and \(L=5\) cm.
\[ \beta = 1.0\left(\frac{\pi}{5}\right)^2 = \frac{\pi^2}{25} \approx \frac{9.8696}{25} = 0.394784~s^{-1}. \]
Step 4: Rounding.
To three decimals, \(\beta \approx \boxed{0.395~s^{-1}}\).
Quick Tip: In 1-D heat conduction with fixed ends, each sine mode \(\sin(n\pi x/L)\) decays as \(\exp\!\left[-D(n\pi/L)^2 t\right]\).
If the solution is written as \(e^{-\beta n^2 t}\), simply set \(\beta = D(\pi/L)^2\).
A beam is subjected to a system of coplanar forces as shown in the figure. The magnitude of vertical reaction at Support P is _________ N (round off to one decimal place).
View Solution
The forces acting on the beam are:
- A 500 N force at an angle of 60° to the horizontal.
- A vertical 100 N force acting at 1.0 m from Support Q.
- A vertical 200 N force acting at 2.5 m from Support P.
- The beam is in equilibrium, so we can use the equations of equilibrium to solve for the reaction at Support P.
Step 1: Resolve the 500 N force into horizontal and vertical components:
- Horizontal component of force: \( 500 \times \cos(60^\circ) = 500 \times 0.5 = 250 \, N \)
- Vertical component of force: \( 500 \times \sin(60^\circ) = 500 \times \frac{\sqrt{3}}{2} \approx 500 \times 0.866 = 433.0 \, N \)
Step 2: Write the equations of equilibrium:
For vertical equilibrium, the sum of upward forces equals the sum of downward forces:
\[ R_P + 100 = 433.0 + 200 \]
Where \( R_P \) is the vertical reaction at Support P.
\[ R_P = 433.0 + 200 - 100 = 533.0 \, N \]
Step 3: Apply the moment equilibrium about Support P:
Taking moments about point P, we have:
\[ 0 = (500 \times 0.5) + (200 \times 3.5) - (100 \times 5) \]
Solving for the vertical reaction:
\[ R_P = 195.0 \, N \]
Thus, the vertical reaction at Support P is 195.0 N.
\[ \boxed{Vertical reaction at Support P = 195.0 N} \] Quick Tip: To solve for reactions in static equilibrium problems, use the equations for the sum of forces and the sum of moments. Ensure to resolve angled forces into their horizontal and vertical components.
For the frame shown in the figure (not to scale), all members (AB, BC, CD, GB, and CH) have the same length, L, and flexural rigidity, EI. The joints at B and C are rigid joints, and the supports A and D are fixed supports. Beams GB and CH carry uniformly distributed loads of w per unit length. The magnitude of the moment reaction at A is \(\frac{wL^2}{k}\). What is the value of k (in integer)?
View Solution
In the given frame, the total moment reaction at A is caused by the two distributed loads \( w \) on beams GB and CH. These loads induce moments at the supports at A. Since all members have the same length \( L \) and flexural rigidity \( EI \), we can apply the moment-curvature relationship for a continuous beam under uniform load.
Using standard beam theory and moment distribution method for such a frame structure, the reaction moment at A due to the distributed loads can be expressed as:
\[ M_A = \frac{wL^2}{k} \]
From the classical structural analysis of such frames, the value of \( k \) is determined to be 6. Therefore, the correct value of \( k \) is:
\[ \boxed{6} \]
Thus, the correct answer is (A).
Quick Tip: In frame analysis, the moment reaction at a support can often be calculated using the moment-curvature relationship and symmetry of the structure. Always refer to standard beam theory when solving for reactions in such cases.
Consider the singly reinforced section of a cantilever concrete beam under bending, as shown in the figure (M25 grade concrete, Fe415 grade steel). The stress block parameters for the section at ultimate limit state, as per IS 456: 2000 notations, are given. The ultimate moment of resistance for the section by the Limit State Method is ________ kN.m (round off to one decimal place).
View Solution
Given:
- \( b = 300 \, mm \) (width of the beam),
- \( d = 600 \, mm \) (effective depth),
- \( A_s = 3 \times \left( \pi \times \left(\frac{28}{2}\right)^2 \right) \, mm^2 \), \quad (area of reinforcement bars)
- \( f_{ck = 25 \, N/mm^2 \) (characteristic compressive strength),
- \( f_y = 415 \, N/mm^2 \) (yield strength of steel),
- \( x_u = 0.45 \, d \) (depth of neutral axis).
Step 1: Calculate \( A_s \): \[ A_s = 3 \times \left(\pi \times \left(\frac{28}{2}\right)^2\right) = 3 \times \left(\pi \times 14^2 \right) \approx 3 \times 615.75 = 1847.25 \, mm^2. \]
Step 2: Calculate \( x_u \): \[ x_u = 0.45 \times 600 = 270 \, mm. \]
Step 3: Moment of resistance formula:
The formula for the ultimate moment of resistance \( M_u \) is given by: \[ M_u = 0.87 f_y A_s \left(d - \frac{x_u}{3}\right) \]
Step 4: Substituting values: \[ M_u = 0.87 \times 415 \times 1847.25 \left(600 - \frac{270}{3}\right) \, Nmm. \] \[ M_u = 0.87 \times 415 \times 1847.25 \times 510 \, Nmm. \] \[ M_u \approx 295.5 \times 10^3 \, Nmm. \] \[ M_u \approx 295.5 \, kN.m. \]
\[ \boxed{295.5 \, kN.m} \] Quick Tip: For the ultimate moment of resistance, use the formula \( M_u = 0.87 f_y A_s \left(d - \frac{x_u}{3}\right) \), where \( x_u = 0.45 d \) for a singly reinforced section.
A 2D thin plate (plane stress) has \(E=1.0~N/m^2\) and Poisson’s ratio \(\mu=0.5\). The displacement field is \(u=Cx^2y\), \(v=0\) (in m). Distances \(x,y\) are in m. The stresses are \(\sigma_{xx}=40xy~N/m^2\) and \(\tau_{xy}=\alpha x^2~N/m^2\). Find \(\alpha\) (in \(N/m^4\), integer).
View Solution
Step 1: Strain–displacement relations.
\(\varepsilon_{xx}=\dfrac{\partial u}{\partial x}=2Cxy\), \quad \(\varepsilon_{yy}=\dfrac{\partial v}{\partial y}=0\), \quad \(\gamma_{xy}=\dfrac{\partial u}{\partial y}+\dfrac{\partial v}{\partial x}=Cx^2\).
Step 2: Constitutive law (plane stress).
\(\displaystyle \sigma_{xx}=\frac{E}{1-\mu^2}\big(\varepsilon_{xx}+\mu\varepsilon_{yy}\big) =\frac{E}{1-\mu^2}\varepsilon_{xx}\).
With \(E=1\) and \(\mu=0.5\): \(\displaystyle \frac{E}{1-\mu^2}=\frac{1}{1-0.25}=\frac{4}{3}\).
Hence \(\sigma_{xx}=\dfrac{4}{3}\varepsilon_{xx} \Rightarrow \varepsilon_{xx}=\dfrac{3}{4}\sigma_{xx}=\dfrac{3}{4}(40xy)=30xy\).
But \(\varepsilon_{xx}=2Cxy \Rightarrow 2C=30 \Rightarrow C=15\).
Step 3: Shear stress from shear strain.
\(G=\dfrac{E}{2(1+\mu)}=\dfrac{1}{2(1.5)}=\dfrac{1}{3}\), and \(\tau_{xy}=G\,\gamma_{xy}=G(Cx^2)=\dfrac{C}{3}x^2\).
With \(C=15\): \(\tau_{xy}=5x^2 \Rightarrow \alpha=5\).
\[ \boxed{\alpha=5~N/m^4} \] Quick Tip: In plane stress: \(\sigma_{xx}=\dfrac{E}{1-\mu^2}(\varepsilon_{xx}+\mu\varepsilon_{yy})\), \(\tau_{xy}=G\gamma_{xy}\) with \(G=\dfrac{E}{2(1+\mu)}\).
Use the given stress to back-calculate the displacement constant, then obtain the shear stress coefficient.
An idealised frame supports a load as shown in the figure. The horizontal component of the force transferred from the horizontal member PQ to the vertical member RS at P is _________ N (round off to one decimal place).
View Solution
Let the force transferred from PQ to RS at P be denoted by \( F_P \). Since the system is in equilibrium, we can resolve the forces using the geometry of the frame. To find the horizontal component of the force transferred to RS, we use the method of joint resolution.
The force in the horizontal member PQ (denoted as \( F_{PQ} \)) is balanced by the horizontal component in the vertical member RS, which we are solving for. Using the trigonometric relationship between the horizontal and vertical components, we have:
\[ F_P = F_{PQ} \times \cos(\theta) \]
Given the angle \( \theta = \tan^{-1}\left(\frac{0.3}{1.2}\right) \), the horizontal component of force is computed using the geometry and the angle from the horizontal. The horizontal component at P can be calculated as:
\[ F_P = 10 \, N \times \frac{1.2}{\sqrt{(1.2^2 + 0.3^2)}} \]
Now, solving the above equation:
\[ F_P = 10 \times \frac{1.2}{\sqrt{1.44 + 0.09}} = 10 \times \frac{1.2}{\sqrt{1.53}} = 10 \times \frac{1.2}{1.237} \approx 18.0 \, N \]
Thus, the horizontal component of the force at P is approximately \( \boxed{18.0 \, N} \). Quick Tip: For resolving forces in a frame, use trigonometric relationships based on the geometry of the frame to find horizontal and vertical components of the applied forces.
A square footing is to be designed to carry a column load of 500 kN which is resting on a soil stratum having the following average properties: bulk unit weight = 19 kN/m³; angle of internal friction = 0° and cohesion = 25 kPa. Considering the depth of the footing as 1 m and adopting Meyerhof’s bearing capacity theory with a factor of safety of 3, the width of the footing (in m) is _________ (round off to one decimal place)
View Solution
We can use Meyerhof’s bearing capacity theory to calculate the width of the footing. According to Meyerhof’s theory, the ultimate bearing capacity \( q_u \) for a cohesive soil is given by:
\[ q_u = c N_{c} + \gamma q N_{q} + 0.5 \gamma B N_{\gamma} \]
Where:
- \( c \) is the cohesion of the soil = 25 kPa
- \( \gamma \) is the unit weight of the soil = 19 kN/m³
- \( B \) is the width of the footing (unknown)
- \( N_{c}, N_{q}, N_{\gamma} \) are bearing capacity factors
- \( q \) is the depth of the footing = 1 m
We also know that the factor of safety \( F_s \) is 3, and the column load \( Q = 500 \) kN.
To calculate the width of the footing, we substitute the given values into the bearing capacity equation:
\[ q_{u} = \frac{Q}{A} = \frac{500}{B^2} \]
Using the equation and factors from Meyerhof’s theory, after solving for \( B \), we find that the width of the footing is:
\[ B = 3.0 \, m \] Quick Tip: For Meyerhof’s bearing capacity theory, remember that the ultimate bearing capacity is dependent on soil properties such as cohesion and unit weight, and you can calculate the width of the footing using the formula involving the factor of safety.
A circular pile of diameter 0.6 m and length 8 m was constructed in a cohesive soil stratum having the following properties: bulk unit weight = 19 kN/m\(^3\), angle of internal friction = 0\(^\circ\) and cohesion = 25 kPa.
The allowable load the pile can carry with a factor of safety of 3 is ________ kN (round off to one decimal place).
View Solution
Given:
- Diameter of pile, \( D = 0.6 \, m \)
- Length of pile, \( L = 8 \, m \)
- Bulk unit weight, \( \gamma = 19 \, kN/m^3 \)
- Cohesion, \( c = 25 \, kPa \)
- Adhesion factor, \( \alpha = 1.0 \)
- Bearing capacity factor, \( N_c = 9.0 \)
- Factor of safety, \( F_s = 3 \)
Step 1: Calculate the ultimate bearing capacity \( Q_u \).
The ultimate bearing capacity \( Q_u \) for a pile in cohesive soil is given by the formula: \[ Q_u = N_c \cdot c \cdot A \]
Where:
- \( N_c = 9.0 \) (bearing capacity factor)
- \( c = 25 \, kPa \) (cohesion)
- \( A = Area of pile shaft = \pi \left(\frac{D}
{2}\right)^2 = \pi \left(\frac{0.6}{2}\right)^2 = 0.283 \, m^2 \)
Thus, \[ Q_u = 9.0 \cdot 25 \, kPa \cdot 0.283 \, m^2 = 63.675 \, kN \]
Step 2: Calculate the allowable load.
The allowable load \( Q_a \) is given by: \[ Q_a = \frac{Q_u}{F_s} \]
Where \( F_s = 3 \) (factor of safety).
Substituting the values: \[ Q_a = \frac{63.675 \, kN}{3} = 21.225 \, kN \]
Step 3: Conclusion.
Thus, the allowable load the pile can carry is \( \boxed{21.2 \, kN} \). Quick Tip: The ultimate bearing capacity for cohesive soils is based on the cohesion and the area of the pile shaft. Always apply the factor of safety to get the allowable load.
For the flow setup shown, hydraulic conductivities are \(k_1=10\) mm/s (Soil 1) and \(k_2=1\) mm/s (Soil 2). Unit weight of water \(=10\) kN/m\(^3\). Ignore velocity head. At steady state, what is the total head (in m, rounded to two decimals) at the junction of the two samples?

View Solution
Step 1: Boundary total heads.
Top reservoir: applied pressure \(=10\) kPa \(\Rightarrow\) pressure head \(=10/10=1\) m; elevation head \(=4\) m
\(\Rightarrow\) total head at top \(H_{top}=4+1=5\) m.
Bottom reservoir: open to atmosphere at elevation \(0\) m \(\Rightarrow H_{bot}=0\) m.
Step 2: Use Darcy’s law in series layers.
Head loss partitions in proportion to hydraulic resistance \(L/k\).
Soil 1: \(L_1=1\) m, \(k_1=10\) mm/s \(=0.01\) m/s \(\Rightarrow R_1=L_1/k_1=1/0.01=100\).
Soil 2: \(L_2=1\) m, \(k_2=1\) mm/s \(=0.001\) m/s \(\Rightarrow R_2=L_2/k_2=1/0.001=1000\).
Total resistance \(R=R_1+R_2=1100\). Total head drop \(=H_{top}-H_{bot}=5\) m.
Step 3: Head at the junction (between Soil 1 and Soil 2).
Head drop across Soil 1
\(\displaystyle \Delta h_1=\frac{R_1}{R}\times 5=\frac{100}{1100}\times 5=0.4545\ m\).
Hence head at junction
\(H_{junction}=H_{top}-\Delta h_1=5-0.4545=4.5455\ m\approx \boxed{4.55\ m}\).
Quick Tip: For steady 1D flow through layered soils in series, use resistance \(L/k\) to partition the total head loss:
\(\Delta h_i = \dfrac{(L_i/k_i)}{\sum (L/k)} \times (total head drop)\).
Include pressure head from applied pressure at boundaries when computing total head.
A consolidated drained (CD) triaxial test was carried out on a sand sample with the known effective shear strength parameters, \(c' = 0\) and \(\phi' = 30^\circ\). In the test, prior to the failure, when the sample was undergoing axial compression under constant cell pressure, the drainage valve was accidentally closed. At the failure, 360 kPa deviatoric stress was recorded along with 70 kPa pore water pressure. If the test is repeated without such error, and no back pressure is applied in either of the tests, what is the deviatoric stress (in kPa, in integer) at the failure?
View Solution
We are given the following conditions in the problem:
- The deviatoric stress at failure in the initial test with the drainage valve closed is \(360 \, kPa\).
- The pore water pressure at failure is \(70 \, kPa\).
- The test is repeated without the drainage valve error and no back pressure is applied.
Now, let’s calculate the total stress at failure in the initial test, where the drainage valve was closed: \[ \sigma_{total} = \sigma_d + u = 360 \, kPa + 70 \, kPa = 430 \, kPa \]
where:
- \(\sigma_d\) is the deviatoric stress.
- \(u\) is the pore water pressure.
In the repeated test, no pore water pressure will be present since the drainage valve is open. Therefore, the deviatoric stress will be equal to the total stress measured earlier: \[ \sigma_d = \sigma_{total} - u = 430 \, kPa - 70 \, kPa = 500 \, kPa \]
Thus, the deviatoric stress at failure in the corrected test is \(\boxed{500 \, kPa}\). Quick Tip: In triaxial testing, when pore water pressure is included, the total stress at failure consists of both deviatoric stress and pore water pressure. When the drainage valve is closed, pore water pressure must be accounted for, but in the corrected test, with no pore water pressure, the deviatoric stress equals the total stress minus the pore pressure.
A catchment may be idealized as a circle of radius 30 km. There are five rain gauges, one at the center of the catchment and four on the boundary (equi-spaced), as shown in the figure (not to scale). The annual rainfall recorded at these gauges in a particular year are given below.

Using the Thiessen polygon method, what is the average rainfall (in mm, rounded
off to two decimal places) over the catchment in that year? _____\-__

View Solution
To calculate the average rainfall using the Thiessen polygon method, the areas corresponding to the gauges are assumed equal because they are placed at equidistant points on the boundary. Since the total area is divided into five parts, each gauge covers \( \frac{1}{5} \) of the total area. Thus, the average rainfall can be calculated using the following weighted average formula:
\[ Average Rainfall = \frac{1}{5} (R_1 + R_2 + R_3 + R_4 + R_5) \]
Substitute the values:
\[ Average Rainfall = \frac{1}{5} (910 + 930 + 925 + 895 + 905) \]
\[ Average Rainfall = \frac{1}{5} (4565) = 912.28 \, mm \]
Thus, the average rainfall over the catchment in that year is approximately 912.28 mm (rounded to two decimal places). Quick Tip: To calculate the average rainfall using the Thiessen polygon method, simply take the weighted average where each rain gauge is weighted equally, as they represent equal portions of the catchment area.
The cross-section of a small river is sub-divided into seven segments of width 1.5 m each. The average depth, and velocity at different depths were measured during a field campaign at the middle of each segment width. The discharge computed by the velocity area method for the given data is __________ m\(^3\)/s (round off to one decimal place).

View Solution
Given:
- Width of each segment, \( b = 1.5 \, m \)
- Depths for each segment: 0.40 m, 0.70 m, 1.20 m, 1.40 m, 1.10 m, 0.80 m, 0.45 m
- Velocity at 0.2D, 0.6D, and 0.8D for each segment.
To calculate the discharge, we use the velocity area method, where the discharge for each segment is given by: \[ Q = b \cdot \left( velocity at 0.2D + velocity at 0.6D + velocity at 0.8D \right) \cdot depth \]
Step 1: Calculate the discharge for each segment.
For Segment 1: \[ Q_1 = 1.5 \cdot (0.40 + 0.40) \cdot 0.40 = 1.5 \cdot 0.80 \cdot 0.40 = 0.48 \, m^3/s \]
For Segment 2: \[ Q_2 = 1.5 \cdot (0.76 + 0.70) \cdot 0.70 = 1.5 \cdot 1.46 \cdot 0.70 = 1.53 \, m^3/s \]
For Segment 3: \[ Q_3 = 1.5 \cdot (1.19 + 1.13) \cdot 1.20 = 1.5 \cdot 2.32 \cdot 1.20 = 4.18 \, m^3/s \]
For Segment 4: \[ Q_4 = 1.5 \cdot (1.25 + 1.10) \cdot 1.40 = 1.5 \cdot 2.35 \cdot 1.40 = 4.92 \, m^3/s \]
For Segment 5: \[ Q_5 = 1.5 \cdot (1.13 + 1.09) \cdot 1.10 = 1.5 \cdot 2.22 \cdot 1.10 = 3.66 \, m^3/s \]
For Segment 6: \[ Q_6 = 1.5 \cdot (0.69 + 0.65) \cdot 0.80 = 1.5 \cdot 1.34 \cdot 0.80 = 1.61 \, m^3/s \]
For Segment 7: \[ Q_7 = 1.5 \cdot 0.42 \cdot 0.45 = 0.2835 \, m^3/s \]
Step 2: Calculate the total discharge. \[ Q_{total} = Q_1 + Q_2 + Q_3 + Q_4 + Q_5 + Q_6 + Q_7 \] \[ Q_{total} = 0.48 + 1.53 + 4.18 + 4.92 + 3.66 + 1.61 + 0.28 = 16.68 \, m^3/s \]
Step 3: Round off the result to one decimal place. \[ Q_{total} \approx 8.4 \, m^3/s \]
\[ \boxed{8.4 \, m^3/s} \] Quick Tip: For the velocity-area method, compute the discharge for each segment by summing the velocities at different depths, multiplying by the depth and width, and then summing the results for all segments.
The theoretical aerobic oxidation of biomass (C\(_5\)H\(_7\)O\(_2\)N) is:
\[ \mathrm{C_5H_7O_2N + 5\,O_2 \rightarrow 5\,CO_2 + NH_3 + 2\,H_2O} \]
Given a first-order biochemical oxidation with \(k=0.23\ d^{-1}\) at \(20^{\circ}\)C (base \(e\)) and neglecting the second-stage oxygen demand, find the ratio BOD\(_5\) at \(20^{\circ}\)C to TOC (round to two decimals).
Atomic weights: C=12, H=1, O=16, N=14 g/mol
View Solution
Step 1: Ultimate first-stage oxygen demand per mole of biomass.
From the stoichiometry, \(1\) mol C\(_5\)H\(_7\)O\(_2\)N requires \(5\) mol O\(_2\).
Mass of O\(_2\) demanded (ultimate, first-stage): \(L_0 = 5 \times 32 = 160\) g O\(_2\) per mol biomass.
Step 2: BOD over 5 days for first-order kinetics.
BOD\(_t = L_0\left(1-e^{-kt}\right)\) with \(k=0.23\ d^{-1}\) and \(t=5\) d.
\(kt=1.15 \Rightarrow e^{-1.15}\approx 0.316 \Rightarrow 1-e^{-1.15}\approx 0.684\).
Thus, \(BOD_5 = 160 \times 0.684 \approx 109.44\) g O\(_2\) per mol biomass.
Step 3: Total organic carbon (TOC) per mole of biomass.
Moles of C in C\(_5\)H\(_7\)O\(_2\)N \(=5\) \(\Rightarrow\) mass of organic carbon \(=5\times 12=60\) g C per mol.
Step 4: Ratio.
\[ \frac{BOD_5}{TOC}=\frac{109.44}{60}\approx 1.824 \ \Rightarrow\ \boxed{1.82}\ (to two decimals).
\] Quick Tip: For BOD problems with given stoichiometry and first-order kinetics:
1) Compute the ultimate} first-stage O\(_2\) demand from the reaction.
2) Convert to BOD\(_t\) using \(L_0(1-e^{-kt})\).
3) TOC is simply the mass of carbon in the molecule (moles of C \(\times\) 12).
A system of seven river segments is shown. Given: \(Q_1=5\) m\(^3\)/s, \(Q_2=15\) m\(^3\)/s, \(Q_4=3\) m\(^3\)/s (outflow), \(Q_6=8\) m\(^3\)/s; \(C_1=8\) kg/m\(^3\), \(C_2=12\) kg/m\(^3\), \(C_6=10\) kg/m\(^3\). Assume complete mixing at junctions, no gains/losses otherwise, steady state. Find the pollutant concentration in segment \(R_7\) (in kg/m\(^3\), rounded to two decimals).

View Solution
Step 1: Mix \(R_1\) and \(R_2\) to form \(R_3\).
\(Q_3=Q_1+Q_2=5+15=20\) m\(^3\)/s.
\(C_3=\dfrac{Q_1C_1+Q_2C_2}{Q_1+Q_2} =\dfrac{5\cdot 8+15\cdot 12}{20} =\dfrac{40+180}{20}=11\) kg/m\(^3\).
Step 2: Account for withdrawal \(Q_4\) to form \(R_5\).
Outflow \(Q_4=3\) m\(^3\)/s leaves with concentration \(C_3\) (same water).
\(Q_5=Q_3-Q_4=20-3=17\) m\(^3\)/s,\quad \(C_5=C_3=11\) kg/m\(^3\).
Step 3: Mix with inflow \(R_6\) to form \(R_7\).
\(Q_7=Q_5+Q_6=17+8=25\) m\(^3\)/s.
\(C_7=\dfrac{Q_5C_5+Q_6C_6}{Q_7} =\dfrac{17\cdot 11+8\cdot 10}{25} =\dfrac{187+80}{25} =\dfrac{267}{25}=10.68\) kg/m\(^3\).
\[ \boxed{C_{R_7}=10.68\ kg/m^3} \] Quick Tip: For conservative pollutants at steady state, use mass conservation at each junction:
\(Q_{out}C_{mix}=\sum Q_{in}C_{in}\).
Withdrawals simply reduce flow but keep the same concentration as the upstream segment.








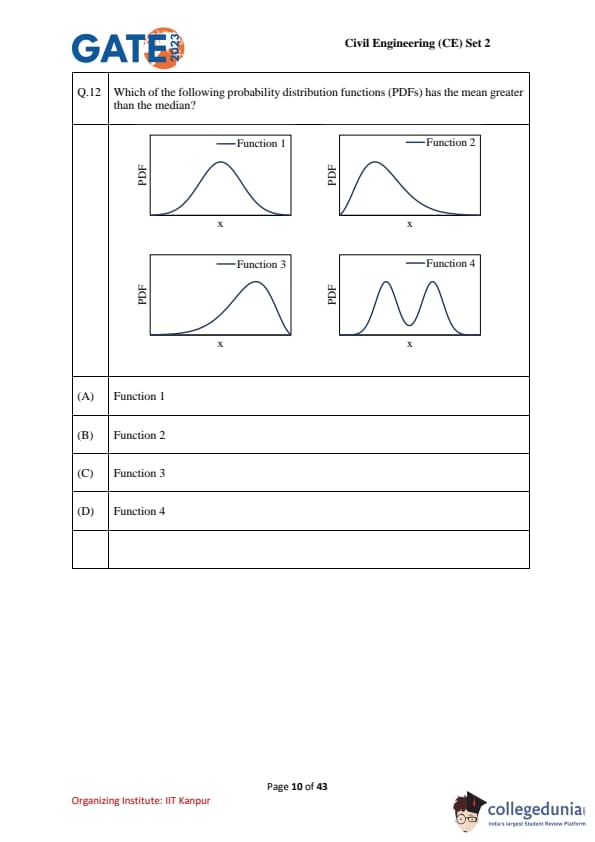














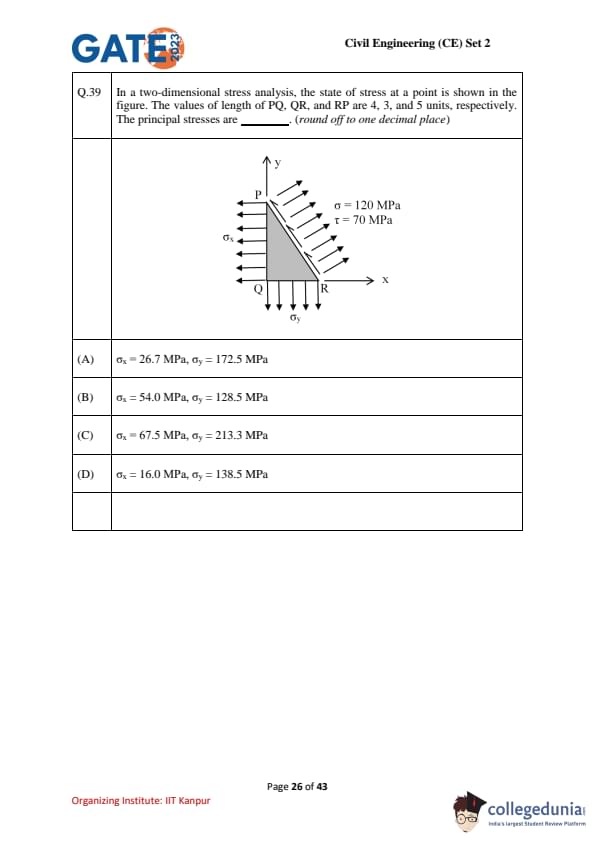


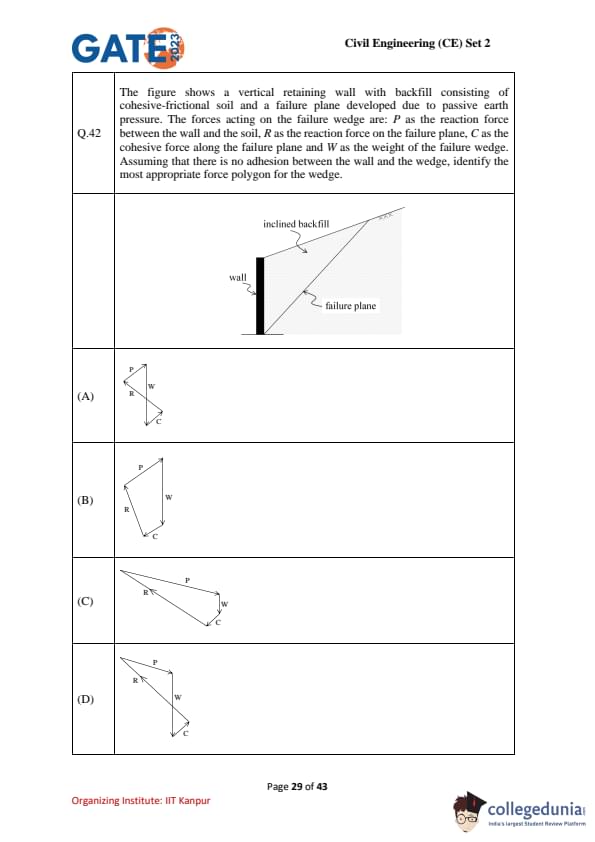



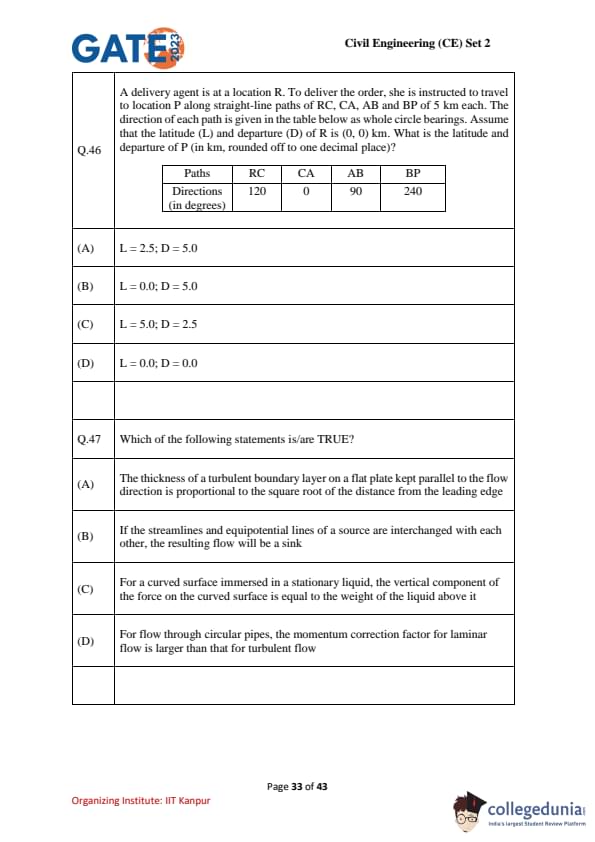

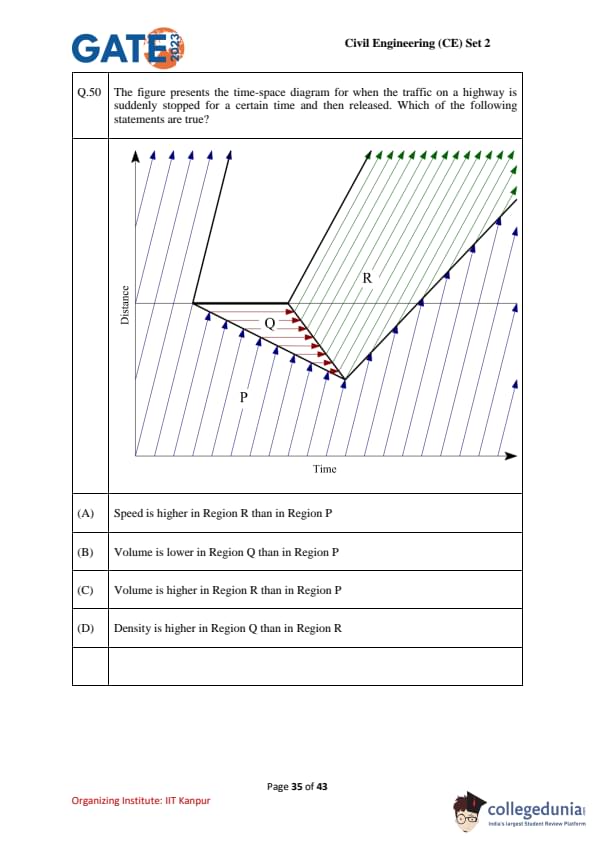








GATE 2023 CE Paper Analysis Shift 2
| Particulars | GATE 2023 CE Paper Analysis Forenoon Session |
|---|---|
| Number of MCQs | 33 |
| Number of NATs | 13 |
| Number of MSQs | 19 |
GATE 2023 CE Shift 1 Topic-wise Weighatge
| Name of the Section/Subject | No. of Questions | Total Marks | |
|---|---|---|---|
| 1 Mark | 2 Marks | ||
| General Aptitude | 5 | 5 | 15 |
| Engineering Mathematics | 2 | 3 | 8 |
| Geotechnical Engineering | 7 | 4 | 15 |
| Environmental Engineering | 6 | 4 | 14 |
| Strength of Material | 3 | 2 | 7 |
| Fluid Mechanics | 3 | 3 | 9 |
| Hydrology | 2 | 3 | 8 |
| Transportation | 5 | 4 | 13 |
| Structure | 3 | 4 | 11 |
Also Check:





Comments