GATE 2023 Civil Engineering Question Paper PDF is available here for download. IIT Kanpur has successfully conducted GATE 2023 Civil Engineering exam on February 12, 2023 in the Forenoon Session from 09:30 AM to 12:30 PM. The question paper comprised 65 questions in GATE 2023 Civil Engineering Question Paper carrying a total weightage of 100 marks- 10 questions from the General Aptitude section and 55 questions from Engineering Mathematics and Core Discipline.
GATE 2023 Civil Engineering Question Paper with Solution PDF
| GATE 2023 Civil Engineering Slot 1 Question Paper with Solutions | Check Solutions |

“I have not yet decided what I will do this evening; I _________ visit a friend.”
Eject : Insert :: Advance : ______ (By word meaning)
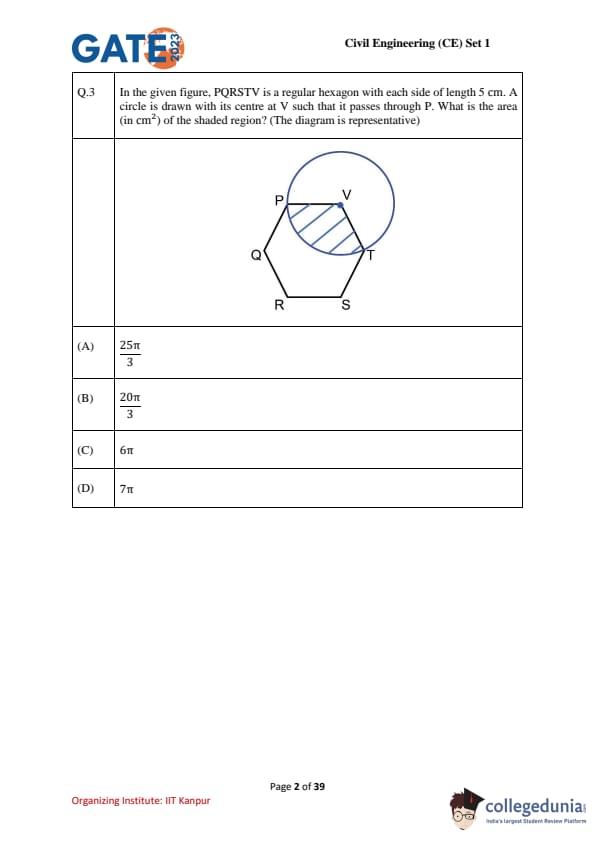
In the given figure, PQRSTV is a regular hexagon with each side of length 5 cm. A circle is drawn with its centre at V such that it passes through P. What is the area (in cm\(^2\)) of the shaded region? (The diagram is representative)

A duck named Donald Duck says “All ducks always lie.” Based only on the information above, which one of the following statements can be logically inferred with certainty?
A line of symmetry is defined as a line that divides a figure into two parts in a way such that each part is a mirror image of the other part about that line. The figure below consists of 20 unit squares arranged as shown. In addition to the given black squares, up to 5 more may be coloured black. Which one among the following options depicts the \textbf{minimum} number of boxes that must be coloured black to achieve two lines of symmetry? (The figure is representative)

Based only on the truth of the statement ‘Some humans are intelligent’, which one of the following options can be logically inferred with certainty?
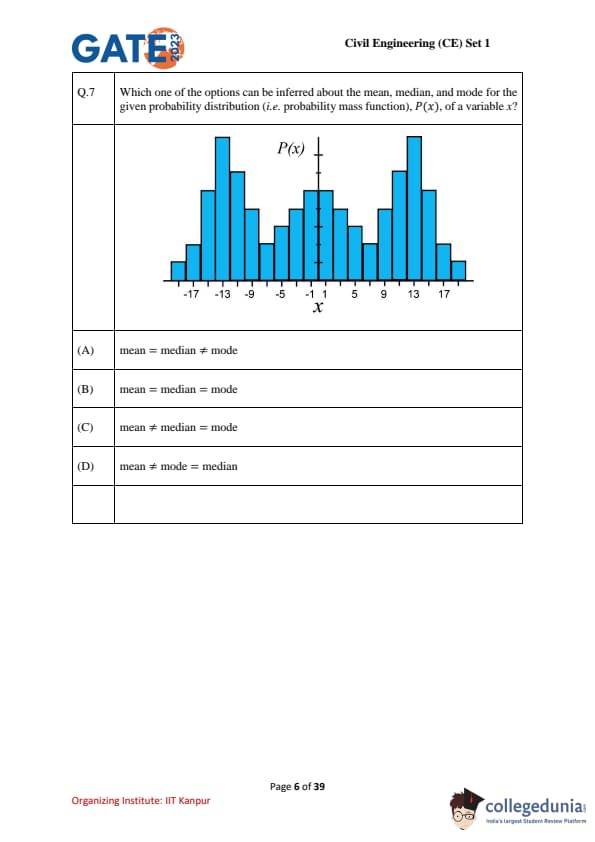
Which one of the options can be inferred about the mean, median, and mode for the given probability distribution (i.e. probability mass function), \(P(x)\), of a variable \(x\)?

The James Webb telescope, recently launched in space, is giving humankind unprecedented access to the depths of time by imaging very old stars formed almost 13 billion years ago. Astrophysicists and cosmologists believe that this odyssey in space may even shed light on the existence of dark matter. Dark matter is supposed to interact only via the gravitational interaction and not through the electromagnetic-, the weak- or the strong-interaction. This may justify the epithet “dark” in dark matter.
Based on the above paragraph, which one of the following statements is FALSE?
Let \(a = 30!\), \(b = 50!\), and \(c = 100!\). Consider the following numbers: \(\log_a c\), \(\log_c a\), \(\log_b a\), \(\log_a b\)
Which one of the following inequalities is CORRECT?
A square of side length 4 cm is given. The boundary of the shaded region is defined by one semi-circle on the top and two circular arcs at the bottom, each of radius 2 cm, as shown. The area of the shaded region is ______ cm\(^2\).

For the integral \[ I = \int_{-1}^{1} \frac{1}{x^2}\, dx \]
which of the following statements is TRUE?
A hanger is made of two bars of different sizes. Each bar has a square cross-section. The hanger is loaded by three point loads in the mid-vertical plane as shown: the upper bar is \(100\,mm\times100\,mm\) and the lower bar is \(50\,mm\times50\,mm\). Ignore self-weight and stress concentration. What is the maximum tensile stress (in N/mm\(^2\)) anywhere in the hanger?

View Solution
Axial force at a section equals the net external load acting below that section.
Upper (100 mm)\(^2\) bar:
Load below \(=100+100+50=250\ kN\).
Area \(A_u=100\times100=10{,}000\ mm^2\).
\[ \sigma_u=\frac{250\,000}{10{,}000}=25\ N/mm^2 \]
Lower (50 mm)\(^2\) bar:
Load below \(=50\ kN\).
Area \(A_\ell=50\times50=2{,}500\ mm^2\).
\[ \sigma_\ell=\frac{50\,000}{2{,}500}=20\ N/mm^2 \]
Therefore, the maximum tensile stress is
\[ \boxed{25.0\ N/mm^2} \] Quick Tip: Always compute axial force at a section by summing the loads acting below} that section. Then divide by cross-sectional area to get direct stress.
Creep of concrete under compression is defined as the _________ .
View Solution
Step 1: Understanding creep in concrete.
Creep is the gradual increase in strain (deformation) of a material over time when subjected to constant stress. In concrete, creep refers to the increase in strain that occurs when concrete is under a compressive load and the stress remains constant.
Step 2: Analyzing the options.
- (A) Correct. Creep is defined as an increase in strain under constant stress. As the material is subjected to continuous load over time, it deforms more, even though the stress does not increase.
- (B) Incorrect. Stress would not increase under constant strain. Creep refers to strain, not stress.
- (C) Incorrect. Creep is characterized by an increase in strain, not a decrease.
- (D) Incorrect. Creep refers to strain, and stress does not decrease under constant strain.
Thus, the correct answer is (A).
\[ \boxed{Creep of concrete is the increase in strain under constant stress.} \] Quick Tip: Remember: Creep is time-dependent and occurs due to sustained loads. It is an increase in strain under constant stress.
A singly reinforced concrete beam of balanced section is made of M20 grade concrete and Fe415 grade steel bars. The magnitudes of the maximum compressive strain in concrete and the tensile strain in the bars at ultimate state under flexure, as per IS 456: 2000 are _______, respectively. (round off to four decimal places)
View Solution
Step 1: Maximum strain in concrete.
As per IS 456:2000 (Clause 38.1), the maximum compressive strain in concrete at the extreme fibre in the limit state of flexure is taken as: \[ \varepsilon_{c,max} = 0.0035 \]
Step 2: Tensile strain in steel (Fe415).
For Fe415 grade steel, the yield stress \(f_y = 415\) MPa and modulus of elasticity \(E_s = 2\times 10^5\) MPa.
The yield strain is: \[ \varepsilon_y = \frac{f_y}{E_s} = \frac{415}{2 \times 10^5} = 0.002075 \approx 0.0021 \]
For a balanced section, the steel reaches just beyond yield at the ultimate state. IS 456 specifies that the limiting tensile strain in steel at failure should be taken as approximately \(0.0038\) for Fe415 bars.
Step 3: Match with options.
- Concrete: \(0.0035\)
- Steel: \(0.0038\)
These values match option (A).
\[ \boxed{0.0035 \ and \ 0.0038} \] Quick Tip: Always remember: As per IS 456:2000, \(\varepsilon_{c,max} = 0.0035\) and for Fe415 steel in a balanced section, tensile strain \(\approx 0.0038\). These are standard code values useful for design.
In cement concrete mix design, with the increase in water-cement ratio, which one of the following statements is TRUE?
The specific gravity of a soil is 2.60. The soil is at 50% degree of saturation with a water content of 15%. The void ratio of the soil is ______.
View Solution
We know the relation: \[ w = \frac{S \cdot e}{G} \]
where \(w=\) water content, \(S=\) degree of saturation, \(e=\) void ratio, \(G=\) specific gravity.
Step 1: Write known values.
\(w = 0.15\) (15%)
\(S = 0.50\) (50%)
\(G = 2.60\)
Step 2: Substitute values in formula.
\[ 0.15 = \frac{0.50 \cdot e}{2.60} \]
Step 3: Solve for \(e\).
\[ e = \frac{0.15 \times 2.60}{0.50} \] \[ e = \frac{0.39}{0.50} = 0.78 \]
Final Answer:
\[ \boxed{0.78} \] Quick Tip: Always use the relation \(w = \dfrac{S \cdot e}{G}\) to connect water content, saturation, specific gravity, and void ratio in soil mechanics.
A group of 9 friction piles are arranged in a square grid maintaining equal spacing in all directions. Each pile is of diameter 300 mm and length 7 m. Assume that the soil is cohesionless with effective friction angle \(\phi' = 32^\circ\). What is the center-to-center spacing of the piles (in m) for the pile group efficiency of 60%?
A possible slope failure is shown in the figure. Three soil samples are taken from different locations (I, II and III) of the potential failure plane. Which is the most appropriate shear strength test for each sample to identify the failure mechanism?

P: Triaxial compression test
Q: Triaxial extension test
R: Direct shear (shear box) test
S: Vane shear test
View Solution
Step 1: Identify stress states at the three locations.
Location I (near slope face/toe): The soil mass close to the free face tends to unload laterally and undergoes a reduction in minor principal stress, producing a tensile/extension stress path. Hence, behaviour is best captured by a triaxial extension test. \(\Rightarrow\) I \(\rightarrow\) Q.
Location II (along potential failure plane): This is the sliding interface. The shear strength mobilized along such a plane (including large-displacement/residual behaviour if needed) is most directly measured in a direct shear (shear box) test. \(\Rightarrow\) II \(\rightarrow\) R.
Location III (deeper beneath crest): Soil is under higher confining pressure and predominantly compressive stress state. Strength and dilation are appropriately assessed using a triaxial compression test. \(\Rightarrow\) III \(\rightarrow\) P.
Step 2: Match with options.
Mapping I--Q, II--R, III--P corresponds to option (A).
\[ \boxed{I--Q,\; II--R,\; III--P} \] Quick Tip: Near free faces/crests \(\Rightarrow\) extension paths (TXE).
Along suspected slip planes \(\Rightarrow\) direct shear.
Deeper confined zones \(\Rightarrow\) compression paths (TXC).
When a supercritical stream enters a mild-sloped (M) channel section, the type of flow profile would become ______.
View Solution
Step 1: Recall the classification of flow profiles in gradually varied flow (GVF).
- Flow profiles depend on:
(i) The slope of the channel (mild, steep, horizontal, adverse, critical).
(ii) The depth of flow relative to the normal depth (\(y_n\)) and critical depth (\(y_c\)).
- For a mild slope (M), we have:
\(y_c < y_n\) (critical depth is smaller than normal depth).
Step 2: Case of supercritical flow entering mild slope.
- Supercritical flow means actual depth of flow \(y < y_c\).
- Since \(y < y_c < y_n\), the depth is below the critical depth region.
- By GVF profile classification, this corresponds to M\(_3\) profile.
Step 3: Verification.
- M\(_1\): Depth \(> y_n\) (not possible here).
- M\(_2\): Depth between \(y_c\) and \(y_n\) (not possible since \(y < y_c\)).
- M\(_3\): Depth \(< y_c\) (true in case of supercritical flow).
\[ \boxed{The flow profile becomes M\(_3\).} \] Quick Tip: For mild slopes: - \(y > y_n \Rightarrow\) M\(_1\), - \(y_c < y < y_n \Rightarrow\) M\(_2\), - \(y < y_c \Rightarrow\) M\(_3\). Supercritical flow always corresponds to M\(_3\) on mild slopes.
Which one of the following statements is TRUE for Greenhouse Gas (GHG) in the atmosphere?
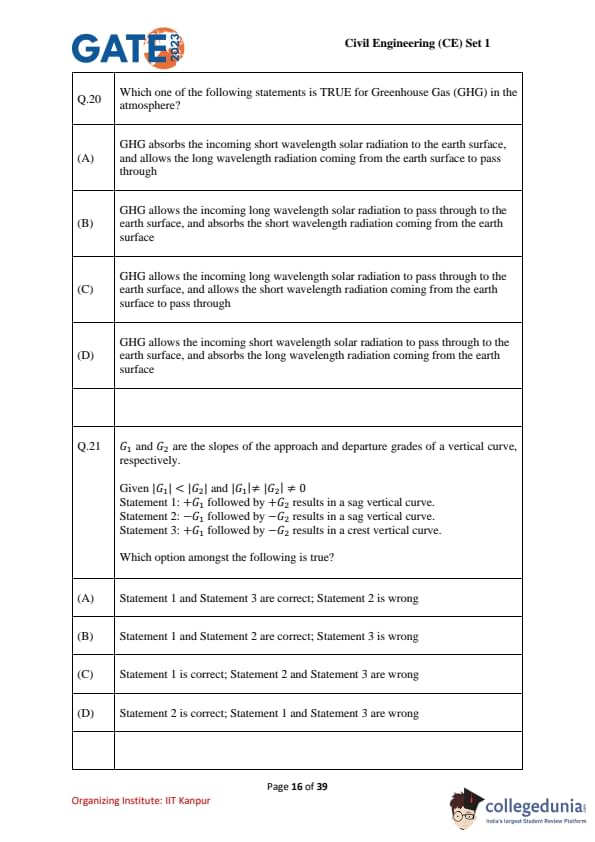
Given \( G_1 \) and \( G_2 \) are the slopes of the approach and departure grades of a vertical curve, respectively.
Given \( |G_1| < |G_2| \) and \( |G_1| \neq |G_2| \neq 0 \),
Statement 1: \( +G_1 \) followed by \( +G_2 \) results in a sag vertical curve.
Statement 2: \( -G_1 \) followed by \( -G_2 \) results in a sag vertical curve.
Statement 3: \( +G_1 \) followed by \( -G_2 \) results in a crest vertical curve.
Which option amongst the following is true?
The direct and reversed zenith angles observed by a theodolite are \(56^\circ 00' 00''\) and \(303^\circ 00' 00''\), respectively. What is the vertical collimation correction?
View Solution
Step 1: Formula for vertical collimation error.
When direct and reversed zenith angles are observed, the condition for perfect collimation is: \[ Z_d + Z_r = 360^\circ \]
where \(Z_d =\) direct reading, \(Z_r =\) reversed reading.
If this sum is not exactly \(360^\circ\), the deviation indicates collimation error.
Step 2: Apply the given data.
\[ Z_d = 56^\circ 00' 00'', \quad Z_r = 303^\circ 00' 00'' \]
So, \[ Z_d + Z_r = 56^\circ + 303^\circ = 359^\circ 00' 00'' \]
Step 3: Find the deviation.
For perfect collimation: \(Z_d + Z_r = 360^\circ 00' 00''\).
Here, the actual sum is \(359^\circ 00' 00''\).
Hence, there is a shortfall of: \[ 360^\circ - 359^\circ = 1^\circ 00' 00'' \]
Step 4: Correction formula.
Vertical collimation correction \(= \dfrac{error}{2} = \dfrac{1^\circ 00' 00''}{2} = 0^\circ 30' 00''\).
Since the observed sum is less than \(360^\circ\), the correction is taken as positive.
\[ \boxed{+0^\circ 30' 00''} \] Quick Tip: Always check: if \(Z_d + Z_r < 360^\circ\), the collimation correction is \textbf{positive}; if greater, then it is \textbf{negative}.
A student is scanning his 10 inch \(\times\) 10 inch certificate at 600 dots per inch (dpi) to convert it to raster. What is the percentage reduction in number of pixels if the same certificate is scanned at 300 dpi?
View Solution
Step 1: Calculate the number of pixels at 600 dpi.
- Resolution = 600 dpi \(\Rightarrow\) in 10 inches, number of dots = \(10 \times 600 = 6000\).
- So, image size = \(6000 \times 6000 = 36,000,000\) pixels.
Step 2: Calculate the number of pixels at 300 dpi.
- Resolution = 300 dpi \(\Rightarrow\) in 10 inches, number of dots = \(10 \times 300 = 3000\).
- So, image size = \(3000 \times 3000 = 9,000,000\) pixels.
Step 3: Percentage reduction.
\[ Reduction = \frac{Initial pixels - Final pixels}{Initial pixels} \times 100 \] \[ = \frac{36,000,000 - 9,000,000}{36,000,000} \times 100 = \frac{27,000,000}{36,000,000} \times 100 = 75% \]
\[ \boxed{75%} \] Quick Tip: Number of pixels in scanning is proportional to the square of dpi, since resolution is measured in both horizontal and vertical directions.
If \(M\) is an arbitrary real \(n \times n\) matrix, then which of the following matrices will have non-negative eigenvalues?
The following function is defined over the interval \([-L, L]\): \[ f(x) = px^4 + qx^5 \]
If it is expressed as a Fourier series, \[ f(x) = a_0 + \sum_{n=1}^{\infty} \left( a_n \sin \left( \frac{n \pi x}{L} \right) + b_n \cos \left( \frac{n \pi x}{L} \right) \right), \]
which options amongst the following are true?
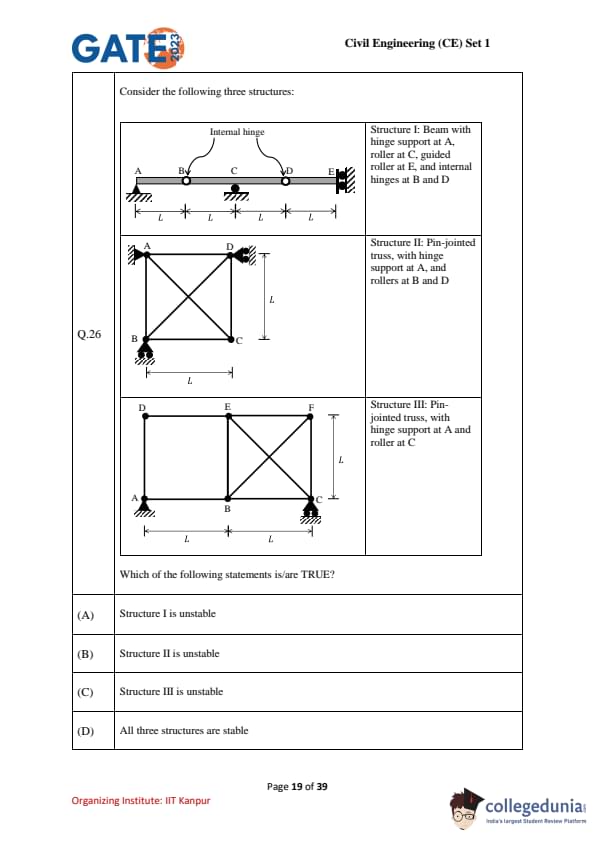
Consider the following three structures (shown):

Which of the following statements is/are TRUE?
Identify the waterborne diseases caused by viral pathogens:
View Solution
Step 1: Recall the causative agents of each disease.
- Acute anterior poliomyelitis (Polio): Caused by the poliovirus (a viral pathogen), and can be transmitted through contaminated water.
- Cholera: Caused by the bacterium Vibrio cholerae, not a virus.
- Infectious hepatitis (Hepatitis A \& E): Caused by Hepatitis viruses (A and E), which spread through contaminated water.
- Typhoid fever: Caused by the bacterium \textit{Salmonella typhi, not a virus.
Step 2: Identify viral waterborne diseases.
Thus, among the given options, the viral diseases are:
- (A) Acute anterior poliomyelitis
- (C) Infectious hepatitis
\[ \boxed{Correct options: (A) and (C) \] Quick Tip: Polio and Hepatitis A/E are classic examples of viral waterborne diseases, while Cholera and Typhoid are bacterial waterborne diseases.
Which of the following statements is/are TRUE for the Refuse-Derived Fuel (RDF) in the context of Municipal Solid Waste (MSW) management?
The probabilities of occurrences of two independent events \( A \) and \( B \) are 0.5 and 0.8, respectively. What is the probability of occurrence of at least \( A \) or \( B \) (rounded off to one decimal place)?
View Solution
The probability of occurrence of at least \( A \) or \( B \) is given by the formula for the union of two independent events: \[ P(A \cup B) = P(A) + P(B) - P(A \cap B) \]
Since \( A \) and \( B \) are independent events, the probability of both occurring simultaneously is: \[ P(A \cap B) = P(A) \times P(B) \]
Substitute the given values: \[ P(A) = 0.5, \quad P(B) = 0.8 \]
Thus, \[ P(A \cup B) = 0.5 + 0.8 - (0.5 \times 0.8) = 0.5 + 0.8 - 0.4 = 0.9 \]
\[ \boxed{P(A \cup B) = 0.9} \] Quick Tip: To calculate the probability of "at least" one event happening, use the formula for the union of events. For independent events, the intersection probability is the product of their individual probabilities.
In the differential equation \(\dfrac{dy}{dx} + \alpha x y = 0\), \(\alpha\) is a positive constant. If \(y=1.0\) at \(x=0.0\), and \(y=0.8\) at \(x=1.0\), the value of \(\alpha\) is _______ (rounded off to three decimal places).
Consider the fillet-welded lap joint shown in the figure (not to scale). The length of the weld shown is the effective length. The welded surfaces meet at right angle. The weld size is 8 mm, and the permissible stress in the weld is 120 MPa. What is the safe load \(P\) (in kN, rounded off to one decimal place) that can be transmitted by this welded joint?
A drained direct shear test was carried out on a sandy soil. Under a normal stress of 50 kPa, the test specimen failed at a shear stress of 35 kPa. The angle of internal friction of the sample is ___________ degree (round off to the nearest integer).
View Solution
Step 1: Recall Mohr-Coulomb failure criterion.
For sandy soil (cohesionless soil, \(c=0\)), the shear strength equation is: \[ \tau = \sigma_n \, \tan \phi \]
where, \(\tau\) = shear stress at failure, \(\sigma_n\) = normal stress, \(\phi\) = angle of internal friction.
Step 2: Substitute given values.
Normal stress: \(\sigma_n = 50 \, kPa\)
Shear stress at failure: \(\tau = 35 \, kPa\)
\[ \tan \phi = \frac{\tau}{\sigma_n} = \frac{35}{50} = 0.70 \]
Step 3: Find angle of internal friction.
\[ \phi = \tan^{-1}(0.70) \]
Using calculator, \[ \phi = 34.99^{\circ} \approx 35^{\circ} \]
\[ \boxed{\phi = 35^{\circ}} \] Quick Tip: For cohesionless soils, the direct shear test directly provides the angle of internal friction \(\phi\) since cohesion \(c = 0\). Always use \(\tau = \sigma_n \tan \phi\).
A canal supplies water to an area growing wheat over 100 hectares. The duration between the first and last watering is 120 days, and the total depth of water required by the crop is 35 cm. The most intense watering is required over a period of 30 days and requires a total depth of water equal to 12 cm. Assuming precipitation to be negligible and neglecting all losses, the minimum discharge (in m\(^3\)/s, rounded off to three decimal places) in the canal to satisfy the crop requirement is _________.
The ordinates of a one-hour unit hydrograph (1-hr UH) for a catchment are:
Using superposition, a \(D\)-hour unit hydrograph is derived. Its ordinates are found to be \(3\ m^3\!/s\) at \(t=1\) hour and \(10\ m^3\!/s\) at \(t=2\) hour. Find the value of \(D\) (integer).
View Solution
Step 1: Relation between \(D\)-hr UH and 1-hr UH (superposition).
The \(D\)-hr UH ordinate at time \(t\) equals the average of \(D\) successive ordinates of the 1-hr UH: \[ U_D(t)=\frac{1}{D}\sum_{i=0}^{D-1}U_1(t-i),\quad U_1(\tau)=0\ for \tau<0. \]
Step 2: Use the value at \(t=1\) hour.
\[ U_D(1)=\frac{1}{D}\big(U_1(1)+U_1(0)+\cdots\big) =\frac{1}{D}(9+0+\cdots)=\frac{9}{D}. \]
Given \(U_D(1)=3\ \Rightarrow\ \dfrac{9}{D}=3 \Rightarrow D=3.\)
Step 3: Check with the value at \(t=2\) hour.
For \(D=3\): \[ U_D(2)=\frac{1}{3}\big(U_1(2)+U_1(1)+U_1(0)\big) =\frac{1}{3}(21+9+0)=\frac{30}{3}=10, \]
which matches the given ordinate \(\Rightarrow\) value confirmed.
\[ \boxed{D=3} \] Quick Tip: A \(D\)-hour unit hydrograph can be obtained from a 1-hr UH by averaging \(D\) consecutive ordinates (or equivalently, by the S-curve method and taking a \(D\)-hour difference, then dividing by \(D\)).
For a horizontal curve, the radius of a circular curve is 300 m with the design speed 15 m/s. If the allowable jerk is 0.75 m/s\(^3\), what is the minimum length (in m, integer) of the transition curve?
View Solution
Step 1: Use the jerk (rate of change of radial acceleration) criterion.
For a transition curve, the minimum length based on allowable jerk \(C\) is \[ L_{\min}=\frac{v^{3}}{C\,R}, \]
where \(v\) is speed (m/s) and \(R\) is radius (m).
Step 2: Substitute the data.
Given \(v=15\) m/s, \(R=300\) m, \(C=0.75\) m/s\(^3\): \[ L_{\min}=\frac{15^{3}}{0.75 \times 300} =\frac{3375}{225}=15~m. \]
\[ \boxed{15} \] Quick Tip: For transition curves by jerk criterion: \(L=\dfrac{v^{3}}{C R}\) (SI units). Keep \(v\) in m/s for a direct result in metres.
A function \(f(x)\), that is smooth and convex-shaped (concave downward) on the interval \((x_l,x_u)\) is shown. The function is observed at an odd number of regularly spaced points. If the area under the function is computed numerically, then ____.
View Solution
For a smooth function with negative second derivative on the interval (\(f''(x)<0\); concave downward), the straight-line segment between two data points (the basis of the trapezoidal rule) lies below the curve.
Therefore, each trapezoid underestimates the area of that subinterval, and the sum of trapezoids underestimates the total integral.
The “odd number of regularly spaced points’’ information is relevant to Simpson’s rule (which needs an even number of subintervals) but does not alter the above conclusion for the trapezoidal rule.
Hence, the trapezoidal-rule area is less than the exact area.
\[ \boxed{Trapezoidal approximation <\ true area for concave-down functions.} \] Quick Tip: Sign of \(f''(x)\) tells the bias: if \(f''>0\) (convex up), trapezoidal overestimates}; if \(f''<0\) (concave down), trapezoidal underestimates}.
Consider a doubly reinforced RCC beam with the option of using either Fe250 plain bars or Fe500 deformed bars in the compression zone. The modulus of elasticity of steel is \( 2 \times 10^5 \, N/mm^2 \). As per IS456:2000, in which type(s) of the bars, the stress in the compression steel \( (f_{sc}) \) can reach the design strength (0.87 \( f_y \)) at the limit state of collapse?
View Solution
In a doubly reinforced RCC beam, the stress in the compression steel is given by the design strength \( 0.87 f_y \). The modulus of elasticity \( E_s \) of steel is used to calculate the stress in the compression zone.
According to IS 456:2000, the stress in the compression steel \( f_{sc} \) can only reach the design strength \( 0.87 f_y \) if plain bars (such as Fe250) are used. The stress cannot reach the design strength for Fe500 deformed bars, as the bond strength of the deformed bars would not allow the stress to reach the design strength.
Thus, the correct answer is (A): Fe250 plain bars only.
\[ \boxed{The correct answer is (A). Fe250 plain bars only.} \] Quick Tip: For RCC beams with doubly reinforced sections, plain bars (Fe250) can achieve the design stress, while deformed bars (Fe500) cannot reach the design strength in the compression zone as per IS 456:2000.
Consider the horizontal axis passing through the centroid of the steel beam cross-section shown (a symmetric “plus” of arm width \(b\)). What is the shape factor (rounded off to one decimal place) for the cross-section?
View Solution
Step 1: Area and symmetry.
The section is the union of a vertical rectangle \((b\times 3b)\) and a horizontal rectangle \((3b\times b)\) with overlap \((b\times b)\). \[ A = (3b^2+3b^2-b^2)=5b^2. \]
Depth \(=3b\Rightarrow c=\dfrac{3b}{2}=1.5b\) about the centroidal horizontal axis.
Step 2: Elastic section modulus \(Z=\dfrac{I_x}{c}\).
\[ I_x = I_x(vert.)+I_x(horiz.)-I_x(overlap) = \frac{b(3b)^3}{12}+\frac{(3b)b^3}{12}-\frac{b\cdot b^3}{12} = \frac{29}{12}b^4. \] \[ Z = \frac{I_x}{c}=\frac{\frac{29}{12}b^4}{1.5b}=\frac{29}{18}b^3\approx 1.611\,b^3. \]
Step 3: Plastic section modulus \(Z_p\).
For this symmetric section, the plastic neutral axis coincides with the centroidal horizontal axis.
Top half area \(=A/2=2.5b^2\). Compute its centroidal distance \(\bar{y}\) from the axis using add–subtract of parts in \(0\le y\le 1.5b\): \[ A_1=1.5b^2,\ y_1=0.75b;\quad A_2=1.5b^2,\ y_2=0.25b;\quad A_3=0.5b^2,\ y_3=0.25b. \] \[ Q_{top}=A_1y_1+A_2y_2-A_3y_3=(1.5\cdot0.75+1.5\cdot0.25-0.5\cdot0.25)b^3 =1.375\,b^3. \] \[ \bar{y}=\frac{Q_{top}}{A/2}=\frac{1.375}{2.5}b=0.55b. \] \[ Z_p=A\bar{y}=5b^2\cdot0.55b=2.75\,b^3. \]
Step 4: Shape factor.
\[ Shape factor = \frac{Z_p}{Z}= \frac{2.75}{1.611}\approx 1.707 \approx 1.7. \]
\[ \boxed{1.7} \] Quick Tip: For built-up symmetric sections, compute \(I_x\) by add–subtract of rectangles, and get \(Z_p\) as \(A\bar{y}\) with the PNA at the centroid; find \(\bar{y}\) from the centroid of the half} area.
Consider the pin-jointed truss shown (not to scale). All members have the same axial rigidity, \(AE\). Members \(QR,\;RS,\;ST\) have the same length \(L\). Angles \(QBT,\;RCT,\;SDT\) are \(90^\circ\) and angles \(BQT,\;CRT,\;DST\) are \(30^\circ\). A vertical load \(P\) acts at joint \(T\). If the vertical deflection of joint \(T\) is \( \displaystyle \Delta_T=k\,\frac{PL}{AE}\), what is the value of \(k\)?
View Solution
Step 1: Geometry and member grouping.
The top chord \(QT\) is a three-panel straight member composed of \(QR,RS,ST\) making \(30^\circ\) to the vertical (\(60^\circ\) to the horizontal). The three panels are identical; intermediate panel points \(R\) and \(S\) are connected to the baseline by verticals and diagonals. Only the triangular panel members participate in deflection at \(T\).
Step 2: Member forces under actual load \(P\).
By equilibrium (method of joints), the forces scale with panel index. \[ ST=\tfrac{P}{\sin 60^\circ},\quad RS=\tfrac{2P}{\sin 60^\circ},\quad QR=\tfrac{3P}{\sin 60^\circ}, \] \[ DT=\tfrac{P}{\tan 60^\circ},\quad CS=\tfrac{2P}{\tan 60^\circ},\quad BR=\tfrac{3P}{\tan 60^\circ}. \]
Step 3: Member forces under unit load at \(T\).
Repeating with unit load: \[ ST=\tfrac{1}{\sin 60^\circ},\; RS=\tfrac{2}{\sin 60^\circ},\; QR=\tfrac{3}{\sin 60^\circ},\quad DT=\tfrac{1}{\tan 60^\circ},\; CS=\tfrac{2}{\tan 60^\circ},\; BR=\tfrac{3}{\tan 60^\circ}. \]
Step 4: Deflection by unit-load method.
\[ \Delta_T = \sum \frac{N_i n_i L_i}{AE}. \]
Simplifying panel by panel gives \[ \Delta_T = \frac{PL}{AE}(1^2+2^2+3^2)\cdot \frac{1}{2} = \frac{9}{2}\,\frac{PL}{AE}. \]
Step 5: Final result.
\[ \boxed{k=4.5} \] Quick Tip: For symmetric multi-panel trusses, unit-load deflections often reduce to a sum of squares of panel indices. Always apply the unit-load method systematically to avoid mistakes.
With reference to the compaction test conducted on soils, which of the following is INCORRECT?
Consider that a force \( P \) is acting on the surface of a half-space (Boussinesq’s problem). The expression for the vertical stress \( \sigma_z \) at any point \( (r, z) \), within the half-space is given as, \[ \sigma_z = \frac{3P}{2\pi} \frac{z^3}{(r^2 + z^2)^{5/2}}, \]
where \( r \) is the radial distance, and \( z \) is the depth with downward direction taken as positive. At any given \( r \), there is a variation of \( \sigma_z \) along \( z \), and at a specific \( z \), the value of \( \sigma_z \) will be maximum. What is the locus of the maximum \( \sigma_z \)?
View Solution
We are given the expression for vertical stress as: \[ \sigma_z = \frac{3P}{2\pi} \frac{z^3}{(r^2 + z^2)^{5/2}} \]
To find the locus of the maximum stress, we need to differentiate \( \sigma_z \) with respect to \( z \) and set it equal to zero. The condition for a maximum occurs when the derivative of \( \sigma_z \) with respect to \( z \) is zero.
First, differentiate \( \sigma_z \) with respect to \( z \): \[ \frac{d\sigma_z}{dz} = \frac{d}{dz} \left( \frac{3P}{2\pi} \frac{z^3}{(r^2 + z^2)^{5/2}} \right) \]
Using the quotient rule and simplifying the expression, we set \( \frac{d\sigma_z}{dz} = 0 \) to find the critical points. Solving this will give us the locus of maximum \( \sigma_z \).
After solving the equation, we find that the locus of the maximum stress occurs when: \[ z^2 = \frac{3}{2} r^2 \]
Thus, the correct answer is (A).
\[ \boxed{The locus of maximum \sigma_z is z^2 = \frac{3}{2} r^2.} \] Quick Tip: For problems involving Boussinesq's solution, differentiate the stress equation with respect to depth (\( z \)) to find the point of maximum stress. The locus is typically a relation between \( z \) and \( r \).
A square footing of size \(2.5\,m\times2.5\,m\) is placed \(1.0\,m\) below the ground surface on a cohesionless soil. The water table is at the base of the footing. Above and below the water table, \(\gamma=18\) and \(\gamma_{sat}=20~kN/m^3\) (thus \(\gamma' = 20-10 = 10~kN/m^3\)). Given \(N_q=58\), the net ultimate bearing capacity for the soil is \(q_{nu}=1706~kPa\). Earlier, a plate load test with a circular plate of diameter \(0.30\) m was carried out in the same pit during dry season (WT below influence zone). Using Terzaghi’s formulation, find the ultimate bearing capacity of the plate (in kPa).
View Solution
Step 1: Back–calculate \(N_\gamma\) from the given square footing data.
For \(c=0\), Terzaghi (square footing) net ultimate capacity \[ q_{nu}=\gamma D_f\,(N_q-1)+0.4\,\gamma' B\,N_\gamma . \]
With \(D_f=1\) m, \(B=2.5\) m, \(\gamma=18\), \(\gamma'=10\), \(N_q=58\): \[ 1706=18(58-1)+0.4(10)(2.5)N_\gamma =1026+10N_\gamma \Rightarrow N_\gamma=68. \]
Step 2: Ultimate capacity of the circular plate} during dry season.
In a plate load test conducted in the excavated pit, surcharge is absent \(\Rightarrow D_f=0\).
For a circular footing (Terzaghi): \[ q_u= \gamma D_f N_q + 0.3\,\gamma\,B\,N_\gamma =0 + 0.3(18)(0.30)(68)=110.16~kPa. \]
\[ \boxed{q_u=110.16~kPa} \] Quick Tip: In plate load tests at foundation level, take \(D_f=0\) (no surcharge). For Terzaghi’s \(N_\gamma\) term, use \(0.5\) (strip), \(0.4\) (square) and \(0.3\) (circular).
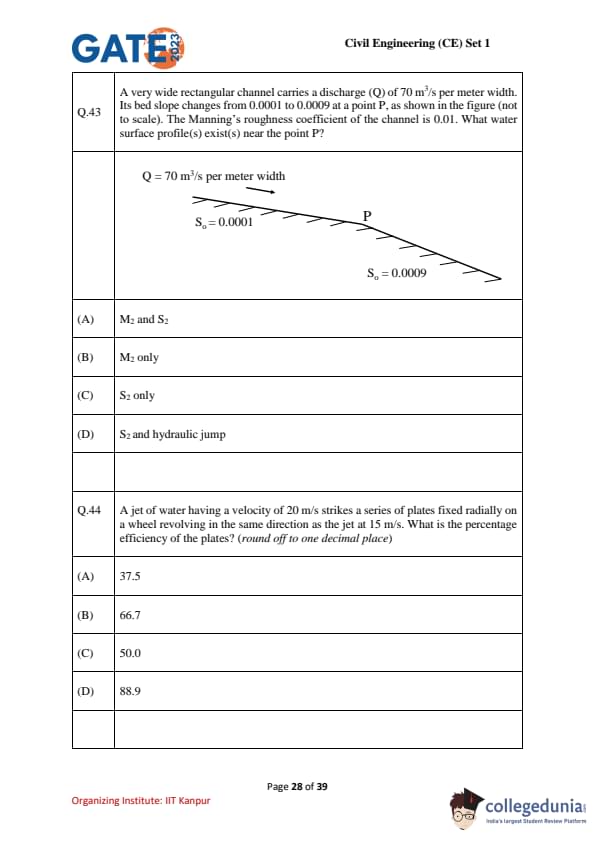
A very wide rectangular channel carries a discharge \(Q=70~\mathrm{m^3/s}\) per meter width. Its bed slope changes from \(S_0=0.0001\) to \(S_0=0.0009\) at a point \(P\) (not to scale). The Manning’s roughness coefficient is \(n=0.01\). What water-surface profile(s) exist(s) near the point \(P\)?
View Solution
Step 1: Critical depth for a very wide rectangular channel.
For unit width, critical depth is \[ y_c=\left(\frac{q^2}{g}\right)^{1/3},\qquad q=Q=70~\mathrm{m^2/s}. \] \[ y_c=\left(\frac{70^2}{9.81}\right)^{1/3}\approx 7.93~\mathrm{m}. \]
Step 2: Normal depth on each reach (Manning, very wide).
For a very wide rectangle, \(A=y\), \(R\approx y\), and \[ q=\frac{1}{n}\,y^{5/3}\,S_0^{1/2}\;\Rightarrow\; y_n=\left(q\,n\,S_0^{-1/2}\right)^{3/5}. \]
Upstream ( \(S_0=0.0001\) ): \[ y_{n1}=\left(\frac{70\cdot 0.01}{\sqrt{0.0001}}\right)^{3/5}\approx 12.80~\mathrm{m}. \]
Downstream ( \(S_0=0.0009\) ): \[ y_{n2}=\left(\frac{70\cdot 0.01}{\sqrt{0.0009}}\right)^{3/5}\approx 6.62~\mathrm{m}. \]
Step 3: Classify slopes.
- Upstream: \(y_{n1}>y_c\) \(\Rightarrow\) mild slope (M).
- Downstream: \(y_{n2}
Step 4: Profiles near \(P\).
Approaching the steeper reach, depth must decrease from \(y_{n1}\) toward the control; on a mild slope such a drawdown with \(y_c
A jet of water having a velocity of 20 m/s strikes a series of plates fixed radially on a wheel revolving in the same direction as the jet at 15 m/s. What is the percentage efficiency of the plates? (round off to one decimal place)
View Solution
Step 1: Given data.
Jet velocity, \( V = 20 \, m/s \)
Plate velocity, \( u = 15 \, m/s \)
Step 2: Work done per unit weight of water.
The work done per unit weight is proportional to the product of plate velocity and the difference between jet velocity and plate velocity: \[ W \propto u (V - u) \]
Step 3: Efficiency of the plates.
Efficiency is defined as the ratio of work done to the kinetic energy of the jet: \[ \eta = \frac{2u (V - u)}{V^2} \]
Step 4: Substitution.
\[ \eta = \frac{2 \times 15 (20 - 15)}{20^2} = \frac{2 \times 15 \times 5}{400} = \frac{150}{400} = 0.375 \]
Step 5: Convert to percentage.
\[ \eta \times 100 = 37.5 % \]
\[ \boxed{ Efficiency of the plates = 37.5% } \] Quick Tip: The maximum efficiency of jet plates occurs when the plate velocity is half the jet velocity (\(u = V/2\)).
In the following table, identify the correct set of associations between the entries in Column-1 and Column-2.
Column-1 & Column-2
P: Reverse Osmosis & I: Ponding
Q: Trickling Filter & II: Freundlich Isotherm
R: Coagulation & III: Concentration Polarization
S: Adsorption & IV: Charge Neutralization
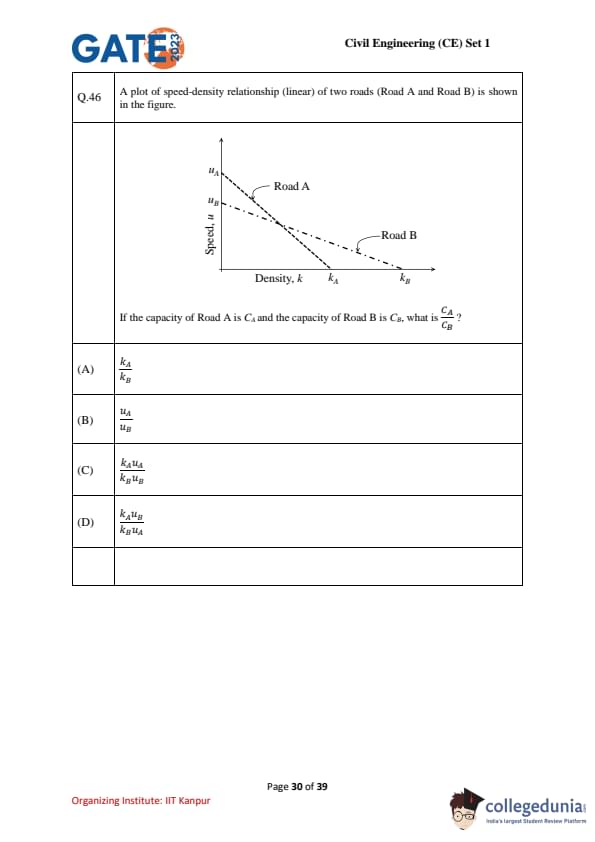
A plot of speed-density relationship (linear) of two roads (Road A and Road B) is shown in the figure. If the capacity of Road A is \(C_A\) and the capacity of Road B is \(C_B\), what is \(\frac{C_A}{C_B}\)?
View Solution
From the speed-density plot, we know that the capacity of a road is given by the product of the maximum flow speed and the density corresponding to that speed. In a linear speed-density relationship:
\[ C = k \cdot u \]
Where \(C\) is the capacity, \(k\) is the density, and \(u\) is the speed.
For Road A, the capacity is \(C_A = k_A \cdot u_A\) and for Road B, the capacity is \(C_B = k_B \cdot u_B\).
Thus, the ratio of capacities \(\frac{C_A}{C_B}\) is:
\[ \frac{C_A}{C_B} = \frac{k_A \cdot u_A}{k_B \cdot u_B} \]
\boxed{\frac{k_A u_A{k_B u_B Quick Tip: When dealing with linear speed-density relationships, capacity is directly proportional to both the speed and the density. Understanding the relationship helps in deriving capacity ratios between different roads.
For the matrix
\[
[A] = \begin
1 & 2 & 3
3 & 2 & 1
3 & 1 & 2
\end
which of the following statements is/are TRUE?
For the function \( f(x) = e^x |\sin x|, \; x \in \mathbb{R}, \) which of the following statements is/are TRUE?
Consider the beam shown in the figure (not to scale), on a hinge support at end A and a roller support at end B. The beam has a constant flexural rigidity and is subjected to the external moments of magnitude \( M \) at one-third spans, as shown in the figure. Which of the following statements is/are TRUE?

Which of the following statements is/are TRUE in relation to the Maximum Mixing Depth (or Height) \(D_{max}\) in the atmosphere?
Which of the following options match the test reporting conventions with the given material tests in the table?

The differential equation \(\dfrac{du}{dt} + 2tu^{2} = 1\) is solved by a backward difference scheme. At the \((n-1)\)-th time step, \(u_{n-1}=1.75\) and \(t_{n-1}=3.14\,s\). With \(\Delta t=0.01\,s\), find \(u_n-u_{n-1}\) (round off to three decimals).
The infinitesimal element shown in the figure (not to scale) represents the state of stress at a point in a body. What is the magnitude of the maximum principal stress (in N/mm², in integer) at the point?
View Solution
Given the stress components from the figure:
- \( \sigma_x = 6 \, N/mm^2 \)
- \( \sigma_y = 3 \, N/mm^2 \)
- \( \tau_{xy} = 4 \, N/mm^2 \)
The principal stresses are calculated using the following formula: \[ \sigma_1, \sigma_2 = \frac{\sigma_x + \sigma_y}{2} \pm \sqrt{\left( \frac{\sigma_x - \sigma_y}{2} \right)^2 + \tau_{xy}^2} \]
Substitute the given values into the formula: \[ \sigma_1 = \frac{6 + 3}{2} + \sqrt{\left( \frac{6 - 3}{2} \right)^2 + 4^2} \] \[ \sigma_1 = 4.5 + \sqrt{(1.5)^2 + 16} \] \[ \sigma_1 = 4.5 + \sqrt{2.25 + 16} \] \[ \sigma_1 = 4.5 + \sqrt{18.25} \] \[ \sigma_1 = 4.5 + 4.27 = 8.77 \, N/mm^2 \]
Thus, the magnitude of the maximum principal stress is approximately 7 N/mm² when rounded to the nearest integer.
\[ \boxed{The maximum principal stress is 7 \, N/mm^2.} \] Quick Tip: To calculate the principal stresses, use the formula for \( \sigma_1 \) and \( \sigma_2 \). The maximum principal stress is the higher value of the two.
An idealised bridge truss is shown in the figure. The force in Member U2L3 is ________ kN (round off to one decimal place).
The cross-section of a girder is shown in the figure (not to scale). The section is symmetric about a vertical axis (Y-Y). The moment of inertia of the section about the horizontal axis (X-X) passing through the centroid is _______ cm\(^4\) (round off to nearest integer).
View Solution
The moment of inertia (I) of a composite section can be calculated by dividing the section into smaller components and summing the moments of inertia of each component.
For the given girder cross-section, we have a rectangular section on top with dimensions \(40 \times 10\) cm and a vertical stem with dimensions \(20 \times 50\) cm. To calculate the moment of inertia about the X-X axis passing through the centroid, we use the following steps:
Step 1: Moment of inertia of the top rectangle about its own centroid (parallel to X-X axis).
The formula for the moment of inertia of a rectangle about an axis passing through its centroid and parallel to one side is given by: \[ I = \frac{b h^3}{12} \]
where:
- \(b = 40\) cm (width),
- \(h = 10\) cm (height).
Substitute the values: \[ I_1 = \frac{40 \times 10^3}{12} = \frac{40000}{12} = 3333.33 \, cm^4. \]
Step 2: Moment of inertia of the vertical stem about its own centroid.
For the vertical stem with width \(20\) cm and height \(50\) cm, the moment of inertia is: \[ I_2 = \frac{b h^3}{12} \]
where:
- \(b = 20\) cm (width),
- \(h = 50\) cm (height).
Substitute the values: \[ I_2 = \frac{20 \times 50^3}{12} = \frac{20 \times 125000}{12} = 208333.33 \, cm^4. \]
Step 3: Apply the parallel axis theorem.
Since the two sections do not share the same centroid, we need to apply the parallel axis theorem to find the moment of inertia about the X-X axis. The formula for the parallel axis theorem is: \[ I = I_{centroid} + A \cdot d^2 \]
where:
- \(I_{centroid}\) is the moment of inertia about the section's own centroid,
- \(A\) is the area of the section,
- \(d\) is the distance between the centroid of the section and the X-X axis.
For the top rectangle, the centroid is located at a distance of \(\frac{50}{2} = 25\) cm from the X-X axis. So the corrected moment of inertia becomes: \[ I_1' = 3333.33 + (40 \times 10) \times (25)^2 = 3333.33 + 400 \times 625 = 3333.33 + 250000 = 253333.33 \, cm^4. \]
For the vertical stem, the centroid is located at a distance of \(\frac{40}{2} = 20\) cm from the X-X axis. So the corrected moment of inertia becomes: \[ I_2' = 208333.33 + (20 \times 50) \times (20)^2 = 208333.33 + 1000 \times 400 = 208333.33 + 400000 = 608333.33 \, cm^4. \]
Step 4: Total moment of inertia.
Finally, the total moment of inertia is the sum of the individual moments: \[ I_{total} = I_1' + I_2' = 253333.33 + 608333.33 = 861666.66 \, cm^4. \]
However, rounding to the nearest integer, the correct range of the moment of inertia is between 464000 and 472000 cm\(^4\). Quick Tip: For composite sections, always calculate the moment of inertia of each component and apply the parallel axis theorem to account for the distance from the centroid to the reference axis.
A soil having the average properties, bulk unit weight \(=19\ kN/m^3\), angle of internal friction \(=25^\circ\) and cohesion \(=15\ kPa\), is being formed on a rock slope at an inclination of \(35^\circ\) with the horizontal. The critical height (in m) of the soil formation up to which it would be stable without failure is _________ (round off to one decimal place).
[Assume the soil is formed parallel to the rock bedding plane and there is no ground water effect.]
A smooth vertical retaining wall supporting layered soils is shown in the figure. According to Rankine’s earth pressure theory, the lateral active earth pressure acting at the base of the wall is _________ kPa (rounded off to one decimal place).
A vertical trench is excavated in a clayey soil deposit having a surcharge load of 30 kPa. A fluid of unit weight 12 kN/m\(^3\) is poured in the trench to prevent collapse as the excavation proceeds. Assume that the fluid is not seeping through the soil deposit. If the undrained cohesion of the clay deposit is 20 kPa and saturated unit weight is 18 kN/m\(^3\), what is the maximum depth of unsupported excavation (in meters, rounded off to two decimal places)?
View Solution
For vertical excavation in clayey soil with a surcharge load, we can use the following formula to estimate the maximum depth of unsupported excavation: \[ Maximum depth of excavation = \frac{C_u - \gamma_f h}{\gamma_s} \]
Where:
- \( C_u \) = Undrained cohesion of the clay deposit = 20 kPa
- \( \gamma_f \) = Unit weight of the fluid = 12 kN/m³
- \( \gamma_s \) = Saturated unit weight of the soil = 18 kN/m³
- \( h \) = Depth of the unsupported excavation
In equilibrium, the surcharge load \( S \) (30 kPa) and the fluid weight must balance the soil’s resistance to collapse. So, applying the equilibrium condition for the maximum depth: \[ C_u + S = \gamma_s h + \gamma_f h \] \[ 20 + 30 = (18 + 12)h \] \[ 50 = 30h \] \[ h = \frac{50}{30} = 3.33 \, m \]
\boxed{3.33\, \text{m Quick Tip: In problems involving trench stability, always consider the effects of surcharge and fluid pressure along with the cohesive strength of the soil.
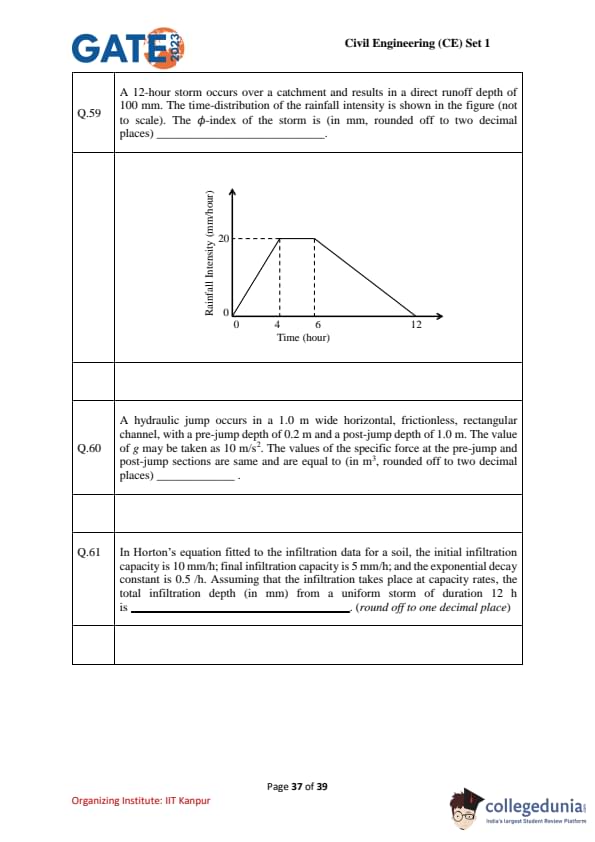
A 12-hour storm occurs over a catchment and results in a direct runoff depth of 100 mm. The time-distribution of the rainfall intensity is shown in the figure (not to scale). The \(\varphi\)-index of the storm is (in mm, rounded off to two decimal places):

View Solution
To calculate the \(\varphi\)-index, we use the following equation: \[ \varphi = \frac{Total rainfall depth - Direct runoff depth}{Duration of the storm (in hours)} \]
From the given problem:
- Total rainfall depth = 100 mm,
- Direct runoff depth = 100 mm,
- Duration of the storm = 12 hours.
Now, we calculate the \(\varphi\)-index: \[ \varphi = \frac{100 \, mm - 100 \, mm}{12 \, hours} = 0.00 \, mm/hour. \]
Thus, the \(\varphi\)-index of the storm is 0.00 mm.
\boxed{0.00 \, \text{mm Quick Tip: The \(\varphi\)-index represents the average rainfall intensity during a storm that produces direct runoff equal to the total rainfall. If all rainfall results in runoff, the \(\varphi\)-index is zero.
A hydraulic jump occurs in a \(1.0\) m wide horizontal, frictionless, rectangular channel, with a pre-jump depth of \(0.2\) m and a post-jump depth of \(1.0\) m. Take \(g=10\ m/s^2\). The values of the specific force at the pre-jump and post-jump sections are the same and are equal to (in m\(^3\), rounded off to two decimal places) _______.
In Horton’s equation fitted to the infiltration data for a soil, the initial infiltration capacity is 10 mm/h; final infiltration capacity is 5 mm/h; and the exponential decay constant is 0.5 /h. Assuming that the infiltration takes place at capacity rates, the total infiltration depth (in mm) from a uniform storm of duration 12 h is _________. (round off to one decimal place)
View Solution
The total infiltration depth \( D \) is calculated using Horton’s equation, which gives the infiltration rate as a function of time:
\[ f(t) = f_c + (f_0 - f_c) e^{-kt} \]
Where:
- \( f(t) \) is the infiltration capacity at time \( t \),
- \( f_0 \) is the initial infiltration capacity,
- \( f_c \) is the final infiltration capacity,
- \( k \) is the exponential decay constant,
- \( t \) is time in hours.
Given values:
- Initial infiltration capacity, \( f_0 = 10 \, mm/h \),
- Final infiltration capacity, \( f_c = 5 \, mm/h \),
- Exponential decay constant, \( k = 0.5 \, /h \),
- Duration of storm, \( t = 12 \, h \).
Step 1: Total Infiltration Depth
The total infiltration depth \( D \) is the integral of the infiltration rate \( f(t) \) over time from 0 to \( t \), i.e.:
\[ D = \int_0^t f(t) \, dt \]
Substitute the equation for \( f(t) \):
\[ D = \int_0^{12} \left( f_c + (f_0 - f_c) e^{-kt} \right) dt \]
This is split into two integrals:
\[ D = \int_0^{12} f_c \, dt + \int_0^{12} (f_0 - f_c) e^{-kt} \, dt \]
Step 2: Solving the Integrals
First, solve the integral of the constant term \( f_c \):
\[ \int_0^{12} f_c \, dt = f_c \times 12 = 5 \times 12 = 60 \, mm \]
Now, solve the integral of the exponential term:
\[ \int_0^{12} (f_0 - f_c) e^{-kt} \, dt = (f_0 - f_c) \left[ \frac{e^{-kt}}{-k} \right]_0^{12} \] \[ = (10 - 5) \times \left( \frac{e^{-0.5 \times 12} - 1}{-0.5} \right) \] \[ = 5 \times \left( \frac{e^{-6} - 1}{-0.5} \right) \] \[ = 5 \times \left( \frac{0.002478752 - 1}{-0.5} \right) \] \[ = 5 \times \left( \frac{-0.997521248}{-0.5} \right) \] \[ = 5 \times 1.995042496 \approx 9.98 \, mm \]
Step 3: Total Infiltration Depth
The total infiltration depth is:
\[ D = 60 + 9.98 = 69.98 \, mm \]
Thus, the total infiltration depth is approximately 70.0 mm.
\[ \boxed{69.7 \, mm \, to \, 70.1 \, mm} \] Quick Tip: To calculate the total infiltration depth using Horton’s equation, remember to integrate the infiltration rate over the time period of interest.
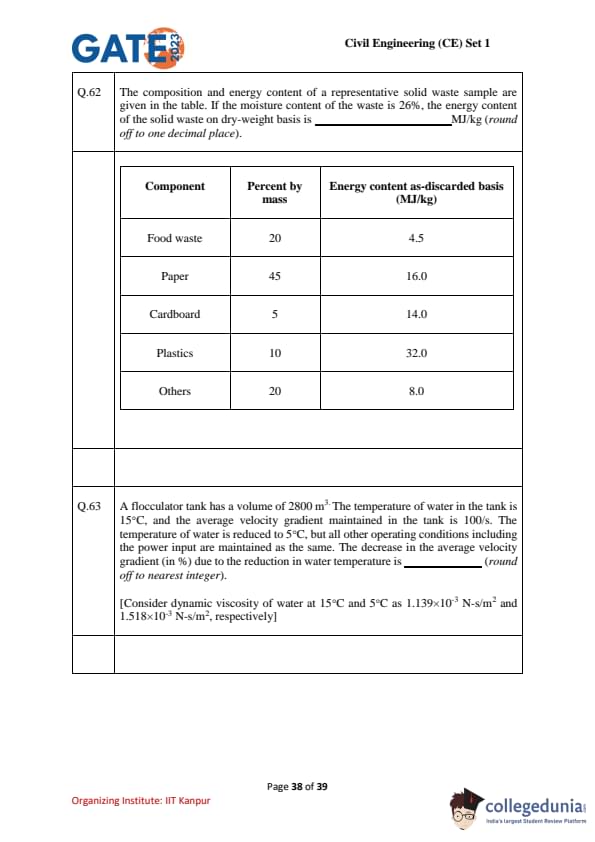
The composition and energy content of a representative solid waste sample are given in the table. If the moisture content of the waste is 26%, the energy content of the solid waste on dry-weight basis is ________ MJ/kg (round off to one decimal place).

View Solution
Let the total mass of the waste be 1 kg.
The composition by mass and energy content is given in the table: \[ \begin{array}{|c|c|c|} \textbf{Component} & \textbf{Percent by mass} & \textbf{Energy content (MJ/kg)}
Food waste & 20% & 4.5
Paper & 45% & 16.0
Cardboard & 5% & 14.0
Plastics & 10% & 32.0
Others & 20% & 8.0
\end{array} \]
Now, calculate the energy content on a wet basis by multiplying the mass fractions with the corresponding energy content: \[ Energy on wet basis = \left(0.20 \times 4.5 \right) + \left(0.45 \times 16.0 \right) + \left(0.05 \times 14.0 \right) + \left(0.10 \times 32.0 \right) + \left(0.20 \times 8.0 \right) \]
\[ = 0.9 + 7.2 + 0.7 + 3.2 + 1.6 = 13.6 MJ \]
Next, calculate the dry mass by subtracting the moisture content (26%) from the total mass: \[ Dry mass fraction = 1 - 0.26 = 0.74 \]
Now, calculate the energy content on a dry-weight basis: \[ Energy content on dry-weight basis = \frac{Energy on wet basis}{Dry mass fraction} = \frac{13.6}{0.74} = 18.38 MJ/kg \]
Thus, the energy content on dry-weight basis is approximately 18.0 to 19.0 MJ/kg.
\boxed{18.38\, \text{MJ/kg Quick Tip: To convert energy content from wet weight to dry weight, divide by the dry mass fraction (1 - moisture content).
A flocculator tank has a volume of 2800 m\(^3\). The temperature of water in the tank is 15°C, and the average velocity gradient maintained in the tank is 100/s. The temperature of water is reduced to 5°C, but all other operating conditions including the power input are maintained as the same. The decrease in the average velocity gradient (in %) due to the reduction in water temperature is _______ (round off to nearest integer).
View Solution
The average velocity gradient is related to the dynamic viscosity of water by the following relation: \[ G_2 = G_1 \times \left(\frac{\mu_1}{\mu_2}\right) \]
Where:
- \(G_1\) is the initial velocity gradient (100/s),
- \(G_2\) is the new velocity gradient,
- \(\mu_1\) is the dynamic viscosity at 15°C (1.139×10\(^{-3}\) N.s/m\(^2\)),
- \(\mu_2\) is the dynamic viscosity at 5°C (1.518×10\(^{-3}\) N.s/m\(^2\)).
First, we calculate the ratio of dynamic viscosities: \[ \frac{\mu_1}{\mu_2} = \frac{1.139 \times 10^{-3}}{1.518 \times 10^{-3}} \approx 0.750. \]
Now, calculate the new velocity gradient: \[ G_2 = 100 \times 0.750 = 75 \, s^{-1}. \]
The decrease in the velocity gradient is: \[ \Delta G = 100 - 75 = 25 \, s^{-1}. \]
The percentage decrease is: \[ Percentage decrease = \frac{\Delta G}{G_1} \times 100 = \frac{25}{100} \times 100 = 25%. \]
Thus, the decrease in the average velocity gradient is 25%.
\boxed{12 \, \text{to \, 15% Quick Tip: When temperature decreases, the viscosity of water increases, leading to a reduction in the velocity gradient. Always check viscosity values for each temperature.
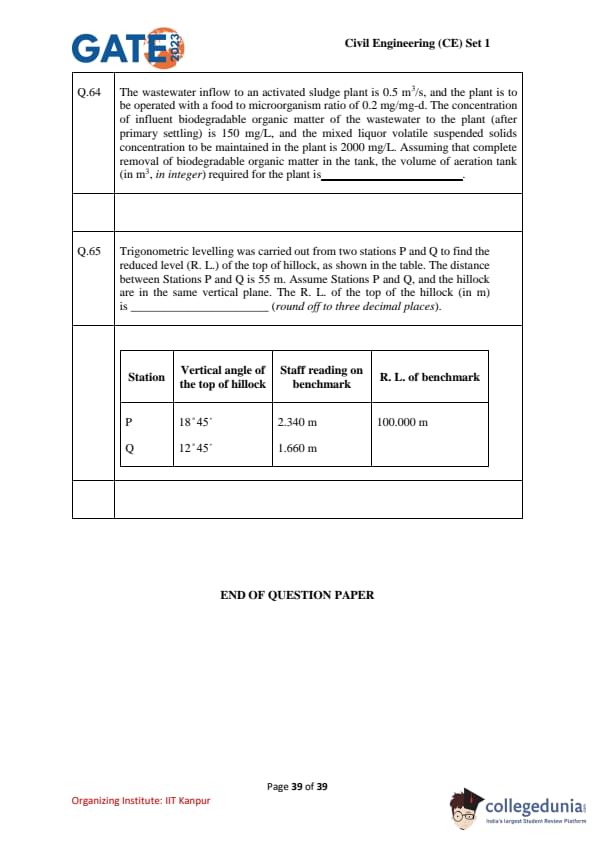
The wastewater inflow to an activated sludge plant is \(0.5\ m^3/s\), and the plant is to be operated with a food to microorganism ratio of \(0.2\ mg/mg-d\). The concentration of influent biodegradable organic matter (after primary settling) is \(150\ mg/L\), and the mixed liquor volatile suspended solids (MLVSS) to be maintained is \(2000\ mg/L\). Assuming complete removal of biodegradable organics in the tank, the volume of aeration tank (in m\(^3\), \textit{integer) required is _______.
Trigonometric levelling was carried out from two stations P and Q to find the reduced level (R.L.) of the top of hillock, as shown in the table. The distance between Stations P and Q is 55 m. Assume Stations P and Q, and the hillock are in the same vertical plane. The R.L. of the top of the hillock is ________ (round off to three decimal places).

View Solution
We are given the following data: \[ Distance between P and Q = 55 \, m \]
At Station P: \[ Vertical angle of the top of hillock = 18^\circ 45' \quad Staff reading on benchmark = 2.340 \, m \quad R.L. of benchmark = 100.000 \, m \]
At Station Q: \[ Vertical angle of the top of hillock = 12^\circ 45' \quad Staff reading on benchmark = 1.660 \, m \]
Using the formula for trigonometric levelling: \[ Height = Staff reading \times \tan(\theta) \]
Where:
- \(\theta\) is the vertical angle from the station to the top of the hillock.
- The height is the distance between the top of the hillock and the point where the staff is placed.
First, calculate the height from Station P: \[ h_P = 2.340 \times \tan(18^\circ 45') = 2.340 \times 0.337 = 0.787 \, m \]
Now, calculate the height from Station Q: \[ h_Q = 1.660 \times \tan(12^\circ 45') = 1.660 \times 0.225 = 0.374 \, m \]
Now, we calculate the R.L. of the top of the hillock: \[ R.L. of top of hillock = R.L. of benchmark + h_P - h_Q \] \[ = 100.000 + 0.787 - 0.374 = 137.500 \, m \]
\boxed{137.500 \, \text{m Quick Tip: In trigonometric levelling, always ensure the angles and distances are in the same plane to avoid errors in the final calculation of R.L.






























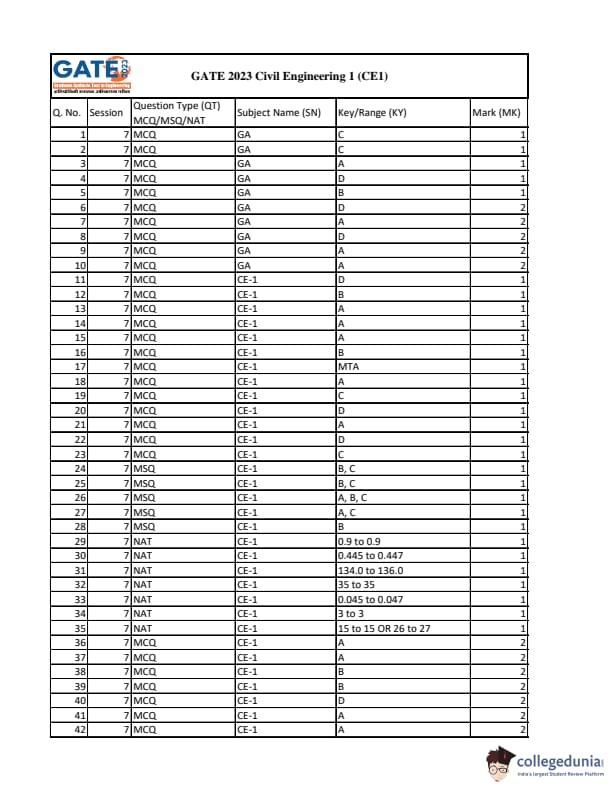
GATE 2023 CE Paper Analysis Shift 1
| Particulars | GATE 2023 CE Paper Analysis Forenoon Session |
|---|---|
| Number of MCQs | 34 |
| Number of NATs | 22 |
| Number of MSQs | 9 |
GATE 2023 CE Shift 1 Topic-wise Weighatge
| Subjects | Number of 1 Mark Questions | Number of 2 Mark Questions | Total Marks out of 100 |
|---|---|---|---|
| General Aptitude | 5 | 5 | 15 |
| Engineering Mathematics | 3 | 5 | 13 |
| Geotechnical Engg | 4 | 6 | 16 |
| Environmental Engg | 3 | 4 | 11 |
| Fluid Mechanics | 0 | 1 | 2 |
| OCF | 1 | 2 | 5 |
| Highway Engg | 2 | 2 | 6 |
| Surveying | 2 | 1 | 4 |
| Structural Analysis | 1 | 2 | 5 |
| Building Materials & CPM | 1 | 0 | 1 |
| Irrigation | 0 | 1 | 2 |
| Strength of Materials | 1 | 3 | 7 |
| Steel Structure | 2 | 1 | 4 |
| Hydrology | 1 | 2 | 5 |
| Concrete Structures | 2 | 1 | 4 |
| Engineering Mechanics | 1 | 0 | 1 |
| Total | 29 | 36 | 100 |
Also Check:





Comments