GATE 2023 Chemistry Question Paper PDF is available here for download. IIT Kanpur conducted GATE 2023 Chemistry exam on February 5, 2023 in the Afternoon Session from 02:30 PM to 05:30 PM. Students have to answer 65 questions in GATE 2023 Chemistry Question Paper carrying a total weightage of 100 marks. 10 questions are from the General Aptitude section and 55 questions are from Core Discipline.
GATE 2023 Chemistry Question Paper with Answer Key PDF
| GATE 2023 Chemistry Question Paper with Solutions PDF | Download PDF | Check Solutions |
GATE 2023 Chemistry Question Paper with Solutions
“I cannot support this proposal. My ______ will not permit it.”
View Solution
Step 1: The sentence implies a moral or ethical reason for not supporting the proposal. The word required should relate to inner moral sense.
Step 2: Option (A) conscious means being awake or aware, which does not fit the context.
Step 3: Option (B) consensus means general agreement, which is collective, not individual, hence incorrect.
Step 4: Option (C) conscience means moral sense of right and wrong, which perfectly fits the sentence.
Step 5: Option (D) consent means permission, which is not applicable here.
Thus, the correct word is conscience. Quick Tip: When filling blanks in context-based questions, check whether the word refers to individual moral reasoning, group agreement, awareness, or permission — this helps eliminate confusing similar words.
Courts : _____ : : Parliament : Legislature (By word meaning)
View Solution
Step 1: The relationship is: Parliament is the institution that represents the Legislature.
Step 2: Similarly, Courts represent the Judiciary.
Step 3: Hence, the correct word to complete the analogy is Judiciary.
Final Answer: \(\boxed{Judiciary}\). Quick Tip: For analogy-based word problems, always identify the relationship between the second pair and apply the same to the first pair.
What is the smallest number with distinct digits whose digits add up to 45?
View Solution
Step 1: The maximum sum of distinct digits is obtained by adding digits from 1 to 9:
\[ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. \]
Step 2: Therefore, the number must use all digits from 1 to 9 exactly once.
Step 3: To get the smallest number, arrange these digits in ascending order: \(123456789\).
Final Answer: \(\boxed{123456789}\). Quick Tip: When asked to form the smallest number with given digits, always arrange the digits in ascending order.
In a class of 100 students,
View Solution
Step 1: Total students = 100. Those who like at least one type of movie = \(100 - 30 = 70\).
Step 2: Let number of students who like comedy movies = \(x\).
Then students who like romantic movies = \(2x\).
Students who like both = 20.
Step 3: By inclusion-exclusion principle:
\[ (2x) + (x) - 20 = 70 \] \[ 3x - 20 = 70 \quad \Rightarrow \quad 3x = 90 \quad \Rightarrow \quad x = 30. \]
Step 4: So, number of students who like romantic movies = \(2x = 60\).
Final Answer: \(\boxed{60}\). Quick Tip: For set problems with overlapping groups, always apply the inclusion-exclusion principle: \( |A \cup B| = |A| + |B| - |A \cap B| \).
How many rectangles are present in the given figure?

View Solution
Step 1: Observe that every rectangle in the figure is a square (possibly tilted). There is one outer square (axis-aligned). Inside, the two families of diagonal lines (\(/\) and \(\backslash\)) form a lattice of tilted squares (diamonds).
Step 2: Count tilted squares:
\(1\) large central diamond.
\(4\) medium diamonds adjacent to the central one (top, right, bottom, left).
\(4\) small corner diamonds formed near the vertices of the outer square.
Step 3: Adding the axis-aligned outer square gives the total number of rectangles: \[ 1\ (outer) + 1\ (central) + 4\ (medium) + 4\ (small) = 10. \]
Hence, the figure contains \(\boxed{10}\) rectangles. Quick Tip: When counting rectangles in diagonal grids, note that all rectangles appear as tilted squares formed by intersections of two perpendicular families of parallel lines; count by size (large/medium/small) and then include any axis-aligned boundary squares.
Forestland is a planet inhabited by different kinds of creatures. Among other creatures, it is populated by animals all of whom are ferocious. There are also creatures that have claws, and some that do not. All creatures that have claws are ferocious.
Based only on the information provided above, which one of the following options can be logically inferred with certainty?
View Solution
Step 1: Translate statements into set relations. Let \(A\) be animals, \(F\) ferocious, and \(C\) creatures with claws. The statements imply \(A \subseteq F\) and \(C \subseteq F\). Also, there exist creatures with claws (i.e., \(C\neq \varnothing\)).
Step 2: Evaluate options.
(A) \(C \subseteq A\) is not implied; clawed creatures could be non-animals. Not certain.
(B) Says \(C \cap F^{c}\neq \varnothing\), contradicting \(C \subseteq F\). False.
(C) Also contradicts \(C \subseteq F\). False.
(D) Since \(C\neq\varnothing\) and \(C\subseteq F\), it follows that \(C \subseteq F\) implies \(F\) contains members from \(C\); hence \(\exists\) ferocious creatures with claws. True.
Thus, (D) is the only statement that follows with certainty. Quick Tip: When tackling syllogism-style questions, convert statements into set relations (\(\subseteq\), existence) and check each option against these relations for necessity or contradiction.
Which one of the following options represents the given graph?

View Solution
Step 1: Observe the symmetry of the graph. The function shown is symmetric about the \(y\)-axis, meaning it is an even function. Therefore, the function must involve \(|x|\) or \(x^2\).
Step 2: Eliminate odd functions. Option (B) \(f(x) = x 2^{-|x|}\) and (D) \(f(x) = x 2^{-x}\) are odd functions, not symmetric about the \(y\)-axis. So, these are not correct.
Step 3: Check behavior near \(x=0\). The graph touches the \(x\)-axis at \(x=0\). For \(f(x) = x^2 2^{-|x|}\), we have \(f(0) = 0^2 \cdot 2^0 = 0\), matching the graph.
Step 4: Growth and decay. For large \(|x|\), the exponential factor \(2^{-|x|}\) decays rapidly, and the function tends to \(0\). This matches the graph where values go to \(0\) as \(x \to \pm \infty\). The quadratic term \(x^2\) causes the "bell-like" rise near the origin, before decay sets in.
Thus, the correct representation is \(f(x) = x^2 2^{-|x|}\). Quick Tip: When identifying graphs: Check symmetry (even/odd functions). Verify behavior near \(x=0\). Analyze growth/decay for large \(|x|\). These help quickly eliminate wrong options.
Which one of the following options can be inferred from the given passage alone?
When I was a kid, I was partial to stories about other worlds and interplanetary travel. I used to imagine that I could just gaze off into space and be whisked to another planet.
[Excerpt from The Truth about Stories by T. King]
View Solution
Step 1: The passage uses the phrase "When I was a kid", indicating that the narrator is now reflecting back on childhood. This shows it is written from an adult’s perspective.
Step 2: The narrator recalls being partial to stories about other worlds and interplanetary travel. This is clearly a memory of past preferences.
Step 3: Option (A) is incorrect because it is not a child describing in the present but an adult reminiscing. Option (C) is not supported because there is no mention of “only in parts.” Option (D) makes a general claim beyond the passage.
Step 4: Hence, the correct inference is that it is an adult’s memory of what he or she liked as a child. Quick Tip: For inference questions: Focus on verb tense to identify whether it’s present or past reflection. Avoid adding assumptions not present in the passage. Choose the option that strictly follows the passage without generalization.
Out of 1000 individuals in a town, 100 unidentified individuals are covid positive. Due to lack of adequate covid-testing kits, the health authorities of the town devised a strategy to identify these covid-positive individuals. The strategy is to:
(i) Collect saliva samples from all 1000 individuals and randomly group them into sets of 5.(ii) Mix the samples within each set and test the mixed sample for covid.
(iii) If the test done in (ii) gives a negative result, then declare all the 5 individuals to be covid negative.
(iv) If the test done in (ii) gives a positive result, then all the 5 individuals are separately tested for covid.
Given this strategy, no more than _____ testing kits will be required to identify all the 100 covid positive individuals irrespective of how they are grouped.
View Solution
Step 1: The 1000 people are split into \(1000/5=200\) groups. Testing each pooled sample needs \(200\) kits.
Step 2: Any group that tests positive requires 5 additional tests (one per individual). To maximize the total number of tests regardless of grouping, distribute the 100 positives so that the number of positive groups is as large as possible—i.e., one positive in each group. This yields \(100\) positive groups.
Step 3: Additional individual tests \(= 100 \times 5 = 500\). Hence, maximum total kits required \[ 200 + 500 = 700. \]
Therefore, no more than \(\boxed{700}\) kits are needed. Quick Tip: For worst-case counts in pooled testing, spread positives across groups to maximize the number of positive pools (each triggers extra individual tests).
A \(100 cm \times 32 cm\) rectangular sheet is folded 5 times. Each time the sheet is folded, the long edge aligns with its opposite side. Eventually, the folded sheet is a rectangle of dimensions \(100 cm \times 1 cm\).
The total number of creases visible when the sheet is unfolded is _____.
View Solution
Step 1: Each fold aligns the long edge with its opposite side; hence every fold halves the shorter side (32 cm). After 5 folds the shorter side becomes \(32/2^5=1\) cm, matching the final size \(100\times1\) cm.
Step 2: Unfolding reveals creases perpendicular to the long edge that partition the 32-cm side into \(2^5=32\) equal strips of 1 cm each. The number of creases equals the number of partitions minus one: \(32-1=31\).
Therefore, the number of creases is \(\boxed{31}\). Quick Tip: Repeated halving into \(2^n\) equal parts produces \(2^n-1\) crease lines when fully unfolded.
The major product formed in the given reaction is: \[ TiCl_3(DME)_2 \quad Zn-Cu \quad DME, r.t. \quad \longrightarrow \quad 1,2-Dimethoxyethane. \]
View Solution
In this reaction, TiCl\(_3\)(DME)\(_2\) with Zn-Cu is used to reduce the aldehyde groups. This type of reaction typically results in the formation of 1,2-butanediol via a coupling reaction between two molecules of an aldehyde. The reaction conditions involve the use of DME as a solvent and mild room temperature conditions.
Thus, the major product formed in this case is 1,2-butanediol, corresponding to option (A). Quick Tip: TiCl\(_3\) and Zn-Cu are commonly used to couple aldehydes or ketones to form diols. The reaction type here involves coupling aldehydes to form a 1,2-diol product.
The compound which gives a fragment at \(m/z = 124 [M+H]^+\) is:

View Solution
The fragment at \(m/z = 124\) corresponds to a specific molecular weight, and by examining the structures of the compounds and their likely fragmentation patterns, Compound B matches the observed mass for the fragment ion at \(m/z = 124 [M+H]^+\). Quick Tip: In mass spectrometry, identifying the correct fragmentation pattern requires understanding the molecular structure and typical mass loss during ionization. Compounds with similar molecular weights can often yield different fragment ions based on their structural features.
The major product formed in the given reaction is

View Solution
The reaction involves a palladium-catalyzed transformation under the conditions given, which suggests that the product will likely result from a coupling reaction or reduction mechanism. Given that the functional groups and the provided conditions favor the hydrogenation or cyclization of the substrate, the major product is the one corresponding to the first structure (Option A), which matches the expected outcome based on the reaction type and conditions. Quick Tip: Palladium catalysts, especially \(Pd(PPh_3)_4\), are often used in hydrogenation reactions. The reaction typically leads to cyclization, forming a bicyclic structure in this case.
The major product formed when the \(\,o\)-(\(\mathrm{Me_3Si}\))-aryl triflate (a Kobayashi benzyne precursor) is treated with Ph–substituted cyclohexene in the presence of \(\mathrm{CsF}\) in \(\mathrm{CH_3CN}\) at r.t. is (A)–(D) as shown in the figure.

View Solution
Step 1: \(\mathrm{CsF}\) activates the \(o\)-silyl aryl triflate by forming a strong \(\mathrm{Si\!-\!F}\) bond and expelling \(\mathrm{OTf^-}\), generating benzyne (\(o\)-aryne).
Step 2: Benzyne reacts with alkenes bearing an allylic H via an ene reaction (not a Diels–Alder in this case). In the concerted TS, (i) the allylic \(\mathrm{C_{allyl}-H}\) migrates to one benzyne carbon, (ii) a new C–C bond forms between the allylic carbon and the other benzyne carbon, and (iii) the alkene shifts position.
Step 3: Regiochemistry is controlled by stabilization of the developing cationic character at the allylic carbon in the ene TS. Bond formation at the allylic carbon already substituted with Ph is favored because the benzylic/aryl group stabilizes the partial positive charge by resonance/induction. Thus the new aryl group (from benzyne) is introduced at the same carbon, giving a geminal diaryl center.
Step 4: The resultant product therefore bears two phenyl groups on the same allylic carbon with the C=C bond migrated within the cyclohexene ring—exactly the connectivity drawn in option (A). Alternatives (B) and (D) (1,3- or 1,2-diphenyl) arise from disfavored regiochemical courses, and (C) does not match the ene-reaction connectivity.
Quick Tip: \(o\)-Silyl aryl triflate + F\(^{-}\) \(\Rightarrow\) benzyne (Kobayashi conditions). With allylic H alkenes, expect an \(\textbf{ene reaction}\): H transfer + C–C bond formation + alkene migration. Choose the site that best stabilizes positive charge in the TS (often the \(\mathrm{Ph}\)-substituted allylic carbon) to predict geminal vs vicinal outcomes.
On irradiation using UV light (\(>300\) nm), compounds X and Y predominantly undergo which photochemical pathway? (Structures as shown in the figure)

View Solution
Step 1: Identify possibilities. Norrish type I = \(\alpha\)-cleavage next to \(C{=}O\) (acyl–\(\alpha\) bond scission). Norrish type II = intramolecular \(\gamma\)-H abstraction by the excited carbonyl oxygen through a six-membered transition state, giving a 1,4-biradical and alkene migration/fragmentation.
Step 2: Analyze \(X\). In \(X\), the carbonyl has a properly aligned \(\gamma\)-hydrogen on the side chain (tertiary/benzylic-like) and the conformation allows the classic six-membered cyclic abstraction. This strongly favors the Type II pathway over \(\alpha\)-cleavage.
Step 3: Analyze \(Y\). In \(Y\), the carbonyl is embedded such that an accessible \(\gamma\)-H is absent/misaligned (substitution places a quaternary/sterically hindered center at \(\gamma\)), suppressing the Type II abstraction. Aldehydes/ketones in such cases undergo facile \(\alpha\)-cleavage (Type I), giving acyl and \(\alpha\)-alkyl radicals.
Step 4: Hence \(X\) predominantly shows Norrish II, while \(Y\) undergoes Norrish I \(\Rightarrow\) option (B).
Quick Tip: Look for an accessible, properly aligned \(\gamma\)-H (six-membered TS) \(\Rightarrow\) Type II likely. If \(\gamma\)-H is missing or geometrically blocked, expect \(\alpha\)-cleavage \(\Rightarrow\) Type I. Aldehydes often favor Type I; bulky \(\gamma\)-substitution disfavors Type II.
The topicity relationship of \(H_a\) and \(H_b\) in X, Y and Z (as drawn in the figure) are, respectively,

View Solution
Step 1: Molecule X. The two hydrogens \(H_a\) and \(H_b\) lie on a carbon in a highly symmetric (meso/C\(_2\)) environment bearing identical \({HO-}\) and \({-CO2H}\) substituent sets on opposite sides. A \(C_2\) rotation superposes \(H_a\) and \(H_b\); replacing either gives the same molecule \(\Rightarrow\) homotopic.
Step 2: Molecule Y. In the bridged/aromatic framework, \(H_a\) and \(H_b\) are related by an improper/mirror operation: replacement of \(H_a\) versus \(H_b\) generates non-superposable mirror-image products, while the parent is achiral. Thus they are enantiotopic.
Step 3: Molecule Z. For the prochiral vinyl \({CH_2}\) adjacent to \({Cl}\), the two vinylic hydrogens are in an enantiotopic relationship (replacing one or the other creates enantiomeric \(E/R_e\) vs \(S_i\) labeled products). Hence enantiotopic.
Step 4: Collecting: \(X\) homotopic, \(Y\) enantiotopic, \(Z\) enantiotopic \(\Rightarrow\) option (B).
Quick Tip: \(\textbf{Homotopic:}\) related by a symmetry element of the molecule (e.g., \(C_2\), mirror plane); substitution gives identical products. \(\textbf{Enantiotopic:}\) substitution gives enantiomers (common for prochiral \({CH2}\) next to a stereogenic plane/center). \(\textbf{Diastereotopic:}\) substitution gives diastereomers; arises when the environment is already chiral (no symmetry relating the two sites).
Compound \(\mathbf{P}\) was prepared based on a four-component reaction at room temperature in methanol. The required starting materials for the synthesis are (structure of \(\mathbf{P}\) shown).

View Solution
Step 1: Identify the reaction type. Compound \(\mathbf{P}\) clearly bears the hallmark structure of an Ugi four-component reaction (Ugi-4CR) product, which arises from the condensation of: \[ Amine + Aldehyde + Carboxylic Acid + Isocyanide. \]
Step 2: Match fragments.
The indole-ethylamine side chain in \(\mathbf{P}\) corresponds to tryptamine, i.e., 2-(1H-indol-3-yl)ethylamine.
The benzylic substituent (–CHPh) in the central scaffold must originate from benzaldehyde (PhCHO).
The acyl group in the final amide unit comes from the carboxylic acid, which is acetic acid (MeCO\(_2\)H).
The distal N-substituent is derived from the isocyanide, here cyclohexyl isocyanide.
Step 3: Rationalize the option. Although isocyanides are neutral species, the problem statement’s option (A) represents cyclohexyl isocyanide with a cationic drawing. Since the structural mapping of the fragments in compound \(\mathbf{P}\) exactly matches (A), it must be considered the correct answer in this context.
Step 4: Conclusion. Therefore, the correct set of four building blocks is given in option (A). Quick Tip: The Ugi reaction is a powerful multicomponent method to rapidly assemble peptide-like scaffolds. The amine provides the \(-NH\)-link, the aldehyde contributes the substituent on the \(\alpha\)-carbon, the carboxylic acid contributes the acyl group, and the isocyanide provides the distal N-substituent. Always map each fragment of the product back to the corresponding starting material to verify correctness.
The major product formed in the following reaction is \(\; \mathrm{nBu_3SnH,\ AIBN,\ C_6H_6,\ heat}\)

View Solution
Step 1: Radical generation under \(\mathrm{nBu_3SnH/AIBN}\).
Thermal initiation gives the \(\mathrm{Bu_3Sn\cdot}\) radical, which abstracts iodine from the substrate to produce a carbon radical at the iodo-substituted carbon:
\[ \mathrm{R{-}CH{-}I} \xrightarrow[AIBN, heat]{\mathrm{Bu_3Sn\cdot}} \mathrm{R{-}CH\cdot} + \mathrm{Bu_3SnI}. \]
Step 2: Intramolecular radical addition follows Baldwin’s rules.
The tether bears a terminal alkene; the carbon radical undergoes 5-exo-trig cyclization onto the alkene to form a new \(\mathrm{C{-}C}\) bond and a radical at the adjacent carbon. According to Baldwin’s rules for radical cyclizations, \(5-exo-trig \gg 6-endo-trig\); thus formation of a \(\mathrm{THF}\)-like five-membered O-heterocycle is preferred.
Step 3: Stereochemical outcome (chairlike transition state).
The cyclohexane adopts a chair; the radical approaches the alkene from the less hindered face, placing the newly formed bond in a pseudo-equatorial orientation. This minimizes A\(^{1,3}\) strain and gives the trans relationship between the substituents depicted in option (B).
Step 4: Radical termination (hydrogen transfer).
The newly formed carbon radical is quenched by \(\mathrm{nBu_3SnH}\): \(\mathrm{C\cdot + Bu_3SnH \to C{-}H + Bu_3Sn\cdot}\), delivering the saturated product corresponding to (B). Quick Tip: Under \(\mathrm{nBu_3SnH/AIBN}\), intramolecular \(\mathrm{C{-}C}\) bond formation usually follows Baldwin’s rules: \(5\)-exo-trig \(>\) \(6\)-endo-trig. For chair substrates, prefer transition states that place forming bonds pseudo-equatorial to minimize A\(^{1,3}\) strain—this often dictates the trans product. Tin hydride steps: (i) halogen abstraction to make a radical, (ii) cyclization, (iii) H-atom transfer to cap the radical.
The reaction of Ph\(_3\)PCl\(_2\) with PhNH\(_2\) primarily produces
View Solution
Step 1: The compound given is Ph\(_3\)PCl\(_2\), which is triphenylphosphine dichloride. It has the structure where phosphorus is bonded to three phenyl groups and two chlorides.
Step 2: When Ph\(_3\)PCl\(_2\) reacts with a primary aromatic amine (PhNH\(_2\)), nucleophilic substitution takes place. The amine nitrogen attacks the phosphorus center, leading to displacement of chloride ions.
Step 3: After elimination of two molecules of HCl, a double bond between P and N is formed, yielding a phosphinimine derivative.
\[ Ph_3PCl_2 + PhNH_2 \;\;\longrightarrow\;\; Ph_3P=NPh + 2HCl \]
Step 4: Thus, the primary product of this reaction is \(Ph_3P=NPh\), which corresponds to option (A). Quick Tip: Triphenylphosphine dichloride reacts with amines to give phosphinimines by elimination of HCl. Remember that the strong nucleophilicity of amines allows them to attack electrophilic phosphorus centers effectively. Phosphinimines are an important class of organophosphorus compounds with P=N double bonds.
Formation of [M(en)\(_3\)]\(^{2+}\) from [M(H\(_2\)O)\(_6\)]\(^{2+}\) and three equivalents of ethylenediamine (en) is LEAST favored when M is
View Solution
Step 1: Apply the Irving--Williams series for M\(^{2+}\) (3d) complexes.
For high-spin octahedral divalent first-row transition metals, the thermodynamic stabilities of complexes (including chelates like en) follow:
\[ Mn^{2+} < Fe^{2+} < Co^{2+} < Ni^{2+} < Cu^{2+} > Zn^{2+}. \]
Thus, among Co, Ni, Cu, and Fe, the least stable chelate is for Fe\(^{2+}\).
Step 2: Rationalize using LFSE and additional stabilization.
The chelate effect favors \([M(en)_3]^{2+}\) for all M, but relative stabilities are governed by metal-dependent factors. Approximate octahedral LFSE (high spin) values:
\[Fe^{2+} (d^6\ HS) : -0.4\,\Delta_o,\] \[Co^{2+} (d^7\ HS) : -0.8\,\Delta_o,\] \[Ni^{2+} (d^8) : -1.2\,\Delta_o,\] \[Cu^{2+} (d^9) : JT stabilization (very strong).\]
Smaller (less negative) LFSE for Fe\(^{2+}\) leads to a less stable octahedral complex than Co\(^{2+}\) and Ni\(^{2+}\). Cu\(^{2+}\) is exceptionally stabilized overall despite Jahn--Teller distortion, consistent with the Irving--Williams series.
Step 3: Conclusion.
Therefore, the formation of \([M(en)_3]^{2+}\) from \([M(H_2O)_6]^{2+}\) is least favored when \(M=Fe\). Quick Tip: - For first-row M\(^{2+}\) octahedral complexes, remember the Irving--Williams order: Mn \(<\) Fe \(<\) Co \(<\) Ni \(<\) Cu \(>\) Zn.
- Chelate effect increases stability for all metals, but comparative stability still follows this metal-dependent trend.
- Use LFSE (and Jahn--Teller for d\(^9\)) to rationalize deviations and strengths.
Wacker oxidation of alkenes is catalyzed by a combination of
View Solution
Step 1: The Wacker oxidation is an industrially important reaction that converts alkenes (like ethylene) into aldehydes or ketones by oxidation. For example, ethylene gets oxidized to acetaldehyde.
Step 2: The reaction proceeds with the help of a palladium catalyst. Pd(II) species first coordinates to the alkene and facilitates the insertion of water, forming an alcohol group.
Step 3: During the process, Pd(II) gets reduced to Pd(0). To regenerate Pd(II) from Pd(0), a co-catalyst is needed. This role is played by Cu(II), which oxidizes Pd(0) back to Pd(II).
Step 4: Thus, the overall catalytic system requires both Pd(II) and Cu(II). Without Cu(II), the cycle would stop because Pd(0) would accumulate and the oxidation would not proceed efficiently.
\[ {CH2=CH2 + 1/2 O2 + H2O ->[PdCl2/CuCl2] CH3CHO} \]
Hence, the correct catalytic combination is Pd(II) and Cu(II). Quick Tip: The Wacker process is widely used in industry to manufacture acetaldehyde from ethylene. Always remember: Pd(II) is the main catalyst, while Cu(II) is a co-catalyst to regenerate Pd(II) from Pd(0). Oxidizing conditions are maintained using molecular oxygen in the reaction medium.
For the conversion of [Pt(L)Cl\(_3\)]\(^-\) to trans-[Pt(L)Cl\(_2\)(H\(_2\)O)], the trans-effect is LEAST when the ligand L is
View Solution
Step 1: Recall the trans-effect. In square-planar Pt(II) complexes, ligands differ in their ability to accelerate substitution of the ligand positioned trans to them (kinetic trans-effect). Strong \(\pi\)-acceptors and soft donors show a large trans-effect; hard, weak \(\sigma\)-donors show a small one.
Step 2: Rank the given ligands qualitatively. \[ (weak)\quad H_2O \;<\; NH_3 \;<\; DMSO (via S) \;<\; C_2H_4 \quad (strong) \]
\(\mathbf{H_2O}\): very weak \(\sigma\)-donor (hard base) \(\Rightarrow\) least trans-effect.
\(\mathbf{NH_3}\): slightly stronger \(\sigma\)-donor than water \(\Rightarrow\) larger effect than H\(_2\)O.
\(\mathbf{DMSO}\) (S-bound): softer donor, moderate trans-effect.
\(\mathbf{C_2H_4}\): \(\pi\)-acceptor olefin, strong trans-effect.
Step 3: Conclusion. Since H\(_2\)O has the smallest trans-effect in this set, the conversion will be slowest when \(L = H_2O\). Hence, option (A) is correct. Quick Tip: A handy fragment of the trans-effect series: \(CO, C_2H_4 \gg PR_3 \gg I^- \gg Br^- \gg Cl^- \gg NH_3 \gtrsim H_2O\). When unsure, remember: hard, weak \(\sigma\)-donors (e.g., H\(_2\)O) \(\Rightarrow\) least trans-effect; soft/\(\pi\)-acceptor ligands \(\Rightarrow\) strong trans-effect.
The tetracoordinated copper center in the oxidized and reduced forms of plastocyanin exhibits longest bond with
View Solution
Step 1: Structure of plastocyanin.
Plastocyanin is a blue copper protein with a \(Cu^{2+/+}\) center coordinated by two histidine imidazoles (N donors), one cysteine thiolate (S), and one methionine thioether (S). This gives a distorted tetrahedral geometry around the Cu center.
Step 2: Bonding considerations.
- The cysteine thiolate provides a strong covalent bond with Cu due to strong \(\pi\)-donation.
- The histidine N donors also form strong bonds.
- The methionine S is a weak thioether donor and interacts more weakly with the copper center.
Step 3: Oxidized vs reduced state.
In both oxidation states (\(Cu^{2+}\) and \(Cu^{+}\)), the \(\mathrm{Cu{-}S_{Met}}\) bond remains the longest bond because of weak donation from methionine compared to cysteine. The geometry is often described as “entatic state” where bond lengths are tuned for efficient electron transfer, but still the Cu–S(Met) bond is the longest in both states.
Step 4: Conclusion.
Therefore, in both oxidized and reduced plastocyanin, the longest bond is with methionine-S.
\[ \boxed{Answer: (D) methionine-S and methionine-S, respectively} \] Quick Tip: - In blue copper proteins like plastocyanin, the axial Cu–S(Met) bond is always longer than the equatorial Cu–S(Cys) and Cu–N(His) bonds.
- Remember: \(\mathrm{Cys{-}S}\) is strong, \(\mathrm{Met{-}S}\) is weak.
- The entatic state enforces a geometry optimal for fast electron transfer, but the longest bond remains Cu–S(Met).
The packing efficiency (in %) of spheres for a body-centered cubic (bcc) lattice is approximately
View Solution
Step 1: Relation between atomic radius and unit cell edge in BCC
In a body-centered cubic lattice, atoms touch each other along the body diagonal. The body diagonal has length \( \sqrt{3}a \), where \(a\) is the edge length.
Along the body diagonal, we have 2 atomic radii from corner atoms and 2 radii from the center atom, i.e. total \(4r\). Hence, \[ \sqrt{3}a = 4r \quad \Rightarrow \quad a = \frac{4r}{\sqrt{3}} \]
Step 2: Number of atoms per unit cell in BCC
A BCC unit cell contains 2 atoms (8 corners \(\times \frac{1}{8} = 1\), plus 1 body-centered atom).
Step 3: Volume occupied by atoms in the unit cell
The volume of 1 atom = \(\frac{4}{3}\pi r^3\).
For 2 atoms, total volume of spheres = \[ V_{atoms} = 2 \times \frac{4}{3}\pi r^3 = \frac{8}{3}\pi r^3 \]
Step 4: Volume of the unit cell
\[ V_{cell} = a^3 = \left(\frac{4r}{\sqrt{3}}\right)^3 = \frac{64r^3}{3\sqrt{3}} \]
Step 5: Packing efficiency
\[ \eta = \frac{V_{atoms}}{V_{cell}} \times 100 = \frac{\frac{8}{3}\pi r^3}{\frac{64r^3}{3\sqrt{3}}} \times 100 = \frac{\pi \sqrt{3}}{8} \times 100 \]
\[ \eta \approx 0.680 \times 100 = 68% \]
Hence, the packing efficiency of a BCC lattice is approximately 68%. Quick Tip: Packing efficiency for SC (simple cubic) = 52%. Packing efficiency for BCC = 68%. Packing efficiency for FCC/HCP = 74% (maximum possible for identical spheres).
The magnitudes of CFSE in \([\mathrm{M}(\mathrm{H}_2\mathrm{O})_6]^{n+}\) for Mn and Fe ions satisfy the relations
View Solution
Step 1: \(\mathrm{H_2O}\) is a weak-field ligand, so octahedral complexes are high-spin. Compute CFSE using \[ CFSE = (-0.4\Delta_o)\,n_{t_{2g}} + (0.6\Delta_o)\,n_{e_g}. \]
Step 2: Determine \(d^n\) counts and high-spin configurations.
\[ \mathrm{Mn}^{2+}: d^5 \Rightarrow t_{2g}^3e_g^2 \ \Rightarrow \ CFSE=3(-0.4)+2(0.6)=0, \]
\[ \mathrm{Mn}^{3+}: d^4 \Rightarrow t_{2g}^3e_g^1 \ \Rightarrow \ CFSE=3(-0.4)+1(0.6)=-0.6\Delta_o, \]
\[ \mathrm{Fe}^{2+}: d^6 \Rightarrow t_{2g}^4e_g^2 \ \Rightarrow \ CFSE=4(-0.4)+2(0.6)=-0.4\Delta_o, \]
\[ \mathrm{Fe}^{3+}: d^5 \Rightarrow t_{2g}^3e_g^2 \ \Rightarrow \ CFSE=0.\]
Step 3: Compare magnitudes. \(|CFSE|\) values: \(\mathrm{Mn}^{2+}=0\), \(\mathrm{Mn}^{3+}=0.6\Delta_o\), \(\mathrm{Fe}^{2+}=0.4\Delta_o\), \(\mathrm{Fe}^{3+}=0\). Hence, \[ \mathrm{Mn}^{2+} < \mathrm{Mn}^{3+} \quad and \quad \mathrm{Fe}^{2+} > \mathrm{Fe}^{3+}. \]
Therefore, option (C) is correct. Quick Tip: For high-spin octahedral complexes: \(d^5 \Rightarrow CFSE=0\); \(d^4 \Rightarrow 0.6\Delta_o\) (magnitude); \(d^6 \Rightarrow 0.4\Delta_o\). With weak-field ligands (e.g., H\(_2\)O), assume high spin unless stated otherwise.
The organometallic catalyst for the following transformation is (intramolecular olefin closure giving a cyclohexene and ethylene, i.e., ring-closing metathesis):
View Solution
Step 1: Identify the reaction manifold.
The substrate bears a terminal alkene tether that cyclizes to a cyclohexene with concurrent formation of \(\mathrm{C_2H_4}\). Formation of ethylene as a by-product and construction of a new internal C=C by intramolecular exchange of alkylidenes is diagnostic of ring-closing metathesis (RCM).
Step 2: Match to the appropriate catalyst class.
RCM is catalyzed by \(\mathrm{Ru}\)-alkylidene (Grubbs/Grubbs–Hoveyda) complexes. The classic first-generation Grubbs' catalyst, \(\mathrm{RuCl_2(=CHPh)(PCy_3)_2}\), mediates metathesis to give cyclohexene and releases ethylene, exactly as depicted. Hence option (A).
Step 3: Exclude the other options.
- (B) Wilkinson's catalyst \(\mathrm{RhCl(PPh_3)_3}\) promotes hydrogenation/isomerization of alkenes, not olefin metathesis.
- (C) \(\mathrm{HCo(CO)_4}\) is a hydroformylation catalyst for adding \(\mathrm{CHO}\) under CO/H\(_2\).
- (D) \([\mathrm{RhI(CO)_2}]^{-}\) is associated with carbonylation chemistry (e.g., acylations), not C=C metathesis. Quick Tip: If a transformation forms a new ring alkene and expels \(\mathrm{C_2H_4}\), think \(\textbf{RCM}\) \(\Rightarrow\) \(\mathrm{Ru}\)-alkylidene (Grubbs/Hoveyda) catalyst. Wilkinson's = hydrogenation; \(\mathrm{HCo(CO)_4}\) = hydroformylation; Rh carbonyl/iodide = carbonylation.
Point group of naphthalene \(C_{10}H_8\) is
View Solution
Step 1: Naphthalene is a polycyclic aromatic hydrocarbon consisting of two fused benzene rings. Its structure is planar and symmetric.
Step 2: To determine its point group, we analyze symmetry elements:
It has a principal \(C_2\) axis along the long axis of the molecule.
Two additional \(C_2\) axes are present perpendicular to the principal axis (orthogonal directions).
It possesses a horizontal mirror plane (\(\sigma_h\)) due to its planarity.
It also has inversion symmetry (\(i\)).
Step 3: The presence of three mutually perpendicular \(C_2\) axes and inversion center (\(i\)) characterizes the \(D_{2h}\) point group.
Therefore, the point group of naphthalene is \(D_{2h}\). Quick Tip: Aromatic planar molecules like benzene belong to \(D_{6h}\). Naphthalene, due to reduced symmetry compared to benzene, falls under \(D_{2h}\). Always check for: principal axis, perpendicular axes, inversion center, and mirror planes.
The \(\textbf{INCORRECT}\) statement is
View Solution
Step 1: Statement (A) is correct. The zero-point energy of a quantum harmonic oscillator is \(\tfrac{1}{2}h\nu\).
Step 2: Statement (B) is correct. The energy of a rigid rotor is given by \[ E_J = \frac{h^2}{8\pi^2 I} J(J+1) \]
where \(I\) is the moment of inertia. Clearly, \(E \propto \tfrac{1}{I}\).
Step 3: Statement (C) is incorrect. The Li\(^ {2+}\) ion is a hydrogen-like species (one electron system with \(Z=3\)). The Schrödinger equation for hydrogen-like atoms can be solved exactly. Hence, this statement is false.
Step 4: Statement (D) is correct. The total angular momentum of an atom is indeed the sum of orbital (\(L\)) and spin (\(S\)) angular momenta: \(\vec{J} = \vec{L} + \vec{S}\).
Thus, the incorrect statement is (C). Quick Tip: Hydrogen-like ions (\(H, He^+, Li^{2+}, Be^{3+}\), etc.) are exactly solvable in quantum mechanics. Multi-electron atoms cannot be solved exactly due to electron–electron repulsion; approximations are used. Always recall: Zero-point energy for a harmonic oscillator = \(\tfrac{1}{2} h\nu\).
For an ideal gas, the molecular partition function in the canonical ensemble, that is proportional to the system volume (V), is the
View Solution
Step 1: Recall definition. The molecular partition function is the product of contributions from translational, rotational, vibrational, and electronic motions: \[ q = q_{trans} \cdot q_{rot} \cdot q_{vib} \cdot q_{elec}. \]
Step 2: Translational partition function. For a particle in a box of volume \(V\), \[ q_{trans} = \left( \frac{2\pi m k_B T}{h^2} \right)^{3/2} V. \]
Thus, it is directly proportional to system volume \(V\).
Step 3: Others. Rotational, vibrational, and electronic partition functions depend only on temperature and energy-level spacings, not on system volume.
Conclusion: The translational partition function is the one proportional to \(V\). Quick Tip: Partition function separates into translational, rotational, vibrational, electronic parts. Only translational motion depends on system volume; others depend on temperature and level spacings.
Assertion (S): The total angular momentum for light atoms (low atomic number) is obtained by Russell–Saunders coupling, whereas \(jj\)-coupling is used for heavy atoms (high atomic number).
Reasoning (R): The spin–orbit interactions are weak in light atoms (low atomic number) and strong in heavy atoms (high atomic number).
The correct option is
View Solution
Step 1: Understand coupling schemes.
- In light atoms: Spin–orbit interaction is weak compared to electrostatic interactions, so orbital angular momenta first couple (\(L\)), spins couple (\(S\)), then total \(J = L+S\) is formed. This is Russell–Saunders (\(LS\)) coupling.
- In heavy atoms: Spin–orbit interaction is strong, so each electron’s \(l_i\) couples with \(s_i\) to form \(j_i\). Then, total \(J\) is the vector sum of individual \(j_i\). This is \(jj\)-coupling.
Step 2: Evaluate assertion and reason.
- Assertion (S): Correct.
- Reason (R): Correct, because the weak spin–orbit coupling in light atoms vs strong in heavy atoms explains the choice of coupling scheme.
Step 3: Logical connection. Since R correctly explains why S is true, option (A) is correct. Quick Tip: For light atoms (\(Z\) small): Russell–Saunders coupling applies (\(LS\)-coupling). For heavy atoms (\(Z\) large): \(jj\)-coupling dominates due to strong spin–orbit interactions. Remember: strength of spin–orbit interaction \(\propto Z^4\).
The acetolysis product(s) of the given reaction (solvolysis of the benzylic tosylate in AcOH) is(are)

View Solution
Step 1: Ionization and anchimeric assistance.
In \(\mathrm{AcOH}\), the benzylic tosylate undergoes solvolysis. Departure of \(\mathrm{OTs^-}\) generates a benzylic cation that is anchimerically assisted by the adjacent phenyl ring to form a bridged phenonium intermediate. This “neighboring-group participation” shields one face of the cationic center.
Step 2: Regio-/stereochemical capture.
Nucleophilic attack by \({AcO^-}\) occurs by anti opening of the phenonium bridge at the reacting carbon. Anti opening gives overall inversion at the substitution center (SN2-like outcome), while the other stereocenter—whose bonds are not broken—retains its configuration.
Step 3: Products formed.
Therefore, the acetolysis furnishes the two diastereomers that both reflect inversion at the reacting center (attack from the two accessible conformers), corresponding to options (A) and (C). The alternatives (B) and (D) depict retention at the reacting center and are not favored under anchimeric assistance.
\[ \boxed{Anchimeric assistance by Ph \Rightarrow\ anti attack and inversion at the benzylic center \Rightarrow\ (A) and (C).} \] Quick Tip: Benzylic solvolysis next to an aryl group often proceeds via a \(\textbf{phenonium}\) ion; nucleophiles open the bridge anti, giving net inversion at that carbon. Stereocenters not involved in bond making/breaking retain configuration. When options show pairs, look for “inversion vs retention” at the reacting center to decide.
Product(s) formed in the given reaction is(are):

View Solution
Step 1: Base generates a neighboring alkoxide.
\({MeO^-}\) deprotonates the free vicinal \({3-OH}\) to give the C-3 alkoxide. Intramolecular attack of this alkoxide on the adjacent tosylate-bearing C-2 proceeds by \(\mathrm{S_N2}\) with inversion at C-2, expelling \({TsO^-}\). This produces a \(2,3\)-anhydrosugar (epoxide across C-2/C-3). Depending on the chair conformer adopted at the moment of attack, two equivalent drawings of the same \(2,3\)-epoxide connectivity are obtained (depicted as (A) and (B)).
Step 2: Competing neighboring-group participation by the ring oxygen.
Under strongly basic, intramolecularly favored conditions, the endocyclic ring oxygen can also act as a neighboring nucleophile and attack C-2, giving a \(1,2\)-epoxide fused to the ring (a \(1,2\)-anhydrosugar). This pathway corresponds to structure (C).
Step 3: Why (D) is not chosen.
Direct intermolecular substitution by \({MeO^-}\) at C-2 to furnish a simple \(2\)-\({OMe}\) product (D) is disfavored relative to the much faster intramolecular cyclizations that give epoxides. In basic methanol, the epoxide-opening by \({MeO^-}\) is slower and requires additional conditions; thus the epoxide products (A/B/C) are the observed outcomes.
Hence, the reaction yields the epoxides in (A), (B), and (C), not the solvolysis product (D). Quick Tip: Vicinal \({RO^-}\) adjacent to \({R-OTs}\) prefers intramolecular \(\mathrm{S_N2}\) \(\Rightarrow\) \({epoxide}\) (anhydrosugar) formation. Under basic conditions, epoxide formation (intramolecular) usually outcompetes intermolecular substitution by external nucleophiles. In carbohydrate scaffolds, both \(2,3\)- and \(1,2\)-anhydrosugars can arise via neighboring-group participation from \({O3^-}\) and the ring oxygen, respectively.
The choice(s) that correctly identify radioisotopes (P, Q, R, S) shown in the following nuclear reaction is(are):
\[ ^{60}_{28}Ni + \alpha \;\; \longrightarrow \;\; P \; (unstable) \] \[ P \;\longrightarrow\; n + Q, \qquad P \;\longrightarrow\; 2n + R, \qquad P \;\longrightarrow\; p + n + S \]
View Solution
Step 1: Determine \(P\). Add mass and atomic numbers: \[ ^{60}_{28}Ni + ^{4}_{2}He \Rightarrow A=60+4=64,\; Z=28+2=30 \Rightarrow P=\,^{64}_{30}Zn. \]
Thus (A) is correct.
Step 2: First decay channel (\(n+Q\)). Emission of one neutron keeps \(Z\) the same and reduces \(A\) by 1: \[ ^{64}_{30}Zn \rightarrow n + \,^{63}_{30}Zn (=Q). \]
So (B) is correct.
Step 3: Second decay channel (\(2n+R\)). Emission of two neutrons keeps \(Z=30\) and reduces \(A\) to 62, hence \[ R = \,^{62}_{30}Zn, \]
not \(^{62}_{29}Cu\). Therefore option (C) is false.
Step 4: Third decay channel (\(p+n+S\)). Emission of a proton and a neutron reduces \(A\) by 2 and \(Z\) by 1: \[ ^{64}_{30}Zn \rightarrow p + n + \,^{62}_{29}Cu (=S), \]
so (D) is correct. Quick Tip: In nuclear equations, conserve both mass number \(A\) and atomic number \(Z\) for each channel. Neutron emission: \(A \downarrow 1\), \(Z\) unchanged. ; Proton emission: \(A \downarrow 1\), \(Z \downarrow 1\). Use these bookkeeping rules to test each proposed isotope quickly.
For the Lindemann–Hinshelwood mechanism of gas phase unimolecular reactions, the true statement(s) is(are)
View Solution
Step 1: Nature of species that show unimolecular behavior.
The Lindemann–Hinshelwood (L–H) scheme explains unimolecular reactions such as isomerizations and decompositions in the gas phase. Energy randomization within an activated molecule requires multiple internal degrees of freedom; therefore it is typically valid for polyatomic (\(\ge 3\)-atom) molecules. Hence statement (A) is true.
Step 2: Elementary steps in the L–H mechanism.
The mechanism proceeds via:
\[ \mathrm{A + M [k_{-1}]{k_1} A^{*} + M} \quad (bimolecular activation/deactivation) \] \[ \mathrm{A^{*} \xrightarrow{k_2} Products} \quad (unimolecular decomposition) \]
Thus, it does involve bimolecular elementary steps (A + M), so (B) is true.
Step 3: Pressure dependence of the overall rate law.
At low pressure, activation collisions are infrequent, and the rate is proportional to \([A][M]\), i.e., second order. Hence (C) is true.
At high pressure, rapid activation makes decomposition of \(A^{*}\) rate-determining, giving a first-order overall rate. Therefore (D) is false.
\[ \boxed{True statements: A, B, and C.} \] Quick Tip: L–H = bimolecular activation (A + M) followed by unimolecular breakdown (A* → P). Low \(p\): rate \(\propto [A][M]\) (2nd order); high \(p\): rate \(\propto [A]\) (1st order). Polyatomic molecules (\(\geq\) 3 atoms) efficiently redistribute vibrational energy needed for unimolecular decay.
The calculated magnetic moment of \([Ce(NO_3)_5]^{2-}\) is _____ BM (rounded off to two decimal places).
(Given: atomic number of Ce is 58)
View Solution
Step 1: Determine oxidation state of Ce.
The complex is \([Ce(NO_3)_5]^{2-}\). Each nitrate group (\({NO3^-}\)) has a charge of \(-1\). With 5 nitrates, total = \(-5\). The overall charge is \(-2\). Let Ce oxidation state = \(x\).
\[ x + (-5) = -2 \quad \Rightarrow \quad x = +3 \]
So Ce is in +3 oxidation state.
Step 2: Write electronic configuration.
Cerium (Z = 58): ground state = [Xe] \(4f^1 5d^1 6s^2\).
For Ce\(^ {3+}\): remove 3 electrons (first from 6s and 5d). Configuration = [Xe] \(4f^1\).
Thus, Ce\(^ {3+}\) has 1 unpaired electron.
Step 3: Apply spin-only formula for magnetic moment.
The spin-only magnetic moment is: \[ \mu = \sqrt{n(n+2)} \ BM \]
where \(n =\) number of unpaired electrons.
Here, \(n = 1\).
\[ \mu = \sqrt{1(1+2)} = \sqrt{3} = 1.732 \]
However, for lanthanides, orbital contribution is significant. The experimental effective moment is calculated using the L-S coupling formula: \[ \mu_{eff} = g \sqrt{J(J+1)} \ BM \]
with \(g = 1 + \dfrac{J(J+1) + S(S+1) - L(L+1)}{2J(J+1)}\)
Step 4: Term symbol for Ce\(^ {3+}\) (4f\(^1\)).
- For \(4f^1\): \(L = 3\) (since f-orbital).
- \(S = \tfrac{1}{2}\) (1 unpaired electron).
- \(J = L - S = \tfrac{5}{2}\) (because for less than half-filled shells, \(J = |L - S|\)).
Step 5: Calculate Landé g-factor.
\[ g = 1 + \frac{J(J+1) + S(S+1) - L(L+1)}{2J(J+1)} \] \[ = 1 + \frac{\tfrac{5}{2}\left(\tfrac{7}{2}\right) + \tfrac{1}{2}\left(\tfrac{3}{2}\right) - 3(4)}{2 \times \tfrac{5}{2}\times \tfrac{7}{2}} \] \[ = 1 + \frac{\tfrac{35}{4} + \tfrac{3}{4} - 12}{2 \times \tfrac{35}{4}} = 1 + \frac{\tfrac{38}{4} - 12}{\tfrac{35}{2}} = 1 + \frac{9.5 - 12}{17.5} = 1 - \tfrac{2.5}{17.5} = 1 - 0.1428 = 0.857 \]
Step 6: Calculate magnetic moment.
\[ \mu_{eff} = g \sqrt{J(J+1)} = 0.857 \times \sqrt{\tfrac{5}{2}\left(\tfrac{7}{2}\right)} = 0.857 \times \sqrt{\tfrac{35}{4}} = 0.857 \times \sqrt{8.75} \] \[ = 0.857 \times 2.958 = 2.54 \ BM \]
Thus, the calculated magnetic moment = \(\boxed{2.54 \ BM}\). Quick Tip: For transition metals, the spin-only formula \(\mu = \sqrt{n(n+2)}\) BM is usually sufficient. For lanthanides (4f block), orbital contribution is significant, so one must use the L-S coupling approach. Ce\(^ {3+}\) (4f\(^1\)) has \(\mu_{eff} \approx 2.54\) BM, a classic textbook value.
A compound, \(\mathrm{C_{15}H_{16}O_2}\), has the following spectral data;
\(^1\)H NMR (ppm): 9.16 (s), 6.89 (d, \(J = 8\) Hz), 6.64 (d, \(J = 8\) Hz), 1.53 (s)
\(^ {13}\)C NMR (ppm): 154.7, 140.9, 127.1, 114.4, 40.7, 30.7
The structure of the compound is

View Solution
Step 1: Use formula and unsaturation. For \(\mathrm{C_{15}H_{16}O_2}\), the double-bond equivalents (DBE) are \[ DBE=\frac{2C+2-H}{2}=\frac{2(15)+2-16}{2}=8, \]
consistent with two benzene rings (8 DBE). Thus two phenyl rings plus two oxygens are likely.
Step 2: Interpret \(^1\)H NMR.
\(\delta 9.16\) (s) \(\Rightarrow\) strongly deshielded phenolic \(\mathrm{OH}\) (often a singlet). One signal suggests two equivalent OH groups.
\(\delta 6.89\) (d, \(J=8\) Hz) and \(\delta 6.64\) (d, \(J=8\) Hz) \(\Rightarrow\) AA'BB' pattern of a para-disubstituted phenyl ring; equivalence on both rings implies a symmetric molecule.
\(\delta 1.53\) (s) \(\Rightarrow\) six protons of two equivalent methyl groups on a quaternary carbon \(\big(\mathrm{C(Me)_2}\big)\).
Step 3: Interpret \(^ {13}\)C NMR.
154.7 ppm: phenolic \(\mathrm{C{-}O}\) ipso carbon.
140.9 ppm: quaternary aromatic carbon (para junction).
127.1, 114.4 ppm: substituted aromatic CH carbons of a para-disubstituted ring (two unique signals due to symmetry).
40.7 ppm: quaternary \(\mathrm{C(Me)_2}\) carbon.
30.7 ppm: methyl carbons of \(\mathrm{C(Me)_2}\).
Step 4: Match with options.
(B) and (C) would show OMe singlets near \(\sim 3.7\) ppm in \(^1\)H NMR, absent here \(\Rightarrow\) not possible.
(D) has additional ring–\(\mathrm{CH_3}\) groups that would give \(\sim 2.3\) ppm benzylic methyl signals, not observed.
(A) \(\mathrm{HO{-}Ph{-}C(Me)_2{-}Ph{-}OH}\) (bisphenol A core) fits all: symmetric para-disubstituted rings, two equivalent phenolic OH (\(\delta \sim 9\) ppm), and a \(\mathrm{C(Me)_2}\) singlet at \(\delta 1.5\) ppm, with matching \(^ {13}\)C shifts (30.7, 40.7 ppm).
Therefore, the structure is option (A). Quick Tip: Para-disubstituted benzene often shows two aromatic doublets (AA'BB') with \(J \approx 7\!-\!9\) Hz. A singlet near \(1.4\!-\!1.6\) ppm integrating to 6H commonly signals a gem-dimethyl \(\mathrm{C(Me)_2}\) attached to an sp\(^2\)/heteroatom center. Phenolic OH in non-deuterated solvents can appear broad/singlet near \(9\!-\!10\) ppm.
The major product formed in the given reaction sequence is

View Solution
Step 1: N-alkylation of potassium phthalimide.
The starting anion is the \(\mathrm{K^+}\) salt of phthalimide (\(\mathrm{PhthN^-K^+}\)). With the primary \(\alpha\)-bromoketone (phenacyl bromide derivative), it undergoes an S\(_\mathrm{N}2\) reaction to give an \(\mathbf{N}\)-phenacethyl phthalimide:
\[ {PhthN^- + PhCOCH2CH2Br -> PhthN-CH2CH2COPh}. \]
Step 2: Methoxide-promoted opening of the imide.
Under \(\mathrm{NaOMe/MeOH}\) (reflux), methoxide attacks one imide carbonyl to give a phthalamate (ring-opened imide) bearing an amide and a methyl imidate/ester. This step renders the carbonyls \(\beta\) to the benzylic methylene.
Step 3: Intramolecular condensation (cyclization).
Deprotonation at the \(\alpha\)-position of the phenacyl unit (\({PhCO–CH2–}\)) generates an enolate that intramolecularly attacks the amide carbonyl of the opened phthalamate, closing onto the aromatic ortho position of the phthal framework (acyl transfer to the ring–N). Subsequent proton transfers/tautomerization furnish the 2-hydroxy benzamide skeleton (quinazolinone‐type enol), with the \({C{=}O(Ph)}\) placed as in option (B).
Step 4: Regioselectivity.
Cyclization occurs onto the amide carbonyl that positions the benzyloyl group adjacent to the ring nitrogen, minimizing strain and maximizing conjugation with the aromatic ring; this gives the regiochemical outcome depicted in (B) rather than (A).
\[ \boxed{Major product is the hydroxybenzamide shown in option (B).} \] Quick Tip: Potassium phthalimide first alkylates (Gabriel-type), but under alkoxide reflux the imide opens, enabling intramolecular condensations. With phenacyl bromides, base triggers enolate formation and cyclization to hydroxybenzamide/quinazolinone-type products; regiochemistry follows the most stabilized conjugation path.
E and F in the given reaction scheme are determined for the photolysis (\(h\nu\)) of the fused N–O heterocycle bearing an N-phenyl group, followed by thermolysis (\(\Delta\)).

View Solution
Step 1: Photochemical N–O bond cleavage and acyl migration.
Irradiation (\(h\nu\)) of N–O heterocycles of the anthranil/benzisoxazole family promotes homolytic/diradical cleavage of the N–O bond to an acyl-nitrene/diradical that rapidly undergoes acyl migration (Bucherer–type/ESIPT assisted) to give the o-acyl anilide (ring-opened \({Ar–C(=O)–NPh}\)). This matches structure \(\mathbf{E}\) in option (A).
Step 2: Thermal recyclization to the N–O five-membered ring.
On heating (\(\Delta\)), the o-acyl anilide cyclizes intramolecularly (nucleophilic attack of the carbonyl oxygen on the adjacent imidoyl carbon followed by N–O bond formation) furnishing the 1,2-benzisoxazole skeleton shown as \(\mathbf{F}\) in option (A).
Step 3: Elimination of other options.
Options (C) and (D) propose oxime or hydroxylamine products for the photolysis step, which are not formed in this photorearrangement; the primary process is N–O cleavage with acyl transfer to the amide (not simple \({N–O}\) reduction/tautomerization). Option (B) shows an incorrect regiochemistry for the amide intermediate.
Therefore, \(\boxed{(A) is correct: E=o-acyl anilide (amide), F=benzisoxazole}\). Quick Tip: Anthranil/benzisoxazole systems often undergo photochemical N–O bond cleavage to amide (o-acyl anilide) intermediates. Subsequent heating typically promotes intramolecular recyclization to regenerate an N–O heterocycle (benzisoxazole). Remember: \(h\nu\) opens the ring (amide), \(\Delta\) closes it (isoxazole).
M and N in the given reaction scheme are (Simmons–Smith on the alkene, then OsO\(_4\)/NMO):

View Solution
Step 1: Simmons–Smith (CH\(_2\)I\(_2\), Zn–Cu). Allylic alcohols direct Simmons–Smith cyclopropanation to the same face as the OH (chelation of the carbenoid to the alcohol). Therefore, the double bond of the cyclohexene is converted to a fused cyclopropane (bicyclo[4.1.0]heptane framework) with the newly formed CH\(_2\) group syn to the existing OH. This matches the structure of M shown in option (C).
Step 2: OsO\(_4\)/NMO dihydroxylation. Osmium tetroxide adds syn across the C=C to give a vicinal cis-diol. Applying this to the substrate furnishes a triol in which the two newly introduced OH groups are on the same face (cis to each other), as depicted for N in option (C).
Step 3: Eliminate other options.
(A) and (D) depict cyclopropanation from the face anti to the directing OH (contrary to Simmons–Smith OH-directing effect).
(B) and (D) show triol stereochemistries inconsistent with syn dihydroxylation.
Hence, (C) correctly represents both M and N. Quick Tip: Simmons–Smith on allylic alcohols is \(\textbf{directed}\): the cyclopropane forms \(\textbf{syn}\) to the OH-bearing face. OsO\(_4\) (with NMO) adds \(\textbf{syn}\) to alkenes, giving \(\textbf{cis}\)-1,2-diols. Combine directing/syn rules to set relative configurations in sequences.
In the \(^{1}\)H NMR spectrum, multiplicity of the signal (bold and underlined H atom) in the following species is
(I) \([\mathbf{H}\mathrm{Ni(OPEt_3)_4}]^{+}\)
(II) \(\mathrm{Ph_2Si(Me)\mathbf{H}}\)
(III) \(\mathrm{PH_3}\)
(IV) \((\mathrm{Cp^*})_2\mathrm{Zr}\mathbf{H}_2\) (Cp\(^*\)=pentamethylcyclopentadienyl)
View Solution
Step 1: Complex \([\mathrm{HNi(OPEt_3)_4}]^{+}\).
The hydride couples to four equivalent \(^{31}\)P nuclei (\(I=\tfrac12\)). Thus \(n=4 \Rightarrow n{+}1=5\) lines: pentet.
Step 2: \(\mathrm{Ph_2Si(Me)H}\).
The Si–H proton is three bonds from the three equivalent \(\mathrm{Me}\) protons and shows \({}^{3}J_{H–H}\) coupling, giving a quartet. (Coupling to \(^{29}\)Si gives only weak satellite doublets because \(^{29}\)Si is 4.7% abundant.)
Step 3: \(\mathrm{PH_3}\).
Each H couples to one \(^{31}\)P nucleus (\(I=\tfrac12\)), giving a doublet. (H–H coupling is not observed among equivalent protons.)
Step 4: \((\mathrm{Cp^*})_2\mathrm{ZrH_2}\).
The two Zr–H hydrides are equivalent; equivalent protons do not split each other, hence the hydride resonance is a singlet.
\[ \boxed{I pentet, II quartet, III doublet, IV singlet \Rightarrow option (A).} \] Quick Tip: Equivalent nuclei never split each other. Metal–hydrides often couple strongly to X (P, Si) nuclei; check the number of equivalent heteronuclei (\(n{+}1\) rule). Low-abundance heteronuclei (e.g., \(^{29}\)Si) give satellite patterns; the main peak multiplicity is set by high-abundance neighbors.
The major product obtained by the treatment of \((\eta^{5}-\mathrm{C_5H_5})_2\mathrm{Ni}\) with Na/Hg in ethanol is
View Solution
Step 1: Reduction and ring‐slip.
Sodium amalgam reduces nickelocene to an anionic species that undergoes \(\eta^{5}\!\to\!\eta^{3}\) ring slip on one Cp ring.
Step 2: Protonation by ethanol.
The reduced, slipped ring is then protonated by \(\mathrm{EtOH}\), converting \(\mathrm{C_5H_5^-}\) to \(\mathrm{C_5H_7^-}\) while retaining \(\eta^{3}\)-coordination on that ring. The other ring stays \(\eta^{5}\)-bound.
Step 3: Product identity.
The resulting mixed-sandwich complex is \((\eta^{5}-\mathrm{C_5H_5})(\eta^{3}-\mathrm{C_5H_7})\mathrm{Ni}\), which matches option (C).
\[ \boxed{(\eta^{5}-\mathrm{C_5H_5})(\eta^{3}-\mathrm{C_5H_7})\mathrm{Ni}} \] Quick Tip: Reductions of metallocenes often induce \(\eta^{5}\!\rightarrow\!\eta^{3}\) ring slip; protic solvents can trap the reduced ring by protonation. Look for “Na/Hg + ROH” \(\Rightarrow\) reduce then protonate: mixed \(\eta^{5}/\eta^{3}\) complexes are common outcomes.
The number of shared corners of the constituent \(SiO_4\) units in orthosilicate, pyrosilicate, cyclic silicate and sheet silicate, respectively, are
View Solution
Step 1: In silicates, connectivity is described by how many corners (oxygen atoms) each \(\mathrm{SiO_4}\) tetrahedron shares.
Step 2: Orthosilicates (nesosilicates) have isolated tetrahedra \(\Rightarrow\) share \(0\) corners.
Step 3: Pyrosilicates (\(\mathrm{Si_2O_7^{6-}}\)) have two tetrahedra sharing one oxygen \(\Rightarrow\) share \(1\) corner.
Step 4: Cyclic silicates (\(\mathrm{(SiO_3)_n^{2n-}}\)) form rings where each tetrahedron shares two corners \(\Rightarrow\) \(2\).
Step 5: Sheet (phyllo) silicates (\(\mathrm{(Si_2O_5)_{n}^{2n-}}\)) have extended sheets with each tetrahedron sharing three corners \(\Rightarrow\) \(3\).
Thus the sequence is \(0,1,2,3\). Quick Tip: Isolated (ortho) = 0; paired (pyro) = 1; rings (cyclo) = 2; sheets = 3; frameworks (tecto) = 4.
Concentration of Q in a consecutive reaction \(P \xrightarrow{k_1} Q \xrightarrow{k_2} R\) is given by \([Q]=\dfrac{k_1[P]_0}{k_2-k_1}\left(e^{-k_1 t}-e^{-k_2 t}\right)\). If \(k_2=25~\mathrm{s^{-1}}\), the value of \(k_1\) that leads to the longest waiting time for Q to reach its maximum is
View Solution
Step 1: Time for \([Q]\) to be maximum. Differentiating and setting \(\dfrac{d[Q]}{dt}=0\) gives the time of maximum: \[ t_{\max}=\frac{\ln\!\left(\dfrac{k_2}{k_1}\right)}{k_2-k_1} \quad (k_1\neq k_2). \]
Step 2: Monotonicity with respect to \(k_1\) (for fixed \(k_2\)). For \(k_1 < k_2\), \[ \frac{d t_{\max}}{d k_1}=\frac{\frac{k_1-k_2}{k_1}+\ln\!\left(\frac{k_2}{k_1}\right)}{(k_2-k_1)^2}. \]
Let \(x=\dfrac{k_2}{k_1}>1\). Using \(\ln x \le x-1\) (equality only at \(x=1\)), \[ \frac{k_1-k_2}{k_1}+\ln\!\left(\frac{k_2}{k_1}\right)= -\left(x-1-\ln x\right)\le 0, \]
so \(t_{\max}\) decreases as \(k_1\) increases. Therefore, the longest waiting time occurs at the smallest \(k_1\).
Step 3: Choose from options. Among the choices, the smallest \(k_1\) is \(20~\mathrm{s^{-1}}\). Hence the longest waiting time is obtained for \(k_1=20~\mathrm{s^{-1}}\). Quick Tip: For \(P \to Q \to R\), \(t_{\max}\) is largest when formation of \(Q\) is slow relative to its consumption (\(k_1\) as small as possible vs fixed \(k_2\)). If \(k_1 \to k_2\), \(t_{\max} \to 1/k_2\) (l’Hôpital’s rule).
The wavefunction for Be\(^{3+}\) in a certain state is given by \(\psi = N e^{-\left(\tfrac{4}{a_0}\right)r}\), where \(N\) is the normalization constant, \(r\) is the distance of electron from the nucleus and \(a_0\) is the Bohr radius. The most probable distance of the electron from the nucleus in this state is
View Solution
Step 1: Identify the type of wavefunction.
The given wavefunction is \[ \psi(r) = N e^{-\frac{4r}{a_0}}. \]
This is of the form \(\psi(r) \propto e^{-Zr/a_0}\), which corresponds to a hydrogenic 1s orbital with nuclear charge \(Z=4\) (for Be\(^{3+}\)).
Step 2: Radial probability distribution.
The probability of finding the electron at a distance \(r\) is given by: \[ P(r) = 4\pi r^2 |\psi(r)|^2. \]
So, \[ P(r) \propto r^2 e^{-\frac{8r}{a_0}}. \]
Step 3: Find most probable radius.
To maximize \(P(r)\), set derivative to zero: \[ \frac{d}{dr} \left(r^2 e^{-\frac{8r}{a_0}}\right) = 0. \] \[ \Rightarrow 2r e^{-\frac{8r}{a_0}} - \frac{8}{a_0} r^2 e^{-\frac{8r}{a_0}} = 0. \] \[ \Rightarrow 2r - \frac{8}{a_0} r^2 = 0. \] \[ \Rightarrow r \left(2 - \frac{8r}{a_0}\right) = 0. \]
Ignoring \(r=0\), \[ r = \frac{a_0}{4}. \]
Step 4: Conclusion.
Thus, the most probable distance of the electron from the nucleus in this state is \(\tfrac{a_0}{4}\). Quick Tip: For hydrogen-like ions, the 1s most probable radius is given by \(\tfrac{a_0}{Z}\). For Be\(^{3+}\) (\(Z=4\)), the most probable distance is \(\tfrac{a_0}{4}\).
Match the following

View Solution
Step 1: Recall the forms of special functions in quantum mechanics.
- The angular part of the hydrogen atom wavefunction (spherical harmonics) involves Associated Legendre polynomials.
- The harmonic oscillator solutions are expressed in terms of Hermite polynomials.
- The radial part of the hydrogen atom wavefunction involves Associated Laguerre polynomials.
- The particle in a box has solutions in terms of trigonometric functions (sine and cosine).
Step 2: Match each entry.
- \(P \to III\): Associated Legendre polynomials → angular part of H atom.
- \(Q \to I\): Hermite polynomials → harmonic oscillator.
- \(R \to IV\): Associated Laguerre polynomials → radial part of H atom.
- \(S \to II\): Trigonometric functions → particle in a box.
\[ \boxed{P→III, Q→I, R→IV, S→II = Option (A)} \] Quick Tip: Hydrogen atom: Angular \(\Rightarrow\) Legendre, Radial \(\Rightarrow\) Laguerre. Harmonic oscillator: Hermite polynomials. Particle in a box: Sine and cosine (trigonometric).
In the scheme \( \mathrm{P_2} [\;k_1\;]{\;I_a\;} 2\mathrm{Q} \xrightarrow{k_2} \mathrm{R} \), \(I_a\) represents the intensity of light absorbed. Assuming the quantum yield of the first step is one, the steady-state concentration of \(\mathrm{Q}\) is given by
View Solution
Step 1: Write formation and consumption rates of \( \mathrm{Q} \).
Quantum yield of step 1 is 1, and \(I_a\) is the absorbed light intensity; hence the photochemical production rate of the pair \(2\mathrm{Q}\) is simply \(I_a\) (already normalized to the amount of light absorbed by \(\mathrm{P_2}\)). Therefore, the formation rate of \(\mathrm{Q}\) is \(I_a\).
Loss of \(\mathrm{Q}\) occurs via two bimolecular steps that consume two \(\mathrm{Q}\) at a time: \(2\mathrm{Q}\xrightarrow{k_1}\mathrm{P_2}\) and \(2\mathrm{Q}\xrightarrow{k_2}\mathrm{R}\). The total consumption rate is \((k_1+k_2)[\mathrm{Q}]^2\).
Step 2: Apply steady state and solve.
At steady state, formation = consumption: \[ I_a = (k_1+k_2)\,[\mathrm{Q}]^2 \quad \Rightarrow \quad [\mathrm{Q}] = \sqrt{\frac{I_a}{k_1+k_2}}. \]
This corresponds to option (A). Quick Tip: If \(I_a\) is the absorbed intensity and quantum yield \(=1\), it equals the rate of creating one event of \(2\mathrm{Q}\) formation—no extra \([\mathrm{P_2}]\) factor. When intermediates are made/consumed in pairs, steady-state often gives a square-root dependence: \([\mathrm{Q}] \propto \sqrt{generation/bimolecular loss}\).
Product(s) formed in the given reaction sequence is(are)

View Solution
Step 1: Ozonolysis outcome.
Cleavage of the endocyclic C=C by O\(_3\) gives a 1,6-dicarbonyl (dialdehyde/aldehyde–ketone) embedded in the bicyclic framework. The tertiary alcohol is retained under these conditions (no oxidative removal of –OH).
Step 2: Base-promoted intramolecular aldol and aromatization.
In NaOH, the 1,6-dicarbonyl undergoes intramolecular aldol cyclization. Two regioisomeric closures are possible (attack of either carbonyl), each followed by dehydration and keto–enol tautomerization to the phenolic form. This furnishes two alkyl-substituted naphthols (positional isomers).
Step 3: Final Pd/C step.
Pd/C here acts as a dehydrogenation/aromatization catalyst to ensure full aromaticity of the newly formed ring; it does not remove the phenolic OH under these conditions. Hence, the products remain as naphthols.
Conclusion: The reaction delivers two positional naphthol isomers, corresponding to options (A) and (B); options without –OH (e.g., (C)) are not consistent with the sequence. Quick Tip: Ozonolysis of a ring alkene \(\Rightarrow\) 1,6-dicarbonyl; under base, intramolecular aldol can “stitch” an aromatic ring. Keto–enol tautomerization of a conjugated diketone generated in such annulations often favors the \(\textbf{phenol}\) (naphthol) form. Pd/C commonly serves to aromatize dihydroarenes; it doesn’t remove phenolic OH in the absence of specific reagents.
Product(s) formed in the reaction below is(are)

View Solution
Step 1: Initial reduction under \(\mathrm{Sn/HCl}\).
Quinolines are chemoselectively reduced by \(\mathrm{Sn/HCl}\) to the corresponding 1,2,3,4-tetrahydroquinolines via protonation at N followed by stepwise electron transfer. The process generates a benzylic iminium at C-2 that can be either reduced further or trapped intramolecularly.
Step 2: Two competing fates of the C-2 iminium.
(i) Direct reduction of the C-2 iminium to the saturated side chain (no C–C bond formation) furnishes the open product shown in option (A).
(ii) Because the pendant \(3,4\)-dimethoxybenzyl arene is strongly activated, intramolecular electrophilic attack onto the C-2 iminium can also occur. Closure across the side chain forms a medium ring (benzazocine) bearing an \(\mathrm{NH}\) bridge, which corresponds to option (C). Under the strongly acidic, reducing conditions both pathways operate, giving a mixture dominated by (A) with significant (C) from cyclization.
\[ \boxed{Products formed: A and C.} \] Quick Tip: \(\mathrm{Sn/HCl}\) reduces N-heteroarenes to tetrahydro derivatives via iminium intermediates. Highly activated aryl tethers can trap iminium ions intramolecularly, giving ring-closed products alongside the simply reduced product.
The stereoisomer(s) of G giving the depicted product is(are):

View Solution
Step 1: Reaction type.
The transformation shown is an acid-catalyzed elimination (\(E1cb/E2\)-like, via BF\(_3\)·OEt\(_2\)) of the alcohol to form an alkene. For stereospecific elimination, the \(\beta\)-hydrogen and the leaving group (OH after activation) must be in an anti-periplanar orientation.
Step 2: Analyze stereochemistry of G.
The substrate G has two adjacent stereocenters: one bearing the OH group and a methyl, the other with bulky substituents. To generate the observed alkene product, only those stereoisomers where the \(\beta\)-H is anti-periplanar to the OH can undergo elimination.
Step 3: Evaluate the options.
(A): Conformation allows the required anti-periplanar alignment → productive.
(B): Has syn-periplanar OH–H alignment → not productive.
(C): Mirror stereoisomer of (A) with correct anti arrangement → productive.
(D): Syn relationship again → not productive.
Step 4: Conclusion.
Therefore, only stereoisomers (A) and (C) give the depicted alkene product. Quick Tip: In stereospecific \(E2\) eliminations, anti-periplanar geometry is crucial: leaving group and \(\beta\)-H must be opposite in the same plane. Always check relative positions of OH (leaving group) and adjacent hydrogens when predicting alkene formation. Enantiomeric stereoisomers that maintain this anti geometry will both lead to the same achiral alkene product.
Product(s) formed in the given reaction sequence is(are)

View Solution
Step 1: Formation of a bromohydrin (anti addition).
Br\(_2\)/KBr/H\(_2\)O adds across the \(\alpha,\beta\)-unsaturated double bond via a bromonium ion followed by attack of water. Opening occurs anti to the bromonium, giving a trans–bromohydrin with Markovnikov placement of OH (at the more substituted carbon). This creates two adjacent stereocenters.
Step 2: Base-promoted intramolecular epoxidation.
With aq. KOH in THF, the alcohol is deprotonated to an alkoxide, which displaces the anti bromide in an \(\mathrm{S_N2}\) fashion to form the epoxide. Because the bromohydrin was formed anti, intramolecular \(\mathrm{S_N2}\) ring closure preserves the overall anti relationship required for epoxide formation.
Step 3: Stereochemical outcome.
Attack of water in Step 1 can occur from either face of the planar bromonium, giving two diastereomeric bromohydrins that each cyclize to an epoxide. Thus, two epoxide diastereomers are produced—those depicted in (A) and (C). Options (B) and (D) are not obtained under these conditions (the former has an incorrect relative configuration; the latter would require oxidation/hydrolysis rather than intramolecular \(\mathrm{S_N2}\)).
\[ \boxed{Products: two epoxides from anti bromohydrin formation \Rightarrow (A) and (C).} \] Quick Tip: Br\(_2\)/H\(_2\)O gives \(\textbf{anti}\) bromohydrins via bromonium-ion opening by water. Base converts bromohydrins to epoxides by intramolecular \(\mathrm{S_N2}\) displacement of Br by the alkoxide. Attack on the bromonium from either face \(\Rightarrow\) two epoxide diastereomers.
The reaction(s) in which inversion of configuration occur(s) is(are)

View Solution
Step 1: Option (A) — Mitsunobu reaction.
\(Ph_{3}\)P/DEAD with a carboxylic acid converts an alcohol \({R^{–OH}}\) into the corresponding ester \({R^{–O_2CR'}}\) via an \(\mathrm{S_N2}\) displacement of the \({O–PPh_3}\) activated intermediate. The chiral center at carbon undergoes a single backside attack \(\Rightarrow\) Walden inversion.
Step 2: Option (B) — Anchimeric assistance (acyloxonium) under heat.
On heating, the neighboring acetate participates to form a cyclic acyloxonium intermediate; subsequent intramolecular/backside attack (or acetate capture) occurs \(\mathrm{S_N2}\)-like. The carbon bearing the leaving group is attacked from the opposite face \(\Rightarrow\) inversion at that stereocenter. (This is the classic neighboring-group participation in constrained bicyclic/allylic systems.)
Step 3: Option (C) — Hofmann rearrangement.
\({NaOBr}\) converts an amide to a \({C{-}1}\) shorter amine via \({N}\)-bromoamide, rearrangement, and isocyanate. Stereochemical information at a migrating \(\alpha\)-carbon (if present) is retained through the concerted migration; no inversion is involved.
Step 4: Option (D) — Baeyer–Villiger oxidation.
Peracid inserts an oxygen adjacent to a carbonyl with migration of one substituent. The migrating stereocenter (if any) migrates with retention (concerted rearrangement), not inversion.
Therefore, only (A) and (B) involve inversion of configuration. Quick Tip: \(\textbf{Mitsunobu}\) \(=\) activated alcohol \(\mathrm{S_N2}\) \(\Rightarrow\) inversion. \(\textbf{Neighboring-group participation}\) (acyloxonium/thiiranium/halonium) often leads to backside opening \(\Rightarrow\) inversion at the attacked carbon. \(\textbf{Rearrangements}\) like Hofmann and Baeyer–Villiger are concerted migrations \(\Rightarrow\) retention of configuration at the migrating center.
The correct statement(s) regarding myoglobin (Mb) and haemoglobin (Hb) is(are)
View Solution
Step 1: Bohr effect. Lowering the pH decreases Hb’s affinity for O\(_2\) (right shift of the O\(_2\)-binding curve), especially relevant at low \(p\)O\(_2\). Hence (A) is true.
Step 2: Cooperativity of Hb. Hb displays positive cooperativity: binding of the first O\(_2\) increases affinity for subsequent O\(_2\) molecules. Thus (B) is false.
Step 3: Spin state changes. In deoxy-Mb, Fe(II) is high-spin; upon O\(_2\) binding (oxy-Mb), iron becomes low-spin due to strong-field interaction. Statement (C) reverses this and is false.
Step 4: Distal His H-bond. In oxy-Mb/Hb, bound O\(_2\) is hydrogen-bonded to the distal histidine (His E7) N–H, stabilizing the adduct. Therefore (D) is true. Quick Tip: Bohr effect: \(\downarrow\)pH or \(\uparrow\)CO\(_2\) \(\Rightarrow\) \(\downarrow\) Hb–O\(_2\) affinity. Hb: positive cooperativity; Mb: hyperbolic, non-cooperative binding. Deoxy Fe(II) is high-spin; O\(_2\) binding leads to low-spin and movement of Fe into the porphyrin plane.
The correct statement(s) regarding Co\(_2\)(CO)\(_8\) is(are)
View Solution
Step 1: Reduction with alkali metals. Co\(_2\)(CO)\(_8\) is reduced by Na to give the cobaltate carbonyl anion: \[ \mathrm{Co_2(CO)_8 + 2\,Na \rightarrow 2\,Na[Co(CO)_4],} \]
so (A) is true.
Step 2: Carbonyl structure. One isomer of Co\(_2\)(CO)\(_8\) has two bridging CO ligands (not three); the other isomer has all terminal CO ligands. Therefore (B) is false.
Step 3: Preparation. Co\(_2\)(CO)\(_8\) is prepared by reductive carbonylation of cobalt(II) salts (e.g., cobalt acetate) under CO pressure \(\Rightarrow\) (C) true.
Step 4: Isomerism in solution. In nonpolar solvents like hexane, Co\(_2\)(CO)\(_8\) exists as an equilibrium mixture of the bridged and unbridged isomers \(\Rightarrow\) (D) true. Quick Tip: Remember: Co\(_2\)(CO)\(_8\) \(\leftrightharpoons\) bridged (2 \(\mu-CO)\) and unbridged (all terminal) isomers. Alkali metals convert many metal carbonyl dimers to anionic monocarbonylates, e.g., Na[Co(CO)\(_4\)].
The compound(s) having [Xe]4f\(^1\) configuration is(are)
(Given the atomic numbers Ce:58, Lu:71, Pr:59 and Nd:60)
View Solution
Step 1: Determine oxidation states.
(A) \([{\rm Ce(NO_3)_6}]^{3-}\Rightarrow {\rm Ce}^{3+}\).
(B) \([{\rm LuCl_6}]^{3-}\Rightarrow {\rm Lu}^{3+}\).
(C) \({\rm PrO_2}\Rightarrow {\rm Pr}^{4+}\) (since O is \(-2\)).
(D) \({\rm Nd(NR_2)_3}\Rightarrow {\rm Nd}^{3+}\).
Step 2: Write 4f electron counts.
Ce: \([{\rm Xe}]4f^1 5d^1 6s^2 \Rightarrow {\rm Ce}^{3+}:[{\rm Xe}]4f^1\).
Lu: \([{\rm Xe}]4f^{14}5d^1 6s^2 \Rightarrow {\rm Lu}^{3+}:[{\rm Xe}]4f^{14}\).
Pr: \([{\rm Xe}]4f^3 6s^2 \Rightarrow {\rm Pr}^{4+}:[{\rm Xe}]4f^1\).
Nd: \([{\rm Xe}]4f^4 6s^2 \Rightarrow {\rm Nd}^{3+}:[{\rm Xe}]4f^3\).
Step 3: Pick compounds with 4f\(^1\).
Ce\(^{3+}\) and Pr\(^{4+}\) give \([{\rm Xe}]4f^1\) \(\Rightarrow\) (A) and (C). Quick Tip: Lanthanide \(3+\) oxidation state usually reflects \(4f^n\) of the element (Ce\(^{3+}\,{\to}\,4f^1\); Nd\(^{3+}\,{\to}\,4f^3\)). Higher oxidation states remove 5d/6s first, then 4f (Pr\(^{4+}\,{\to}\,4f^1\)).
The correct statement(s) for XeF\(_2\) is(are)
View Solution
Step 1: Bonding model.
XeF\(_2\) is linear with an \(AX_2E_3\) arrangement about Xe. The two Xe–F bonds are best described by 3-center–4-electron (3c–4e) bonding over the F–Xe–F framework, not by two independent 2c–2e bonds. Thus (B) is true, (A) is false.
Step 2: Lone-pair count.
Each F has three lone pairs (\(2\times3=6\)), and Xe has three lone pairs in the equatorial positions of a trigonal bipyramidal electron geometry. Total \(=6+3=\mathbf{9}\) lone pairs \(\Rightarrow\) (C) true.
Step 3: Symmetry.
A linear, centrosymmetric F–Xe–F molecule has point group \(\mathbf{D_{\infty h}}\). Hence (D) is true. Quick Tip: Hypervalent AX\(_2\) species like XeF\(_2\) are classic examples of 3c–4e bonding; remember the linear geometry (AX\(_2\)E\(_3\)) and \(D_{\infty h}\) symmetry.
For the non-dissociative adsorption of a gas on solid,
View Solution
Step 1: Langmuir at low coverage.
Langmuir: \(\displaystyle \theta=\frac{Kp}{1+Kp}\). For \(Kp\ll1\), \(\theta\approx Kp\), i.e., \(\theta\propto p\). This is the Freundlich form with \(n=1\) (and \(k=K\)). Hence (A) is true.
Step 2: Langmuir at high coverage.
For \(Kp\gg1\), \(\theta\to\theta_s\) (saturation, a constant). The Freundlich expression \(\theta=k\,p^{1/n}\) with \(n\to\infty\) gives \(\theta=k\,p^{0}=k\) (a constant). Choosing \(k=\theta_s\) reproduces the Langmuir high-coverage limit. Thus, in this limiting sense, (B) is true.
Step 3: BET at very low pressure.
From the given BET form, \[ \frac{p}{p^{\ast}-p}=\frac{\theta}{c}+\theta(c-1)\left(\frac{p}{p^{\ast}}\right). \]
If \(p\ll p^{\ast}\), then \(\dfrac{p}{p^{\ast}-p}\approx\dfrac{p}{p^{\ast}}\) and the term \(\theta(c-1)\dfrac{p}{p^{\ast}}\) is negligible. Hence \[ \frac{p}{p^{\ast}}\approx \frac{\theta}{c}\quad\Rightarrow\quad \theta\approx \frac{c}{p^{\ast}}\,p, \]
which is the Langmuir (monolayer, linear low-\(p\)) limit. Therefore (C) is true.
Step 4: BET near saturation.
As \(p\to p^{\ast}\), multilayer adsorption dominates and the BET equation does not collapse to the monolayer Langmuir form; thus (D) is false. Quick Tip: Langmuir limits: low \(p\Rightarrow \theta\propto p\) (Freundlich with \(n=1\)); high \(p\Rightarrow \theta\to\theta_s\) (Freundlich with \(n\to\infty\), \(k=\theta_s\)). BET reduces to Langmuir only in the very-low-pressure (monolayer) regime.
Two different enzyme catalysis reactions I and II have identical Y-intercepts for the Lineweaver–Burke plots. The slope for reaction I is twice that of reaction II. If the initial concentrations of enzymes in I and II are same, the correct statement(s) is(are)
\[ \frac{1}{v}=\frac{1}{v_{\max}}+\frac{K_M}{v_{\max}}\frac{1}{[S]} \]
View Solution
Step 1: Use the Lineweaver–Burke form. The intercept equals \(1/v_{\max}\). Identical Y-intercepts \(\Rightarrow v_{\max}^{(I)}=v_{\max}^{(II)}\). With equal enzyme concentrations \([\mathrm{E}]_0\), the turnover number \(k_{cat}=v_{\max}/[\mathrm{E}]_0\) is the same for I and II \(\Rightarrow\) (A) true.
Step 2: Compare the slopes. Slope \(=K_M/v_{\max}\).
Since \(v_{\max}\) is the same and slope(I) \(=2\times\) slope(II), we get \(K_M^{(I)}=2K_M^{(II)}\) \(\Rightarrow\) (C) true; (B) false.
Step 3: Elementary steps. Equality of \(v_{\max}\) and the slope relation gives no information about the detailed microscopic steps; therefore (D) cannot be concluded (false). Quick Tip: In a Lineweaver–Burke plot: intercept \(=1/v_{\max}\), slope \(=K_M/v_{\max}\). If intercepts are equal, differences in slope reflect differences in \(K_M\) only.
The enthalpy change for the exothermic reaction between BeI\(_2\) and HgF\(_2\) is _____ kJ mol\(^{-1}\) (rounded off to the nearest integer).
(Given bond dissociation energies in kJ mol\(^{-1}\): Be–F = 632, Be–I = 289, Hg–F = 268, Hg–I = 145)
View Solution
Step 1: Write the reaction using halide exchange. \[ \mathrm{BeI_2 + HgF_2 \rightarrow BeF_2 + HgI_2} \]
Step 2: Apply the bond-energy method.
Break: \(2\times\)Be–I \(=2(289)=578\) kJ; \(2\times\)Hg–F \(=2(268)=536\) kJ. \[ E_{broken}=578+536=1114\ kJ \]
Form: \(2\times\)Be–F \(=2(632)=1264\) kJ; \(2\times\)Hg–I \(=2(145)=290\) kJ. \[ E_{formed}=1264+290=1554\ kJ \]
Step 3: Compute \(\Delta H\). \[ \Delta H \approx E_{broken}-E_{formed} =1114-1554=-440\ kJ mol^{-1}. \]
Thus the reaction is exothermic by approximately \(-440\ kJ mol^{-1}\). Quick Tip: For bond-energy estimates: \(\Delta H \approx \sum D(bonds broken)-\sum D(bonds formed)\). Halogen exchange tends to form the stronger metal–halogen bonds (here, Be–F and Hg–I), driving the reaction exothermic.
Number of carbon atoms connected to the metal center in [W(C\(_{60}\))(CO)\(_5\)] is ____ (rounded off to the nearest integer).
(Given: atomic number of W = 74)
View Solution
Step 1: Nature of the complex.
The complex is \([W(C_{60})(CO)_5]\), where tungsten is coordinated to 5 terminal carbonyls and the fullerene (C\(_{60}\)). Each CO contributes one carbon donor. The question is about the number of carbon atoms of the fullerene directly bonded to W.
Step 2: Electron-counting perspective.
W has atomic number 74; in zero oxidation state it has 6 valence electrons (group 6). The five CO ligands donate \(5 \times 2 = 10\) electrons. For the stable 18-electron configuration, the metal must receive 2 additional electrons from the C\(_{60}\).
Thus, C\(_{60}\) as a ligand provides \(\eta^2\)-type coordination (a C=C double bond). Hence, W is connected to two adjacent carbon atoms of C\(_{60}\).
Step 3: Interpretation of “number of carbon atoms connected.”
In such \(\eta\)\(^2\)-binding, the metal simultaneously bonds to both carbons of the C=C bond. Therefore, the number of C atoms directly connected to W = 5 (from CO) + 2 (from C\(_{60}\)) = 7.
However, the question asks only for the number of carbon atoms (not counting O of CO), i.e., the carbon donors:
- 5 carbons from the CO ligands
- 2 carbons from the \(\eta\)\(^2\)-C\(_{60}\) bond
Total = \(\mathbf{7}\).
Rounded off to the nearest integer → \(\mathbf{7}\).
\[ \boxed{7} \] Quick Tip: In organometallic complexes, each CO ligand donates its carbon atom. C\(_{60}\) typically coordinates in an \(\eta^2\) fashion through a double bond (2 carbons to the metal). Always include both CO carbons and fullerene carbons when asked for “number of carbons connected to the metal.”
Two-component solid–liquid system of naphthalene–benzene forms a simple eutectic mixture. Assuming an ideal solution, the mole fraction of naphthalene in benzene at \(300~K\) and \(1~bar\) is _____ (rounded off to two decimal places).
(Given: freezing point \(T_{\mathrm{fp}}\) and enthalpy of fusion \(\Delta H_{\mathrm{fus}}\) of naphthalene are \(353~K\) and \(19.28~kJ mol^{-1}\), respectively; \(R=8.31~J K^{-1}mol^{-1}\))
View Solution
Step 1: Ideal solubility relation for a solid in a liquid.
For equilibrium between solid naphthalene and its ideal solution at temperature \(T < T_{\mathrm{m}}\), \[ \ln x_{\mathrm{Naph}}=-\frac{\Delta H_{\mathrm{fus}}}{R}\left(\frac{1}{T}-\frac{1}{T_{\mathrm{m}}}\right), \]
where \(x_{\mathrm{Naph}}\) is the mole fraction of naphthalene in the liquid phase and \(T_{\mathrm{m}}=T_{\mathrm{fp}}=353~K\).
Step 2: Insert data.
\[ \frac{1}{T}-\frac{1}{T_{\mathrm{m}}}=\frac{1}{300}-\frac{1}{353}\approx 4.99\times10^{-4}\ K^{-1}, \] \[ \frac{\Delta H_{\mathrm{fus}}}{R}=\frac{19.28\times10^{3}}{8.31}\approx 2.32\times10^{3}. \]
Hence, \[ \ln x_{\mathrm{Naph}}\approx - (2.32\times10^{3})(4.99\times10^{-4})\approx -1.16. \]
Step 3: Solve for \(x_{\mathrm{Naph}}\).
\[ x_{\mathrm{Naph}}=\exp(-1.16)\approx 0.313 \ \Rightarrow \ \boxed{0.31}\ (to two decimals). \] Quick Tip: Ideal solubility of a solid: \(\ln x = -\dfrac{\Delta H_{\mathrm{fus}}}{R}\left(\dfrac{1}{T}-\dfrac{1}{T_{\mathrm{m}}}\right)\). Works well for simple eutectic systems far from solid–solid interactions and at pressures near 1 bar.
The intrinsic viscosity of a sample of polystyrene in toluene is \(84\ cm^3\ g^{-1}\) at \(30\,^{\circ}C\). It follows the Mark–Houwink equation with empirical constants \(K = 1.05\times 10^{-2}\ cm^3\ g^{-1}\) and \(a = 0.75\). The molecular weight of the polymer is \(\_\_\_\_\_\_\times10^{3}\ g mol^{-1}\) (rounded off to the nearest integer).
View Solution
Step 1: Use the Mark–Houwink relation \([\,\eta\,] = K\,M^{a}\). Given \([\,\eta\,]=84\), \(K=1.05\times10^{-2}\), \(a=0.75\).
Step 2: Solve for \(M\): \[ M=\left(\frac{[\,\eta\,]}{K}\right)^{1/a} =\left(\frac{84}{1.05\times10^{-2}}\right)^{\!1/0.75} =\left(8000\right)^{4/3}. \]
Step 3: Compute: \[ 8000^{1/3}=20 \;\Rightarrow\; M=20^{4}=160\,000\ g mol^{-1}=160\times10^{3}\ g mol^{-1}. \]
Step 4: Rounded to the nearest integer for the \(\times10^{3}\) form gives \(\boxed{160}\). Quick Tip: For Mark–Houwink, if \(1/a=\tfrac{4}{3}\), rewrite \(M=(x)^{4/3}=(x^{1/3})^{4}\) to compute quickly by taking a cube root first and then raising to the 4th power.
According to Debye–Hückel limiting law, the mean molal activity coefficient for 0.87 g K\(_2\)SO\(_4\) (molar mass = 174 g mol\(^{-1}\)) in 1 kg of water at 25 °C is ____ (rounded off to two decimal places).
View Solution
Step 1: Molality.
Moles of salt \(= \frac{0.87}{174} = 0.005\ mol\). In 1 kg water, \(m = 0.005\ mol kg^{-1}\).
Step 2: Ionic strength \(I\).
\(\mathrm{K_2SO_4 \to 2K^+ + SO_4^{2-}}\). Using \(I = \tfrac12 \sum m_i z_i^2\):
\[ I=\tfrac12[(2m)\cdot(1)^2 + (m)\cdot(2)^2] = \tfrac12(0.01 + 0.02)=0.015. \]
Step 3: Debye–Hückel limiting law (25 °C).
\[ \log_{10}\gamma_{\pm} = -A|z_+z_-|\sqrt{I} = -0.509\times 2 \times \sqrt{0.015}. \] \[ \sqrt{0.015}=0.1225\Rightarrow \log_{10}\gamma_{\pm}\approx -0.1247. \]
Step 4: Evaluate \(\gamma_{\pm}\).
\[ \gamma_{\pm}=10^{-0.1247}\approx 0.75 \ (to two decimals). \] Quick Tip: For \(\mathrm{A_xB_y}\) electrolytes, use \(m_i=\nu_i m\) in \(I=\tfrac12\sum m_i z_i^2\). At 25 °C, \(A=0.509\) in the Debye–Hückel limiting law.
A solution is prepared by dissolving 128 g of naphthalene \(C_{10}H_8\) in 780 g of benzene \(C_6H_6\). The vapor pressure of pure benzene is 12.6 kPa at 25\(^\circ\)C. Assuming that naphthalene in benzene is an ideal solution, the partial vapor pressure of benzene is _____ kPa (rounded off to two decimal places).
View Solution
Step 1: Calculate moles.
Molar masses: \(M_{\mathrm{benz}} \approx 78.11~\mathrm{g\,mol^{-1}}\), \(M_{\mathrm{naph}} \approx 128.17~\mathrm{g\,mol^{-1}}\).
\[ n_{\mathrm{benz}}=\frac{780}{78.11}\approx 9.986~\mathrm{mol}, \qquad n_{\mathrm{naph}}=\frac{128}{128.17}\approx 0.999~\mathrm{mol}. \]
Step 2: Mole fraction of benzene.
\[ x_{\mathrm{benz}}=\frac{n_{\mathrm{benz}}}{n_{\mathrm{benz}}+n_{\mathrm{naph}}} =\frac{9.986}{9.986+0.999}\approx 0.9091. \]
Step 3: Apply Raoult's law.
\[ p_{\mathrm{benz}}=x_{\mathrm{benz}}\,P^{\ast}_{\mathrm{benz}} =0.9091\times 12.6~\mathrm{kPa}\approx 11.454~\mathrm{kPa} \Rightarrow \boxed{11.45~\mathrm{kPa}} (to two decimals). \] Quick Tip: For ideal solutions: \(p_i=x_i P_i^\ast\) (Raoult's law). Nonvolatile solutes (like naphthalene here) lower the solvent vapor pressure in proportion to the solvent mole fraction.
For the galvanic cell: H\(_2\)(g) | HCl(aq) | Cl\(_2\)(g), the standard electromotive force is \[ E^0 = 1.73 - (1.25\times10^{-3})T + (1.00\times10^{-6})T^2 \quad (V, with T in K). \]
Find the standard enthalpy change \(\Delta_r H^0\) at \(300\ K\) (kJ mol\(^{-1}\)). Assume the cell reaction is written per mole of HCl, i.e., \(\tfrac12\mathrm{H_2} + \tfrac12\mathrm{Cl_2} \rightarrow \mathrm{HCl(aq)}\) so that \(n=1\). (Given \(F=96500\ C mol^{-1}\)).
View Solution
Step 1: Evaluate \(E^0\) and its temperature derivative at \(T=300\ K\). \[ E^0 = 1.73-(1.25\times10^{-3})(300)+(1.00\times10^{-6})(300)^2 =1.445\ V, \] \[ \left(\frac{dE^0}{dT}\right)_P = -1.25\times10^{-3}+2(1.00\times10^{-6})(300) = -6.5\times10^{-4}\ V K^{-1}. \]
Step 2: Use thermodynamic relations. \[ \Delta G^0=-nFE^0,\qquad \Delta S^0=nF\left(\frac{dE^0}{dT}\right), \] \[ \Rightarrow\ \Delta H^0=\Delta G^0+T\Delta S^0 = -nFE^0 + nFT\left(\frac{dE^0}{dT}\right). \]
Step 3: Insert \(n=1\). \[ \Delta H^0 = -(96500)(1.445) + (96500)(300)(-6.5\times10^{-4}) = -1.394\times10^{5} - 1.882\times10^{4}\ J mol^{-1} \] \[ = -1.5826\times10^{5}\ J mol^{-1} \approx -1.58\times10^{5}\ J mol^{-1} = \boxed{-158\ kJ mol^{-1}}. \] Quick Tip: For EMF that depends on \(T\): \(\Delta H^0=-nF\big[E^0 - T(dE^0/dT)\big]\). Be clear whether the cell reaction is written per mole of product (here, per mole of HCl so \(n=1\)) or for the full \(2e^-\) process.
A solution of three non-interacting compounds P, Q, and R is taken in a cuvette of 1 cm path length. Their concentrations are [P] = \(1\times10^{-6}\) M, [Q] = \(2\times10^{-6}\) M, [R] = \(3\times10^{-6}\) M and the molar extinction coefficients at 300 nm are \(\varepsilon_P = 1\times10^{5}\ \mathrm{M^{-1}\,cm^{-1}}\), \(\varepsilon_Q = 2\times10^{5}\ \mathrm{M^{-1}\,cm^{-1}}\) and \(\varepsilon_R = 3\times10^{5}\ \mathrm{M^{-1}\,cm^{-1}}\). The % transmittance at 300 nm is ___________ (rounded off to two decimal places)
View Solution
Step 1: Use Beer–Lambert law and add absorbances.
For non-interacting species, \(A = \sum \varepsilon_i\,c_i\,l\). With \(l=1\,cm\):
\[ A = (1\times10^{5})(1\times10^{-6}) + (2\times10^{5})(2\times10^{-6}) + (3\times10^{5})(3\times10^{-6}) \] \[ A = 0.10 + 0.40 + 0.90 = 1.40 \]
Step 2: Convert absorbance to transmittance.
\(T = 10^{-A} = 10^{-1.40} \approx 0.03981\). Hence, \(\%T = 100\,T \approx 3.981\%\).
\[ \boxed{\%T \approx 3.98\%} \] Quick Tip: - For mixtures, total absorbance is additive: \(A_total = \sum \varepsilon c l\).
- Convert using \(T = 10^{-A}\) and \(%T = 100\times T\).


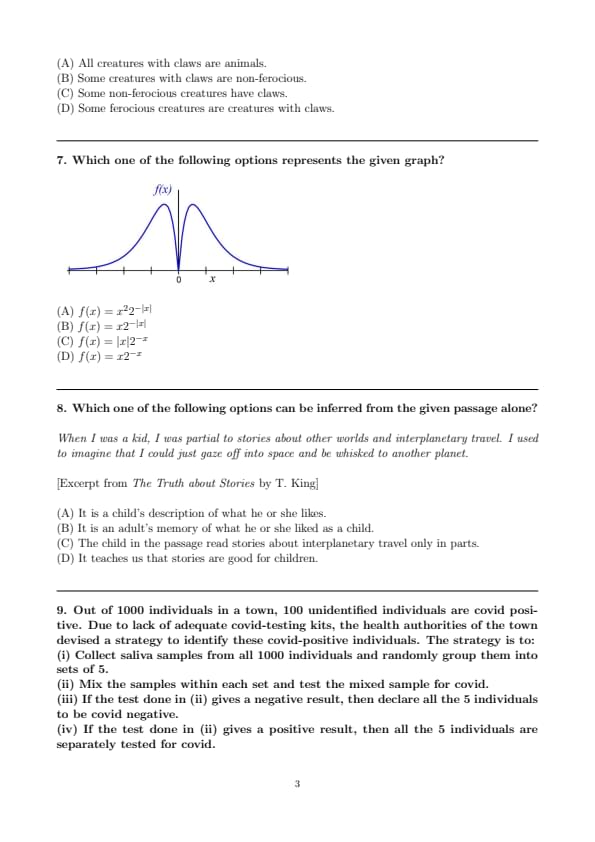







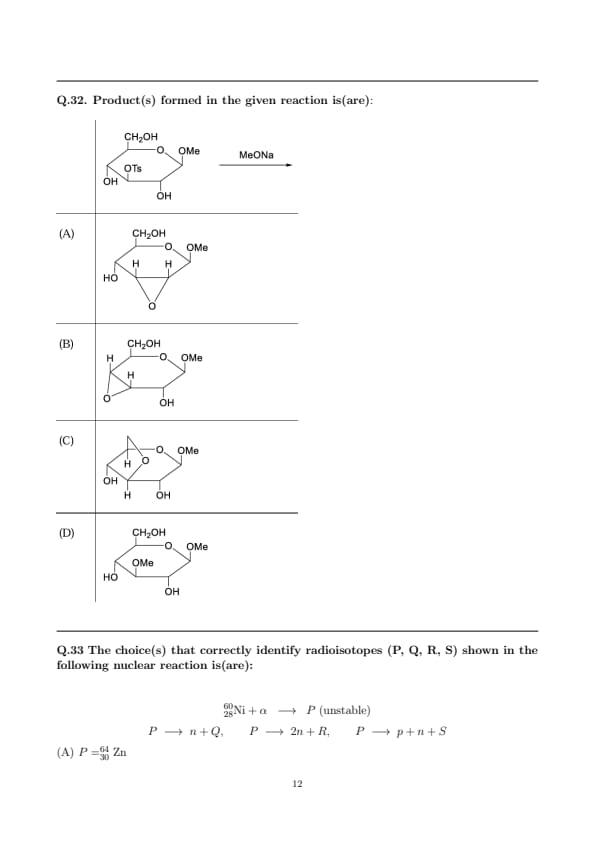




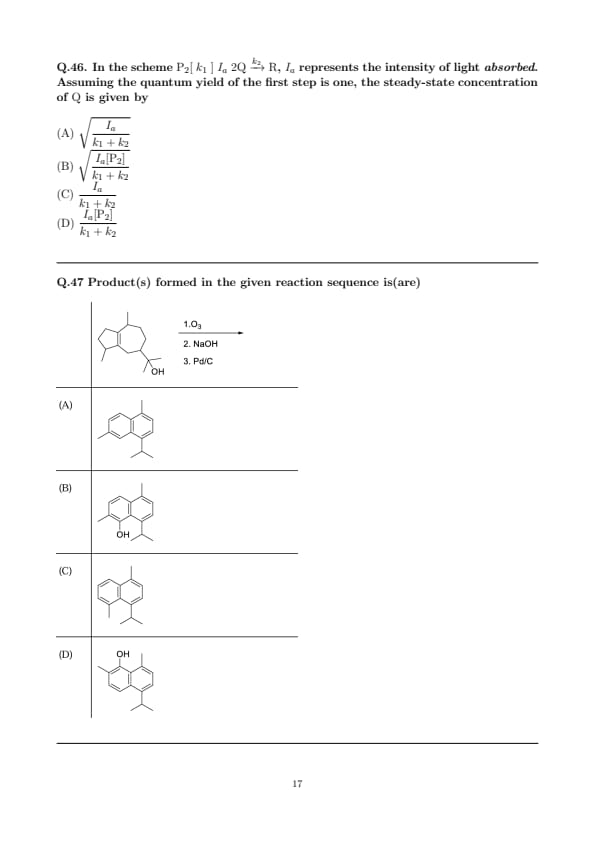
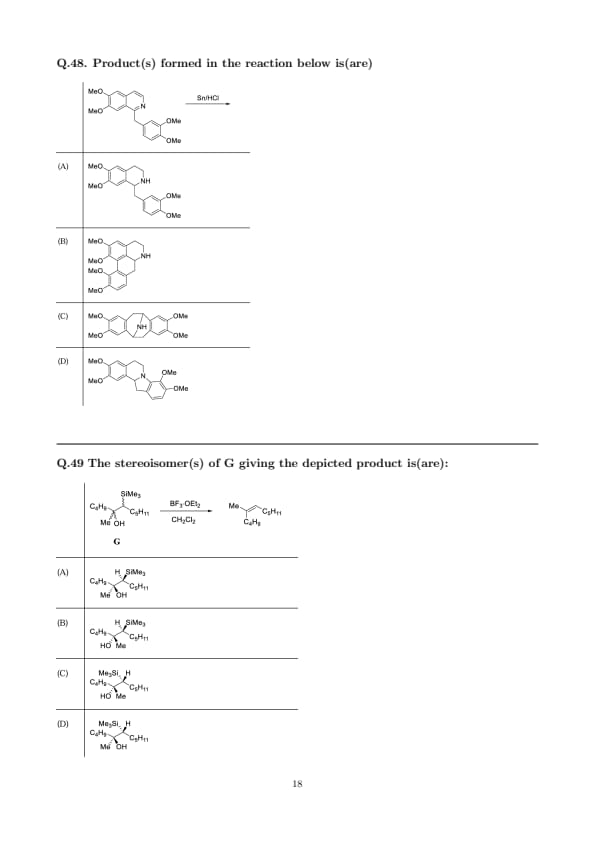
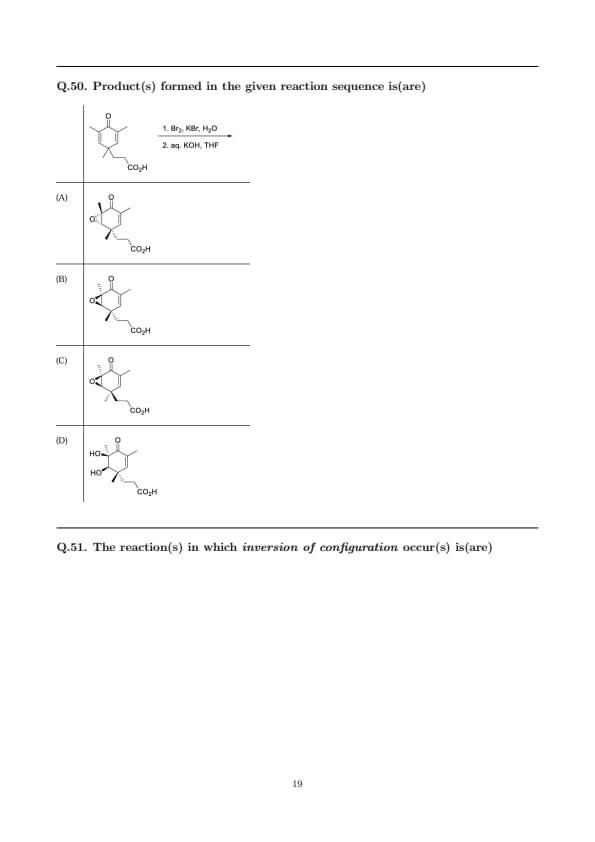







Comments