JEE Main 2025 28 Jan Shift 1 Question Paper is now available for download with Solution PDF. NTA conducted the exam successfully on 28 Jan 2025 from 09:00 AM to 12:00 PM.
You can also match your JEE Main 2025 solutions with Collegdunia’s JEE Main 2025 Question Paper Solutions pdf for free and analyse your expected JEE Main Marks Vs Percentile in JEE Main Session 1.
| JEE Main 2025 Jan 28 Shift 1 Question Paper with Solution | Check Solution |
Also Check
- Download JEE Main 2025 PYQ for all shifts
- Download JEE Main Last 10 Year Question Papers for all shifts

Check – JEE Main 2025 Jan 28 Shift 2 Question Paper Solutions Pdf
JEE Main 2025 Jan 28 Shift 1 Questions with Solutions
Let for some function \( y = f(x) \), \(\int_0^x t f(t) \, dt = x^2 f(x), x > 0\) and \( f(2) = 3 \). Then \( f(6) \) is equal to:
View Solution
The sum of the squares of all the roots of the equation \( x^2 + [2x - 3] - 4 = 0 \) is:
View Solution
The sum of all local minimum values of the function \( f(x) \) as defined below is: \[ f(x) = \left\{ \begin{array}{ll} 1 - 2x & \text{if } x < -1
\frac{1}{3}(7 + 2|x|) & \text{if } -1 \leq x \leq 2
\frac{11}{18} (x-4)(x-5) & \text{if } x > 2 \end{array} \right. \]
View Solution
Let \( \langle a_n \rangle \) be a sequence such that \( a_0 = 0 \), \( a_1 = \frac{1}{2} \), and \( 2a_{n+2} = 5a_{n+1} - 3a_n \).n= 0,1,2,3.... Then \( \sum_{k=1}^{100} a_k \) is equal to:
View Solution
If the image of the point \( (4, 4, 3) \) in the line \( \frac{x-1}{2} = \frac{y-2}{1} = \frac{z-1}{3} \) is \( (a, \beta, \gamma) \), then \( a + \beta + \gamma \) is equal to:
View Solution
The value of \( \cos \left( \sin^{-1} \left(-\frac{3}{5}\right) + \sin^{-1} \left(\frac{5}{13}\right) + \sin^{-1} \left(-\frac{33}{65}\right) \right) \) is:
View Solution
Three defective oranges are accidentally mixed with seven good ones and on looking at them, it is not possible to differentiate between them. Two oranges are drawn at random from the lot. If \( x \) denotes the number of defective oranges, then the variance of \( x \) is:
View Solution
Let the equation of the circle, which touches x-axis at the point \( (a, 0) \) and cuts off an intercept of length \( b \) on y-axis be \( x^2 + y^2 - cx + dy + e = 0 \). If the circle lies below x-axis, then the ordered pair \( (2a, b^2) \) is equal to:
View Solution
Let O be the origin, the point A be \( z_1 = \sqrt{3} + 2\sqrt{2}i \), the point B \( z_2 \) be such that \( \sqrt{3}|z_2| = |z_1| \) and \( \arg(z_2) = \arg(z_1) + \frac{\pi}{6} \). Then:
View Solution
The area (in sq. units) of the region \((x, y) : 0 \leq y \leq 2|x| + 1, 0 \leq y \leq x^2 + 1, |x| \leq 3\) is:
View Solution
Let \(T_{n-1} = 28\), \(T_n = 56\), and \(T_{n+1} = 70\). Let A \((4\cos t, 4\sin t)\), B \((2\sin t, -2\cos t)\), and C \((3r_n - 1, r^2_n - n - 1)\) be the vertices of a triangle ABC, where \(t\) is a parameter. If \((3x - 1)^2 + (3y)^2 = a\), is the locus of the centroid of triangle ABC, then \(a\) equals:
View Solution
The number of different 5 digit numbers greater than 50000 that can be formed using the digits 0, 1, 2, 3, 4, 5, 6, 7, such that the sum of their first and last digits should not be more than 8, is:
View Solution
If \( f(x) = \frac{2^x}{2^x + \sqrt{2}} \), \(x \in \mathbb{R}\), then \(\sum_{k=1}^{81} f\left(\frac{k}{82}\right)\) is equal to:
View Solution
Two numbers \(k_1\) and \(k_2\) are randomly chosen from the set of natural numbers. Then, the probability that the value of \(i^{k_1} + i^{k_2}\) (where \(i = \sqrt{-1}\)) is non-zero equals:
View Solution
Let A \((x, y, z)\) be a point in \(xy\)-plane, which is equidistant from three points (0, 3, 2), (2, 0, 3) and (0, 0, 1). Let B \((1, 4, -1)\) and C \((2, 0, -2)\). Then among the statements: (S1): ABC is an isosceles right angled triangle, and
(S2): the area of \(\triangle ABC\) is \( \frac{9\sqrt{2}}{2} \).
View Solution
Let \( f: \mathbb{R} \to \mathbb{R} \) be a function defined by \( f(x) = \left( 2 + 3a \right)x^2 + \left( \frac{a+2}{a-1} \right)x + b, a \neq 1 \). If \[ f(x + y) = f(x) + f(y) + 1 - \frac{2}{7}xy, \] then the value of \( 28 \sum_{i=1}^5 f(i) \) is:
View Solution
If \[ \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{96x^2 \cos^2 x}{1 + e^x} dx = \pi(a\pi^2 + \beta), \quad a, \beta \in \mathbb{Z}, \] then \( (a + \beta)^2 \) equals:
View Solution
Let \( T_r \) be the \( r^{th} \) term of an A.P. If for some \( m \), \( T_m = \frac{1}{25} \), \( T_{25} = \frac{1}{20} \), and \( \sum_{r=1}^{25} T_r = 13 \), then \[ 5m \sum_{r=m}^{2m} T_r \text{ is equal to:} \]
View Solution
Let ABCD be a trapezium whose vertices lie on the parabola \( y^2 = 4x \). Let the sides AD and BC of the trapezium be parallel to the y-axis. If the diagonal AC is of length \( \frac{25}{4} \) and it passes through the point \( (1, 0) \), then the area of ABCD is:
View Solution
The relation \( R = \{(x, y) : x, y \in \mathbb{Z} \text{ and } x + y \text{ is even} \} \) is:
View Solution
If \(a = 1 + \sum_{r=1}^{6} (-3)^{r-1} \binom{12}{2r-1}\), then the distance of the point \((12, \sqrt{3})\) from the line \(\alpha x - \sqrt{3}y + 1 = 0\) is:
View Solution
Let \(E_1: \frac{x^2}{9} + \frac{y^2}{4} = 1\) be an ellipse. Ellipses \(E_i\) are constructed such that their centers and eccentricities are the same as that of \(E_1\), and the length of the minor axis of \(E_{i+1}\) is the length of the major axis of \(E_i\). If \(A_i\) is the area of the ellipse \(E_i\), then \(\frac{5}{\pi} \sum_{i=1}^{\infty} A_i\) is equal to:
View Solution
Let \(\vec{a} = i + j + k\), \(\vec{b} = 2i + 2j + k\) and \(\vec{d} = \vec{a} \times \vec{b}\). If \(\vec{c}\) is a vector such that \(\vec{a} \cdot \vec{c} = |\vec{c}|\), \(\|\vec{c} - 2\vec{d}\| = 8\) and the angle between \(\vec{d}\) and \(\vec{c}\) is \(\frac{\pi}{4}\), then \(\left|10 - 3\vec{b} \cdot \vec{c} + |\vec{d}|\right|^2\) is equal to:
View Solution
Let \(f(x)\) be defined as follows: \[ f(x) = \begin{cases} 3x, & \text{if } x < 0
\min(1+x+\lfloor x \rfloor, 2+x\lfloor x \rfloor), & \text{if } 0 \leq x \leq 2
5, & \text{if } x > 2 \end{cases} \] where \(\lfloor . \rfloor\) denotes the greatest integer function. If \(\alpha\) and \(\beta\) are the number of points, where \(f\) is not continuous and is not differentiable, respectively, then \(\alpha + \beta\) equals:
View Solution
Let \(M\) denote the set of all real matrices of order 3 x 3 and let \(S = \{-3, -2, -1, 1, 2\}\). Let \[ S_1 = \{A = [a_{ij}] \in M : A = A^T \text{ and } a_{ij} \in S, \forall i, j\}, \] \[ S_2 = \{A = [a_{ij}] \in M : A = -A^T \text{ and } a_{ij} \in S, \forall i, j\}, \] \[ S_3 = \{A = [a_{ij}] \in M : a_{11} + a_{22} + a_{33} = 0 \text{ and } a_{ij} \in S, \forall i, j\}. \] If \(n(S_1 \cup S_2 \cup S_3) = 125\), then \(\alpha\) equals:
View Solution
Consider a long thin conducting wire carrying a uniform current \( I \). A particle having mass \( M \) and charge \( q \) is released at a distance \( a \) from the wire with a speed \( v_0 \) along the direction of current in the wire. The particle gets attracted to the wire due to magnetic force. The particle turns round when it is at distance \( x \) from the wire. The value of \( x \) is:
View Solution
A thin prism \( P_1 \) with angle \( 4^\circ \) made of glass having refractive index 1.54 is combined with another thin prism \( P_2 \) made of glass having refractive index 1.72 to get dispersion without deviation. The angle of the prism \( P_2 \) in degrees is:
View Solution
A hemispherical vessel is completely filled with a liquid of refractive index \( \mu \). A small coin is kept at the lowest point \( O \) of the vessel as shown in the figure. The minimum value of the refractive index of the liquid so that a person can see the coin from point \( E \) (at the level of the vessel) is:

View Solution
A particle of mass \( m \) and charge \( q \) is fastened to one end \( A \) of a massless string having equilibrium length \( l \), whose other end is fixed at point \( O \). The whole system is placed on a frictionless horizontal plane and is initially at rest. If a uniform electric field is switched on along the direction as shown in the figure, then the speed of the particle when it crosses the x-axis is:

View Solution
Which of the following circuits has the same output as that of the given circuit?

View Solution
For a particular ideal gas, which of the following graphs represents the variation of mean squared velocity of the gas molecules with temperature?

View Solution
A bead of mass \( m \) slides without friction on the wall of a vertical circular hoop of radius \( R \) as shown in figure. The bead moves under the combined action of gravity and a massless spring \( k \) attached to the bottom of the hoop. The equilibrium length of the spring is \( R \). If the bead is released from the top of the hoop with (negligible) zero initial speed, the velocity of the bead, when the length of spring becomes \( R \), would be (spring constant is \( k \), \( g \) is acceleration due to gravity):
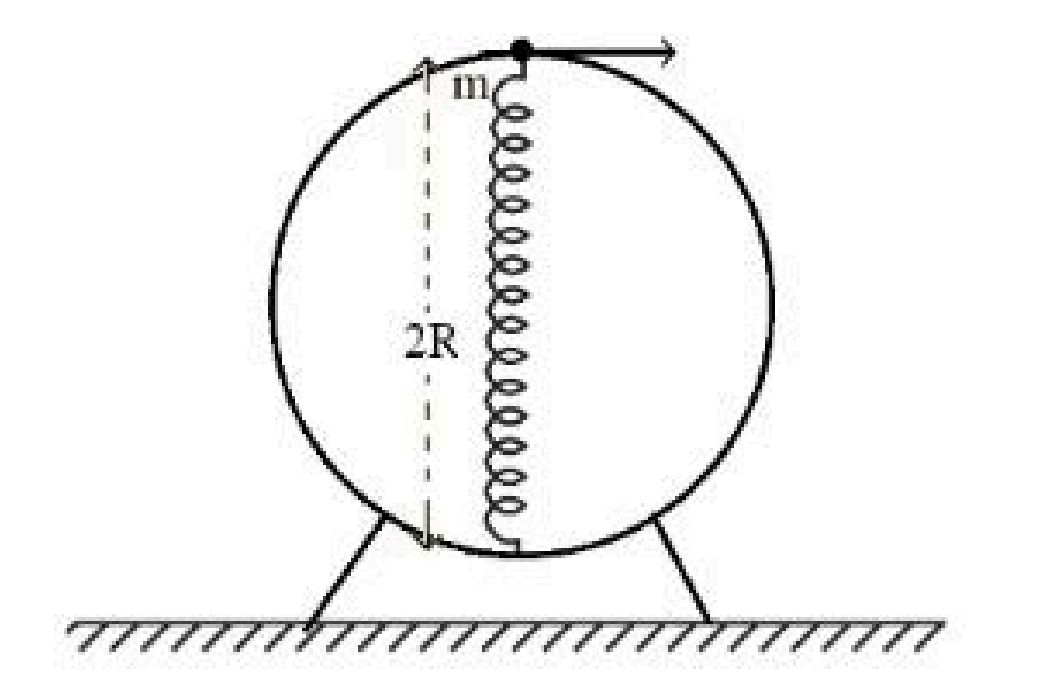
View Solution
Due to presence of an em-wave whose electric component is given by \( E = 100 \sin(\omega t - kx) \, \text{NC}^{-1} \), a cylinder of length 200 cm holds certain amount of em-energy inside it. If another cylinder of same length but half diameter than previous one holds same amount of em-energy, the magnitude of the electric field of the corresponding em-wave should be modified as:
View Solution
Three infinitely long wires with linear charge density \( \lambda \) are placed along the x-axis, y-axis and z-axis respectively. Which of the following denotes an equipotential surface?
View Solution
Consider the following statements: Surface tension arises due to extra energy of the molecules at the interior as compared to the molecules at the surface of a liquid. As the temperature of liquid rises, the coefficient of viscosity increases. As the temperature of gas increases, the coefficient of viscosity increases. The onset of turbulence is determined by Reynolds number. In a steady flow, two streamlines never intersect. Choose the correct answer from the options given below:
View Solution
Find the equivalent resistance between two ends of the following circuit: % Circuit Description \textit{The circuit consists of three resistors, two of \(\frac{r}{3}\) in series connected in parallel with another resistor of \(r\).
Choose the correct nuclear process from the below options:
View Solution
A Carnot engine (E) is working between two temperatures 473K and 273K. In a new system two engines - engine \(E_1\) works between 473K to 373K and engine \(E_2\) works between 373K to 273K. If \(\eta_{12}\), \(\eta_1\) and \(\eta_2\) are the efficiencies of the engines \(E\), \(E_1\) and \(E_2\), respectively, then:
View Solution
Given below are two statements: one is labelled as Assertion \(A\) and the other as Reason \(R\): Assertion \(A\): A sound wave has higher speed in solids than in gases.
Reason \(R\): Gases have higher value of Bulk modulus than solids.
View Solution
In the experiment for measurement of viscosity \( \eta \) of a given liquid with a ball having radius \( R \), consider following statements: A. Graph between terminal velocity \( V \) and \( R \) will be a parabola.
B. The terminal velocities of different diameter balls are constant for a given liquid.
C. Measurement of terminal velocity is dependent on the temperature.
D. This experiment can be utilized to assess the density of a given liquid.
E. If balls are dropped with some initial speed, the value of \( \eta \) will change.
View Solution
Two capacitors \( C_1 \) and \( C_2 \) are connected in parallel to a battery. Charge-time graph is shown below for the two capacitors. The energy stored with them are \( U_1 \) and \( U_2 \), respectively. Which of the given statements is true?

View Solution
A wire of resistance R is bent into an equilateral triangle and an identical wire is bent into a square. The ratio of resistance between the two end points of an edge of the triangle to that of the square is:
View Solution
The center of mass of a thin rectangular plate (fig - x) with sides of length \( a \) and \( b \), whose mass per unit area (\( \sigma \)) varies as \( \sigma = \sigma_0 \frac{x}{ab} \) (where \( \sigma_0 \) is a constant), would be

View Solution
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R. Assertion A: In a central force field, the work done is independent of the path chosen. Reason R: Every force encountered in mechanics does not have an associated potential energy. In the light of the above statements, choose the most appropriate answer from the options given below.
View Solution
A proton of mass 'mp' has same energy as that of a photon of wavelength 'λ'. If the proton is moving at non-relativistic speed, then ratio of its de Broglie wavelength to the wavelength of photon is.
View Solution
In a measurement, it is asked to find the modulus of elasticity per unit torque applied on the system. The measured quantity has the dimension of \( [M^a L^b T^c] \). If \( b = 3 \), the value of \( c \) is:
View Solution
A tiny metallic rectangular sheet has length and breadth of 5 mm and 2.5 mm, respectively. Using a specially designed screw gauge which has pitch of 0.75 mm and 15 divisions in the circular scale, you are asked to find the area of the sheet. In this measurement, the maximum fractional error will be \( \frac{x}{100} \), where \( x \) is:
View Solution
The moment of inertia of a solid disc rotating along its diameter is 2.5 times higher than the moment of inertia of a ring rotating in a similar way. The moment of inertia of a solid sphere which has the same radius as the disc and rotating in similar way, is \( n \) times higher than the moment of inertia of the given ring. Here, \( n = \):
View Solution
Two iron solid discs of negligible thickness have radii \( R_1 \) and \( R_2 \) and moment of inertia \( I_1 \) and \( I_2 \), respectively. For \( R_2 = 2R_1 \), the ratio of \( I_1 \) and \( I_2 \) would be \( \frac{1}{x} \), where \( x \) is:
View Solution
A double slit interference experiment performed with a light of wavelength 600 nm forms an interference fringe pattern on a screen with 10th bright fringe having its centre at a distance of 10 mm from the central maximum. Distance of the centre of the same 10th bright fringe from the central maximum when the source of light is replaced by another source of wavelength 660 nm would be:
View Solution
The products A and B in the following reactions, respectively, are:

View Solution
The correct order of stability of following carbocations is:

View Solution
Given below are two statements:
Statement I: In the oxalic acid vs KMnO$_4$ (in the presence of dil H$_2$SO$_4$) titration the solution needs to be heated initially to 60°C, but no heating is required in Ferrous ammonium sulphate (FAS) vs KMnO$_4$ titration (in the presence of dil H$_2$SO$_4$). Statement II: In oxalic acid vs KMnO$_4$ titration, the initial formation of MnSO$_4$ takes place at high temperature, which then acts as catalyst for further reaction. In the case of FAS vs KMnO$_4$, heating oxidizes Fe$^{2+$ into Fe$^{3+$ by oxygen of air and error may be introduced in the experiment. In the light of the above statements, choose the correct answer from the options given below:
View Solution
A molecule (P) on treatment with acid undergoes rearrangement and gives (Q). (Q) on ozonolysis followed by reflux under alkaline condition gives (R). The structure of (R) is given below. The structure of (P) is:
View Solution
Given below are two statements:

View Solution
In a multielectron atom, which of the following orbitals described by three quantum numbers will have the same energy in absence of electric and magnetic fields? A. \( n = 1, l = 0, m_l = 0 \) B. \( n = 2, l = 0, m_l = 0 \) C. \( n = 2, l = 1, m_l = 1 \) D. \( n = 3, l = 2, m_l = 1 \) E. \( n = 3, l = 2, m_l = 0 \) Choose the correct answer from the options given below:
View Solution
Given below are two statements: Statement I: D-glucose pentaacetate reacts with 2,4-dinitrophenylhydrazine. Statement II: Starch, on heating with concentrated sulfuric acid at 100°C and 2-3 atmosphere pressure, produces glucose. In the light of the above statements, choose the correct answer from the options given below:
View Solution
Both acetaldehyde and acetone (individually) undergo which of the following reactions? A. Iodoform Reaction B. Cannizzaro Reaction C. Aldol Condensation D. Tollen's Test E. Clemmensen Reduction Choose the correct answer from the options given below:
View Solution
Which of the following oxidation reactions are carried out by both \( K_2Cr_2O_7 \) and \( KMnO_4 \) in acidic medium? A. \( I^- \rightarrow I_2 \) B. \( S^{2-} \rightarrow S \) C. \( Fe^{2+} \rightarrow Fe^{3+} \) D. \( I^- \rightarrow IO_3^- \) E. \( S_2O_3^{2-} \rightarrow SO_4^{2-} \) Choose the correct answer from the options given below:
View Solution
Match the LIST-I with LIST-II (Redox Reactions). \begin{tabular{|c|c| \hline LIST-I (Redox Reaction) & LIST-II (Type of Redox Reaction)
\hline A. \( CH_4(g) + 2O_2(g) \rightarrow CO_2(g) + 2H_2O(l) \) & I. Disproportionation reaction
B. \( 2NaH(s) \rightarrow 2Na(s) + H_2(g) \) & II. Combination reaction
C. \( V_2O_5(s) + 5Ca(s) \rightarrow 2V(s) + 5CaO(s) \) & III. Decomposition reaction
D. \( 2H_2O(aq) \rightarrow 2H_2(g) + O_2(g) \) & IV. Displacement reaction
\hline \end{tabular Choose the correct answer from the options given below:
View Solution
Consider the following elements In, Tl, Al, Pb, and Ge. The most stable oxidation states of elements with highest and lowest first ionisation enthalpies, respectively, are:
View Solution
The metal ion whose electronic configuration is not affected by the nature of the ligand and which gives a violet color in non-luminous flame under hot condition in borax bead test is:
View Solution
A weak acid HA has degree of dissociation x. Which option gives the correct expression of \(pH - pK_a\)?
View Solution
The molecules having square pyramidal geometry are:
View Solution
The compounds that produce CO$_2$ with aqueous NaHCO$_3$ solution are:

View Solution
Consider ‘n’ is the number of lone pair of electrons present in the equatorial position of the most stable structure of \( \text{ClF}_3 \). The ions from the following with ‘n’ number of unpaired electrons are: A. \( \text{V}^{3+} \)
B. \( \text{Ti}^{3+} \)
C. \( \text{Cu}^{2+} \)
D. \( \text{Ni}^{2+} \)
E. \( \text{Ti}^{2+} \)
Choose the correct answer from the options given below:
View Solution
The incorrect decreasing order of atomic radii is:
View Solution
What is the freezing point depression constant of a solvent, 50 g of which contain 1 g non-volatile solute (molar mass 256 g mol\(^{-1}\)) and the decrease in freezing point is 0.40 K?
View Solution
Ice and water are placed in a closed container at a pressure of 1 atm and temperature 273.15K. If pressure of the system is increased 2 times, keeping temperature constant, then identify correct observation from the following:
View Solution
For a given reaction \( R \rightarrow P \), \( t_{1/2} \) is related to \([A_0]\) as given in table. Given: \( \log 2 = 0.30 \). Which of the following is true? \begin{tabular{|c|c| \hline [A] (mol/L) & t$_{1/2}$ (min)
\hline 0.100 & 200
0.025 & 100
\hline \end{tabular
View Solution
The formation enthalpies, \( \Delta H_f^\circ \) for \( \text{H}_2 \) and \( \text{O}_2 \) are 220.0 and 250.0 kJ mol\(^{-1}\), respectively, at 298.15 K, and \( \Delta H_f^\circ \) for \( \text{H}_2\text{O} \) (g) is -242.0 kJ mol\(^{-1}\) at the same temperature. The average bond enthalpy of the O-H bond in water at 298.15 K is:
View Solution
Quantitative analysis of an organic compound (X) shows the following percentage composition. C: 14.5% Cl: 64.46% H: 1.8% Empirical formula mass of the compound (X) is:
View Solution
Given below is the plot of the molar conductivity vs \( \sqrt{c} \) concentration for KCl in aqueous solution. If, for the higher concentration of KCl solution, the resistance of the conductivity cell is 100 \( \Omega \), then the resistance of the same cell with the dilute solution is 'x' \( \Omega \). The value of \( x \) is:

View Solution
Consider the following sequence of reactions: \includegraphics[width=0.5\linewidth]{74.png 11.25 mg of chlorobenzene will produce \( x \times 10^{-1} \) mg of product B. Consider the reactions result in complete conversation. Given molar mass of C, H, O, N, and Cl as 12, 1, 16, 14, and 35.5 g mol\(^{-1}\), respectively, the value of \( x \) is:
View Solution
The molarity of a 70% (mass/mass) aqueous solution of a monobasic acid (X) is:
{Given: Density of aqueous solution of \( X \) is 1.25 g/mL Molar mass of the acid \( X \) is 70 g/mol
View Solution








































Also Check: Good Score in JEE Main 2025
JEE Main 28th Jan Shift 1 Paper Analysis- Check Difficulty Level and Good Score
The question paper consisted of a total of 75 questions, divided equally across the three subjects:
- The Mathematics section in JEE Main 2025 28th Jan Shift 1 Question Paper was Tough with 9 questions coming majorly from topics like Integration, Co-ordinate Geometry, etc.
- Physics was Tough with 7 questions coming majorly from topics like Modern Physics, Thermodynamics, etc.
- Chemistry was Easy with 8 questions coming majorly from topics like Organic Chemistry, Physical Chemistry, etc.
Each section included a mix of multiple-choice questions (MCQs) and numerical value-based questions, offering a balanced challenge for students.
Check: JEE Main 28th Jan Shift 2 Question Paper
JEE Main 2025: Shift-Wise Analysis
| Session | Shift | Difficulty Trend (Physics, Chemistry, Mathematics) |
Overall Difficulty |
|---|---|---|---|
| January | 22nd January Shift 1 |
|
Moderate |
| January | 22nd January Shift 2 |
|
Moderate |
| January | 23rd January Shift 1 |
|
Moderate |
| January | 23rd January Shift 2 |
|
Moderate |
| January | 24th January Shift 1 |
|
Moderate |
| January | 24th January Shift 2 |
|
Moderate |
| January | 28th January Shift 1 |
|
Tough |
| January | 28th January Shift 2 |
|
Tough |
| January | 29th January Shift 1 |
|
Moderate to Tough |
| January | 29th January Shift 2 |
|
Moderate to Tough |





Comments