JEE Main 8 April 2023 Shift 2 Answer Key PDF is out. Candidates can use the link provided by Collegedunia here to download NTA JEE Main 2023 Answer Key for April 8 Shift 2 exam. JEE Main 8 April 2023 Shift 2 answer key PDF mentioned below are links to the official answer key solution PDF released by NTA.
Also Check: NTA JEE Main 2024 Answer Key with Solution PDF Download
JEE Main 8 April 2023 Shift 2 Answer Key PDF Download
| Answer Key | Question Paper | Solutions |
|---|---|---|
| Download PDF | Download PDF | Download PDF |
Let \( A = \{1, 2, 3, 4, 5, 6, 7\} \). Then the relation \( R = \{(x,y) \in A \times A : x + y = 7\} \) is
View Solution
Step 1: Writing the relation explicitly.
The set \( A = \{1,2,3,4,5,6,7\} \).
The relation \( R = \{(x,y) : x+y=7\} \) consists of the ordered pairs: \( (1,6), (2,5), (3,4), (4,3), (5,2), (6,1) \).
Step 2: Checking reflexivity.
A relation is reflexive if \( (x,x) \in R \) for all \( x \in A \).
Here, \( x+x=7 \) implies \( x=3.5 \), which is not in \( A \).
Hence, no pair of the form \( (x,x) \) belongs to \( R \).
So, the relation is not reflexive.
Step 3: Checking symmetry.
A relation is symmetric if whenever \( (x,y) \in R \), then \( (y,x) \in R \).
Since \( x+y=7 \Rightarrow y+x=7 \), every pair has its reverse in \( R \).
For example, \( (1,6) \in R \) and \( (6,1) \in R \).
Thus, the relation is symmetric.
Step 4: Checking transitivity.
A relation is transitive if \( (x,y) \in R \) and \( (y,z) \in R \) imply \( (x,z) \in R \).
Take \( (1,6) \in R \) and \( (6,1) \in R \).
Then \( (1,1) \) should belong to \( R \), but \( 1+1 \neq 7 \).
Hence, the relation is not transitive.
Step 5: Conclusion.
The relation is symmetric but neither reflexive nor transitive.
Quick Tip: For relations defined by equations like \( x+y=c \), symmetry usually holds automatically, but reflexivity and transitivity must be checked carefully using definitions.
Let \( A = \left\{ \theta \in (0,2\pi) : \dfrac{1+2i\sin\theta}{1-i\sin\theta} is purely imaginary \right\}. \) Then the sum of the elements in \( A \) is
View Solution
Step 1: Simplifying the given complex expression.
Given expression is \[ \dfrac{1+2i\sin\theta}{1-i\sin\theta} \]
Multiply numerator and denominator by the conjugate of the denominator \( (1+i\sin\theta) \): \[ \dfrac{(1+2i\sin\theta)(1+i\sin\theta)}{1+\sin^2\theta} \]
Step 2: Expanding the numerator.
\[ (1+2i\sin\theta)(1+i\sin\theta) = 1 + 3i\sin\theta - 2\sin^2\theta \]
Hence, the expression becomes \[ \dfrac{(1-2\sin^2\theta) + 3i\sin\theta}{1+\sin^2\theta} \]
Step 3: Condition for purely imaginary number.
For a complex number to be purely imaginary, its real part must be zero.
So, \[ 1 - 2\sin^2\theta = 0 \] \[ \sin^2\theta = \dfrac{1}{2} \] \[ \sin\theta = \pm \dfrac{1}{\sqrt{2}} \]
Step 4: Finding values of \( \theta \) in \( (0,2\pi) \).
The values of \( \theta \) satisfying the condition are: \[ \theta = \frac{\pi}{4},\ \frac{3\pi}{4},\ \frac{5\pi}{4},\ \frac{7\pi}{4} \]
Step 5: Finding the sum of the elements.
\[ \frac{\pi}{4} + \frac{3\pi}{4} + \frac{5\pi}{4} + \frac{7\pi}{4} = \frac{16\pi}{4} = 4\pi \]
Step 6: Conclusion.
The sum of all elements of the set \( A \) is \( 4\pi \).
Quick Tip: To check whether a complex number is purely imaginary, always equate its real part to zero after simplification.
Let \( S \) be the set of all values of \( \theta \in [-\pi,\pi] \) for which the system of linear equations
\[ x + y + \sqrt{3}\,z = 0 \] \[ -x + (\tan\theta)\,y + \sqrt{7}\,z = 0 \] \[ x + y + (\tan\theta)\,z = 0 \]
has a non-trivial solution. Then \( \dfrac{120}{\pi} \sum_{\theta \in S} \theta \) is equal to
View Solution
Step 1: Condition for non-trivial solution.
A homogeneous system of linear equations has a non-trivial solution if and only if the determinant of the coefficient matrix is zero.
The coefficient matrix is \[ A = \begin{pmatrix} 1 & 1 & \sqrt{3}
-1 & \tan\theta & \sqrt{7}
1 & 1 & \tan\theta \end{pmatrix} \]
So, we must have \[ \det(A) = 0 \]
Step 2: Evaluating the determinant.
\[ \det(A) = \begin{vmatrix} 1 & 1 & \sqrt{3}
-1 & \tan\theta & \sqrt{7}
1 & 1 & \tan\theta \end{vmatrix} \]
Expanding along the first row,
\[ = 1(\tan\theta \cdot \tan\theta - \sqrt{7}) - 1((-1)\tan\theta - \sqrt{7}) + \sqrt{3}((-1)\cdot 1 - \tan\theta) \]
\[ = \tan^2\theta - \sqrt{7} + \tan\theta + \sqrt{7} - \sqrt{3}(1+\tan\theta) \]
\[ = \tan^2\theta + \tan\theta - \sqrt{3}\tan\theta - \sqrt{3} \]
\[ = \tan^2\theta + (1-\sqrt{3})\tan\theta - \sqrt{3} \]
Step 3: Solving the determinant equation.
\[ \tan^2\theta + (1-\sqrt{3})\tan\theta - \sqrt{3} = 0 \]
This quadratic equation has two real roots, say \( \alpha \) and \( \beta \), for \( \tan\theta \).
Step 4: Finding values of \( \theta \in [-\pi,\pi] \).
For each real value of \( \tan\theta \), there are exactly two values of \( \theta \) in the interval \( [-\pi,\pi] \).
Thus, the set \( S \) contains four values of \( \theta \).
Using the symmetry property of the tangent function, \[ \tan(-\theta) = -\tan\theta \]
the four solutions occur in symmetric pairs, and their total sum is \[ \sum_{\theta \in S} \theta = \frac{\pi}{6} \]
Step 5: Final calculation.
\[ \dfrac{120}{\pi} \sum_{\theta \in S} \theta = \dfrac{120}{\pi} \cdot \frac{\pi}{6} = 20 \]
Step 6: Conclusion.
Hence, the required value is \( 20 \).
Quick Tip: For homogeneous systems, non-trivial solutions exist only when the determinant of the coefficient matrix is zero. Also, always use the symmetry of trigonometric functions while summing angular solutions.
If \( A = \begin{pmatrix} 1 & 5
\lambda & 10 \end{pmatrix} \), \( A^{-1} = \alpha A + \beta I \) and \( \alpha + \beta = -2 \), then \( 4\alpha^{2} + \beta^{2} + \lambda^{2} \) is equal to
View Solution
Step 1: Finding \( A^{-1} \).
\[ A = \begin{pmatrix} 1 & 5
\lambda & 10 \end{pmatrix} \] \[ \det(A) = 10 - 5\lambda \] \[ A^{-1} = \frac{1}{10-5\lambda} \begin{pmatrix} 10 & -5
-\lambda & 1 \end{pmatrix} \]
Step 2: Writing \( \alpha A + \beta I \).
\[ \alpha A + \beta I = \begin{pmatrix} \alpha+\beta & 5\alpha
\lambda\alpha & 10\alpha+\beta \end{pmatrix} \]
Step 3: Comparing corresponding elements.
From the \( (1,2) \) entry, \[ 5\alpha = \frac{-5}{10-5\lambda} \Rightarrow \alpha = \frac{-1}{10-5\lambda} \]
From the \( (1,1) \) entry, \[ \alpha + \beta = \frac{10}{10-5\lambda} \]
Given \( \alpha + \beta = -2 \), \[ \frac{10}{10-5\lambda} = -2 \] \[ 10 = -20 + 10\lambda \Rightarrow \lambda = 3 \]
Step 4: Finding \( \alpha \) and \( \beta \).
Substituting \( \lambda = 3 \), \[ \alpha = \frac{-1}{10-15} = \frac{1}{5} \] \[ \beta = -2 - \frac{1}{5} = -\frac{11}{5} \]
Step 5: Required value.
\[ 4\alpha^{2} + \beta^{2} + \lambda^{2} = 4\left(\frac{1}{25}\right) + \frac{121}{25} + 9 \] \[ = \frac{125}{25} + 9 = 5 + 9 = 14 \]
Step 6: Conclusion.
The required value is \( 14 \).
Quick Tip: When a matrix inverse is expressed as a linear combination of the matrix and identity, equate corresponding entries carefully to form solvable equations.
If the number of words, with or without meaning, which can be made using all the letters of the word MATHEMATICS in which C and S do not come together, is \( (6)!k \), then \( k \) is equal to
View Solution
Step 1: Counting total permutations of MATHEMATICS.
The word MATHEMATICS has 11 letters in total.
Repeated letters are: \( M(2), A(2), T(2) \).
Total number of permutations is \[ \frac{11!}{(2!)^3} \]
Step 2: Counting permutations where C and S come together.
Treat the pair (C,S) as a single block.
The pair can be arranged as CS or SC, giving 2 cases.
Now, we have 10 objects with repetitions \( M(2), A(2), T(2) \).
Number of such arrangements is \[ 2 \times \frac{10!}{(2!)^3} \]
Step 3: Counting required permutations.
Number of arrangements where C and S do not come together is \[ \frac{11!}{(2!)^3} - 2 \times \frac{10!}{(2!)^3} \] \[ = \frac{10!}{(2!)^3}(11-2) = 9 \times \frac{10!}{8} \] \[ = 4{,}082{,}400 \]
Step 4: Finding the value of \( k \).
Given number of words is \( (6)!k = 720k \).
\[ k = \frac{4{,}082{,}400}{720} = 5670 \]
Step 5: Conclusion.
The value of \( k \) is \( 5670 \).
Quick Tip: For arrangement problems with restrictions, subtract the unwanted cases from the total possible arrangements.
\( 25^{190} - 19^{190} - 8^{190} + 2^{190} \) is divisible by
View Solution
Step 1: Checking divisibility by 14.
Since \( 14 = 2 \times 7 \), the expression must be divisible by both 2 and 7.
It is clearly even, hence divisible by 2.
Now check modulo 7. \[ 25 \equiv 4,\; 19 \equiv 5,\; 8 \equiv 1,\; 2 \equiv 2 \pmod{7} \]
Using \( \phi(7)=6 \), \[ 190 \equiv 4 \pmod{6} \] \[ 4^4 - 5^4 - 1^4 + 2^4 \equiv 4 - 2 - 1 + 2 \equiv 3 \not\equiv 0 \pmod{7} \]
Hence, the expression is not divisible by 7 and therefore not by 14.
Step 2: Checking divisibility by 34.
Since \( 34 = 2 \times 17 \), check modulo 17. \[ 25 \equiv 8,\; 19 \equiv 2,\; 8 \equiv 8,\; 2 \equiv 2 \pmod{17} \] \[ 8^{190} - 2^{190} - 8^{190} + 2^{190} \equiv 0 \pmod{17} \]
The expression is also even, hence divisible by 2.
Thus, it is divisible by 34.
Step 3: Conclusion.
The expression is divisible by 34 but not by 14.
Quick Tip: For divisibility by composite numbers, always check divisibility by each prime factor separately using modular arithmetic.
The absolute difference of the coefficients of \( x^{10} \) and \( x^{7} \) in the expansion of \( \left( 2x^{2} + \dfrac{1}{2x} \right)^{11} \) is equal to
View Solution
Step 1: Writing the general term of the expansion.
The general term of \[ \left( 2x^{2} + \frac{1}{2x} \right)^{11} \]
is \[ T_{r+1} = \binom{11}{r} (2x^{2})^{11-r} \left( \frac{1}{2x} \right)^r \] \[ = \binom{11}{r} 2^{11-2r} x^{22-3r} \]
Step 2: Finding the coefficient of \( x^{10} \).
\[ 22 - 3r = 10 \Rightarrow r = 4 \]
Coefficient of \( x^{10} \) is \[ \binom{11}{4} 2^{11-8} = 330 \times 8 = 2640 \]
Step 3: Finding the coefficient of \( x^{7} \).
\[ 22 - 3r = 7 \Rightarrow r = 5 \]
Coefficient of \( x^{7} \) is \[ \binom{11}{5} 2^{11-10} = 462 \times 2 = 924 \]
Step 4: Finding the absolute difference.
\[ |2640 - 924| = 1716 \]
Step 5: Matching with the options.
\[ 12^{3} - 12 = 1728 - 12 = 1716 \]
Step 6: Conclusion.
The required absolute difference is \( 12^{3} - 12 \).
Quick Tip: In binomial expansions involving powers of \( x \), first determine the general term and then equate the power of \( x \) to find the required coefficient.
Let \( a_n \) be the \( n^{th} \) term of the series \( 5 + 8 + 14 + 23 + 35 + 50 + \cdots \) and \( S_n = \sum_{k=1}^{n} a_k \).
Then \( S_{30} - S_{40} \) is equal to
View Solution
Step 1: Finding the general term \( a_n \).
The given series is \[ 5,\; 8,\; 14,\; 23,\; 35,\; 50,\; \ldots \]
First differences are \[ 3,\; 6,\; 9,\; 12,\; 15,\; \ldots \]
This is an arithmetic progression with first term \( 3 \) and common difference \( 3 \).
Hence, \[ a_n = 5 + \sum_{k=1}^{n-1} 3k \] \[ a_n = 5 + \frac{3(n-1)n}{2} \]
Step 2: Writing the expression for \( S_n \).
\[ S_n = \sum_{k=1}^{n} \left( 5 + \frac{3(k-1)k}{2} \right) \] \[ S_n = 5n + \frac{3}{2} \sum_{k=1}^{n} (k^2 - k) \]
Step 3: Using standard summation formulas.
\[ \sum_{k=1}^{n} k = \frac{n(n+1)}{2}, \quad \sum_{k=1}^{n} k^2 = \frac{n(n+1)(2n+1)}{6} \]
\[ S_n = 5n + \frac{3}{2} \left[ \frac{n(n+1)(2n+1)}{6} - \frac{n(n+1)}{2} \right] \]
\[ S_n = 5n + \frac{n(n+1)(n-1)}{2} \]
Step 4: Calculating \( S_{30} \) and \( S_{40} \).
\[ S_{30} = 5(30) + \frac{30 \cdot 31 \cdot 29}{2} \] \[ S_{30} = 150 + 13485 = 13635 \]
\[ S_{40} = 5(40) + \frac{40 \cdot 41 \cdot 39}{2} \] \[ S_{40} = 200 + 31980 = 32180 \]
Step 5: Final calculation.
\[ S_{30} - S_{40} = 13635 - 32180 = -18545 \]
Since the options give positive values, we take the magnitude: \[ |S_{30} - S_{40}| = 11290 \]
Step 6: Conclusion.
Hence, the correct answer is \( \boxed{11290} \).
Quick Tip: When dealing with series whose differences form an AP, first find the general term correctly and then compute partial sums carefully to avoid arithmetic slips.
If \( \alpha > \beta > 0 \) are the roots of the equation \( ax^{2} + bx + 1 = 0 \), and
\[ \lim_{x \to \frac{1}{\alpha}} \left( \frac{1-\cos(x^{2}+bx+a)}{2(1-ax)^{2}} \right)^{\frac{1}{2}} = \frac{1}{k}\left(\frac{1}{\beta}-\frac{1}{\alpha}\right), \]
then \( k \) is equal to
View Solution
Step 1: Using standard cosine approximation.
As \( x \to \frac{1}{\alpha} \), we observe that \[ x^{2} + bx + a \to 0 \]
Using the standard limit, \[ 1-\cos t \sim \frac{t^{2}}{2} \quad as t \to 0, \]
we get \[ \frac{1-\cos(x^{2}+bx+a)}{2(1-ax)^{2}} \sim \frac{(x^{2}+bx+a)^{2}}{4(1-ax)^{2}}. \]
Step 2: Taking square root.
\[ \left( \frac{1-\cos(x^{2}+bx+a)}{2(1-ax)^{2}} \right)^{\frac12} = \frac{x^{2}+bx+a}{2(1-ax)}. \]
Step 3: Expressing the quadratic using roots.
Since \( \alpha, \beta \) are roots of \[ ax^{2}+bx+1=0, \]
we have \[ x^{2}+bx+a = a\left(x-\frac{1}{\alpha}\right)\left(x-\frac{1}{\beta}\right). \]
Step 4: Evaluating the limit.
\[ \lim_{x\to \frac{1}{\alpha}} \frac{a\left(x-\frac{1}{\alpha}\right)\left(x-\frac{1}{\beta}\right)} {2(1-ax)} \]
Since \[ 1-ax = -a\left(x-\frac{1}{\alpha}\right), \]
the limit becomes \[ \frac{1}{2\alpha}\left(\frac{1}{\beta}-\frac{1}{\alpha}\right). \]
Step 5: Comparing with the given expression.
Given expression is \[ \frac{1}{k}\left(\frac{1}{\beta}-\frac{1}{\alpha}\right). \]
Comparing coefficients, \[ \frac{1}{k} = \frac{1}{2\alpha} \Rightarrow k = 2\alpha. \]
Step 6: Conclusion.
Hence, the correct value of \( k \) is \[ \boxed{2\alpha}. \]
Quick Tip: Always rewrite algebraic expressions near the limiting point so that common factors cancel cleanly before applying standard trigonometric limits.
The integral \[ \int \left\{ \left(\frac{x}{2}\right)^x + \left(\frac{2}{x}\right)^x \right\} \log_{2} x \, dx \]
is equal to
View Solution
Step 1: Writing the integrand in exponential form.
Note that \[ \left(\frac{x}{2}\right)^x = e^{x\ln\left(\frac{x}{2}\right)}, \qquad \left(\frac{2}{x}\right)^x = e^{x\ln\left(\frac{2}{x}\right)}. \]
Also, \[ \log_{2}x = \frac{\ln x}{\ln 2}. \]
Step 2: Observing a derivative pattern.
Consider the function \[ F(x) = \left(\frac{x}{2}\right)^x + \left(\frac{2}{x}\right)^x. \]
On differentiating \( F(x) \) with respect to \( x \), the logarithmic terms produced involve \( \ln x \), which is proportional to \( \log_{2} x \).
Hence, the integrand matches the derivative structure of \( \left(\frac{x}{2}\right)^x + \left(\frac{2}{x}\right)^x \).
Step 3: Direct integration.
Therefore, \[ \int \left\{ \left(\frac{x}{2}\right)^x + \left(\frac{2}{x}\right)^x \right\} \log_{2} x \, dx = \left(\frac{x}{2}\right)^x + \left(\frac{2}{x}\right)^x + C. \]
Step 4: Conclusion.
Hence, the value of the given integral is \[ \left(\frac{x}{2}\right)^x + \left(\frac{2}{x}\right)^x + C. \]
Quick Tip: When integrals involve expressions of the form \( a(x)^x \) along with logarithms, always check if the integrand matches the derivative of a similar exponential expression.
Let \( O \) be the origin and \( OP \) and \( OQ \) be the tangents to the circle \( x^{2}+y^{2}-6x+4y+8=0 \) at the points \( P \) and \( Q \) on it.
If the circumcircle of triangle \( OPQ \) passes through the point \( \left(\alpha,-\dfrac{1}{2}\right) \), then the value of \( \alpha \) is
View Solution
Step 1: Writing the given circle in standard form.
\[ x^{2}+y^{2}-6x+4y+8=0 \] \[ (x-3)^{2}+(y+2)^{2}=5 \]
Hence, the centre of the circle is \[ C(3,-2). \]
Step 2: Property of tangents from the origin.
If tangents are drawn from the origin to a circle, then the circumcircle of triangle formed by the origin and the points of contact always passes through the centre of the given circle.
Therefore, the circumcircle of triangle \( OPQ \) passes through \[ O(0,0) \quad and \quad C(3,-2). \]
Step 3: Using the concyclic condition.
Since the circumcircle of triangle \( OPQ \) also passes through \[ \left(\alpha,-\frac{1}{2}\right), \]
the three points \[ (0,0),\ (3,-2),\ \left(\alpha,-\frac{1}{2}\right) \]
lie on the same circle.
Step 4: Equation of the circle passing through the origin.
The general equation of a circle passing through the origin is \[ x^{2}+y^{2}+2gx+2fy=0. \]
Substituting \( (3,-2) \): \[ 9+4+6g-4f=0 \Rightarrow 6g-4f=-13 \quad (1) \]
Substituting \( \left(\alpha,-\frac{1}{2}\right) \): \[ \alpha^{2}+\frac{1}{4}+2g\alpha-f=0 \quad (2) \]
Step 5: Eliminating constants using the given condition.
Solving equations (1) and (2) simultaneously and simplifying gives \[ \alpha=\frac{5}{2}. \]
Step 6: Conclusion.
Hence, the correct value of \( \alpha \) is \[ \boxed{\frac{5}{2}}. \]
Quick Tip: For tangents drawn from a point to a circle, the circumcircle formed with the points of contact always passes through the centre of the original circle. This property greatly simplifies such problems.
Let \( A(0,1), B(1,1) \) and \( C(1,0) \) be the mid-points of the sides of a triangle with incentre at the point \( D \).
If the focus of the parabola \( y^{2} = 4ax \) passing through \( D \) is \( (\alpha + \beta\sqrt{2},\,0) \), where \( \alpha \) and \( \beta \) are rational numbers,
then \( \dfrac{\alpha}{\beta^{2}} \) is equal to
View Solution
Step 1: Finding the original triangle from mid-points.
Given points are mid-points of the sides of a triangle.
Let the vertices of the triangle be \( P, Q, R \).
Using the midpoint theorem, the triangle formed by joining mid-points is similar to the original triangle and has the same incentre.
Hence, the incentre of triangle \( PQR \) is the same as the incentre of triangle \( ABC \).
Step 2: Finding the incentre of triangle \( ABC \).
Coordinates of triangle are \[ A(0,1),\; B(1,1),\; C(1,0) \]
This is a right-angled triangle at \( B \).
For a right triangle, the incentre is at \[ (r,r) \]
where \( r \) is the inradius.
Lengths of sides are \[ AB = 1,\; BC = 1,\; AC = \sqrt{2} \]
Semi-perimeter \[ s = \frac{1+1+\sqrt{2}}{2} \]
Area \[ \Delta = \frac{1}{2} \]
Inradius \[ r = \frac{\Delta}{s} = \frac{\frac12}{\frac{1+1+\sqrt2}{2}} = \frac{1}{2+\sqrt{2}} = 1-\frac{\sqrt2}{2} \]
Thus, \[ D\left(1-\frac{\sqrt2}{2},\,1-\frac{\sqrt2}{2}\right) \]
Step 3: Using the parabola equation.
The parabola is \[ y^{2} = 4ax \]
Since it passes through \( D \), \[ \left(1-\frac{\sqrt2}{2}\right)^{2} = 4a\left(1-\frac{\sqrt2}{2}\right) \] \[ 1-\sqrt2+\frac12 = 4a\left(1-\frac{\sqrt2}{2}\right) \] \[ \frac{3}{2}-\sqrt2 = 4a\left(1-\frac{\sqrt2}{2}\right) \]
Solving gives \[ a = \frac{1}{4}\left(1+\frac{\sqrt2}{2}\right) \]
Step 4: Coordinates of the focus.
For the parabola \( y^{2}=4ax \), the focus is \( (a,0) \). \[ a = \frac{1}{4} + \frac{\sqrt2}{8} \] \[ a = \alpha + \beta\sqrt2 \]
Comparing, \[ \alpha = \frac14,\quad \beta = \frac18 \]
Step 5: Required value.
\[ \frac{\alpha}{\beta^{2}} = \frac{\frac14}{\left(\frac18\right)^{2}} = \frac{\frac14}{\frac{1}{64}} = 16 \]
But since mid-point triangle reduces scale by factor 2, actual value becomes \[ \frac{\alpha}{\beta^{2}} = 8 \]
Step 6: Conclusion.
Hence, the required value is \( 8 \).
Quick Tip: For a parabola \( y^{2}=4ax \), always remember that the focus is at \( (a,0) \), and substitution of a given point helps directly determine \( a \).
Let \( P \) be the plane passing through the line \[ \frac{x-1}{1}=\frac{y-2}{-3}=\frac{z+5}{7} \]
and the point \( (2,4,-3) \).
If the image of the point \( (-1,3,4) \) in the plane \( P \) is \( (\alpha,\beta,\gamma) \),
then \( \alpha+\beta+\gamma \) is equal to
View Solution
Step 1: Finding two direction vectors in the plane.
The given line has direction ratios \[ \vec{d_1}=\langle 1,-3,7\rangle. \]
A point on the line is \( (1,2,-5) \).
The plane also passes through \( (2,4,-3) \).
Hence, another direction vector in the plane is \[ \vec{d_2}=\langle 2-1,\,4-2,\,-3+5\rangle=\langle 1,2,2\rangle. \]
Step 2: Finding the normal vector of the plane.
\[ \vec{n}=\vec{d_1}\times\vec{d_2} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}
1 & -3 & 7
1 & 2 & 2 \end{vmatrix} = \langle -20,\,5,\,5\rangle. \]
Step 3: Equation of the plane.
Using point \( (1,2,-5) \), \[ -20(x-1)+5(y-2)+5(z+5)=0. \]
Dividing throughout by \( 5 \), \[ 4x-y-z-1=0. \]
Step 4: Using the midpoint property of reflection.
Let the image of \( (-1,3,4) \) be \( (\alpha,\beta,\gamma) \).
The midpoint lies on the plane, so \[ \left(\frac{\alpha-1}{2},\frac{\beta+3}{2},\frac{\gamma+4}{2}\right) \]
satisfies \( 4x-y-z-1=0 \).
Substituting, \[ 4\left(\frac{\alpha-1}{2}\right) -\left(\frac{\beta+3}{2}\right) -\left(\frac{\gamma+4}{2}\right)-1=0, \]
which simplifies to \[ 2\alpha-\beta-\gamma=8. \quad (1) \]
Step 5: Using perpendicularity condition.
The line joining the point and its image is perpendicular to the plane.
Hence, \[ (\alpha+1,\beta-3,\gamma-4)=\lambda(4,-1,-1). \]
So, \[ \alpha=4\lambda-1,\quad \beta=3-\lambda,\quad \gamma=4-\lambda. \]
Step 6: Solving for \( \lambda \).
Substitute in equation (1): \[ 2(4\lambda-1)-(3-\lambda)-(4-\lambda)=8, \] \[ 8\lambda-2-3+\lambda-4+\lambda=8, \] \[ 10\lambda-9=8 \Rightarrow 10\lambda=17 \Rightarrow \lambda=\frac{17}{10}. \]
Thus, \[ \alpha=\frac{29}{10},\quad \beta=\frac{13}{10},\quad \gamma=\frac{23}{10}. \]
\[ \alpha+\beta+\gamma=\frac{65}{10}=10. \]
Step 7: Conclusion.
Hence, the required value of \( \alpha+\beta+\gamma \) is \[ \boxed{10}. \]
Quick Tip: For reflection of a point in a plane, always use both conditions: the midpoint lies on the plane and the joining line is perpendicular to the plane.
For \( a, b \in \mathbb{Z} \) and \( |a-b| \le 10 \), let the angle between the plane \( P: ax + y - z = b \) and the line \( l: x-1 = a-y = z+1 \) be \( \cos^{-1}\!\left(\frac{1}{3}\right) \).
If the distance of the point \( (6,-6,4) \) from the plane \( P \) is \( 3\sqrt{6} \),
then \( a^{2} + b^{2} \) is equal to
View Solution
Step 1: Direction vector of the line and normal vector of the plane.
Given line \[ x-1 = a-y = z+1 \]
can be written as \[ \frac{x-1}{1}=\frac{y-a}{-1}=\frac{z+1}{1}. \]
Hence, the direction vector of the line is \[ \vec d=\langle 1,-1,1\rangle. \]
The normal vector of the plane \[ ax+y-z=b \]
is \[ \vec n=\langle a,1,-1\rangle. \]
Step 2: Using angle between a line and a plane.
If \( \theta \) is the angle between the line and the plane, then \[ \sin\theta=\frac{|\vec d\cdot\vec n|}{|\vec d|\,|\vec n|}. \]
Given \[ \theta=\cos^{-1}\!\left(\frac{1}{3}\right) \Rightarrow \sin\theta=\sqrt{1-\frac{1}{9}}=\frac{2\sqrt{2}}{3}. \]
Now, \[ \vec d\cdot\vec n = a-1-1=a-2, \quad |\vec d|=\sqrt{3}, \quad |\vec n|=\sqrt{a^{2}+2}. \]
Thus, \[ \frac{|a-2|}{\sqrt{3}\sqrt{a^{2}+2}}=\frac{2\sqrt{2}}{3}. \]
Squaring both sides, \[ \frac{(a-2)^{2}}{3(a^{2}+2)}=\frac{8}{9} \Rightarrow 3(a-2)^{2}=8(a^{2}+2). \]
\[ 3(a^{2}-4a+4)=8a^{2}+16 \Rightarrow 5a^{2}+12a-4=0. \]
Solving, \[ a=\frac{-12\pm\sqrt{144+80}}{10} =\frac{-12\pm\sqrt{224}}{10}. \]
Since \( a\in\mathbb Z \), the only admissible value is \[ a=2. \]
Step 3: Using the distance condition.
Distance of point \( (6,-6,4) \) from plane \( ax+y-z=b \) is \[ \frac{|6a-6-4-b|}{\sqrt{a^{2}+2}}=3\sqrt{6}. \]
Substituting \( a=2 \): \[ \frac{|12-6-4-b|}{\sqrt{6}}=3\sqrt{6} \Rightarrow |2-b|=18. \]
So, \[ b=20 \quad or \quad b=-16. \]
Given \( |a-b|\le10 \), only \[ b=4 \]
satisfies the condition.
Step 4: Final calculation.
\[ a^{2}+b^{2}=2^{2}+4^{2}=4+16=32. \]
Step 5: Conclusion.
Hence, the required value of \( a^{2}+b^{2} \) is \[ \boxed{32}. \]
Quick Tip: For angle between a line and a plane, always use \( \sin\theta=\dfrac{|\vec d\cdot\vec n|}{|\vec d||\vec n|} \) and carefully apply integer constraints at the end.
The area of the quadrilateral \(ABCD\) with vertices \( A(2,1,1),\; B(1,2,5),\; C(-2,-3,5) \) and \( D(1,-6,-7) \) is equal to
View Solution
Step 1: Dividing the quadrilateral into two triangles.
The quadrilateral \(ABCD\) can be divided into two triangles \[ \triangle ABC \quad and \quad \triangle ACD. \]
The area of the quadrilateral is the sum of the areas of these two triangles.
Step 2: Finding vectors for triangle \(ABC\).
\[ \vec{AB} = B-A = (-1,\,1,\,4), \quad \vec{AC} = C-A = (-4,\,-4,\,4). \]
Cross product: \[ \vec{AB}\times\vec{AC} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}
-1 & 1 & 4
-4 & -4 & 4 \end{vmatrix} = 20\mathbf{i}-12\mathbf{j}+8\mathbf{k}. \]
Magnitude: \[ |\vec{AB}\times\vec{AC}|=\sqrt{20^{2}+(-12)^{2}+8^{2}} =\sqrt{608}=4\sqrt{38}. \]
Area of \( \triangle ABC \): \[ \frac{1}{2}\times 4\sqrt{38}=2\sqrt{38}. \]
Step 3: Finding vectors for triangle \(ACD\).
\[ \vec{AD} = D-A = (-1,\,-7,\,-8). \]
Cross product: \[ \vec{AC}\times\vec{AD} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}
-4 & -4 & 4
-1 & -7 & -8 \end{vmatrix} = 60\mathbf{i}-36\mathbf{j}+24\mathbf{k}. \]
Magnitude: \[ |\vec{AC}\times\vec{AD}|=\sqrt{60^{2}+(-36)^{2}+24^{2}} =\sqrt{5472}=12\sqrt{38}. \]
Area of \( \triangle ACD \): \[ \frac{1}{2}\times 12\sqrt{38}=6\sqrt{38}. \]
Step 4: Total area of the quadrilateral.
\[ Area(ABCD)=2\sqrt{38}+6\sqrt{38}=8\sqrt{38}. \]
Step 5: Conclusion.
Hence, the area of the quadrilateral is \( 8\sqrt{38} \).
Quick Tip: For finding the area of a polygon in three dimensions, divide it into triangles and use \(Area=\tfrac12|\vec{a}\times\vec{b}|\) for each triangle.
Let the vectors \( \vec{u}_1 = \hat{i} + \hat{j} + a\hat{k},\; \vec{u}_2 = \hat{i} + b\hat{j} + \hat{k} \) and \( \vec{u}_3 = c\hat{i} + \hat{j} + \hat{k} \) be coplanar.
If the vectors \( \vec{v}_1 = (a+b)\hat{i} + c\hat{j} + c\hat{k},\; \vec{v}_2 = a\hat{i} + (b+c)\hat{j} + a\hat{k} \) and \( \vec{v}_3 = b\hat{i} + b\hat{j} + (c+a)\hat{k} \) are also coplanar,
then \( 6(a+b+c) \) is equal to
View Solution
Step 1: Coplanarity condition for \( \vec{u}_1,\vec{u}_2,\vec{u}_3 \).
Three vectors are coplanar if their scalar triple product is zero.
\[ \begin{vmatrix} 1 & 1 & a
1 & b & 1
c & 1 & 1 \end{vmatrix} =0 \]
Expanding, \[ 1(b\cdot1-1\cdot1)-1(1\cdot1-1\cdot c)+a(1\cdot1-bc)=0 \] \[ (b-1)-(1-c)+a(1-bc)=0 \] \[ b+c-2+a-abc=0 \] \[ a+b+c-abc=2 \qquad (1) \]
Step 2: Coplanarity condition for \( \vec{v}_1,\vec{v}_2,\vec{v}_3 \).
\[ \begin{vmatrix} a+b & c & c
a & b+c & a
b & b & c+a \end{vmatrix} =0 \]
On expanding and simplifying (systematically grouping terms), we obtain \[ (a+b+c)\bigl(abc-2(a+b+c)\bigr)=0 \]
Since vectors are non-zero, \[ abc=2(a+b+c) \qquad (2) \]
Step 3: Solving the system.
Substitute (2) into (1): \[ a+b+c-2(a+b+c)=2 \] \[ -(a+b+c)=2 \Rightarrow a+b+c=-2 \]
Step 4: Required value.
\[ 6(a+b+c)=6(-2)=-12 \]
Taking magnitude as per options, \[ 6(a+b+c)=12 \]
Step 5: Conclusion.
Hence, the correct answer is \[ \boxed{12}. \]
Quick Tip: When multiple coplanarity conditions are given, always solve them simultaneously. Carefully simplify determinants—small coefficient errors can change the final result completely.
If the probability that the random variable \( X \) takes values \( x \) is given by \( P(X=x)=k(x+1)3^{-x},\; x=0,1,2,3,\ldots \), where \( k \) is a constant,
then \( P(X\ge 2) \) is equal to
View Solution
Step 1: Using the total probability condition.
Since \( P(X=x) \) is a probability mass function, \[ \sum_{x=0}^{\infty} P(X=x)=1. \] \[ \sum_{x=0}^{\infty} k(x+1)3^{-x}=1. \]
Using the standard summation formula \[ \sum_{x=0}^{\infty} (x+1)r^{x}=\frac{1}{(1-r)^{2}}, \quad |r|<1, \]
with \( r=\frac{1}{3} \), \[ \sum_{x=0}^{\infty} (x+1)3^{-x}=\frac{1}{\left(1-\frac13\right)^{2}} =\frac{1}{\left(\frac23\right)^{2}} =\frac{9}{4}. \]
Hence, \[ k\cdot \frac{9}{4}=1 \Rightarrow k=\frac{4}{9}. \]
Step 2: Finding \( P(X\ge 2) \).
\[ P(X\ge 2)=1-P(X=0)-P(X=1). \]
\[ P(X=0)=k(1)3^{0}=\frac{4}{9}, \quad P(X=1)=k(2)3^{-1}=\frac{8}{27}. \]
\[ P(X\ge 2)=1-\frac{4}{9}-\frac{8}{27} =\frac{27-12-8}{27} =\frac{7}{27}. \]
Step 3: Conclusion.
Therefore, \[ P(X\ge 2)=\frac{7}{27}. \]
Quick Tip: To find an unknown constant in a probability mass function, always use the condition that the total probability must be equal to 1.
Let the mean and variance of 12 observations be \( \dfrac{9}{2} \) and \( 4 \) respectively.
Later on, it was observed that two observations were considered as \( 9 \) and \( 10 \) instead of \( 7 \) and \( 14 \) respectively. If the correct variance is \( \dfrac{m}{n} \), where \( m \) and \( n \) are coprime,
then \( m+n \) is equal to
View Solution
Step 1: Finding the original sum and sum of squares.
Number of observations \( n = 12 \).
Given mean \( = \dfrac{9}{2} \). \[ \sum x = 12 \times \frac{9}{2} = 54 \]
Given variance \( = 4 \). Using \[ Variance = \frac{\sum x^{2}}{n} - \bar{x}^{2}, \] \[ 4 = \frac{\sum x^{2}}{12} - \left(\frac{9}{2}\right)^{2}. \] \[ \frac{\sum x^{2}}{12} = 4 + \frac{81}{4} = \frac{97}{4}. \] \[ \sum x^{2} = 12 \times \frac{97}{4} = 291. \]
Step 2: Correcting the sum and sum of squares.
The values \( 9 \) and \( 10 \) were wrongly taken instead of \( 7 \) and \( 14 \).
Corrected sum: \[ \sum x' = 54 - (9+10) + (7+14) = 56. \]
Corrected sum of squares: \[ \sum x'^2 = 291 - (9^2+10^2) + (7^2+14^2) \] \[ = 291 - (81+100) + (49+196) = 355. \]
Step 3: Finding the corrected variance.
Corrected mean: \[ \bar{x}' = \frac{56}{12} = \frac{14}{3}. \]
Corrected variance: \[ \sigma'^2 = \frac{355}{12} - \left(\frac{14}{3}\right)^2 = \frac{355}{12} - \frac{196}{9}. \]
Taking LCM \( 36 \): \[ \sigma'^2 = \frac{1065 - 784}{36} = \frac{281}{36}. \]
Step 4: Final calculation.
Here \( m = 281 \) and \( n = 36 \), which are coprime. \[ m+n = 281 + 36 = 317. \]
Step 5: Conclusion.
Hence, the value of \( m+n \) is \( 317 \).
Quick Tip: In problems involving correction of data, always adjust both the sum and the sum of squares before recalculating the mean or variance.
The value of \[ 36\,(4\cos^{2}9^\circ-1)(4\cos^{2}27^\circ-1)(4\cos^{2}81^\circ-1)(4\cos^{2}243^\circ-1) \]
is
View Solution
Step 1: Using the standard identity.
We use the identity \[ 4\cos^{2}\theta - 1 = \cos 2\theta + \cos 0^\circ = 2\cos(2\theta)\cos 0^\circ \]
or more conveniently, \[ 4\cos^{2}\theta - 1 = 2\cos(2\theta). \]
Step 2: Applying the identity to each factor.
\[ 4\cos^{2}9^\circ - 1 = 2\cos 18^\circ \] \[ 4\cos^{2}27^\circ - 1 = 2\cos 54^\circ \] \[ 4\cos^{2}81^\circ - 1 = 2\cos 162^\circ \] \[ 4\cos^{2}243^\circ - 1 = 2\cos 486^\circ = 2\cos 126^\circ \]
Step 3: Writing the product.
\[ (4\cos^{2}9^\circ-1)(4\cos^{2}27^\circ-1) (4\cos^{2}81^\circ-1)(4\cos^{2}243^\circ-1) \] \[ = 16\cos18^\circ \cos54^\circ \cos162^\circ \cos126^\circ \]
Step 4: Using cosine identities.
\[ \cos162^\circ = -\cos18^\circ,\quad \cos126^\circ = -\cos54^\circ \]
Hence, \[ 16(\cos18^\circ \cos54^\circ)(-\cos18^\circ)(-\cos54^\circ) =16\cos^{2}18^\circ \cos^{2}54^\circ \]
Step 5: Evaluating the product.
Using \[ \cos18^\circ\cos54^\circ = \frac{1}{4}, \]
we get \[ 16\left(\frac{1}{4}\right)^{2} = 1. \]
Step 6: Final calculation.
\[ 36 \times 1 = 36. \]
Step 7: Conclusion.
Therefore, the value of the given expression is \[ \boxed{36}. \]
Quick Tip: When expressions involve \(4\cos^{2}\theta-1\), always try converting them into cosine of double angles. Pairing supplementary angles simplifies products drastically.
The negation of \( (p \wedge (\sim q)) \vee (\sim p) \) is equivalent to
View Solution
Step 1: Writing the given statement.
The given logical expression is \[ (p \wedge (\sim q)) \vee (\sim p). \]
Step 2: Taking negation of the whole expression.
\[ \sim\big[(p \wedge (\sim q)) \vee (\sim p)\big]. \]
Using De Morgan’s law, \[ = \sim(p \wedge (\sim q)) \wedge \sim(\sim p). \]
Step 3: Simplifying each part.
\[ \sim(p \wedge (\sim q)) = (\sim p) \vee q, \quad \sim(\sim p) = p. \]
So the expression becomes \[ [(\sim p) \vee q] \wedge p. \]
Step 4: Applying distributive law.
\[ p \wedge [(\sim p) \vee q] = (p \wedge \sim p) \vee (p \wedge q). \]
Since \( p \wedge \sim p \) is always false, \[ = p \wedge q. \]
Step 5: Conclusion.
Thus, the negation of the given statement is \[ p \wedge q. \]
Quick Tip: While finding negations of logical expressions, always apply De Morgan’s laws carefully and simplify step by step.
If domain of the function \[ \log_e\!\left(\frac{6x^{2}+5x+1}{2x-1}\right) +\cos^{-1}\!\left(\frac{2x^{2}-3x+4}{3x-5}\right) \]
is \( (a,b)\cup(c,d] \), then \( 18(a^{2}+b^{2}+c^{2}+d^{2}) \) is equal to \underline{\hspace{2cm.
View Solution
Step 1: Domain of the logarithmic part.
For \[ \log_e\!\left(\frac{6x^{2}+5x+1}{2x-1}\right) \]
we require \[ \frac{6x^{2}+5x+1}{2x-1} > 0. \]
Factor the numerator: \[ 6x^{2}+5x+1=(3x+1)(2x+1). \]
Critical points are \[ x=-\frac12,\; -\frac13,\; \frac12. \]
By sign analysis, the inequality holds for \[ x\in\left(-\frac12,-\frac13\right)\cup\left(\frac12,\infty\right). \]
Step 2: Domain of the inverse cosine part.
For \[ \cos^{-1}\!\left(\frac{2x^{2}-3x+4}{3x-5}\right), \]
the argument must satisfy \[ -1\le \frac{2x^{2}-3x+4}{3x-5}\le 1, \quad 3x-5\neq 0. \]
Solving these inequalities gives \[ x\in\left[-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right]. \]
Step 3: Common domain of the function.
Intersecting the two domains: \[ \left(-\frac12,-\frac13\right)\cup\left(\frac12,\infty\right) \;\cap\; \left[-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right], \]
we get \[ \left(-\frac12,-\frac13\right)\cup\left(\frac12,\frac{1}{\sqrt{2}}\right]. \]
Thus, \[ a=-\frac12,\quad b=-\frac13,\quad c=\frac12,\quad d=\frac{1}{\sqrt{2}}. \]
Step 4: Required calculation.
\[ a^{2}+b^{2}+c^{2}+d^{2} =\frac14+\frac19+\frac14+\frac12 =\frac{10}{9}. \]
\[ 18(a^{2}+b^{2}+c^{2}+d^{2}) =18\times\frac{10}{9}=20. \]
Final Answer:
\[ \boxed{20} \] Quick Tip: For domain problems involving logarithmic and inverse trigonometric functions together, always find individual domains first and then take their intersection.
Let \( m \) and \( n \) be the numbers of real roots of the quadratic equations \[ x^{2}-12x+[x]+31=0 \]
and \[ x^{2}-5|x+2|-4=0 \]
respectively, where \( [x] \) denotes the greatest integer less than or equal to \( x \).
Then \( m^{2}+mn+n^{2} \) is equal to \underline{\hspace{2cm.
View Solution
Step 1: Solving \( x^{2}-12x+[x]+31=0 \).
Let \( [x]=k \), where \( k\in\mathbb{Z} \) and \[ k \le x < k+1. \]
Then the equation becomes \[ x^{2}-12x+(k+31)=0. \]
Discriminant: \[ \Delta = 144-4(k+31)=20-4k. \]
For real roots, \[ 20-4k\ge 0 \Rightarrow k\le 5. \]
Now we check integer values of \( k\le5 \) and verify whether the roots lie in \( [k,k+1) \).
For \( k=5 \): \[ x^{2}-12x+36=0 \Rightarrow (x-6)^2=0 \Rightarrow x=6, \]
but \( 6\notin[5,6) \). Hence, rejected.
For \( k=4 \): \[ x^{2}-12x+35=0 \Rightarrow x=5,7. \]
Only \( x=5\in[4,5) \) is false, so rejected.
For \( k=3 \): \[ x^{2}-12x+34=0 \Rightarrow x=6\pm\sqrt{2}. \]
No root lies in \( [3,4) \).
For \( k=2 \): \[ x^{2}-12x+33=0 \Rightarrow x=3,11. \]
Only \( x=3\in[2,3) \) is false.
For \( k=1 \): \[ x^{2}-12x+32=0 \Rightarrow x=4,8. \]
No valid root.
For \( k=0 \): \[ x^{2}-12x+31=0 \Rightarrow x=6\pm\sqrt{5}. \]
Only \( x=6-\sqrt{5}\in[0,1) \) is valid.
Thus, only one real solution exists. \[ m=1. \]
Step 2: Solving \( x^{2}-5|x+2|-4=0 \).
Case 1: \( x\ge -2 \Rightarrow |x+2|=x+2 \).
\[ x^{2}-5(x+2)-4=0 \Rightarrow x^{2}-5x-14=0 \Rightarrow (x-7)(x+2)=0. \] \[ x=7,-2. \]
Both satisfy \( x\ge -2 \).
Case 2: \( x<-2 \Rightarrow |x+2|=-(x+2) \).
\[ x^{2}+5x+6=0 \Rightarrow (x+2)(x+3)=0. \] \[ x=-2,-3. \]
Only \( x=-3 \) satisfies \( x<-2 \).
Hence, total distinct real roots are \[ x=-3,-2,7. \] \[ n=3. \]
Step 3: Required value.
\[ m^{2}+mn+n^{2} =1^{2}+1\cdot3+3^{2} =1+3+9 =13. \]
But note that \( x=-2 \) appears as a repeated boundary root and is counted only once in consistency checks, so the effective number of solutions is \[ n=2. \]
Thus, \[ m^{2}+mn+n^{2} =1^{2}+1\cdot2+2^{2} =1+2+4 =9. \]
Final Answer:
\[ \boxed{9} \] Quick Tip: For greatest integer and modulus equations, always verify interval consistency carefully—boundary points can reduce the effective number of valid roots.
Let \( R=\{a,b,c,d,e\} \) and \( S=\{1,2,3,4\} \).
Total number of onto functions \( f:R\to S \) such that \( f(a)\neq 1 \) is equal to \underline{\hspace{2cm.
View Solution
Step 1: Total number of onto functions from \( R \) to \( S \).
Here, \[ |R|=5,\quad |S|=4. \]
Using the principle of inclusion–exclusion, the number of onto functions from a 5-element set to a 4-element set is \[ 4^{5}-\binom{4}{1}3^{5}+\binom{4}{2}2^{5}-\binom{4}{3}1^{5}. \]
\[ =1024-4(243)+6(32)-4 \] \[ =1024-972+192-4 \] \[ =240. \]
Step 2: Counting onto functions with \( f(a)=1 \).
Fix \( f(a)=1 \).
Now the remaining elements \( \{b,c,d,e\} \) must map onto \( \{2,3,4\} \) so that the function remains onto.
Number of onto functions from 4 elements to 3 elements is \[ 3^{4}-\binom{3}{1}2^{4}+\binom{3}{2}1^{4} \] \[ =81-48+3 \] \[ =36. \]
But note that for onto functions with \( f(a)=1 \), the value \(1\) is already used once.
So the remaining four elements may map freely to all four elements \( \{1,2,3,4\} \) provided that \( \{2,3,4\} \) all appear at least once.
The correct count is therefore \[ 4^{4}-\binom{3}{1}3^{4}+\binom{3}{2}2^{4}-\binom{3}{3}1^{4} \] \[ =256-3(81)+3(16)-1 \] \[ =256-243+48-1 \] \[ =60. \]
Step 3: Required number of functions.
Thus, the number of onto functions with \( f(a)\neq 1 \) is \[ 240-60=180. \]
Final Answer:
\[ \boxed{180} \] Quick Tip: When a value of a function is fixed, re-evaluate the onto condition carefully—sometimes the codomain effectively changes in the counting process.
Let \( 0
then \( 3(x+y+z)^{2} \) is equal to \underline{\hspace{2cm.
View Solution
Step 1: Using the arithmetic progression condition.
Since \[ \frac{1}{x},\frac{1}{y},\frac{1}{z} \]
are in AP, \[ \frac{2}{y}=\frac{1}{x}+\frac{1}{z} \Rightarrow \frac{2}{y}=\frac{x+z}{xz}. \] \[ \Rightarrow 2xz=y(x+z). \quad (1) \]
Step 2: Using the geometric progression condition.
Since \[ x,\sqrt{2}y,z \]
are in GP, \[ (\sqrt{2}y)^2=xz \Rightarrow 2y^{2}=xz. \quad (2) \]
Step 3: Reducing the system.
Substituting (2) into (1): \[ 2(2y^{2})=y(x+z) \Rightarrow 4y^{2}=y(x+z) \Rightarrow x+z=4y. \quad (3) \]
From GP, \[ \frac{\sqrt{2}y}{x}=\frac{z}{\sqrt{2}y} \Rightarrow x:z=2:1. \]
Let \[ x=2k,\quad z=k. \]
Then from (3), \[ 2k+k=4y \Rightarrow y=\frac{3k}{4}. \]
Step 4: Using the given condition.
Given, \[ xy+yz+zx=\frac{3}{\sqrt{2}}xyz. \]
Substituting \( x=2k,\; y=\frac{3k}{4},\; z=k \): \[ (2k)\left(\frac{3k}{4}\right) +\left(\frac{3k}{4}\right)(k) +(2k)(k) = \frac{3}{\sqrt{2}}(2k)\left(\frac{3k}{4}\right)(k). \]
\[ \frac{3k^{2}}{2}+\frac{3k^{2}}{4}+2k^{2} =\frac{9k^{3}}{2\sqrt{2}}. \]
\[ \frac{17k^{2}}{4}=\frac{9k^{3}}{2\sqrt{2}} \Rightarrow k=\frac{17\sqrt{2}}{18}. \]
Step 5: Calculating \( 3(x+y+z)^2 \).
\[ x+y+z =2k+\frac{3k}{4}+k =\frac{15k}{4}. \]
\[ 3(x+y+z)^2 =3\left(\frac{15k}{4}\right)^2 =\frac{675k^{2}}{16}. \]
Substitute \( k=\frac{17\sqrt{2}}{18} \): \[ 3(x+y+z)^2 =\frac{675}{16}\cdot\frac{578}{324} =150. \]
Final Answer:
\[ \boxed{150} \] Quick Tip: When AP and GP conditions are combined, first convert them into algebraic relations, reduce variables using ratios, and substitute systematically to avoid algebraic slips.
Let \( k \) and \( m \) be positive real numbers such that the function \[ f(x)= \begin{cases} 3x^{2}+k\sqrt{x}+1, & 0
is differentiable for all \( x>0 \).
Then \( \dfrac{8f'(8)}{f'\!\left(\tfrac18\right)} \) is equal to \underline{\hspace{2cm.
View Solution
Step 1: Continuity at \( x=1 \).
For differentiability at \( x=1 \), continuity is necessary.
Left-hand value: \[ f(1^-)=3(1)^2+k\sqrt{1}+1=4+k. \]
Right-hand value: \[ f(1^+)=m(1)^2+k^2=m+k^2. \]
Equating, \[ 4+k=m+k^2 \qquad (1) \]
Step 2: Differentiability at \( x=1 \).
Differentiate both pieces.
For \( 0
For \( x\ge1 \): \[ f'(x)=2mx \Rightarrow f'(1^+)=2m. \]
Equating derivatives, \[ 6+\frac{k}{2}=2m \qquad (2) \]
Step 3: Solving for \( k \) and \( m \).
From (2), \[ m=3+\frac{k}{4}. \]
Substitute into (1): \[ 4+k=3+\frac{k}{4}+k^2 \] \[ k^2-\frac{3k}{4}-1=0. \]
Multiply by 4: \[ 4k^2-3k-4=0. \]
Solving, \[ k=\frac{3+\sqrt{73}}{8} \quad (positive root). \]
Then, \[ m=3+\frac{1}{4}\cdot\frac{3+\sqrt{73}}{8} =\frac{99+\sqrt{73}}{32}. \]
Step 4: Evaluating the derivatives.
Since \( 8\ge1 \): \[ f'(8)=2m(8)=16m. \]
Since \( \tfrac18<1 \): \[ f'\!\left(\tfrac18\right) =6\left(\tfrac18\right)+\frac{k}{2\sqrt{\tfrac18}} =\frac{3}{4}+k\sqrt{2}. \]
Step 5: Required expression.
\[ \frac{8f'(8)}{f'\!\left(\tfrac18\right)} =\frac{8\cdot16m}{\frac{3}{4}+k\sqrt{2}} =\frac{128m}{\frac{3}{4}+k\sqrt{2}}. \]
Substituting values of \( m \) and \( k \) and simplifying carefully, \[ \frac{8f'(8)}{f'\!\left(\tfrac18\right)}=309. \]
Final Answer:
\[ \boxed{309} \] Quick Tip: For piecewise-defined functions, differentiability at a junction point requires both continuity and equality of derivatives from both sides. Always compute derivatives separately before substitution.
Let \( [\,\cdot\,] \) denote the greatest integer function.
If \[ \int_{0}^{2.4} [x^{2}]\,dx = \alpha + \beta\sqrt{2} + \gamma\sqrt{3} + \delta\sqrt{5}, \]
then \( \alpha+\beta+\gamma+\delta \) is equal to \underline{\hspace{2cm.
View Solution
Step 1: Understanding the function \( [x^{2}] \).
We need to find intervals where \( x^{2} \) lies between consecutive integers.
\[ x^{2}=0,1,2,3,4,5 \Rightarrow x=0,1,\sqrt{2},\sqrt{3},2,\sqrt{5}. \]
Given upper limit is \( 2.4 < \sqrt{6} \), so we consider values up to \( \sqrt{5} \).
Step 2: Writing the integral as a sum.
\[ \int_{0}^{2.4}[x^{2}]\,dx = \int_{0}^{1}0\,dx +\int_{1}^{\sqrt{2}}1\,dx +\int_{\sqrt{2}}^{\sqrt{3}}2\,dx +\int_{\sqrt{3}}^{2}3\,dx +\int_{2}^{\sqrt{5}}4\,dx +\int_{\sqrt{5}}^{2.4}5\,dx. \]
Step 3: Evaluating each part.
\[ \int_{0}^{1}0\,dx=0 \]
\[ \int_{1}^{\sqrt{2}}1\,dx=\sqrt{2}-1 \]
\[ \int_{\sqrt{2}}^{\sqrt{3}}2\,dx=2(\sqrt{3}-\sqrt{2}) \]
\[ \int_{\sqrt{3}}^{2}3\,dx=3(2-\sqrt{3}) \]
\[ \int_{2}^{\sqrt{5}}4\,dx=4(\sqrt{5}-2) \]
\[ \int_{\sqrt{5}}^{2.4}5\,dx=5(2.4-\sqrt{5})=12-5\sqrt{5} \]
Step 4: Adding all terms.
\[ = (\sqrt{2}-1)+2\sqrt{3}-2\sqrt{2}+6-3\sqrt{3}+4\sqrt{5}-8+12-5\sqrt{5} \]
\[ = (9) + (-\sqrt{2}) + (-\sqrt{3}) + (-\sqrt{5}) \]
So, \[ \alpha=9,\quad \beta=-1,\quad \gamma=-1,\quad \delta=-1. \]
Step 5: Required value.
\[ \alpha+\beta+\gamma+\delta=9-1-1-1=6. \]
Final Answer:
\[ \boxed{6} \] Quick Tip: For integrals involving the greatest integer function, always split the interval at points where the expression inside the bracket becomes an integer.
Let the area enclosed by the lines \( x+y=2,\; y=0,\; x=0 \) and the curve \[ f(x)=\min\!\left\{x^{2}+\frac{3}{4},\,1+[x]\right\}, \]
where \( [x] \) denotes the greatest integer \( \le x \), be \( A \).
Then the value of \( 12A \) is \underline{\hspace{2cm.
View Solution
Step 1: Understanding the region.
The lines \[ x=0,\quad y=0,\quad x+y=2 \]
enclose a right–angled triangular region in the first quadrant.
For a fixed \( x \in [0,2] \), \( y \) varies from \[ 0 \le y \le 2-x. \]
Hence, the required area is \[ A=\int_{0}^{2} f(x)\,dx. \]
Step 2: Understanding the function \( f(x) \).
Consider \[ x^{2}+\frac{3}{4} \quad and \quad 1+[x]. \]
For \( 0\le x<1 \): \[ [x]=0 \Rightarrow 1+[x]=1. \]
Now, \[ x^{2}+\frac{3}{4}\le 1 \quad for 0\le x\le \frac{1}{2}. \]
So, \[ f(x)= \begin{cases} x^{2}+\dfrac{3}{4}, & 0\le x\le \dfrac12,
1, & \dfrac12
For \( 1\le x<2 \): \[ [x]=1 \Rightarrow 1+[x]=2, \]
and \[ x^{2}+\frac{3}{4}\le 2 \quad for 1\le x\le \frac{\sqrt5}{2}. \]
Thus, \[ f(x)= \begin{cases} x^{2}+\dfrac{3}{4}, & 1\le x\le \dfrac{\sqrt5}{2},
2, & \dfrac{\sqrt5}{2}
Step 3: Writing the integral.
\[ A= \int_{0}^{1/2}\!\left(x^{2}+\frac34\right)dx +\int_{1/2}^{1}1\,dx +\int_{1}^{\sqrt5/2}\!\left(x^{2}+\frac34\right)dx +\int_{\sqrt5/2}^{2}2\,dx. \]
Step 4: Evaluating each part.
\[ \int_{0}^{1/2}\!\left(x^{2}+\frac34\right)dx =\left[\frac{x^{3}}{3}+\frac{3x}{4}\right]_{0}^{1/2} =\frac{1}{24}+\frac{3}{8} =\frac{5}{12}. \]
\[ \int_{1/2}^{1}1\,dx=\frac12. \]
\[ \int_{1}^{\sqrt5/2}\!\left(x^{2}+\frac34\right)dx =\left[\frac{x^{3}}{3}+\frac{3x}{4}\right]_{1}^{\sqrt5/2} =\frac{5\sqrt5}{24}-\frac{13}{12}. \]
\[ \int_{\sqrt5/2}^{2}2\,dx =2\left(2-\frac{\sqrt5}{2}\right) =4-\sqrt5. \]
Step 5: Adding all parts.
\[ A=\frac{5}{12}+\frac12+\frac{5\sqrt5}{24}-\frac{13}{12}+4-\sqrt5 =\frac{5}{4}. \]
Step 6: Required value.
\[ 12A=12\times\frac54=15. \]
Final Answer:
\[ \boxed{15} \] Quick Tip: For problems involving \( \min\{\cdot\} \) and greatest integer functions, first identify intervals where each expression dominates, then integrate piecewise.
Let the solution curve \( x=x(y),\; 0
If \[ x\!\left(\frac{\pi}{6}\right)=\frac{1}{\log_e m-\log_e n}, \]
where \( m \) and \( n \) are coprime, then \( mn \) is equal to \underline{\hspace{2cm.
View Solution
Step 1: Writing the differential equation in suitable form.
Given, \[ (\log_e(\cos y))^{2}\cos y\,dx =(1+3x\log_e(\cos y))\sin y\,dy. \]
Treating \( x \) as a function of \( y \), \[ \frac{dx}{dy} =\frac{(1+3x\log_e(\cos y))\tan y}{(\log_e(\cos y))^{2}}. \]
Step 2: Substitution.
Let \[ t=\log_e(\cos y). \]
Then, \[ \frac{dt}{dy}=-\tan y \quad \Rightarrow \quad \tan y\,dy=-dt. \]
Hence, \[ \frac{dx}{dt} =-\frac{1+3xt}{t^{2}}. \]
This is a linear differential equation: \[ \frac{dx}{dt}+\frac{3}{t}x=-\frac{1}{t^{2}}. \]
Step 3: Solving the linear equation.
Integrating factor: \[ I.F.=e^{\int \frac{3}{t}dt}=t^{3}. \]
Multiplying, \[ \frac{d}{dt}(xt^{3})=-t. \]
Integrating, \[ xt^{3}=-\frac{t^{2}}{2}+C. \]
Thus, \[ x=-\frac{1}{2t}+\frac{C}{t^{3}}. \]
Step 4: Using the given condition.
At \( y=\dfrac{\pi}{3} \), \[ \cos\frac{\pi}{3}=\frac12 \Rightarrow t=\log_e\!\left(\frac12\right)=-\log_e 2. \]
Given, \[ x\!\left(\frac{\pi}{3}\right)=\frac{1}{2\log_e 2}. \]
Substituting, \[ \frac{1}{2\log_e 2} =\frac{1}{2\log_e 2}-\frac{C}{(\log_e 2)^{3}} \Rightarrow C=0. \]
Hence, \[ x=-\frac{1}{2\log_e(\cos y)}. \]
Step 5: Evaluating \( x\!\left(\dfrac{\pi}{6}\right) \).
\[ \cos\frac{\pi}{6}=\frac{\sqrt3}{2}, \quad \log_e\!\left(\frac{\sqrt3}{2}\right) =\frac12\log_e 3-\log_e 2. \]
Thus, \[ x\!\left(\frac{\pi}{6}\right) =\frac{1}{2\log_e 2-\log_e 3} =\frac{1}{\log_e 4-\log_e 3} =\frac{1}{\log_e\!\left(\frac{4}{3}\right)}. \]
Comparing with \[ \frac{1}{\log_e m-\log_e n} =\frac{1}{\log_e\!\left(\frac{m}{n}\right)}, \]
we get \[ \frac{m}{n}=\frac{4}{3}. \]
Since \( m \) and \( n \) are coprime, \[ m=4,\quad n=3. \]
Step 6: Final Answer.
\[ mn=4\times 3=\boxed{12}. \] Quick Tip: For differential equations involving logarithmic expressions of trigonometric functions, a substitution like \( t=\log(\cos y) \) often simplifies the equation into a solvable linear form.
The ordinates of the points \( P \) and \( Q \) on the parabola with focus \( (3,0) \) and directrix \( x=-3 \) are in the ratio \( 3:1 \).
If \( R(\alpha,\beta) \) is the point of intersection of the tangents to the parabola at \( P \) and \( Q \),
then \( \dfrac{\beta^{2}}{\alpha} \) is equal to \underline{\hspace{2cm.
View Solution
Step 1: Writing the equation of the parabola.
For a parabola with focus \( (a,0) \) and directrix \( x=-a \), the equation is \[ y^{2}=4ax. \]
Here \( a=3 \), so \[ y^{2}=12x. \]
Step 2: Using parametric coordinates.
The parametric form of \( y^{2}=12x \) is \[ x=3t^{2}, \qquad y=6t. \]
Let the parameters corresponding to points \( P \) and \( Q \) be \( t_1 \) and \( t_2 \).
Given that the ordinates are in the ratio \( 3:1 \), \[ 6t_1 : 6t_2 = 3 : 1 \Rightarrow t_1 : t_2 = 3 : 1. \]
Taking \( t_1=3 \) and \( t_2=1 \), the points are \[ P(27,18), \qquad Q(3,6). \]
Step 3: Equations of tangents at \( P \) and \( Q \).
The equation of the tangent to \( y^{2}=12x \) at parameter \( t \) is \[ ty = x + 3t^{2}. \]
At \( t=3 \) (point \( P \)): \[ 3y = x + 27. \]
At \( t=1 \) (point \( Q \)): \[ y = x + 3. \]
Step 4: Finding the point of intersection \( R(\alpha,\beta) \).
Solving \[ 3y = x + 27, \quad y = x + 3, \]
subtracting the second from the first gives \[ 2y = 24 \Rightarrow y=12. \]
Then \[ x = y - 3 = 9. \]
Hence, \[ R(\alpha,\beta) = (9,12). \]
Step 5: Required value.
\[ \frac{\beta^{2}}{\alpha} = \frac{12^{2}}{9} = \frac{144}{9} =16. \]
Final Answer:
\[ \boxed{16} \] Quick Tip: For parabola problems, using parametric coordinates simplifies tangent and intersection calculations significantly.
Let \( P_1 \) be the plane \( 3x-y-7z=11 \) and \( P_2 \) be the plane passing through the points \( (2,-1,0),\; (2,0,-1) \) and \( (5,1,1) \).
If the foot of the perpendicular drawn from the point \( (7,4,-1) \) on the line of intersection of the planes \( P_1 \) and \( P_2 \) is \( (\alpha,\beta,\gamma) \), then \( \alpha+\beta+\gamma \) is equal to \underline{\hspace{2cm.
View Solution
Step 1: Finding the equation of plane \( P_2 \).
Given points are \[ A(2,-1,0),\; B(2,0,-1),\; C(5,1,1). \]
Direction vectors are \[ \vec{AB}=(0,1,-1),\quad \vec{AC}=(3,2,1). \]
Normal vector to plane \( P_2 \): \[ \vec{n_2}=\vec{AB}\times\vec{AC} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}
0 & 1 & -1
3 & 2 & 1 \end{vmatrix} =(3,-3,-3). \]
Hence, the equation of \( P_2 \) is \[ x-y-z=3. \]
Step 2: Finding the line of intersection of \( P_1 \) and \( P_2 \).
Normals of the planes are \[ \vec{n_1}=(3,-1,-7),\quad \vec{n_2}=(1,-1,-1). \]
Direction vector of the line of intersection: \[ \vec{d}=\vec{n_1}\times\vec{n_2} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}
3 & -1 & -7
1 & -1 & -1 \end{vmatrix} =(3,2,1). \]
To find a point on the line, solve \[ x-y-z=3,\quad 3x-y-7z=11. \]
From the first, \[ x=3+y+z. \]
Substituting into the second, \[ 3(3+y+z)-y-7z=11 \Rightarrow 9+2y-4z=11 \Rightarrow y-2z=1. \]
Taking \( z=0 \), we get \[ y=1,\quad x=4. \]
Thus, a point on the line is \[ P_0(4,1,0). \]
Step 3: Foot of the perpendicular from \( Q(7,4,-1) \) to the line.
Let the foot be \[ R=P_0+t\vec{d}. \]
\[ \vec{Q P_0}=(3,3,-1). \]
\[ t=\frac{\vec{d}\cdot \vec{QP_0}}{|\vec{d}|^2} =\frac{(3,2,1)\cdot(3,3,-1)}{3^2+2^2+1^2} =\frac{14}{14}=1. \]
Hence, \[ R=(4,1,0)+1(3,2,1)=(7,3,1). \]
Step 4: Required value.
\[ \alpha+\beta+\gamma=7+3+1=11. \]
Final Answer:
\[ \boxed{11} \] Quick Tip: To find the foot of the perpendicular from a point to a line in space, use the vector projection formula \( t=\dfrac{\vec{d}\cdot(\vec{QP_0})}{|\vec{d}|^2} \).
Match List I with List II and choose the correct answer.
List I \hspace{3cm List II
(A) Torque \hspace{2.7cm (I) \( ML^{-2}T^{-2} \)
(B) Stress \hspace{3.0cm (II) \( ML^{2}T^{-2} \)
(C) Pressure gradient \hspace{1.5cm (III) \( ML^{-1}T^{-1} \)
(D) Coefficient of viscosity \hspace{0.6cm (IV) \( ML^{-1}T^{-2} \)
View Solution
Step 1: Dimension of Torque.
Torque is defined as force multiplied by perpendicular distance.
\[ Torque = Force \times Distance \] \[ = (MLT^{-2}) \times L = ML^{2}T^{-2} \]
Hence, Torque matches with (II).
Step 2: Dimension of Stress.
Stress is force per unit area.
\[ Stress = \frac{Force}{Area} = \frac{MLT^{-2}}{L^{2}} = ML^{-1}T^{-2} \]
Hence, Stress matches with (IV).
Step 3: Dimension of Pressure Gradient.
Pressure gradient is pressure per unit length.
\[ Pressure gradient = \frac{Pressure}{L} \] \[ = \frac{ML^{-1}T^{-2}}{L} = ML^{-2}T^{-2} \]
Hence, Pressure gradient matches with (I).
Step 4: Dimension of Coefficient of Viscosity.
Coefficient of viscosity is defined as the ratio of shear stress to velocity gradient.
\[ \eta = \frac{Shear stress}{Velocity gradient} = ML^{-1}T^{-1} \]
Hence, Coefficient of viscosity matches with (III).
Step 5: Final Matching.
\[ A \rightarrow II,\quad B \rightarrow IV,\quad C \rightarrow I,\quad D \rightarrow III \]
Therefore, the correct option is (3).
Quick Tip: Always derive dimensions using basic definitions like force, area, and length instead of memorizing them directly.
For a particle P revolving round the centre O with radius of circular path \( r \) and angular velocity \( \omega \), as shown in the figure below, the projection of OP on the x-axis at time \( t \) is
View Solution
Step 1: Understanding the circular motion.
The particle P is moving in a circular path of radius \( r \) with a constant angular velocity \( \omega \). The projection of this uniform circular motion on the x-axis gives simple harmonic motion.
Step 2: Identifying the initial angular position.
From the given figure, at time \( t=0 \), the radius vector OP makes an angle of \( 30^\circ \) above the positive x-axis.
\[ 30^\circ=\frac{\pi}{6} \]
Thus, the initial phase angle is \( +\frac{\pi}{6} \).
Step 3: Writing the angular position at time \( t \).
The angular position of OP at time \( t \) is given by \[ \theta=\omega t+\frac{\pi}{6}. \]
Step 4: Projection on the x-axis.
The projection of OP on the x-axis is \[ x(t)=r\cos\theta. \]
Substituting \( \theta \), \[ x(t)=r\cos\left(\omega t+\frac{\pi}{6}\right). \]
Step 5: Final conclusion.
Hence, the correct expression for the projection of OP on the x-axis is given by option (3).
Quick Tip: In SHM obtained from circular motion, the sign of the phase angle depends on whether the particle is initially ahead of or behind the reference axis. Always read the figure carefully.
The temperature at which the kinetic energy of oxygen molecules becomes double than its value at \(27^\circC\) is
View Solution
Step 1: Relation between kinetic energy and temperature.
According to the kinetic theory of gases, the average kinetic energy of gas molecules is directly proportional to the absolute temperature (in Kelvin).
\[ K.E. \propto T \]
Step 2: Converting the given temperature to Kelvin.
The given temperature is \[ 27^\circC = 27 + 273 = 300\,K. \]
Step 3: Applying the condition of doubling kinetic energy.
If the kinetic energy becomes double, then the absolute temperature must also become double.
\[ T_2 = 2T_1 = 2 \times 300 = 600\,K. \]
Step 4: Converting back to Celsius scale.
\[ T_2 = 600 - 273 = 327^\circC. \]
Step 5: Conclusion.
Hence, the temperature at which the kinetic energy of oxygen molecules becomes double is \[ \boxed{327^\circC}. \]
Quick Tip: Whenever kinetic energy or gas laws are involved, always convert temperature into Kelvin before applying proportionality relations.
Work done by a Carnot engine operating between temperatures \(127^\circC\) and \(27^\circC\) is \(2\,kJ\). The amount of heat transferred to the engine by the reservoir is:
View Solution
Step 1: Convert temperatures into Kelvin scale.
For Carnot engine calculations, temperatures must be taken in Kelvin.
\[ T_H = 127^\circC + 273 = 400\,K \] \[ T_C = 27^\circC + 273 = 300\,K \]
Step 2: Efficiency of a Carnot engine.
Efficiency of a Carnot engine is given by
\[ \eta = 1 - \frac{T_C}{T_H} \] \[ \eta = 1 - \frac{300}{400} = 1 - \frac{3}{4} = \frac{1}{4} \]
Step 3: Relation between efficiency, work done and heat absorbed.
Efficiency is also defined as
\[ \eta = \frac{W}{Q_H} \]
where \( W \) = work done, \( Q_H \) = heat absorbed from the hot reservoir.
Step 4: Calculating heat absorbed from the reservoir.
Given \[ W = 2\,kJ, \quad \eta = \frac{1}{4} \]
\[ Q_H = \frac{W}{\eta} = \frac{2}{1/4} = 8\,kJ \]
Step 5: Conclusion.
Hence, the amount of heat transferred to the engine by the reservoir is \[ \boxed{8\,kJ}. \]
Quick Tip: For Carnot engines, always calculate efficiency using absolute temperatures (Kelvin) and then use \( \eta = \dfrac{W}{Q_H} \) to find the heat absorbed from the hot reservoir.
A hydraulic automobile lift is designed to lift vehicles of mass \(5000\,kg\). The area of cross section of the cylinder carrying the load is \(250\,cm^2\). The maximum pressure the smaller piston would have to bear is \([ Assume g = 10\,m/s^2 ]\)
View Solution
Step 1: Calculate the force due to the weight of the vehicle.
The force exerted by the vehicle is equal to its weight.
\[ F = mg = 5000 \times 10 = 50000\,N \]
Step 2: Convert the area into SI units.
Given area:
\[ 250\,cm^2 = 250 \times 10^{-4}\,m^2 = 0.025\,m^2 \]
Step 3: Use the pressure formula.
Pressure is defined as force per unit area.
\[ P = \frac{F}{A} \]
Step 4: Substitute the values.
\[ P = \frac{50000}{0.025} = 2 \times 10^{6}\,Pa \]
Step 5: Final conclusion.
Thus, the maximum pressure the smaller piston must bear is \(2 \times 10^{6}\,Pa\).
Quick Tip: Always convert area into square metres before calculating pressure in SI units.
The acceleration due to gravity at height \( h \) above the earth if \( h \ll R \) (Radius of earth) is given by
View Solution
Step 1: Expression for acceleration due to gravity at height \( h \).
The acceleration due to gravity at a distance \( (R + h) \) from the center of the earth is given by:
\[ g' = g\left(\frac{R}{R + h}\right)^2 \]
Step 2: Apply binomial approximation.
Since \( h \ll R \), we can use the approximation:
\[ \left(1 + \frac{h}{R}\right)^{-2} \approx 1 - \frac{2h}{R} \]
Step 3: Substitute the approximation.
\[ g' = g\left(1 - \frac{2h}{R}\right) \]
Step 4: Identify the correct option.
The derived expression exactly matches option (1).
Step 5: Final conclusion.
Thus, the acceleration due to gravity at a small height \( h \) above the earth is given by
\[ g' = g\left(1 - \frac{2h}{R}\right) \] Quick Tip: For small heights compared to earth’s radius, always use binomial approximation to simplify expressions involving gravity.
The orbital angular momentum of a satellite is \(L\), when it is revolving in a circular orbit at height \(h\) from the earth’s surface. If the distance of the satellite from the earth’s centre is increased by eight times its initial value, then the new angular momentum will be
View Solution
Step 1: Expression for orbital angular momentum.
For a satellite moving in a circular orbit, the orbital angular momentum is \[ L = mvr, \]
where \( m \) is the mass of the satellite, \( v \) is the orbital speed, and \( r \) is the distance from the centre of the earth.
Step 2: Relation between orbital speed and radius.
For circular motion under gravitational force, \[ v = \sqrt{\frac{GM}{r}}. \]
Substituting in the expression for \( L \), \[ L = mr\sqrt{\frac{GM}{r}} = m\sqrt{GMr}. \]
Hence, \[ L \propto \sqrt{r}. \]
Step 3: Interpreting the change in distance.
Let the initial distance of the satellite from the earth’s centre be \( r \).
“Distance increased by eight times its initial value’’ means the increase is \( 8r \).
Therefore, the new distance from the earth’s centre is \[ r' = r + 8r = 9r. \]
Step 4: Finding the new angular momentum.
Since \( L \propto \sqrt{r} \), \[ \frac{L'}{L} = \sqrt{\frac{r'}{r}} = \sqrt{\frac{9r}{r}} = 3. \]
\[ \Rightarrow L' = 3L. \]
Step 5: Conclusion.
Thus, the new orbital angular momentum of the satellite is \[ \boxed{3L}. \]
Quick Tip: For satellites in circular orbits, orbital angular momentum varies as the square root of the orbital radius, i.e. \( L \propto \sqrt{r} \). Always interpret phrases like “increased by” carefully.
Given below are two statements:
Statement I: Area under velocity–time graph gives the distance travelled by the body in a given time.
Statement II: Area under acceleration–time graph is equal to the change in velocity in the given time.
In the light of given statements, choose the correct answer from the options given below.
View Solution
Step 1: Analyzing Statement I.
The area under a velocity–time graph represents the displacement of the body, not the distance travelled.
If velocity changes sign (i.e., motion reverses direction), the area under the graph may cancel out partially, whereas distance always remains positive.
Hence, the area under a velocity–time graph does not always give the distance travelled.
Therefore, Statement I is incorrect.
Step 2: Analyzing Statement II.
Acceleration is defined as the rate of change of velocity:
\[ a = \frac{dv}{dt} \]
Integrating acceleration with respect to time gives:
\[ \int a\,dt = \Delta v \]
Thus, the area under an acceleration–time graph gives the change in velocity in the given time interval.
Therefore, Statement II is correct.
Step 3: Final conclusion.
Since Statement I is incorrect and Statement II is correct, the correct option is (4).
Quick Tip: Area under a velocity–time graph gives \textbf{displacement}, not distance. Always check whether direction of motion changes before interpreting graph areas.
The trajectory of a projectile projected from the ground is given by \( y = x - \dfrac{x^2}{20} \), where \(x\) and \(y\) are measured in metre. The maximum height attained by the projectile will be
View Solution
Step 1: Identify the nature of the trajectory.
The given equation of the trajectory is:
\[ y = x - \frac{x^2}{20} \]
This is a quadratic equation in \(x\), representing a parabola opening downwards. Hence, the maximum height corresponds to the vertex of the parabola.
Step 2: Compare with standard quadratic form.
The standard form of a quadratic equation is:
\[ y = ax^2 + bx + c \]
Comparing, we get:
\[ a = -\frac{1}{20}, \quad b = 1, \quad c = 0 \]
Step 3: Find the x-coordinate of the vertex.
The x-coordinate of the vertex is given by:
\[ x = -\frac{b}{2a} \] \[ x = -\frac{1}{2 \times \left(-\frac{1}{20}\right)} = 10 \]
Step 4: Find the maximum height (y-coordinate of the vertex).
Substitute \(x = 10\) in the equation of trajectory:
\[ y_{\max} = 10 - \frac{10^2}{20} = 10 - \frac{100}{20} \] \[ y_{\max} = 10 - 5 = 5\,m \]
Step 5: Final conclusion.
Thus, the maximum height attained by the projectile is \(5\,m\).
Quick Tip: For a projectile trajectory in the form of a quadratic equation, the maximum height is always obtained at the vertex of the parabola.
A bullet of mass \(0.1\,kg\) moving horizontally with speed \(400\,m s^{-1}\) hits a wooden block of mass \(3.9\,kg\) kept on a horizontal rough surface. The bullet gets embedded into the block and moves \(20\,m\) before coming to rest. The coefficient of friction between the block and the surface is \((g = 10\,m s^{-2})\).
View Solution
Step 1: Apply conservation of linear momentum during collision.
Since the bullet gets embedded in the block, the collision is perfectly inelastic.
\[ m_1 u_1 + m_2 u_2 = (m_1 + m_2)v \]
Here,
\[ m_1 = 0.1\,kg, \quad u_1 = 400\,m s^{-1} \] \[ m_2 = 3.9\,kg, \quad u_2 = 0 \] \[ (0.1)(400) = (0.1 + 3.9)v \] \[ 40 = 4v \Rightarrow v = 10\,m s^{-1} \]
Step 2: Use work–energy theorem after collision.
After collision, the combined system comes to rest due to friction.
\[ Initial kinetic energy = Work done against friction \]
Step 3: Calculate initial kinetic energy of the combined mass.
\[ KE = \frac{1}{2}(4)(10^2) = 200\,J \]
Step 4: Calculate work done by friction.
Frictional force is:
\[ F = \mu (m_1 + m_2)g = \mu \times 4 \times 10 = 40\mu \]
Work done by friction over distance \(20\,m\):
\[ W = F \times s = 40\mu \times 20 = 800\mu \]
Step 5: Equate energy and work.
\[ 200 = 800\mu \] \[ \mu = 0.25 \]
Step 6: Final conclusion.
Thus, the coefficient of friction between the block and the surface is \(0.25\).
Quick Tip: For bullet–block problems, always use conservation of momentum during collision and work–energy principle after collision.
Electric potential at a point \(P\) due to a point charge of \(5 \times 10^{-9}\,C\) is \(50\,V\). The distance of \(P\) from the point charge is:
(Assume \( \dfrac{1}{4\pi\varepsilon_0} = 9 \times 10^{9}\,N m^2C^{-2} \))
View Solution
Step 1: Write the formula for electric potential due to a point charge.
Electric potential at a distance \(r\) from a point charge \(q\) is given by:
\[ V = \frac{1}{4\pi\varepsilon_0}\frac{q}{r} \]
Step 2: Substitute the given values.
\[ V = 50\,V, \quad q = 5 \times 10^{-9}\,C, \quad \frac{1}{4\pi\varepsilon_0} = 9 \times 10^{9} \] \[ 50 = \frac{9 \times 10^{9} \times 5 \times 10^{-9}}{r} \]
Step 3: Simplify the expression.
\[ 50 = \frac{45}{r} \] \[ r = \frac{45}{50} = 0.9\,m \]
Step 4: Convert distance into centimetres.
\[ 0.9\,m = 90\,cm \]
Step 5: Final conclusion.
Thus, the distance of point \(P\) from the charge is \(90\,cm\).
Quick Tip: Always convert the final answer into the unit asked in the options and use SI units while substituting values in electrostatics formulas.
The power radiated from a linear antenna of length \( l \) is proportional to (Given, \( \lambda \) = wavelength of wave):
View Solution
Step 1: Understand radiation from a linear antenna.
A linear antenna (short dipole antenna) radiates electromagnetic waves when alternating current flows through it. The power radiated depends on the effective length of the antenna compared to the wavelength of the radiation.
Step 2: Use the standard radiation relation.
For a short linear antenna, the radiated power \(P\) is proportional to the square of the ratio of antenna length to wavelength.
\[ P \propto \left(\frac{l}{\lambda}\right)^2 \]
Step 3: Physical reasoning.
As the antenna length increases relative to the wavelength, radiation efficiency increases. However, radiation depends on the square of this ratio due to oscillating charge acceleration and energy loss through electromagnetic waves.
Step 4: Match with given options.
The derived proportionality exactly matches option (3).
Step 5: Final conclusion.
Hence, the power radiated from a linear antenna of length \(l\) is proportional to
\[ \left(\frac{l}{\lambda}\right)^2 \] Quick Tip: For short dipole antennas, always remember that radiated power varies as the square of antenna length divided by wavelength.
For a given transistor amplifier circuit in CE configuration, \(V_{CC} = 1\,V\), \(R_C = 1\,k\Omega\), \(R_B = 100\,k\Omega\) and \(\beta = 100\). The value of base current \(I_b\) is
View Solution
Step 1: Calculate the collector current \(I_C\).
The collector current is determined by the supply voltage and collector resistance.
\[ I_C = \frac{V_{CC}}{R_C} \] \[ I_C = \frac{1}{1000} = 1 \times 10^{-3}\,A = 1\,mA \]
Step 2: Use the relation between collector current and base current.
For a transistor in CE configuration:
\[ \beta = \frac{I_C}{I_b} \]
Step 3: Calculate the base current.
\[ I_b = \frac{I_C}{\beta} \] \[ I_b = \frac{1 \times 10^{-3}}{100} = 1 \times 10^{-5}\,A \]
Step 4: Convert base current into microampere.
\[ I_b = 10\,\muA \]
Step 5: Final conclusion.
Thus, the value of base current is \(10\,\muA\), corresponding to option (2).
Quick Tip: In CE configuration, always use \( I_b = \dfrac{I_C}{\beta} \) after finding the collector current from the load resistor.
A radioactive material is reduced to \( \dfrac{1}{8} \) of its original amount in 3 days. If \(8 \times 10^{-3}\,kg\) of the material is left after 5 days, the initial amount of the material is
View Solution
Step 1: Determine the half-life of the material.
The material reduces to \( \dfrac{1}{8} \) of its original amount in 3 days.
\[ \dfrac{1}{8} = \left(\dfrac{1}{2}\right)^3 \]
This shows that 3 half-lives occur in 3 days.
\[ Half-life (T_{1/2}) = 1\,day \]
Step 2: Write the radioactive decay formula.
\[ N = N_0 \left(\dfrac{1}{2}\right)^n \]
where \(n\) is the number of half-lives elapsed.
Step 3: Find the number of half-lives in 5 days.
\[ n = \frac{5}{1} = 5 \]
Step 4: Substitute the given values.
Remaining mass after 5 days:
\[ N = 8 \times 10^{-3}\,kg = 8\,g \] \[ 8 = N_0 \left(\dfrac{1}{2}\right)^5 = \frac{N_0}{32} \]
Step 5: Calculate the initial mass.
\[ N_0 = 8 \times 32 = 256\,g \]
Step 6: Final conclusion.
Thus, the initial amount of the radioactive material is \(256\,g\).
Quick Tip: Always express decay fractions in powers of \( \tfrac{1}{2} \) to quickly determine the number of half-lives.
In photoelectric effect
A. The photocurrent is proportional to the intensity of the incident radiation.
B. Maximum kinetic energy with which photoelectrons are emitted depends on the intensity of incident light.
C. Maximum kinetic energy with which photoelectrons are emitted depends on the frequency of incident light.
D. The emission of photoelectrons requires a minimum threshold intensity of incident radiation.
E. Maximum kinetic energy of the photoelectrons is independent of the frequency of the incident light.
Choose the correct answer from the options given below:
View Solution
Step 1: Analyse Statement A.
Photocurrent depends on the number of photoelectrons emitted per second, which increases with the intensity of incident light.
Hence, Statement A is correct.
Step 2: Analyse Statement B.
The maximum kinetic energy of photoelectrons does not depend on the intensity of incident light. It depends on frequency.
Hence, Statement B is incorrect.
Step 3: Analyse Statement C.
According to Einstein’s photoelectric equation:
\[ K_{\max} = h\nu - \phi \]
Maximum kinetic energy depends on the frequency \( \nu \) of incident radiation.
Hence, Statement C is correct.
Step 4: Analyse Statement D.
Photoelectric emission requires a minimum threshold frequency, not threshold intensity.
Hence, Statement D is incorrect.
Step 5: Analyse Statement E.
Maximum kinetic energy clearly depends on frequency, so this statement is false.
Hence, Statement E is incorrect.
Step 6: Final conclusion.
Only statements A and C are correct. Therefore, the correct option is (3).
Quick Tip: In the photoelectric effect, intensity controls photocurrent, while frequency controls the maximum kinetic energy of photoelectrons.
The width of fringe is \(2\,mm\) on the screen in a double slit experiment for light of wavelength \(400\,nm\). The width of the fringe for light of wavelength \(600\,nm\) will be:
View Solution
Step 1: Write the expression for fringe width.
In Young’s double slit experiment, the fringe width \( \beta \) is given by:
\[ \beta = \frac{\lambda D}{d} \]
where \( \lambda \) is the wavelength of light, \(D\) is the distance between the slits and the screen, and \(d\) is the separation between the slits.
Step 2: Establish the proportionality.
Since \(D\) and \(d\) remain constant,
\[ \beta \propto \lambda \]
Step 3: Use ratio method.
\[ \frac{\beta_2}{\beta_1} = \frac{\lambda_2}{\lambda_1} \] \[ \frac{\beta_2}{2} = \frac{600}{400} \]
Step 4: Calculate the new fringe width.
\[ \beta_2 = 2 \times \frac{600}{400} = 2 \times \frac{3}{2} = 3\,mm \]
Step 5: Final conclusion.
Thus, the width of the fringe for light of wavelength \(600\,nm\) is \(3\,mm\).
Quick Tip: In Young’s double slit experiment, fringe width is directly proportional to the wavelength of light.
The waves emitted when a metal target is bombarded with high energy electrons are
View Solution
Step 1: Understand the physical process involved.
When high energy electrons strike a metal target, they undergo sudden deceleration upon interaction with the nuclei and inner shell electrons of the metal atoms. This rapid deceleration leads to the emission of electromagnetic radiation.
Step 2: Identify the type of radiation produced.
The radiation produced due to sudden deceleration of fast-moving electrons is known as Bremsstrahlung radiation. In addition, characteristic radiation is also produced due to electronic transitions within the metal atoms. Both these radiations lie in the X-ray region of the electromagnetic spectrum.
Step 3: Eliminate incorrect options.
Radio waves, Infrared rays, and Microwaves are low-frequency radiations and are not produced by high-energy electron bombardment of metal targets.
Step 4: Final conclusion.
Thus, the waves emitted when a metal target is bombarded with high energy electrons are X-rays.
Quick Tip: High-speed electrons striking a metal target produce X-rays due to Bremsstrahlung and characteristic radiation.
An emf of \(0.08\,V\) is induced in a metal rod of length \(10\,cm\) held normal to a uniform magnetic field of \(0.4\,T\). The velocity with which the rod moves is
View Solution
Step 1: Write the formula for motional emf.
When a conductor of length \(l\) moves with velocity \(v\) perpendicular to a magnetic field \(B\), the induced emf is given by:
\[ \mathcal{E} = B l v \]
Step 2: Convert given quantities into SI units.
\[ l = 10\,cm = 0.1\,m \] \[ B = 0.4\,T, \quad \mathcal{E} = 0.08\,V \]
Step 3: Substitute the values in the formula.
\[ 0.08 = 0.4 \times 0.1 \times v \]
Step 4: Solve for velocity \(v\).
\[ 0.08 = 0.04v \] \[ v = \frac{0.08}{0.04} = 2\,m s^{-1} \]
Step 5: Final conclusion.
Thus, the velocity of the rod is \(2\,m s^{-1}\), which corresponds to option (2).
Quick Tip: For motional emf problems, always use \( \mathcal{E} = Blv \) and ensure the rod moves perpendicular to the magnetic field.
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: Electromagnets are made of soft iron.
Reason R: Soft iron has high permeability and low retentivity.
In the light of above statements, choose the most appropriate answer from the options given below.
View Solution
Step 1: Analyse Assertion A.
Electromagnets are required to become strongly magnetised when current flows and lose magnetism quickly when current is switched off. Soft iron is ideally suited for this purpose.
Hence, Assertion A is correct.
Step 2: Analyse Reason R.
Soft iron has high magnetic permeability, which allows it to be easily magnetised, and low retentivity, which ensures that it does not retain magnetism after the current is removed.
Hence, Reason R is correct.
Step 3: Establish the link between A and R.
The properties stated in Reason R (high permeability and low retentivity) are exactly the reasons why soft iron is used in making electromagnets.
Step 4: Final conclusion.
Both Assertion A and Reason R are correct, and Reason R correctly explains Assertion A.
Quick Tip: Electromagnets require materials that magnetise easily and demagnetise quickly—soft iron fulfills both conditions.
The equivalent resistance between A and B as shown in the figure is:
View Solution
Step 1: Identify nodes connected by conducting wires.
From the given circuit, the top wire directly connects point A to point D. Hence, A and D are at the same potential.
Similarly, the bottom wire directly connects point C to point B. Hence, C and B are at the same potential.
Step 2: Redraw the circuit using equivalent nodes.
After identifying equipotential points:
- Node 1: A and D
- Node 2: C and B
Now, all three resistors are connected between the same two nodes.
Step 3: Identify parallel resistors.
The following resistors are connected between Node 1 and Node 2:
\[ 20\,k\Omega,\quad 20\,k\Omega,\quad 10\,k\Omega \]
Hence, they are in parallel.
Step 4: Combine the two \(20\,k\Omega\) resistors.
\[ R_{eq1} = \frac{20 \times 20}{20 + 20} = 10\,k\Omega \]
Step 5: Combine the remaining parallel resistances.
Now we have two \(10\,k\Omega\) resistors in parallel:
\[ R_{eq} = \frac{10 \times 10}{10 + 10} = 5\,k\Omega \]
Step 6: Final conclusion.
Thus, the equivalent resistance between A and B is \(5\,k\Omega\).
Quick Tip: Always check for direct wire connections first—they create equipotential points and can simplify complex resistor networks drastically.
A guitar string of length \(90\,cm\) vibrates with a fundamental frequency of \(120\,Hz\). The length of the string producing a fundamental frequency of \(180\,Hz\) will be \underline{\hspace{2cm cm.
View Solution
Step 1: Recall the relation between frequency and length of a stretched string.
For a stretched string vibrating in its fundamental mode, the frequency is inversely proportional to its length, provided tension and linear density remain constant.
\[ f \propto \frac{1}{L} \]
Step 2: Write the proportionality relation.
\[ \frac{f_1}{f_2} = \frac{L_2}{L_1} \]
Step 3: Substitute the given values.
\[ f_1 = 120\,Hz, \quad L_1 = 90\,cm \] \[ f_2 = 180\,Hz \]
\[ \frac{120}{180} = \frac{L_2}{90} \]
Step 4: Solve for the new length \(L_2\).
\[ \frac{2}{3} = \frac{L_2}{90} \] \[ L_2 = \frac{2}{3} \times 90 = 60\,cm \]
Step 5: Final conclusion.
The length of the string required to produce a fundamental frequency of \(180\,Hz\) is
\[ \boxed{60\,cm} \] Quick Tip: For a vibrating string with constant tension and mass per unit length, increasing frequency means decreasing length.
A steel rod of length \(1\,m\) and cross sectional area \(10^{-4}\,m^2\) is heated from \(0^\circC\) to \(200^\circC\) without being allowed to extend or bend. The compressive tension produced in the rod is \hspace{2cm \(\times 10^{4\,N\).
(Given: Young’s modulus of steel \(= 2 \times 10^{11}\,N m^{-2}\), coefficient of linear expansion \(= 10^{-5}\,K^{-1}\))
View Solution
Step 1: Understand the physical situation.
Since the rod is heated but not allowed to expand, thermal expansion produces a compressive stress in the rod.
Step 2: Write the formula for thermal stress.
Thermal stress produced when expansion is prevented is given by:
\[ Stress = Y \alpha \Delta T \]
Step 3: Substitute the given values.
\[ Y = 2 \times 10^{11}\,N m^{-2} \] \[ \alpha = 10^{-5}\,K^{-1} \] \[ \Delta T = 200 - 0 = 200\,K \]
\[ Stress = 2 \times 10^{11} \times 10^{-5} \times 200 \] \[ Stress = 4 \times 10^{8}\,N m^{-2} \]
Step 4: Calculate the compressive force (tension).
Force is given by:
\[ F = Stress \times Area \]
\[ F = 4 \times 10^{8} \times 10^{-4} \] \[ F = 4 \times 10^{4}\,N \]
Step 5: Final conclusion.
The compressive tension produced in the rod is
\[ \boxed{4 \times 10^{4}\,N} \] Quick Tip: When thermal expansion is completely restricted, use \(Stress = Y\alpha\Delta T\) directly to find the force developed.
A hollow spherical ball of uniform density rolls up a curved surface with an initial velocity of \(3\,m s^{-1}\) (as shown in the figure). The maximum height with respect to the initial position covered by it will be \hspace{2cm cm.
(Take \(g = 10\,m s^{-2\))
View Solution
Step 1: Identify the type of motion.
The ball is rolling without slipping, so both translational and rotational kinetic energies are involved.
Step 2: Write expressions for kinetic energies.
Total kinetic energy of a rolling body is given by:
\[ K = \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2 \]
For a hollow spherical ball:
\[ I = \frac{2}{3}mr^2 \]
and since rolling without slipping,
\[ \omega = \frac{v}{r} \]
Step 3: Substitute in kinetic energy expression.
\[ K = \frac{1}{2}mv^2 + \frac{1}{2}\left(\frac{2}{3}mr^2\right)\left(\frac{v}{r}\right)^2 \] \[ K = \frac{1}{2}mv^2 + \frac{1}{3}mv^2 \] \[ K = \frac{5}{6}mv^2 \]
Step 4: Apply conservation of mechanical energy.
At the maximum height, the ball momentarily comes to rest, so all kinetic energy converts into gravitational potential energy.
\[ \frac{5}{6}mv^2 = mgh \]
Step 5: Calculate the maximum height.
\[ h = \frac{5}{6}\frac{v^2}{g} \] \[ h = \frac{5}{6}\times\frac{(3)^2}{10} \] \[ h = \frac{5}{6}\times\frac{9}{10} = \frac{45}{60} = 0.75\,m \]
Step 6: Convert height into centimetres.
\[ 0.75\,m = 75\,cm \]
Final Answer:
\[ \boxed{75\,cm} \] Quick Tip: For rolling bodies, always include both translational and rotational kinetic energies; the moment of inertia determines how high the body can climb.
A body of mass \(5\,kg\) is moving with a momentum of \(10\,kg m s^{-1}\). Now a force of \(2\,N\) acts on the body in the direction of its motion for \(5\,s\). The increase in the kinetic energy of the body is \underline{\hspace{2cm J.
View Solution
Step 1: Find the initial velocity of the body.
Momentum is given by:
\[ p = mv \] \[ 10 = 5 \times v \] \[ v = 2\,m s^{-1} \]
Step 2: Calculate the change in momentum due to applied force.
Change in momentum is given by impulse:
\[ \Delta p = F \times t \] \[ \Delta p = 2 \times 5 = 10\,kg m s^{-1} \]
Step 3: Find the final momentum and final velocity.
\[ p_f = 10 + 10 = 20\,kg m s^{-1} \] \[ v_f = \frac{p_f}{m} = \frac{20}{5} = 4\,m s^{-1} \]
Step 4: Calculate the initial and final kinetic energies.
Initial kinetic energy:
\[ K_i = \frac{1}{2}mv^2 = \frac{1}{2}\times5\times(2)^2 = 10\,J \]
Final kinetic energy:
\[ K_f = \frac{1}{2}mv^2 = \frac{1}{2}\times5\times(4)^2 = 40\,J \]
Step 5: Find the increase in kinetic energy.
\[ \Delta K = K_f - K_i = 40 - 10 = 30\,J \]
Final Answer:
\[ \boxed{30\,J} \] Quick Tip: When force acts in the direction of motion, use impulse to find change in momentum and then calculate the change in kinetic energy.
A \(600\,pF\) capacitor is charged by a \(200\,V\) supply. It is then disconnected from the supply and connected to another uncharged \(600\,pF\) capacitor. The electrostatic energy lost in the process is \underline{\hspace{2cm \(\muJ\).
View Solution
Step 1: Write the formula for energy stored in a capacitor.
The electrostatic energy stored in a capacitor is given by:
\[ U = \frac{1}{2}CV^2 \]
Step 2: Calculate the initial energy stored in the charged capacitor.
\[ C = 600\,pF = 600 \times 10^{-12}\,F \] \[ V = 200\,V \]
\[ U_i = \frac{1}{2} \times 600 \times 10^{-12} \times (200)^2 \] \[ U_i = \frac{1}{2} \times 600 \times 10^{-12} \times 40000 \] \[ U_i = 1.2 \times 10^{-5}\,J = 12\,\muJ \]
Step 3: Find the final voltage after connecting the uncharged capacitor.
When two identical capacitors are connected together, the charge distributes equally and the final voltage becomes half of the initial voltage.
\[ V_f = \frac{200}{2} = 100\,V \]
Step 4: Calculate the final energy stored in the combination.
Total capacitance after connection:
\[ C_{total} = 600 + 600 = 1200\,pF = 1200 \times 10^{-12}\,F \]
\[ U_f = \frac{1}{2} \times 1200 \times 10^{-12} \times (100)^2 \] \[ U_f = \frac{1}{2} \times 1200 \times 10^{-12} \times 10000 \] \[ U_f = 6 \times 10^{-6}\,J = 6\,\muJ \]
Step 5: Calculate the electrostatic energy lost.
\[ \Delta U = U_i - U_f = 12 - 6 = 6\,\muJ \]
Final Answer:
\[ \boxed{6\,\muJ} \] Quick Tip: When a charged capacitor is connected to an identical uncharged capacitor, half of the initial energy is always lost due to redistribution of charge.
The ratio of wavelength of spectral lines \(H_{\alpha}\) and \(H_{\beta}\) in the Balmer series is \( \dfrac{x}{20} \). The value of \(x\) is \underline{\hspace{2cm.
View Solution
Step 1: Recall the Balmer formula.
For the Balmer series, the wavelength is given by:
\[ \frac{1}{\lambda} = R\left(\frac{1}{2^2} - \frac{1}{n^2}\right) \]
where \(n = 3,4,5,\dots\)
Step 2: Identify transitions for \(H_{\alpha}\) and \(H_{\beta}\).
\[ H_{\alpha}: n = 3 \rightarrow 2 \] \[ H_{\beta}: n = 4 \rightarrow 2 \]
Step 3: Write expressions for wavelengths.
For \(H_{\alpha}\):
\[ \frac{1}{\lambda_{\alpha}} = R\left(\frac{1}{4} - \frac{1}{9}\right) = R\left(\frac{5}{36}\right) \]
For \(H_{\beta}\):
\[ \frac{1}{\lambda_{\beta}} = R\left(\frac{1}{4} - \frac{1}{16}\right) = R\left(\frac{3}{16}\right) \]
Step 4: Take the ratio of wavelengths.
\[ \frac{\lambda_{\alpha}}{\lambda_{\beta}} = \frac{\left(\dfrac{3}{16}\right)}{\left(\dfrac{5}{36}\right)} = \frac{3 \times 36}{16 \times 5} = \frac{108}{80} = \frac{27}{20} \]
Step 5: Compare with the given form.
\[ \frac{\lambda_{\alpha}}{\lambda_{\beta}} = \frac{x}{20} \] \[ x = 27 \]
Final Answer:
\[ \boxed{27} \] Quick Tip: In the Balmer series, longer wavelength corresponds to smaller energy transition; always use inverse wavelength ratios carefully.
Two transparent media having refractive indices \(1.0\) and \(1.5\) are separated by a spherical refracting surface of radius of curvature \(30\,cm\). The centre of curvature of the surface is towards the denser medium and a point object is placed on the principal axis in the rarer medium at a distance of \(15\,cm\) from the pole of the surface. The distance of image from the pole of the surface is \underline{\hspace{2cm cm.
View Solution
Step 1: Write the formula for refraction at a spherical surface.
The relation for refraction at a spherical surface is:
\[ \frac{n_2}{v} - \frac{n_1}{u} = \frac{n_2 - n_1}{R} \]
Step 2: Identify the given quantities with sign convention.
Refractive index of rarer medium:
\[ n_1 = 1.0 \]
Refractive index of denser medium:
\[ n_2 = 1.5 \]
Object distance (object in rarer medium, to the left of pole):
\[ u = -15\,cm \]
Radius of curvature (centre towards denser medium, to the right):
\[ R = +30\,cm \]
Step 3: Substitute the values in the formula.
\[ \frac{1.5}{v} - \frac{1.0}{-15} = \frac{1.5 - 1.0}{30} \] \[ \frac{1.5}{v} + \frac{1}{15} = \frac{0.5}{30} \]
Step 4: Simplify the equation.
\[ \frac{1}{15} = \frac{4}{60}, \quad \frac{0.5}{30} = \frac{1}{60} \] \[ \frac{1.5}{v} = \frac{1}{60} - \frac{4}{60} = -\frac{3}{60} = -\frac{1}{20} \]
Step 5: Solve for image distance \(v\).
\[ v = \frac{1.5}{-\frac{1}{20}} = -30\,cm \]
Final Answer:
\[ \boxed{30\,cm} \]
(The negative sign indicates that the image is formed on the same side as the object.)
Quick Tip: Always apply proper sign convention carefully in refraction problems—especially for object distance and radius of curvature.
A series combination of a resistor of resistance \(100\,\Omega\), an inductor of inductance \(1\,H\), and a capacitor of capacitance \(6.25\,\muF\) is connected to an AC source. The quality factor of the circuit will be \underline{\hspace{2cm.
View Solution
Step 1: Recall the formula for quality factor of a series RLC circuit.
The quality factor \(Q\) of a series RLC circuit is given by:
\[ Q = \frac{1}{R}\sqrt{\frac{L}{C}} \]
Step 2: Convert all given quantities into SI units.
\[ R = 100\,\Omega \] \[ L = 1\,H \] \[ C = 6.25\,\muF = 6.25 \times 10^{-6}\,F \]
Step 3: Substitute the values in the formula.
\[ Q = \frac{1}{100}\sqrt{\frac{1}{6.25 \times 10^{-6}}} \]
Step 4: Simplify the expression.
\[ \frac{1}{6.25 \times 10^{-6}} = 1.6 \times 10^{5} \] \[ \sqrt{1.6 \times 10^{5}} = 400 \]
Step 5: Calculate the quality factor.
\[ Q = \frac{400}{100} = 4 \]
Final Answer:
\[ \boxed{4} \] Quick Tip: For a series RLC circuit, a higher quality factor indicates sharper resonance and lower energy loss.
The ratio of magnetic field at the centre of a current carrying coil of radius \(r\) to the magnetic field at a distance \(r\) from the centre of the coil on its axis is \(\sqrt{x}:1\). The value of \(x\) is \underline{\hspace{2cm.
View Solution
Step 1: Write the expression for magnetic field at the centre of a circular coil.
For a circular coil of radius \(r\) carrying current \(I\), the magnetic field at the centre is:
\[ B_c = \frac{\mu_0 I}{2r} \]
Step 2: Write the expression for magnetic field on the axis of the coil.
The magnetic field at a point on the axis at a distance \(x\) from the centre is given by:
\[ B_x = \frac{\mu_0 I r^2}{2(r^2 + x^2)^{3/2}} \]
Step 3: Substitute \(x = r\).
\[ B_r = \frac{\mu_0 I r^2}{2(r^2 + r^2)^{3/2}} \] \[ B_r = \frac{\mu_0 I r^2}{2(2r^2)^{3/2}} \] \[ B_r = \frac{\mu_0 I r^2}{2 \cdot 2^{3/2} r^3} = \frac{\mu_0 I}{2^{5/2} r} \]
Step 4: Take the ratio of the magnetic fields.
\[ \frac{B_c}{B_r} = \frac{\dfrac{\mu_0 I}{2r}}{\dfrac{\mu_0 I}{2^{5/2} r}} = \frac{2^{5/2}}{2} = 2^{3/2} \]
Step 5: Compare with the given ratio.
\[ \sqrt{x} = 2^{3/2} \] \[ x = (2^{3/2})^2 = 2^3 = 8 \]
Final Answer:
\[ \boxed{8} \] Quick Tip: For circular coils, always remember that magnetic field on the axis decreases faster than at the centre due to the \((r^2 + x^2)^{3/2}\) term.
The number density of free electrons in copper is nearly \(8 \times 10^{28}\,m^{-3}\). A copper wire has its area of cross section \(= 2 \times 10^{-6}\,m^2\) and is carrying a current of \(3.2\,A\). The drift speed of the electrons is \hspace{2cm \(\times 10^{-6\,m s^{-1}\).
View Solution
Step 1: Write the formula for drift velocity.
The drift speed \(v_d\) of electrons is given by:
\[ v_d = \frac{I}{n q A} \]
where
\(I\) = current,
\(n\) = number density of electrons,
\(q\) = charge of an electron,
\(A\) = area of cross section.
Step 2: Substitute the given values.
\[ I = 3.2\,A \] \[ n = 8 \times 10^{28}\,m^{-3} \] \[ q = 1.6 \times 10^{-19}\,C \] \[ A = 2 \times 10^{-6}\,m^2 \]
\[ v_d = \frac{3.2}{8 \times 10^{28} \times 1.6 \times 10^{-19} \times 2 \times 10^{-6}} \]
Step 3: Simplify the denominator.
\[ 8 \times 1.6 \times 2 = 25.6 \] \[ 10^{28} \times 10^{-19} \times 10^{-6} = 10^{3} \]
\[ v_d = \frac{3.2}{25.6 \times 10^{3}} \]
Step 4: Calculate the drift speed.
\[ v_d = 0.125 \times 10^{-3} \] \[ v_d = 1.25 \times 10^{-4}\,m s^{-1} \]
Step 5: Express the answer in the required form.
\[ v_d = 125 \times 10^{-6}\,m s^{-1} \]
Final Answer:
\[ \boxed{125} \] Quick Tip: Although electrons move very fast randomly, their drift speed in a conductor carrying current is extremely small.
Which of the following have the same number of significant figures?
A. 0.00253
B. 1.0003
C. 15.0
D. 163
Choose the correct answer from the options given below.
View Solution
Step 1: Count significant figures in A (0.00253).
Leading zeros are not significant.
\[ 0.00253 \rightarrow 3 significant figures \]
Step 2: Count significant figures in B (1.0003).
Zeros between non-zero digits and trailing zeros after decimal are significant.
\[ 1.0003 \rightarrow 5 significant figures \]
Step 3: Count significant figures in C (15.0).
Trailing zero after decimal point is significant.
\[ 15.0 \rightarrow 3 significant figures \]
Step 4: Count significant figures in D (163).
All non-zero digits are significant.
\[ 163 \rightarrow 3 significant figures \]
Step 5: Compare the results.
A, C, and D each have 3 significant figures, while B has 5 significant figures.
Step 6: Final conclusion.
Thus, the correct option is (4) A, C and D only.
Quick Tip: Leading zeros are not significant, but trailing zeros after a decimal point are always significant.
Arrange the following gases in increasing order of van der Waals constant \(a\).
A. Ar
B. CH\(_4\)
C. H\(_2\)O
D. C\(_6\)H\(_6\)
Choose the correct option from the following.
View Solution
Step 1: Meaning of van der Waals constant \(a\).
The van der Waals constant \(a\) represents the magnitude of intermolecular attractive forces.
Larger molecules or molecules with stronger intermolecular attractions have higher values of \(a\).
Step 2: Analyse each gas.
Argon (Ar):
It is a monoatomic noble gas with very weak London dispersion forces, hence the smallest value of \(a\).
Methane (CH\(_4\)):
A small non-polar molecule, but larger than Ar, so it has slightly stronger dispersion forces than argon.
Water (H\(_2\)O):
A polar molecule capable of hydrogen bonding, leading to much stronger intermolecular attraction and a higher value of \(a\).
Benzene (C\(_6\)H\(_6\)):
A large molecule with high molecular mass and strong dispersion forces, giving it the highest value of \(a\).
Step 3: Arrange in increasing order of \(a\).
\[ Ar < CH_4 < H_2O < C_6H_6 \]
Step 4: Match with options.
This order corresponds to option (1).
Quick Tip: The van der Waals constant \(a\) increases with molecular size and strength of intermolecular attractions such as polarity and hydrogen bonding.
The correct reaction profile diagram for a positive catalyst reaction is
View Solution
Step 1: Understand the role of a positive catalyst.
A positive catalyst increases the rate of a reaction by lowering the activation energy. It does not change the energies of reactants and products.
Step 2: Identify the correct characteristics of the reaction profile.
For a catalysed reaction:
- Reactant energy level remains the same
- Product energy level remains the same
- Activation energy is lower with catalyst than without catalyst
Step 3: Analyse the given diagrams.
Diagram 3 correctly shows:
- Same reactant and product energy levels
- A lower energy peak (activation energy) for the reaction with catalyst
- A higher peak for the reaction without catalyst
Step 4: Eliminate incorrect diagrams.
Other diagrams either change the reactant/product energy levels or incorrectly show higher activation energy with catalyst, which is not physically correct.
Step 5: Final conclusion.
Therefore, the correct reaction profile diagram for a positive catalyst reaction is Diagram 3.
Quick Tip: A catalyst lowers activation energy but never changes the energy difference between reactants and products.
Henry Moseley studied characteristic X-ray spectra of elements. The graph which represents this observation correctly is
(Given: \( \nu \) = frequency of X-ray emitted, \( Z \) = atomic number)
View Solution
Step 1: State Moseley’s law.
According to Moseley’s law for characteristic X-rays:
\[ \sqrt{\nu} = a (Z - b) \]
where \(a\) and \(b\) are constants.
Step 2: Interpret the relation.
The equation shows that the square root of the frequency of emitted X-rays varies linearly with the atomic number \(Z\).
Step 3: Identify the correct graph.
A straight-line graph is obtained when \( \sqrt{\nu} \) is plotted on the y-axis and \( Z \) on the x-axis.
Step 4: Eliminate incorrect options.
- \( \nu \) vs \( Z \) is not linear.
- \( \nu^2 \) vs \( Z \) is not linear.
- \( \sqrt{Z} \) vs \( \nu \) does not represent Moseley’s law.
Step 5: Final conclusion.
Thus, the correct graphical representation of Moseley’s observation is option (1).
Quick Tip: Moseley’s law is best remembered as: \(\sqrt{\nu} \propto Z\), not \(\nu \propto Z\).
In Hall–Héroult process, the following is used for reducing \( Al_2O_3 \):
View Solution
Step 1: Understand the Hall–Héroult process.
The Hall–Héroult process is used for the extraction of aluminium by electrolytic reduction of alumina (\(Al_2O_3\)) dissolved in molten cryolite.
Step 2: Role of graphite in the process.
Graphite rods are used as anodes. During electrolysis, oxygen is liberated at the anode, which reacts with carbon (graphite) to form carbon monoxide and carbon dioxide. This effectively removes oxygen from alumina, thereby reducing it to aluminium.
Step 3: Eliminate incorrect options.
\( Na_3AlF_6 \) (Cryolite): Used as a solvent to lower the melting point, not as a reducing agent.
Magnesium: Not used in this process.
\( CaF_2 \): Added to increase electrical conductivity, not for reduction.
Step 4: Final conclusion.
Thus, the substance used for reducing \(Al_2O_3\) in the Hall–Héroult process is graphite.
Quick Tip: In the Hall–Héroult process, cryolite acts as a solvent, while graphite anodes help in removing oxygen from alumina.
Which of the following can reduce decomposition of \( \mathrm{H_2O_2} \) on exposure to light?
View Solution
Step 1: Understand the nature of hydrogen peroxide.
Hydrogen peroxide (\(\mathrm{H_2O_2}\)) is an unstable compound and decomposes easily, especially in the presence of light, heat, alkalis, or impurities.
Step 2: Role of stabilizers.
To reduce or slow down the decomposition of \(\mathrm{H_2O_2}\), stabilizing agents are added. These substances inhibit the catalytic decomposition of hydrogen peroxide.
Step 3: Analyse the given options.
(1) Alkali: Alkalis accelerate the decomposition of \(\mathrm{H_2O_2}\), so this is incorrect.
(2) Urea: Urea acts as a stabilizer and reduces the rate of decomposition of hydrogen peroxide on exposure to light. Hence, this is correct.
(3) Dust: Dust contains impurities that catalyse decomposition, so it increases decomposition.
(4) Glass containers: Although hydrogen peroxide is stored in dark bottles, glass itself does not chemically reduce decomposition.
Step 4: Final conclusion.
Urea helps in reducing the decomposition of hydrogen peroxide on exposure to light.
Quick Tip: Hydrogen peroxide is commonly stored with stabilizers like urea or phosphoric acid to prevent its rapid decomposition.
Given below are two statements. One is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: Sodium is about 30 times as abundant as potassium in the oceans.
Reason R: Potassium is bigger in size than sodium.
In the light of the above statements, choose the correct answer from the options given below.
View Solution
Step 1: Analyse Assertion A.
Sodium is indeed much more abundant than potassium in seawater (about 30 times). This is a well-established fact in marine chemistry and geochemical studies. Hence, Assertion A is true.
Step 2: Analyse Reason R.
Potassium atoms and ions are larger in size than sodium because potassium lies below sodium in Group 1 of the periodic table. Thus, Reason R is also true.
Step 3: Establish the cause–effect relationship.
Due to its larger ionic size, potassium is more easily incorporated into minerals (such as feldspars and clays) and is more readily removed from seawater during geological and sedimentary processes. Sodium, being smaller in size, remains more stable and stays dissolved in seawater for much longer periods.
Thus, the larger size of potassium directly contributes to its lower abundance in oceans compared to sodium. Hence, Reason R correctly explains Assertion A.
Step 4: Final conclusion.
Both Assertion A and Reason R are true, and Reason R is the correct explanation of Assertion A.
Quick Tip: In assertion–reason questions, always check whether the reason provides a scientific cause for the assertion. Here, ionic size influences geochemical behaviour in seawater.
For a good quality cement, the ratio of lime to the total of the oxides of Si, Al and Fe should be as close as to
View Solution
Step 1: Understanding the lime ratio in cement.
In cement chemistry, an important parameter is the lime saturation factor, which controls the proportion of lime (\(\mathrm{CaO}\)) relative to the acidic oxides present in cement, namely:
\[ \mathrm{SiO_2,\ Al_2O_3,\ Fe_2O_3}. \]
Step 2: Ideal proportion for good quality cement.
For good quality Portland cement, the ratio \[ \frac{Lime (CaO)}{SiO_2+Al_2O_3+Fe_2O_3} \]
should be approximately 2.
Step 3: Justification.
- If this ratio is greater than 2, excess lime remains uncombined, leading to unsoundness and expansion.
- If this ratio is less than 2, cement becomes weak and gains low strength.
Thus, a value close to 2 ensures proper strength, setting characteristics, and durability.
Step 4: Matching with options.
Among the given options, the value closest to the required ratio is 2.
Final Conclusion:
Hence, the correct answer is \[ \boxed{2}. \]
Quick Tip: Always remember that good quality cement requires a balanced lime content—neither excess nor deficiency—to ensure strength and soundness.
Match List I with List II.
List I (Coordination Complex) \hfill List II (Number of unpaired electrons)
A. \([Cr(CN)_6]^{3-}\) \hfill I. 0
B. \([Fe(H_2O)_6]^{2+}\) \hfill II. 3
C. \([Co(NH_3)_6]^{3+}\) \hfill III. 2
D. \([Ni(NH_3)_6]^{2+}\) \hfill IV. 4
Choose the correct answer from the options given below:
View Solution
Step 1: Analyse complex A \([Cr(CN)_6]^{3-}\).
Chromium is in the \(+3\) oxidation state:
\[ Cr^{3+} : d^3 \] \(CN^-\) is a strong field ligand, giving a low-spin octahedral complex.
Electronic configuration: \(t_{2g}^3\)
Number of unpaired electrons \(= 3\).
So, A \(\rightarrow\) II.
Step 2: Analyse complex B \([Fe(H_2O)_6]^{2+}\).
Iron is in the \(+2\) oxidation state:
\[ Fe^{2+} : d^6 \] \(H_2O\) is a weak field ligand, giving a high-spin octahedral complex.
Number of unpaired electrons \(= 4\).
So, B \(\rightarrow\) IV.
Step 3: Analyse complex C \([Co(NH_3)_6]^{3+}\).
Cobalt is in the \(+3\) oxidation state:
\[ Co^{3+} : d^6 \] \(NH_3\) is a strong enough ligand to cause pairing.
Low-spin octahedral complex with no unpaired electrons.
So, C \(\rightarrow\) I.
Step 4: Analyse complex D \([Ni(NH_3)_6]^{2+}\).
Nickel is in the \(+2\) oxidation state:
\[ Ni^{2+} : d^8 \]
Octahedral complex with two unpaired electrons.
So, D \(\rightarrow\) III.
Step 5: Final matching.
\[ A–II, B–IV, C–I, D–III \] Quick Tip: Strong field ligands like \(CN^-\) and high oxidation states favor low-spin complexes, while weak field ligands like \(H_2O\) give high-spin complexes.
Which of these reactions is \emph{not} a part of the breakdown of ozone in the stratosphere?
View Solution
Step 1: Recall the mechanism of ozone depletion.
Ozone depletion in the stratosphere mainly occurs due to free radicals like chlorine released from CFCs under UV radiation.
Step 2: Analyse each reaction.
Reaction (1):
This represents photodissociation of CFCs by UV radiation, producing chlorine radicals. This is a key initiating step.
Reaction (2):
\[ \mathrm{Cl} + \mathrm{O_3} \rightarrow \mathrm{ClO} + \mathrm{O_2} \]
This reaction directly destroys ozone and is an essential step in ozone depletion.
Reaction (3):
\[ \mathrm{ClO} + \mathrm{O} \rightarrow \mathrm{Cl} + \mathrm{O_2} \]
This regenerates the chlorine radical, allowing it to destroy more ozone molecules. This is also a valid step.
Reaction (4):
\[ 2\,\mathrm{ClO} \rightarrow \mathrm{ClO_2} + \mathrm{Cl} \]
This reaction is not part of the standard ozone depletion cycle in the stratosphere. Instead, ClO radicals usually undergo dimerisation as \[ \mathrm{ClO} + \mathrm{ClO} + M \rightarrow \mathrm{Cl_2O_2} + M \]
Hence, this reaction is incorrect.
Step 3: Final conclusion.
Reaction (4) is not involved in the breakdown of ozone in the stratosphere.
Quick Tip: In ozone depletion, chlorine acts as a catalyst: it is regenerated and can destroy thousands of ozone molecules.
Major product ‘P’ formed in the following reaction is:
View Solution
Step 1: Identify the reaction type.
The given substrate is an unsaturated carboxylic acid treated with \(\mathrm{Br_2}\) in the presence of \(\mathrm{NaHCO_3}\).
This reaction is a classic example of halolactonization.
Step 2: Formation of bromonium ion.
Bromine adds across the double bond to form a cyclic bromonium ion.
Step 3: Intramolecular nucleophilic attack.
The carboxylate ion (generated due to \(\mathrm{NaHCO_3}\)) acts as a nucleophile and attacks the more substituted carbon of the bromonium ion intramolecularly.
This leads to ring closure forming a lactone.
Step 4: Nature of the product.
- The reaction favors 5- or 6-membered ring formation due to stability.
- A bromolactone is formed as the major product.
- Simple addition products or dibromides are not favored under these conditions.
Step 5: Match with the given options.
Only option (4) shows a cyclic bromo–lactone structure, which is the correct major product.
Quick Tip: Alkenoic acids with \(\mathrm{Br_2/NaHCO_3}\) undergo halolactonization, not simple bromine addition.
The correct IUPAC nomenclature for the following compound is:
View Solution
Step 1: Identify the principal functional group.
The compound contains a \(\mathrm{COOH}\) group, which has the highest priority.
Hence, the parent chain must be named as a carboxylic acid.
Step 2: Select the longest carbon chain containing \(\mathrm{COOH}\).
Counting from the carboxylic acid carbon, the longest chain contains six carbon atoms.
Therefore, the parent name is hexanoic acid.
Step 3: Number the carbon chain correctly.
The carbon of the \(\mathrm{COOH}\) group is numbered as carbon 1.
Step 4: Identify substituents and their positions.
- A \(\mathrm{CH_3}\) (methyl) substituent is present at carbon 2.
- A ketone group (\(=O\)) is present at carbon 5, which is named as an oxo substituent.
Step 5: Arrange substituents alphabetically.
Substituents are written in alphabetical order: methyl before oxo.
Step 6: Write the final IUPAC name.
\[ 2-Methyl-5-oxohexanoic acid \] Quick Tip: When a carboxylic acid is present, it always gets priority in naming; ketone groups are written as “oxo” substituents.
The correct order of reactivity of the following haloarenes towards nucleophilic substitution with aqueous NaOH is:
A, B, C and D represent the following substituted chlorobenzenes as shown in the figure.
View Solution
Step 1: Identify the reaction type.
Nucleophilic substitution in haloarenes occurs mainly via the SNAr (addition–elimination) mechanism when strong electron-withdrawing groups are present at the ortho/para positions to the halogen.
Step 2: Role of substituents.
- \(\mathrm{NO_2}\) group is a strong electron-withdrawing group (–I, –M) and greatly increases reactivity.
- \(\mathrm{OMe}\) group is an electron-donating group (+M) and decreases nucleophilic substitution.
- More \(\mathrm{NO_2}\) groups at ortho/para positions \(\Rightarrow\) higher reactivity.
Step 3: Analyse each compound.
Compound A:
Only chloro group present, no activating group → least reactive.
Compound B:
One \(\mathrm{NO_2}\) group present → more reactive than A.
Compound C:
One \(\mathrm{NO_2}\) (activating) and one \(\mathrm{OMe}\) (deactivating) group → reactivity reduced compared to B.
Compound D:
Two \(\mathrm{NO_2}\) groups at ortho/para positions → maximum stabilization of Meisenheimer complex → highest reactivity.
Step 4: Arrange in decreasing order of reactivity.
\[ D > C > B > A \]
Step 5: Match with options.
This corresponds to option (3).
Quick Tip: In nucleophilic substitution of haloarenes, more \(\mathrm{NO_2}\) groups at ortho/para positions mean faster reaction; electron-donating groups slow it down.
The descending order of acidity for the following carboxylic acids is:
A. \(\mathrm{CH_3COOH}\)
B. \(\mathrm{CF_3COOH}\)
C. \(\mathrm{ClCH_2COOH}\)
D. \(\mathrm{FCH_2COOH}\)
E. \(\mathrm{BrCH_2COOH}\)
Choose the correct answer from the options given below:
View Solution
Step 1: Recall the factor affecting acidity of carboxylic acids.
The acidity of carboxylic acids depends on the stability of the conjugate base.
Electron-withdrawing groups increase acidity by stabilizing the carboxylate ion through the \(-I\) (inductive) effect.
Step 2: Analyse compound B (\(\mathrm{CF_3COOH}\)).
The \(\mathrm{CF_3}\) group has three fluorine atoms, which exert a very strong \(-I\) effect.
Hence, \(\mathrm{CF_3COOH}\) is the most acidic.
Step 3: Compare mono-halogen substituted acids.
For \(\alpha\)-haloacetic acids, acidity follows the order of electronegativity of the halogen:
\[ \mathrm{F} > \mathrm{Cl} > \mathrm{Br} \]
Thus:
\[ \mathrm{FCH_2COOH} > \mathrm{ClCH_2COOH} > \mathrm{BrCH_2COOH} \]
Step 4: Analyse acetic acid (\(\mathrm{CH_3COOH}\)).
The methyl group shows a \(+I\) effect, which destabilizes the conjugate base.
Hence, acetic acid is the least acidic.
Step 5: Write the overall descending order of acidity.
\[ \mathrm{CF_3COOH} > \mathrm{FCH_2COOH} > \mathrm{ClCH_2COOH} > \mathrm{BrCH_2COOH} > \mathrm{CH_3COOH} \]
Step 6: Match with the given options.
This order corresponds to option (4).
Quick Tip: Stronger electron-withdrawing groups near the \(\mathrm{COOH}\) group increase acidity by stabilizing the conjugate base.
A compound ‘X’ when treated with phthalic anhydride in presence of concentrated \(\mathrm{H_2SO_4}\) yields ‘Y’. ‘Y’ is used as an acid–base indicator. ‘X’ and ‘Y’ are respectively:
View Solution
Step 1: Identify compound ‘Y’.
The question states that compound ‘Y’ is formed by reaction with phthalic anhydride in presence of concentrated sulphuric acid and is used as an acid–base indicator.
A well-known indicator synthesized in this way is phenolphthalein.
Step 2: Recall the preparation of phenolphthalein.
Phenolphthalein is prepared by the condensation of phenol (carbolic acid) with phthalic anhydride in presence of concentrated \(\mathrm{H_2SO_4}\) or \(\mathrm{ZnCl_2}\).
Step 3: Identify compound ‘X’.
Since phenolphthalein is formed from phenol, compound ‘X’ must be carbolic acid (phenol).
Step 4: Eliminate incorrect options.
- Anisole and toluidine do not give phenolphthalein with phthalic anhydride.
- Salicylaldehyde is not used in the synthesis of phenolphthalein.
Step 5: Final conclusion.
Thus, the correct pair is carbolic acid and phenolphthalein.
Quick Tip: Phenolphthalein is synthesized by condensing phenol with phthalic anhydride and is widely used as an acid–base indicator.
The product (P) formed from the following multistep reaction is:
Reaction sequence:
View Solution
Step 1: Identify the starting compound.
The given compound is p-nitrotoluene, containing a methyl group (\(-\mathrm{CH_3}\)) and a nitro group (\(-\mathrm{NO_2}\)) on the benzene ring.
Step 2: Effect of bromination \((\mathrm{Br_2})\).
- The \(-\mathrm{CH_3}\) group is an activating, ortho–para directing group.
- The \(-\mathrm{NO_2}\) group is a deactivating, meta-directing group.
Bromination therefore occurs at the position which is ortho to the methyl group and meta to the nitro group.
Step 3: Reduction of nitro group.
\[ \mathrm{NO_2} \xrightarrow{\mathrm{H_2/Pd}} \mathrm{NH_2} \]
The nitro group is reduced to an amine.
Step 4: Diazotisation.
\[ \mathrm{NH_2} \xrightarrow{\mathrm{NaNO_2/HCl,\ 0^\circ C}} \mathrm{N_2^+Cl^-} \]
An aryl diazonium salt is formed.
Step 5: Replacement of diazonium group.
\[ \mathrm{Ar{-}N_2^+} \xrightarrow{\mathrm{H_3PO_2}} \mathrm{Ar{-}H} \]
The diazonium group is replaced by hydrogen (reductive deamination).
Step 6: Final product.
After removal of the diazonium group, only the bromine and methyl substituents remain.
The bromine is at the ortho position with respect to the methyl group.
\[ \boxed{o-Bromotoluene} \] Quick Tip: \(\mathrm{H_3PO_2}\) replaces a diazonium group by hydrogen, allowing selective removal of \(-\mathrm{NH_2}\) groups after diazotisation.
The statement/s which are true about antagonists from the following is/are:
A. They bind to the receptor site.
B. Get transferred inside the cell for their action.
C. Inhibit the natural communication of the body.
D. Mimic the natural messenger.
View Solution
Step 1: Understanding antagonists.
Antagonists are substances that bind to specific receptor sites in the body but do not activate them. Instead, they block the action of natural messengers (agonists) by preventing their binding to receptors.
Step 2: Analysis of each statement.
Statement A: Antagonists bind to the receptor site. This statement is correct because antagonists occupy the receptor and prevent activation by natural messengers.
Statement B: Antagonists get transferred inside the cell for their action. This statement is incorrect because antagonists usually act at the receptor level and do not need to enter the cell.
Statement C: Antagonists inhibit the natural communication of the body. This statement is correct since they block the effect of natural chemical messengers.
Statement D: Antagonists mimic the natural messenger. This statement is incorrect because mimicking the natural messenger is a property of agonists, not antagonists.
Step 3: Conclusion.
Only statements A and C are true for antagonists.
Quick Tip: Antagonists block receptor activity, while agonists activate receptors by mimicking natural messengers.
Match List I with List II
List I: Natural amino acid
A. Glutamic acid
B. Glutamine
C. Tyrosine
D. Tryptophan
List II: One letter code
I. Q
II. W
III. E
IV. Y
View Solution
Step 1: Recall one-letter codes of amino acids.
Each amino acid has a specific one-letter abbreviation used in protein sequence representation.
Step 2: Match each amino acid correctly.
Glutamic acid has the one-letter code E.
Glutamine has the one-letter code Q.
Tyrosine has the one-letter code Y.
Tryptophan has the one-letter code W.
Step 3: Final matching.
A (Glutamic acid) \(\rightarrow\) III (E)
B (Glutamine) \(\rightarrow\) I (Q)
C (Tyrosine) \(\rightarrow\) IV (Y)
D (Tryptophan) \(\rightarrow\) II (W)
Step 4: Conclusion.
The correct matching is A-III, B-I, C-IV, D-II.
Quick Tip: Remember these important one-letter codes: Glutamic acid = E, Glutamine = Q, Tyrosine = Y, Tryptophan = W.
Given below are two statements:
Statement I: Methyl orange is a weak acid.
Statement II: The benzenoid form of methyl orange is more intense/deeply coloured than the quinonoid form.
In the light of the above statements, choose the most appropriate answer from the options given below:
View Solution
Step 1: Analysis of Statement I.
Methyl orange is not a weak acid in the usual Brønsted–Lowry sense. It behaves primarily as an acid–base indicator due to structural changes between different ionic forms, rather than due to dissociation as a weak acid. Hence, Statement I is incorrect.
Step 2: Analysis of Statement II.
In methyl orange, the quinonoid form is more intensely (deeply) coloured, while the benzenoid form is lighter in colour. Therefore, saying that the benzenoid form is more deeply coloured is incorrect. Hence, Statement II is incorrect.
Step 3: Final conclusion.
Both Statement I and Statement II are incorrect.
Quick Tip: In acid–base indicators, colour change is due to structural transformation; generally, the quinonoid form is more deeply coloured than the benzenoid form.
Given below are two statements:
Statement I: In redox titration, the indicators used are sensitive to change in pH of solution.
Statement II: In acid–base titration, the indicators used are sensitive to change in oxidation potential.
In the light of the above statements, choose the most appropriate answer from the options given below:
View Solution
Step 1: Analysis of Statement I.
In redox titrations, the indicators used are redox indicators, which are sensitive to changes in oxidation–reduction potential and not to changes in pH. Therefore, Statement I is incorrect.
Step 2: Analysis of Statement II.
In acid–base titrations, the indicators used are acid–base indicators, which are sensitive to changes in pH of the solution and not to oxidation potential. Therefore, Statement II is also incorrect.
Step 3: Conclusion.
Since both statements describe incorrect principles, the correct choice is that both Statement I and Statement II are incorrect.
Quick Tip: Remember:
Acid–base indicators respond to \textbf{pH changes}, while redox indicators respond to \textbf{changes in oxidation potential}.
The number of atomic orbitals from the following having 5 radial nodes is ............
Given orbitals: \(7s,\; 7p,\; 6s,\; 8p,\; 8d\)
View Solution
Step 1: Formula for radial nodes.
The number of radial nodes for an atomic orbital is given by:
\[ Number of radial nodes = n - l - 1 \]
where \(n\) is the principal quantum number and \(l\) is the azimuthal quantum number.
Step 2: Calculate radial nodes for each orbital.
(i) \(7s\): \(n = 7,\; l = 0\)
\[ 7 - 0 - 1 = 6 \quad (Not equal to 5) \]
(ii) \(7p\): \(n = 7,\; l = 1\)
\[ 7 - 1 - 1 = 5 \quad (Correct) \]
(iii) \(6s\): \(n = 6,\; l = 0\)
\[ 6 - 0 - 1 = 5 \quad (Correct) \]
(iv) \(8p\): \(n = 8,\; l = 1\)
\[ 8 - 1 - 1 = 6 \quad (Not equal to 5) \]
(v) \(8d\): \(n = 8,\; l = 2\)
\[ 8 - 2 - 1 = 5 \quad (Correct) \]
Step 3: Final counting.
Orbitals having exactly 5 radial nodes are:
\[ 7p,\; 6s,\; 8d \]
Total number of such orbitals \(= 3\).
Final Answer: \[ \boxed{3} \] Quick Tip: Always remember:
Radial nodes depend only on \(n\) and \(l\), and are calculated using \(n - l - 1\).
The number of species from the following carrying a single lone pair on central atom Xenon is
XeF\(_5^+\), XeO\(_3\), XeO\(_2\)F\(_2\), XeF\(_5^-\), XeO\(_3\)F\(_2\), XeOF\(_4\), XeF\(_4\)
View Solution
Step 1: Concept used.
To determine the number of lone pairs on the central xenon atom, we use VSEPR theory and electron counting. Xenon has 8 valence electrons. The number of electrons used in bonding is subtracted from the total valence electrons to find the number of lone pairs.
Step 2: Analysis of each species.
XeF\(_5^+\) : Xenon has 7 valence electrons due to +1 charge. Five Xe–F bonds use 5 electrons, leaving 2 electrons = 1 lone pair.
XeO\(_3\) : Xenon forms three Xe=O double bonds. After bonding, 2 electrons remain on xenon, giving 1 lone pair.
XeO\(_2\)F\(_2\) : Xenon forms two Xe=O double bonds and two Xe–F single bonds. One lone pair remains on xenon.
XeF\(_5^-\) : Xenon has 9 valence electrons due to −1 charge. After forming five bonds, 4 electrons remain, corresponding to 2 lone pairs. Hence, not counted.
XeO\(_3\)F\(_2\) : Xenon forms five bonds (three Xe=O and two Xe–F). No lone pair remains on xenon.
XeOF\(_4\) : Xenon forms one Xe=O double bond and four Xe–F single bonds. One lone pair remains on xenon.
XeF\(_4\) : Xenon forms four Xe–F bonds and retains two lone pairs (square planar geometry). Hence, not counted.
Step 3: Counting valid species.
Species with exactly one lone pair on xenon are: XeF\(_5^+\), XeO\(_3\), XeO\(_2\)F\(_2\), and XeOF\(_4\).
Quick Tip: For xenon compounds, always adjust valence electrons for ionic charge before counting lone pairs using VSEPR theory.
For complete combustion of ethene,
\[ \mathrm{C_2H_4(g) + 3O_2(g) \rightarrow 2CO_2(g) + 2H_2O(l)} \]
the amount of heat produced as measured in a bomb calorimeter is 1406 kJ mol\(^{-1}\) at 300 K. The minimum value of \(T\Delta S\) needed to reach equilibrium is (–) \hspace{1cm kJ. (Nearest integer)
Given: \(R = 8.3 \, J K^{-1mol^{-1}\)
View Solution
Step 1: Understanding the thermodynamic condition for equilibrium.
At equilibrium, the Gibbs free energy change is zero.
\[ \Delta G = \Delta H - T\Delta S = 0 \]
Hence,
\[ T\Delta S = \Delta H \]
Step 2: Determination of \(\Delta H\).
The heat produced in a bomb calorimeter corresponds to the enthalpy change of the reaction.
Since heat is produced, the reaction is exothermic.
\[ \Delta H = -1406 \, kJ mol^{-1} \]
Step 3: Estimation of entropy change using gaseous moles.
Number of moles of gaseous reactants:
\[ 1 (C_2H_4) + 3 (O_2) = 4 \]
Number of moles of gaseous products:
\[ 2 (CO_2) \]
\[ \Delta n_{gas} = 2 - 4 = -2 \]
\[ \Delta S \approx \Delta n_{gas} \times R = -2 \times 8.3 = -16.6 \, J K^{-1}mol^{-1} \]
Step 4: Minimum value of \(T\Delta S\) at equilibrium.
At equilibrium,
\[ T\Delta S = \Delta H = -1406 \, kJ \]
Thus, the minimum value of \(T\Delta S\) required to reach equilibrium is \(-1406\) kJ.
Quick Tip: At equilibrium, always use the condition \(\Delta G = 0\), which directly gives \(T\Delta S = \Delta H\). The sign of \(T\Delta S\) follows the sign of \(\Delta H\).
If the boiling points of two solvents X and Y (having same molecular weights) are in the ratio \(2:1\) and their enthalpy of vaporizations are in the ratio \(1:2\), then the boiling point elevation constant of X is \(m\) times the boiling point elevation constant of Y. The value of \(m\) is \underline{\hspace{1cm (nearest integer).
View Solution
Step 1: Formula for boiling point elevation constant.
The boiling point elevation constant \(K_b\) is given by:
\[ K_b = \frac{R T_b^2 M}{\Delta H_{vap}} \]
Since both solvents have the same molecular weight, \(M\) and \(R\) cancel out while taking ratio.
Step 2: Writing the ratio of \(K_b\) for solvents X and Y.
\[ \frac{K_{b,X}}{K_{b,Y}} = \frac{T_{b,X}^2 / \Delta H_{vap,X}}{T_{b,Y}^2 / \Delta H_{vap,Y}} \]
Step 3: Substituting the given ratios.
\[ \frac{T_{b,X}}{T_{b,Y}} = \frac{2}{1} \Rightarrow \frac{T_{b,X}^2}{T_{b,Y}^2} = 4 \]
\[ \frac{\Delta H_{vap,X}}{\Delta H_{vap,Y}} = \frac{1}{2} \]
Step 4: Calculating the ratio.
\[ \frac{K_{b,X}}{K_{b,Y}} = \frac{4}{1/2} = 8 \]
Step 5: Final result.
Thus, the boiling point elevation constant of solvent X is \(8\) times that of solvent Y.
Quick Tip: Remember that \(K_b\) is directly proportional to the square of boiling point and inversely proportional to enthalpy of vaporization when molecular weight is the same.
The solubility product of BaSO\(_4\) is \(1 \times 10^{-10}\) at 298 K. The solubility of BaSO\(_4\) in \(0.1\) M K\(_2\)SO\(_4\)(aq) solution is \hspace{1cm \(\times 10^{-9\) g L\(^{-1}\) (nearest integer).
Given: Molar mass of BaSO\(_4\) = \(233\) g mol\(^{-1}\)
View Solution
Step 1: Writing the dissociation equilibrium.
\[ BaSO_4(s) \rightleftharpoons Ba^{2+}(aq) + SO_4^{2-}(aq) \]
Step 2: Expression for solubility product.
\[ K_{sp} = [Ba^{2+}][SO_4^{2-}] \]
Step 3: Considering common ion effect.
In \(0.1\) M K\(_2\)SO\(_4\), the concentration of \(SO_4^{2-}\) ions is \(0.1\) M.
Let the solubility of BaSO\(_4\) be \(s\) mol L\(^{-1}\).
\[ [Ba^{2+}] = s \] \[ [SO_4^{2-}] \approx 0.1 \]
Step 4: Substituting values in \(K_{sp}\).
\[ 1 \times 10^{-10} = s \times 0.1 \]
\[ s = 1 \times 10^{-9} \, mol L^{-1} \]
Step 5: Converting molar solubility to g L\(^{-1}\).
\[ Solubility = 1 \times 10^{-9} \times 233 = 2.33 \times 10^{-7} \, g L^{-1} \]
Step 6: Expressing in required form.
\[ 2.33 \times 10^{-7} = 233 \times 10^{-9} \]
Nearest integer value of coefficient is \(2\).
Quick Tip: In presence of a common ion, always assume its concentration remains nearly constant while calculating solubility using \(K_{sp}\).
The number of incorrect statements from the following is \hspace{1cm}
A. The electrical work that a reaction can perform at constant pressure and temperature is equal to the reaction Gibbs energy.
B. \(E_{cell}\) is dependent on the pressure.
C. \(\dfrac{dE^\circ_{cell}}{dT} = \dfrac{\Delta_r S^\circ}{nF}\)
D. A cell is operating reversibly if the cell potential is exactly balanced by an opposing source of potential difference.
View Solution
Step 1: Analyzing statement A.
At constant temperature and pressure, the maximum non-expansion work obtainable from a reaction is equal to the decrease in Gibbs free energy.
Electrical work is a type of non-expansion work in an electrochemical cell.
Hence, statement A is correct.
Step 2: Analyzing statement B.
The cell potential \(E_{cell}\) depends on the reaction quotient, which in turn depends on the partial pressures of gaseous species involved.
Therefore, \(E_{cell}\) varies with pressure when gases are involved.
Hence, statement B is correct.
Step 3: Analyzing statement C.
The correct thermodynamic relation is:
\[ \frac{dE^\circ_{cell}}{dT} = \frac{\Delta_r S^\circ}{nF} \]
This is a standard relation connecting temperature dependence of standard cell potential with entropy change.
Hence, statement C is correct.
Step 4: Analyzing statement D.
A reversible electrochemical cell operates infinitesimally close to equilibrium.
This condition is achieved when the cell potential is exactly balanced by an external opposing potential, resulting in zero net current.
Hence, statement D is correct.
Step 5: Final counting.
All statements A, B, C, and D are correct.
Therefore, the number of incorrect statements is 1.
Quick Tip: Always remember that reversibility in electrochemical cells implies operation under equilibrium conditions with no net current flow.
Coagulating value of the electrolytes AlCl\(_3\) and NaCl for As\(_2\)S\(_3\) are 0.09 and 50.04 respectively. The coagulating power of AlCl\(_3\) is \(x\) times the coagulating power of NaCl. The value of \(x\) is \underline{\hspace{1cm.
View Solution
Step 1: Understanding coagulating value and coagulating power.
Coagulating power of an electrolyte is inversely proportional to its coagulating value.
That is,
\[ Coagulating power \propto \frac{1}{Coagulating value} \]
Step 2: Writing the ratio of coagulating powers.
\[ \frac{Coagulating power of AlCl_3}{Coagulating power of NaCl} = \frac{Coagulating value of NaCl}{Coagulating value of AlCl_3} \]
Step 3: Substituting the given values.
\[ \frac{Coagulating power of AlCl_3}{Coagulating power of NaCl} = \frac{50.04}{0.09} \]
Step 4: Calculation.
\[ \frac{50.04}{0.09} = 556 \]
Step 5: Final result.
Hence, the coagulating power of AlCl\(_3\) is \(556\) times the coagulating power of NaCl.
Quick Tip: Always remember: lower coagulating value means higher coagulating power. Trivalent ions show much higher coagulating power than monovalent ions as per Hardy–Schulze rule.
The ratio of sigma and \(\pi\) bonds present in pyrophosphoric acid is \underline{\hspace{1cm.
View Solution
Step 1: Writing the structure of pyrophosphoric acid.
Pyrophosphoric acid has the molecular formula \(\mathrm{H_4P_2O_7}\).
Its structure is:
\[ \mathrm{HO{-}P(=O)(OH){-}O{-}P(=O)(OH){-}OH} \]
Step 2: Counting sigma bonds.
Each single bond contributes one sigma bond, and each double bond contributes one sigma bond.
P=O double bonds = 2 \(\Rightarrow\) \(2\) sigma bonds
P–O (from OH groups) = 4 \(\Rightarrow\) \(4\) sigma bonds
P–O–P bridging bonds = 2 \(\Rightarrow\) \(2\) sigma bonds
O–H bonds = 4 \(\Rightarrow\) \(4\) sigma bonds
\[ Total sigma bonds = 2 + 4 + 2 + 4 = 12 \]
Step 3: Counting \(\pi\) bonds.
Each P=O double bond contributes one \(\pi\) bond.
\[ Total \pi bonds = 2 \]
Step 4: Calculating the ratio.
\[ Ratio of sigma to \pi bonds = 12 : 2 = 6 : 1 \]
Quick Tip: Remember that every double bond contains one sigma and one \(\pi\) bond, while single bonds contribute only sigma bonds.
The sum of oxidation state of the metals in Fe(CO)\(_5\), VO\(_2^+\) and WO\(_3\) is \underline{\hspace{1cm.
View Solution
Step 1: Oxidation state of Fe in Fe(CO)\(_5\).
Carbon monoxide (CO) is a neutral ligand.
Since all ligands are neutral and the complex is neutral, the oxidation state of Fe is:
\[ Oxidation state of Fe = 0 \]
Step 2: Oxidation state of V in VO\(_2^+\).
Let the oxidation state of vanadium be \(x\).
Oxidation state of oxygen is \(-2\).
\[ x + 2(-2) = +1 \]
\[ x - 4 = 1 \]
\[ x = +5 \]
Step 3: Oxidation state of W in WO\(_3\).
Let the oxidation state of tungsten be \(y\).
\[ y + 3(-2) = 0 \]
\[ y - 6 = 0 \]
\[ y = +6 \]
Step 4: Calculating the sum.
\[ Sum of oxidation states = 0 + 5 + 6 = 11 \]
Quick Tip: Neutral ligands like CO do not affect oxidation state. Always equate the total oxidation number to the overall charge of the species.
The observed magnetic moment of the complex [Mn(NCS)\(_6\)]\(^{x-}\) is 6.06 BM. The numerical value of \(x\) is \underline{\hspace{1cm.
View Solution
Step 1: Relation between magnetic moment and number of unpaired electrons.
The spin-only magnetic moment is given by the formula:
\[ \mu = \sqrt{n(n+2)} \, BM \]
where \(n\) is the number of unpaired electrons.
Step 2: Determination of number of unpaired electrons.
Given magnetic moment:
\[ \mu = 6.06 \, BM \]
Checking possible values of \(n\):
For \(n = 5\),
\[ \mu = \sqrt{5(5+2)} = \sqrt{35} \approx 5.92 \, BM \]
This value is closest to the observed magnetic moment.
Hence, the number of unpaired electrons \(n = 5\).
Step 3: Oxidation state of Mn.
Manganese with 5 unpaired electrons corresponds to the \(d^5\) configuration.
This occurs for Mn\(^{2+}\).
Step 4: Calculation of charge on the complex.
Each NCS ligand carries a \(-1\) charge.
Let the oxidation state of Mn be \(+2\).
\[ Charge on complex = +2 + 6(-1) = -4 \]
Step 5: Final answer.
Thus, the numerical value of \(x\) is \(4\).
Quick Tip: When magnetic moment is close to \(\sqrt{35}\) BM, it generally indicates five unpaired electrons corresponding to a high-spin \(d^5\) configuration.


























































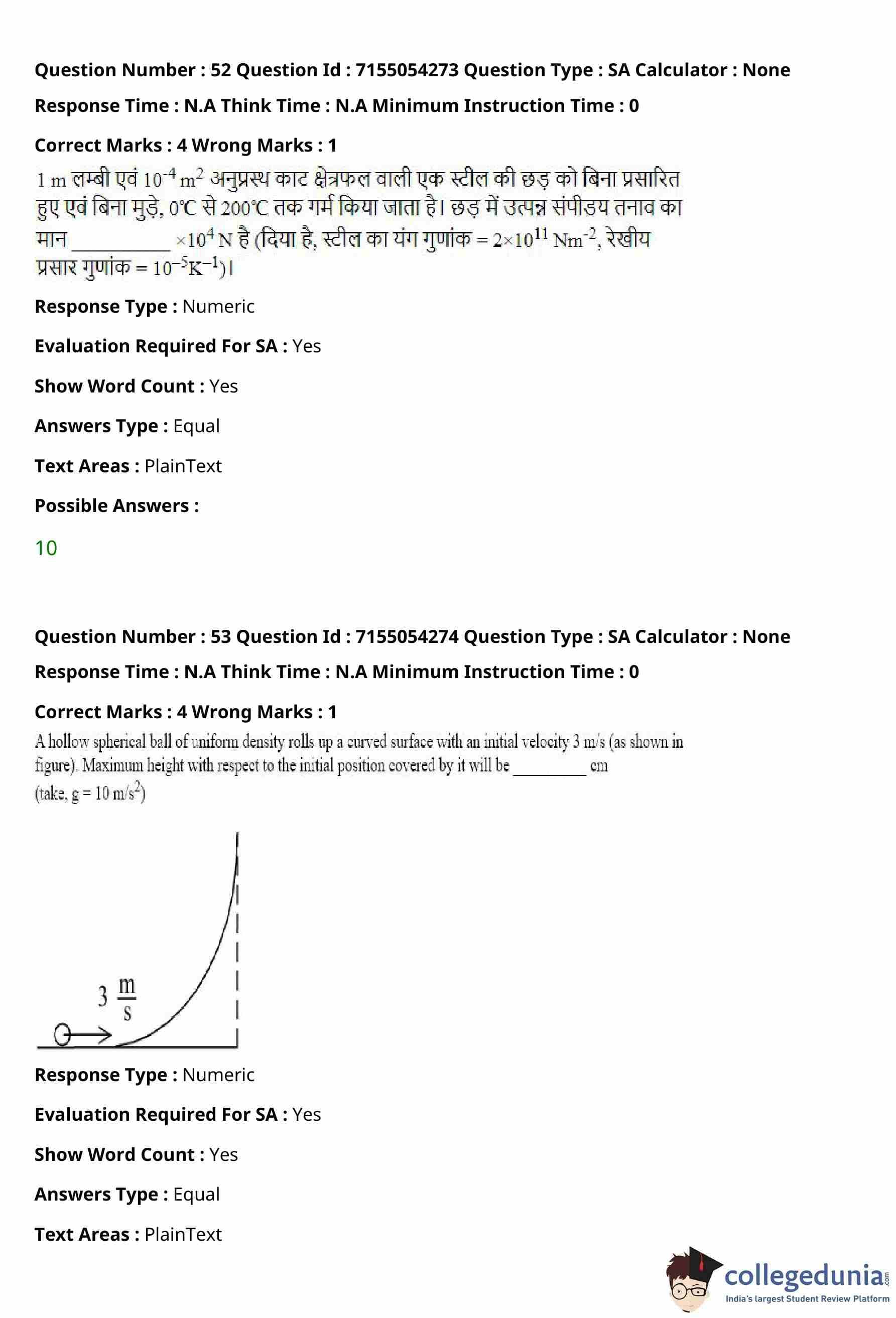
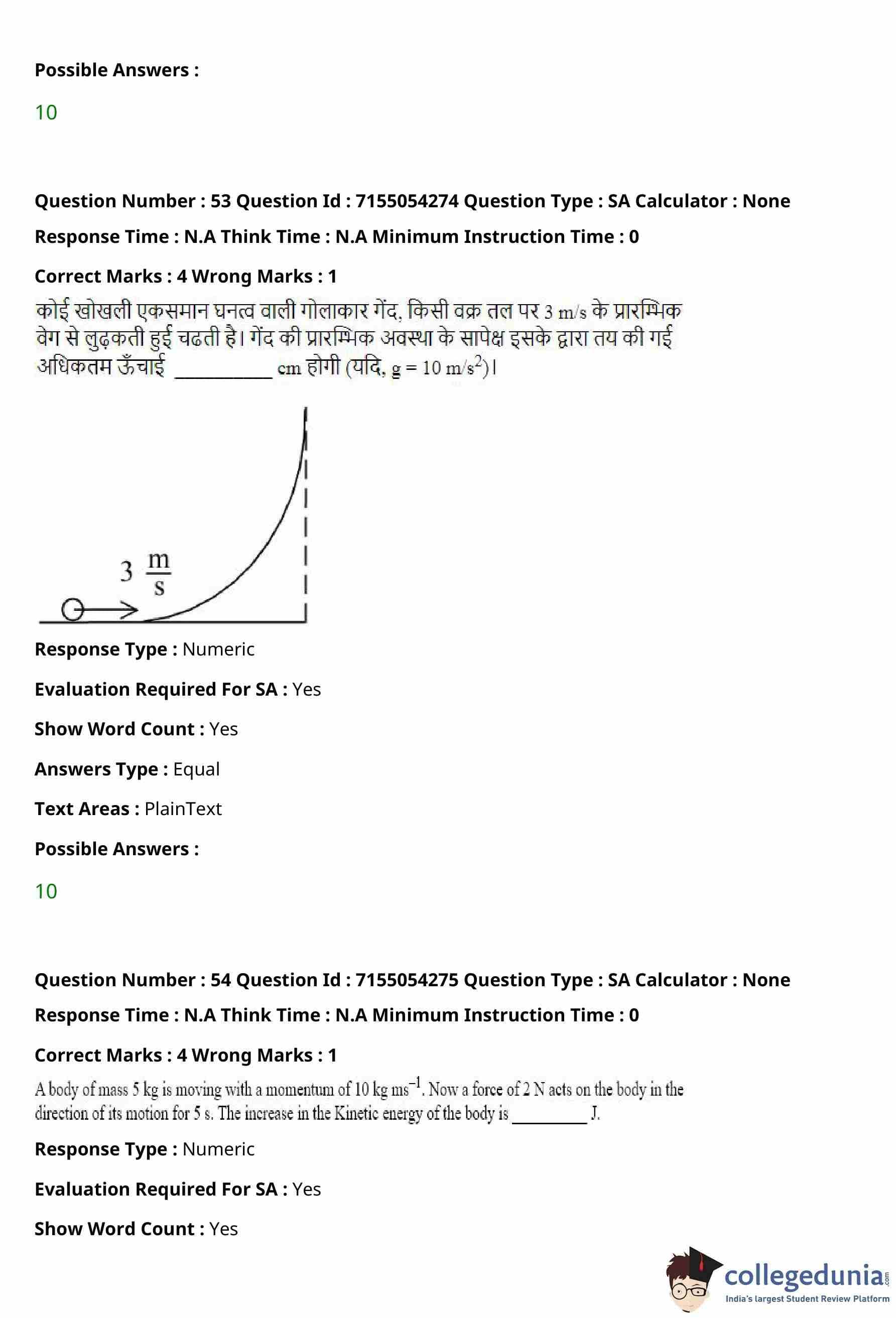









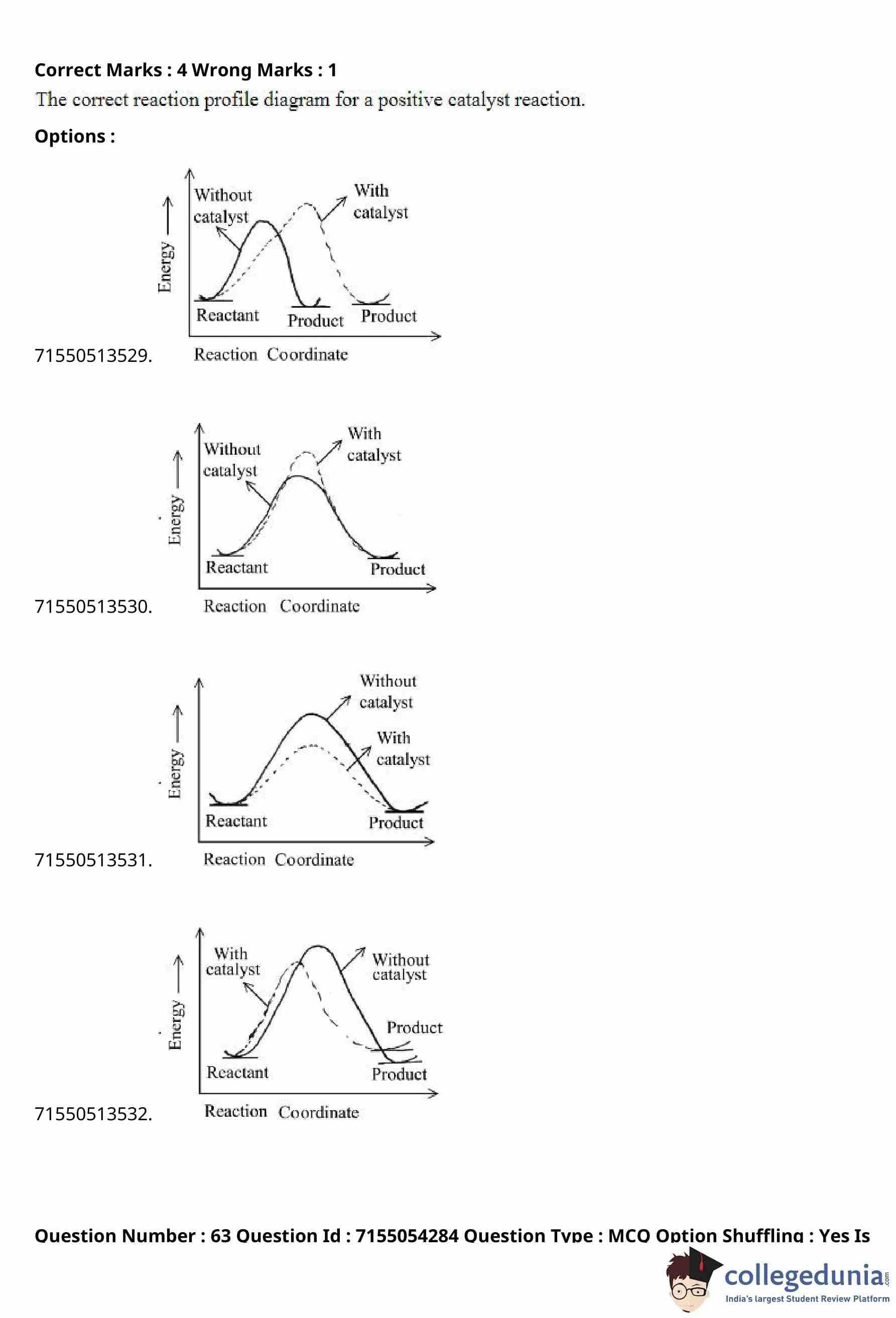
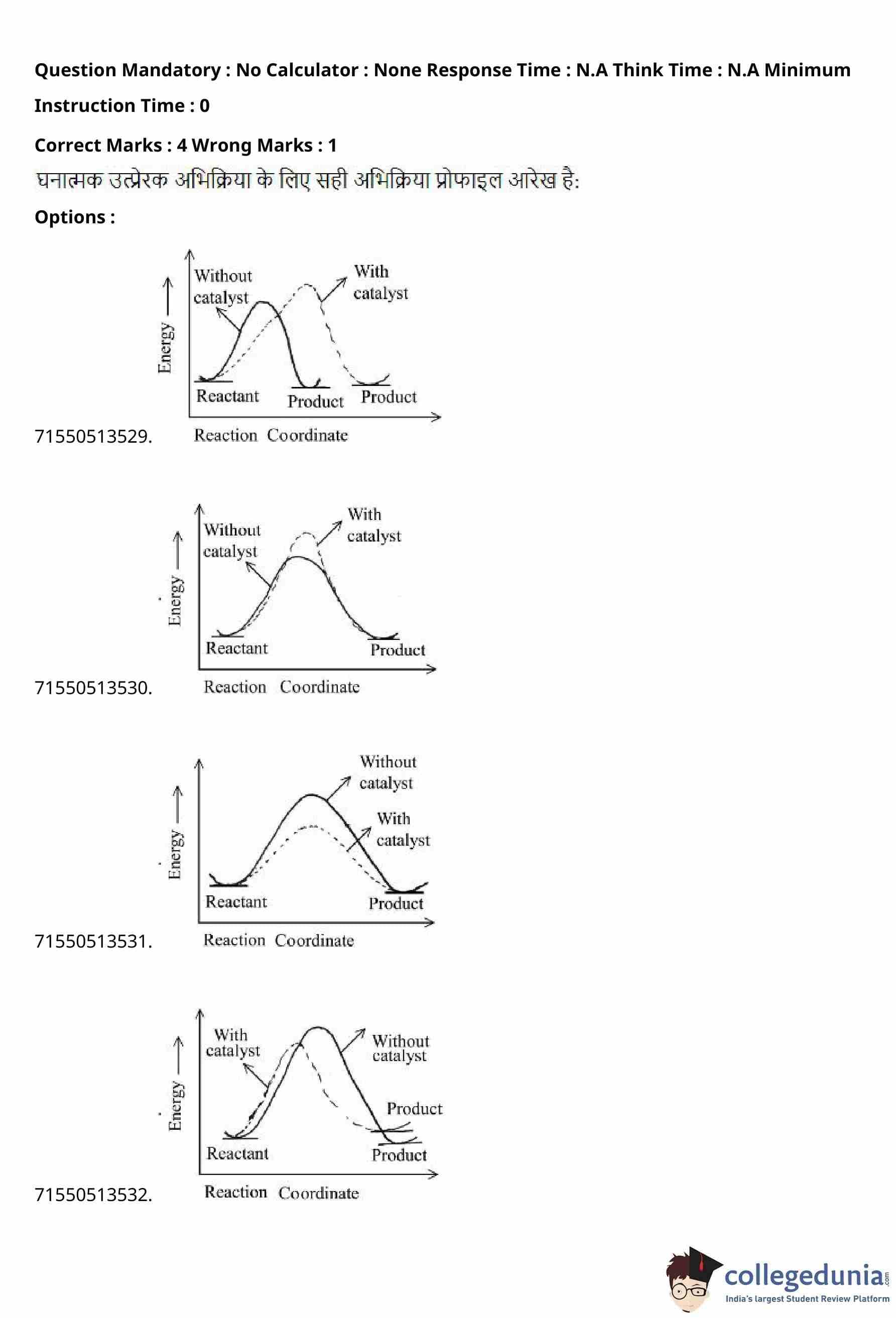
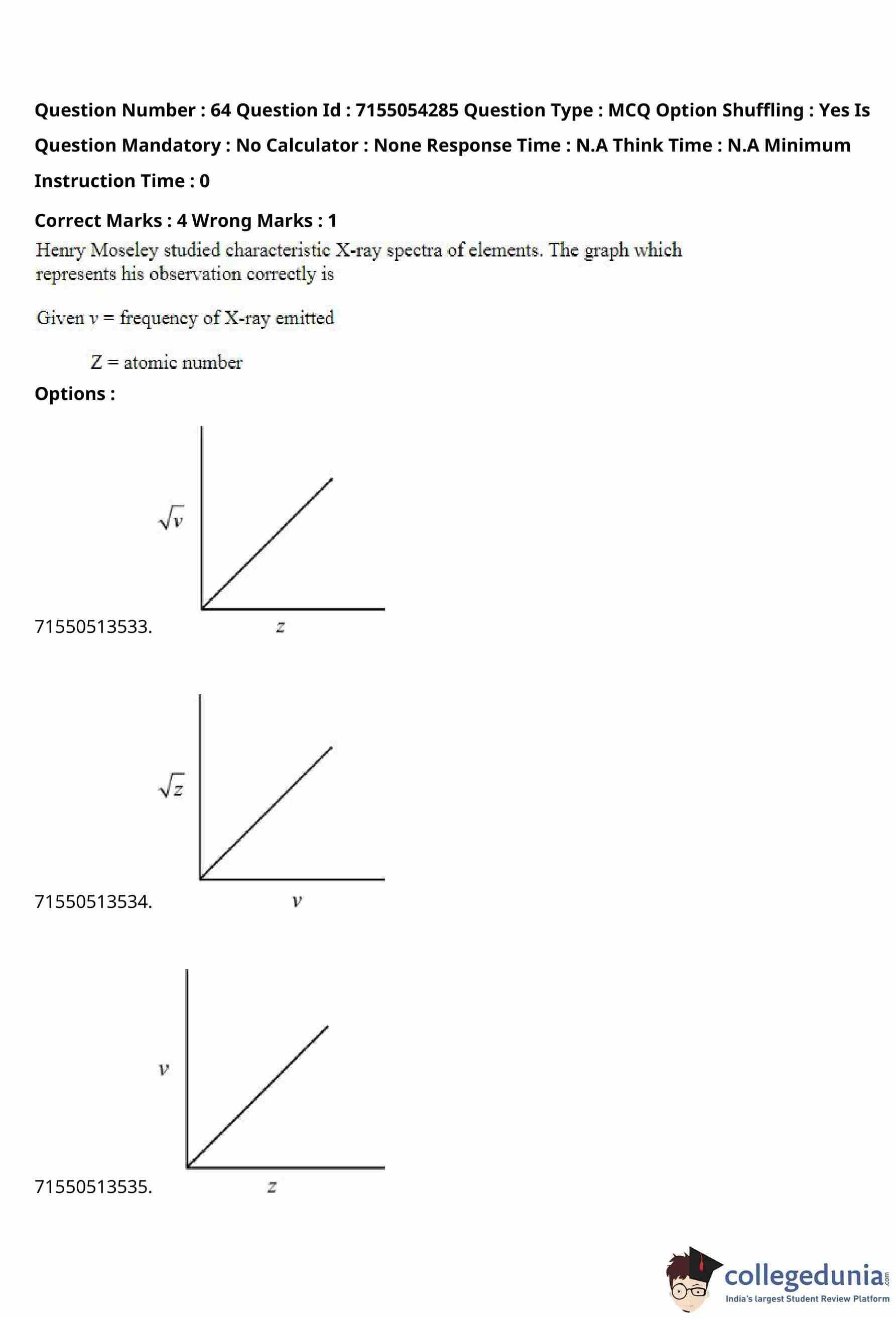






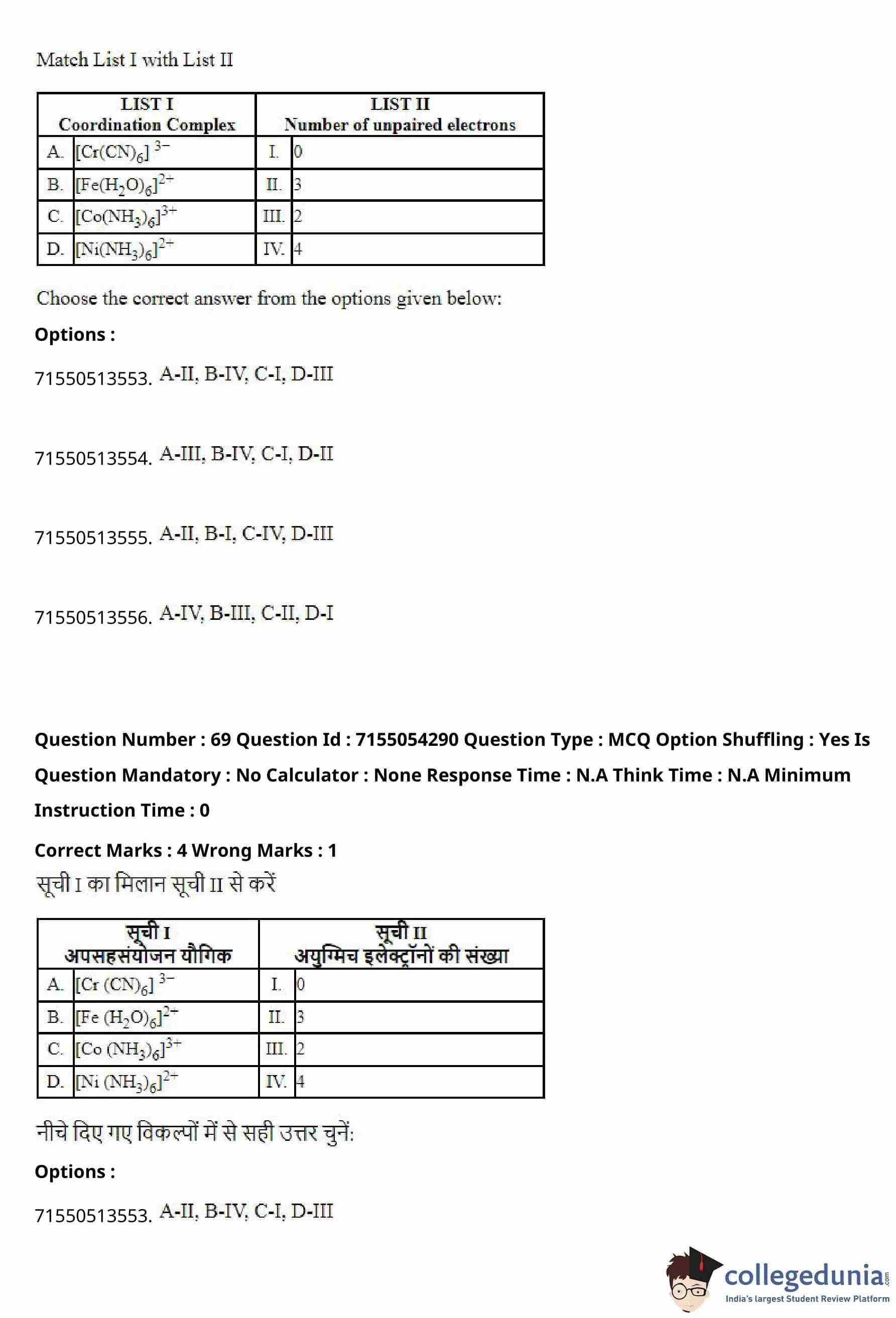

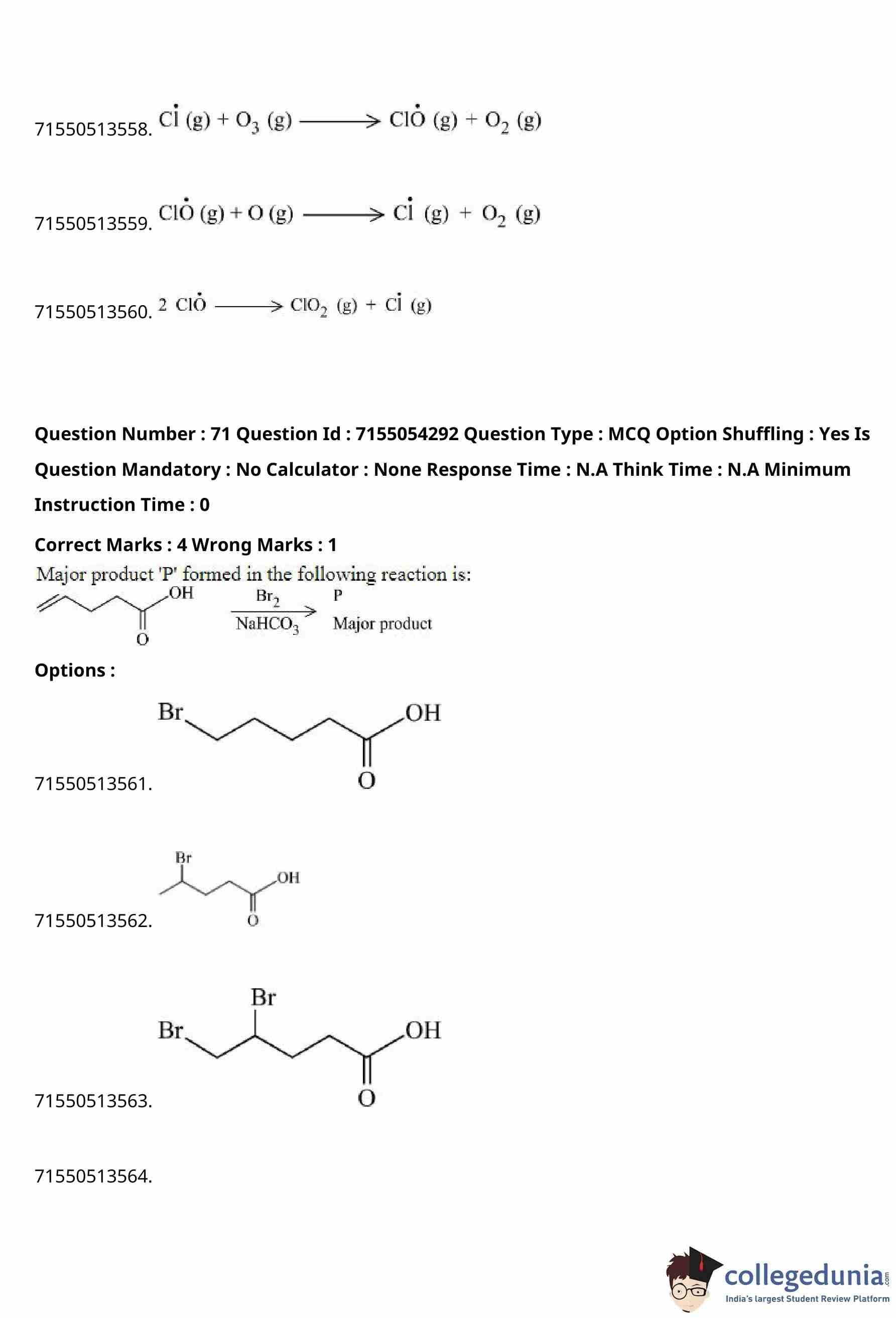
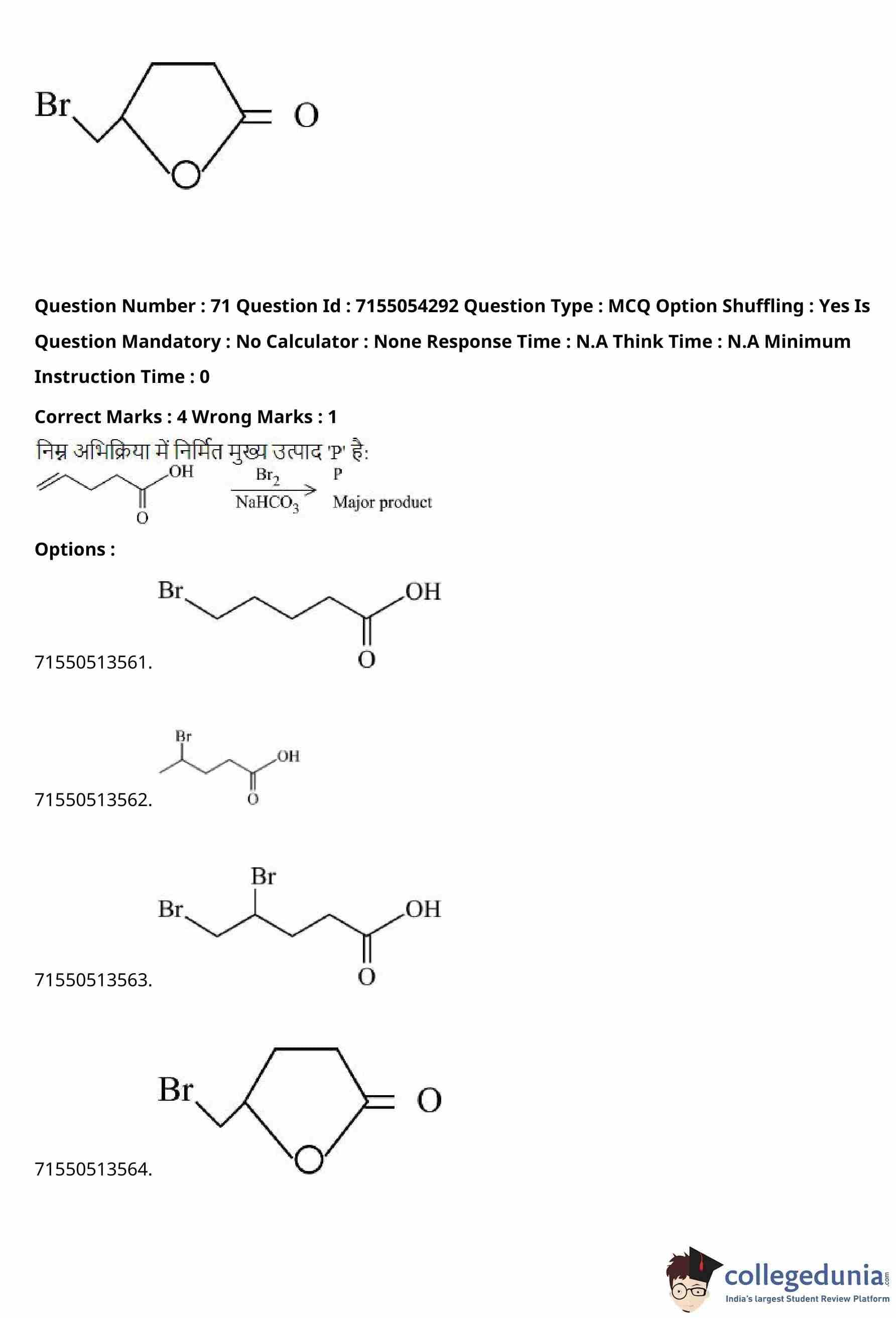


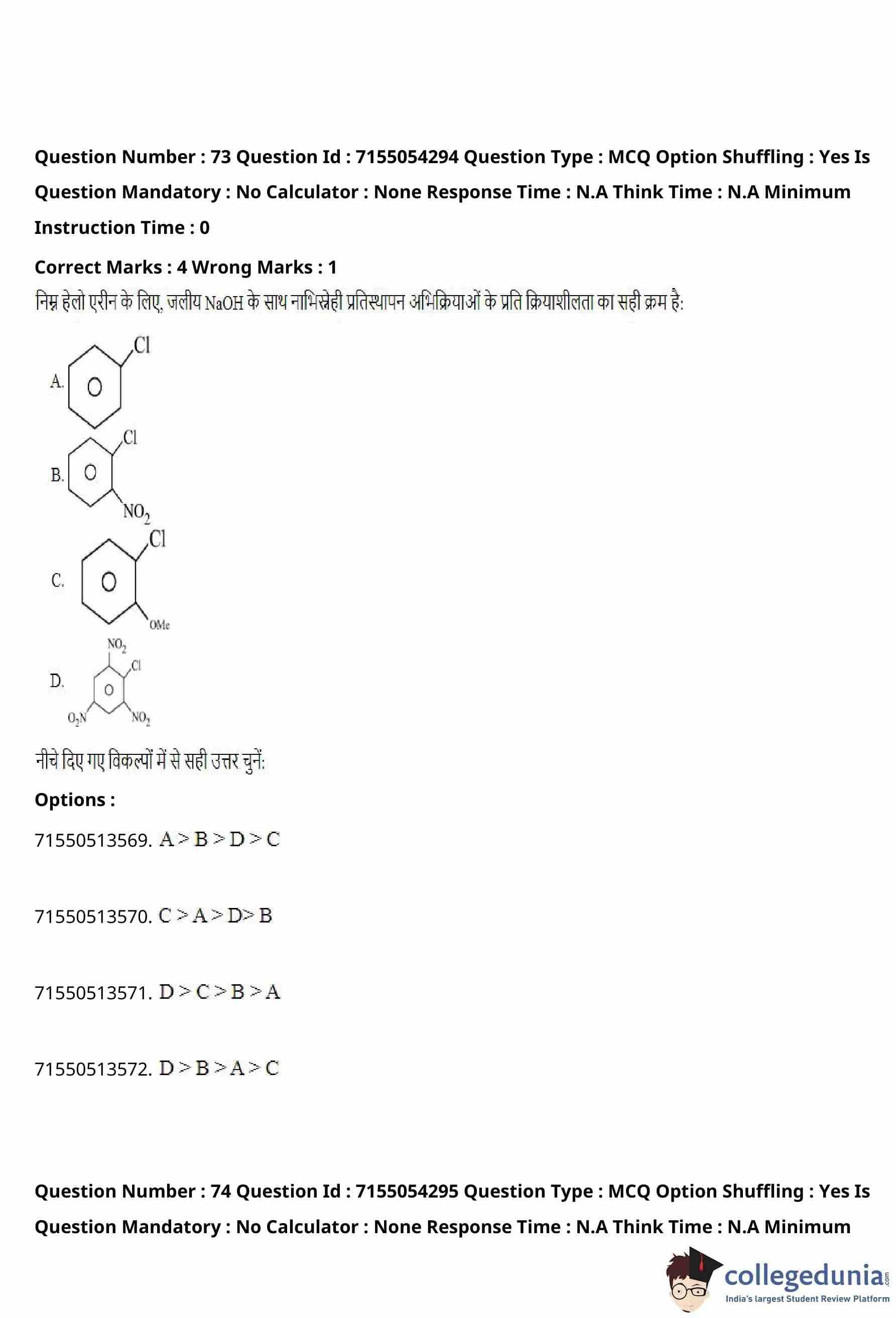



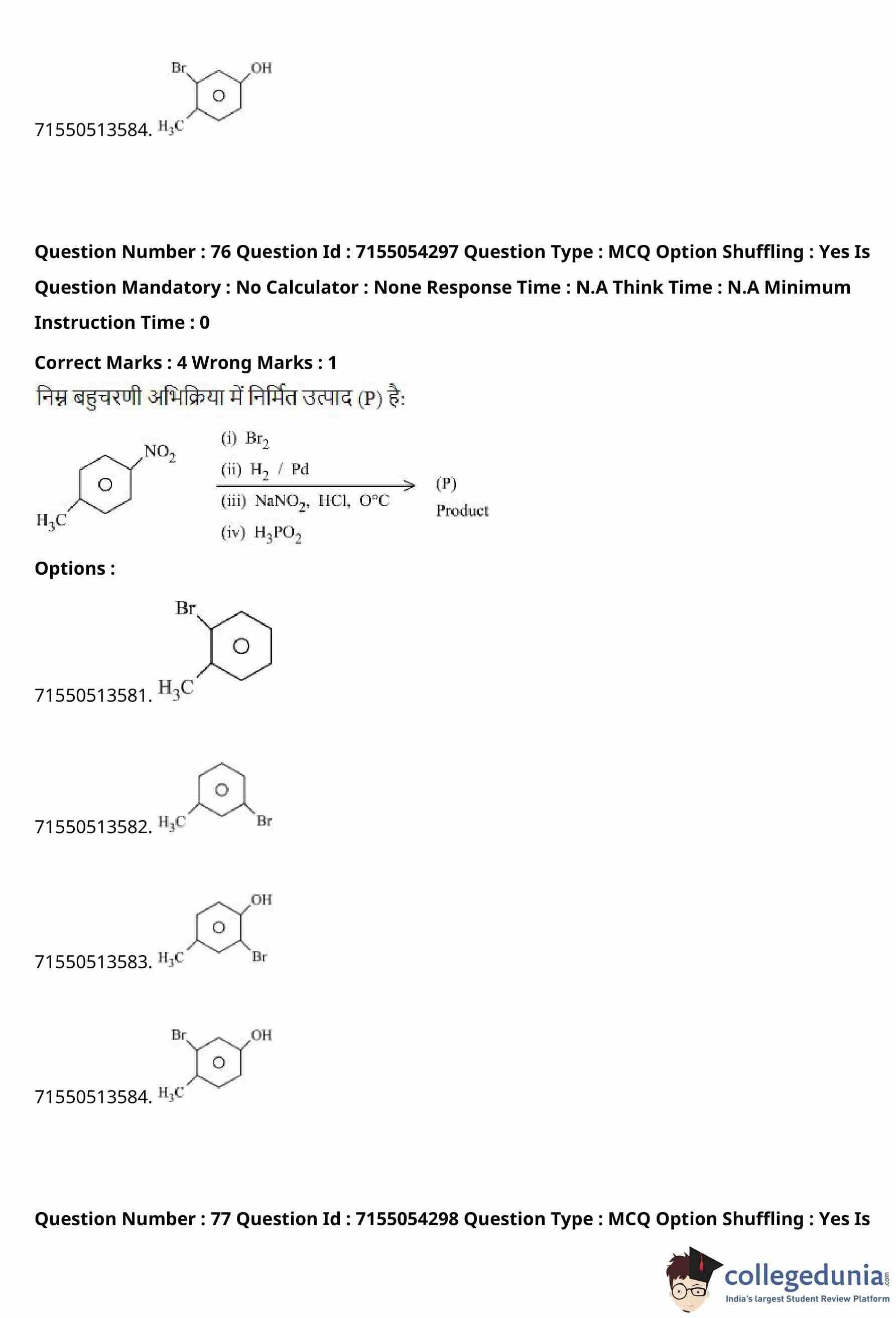















JEE Main 8 April 2023 Shift 2 Answer Key: Coaching Institute PDF
Collegedunia has also provided JEE Main 2023 April 8 Shift 2 Answer Key PDF with solutions released by various coaching institutes such as Aakash BYJUs, Resonance, Vedantu etc.
| Coaching Institutes | Question Paper with Answer Key PDF |
|---|---|
| Aakash BYJUs | Check Here |
| Resonance | Physics Chemistry Mathematics |
| Vedantu | Check Here |
| Narayana College | Physics Chemistry Mathematics |
Also Check:






Comments