Jasmine Grover Study Abroad Expert
Study Abroad Expert
Magnetic field in a solenoid formula is calculated as B = μ0 nl. In the formula, B represents the magnetic flux density, μ0 is the magnetic constant whose value is 4π x 10-7 Hm-1 or 12.57 x 10-7 Hm-1, N represents the number of turns, and I is the current flowing through the solenoid.
- A solenoid is a long thin loop of wire that is mostly wrapped around a metallic core.
- The core of a solenoid produces a magnetic field when an electric current passes through it.
- Magnetic field in a long solenoid is homogeneous.
- Its strength doesn’t depend on the distance from the axis or on the cross-sectional area of the solenoid.
- Solenoids can create controlled magnetic fields and therefore can be used as electromagnets.
- Electromagnets are formed by wrapping a coil of wire (solenoid) around a ferromagnetic core.
- They can be easily controlled by adjusting the current flowing through the solenoid.
- Magnetic field in a solenoid formula indicates that the magnetic field strength is directly proportional to the number of turns and the current.
The solenoid's magnetic field formula provides a quantitative relationship between magnetic flux density, the magnetic constant, the number of turns, and the current.
Also Read: Electromagnetic Induction
| Table of Content |
Key Terms: Magnetic Field, Solenoid, Solenoid Formula, Ampere’s Law, Magnetism, Electric Current, Electric charges, Magnetic constant, Solenoid
Magnetic Field in a Solenoid Formula
[Click Here for Sample Questions]
A vector field, which exhibits the magnetic influence on moving electric charges, electric currents, and materials that are magnetic, is called Magnetic Field. A solenoid is a coil of wire that is able to produce a strong magnetic field within the coil. Covering the wire around a cylindrical material generates a stronger magnetic field when the current is allowed to pass through. The magnetic field inside the solenoid is maximum, and the magnetic field in a solenoid formula is,
B = \(\mu_0\)IN/L
- Where, B is the magnetic field
- I is the current in the coil
- N is the number of turns in the solenoid
- L is the length of the coil
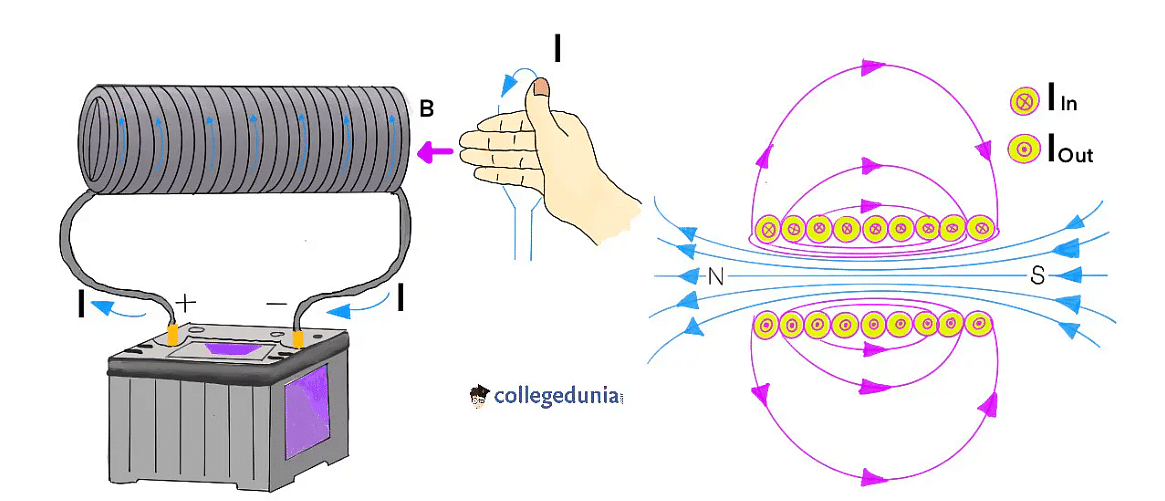
Magnetic Field Around A Solenoid
The video below explains this:
Magnetic Field in A Solenoid Detailed Video Explanation:
Read More:
Magnetic Field Outside a Solenoid
[Click Here for Previous Year Questions]
Magnetic field lines are present in the form of loops, wherein they cannot diverge or converge to a point compared to electric field lines.
- The magnetic field lines in the solenoid follow the longitudinal path, hence, these magnetic field lines must move in the opposite direction outside the solenoid.
- The longitudinal path of magnetic field lines is due to the formation of the loop from the lines.
- Therefore, the density of the magnetic field lines outside the solenoid is decreased greatly.
- As a result of which, the field outside the solenoid is constant.
- For the entire number of field lines to be contained, the magnetic field outside must be zero, because the solenoid gets longer.
The magnetic field outside a solenoid is:
B = μ0 nl
Since the field outside the solenoid is comparatively less than that it is present inside, we can consider it as zero as the length of the solenoid increases, and hence B = 0.

Magnetic Field Outside a Solenoid
Also Read: Parallel Current Carrying Conductor
Ampere’s Law
[Click Here for Sample Questions]
Ampere’s Law states that:
“The integration of a magnetic field around a loop is directly proportional to the current enclosed in the loop.”
∮ \(\overrightarrow {B}. \overrightarrow {dl}\)= \(\mu_0\)Ienc
Where, \(\mu_0\) is the constant of proportionality.

Ampere’s Law
Read More: Magnetic Flux Formula and Solved Example
Ampere’s Law Derivation
[Click Here for Previous Year Questions]
The equation of magnetic field is derived from Ampere’s law. Consider an amperian rectangular path, the integral over the closed path will be:
\(\oint \overrightarrow{B} . \overrightarrow{dl} = Bh\)…(1)
Now, Ienc = (number of turns inside the area) x (current through each turn)
Therefore, Ienc = nh x I…(2)
Considering, \(\oint \overrightarrow{B} . \overrightarrow{dl}\)l= \(\mu_0\)Ienc
Comparing (1) and (2)
Bh = \(\mu_0\)Ienc
Bh = \(\mu_0\)I x nh
B = \(\mu_0\)nI
The above equation is used to determine the magnitude of the magnetic field in a long solenoid.
Ampere’s Circuital Law Video Explanation
Also Read: Moving Charges and Magnetism MCQ
Solved ExamplesExample 1: Find out the magnetic field produced by the solenoid of length 80 cm under the number of turns of the coil is 360 and the current passing through is 15 A. Solution: Given: Number of turns N = 360 Current I = 15 A Permeability μo = 1.26 × 10−6 T/m Length L = 0.8 m The magnetic field in a solenoid formula is given by, B = μoIN / L B = (1.26×10−6 × 15 × 360) / 0.8 B = 8.505 × 10−3 N/Amps m The magnetic field generated by the solenoid is 8.505 × 10−4 N/Amps m. Example 2: A solenoid of diameter 40 cm has a magnetic field of 2.9 × 10−5 N/Amps m. If it has 300 turns, determine the current flowing through it. Solution: Given: Number of turns N = 300 Length L = 0.4 m Magnetic field B = 2.9 × 10−5 N/Amps m The magnetic field formula is given by B = μoIN /L The current flowing through the coil can be expressed by I = BL / μoN I = (2.9×10−5 x 0.4 )/ (1.26×10−6 × 300) I = 30.6 mA |
Read more: Magnetism Formula
Notes on Magnetic Fields in a Solenoid
[Click Here for Sample Questions]
Provided below are some handwritten notes on magnetic field in a solenoid and other important concepts.







Things to Remember
- The magnetic field is proportional to the current applied and the number of turns per unit length in the coil.
- A solenoid produces a controlled magnetic field and acts as an electromagnet.
- As the number of turns in the solenoid increases, the magnetic field gets stronger.
- The magnetic field is maximum inside the solenoid and is given by B = \(\mu_0\)In.
- \(\mu_0\) is the magnetic constant, whose value is 4 x 10-7 Tm-1.
- The total magnetic field relies on the number of turns and the length of the solenoid.
- Ampere’s law is used to obtain an expression for the interior magnetic field in a solenoid.
- The unit of Magnetic field is Tesla (T).
- The right-hand thumb rule is used to determine the magnetic field.
Also Read:
Previous Year Questions
- A part of a long wire carrying a current i is bent into a circle of radius … [JCECE 2010]
- The magnetic field intensity at the centre of cubical cage … [WBJEE 2016]
- A thin flexible wire of length L is connected to two adjacent fixed points … [KCET 2010]
- The magnetic fields at two points on the axis of a circular coil … [KCET 2001]
- A 100 millihenry coil carries a current of 1 A … [NEET 1991]
- A bar magnet placed in a uniform magnetic field making an angle … [NEET 2019]
- A proton is fired through a magnetic field in a direction opposite … [JIPMER 1996]
- An electron moves in a circular path of radius … [DUE 2013]
- The magnetic field at a distance r from a long wire carrying … [VITEEE 2019]
- In a potentiometer experiment, the balancing length of a cell is … [VITEEE 2015]
- A proton with energy of 2 MeV enters a uniform … [VITEEE 2007]
- A conducting circular loop of radius r carries … [JEE Advanced 2017]
- A particle enters uniform constant magnetic field … [UPSEE 2016]
- Two solenoids are given - 1st has 1 turn per unit … [VITEEE 2016]
- Two sources of equal emf are connected … [VITEEE 2015]
Also Read: Derivation of Lorentz Transformation
Sample Questions
Ques 1. Find the magnetic field if the current passes through the solenoid id 8 A? Consider that the length of the solenoid is 0.4m with 320 turns. (2 Marks)
Ans. n = 320/0.4
Therefore, n = 800 turns per meter
According to the formula, B = \(\mu_0\)In
B = \(\pi \) x 10-7 x 8 x 800
B = 8.03 x 10-3 T
Ques 2. The line integral \(\int \overrightarrow{B}. \overrightarrow{dl}\) Is 6.23 x 10-7 around the close curve with various conductors, find the current passing through. (2 Marks)
Ans. Applying the formula,\(\oint \overrightarrow{B} . \overrightarrow{dl} = \mu_0 l\)
Inet = \(\frac{\int \overrightarrow{B} . \overrightarrow{dl}}{\mu_0} = \frac{6.23 \times 10^{-7}}{4 \pi \times 10{-7}}\)= 0.5A
I = 0.5A
Ques 3. Find the number of turns the solenoid has if the current passing through is 0.3A and magnetic field around is 3.21x10-7 T. (2 Marks)
Ans. According to the formula, B = \(\mu_0\)In
3.21x10-7 = 4\(\pi \) x 10-7 x 0.3 x n
n = 3.21x10-7/ 4\(\pi \) x 10-7 x 0.3
n = 0.85 turns
Ques 4. If n = 400, I = 0.6A, and B = 3 x 10-4 T, prove that the magnetic constant value is 4x 10-7 Tm-1. (2 Marks)
Ans. B = \(\mu_0\)In
On applying the given values,
3 x 10-4 =\(\mu_0\) x 0.6 x 400
Therefore, \(\mu_0\)= 3 x 10-4/0.6 x 400
\(\mu_0\) = 1.25 x 10-6 Tm-1 (4 x 10-7 = 1.256 x 10-6)
Hence proved.
Ques 5. How is the magnetic field inside and outside an ideal solenoid? (2 Marks)
Ans. The magnetic field inside an ideal solenoid is uniform and the field lines are straight and parallel lines. The magnetic field line outside the solenoid is present, but considering the number of field lines per unit area, which is negligible compared to the lines per unit area inside the solenoid, the total magnetic field outside the solenoid is considered to be 0.
Ques 6. List three uses of Magnetic fields. (3 Marks)
Ans. Magnetic Fields are used as:
- Electromagnets:
Application of electromagnets in doorbells where the striker hits the bell due to electromagnet and in speakers, where paper cones are used, in which the electromagnet receives a rhythmic input and reproduces the sound.
- Motors:
In motors magnetic fields are used to rotate the shaft in industrial machines, motors using magnetic fields can also be seen in automatic doors, cars and in computers.
- Magnetic Levitation:
Used in electric trains, the train is allowed to ride above the rail only with the help of a magnetic field. Therefore very less friction falls on the train and it moves easily.
Ques 7. What are the uses and advantages of a Solenoid? (3 Marks)
Ans. Uses of Solenoid:
- As switch
- In inductors, valves, antennas, etc.
- As fuel injection gears in automobiles
- As electromagnets
Advantages of Solenoid:
- When the solenoid is used in the engines of automobiles, the pollution produced by the car is drastically reduced. Fossil fuel can be replaced by Solenoid engines.
- When electricity is passed through or applied to a solenoid, it reacts immediately.
Ques 8. Mention the properties of a solenoid. (2 Marks)
Ans. The characteristics of a solenoid are –
- Solenoids are useful in converting electric current into mechanical action.
- The magnetic field of a material is determined by the density of coils, number of turns, and current.
- A force of a few newtons is generated by even a simpler solenoid.
- The uniform and parallel magnetic fields are found in the centre of the solenoid.
Ques 9. A solenoid is 2 m long and 3 cm in diameter. It has 5 layers of windings of 1000 turns each and carries a current of 5 A. What is the magnetic field at its center? (3 Marks)
Ans. Given
- Length of the solenoid, L = 2 m
- Current flowing through the solenoid, I = 5 A
- Number of turns in each layer, N = 1000 turns
The magnetic field at the center of a solenoid for one layer of winding is given by
B = µ0NI/L
On substituting the values, we get
B = [(4π x 10-7) x 1000 x 5]/2
⇒ B = 0.314 x 10-2 T
Since there are 5 layers of winding present in the solenoid, the net magnetic field at the center is given by
Bnet = 5 x 0.314 x 10-2 = 1.57 x 10-2 T
Ques 10. What happens to the magnetic field in the solenoid when the number of turns increases? (2 Marks)
(a) Decreases
(b) Becomes zero
(c) Remains constant
(d) Increases
Ans. The correct answer is d. Increases
Explanation: The magnetic field of a solenoid is directly proportional to the number of turns in it. As a result, as the number of turns increases, the strength of the magnetic field also increases.
Ques 11. A long solenoid has 200 turns per cm and carries a current of 2.5 amps. What is the value of the magnetic field at its center? (3 Marks)
Ans. Given
- The number density of turns of the solenoid, n = 200 turns per cm
- Current flowing through the solenoid, I = 2.5 A
The magnetic field at the center of a solenoid in terms of the number density of turns is given by
B = µ0nI
On substituting the values, we get
B = (4π x 10-7) x (200/10-2) x 2.5
⇒ B = 6.28 x 10-2 Wb/m2
Ques 12. The magnetic field strength of a solenoid can be increased by inserting which of the following materials as the core? (2 Marks)
(a) Silver
(b) Iron
(c) Copper
(d) Aluminum
Ans. The correct answer is b. Iron
Explanation: When we place an iron core into a solenoid, the magnetic field increases because iron is a ferromagnetic material, and ferromagnetic elements help in increasing the magnetic property.
For Latest Updates on Upcoming Board Exams, Click Here:https://t.me/class_10_12_board_updates
Check Out:





Comments