Pressure is something we use in many things in our daily lives. For example, when we open solid jars and seal the object, we put pressure on them to open them. The normal force acting per unit on a surface is called pressure. Also, it is important to note down that pressure is exerted by solids, liquids as well as gases. For example, drawing pins, nails, sewing needles, etc. have pointed tips so that they penetrate easily into the surface. Another example to make it more clear - skiers use long and flat skis to slide over the snow to slide comfortably without sinking into the snow.
| Table of Content |
What is Pressure?
The term ‘pressure’ is applied to one thing over another. Pressure is defined as the force in each area of the unit. We can define pressure as a powerful force for good. Also, the force applied to an object is perpendicular to the surface of an object in the area of each unit. Therefore, pressure is the energy per unit applied to the surface of an object. It increases as the applied power increases and decreases as the contact area increases. In addition, the pressure unit in Pascals (Pa).

The video below explains this:
Pressure Formula Detailed Video Explanation:
SI Unit of Pressure
The unit of force is Newton, and the unit of area is square meters (m2). So, the SI unit of pressure newton per meter square (N/m2). Also, it is known as Pascals (Pa), i.e., 1 Pa = 1 N/m2.
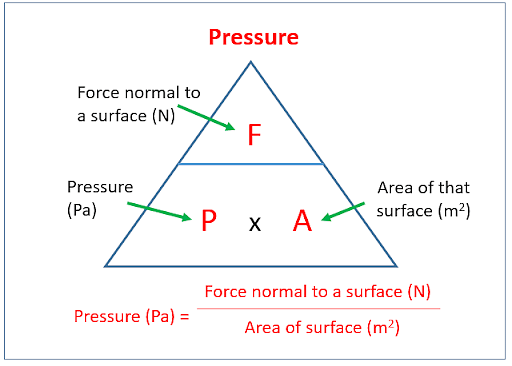
Formula of Pressure
Pressure can be calculated with the help of the following formula -
P = F/A
Where P = pressure exerted
F = force applied by the body (N)
A = total area of the object (m2)
Partial Pressure
The molecule and atoms in a solid space are close together and there is an important force between these molecules. The solids will take the form of what is said to be determined by the type of energy in the molecules. Even the strongest forces are said to produce only small atoms in lattice molecules or atoms as well as solid metals and their structure. Moreover, solid is also said to withstand the force of the shear. Shearing power is a powerful force used in the environment as described in static equilibrium and elasticity.
Also Read: Partial Pressure
Osmotic Pressure
Gases and Liquids are said to be considered liquid because they allow the shaft to be strong enough to withstand them. Just as we can say that solids and liquid molecules are not bound to neighbour molecules, but we can say that they have a few more of these bonds. Unlocked fluid molecules exist and can move with respect. The distance between the molecules is said to be the same as the distances in a solid-state so the liquid has a specific volume. but we need to note that the composition of the liquid changes depending on the shape of the vessel. These gases are said to be unrelated to neighbouring atoms and may have significant differences between molecules. Gases usually do not have specific conditions or volumes as we can say that their molecules usually travel to fill the container where they are stored.
Also Read: Hydrostatic Pressure
Absolute Pressure
Pressure (P) power is applied upwards (perpendicular) which is the area of each unit that is said to be where those energies are distributed. A pressure gauge that also records ‘gage’ pressure is said to be the pressure that is said to be accompanied by ambient pressure.
The video below explains this:
Absolute Pressure Detailed Video Explanation:
Things to Remember
Following are some important points:
- A normal force acting per unit area of a surface sue to an object placed on it, it is known as pressure.
- The formula of pressure is P = F/A.
- The SI unit of pressure is Pascal (Pa) or N/m2.
- Thrust or force is the pressure exerted on a wooden block in its target, while the pressure is a continuous force applied to an object against a connected body. Therefore, thrust is a kind of force acting on an object and pressure is the force acting on an object in each area.
Also Read:
| Pressure of an Ideal Gas | Different Properties of Fluids | Fluid Pressure |
| Viscosity | Surface Tension | Buoyant Force |
Sample Questions
Ques: A boy weighs 600 N. The student’s shoes are in contact with the. floor over a surface area of 0.012m². Calculate the pressure exerted by the boy on the floor.
Ans: F = 600 N
A = 0.012m2
P = F/A = 600/0.012 N/m2 = 5 * 10 x 4 Pa.
Ques: Calculate the force which exerts a pressure of 60 Pa on an area of 5m2.
Ans: P = 60 Pa, A = 5 m2
As we know, P = F/A
Hence, F = P * A
= 60Pa * 5m2
= 300 N.
Ques: A force of 300 N produces a pressure of 10000 Pa. Calculate the area of the surface on which the force acts.
Ans: F = 300 N, P = 10000 Pa
A = F/P
= 300/10000
= 3/100 m2 = 0.03 m2
Ques: Acceleration due to gravity is 10 N/kg. The surface area of fish pressed by the water above it is 6 cm2. Determine the force of water above fish that acts on fish.
Ans: Acceleration due to gravity (g) = 10 N/kg
Surface area of fish (A) = 6cm2 = 6 x 10-4 m2
Density of water = 1 gram/cm3 = 1 (10-3 kg) / 10-6 m3 = 103 kg/m3 = 1000 kg/m3
Height of water = 100 cm – 15 cm = 85 cm = 85 x 10-2 meters
F = pghA
F = (1000) (10) (85 x 10-2) (6 x 10-4 m2)
F = (104) (510 x 10-6)
F = 510 x 10-2
F = 5.1 N
Ques: A water glass lying on a table weighs 4 N. The bottom of the water glass has a surface area of 0.003 m². Calculate the pressure the glass exerts on the table.
Ans: F = 4 N and A = 0.003 m2
P = F/A = 4/0.003 = 1333.33 Pa.
Ques: Give some examples of pressure from daily life.
Ans: Examples of Pressure are as follows:
- Your school bag and your shopping bag have broad straps to reduce pressure on your hands or the shoulders.
- Shoes and Sandals having pointed heels are not comfortable to wear because they exert more pressure on the ground than normal flat heels.
Ques: Explain the following statement - It is easier to cut with a sharp knife than a blunt knife.
Ans: This is because even a small amount of force causes great pressure at the edges and cutting can be done with less effort.





Comments