An electric dipole of dipole moment p is lying along uniform electric field E. Calculate the work done in rotating the dipole by 90 degrees.

Study Abroad Expert

Ques: An electric dipole of dipole moment p is lying along uniform electric field E. Calculate the work done in rotating the dipole by 90 degrees.

Ans: The work done in rotating the dipole by 90 degrees when dipole moment is lying along uniform electric field is “pE”.

Explanation: The potential energy of an electric dipole in a uniform electric field is given by an expression: U = -pEcosθ.

where p is the dipole moment,
E is the electric field strength,
θ is the angle between the dipole moment and the electric field.

Initially, the dipole moment is aligned with the electric field, so θ = 0, and the potential energy is:

U1 = -pEcos0 = -pE

When the dipole is rotated by 90 degrees, the angle between the dipole moment and the electric field becomes θ = 90 degrees, and the potential energy becomes:

U2 = -pEcos90 = 0

The change in potential energy is then equal to the work done

Work Done = ΔU = U2 - U1 = 0 - (-pE) = pE

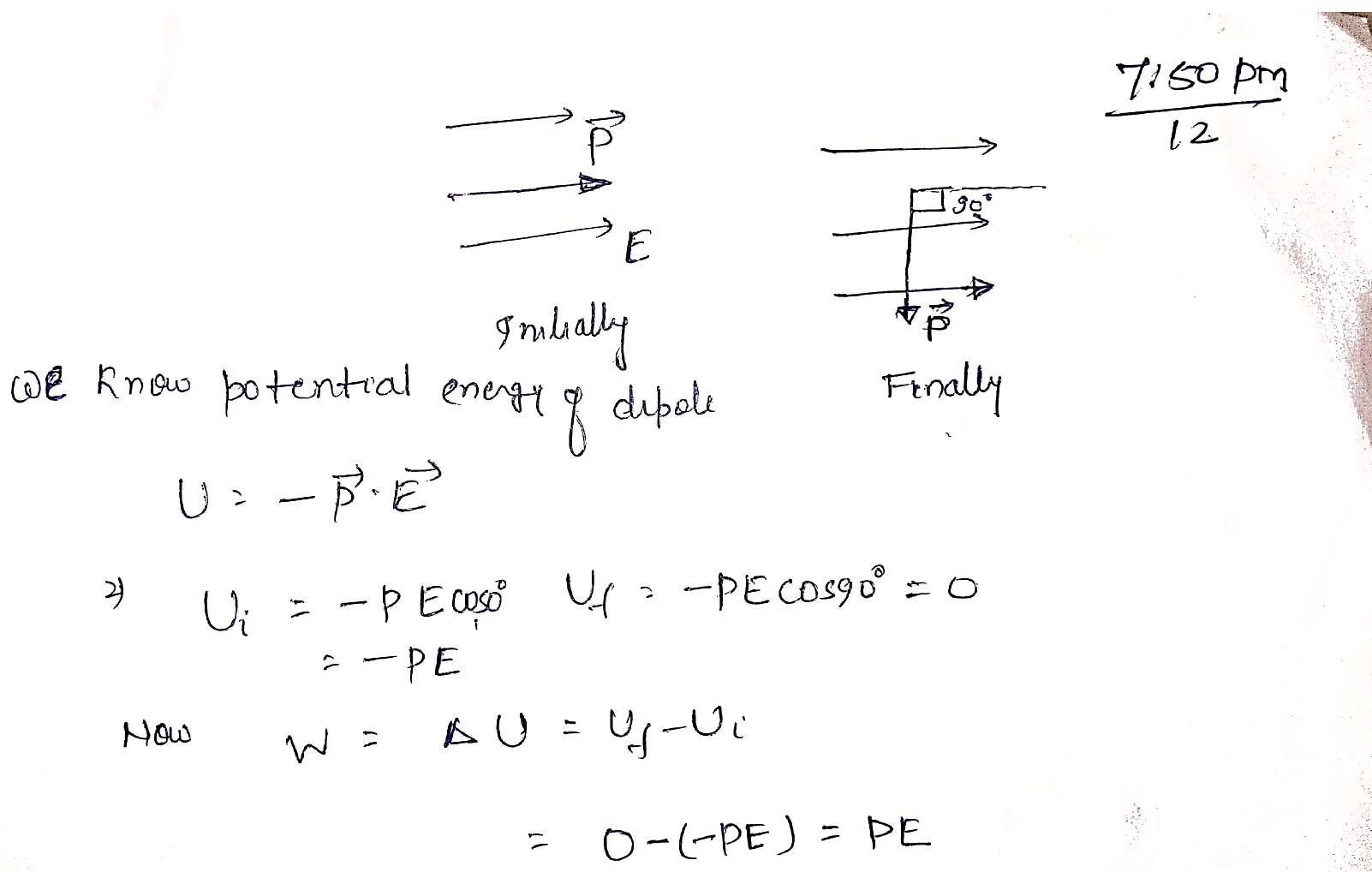
electric dipole of dipole moment p is lying along uniform electric field E

Therefore, the potential energy of the dipole in rotating it by 90 degrees is pE.

CBSE CLASS XII Related Questions

1.
Four long straight thin wires are held vertically at the corners A, B, C and D of a square of side \( a \), kept on a table and carry equal current \( I \). The wire at A carries current in upward direction whereas the current in the remaining wires flows in downward direction. The net magnetic field at the centre of the square will have the magnitude:

\( \dfrac{\mu_0 I}{\pi a} \) and directed along OC
\( \dfrac{\mu_0 I}{\pi a \sqrt{2}} \) and directed along OD
\( \dfrac{\mu_0 I \sqrt{2}}{\pi a} \) and directed along OB
\( \dfrac{2\mu_0 I}{\pi a} \) and directed along OA

View Solution

2.
Determine the current in the \( 3 \, \Omega \) branch of a Wheatstone Bridge in the circuit shown in the figure.

View Solution

3.
Write any two features of nuclear forces.

View Solution

4.
When monochromatic light is incident on a surface separating two media, the refracted and reflected light both have the same frequency as the incident frequency but the wavelength of refracted light is different. Explain why.

View Solution

5.
Suppose a pure Si crystal has \( 5 \times 10^{28} \) atoms per \( \text{m}^3 \). It is doped with \( 5 \times 10^{22} \) atoms per \( \text{m}^3 \) of Arsenic. Calculate majority and minority carrier concentration in the doped silicon. (Given: \( n_i = 1.5 \times 10^{16} \, \text{m}^{-3} \))

View Solution

6.
Assertion : Photoelectric effect is a spontaneous phenomenon. Reason (R): According to the wave picture of radiation, an electron would take hours/days to absorb sufficient energy to overcome the work function and come out from a metal surface.

Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Both Assertion (A) and Reason (R) are false.

View Solution

An electric dipole of dipole moment p is lying along uniform electric field E. Calculate the work done in rotating the dipole by 90 degrees.

CBSE CLASS XII Related Questions

2.
Determine the current in the \( 3 \, \Omega \) branch of a Wheatstone Bridge in the circuit shown in the figure.

3.
Write any two features of nuclear forces.

4.
When monochromatic light is incident on a surface separating two media, the refracted and reflected light both have the same frequency as the incident frequency but the wavelength of refracted light is different. Explain why.

5.
Suppose a pure Si crystal has \( 5 \times 10^{28} \) atoms per \( \text{m}^3 \). It is doped with \( 5 \times 10^{22} \) atoms per \( \text{m}^3 \) of Arsenic. Calculate majority and minority carrier concentration in the doped silicon. (Given: \( n_i = 1.5 \times 10^{16} \, \text{m}^{-3} \))

6.
Assertion : Photoelectric effect is a spontaneous phenomenon. Reason (R): According to the wave picture of radiation, an electron would take hours/days to absorb sufficient energy to overcome the work function and come out from a metal surface.

Similar Physics Concepts

Comments

dOGVmW

An electric dipole of dipole moment p is lying along uniform electric field E. Calculate the work done in rotating the dipole by 90 degrees.

CBSE CLASS XII Related Questions

2. Determine the current in the \( 3 \, \Omega \) branch of a Wheatstone Bridge in the circuit shown in the figure.

3. Write any two features of nuclear forces.

4.When monochromatic light is incident on a surface separating two media, the refracted and reflected light both have the same frequency as the incident frequency but the wavelength of refracted light is different. Explain why.

5.Suppose a pure Si crystal has \( 5 \times 10^{28} \) atoms per \( \text{m}^3 \). It is doped with \( 5 \times 10^{22} \) atoms per \( \text{m}^3 \) of Arsenic. Calculate majority and minority carrier concentration in the doped silicon. (Given: \( n_i = 1.5 \times 10^{16} \, \text{m}^{-3} \))

6.Assertion : Photoelectric effect is a spontaneous phenomenon. Reason (R): According to the wave picture of radiation, an electron would take hours/days to absorb sufficient energy to overcome the work function and come out from a metal surface.

Similar Physics Concepts

Comments

dOGVmW

2.
Determine the current in the \( 3 \, \Omega \) branch of a Wheatstone Bridge in the circuit shown in the figure.

3.
Write any two features of nuclear forces.

4.
When monochromatic light is incident on a surface separating two media, the refracted and reflected light both have the same frequency as the incident frequency but the wavelength of refracted light is different. Explain why.

5.
Suppose a pure Si crystal has \( 5 \times 10^{28} \) atoms per \( \text{m}^3 \). It is doped with \( 5 \times 10^{22} \) atoms per \( \text{m}^3 \) of Arsenic. Calculate majority and minority carrier concentration in the doped silicon. (Given: \( n_i = 1.5 \times 10^{16} \, \text{m}^{-3} \))

6.
Assertion : Photoelectric effect is a spontaneous phenomenon. Reason (R): According to the wave picture of radiation, an electron would take hours/days to absorb sufficient energy to overcome the work function and come out from a metal surface.