JEE Main 2025 22nd Jan Shift 2 Question Paper is available for download. NTA conducted the exam successfully on 22nd Jan 2025 from 03:00 PM to 06:00 PM. The JEE Main 2025 22nd Jan Shift 2 Question Paper is expected to be Moderately tough. A comprehensive paper analysis including subject-wise question breakdown will be added in due time.
| JEE Main 2025 Jan 22 Shift 2 Question Paper with Solution | Check Solution |
The JEE Main 2025 Question Paper for 22nd Jan Shift 1 was reported as Moderately tough. No question was reported as “out of syllabus”. The role of NCERT was crucial in solving Organic Chemistry questions.
Also Check
- Download JEE Main 2025 PYQ for all shifts
- Download JEE Main Last 10 Year Question Papers for all shifts

Check – JEE Main 2025 Jan 22 Shift 1 Question Paper Solutions Pdf
JEE Main 2025 Jan 22 Shift 2 Questions with Solutions
Let \( \alpha_1 \) and \( \beta_1 \) be the distinct roots of \( 2x^2 + (\cos\theta)x - 1 = 0, \ \theta \in (0, 2\pi) \). If \( m \) and \( M \) are the minimum and the maximum values of \( \alpha_1 + \beta_1 \), then \( 16(M + m) \) equals:
View Solution
Let \( \alpha, \beta, \gamma \) and \( \delta \) be the coefficients of \( x^7, x^5, x^3, x \) respectively in the expansion of \( (x + \sqrt{x^3 - 1})^5 + (x - \sqrt{x^3 - 1})^5, \, x > 1 \). If \( \alpha u + \beta v = 18 \), \( \gamma u + \delta v = 20 \), then \( u + v \) equals:
View Solution
Let \( f(x) = \int_0^{x^2} \frac{t^2 - 8t + 15}{e^t} dt, \, x \in \mathbb{R} \). Then the numbers of local maximum and local minimum points of \( f \), respectively, are:
View Solution
Let \( A = \{1, 2, 3, 4\} \) and \( B = \{1, 4, 9, 16\} \). Then the number of many-one functions \( f: A \to B \) such that \( 1 \in f(A) \) is equal to:
View Solution
The perpendicular distance of the line \( \frac{x - 1}{2} = \frac{y + 2}{-1} = \frac{z + 3}{2} \) from the point \( P(2, -10, 1) \) is:
View Solution
Suppose that the number of terms in an A.P. is \( 2k, k \in \mathbb{N} \). If the sum of all odd terms of the A.P. is 40, the sum of all even terms is 55, and the last term of the A.P. exceeds the first term by 27, then \( k \) is equal to:
View Solution
Let \( \mathbf{a} \) and \( \mathbf{b} \) be two unit vectors such that the angle between them is \( \frac{\pi}{3} \). If \( \lambda \mathbf{a} + 2 \mathbf{b} \) and \( 3 \mathbf{a} - \lambda \mathbf{b} \) are perpendicular to each other, then the number of values of \( \lambda \) in \( [-1, 3] \) is:
View Solution
Let \( P(4, 4\sqrt{3}) \) be a point on the parabola \( y^2 = 4ax \) and PQ be a focal chord of the parabola. If M and N are the foot of the perpendiculars drawn from P and Q respectively on the directrix of the parabola, then the area of the quadrilateral PQMN is equal to:
View Solution
If \( \int \left( x \sin^{-1} x + \sin^{-1} x (1 - x^2)^{3/2} + \frac{x}{1 - x^2} \right) dx = g(x) + C \), where C is the constant of integration, then \( g\left(\frac{1}{2}\right) \) equals:
View Solution
If A and B are two events such that \( P(A \cap B) = 0.1 \), and \( P(A|B) \) and \( P(B|A) \) are the roots of the equation \( 12x^2 - 7x + 1 = 0 \), then the value of \( \frac{P(A \cup B)}{P(A \cap B)} \) is:
View Solution
Let the curve \( z(1 + i) + \overline{z}(1 - i) = 4, \, z \in \mathbb{C} \), divide the region \( |z - 3| \leq 1 \) into two parts of areas \( \alpha \) and \( \beta \). Then \( |\alpha - \beta| \) equals:
View Solution
The sum of all values of \( \theta \in [0, 2\pi] \) satisfying \( 2\sin^2\theta = \cos 2\theta \) and \( 2\cos^2\theta = 3\sin\theta \) is:
View Solution
If \( x = f(y) \) is the solution of the differential equation \[ (1 + y^2) + (x - 2e^{\tan^{-1}y}) \frac{dy}{dx} = 0, \quad y \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right), \] with \( f(0) = 1 \), then \( f\left( \frac{1}{\sqrt{3}} \right) \) is equal to:
View Solution
If \[ \lim_{x \to \infty} \left( \frac{e}{1 - e} \left( \frac{1}{e} - \frac{x}{1 + x} \right) \right)^x = \alpha, \] then the value of \[ \frac{\log_e \alpha}{1 + \log_e \alpha} \] equals:
View Solution
Let \[ E: \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \quad a > b \quad \text{and} \quad H: \frac{x^2}{A^2} - \frac{y^2}{B^2} = 1. \] Let the distance between the foci of \( E \) and the foci of \( H \) be \( 2\sqrt{3} \). If \( a - A = 2 \), and the ratio of the eccentricities of \( E \) and \( H \) is \( \frac{1}{3} \), then the sum of the lengths of their latus rectums is equal to:
View Solution
The area of the region enclosed by the curves \( y = x^2 - 4x + 4 \) and \( y^2 = 16 - 8x \) is:
View Solution
If the system of linear equations: \[ x + y + 2z = 6, \] \[ 2x + 3y + az = a + 1, \] \[ -x - 3y + bz = 2b, \] where \( a, b \in \mathbb{R} \), has infinitely many solutions, then \( 7a + 3b \) is equal to:
View Solution
In a group of 3 girls and 4 boys, there are two boys \( B_1 \) and \( B_2 \). The number of ways in which these girls and boys can stand in a queue such that all the girls stand together, all the boys stand together, but \( B_1 \) and \( B_2 \) are not adjacent to each other, is:
View Solution
Let a line pass through two distinct points \( P(-2, -1, 3) \) and \( Q \), and be parallel to the vector \( 3\hat{i} + 2\hat{j} + 2\hat{k} \). If the distance of the point \( Q \) from the point \( R(1, 3, 3) \) is 5, then the square of the area of \( \triangle PQR \) is equal to:
View Solution
For a \( 3 \times 3 \) matrix \( M \), let trace(M) denote the sum of all the diagonal elements of \( M \). Let \( A \) be a \( 3 \times 3 \) matrix such that \( |A| = \frac{1}{2} \) and \( \text{trace}(A) = 3 \). If \( B = \text{adj}(\text{adj}(2A)) \), then the value of \( |B| + \text{trace}(B) \) equals:
View Solution
Let \( A(6,8) \), \( B(10\cos\alpha, -10\sin\alpha) \), and \( C(-10\sin\alpha, 10\cos\alpha) \) be the vertices of a triangle. If \( L(a,9) \) and \( G(h,k) \) be its orthocenter and centroid respectively, then \( 5a - 3h + 6k + 100\sin2\alpha \) is equal to ______.
View Solution
Let \( y = f(x) \) be the solution of the differential equation\[\frac{dy}{dx} + \frac{xy}{x^2 - 1} = \frac{x^6 + 4x}{\sqrt{1 - x^2}}, \quad -1 < x < 1\] such that \( f(0) = 0 \). If \[6 \int_{-1/2}^{1/2} f(x)dx = 2\pi - \alpha\] then \( \alpha^2 \) is equal to ______.
View Solution
Let the distance between two parallel lines be 5 units and a point \( P \) lies between the lines at a unit distance from one of them. An equilateral triangle \( POR \) is formed such that \( Q \) lies on one of the parallel lines, while \( R \) lies on the other. Then \( (QR)^2 \) is equal to ______.
View Solution
If \[ \sum_{r=1}^{30} r^2 \left( \binom{30}{r} \right)^2 = \alpha \times 2^{29}, \] then \( \alpha \) is equal to ______.
View Solution
Let \( A = \{1,2,3\} \). The number of relations on \( A \), containing \( (1,2) \) and \( (2,3) \), which are reflexive and transitive but not symmetric, is ______.
View Solution
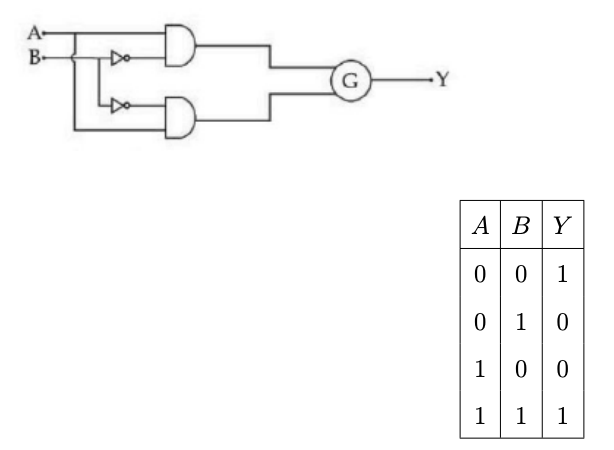
To obtain the given truth table, the following logic gate should be placed at \( G \):
View Solution
A rectangular metallic loop is moving out of a uniform magnetic field region to a field-free region with a constant speed. When the loop is partially inside the magnetic field, the plot of the magnitude of the induced emf \( (\varepsilon) \) with time \( (t) \) is given by:
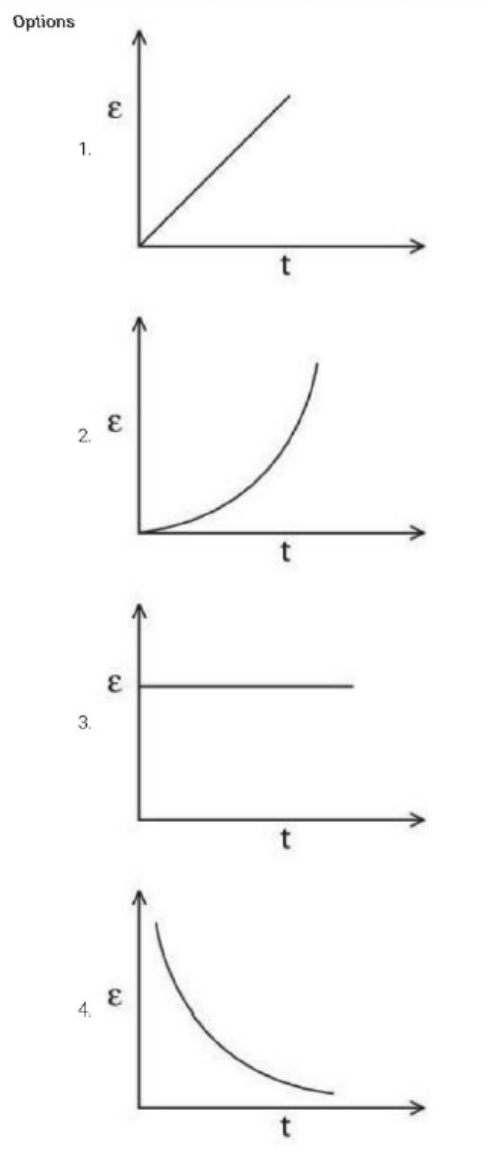
View Solution
A light source of wavelength \( \lambda \) illuminates a metal surface, and electrons are ejected with a maximum kinetic energy of 2 eV. If the same surface is illuminated by a light source of wavelength \( \frac{\lambda}{2} \), then the maximum kinetic energy of ejected electrons will be (The work function of the metal is 1 eV).
View Solution
For a short dipole placed at origin \( O \), the dipole moment \( P \) is along the \( x \)-axis, as shown in the figure. If the electric potential and electric field at \( A \) are \( V_0 \) and \( E_0 \) respectively, then the correct combination of the electric potential and electric field, respectively, at point \( B \) on the \( y \)-axis is given by:
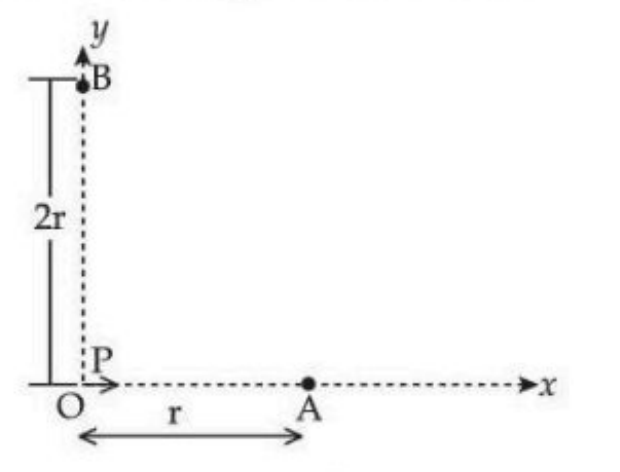
View Solution
An electron projected perpendicular to a uniform magnetic field \( B \) moves in a circle. If Bohr’s quantization is applicable, then the radius of the electronic orbit in the first excited state is:
View Solution
Given below are two statements, one labeled as Assertion (A) and the other as Reason (R). Assertion (A): In Young’s double slit experiment, the fringes produced by red light are closer compared to those produced by blue light. Reason (R): The fringe width is directly proportional to the wavelength of light. In the light of the above statements, choose the correct answer from the options given below:
View Solution
The maximum percentage error in the measurement of the density of a wire is: \[ \text{Given, mass of wire} = (0.60 \pm 0.003) \, \text{g}, \quad \text{radius of wire} = (0.50 \pm 0.01) \, \text{cm}, \quad \text{length of wire} = (10.00 \pm 0.05) \, \text{cm}. \]
View Solution
Given are statements for certain thermodynamic variables: [(A)] Internal energy, volume \( V \), and mass \( M \) are extensive variables. [(B)] Pressure \( P \), temperature \( T \), and density \( \rho \) are intensive variables. [(C)] Volume \( V \), temperature \( T \), and density \( \rho \) are intensive variables. [(D)] Mass \( M \), temperature \( T \), and internal energy are extensive variables. Choose the correct answer from the options given below:
View Solution
The torque due to the force \( \left( 2\hat{i} + \hat{j} + 2\hat{k} \right) \) about the origin, acting on a particle whose position vector is \( \hat{i} + \hat{j} + \hat{k} \), would be:
View Solution
Which one of the following is the correct dimensional formula for the capacitance in F? M, L, T, and C stand for unit of mass, length, time, and charge.
View Solution
A transparent film of refractive index 2.0 is coated on a glass slab of refractive index 1.45. What is the minimum thickness of transparent film to be coated for the maximum transmission of green light of wavelength 550 nm?
View Solution
Given below are two statements, one is labelled as Assertion (A) and the other is labelled as Reason (R): [(A)] A simple pendulum is taken to a planet of mass and radius, 4 times and 2 times, respectively, than the Earth. The time period of the pendulum remains same on earth and the planet. [(R)] The mass of the pendulum remains unchanged at Earth and the other planet. In light of the above statements, choose the correct answer from the options given below:
View Solution
A small rigid spherical ball of mass \( M \) is dropped in a long vertical tube containing glycerine. The velocity of the ball becomes constant after some time. If the density of glycerine is half of the density of the ball, then the viscous force acting on the ball will be (consider \( g \) as acceleration due to gravity):
View Solution
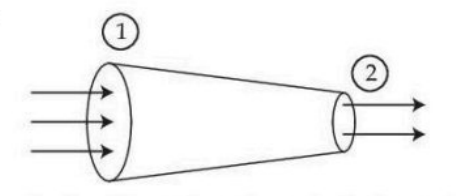
A tube of length \( L \) is shown in the figure. The radius of cross section at point (1) is 2 cm and at the point (2) is 1 cm, respectively. If the velocity of water entering at point (1) is 2 m/s, then velocity of water leaving the point (2) will be:
A force \( \mathbf{F} = 2\hat{i} + b\hat{j} + \hat{k} \) is applied on a particle and it undergoes a displacement \( \mathbf{r} = \hat{i} - 2\hat{j} - \hat{k} \). What will be the value of \( b \), if the work done on the particle is zero?
View Solution
A ball of mass 100 g is projected with velocity 20 m/s at \( 60^\circ \) with horizontal. The decrease in kinetic energy of the ball during the motion from point of projection to highest point is:
View Solution
A body of mass 100 g is moving in a circular path of radius 2 m on a vertical plane as shown in the figure. The velocity of the body at point A is 10 m/s. The ratio of its kinetic energies at point B and C is: (Take acceleration due to gravity as 10 m/s\(^2\))
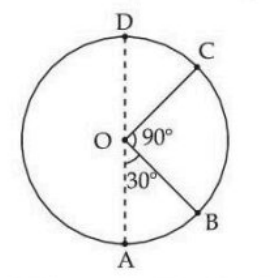
View Solution
For a diatomic gas, if \( \gamma_1 = \frac{C_P}{C_V} \) for rigid molecules and \( \gamma_2 = \frac{C_P}{C_V} \) for another diatomic molecules, but also having vibrational modes. Then, which one of the following options is correct? (where \( C_P \) and \( C_V \) are specific heats of the gas at constant pressure and volume)
View Solution
A series LCR circuit is connected to an alternating source of emf \( E \). The current amplitude at resonance frequency is \( I_0 \). If the value of resistance \( R \) becomes twice of its initial value, then amplitude of current at resonance will be:
View Solution
A symmetric thin biconvex lens is cut into four equal parts by two planes AB and CD as shown in the figure. If the power of the original lens is 4D, then the power of a part of the divided lens is:
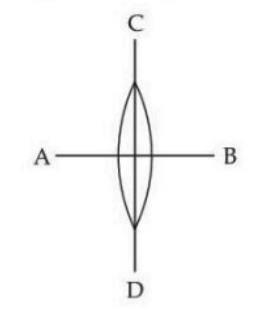
View Solution
Two long parallel wires X and Y, separated by a distance of 6 cm, carry currents of 5 A and 4 A, respectively, in opposite directions as shown in the figure. Magnitude of the resultant magnetic field at point P at a distance of 4 cm from wire Y is \( 3 \times 10^{-5} \) T. The value of \( x \), which represents the distance of point P from wire X, is _____ cm. (Take permeability of free space as \( \mu_0 = 4\pi \times 10^{-7} \) SI units.)
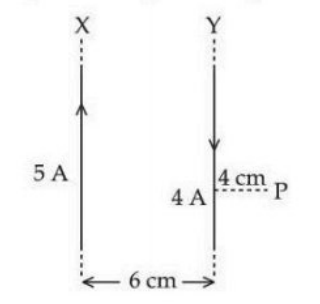
View Solution
A tube of length 1m is filled completely with an ideal liquid of mass 2M, and closed at both ends. The tube is rotated uniformly in horizontal plane about one of its ends. If the force exerted by the liquid at the other end is \( F \) and the angular velocity of the tube is \( \omega \), then the value of \( \alpha \) is _____ in SI units.
View Solution
A proton is moving undeflected in a region of crossed electric and magnetic fields at a constant speed of \( 2 \times 10^5 \, \text{m/s} \). When the electric field is switched off, the proton moves along a circular path of radius 2 cm. The magnitude of electric field is \( x \times 10^4 \, \text{N/C} \). The value of \( x \) is _____. (Take the mass of the proton as \( 1.6 \times 10^{-27} \, \text{kg} \)).
View Solution
A parallel plate capacitor of area \( A = 16 \, \text{cm}^2 \) and separation between the plates \( 10 \, \text{cm} \), is charged by a DC current. Consider a hypothetical plane surface of area \( A_0 = 3.2 \, \text{cm}^2 \) inside the capacitor and parallel to the plates. At an instant, the current through the circuit is 6A. At the same instant the displacement current through \( A_0 \) is _____ mA.
View Solution
The most stable carbocation from the following is:
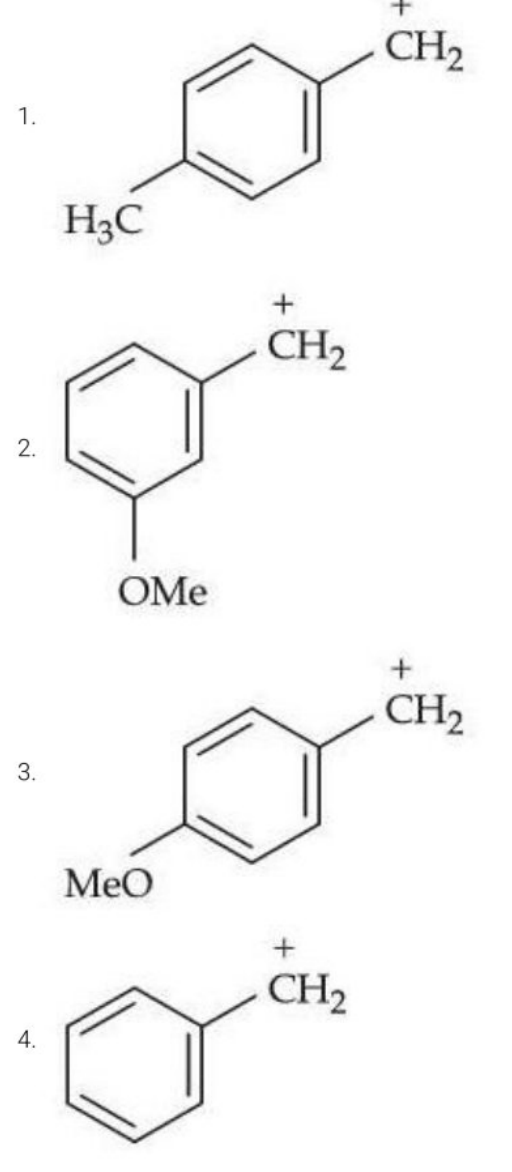
View Solution
Match the Compounds (List - I) with the appropriate Catalyst/Reagents (List - II) for their reduction into corresponding amines.
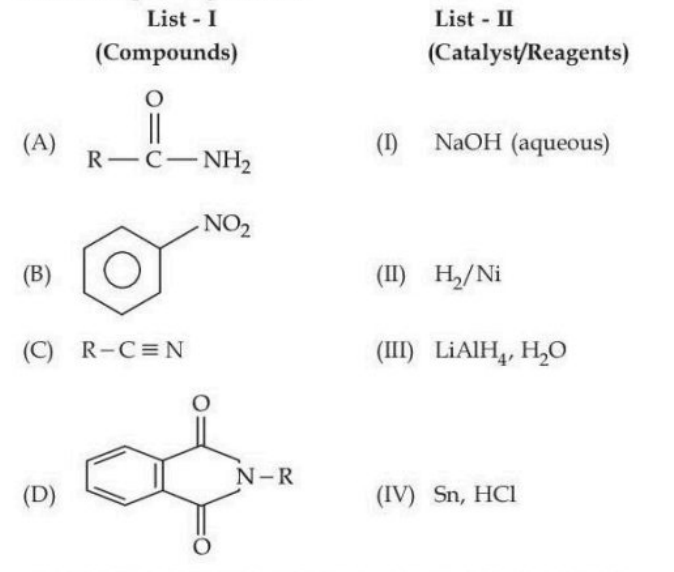
View Solution
Given below are two statements: Statement (I): \textit{Corrosion is an electrochemical phenomenon in which pure metal acts as an anode and impure metal as a cathode.
Statement (II): \textit{The rate of corrosion is more in alkaline medium than in acidic medium. In the light of the above statements, choose the correct answer from the options given below:
View Solution
When sec-butylcyclohexane reacts with bromine in the presence of sunlight, the major product is:
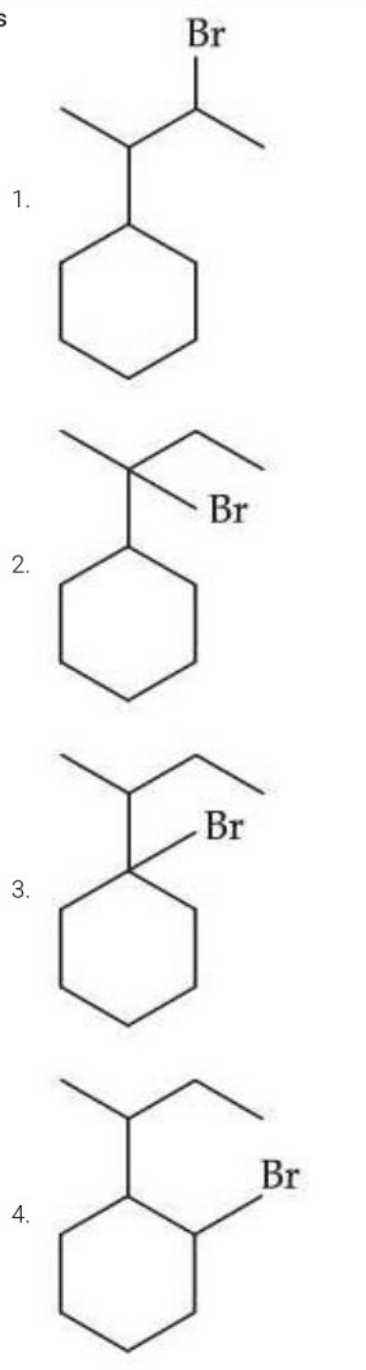
View Solution
The molar solubility(s) of zirconium phosphate with molecular formula \( \text{Zr}^{4+} \text{PO}_4^{3-} \) is given by relation:

View Solution
Identify the homoleptic complex(es) that is/are low spin.
View Solution

Given below are two statements: Statement (I): \textit{A spectral line will be observed for a 2p\(_x\) \(\rightarrow\) 2p\(_y\) transition.
Statement (II): \textit{2p\(_x\) and 2p\(_y\) are degenerate orbitals. In the light of the above statements, choose the correct answer from the options given below:
View Solution
The alkane from below having two secondary hydrogens is:
View Solution
Match List - I with List - II. List - I (Partial Derivatives) \quad List - II (Thermodynamic Quantity)
View Solution
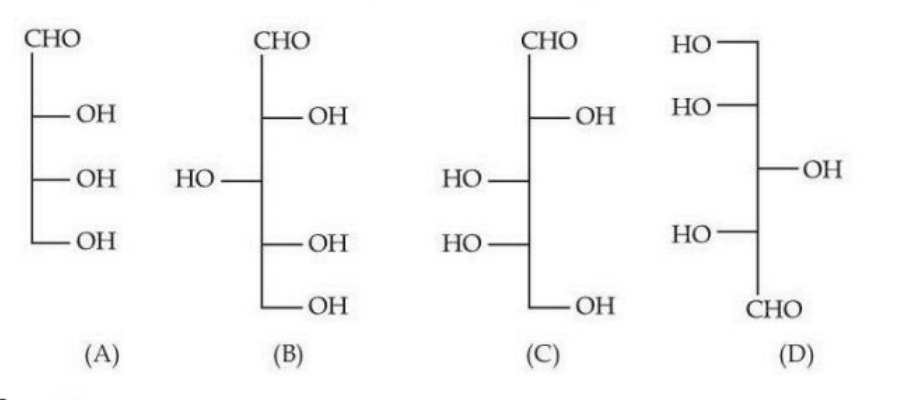
Identify the number of structure/s from the following which can be correlated to D-glyceraldehyde.
View Solution
Arrange the following compounds in increasing order of their dipole moment:
HBr, H\(_2\)S, NF\(_3\), and CCl\(_3\)
View Solution
Given below are two statements: Statement (I): \textit{An element in the extreme left of the periodic table forms acidic oxides.
Statement (II): \textit{Acid is formed during the reaction between water and oxide of a reactive element present in the extreme right of the periodic table. In the light of the above statements, choose the correct answer from the options given below:
View Solution
Given below are two statements: Statement (I): \textit{Nitrogen, sulphur, halogen, and phosphorus present in an organic compound are detected by Lassaigne's Test.
Statement (II): \textit{The elements present in the compound are converted from covalent form into ionic form by fusing the compound with Magnesium in Lassaigne's test. In the light of the above statements, choose the correct answer from the options given below:
View Solution
The correct order of the following complexes in terms of their crystal field stabilization energies is:
View Solution
Density of 3 M NaCl solution is 1.25 g/mL. The molality of the solution is:
View Solution

View Solution
Step 1: The reaction involves the oxidation of toluene with \(\text{CrO}_2\text{Cl}_2\) and \(\text{CS}_2\). \(\text{CrO}_2\text{Cl}_2\) is a strong oxidizing agent, typically oxidizing the methyl group (\(\text{-CH}_3\)) in toluene to a carboxylic acid (\(\text{COOH}\)) group. This results in a formyl group (\(\text{CHO}\)) being left behind in residue (A), as toluene is partially oxidized. Step 2: The treatment with water and NaHSO\(_3\) ensures further oxidation of the formyl group (\(\text{CHO}\)) into a carboxyl group (\(\text{COOH}\)). Diluting with HCl gives a sodium salt of the carboxyl group (\(\text{COONa}\)) in compound (B). Thus, the structures of residue (A) and compound (B) are as follows: Residue (A) has a formyl group (\(\text{CHO}\)) and compound (B) has a carboxylate group (\(\text{COONa}\)). Quick Tip: When toluene is oxidized with chromium reagents like CrO\(_2\)Cl\(_2\), the methyl group is oxidized to a carboxyl group. Sodium bisulfite is often used to convert aldehydes to carboxylates.
Consider the given figure and choose the correct option:
View Solution
The species which does not undergo disproportionation reaction is:
View Solution
The maximum covalency of a non-metallic group 15 element 'E' with the weakest E-E bond is:
View Solution
Niobium (Nb) and ruthenium (Ru) have "x" and "y" number of electrons in their respective 4d orbitals. The value of \( x + y \) is:
View Solution
The compound with molecular formula C\(_6\)H\(_6\), which gives only one monobromo derivative and takes up four moles of hydrogen per mole for complete hydrogenation has _____\( \pi \) electrons.
View Solution
Consider the following cases of standard enthalpy of reaction (\( \Delta H_f^\circ \) in kJ mol\(^{-1}\)): \[ \text{C}_2\text{H}_6(g) + 7 \text{O}_2(g) \rightarrow 2 \text{CO}_2(g) + 3 \text{H}_2\text{O}(l) \quad \Delta H_1^\circ = -1550 \] \[ \text{C(graphite)} + \text{O}_2(g) \rightarrow \text{CO}_2(g) \quad \Delta H_2^\circ = -393.5 \] \[ \text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \rightarrow \text{H}_2\text{O}(g) \quad \Delta H_3^\circ = -286 \] The magnitude of \( \Delta H_f^\circ \) of \( \text{C}_2\text{H}_6(g) \) is _____ kJ mol\(^{-1}\) (Nearest integer).
View Solution
The complex of Ni\(^{2+}\) ion and dimethyl glyoxime contains _____ number of Hydrogen (H) atoms.
View Solution
20 mL of 2 M NaOH solution is added to 400 mL of 0.5 M NaOH solution. The final concentration of the solution is _____ x \( 10^{-2} \) M. (Nearest integer)
View Solution


























Also Check: JEE Main 2025 22 Jan Shift 1 Question Paper Solutions Pdf
JEE Main 2025 22nd Jan Shift 2 Question Paper Analysis- Check Difficulty Level and Good Score
The question paper consisted of a total of 75 questions, divided equally across the three subjects:
- The Mathematics section in JEE Main 2025 22nd Jan Shift 2 Question Paper was reported as Moderate with 9 questions coming majorly from topics like Integration, Co-ordinate Geometry, etc.
- Physics was reported as Tough with 8 questions coming majorly from topics like Modern Physics, Thermodynamics, etc.
- Chemistry was reported as Moderate with 7 questions coming majorly from topics like Organic Chemistry, Physical Chemistry, etc.
Each section included a mix of multiple-choice questions (MCQs) and numerical value-based questions, offering a balanced challenge for students.
Check: JEE Main 2025 22nd Jan Shift 1 Question Paper
Is 241 a good score in JEE Mains?
For a score of 241, this is considered an excellent score with a likely percentile of 99.96+ and an estimated rank of 500–1400. Candidates scoring in this range have strong chances of securing admission to top colleges such as NIT Trichy (Computer Science), NIT Surathkal (ECE), IIIT Hyderabad (ECE), and IIIT Allahabad (IT). Additionally, they are most likely to qualify for JEE Advanced.
| Parameter | Details |
|---|---|
| Evaluation | Excellent score |
| Likely Percentile | 99.96+ |
| Estimated Rank | 500–1400 |
Is 120 a bad score in JEE Mains?
A score of 120 is not bad but considered moderate, with a likely percentile of 80–85 and an estimated rank of 35,000–45,000. While admission to top NITs is challenging, candidates may secure seats in lower-tier NITs like NIT Nagaland or NIT Mizoram (Civil, Mechanical, or Electrical). Other options include state colleges like DTU or NSUT under the state quota and private institutions such as VIT (lower campuses) or Shiv Nadar University.
| Parameter | Details |
|---|---|
| Evaluation | Moderate score |
| Likely Percentile | 80–85 |
| Estimated Rank | 35,000–45,000 |
Is 170 a good score in JEE Mains?
For a score of 170, this is considered a good score with a likely percentile of 90–95 and an estimated rank of 8,000–15,000. Candidates scoring in this range have decent chances at mid-tier NITs like NIT Calicut (ECE, Mechanical) and NIT Raipur (CSE, Electrical), as well as IIITs like IIIT Pune or IIIT Jabalpur (ECE, CSE). Additionally, they are likely to qualify for JEE Advanced.
| Parameter | Details |
|---|---|
| Evaluation | Good score |
| Likely Percentile | 90–95 |
| Estimated Rank | 8,000–15,000 |
Is 150 a bad score in JEE Mains?
A score of 150 is considered average, with a likely percentile of 85–90 and an estimated rank of 15,000–25,000. Candidates may secure admission to mid-tier NITs such as NIT Patna or NIT Silchar (Civil, Electrical, Mechanical) or GFTIs like BIT Mesra and IIEST Shibpur (Mechanical, Chemical). Private colleges like SRM or Manipal also offer good opportunities.
| Parameter | Details |
| Evaluation | Average score |
| Likely Percentile | 85–90 |
| Estimated Rank | 15,000–25,000 |
JEE Main 2025:Shift-Wise Analysis
| Session | Shift | Difficulty Trend (Physics, Chemistry, Mathematics) |
Overall Difficulty |
|---|---|---|---|
| January | 22nd January Shift 1 |
|
Moderate |
| January | 22nd January Shift 2 |
|
Moderate |
| January | 23rd January Shift 1 |
|
Moderate |
| January | 23rd January Shift 2 |
|
Moderate |
| January | 24th January Shift 1 |
|
Moderate |
| January | 24th January Shift 2 |
|
Moderate |
| January | 28th January Shift 1 |
|
Tough |
| January | 28th January Shift 2 |
|
Tough |
| January | 29th January Shift 1 |
|
Moderate to Tough |
| January | 29th January Shift 2 |
|
Moderate to Tough |





Comments