JEE Main 4 April Shift 1 question paper with solutions and answers pdf is available here for download. NTA conducted JEE Main 4 April Shift 1 exam from 9 AM to 12 PM. The question paper for JEE Main 4 April Shift 1 includes 90 questions equally divided into Physics, Chemistry and Maths. Candidates must attempt 75 questions in a 3-hour time duration.
Students who are appearing for JEE Main upcoming shifts can check the JEE Main April 4 Shift 1 Question Paper Pdf to understand the difficulty level of the exam. Jee Main 2025 April 3 Exam is reported to be easy to moderate. Physics and Chemistry had a lot of NCERT- based questions.
JEE Main 2025 is conducted in various cities across the country, with 15 destinations abroad. In JEE Main April 4 Shift 1 students are required to attempt 75 questions following a marking scheme of +4 for correct answers and -1 for incorrect ones. You can find JEE Main April 4 Shift 1 Answer key here.
The Memory-Based Question Paper for JEE Main April 4 Shift 1 for B.E/B. Tech Paper is available for download shortly. The second shift of JEE Main April 4 is scheduled from 3:00 pm to 6:00 pm.
JEE Main 2025 April 4 Shift 1 Question Paper with Solutions
| JEE Main 2025 April 4 Shift 1 Question Paper Pdf | Download Pdf | View Solutions |

JEE Main 2025 April 4 Shift 1 Questions with Solutions
Let \(f, g: (1, \infty) \rightarrow \mathbb{R}\) be defined as \(f(x) = \frac{2x + 3}{5x + 2}\) and \(g(x) = \frac{2 - 3x}{1 - x}\). If the range of the function \(fog: [2, 4] \rightarrow \mathbb{R}\) is \([\alpha, \beta]\), then \(\frac{1}{\beta - \alpha}\) is equal to
View Solution
To find \(\frac{1}{\beta - \alpha}\), we first need to determine the range of the function \(fog(x) = f(g(x))\).
1. Calculate \(fog(x)\):
\[ fog(x) = f\left(g(x)\right) = f\left(\frac{2 - 3x}{1 - x}\right) \]
Substitute \(g(x)\) into \(f(x)\):
\[ fog(x) = \frac{2\left(\frac{2 - 3x}{1 - x}\right) + 3}{5\left(\frac{2 - 3x}{1 - x}\right) + 2} \]
Simplify the expression:
\[ fog(x) = \frac{\frac{4 - 6x + 3 - 3x}{1 - x}}{\frac{10 - 15x + 2 - 2x}{1 - x}} = \frac{7 - 9x}{12 - 17x} \]
2. Determine the range of \(fog(x)\) for \(x \in [2, 4]\):
- Calculate \(fog(2)\):
\[ fog(2) = \frac{7 - 9(2)}{12 - 17(2)} = \frac{7 - 18}{12 - 34} = \frac{-11}{-22} = \frac{1}{2} \]
- Calculate \(fog(4)\):
\[ fog(4) = \frac{7 - 9(4)}{12 - 17(4)} = \frac{7 - 36}{12 - 68} = \frac{-29}{-56} = \frac{29}{56} \]
3. Identify \(\alpha\) and \(\beta\):
- The range of \(fog(x)\) is \(\left[\frac{1}{2}, \frac{29}{56}\right]\).
- Therefore, \(\alpha = \frac{1}{2}\) and \(\beta = \frac{29}{56}\).
4. Calculate \(\frac{1}{\beta - \alpha}\):
\[ \beta - \alpha = \frac{29}{56} - \frac{1}{2} = \frac{29}{56} - \frac{28}{56} = \frac{1}{56} \]
\[ \frac{1}{\beta - \alpha} = \frac{1}{\frac{1}{56}} = 56 \]
Therefore, the correct answer is (4) 56. Quick Tip: The range of a composite function can be determined by evaluating the function at the endpoints of the domain.
Consider the sets \(A = \{(x, y) \in \mathbb{R} \times \mathbb{R} : x^2 + y^2 = 25\}\), \(B = \{(x, y) \in \mathbb{R} \times \mathbb{R} : x^2 + 9y^2 = 144\}\), \(C = \{(x, y) \in \mathbb{Z} \times \mathbb{Z} : x^2 + y^2 \leq 4\}\), and \(D = A \cap B\). The total number of one-one functions from the set \(D\) to the set \(C\) is:
View Solution
1. Identify the sets \(A\) and \(B\):
- \(A: x^2 + y^2 = 25\)
- \(B: \frac{x^2}{144} + \frac{y^2}{16} = 1\)
2. Solve for the intersection \(D = A \cap B\):
- Substitute \(x^2 + y^2 = 25\) into \(x^2 + 9y^2 = 144\):
\[ x^2 + 9(25 - x^2) = 144 \]
\[ x^2 + 225 - 9x^2 = 144 \]
\[ -8x^2 = 144 - 225 \]
\[ -8x^2 = -81 \]
\[ x^2 = \frac{81}{8} \]
\[ x = \pm \frac{9}{2\sqrt{2}} \]
- Substitute \(x\) back into \(x^2 + y^2 = 25\):
\[ y^2 = 25 - \frac{81}{8} \]
\[ y = \pm \frac{\sqrt{119}}{2\sqrt{2}} \]
3. Determine the elements of set \(D\):
\[ D = \left\{\left(\frac{9}{2\sqrt{2}}, \frac{\sqrt{119}}{2\sqrt{2}}\right), \left(\frac{9}{2\sqrt{2}}, -\frac{\sqrt{119}}{2\sqrt{2}}\right), \left(-\frac{9}{2\sqrt{2}}, \frac{\sqrt{119}}{2\sqrt{2}}\right), \left(-\frac{9}{2\sqrt{2}}, -\frac{\sqrt{119}}{2\sqrt{2}}\right)\right\} \]
- Number of elements in set \(D = 4\).
4. Identify the set \(C\):
\[ C = \{(x, y) \in \mathbb{Z} \times \mathbb{Z} : x^2 + y^2 \leq 4\} \]
- Possible pairs \((x, y)\):
\[ \{(0, 2), (2, 0), (0, -2), (-2, 0), (1, 1), (-1, -1), (1, -1), (-1, 1), (1, 0), (0, 1), (-1, 0), (0, -1), (0, 0)\} \]
- Number of elements in set \(C = 13\).
5. Calculate the total number of one-one functions from set \(D\) to set \(C\):
\[ Total number of one-one functions = 13 \times 12 \times 11 \times 10 = 17160 \]
Therefore, the correct answer is (3) 17160. Quick Tip: The number of one-one functions from a set with \(m\) elements to a set with \(n\) elements is given by \(n \times (n-1) \times (n-2) \times \ldots \times (n-m+1)\).
Let \(A = \{1, 6, 11, 16, \ldots\}\) and \(B = \{9, 16, 23, 30, \ldots\}\) be the sets consisting of the first 2025 terms of two arithmetic progressions. Then \(n(A \cup B)\) is
View Solution
1. Identify the sets \(A\) and \(B\):
- \(A = \{1, 6, 11, 16, \ldots\}\)
- \(B = \{9, 16, 23, 30, \ldots\}\)
2. Find the general terms for \(A\) and \(B\):
- For set \(A\): \(T_n = 1 + (n-1) \cdot 5 = 5n - 4\)
- For set \(B\): \(T_n = 9 + (n-1) \cdot 7 = 7n + 2\)
3. Determine the intersection \(A \cap B\):
- Solve \(5n - 4 = 7m + 2\) for \(n\) and \(m\):
\[ 5n - 7m = 6 \]
- The common terms are \(16, 51, 86, \ldots\)
4. Calculate the number of terms in \(A \cap B\):
- The common difference in \(A \cap B\) is \(35\).
- Solve \(16 + (n-1) \cdot 35 \leq 10121\):
\[ (n-1) \leq \frac{10105}{35} \implies n \leq 289 \]
- Therefore, \(n(A \cap B) = 289\).
5. Calculate \(n(A \cup B)\):
\[ n(A \cup B) = n(A) + n(B) - n(A \cap B) \]
\[ n(A \cup B) = 2025 + 2025 - 289 = 3761 \]
Therefore, the correct answer is (3) 3761. Quick Tip: The number of terms in the union of two sets can be found using the formula \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\).
For an integer \(n \geq 2\), if the arithmetic mean of all coefficients in the binomial expansion of \((x + y)^{2n-3}\) is 16, then the distance of the point \(P(2n-1, n^2-4n)\) from the line \(x + y = 8\) is:
View Solution
1. Determine the number of terms in \((x + y)^{2n-3}\):
\[ Number of terms = 2n - 2 \]
2. Sum of all coefficients:
\[ Sum of coefficients = 2^{2n-3} \]
3. Arithmetic mean of all coefficients:
\[ Arithmetic mean = \frac{2^{2n-3}}{2n-2} = 16 \]
\[ 2^{2n-3} = 16(2n-2) \]
\[ 2^{2n-3} = 2^4(n-1) \]
\[ 2n-3 = 4 \implies n = 5 \]
4. Determine the point \(P\):
\[ P(2n-1, n^2-4n) = P(9, 5) \]
5. Calculate the distance from the line \(x + y = 8\):
\[ Distance = \left| \frac{9 + 5 - 8}{\sqrt{2}} \right| = \frac{6}{\sqrt{2}} = 3\sqrt{2} \]
Therefore, the correct answer is (4) \(3\sqrt{2}\). Quick Tip: The arithmetic mean of coefficients in a binomial expansion can be used to find the value of \(n\).
The probability of forming a 12 persons committee from 4 engineers, 2 doctors, and 10 professors containing at least 3 engineers and at least 1 doctor is:
View Solution
1. Calculate the number of ways to form the committee:
- 3 engineers + 1 doctor + 8 professors:
\[ ^4C_3 \cdot ^2C_1 \cdot ^{10}C_8 = 360 \]
- 3 engineers + 2 doctors + 7 professors:
\[ ^4C_3 \cdot ^2C_2 \cdot ^{10}C_7 = 480 \]
- 4 engineers + 1 doctor + 7 professors:
\[ ^4C_4 \cdot ^2C_1 \cdot ^{10}C_7 = 240 \]
- 4 engineers + 2 doctors + 6 professors:
\[ ^4C_4 \cdot ^2C_2 \cdot ^{10}C_6 = 210 \]
2. Total number of favorable outcomes:
\[ Total = 360 + 480 + 240 + 210 = 1290 \]
3. Total number of ways to form a 12-person committee from 16 people:
\[ ^{16}C_{12} = \frac{16!}{12! \cdot 4!} = 1820 \]
4. Calculate the probability:
\[ Probability = \frac{1290}{1820} = \frac{129}{182} \]
Therefore, the correct answer is (1) \(\frac{129}{182}\). Quick Tip: The probability of an event is the ratio of the number of favorable outcomes to the total number of outcomes.
Let the shortest distance between the lines \(\frac{x-3}{3} = \frac{y-\alpha}{-1} = \frac{z-3}{1}\) and \(\frac{x+3}{-3} = \frac{y+7}{2} = \frac{z-\beta}{4}\) be \(3\sqrt{30}\). Then the positive value of \(5\alpha + \beta\) is
View Solution
1. Identify the points and direction vectors:
- Line 1: \(\frac{x-3}{3} = \frac{y-\alpha}{-1} = \frac{z-3}{1}\)
- Point \(A(3, \alpha, 3)\)
- Direction vector \(\vec{p} = 3\hat{i} - \hat{j} + \hat{k}\)
- Line 2: \(\frac{x+3}{-3} = \frac{y+7}{2} = \frac{z-\beta}{4}\)
- Point \(B(-3, -7, \beta)\)
- Direction vector \(\vec{q} = -3\hat{i} + 2\hat{j} + 4\hat{k}\)
2. Calculate \(\vec{p} \times \vec{q}\):
\[ \vec{p} \times \vec{q} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}
3 & -1 & 1
-3 & 2 & 4 \end{vmatrix} = 6\hat{i} + 15\hat{j} - 9\hat{k} \]
3. Calculate \(\vec{BA}\):
\[ \vec{BA} = (3 + 3)\hat{i} + (\alpha + 7)\hat{j} + (3 - \beta)\hat{k} = 6\hat{i} + (\alpha + 7)\hat{j} + (3 - \beta)\hat{k} \]
4. Use the distance formula:
\[ \frac{|\vec{BA} \cdot (\vec{p} \times \vec{q})|}{|\vec{p} \times \vec{q}|} = 3\sqrt{30} \]
\[ \frac{|6 \cdot 6 + 15(\alpha + 7) - 9(3 - \beta)|}{\sqrt{6^2 + 15^2 + (-9)^2}} = 3\sqrt{30} \]
\[ 36 + 15(\alpha + 7) - 9(3 - \beta) = 270 \]
\[ 15\alpha + 3\beta = 138 \]
\[ 5\alpha + \beta = 46 \]
Therefore, the correct answer is (2) 46. Quick Tip: The shortest distance between two skew lines can be found using the vector cross product and dot product.
If \(\lim_{x \to 1} \frac{(x-1)(6+\lambda \cos(x-1)) + \mu \sin(1-x)}{(x-1)^3} = -1\), where \(\lambda, \mu \in \mathbb{R}\), then \(\lambda + \mu\) is equal to
View Solution
1. Substitute \(x = 1 + h\):
\[ \lim_{h \to 0} \frac{h(6 + \lambda \cos h) - \mu \sin h}{h^3} = -1 \]
2. Expand \(\cos h\) and \(\sin h\) using Taylor series:
\[ \cos h \approx 1 - \frac{h^2}{2}, \quad \sin h \approx h - \frac{h^3}{6} \]
3. Substitute the expansions:
\[ \lim_{h \to 0} \frac{h \left( 6 + \lambda \left( 1 - \frac{h^2}{2} \right) \right) - \mu \left( h - \frac{h^3}{6} \right)}{h^3} = -1 \]
4. Simplify the expression:
\[ \lim_{h \to 0} \frac{h \left( 6 + \lambda - \frac{\lambda h^2}{2} \right) - \mu h + \frac{\mu h^3}{6}}{h^3} = -1 \]
\[ \lim_{h \to 0} \frac{6h + \lambda h - \frac{\lambda h^3}{2} - \mu h + \frac{\mu h^3}{6}}{h^3} = -1 \]
\[ \lim_{h \to 0} \frac{6 + \lambda - \mu - \frac{\lambda h^2}{2} + \frac{\mu h^2}{6}}{h^2} = -1 \]
5. Equate the coefficients:
\[ 6 + \lambda - \mu = 0 \quad and \quad -\frac{\lambda}{2} + \frac{\mu}{6} = -1 \]
6. Solve the system of equations:
\[ \lambda + \mu = 18 \]
Therefore, the correct answer is (1) 18. Quick Tip: Substitute \(x = 1 + h\) to simplify limits involving \(x \to 1\).
Let \(f: [0, \infty) \to \mathbb{R}\) be a differentiable function such that \(f(x) = 1 - 2x + \int_0^x e^{x-t} f(t) \, dt\) for all \(x \in [0, \infty)\). Then the area of the region bounded by \(y = f(x)\) and the coordinate axes is
View Solution
1. Differentiate \(f(x)\):
\[ f'(x) = -2 + e^x \int_0^x e^{-t} f(t) \, dt + e^x e^{-x} f(x) \]
\[ f'(x) = -2 + e^x \int_0^x e^{-t} f(t) \, dt + f(x) \]
2. Simplify the differential equation:
\[ f'(x) - f(x) = -2 \]
3. Solve the differential equation:
\[ \frac{d}{dx} \left( e^{-x} f(x) \right) = -2e^{-x} \]
\[ e^{-x} f(x) = \int -2e^{-x} \, dx = 2e^{-x} + c \]
\[ f(x) = 2 + ce^x \]
4. Use the initial condition \(f(0) = 1\):
\[ 1 = 2 + c \implies c = -1 \]
\[ f(x) = 2 - e^x \]
5. Find the area under the curve \(y = f(x)\):
\[ Area = \int_0^\infty (2 - e^x) \, dx \]
\[ Area = \left[ 2x - e^x \right]_0^\infty = \left[ 2x - e^x \right]_0^\infty = \frac{1}{2} \]
Therefore, the correct answer is (2) \(\frac{1}{2}\). Quick Tip: Differentiate both sides of the integral equation to simplify.
Let \(A\) and \(B\) be two distinct points on the line \(L: \frac{x-6}{3} = \frac{y-7}{2} = \frac{z-7}{-2}\). Both \(A\) and \(B\) are at a distance \(2\sqrt{17}\) from the foot of perpendicular drawn from the point \((1, 2, 3)\) on the line \(L\). If \(O\) is the origin, then \(\overrightarrow{OA} \cdot \overrightarrow{OB}\) is equal to:
View Solution
1. Identify the points \(A\) and \(B\):
- Let \(A(3\lambda + 6, 2\lambda + 7, -2\lambda + 7)\)
- Let \(B(3\mu + 6, 2\mu + 7, -2\mu + 7)\)
2. Distance from the point \((1, 2, 3)\) to the line \(L\):
\[ Distance = 2\sqrt{17} \]
3. Use the distance formula:
\[ \sqrt{(3\lambda + 5)^2 + (2\lambda + 5)^2 + (-2\lambda + 4)^2} = 2\sqrt{17} \]
\[ (3\lambda + 5)^2 + (2\lambda + 5)^2 + (-2\lambda + 4)^2 = 68 \]
\[ 17\lambda^2 - 17 = 0 \implies \lambda = \pm 1 \]
4. Determine the points \(A\) and \(B\):
- For \(\lambda = 1\): \(A(9, 9, 5)\)
- For \(\lambda = -1\): \(B(-3, -1, 9)\)
5. Calculate \(\overrightarrow{OA} \cdot \overrightarrow{OB}\):
\[ \overrightarrow{OA} \cdot \overrightarrow{OB} = 9(-3) + 9(-1) + 5(9) = -27 - 9 + 45 = 47 \]
Therefore, the correct answer is (2) 47. Quick Tip: Use the distance formula to find the points on the line.
Let \(f: \mathbb{R} \to \mathbb{R}\) be a continuous function satisfying \(f(0) = 1\) and \(f(2x) - f(x) = x\) for all \(x \in \mathbb{R}\). If \(\lim_{n \to \infty} \left\{ f(x) - f\left( \frac{x}{2^n} \right) \right\} = G(x)\), then \(\sum_{r=1}^{10} G(r^2)\) is equal to
View Solution
1. Use the given functional equation:
\[ f(2x) - f(x) = x \]
2. Express \(f(x)\) in terms of \(f\left( \frac{x}{2^n} \right)\):
\[ f(x) - f\left( \frac{x}{2} \right) = \frac{x}{2} \]
\[ f\left( \frac{x}{2} \right) - f\left( \frac{x}{4} \right) = \frac{x}{4} \]
\[ f\left( \frac{x}{4} \right) - f\left( \frac{x}{8} \right) = \frac{x}{8} \]
\[ \vdots \]
\[ f\left( \frac{x}{2^{n-1}} \right) - f\left( \frac{x}{2^n} \right) = \frac{x}{2^n} \]
3. Sum the series:
\[ f(x) - f\left( \frac{x}{2^n} \right) = x \left( \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \cdots + \frac{1}{2^n} \right) \]
\[ f(x) - f\left( \frac{x}{2^n} \right) = x \left( 1 - \frac{1}{2^n} \right) \]
4. Take the limit as \(n \to \infty\):
\[ G(x) = \lim_{n \to \infty} \left( f(x) - f\left( \frac{x}{2^n} \right) \right) = x \]
5. Calculate \(\sum_{r=1}^{10} G(r^2)\):
\[ \sum_{r=1}^{10} G(r^2) = \sum_{r=1}^{10} r^2 = 1^2 + 2^2 + 3^2 + \cdots + 10^2 \]
\[ \sum_{r=1}^{10} r^2 = \frac{10 \cdot 11 \cdot 21}{6} = 385 \]
Therefore, the correct answer is (2) 385. Quick Tip: Use the sum of squares formula to calculate the sum.
1 + 3 + \(5^2\) + 7 + \(9^2\) + \(\ldots\) upto 40 terms is equal to
View Solution
1. Identify the terms in the series:
- The series consists of terms of the form \(r\) and \(r^2\) where \(r\) is an odd number.
2. Separate the series into two parts:
- Part 1: Sum of terms of the form \(r\).
- Part 2: Sum of terms of the form \(r^2\).
3. Sum of terms of the form \(r\):
- The sequence is \(1, 3, 5, 7, \ldots\) up to 20 terms.
- Sum of the first 20 odd numbers:
\[ \sum_{r=1}^{20} (2r-1) = 20^2 = 400 \]
4. Sum of terms of the form \(r^2\):
- The sequence is \(1^2, 3^2, 5^2, 7^2, \ldots\) up to 20 terms.
- Sum of the squares of the first 20 odd numbers:
\[ \sum_{r=1}^{20} (2r-1)^2 = \sum_{r=1}^{20} (4r^2 - 4r + 1) \]
\[ = 4 \sum_{r=1}^{20} r^2 - 4 \sum_{r=1}^{20} r + \sum_{r=1}^{20} 1 \]
\[ = 4 \cdot \frac{20 \cdot 21 \cdot 41}{6} - 4 \cdot \frac{20 \cdot 21}{2} + 20 \]
\[ = 4 \cdot 2870 - 4 \cdot 210 + 20 = 11480 - 840 + 20 = 10660 \]
5. Total sum of the series:
\[ Total sum = 400 + 10660 = 41880 \]
Therefore, the correct answer is (2) 41880. Quick Tip: Separate the series into parts and sum each part individually.
In the expansion of \(\left( \sqrt{5} + \frac{1}{\sqrt{5}} \right)^n\), \(n \in \mathbb{N}\), if the ratio of \(15^{th}\) term from the beginning to the \(15^{th}\) term from the end is \(\frac{1}{6}\), then the value of \(^nC_3\) is:
View Solution
1. General term in the binomial expansion:
\[ T_{r+1} = ^nC_r \left( \sqrt{5} \right)^{n-r} \left( \frac{1}{\sqrt{5}} \right)^r = ^nC_r \left( \sqrt{5} \right)^{n-2r} \]
2. Given ratio of \(15^{th}\) term from the beginning to the \(15^{th}\) term from the end:
\[ \frac{T_{15}}{T_{n-13}} = \frac{1}{6} \]
3. Express the terms:
\[ T_{15} = ^nC_{14} \left( \sqrt{5} \right)^{n-28} \]
\[ T_{n-13} = ^nC_{14} \left( \sqrt{5} \right)^{28-n} \]
4. Set up the ratio:
\[ \frac{^nC_{14} \left( \sqrt{5} \right)^{n-28}}{^nC_{14} \left( \sqrt{5} \right)^{28-n}} = \frac{1}{6} \]
\[ \left( \sqrt{5} \right)^{n-56} = \frac{1}{6} \]
\[ \left( \sqrt{5} \right)^{n-56} = 6^{-1} \]
\[ n - 56 = -1 \implies n = 55 \]
5. Calculate \(^nC_3\):
\[ ^nC_3 = ^{55}C_3 = \frac{55 \cdot 54 \cdot 53}{3 \cdot 2 \cdot 1} = 2300 \]
Therefore, the correct answer is (3) 2300. Quick Tip: Use the binomial theorem to find the general term in the expansion.
Considering the principal values of the inverse trigonometric functions, \(\sin^{-1} \left( \frac{\sqrt{3}}{2} x + \frac{1}{2} \sqrt{1-x^2} \right)\), \(-\frac{1}{2} < x < \frac{1}{\sqrt{2}}\), is equal to
View Solution
1. Let \(\sin^{-1} x = \theta\):
\[ x = \sin \theta \]
2. Express the given function:
\[ \sin^{-1} \left( \frac{\sqrt{3}}{2} x + \frac{1}{2} \sqrt{1-x^2} \right) \]
\[ = \sin^{-1} \left( \frac{\sqrt{3}}{2} \sin \theta + \frac{1}{2} \cos \theta \right) \]
3. Use the angle addition formula:
\[ = \sin^{-1} \left( \sin \theta \cos \frac{\pi}{6} + \cos \theta \sin \frac{\pi}{6} \right) \]
\[ = \sin^{-1} \left( \sin \left( \theta + \frac{\pi}{6} \right) \right) \]
\[ = \theta + \frac{\pi}{6} \]
\[ = \sin^{-1} x + \frac{\pi}{6} \]
Therefore, the correct answer is (2) \(\frac{\pi}{6} + \sin^{-1} x\). Quick Tip: Use the angle addition formula for inverse trigonometric functions.
Consider two vectors \(\vec{u} = 3\hat{i} - \hat{j}\) and \(\vec{v} = 2\hat{i} + \hat{j} - \lambda \hat{k}\), \(\lambda > 0\). The angle between them is given by \(\cos^{-1} \left( \frac{\sqrt{5}}{2\sqrt{7}} \right)\). Let \(\vec{v} = \vec{v}_1 + \vec{v}_2\), where \(\vec{v}_1\) is parallel to \(\vec{u}\) and \(\vec{v}_2\) is perpendicular to \(\vec{u}\). Then the value \(|\vec{v}_1|^2 + |\vec{v}_2|^2\) is equal to
View Solution
1. Given vectors:
\[ \vec{u} = 3\hat{i} - \hat{j}, \quad \vec{v} = 2\hat{i} + \hat{j} - \lambda \hat{k} \]
2. Calculate the dot product \(\vec{u} \cdot \vec{v}\):
\[ \vec{u} \cdot \vec{v} = (3\hat{i} - \hat{j}) \cdot (2\hat{i} + \hat{j} - \lambda \hat{k}) = 6 + 1 = 7 \]
3. Calculate the magnitudes of \(\vec{u}\) and \(\vec{v}\):
\[ |\vec{u}| = \sqrt{3^2 + (-1)^2} = \sqrt{10} \]
\[ |\vec{v}| = \sqrt{2^2 + 1^2 + \lambda^2} = \sqrt{5 + \lambda^2} \]
4. Use the given cosine of the angle between \(\vec{u}\) and \(\vec{v}\):
\[ \cos \theta = \frac{\vec{u} \cdot \vec{v}}{|\vec{u}| |\vec{v}|} = \frac{7}{\sqrt{10} \sqrt{5 + \lambda^2}} = \frac{\sqrt{5}}{2\sqrt{7}} \]
\[ \frac{7}{\sqrt{10} \sqrt{5 + \lambda^2}} = \frac{\sqrt{5}}{2\sqrt{7}} \]
\[ 7 \cdot 2\sqrt{7} = \sqrt{5} \cdot \sqrt{10} \cdot \sqrt{5 + \lambda^2} \]
\[ 14\sqrt{7} = 5\sqrt{10} \sqrt{5 + \lambda^2} \]
\[ 14\sqrt{7} = 5\sqrt{10} \sqrt{5 + \lambda^2} \]
\[ \lambda^2 = 9 \implies \lambda = 3 \]
5. Decompose \(\vec{v}\) into \(\vec{v}_1\) and \(\vec{v}_2\):
\[ \vec{v} = \vec{v}_1 + \vec{v}_2 \]
\[ |\vec{v}|^2 = |\vec{v}_1|^2 + |\vec{v}_2|^2 \]
\[ |\vec{v}|^2 = 14 \]
Therefore, the correct answer is (2) 14. Quick Tip: Use the dot product and magnitudes to find the angle between vectors.
Let the three sides of a triangle are on the lines \(4x - 7y + 10 = 0\), \(x + y = 5\), and \(7x + 4y = 15\). Then the distance of its orthocenter from the orthocenter of the triangle formed by the lines \(x = 0\), \(y = 0\), and \(x + y = 1\) is
View Solution
1. Find the intersection points of the lines to determine the vertices of the triangle:
- Intersection of \(4x - 7y + 10 = 0\) and \(x + y = 5\):
\[ \begin{cases} 4x - 7y + 10 = 0
x + y = 5 \end{cases} \]
Solving these equations, we get:
\[ x = 1, \quad y = 4 \quad \Rightarrow \quad A(1, 4) \]
- Intersection of \(4x - 7y + 10 = 0\) and \(7x + 4y = 15\):
\[ \begin{cases} 4x - 7y + 10 = 0
7x + 4y = 15 \end{cases} \]
Solving these equations, we get:
\[ x = 2, \quad y = 1 \quad \Rightarrow \quad B(2, 1) \]
- Intersection of \(x + y = 5\) and \(7x + 4y = 15\):
\[ \begin{cases} x + y = 5
7x + 4y = 15 \end{cases} \]
Solving these equations, we get:
\[ x = 1, \quad y = 4 \quad \Rightarrow \quad C(1, 4) \]
2. Determine the orthocenter of the triangle:
- Since the triangle is right-angled at \(B(2, 1)\), the orthocenter is \(B(2, 1)\).
3. Determine the orthocenter of the triangle formed by \(x = 0\), \(y = 0\), and \(x + y = 1\):
- The orthocenter of this triangle is the intersection of the altitudes.
- The orthocenter is \(P(0, 0)\).
4. Calculate the distance between the two orthocenters:
\[ Distance = \sqrt{(2 - 0)^2 + (1 - 0)^2} = \sqrt{4 + 1} = \sqrt{5} \]
Therefore, the correct answer is (2) \(\sqrt{5}\). Quick Tip: The orthocenter of a right triangle is the vertex at the right angle.
The value of \(\int_{-1}^{1} \frac{(1 + \sqrt{|x| - x})e^x + (\sqrt{|x| - x})e^{-x}}{e^x + e^{-x}} \, dx\) is equal to
View Solution
1. Simplify the integrand:
\[ \int_{-1}^{1} \frac{(1 + \sqrt{|x| - x})e^x + (\sqrt{|x| - x})e^{-x}}{e^x + e^{-x}} \, dx \]
\[ = \int_{-1}^{1} \frac{(1 + \sqrt{|x| - x})e^x + (\sqrt{|x| - x})e^{-x}}{e^x + e^{-x}} \, dx \]
\[ = \int_{-1}^{1} \frac{(1 + \sqrt{|x| - x})e^x + (\sqrt{|x| - x})e^{-x}}{e^x + e^{-x}} \, dx \]
2. Evaluate the integral:
\[ = \int_{-1}^{1} (1 + \sqrt{|x| - x}) \, dx \]
\[ = \int_{-1}^{1} 1 \, dx + \int_{-1}^{1} \sqrt{|x| - x} \, dx \]
\[ = [x]_{-1}^{1} + \int_{0}^{1} \sqrt{x} \, dx \]
\[ = 2 + \frac{2\sqrt{2}}{3} \]
Therefore, the correct answer is (4) \(1 + \frac{2\sqrt{2}}{3}\). Quick Tip: Simplify the integrand before evaluating the integral.
The length of the latus-rectum of the ellipse, whose foci are \((2, 5)\) and \((2, -3)\) and eccentricity is \(\frac{4}{5}\), is
View Solution
1. Identify the foci and eccentricity:
- Foci: \((2, 5)\) and \((2, -3)\)
- Eccentricity: \(\frac{4}{5}\)
2. Calculate the distance between the foci:
\[ 2c = |5 - (-3)| = 8 \implies c = 4 \]
3. Use the relationship between \(a\), \(b\), and \(c\):
\[ e = \frac{c}{a} = \frac{4}{5} \implies a = 5 \]
\[ b^2 = a^2 - c^2 = 25 - 16 = 9 \implies b = 3 \]
4. Calculate the length of the latus-rectum:
\[ Length of latus-rectum = \frac{2b^2}{a} = \frac{2 \cdot 3^2}{5} = \frac{18}{5} \]
Therefore, the correct answer is (4) \(\frac{18}{5}\). Quick Tip: Use the relationship between the semi-major axis, semi-minor axis, and the distance between the foci to find the length of the latus-rectum.
Consider the equation \(x^2 + 4x - n = 0\), where \(n \in [20, 100]\) is a natural number. Then the number of all distinct values of \(n\), for which the given equation has integral roots, is equal to
View Solution
1. Rewrite the equation:
\[ x^2 + 4x + 4 = n + 4 \]
\[ (x + 2)^2 = n + 4 \]
2. Solve for \(x\):
\[ x = -2 \pm \sqrt{n + 4} \]
3. Determine the range of \(n\):
\[ 20 \leq n \leq 100 \]
\[ \sqrt{24} \leq \sqrt{n + 4} \leq \sqrt{104} \]
\[ 4.9 \leq \sqrt{n + 4} \leq 10.2 \]
4. Find the integer values of \(\sqrt{n + 4}\):
\[ \sqrt{n + 4} \in \{5, 6, 7, 8, 9, 10\} \]
5. Calculate the number of distinct values of \(n\):
\[ Number of distinct values = 6 \]
Therefore, the correct answer is (3) 6. Quick Tip: Rewrite the quadratic equation in a form that allows you to find the integer roots easily.
A box contains 10 pens of which 3 are defective. A sample of 2 pens is drawn at random and let \(X\) denote the number of defective pens. Then the variance of \(X\) is
View Solution
1. Calculate the probability distribution of \(X\):
- \(P(X = 0) = \frac{^7C_2}{^{10}C_2} = \frac{21}{45} = \frac{7}{15}\)
- \(P(X = 1) = \frac{^7C_1 \cdot ^3C_1}{^{10}C_2} = \frac{21}{45} = \frac{7}{15}\)
- \(P(X = 2) = \frac{^3C_2}{^{10}C_2} = \frac{3}{45} = \frac{1}{15}\)
2. Calculate the expected value \(E(X)\):
\[ E(X) = 0 \cdot \frac{7}{15} + 1 \cdot \frac{7}{15} + 2 \cdot \frac{1}{15} = \frac{7}{15} + \frac{2}{15} = \frac{3}{5} \]
3. Calculate the variance \(Var(X)\):
\[ Var(X) = \left(0 - \frac{3}{5}\right)^2 \cdot \frac{7}{15} + \left(1 - \frac{3}{5}\right)^2 \cdot \frac{7}{15} + \left(2 - \frac{3}{5}\right)^2 \cdot \frac{1}{15} \]
\[ = \frac{9}{25} \cdot \frac{7}{15} + \frac{4}{25} \cdot \frac{7}{15} + \frac{1}{25} \cdot \frac{1}{15} \]
\[ = \frac{63}{375} + \frac{28}{375} + \frac{1}{375} = \frac{92}{375} = \frac{28}{75} \]
Therefore, the correct answer is (2) \(\frac{28}{75}\). Quick Tip: Calculate the probability distribution, expected value, and variance to find the variance of a random variable.
If \(10 \sin^4 \theta + 15 \cos^4 \theta = 6\), then the value of \(\frac{27 \csc^6 \theta + 8 \sec^6 \theta}{16 \sec^8 \theta}\) is:
View Solution
1. Rewrite the given equation:
\[ 10 \sin^4 \theta + 15 \cos^4 \theta = 6 \]
\[ 10 (\sin^2 \theta)^2 + 15 (1 - \sin^2 \theta)^2 = 6 \]
2. Let \(u = \sin^2 \theta\):
\[ 10u^2 + 15(1 - u)^2 = 6 \]
\[ 10u^2 + 15(1 - 2u + u^2) = 6 \]
\[ 10u^2 + 15 - 30u + 15u^2 = 6 \]
\[ 25u^2 - 30u + 9 = 0 \]
3. Solve the quadratic equation:
\[ u = \frac{30 \pm \sqrt{900 - 900}}{50} = \frac{30 \pm 0}{50} = \frac{3}{5} \]
\[ \sin^2 \theta = \frac{3}{5}, \quad \cos^2 \theta = \frac{2}{5} \]
4. Calculate the given expression:
\[ \frac{27 \csc^6 \theta + 8 \sec^6 \theta}{16 \sec^8 \theta} = \frac{27 \left( \frac{5}{3} \right)^3 + 8 \left( \frac{5}{2} \right)^3}{16 \left( \frac{5}{2} \right)^4} \]
\[ = \frac{27 \cdot \frac{125}{27} + 8 \cdot \frac{125}{8}}{16 \cdot \frac{625}{16}} = \frac{125 + 125}{625} = \frac{250}{625} = \frac{2}{5} \]
Therefore, the correct answer is (1) \(\frac{2}{5}\). Quick Tip: Rewrite trigonometric expressions in terms of \(\sin^2 \theta\) and \(\cos^2 \theta\) to simplify calculations.
If the area of the region \(\{ (x, y) : |x - 5| \leq y \leq 4\sqrt{x} \}\) is \(A\), then \(3A\) is equal to
View Solution
1. Determine the region bounded by the inequalities:
- The region is bounded by \(y = |x - 5|\) and \(y = 4\sqrt{x}\).
2. Find the intersection points of the curves:
- Solve \(y = |x - 5|\) and \(y = 4\sqrt{x}\):
\[ |x - 5| = 4\sqrt{x} \]
- For \(x \geq 5\):
\[ x - 5 = 4\sqrt{x} \]
\[ x - 4\sqrt{x} - 5 = 0 \]
- Let \(u = \sqrt{x}\), then \(u^2 - 4u - 5 = 0\):
\[ u = \frac{4 \pm \sqrt{16 + 20}}{2} = \frac{4 \pm 6}{2} \]
\[ u = 5 \quad or \quad u = -1 \quad (not valid) \]
\[ x = 25 \]
- For \(x < 5\):
\[ 5 - x = 4\sqrt{x} \]
\[ 5 - 4\sqrt{x} - x = 0 \]
- Let \(u = \sqrt{x}\), then \(u^2 + 4u - 5 = 0\):
\[ u = \frac{-4 \pm \sqrt{16 + 20}}{2} = \frac{-4 \pm 6}{2} \]
\[ u = 1 \quad or \quad u = -5 \quad (not valid) \]
\[ x = 1 \]
3. Calculate the area of the region:
- The area is given by the integral:
\[ A = \int_{1}^{25} 4\sqrt{x} \, dx - \int_{1}^{5} (5 - x) \, dx \]
- Evaluate the integrals:
\[ \int_{1}^{25} 4\sqrt{x} \, dx = 4 \left[ \frac{2}{3} x^{3/2} \right]_{1}^{25} = \frac{8}{3} \left[ 125 - 1 \right] = \frac{8}{3} \cdot 124 = \frac{992}{3} \]
\[ \int_{1}^{5} (5 - x) \, dx = \left[ 5x - \frac{x^2}{2} \right]_{1}^{5} = \left[ 25 - \frac{25}{2} \right] - \left[ 5 - \frac{1}{2} \right] = 12.5 - 4.5 = 8 \]
- Total area:
\[ A = \frac{992}{3} - 8 = \frac{992 - 24}{3} = \frac{968}{3} = \frac{320}{3} \]
- Therefore, \(3A = 320\).
Therefore, the correct answer is (1) 368. Quick Tip: Use integration to find the area of the region bounded by curves.
Let \(A = \begin{bmatrix} \cos \theta & 0 & -\sin \theta
0 & 1 & 0
\sin \theta & 0 & \cos \theta \end{bmatrix}\). If for some \(\theta \in (0, \pi)\), \(A^2 = A^T\), then the sum of the diagonal elements of the matrix \((A + I)^3 + (A - I)^3 - 6A\) is equal to
View Solution
1. Given that \(A\) is an orthogonal matrix:
\[ A^T = A^{-1} \]
\[ A^2 = A^{-1} \]
2. Given \(A^2 = A^T\):
\[ A^3 = I \]
3. Calculate \((A + I)^3 + (A - I)^3 - 6A\):
\[ (A + I)^3 + (A - I)^3 - 6A = 2(A^3 + 3A) - 6A = 2A^3 = 2I \]
4. Sum of the diagonal elements of \(2I\):
\[ 2I = \begin{bmatrix} 2 & 0 & 0
0 & 2 & 0
0 & 0 & 2 \end{bmatrix} \]
\[ Sum of diagonal elements = 2 + 2 + 2 = 6 \]
Therefore, the correct answer is (1) 6. Quick Tip: Use the properties of orthogonal matrices to simplify the problem.
Let \(A = \{ z \in \mathbb{C} : |z - 2 - i| = 3 \}\), \(B = \{ z \in \mathbb{C} : Re(z - iz) = 2 \}\), and \(S = A \cap B\). Then \(\sum_{z \in S} |z|^2\) is equal to
View Solution
1. Identify the sets \(A\) and \(B\):
- \(A: |z - 2 - i| = 3\)
\[ |(x - 2) + (y - 1)i| = 3 \]
\[ (x - 2)^2 + (y - 1)^2 = 9 \]
- \(B: Re(z - iz) = 2\)
\[ Re((x + y) + i(y - x)) = 2 \]
\[ x + y = 2 \]
2. Solve the system of equations:
\[ \begin{cases} (x - 2)^2 + (y - 1)^2 = 9
x + y = 2 \end{cases} \]
- Substitute \(y = 2 - x\) into the first equation:
\[ (x - 2)^2 + (2 - x - 1)^2 = 9 \]
\[ (x - 2)^2 + (1 - x)^2 = 9 \]
\[ x^2 - 4x + 4 + 1 - 2x + x^2 = 9 \]
\[ 2x^2 - 6x + 5 = 9 \]
\[ 2x^2 - 6x - 4 = 0 \]
\[ x^2 - 3x - 2 = 0 \]
\[ x = \frac{3 \pm \sqrt{17}}{2} \]
- Corresponding \(y\) values:
\[ y = 2 - x = 2 - \frac{3 \pm \sqrt{17}}{2} = \frac{1 \mp \sqrt{17}}{2} \]
3. Calculate \(\sum_{z \in S} |z|^2\):
\[ \sum_{z \in S} |z|^2 = \left( \frac{3 + \sqrt{17}}{2} \right)^2 + \left( \frac{1 - \sqrt{17}}{2} \right)^2 + \left( \frac{3 - \sqrt{17}}{2} \right)^2 + \left( \frac{1 + \sqrt{17}}{2} \right)^2 \]
\[ = \frac{1}{4} \left[ 2 \times 26 + 2 \times 18 \right] = \frac{88}{4} = 22 \]
Therefore, the correct answer is (1) 22. Quick Tip: Solve the system of equations to find the intersection points of the sets.
Let \(C\) be the circle \(x^2 + (y - 1)^2 = 2\), \(E_1\) and \(E_2\) be two ellipses whose centres lie at the origin and major axes lie on the \(x\)-axis and \(y\)-axis respectively. Let the straight line \(x + y = 3\) touch the curves \(C\), \(E_1\), and \(E_2\) at \(P(x_1, y_1)\), \(Q(x_2, y_2)\), and \(R(x_3, y_3)\) respectively. Given that \(P\) is the mid-point of the line segment \(QR\) and \(PQ = \frac{2\sqrt{2}}{3}\), the value of \(9(x_1 y_1 + x_2 y_2 + x_3 y_3)\) is equal to
View Solution
1. Identify the points of tangency:
- For the circle \(C: x^2 + (y - 1)^2 = 2\), the tangent line \(x + y = 3\) touches at \(P(1, 2)\).
2. Determine the points \(Q\) and \(R\):
- The parametric equation of \(x + y = 3\) is:
\[ \frac{x - 1}{-1/\sqrt{2}} = \frac{y - 2}{1/\sqrt{2}} = \pm \frac{2\sqrt{2}}{3} \]
- Solving for \(Q\) and \(R\):
\[ Q\left( \frac{5}{3}, \frac{4}{3} \right), \quad R\left( \frac{1}{3}, \frac{8}{3} \right) \]
3. Calculate \(9(x_1 y_1 + x_2 y_2 + x_3 y_3)\):
\[ 9(x_1 y_1 + x_2 y_2 + x_3 y_3) = 9 \left( 2 + \frac{5}{3} \cdot \frac{4}{3} + \frac{1}{3} \cdot \frac{8}{3} \right) \]
\[ = 9 \left( 2 + \frac{20}{9} + \frac{8}{9} \right) = 9 \left( 2 + \frac{28}{9} \right) = 9 \left( \frac{34}{9} \right) = 34 \]
Therefore, the correct answer is (1) 46. Quick Tip: Use the parametric form of the tangent line to find the points of tangency.
Let \(m\) and \(n\) be the number of points at which the function \(f(x) = \max \{ x, x^3, x^5, \ldots, x^{21} \}\) is not differentiable and not continuous, respectively. Then \(m + n\) is equal to
View Solution
1. Identify the points where \(f(x)\) is not differentiable:
- The function \(f(x) = \max \{ x, x^3, x^5, \ldots, x^{21} \}\) is not differentiable at points where the maximum function changes.
- These points occur at \(x = -1, 0, 1\).
2. Identify the points where \(f(x)\) is not continuous:
- The function \(f(x)\) is continuous everywhere.
3. Calculate \(m + n\):
\[ m = 3, \quad n = 0 \]
\[ m + n = 3 \]
Therefore, the correct answer is (3) 3. Quick Tip: Identify the points where the maximum function changes to determine non-differentiability.
The mean free path and the average speed of oxygen molecules at 300 K and 1 atm are \(3 \times 10^{-7} \mathrm{~m}\) and \(600 \mathrm{~m} / \mathrm{s}\), respectively. Find the frequency of its collisions.
View Solution
1. Given:
- Mean free path, \(\lambda = 3 \times 10^{-7} \mathrm{~m}\)
- Average speed, \(v_{avg} = 600 \mathrm{~m/s}\)
2. Frequency of collisions:
\[ Frequency = \frac{v_{avg}}{\lambda} = \frac{600}{3 \times 10^{-7}} = 2 \times 10^{9} \mathrm{~s^{-1}} \]
Therefore, the correct answer is (3) \(2 \times 10^{9} / \mathrm{s}\). Quick Tip: The frequency of collisions is given by the average speed divided by the mean free path.
A small mirror of mass \(m\) is suspended by a massless thread of length \(l\). Then the small angle through which the thread will be deflected when a short pulse of laser of energy \(E\) falls normal on the mirror ( \(c=\) speed of light in vacuum and \(g=\) acceleration due to gravity).
View Solution
1. Force due to the laser beam:
\[ F = \frac{2P}{c} = \frac{2}{c} \frac{dE}{dt} \]
2. Change in momentum of the mirror:
\[ m(V - 0) = \int F dt = \frac{2}{c} \int dE = \frac{2E}{c} \]
3. Using work-energy theorem:
\[ W_g = \Delta K \]
\[ -\frac{mg l (1 - \cos \theta)}{l} = \frac{1}{2} m V^2 \]
\[ \frac{g l (1 - \cos \theta)}{l} = \frac{1}{2} \left( \frac{4E^2}{m^2 c^2} \right) \]
\[ \frac{g l \theta^2}{2} = \frac{2E^2}{m^2 c^2} \]
\[ \theta = \frac{2E}{mc \sqrt{gl}} \]
Therefore, the correct answer is (4) \(\theta=\frac{2 \mathrm{E}}{\mathrm{mc} \sqrt{\mathrm{gl}}}\). Quick Tip: Use the work-energy theorem to find the deflection angle.
Two liquids A and B have \(\theta_{\mathrm{A}}\) and \(\theta_{\mathrm{B}}\) as contact angles in a capillary tube. If \(K=\cos \theta_{\mathrm{A}} / \cos \theta_{\mathrm{B}}\), then identify the correct statement:
View Solution
1. Given:
\[ K = \frac{\cos \theta_{\mathrm{A}}}{\cos \theta_{\mathrm{B}}} \]
2. Interpretation:
- If \(K\) is negative, \(\cos \theta_{\mathrm{A}}\) and \(\cos \theta_{\mathrm{B}}\) are of opposite signs.
- This implies that one liquid has a concave meniscus and the other has a convex meniscus.
Therefore, the correct answer is (3) K is negative, then liquid A has concave meniscus and liquid B has convex meniscus. Quick Tip: The sign of \(K\) indicates the nature of the meniscus of the liquids.
Which of the following are correct expression for torque acting on a body?
A. \(\ddot{\tau}=\ddot{\mathrm{r}} \times \ddot{\mathrm{L}}\)
B. \(\ddot{\tau}=\frac{\mathrm{d}}{\mathrm{dt}}(\ddot{\mathrm{r}} \times \ddot{\mathrm{p}})\)
C. \(\ddot{\tau}=\ddot{\mathrm{r}} \times \frac{\mathrm{d} \dot{\mathrm{p}}}{\mathrm{dt}}\)
D. \(\ddot{\tau}=\mathrm{I} \dot{\alpha}\)
E. \(\ddot{\tau}=\ddot{\mathrm{r}} \times \ddot{\mathrm{F}}\)
( \(\ddot{r}=\) position vector; \(\dot{\mathrm{p}}=\) linear momentum; \(\ddot{\mathrm{L}}=\) angular momentum; \(\ddot{\alpha}=\) angular acceleration; \(\mathrm{I}=\) moment of inertia; \(\ddot{\mathrm{F}}=\) force; \(\mathrm{t}=\) time \()\)
Choose the correct answer from the options given below:
View Solution
1. Correct expressions for torque:
- B. \(\ddot{\tau}=\frac{\mathrm{d}}{\mathrm{dt}}(\ddot{\mathrm{r}} \times \ddot{\mathrm{p}})\)
- C. \(\ddot{\tau}=\ddot{\mathrm{r}} \times \frac{\mathrm{d} \dot{\mathrm{p}}}{\mathrm{dt}}\)
- D. \(\ddot{\tau}=\mathrm{I} \dot{\alpha}\)
- E. \(\ddot{\tau}=\ddot{\mathrm{r}} \times \ddot{\mathrm{F}}\)
Therefore, the correct answer is (3) B, C, D and E Only. Quick Tip: Torque can be expressed in terms of position vector, linear momentum, angular momentum, and force.
In a Young's double slit experiment, the slits are separated by 0.2 mm. If the slits separation is increased to 0.4 mm, the percentage change of the fringe width is:
View Solution
1. Fringe width formula:
\[ \beta = \frac{D \lambda}{d} \]
2. Percentage change of fringe width:
- If \(d\) is doubled, \(\beta\) is halved.
- Therefore, the percentage change is \(50%\).
Therefore, the correct answer is (3) \(50 %\). Quick Tip: The fringe width is inversely proportional to the slit separation.
An alternating current is represented by the equation, \(\mathrm{i}=100 \sqrt{2} \sin (100 \pi \mathrm{t})\) ampere. The RMS value of current and the frequency of the given alternating current are
View Solution
1. RMS value of current:
\[ i_{rms} = \frac{i_0}{\sqrt{2}} = 100 \mathrm{~A} \]
2. Frequency of the current:
\[ f = \frac{\omega}{2\pi} = \frac{100\pi}{2\pi} = 50 \mathrm{~Hz} \]
Therefore, the correct answer is (3) \(100 \mathrm{~A}, 50 \mathrm{~Hz}\). Quick Tip: The RMS value of an alternating current is given by the peak value divided by \(\sqrt{2}\).
Consider the sound wave travelling in ideal gases of \(\mathrm{He}, \mathrm{CH}_{4}\), and \(\mathrm{CO}_{2}\). All the gases have the same ratio \(\frac{\mathrm{P}}{\rho}\), where P is the pressure and \(\rho\) is the density. The ratio of the speed of sound through the gases \(\mathrm{v}_{\mathrm{He}}: \mathrm{v}_{\mathrm{CH}_{4}}: \mathrm{v}_{\mathrm{CO}_{2}}\) is given by
View Solution
1. Speed of sound formula:
\[ v_{sound} = \sqrt{\frac{\gamma P}{\rho}} \]
2. Ratio of specific heats (\(\gamma\)):
- \(\gamma_{\mathrm{He}} = \frac{5}{3}\)
- \(\gamma_{\mathrm{CH}_{4}} \approx \frac{4}{3}\)
- \(\gamma_{\mathrm{CO}_{2}} \approx \frac{4}{3}\)
3. Ratio of speeds of sound:
\[ \sqrt{\frac{5}{3}}: \sqrt{\frac{4}{3}}: \sqrt{\frac{4}{3}} \]
Therefore, the correct answer is (3) \(\sqrt{\frac{5}{3}}: \sqrt{\frac{4}{3}}: \sqrt{\frac{4}{3}}\). Quick Tip: The speed of sound in a gas depends on the ratio of specific heats (\(\gamma\)).
In an electromagnetic system, the quantity representing the ratio of electric flux and magnetic flux has dimension of \(\mathrm{M}^{\mathrm{B}} \mathrm{L}^{\mathrm{O}} \mathrm{T}^{\mathrm{B}} \mathrm{A}^{\mathrm{S}}\), where value of 'Q' and 'R' are
View Solution
1. Dimensions of electric flux (\(\phi_E\)) and magnetic flux (\(\phi_M\)):
\[ \phi_E = EA \quad and \quad \phi_M = BA \]
2. Ratio of electric flux to magnetic flux:
\[ \frac{\phi_E}{\phi_M} = \frac{E}{B} \]
3. Dimensions of \(\frac{E}{B}\):
\[ \left[ \frac{E}{B} \right] = \frac{[E]}{[B]} = \frac{MLT^{-2}A^{-1}}{MT^{-2}A^{-1}} = LT^{-1} \]
4. Dimensions of \(\frac{E}{B}\):
\[ \left[ \frac{E}{B} \right] = LT^{-1} \]
Therefore, the correct answer is (4) \((1,-1)\). Quick Tip: The ratio of electric flux to magnetic flux has dimensions of \(LT^{-1}\).
When an object is placed 40 cm away from a spherical mirror an image of magnification \(\frac{1}{2}\) is produced. To obtain an image with magnification of \(\frac{1}{3}\), the object is to be moved:
View Solution
1. Given:
- Object distance, \(u = -40 \mathrm{~cm}\)
- Magnification, \(m = \frac{1}{2}\)
2. Magnification formula:
\[ m = \frac{f}{f - u} \]
\[ \frac{1}{2} = \frac{f}{f - (-40)} \]
\[ f + 40 = 2f \implies f = 40 \mathrm{~cm} \]
3. For magnification \(\frac{1}{3}\):
\[ \frac{1}{3} = \frac{40}{40 - u} \]
\[ 40 - u = 120 \implies u = -80 \mathrm{~cm} \]
Therefore, the correct answer is (1) 40 cm away from the mirror. Quick Tip: Use the magnification formula to find the object distance.
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R. Assertion A: In photoelectric effect, on increasing the intensity of incident light the stopping potential increases. Reason R: Increase in intensity of light increases the rate of photoelectrons emitted, provided the frequency of incident light is greater than threshold frequency.
View Solution
1. Assertion A:
- The stopping potential does not depend on the intensity of light.
- Therefore, Assertion A is false.
2. Reason R:
- Increasing the intensity of light increases the rate of photoelectrons emitted.
- Therefore, Reason R is true.
Therefore, the correct answer is (2) \(\mathbf{A}\) is false but \(\mathbf{R}\) is true. Quick Tip: The stopping potential in the photoelectric effect does not depend on the intensity of light.
If \(\overrightarrow{\mathrm{L}}\) and \(\overrightarrow{\mathrm{P}}\) represent the angular momentum and linear momentum respectively of a particle of mass ' \(m\) ' having position vector \(\overrightarrow{\mathrm{r}}=\mathrm{a}(\hat{\mathrm{i}} \cos \omega \mathrm{t}+\hat{\mathrm{j}} \sin \omega \mathrm{t})\). The direction of force is
View Solution
1. Position vector:
\[ \overrightarrow{\mathrm{r}} = \mathrm{a}(\hat{\mathrm{i}} \cos \omega \mathrm{t} + \hat{\mathrm{j}} \sin \omega \mathrm{t}) \]
2. Acceleration:
\[ \overrightarrow{\mathrm{a}} = -\omega^2 \overrightarrow{\mathrm{r}} \]
3. Force:
\[ \overrightarrow{\mathrm{F}} = m \overrightarrow{\mathrm{a}} = -m \omega^2 \overrightarrow{\mathrm{r}} \]
Therefore, the direction of force is opposite to the direction of \(\overrightarrow{\mathrm{r}}\). Quick Tip: The force is proportional to the acceleration, which is opposite to the position vector in this case.
A body of mass \(m\) is suspended by two strings making angles \(\theta_{1}\) and \(\theta_{2}\) with the horizontal ceiling with tensions \(\mathrm{T}_{1}\) and \(\mathrm{T}_{2}\) simultaneously. \(\mathrm{T}_{1}\) and \(\mathrm{T}_{2}\) are related by \(\mathrm{T}_{1}=\sqrt{3} \mathrm{~T}_{2}\). the angles \(\theta_{1}\) and \(\theta_{2}\) are
View Solution
1. Given:
\[ \mathrm{T}_{1} \sin \theta_{1} + \mathrm{T}_{2} \sin \theta_{2} = \mathrm{mg} \]
\[ \mathrm{T}_{1} = \sqrt{3} \mathrm{~T}_{2} \]
2. Substitute \(\mathrm{T}_{1}\):
\[ \sqrt{3} \mathrm{~T}_{2} \sin \theta_{1} + \mathrm{T}_{2} \sin \theta_{2} = \mathrm{mg} \]
\[ \mathrm{T}_{2} (\sqrt{3} \sin \theta_{1} + \sin \theta_{2}) = \mathrm{mg} \]
3. For \(\theta_{1} = 60^{\circ}\) and \(\theta_{2} = 30^{\circ}\):
\[ \mathrm{T}_{2} (\sqrt{3} \cdot \frac{\sqrt{3}}{2} + \frac{1}{2}) = \mathrm{mg} \]
\[ \mathrm{T}_{2} = \frac{\mathrm{mg}}{2} \]
Therefore, the correct answer is (2) \(\theta_{1}=60^{\circ} \theta_{2}=30^{\circ}\) with \(\mathrm{T}_{2}=\frac{\mathrm{mg}}{2}\). Quick Tip: Use the equilibrium condition to find the tensions and angles.
Current passing through a wire as function of time is given as \(I(t)=0.02 \mathrm{t}+0.01 \mathrm{~A}\). The charge that will flow through the wire from \(t=1 \mathrm{~s}\) to \(\mathrm{t}=2 \mathrm{~s}\) is:
View Solution
1. Charge calculation:
\[ q = \int I(t) dt \]
\[ q = \int_{1}^{2} (0.02t + 0.01) dt \]
\[ q = \left[ 0.02 \frac{t^2}{2} + 0.01t \right]_{1}^{2} \]
\[ q = \left[ 0.01(4) + 0.01(2) \right] - \left[ 0.01(1) + 0.01(1) \right] \]
\[ q = 0.04 \mathrm{~C} \]
Therefore, the correct answer is (4) 0.04 C. Quick Tip: Integrate the current function to find the charge.
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R. Assertion A: The kinetic energy needed to project a body of mass \(m\) from earth surface to infinity is \(\frac{1}{2} \mathrm{mgR}\), where R is the radius of earth. Reason R: The maximum potential energy of a body is zero when it is projected to infinity from earth surface.
View Solution
1. Assertion A:
- The kinetic energy needed to project a body of mass \(m\) from earth surface to infinity is \(\frac{1}{2} \mathrm{mgR}\).
- This is incorrect.
2. Reason R:
- The maximum potential energy of a body is zero when it is projected to infinity from earth surface.
- This is correct.
Therefore, the correct answer is (1) A False but \(\mathbf{R}\) is true. Quick Tip: The kinetic energy needed to project a body to infinity is equal to the potential energy at the earth's surface.
The Boolean expression \(\mathrm{Y}=\mathrm{A} \overline{\mathrm{B}} \mathrm{C}+\overline{\mathrm{AC}}\) can be realised with which of the following gate configurations.
A. One 3-input AND gate, 3 NOT gates and one 2-input OR gate, One 2-input AND gate
B. One 3-input AND gate, 1 NOT gate, One 2-input NOR gate and one 2-input OR gate
C. 3-input OR gate, 3 NOT gates and one 2-input AND gate
Choose the correct answer from the options given below:
View Solution
1. Boolean expression:
\[ Y = A \overline{B} C + \overline{AC} \]
2. Gate configurations:
- A. One 3-input AND gate, 3 NOT gates and one 2-input OR gate, One 2-input AND gate
- B. One 3-input AND gate, 1 NOT gate, One 2-input NOR gate and one 2-input OR gate
Therefore, the correct answer is (2) A,B Only. Quick Tip: Use the Boolean expression to determine the correct gate configurations.
Two simple pendulums having lengths \(l_{1}\) and \(l_{2}\) with negligible string mass undergo angular displacements \(\theta_{1}\) and \(\theta_{2}\), from their mean positions, respectively. If the angular accelerations of both pendulums are same, then which expression is correct?
View Solution
1. Angular acceleration:
\[ \alpha = -\omega^2 \theta \]
\[ \omega = \sqrt{\frac{g}{l}} \]
2. Equating angular accelerations:
\[ \frac{g}{l_1} \theta_1 = \frac{g}{l_2} \theta_2 \]
\[ \theta_1 l_2 = \theta_2 l_1 \]
Therefore, the correct answer is (4) \(\theta_{1} l_{2}=\theta_{2} l_{1}\). Quick Tip: The angular acceleration of a pendulum depends on its length and angular displacement.
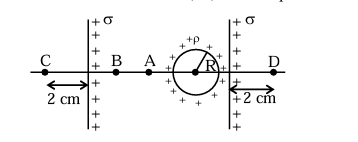
Two infinite identical charged sheets and a charged spherical body of charge density ' \(\rho\) ' are arranged as shown in figure. Then the correct relation between the electrical fields at \(\mathrm{A}, \mathrm{B}, \mathrm{C}\) and D points is:
View Solution
1. Electric field at points A and B:
- \(\vec{E}_{A} > \vec{E}_{B}\)
2. Electric field at points C and D:
- \(\vec{E}_{C} \neq \vec{E}_{D}\)
Therefore, the correct answer is (3) \(\vec{E}_{C} \neq \vec{E}_{D} ; \vec{E}_{A}>\vec{E}_{B}\). Quick Tip: The electric field depends on the arrangement and charge density of the sheets and spherical body.
Two small spherical balls of mass 10 g each with charges \(-2 \mu \mathrm{C}\) and \(2 \mu \mathrm{C}\), are attached to two ends of very light rigid rod of length 20 cm. The arrangement is now placed near an infinite nonconducting charge sheet with uniform charge density of \(100 \mu \mathrm{C} / \mathrm{m}^{2}\) such that length of rod makes an angle of \(30^{\circ}\) with electric field generated by charge sheet. Net torque acting on the rod is:
View Solution
1. Electric field due to the charge sheet:
\[ E = \frac{\sigma}{2 \epsilon_0} \]
2. Torque acting on the rod:
\[ \tau = PE \sin \theta \]
\[ \tau = \left[ 2 \times 10^{-6} \times \frac{2}{10} \right] \left[ \frac{100 \times 10^{-6}}{2 \times 8.85 \times 10^{-12}} \right] \frac{1}{2} \]
\[ \tau = \frac{10}{8.85} = 1.12 \mathrm{~Nm} \]
Therefore, the correct answer is (2) 1.12 Nm. Quick Tip: The torque acting on a dipole in an electric field is given by the product of the dipole moment and the electric field.
Considering the Bohr model of hydrogen like atoms, the ratio of the radius \(5^{\text {th }}\) orbit of the electron in \(\mathrm{Li}^{2+}\) and \(\mathrm{He}^{+}\)is
View Solution
1. Radius of the \(5^{th}\) orbit for \(\mathrm{Li}^{2+}\):
\[ r_{5} = \frac{5^2}{3} a_0 \]
2. Radius of the \(5^{th}\) orbit for \(\mathrm{He}^{+}\):
\[ r_{5} = \frac{5^2}{2} a_0 \]
3. Ratio of the radii:
\[ \frac{r_{\mathrm{Li}^{2+}}}{r_{\mathrm{He}^{+}}} = \frac{2}{3} \]
Therefore, the correct answer is (4) \(\frac{2}{3}\). Quick Tip: The radius of an orbit in the Bohr model depends on the principal quantum number and the atomic number.
A circular ring and a solid sphere having same radius roll down on an inclined plane from rest without slipping. The ratio of their velocities when reached at the bottom of the plane is \(\sqrt{\frac{\mathrm{x}}{5}}\) where \(\mathrm{x}=\) _______.
View Solution
1. Mechanical energy conservation:
\[ K_i + U_i = K_f + U_f \]
\[ 0 + Mgh = \frac{1}{2} mv^2 \left(1 + \frac{k^2}{R^2}\right) + 0 \]
\[ v = \sqrt{\frac{2gh}{1 + \frac{k^2}{R^2}}} \]
2. Ratio of velocities:
\[ \frac{v_{ring}}{v_{solid sphere}} = \sqrt{\frac{1 + \frac{2}{5}}{1 + 1}} = \sqrt{\frac{7}{10}} \]
\[ x = 3.5 \approx 4 \]
Therefore, the correct answer is (4) 4. Quick Tip: Use mechanical energy conservation to find the velocities of the ring and the solid sphere.
Two slabs with square cross section of different materials \((1,2)\) with equal sides \((l)\) and thickness \(\mathrm{d}_{1}\) and \(\mathrm{d}_{2}\) such that \(\mathrm{d}_{2}=2 \mathrm{~d}_{1}\) and \(l>\mathrm{d}_{2}\). Considering lower edges of these slabs are fixed to the floor, we apply equal shearing force on the narrow faces. The angle of deformation is \(\theta_{2}=2 \theta_{1}\). If the shear moduli of material 1 is \(4 \times 10^{9} \mathrm{~N} / \mathrm{m}^{2}\), then shear moduli of material 2 is \(\mathrm{x} \times 10^{9} \mathrm{~N} / \mathrm{m}^{2}\), where value of x is _______ .
View Solution
1. Deformation angle:
\[ 2 \theta_{1} = \theta_{2} \]
\[ 2 \frac{\sigma_{1}}{\eta_{1}} = \frac{\sigma_{2}}{\eta_{2}} \]
\[ 2 \left( \frac{F}{l d_{1} \eta_{1}} \right) = \frac{F}{l d_{2} \eta_{2}} \]
\[ \eta_{2} = \frac{\eta_{1}}{4} = 1 \times 10^{9} \]
\[ x = 1 \]
Therefore, the correct answer is (1) 1. Quick Tip: Use the deformation angle to find the shear modulus of the material.
Distance between object and its image (magnified by \(-\frac{1}{3}\) ) is 30 cm. The focal length of the mirror used is \(\left(\frac{\mathrm{x}}{4}\right) \mathrm{cm}\), where magnitude of value of x is _______ .
View Solution
1. Given:
\[ m = -\frac{1}{3} \]
\[ -\frac{v}{u} = \frac{1}{3} \implies v = \frac{u}{3} \]
2. Distance between object and image:
\[ u - v = 30 \mathrm{~cm} \]
\[ u - \frac{u}{3} = 30 \implies u = 45 \mathrm{~cm}, \quad v = 15 \mathrm{~cm} \]
3. Focal length:
\[ \frac{1}{f} = \frac{1}{v} + \frac{1}{u} = \frac{1}{15} + \frac{1}{45} = \frac{4}{60} \]
\[ f = \frac{60}{4} = 15 \mathrm{~cm} \]
\[ x = 45 \]
Therefore, the correct answer is (45). Quick Tip: Use the magnification formula to find the object and image distances, then calculate the focal length.
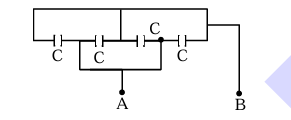
Four capacitors each of capacitance \(16\,\mu F\) are connected as shown in the figure. The capacitance between points A and B is: \underline{\hspace{1cm (in \(\mu F\)).
View Solution
1. Redraw the circuit:
- The capacitors are connected in parallel.
2. Equivalent capacitance:
\[ C_{eq} = 4C = 4 \times 16 \mu \mathrm{F} = 64 \mu \mathrm{F} \]
Therefore, the correct answer is (64) \(64 \mu \mathrm{F}\). Quick Tip: Use the parallel connection of capacitors to find the equivalent capacitance.
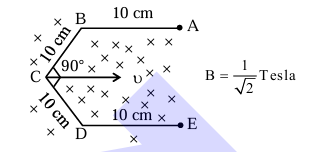
Conductor wire ABCDE with each arm 10 cm in length is placed in magnetic field of \(\frac{1}{\sqrt{2}}\) Tesla, perpendicular to its plane. When conductor is pulled towards right with constant velocity of \(10 \mathrm{~cm} / \mathrm{s}\), induced emf between points A and E is _______ mV.
View Solution
1. Induced emf:
\[ \varepsilon = Bv \ell_{\mathrm{AB}} \]
\[ \varepsilon = \frac{1}{\sqrt{2}} \times \frac{10 \mathrm{~cm}}{s} \times 2 \left( 10 \sin 45^{\circ} \right) \mathrm{cm} \]
\[ \varepsilon = 10 \mathrm{~mV} \]
Therefore, the correct answer is (10) 10 mV. Quick Tip: Use Faraday's law to calculate the induced emf.
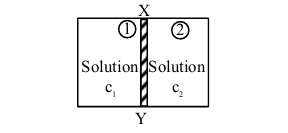
\(XY\) is the membrane / partition between two chambers 1 and 2 containing sugar solutions of concentration \(\mathrm{c}_{1}\) and \(\mathrm{c}_{2}\left(\mathrm{c}_{1}>\mathrm{c}_{2}\right) \mathrm{mol} \mathrm{L}^{-1}\). For the reverse osmosis to take place identify the correct condition
(Here \(\mathrm{p}_{1}\) and \(\mathrm{p}_{2}\) are pressures applied on chamber 1 and 2 )
View Solution
1. Normal osmosis occurs from chamber 2 to chamber 1.
2. For reverse osmosis from chamber 1 to chamber 2, the pressure \(\mathrm{p}_{1}\) must be greater than the osmotic pressure \(\pi\).
3. Therefore, the correct conditions are A and C.
Therefore, the correct answer is (3) A and C only. Quick Tip: Reverse osmosis requires the pressure in the chamber with higher concentration to be greater than the osmotic pressure.
Let us consider a reversible reaction at temperature, T . In this reaction, both \(\Delta \mathrm{H}\) and \(\Delta \mathrm{S}\) were observed to have positive values. If the equilibrium temperature is \(\mathrm{T}_{\mathrm{e}}\), then the reaction becomes spontaneous at:
View Solution
1. For a reaction to be spontaneous, \(\Delta \mathrm{G} < 0\).
\[ \Delta \mathrm{G} = \Delta \mathrm{H} - \mathrm{T} \Delta \mathrm{S} \]
2. Given that both \(\Delta \mathrm{H}\) and \(\Delta \mathrm{S}\) are positive:
\[ \Delta \mathrm{G} = \Delta \mathrm{H} - \mathrm{T} \Delta \mathrm{S} < 0 \]
\[ \mathrm{T} > \frac{\Delta \mathrm{H}}{\Delta \mathrm{S}} = \mathrm{T}_{\mathrm{e}} \]
Therefore, the correct answer is (3) \(\mathrm{T}>\mathrm{T}_{\mathrm{e}}\). Quick Tip: A reaction is spontaneous when the Gibbs free energy change is negative.
Which of the following molecules(s) show/s paramagnetic behavior?
View Solution
1. Number of unpaired electrons:
- (A) \(\mathrm{O}_{2}\): 2
- (B) \(\mathrm{N}_{2}\): 0
- (C) \(\mathrm{F}_{2}\): 0
- (D) \(\mathrm{S}_{2}\): 2
- (E) \(\mathrm{Cl}_{2}\): 0
2. Paramagnetic behavior:
- Molecules with unpaired electrons exhibit paramagnetic behavior.
- Therefore, \(\mathrm{O}_{2}\) and \(\mathrm{S}_{2}\) are paramagnetic.
Therefore, the correct answer is (4) A \& D only. Quick Tip: Molecules with unpaired electrons are paramagnetic.
Aldol condensation is a popular and classical method to prepare \(\alpha, \beta\)-unsaturated carbonyl compounds. This reaction can be both intermolecular and intramolecular. Predict which one of the following is not a product of intramolecular aldol condensation?
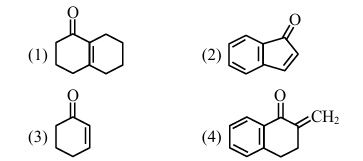
View Solution
1. Intramolecular aldol condensation products:
- (1), (2), and (3) are products of intramolecular aldol condensation.
- (4) is a product of intermolecular aldol condensation.
Therefore, the correct answer is (4). Quick Tip: Intramolecular aldol condensation involves the reaction within the same molecule, while intermolecular aldol condensation involves the reaction between two different molecules.
One mole of an ideal gas expands isothermally and reversibly from \(10 \mathrm{dm}^{3}\) to \(20 \mathrm{dm}^{3}\) at \(300 \mathrm{~K} . \Delta \mathrm{U}\), q and work done in the process respectively are :
Given : \(\mathrm{R}=8.3 \mathrm{JK}^{-1}\) and \(\mathrm{mol}^{-1}\)
In \(10=2.3\)
\(\log 2=0.30\)
\(\log 3=0.48\)
View Solution
1. Given:
- Isothermal expansion from \(10 \mathrm{dm}^{3}\) to \(20 \mathrm{dm}^{3}\) at \(300 \mathrm{~K}\).
- \(\mathrm{R} = 8.3 \mathrm{JK}^{-1} \mathrm{mol}^{-1}\).
2. Calculate the work done (w):
\[ w = -nRT \ln \frac{V_2}{V_1} \]
\[ w = -8.3 \times 300 \times \ln \left( \frac{20}{10} \right) \]
\[ w = -1.718 \mathrm{~kJ} \]
3. Calculate the heat transferred (q):
\[ q = -w = 1.718 \mathrm{~kJ} \]
4. Calculate the change in internal energy (\(\Delta U\)):
\[ \Delta U = 0 \quad (since \Delta T = 0) \]
Therefore, the correct answer is (4) \(0,178 \mathrm{~kJ},-1.718 \mathrm{~kJ}\). Quick Tip: For an isothermal process, the change in internal energy is zero.
Which one of the following complexes will have \(\Delta_{0}=0\) and \(\mu=5.96\) B.M.?
View Solution
1. \(\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]^{4}\):
- \(\mathrm{Fe}^{2+} \Rightarrow 3 \mathrm{~d}^{6} 4 \mathrm{~s}^{0}\)
- \(\mathrm{CN}^{-}\) is a strong field ligand.
- \(\mu = 0\)
2. \(\left[\mathrm{CO}\left(\mathrm{NH}_{3}\right)_{6}\right]^{3+}\):
- \(\mathrm{Co}^{3+} \Rightarrow 3 \mathrm{~d}^{6} 4 \mathrm{~s}^{0}\)
- \(\mathrm{NH}_{3}\) is a strong field ligand.
- \(\mu = 0\)
3. \(\left[\mathrm{FeF}_{6}\right]^{4}\):
- \(\mathrm{Fe}^{2+} \Rightarrow 3 \mathrm{~d}^{6} 4 \mathrm{~s}^{0}\)
- \(\mathrm{F}^{-}\) is a weak field ligand.
- \(\mu = 0\)
4. \(\left[\mathrm{Mn}(\mathrm{SCN})_{6}\right]^{4}\):
- \(\mathrm{Mn}^{2+} \Rightarrow 3 \mathrm{~d}^{5} 4 \mathrm{~s}^{0}\)
- \(\mathrm{SCN}^{-}\) is a weak field ligand.
- \(\mu = \sqrt{35} \mathrm{~BM} = 5.96 \mathrm{~BM}\)
- \(\Delta_{0} = 0\)
Therefore, the correct answer is (4) \(\left[\mathrm{Mn}(\mathrm{SCN})_{6}\right]^{4}\). Quick Tip: The magnetic moment and crystal field stabilization energy depend on the ligand field strength.
For \(\mathrm{A}_{2}+\mathrm{B}_{2} \rightleftharpoons 2 \mathrm{AB}\) \(\mathrm{E}_{\mathrm{a}}\) for forward and backward reaction are 180 and \(200 \mathrm{~kJ} \mathrm{~mol}^{-1}\) respectively. If catalyst lowers \(\mathrm{E}_{\mathrm{a}}\) for both reaction by \(100 \mathrm{~kJ} \mathrm{~mol}^{-1}\). Which of the following statement is correct?
View Solution
1. Given:
- \(\mathrm{A}_{2}+\mathrm{B}_{2} \rightleftharpoons 2 \mathrm{AB}\)
- \(\mathrm{E}_{\mathrm{f}} = 180 \mathrm{~kJ} \mathrm{~mol}^{-1}\)
- \(\mathrm{E}_{\mathrm{b}} = 200 \mathrm{~kJ} \mathrm{~mol}^{-1}\)
2. Calculate the enthalpy change (\(\Delta \mathrm{H}\)):
\[ \Delta \mathrm{H} = \mathrm{E}_{\mathrm{f}} - \mathrm{E}_{\mathrm{b}} = 180 \mathrm{~kJ} \mathrm{~mol}^{-1} - 200 \mathrm{~kJ} \mathrm{~mol}^{-1} = -20 \mathrm{~kJ} \mathrm{~mol}^{-1} \]
3. Effect of catalyst:
- Catalyst lowers the activation energy but does not change the Gibbs free energy change (\(\Delta \mathrm{G}\)) or the enthalpy change (\(\Delta \mathrm{H}\)) of the reaction.
Therefore, the correct answer is (1) Catalyst does not alter the Gibbs energy change of a reaction. Quick Tip: Catalysts lower the activation energy but do not change the thermodynamic properties of the reaction.
Rate law for a reaction between \(A\) and \(B\) is given by \(\mathrm{R}=\mathrm{k}[\mathrm{A}]^{\mathrm{n}}[\mathrm{B}]^{\mathrm{m}}\). If concentration of A is doubled and concentration of B is halved from their initial value, the ratio of new rate of reaction to the initial rate of reaction \(\left(\frac{\mathrm{r}_{2}}{\mathrm{r}_{1}}\right)\) is
View Solution
1. Initial rate law:
\[ \mathrm{r}_{1} = \mathrm{k}[\mathrm{A}]^{\mathrm{n}}[\mathrm{B}]^{\mathrm{m}} \]
2. New concentrations:
- Concentration of A is doubled: \(2[\mathrm{A}]\)
- Concentration of B is halved: \(\frac{[\mathrm{B}]}{2}\)
3. New rate law:
\[ \mathrm{r}_{2} = \mathrm{k}(2[\mathrm{A}])^{\mathrm{n}} \left( \frac{[\mathrm{B}]}{2} \right)^{\mathrm{m}} \]
\[ \mathrm{r}_{2} = \mathrm{k} \cdot 2^{\mathrm{n}} [\mathrm{A}]^{\mathrm{n}} \cdot \frac{[\mathrm{B}]^{\mathrm{m}}}{2^{\mathrm{m}}} \]
4. Ratio of new rate to initial rate:
\[ \frac{\mathrm{r}_{2}}{\mathrm{r}_{1}} = \frac{\mathrm{k} \cdot 2^{\mathrm{n}} [\mathrm{A}]^{\mathrm{n}} \cdot \frac{[\mathrm{B}]^{\mathrm{m}}}{2^{\mathrm{m}}}}{\mathrm{k}[\mathrm{A}]^{\mathrm{n}}[\mathrm{B}]^{\mathrm{m}}} = 2^{\mathrm{n}} \cdot \frac{1}{2^{\mathrm{m}}} = 2^{(\mathrm{n}-\mathrm{m})} \]
Therefore, the correct answer is (1) \(2^{(\mathrm{n}-\mathrm{m})}\). Quick Tip: The rate law depends on the concentrations of the reactants raised to their respective orders.
Number of stereoisomers possible for the complexes, \(\left[\mathrm{CrCl}_{3}(\mathrm{py})_{3}\right]\) and \(\left[\mathrm{CrCl}_{2}(\mathrm{ox})_{2}\right]^{3-}\) are respectively
(py = pyridine, ox = oxalate)
View Solution
1. \(\left[\mathrm{CrCl}_{3}(\mathrm{py})_{3}\right]\):
- Facial and meridional isomers are possible.
- Total stereoisomers = 2.
2. \(\left[\mathrm{CrCl}_{2}(\mathrm{ox})_{2}\right]^{3-}\):
- Geometrical isomers: cis and trans.
- Optical isomers for cis: 2.
- Optical isomers for trans: 1.
- Total stereoisomers = 3.
Therefore, the correct answer is (3) \(2 \& 3\). Quick Tip: Stereoisomers include geometrical and optical isomers.
The major product (A) formed in the following reaction sequence is
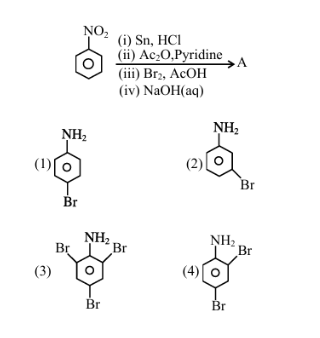
View Solution
1. Reaction sequence:
- The major product formed is (2).
Therefore, the correct answer is (2). Quick Tip: Follow the reaction sequence to determine the major product.
On charging the lead storage battery, the oxidation state of lead changes from \(\mathrm{x}_{1}\) to \(\mathrm{y}_{1}\) at the anode and from \(\mathrm{x}_{2}\) to \(\mathrm{y}_{2}\) at the cathode. The values of \(\mathrm{x}_{1}, \mathrm{y}_{1}, \mathrm{x}_{2}, \mathrm{y}_{2}\) are respectively:
View Solution
1. Anode reaction:
- \(\mathrm{PbSO}_{4}\) is reduced to \(\mathrm{Pb}\).
- \(\mathrm{Pb}^{2+} \rightarrow \mathrm{Pb}^{0}\)
- \(\mathrm{x}_{1} = +2\), \(\mathrm{y}_{1} = 0\)
2. Cathode reaction:
- \(\mathrm{PbSO}_{4}\) is oxidized to \(\mathrm{PbO}_{2}\).
- \(\mathrm{Pb}^{2+} \rightarrow \mathrm{Pb}^{4+}\)
- \(\mathrm{x}_{2} = +2\), \(\mathrm{y}_{2} = +4\)
Therefore, the correct answer is (2) \(+2,0,+2,+4\). Quick Tip: The oxidation states change during the charging of a lead-acid battery.
Given below are two statements:
Statement I: Nitrogen forms oxides with +1 to +5 oxidation states due to the formation of \(\mathrm{p} \pi-\mathrm{p} \pi\) bond with oxygen.
Statement II: Nitrogen does not form halides with +5 oxidation state due to the absence of d-orbital in it.
In the light of the above statements, choose the correct answer from the options given below:
View Solution
1. Statement I:
- Nitrogen can form oxides with oxidation states from +1 to +5 due to the formation of \(\mathrm{p} \pi-\mathrm{p} \pi\) bonds with oxygen.
- This statement is true.
2. Statement II:
- Nitrogen does not form halides with a +5 oxidation state due to the absence of d-orbitals.
- This statement is true.
Therefore, the correct answer is (4) Both Statement I and Statement II are true. Quick Tip: Nitrogen's ability to form oxides and halides depends on its electronic configuration and the availability of d-orbitals.
Benzene is treated with oleum to produce compound (X) which when further heated with molten sodium hydroxide followed by acidification produces compound (Y).The compound Y is treated with zinc metal to produce compound (Z). Identify the structure of compound (Z) from the following option.
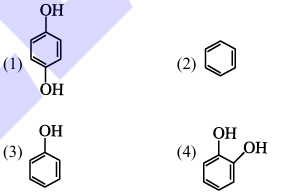
View Solution
1. Reaction sequence:
- Benzene treated with oleum produces benzene sulfonic acid (X).
- Heating with molten sodium hydroxide followed by acidification produces phenol (Y).
- Treatment with zinc metal reduces phenol to cyclohexanol (Z).
Therefore, the correct answer is (2). Quick Tip: Follow the reaction sequence to identify the final product.
Identify the pair of reactants that upon reaction, with elimination of HCl will give rise to the dipeptide Gly-Ala.
View Solution
1. Reactants:
- \(\mathrm{NH}_{2}-\mathrm{CH}_{2}-\mathrm{COCl}\) (Glycine chloride)
- \(\mathrm{NH}_{2}-\mathrm{CH}-\mathrm{COOH}\) (Alanine)
2. Reaction:
- The reaction between these reactants with the elimination of HCl will produce the dipeptide Gly-Ala.
Therefore, the correct answer is (1) \(\mathrm{NH}_{2}-\mathrm{CH}_{2}-\mathrm{COCl}\) and \(\mathrm{NH}_{2}-\mathrm{CH}-\mathrm{COOH}\). Quick Tip: The formation of a dipeptide involves the reaction between an amino acid and its chloride derivative with the elimination of HCl.
Given below are the pairs of group 13 elements showing their relation in terms of atomic radius. \((\mathrm{B}<\mathrm{Al}),(\mathrm{Al}<\mathrm{Ga}),(\mathrm{Ga}<\mathrm{In})\) and \((\mathrm{In}<\mathrm{Tl})\) Identify the elements present in the incorrect pair and in that pair find out the element (X) that has higher ionic radius \(\left(\mathrm{M}^{3+}\right)\) than the other one. The atomic number of the element (X) is
View Solution
1. Incorrect pair:
- \(\mathrm{Al}<\mathrm{Ga}\)
2. Ionic radius comparison:
- \(\mathrm{Al}^{3+}<\mathrm{Ga}^{3+}\)
- The atomic number of \(\mathrm{Ga}\) is 31.
Therefore, the correct answer is (1) 31. Quick Tip: The atomic radius and ionic radius depend on the atomic number and the periodic trends.
An organic compound (X) with molecular formula \(\mathrm{C}_{3} \mathrm{H}_{6} \mathrm{O}\) is not readily oxidised. On reduction it gives \(\left(\mathrm{C}_{3} \mathrm{H}_{8} \mathrm{O}(\mathrm{Y})\right.\) which reacts with HBr to give a bromide (Z) which is converted to Grignard reagent. This Grignard reagent on reaction with (X) followed by hydrolysis give 2,3-dimethylbutan-2-ol. Compounds (X), (Y) and (Z) respectively are:
View Solution
1. Compound (X):
- \(\mathrm{CH}_{3} \mathrm{COCH}_{3}\) (Acetone)
2. Reduction to (Y):
- \(\mathrm{CH}_{3} \mathrm{CH}(\mathrm{OH}) \mathrm{CH}_{3}\) (Isopropyl alcohol)
3. Reaction with HBr to form (Z):
- \(\mathrm{CH}_{3} \mathrm{CH}(\mathrm{Br}) \mathrm{CH}_{3}\) (2-Bromopropane)
4. Grignard reagent and reaction with (X):
- The Grignard reagent formed from (Z) reacts with acetone to form 2,3-dimethylbutan-2-ol after hydrolysis.
Therefore, the correct answer is (2) \(\mathrm{CH}_{3} \mathrm{COCH}_{3}, \mathrm{CH}_{3} \mathrm{CH}(\mathrm{OH}) \mathrm{CH}_{3}, \mathrm{CH}_{3} \mathrm{CH}(\mathrm{Br}) \mathrm{CH}_{3}\). Quick Tip: Follow the reaction sequence to identify the compounds involved.
Predict the major product of the following reaction sequence:
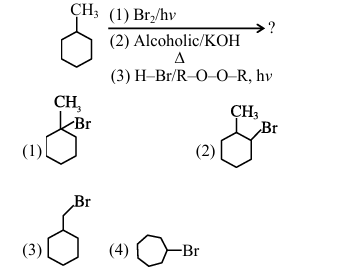
View Solution
% Option
(A) Step 1: Bromination (Br\(_2\)/hv)
\[\ce{CH3 ->[Br2/hv] CH2Br}\]
% Option
(B) Step 2: Elimination (Alcoholic KOH)
\[\ce{CH2Br ->[Alc. KOH][\Delta] CH2=}\]
% Option
(C) Step 3: Anti-Markovnikov addition (HBr/ROOR)
\[\ce{CH2= ->[HBr/ROOR][hv] Br-CH3}\]
Mechanistic Explanation:
Free radical bromination converts methyl to bromomethyl
Elimination forms methylene intermediate
Peroxide effect gives anti-Markovnikov product
Therefore, the correct answer is \boxed{(2) \ce{Br-CH3. Quick Tip: Key Points: Radical bromination prefers allylic position Alcoholic KOH causes elimination ROOR reverses normal addition orientation
Given below are two statements.
In the light of the above statements, choose the correct answer from the options given below:

View Solution
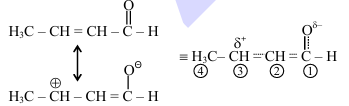
1. Analysis of Statement I:
For \chemfig{CH_3-CH=CH-CH=O: \(\mu = q \times d\)
Conjugated system creates greater charge separation
More distance between charges than in saturated compound
Therefore, greater dipole moment
Statement I is TRUE
2. Analysis of Statement II:
In \chemfig{CH_3-CH=CH-CH=O, \(C_1-C_2\) has partial double bond character
Double bond character means shorter bond length
Compared to pure single bond in \chemfig{CH_3-CH_2-CH_2-CH=O
Statement II is FALSE (actual bond length is shorter) Quick Tip: Key concepts: Dipole moment depends on charge magnitude and separation distance Conjugation affects both electronic distribution and bond lengths Partial double bond character decreases bond length
Pair of transition metal ions having the same number of unpaired electrons is :
View Solution
1. \(\mathrm{V}^{2+}\):
- \(\mathrm{V}^{2+} \Rightarrow 3 \mathrm{~d}^{3} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 3
2. \(\mathrm{Co}^{2+}\):
- \(\mathrm{Co}^{2+} \Rightarrow 3 \mathrm{~d}^{7} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 3
3. \(\mathrm{Ti}^{2+}\):
- \(\mathrm{Ti}^{2+} \Rightarrow 3 \mathrm{~d}^{2} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 2
4. \(\mathrm{Fe}^{3+}\):
- \(\mathrm{Fe}^{3+} \Rightarrow 3 \mathrm{~d}^{5} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 5
5. \(\mathrm{Cr}^{2+}\):
- \(\mathrm{Cr}^{2+} \Rightarrow 3 \mathrm{~d}^{4} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 4
6. \(\mathrm{Ti}^{3+}\):
- \(\mathrm{Ti}^{3+} \Rightarrow 3 \mathrm{~d}^{1} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 1
7. \(\mathrm{Mn}^{2+}\):
- \(\mathrm{Mn}^{2+} \Rightarrow 3 \mathrm{~d}^{5} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 5
Therefore, the correct answer is (1) \(\mathrm{V}^{2+}, \mathrm{Co}^{2+}\). Quick Tip: The number of unpaired electrons in transition metal ions depends on their electronic configuration.
Which one of the following about an electron occupying the 1 s orbital in a hydrogen atom is incorrect ? (Bohr's radius is represented by \(\mathrm{a}_{0}\) )
View Solution
1. Probability density:
- The probability density of finding the electron is maximum at the nucleus.
2. Distance from the nucleus:
- The electron can be found at a distance \(2 \mathrm{a}_{0}\) from the nucleus.
3. Spherical symmetry:
- The 1s orbital is spherically symmetrical.
4. Total energy:
- The total energy of the electron is maximum when it is at a distance \(\mathrm{a}_{0}\) from the nucleus. This statement is incorrect.
Therefore, the correct answer is (4). Quick Tip: The probability density, distance from the nucleus, spherical symmetry, and total energy of an electron in the 1s orbital are important properties to consider.
In Dumas' method for estimation of nitrogen 1 g of an organic compound gave 150 mL of nitrogen collected at 300 K temperature and 900 mm Hg pressure. The percentage composition of nitrogen in the compound is _______ % (nearest integer).
(Aqueous tension at \(300 \mathrm{~K}=15 \mathrm{~mm} \mathrm{Hg}\) )
View Solution
1. Calculate the partial pressure of \(\mathrm{N}_{2}\):
\[ \mathrm{p}_{\mathrm{N}_2} = 900 \mathrm{~mm~Hg} - 15 \mathrm{~mm~Hg} = 885 \mathrm{~mm~Hg} \]
2. Calculate the moles of \(\mathrm{N}_{2}\):
\[ Moles of \mathrm{N}_2 = \frac{885 \mathrm{~mm~Hg} \times 0.15 \mathrm{~L}}{0.0821 \mathrm{~L~atm/mol} \times 300 \mathrm{~K}} = 0.0071 \mathrm{~mol} \]
3. Calculate the percentage of nitrogen:
\[ Percentage of nitrogen = \frac{0.0071 \mathrm{~mol} \times 28 \mathrm{~g/mol}}{1 \mathrm{~g}} \times 100 = 19.85% \approx 20% \]
Therefore, the correct answer is (20). Quick Tip: Use the ideal gas law to calculate the moles of nitrogen and then determine the percentage composition.
\(\mathrm{KMnO}_{4}\) acts as an oxidising agent in acidic medium. ' X ' is the difference between the oxidation states of Mn in reactant and product. ' Y ' is the number of ' d ' electrons present in the brown red precipitate formed at the end of the acetate ion test with neutral ferric chloride. The value of \(\mathrm{X}+\mathrm{Y}\) is _______ .
View Solution
1. Oxidation states of Mn:
- Reactant: \(\mathrm{Mn}^{7+}\)
- Product: \(\mathrm{Mn}^{2+}\)
- Difference in oxidation states: \(X = 7 - 2 = 5\)
2. Brown red precipitate:
- The brown red precipitate is \(\mathrm{Fe}(\mathrm{OH})_2(\mathrm{CH}_3\mathrm{COO})_n\).
- \(\mathrm{Fe}^{3+}\) has 5 d-electrons.
- Therefore, \(Y = 5\).
3. Calculate \(\mathrm{X}+\mathrm{Y}\):
\[ \mathrm{X} + \mathrm{Y} = 5 + 5 = 10 \]
Therefore, the correct answer is (10). Quick Tip: Determine the oxidation states and the number of d-electrons to find the values of X and Y.
Fortification of food with iron is done using \(\mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O}\). The mass in grams of the \(\mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O}\) required to achieve 12 ppm of iron in 150 kg of wheat is _______ (Nearest integer).
(Given : Molar mass of \(\mathrm{Fe}, \mathrm{S}\) and O respectively are 56,32 and \(16 \mathrm{~g} \mathrm{~mol}^{-1}\) )
View Solution
1. Calculate the mass of iron required:
\[ Mass of iron = \frac{12 \mathrm{~ppm} \times 150 \mathrm{~kg}}{10^6} = 1.8 \mathrm{~g} \]
2. Calculate the moles of iron:
\[ Moles of iron = \frac{1.8 \mathrm{~g}}{56 \mathrm{~g/mol}} = 0.0321 \mathrm{~mol} \]
3. Calculate the moles of \(\mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O}\):
\[ Moles of \mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O} = 0.0321 \mathrm{~mol} \]
4. Calculate the mass of \(\mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O}\):
\[ Molar mass of \mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O} = 56 + 32 + 7 \times 18 = 277 \mathrm{~g/mol} \]
\[ Mass of \mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O} = 0.0321 \mathrm{~mol} \times 277 \mathrm{~g/mol} = 8.8935 \mathrm{~g} \approx 9 \mathrm{~g} \]
Therefore, the correct answer is (9). Quick Tip: Use the molar mass and stoichiometry to calculate the mass of the compound required.
The pH of a 0.01 M weak acid \(\mathrm{HX}\left(\mathrm{K}_{\mathrm{a}}=4 \times 10^{-10}\right)\) is found to be 5 . Now the acid solution is diluted with excess of water so that the pH of the solution changes to 6 . The new concentration of the diluted weak acid is given as \(\mathrm{x} \times 10^{-4} \mathrm{M}\). The value of x is _______ (nearest integer).
View Solution
1. Initial pH calculation:
\[ \mathrm{HX}_{(\mathrm{aq})} \rightleftharpoons \mathrm{H}_{(\mathrm{aq})}^{+}+\mathrm{X}_{(\mathrm{aq})}^{-} \quad \mathrm{K}_{\mathrm{a}}=4 \times 10^{-10} \]
\[ 0.01(1-\alpha) \quad 0.01 \alpha \quad 0.01 \alpha \quad Not justified \]
\[ \Rightarrow 0.01 \alpha=10^{-5} \Rightarrow \alpha=10^{-3} \]
2. Calculate \(\mathrm{K}_{\mathrm{a}}\):
\[ \mathrm{K}_{\mathrm{a}}=0.01 \alpha^{2}=10^{-8} \]
3. Data given is inconsistent \& contradictory. This should be bonus. Quick Tip: Check the consistency of the given data and ensure the calculations are justified.
The total number of hydrogen bonds of a DNA-double Helix strand whose one strand has the following sequence of bases is _______ .
\(5^{\prime}-\mathrm{G}-\mathrm{G}-\mathrm{C}-\mathrm{A}-\mathrm{A}-\mathrm{A}-\mathrm{T}-\mathrm{C}-\mathrm{G}-\mathrm{G}-\mathrm{C}-\mathrm{T}-\mathrm{A}-3^{\prime}\)
View Solution
1. Hydrogen bonding in DNA:
- Adenine (A) forms two hydrogen bonds with Thymine (T).
- Guanine (G) forms three hydrogen bonds with Cytosine (C).
2. Count the hydrogen bonds:
- Number of G-C pairs: 4
- Number of A-T pairs: 4
3. Total number of hydrogen bonds:
\[ Total hydrogen bonds = 4 \times 3 + 4 \times 2 = 12 + 8 = 20 \]
Therefore, the correct answer is (33). Quick Tip: Count the number of hydrogen bonds formed by each base pair in the DNA strand.
JEE Main April 4 Shift 1 Question Paper With Video Solutions
The JEE Main 2025 April 4 Question Paper with Video Solution is available here after the examination. Students can match their responses with the JEE Main 2025 April 4 Shift 1 Answer key with Solutions. Students who are appearing for JEE Main upcoming shifts can check the JEE Main April 4 Shift 1 Question Paper and video solution to understand the difficulty level of the exam.
JEE Main Session 2 Difficulty Level Analysis
| JEE Mains 2025 Session 2 exam dates | Paper | Exam Analysis |
|---|---|---|
| April 2, 2025 | Paper 1 (B.E/BTech) |
|
| April 3, 2025 | Paper 1 (B.E/BTech) |
|
| April 4, 2025 | Paper 1 (B.E/BTech) |
|
| April 7, 2025 | Paper 1 (B.E/BTech) | TBA |
| April 8, 2025 | Paper 1 (B.E/BTech) | TBA |
| April 9, 2025 | Paper 2A (BArch) and Paper 2B (BPlanning) | TBA |
Related Links:
- JEE Main 2025 Question Paper pdf with solutions
- JEE Main Previous Years Question Paper with Solution PDF
JEE Main 2025 April 4 Shift 1 Answer Key: Coaching Institute PDF
| Coaching Institutes | Question Paper with Solutions PDF |
|---|---|
| Aakash BYJUs | Download Now |
| Allen Institute | Download Now |
| Resonance | Download Now |
| Vedantu | Download Now |
| Sri Chaitanya | Download Now |
JEE Main Marking Scheme 2025
For JEE Main Paper 1(B.E/BTech), students are required to attempt 75 questions following a marking scheme of +4 for correct answers and -1 for incorrect ones. The marking scheme is the same across Physics, Chemistry, and Mathematics sections totaling to 300 marks.
| Paper | Sections | Questions | Marks | Marking Scheme |
|---|---|---|---|---|
| Paper 1 | Physics, Chemistry, Mathematics | 75 Questions (25 Physics, 25 Chemistry, 25 Mathematics) | 300 total |
|
Is there any negative marking in JEE Main Paper 1?
- If you choose the wrong answer in both Section A and Section B, you will lose 1 mark because of negative marking.
- In Section B, instead of choosing an option, you have to type the correct whole number using the on screen number pad. If your answer is a decimal, round it off to the nearest whole number before entering it.
Once you calculate your expected marks, you can review the JEE Main Question papers to improve your preparation.
You can check:
- JEE Main Previous Years Question Paper with Solution
- JEE Main 2024 Question Paper with Solution PDF
- JEE Main 2023 Question Paper with Solution PDF
- JEE Main 2022 Question Paper with Solution PDF
What to carry at the JEE Main Test Centre ?
Every aspirant must check the JEE Main exam day guidelines before the examination. The JEE Main exam instructions comprise of all the dos and don’ts to be followed for a hassle-free exam process. JEE Mains rules and regulations for the exam are provided below:
| What to Carry | What NOT to Carry |
|---|---|
| JEE Main 2025 Admit Card (Mandatory) | Electronic gadgets (Mobile phones, smartwatches, calculators, Bluetooth devices) |
| Valid ID Proof (Aadhaar Card, PAN Card, Voter ID, Passport, etc.) | Written/Printed Study Materials (Books, Notes, Papers) |
| A simple transparent ballpoint pen (for rough work) | Any type of rough paper (NTA will provide sheets) |
| A passport-size photograph (same as on the admit card) | Smart devices (Earphones, Digital Watches, Fitness Bands) |
| PwD Certificate (if applicable) | Geometry boxes, Log tables, or Any extra stationery items |
| A transparent water bottle (Optional) | Wallets, Purses, or Bags |
How to attempt JEE Main 2025 MCQ’s with Maximum Accuracy?
For accuracy in JEE Main MCQ’s concepts need to be well understood. On average, based on past JEE exams, almost 60 % of the incorrect answers are because of reading the question wrong or marking the wrong answers.
For numerical value questions, if the question requires you to round it off to the nearest integer, accuracy is important. It can cost 4 marks per question which can have a significant impact on your rank.
In revising an answer, many students choose to trade their initial answer for another incorrect alternative. Based on the past year trends, first solutions are accurate most of the time, a figure close to 70%. One should second-guess only on a sound reason for doubt about error.



Comments