JEE Main 2025 April 4 Chemistry Question Paper is available for download. NTA conducted JEE Main 2025 Shift 1 B.Tech Exam on 3rd April 2025 from 9:00 AM to 12:00 PM and for JEE Main 2025 B.Tech Shift 2 appearing candidates from 3:00 PM to 6:00 PM. The JEE Main 2025 3rd April B.Tech Question Paper was Moderate to Tough.
Also Check: JEE Main 2025 Question Paper with Solution PDF Download
JEE Main 2025 April 4 Shift 1 Chemistry Question Paper with Solutions
| JEE Main 2025 April 4 Shift 1 Chemistry Question Paper Pdf | Download PDF | View Solution |

JEE Main 2025 Chemistry Questions with Solutions
Question 1:
\(XY\) is the membrane / partition between two chambers 1 and 2 containing sugar solutions of concentration \(\mathrm{c}_{1}\) and \(\mathrm{c}_{2}\left(\mathrm{c}_{1}>\mathrm{c}_{2}\right) \mathrm{mol} \mathrm{L}^{-1}\). For the reverse osmosis to take place identify the correct condition
(Here \(\mathrm{p}_{1}\) and \(\mathrm{p}_{2}\) are pressures applied on chamber 1 and 2 )
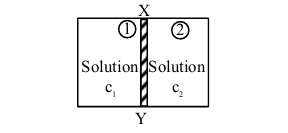
View Solution
1. Normal osmosis occurs from chamber 2 to chamber 1.
2. For reverse osmosis from chamber 1 to chamber 2, the pressure \(\mathrm{p}_{1}\) must be greater than the osmotic pressure \(\pi\).
3. Therefore, the correct conditions are A and C.
Therefore, the correct answer is (3) A and C only. Quick Tip: Reverse osmosis requires the pressure in the chamber with higher concentration to be greater than the osmotic pressure.
Let us consider a reversible reaction at temperature, T . In this reaction, both \(\Delta \mathrm{H}\) and \(\Delta \mathrm{S}\) were observed to have positive values. If the equilibrium temperature is \(\mathrm{T}_{\mathrm{e}}\), then the reaction becomes spontaneous at:
View Solution
1. For a reaction to be spontaneous, \(\Delta \mathrm{G} < 0\).
\[ \Delta \mathrm{G} = \Delta \mathrm{H} - \mathrm{T} \Delta \mathrm{S} \]
2. Given that both \(\Delta \mathrm{H}\) and \(\Delta \mathrm{S}\) are positive:
\[ \Delta \mathrm{G} = \Delta \mathrm{H} - \mathrm{T} \Delta \mathrm{S} < 0 \]
\[ \mathrm{T} > \frac{\Delta \mathrm{H}}{\Delta \mathrm{S}} = \mathrm{T}_{\mathrm{e}} \]
Therefore, the correct answer is (3) \(\mathrm{T}>\mathrm{T}_{\mathrm{e}}\). Quick Tip: A reaction is spontaneous when the Gibbs free energy change is negative.
Which of the following molecules(s) show/s paramagnetic behavior?
View Solution
1. Number of unpaired electrons:
- (A) \(\mathrm{O}_{2}\): 2
- (B) \(\mathrm{N}_{2}\): 0
- (C) \(\mathrm{F}_{2}\): 0
- (D) \(\mathrm{S}_{2}\): 2
- (E) \(\mathrm{Cl}_{2}\): 0
2. Paramagnetic behavior:
- Molecules with unpaired electrons exhibit paramagnetic behavior.
- Therefore, \(\mathrm{O}_{2}\) and \(\mathrm{S}_{2}\) are paramagnetic.
Therefore, the correct answer is (4) A \& D only. Quick Tip: Molecules with unpaired electrons are paramagnetic.
Aldol condensation is a popular and classical method to prepare \(\alpha, \beta\)-unsaturated carbonyl compounds. This reaction can be both intermolecular and intramolecular. Predict which one of the following is not a product of intramolecular aldol condensation?
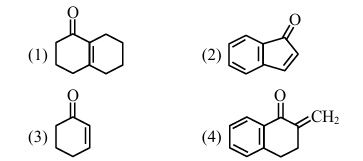
View Solution
1. Intramolecular aldol condensation products:
- (1), (2), and (3) are products of intramolecular aldol condensation.
- (4) is a product of intermolecular aldol condensation.
Therefore, the correct answer is (4). Quick Tip: Intramolecular aldol condensation involves the reaction within the same molecule, while intermolecular aldol condensation involves the reaction between two different molecules.
One mole of an ideal gas expands isothermally and reversibly from \(10 \mathrm{dm}^{3}\) to \(20 \mathrm{dm}^{3}\) at \(300 \mathrm{~K} . \Delta \mathrm{U}\), q and work done in the process respectively are :
Given : \(\mathrm{R}=8.3 \mathrm{JK}^{-1}\) and \(\mathrm{mol}^{-1}\)
In \(10=2.3\)
\(\log 2=0.30\)
\(\log 3=0.48\)
View Solution
1. Given:
- Isothermal expansion from \(10 \mathrm{dm}^{3}\) to \(20 \mathrm{dm}^{3}\) at \(300 \mathrm{~K}\).
- \(\mathrm{R} = 8.3 \mathrm{JK}^{-1} \mathrm{mol}^{-1}\).
2. Calculate the work done (w):
\[ w = -nRT \ln \frac{V_2}{V_1} \]
\[ w = -8.3 \times 300 \times \ln \left( \frac{20}{10} \right) \]
\[ w = -1.718 \mathrm{~kJ} \]
3. Calculate the heat transferred (q):
\[ q = -w = 1.718 \mathrm{~kJ} \]
4. Calculate the change in internal energy (\(\Delta U\)):
\[ \Delta U = 0 \quad (since \Delta T = 0) \]
Therefore, the correct answer is (4) \(0,178 \mathrm{~kJ},-1.718 \mathrm{~kJ}\). Quick Tip: For an isothermal process, the change in internal energy is zero.
Which one of the following complexes will have \(\Delta_{0}=0\) and \(\mu=5.96\) B.M.?
View Solution
1. \(\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]^{4}\):
- \(\mathrm{Fe}^{2+} \Rightarrow 3 \mathrm{~d}^{6} 4 \mathrm{~s}^{0}\)
- \(\mathrm{CN}^{-}\) is a strong field ligand.
- \(\mu = 0\)
2. \(\left[\mathrm{CO}\left(\mathrm{NH}_{3}\right)_{6}\right]^{3+}\):
- \(\mathrm{Co}^{3+} \Rightarrow 3 \mathrm{~d}^{6} 4 \mathrm{~s}^{0}\)
- \(\mathrm{NH}_{3}\) is a strong field ligand.
- \(\mu = 0\)
3. \(\left[\mathrm{FeF}_{6}\right]^{4}\):
- \(\mathrm{Fe}^{2+} \Rightarrow 3 \mathrm{~d}^{6} 4 \mathrm{~s}^{0}\)
- \(\mathrm{F}^{-}\) is a weak field ligand.
- \(\mu = 0\)
4. \(\left[\mathrm{Mn}(\mathrm{SCN})_{6}\right]^{4}\):
- \(\mathrm{Mn}^{2+} \Rightarrow 3 \mathrm{~d}^{5} 4 \mathrm{~s}^{0}\)
- \(\mathrm{SCN}^{-}\) is a weak field ligand.
- \(\mu = \sqrt{35} \mathrm{~BM} = 5.96 \mathrm{~BM}\)
- \(\Delta_{0} = 0\)
Therefore, the correct answer is (4) \(\left[\mathrm{Mn}(\mathrm{SCN})_{6}\right]^{4}\). Quick Tip: The magnetic moment and crystal field stabilization energy depend on the ligand field strength.
For \(\mathrm{A}_{2}+\mathrm{B}_{2} \rightleftharpoons 2 \mathrm{AB}\) \(\mathrm{E}_{\mathrm{a}}\) for forward and backward reaction are 180 and \(200 \mathrm{~kJ} \mathrm{~mol}^{-1}\) respectively. If catalyst lowers \(\mathrm{E}_{\mathrm{a}}\) for both reaction by \(100 \mathrm{~kJ} \mathrm{~mol}^{-1}\). Which of the following statement is correct?
View Solution
1. Given:
- \(\mathrm{A}_{2}+\mathrm{B}_{2} \rightleftharpoons 2 \mathrm{AB}\)
- \(\mathrm{E}_{\mathrm{f}} = 180 \mathrm{~kJ} \mathrm{~mol}^{-1}\)
- \(\mathrm{E}_{\mathrm{b}} = 200 \mathrm{~kJ} \mathrm{~mol}^{-1}\)
2. Calculate the enthalpy change (\(\Delta \mathrm{H}\)):
\[ \Delta \mathrm{H} = \mathrm{E}_{\mathrm{f}} - \mathrm{E}_{\mathrm{b}} = 180 \mathrm{~kJ} \mathrm{~mol}^{-1} - 200 \mathrm{~kJ} \mathrm{~mol}^{-1} = -20 \mathrm{~kJ} \mathrm{~mol}^{-1} \]
3. Effect of catalyst:
- Catalyst lowers the activation energy but does not change the Gibbs free energy change (\(\Delta \mathrm{G}\)) or the enthalpy change (\(\Delta \mathrm{H}\)) of the reaction.
Therefore, the correct answer is (1) Catalyst does not alter the Gibbs energy change of a reaction. Quick Tip: Catalysts lower the activation energy but do not change the thermodynamic properties of the reaction.
Rate law for a reaction between \(A\) and \(B\) is given by \(\mathrm{R}=\mathrm{k}[\mathrm{A}]^{\mathrm{n}}[\mathrm{B}]^{\mathrm{m}}\). If concentration of A is doubled and concentration of B is halved from their initial value, the ratio of new rate of reaction to the initial rate of reaction \(\left(\frac{\mathrm{r}_{2}}{\mathrm{r}_{1}}\right)\) is
View Solution
1. Initial rate law:
\[ \mathrm{r}_{1} = \mathrm{k}[\mathrm{A}]^{\mathrm{n}}[\mathrm{B}]^{\mathrm{m}} \]
2. New concentrations:
- Concentration of A is doubled: \(2[\mathrm{A}]\)
- Concentration of B is halved: \(\frac{[\mathrm{B}]}{2}\)
3. New rate law:
\[ \mathrm{r}_{2} = \mathrm{k}(2[\mathrm{A}])^{\mathrm{n}} \left( \frac{[\mathrm{B}]}{2} \right)^{\mathrm{m}} \]
\[ \mathrm{r}_{2} = \mathrm{k} \cdot 2^{\mathrm{n}} [\mathrm{A}]^{\mathrm{n}} \cdot \frac{[\mathrm{B}]^{\mathrm{m}}}{2^{\mathrm{m}}} \]
4. Ratio of new rate to initial rate:
\[ \frac{\mathrm{r}_{2}}{\mathrm{r}_{1}} = \frac{\mathrm{k} \cdot 2^{\mathrm{n}} [\mathrm{A}]^{\mathrm{n}} \cdot \frac{[\mathrm{B}]^{\mathrm{m}}}{2^{\mathrm{m}}}}{\mathrm{k}[\mathrm{A}]^{\mathrm{n}}[\mathrm{B}]^{\mathrm{m}}} = 2^{\mathrm{n}} \cdot \frac{1}{2^{\mathrm{m}}} = 2^{(\mathrm{n}-\mathrm{m})} \]
Therefore, the correct answer is (1) \(2^{(\mathrm{n}-\mathrm{m})}\). Quick Tip: The rate law depends on the concentrations of the reactants raised to their respective orders.
Number of stereoisomers possible for the complexes, \(\left[\mathrm{CrCl}_{3}(\mathrm{py})_{3}\right]\) and \(\left[\mathrm{CrCl}_{2}(\mathrm{ox})_{2}\right]^{3-}\) are respectively
(py = pyridine, ox = oxalate)
View Solution
1. \(\left[\mathrm{CrCl}_{3}(\mathrm{py})_{3}\right]\):
- Facial and meridional isomers are possible.
- Total stereoisomers = 2.
2. \(\left[\mathrm{CrCl}_{2}(\mathrm{ox})_{2}\right]^{3-}\):
- Geometrical isomers: cis and trans.
- Optical isomers for cis: 2.
- Optical isomers for trans: 1.
- Total stereoisomers = 3.
Therefore, the correct answer is (3) \(2 \& 3\). Quick Tip: Stereoisomers include geometrical and optical isomers.
The major product (A) formed in the following reaction sequence is

View Solution
1. Reaction sequence:
- The major product formed is (2).
Therefore, the correct answer is (2). Quick Tip: Follow the reaction sequence to determine the major product.
On charging the lead storage battery, the oxidation state of lead changes from \(\mathrm{x}_{1}\) to \(\mathrm{y}_{1}\) at the anode and from \(\mathrm{x}_{2}\) to \(\mathrm{y}_{2}\) at the cathode. The values of \(\mathrm{x}_{1}, \mathrm{y}_{1}, \mathrm{x}_{2}, \mathrm{y}_{2}\) are respectively:
View Solution
1. Anode reaction:
- \(\mathrm{PbSO}_{4}\) is reduced to \(\mathrm{Pb}\).
- \(\mathrm{Pb}^{2+} \rightarrow \mathrm{Pb}^{0}\)
- \(\mathrm{x}_{1} = +2\), \(\mathrm{y}_{1} = 0\)
2. Cathode reaction:
- \(\mathrm{PbSO}_{4}\) is oxidized to \(\mathrm{PbO}_{2}\).
- \(\mathrm{Pb}^{2+} \rightarrow \mathrm{Pb}^{4+}\)
- \(\mathrm{x}_{2} = +2\), \(\mathrm{y}_{2} = +4\)
Therefore, the correct answer is (2) \(+2,0,+2,+4\). Quick Tip: The oxidation states change during the charging of a lead-acid battery.
Given below are two statements:
Statement I: Nitrogen forms oxides with +1 to +5 oxidation states due to the formation of \(\mathrm{p} \pi-\mathrm{p} \pi\) bond with oxygen.
Statement II: Nitrogen does not form halides with +5 oxidation state due to the absence of d-orbital in it.
In the light of the above statements, choose the correct answer from the options given below:
View Solution
1. Statement I:
- Nitrogen can form oxides with oxidation states from +1 to +5 due to the formation of \(\mathrm{p} \pi-\mathrm{p} \pi\) bonds with oxygen.
- This statement is true.
2. Statement II:
- Nitrogen does not form halides with a +5 oxidation state due to the absence of d-orbitals.
- This statement is true.
Therefore, the correct answer is (4) Both Statement I and Statement II are true. Quick Tip: Nitrogen's ability to form oxides and halides depends on its electronic configuration and the availability of d-orbitals.
Benzene is treated with oleum to produce compound (X) which when further heated with molten sodium hydroxide followed by acidification produces compound (Y).The compound Y is treated with zinc metal to produce compound (Z). Identify the structure of compound (Z) from the following option.
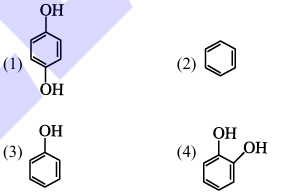
View Solution
1. Reaction sequence:
- Benzene treated with oleum produces benzene sulfonic acid (X).
- Heating with molten sodium hydroxide followed by acidification produces phenol (Y).
- Treatment with zinc metal reduces phenol to cyclohexanol (Z).
Therefore, the correct answer is (2). Quick Tip: Follow the reaction sequence to identify the final product.
Identify the pair of reactants that upon reaction, with elimination of HCl will give rise to the dipeptide Gly-Ala.
View Solution
1. Reactants:
- \(\mathrm{NH}_{2}-\mathrm{CH}_{2}-\mathrm{COCl}\) (Glycine chloride)
- \(\mathrm{NH}_{2}-\mathrm{CH}-\mathrm{COOH}\) (Alanine)
2. Reaction:
- The reaction between these reactants with the elimination of HCl will produce the dipeptide Gly-Ala.
Therefore, the correct answer is (1) \(\mathrm{NH}_{2}-\mathrm{CH}_{2}-\mathrm{COCl}\) and \(\mathrm{NH}_{2}-\mathrm{CH}-\mathrm{COOH}\). Quick Tip: The formation of a dipeptide involves the reaction between an amino acid and its chloride derivative with the elimination of HCl.
Given below are the pairs of group 13 elements showing their relation in terms of atomic radius. \((\mathrm{B}<\mathrm{Al}),(\mathrm{Al}<\mathrm{Ga}),(\mathrm{Ga}<\mathrm{In})\) and \((\mathrm{In}<\mathrm{Tl})\) Identify the elements present in the incorrect pair and in that pair find out the element (X) that has higher ionic radius \(\left(\mathrm{M}^{3+}\right)\) than the other one. The atomic number of the element (X) is
View Solution
1. Incorrect pair:
- \(\mathrm{Al}<\mathrm{Ga}\)
2. Ionic radius comparison:
- \(\mathrm{Al}^{3+}<\mathrm{Ga}^{3+}\)
- The atomic number of \(\mathrm{Ga}\) is 31.
Therefore, the correct answer is (1) 31. Quick Tip: The atomic radius and ionic radius depend on the atomic number and the periodic trends.
An organic compound (X) with molecular formula \(\mathrm{C}_{3} \mathrm{H}_{6} \mathrm{O}\) is not readily oxidised. On reduction it gives \(\left(\mathrm{C}_{3} \mathrm{H}_{8} \mathrm{O}(\mathrm{Y})\right.\) which reacts with HBr to give a bromide (Z) which is converted to Grignard reagent. This Grignard reagent on reaction with (X) followed by hydrolysis give 2,3-dimethylbutan-2-ol. Compounds (X), (Y) and (Z) respectively are:
View Solution
1. Compound (X):
- \(\mathrm{CH}_{3} \mathrm{COCH}_{3}\) (Acetone)
2. Reduction to (Y):
- \(\mathrm{CH}_{3} \mathrm{CH}(\mathrm{OH}) \mathrm{CH}_{3}\) (Isopropyl alcohol)
3. Reaction with HBr to form (Z):
- \(\mathrm{CH}_{3} \mathrm{CH}(\mathrm{Br}) \mathrm{CH}_{3}\) (2-Bromopropane)
4. Grignard reagent and reaction with (X):
- The Grignard reagent formed from (Z) reacts with acetone to form 2,3-dimethylbutan-2-ol after hydrolysis.
Therefore, the correct answer is (2) \(\mathrm{CH}_{3} \mathrm{COCH}_{3}, \mathrm{CH}_{3} \mathrm{CH}(\mathrm{OH}) \mathrm{CH}_{3}, \mathrm{CH}_{3} \mathrm{CH}(\mathrm{Br}) \mathrm{CH}_{3}\). Quick Tip: Follow the reaction sequence to identify the compounds involved.
Predict the major product of the following reaction sequence:
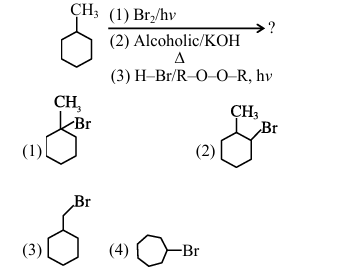
View Solution
% Option
(A) Step 1: Bromination (Br\(_2\)/hv)
\[\ce{CH3 ->[Br2/hv] CH2Br}\]
% Option
(B) Step 2: Elimination (Alcoholic KOH)
\[\ce{CH2Br ->[Alc. KOH][\Delta] CH2=}\]
% Option
(C) Step 3: Anti-Markovnikov addition (HBr/ROOR)
\[\ce{CH2= ->[HBr/ROOR][hv] Br-CH3}\]
Mechanistic Explanation:
Free radical bromination converts methyl to bromomethyl
Elimination forms methylene intermediate
Peroxide effect gives anti-Markovnikov product
Therefore, the correct answer is \boxed{(2) \ce{Br-CH3. Quick Tip: Key Points: Radical bromination prefers allylic position Alcoholic KOH causes elimination ROOR reverses normal addition orientation
Given below are two statements.

In the light of the above statements, choose the correct answer from the options given below:
View Solution
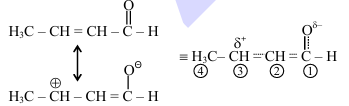
1. Analysis of Statement I:
For \chemfig{CH_3-CH=CH-CH=O: \(\mu = q \times d\)
Conjugated system creates greater charge separation
More distance between charges than in saturated compound
Therefore, greater dipole moment
Statement I is TRUE
2. Analysis of Statement II:
In \chemfig{CH_3-CH=CH-CH=O, \(C_1-C_2\) has partial double bond character
Double bond character means shorter bond length
Compared to pure single bond in \chemfig{CH_3-CH_2-CH_2-CH=O
Statement II is FALSE (actual bond length is shorter) Quick Tip: Key concepts: Dipole moment depends on charge magnitude and separation distance Conjugation affects both electronic distribution and bond lengths Partial double bond character decreases bond length
Pair of transition metal ions having the same number of unpaired electrons is :
View Solution
1. \(\mathrm{V}^{2+}\):
- \(\mathrm{V}^{2+} \Rightarrow 3 \mathrm{~d}^{3} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 3
2. \(\mathrm{Co}^{2+}\):
- \(\mathrm{Co}^{2+} \Rightarrow 3 \mathrm{~d}^{7} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 3
3. \(\mathrm{Ti}^{2+}\):
- \(\mathrm{Ti}^{2+} \Rightarrow 3 \mathrm{~d}^{2} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 2
4. \(\mathrm{Fe}^{3+}\):
- \(\mathrm{Fe}^{3+} \Rightarrow 3 \mathrm{~d}^{5} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 5
5. \(\mathrm{Cr}^{2+}\):
- \(\mathrm{Cr}^{2+} \Rightarrow 3 \mathrm{~d}^{4} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 4
6. \(\mathrm{Ti}^{3+}\):
- \(\mathrm{Ti}^{3+} \Rightarrow 3 \mathrm{~d}^{1} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 1
7. \(\mathrm{Mn}^{2+}\):
- \(\mathrm{Mn}^{2+} \Rightarrow 3 \mathrm{~d}^{5} 4 \mathrm{~s}^{0}\)
- Number of unpaired electrons = 5
Therefore, the correct answer is (1) \(\mathrm{V}^{2+}, \mathrm{Co}^{2+}\). Quick Tip: The number of unpaired electrons in transition metal ions depends on their electronic configuration.
Which one of the following about an electron occupying the 1 s orbital in a hydrogen atom is incorrect ? (Bohr's radius is represented by \(\mathrm{a}_{0}\) )
View Solution
1. Probability density:
- The probability density of finding the electron is maximum at the nucleus.
2. Distance from the nucleus:
- The electron can be found at a distance \(2 \mathrm{a}_{0}\) from the nucleus.
3. Spherical symmetry:
- The 1s orbital is spherically symmetrical.
4. Total energy:
- The total energy of the electron is maximum when it is at a distance \(\mathrm{a}_{0}\) from the nucleus. This statement is incorrect.
Therefore, the correct answer is (4). Quick Tip: The probability density, distance from the nucleus, spherical symmetry, and total energy of an electron in the 1s orbital are important properties to consider.
In Dumas' method for estimation of nitrogen 1 g of an organic compound gave 150 mL of nitrogen collected at 300 K temperature and 900 mm Hg pressure. The percentage composition of nitrogen in the compound is _______ % (nearest integer).
(Aqueous tension at \(300 \mathrm{~K}=15 \mathrm{~mm} \mathrm{Hg}\) )
View Solution
1. Calculate the partial pressure of \(\mathrm{N}_{2}\):
\[ \mathrm{p}_{\mathrm{N}_2} = 900 \mathrm{~mm~Hg} - 15 \mathrm{~mm~Hg} = 885 \mathrm{~mm~Hg} \]
2. Calculate the moles of \(\mathrm{N}_{2}\):
\[ Moles of \mathrm{N}_2 = \frac{885 \mathrm{~mm~Hg} \times 0.15 \mathrm{~L}}{0.0821 \mathrm{~L~atm/mol} \times 300 \mathrm{~K}} = 0.0071 \mathrm{~mol} \]
3. Calculate the percentage of nitrogen:
\[ Percentage of nitrogen = \frac{0.0071 \mathrm{~mol} \times 28 \mathrm{~g/mol}}{1 \mathrm{~g}} \times 100 = 19.85% \approx 20% \]
Therefore, the correct answer is (20). Quick Tip: Use the ideal gas law to calculate the moles of nitrogen and then determine the percentage composition.
\(\mathrm{KMnO}_{4}\) acts as an oxidising agent in acidic medium. ' X ' is the difference between the oxidation states of Mn in reactant and product. ' Y ' is the number of ' d ' electrons present in the brown red precipitate formed at the end of the acetate ion test with neutral ferric chloride. The value of \(\mathrm{X}+\mathrm{Y}\) is _______ .
View Solution
1. Oxidation states of Mn:
- Reactant: \(\mathrm{Mn}^{7+}\)
- Product: \(\mathrm{Mn}^{2+}\)
- Difference in oxidation states: \(X = 7 - 2 = 5\)
2. Brown red precipitate:
- The brown red precipitate is \(\mathrm{Fe}(\mathrm{OH})_2(\mathrm{CH}_3\mathrm{COO})_n\).
- \(\mathrm{Fe}^{3+}\) has 5 d-electrons.
- Therefore, \(Y = 5\).
3. Calculate \(\mathrm{X}+\mathrm{Y}\):
\[ \mathrm{X} + \mathrm{Y} = 5 + 5 = 10 \]
Therefore, the correct answer is (10). Quick Tip: Determine the oxidation states and the number of d-electrons to find the values of X and Y.
Fortification of food with iron is done using \(\mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O}\). The mass in grams of the \(\mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O}\) required to achieve 12 ppm of iron in 150 kg of wheat is _______ (Nearest integer).
(Given : Molar mass of \(\mathrm{Fe}, \mathrm{S}\) and O respectively are 56,32 and \(16 \mathrm{~g} \mathrm{~mol}^{-1}\) )
View Solution
1. Calculate the mass of iron required:
\[ Mass of iron = \frac{12 \mathrm{~ppm} \times 150 \mathrm{~kg}}{10^6} = 1.8 \mathrm{~g} \]
2. Calculate the moles of iron:
\[ Moles of iron = \frac{1.8 \mathrm{~g}}{56 \mathrm{~g/mol}} = 0.0321 \mathrm{~mol} \]
3. Calculate the moles of \(\mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O}\):
\[ Moles of \mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O} = 0.0321 \mathrm{~mol} \]
4. Calculate the mass of \(\mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O}\):
\[ Molar mass of \mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O} = 56 + 32 + 7 \times 18 = 277 \mathrm{~g/mol} \]
\[ Mass of \mathrm{FeSO}_{4} .7 \mathrm{H}_{2} \mathrm{O} = 0.0321 \mathrm{~mol} \times 277 \mathrm{~g/mol} = 8.8935 \mathrm{~g} \approx 9 \mathrm{~g} \]
Therefore, the correct answer is (9). Quick Tip: Use the molar mass and stoichiometry to calculate the mass of the compound required.
The pH of a 0.01 M weak acid \(\mathrm{HX}\left(\mathrm{K}_{\mathrm{a}}=4 \times 10^{-10}\right)\) is found to be 5 . Now the acid solution is diluted with excess of water so that the pH of the solution changes to 6 . The new concentration of the diluted weak acid is given as \(\mathrm{x} \times 10^{-4} \mathrm{M}\). The value of x is _______ (nearest integer).
View Solution
1. Initial pH calculation:
\[ \mathrm{HX}_{(\mathrm{aq})} \rightleftharpoons \mathrm{H}_{(\mathrm{aq})}^{+}+\mathrm{X}_{(\mathrm{aq})}^{-} \quad \mathrm{K}_{\mathrm{a}}=4 \times 10^{-10} \]
\[ 0.01(1-\alpha) \quad 0.01 \alpha \quad 0.01 \alpha \quad Not justified \]
\[ \Rightarrow 0.01 \alpha=10^{-5} \Rightarrow \alpha=10^{-3} \]
2. Calculate \(\mathrm{K}_{\mathrm{a}}\):
\[ \mathrm{K}_{\mathrm{a}}=0.01 \alpha^{2}=10^{-8} \]
3. Data given is inconsistent \& contradictory. This should be bonus. Quick Tip: Check the consistency of the given data and ensure the calculations are justified.
The total number of hydrogen bonds of a DNA-double Helix strand whose one strand has the following sequence of bases is _______ .
\(5^{\prime}-\mathrm{G}-\mathrm{G}-\mathrm{C}-\mathrm{A}-\mathrm{A}-\mathrm{A}-\mathrm{T}-\mathrm{C}-\mathrm{G}-\mathrm{G}-\mathrm{C}-\mathrm{T}-\mathrm{A}-3^{\prime}\)
View Solution
1. Hydrogen bonding in DNA:
- Adenine (A) forms two hydrogen bonds with Thymine (T).
- Guanine (G) forms three hydrogen bonds with Cytosine (C).
2. Count the hydrogen bonds:
- Number of G-C pairs: 4
- Number of A-T pairs: 4
3. Total number of hydrogen bonds:
\[ Total hydrogen bonds = 4 \times 3 + 4 \times 2 = 12 + 8 = 20 \]
Therefore, the correct answer is (33). Quick Tip: Count the number of hydrogen bonds formed by each base pair in the DNA strand.
















Comments