JEE Main 2025 April 3 Chemistry Question Paper is available for download. NTA conducted JEE Main 2025 Shift 1 B.Tech Exam on 3rd April 2025 from 9:00 AM to 12:00 PM and for JEE Main 2025 B.Tech Shift 2 appearing candidates from 3:00 PM to 6:00 PM. The JEE Main 2025 3rd April B.Tech Question Paper was Moderate to Tough.
Also Check: JEE Main 2025 Question Paper with Solution PDF Download
JEE Main 2025 April 3 Shift 2 Chemistry Question Paper with Solutions
| JEE Main 2025 April 3 Shift 2 Chemistry Question Paper Pdf | Download PDF | View Solution |

JEE Main 2025 Chemistry Questions with Solutions
Question 1:
40 mL of a mixture of CH\(_3\)COOH and HCl (aqueous solution) is titrated against 0.1 M NaOH solution conductometrically. Which of the following statement is correct?
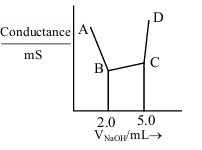
10 mL of 2 M NaOH solution is added to 20 mL of 1 M HCl solution kept in a beaker. Now, 10 mL of this mixture is poured into a volumetric flask of 100 mL containing 2 moles of HCl and made the volume upto the mark with distilled water. The solution in this flask is :
Fat soluble vitamins are :
A. Vitamin B\( _1 \)
B. Vitamin C
C. Vitamin E
D. Vitamin B\( _{12} \)
E. Vitamin K
Choose the correct answer from the options given below :
- Match the LIST-I with LIST-II.
LIST-I LIST-II
A. Pnicogen (group 15) I. Ts
B. & Chalcogen (group 16) II. Og
C. & Halogen (group 17) III. Lv
D. & Noble gas (group 18) IV. Mc
Choose the correct answer from the options given below :
For electron in '2s' and '2p' orbitals, the orbital angular momentum values, respectively are :
Compounds that should not be used as primary standards in titrimetric analysis are :
A. Na\( _2 \)Cr\( _2 \)O\( _7 \)
B. Oxalic acid
C. NaOH
D. FeSO\( _4 \).6H\( _2 \)O
E. Sodium tetraborate
Choose the most appropriate answer from the options given below :
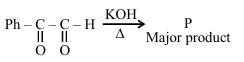
The major product (P) in the following reaction is :
In the following series of reactions identify the major products A and B respectively.
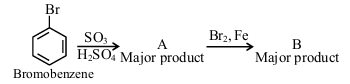
The standard cell potential (E\(^\circ_{cell}\)) of a fuel cell based on the oxidation of methanol in air that has been used to power a television relay station is measured as 1.21 V. The standard half cell reduction potential for O\( _2 \)/H\( _2 \)O (E\(^\circ_{O_2/H_2O}\)) is 1.229 V. Choose the correct statement:
Identify the diamagnetic octahedral complex ions from below ;
A. [Mn(CN)\(_6\)]\(^{3-}\)
B. [Co(NH\(_3\))\(_6\)]\(^{3+}\)
C. [Fe(CN)\(_6\)]\(^{4-}\)
D. [Co(H\(_2\)O)\(_3\)F\(_3\)]
Choose the correct answer from the options given below :
In Dumas' method for estimation of nitrogen 0.4 g of an organic compound gave 60 mL of nitrogen collected at 300 K temperature and 715 mm Hg pressure. The percentage composition of nitrogen in the compound is
(Given : Aqueous tension at 300 K = 15 mm Hg)
Mass of magnesium required to produce 220 mL of hydrogen gas at STP on reaction with excess of dil. HCl is
Given : Molar mass of Mg is 24 g mol\(^{-1}\).
Given below are two statements :
Statement I : Wet cotton clothes made of cellulose based carbohydrate takes comparatively longer time to get dried than wet nylon polymer based clothes.
Statement II : Intermolecular hydrogen bonding with water molecule is more in nylon-based clothes than in the case of cotton clothes.
In the light of the above statements, choose the Correct answer from the options given below
(1) Statement I is false but Statement II is true
(2) Statement I is true but Statement II is false
(3) Both Statement I and Statement II are true
(4) Both Statement I and Statement II are false
Given below are two statements :
Statement I : CrO\( _3 \) is a stronger oxidizing agent than MoO\( _3 \)
Statement II : Cr(VI) is more stable than Mo(VI)
In the light of the above statements, choose the correct answer from the options given below
(1) Statement I is false but Statement II is true
(2) Statement I is true but Statement II is false
(3) Both Statement I and Statement II are true
(4) Both Statement I and Statement II are false
Given below are two statements :
Statement I : Hyperconjugation is not a permanent effect.
Statement II : In general, greater the number of alkyl groups attached to a positively charged C-atom, greater is the hyperconjugation interaction and stabilization of the cation.
In the light of the above statements, choose the correct answer from the options given below
(1) Statement I is true but Statement II is false
(2) Both Statement I and Statement II are false
(3) Statement I is false but Statement II is true
(4) Both Statement I and Statement II are true
Given below are two statements :
Statement I : When a system containing ice in equilibrium with water (liquid) is heated, heat is absorbed by the system and there is no change in the temperature of the system until whole ice gets melted.
Statement II : At melting point of ice, there is absorption of heat in order to overcome intermolecular forces of attraction within the molecules of water in ice and kinetic energy of molecules is not increased at melting point.
In the light of the above statements, choose the correct answer from the options given below:
(1) Statement I is true but Statement II is false
(2) Statement I is false but Statement II is true
(3) Both Statement I and Statement II are true
(4) Both Statement I and Statement II are false
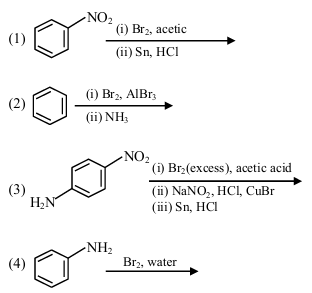
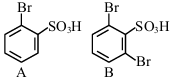
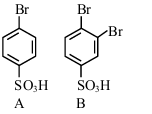
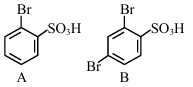
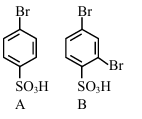
The sequence from the following that would result in giving predominantly 3, 4, 5 -Tribromoaniline is :
The correct orders among the following are:
[A.] Atomic radius : B < Al < Ga < In < Tl
[B.] Electronegativity : Al < Ga < In < Tl < B
[C.] Density : Tl < In < Ga < Al < B
[D.] 1st Ionisation Energy : In < Al < Ga < Tl < B
Choose the correct answer from the options given below :
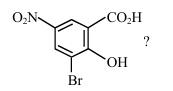
What is the correct IUPAC name of
Consider the following statements related to temperature dependence of rate constants.
Identify the correct statements,
A. The Arrhenius equation holds true only for an elementary homogeneous reaction.
B. The unit of A is same as that of k in Arrhenius equation.
C. At a given temperature, a low activation energy means a fast reaction.
D. A and Ea as used in Arrhenius equation depend on temperature.
E. When Ea >> RT. A and Ea become interdependent.
Choose the correct answer from the options given below :
X g of nitrobenzene on nitration gave 4.2 g of m-dinitrobenzene.
X = ____________ g. (nearest integer)
[Given : molar mass (in g mol\(^{-1}\)) C : 12, H : 1, O : 16, N : 14]
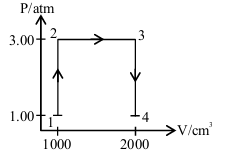
A perfect gas (0.1 mol) having \( \bar{C}_V = 1.50 \) R (independent of temperature) undergoes the above transformation from point 1 to point 4. If each step is reversible, the total work done (w) while going from point 1 to point 4 is (____________) J (nearest integer)
[Given : R = 0.082 L atm K\(^{-1}\)]
A sample of n-octane (1.14 g) was completely burnt in excess of oxygen in a bomb calorimeter, whose heat capacity is 5 kJ K\(^{-1}\). As a result of combustion, the temperature of the calorimeter increased by 5 K. The magnitude of the heat of combustion at constant volume is ____________ kJ mol\(^{-1}\) (nearest integer).
Among, Sc, Mn, Co and Cu, identify the element with highest enthalpy of atomisation. The spin only magnetic moment value of that element in its +2 oxidation state is ____________ BM (in nearest integer).
The total number of structural isomers possible for the substituted benzene derivatives with the molecular formula C\( _7 \)H\( _{12} \) is ____________ .










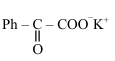
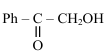

Comments