Collegedunia Team Content Curator
Content Curator
Wave function in quantum physics is the variable quantity that mathematically describes the wave characteristics of a particle. Value of a particle’s wave function at a given point of space and time is related to the possibility of the particle being there at the time. It describes the quantum state of the particle as a function of momentum, spin, position, and time. It is denoted by Ψ, a Greek letter known as psi.
Key Terms: Wave Function, Quantum State, Momentum, Particle, Schrodinger Equation, Spin,
What is Wave Function?
[Click Here for Previous Year Questions]
The wave function is a mathematical description of the quantum state of a particle as a function of momentum, time, position, and spin.
- We can denote it using a Greek letter called psi, Ψ.
- The value of the wave function of a particle at a given time is related to the likelihood of the particle being there at the time.
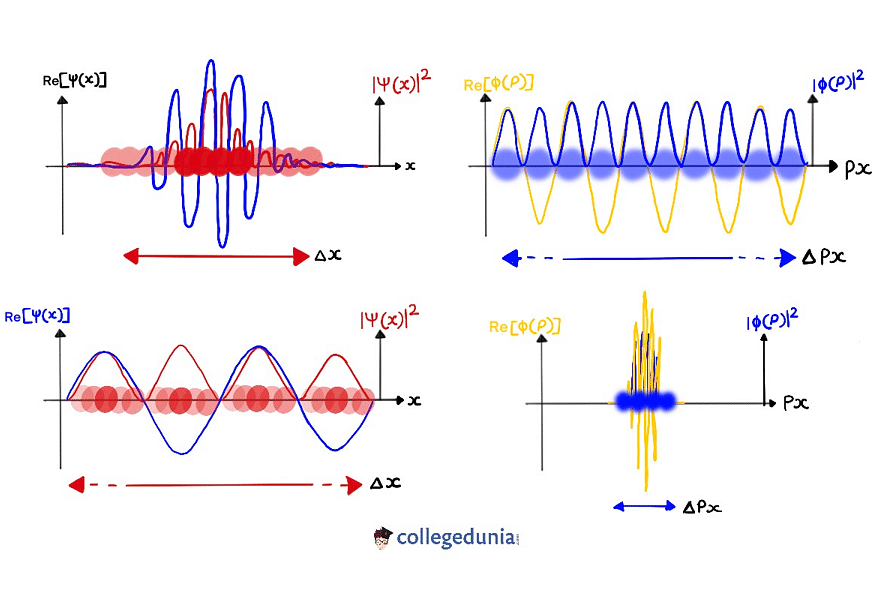
Wave Function
- The probability of finding an electron within the matter can be explained with the use of the wave function.
- This can be done if we include an imaginary number that is squared to get one real solution which results in the position of the electron.
- The probability of finding the particles described by a specific wave function at a given point is proportional to the square of the value of the wave function.
- The concept of wave function was given with the development of the Schrodinger equation in 1925.
| Frequently Asked Questions on Wave Function Ques. What is the importance of wave function? Ans. Ψ2 is the physical interpretation of wave function as it provides the probability information of locating a particle at allocation in a given time. Ques. What are the limitations of wave function? Ans. Following are the limitations of wave function:
|
Properties of Wave Function
[Click Here for Sample Questions]
The important characteristics of wave function include:
- All energy calculations become very easy using the Schrodinger equation.
- Using the wave function the probability distribution in three-dimensional is established.
- All measurable information is available about the particle.
- The wave function, Ψ, should be continuous and single-valued.
- Probability distribution using the wave function in the three dimensions is established.
- If a particle exists, then the probability of finding a particle is 1.
Also Read:
What is Schrodinger Equation?
[Click Here for Previous Year Questions]
Schrodinger equation is defined as the linear partial differential equation describing the wave function, Ψ.
- The Schrodinger equation is named after Erwin Schrodinger.
- Schrodinger could work on the wave function by using the postulates of quantum mechanics.

Schrodinger Equation
Following is the equation of the Schrodinger equation or the formula for wave function:
Time-dependent Schrodinger equation:
ih \({\partial \over \partial t}\) Ψ(r, t) = [ \({-h^2\over 2m}\)∇2 + V (r, t)] Ψ(r,t)
Time-independent Schrodinger equation:
[\({-h^2\over 2m}\) ∇2+ V (r)] Ψ(r) = EΨ(r)
Where,
- m = mass of the particle
- ∇ = laplacian
- i = imaginary unit
- h = h/2π: reduced Planck constant
- E = constant equal to the energy level of the system
Read More: NCERT Solutions for Class 11 Physics Chapter 15 Waves
Postulates of Quantum Mechanics
[Click Here for Sample Questions]
The six postulates of quantum mechanics are listed below:
- The time evolution of the wave is given with the help of the time-dependent Schrodinger equation.
- The linear set of independent functions is formed from the set of eight functions of operator Q.
- Operator Q which is associated with a physically measurable property q is Hermitian.
- Using wave function it becomes very understand the system of a particle in a conservative field of force systems.
- The expectation value of the property q can be determined by performing the expectation value integral concerning the wavenumber which is associated with the system.
- For every physical observable q, there is an operator Q operating on the wave function associated with a definite value of that observable such that it yields a wave function of it numerous times.
Read More: Beats
Derivation of Formula of Wave Function
Wave function of a particle of fixed energy E can be written as a linear combination of wave functions of the form:
\(\Psi (x,t) = Ae^{i(kx-wt)}\) (1)
This is representative of a wave that travels in the positive x direction. A corresponding wave travels in the opposite direction. Thus, the result is a standing wave that stands true to the boundary conditions.
This corresponds, in an intuitive manner, to the classical notion of a particle bouncing. This particle bounces back and forth between the potential well walls. It is also possible to adopt the wave function as being the suitable wave function for a particle that is free.
The momentum of this free particle is p = hk and its energy is E = hω. So, one can see that:
\(\frac{\vartheta \Psi}{\vartheta x^2} = -k^2 \Psi\) (2)
By using E = p2/2m = h2k2/2m, one can write:
\(\frac{-h^2 \vartheta ^2 \Psi}{2m \vartheta x^2} = \frac{p^2 \Psi}{2m}\) (3)
Furthermore, similarly
\(\frac{\vartheta \Psi}{\vartheta t} = -i w \Psi\) (4)
One can also write this, using E = hω:
\(ih \frac{\vartheta \Psi}{\vartheta t} = hw \psi =E \Psi\) (5)
Now generalizing that this is possible to the situation in which there is a potential energy as well as a kinetic energy present, then E = p2/2m + V (x) so that
\(E \Psi = \frac{P^2 \Psi}{2m} + V(x) \Psi\) (6)
where Ψ is now the wave function of a particle whose movement takes place in the presence of a potential V (x). However, considering the results Eq. (6.3) and Eq. (6.5) still apply in this case, then what we are left with is:
\(-\frac{h^{2}\vartheta ^{2}\psi }{2m\vartheta x^{2}} + V\left ( x \right )\Psi = ih\frac{\vartheta \psi }{\vartheta t} \) (7)
Significance of Wave Function
[Click Here for Sample Questions]
In the case of light or sound, the square of the amplitude of the wave at any point will give us the intensity of the sound or light at that particular point.
- Similarly, the square of the amplitude of the given electron wave at any point will give us the intensity of the electron wave at that point which due to the Heisenberg Uncertainty Principle means the probability of finding the electron at that particular point.
- The square of the amplitude of electrons at any point gives the probability of finding the electron at that point that is electron density at that point.
- The region around the nucleus representing the electron density at different points is called an orbital.

Amplitude of Wave Function
- The wave function for an electron in an atom is called the orbital wave function or atomic orbital.
- Since electrons can have any wave function, there are many atomic orbitals in an atom.
- The probability will provide the best possible description of any such situation which we will be unable to describe with certainty.
- Most of the time electrons are used to spend in the volume of the sphere which is bounded by that distance and for the rest of the time, the electrons can be found outside the volume of the sphere.
- The electron cloud is the region of space around the nucleus that can describe the probability of finding an electron of given energy which is given in terms of dots.
- An atomic orbital can be defined as the three-dimensional space around the nucleus within which the probability of finding an electron of a given energy is then maximum.
Normalization of Wave Function
In the case of normalization of the wave function, the probability of finding a particle if it is existing in the system becomes 1. This depicts that the exact form of wave function Ψ is found.
Read More: Period angular frequencyPhysical Significance of Wave Function
[Click Here for Sample Questions]
- As the wave function is not a quantity that can be observed there is no physical meaning to the wave function. Instead, it is complex.
- It is expressed as ψ(x, y, z, t) = a + ib, and the complex conjugate of the wave function is expressed as ψ*(x, y, z, t) = a – ib.
- The product of these two of them indicates the probability density of finding a particle in space at a time.
- Whereas, ψ2 is a physical interpretation of wave function as it is providing the probability information for locating a particle at allocation in a given time.
Also Check Out: Transverse and Longitudinal waves
Previous Year Questions
- The maximum particle velocity in a wavemotion … (KCET 2007)
- The equation of progressive wave is y=0.2 sin 2π … (BITSAT 2007)
- A wave along a string has the following equation y … (KEAM 2019)
- The phase velocity of a wave described by the equation … (KEAM)
- The principle of superposition is basic to the phenomenon … (KEAM)
- Suppose that the electric field amplitude of electromagnetic wave is… (KCET 2021)
- A light beam of intensity 20W/cm2 is incident normally on… (KCET 2020)
- For a plane electromagnetic wave propagating in x-direction… (NEET 2021)
- The magnetic field in a travelling electromagnetic wave… (VITEEE 2018)
- For sky wave propagation of 10 MHz signal… (JCECE 2007)
- If \(\overrightarrow{E}\) and \(\overrightarrow{B}\) are the electric and magnetic field vectors of e.m. waves… (BITSAT 2019)
- Which of the following rays is emitted by a human body… (VITEEE 2010)
- A pipe open at both ends and a pipe closed at one end have same… (MHT CET 2019)
- A wave travelling along a string is described by the equation… (MHT CET 2008)
- An object flying in air with velocity… (NEET 2019)
Things to Remember
[Click Here for Sample Questions]
- Wave function is a mathematical description of the quantum state of a particle as a function of momentum, time, position, and spin.
- We can denote the wave function using a Greek letter called psi, Ψ.
- The probability of finding an electron within the matter can be explained with the use of the wave function.
- The Schrodinger equation is defined as the linear partial differential equation describing the wave function, Ψ.
- The linear set of independent functions is formed from the set of eight functions of operator Q.
- As the wave function is not a quantity that can be observed, there is no physical meaning to the wave function.
Wave Function PDF
Read More:
Sample Questions
Ques. What is meant by the wave function? (1 mark)
Ans. A wave function is a mathematical description of the quantum state of any quantum system which is isolated. However, it is a complex-valued probability amplitude.
Ques. What is an acceptable wave function? (1 mark)
Ans. An acceptable wave function must be single-valued, must be normalized, and has to be continuous in the given time interval.
Ques. What is meant by the harmonic wave function? (1 mark)
Ans. A harmonic wave function is defined as a periodic function whose functional form is "sine" or "cosine".
Ques. How do we measure wave function? (1 mark)
Ans. The wave function can be measured with the help of the Schrodinger equation. The Schrodinger equation is the linear partial differential equation that describes the wave function.
Ques. Does the wave function is having any physical significance? (2 marks)
Ans. The wave function is a complex quantity. Also, this section is not an observable quantity when it has an association with a moving particle. Also, it doesn’t have any direct physical meaning.
Ques. What is the Schrodinger equation? (3 marks)
Ans. This Schrodinger equation is defined as the linear partial differential equation describing the wave function, Ψ. This equation is named after Erwin Schrodinger. Schrodinger could work on the wave function using the postulates of quantum mechanics.
Following is the equation of Schrodinger equation:
- Time dependent Schrodinger equation: ih \({\partial \over \partial t}\) Ψ(r, t) = [ \({-h^2\over 2m}\)∇2 + V (r, t)] Ψ (r,t)
- Time independent Schrodinger equation: [\({-h^2\over 2m}\) ∇2+ V (r)] Ψ (r) = E Ψ (r)
Where,
m = mass of the particle
∇ = laplacian
i = imaginary unit
h = h/2π: reduced Planck constant
E = constant equal to the energy level of the system
Ques. What is a wave function and how can its value be found? (3 marks)
Ans. A wave function is a mathematical tool that is used in quantum mechanics to describe any physical system. It is a function from a space that maps the possible states of the system in complex numbers. The law of quantum mechanics describes how the wave function had evolved. The value of the wave function is probability amplitude, complex numbers, and the square of the absolute values which, gives the probability distribution that the system will be in any of these possible states.
Ques. What is a normalization of the wave function? (2 marks)
Ans. It is the situation wherein all the probabilities add up to make it 1. In case it adds up to some other constant, then this value is incorporated in the wave function to make the probability 1 and attain the state of normalization.
Ques. State the properties and characteristics of the wave function. (5 marks)
Ans. The properties of the wave function are:
- All measurable information is available about the particle.
- The wave function should be continuous and only single-valued.
- Every calculation becomes very easy using the Schrodinger equation.
- Using the wave function the probability distribution in three-dimensional is established.
- The probability distribution in the three-dimensional is established using the wave function.
Ques. Write the importance of wave function. (5 marks)
Ans. In the case of light or sound, the square of the amplitude of the wave at any point will give us the intensity of the sound or light at that particular point. Similarly, the square of the amplitude of the given electron wave at any point will give us the intensity of the electron wave at that point which because of the Heisenberg Uncertainty Principle means the probability of finding the electron at that particular point. The square of the amplitude of electrons at any point gives the probability of finding the electron at that point that is electron density at that point. The region around the nucleus which represents the electron density at different points is called an orbital.
The wave function for an electron in an atom is called the orbital wave function or atomic orbital. Since electrons can have any wave function, thus there are many atomic orbitals in an atom. The probability will provide the best possible description of any such situation which we will be unable to describe with certainty.
Ques. What are the postulates of the wave function? (5 marks)
Ans. The postulates of the wave function are as follows:
- The time evolution of the wave is given with the help of the time-dependent Schrodinger equation.
- Using wave function it becomes very understand the system of a particle in a conservative field of force systems.
- The linear set of independent functions is formed from the set of eight functions of operator Q.
- Operator Q which is associated with a physically measurable property q is Hermitian.
- The expectation value of the property q can be determined by performing the expectation value integral concerning the wavenumber which is associated with the system.
Do Check Out:







Comments