Jasmine Grover Content Strategy Manager
Content Strategy Manager
Stress in physics refers to the force that acts on a unit area of a material. Stress can deform a given body. The effect that stress has on the body is known as strain. An opposing force known as restoring force is generated inside the object to bring back the object to its original shape and size. Stress is a physical quantity denoted by the symbol ‘\(\sigma\)’. The SI unit of stress is N/m².
The ability of an object to face the applied stress, to the extent it can bear is known as its ‘Strength’. On the basis of the direction of the deforming forces that act on a body, stress in physics is of 2 types – Normal Stress and Tangential or Shearing Stress. The stress formula is given as –
Stress \(\sigma\) = \(F\over A\)
Here, F refers to Force and A denotes Area.
Key Terms: Stress, Stress formula, Longitudinal Stress, Sheer Stress, Bulking Stress, Hydraulic Stress
What is Stress?
[Click Here for Sample Questions]
In physics, stress is the restoring force per unit area of the material. Stress units can be used to discover how much force an object has experienced.
- Stress consistently relies upon strain, which means, stress is a reason for the strain.
- If a body doesn't see disfigurement by the strain it won't deliver stress.
- Stress in Physics is the internal force that is developed per unit area within the deformed object.
- This internal force known as stress is equal in magnitude and opposite to the applied deforming force.
For instance, when we squeeze and leave a cushion (external force), instantly some force develops in the cushion which acts in the opposite way. This opposite force that develops in the cushion when an external force is applied is known as restoring force.

Read More:
Stress Formula
[Click Here for Previous Year Questions]
The mathematical formula of stress is represented as –
\(Stress = {Restoring\ force \over Cross\ sectional\ area}\)
It can also be represented as \(\sigma\) = F/A
- Where Restoring force is represented in Newton
- The cross-sectional area, A is represented in m2
Solved ExampleQues. A rod has a 10 mm radius and 10 cm length. A 200N force is compressed along its length. Calculate the stress in the rod. Solution: Stress = Force/area Stress = (200/(\(\pi\) x 10 x 10-3)2 Stress = 6.36 x 105 Nm-2 |
Important formulas relating to stress are tabulated below.
| Stress | Formula |
|---|---|
| Normal Stress | Axial force/Cross-Sectional Area or σ =P/A |
| Longitudinal Stress | Deforming Force/Area of cross-section |
| Shearing Stress | Force/Surface Area |
SI Unit of Stress
[Click Here for Sample Questions]
Stress is expressed usually in Nm2.
| System of Units | Stress Unit |
|---|---|
| Fundamental units | Kgm-1s-2 |
| SI unit (derived units) | Nm2 or Pa (Pascal) |
Types of Stress
[Click Here for Previous Year Questions]
There are different types of stress in physics, some of them are as explained below –
Normal Stress
Stress is considered to be normal when the deforming force’s direction is perpendicular to the cross-sectional area of the body.
- When the length of the wire or the volume of the body changes, the stress level will return to normal.
-
Normal stress can further be classified on the basis of the dimension of force as – Longitudinal stress and Bulk or Volumetric stress.

Longitudinal Stress
Consider a cylinder with longitudinal stress. When two cross-sectional regions of a cylinder are exposed to equal and opposite forces, the cylinder experiences longitudinal stress. The formula for longitudinal stress is as follows.
Longitudinal Stress = Deforming Force/Cross-Section Area = F/A
- When the body is subjected to longitudinal stress, the deforming force acts along the length of the body, as the name implies.
- Longitudinal tension causes the body's length to alter. As a result, it affects a minor variation in diameter.
- Longitudinal stress either stretches or compresses an item along its length.
Read More:
Therefore, Longitudinal stress can be further classified into two types on the basis of the direction of deforming force –
Tensile Stress
Tensile Stress is the force per unit area. When stress is applied, the length of the body increases due to the force.
- Tensile stress is measured when a rod is stretched in accordance with the third law of motion.
- Rubber is a frequent example of tensile stress.
- It is the amount related to stretching. It is generally represented by the σ symbol.
Compression Stress
When a tangential force is applied to a body, the form and volume of the body change.
- The length of the body is reduced when compression tension is applied.
- Tensile stress is the inverse of compression stress.
- If you've ever squeezed a squeaky toy, you've experienced compressive stress on the body.
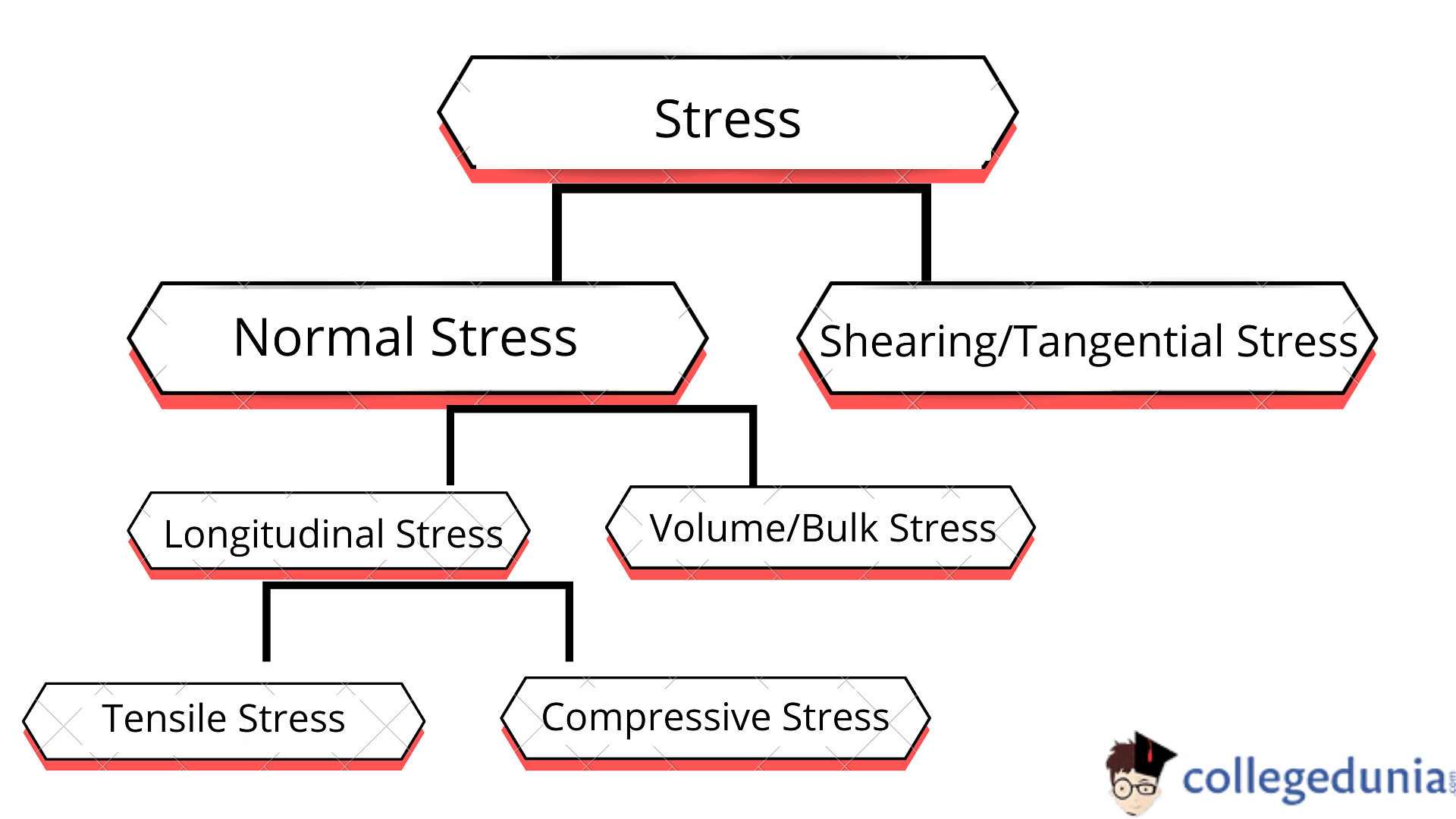
Bulk Stress
Volumetric stress is a type of stress in which the volume of the body varies as a result of stress. Normal stress on a body generates a change in length or volume, whereas tangential stress causes a change in the form of the body. When a body under the force of pressure p is submerged in a liquid, the body is confronted with a force that is perpendicular to the body's surface.

Bulk Stress
The bulk stress formula is as follows
Bulk Stress = Force /Area = Pressure
Shearing Stress
When the force exerted is parallel to the cross-sectional area of the body, it restores force per unit area known as tangential stress. Relative displacement occurs between opposing body faces. This changes the shape of the body
Hydraulic Stress
When a fluid applies force to the body, hydraulic stress is the restoring force per unit area.
Consider a rubber ball that has been dipped in a pond. As a consequence of the strain exerted on the ball by the pressure of water from all directions, the ball seems to be somewhat constricted. Because of the force exerted by the water, a restoring force arises in the ball, equivalent in size to the force exerted by the water but in the opposite direction. This is referred to as hydraulic stress.
Things to Remember
- Stress in physics is the force acting on a unit area of a material.
- The formula of stress is Stress \(\sigma\) = \( F \over A\)
- Stress is denoted by the symbol ‘\(\sigma\)’ and its unit is N/m².
- Strain is used to portray the effect of weight on the body.
- Stress is considered normal stress when the deforming force’s direction is perpendicular to the cross-sectional area of the body.
- When the force exerted is parallel to the cross-sectional area of the body, it restores force per unit area, known as shearing or tangential stress.
Previous Year Questions
- A copper wire of length 2.2m and a steel wire … [KCET 2013]
- One end of a horizontal thick copper wire of length … [JEE Advanced 2013]
- When a rod is heated but prevented from expanding the stress … [BHU UET]
- The breaking stress of a wire of length ll and radius r is …
- A steel wire can withstand a load up to … [BITSAT 2008]
- A light rod of length 100 cm is suspended from the ceiling horizontally … [AP EAPCET]
- Two wires are made of the same material and have the same volume … [NEET 2018]
- Elastic strain energy of 10 J is stored in a loaded copper rod … [TS EAMCET 2018]
- If the ratio of diameters, lengths and Young's modulus of steel … [NEET 2003]
- Two wires A and B are stretched by the same load … [KCET 2018]
Sample Questions
Ques 1. The shear modulus of a coil spring determines its stretching. How? (2 marks)
Ans. When a coil spring is extended, neither its length nor volume changes; only its form changes. As a result, shear modulus determines coil spring stretching.
Ques 2. A police jeep on a petrol duty on a national highway was traveling in the same direction at a speed of 54km/hr. It discovers a burglar speeding up in a car at 126km/hr in the same direction. The police sub-inspector used his service pistol with a muzzle speed of 100m/s to shoot at the thief's vehicle. How fast will the bullet hit the thief's car? (3 marks)
Ans. VPJ = 54km/hr = 15m/s
VTC = 126 km/hr = 35 m/s
VCP = 35 – 15 = 20m/s
The bullet's muzzle speed= 100m/s
VCP = Velocity of the automobile in relation to the police.
VBC = Bullet Velocity in Relation to Car
= 100 – 20 m/s
As a result, the bullet will strike the vehicle at a speed of 80 m/s.
Ques 3. If a steel rod of 1 m length has a radius of 10 mm and a 100 kN force stretches the rod along its length, then calculate its (3 marks)
a) Stress
b) Elongation
c) Strain of the rod
It is given that Y = 2.0 x 1011N/m2
Ans. a) Stress = FA=F.πr2
= 3.18 x 108 N/m2
b) Elongation
ΔL = (FA)LY
= 1.59 mm
c) Strain = Δ LL
= 0.16%
Ques 4. For the following statements, state True or False. Give a reason for the same. (3 marks)
(a) The rubber’s Young’s modulus is greater than Young’s modulus of steel;
(b) Shear Modulus determines the stretching of a coil
Ans. The answers are –
(a) False. The reason for this is that when steel and rubber wires of the same cross-sectional area and length are subjected to the same deforming force, then the extension that is produced in steel is less than the extension produced in rubber. So Ys> Yr. Hence, for producing the same strain in steel and rubber, more stress is required in the case of steel.
(b) True. This is because when a coil spring is stretched, there is neither a change in the volume of the coil nor a change in its length (i.e., the length of the wire forming the coil spring). Now, since the change takes place in the shape of the coil spring, the shear modulus is responsible for determining its stretching.
Ques 5. Calculate the bulk modulus of water if it is given that the initial volume of the water is 100 L, the increase in pressure is 100.0 atm (1 atm = 1.013 x 105 Pa), and the final volume is 100.5 L. At a constant temperature, compare the bulk modulus of water and air. Explain why the ratio is so large. (5 marks)
Ans. P = 100 atm
= 100 x 1.013 x105 Pa
Initial volume (V1) = 100 L
= 100 x 10-3m3
Final volume (V2) = 100.5 L
= 100.5 x 10-3m3
Therefore, ΔV= V2 - V1
= 0.5 x 10-3m3
We know that, Bulk Modulus (B) = P/(ΔV/V)
![]()
= 2.06 x 109 Pa
Also, the bulk modulus of air at STP is
Bair = 105 Pa
Therefore, \(\frac{Bw}{Bair}\)= 2.026 x 109105
= 20260
This ratio is too large. as the strain for air is comparatively larger than for water at the same temperature. Also, the intermolecular distances in the case of liquids are very small than those in the case of gases. Hence, in liquids, there are larger interatomic forces than in gases.
Ques 6. A steel wire with a cross-sectional area of 3.0 x 10-5 m2 and length 4.7 m stretches the same amount as a copper wire of a cross-sectional area of 4.0 x 10-5 m2 and length 3.5 m under a given load. What is the ratio of Young’s modulus of steel to young’s modulus of copper? (5 marks)
Ans. Here, for steel wire,
Length of wire, l1= 4.7 m
Area of cross-section, i.e A1 = 3.0 x 10-5 m2
Stretching, Δl1= Δl(say)
Stretching force on steel, F1 = F
For the copper wire, the length of wire, l2 = 3.5 m
Cross-section area, A2 = 4.0 x 10-5m2
Stretching, Δl2 = Δl (given);
Stretching force on copper, F2 = F
Let Y1 Young’s modulus of steel and Y2 of copper wire respectively
Therefore,
Y1 = (F1/A1)/(Δl1/l1) = (F1 x l1)/(A1 x Δl1) --- 1)
Y2 = (F2/A2)/(Δl2/l2) = (F2 x l2)/(A2 x Δl2) --- 2)
Dividing 1 by 2,
\(\frac{Y1}{Y2}\)= \(\frac{F * 4.7}{3 * 10^{-5} * \Delta l}\)x \(\frac{4 * 10^{-5} * \Delta l}{F * 3.5}\)
Thus, Y1:Y2 = 1.8:1
Ques 7. Define longitudinal stress. (1 mark)
Ans. Longitudinal stress is the stress experienced by an object along its length when equal and opposite deforming forces perpendicular to the area of the cross-section are present.
Ques 8. What is the effect of tangential stress on an object? (1 mark)
Ans. Tangential stress leads to a change in the shape of the object.
Ques 9. What is the direction of the deforming force in the case of shearing stress? (1 mark)
Ans. In shearing stress, the deforming force is parallel to the cross-sectional area.
Ques 10. What is the unit of Stress? (1 mark)
Ans. The SI unit of stress is N/m2 or Pascal.
Read More:






Comments