
Jasmine Grover Content Strategy Manager
Content Strategy Manager
Strain refers to the deformity or change in length of a body when it is subjected to stress. Strain occurs when stress is applied to the body that is still in equilibrium state (it means that the net force acting on the body is zero). The strain applied to a body can cause both reduction or elongation of the body. Strain is considered as a fractional change in either the volume, length or geometry. Hence it is a dimensionless number. The three types of strain are:
- Longitudinal Strain
- Shearing Strain
- Volumetric Strain
The formula for Strain is given by,
Strain = \(\frac{Deformity \ or \ Change\ in\ the\ dimension\ due\ to\ applied\ stress}{Actual\ Dimension}\)= \(\frac{\triangle x}{x}\)
Related Links
- Appearing for JEE Main, Download JEE Mains PYQ for all sabjects
- Appearing for NEET, Download NEET PYQ for all subjects
| Table of Content |
What is Strain?
[Click Here for Sample Questions]
When a body is subjected to a force that causes a change in physical structure of the body, there lies an equally restoring force. This restoring force that acts internally is in response to the deforming force applied on the body externally and sort of opposes the deforming force. Hence, this internal restoring force acting per unit area is called Stress applied on the body.
Strain can be defined as:
| “The amount of deformation a body undergoes in the direction of applied force, divided by the body’s initial dimensions.” |
Even though the restoring force acts opposite to the direction of the deforming force, they both have equal magnitude.

Strain
As a result of stress, change occurs in the body. The change or deformity consequential to the stress acting on the body is called strain. Strain can be defined as the amount or measure of deformity that takes place due to the force applied on the object.
|Restoring Force| = |Deforming Force|
Strain is denoted with (ε). It has no units.
Also Read:
Strain Formula and Derivation
[Click Here for Previous Year's Questions]
The strain formula in physics in general is given by:
| Strain = Δx/x |
Where,
- Δx is the change or deformity formed in the dimension of the body
- x is the actual dimension of the body before the stress or restoring force was applied
Strain can also be represented as: “Change in Dimension of the body/Original Dimension of the body”
Strain can be dimensionally analyzed as follows:
Strain = Δ x/x
= L/L
= M0 L1 T0 / M0 L1 T0
= M0 L0 T0
Hence, it is proven that Strain has no units [M = Mass, T = Time, L = Length].
Also Read: Strain Energy FormulaType of Strain
[Click Here for Sample Questions]
Strain is mainly classified into three types:
Longitudinal Strain
Longitudinal strain is produced as a result of longitudinal stress. In this peculiar case, the stress or restoring force per unit area acts on the length basis of the object. It means that the applied deforming force will cause a change in the length of the object.
Therefore, the strain developed will be called longitudinal because the physical change in the object has occurred on the parameters of length. It can either be compressive (reduction in length) or tensile (increase in length). It is represented as:
| Longitudinal Strain = Δ L/L |
Where,
- Δ L is the change in length of the object that can be calculated by subtracting the original length from the newly produced length
- L is the actual length of the object before stress was applied at its equilibrium state

Longitudinal Strain
Shearing Strain
When the stress applied on the body appears to work tangentially on the object, it gives rise to shearing strain. Stemmed from tangential stress or shearing stress, the shearing strain is the result of change in the body that occurred tangentially on the body. It is represented as Shearing Strain = Shearing Stress/Shearing Strain, thus
| Δx/L = tanθ |
Where,
- Δ x is the change induced tangentially
- L is the length of the object
- Θ is the angular displacement of the object from its vertical position

Shearing Strain
Volumetric Strain
This strain is produced particularly when volume-based changes take place in an object.
The stress applied here is called hydraulic stress which causes compression in the volume of the object. Here, the objects taken are particularly fluid (like water and gas or any substance that can be compressed to induce a change in volume).
Therefore,
| Volumetric Strain = Δ V/V |
Where,
- Δ V is the change in volume formed due to hydraulic stress in the geometric shape of the body
- V is the actual volume of the body before hydraulic stress or hydraulic pressure was applied
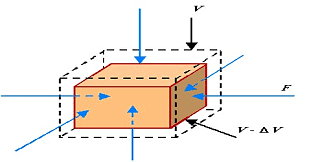
Volumetric Strain
Also Read:
| Important Concept Related Links | ||
|---|---|---|
| Stress | Tensile Stress | Elastic moduli |
| Shear Modulus | Stress and strain | Hooke’s law |
Stress-Strain Curve
[Click Here for Previous year's Questions]
The stress-strain curve is regarded as the graphical representation of the relationship between tensile stress and strain. The graph is plotted on the basis of Hooke’s Law
(Hooke’s Law suggest that, Stress = K x Strain, where K is proportionality constant represented as modulus of elasticity)

Stress-Strain Curve
Observations Drawn from the Graph:
- From 0 to A, the stress and strain move hand-in-hand proportionally by following Hooke's law. The ratio of Stress/Strain remains constant (i.e. K)
- But, from A to B, the proportionality vanishes as strain falls even though the same amount of stress is applied. A, is, therefore, called the proportionality limit. However, the curve continues to rise.
- At point B, which is the yielding point or the elastic limit point, stress is now equal to the strength of the material.
- From B to D, it is the period when the load applied got lifted. Yet, the material did not jump back to its original form. It means that due to the loss of elasticity, the material has a permanent strain.
- When more stress is applied to induce strain, the material ultimately faces a permanent fracture at point C, called the breakeven point or the fracture point.
Points to Note
|
Previous Year Questions
- The upper end of a wire of diameter … [BITSAT 2010]
- When a rod is heated but prevented from expanding the stress … [BHU UET]
- Two wires of same length and same material … [KEAM]
- The breaking stress of a wire of length ll and radius r is …
- Four wires of the same material are stretched by the same load …
- A steel wire can withstand a load up to … [BITSAT 2008]
- A copper wire of length 2.2m and a steel wire … [KCET 2013]
- A light rod of length 100 cm is suspended from the ceiling horizontally … [AP EAPCET]
- A copper wire and a steel wire of the same diameter and length … [BHU UET]
- Two wires are made of the same material and have the …
- Elastic strain energy of 10 J is stored in a loaded copper … [TS EAMCET 2018]
- A load of 1 kg weight is attached to one end … [BITSAT 2008]
- There is some change … [BITSAT 2008]
- If the ratio of lengths, radii and Young's modulus of … [VITEEE 2009]
- One end of a horizontal thick copper wire of length … [JEE Advanced 2013]
Things To Remember
- Strain is defined as the amount of deformation that occurs in a body when stress is applied.
- Strain is of three types: Longitudinal, shearing and volumetric. Each of them is produced by the stress of three kinds: Longitudinal, tangential and hydraulic.
- Strain is a unitless quantity and is represented by the letter epsilon (ε).
- Strain formula = Δ x/x, where, Δ x = change in dimension of the body and x = original dimension of the body.
- Strain is developed in response to the stress produced. More the stress, the more the strain. However, there comes a breaking point when the elasticity of the material gives up and no extra strain is produced even if more stress is applied.
Also Read:
| Important Chapter Related Topics | ||
|---|---|---|
| Bulk Modulus | Pressure | Shear Modulus |
| Surface Energy | Surface tension | Yield Strength |
| Beam Deflection Formula | Mechanical Properties of Solids | Relation between Elastic Constants |
Sample Questions
Ques. Is the stretching of a coil string determined by its shear modulus? (1 Mark)
Ans: Yes, the stretching of the coil string is determined by its shear modulus because only the length experiences change whenever the string is stretched or compressed. There lies no effect on its volume as well as length.
Ques. A spherical ball compresses by 0.5% in volume when a 100 atm pressure is applied. Calculate the strain and bulk modulus of the ball. (2 marks)
Ans: Strain = 0.5% = Δ V/V
Δ V/V = 0.5/100= 0.005
Pressure = F/A = Stress
Stress = Strain x Bulk modulus
100 atm = 0.005 x Bulk modulus
Bulk modulus = 0.005/100 atm
[1 atm = 105 N/m2;100 atm = 100 x 105 N/m2]
Bulk modulus = 0.005/100 x 105
Bulk modulus = 5 x 1010 N/m2
Ques. Compute the strain and elongation when two wires of diameter 0.25 m are subjected to load. One is made up of steel while the other is crafted out of brass (see fig).
Y of steel = 2x1011Pa; Y of brass = 0.9×1011 Pa (5 marks)

Ans: Force exerted on the steel wire = sum of masses of both the loads x acceleration due to gravity
Force on steel wire = (4+6) kg x 9.8 m/s2 = 10 x 9.8
Force on steel wire = 98 N
Stress on Steel wire = Force on Steel wire / area of steel wire
A = Area of steel wire = area of brass wire = \(\pi\)r2
Radius (r) = diameter /2
r = 0.25/2
r = 0.125 m
A = \(\pi\)(0.125)2
A = 0.049 metre square.
Stress on Steel wire = 98/0.049 = 1997.5 N/m2
Force on brass wire = mass of load on brass x acceleration due to gravity
Force on brass wire = 6 x 9.8 = 58.8 N
Stress on brass wire = force on brass wire/area
Stress on brass wire = 58.8/0.049 = 1200 N/m2
Strain on brass wire = stress of brass/young's modulus of brass
Strain on brass wire = 1200/0.9×1011
Strain on brass wire = 1333.33 x 10-11
Elongation of brass wire:
Δ L/L = strain of brass wire
Δ L = strain of brass wire x L (length of brass wire) = 1333.33 x 10-11 x 1 = 1333.33 x 10-11 m
Strain on steel wire = stress of steel wire/ young’s modulus of steel
Strain on steel wire = 1997.5/2 x 1011
Strain on steel wire = 998.75 x 1011
Elongation of steel wire:
Δ L/L = strain on steel wire
Δ L = strain of steel wire x L (length of steel wire) = 998.75 x 10-11 x 1.5
Δ L = 1498.125 x 10-11 m
Ques. A steel rod of length 2 m and having an area of 0.30 cm square suffers the tension of a 550 kg milling machine hung on its lower end. Find the stress, strain and elongation produced in the rod. (Y= 2.0 × 1011 Nm-2) (3 marks)
Ans: Stress = F/A
Force = mass x acceleration due to gravity = 550 x 9.81 = 5395.5 N
A = 0.0003 m2
Stress = 5393.5/0.0003 m2
Stress = 17985000 N/ m2
Strain x Young Modulus = Stress
Strain = Stress/Young Modulus(Y)
Strain = 17985000/2 x 1011
Strain = 8.99 x 105
Elongation Produced = Strain = Δ L/L
Δ L=? L = 2 m
8.99 x 105 = Δ L/2
Δ L = 17.98 x 105 m
Ques. If the length of a wire rises by 16 cm because a load of 5 kg is loaded/hung on it, find the decrease in its length when diameter is 2 times the previous one. (2 marks)
![]()
As we see that l \(\propto\) ¼ of diameter.
Therefore, doubling the diameter will cause ¼th reduction in l.
Ques. If a mass of 14.5 kg is hung at the lowest point on the end of 1 m long steel wire (unstretched), what will be the elongation induced when the wire is turned into a vertical circle of 2 rev/s angular velocity? (3 marks)
Ans. Cross-sectional area of the wire = 0.065 cm2 = 0.0000065 m2
Mass of object, m = 14.5 kg.
Length of wire, L = 1 m
Angular velocity = 2 rev/s = 12.56 rad/s
Area, A = 0.065 cm2
Total force, F = mass x acceleration due to gravity + mass x (angular velocity)2 x L
F = 14.5 x 9.8 + 14.5 x (12.56)2 x 1
F = 2430 N (approx)
Stress = strain x young’s modulus (Y)
Stress = F/A = 2430/0.0000065 = 381,538,461.5 N/m2
Y (for steel wire) = 2 x 1011 Pa
Strain = Δ L/L
381,538,461.5 = (Δ L/1) x 2 x 1011
190,769,230.8 x 10-11 = Δ L
1.9 x 10-3 m = Δ L
Ques. Draw comparison between the density of water on the surface and at 100 m depth, provided that: 1/K (i.e. compressibility) = 1023/22 per atm (1 atm = 1.015 × 105 Pa.) (5 marks)

Now, let V = volume of water at surface
V’ = volume of water at 100 m depth of the lake
Δ V is the difference between V’ and V which shows the change in volume.
Also, let ρs be the density of water at surface and ρb be the density of water at the bottom of the lake (100 m depth)
Ques. If a tensile stress of 5 x 107 m2 is applied on a longitudinal uniform cylindrical wire, find the fractional change in radius if the volume alters by 0.02%. (Y = 2 x 1011 Pa) (5 marks)
Ans. Here,
Stress = 5 x 107 Nm-2
Y = 2 x 1011 Nm-2
\(\frac{\triangle v}{v}\) = 0.02% = 0.02/100
Y = Stress/ \(\frac{\triangle L}{L}\)
\(\frac{\triangle L}{L}\) = Stress/ Y
5 x 107/ 2x1011 = 2.5 x 10-4
V = \(\pi\)r2L
\(\frac{\triangle v}{v}\) = \(\frac{\pi \triangle (r^2 L)}{\pi r^2 L} = \frac{r^2 \triangle L + L \times 2r\triangle r}{r^2 L}\)
\(\frac{\triangle v}{v}\)= \(\frac{\triangle L}{L}\) + 2 (\(\frac{\triangle r}{r}\))
2 (\(\frac{\triangle r}{r}\)) = \(\frac{\triangle v}{v}\)– \(\frac{\triangle L}{L}\)
= 0.02/100 – 2.5 x 10-4
= 2 x 10-4 – 2.5 x 10-4
= -0.5 x 10-4
\(\frac{\triangle r}{r}\) = – 0.5/ 2 x10-4
= -0.25 x 10-4
Also Check:





Comments