
Arpita Srivastava Content Writer
Content Writer
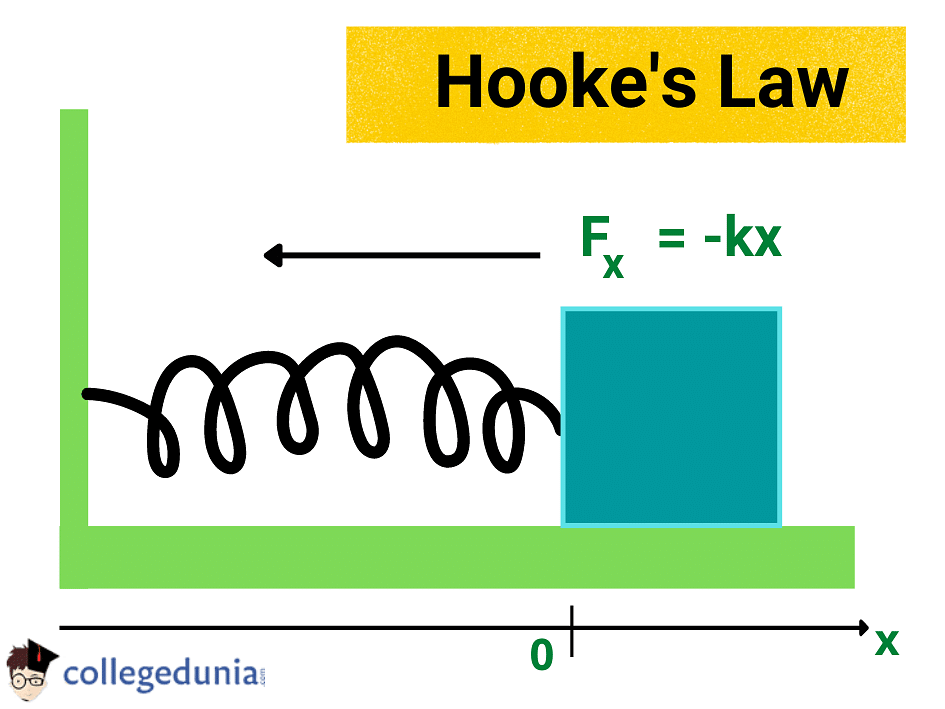
Hooke’s Law is the foundational law of elasticity in Physics. It states that the force required to extend or compress a spring by a certain distance is directly proportional to that distance.
- The object would return to its original shape and size upon the removal of the force.
- Hooke’s law is also known as the elasticity principle or law of elasticity.
- The law was proposed by Robert Hooke, a British physicist, in 1660.
- You can use it to find out the force in a stretched spring, its displacement, and the force or spring constant.
- Hooke’s Law states that the amount of stress applied to an object is equal to the amount of strain observed on it, i.e. Stress-Strain.
Hooke’s Law Formula is given as F = – Kx
- Here, F is the amount of force applied to the object
- k is the force constant or the spring constant
- x denotes the displacement in the spring.
Key Terms: Hooke’s Law, Stress, Strain, Hooke’s Law Formula, Deformation, Spring, Elasticity, Force, Spring Constant, Hooke’s Law Graph, Hooke’s Law Experiment
What is Hooke’s Law?
[Click Here for Sample Questions]
Hooke's Law states that the strain of a material is always proportional to applied stress within the elastic limit of that particular material.
- When an elastic material is stretched, and stress is applied to it, the atoms and molecules constituting the object will deform.
- Once the stress is removed from the object, it will return to its original state.
- The force required to extend or compress a spring by a certain distance is directly proportional to that distance.
- The stiffness of the spring plays an important role in the application of Hooke's Law.
- Stretching a spring twice as long requires twice as much power.
- Hooke's law is the linear relationship of displacement on stretching.
- Mathematically, Hooke's law is expressed as:
Stress ∝ Strain
- It can also be stated as: Stress = Constant × Strain
- Constant = Stress / Strain
- Modulus of Elasticity = Stress / Strain
Hooke’s Law
Read More:
Hooke’s Law Formula
[Click Here for Sample Questions]
Hooke’s law illustrates that the strain of an elastic object is proportional to the stress applied to it.
F = – Kx
Where
- F is the force applied to the object.
- x is the displacement in the spring.
- k is the force constant or the spring constant.
Hooke’s Law Solved ExampleExample: A spring displaced by 10 cm is held in place with a force of 1000 N. Calculate the spring constant of the spring. Solution: As the spring is displaced by 10 cm but the unit of the spring constant is Newtons per meter. We will convert the distance from cm to meters. 10 cm = 0.1 m Substituting these values in the Hooke’s law equation, we get F = – k.x 1000 N = – k x 0.1 m To calculate the spring constant or k and omit the negative sign, we get
Therefore, the spring constant of the given spring is 10000 N/m. |
Hooke’s Law of Elasticity
[Click Here for Previous Year Questions]
Hooke's law especially emphasizes working with a limited amount of force that will lead to temporary object deformation. Thus, the law does not apply to any object's extreme elasticity.
- The relation is completely based on the properties of the intrinsic materials of the objects.
- For instance, a homogeneous rod that has a uniform cross-section is meant to act as a simple spring during the stretching.
- The spring constant (k) of the rod is directly proportional to the area of the cross-section of the rod, as per the convention.
- It is inversely proportional to its length as per the law of elasticity.
- Hooke's law also detects the nature of a wave-like periodic function within the spring.
- It also helps find the frequency and wavelength of the motion generated inside the spring.
Hooke’s Law Experiment
[Click Here for Sample Questions]
To understand Hooke’s Law, we shall perform an experiment. Consider a spring with load application, as shown in the figure.
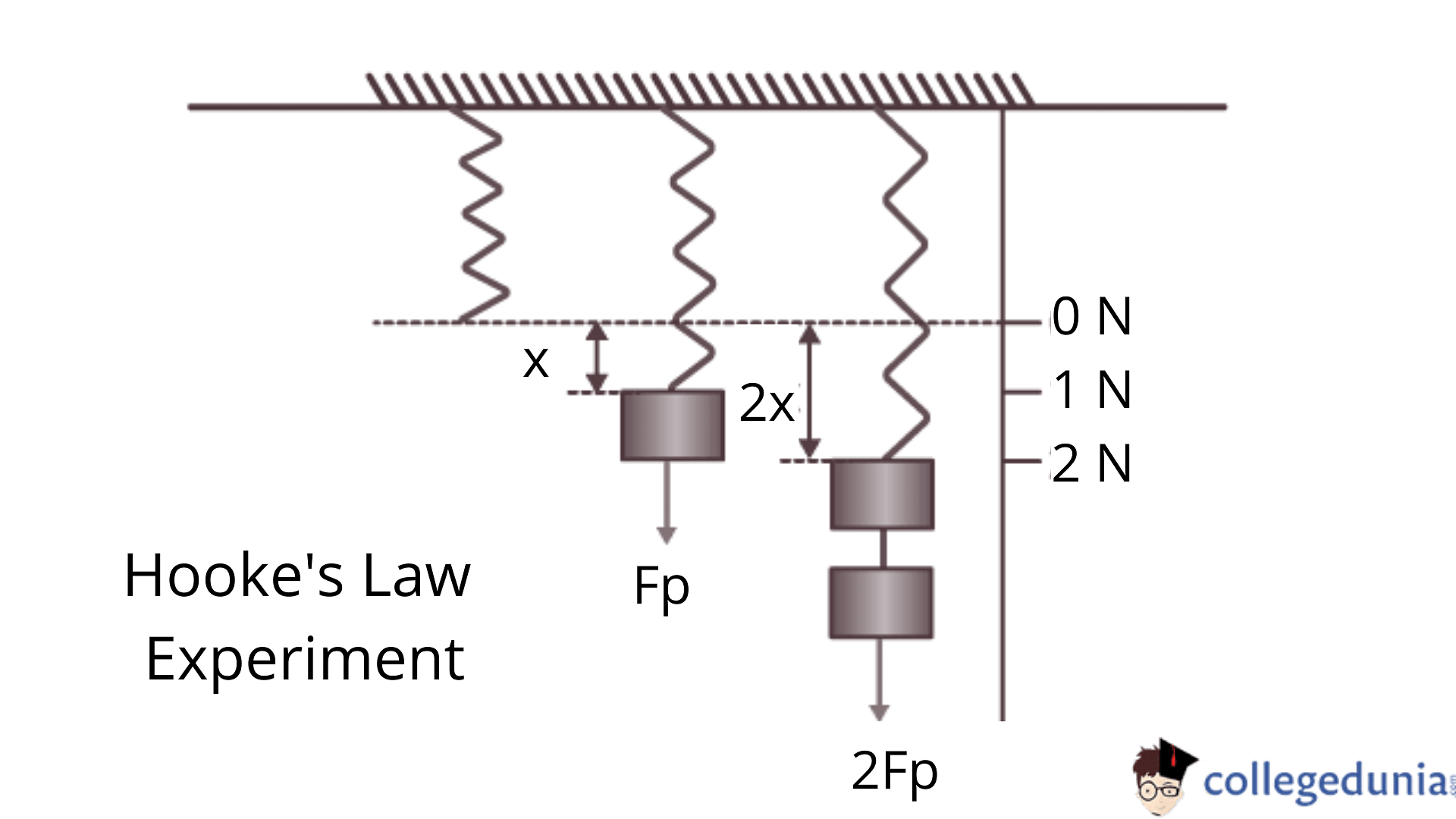
- In the figure, the stable condition of the spring is demonstrated when no load is applied to it.
- It elongates to x when the spring is under the load of 1 N, and the spring is elongated to 2x under the influence of load 2 N.
- Various springs will have different spring constants depending on the material.
- If we substitute the three values given in the figure in Hooke’s law equation, we get the spring constant for the given material.
Hooke’s Law Graph
[Click Here for Previous Year Questions]
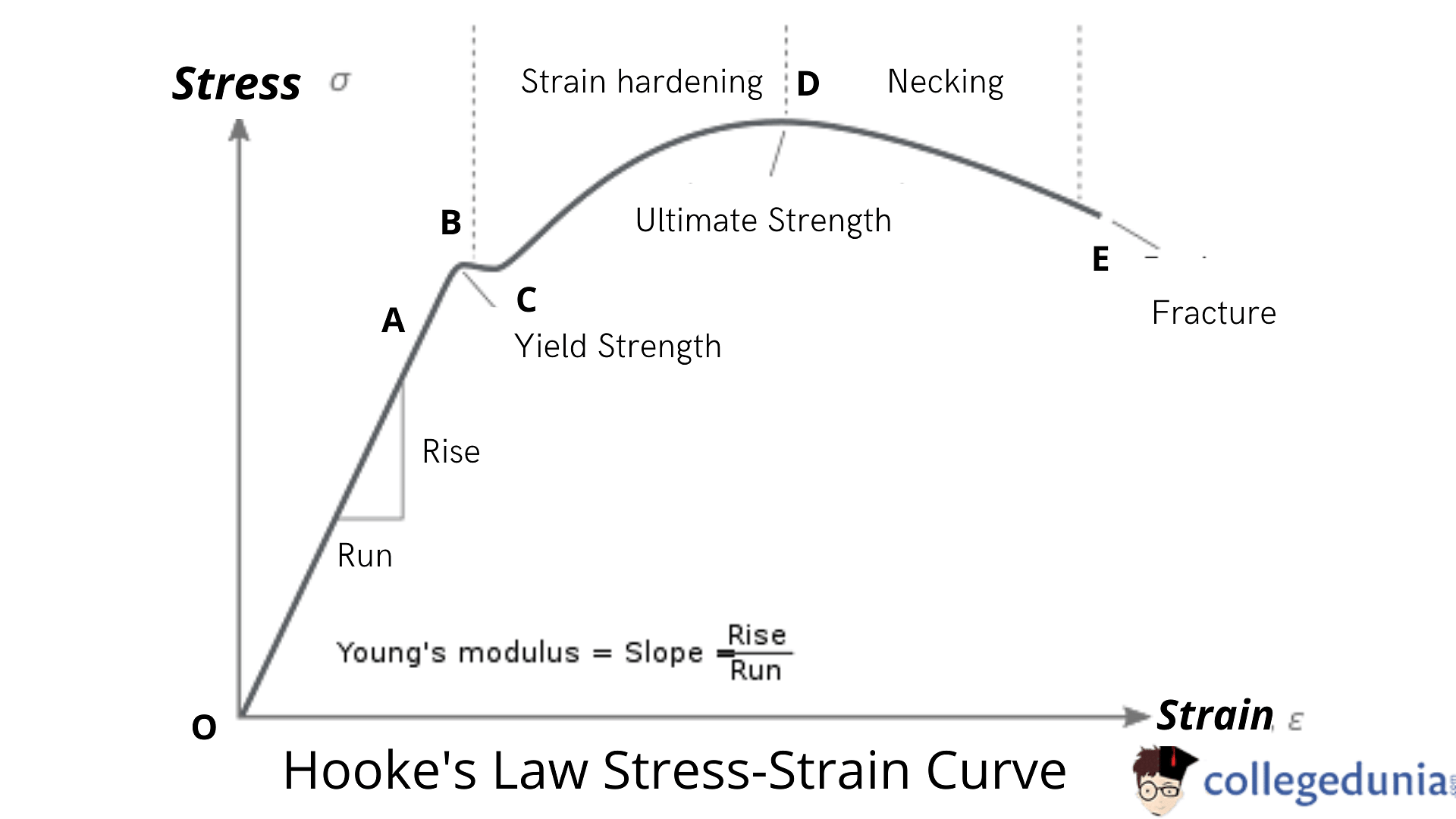
A graph is plotted between the stress, which can be defined as the applied force per unit area and the strain produced. Although, the stress-strain curves vary from material to material, depending on multiple factors.
- The curves help us to understand how a given material deforms with the increasing forms and give justification to Hooke’s law.
- The region between O and A has a linear curve, which proves Hooke’s law.
- The stress and strain are not proportional in the region from A to B.
- The body still returns to its original form when the force is removed.
- Point B in the curve is known as the yield point, which is also known as the elastic limit.
- The stress corresponding to the elasticity is known as the yield strength of the material.
- The region between B and D represents the increase in the yield strength.
- The strain increases due to the increase in the force/load.
- Even after reducing the force, the body's dimensions do not return to normal.
- Such material is said to have a permanent set when a strain is always greater than zero, either in the presence of stress or in its absence.
- Point D in the figure is the tensile strength of the material.
- It marks the increase in the strain even when reducing stress; thus, point E marks the fracture.
- In such cases, the material is either called brittle or ductile.
Hooke’s law graph is represented as follows:
Applications of Hooke’s Law
[Click Here for Sample Questions]
The applications of Hooke’s Law are as follows:
- Hooke’s law is a fundamental principle behind the manometer, the balance wheel of the clock, and the spring scale.
- It sets the foundation for seismology, molecular mechanics, and acoustics.
- Hooke’s Law is used in all branches of science and engineering to understand the behaviour of elastic material.
- It can be used to balance the wheel of a clock.
- Spring scales are made up of a hook suspended by the entity, which uses the law as the scale’s internal arrangement is made up of springs.
- The expansion and compression of a balloon are determined by the force required to fill it with air; hence, it is based on Hooke’s law.
- Retractable pen uses the concept of the law for locking and releasing the ink cartridge as needed.
Read More:
Disadvantages of Hooke’s Law
[Click Here for Previous Year Questions]
The disadvantages of Hooke’s Law are as follows:
- Hooke’s law is not applicable beyond the elastic limit of a material.
- The law is accurate only for solid bodies if the deformations and forces are small.
- It is not a universal principle.
- Hooke’s law only applies to materials as long as they are not stretched past their capacity.
Read More: Solid Deformation
Mechanical Properties of Solids Class 11 Handwritten Notes
Here are the handwritten notes for Mechanical Properties of Solids:















Things to Remember
- Hooke’s law states that for a material, the strain is proportional to the applied stress within its elastic limit.
- The law states that the applied force F is equal to k times the change in length x.
- The law is the foundational principle for elasticity, thus, is known as the law of elasticity.
- It is used as a principle behind the spring scale and manometer.
- A disadvantage of Hooke’s law is that it is accurate only for solid bodies if the forces are small.
Previous Years’ Questions
- A copper wire of length 2.2m and a steel wire … [KCET 2013]
- A copper wire and a steel wire of the same diameter and length … [BHU UET]
- A steel wire can withstand a load up to … [BITSAT 2008]
- A light rod of length 100 cm is suspended from the ceiling horizontally … [AP EAPCET]
- A load of 1 kg weight is attached to one end of a steel wire of area … [BITSAT 2008]
- One end of a horizontal thick copper wire of length … [JEE Advanced 2013]
- When a rod is heated but prevented from expanding the stress … [BHU UET]
- The breaking stress of a wire of length ll and radius r is …
- Two wires are made of the same material and have the same volume … [NEET 2018]
- Two wires A and B are stretched by the same load … [KCET 2018]
- Elastic strain energy of 10 J is stored in a loaded copper rod … [TS EAMCET 2018]
- If the ratio of diameters, lengths and Young's modulus of steel … [NEET 2003]
Sample Questions
Ques. Mention a few applications of Hooke’s law? (2 marks)
Ans. A few applications of Hooke’s Law are as follows:
- Hooke’s Law is usually used in multiple branches of science and engineering, especially for producing mechanical devices.
- It is used as a fundamental principle behind the production of the spring scale, the manometer, and the balance wheel of the clock.
- Hooke’s law also acts as a foundation for seismology, acoustics, and molecular mechanics.
Ques. What is the reason behind the negative value of K in Hooke’s Law? (2 marks)
Ans. In Hooke’s law, K represents the spring constant and it is denoted negative in the corresponding equation. The negative symbol actually represents the direction of the force, as in, the returning force always travels in the opposite direction soon after the release of the applied force in the spring.
Ques. What are the disadvantages of Hooke’s law? (2 marks)
Ans. The disadvantages of Hooke’s Law are as mentioned below:
- One of the major limitations of Hooke’s law is that it ceases to apply after a certain extreme elastic limit of a material.
- The law is majorly accurate only for solid bodies, that is, if the forces and deformations are small.
- It only applies to the materials as long as they are not stretched way past their capacity.
- The law is not universal.
Ques. Which material can be regarded as a non-Hookean material? (1 mark)
Ans. Rubber is generally regarded as a non-Hookean material because its elasticity is dependent on stress and it is also sensitive to temperature and loading rate.
Ques. What shall be the Spring Force of a stretched string whose length is 4m and has a spring constant of 0.2? (2 marks)
Ans. Given: x = 4m, Spring constant k = 0.2
Therefore, Spring force Fs = -k.x
= -0.2*4
= -0.8 N
Ques. What are the types of strain? (2 marks)
Ans. The different types of strain are –
- Volumetric Strain
- Longitudinal Strain
- Shear Strain
Ques. Calculate the force constant if a force of 100 N stretches a spring by 0.8 m? (3 marks)
Ans. It is given that,
- Force Applied (F) = 100 N
- Displacement/Extension of Spring (x) = 0.2 m
- Force Constant (k) =?
Using Hooke’s law Formula,
F = -k x
k = – F / x
k = – 100 / 0.8
k = – 125 N/m.
The force constant will be – 125 N/m.
Ques. How a wire is broken due to repeated bending? (2 marks)
Ans. When a substance is subjected to repeated strain, its elastic properties get impaired. This is known as elastic fatigue. Thus, the wire is broken due to repeated bending. Hooke’s spring law applies to any elastic object, as long as a single number can express the deformation and the stress.
Ques. When does Hooke’s Law fail? (1 mark)
Ans. Hooke’s law is applicable to a perfectly elastic material and doesn’t apply beyond the elastic limit of any material.
Ques. Calculate the force applied to the spring if it is stretched by 10 cm and has a force constant of 2 cm /dyne? (3 marks)
Ans. We are given that,
- Force constant (k) = 2 cm/dyne
- Displacement in Spring (x) = 10 cm
- Force Applied (F) =?
Using Hooke’s Law Formula,
F = – k x
F = – 2 × 10 cm
F = – 20 N
Therefore, the force applied on the string is -20N.
Ques. Is Hooke’s Law linear? (1 mark)
Ans. Hooke’s Law is linear as it states that the restoring force is proportional to the displacement. The stiffness of the spring plays an important role in the application of Hooke's Law. Stretching a spring twice as long requires twice as much power.
Ques. What is modulus of elasticity? (3 marks)
Ans. Modulus of elasticity is defined as the ratio of stress and strain. The SI unit of modulus of elasticity is Nm-2. The dimensional formula of the modulus of elasticity is given as [ML-1T-2]
- Modulus of elasticity is dependent on the nature of the material of the body.
- Modulus of elasticity of a body is independent of its dimensions.
- The dimensional formula of the Modulus of elasticity is the same as that of pressure or stress.
Read More:
| Class 11 Physics Study Guides | ||
|---|---|---|
| NCERT Solutions for Class 11 Physics | Topics for Comparison in Physics | Formulas in Physics |







Comments