Derivation of Bending Equation: Deformation, Factors & Assumptions

Bending equation is considered to be a subsection of the bending theory. Bending theory states that a beam can undergo deformation when there is an external application of any form of force perpendicular to its longitudinal axis. Bending theory is also known as flexure theory. It basically signifies the effects of force on a beam. The bending equation is used to find the amount of stress applied on the beam.

Also Read: Effects of force

Key takeaways: Beam, Force, Stress, Strain, Bending, Pure Bending, Longitudinal axis, Deformation, cross-section, moment of inertia

Beam & its Bending

[Click Here for Sample Questions]

Any structure can be a beam if one dimension of it is larger than the other two dimensions by a factor of 1/10 or less. When force is applied to this beam along its longitudinal axis, it tends to get deformed. 

Bending equation is a mathematical equation that has been formed to calculate the amount of stress being applied to the beam. However, multiple assumptions have been made while forming it. Pure bending of beams is a hypothetical situation where the bending moment is solely applied on the beam without taking into account axial, shear or torsional forces.

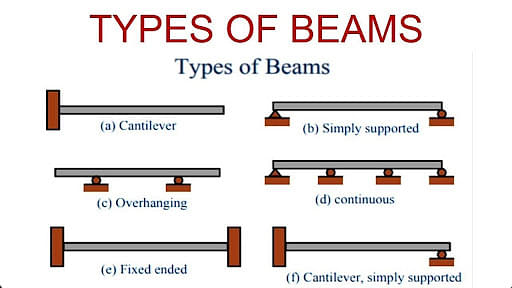
Types of Beams

Read More:

Bending Equation 

[Click Here for Sample Questions]

Bending Equation is given by,

\(\frac{\sigma}{y} = \frac{M}{T} =\frac{E}{R}\)

Where,

• M = Bending Moment
• I = Moment of inertia on the axis of bending
• σ = Stress of fibre at distance ‘y’ from neutral axis
• E = Young’s modulus of the material of beam
• R = Radius of curvature of the bent beam

In case the distance y is replaced by the element c, then

\(\frac{M}{l} = \frac{\sigma max}{c}\)

Hence,

σmax = \(\frac{MC}{l} = \frac{M}{Z}\)

Where, Z = I / c

Z is called the section modulus of the beam.

Derivation of Bending Equation

Consider an unstressed beam subjected to bending. It bends upto a radius R such that the bottom fibres expereince tension and top fibres experience compression as given in the figure below. The points with zero stress have a common locus. This locus is called as neutral axis.

Bending equation computes the bending stress that develops on the beam which experiences a force. 

Strain in fibre AB = \(\frac{\text{ Change in length}}{\text{Original Length}}\)=\(\frac{A'B' - AB}{AB}\)

But, AB = CD and CD=C′D′

Thus, strain = \(\frac{A'B' - C'D'}{C'D'}\)

The stress on the neutral axis is found to be null because of the presence of CD and C′D′. Thus, the neutral axis does not experience any strain due to the applied force.

Bending of Beam

\(\frac{(R+y)\theta - R\theta}{R \theta}\)=\(\frac{R\theta +y \theta - R\theta}{R \theta}\) = \(\frac{y}{R}\)

We know that,

\(\frac{\text{Stress}}{\text{Strain}}\)= E (Young’s Modulus of Elasticity)

\(\frac{\sigma}{y} = \frac{y}{R} =\frac{E}{R}\)  ……………(i)

Taking any arbitrary cross section of the beam, strain on its fibre is at a distance y from the neutral axis. The expression is: 

σ = E / Ry

Considering a strip of area dA, Force on the strip

F = σδA = \(\frac{E}{R}\)yδA

Moment of the bending equation on the neutral axis will be

F y = \(\frac{E}{R}\)y²δA

Therefore, the total moment of bending equation for the entire cross-section will be 

M = ∑  \(\frac{E}{R}\)y²δa = \(\frac{E}{R}\) ∑ y²δa

∑ \(\sigma \)/y²δa is taken to be the material property of the beam. It suggests the second moment of the area of cross section. ‘I’ is used to denote it. 

Thus, 

M = ERl   …………...(ii)

Combining equations (i) and (ii), we get

\(\frac{\sigma}{y} = \frac{M}{I} =\frac{E}{R}\)

This is the derivation of the bending equation. It is also called as flexural formula.

Also Read: Moment of force

Assumptions of Bending Equation

[Click Here for Sample Questions]

Many assumptions were made for the derivation of the bending equation. They are:

1. The cross-section of the beam is constant.
2. The beam is straight.
3. The cross-section is constant before and after the bending.
4. The beam has a symmetrical longitudinal plane.
5. The beam is made of a homogenous material.
6. Elastic limit is the same for tension as well as compression.

Check out:

Things to remember

1. The bending equation is  \(\frac{\sigma}{y} = \frac{M}{I} =\frac{E}{R}\)
2. Bending equation is used to find the stress applied on the beam.
3. Deformation happens when an unstressed beam is subjected to stress acting perpendicular to its axis. 
4. When the direction of force applied is perpendicular to the longitudinal plane of the beam, the upper part of the beam undergoes compression while the lower part is experiences tension. 
5. Certain assumptions are made in the derivation of beam equation such as its straightness, cross section, material homogeneity and elastic limit.

Check out PYQs: