Central Force: Equations, Motions, Fields & Examples

Central force exists when the force between two bodies is directed along the line linking the two bodies' centres of mass. Because most of the fundamental forces we know about are of this type, including gravitational, electrostatic, and some nuclear forces, researching central force motion is critical in physics. 

Keyterms: Central force, Force, Motion, gravitational force, electrostatic force, nuclear force, fundamental force, Planets, comets, stars, satellites

---

What is a Central Force?

[Click Here for Sample Questions]

The force that works along the line connecting the centres of two interacting bodies is known as the central force. A central force is always directed away from a fixed location and towards the centre. The central force is described in classical mechanics as the force applied on an object that focuses along the line connecting the object and the origin. The central force's size is solely determined by the distance between the object and the centre.

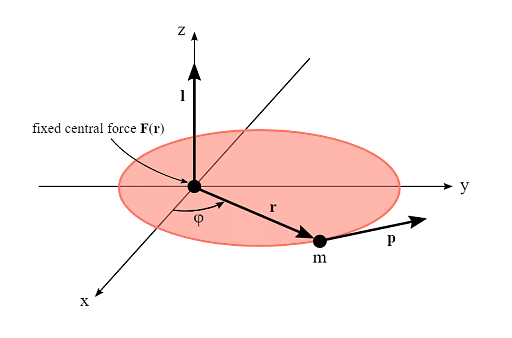
Central Force

Furthermore, one of the few problems in classical mechanics that can be entirely solved is the motion of a system consisting of only two bodies interacting via a central force (once you add a third body it becomes, in general, unsolvable). 

Planets and comets orbiting a star, satellites orbiting a planet, binary stars, and classical scattering of atoms or subatomic particles are examples of such systems. Quantum mechanics is required for a complete explanation of atoms and subatomic particles, yet even here, a classical study of core forces can provide a lot of information.

Also Read: Magnetic field and magnetic force

---

Equation of Central force

[Click Here for Sample Questions]

The central force's mathematical equation is:

\(F = F(r) \hat{r}\)

Where,

F → Conservative central force.

r → Vector magnitude and |r| is the distance to the centre of force

 = r/r → Unit vector in the direction of r.

We created a central force that satisfies two criteria. We can now generate the new equations using these descriptions of the characteristics:

Equation of Central force

1. A central force is solely dependent on the distance between the two bodies.

f₂₁ = -f₁₂ = f(r₂-r₁)r/r

       b. It indicates the direction of the line that connects the two bodies.

F₂₁ = -f₁₂ = f(r₂-r₁) = f(r) 

Central force is a conservative force which is expressed as follows:

F(r)=\(-\frac{du}{dr}\)

Where,

F(r) → Magnitude of a central force

U(r) → Time-independent potential energy

For a particle under central force to be in a uniform circular motion should have centripetal force as follows:

F(r)= \(\frac{mv^2}{r}\)

Where,

r → Initial radius

v → Speed that satisfies the equation of centripetal force

Read More: 

---

Motions in Central force

[Click Here for Sample Questions]

Bounded motion: The distance between two bodies or objects has a similar value in this motion and never exceeds the established values. The motion of the planets around the sun is an example of this type of movement.

Motions in Central force

Unbounded motion: The distance between the two bodies or objects is infinity in the initial and final stages of this motion. The dispersion of alpha particles in the Rutherford experiment is an example of this type of movement.

Also Read: Cyclotron

---

Examples of Central forces

[Click Here for Sample Questions]

Many natural events define the central force in physics such as planets orbiting the sun, Natural satellites that revolve around the earth, In terms of movement against each other two charged particles, Gravitational Force and Projectile Motion, Electrostatic, Magneto static Forces and Simple Harmonic Motion.

Examples of Central forces

Also Read:

---

Things to Remember 

• An object's angular momentum should be conserved if it is solely subjected to the central force.
• The magnitude of the central force is determined solely by the object's distance from the centre.
• When estimating the motion of the planets in the Solar System, the solution to the central-force issue frequently provides a decent first approximation of the true velocity.
• The magnitude of a central force can always be written as the derivative of a time-independent potential energy function if the central force is a conservative force.
• If the initial radius r and speed v satisfy the centripetal force equation, any central force can create uniform circular motion.
• The gravitational connection exemplifies classical activity, whereas the Coulomb interaction exemplifies quantum behaviour.