Jasmine Grover Content Strategy Manager
Content Strategy Manager
Magnetic field refers to the area around a magnet which generates magnetic force due to the movement of electric charges. The magnetic field is represented by the symbol ‘B’ or ‘H’.
- B-field is a magnetic field formed by the force a magnet exerts on a moving charged particle.
- An H-field is similar to a B-field except when the object is inside a material.
The SI Unit of Magnetic Field is tesla (T). Tesla (symbol - T) is a derived unit of the magnetic field strength (also called magnetic flux density) in the International System of Units. One tesla is equal to one weber per square metre. The unit of magnetic field helps in measuring the magnetic force distributed around any object that is magnetic in nature.
Also read: Moving Charges and Magnetism
| Table of Content |
Key Terms: SI unit of magnetic flux, magnetic field intensity, Magnetic Field, Magnetic Flux, Magnetic Induction, Tesla, Electric charge, Ampere, meter, coulomb
What is the SI Unit of Magnetic Field?
[Click Here for Sample Questions]
The magnetic field is denoted by B and H.
- The SI unit of H magnetic field is amperes per meter.
- The SI unit of B magnetic field is Newtons per meter per ampere or Teslas.
The SI unit used to measure the magnetic field is tesla (T). Thus, one tesla is that magnetic field in which a charge of one coulomb moving with a velocity of 1 m/s perpendicular to the magnetic field experiences a force of one newton.
A magnetic field can be defined in several specific ways in relation to its effect on the environment. Accordingly, there are B-fields and H-fields.
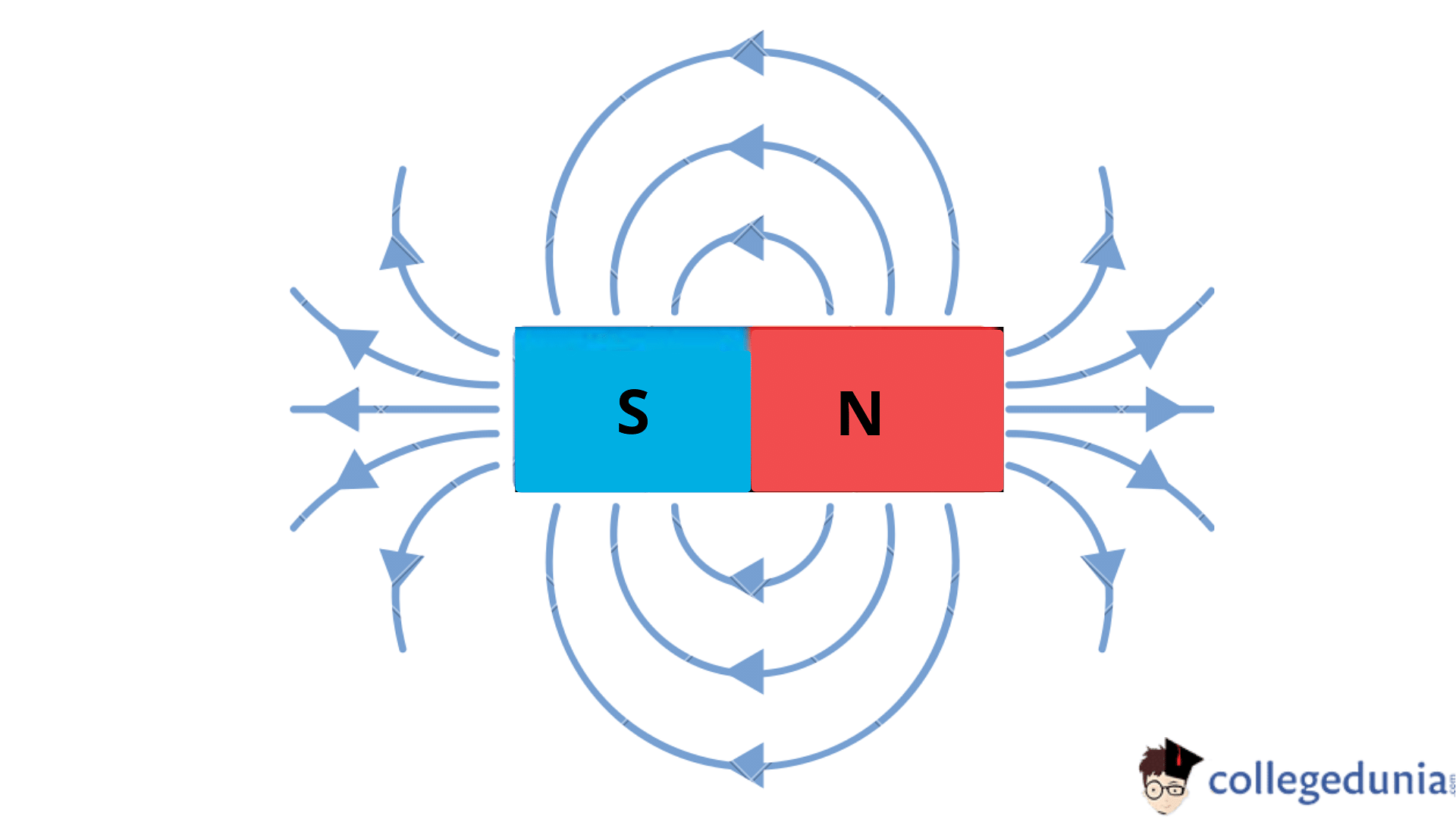
Magnetic Fields
Important Notes about B-fields and H-fields
|
Read More:
Other SI Units of Magnetic Field
[Click Here for Previous Year Questions]
Other Common SI Units of Magnetic Field are:
- Apart from the SI system, the B-field in the Gaussian-CGS system is measured with the unit gauss (G).
- If we look at the conversion it is 1 T = 10000 G.
- Meanwhile, the H-field is measured with the help of Oersted (Oe) in the CGS system.
Representation of Magnetic Field
[Click Here for Sample Questions]
Magnetic fields are represented by the constantly emerging lines of force or magnetic flux from north to south magnetic poles.
- Magnetic poles where the density of the magnetic field is strongest, the field lines are denser.
- Farther away where the magnetic field is weaker, the field lines are less dense.
- The equally spaced parallel straight lines are used to represent magnetic fields.
- The direction of the flux is always the direction in the north-seeking direction of a small magnetic point.
- Mathematically, the magnetic fields can be represented as a vector field.
- Here the magnetic fields are endless; they never stop and never cross each other.
Examples & Uses of Magnetic FieldsIn the case of a bar magnet, the field emerges from the north pole, enters into the south pole and returns back to the north-seeking pole from where the fields had started. Magnetic Fields are very useful, particularly in the mechanisms associated with generators and electric motors. Various electrical devices like transformers require the interaction of magnetic fields. Earth also generates its magnetic field which is required for navigation using a compass. It also protects the ozone layer from solar wind.
|
Magnetic Force
[Click Here for Previous Year Questions]
Magnetic force is the force which emerges due to the interaction of the magnetic fields which can either be an attractive or repulsive force.
- A point of charge (q) with velocity (v) and at a given time (t), located at point (r) in presence of magnetic field B (r) and electric field E (r). The Magnetic force on electric charge q can be written as:
F = q [E (r) + B (r)] = Felectric + Fmagnetic
- This was formulated by H.A Lorentz based on the experiments of Ampere and others. This is also known as the Lorentz Force.

Magnetic Force
Magnetic Field In a Straight Wire due to Current
According to the Biot-Savart Law, the magnetic field through a small wire can be calculated by extending the wire that is carrying current. Let AB be the conductor through which current flows. Consider point P, which is at a specific distance from the midpoint of the conductor. Let us take a small current-carrying element “dl” at point c which is at a distance “r” from p. “l” is the distance between the centre of the coil. dl is the length. Using the biot-savart law, we can calculate the magnetic field at point P due to “dl” as –

\({l}\bar{dB} = \frac{\mu _{0}}{4\pi }. \frac{I\bar{dl}.\bar{r}}{r^{3}}\)
As the angle between I dl and r is 180 degrees, therefore –
\({l}\bar{dB} = \frac{\mu _{0}}{4\pi }. \frac{I\bar{dl}.sin (180 – \Theta )}{r^{2}}\)
The total magnetic field at point P due to the complete length of the conductor is given as \({l}{B} = \frac{\mu _{0}}{4\pi }. \frac{I}{R} \sin\phi\,\)
Magnetic Field on a Current-Carrying Circular Loop
Magnetic field lines can be shown as concentric circles which are carrying current in a circular loop. Here, the direction at every section of the magnetic field of the circular loop can be found using the right-hand thumb rule. The magnet field lines are straight at the center of the loop. The magnetic field in the center of the coil is having a direction perpendicular along the axis of the coil. Also, every segment of the loop which is carrying current in it is producing magnetic field lines in the exact same direction of the loop.
We may say that the magnitude of the current is directly proportional to the magnitude of the magnetic field in the circular loop – B ∝ I. Also, the radius of the circular loop is inversely proportional to the magnitude of the magnetic field – B ∝ 1/r.
In the case of Flat surfaces, m = I (πR2)

With N number of turns in the loop, the magnetic field can be given as \({l}B=\frac{\mu _{0}Nia^{2}}{2(a^{2}+x^{2})^\frac{3}{2}}\)
Magnetic Field in a Solenoid
A solenoid is actually a coil of wire that is designed to create a strong magnetic field within the coil. The same wire is wrapped many times around a cylinder to produce stronger magnetic fields. The number of loops in the solenoid is denoted by N. So the formula can be written for the field inside of the solenoid is:
B = μ°I N/L
The magnetic field present inside a solenoid is proportional to the number of turns per unit length as well as to the applied current. The position inside a solenoid is not dependent upon its strength or its diameter, the field which is inside is constant.

Magnetic Field in a Solenoid
Also Read:
|
Examples Based on SI Unit of Magnetic FieldExample 1: A uniform electric field of magnitude E = 100 N/C exists in the space in the X-direction. Using the Gauss theorem calculate the flux of this field through a plane square area of edge 10 cm placed in the Y-Z plane. Take the normal along the positive X-axis to be positive. Solution: The flux Φ = ∫ E.cosθ ds. As the normal to the area points along the electric field, θ = 0. Also, E is uniform so, Φ = E.ΔS = (100 N/C) (0.10m)2 = 1 N-m2. Example 2: A large plane charge sheet having surface charge density σ = 2.0 × 10-6 C-m-2 lies in the X-Y plane. Find the flux of the electric field through a circular area of radius 1 cm lying completely in the region where x, y, z are all positive and with its normal making an angle of 600 with the Z-axis. Solution: The electric field near the plane charge sheet is E = σ/2ε0 in the direction away from the sheet. At the given area, the field is along the Z-axis. The area = πr2 = 3.14 × 1 cm2 = 3.14 × 10-4 m2. The angle between the normal to the area and the field is 600. Hence, according to the Gauss theorem, the flux = \((\begin{array}{l}\vec{E}.\Delta \vec{S}\end{array})\) = E.ΔS cos θ = σ/2ε0 × pr2 cos 60º = \(\frac{2.0\times10^{-6} C/m^2}{2\times8.85\times10^{-12}C^2/N-m^2}\) = 17.5 N-m2 C-1 |
Things to Remember
- Magnetic fields are represented using two symbols H and B in which H denotes magnetic field strength and B denotes magnetic flux.
- The SI unit of magnetic field – H is amperes per meter while the SI unit of B is Teslas or Newtons per meter per ampere.
- Magnetic field lines cannot cross each other. They are endless continuous loops
- In the CGS system, the smallest unit of the magnetic field is Gauss.
- The Relationship between Gauss & Tesla is 1T = 10000G.
- According to Lorentz Force law, q [v X B] is a vector product of Velocity & magnetic field.
- If v & B are parallel or anti-parallel, the vector product of forces becomes zero. Only any moving charge will feel the magnetic force.
Previous Year Questions
- The ratio of magnetic fields at the centre of coil and at a point at a distance 6R from centre of coil on axis of coil is
- A galvanometer can be converted into a voltmeter by connecting a
- If the total current is 1 A, the part of it passing through the shunt will be
- Find the minimum current in the circuit, so that the ammeter shows maximum deflection
- A uniform electric field and a uniform magnetic field are produced, pointed in the same direction. An electron is projected with its velocity pointing in the same direction
- The coil is placed in a uniform magnetic field B. The maximum torque on the coil can be
- When a charged particle moving with velocity →vv→ is subjected to a magnetic field of induction →BB→ the force on it is non-zero. This implies that
- Who invented the cyclotron?
- Magnetic field intensity H at the centre of a circular loop of radius r carrying current I is
- A third current-carrying wire parallel to both of them is placed in the same plane such that it feels no net magnetic force. It is placed at a distance of
Sample Questions
Ques. What is Magnetic flux? (1 mark)
Ans. Magnetic flux is the measurement of the total magnetic field which passes through a given area. It is useful in determining the effects of the magnetic force on something occupying a given area.
Ques. What is B-field? (2 marks)
Ans. The magnetic field vector B, at a certain point, is known as the vector which when used in Lorentz force law, predicts the force correctly on a charged particle at that point.
Hence, the formula is:
Magnetic torque, τ = m x B
B here is measured in Tesla (T)
Ques. What instruments are used to measure magnetic fields? (2 marks)
Ans. An instrument known as a magnetometer is used to measure local magnetic fields. The various kinds of magnetometers used to measure varying magnetic fields are rotating magnetometer, Hall Effect magnetometer, NMR magnetometer, SQUID magnetometer, a fluxgate magnetometer, and rotating coil magnetometer.
Ques. What is the SI Unit of a magnetic field? (1 mark)
i. Weber
ii. Weber.m
iii. Gauss
iv. Tesla
Ans. SI Unit of Magnetic Field is denoted by the symbol T. The measure of Magnetic flux per unit area is –
1 tesla =1wb/m2
Ques. What is the formula of Lorentz Force Law? (2 marks)
Ans. The formula of Lorentz Force Law is:
Fmagnetic = q [v X B]
Here, q is the electric charge
v is velocity
B is the magnetic field
Ques. (a) Derive the expression for the torque acting on a current-carrying loop placed in a magnetic field.
(b) Explain the significance of a radial magnetic field when a current-carrying coil is kept in it. [2019] (4 Marks)
Ans. The torque acting on a current carrying loop placed in a magnetic field:
Let’s take PQRS as a coil kept in a magnetic field and 0 is the angle between the direction of B and the coil’s plane. When there is a flow of current across the coil every side of the coil experiences a force and these forces on the vertical side will represent a couple.
Torque moment = One of the forces*Perpendicular distance between the action of force lines.
τ = F*QT = F*b sinθ
= I/B b sinθ
τ = I(lb) B sinθ

- A magnetic field having a coil with a plane that remains parallel to the direction of the magnetic field in all positions is known as the radial magnetic field. In the case of a radial magnetic field the magnetic torque remains the highest for all the placement of the coil.
Ques. (a) State Gauss’ law for magnetism. Explain its significance.
(b) Write the four important properties of the magnetic field lines due to a bar magnet. [2019] (4 Marks)
Ans. a. Gauss law for magnetism: If a closed surface is considered to be in the magnetic field, the total number of force lines generated from the surface should be similar to the number of lines entering it. That is zero is the number of net magnetic flux out of the closed surface.
- Four important properties are:
- In every bar magnet every line of force moves eternally from north to south pole and vice versa internally.
- The force lines never intersect each other.
- The lines in a uniform field are parallel and equidistant to each other.
- The force lines are congested near the poles.
Ques. How is a toroid different from a solenoid? [Outside Delhi 2019] (2 Marks)
Ans. Difference between toroid and solenoid are as follows:
| Solenoid | Toroid |
|---|---|
| Solenoid can be termed as a formation within which a conductor wounds around a cylindrical body having limbs. | Toroid can be termed as a formation within which a conductor wounds around a circular body. |
| In the case of the solenoid, the magnetic field creates N and S poles and has some leakage in flux. | Magnetic fields are present within the core and poles are absent. |
| It is used in motors, relays, and electromagnets. | It's used in toroidal transformers and inductors. |
Ques. A bar magnet of the magnetic moment 6 J/T is aligned at 60° with a uniform external magnetic field of 0.44 T. Calculate
(a) the work done in turning the magnet to align its magnetic moment
(i) normal to the magnetic field,
(ii) opposite to the magnetic field, and
(b) the torque on the magnet in the final orientation in case (ii) [2018] (5 Marks)
Ans. Magnetic momentum: m = 6JT-1
External magnetic field: B = 0.44T
Θ1 = 60º cosΘ1 = cos60º = ½
- The work done in turning the magnet to align its magnetic moment:
W = -mB(cosΘ1 -cosΘ1 )
(i) Here Θ1 = 90º
W = +mB cosΘ1
= 6*0.44*½ = 1.32J
(ii) Here Θ1 = 180º
W = -mB(cosΘ1 - cozΘ1)
W = -6*0.44(-1-½ ) = 3.96J
Ques. Write two properties of a material suitable for making
(a) a permanent magnet, and
(b) an electromagnet. [Outside Delhi 2017] (3 Marks)
Ans. a. Permanent magnet:
- Retentivity is high.
- Coercivity is high.
- Electromagnet:
- Permeability is high.
- Retentivity is low.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check Out:








Comments