Jasmine Grover Content Strategy Manager
Content Strategy Manager
Lorentz force is defined as the force exerted on a charged particle moving through an electric field and a magnetic field. Hendrik Lorentz first derived the modern formula of the Lorentz force in the year 1895. Lorentz Force helps find how an electric field and a magnetic field coexist and affect a charged particle. It is the entire electromagnetic force applied to the charged particle. Lorentz force formula can be expressed by:
F = qE + qv \(\times\) B
The electric charges moving through a magnetic field normally experience Lorentz force. Essentially, when there is a motion of a charge in a magnetic field, the magnetic force is perpendicular in the direction to the velocity. So, there is neither any work done nor any change in the magnitude of velocity.
| Table of Content |
Key Terms: Electromagnetic Force, Magnetic Force, Electric Field, Magnetic Field, Motion of a Charge in a Magnetic Field, Velocity, Lorentz force
What is Lorentz Force?
[Click Here for Previous Year Questions]
Lorentz force is defined as the force exerted on a charged particle moving through an electric field and a magnetic field. It is the entire electromagnetic force applied to the charged particle. Hendrik Lorentz derived the modern formula of the Lorentz force in 1895. It is formulated as,
| F = qE + qv \(\times\) B |
where,
- F denotes Lorentz force,
- q denotes the charged particle,
- E is the Electric field,
- B is the magnetic field,
- v is the velocity of the charged particle

Lorentz force
For continuous charge distribution, Lorentz force formula is,
| dF – dq(E + vB) |
where,
- dF = force on a small piece of the charge
- dq = charge of a small piece
Considering that a small piece of charge distribution has been divided by the volume dV, the formula can be obtained:
⇒ f = \(\rho\) (E + vB)
How to Measure Lorentz Force?
There are different ways to measure Lorentz force. Some of them include:
Lorentz force on a moving charge present in a “B” Field
Lorentz force occurs when a charged particle’s movement takes place via a magnetic field and cuts through the field lines during the procedure. It acts at right angles to particle velocity (v) and magnetic field (B). Lorentz force’s direction in different situations relies on the particle’s direction of velocity, magnetic field and sign of the particle’s charge. The rule that helps measure it is the variant of Fleming’s Left hand rule.
- First finger points to the direction of Magnetic Field
- Second finger points to the direction of the Current
- Thumb’s direction is in the direction of Motion, considering the magnetic force is the only force present.
Lorentz Force on a Current-carrying Wire Present in a Magnetic Field
Current can be defined as the movement of charged particles. Thus, if a wire with current is found within a magnetic field, then all the charged particles would undergo Lorentz force.
Thus, in order to determine the solution, the sum of the forces on the moving charged particles is need to be found out. This is due to the fact that the sum of the forces on the moving charged particles is equivalent to the overall force on the wire.
Read More:
Motion in Electric and Magnetic Field
[Click Here for Sample Questions]
Essentially, when there is a motion of a charge in a magnetic field, the magnetic force is perpendicular in direction to the velocity. So, there is neither any work done nor any change in the magnitude of velocity.
Now, when velocity is perpendicular to the magnetic force with the charge moving in a uniform magnetic field, a circular motion perpendicular to the magnetic field is produced. The perpendicular force, which is denoted by qvB, acts as a centripetal force.

Motion of Charges
On the other hand, if there is another component of velocity along with the magnetic field, the component will remain unchanged as the motion along the magnetic field will be unaffected. The motion will be perpendicular to the magnetic field describing a helical motion.
Helical Motion
- The radius of every circular path framed will be derived from the centripetal force and will be denoted by, r = mv/qB.
- The circle formed will be bigger depending on the radius, which in turn, is directly proportional to the momentum.
- The angular frequency will be given as =Bqm.
- The distance travelled along the magnetic field to make another revolution is known as the pitch. It is the product of the component of velocity parallel to the magnetic field and the time taken to make a revolution (T). Thus, \(p = vT = 2m\frac{v}{T} B\).
Applications of Lorentz Force
[Click Here for Previous Year Questions]
There are several applications of Lorentz Force, some of them include:
- J.J. Thomson experiment: Measurement of the specific charge of an electron.
- Cyclotron: Acceleration of charged particle.
- A bubble chamber uses Lorentz force in order to generate the graph to obtain the trajectories of charged particles.
- Cathode ray tube televisions are known to use Lorentz force in order to deviate electrons in a straight line to help it land on specific spots on the screen.
Importance of Lorentz ForceLorentz’s force helps define the mathematical equations alongside the physical importance of forces which act on the charged particles travelling via the space that contains electric and magnetic fields. Thus, this is how the importance of Lorentz force can be shown. Right-Hand RuleThe right-hand rule is often used in order to determine the magnetic force. It is useful because it helps visualize the direction as present in Lorentz force law.
Fleming's Right Hand Rule |
Also Read:
Things to Remember
- Lorentz force is defined as the force exerted on a charged particle moving through an electric field and a magnetic field.
- Lorentz Force is the summation of the force experienced by the moving charge in an electric and magnetic field.
- Lorentz force is given by the formula F = qE + qV x B
- For continuous charge distribution, Lorentz force formula is, dF- dq(E + vB).
- Lorentz force finds its application in JJ Thomson’s measurement of specific charge of an electron experiment and in cyclotron.
Sample Questions
Ques. An electron describing a circle is in a magnetic field of 10-4T. What will be the angular frequency of revolution if mass is 9.1x10-13kg and the charge is 1.6x10-19C? (2 marks)
Ans. On equating the centripetal force and the magnetic force,
mv 2 r=qvB
v=rBqm……..(i)
We know, angular frequency =vr
So, from equation (i), we get =Bqm
=10-41.6x10-19 / 9.1x 10-31rad/sec
=1.758x 107rad/sec
Ques. A beam of protons enters a uniform magnetic field of 0.3 T with a velocity of 4105m/s in a direction making an angle of 60with the direction of the magnetic field. What will be the pitch of the helix formed by moving particles? (Given, charge of proton e=1.6x10-19C, mass m=1.67x10-27kg) (2 marks)
Ans. Let, v be the component of the pitch.
T=2mq
B=2 x1.67x10-27x1.6x10-19 x 0.321.8610-8s
Pitch = 0.043 m
Ques. A thin, 0.638 m long copper rod has a mean of 22g. Find out the minimum current in the rod that will cause it to float in a magnetic field of 2.45T? (2 marks)
Ans. Given data, length of the copper rod: l = 0.638m
The mass of the copper rod: m = 22g = 22g x 1kg/ 103 g = 2.2 x 10-2 kg
Magnetic field around the copper rod: B = 2.45T
The equation to calculate the minimum current present in the road to float in the magnetic field is, BIl= mg
(2.45T). I. (0.638 m) = (2.2 x 10-2 kg) (9.8m/ s2)
I = 0.14A.
Ques. A moving charged particle q travelling along the x-axis, enters a uniform magnetic field B. When the force acting on q will be maximum? (2 marks)
Ans. The magnetic force acting on the charged particle,
F = qvB sinθ
Where θ represents the angle between the velocity of particle v and magnetic field B
Hence, for maximum force sinθ = 1
⇒ θ = 90o
Therefore, the magnetic field must be in the direction which is perpendicular to the velocity of the particle which implies that the magnetic field must either be in the y-axis or z-axis.
Ques. A charged particle is whirled in a horizontal circle on a frictionless table by joining it to a string fixed at one end. Now, if the magnetic field is switched on in the vertical direction, the tension in the string will be, (2 marks)
a) will increase
b) will decrease
c) will remain same
d) may increase or decrease
Ans. Let us assume that the string makes an angle θ with the vertical.
Initially, before the magnetic field is applied, T sin θ = mv2/r
If the particle experiences an outward force in the direction of the radius, tension T will increase. Again, if the particle experiences an inward force in the direction of the radius towards the centre, tension T will decrease.
Ques. An electron moving perpendicular to a uniform magnetic field 0.500 T undergoes circular motion of radius 2.80 mm. What is the speed of electron? (2 marks)
Ans. Charge of an electron q = -1.60 × 10-19 C
→ |q| = 1.60 ×10−19 C
Magnitude of magnetic field B = 0.500 T
Mass of the electron, m = 9.11 × 10-31 kg
Radius of the orbit, r = 2.50 mm = 2.50 × 10-3 m
Velocity of the electron, v = |q| rB/m
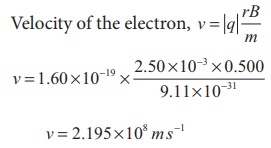
v = 2.195 ×108 m s−1
Ques. Find out the magnitude of the force experienced when the unit charge is kept under the influence of 5 N/C electric fields.(2 marks)
Ans. Force on the charge is given by,
F = qE
F = 1x5
F = 5 N/s
Ques. Find out the magnitude of the force experienced when a 5C charge is kept under the influence of 25 N/C electric fields. (2 marks)
Ans. Force on the charge is given by,
F = qE
F = 5 x 25
F = 125 N/s
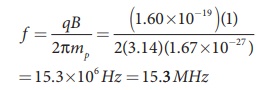
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:








Comments