Jasmine Grover Content Strategy Manager
Content Strategy Manager
Magnetism, an invisible force pulling and pushing matter without contact, holds a unique place in our universe. It arises from the dynamic dance of electrons within atoms. When these tiny charged particles move in specific arrangements, they generate a magnetic field. It is an invisible region influencing other moving charges or magnetic materials.
- Ferromagnetic materials, like iron or nickel, readily align their internal electron spins with an external magnetic field, becoming temporary magnets themselves.
- Electromagnets are powerful temporary magnets created by coiling wire and passing current through it. Electricity interacts with magnets in the motor to create rotational motion, powering everything from fans to high-speed trains.
- The Earth's magnetic field interacts with a compass needle, providing reliable navigation.
Read More:
| Additional Resources for Preparation | |
|---|---|
| Magnetism and Matter | NCERT Solutions for Class 12 Physics Chapter 5 Magnetism and Matter |
| Magnetism and Matter MCQs | Magnetism and Matter Important Questions |
Class 12 Physics Chapter 5 Notes - Magnetism and Matter
Bar Magnet
- A bar magnet is a rectangular piece of magnet having South and North poles of equal strength separated by a small distance.
- The strength with which a magnetic pole attracts is known as pole strength.
- When suspended freely, the north pole of the magnet points toward geographical north and south pole point toward geographical south.
- Line joining the north and south poles of a magnet is called magnetic axis.
- Like poles repel each other and unlike poles attract each other.
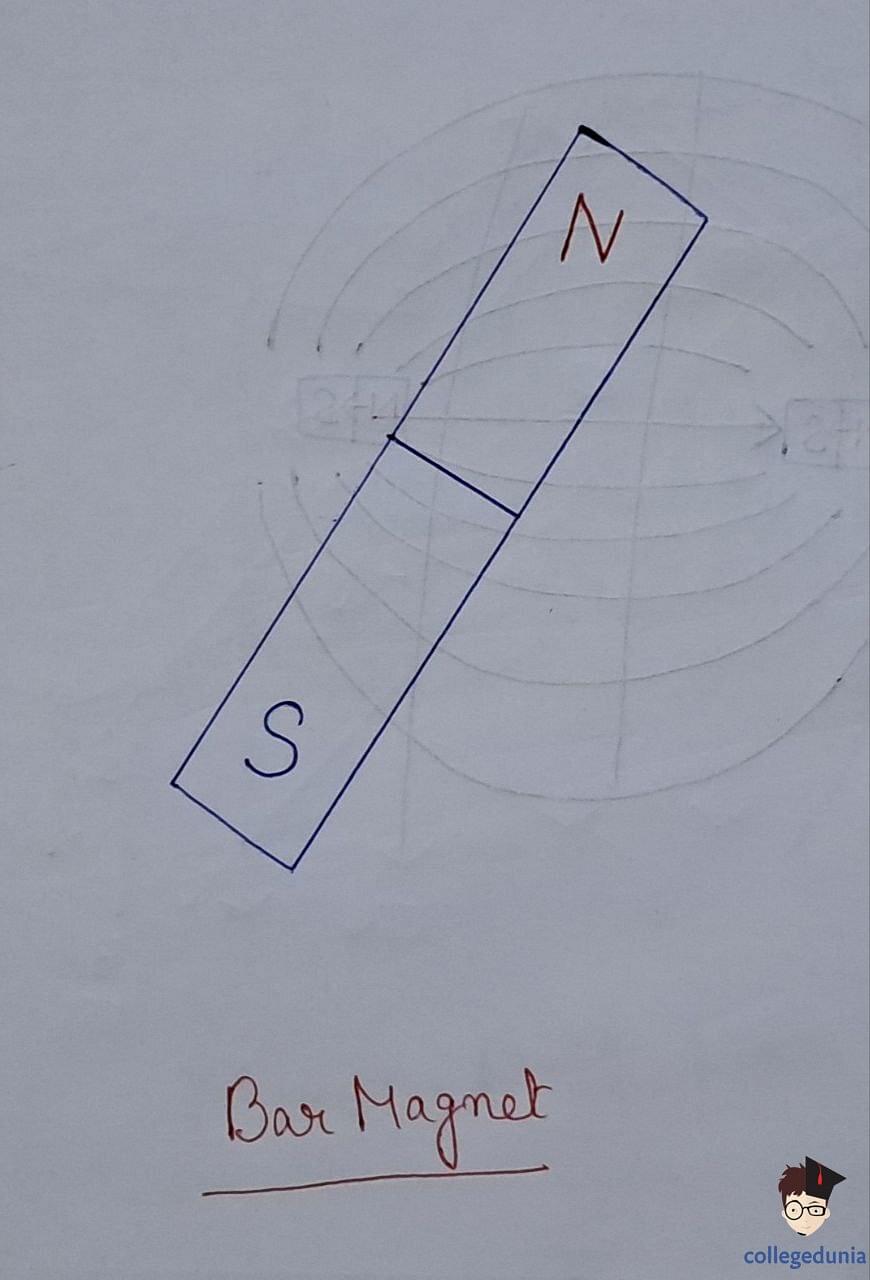
Bar magnet
Magnetic Field Lines
- Magnetic field lines provide a visual representation of the direction a magnetic field takes in a given region.
- The density of magnetic field lines indicates the strength of the magnetic field – closer lines signify stronger fields, while more spaced-out lines suggest weaker fields.
- The orientation of magnetic field lines indicates the polarity of the magnet, with lines emerging from the north pole and entering the south pole in a continuous loop.

Magnetic field lines
Coulomb’s Law of Magnetic Force
- The force between magnetic poles at a distance r is directly proportional to the product of pole strengths and inversely proportional to the square of the distance between their centers.
- Formula:
F = (μo/4π) (qm1 qm2)/r2
Where
- qm1 amd qm2 are the pole strengths
- r is the distance between the pole strengths of two different magnets.
Magnetic Dipole Moment
- It is defined as the product of the pole strength of the either pole and distance between the magnetic poles.
- Formula:
m = qm x 2l
Where
- m is the magnetic moment
- qm is the pole strength
- 2l is the distance between the magnetic poles.
Bar Magnet As An Equivalent Solenoid
- A bar magnet can be considered equivalent to a solenoid due to the alignment of its magnetic field lines.
- Similar to a solenoid, the magnetic field inside the bar magnet runs from its north pole to the south pole.
- The north-seeking pole (north pole) of the bar magnet corresponds to the direction of the magnetic field's exit in a solenoid.
- The south-seeking pole (south pole) of the bar magnet corresponds to the direction of the magnetic field's entry in a solenoid.
- The magnetic moment of a bar magnet aligns with the axial direction, just like the magnetic moment of a solenoid.
- The strength and orientation of the magnetic moment in both structures are critical for understanding their magnetic behavior.
The Dipole In A Uniform Magnetic Field
A magnetic dipole experiences a torque when placed in a uniform magnetic field.
- Formula
\(\tau\) = mB sinθ
Where
- \(\tau\) is the torque acting on a magnetic dipole
- B is the uniform magnetic field
- m is the magnetic moment
- θ is the angle between magnetic field and magnetic moment
- The torque causes the magnetic dipole to align itself with the magnetic field.
- The direction of the torque follows the right-hand rule, where the thumb points along the magnetic dipole moment (m), the forefinger along the magnetic field (B), and the middle finger represents the direction of the torque.
- The potential energy (U) of a magnetic dipole in a uniform magnetic field is given by U = − m ⋅ B.
- The negative sign indicates that the potential energy is minimum when the magnetic dipole is aligned with the magnetic field and maximum when perpendicular.

Torque on a magnetic dipole
The Electrostatic Analog
- The electrostatic analog refers to a conceptual framework where the principles and behaviors of electrical circuits are analogously compared to those of electrostatic systems.
- In this analogy, voltage corresponds to electric potential, current to the flow of charge, and resistors to objects with resistance.
- The electrostatic analog provides a useful way to understand and analyze complex electrical circuits through the lens of simpler electrostatic principles.
Magnetism And Gauss’s Law
- Gauss’s Law for Magnetism states that the magnetic flux through any closed surface is zero, indicating that there are no magnetic monopoles (isolated magnetic charges).
- Unlike electric fields, which can have sources (charges) or sinks (charge densities), magnetic fields only exist as closed loops, and there are no magnetic charges separated from magnetic dipoles.
- Magnetic field lines are continuous loops with no beginning or end, representing the closed nature of magnetic fields.
- Gauss’s Law for Magnetism helps understand that magnetic field lines neither start nor end—they always form complete loops, emphasizing the absence of isolated magnetic poles.
Magnetisation And Magnetic Intensity
- Magnetization refers to the process of inducing magnetic properties in a material, aligning its magnetic domains.
- Achieved by exposing the material to an external magnetic field, causing its atomic magnets to align in the direction of the field.
- Definition: Magnetic intensity, symbolized by H, represents the strength of an external magnetic field applied to a material.
- Measured in Amperes per meter (A/m).
- It depends on the current flowing in a wire and the number of turns in a coil forming the magnetizing solenoid.

Magnetization
Magnetic Properties Of Materials
These properties showcase the diverse magnetic behaviors exhibited by different materials, contributing to their classification based on magnetic response -
Ferromagnetism
- Materials exhibiting ferromagnetism, like iron and nickel, have strong and permanent magnetic moments.
- They can be easily magnetized and retain their magnetic properties even after the removal of an external magnetic field.
Paramagnetism
- Paramagnetic materials, such as aluminum and platinum, possess weak and temporary magnetic moments.
- They get magnetized in the presence of an external magnetic field but lose their magnetization when the field is removed.
Diamagnetism
- Diamagnetic materials, like bismuth and copper, have no intrinsic magnetic moment.
- They are weakly repelled by both permanent magnets and external magnetic fields.

Diamagnetic, Paramagnetic, and Ferromagnetic matrials
In the CBSE Class 12 Physics exam, Units 3 and 4, "Magnetic Effects of Current and Magnetism" and "Electromagnetic Induction and Alternating Currents," hold a significant weight of 17 marks.
There are Some important List Of Top Physics Questions On Magnetism And Matter Asked In CBSE CLASS XII






Comments