
Content Strategy Manager
Brownian Motion refers to the random movements of the particles suspended in a medium. This motion results in random fluctuation of the particle's position inside a fluid subdomain, followed by relocation to a different sub-domain. There is no preferential direction of the movement that exists. The continuous and random unequal bombardment leads to such non-uniform movements. Here, a particle changes its path when it collides with another particle. These collisions cause the particle to follow a random zigzag pattern involving an exchange of momentum/ energy between the particles.
| Table of Content |
Key Takeaways: Brownian Motion, Colloidal Solution, Non uniform motion, Angular Momentum, Motion, Collide, Collision
What is Brownian Motion?
[Click Here for Sample Questions]
Brownian motion, also known as ‘pedesis’ , refers to the random motion of particles suspended in a medium. Here the medium can be air or liquid. This motion results in random fluctuation of the particle's position inside a fluid subdomain, followed by relocation to a different sub-domain. Each such relocation is followed by more fluctuation inside the new closed volume. Here, no preferential direction of flow exists. In other words, fluid’s overall linear and angular momenta remain null over time.
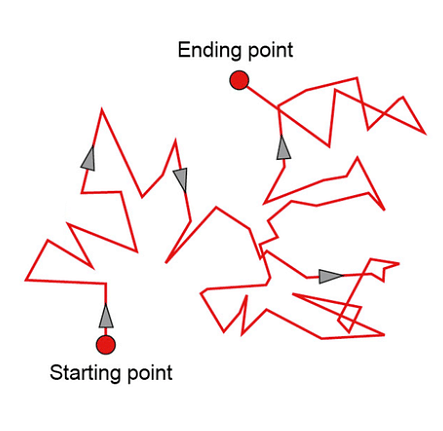
Brownian Movement
The phenomenon is named after the botanist Robert Brown, who first observed the motion in 1827 by looking at the motion of pollen immersed in water. Here, it should be noted that Brownian motion is observed in colloidal substances and not in a real solution where the system is homogeneous and the bombardment is rather uniform. Thus, the particles move uniformly and do not exhibit Brownian Motion.
A particle changes its path when it collides with another particle. These collisions cause the particle to follow a random zigzag pattern. The process involves the exchange of momentum/energy between the particles.
Also Read:
| Related Articles | ||
|---|---|---|
| All about solutions | Types of solutions | Electrolytic cell |
| Concentration cell | Neo-electrolytes | Quadratic Equation |
Causes of Brownian Motion
[Click Here for Sample Questions]
Brownian motion simply denotes randomness and chaos. There are various causes of this motion which are listed below.
- Firstly, the size of the particles is inversely proportional to the speed of the motion which means small particles tend to exhibit faster movements and the bigger ones show slower movements.
- Secondly, it is because the transfer momentum is proportional to the mass of the particles. That is why particles, light in weight, obtain greater speed after collision.
- Thirdly, the speed of the motion is inversely proportional to the viscosity of the fluid it is residing in. The lower the viscosity, the faster the movement of the particle.
- Lastly, viscosity can be considered as a quantity to express the magnitude of the internal friction in a liquid. It measures the fluid’s resistance to flow.
Effects of Brownian Motion
[Click Here for Sample Questions]
The effects of the Brownian motion are listed below-
- Due to Brownian Motion, the particles in the fluid are in constant motion.
- A single particle can be hit by more on one side than another leading to the seemingly random nature of the motion.
- The Brownian motion prevents the particles from settling down, leading to the stability of the colloidal substances.
- Brownian motion can be one of the parameters to distinguish a colloid from a true solution.

Brownian Motion
Brownian Motion in Colloids
[Click Here for Sample Questions]
Brownian Motion is observed in all types of colloidal solutions. Apart from that it explains the randomness of the particles and indicates that the particles are never static. The reason behind this type of random movement is the unequal bombardment of the depress phase particle leading to non-uniform movement in native because of differences in the size of the particles.
Unlike colloidal substances, Brownian motion is not observed in a true solution where the system is homogeneous and the bombardment is rather uniform. The heterogeneous nature of the colloids and the non-uniform bombardments lead to the random measurement.

Collision in Brownian Motion
One of the key advantages of this effect is that it helps to keep the soil particles in continuous, random motion and prevents their settling down. Thus, they prevent the coagulation of the lyophobic sold. This type of motion increases the stability of a solution.
Things to Remember
- Brownian motion refers to the random movement of particles suspended in a medium.
- This motion results in random fluctuation of the particle's position inside a fluid subdomain, followed by relocation to a different sub-domain.
- There is no preferential direction of flow that exists in Brownian Motion. The fluid’s overall linear and angular momenta remain null over time.
- The size of the particles is inversely proportional to the speed of the motion and the transfer of momentum is proportional to the mass of the particles
- The Brownian Motion is observed in all sorts of colloidal solutions. The reason behind this type of random movement is the unequal bombardment of the depressed phase particle leading to non-uniform movement.
Read More:
Sample Question
Ques: What is Brownian Motion? (2 marks)
Ans: Brownian motion refers to the random movement of particles suspended in a medium. This motion results in random fluctuation of the particle's position inside a fluid subdomain, followed by relocation to a different sub-domain.
Ques: State an example of Brownian Motion. (2 marks)
Ans: Brownian motion is primarily observed in a transport system that is affected by a large current. For example, the motion of the pollen grains in still water shows zigzag Brownian motion. Plasma cell particles in the cells also show Brownian motion.
Ques: What is the cause of the Brownian Motion? (2 marks)
Ans: Brownian movement takes place when the particles collide with the surrounding molecules causing them to move randomly. The unequal bombardment of the depressed phase particle leads to non-uniform movement.
Ques: Why does the real solution not follow the Brownian Movement? (2 marks)
Ans: Brownian motion is not observed in a real solution where the system is homogeneous and the bombardment is rather uniform. Thus, the particles move uniformly and do not exhibit Brownian Motion.
Ques: How does the Brownian Motion help in the stability of the colloids? (2 marks)
Ans: Random collisions between water molecules and colloidal particles result in Brownian Motion. This motion is responsible for the stirring effect. Thus, the particles do not settle down which impacts its stability.
Ques: How does temperature affect Brownian motion? (2 marks)
Ans: Temperature is one of the most significant elements to affect Brownian motion. When the temperature of a colloidal solution rises the more energetic the particles become leading to a higher degree of movement.
Ques: Is there any difference between Brownian motion and motility? (2 marks)
Ans: It is a bit tricky to differentiate a movement due to Brownian motion and movement due to other effects. Typically, the process of Brownian motion is a random, jerky, directionless movement whereas true motility appears to have direction. For example, ciliary and flagellar movements have a particular direction of movement.
Ques: How does Brownian motion work in gas? (2 marks)
Ans: Irrespective of whether a substance is a gas or liquid, the particles move randomly and Brownian Motion is responsible for this. The collisions of the particles lead to such directionless random motion.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:





Comments