Jasmine Grover Content Strategy Manager
Content Strategy Manager
Bohr's model of the hydrogen atom is a modification of the model of the atom given by Rutherford. Bohr had closely studied Rutherford’s model and came across several gaps in the theory. He addressed these spaces which newly defined the model of an atom. He emphasized the role of the quantum hypothesis in describing what we today know as Bohr’s model of the hydrogen atom.
| Table of Content |
Keyterms: Bohr Model, Hydrogen Atom, Bohr’s Postulates, Energy levels, Limitations, Planck’s constant, Coulomb’s Law
Bohr’s model of the Hydrogen atom
[Click Here for Sample Questions]
Rutherford had assumed the atom and its components work in a manner similar to the solar system. But, the elementary difference between the two situations is that the planetary system is held by the gravitational force whereas the nucleus-electron system interacts by the Coulomb’s Law of Force. This is because both the nucleus and electrons are charged particles. In addition, it is known that there is a constant acceleration of an object moving in a circle due to centripetal force.
Furthermore, the electromagnetic theory says that an accelerating charged particle will emit radiation in the form of electromagnetic waves. The energy of an accelerating electron must be decreasing. The electron will then revolve towards the nucleus. An atom, in such a case, cannot be stable.
The theory also states that the frequency of the electromagnetic waves discharged by the revolving electrons will be equal to that of the revolution. The angular velocity and frequency of such electrons will keep on changing, alternating the frequency of light released. Thus, a continuous spectrum can be observed.
These were the observations made by Niel Bohr, and that’s when his model of the atom came into the picture.
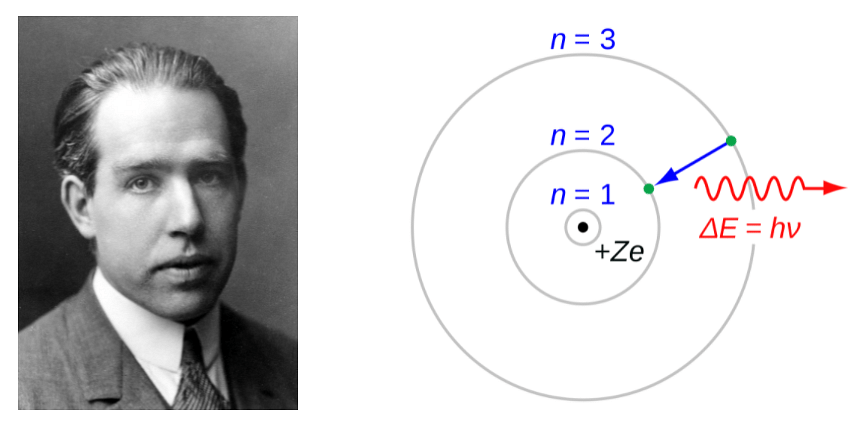
Fig: Niels Bohr and his Atomic Model
Also Read:
| Related Articles | ||
|---|---|---|
| Value of c | Particle Physics | Bohr Radius |
| Energy Level | ionizing radiation | Quantum Mechanics |
Bohr’s Postulates
[Click Here for Sample Questions]
Bohr defined his model using three postulates applying the concepts of classical electromagnetic theory and initial studies on quantum theory together.
Postulate I: An electron in an atom could revolve in certain stable orbits without emission of radiant energy.
According to Bohr, each atom can exist in certain definite stable states and each state has fixed total energy. These are called the stationary states of atoms
Postulate II: The electron revolves around the nucleus only in those orbits for which the angular momentum is some integral multiple of h/2.
The angular momentum of orbiting electron is calculated by L=nh/2
Where, L - angular momentum
h - Planck’s constant (= 6.6 x 10-34Js)
Postulate III: An electron might make transitions from one of its specified non-radiating orbits to another of lower energy. Then, a photon is released having energy equal to energy difference between the initial and final states.
The frequency of the released photon is presented as,
hv = Et – Ef
(Etis the initial state and Efis the final state and Et>Ef)
Limitations of Bohr’s Model of an Atom
[Click Here for Sample Questions]
- Bohr’s model of the atom failed to explain the Zeeman Effect (effect of magnetic field on the spectra of atoms).
- It failed to explain the Stark effect (effect of electric field on the spectra of atoms).
- The spectra obtained from larger atoms weren’t explained.
- It violates the Heisenberg Uncertainty Principle.
Important equations of Bohr’s model
The radius of Bohr’s stationary orbit
\(r_n = n^2 ( \frac {h^2 \epsilon_0}{\pi m Z e^2}) \)
Where,
n is an integer,
rn is the radius of the n-th orbit,
H is the Planck’s constant,
ε0 is the electric constant,
m is the mass of the electron,
Z is the atomic number of the atom (Z = 1 for hydrogen atom),
e is the elementary charge.
The velocity of the electron in Bohr’s stationary orbit

The total energy of an electron in Bohr’s stationary orbit
![]()
The negative sign denotes that the electron is bound to the nucleus.
Energy levels
[Click Here for Sample Questions]
The energy of an atom is the lowest when its electron is revolving in an orbit closest to the nucleus (i.e. when n = 1). The energy levels gradually increase in the outer orbits, when n = 2, 3, …
The state of the atom, in this case, is called the Ground-state where the radius of the orbit (a0) is the least. The energy is equal to – 13.6 eV. This is the minimum energy necessary to release an electron from the ground state of an atom. It is called the Ionisation energy of the hydrogen atom.
As a matter of fact, the hydrogen atom is normally in the Ground-state at room temperature. The energy levels can be increased by electron collision and the electron can be shifted to higher energy orbits. This is the excited state of the hydrogen atom. Thus, the energy required to excite an electron to the first excited state is,
E2 – E1= – 3.40 eV – (- 13.6)eV = 10.2 eV
Again, to excite the electron to the second excited state, the energy required is,
E3 – E1= – 1.51 eV – (- 13.6)eV = 12.09 eV
Therefore, as the excitation of the hydrogen atom increases, the minimum energy needed to free the electron diminishes. Also, the electron can jump to a lower energy level by releasing a photon.
Things to Remember
- .Bohr's model of the hydrogen atom is a modification of the model of the atom given by Rutherford.
- Rutherford had assumed the atom and its components work in a manner similar to the solar system. But, the elementary difference between the two situations is that the planetary system is held by the gravitational force whereas the nucleus-electron system interacts by the Coulomb’s Law of Force.
- The theory also states that the frequency of the electromagnetic waves discharged by the revolving electrons will be equal to that of the revolution.
- Bohr defined his model using three postulates applying the concepts of classical electromagnetic theory and initial studies on quantum theory together.
- Bohr’s model of the atom failed to explain the Zeeman Effect (effect of magnetic field on the spectra of atoms).
- The energy of an atom is the lowest when its electron is revolving in an orbit closest to the nucleus (i.e. when n = 1). The energy levels gradually increase in the outer orbits, when n = 2, 3, …
Also Read:
Sample Questions
Ques: What happens when an electron shifts from an outer orbit to an inner orbit? (1 Mark)
Ans: The energy level drops as the electron moves from a higher orbit to a lower one. The energy is released.
Ques: What is the wavelength (in nm) of the photon emitted when an electron in the hydrogen atom makes a transition from the energy level n = 7 to the energy level n = 4? (2 Marks)
Ans: The wavelength of electron transition is calculated by,
1=RH(1nf2-1nt2)
1=RH(142-172)
1=RH(116-149)
1=RH(33784)
Put, RH=1.09678 x 107m-1
=2.17 x 10-6m(Ans)
Ques: State Bohr’s quantization condition of angular momentum. Calculate the shortest wavelength of the Bracket series and state to which part of the electromagnetic spectrum does it belong. (2019) (2 Marks)
Ans:

Ques: Calculate the orbital period of the electron in the first excited state of the hydrogen atom. (2019) (3 Marks)
Ans: r = 0.53(n²/z) * 10-¹ºm
For the former excited state n = 2
r = 0.53(2²/1) * 10-¹º
r = 2.12 * 10-¹ºm
V = v0 * Z/n (m/s)
V = 2.188 * 106 * Z/n (m/s)
For the initial excited state, n = 2 and Z = 1 for hydrogen atom
Therefore v = 2.188 * 106 * ½(m/s)
V = 1.094 * 106(m/s)
Orbital period = 2r/v = 2*3.14*2.12*10-¹º/1.094*10?
Orbital period = 1.22 * 10-15 sec
Ques: A hydrogen atom in the ground state is excited by an electron beam 12-5 eV energy. Find out the maximum number of lines emitted by an atom from its excited state. (2019 outside Delhi) (3 Marks)
Ans: The energy present in the ground state E1 = -13.6eV
The energy that is being supplied = 12.5eV
THerefore, the energy present in the excited state refers to,
En = -13.6 + 12.5
En = -1.1eV
En = -13.6/n²
Hence, n=3
The max number of lines is equal to 3.
Ques: State Bohr’s postulate defines stable- orbits in hydrogen atoms. How does de Broglie’s hypothesis explain the stability of these orbits? (2018) (3 Marks)
Ans: Bohr’s postulate of Quantisation condition states that the electrons can only revolve in certain particular orbits which have their angular momentum L.

= mvr is a integral multiple of \(\frac{h}{2 \pi}\) i.e.
Therefore the circumference of the electron that has the nth stable orbit can conserve exactly n wavelength of de-Broglie which is in association with the electron in that particular orbit.
Ques: Find out the wavelength of the electron orbiting in the ground state of the hydrogen atom. (2017) (2 Marks)
Ans:

For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:






Comments