The CBSE Class 12th Physics examination for the year 2025 was conducted on February 21, 2025. An estimated 17.88 lakh students are appearing from 7,842 centers in India and 26 other countries.
The exam carries a total of 70 marks for the theory paper, while 30 marks are assigned to internal assessment. The question paper includes multiple-choice questions (1 mark each), short-answer questions (2-3 marks each), and long-answer questions (5 marks each).
The question paper and solution PDF is available for download after the exam.
CBSE Board Class 12 Physics Set- 2 (55/1/2) Question Paper 2025 with Solutions
| CBSE Board Class 12 Physics Question Paper with Answer Key | Check Solutions |
CBSE Class 12 2025 Physics Question Paper with Solutions
In the figure, curved lines represent equipotential surfaces. A charge \( Q \) is moved along different paths A, B, C, and D. The work done on the charge will be maximum along the path:

View Solution
The work done on a charge \( Q \) moving in an electric field is given by:
\[ W = -Q \Delta V \]
Where \( \Delta V \) is the potential difference. Work is maximum when the potential difference is maximum.
Looking at the diagram, path B moves across the largest potential difference (from 25V to 10V) compared to the other paths. Therefore, the work done will be maximum along path B. Quick Tip: The work done on a charge in an electric field depends on the potential difference between the starting and ending points. The larger the potential difference, the greater the work done. In this case, the path with the maximum potential difference will have the maximum work done.
The resistance of a wire of length \( L \) and radius \( r \) is \( R \). Which one of the following would provide a wire of the same material of resistance \( \frac{R}{2} \)?
View Solution
The resistance of a wire is given by:
\[ R = \rho \frac{L}{A} \]
Where \( L \) is the length of the wire, \( A \) is the cross-sectional area, and \( \rho \) is the resistivity of the material.
The cross-sectional area \( A \) is given by:
\[ A = \pi r^2 \]
For a wire of same material and length, resistance will be halved when the radius is doubled, as resistance is inversely proportional to the square of the radius. Therefore, option (C) is correct. Quick Tip: The resistance of a wire depends on its length and cross-sectional area. To reduce the resistance by half, you can increase the radius of the wire, as the resistance is inversely proportional to the square of the radius.
A 1 cm segment of a wire lying along the x-axis carries a current of 0.6 A along the \( +x \) direction. A magnetic field \( \vec{B} = (0.4 \, mT) \hat{j} + (0.6 \, mT) \hat{k} \) is switched on in the region. The force acting on the segment is:
View Solution
The magnetic force on a current-carrying wire segment is given by:
\[ \vec{F} = I \vec{L} \times \vec{B} \]
Where \( I \) is the current, \( \vec{L} \) is the length vector of the wire, and \( \vec{B} \) is the magnetic field.
Using the right-hand rule and calculating the cross product, we find the force acting on the segment to be \( (-3 \hat{j} + 2 \hat{k}) \, \mu N \). Quick Tip: To find the magnetic force on a current-carrying wire, use the formula \( \vec{F} = I \vec{L} \times \vec{B} \), and apply the right-hand rule to determine the direction of the force.
A circular coil of diameter 15 mm having 300 turns is placed in a magnetic field of 30 mT such that the plane of the coil is perpendicular to the direction of the magnetic field. The magnetic field is reduced uniformly to zero in 20 ms and again increased uniformly to 30 mT in 40 ms. If the emfs induced in the two time intervals are \( \varepsilon_1 \) and \( \varepsilon_2 \) respectively, then the value of \( \varepsilon_1 / \varepsilon_2 \) is:
View Solution
The induced emf is given by Faraday’s Law:
\[ \varepsilon = -N \frac{d\Phi}{dt} \]
Where \( N \) is the number of turns, \( \Phi \) is the magnetic flux, and \( \frac{d\Phi}{dt} \) is the rate of change of flux.
Since the number of turns and the change in magnetic field are the same for both intervals, the ratio of the emfs \( \frac{\varepsilon_1}{\varepsilon_2} \) will be 1. Quick Tip: Faraday’s Law tells us that the induced emf is proportional to the rate of change of the magnetic flux. If the magnetic field change is the same, the induced emf will be the same, regardless of the duration of the change.
You are required to design an air-filled solenoid of inductance 0.016 H having a length 0.81 m and radius 0.02 m. The number of turns in the solenoid should be:
View Solution
The inductance \( L \) of a solenoid is given by the formula:
\[ L = \mu_0 \frac{N^2 A}{l} \]
Where:
- \( L \) is the inductance,
- \( \mu_0 \) is the permeability of free space,
- \( N \) is the number of turns,
- \( A \) is the cross-sectional area of the solenoid, and
- \( l \) is the length of the solenoid.
Solving for \( N \), we get:
\[ N = \sqrt{\frac{L l}{\mu_0 A}} \]
Substituting the given values, we find that the number of turns is approximately 2866. Quick Tip: For solenoids, the inductance depends on the number of turns, the cross-sectional area, and the length. Remember that the inductance increases with the square of the number of turns, so use this formula to find the number of turns required for a given inductance.
A voltage \( v = v_0 \sin (\omega t) \) applied to a circuit drives a current \( i = i_0 \sin (\omega t + \phi) \) in the circuit. The average power consumed in the circuit over a cycle is:
View Solution
The average power consumed in an AC circuit is given by:
\[ P_{avg} = \frac{1}{T} \int_0^T v(t) i(t) \, dt \]
For a sinusoidal voltage and current, the average power is:
\[ P_{avg} = \frac{i_0 v_0}{2} \cos \phi \]
Where \( \phi \) is the phase difference between the voltage and the current. Hence, the correct answer is \( \frac{i_0 v_0}{2} \). Quick Tip: When working with AC circuits, remember that the average power over a cycle depends on the amplitude of the voltage and current and their phase difference. For a purely resistive circuit, the phase difference is zero, and the power is maximized.
Which one of the following correctly represents the change in wave characteristics (all in vacuum) from microwaves to X-rays in the electromagnetic spectrum?
View Solution
In the electromagnetic spectrum, all waves travel at the same speed in vacuum, which is the speed of light. As we move from microwaves to X-rays, the wavelength decreases and the frequency increases. Quick Tip: In the electromagnetic spectrum, the speed of light is constant in vacuum. As the wavelength decreases, the frequency must increase to maintain the relationship \( c = \lambda f \), where \( c \) is the speed of light, \( \lambda \) is the wavelength, and \( f \) is the frequency.
The speed of light in two media '1' and '2' are \( v_1 \) and \( v_2 \) (\( v_2 > v_1 \)) respectively. For a ray of light to undergo total internal reflection at the interface of these two media, it must be incident from:
View Solution
For total internal reflection to occur, the incident angle must exceed the critical angle, which is given by:
\[ \sin \theta_c = \frac{v_1}{v_2} \]
Thus, for total internal reflection, the angle of incidence must be greater than \( \sin^{-1} \left( \frac{v_1}{v_2} \right) \). Since the light is traveling from medium 1 to medium 2, the correct condition is \( \theta_i > \sin^{-1} \left( \frac{v_1}{v_2} \right) \), where \( v_1 < v_2 \). Quick Tip: Total internal reflection occurs when the incident angle exceeds the critical angle. The critical angle depends on the ratio of the speeds of light in the two media.
A source produces monochromatic light of frequency \( 5.0 \times 10^{14} \) Hz and the power emitted is 3.31 mW. The number of photons emitted per second by the source, on an average, is:
View Solution
The energy of one photon is given by:
\[ E = h f \]
Where \( h \) is Planck's constant and \( f \) is the frequency of the light.
The number of photons emitted per second, \( n \), is given by:
\[ n = \frac{P}{E} = \frac{P}{h f} \]
Substituting the given values:
\[ n = \frac{3.31 \times 10^{-3}}{6.626 \times 10^{-34} \times 5.0 \times 10^{14}} \approx 10^{10} \]
Thus, the number of photons emitted per second is \( 10^{10} \). Quick Tip: To calculate the number of photons emitted per second, use the relation \( n = \frac{P}{hf} \), where \( P \) is the power, \( h \) is Planck's constant, and \( f \) is the frequency of the light.
Question 10:
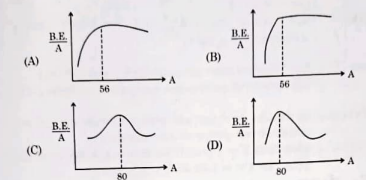
Which of the following figures correctly represent the shape of the curve of binding energy per nucleon as a function of mass number?
View Solution
The curve of binding energy per nucleon as a function of mass number shows a peak around iron (Fe, mass number 56). This is because the binding energy per nucleon increases with mass number up to iron and then decreases for heavier elements. The correct curve is represented by option (B). Quick Tip: The binding energy per nucleon increases with mass number up to iron (Fe) because nuclear fusion releases energy, making nuclei more stable. After iron, nuclear fission becomes more favorable, and binding energy per nucleon decreases.
When a p-n junction diode is forward biased, the barrier height and the depletion layer width both increase.
View Solution
When a p-n junction diode is forward biased, the barrier height decreases as the external voltage opposes the built-in potential. This results in a decrease in the depletion region width, allowing current to flow more easily through the junction. Quick Tip: Forward biasing a p-n junction reduces the potential barrier, making it easier for charge carriers to move across the junction. This results in a decrease in the depletion region width and the barrier height.
Assertion (A): The potential energy of an electron revolving in any stationary orbit in a hydrogen atom is positive.
Reason (R): The total energy of a charged particle is always positive.
View Solution
In a hydrogen atom, the potential energy \( U \) of the electron is negative due to the attractive force between the electron and the nucleus. The total energy \( E \) of the electron is the sum of kinetic energy and potential energy, and for a bound system, it is negative. However, the assertion (A) incorrectly states that the potential energy is positive. Quick Tip: In the Bohr model of the hydrogen atom, the potential energy of the electron is negative, while the total energy (which is the sum of potential and kinetic energy) is also negative for a bound system.
Assertion (A): We cannot form a p-n junction diode by taking a slab of a p-type semiconductor and physically joining it to another slab of a n-type semiconductor.
Reason (R): In a p-type semiconductor \( n_e \gg n_h \) while in a n-type semiconductor \( n_h \gg n_e \).
View Solution
To form a p-n junction, we need to join a p-type semiconductor and an n-type semiconductor. Assertion (A) is correct. However, the Reason (R) incorrectly states that the carrier concentrations are in the reverse order. In a p-type semiconductor, \( n_h \gg n_e \) because holes dominate, and in an n-type semiconductor, \( n_e \gg n_h \), where electrons dominate. Therefore, Reason (R) is false. Quick Tip: In p-type semiconductors, holes (absence of electrons) are the majority carriers, while in n-type semiconductors, electrons are the majority carriers. This is crucial in forming a p-n junction.
Assertion (A): The deflection in a galvanometer is directly proportional to the current passing through it.
Reason (R): The coil of a galvanometer is suspended in a uniform radial magnetic field.
View Solution
The assertion (A) is true because the deflection in a galvanometer is indeed proportional to the current passing through it. However, the reason (R) is not a complete explanation for Assertion (A). The coil of the galvanometer is suspended in a magnetic field, but the deflection also depends on the strength of the current and the sensitivity of the galvanometer, not just the magnetic field. Quick Tip: The deflection of a galvanometer is directly related to the current flowing through it, but other factors like the number of turns in the coil and the magnetic field also play a role.
Assertion (A): It is difficult to move a magnet into a coil of large number of turns when the circuit of the coil is closed.
Reason (R): The direction of induced current in a coil with its circuit closed, due to motion of a magnet, is such that it opposes the cause.
View Solution
The assertion (A) is true because moving a magnet into a coil with a large number of turns will induce an opposing current that resists the motion of the magnet. This is in accordance with Lenz's Law, which states that the induced current always opposes the change causing it. Quick Tip: Lenz's Law states that the direction of induced current in a coil will always oppose the change in magnetic flux that caused it. This is why moving a magnet into a coil with a closed circuit can be difficult.
Show that \( \mathbf{E} = \rho \mathbf{j} \) leads to Ohm's law. Write a condition in which Ohm's law is not valid for a material.
View Solution
The equation \( \mathbf{E} = \rho \mathbf{j} \) represents the relationship between electric field (\( \mathbf{E} \)) and current density (\( \mathbf{j} \)) in a material, where \( \rho \) is the resistivity of the material. This is a form of Ohm's law.
For a material to follow Ohm’s law, the resistivity should be constant and independent of the electric field. However, Ohm's law is not valid for non-ohmic materials, where resistivity varies with the electric field or current. This occurs in materials with nonlinear characteristics, such as semiconductors or materials exhibiting superconductivity. Quick Tip: Ohm's law, \( \mathbf{E} = \rho \mathbf{j} \), is valid only for materials with a constant resistivity. In materials where resistivity varies with current or electric field, Ohm's law doesn't hold.
In a diffraction experiment, the slit is illuminated by light of wavelength 600 nm. The first minimum of the pattern falls at \( \theta = 30^\circ \). Calculate the width of the slit.
View Solution
In a single-slit diffraction pattern, the condition for the first minimum is given by:
\[ a \sin \theta = m \lambda \]
Where:
- \( a \) is the width of the slit,
- \( \theta \) is the angle of the first minimum,
- \( m \) is the order of the minimum (for the first minimum, \( m = 1 \)),
- \( \lambda \) is the wavelength of the light.
Substituting the given values:
- \( \lambda = 600 \, nm = 600 \times 10^{-9} \, m \),
- \( \theta = 30^\circ \).
We can solve for \( a \):
\[ a = \frac{\lambda}{\sin \theta} \]
\[ a = \frac{600 \times 10^{-9}}{\sin 30^\circ} = \frac{600 \times 10^{-9}}{0.5} = 1200 \times 10^{-9} \, m = 1.2 \, μm \] Quick Tip: For single-slit diffraction, the position of the first minimum is given by \( a \sin \theta = \lambda \). Use this formula to calculate the slit width by rearranging it.
In a Young’s double-slit experiment, two light waves, each of intensity \( I_0 \), interfere at a point, having a path difference \( \frac{\lambda}{8} \) on the screen. Find the intensity at this point.
View Solution
In Young's double-slit experiment, the intensity \( I \) at a point on the screen due to two interfering waves is given by the formula:
\[ I = I_0 \left( 1 + \cos \delta \right) \]
Where \( I_0 \) is the intensity of each wave, and \( \delta \) is the phase difference between the waves. The phase difference \( \delta \) can be related to the path difference \( \Delta x \) by:
\[ \delta = \frac{2 \pi \Delta x}{\lambda} \]
Given that the path difference \( \Delta x = \frac{\lambda}{8} \), we can calculate \( \delta \):
\[ \delta = \frac{2 \pi \left( \frac{\lambda}{8} \right)}{\lambda} = \frac{\pi}{4} \]
Now, substituting into the intensity formula:
\[ I = I_0 \left( 1 + \cos \frac{\pi}{4} \right) = I_0 \left( 1 + \frac{\sqrt{2}}{2} \right) = I_0 \left( \frac{2 + \sqrt{2}}{2} \right) \]
\[ I = I_0 \times 1.707 \]
Thus, the intensity at this point is approximately \( 1.707 I_0 \). Quick Tip: In interference problems, the intensity due to two waves is calculated using \( I = I_0 \left( 1 + \cos \delta \right) \), where \( \delta \) is the phase difference corresponding to the path difference.
A spherical convex surface of radius of curvature \( R \) separates glass (refractive index 1.5) from air. Light from a point source placed in air at distance \( \frac{R}{2} \) from the surface falls on it. Find the position and nature of the image formed.
View Solution
N/A Quick Tip: When dealing with spherical mirrors, remember the mirror equation \( \frac{1}{f} = \frac{1}{v} - \frac{1}{u} \), and the focal length of a spherical surface is \( f = \frac{R}{2} \), where \( R \) is the radius of curvature.
The energy of an electron in an orbit of Bohr hydrogen atom is -3.4 eV. Find its angular momentum.
View Solution
For a hydrogen atom, the energy of an electron in the \( n \)-th orbit is given by the formula:
\[ E_n = -\frac{13.6}{n^2} \, eV \]
For \( n = 2 \), the energy is:
\[ E_2 = -\frac{13.6}{2^2} = -3.4 \, eV \]
Now, the angular momentum \( L \) of an electron in the \( n \)-th orbit is given by:
\[ L = n \hbar \]
For \( n = 2 \), the angular momentum is:
\[ L = 2 \hbar = 2 \times 1.0545718 \times 10^{-34} \, J·s = 2.1091436 \times 10^{-34} \, J·s \] Quick Tip: The energy of an electron in a Bohr orbit is inversely proportional to \( n^2 \), and its angular momentum is quantized as \( L = n \hbar \), where \( \hbar \) is the reduced Planck's constant.
A p-type Si semiconductor is made by doping an average of one dopant atom per \( 5 \times 10^7 \) silicon atoms. If the number density of silicon atoms in the specimen is \( 5 \times 10^{28} \) atoms/m\(^3\), find the number of holes created per cubic centimetre in the specimen due to doping. Also give one example of such dopants.
View Solution
The number of dopant atoms per silicon atom is given as \( \frac{1}{5 \times 10^7} \), so the number of dopant atoms per cubic metre is:
\[ Number of dopants per m^3 = \frac{5 \times 10^{28}}{5 \times 10^7} = 10^{21} \, dopants/m^3 \]
Since each dopant atom creates a hole in a p-type semiconductor, the number of holes created per cubic centimetre is:
\[ Number of holes per cm^3 = \frac{10^{21}}{10^6} = 10^{15} \, holes/cm^3 \]
One example of a dopant is Boron (B), which is commonly used to create p-type semiconductors. Quick Tip: In p-type semiconductors, doping with an element like Boron creates holes by substituting a silicon atom with one less valence electron. The number of holes created is equal to the number of dopant atoms.
Two batteries of emf's 3V \& 6V and internal resistances 0.2 \( \Omega \) \& 0.4 \( \Omega \) are connected in parallel. This combination is connected to a 4 \( \Omega \) resistor. Find:
the equivalent emf of the combination
the equivalent internal resistance of the combination
the current drawn from the combination
View Solution
Equivalent emf:
The equivalent emf \( E_{eq} \) of two batteries connected in parallel is given by:
\[ E_{eq} = \frac{E_1 R_2 + E_2 R_1}{R_1 + R_2} \]
Where \( E_1 = 3V \), \( E_2 = 6V \), \( R_1 = 0.2 \, \Omega \), and \( R_2 = 0.4 \, \Omega \). Substituting these values:
\[ E_{eq} = \frac{3 \times 0.4 + 6 \times 0.2}{0.2 + 0.4} = \frac{1.2 + 1.2}{0.6} = \frac{2.4}{0.6} = 4V \]
So, the equivalent emf of the combination is \( 4V \).
Equivalent internal resistance:
The equivalent internal resistance \( r_{eq} \) of the two batteries in parallel is given by:
\[ \frac{1}{r_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} \]
Substituting \( R_1 = 0.2 \, \Omega \) and \( R_2 = 0.4 \, \Omega \):
\[ \frac{1}{r_{eq}} = \frac{1}{0.2} + \frac{1}{0.4} = 5 + 2.5 = 7.5 \]
So,
\[ r_{eq} = \frac{1}{7.5} = 0.133 \, \Omega \]
Current drawn:
The total current drawn from the combination can be calculated using Ohm's law:
\[ I = \frac{E_{eq}}{R + r_{eq}} = \frac{4}{4 + 0.133} = \frac{4}{4.133} \approx 0.968 \, A \] Quick Tip: For parallel connected batteries, use the formulas \( E_{eq} = \frac{E_1 R_2 + E_2 R_1}{R_1 + R_2} \) for the equivalent emf and \( \frac{1}{r_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} \) for the equivalent internal resistance.
A conductor of length \( l \) is connected across an ideal cell of emf \( E \). Keeping the cell connected, the length of the conductor is increased to \( 2l \) by gradually stretching it. If \( R \) and \( R' \) are initial and final values of resistance and \( v_d \) and \( v_d' \) are initial and final values of drift velocity, find the relation between (i) \( R' \) and \( R \) and (ii) \( v_d' \) and \( v_d \).
View Solution
N/A Quick Tip: When stretching a conductor, its resistance increases by the square of the stretching factor, and the drift velocity decreases proportionally because the cross-sectional area decreases and the current density reduces.
When electrons drift in a conductor from lower to higher potential, does it mean that all the 'free electrons' of the conductor are moving in the same direction?
View Solution
No, it does not mean that all the free electrons are moving in the same direction. In a conductor, free electrons are constantly moving in random directions due to thermal motion. However, when an electric field is applied, they experience a net drift in the direction opposite to the electric field (from lower to higher potential). This drift is a superposition of the random motion and the directed movement due to the applied electric field. Quick Tip: In a conductor, the electrons undergo random thermal motion, but the applied electric field causes a net drift in the opposite direction of the field. This results in a small drift velocity while maintaining random thermal movement.
Define magnetic moment of a current-carrying coil. Write its SI unit.
View Solution
The magnetic moment \( \mathbf{M} \) of a current-carrying coil is defined as:
\[ \mathbf{M} = I \times A \]
Where:
- \( I \) is the current flowing through the coil,
- \( A \) is the area of the coil (perpendicular to the magnetic field).
The SI unit of magnetic moment is:
\[ \mathbf{M} = \, Ampere \times meter^2 = \, A \cdot m^2 \] Quick Tip: The magnetic moment is a vector quantity and its direction is perpendicular to the plane of the coil. Its magnitude depends on the current and the area of the coil.
A coil of 60 turns and area \( 1.5 \times 10^{-3} \, m^2 \) carrying 2A current lies in a vertical plane. It experiences a torque of 0.12 Nm when placed in a uniform horizontal magnetic field. The torque acting on the coil changes to 0.05 Nm after the coil is rotated about its diameter by \( 90^\circ \) in the magnetic field. Find the magnitude of the magnetic field.
View Solution
The torque \( \tau \) acting on a coil in a magnetic field is given by:
\[ \tau = NIBA \sin \theta \]
Where:
- \( N \) is the number of turns,
- \( I \) is the current,
- \( B \) is the magnetic field,
- \( A \) is the area of the coil,
- \( \theta \) is the angle between the normal to the coil and the magnetic field.
For the initial torque:
\[ 0.12 = 60 \times 2 \times 1.5 \times 10^{-3} \times B \times \sin(90^\circ) \]
Solving for \( B \):
\[ B = \frac{0.12}{60 \times 2 \times 1.5 \times 10^{-3}} = 0.67 \, T \]
Thus, the magnitude of the magnetic field is \( 0.67 \, T \). Quick Tip: When calculating the torque on a current-carrying coil, use the formula \( \tau = NIBA \sin \theta \), where \( \theta = 90^\circ \) gives the maximum torque.
Consider two long co-axial solenoids \( S_1 \) and \( S_2 \), each of length \( l \gg r_1 \) and \( r_2 \) (where \( r_2 > r_1 \)). The number of turns per unit length are \( n_1 \) and \( n_2 \) respectively. Derive an expression for the mutual inductance \( M_{12} \) of solenoid \( S_1 \) with respect to solenoid \( S_2 \). Show that \( M_{21} = M_{12} \).
View Solution
The mutual inductance \( M_{12} \) between two solenoids is given by the formula:
\[ M_{12} = \mu_0 \frac{n_1 n_2 A l}{l} \]
Where:
- \( n_1 \) and \( n_2 \) are the number of turns per unit length in solenoids \( S_1 \) and \( S_2 \),
- \( A \) is the cross-sectional area of the solenoid,
- \( l \) is the length of the solenoids,
- \( \mu_0 \) is the permeability of free space.
Since the mutual inductance depends on the geometry and the number of turns, it is symmetric, so:
\[ M_{21} = M_{12} \] Quick Tip: The mutual inductance between two solenoids is symmetric, meaning \( M_{12} = M_{21} \). This is because the magnetic field created by one solenoid induces the same flux in the other solenoid.
A parallel plate capacitor is charged by an ac source. Show that the sum of conduction current (\( I_c \)) and the displacement current (\( I_d \)) has the same value at all points of the circuit.
View Solution
In an AC circuit with a capacitor, the conduction current \( I_c \) is given by:
\[ I_c = \frac{dQ}{dt} \]
Where \( Q \) is the charge on the plates of the capacitor. The displacement current \( I_d \) is defined as:
\[ I_d = \epsilon_0 A \frac{dE}{dt} \]
Where \( E \) is the electric field between the plates of the capacitor, and \( A \) is the area of the plates.
Since the current is related to the change in charge and electric field, the conduction current \( I_c \) and the displacement current \( I_d \) are equal:
\[ I_c = I_d \]
Hence, the sum of conduction current and displacement current is constant at all points of the circuit. Quick Tip: The displacement current is introduced to ensure that the continuity equation holds in an AC circuit. It is equal to the conduction current in a capacitor and accounts for the time-varying electric field between the plates.
Question 29:
In case (a), is Kirchhoff’s first rule (junction rule) valid at each plate of the capacitor? Explain.
View Solution
Yes, Kirchhoff’s first rule (junction rule) is valid at each plate of the capacitor. This is because the junction rule states that the sum of currents entering any junction must be equal to the sum of currents leaving the junction. In the case of the capacitor, the conduction current and the displacement current must be balanced, ensuring that the total current entering the capacitor is equal to the total current leaving it. Quick Tip: Kirchhoff's first rule is based on the principle of conservation of charge. In a capacitor, the displacement current ensures that the current is conserved even though no physical current flows through the dielectric.
Draw a plot of frequency \( \nu \) of incident radiation as a function of stopping potential \( V_0 \) for a given photoemissive material. What information can be obtained from the value of the intercept on the stopping potential axis?
View Solution
The plot of frequency \( \nu \) versus stopping potential \( V_0 \) is a straight line with slope \( h/e \) and intercept \( -\frac{\phi}{e} \), where:
- \( h \) is Planck's constant,
- \( e \) is the charge of the electron,
- \( \phi \) is the work function of the material.
The intercept on the \( V_0 \)-axis gives the value of \( -\frac{\phi}{e} \), which can be used to determine the work function of the material. The slope of the graph provides the value of Planck’s constant \( h \). Quick Tip: The plot of stopping potential \( V_0 \) vs frequency \( \nu \) provides important information about the work function and Planck's constant. The slope is related to \( h/e \), and the intercept gives the work function.
Calculate: (i) the momentum and (ii) de Broglie wavelength of an electron with kinetic energy of 80 eV.
View Solution
(i) The momentum \( p \) of the electron can be calculated using the relation between kinetic energy and momentum:
\[ K.E. = \frac{p^2}{2m_e} \]
Solving for \( p \):
\[ p = \sqrt{2m_e K.E.} \]
Where:
- \( m_e = 9.11 \times 10^{-31} \, kg \) (mass of the electron),
- \( K.E. = 80 \, eV = 80 \times 1.602 \times 10^{-19} \, J \).
Substituting the values:
\[ p = \sqrt{2 \times 9.11 \times 10^{-31} \times 80 \times 1.602 \times 10^{-19}} = 4.4 \times 10^{-24} \, kg·m/s \]
(ii) The de Broglie wavelength \( \lambda \) is given by:
\[ \lambda = \frac{h}{p} \]
Where \( h = 6.626 \times 10^{-34} \, J·s \). Substituting the values:
\[ \lambda = \frac{6.626 \times 10^{-34}}{4.4 \times 10^{-24}} = 1.5 \times 10^{-10} \, m \]
Thus, the de Broglie wavelength is \( 1.5 \times 10^{-10} \, m \). Quick Tip: The de Broglie wavelength of a particle is inversely proportional to its momentum. Use the relation \( \lambda = \frac{h}{p} \) to calculate the wavelength from momentum, and \( p = \sqrt{2m_e K.E.} \) to find the momentum.
Define 'Mass defect' and 'Binding energy' of a nucleus. Describe 'Fission process' on the basis of binding energy per nucleon.
View Solution
- Mass defect: The mass defect of a nucleus is the difference between the mass of the completely assembled nucleus and the sum of the masses of the individual protons and neutrons that make it up. This difference in mass is converted into binding energy according to Einstein's equation \( E = mc^2 \).
- Binding energy: The binding energy of a nucleus is the energy required to separate a nucleus into its individual protons and neutrons. It is related to the mass defect and provides a measure of the stability of the nucleus.
- Fission process: Fission is the process in which a heavy nucleus splits into two lighter nuclei, releasing a significant amount of energy. The binding energy per nucleon increases as the nucleus splits, and this release of energy is due to the difference in binding energy between the fission products and the original nucleus. Quick Tip: In the fission process, energy is released because the binding energy per nucleon of the resulting smaller nuclei is higher than that of the original large nucleus. The mass defect is directly related to this released energy.
A deuteron contains a proton and a neutron and has a mass of 2.013553 u. Calculate the mass defect for it in u and its energy equivalence in MeV. \( m_p = 1.007277 \, u \), \( m_n = 1.008665 \, u \), and \( 1u = 931.5 \, MeV/c^2 \).
View Solution
The mass defect \( \Delta m \) is the difference between the total mass of the individual nucleons and the mass of the deuteron:
\[ \Delta m = (m_p + m_n) - m_{deuteron} \]
Substituting the values:
\[ \Delta m = (1.007277 + 1.008665) - 2.013553 = 0.002389 \, u \]
Now, the energy equivalence \( E \) of the mass defect is given by:
\[ E = \Delta m \times 931.5 \, MeV/c^2 \]
Substituting the mass defect:
\[ E = 0.002389 \times 931.5 = 2.226 \, MeV \]
Thus, the mass defect is \( 0.002389 \, u \), and the energy equivalence is \( 2.226 \, MeV \). Quick Tip: The mass defect is the difference between the sum of the masses of individual nucleons and the actual mass of the nucleus. This difference is converted to energy using \( E = \Delta m \times 931.5 \, MeV/c^2 \).
Question 34:
A thin lens is a transparent optical medium bounded by two surfaces, at least one of which should be spherical. Applying the formula for image formation by a single spherical surface successively at the two surfaces of a lens, one can obtain the 'lens maker formula' and then the 'lens formula'. A lens has two foci – called 'first focal point' and 'second focal point' of the lens, one on each side.

View Solution
The arrangement involves a convex lens with the following setup:
- A light box with a plate is placed such that the rays are incident on the lens.
- The convex lens focuses light onto a screen, where the image can be observed.
- The distance between the lens and the screen is adjustable, so that the image formation is studied for different object distances.
- The lens has two focal points: one on each side.
- The convex lens focuses light rays to a point on the screen.
- The 'first focal point' and 'second focal point' are the points where parallel rays of light either converge or diverge after passing through the lens.
Quick Tip: In a convex lens, the image formed is real and inverted when the object is beyond the focal length. The image is virtual and upright when the object is within the focal length.
What are coherent sources? Why are they necessary for observing a sustained interference pattern?
View Solution
Coherent sources are sources of light or waves that emit waves with a constant phase relationship over time. This means the phase difference between the waves remains constant or changes in a predictable way.
Coherent sources are necessary for observing a sustained interference pattern because interference occurs due to the superposition of waves. If the sources are not coherent, the phase difference between the waves will change randomly over time, leading to a rapidly fluctuating interference pattern which cannot be sustained. Quick Tip: For sustained interference patterns, the sources must be coherent, meaning they have a constant phase difference. Coherent sources allow the formation of stable interference fringes.
Lights from two independent sources are not coherent. Explain.
View Solution
Two light sources are said to be incoherent or not coherent when there is no constant phase relationship between them. In other words, the phase difference between the two sources changes randomly over time. This causes the interference pattern to be unstable, and the maxima and minima of the pattern to fluctuate, making it impossible to maintain a sustained pattern. Quick Tip: For stable interference patterns, the sources must have a fixed phase relationship, which is characteristic of coherent sources. Incoherent sources do not have this fixed phase, leading to unstable interference.
Two slits 0.1 m apart are arranged 1.20 m from a screen. Light of wavelength 600 nm from a distant source is incident on the slits. How far apart will adjacent bright interference fringes be on the screen?
View Solution
The distance between adjacent bright fringes (fringe width) in a double-slit interference pattern is given by the formula:
\[ y = \frac{\lambda D}{d} \]
Where:
- \( y \) is the distance between adjacent bright fringes,
- \( \lambda \) is the wavelength of light,
- \( D \) is the distance between the slits and the screen,
- \( d \) is the separation between the slits.
Substituting the given values:
- \( \lambda = 600 \, nm = 600 \times 10^{-9} \, m \),
- \( D = 1.20 \, m \),
- \( d = 0.1 \, m \).
\[ y = \frac{600 \times 10^{-9} \times 1.20}{0.1} = 7.2 \times 10^{-3} \, m = 7.2 \, mm \]
Thus, the adjacent bright interference fringes will be \( 7.2 \, mm \) apart. Quick Tip: The fringe width is directly proportional to the wavelength and the distance to the screen, and inversely proportional to the slit separation. Use the formula \( y = \frac{\lambda D}{d} \) to find the fringe separation.
Find the angular width (in degree) of the first bright fringe.
View Solution
The angular width \( \theta \) of the first bright fringe is given by:
\[ \theta = \frac{\lambda}{d} \]
Substituting the given values:
\[ \theta = \frac{600 \times 10^{-9}}{0.1} = 6 \times 10^{-3} \, radians \]
To convert to degrees:
\[ \theta = 6 \times 10^{-3} \times \frac{180}{\pi} \approx 0.34^\circ \]
Thus, the angular width of the first bright fringe is approximately \( 0.34^\circ \). Quick Tip: The angular width of the first bright fringe is calculated using the formula \( \theta = \frac{\lambda}{d} \). Remember to convert the result from radians to degrees if needed.
A beam of light coming from a distant source is refracted by a spherical glass ball (refractive index 1.5) of radius 15 cm. Draw the ray diagram and obtain the position of the final image formed.
View Solution
The ray diagram for the light passing through the spherical glass ball is shown below:
Explanation:
- The light ray enters the spherical glass ball and gets refracted.
- The refractive index \( n = 1.5 \) and radius \( r = 15 \, cm \).
- Using the lens formula and refractive index, we can calculate the position of the image formed by the spherical ball.
For a spherical ball, the image formation is complex because it involves both refraction at the spherical surface and the curvature of the ball. A detailed calculation can be made using the formula for refraction at a curved surface and the lens-maker’s formula. Quick Tip: When light passes through a spherical lens, both the curvature of the surface and the refractive index of the material affect the image formation. The lens-maker’s formula can be used to find the focal length and hence the image position.
Define a wavefront. An incident plane wave falls on a convex lens and gets refracted through it. Draw a diagram to show the incident and refracted wavefront.
View Solution
A wavefront is the locus of points that are in the same phase of vibration. In simpler terms, it is the surface of constant phase where all points on the wavefront are at the same distance from the source.
In the case of an incident plane wave falling on a convex lens, the wavefront bends (refracts) as it passes through the lens. The convex lens converges parallel rays of light, changing the wavefront's shape.
The diagram below shows the incident and refracted wavefronts:
Explanation:
- The incident plane wavefronts are straight lines.
- After passing through the convex lens, the wavefronts converge to a point (focus), becoming spherical in shape. Quick Tip: A plane wavefront becomes spherical after passing through a convex lens because the lens converges the rays of light to a point. This property is crucial in understanding how lenses focus light.
A beam of light coming from a distant source is refracted by a spherical glass ball (refractive index 1.5) of radius 15 cm. Draw the ray diagram and obtain the position of the final image formed.
View Solution
When light from a distant source strikes a spherical glass ball, it undergoes refraction at both surfaces of the ball. The spherical surface will cause the light rays to bend inward, and the refracted rays will converge to form an image.
Here is the ray diagram showing the process:
Explanation:
- The light rays are incident on the spherical glass ball and refract at the first surface, moving towards the center of the ball.
- The rays refract again at the second surface as they exit the ball.
- The image formed is real and inverted, and its position can be determined by applying the lens formula.
For a spherical glass ball, the effective focal length \( f \) is related to the radius \( r \) of the sphere and the refractive index \( n \) by the formula:
\[ \frac{1}{f} = (n - 1) \left( \frac{2}{r} \right) \]
Substituting the values:
- \( n = 1.5 \),
- \( r = 15 \, cm \),
\[ \frac{1}{f} = (1.5 - 1) \times \frac{2}{15} = \frac{1}{15} \]
Thus, the focal length \( f = 15 \, cm \).
For a distant source, the image will form at the focal point, and the position of the final image will be at a distance of \( 15 \, cm \) from the center of the ball. Quick Tip: For spherical lenses or spherical glass balls, use the formula \( \frac{1}{f} = (n - 1) \left( \frac{2}{r} \right) \) to determine the focal length. The focal length helps in locating the image position for a distant object.
Two point charges \( 5 \, \mu C \) and \( -1 \, \mu C \) are placed at points \( (-3 \, cm, 0, 0) \) and \( (3 \, cm, 0, 0) \) respectively. An external electric field \( \mathbf{E} = \frac{A}{r^2} \hat{r} \) where \( A = 3 \times 10^5 \, V/m \) is switched on in the region. Calculate the change in electrostatic energy of the system due to the electric field.
View Solution
The electrostatic potential energy of a system of point charges is given by:
\[ U = \frac{1}{4\pi \epsilon_0} \sum_{i < j} \frac{q_i q_j}{r_{ij}} \]
Where:
- \( q_i \) and \( q_j \) are the charges,
- \( r_{ij} \) is the distance between the charges,
- \( \epsilon_0 = 8.854 \times 10^{-12} \, C^2/N·m^2 \) is the permittivity of free space.
In the presence of an external electric field, the potential energy of the system changes due to the interaction of the charges with the field. The change in electrostatic potential energy \( \Delta U \) due to the external electric field can be found by calculating the work done by the electric field:
\[ \Delta U = \mathbf{F} \cdot \mathbf{d} \]
Where \( \mathbf{F} \) is the force on the charges due to the field, and \( \mathbf{d} \) is the displacement.
The field is acting symmetrically on the two charges, and the displacement for each charge depends on the direction of the electric field. The total work done can be computed using the above formula and the given field strength. Quick Tip: When an electric field is applied, it changes the potential energy of a charge distribution. The change in energy is related to the work done by the field on the charges. Use the formula \( \Delta U = \mathbf{F} \cdot \mathbf{d} \) to calculate the change in energy.
A system of two conductors is placed in air and they have net charge of \( +80 \, \mu C \) and \( -80 \, \mu C \) which causes a potential difference of 16 V between them. Find the capacitance of the system.
View Solution
The capacitance \( C \) of the system is related to the charge \( Q \) and the potential difference \( V \) by the formula:
\[ C = \frac{Q}{V} \]
Substituting the given values:
\[ C = \frac{80 \times 10^{-6}}{16} = 5 \times 10^{-6} \, F = 5 \, \muF \]
Thus, the capacitance of the system is \( 5 \, \muF \). Quick Tip: The capacitance of a system is given by \( C = \frac{Q}{V} \), where \( Q \) is the total charge and \( V \) is the potential difference. Ensure that the units are consistent when calculating.
If the air between the capacitor is replaced by a dielectric medium of dielectric constant 3, what will be the potential difference between the two conductors?
View Solution
The capacitance of the system with the dielectric material is given by:
\[ C' = K C \]
Where:
- \( C' \) is the new capacitance with the dielectric,
- \( K = 3 \) is the dielectric constant,
- \( C = 5 \, \muF \) is the initial capacitance.
Thus:
\[ C' = 3 \times 5 \, \muF = 15 \, \muF \]
Now, the potential difference \( V' \) is related to the charge and the capacitance by:
\[ V' = \frac{Q}{C'} \]
Substituting the values:
\[ V' = \frac{80 \times 10^{-6}}{15 \times 10^{-6}} = 5.33 \, V \]
Thus, the new potential difference between the conductors is \( 5.33 \, V \). Quick Tip: When a dielectric material is inserted between the conductors, the capacitance increases by a factor of the dielectric constant \( K \). The potential difference decreases because the capacitance increases.
If the charges on two conductors are changed to \( +160 \, \mu C \) and \( -160 \, \mu C \), will the capacitance of the system change? Give reason for your answer.
View Solution
The capacitance of the system depends on the geometry of the conductors and the dielectric material between them, not on the charge. Therefore, changing the charges does not affect the capacitance. The capacitance remains the same unless the dielectric material or the distance between the conductors is altered.
\[ C = \frac{Q}{V} \]
Since the capacitance is independent of the charge, the capacitance remains unchanged when the charges are changed. Quick Tip: Capacitance depends on the geometry of the conductors and the dielectric constant of the material between them. The charge on the conductors does not affect the capacitance.













Comments