CUET Latest Updates
29 Dec, 2025 CUET UG 2026 Syllabus has been released by NTA on December 29, 2025. Check Syllabus Here
NTA released the CUET Mathematics Syllabus on the official website as Mathematics/Applied Mathematics Syllabus with subject code 319. CUET UG syllabus PDF for mathematics includes 3 sections such as Section A1, Section B1 (Mathematics), and Section B2 (Applied Mathematics).
- CUET Mathematics syllabus sections have different weightage with 15 questions asked from Section A1 and 35 questions asked from Section B1 and Section B2.
- Section A1 is compulsory and students can choose to solve Section B1 or Section B2 based on their domain choice.
- You will face a total of 50 questions in CUET Mathematics paper.
- You can score a maximum of 250 marks in CUET Mathematics syllabus with highest weightage give to topics like Calculus, Probability, and Vectors and 3D geometry.
- CUET Syllabus 2026 for Mathematics is expected to remain same as that in last year with no changes.
Based on previous analysis, it is estimated that 60% of the paper is of average difficulty, 30% demands in-depth concept understanding, and 10% is very challenging, similar to the JEE Mains level.
Related Articles:

Official CUET Mathematics Syllabus Download PDF
Aspirants can download the official CUET Mathematics syllabus from the table below.
| Official CUET Mathematics Syllabus PDF 2026 | Download Here |
|---|
Key Summary
|
|---|
CUET Mathematics Syllabus: Section-wise
CUET Syllabus for Mathematics includes 3 sections, such as:
- Section A1: This section includes topics like Algebra, Calculus, Integration and its Applications, Differential Equations, Probability Distributions, and Linear Programming.
- Section B1: This section includes topics like Relations and Functions, Algebra, Calculus, Integrals, Applications of Integrals, Differential Equations, Vectors, and 3D Geometry.
- Section B2: This section includes 8 units named Numbers, Quantification and Numerical Applications, Algebra, Calculus, Probability Distributions, Index Numbers and Time-Based data, Inferential Statistics, Financial Mathematics, and Linear Programming.
“Candidates must attempt questions from either Section B1 or B2, based on their chosen domain.”
CUET Mathematics Syllabus: Section A1
| Algebra | Calculus |
|---|---|
|
|
| Integration and Its Applications | Differential Equations |
|
|
| ProbabilityDistributions | Linear Programming |
|
|
CUET Mathematics Syllabus: Section B1 (Mathematics)
UNIT I: RELATIONS AND FUNCTIONS
- Relations and Functions: Types of relations: Reflexive, symmetric, transitive, and equivalence relations. One-to-one and onto functions.
- Inverse Trigonometric Functions: Definition, range, domain, principal value branches. Graphs of inverse trigonometric functions.
UNIT II: ALGEBRA
- Matrices: Concept, notation, order, equality, types of matrices, zero matrix, transpose of a matrix, symmetric and skew-symmetric matrices. Operations on matrices: Addition, multiplication, and multiplication with a scalar. Simple properties of addition, multiplication, and scalar multiplication. Non-commutativity of multiplication of matrices and existence of non-zero matrices whose product is the zero matrix (restrict to square matrices of order 2). Invertible matrices and proof of the uniqueness of inverse, if it exists; (Here, all matrices will have real entries).
- Determinants: Determinant of a square matrix (up to 3 × 3 matrices), minors, cofactors, and applications of determinants in finding the area of a triangle. Adjoint and inverse of a square matrix. Consistency, inconsistency, and number of solutions of a system of linear equations by examples, solving a system of linear equations in two or three variables (having a unique solution) using the inverse of a matrix.
UNIT III: CALCULUS
- Continuity and Differentiability: Continuity and differentiability, chain rule, derivatives of inverse trigonometric functions, like sin−1 x, cos−1 x, and tan−1 x, derivatives of implicit functions. Concepts of exponential, logarithmic functions. Derivatives of logarithmic and exponential functions. Logarithmic differentiation, the derivative of functions expressed in parametric forms. Second-order derivatives.
- Applications of derivatives: Rate of change of quantities, increasing/decreasing functions, maxima and minima (first derivative test motivated geometrically and second derivative test given as a provable tool). Simple problems (that illustrate basic principles and understanding of the subject as well as real-life situations).
- Integrals: Integration is the inverse process of differentiation. Integration of a variety of functions by substitution, by partial fractions, and by parts. Evaluation of simple integrals of the following types and problems based on them.
Fundamental Theorem of Calculus (without proof). Basic properties of definite integrals and evaluation of definite integrals.
![CALCULUS]()
- Applications of the Integrals: Applications in finding the area under simple curves, especially lines, circles/parabolas/ellipses (in standard form only)
- Differential Equations: Definition, order, and degree, general and particular solutions of a differential equation. Solution of differential equations by the method of separation of variables, solutions of homogeneous differential equations of first order and first degree. Solutions of linear differential equations of the type:
- dy/dx + Py = Q, where P and Q are functions of x or constants
- dx/dy + Px = Q, where P and Q are functions of y or constants
UNIT IV: VECTORS AND THREE-DIMENSIONAL GEOMETRY
- Vectors: Vectors and scalars, the magnitude and direction of a vector. Direction cosines and direction ratios of a vector. Types of vectors (equal, unit, zero, parallel, and collinear vectors), position vector of a point, negative of a vector, components of a vector, addition of vectors, multiplication of a vector by a scalar, and position vector of a point dividing a line segment in a given ratio. Definition, Geometrical interpretation, properties, and application of scalar (dot) product of vectors, vector (cross) product of vectors.
- Three-dimensional Geometry: Direction cosines and direction ratios of a line joining two points. Cartesian equation and vector equation of a line, skew lines, shortest distance between two lines. Angle between two lines.
Unit V: Linear Programming
Introduction, related terminology such as constraints, objective function, optimization, graphical method of solution for problems in two variables, feasible and infeasible regions (bounded or unbounded), feasible and infeasible solutions, optimal feasible solutions (up to three non-trivial constraints).
Unit VI: Probability
Conditional probability, Multiplication theorem on probability, independent events, total probability, Bayes’ theorem. Random variable.
CUET Mathematics Syllabus: Section B2 (Applied Mathematics)
Unit I: Numbers, Quantification, and Numerical Applications
Modulo Arithmetic
- Define the modulus of an integer
- Apply arithmetic operations using modular arithmetic rules
Congruence Modulo
- Define congruence modulo
- Apply the definition in various problems
Allegation and Mixture
- Understand the rule of allegation to produce a mixture at a given price
- Determine the mean price of a mixture
- Apply the rule of allegation
Numerical Problems
- Solve real-life problems mathematically
Boats and Streams
- Distinguish between upstream and downstream
- Express the problem in the form of an equation
Pipes and Cisterns
- Determine the time taken by two or more pipes to fill or empty the tank
Races and Games
- Compare the performance of two players w.r.t. time, distance
H. Numerical Inequalities
- Describe the basic concepts of numerical inequalities
- Understand and write numerical inequalities
UNIT II: ALGEBRA
Matrices and types of matrices
- Define matrix
- Identify different kinds of matrices
Equality of matrices, Transpose of a matrix, Symmetric and Skew-symmetric matrix
- Determine the equality of two matrices
- Write the transpose of given matrix
- Define a symmetric and skew-symmetric matrix
Algebra of Matrices
- Perform operations like addition & subtraction on matrices of the same order
- Perform the multiplication of two matrices of appropriate order
- Perform multiplication of a scalar with a matrix
Determinant of Matrices
- Find the determinant of a square matrix
- Use elementary properties of determinants
- Singular matrix, Non-singular matrix
- |AB|=|A||B|
- Simple problems to find the determinant value
Inverse of a Matrix
- Define the inverse of a square matrix
- Apply the properties of the inverse of matrices
- Inverse of a matrix using: a) cofactors
If A and B are invertible square matrices of the same size,
i) (AB)-1=B-1 A-1
ii) (A-1)-1 =A
iii) (AT) -1 = (A-1) T
F. Solving system of simultaneous equations (up to three variables only (non-homogeneous equations))
UNIT III: CALCULUS
Higher Order Derivatives
- Determine second and higher order derivatives
- Understand the differentiation of parametric functions and implicit functions
Application of Derivatives
- Determine the rate of change of various quantities
- Understand the gradient of the tangent and normal to a curve at a given point
- Write the equations of tangents and normals to a curve at a given point
Marginal Cost and Marginal Revenue using derivatives
- Define marginal cost and marginal revenue
- Find marginal cost and marginal revenue
Increasing/Decreasing Functions
- Determine whether a function is increasing or decreasing
- Determine the conditions for a function to be increasing or decreasing
Maxima and Minima
- Determine critical points of the function
- Find the point(s) of local maxima and local minima, and corresponding local maximum and local minimum values
- Find the absolute maximum and absolute minimum value of a function
- Solve applied problems
Integration
- Understand and determine indefinite integrals of simple functions as anti-derivatives
Indefinite integrals as a family of curves
- Evaluate indefinite integrals of simple algebraic functions by the methods of
(i) substitution
(ii) partial fraction
(iii) by parts
Definite Integral as area under the curve
- Define the definite integral as the area under the curve
- Understand the fundamental theorem of integral calculus and apply it to evaluate the definite integral
- Apply properties of definite integrals to solve problems
Application of Integration
- Identify the region representing C.S. and P.S. graphically
- Apply the definite integral to find consumer surplus-producer surplus
Differential Equations
- Recognize a differential equation
- Find the order and degree of a differential equation
Formulating and solving differential equations
- Formulate differential equations
- Verify the solution of the differential equation
- Solve a simple differential equation
Application of Differential Equations
- Define the growth and decay model
- Apply the differential equations to solve growth and decay models
UNIT IV: PROBABILITY DISTRIBUTIONS
Probability Distribution
- Understand the concept of Random Variables and their Probability Distributions
- Find the probability distribution of a discrete random variable
Mathematical Expectation
- Apply the arithmetic mean of the frequency distribution to find the expected value of a random variable
Variance
- Calculate the Variance and S.D. of a random variable
Binomial Distribution
- Identify the Bernoulli Trials and apply the Binomial Distribution
- Evaluate Mean, Variance, and S.D. of a Binomial Distribution
Poisson Distribution
- Understand the conditions of the Poisson Distribution
- Evaluate the Mean and Variance of the Poisson distribution
Normal Distribution
- Understand that a normal distribution is a continuous distribution
- Evaluate the value of the Standard normal variate
- Area relationship between Mean and Standard Deviation
UNIT V: INDEX NUMBERS AND TIME-BASED DATA
Time Series
- Identify time series as chronological data
Components of Time Series
- Distinguish between different components of a time series
Time Series analysis for univariate data
- Solve practical problems based on statistical data and interpret
Secular trend
- Understand the long-term tendency
Methods of Measuring Trend
- Demonstrate the techniques of finding trends by different methods
UNIT VI: INFERENTIAL STATISTICS
Population and Sample
- Define Population and Sample
- Differentiate between population and sample
- Define a representative sample from a population
- Differentiate between a representative and a non-representative sample
- Draw a representative sample using simple random sampling
- Draw a representative sample using systematic random sampling
Parameter and Statistics, and Statistical Interferences
- Define Parameter with reference to Population
- Define Statistics with reference to the Sample
- Explain the relation between Parameter and Statistic
- Explain the limitations of statistics to generalize the estimation forthe population
- Interpret the concept of Statistical Significance and Statistical Inferences
- State Central Limit Theorem
- Explain the relation between Population-Sampling Distribution-Sample
t-Test (one-sample t-test and two independent groups t-test)
- Define a hypothesis
- Differentiate between the Null and alternative hypotheses
- Define and calculate the degree of freedom
- Test the Null hypothesis and make inferences using the t-test statistic for one group/two independent groups
UNIT VII: FINANCIAL MATHEMATICS
Perpetuity, Sinking Funds
- Explain the concept of perpetuity and sinking fund
- Calculate perpetuity
- Differentiate between a sinking fund and a savings account
B. Calculation of EMI
- Explain the concept of EMI
- Calculate EMI using various methods
Calculation of Returns, Nominal Rate of Return
- Explain the concept of rate of return and nominal rate of return
- Calculate the rate of return and the nominal rate of return
Compound Annual Growth Rate
- Understand the concept of Compound Annual Growth Rate
- Differentiate between Compound Annual Growth Rate and Annual Growth Rate
- Calculate Compound Annual Growth Rate
E. Linear method of Depreciation
- Define the concept of the linear method of Depreciation
- Interpret the cost, residual value, and useful life of an asset from the given information
- Calculate depreciation
UNIT VIII: LINEAR PROGRAMMING
Introduction and related terminology
- Familiarize yourself with terms related to the Linear Programming Problem
Mathematical formulation of Linear Programming Problem
- Formulate Linear Programming Problem
Different Types of Linear Programming Problems
- Identify and formulate different types of LPP
Graphical Method of Solution for problems in two Variables
- Draw the Graph for a system of linear inequalities involving two variables and to find its solution graphically
Feasible and Infeasible Regions
- Identify feasible, infeasible, and bounded regions
Feasible and infeasible solutions, optimal feasible solution
- Understand feasible and infeasible solutions
- Find an optimal feasible solution
![CUET Mathematics Syllabus]()
Ques. What is CUET Maths syllabus for Commerce students?
Ans. For Commerce students, CUET Mathematics Section B2 syllabus is preferred and the syllabus includes topics like Numbers, Quantification and Numerical Applications, Algebra, Calculus, Probability Distributions, Index Numbers and Time-Based data, Inferential Statistics, Financial Mathematics, and Linear Programming.
Ques. What is the CUET core Maths Syllabus 2026?
Ans. Syllabus for CUET Core Mathematics syllabus include:
- Algebra
- Integration and Its Applications
- Probability Distributions
- Calculus
- Differential Equations
- Linear Programming
Ques. How many sections are there in CUET Mathematics syllabus?
Ans. There are 3 sections in CUET Mathematics Syllabus as discussed below.
- Section A1: This section includes topics like Algebra, Calculus, Integration and its Applications, Differential Equations, Probability Distributions, and Linear Programming.
- Section B1: This section includes topics like Relations and Functions, Algebra, Calculus, Integrals, Applications of Integrals, Differential Equations, Vectors, and 3D Geometry.
- Section B2: This section includes 8 units named Numbers, Quantification and Numerical Applications, Algebra, Calculus, Probability Distributions, Index Numbers and Time-Based data, Inferential Statistics, Financial Mathematics, and Linear Programming.
CUET Mathematics Exam Pattern
| Particulars | Details |
|---|---|
| Subject Code | 319 |
| Mode of Examinatuion | CBT |
| Sections | Section A1Section B1: MathematicsSection B2: Applied Mathematics |
| Total Number of Questions | 50 |
| Type of Questions | MCQs |
| Exam Duration | 60 minutes |
| Marking Scheme |
|
| Total Marks | 250 |

Ques. How many questions are there in CUET Mathematics?
Ans. As per the CUET syllabus and exam pattern for Mathematics, there are a total of 50 questions in CUET Maths. 15 questions will be asked from Section A1 and 35 questions will be asked from Section B1 (Mathematics)/Section B2 (Applied Mathematics.
Ques. What is marking scheme in CUET Maths?
Ans. According to CUET Mathematics syllabus and exam pattern, students will be awarded 5 marks for each correct answer and -1 will be deducted for each wrong answer.
Also Read: CUET Exam Pattern
CUET Mathematics Syllabus 2026: Sectional Weightage
CUET Mathematics weightage is different for different sections, including 15 questions from Section A1, 35 questions each from Section B1 and Section B2. Students can choose to solve either the B1 Section or the B2 Section based on their domain chosen at the time of applying for CUET 2026.
- The total questions in the CUET UG Mathematics syllabus is 50.
- Total marks asked from the CUET Mathematics syllabus are 250, with 75 marks in Section A1 and 175 marks in Section B1/Section B2.
| Section | Total Questions | Total Marks |
|---|---|---|
| Section A | 15 | 75 |
| Section B1: Mathematics | 35 | 175 |
| Section B2: Applied Mathematics | 35 | 175 |

Ques. How many marks is Advanced Maths in CUET?
Ans. As per the CUET Maths sectional weightage, Advanced Mathematics (Section B1), a total of 35 questions will be asked. Students can score a maximum of 175 marks in CUET Advanced Mathematics.
Ques. What are the total marks in CUET Mathematics in Section A?
Ans. In section A of CUET Mathematics, a total of 15 questions will be asked. For each question, 5 marks are allotted, and students can score a maximum of 75 marks in CUET Mathematics in Section A.
CUET Mathematics Syllabus: Topic-wise Weightage
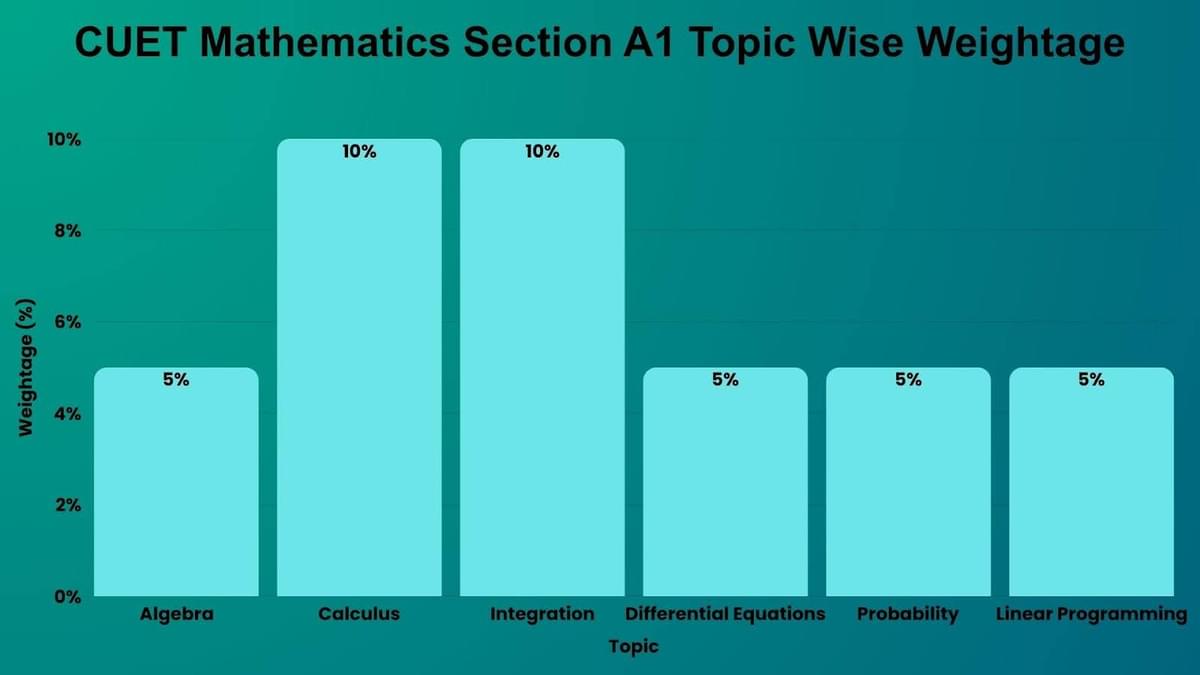
CUET Mathematics Section A1 Topic Wise Weightage
This section builds the foundation of mathematical concepts and is crucial for problem-solving.
- Calculus & Integration (20%) forms the major portion of the CUET 2026 question paper. Prioritize differentiation and integration techniques.
- Probability & Linear Programming are easy to score with proper practice.
- Algebra & Differential Equations are fundamental but require formula retention and application skills.
| Topic | Weightage (%) | Analysis |
|---|---|---|
| Algebra (Matrices & Determinants) | 5% | Important for solving linear equations and transformations. Frequently tested in competitive exams. |
| Calculus (Higher Order Derivatives) | 10% | One of the most scoring topics covers tangent, normals, increasing/decreasing functions. Mastering differentiation is key. |
| Integration (Indefinite & Definite Integrals) | 10% | Focus on the fundamental theorem, area under curves, and applications. Essential for physics and engineering-related studies. |
| Differential Equations | 5% | Involves real-world applications like population growth and cooling laws. Requires understanding of order and degree. |
| Probability (Random Variables & Distributions) | 5% | Covers expected values, variance, and probability distributions. Important for data science and statistics. |
| Linear Programming | 5% | Optimization-based topic; graphical methods are tested. Useful in business and economics. |
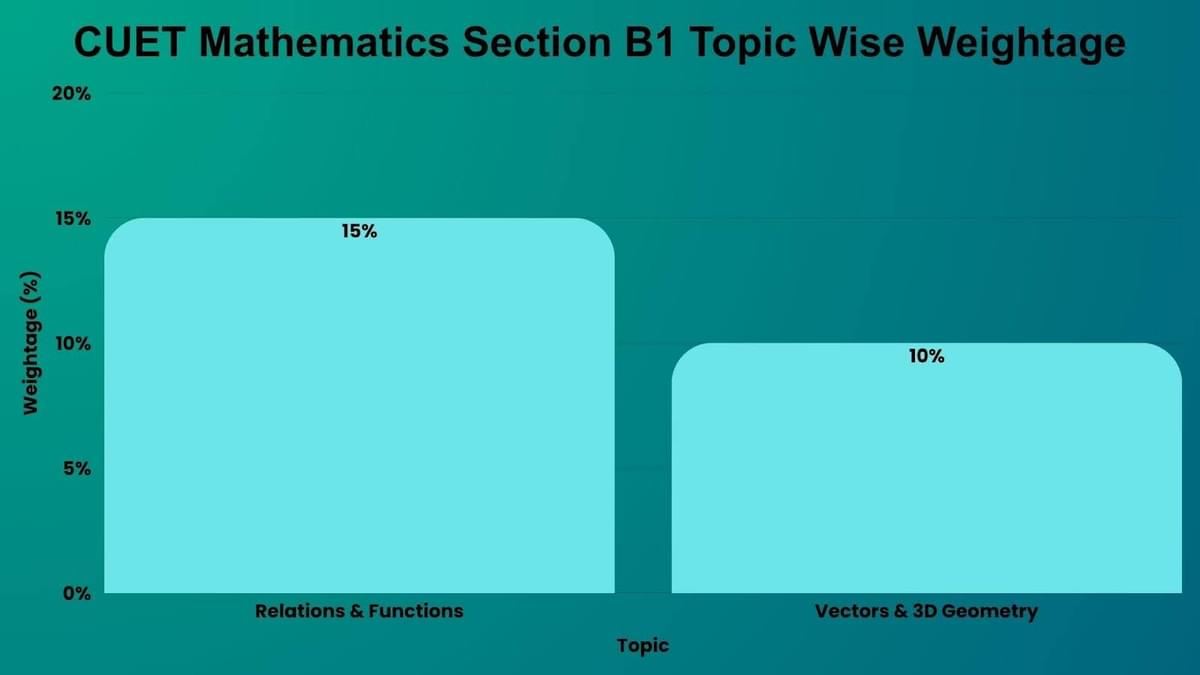
CUET Mathematics Section B1 Topic-Wise Weightage
This section involves advanced problem-solving and abstract mathematical concepts.
- Relations & Functions (15%) need conceptual clarity, especially for inverse functions and graph transformations.
- Vectors & 3D Geometry (10%) is scoring but requires strong spatial visualization skills.
| Topic | Weightage (%) | Analysis |
|---|---|---|
| Relations & Functions | 15% | The highest-weighted topic. Covers types, properties, and inverse functions. Crucial for advanced calculus. |
| Vectors & 3D Geometry | 10% | Focus on direction ratios, equations of planes, and line intersection. Important for engineering and physics applications. |
CUET Mathematics Section B2 Topic-Wise Weightage
This section focuses on practical and real-world mathematical applications.
- Financial Mathematics & Quantification (20%) needs real-world application skills.
- Index Numbers & Data Analysis can be scored with proper interpretation skills.
| Topic | Weightage (%) | Analysis |
|---|---|---|
| Numbers & Quantification | 10% | Includes modulo arithmetic, allegations, and mixtures. Useful for logical reasoning. |
| Financial Mathematics | 10% | Focus on EMI, bond valuation, and sinking funds. Essential for commerce and finance aspirants. |
| Index Numbers & Time-Based Data | 5% | Deals with statistical measures, inflation index, and trend analysis. |

Also Check: CUET Mathematics Paper Analysis
CUET Mathematics Syllabus 2026: Important Topics
The CUET Mathematics Syllabus 2026 comprises several crucial topics categorized into high-weight, medium-weight, and low-weight sections.
High-Weightage Topics (10% or More)
| Topic | Expected Questions | Weightage (%) | Key Concepts |
|---|---|---|---|
| Relations & Functions | 4 - 5 | 15% | Types of relations, inverse trigonometry, domain & range |
| Calculus | 3 - 4 | 10% | Differentiation, continuity, maxima & minima |
| Integration & Its Applications | 3 - 4 | 10% | Indefinite & definite integrals, area under curves |
| Vectors & Three-Dimensional Geometry | 3 - 4 | 10% | Dot & cross product, direction cosines, lines & planes |
| Numbers, Quantification & Numerical Applications | 3 - 4 | 10% | Modular arithmetic, number theory, approximations |
Medium-Weightage Topics (5-10%)
| Topic | Expected Questions | Weightage (%) | Key Concepts |
|---|---|---|---|
| Differential Equations | 2 - 3 | 5% | Order & degree, variable separation method |
| Probability Distributions | 2 - 3 | 5% | Binomial distribution, expected value, variance |
| Linear Programming | 2 - 3 | 5% | Feasible region, optimization, graphical method |
| Probability | 2 - 3 | 5% | Conditional probability, Bayes' theorem |
| Algebra (Matrices & Determinants) | 2 - 3 | 5% | Matrix operations, inverse of matrices, determinants |
Low-Weightage Topics (Below 5%)
| Topic | Expected Questions | Weightage (%) | Key Concepts |
|---|---|---|---|
| Set Theory | 1 - 2 | <5% | Union, intersection, Venn diagrams |
| Complex Numbers | 1 - 2 | <5% | Polar form, De Moivre’s theorem |
| Permutation & Combination | 1 - 2 | <5% | Factorial notation, binomial theorem |
| Statistics | 1 - 2 | <5% | Mean, median, mode, standard deviation |
Ques. What are the high-weightage topics in CUET Mathematics?
Ans. As per the CUET Mathematics topic-wise weightage, some of the high-weightage topics include Relations and Functions, Calculus, Integrals, Financial Mathematics, and Numbers & Quantification. Each of these topics carries 10-15% weightage in the CUET Mathematics question paper.
CUET Mathematics Preparation 2026
Students must attempt either Section B1 or B2 based on their preference for Mathematics (B1) or Applied Mathematics (B2).
To achieve maximum success in the CUET Mathematics 2026 exam, it is necessary to:
- Spend most of your time on high-priority subjects that have the highest weightage and can account for up to 70% of your overall marks.
- Maintain a regular study schedule for medium-priority questions and solve problems regularly to ensure they make up a good 20-25% of your marks.
- Devote the remaining time to low-priority questions, since they can still add worthy marks to your final score.
By adopting this strategy, students can maximize their study time and increase their probability of securing high marks in the CUET 2026 Mathematics exam.
Also Check:
CUET Mathematics 2026 study approach
| Study Priority | Topics to Focus On | Approx. Study Time (%) | Expected Scoring Potential |
|---|---|---|---|
| High Priority (40%) | Relations & Functions, Calculus, Integration, Vectors, 3D Geometry | 40% | 60-70% of the total marks |
| Medium Priority (30%) | Probability, Probability Distributions, Differential Equations | 30% | 20-25% of the total marks |
| Low Priority (20%) | Algebra, Linear Programming, Numerical Applications | 20% | 10-15% of the total marks |
CUET Mathematics Important Books
| Book Name | Author/Publication | Key Features |
|---|---|---|
| NCERT Class 12 Mathematics Textbook | NCERT | Covers fundamental conceptsAligned with the CUET syllabus |
| Complete Mathematics | Lucent's Publication | Covers all CUET topicsIncludes solved examples & MCQs |
| Handbook of Mathematics | Arihant Experts | Quick reference guide summarizes formulas & theorems |
| NCERT Exemplar Problems for Mathematics | NCERT | Includes advanced problemsEnhances problem-solving skills |
| Senior Secondary School Mathematics for Class 12 | R.S. Aggarwal | Detailed explanationsVariety of practice problems |
| Mathematics for Class 12 | R.D. Sharma | Comprehensive coverage of solved & unsolved problems |
Also Check: CUET Books 2026 and Preparation Tips
CUET Mathematics Previous Years Papers
| Year | Question paper PDF |
|---|---|
| 2025 | Download Here |
| 2024 | Download Here |
| 2023 | Download Here |
| 2022 | Download Here |
CUET Mathematics Syllabus FAQs
Ques. What is the syllabus for maths in CUET?
Ans. Syllabus for Maths in CUET 2026 is based on 3 sections, including Section A1, Section B1 (Mathematics), and Section C (Applied Mathematics). Students can check the CUET Mathematics syllabus for each section in the table below.
| Section A1 | Section B1 | Section B2 |
|---|---|---|
| AlgebraIntegration and Its ApplicationsProbability DistributionsCalculusDifferential EquationsLinear Programming | Relations and FunctionsAlgebraCalculusVectors And Three-Dimensional GeometryLinear ProgrammingProbability | Numbers, Quantification, And Numerical ApplicationsAlgebraCalculusProbability DistributionsIndex Numbers And Time-Based DataInferential StatisticsFinancial MathematicsLinear Programming |
Ques. What are the topics of Applied Maths in CUET?
Ans. Topics included in the CUET Mathematics syllabus 2026 include:
- Numbers, Quantification, And Numerical Applications
- Algebra
- Calculus
- Probability Distributions
- Index Numbers And Time-Based Data
- Inferential Statistics
- Financial Mathematics
- Linear Programming
Ques. Is Maths a subject in CUET?
Ans. Yes, Mathematics is a subject in CUET examination for admission to BSc, BSc Hons., etc. courses in Mathematics. CUET Mathematics has a subject code- 319.
Ques. Is CUET maths difficult than JEE?
Ans. Yes, CUET Mathematics is generally considered easier than JEE Main Mathematics. The concepts asked in JEE Main are deeper and higher in level than those asked in CUET Mathematics.
*The article might have information for the previous academic years, which will be updated soon subject to the notification issued by the University/College.







Comments