The CUET Physics exam in 2025 will be conducted between 13th May and 3rd June, and the question paper, answer key, and solution PDF will be available for download after the examination. The Physics paper in CUET tests a student’s understanding of core concepts in mechanics, thermodynamics, electricity and magnetism, optics, modern physics, and problem-solving skills.
According to the revised exam pattern, students must attempt all 50 questions within 60 minutes, with the total marks being 250. Each correct response carries +5 marks, while each incorrect answer incurs a –1 mark penalty.
CUET UG Physics 2025 Question Paper with Answer Key PDF
| CUET UG Physics Question Paper with Solutions PDFs | Download PDF | Check Solutions |
CUET UG Physics 2025 Question Paper with Answer Key PDF
If the protons and electrons are the only basic charges in the universe, all the observable charges have to be integral multiples of e. Thus, if an object contains x electrons and y protons, the net charge on the object will be
View Solution
Step 1: Understanding the Concept:
The net charge on an object is the algebraic sum of the charges of all its constituent particles. The charge of a single electron is -e, and the charge of a single proton is +e.
Step 3: Detailed Explanation:
An object contains 'x' electrons and 'y' protons.
The total charge due to 'x' electrons = \( x \times (charge of one electron) = x \times (-e) = -xe \).
The total charge due to 'y' protons = \( y \times (charge of one proton) = y \times (+e) = +ye \).
The net charge on the object is the sum of these charges:
\[ Net Charge = (Total charge of electrons) + (Total charge of protons) \] \[ Net Charge = -xe + ye \]
Factoring out 'e', we get:
\[ Net Charge = (y - x)e \]
Step 4: Final Answer:
The net charge on the object will be (y - x)e.
Quick Tip: Remember that charge is quantized and additive. Always assign a negative sign to the charge of electrons and a positive sign to the charge of protons before summing them up to find the net charge.
A charge of magnitude \(3 \times 10^{-7}\) C is located at a distance of 0.09 m from a point P. Obtain the work done in bringing a charge of \(2 \times 10^{-9}\) C from infinity to the point P.
View Solution
Step 1: Understanding the Concept:
The work done in bringing a charge 'q' from infinity to a point 'P' in an electric field is equal to the product of the charge 'q' and the electric potential 'V' at that point P. The electric potential at a point P due to a source charge 'Q' at a distance 'r' is given by \( V = \frac{kQ}{r} \).
Step 2: Key Formula or Approach:
1. Calculate the electric potential (V) at point P due to the source charge (Q).
\[ V = \frac{1}{4\pi\epsilon_0} \frac{Q}{r} = k \frac{Q}{r} \]
where \( k = 9 \times 10^9 \, N m^2 C^{-2} \).
2. Calculate the work done (W) in bringing the charge (q) to point P.
\[ W = q \times V \]
Step 3: Detailed Explanation:
Given:
Source charge, \( Q = 3 \times 10^{-7} \) C
Charge to be moved, \( q = 2 \times 10^{-9} \) C
Distance, \( r = 0.09 \) m
First, we calculate the electric potential V at point P:
\[ V = \left(9 \times 10^9 \frac{N m^2}{C^2}\right) \times \frac{3 \times 10^{-7} \, C}{0.09 \, m} \] \[ V = \frac{27 \times 10^2}{0.09} \, V = \frac{27 \times 10^2}{9 \times 10^{-2}} \, V = 3 \times 10^4 \, V \]
Now, we calculate the work done W:
\[ W = q \times V = (2 \times 10^{-9} \, C) \times (3 \times 10^4 \, V) \] \[ W = 6 \times 10^{-5} \, J \]
Step 4: Final Answer:
The work done in bringing the charge from infinity to point P is \(6 \times 10^{-5}\) J.
Quick Tip: The work done to move a charge in an electric field is equivalent to the change in its potential energy. Since the potential at infinity is zero, the work done is simply the final potential energy, which is \(qV\).
In a series combination of capacitors connected across a battery
View Solution
Step 1: Understanding the Concept:
When capacitors are connected in series, they are connected end-to-end, forming a single path for the charge to flow.
Step 3: Detailed Explanation:
When a battery is connected across a series combination of capacitors, the battery supplies a charge +Q to the first plate of the first capacitor. This induces a charge -Q on the second plate of the first capacitor. The positive charge +Q from this second plate is repelled and flows to the first plate of the second capacitor. This process continues down the line. As a result, the charge that accumulates on each capacitor plate has the same magnitude, Q. This occurs because charge is conserved, and there is only one path for the charge to flow. This principle holds true regardless of the individual capacitance values of the capacitors in the series. The voltage across each capacitor will be different (unless they have the same capacitance), but the charge on each is the same.
Step 4: Final Answer:
In a series combination, each capacitor has an equal charge for any value of its capacitance.
Quick Tip: Remember the key rules for combinations: - \(\textbf{Series:}\) Same Charge (Q), Different Voltage (V). \(1/C_{eq} = 1/C_1 + 1/C_2 + ...\) - \(\textbf{Parallel:}\) Same Voltage (V), Different Charge (Q). \(C_{eq} = C_1 + C_2 + ...\)
Two point charges, 4 µC and -3 µC (with no external field) are placed at (-6 cm, 0, 0) and (6 cm, 0, 0), respectively. The amount of work required to separate the two charges infinitely away from each other will be
View Solution
Step 1: Understanding the Concept:
The work required to separate two charges from an initial distance 'r' to an infinite distance is equal to the change in the electrostatic potential energy of the system. This work is the negative of the initial potential energy of the system, as the final potential energy at infinite separation is zero.
Step 2: Key Formula or Approach:
1. Calculate the initial distance (r) between the charges.
2. Calculate the initial potential energy (U\(_i\)) of the two-charge system using the formula:
\[ U_i = k \frac{q_1 q_2}{r} \]
3. The work done (W) to separate the charges to infinity is given by:
\[ W = U_f - U_i \]
Since the final potential energy at infinite separation (U\(_f\)) is 0, the work done is:
\[ W = -U_i \]
Step 3: Detailed Explanation:
Given:
Charge \( q_1 = 4 \, \mu C = 4 \times 10^{-6} \, C \)
Charge \( q_2 = -3 \, \mu C = -3 \times 10^{-6} \, C \)
Position of \(q_1\) is (-6 cm, 0, 0).
Position of \(q_2\) is (6 cm, 0, 0).
First, find the initial distance 'r' between the charges:
\[ r = 6 \, cm - (-6 \, cm) = 12 \, cm = 0.12 \, m \]
Next, calculate the initial potential energy U\(_i\):
\[ U_i = \left(9 \times 10^9 \frac{N m^2}{C^2}\right) \times \frac{(4 \times 10^{-6} \, C) \times (-3 \times 10^{-6} \, C)}{0.12 \, m} \] \[ U_i = \frac{9 \times 10^9 \times (-12 \times 10^{-12})}{0.12} \, J \] \[ U_i = \frac{-108 \times 10^{-3}}{0.12} \, J = \frac{-108 \times 10^{-3}}{12 \times 10^{-2}} \, J \] \[ U_i = -9 \times 10^{-1} \, J = -0.9 \, J \]
The work required to separate the charges to infinity is:
\[ W = -U_i = -(-0.9 \, J) = 0.9 \, J \]
Step 4: Final Answer:
The amount of work required is 0.9 J.
Quick Tip: The work done to assemble a system of charges is equal to its potential energy. The work done to disassemble it (separate to infinity) is the negative of its potential energy. Since the initial potential energy here is negative (due to opposite charges), the work to separate them is positive, meaning you have to supply energy.
If the net flux through a cube is 1.05 N m\(^2\) C\(^{-1}\), what will be the total charge inside the cube? (Given: The permittivity of free space is \(8.85 \times 10^{-12}\) C\(^2\) N\(^{-1}\) m\(^{-2}\)).
View Solution
Step 1: Understanding the Concept:
This problem is a direct application of Gauss's Law of electrostatics. Gauss's Law states that the total electric flux (\(\Phi\)) through any closed surface is equal to the total net electric charge (\(Q_{in}\)) enclosed within that surface, divided by the permittivity of free space (\(\epsilon_0\)).
Step 2: Key Formula or Approach:
According to Gauss's Law:
\[ \Phi = \frac{Q_{in}}{\epsilon_0} \]
To find the total charge inside the cube, we can rearrange the formula:
\[ Q_{in} = \Phi \times \epsilon_0 \]
Step 3: Detailed Explanation:
Given:
Net electric flux, \( \Phi = 1.05 \, N m^2 C^{-1} \)
Permittivity of free space, \( \epsilon_0 = 8.85 \times 10^{-12} \, C^2 N^{-1} m^{-2} \)
Now, we calculate the total charge enclosed, \(Q_{in}\):
\[ Q_{in} = (1.05 \, N m^2 C^{-1}) \times (8.85 \times 10^{-12} \, C^2 N^{-1} m^{-2}) \] \[ Q_{in} = 9.2925 \times 10^{-12} \, C \]
Rounding to two decimal places, we get:
\[ Q_{in} \approx 9.29 \times 10^{-12} \, C \]
Step 4: Final Answer:
The total charge inside the cube will be \(9.29 \times 10^{-12}\) C.
Quick Tip: Gauss's Law provides a powerful link between electric flux and the enclosed charge. The shape of the closed surface (a cube, sphere, etc.) does not matter for the total flux, only the net charge inside does. If you know the flux, you can find the charge, and vice versa.
A parallel plate capacitor having plate area 200 cm² and separation 2.0 mm holds a charge of 0.06 µC on applying a potential difference of 60 V. The dielectric constant of the material filled in between the plates is.
View Solution
Step 1: Understanding the Concept:
This problem involves a parallel plate capacitor filled with a dielectric material. We need to find the dielectric constant (k) using the given physical quantities. The capacitance of a capacitor can be determined from its charge and voltage, and also from its physical dimensions and the dielectric material.
Step 2: Key Formula or Approach:
The capacitance \(C\) of a capacitor is given by the ratio of charge \(Q\) to the potential difference \(V\):
\[ C = \frac{Q}{V} \]
For a parallel plate capacitor with a dielectric material, the capacitance is also given by:
\[ C = \frac{k \varepsilon_0 A}{d} \]
where \(k\) is the dielectric constant, \(\varepsilon_0\) is the permittivity of free space (\(8.854 \times 10^{-12} \, F/m\)), \(A\) is the plate area, and \(d\) is the separation between the plates.
By equating these two expressions for \(C\), we can solve for \(k\).
Step 3: Detailed Explanation:
Given data:
Plate area, \(A = 200 \, cm^2 = 200 \times 10^{-4} \, m^2\).
Plate separation, \(d = 2.0 \, mm = 2.0 \times 10^{-3} \, m\).
Charge, \(Q = 0.06 \, \mu C = 0.06 \times 10^{-6} \, C\).
Potential difference, \(V = 60 \, V\).
Calculation:
First, calculate the capacitance from the charge and voltage:
\[ C = \frac{Q}{V} = \frac{0.06 \times 10^{-6} \, C}{60 \, V} = 1 \times 10^{-9} \, F \]
Next, rearrange the formula for the parallel plate capacitor to solve for the dielectric constant \(k\):
\[ k = \frac{C d}{\varepsilon_0 A} \]
Now, substitute the known values into this equation:
\[ k = \frac{(1 \times 10^{-9} \, F) \times (2.0 \times 10^{-3} \, m)}{(8.854 \times 10^{-12} \, F/m) \times (200 \times 10^{-4} \, m^2)} \] \[ k = \frac{2 \times 10^{-12}}{8.854 \times 10^{-12} \times 2 \times 10^{-2}} \] \[ k = \frac{2 \times 10^{-12}}{17.708 \times 10^{-14}} = \frac{2}{0.17708} \approx 11.294 \]
Step 4: Final Answer:
The calculated value of the dielectric constant is approximately 11.3.
Quick Tip: Always ensure that all given quantities are converted to their standard SI units (meters, Coulombs, Farads, etc.) before substituting them into the formulas. This prevents common errors in calculation.
The electric potential due to an electric dipole
(A) depends on r, where r is the magnitude of position vector \(\vec{r}\)
(B) depends on the angle between the position vector \(\vec{r}\) and the dipole moment vector \(\vec{p}\)
(C) falls off at long distances, as \(1/r^2\)
(D) does not depend upon the distance separating the charges
Choose the correct answer from the options given below:
View Solution
Step 1: Understanding the Concept:
An electric dipole consists of two equal and opposite charges separated by a small distance. The electric potential at a point due to this dipole is the sum of the potentials due to each individual charge. We need to analyze the properties of this potential, especially at large distances from the dipole.
Step 2: Key Formula or Approach:
The electric potential \(V\) at a point with position vector \(\vec{r}\) due to an electric dipole with dipole moment \(\vec{p}\) is given by: \[ V = \frac{1}{4\pi\varepsilon_0} \frac{\vec{p} \cdot \hat{r}}{r^2} = \frac{1}{4\pi\varepsilon_0} \frac{p \cos\theta}{r^2} \]
where \(r = |\vec{r}|\) is the distance from the center of the dipole to the point, and \(\theta\) is the angle between the dipole moment vector \(\vec{p}\) and the position vector \(\vec{r}\). The dipole moment is defined as \(\vec{p} = q\vec{d}\), where \(\vec{d}\) is the vector from the negative to the positive charge.
Step 3: Detailed Explanation:
Let's evaluate each statement based on the formula:
(A) depends on r, where r is the magnitude of position vector \(\vec{r}\):
The formula \(V \propto \frac{1}{r^2}\) clearly shows that the potential depends on the distance \(r\). So, statement (A) is correct.
(B) depends on the angle between the position vector \(\vec{r}\) and the dipole moment vector \(\vec{p}\):
The term \(\cos\theta\) in the formula indicates that the potential depends on the angle \(\theta\) between \(\vec{p}\) and \(\vec{r}\). So, statement (B) is correct.
(C) falls off at long distances, as \(1/r^2\):
The formula shows that \(V\) is inversely proportional to the square of the distance \(r\) (\(V \propto 1/r^2\)). This confirms that the potential falls off as \(1/r^2\) at long distances. So, statement (C) is correct.
(D) does not depend upon the distance separating the charges:
The dipole moment is defined as \(p = qd\), where \(d\) is the distance separating the two charges. Since the potential \(V\) depends on \(p\), it indirectly depends on the separation distance \(d\). Therefore, statement (D) is incorrect.
Step 4: Final Answer:
Statements (A), (B), and (C) are correct, while (D) is incorrect. The correct choice is the option that includes only (A), (B), and (C).
Quick Tip: Remember the distance dependence for different charge distributions: Point charge potential \(V \propto 1/r\), dipole potential \(V \propto 1/r^2\), and quadrupole potential \(V \propto 1/r^3\). This pattern is useful for quickly identifying the correct relationship in multiple-choice questions.
Two point charges placed a distance d apart in vacuum exert a force of magnitude F on each other. One of the two charges is doubled. To keep the magnitude of force same the separation between the charges should be changed to
View Solution
Step 1: Understanding the Concept:
This problem applies Coulomb's Law, which describes the electrostatic force between two point charges. The force is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
Step 2: Key Formula or Approach:
Coulomb's Law states that the force \(F\) between two charges \(q_1\) and \(q_2\) separated by a distance \(d\) is: \[ F = k \frac{q_1 q_2}{d^2} \]
where \(k\) is Coulomb's constant. We will use this relationship to compare the initial and final situations.
Step 3: Detailed Explanation:
Initial situation:
The charges are \(q_1\) and \(q_2\), the distance is \(d\), and the force is \(F\). \[ F = k \frac{q_1 q_2}{d^2} \quad \cdots (1) \]
Final situation:
One charge is doubled, let's say the new charges are \(q'_1 = 2q_1\) and \(q'_2 = q_2\). The new distance is \(d'\). The force \(F'\) must be the same as the initial force \(F\). \[ F' = k \frac{(2q_1) q_2}{(d')^2} \quad \cdots (2) \]
Equating the forces:
We are given that \(F' = F\). Therefore, we can set equation (1) equal to equation (2): \[ k \frac{q_1 q_2}{d^2} = k \frac{2q_1 q_2}{(d')^2} \]
The terms \(k\), \(q_1\), and \(q_2\) cancel out from both sides: \[ \frac{1}{d^2} = \frac{2}{(d')^2} \]
Now, we solve for the new distance \(d'\): \[ (d')^2 = 2d^2 \] \[ d' = \sqrt{2d^2} = \sqrt{2} d \]
Step 4: Final Answer:
To maintain the same force after doubling one of the charges, the new separation distance must be \(\sqrt{2} d\).
Quick Tip: In problems involving ratios and proportions like Coulomb's law (\(F \propto \frac{q_1 q_2}{d^2}\)), you can set up a ratio. If \(F\) is to remain constant, then the ratio \(\frac{q_1 q_2}{d^2}\) must also be constant. So, \(\frac{q_1 q_2}{d_{initial}^2} = \frac{(2q_1) q_2}{d_{final}^2}\), which quickly leads to \(d_{final}^2 = 2d_{initial}^2\).
Conductors develop electric currents in them
View Solution
Step 1: Understanding the Concept:
This question asks about the fundamental cause of electric current in a conductor. An electric current is defined as the net flow of electric charge. Conductors, like metals, have a large number of free electrons that can move throughout the material.
Step 2: Detailed Explanation:
(A) on applying electric field:
When an electric field (\(\vec{E}\)) is applied across a conductor, it exerts an electrostatic force (\(\vec{F} = q\vec{E}\)) on the free charge carriers (electrons). For electrons, \(q = -e\), so the force is \(\vec{F} = -e\vec{E}\). This force causes the electrons to accelerate and drift in a direction opposite to the electric field, resulting in a net flow of charge, which is an electric current. This is the primary mechanism for generating a steady current in a conductor.
(B) on placing the conductor in the magnetic field:
A magnetic field exerts a force (\(\vec{F} = q(\vec{v} \times \vec{B})\)) only on charges that are already in motion (\(\vec{v} \neq 0\)). A static magnetic field applied to a stationary conductor will not initiate the movement of charges, and therefore will not create a current by itself. (Note: A changing magnetic field can induce an electric field and thus a current, but the option refers to placing the conductor in a magnetic field, implying a static field).
(C) on applying gravitational field only:
A gravitational field exerts a force on mass, not on electric charge. It does not cause the ordered motion of charge carriers needed to constitute an electric current.
(D) on applying the magnetic field and gravitational field:
As explained above, neither a static magnetic field nor a gravitational field can independently initiate a current in a stationary conductor. Their combination would also not result in an electric current.
Step 3: Final Answer:
An electric current is produced in a conductor when an electric field is applied, as it provides the necessary force to cause a directed motion of free charges.
Quick Tip: Remember the fundamental forces: Electric fields act on charges. Magnetic fields act on moving charges. Gravitational fields act on masses. Electric current is the flow of charge, so the force that directly causes this flow must be the electric force from an applied electric field.
Resistivity of a conductor depends on
View Solution
Step 1: Understanding the Concept:
This question asks about the factors that determine the electrical resistivity (\(\rho\)) of a conducting material. It is important to distinguish between resistance (\(R\)) and resistivity (\(\rho\)).
Step 2: Detailed Explanation:
Resistivity (\(\rho\)):
Resistivity is an intrinsic property of a material. It quantifies how strongly a given material opposes the flow of electric current.
- Material: Different materials have different atomic structures and numbers of free charge carriers per unit volume. For example, copper has a lower resistivity than iron because it has more free electrons available for conduction. Therefore, resistivity depends on the material.
- Temperature: When the temperature of a conductor increases, the atoms/ions in the material vibrate with greater amplitude. This increases the frequency of collisions between the free electrons and the ions, which impedes the flow of electrons and thus increases the resistivity. Therefore, resistivity depends on temperature.
Resistance (\(R\)):
Resistance is an extrinsic property of an object. It depends not only on the material's resistivity but also on the object's physical dimensions (length \(L\) and cross-sectional area \(A\)). The relationship is given by: \[ R = \rho \frac{L}{A} \]
From this formula, we can see that resistance depends on dimensions, but resistivity (\(\rho\)) does not.
Evaluating the options:
(A) Incorrect. Resistivity does not depend on the dimensions.
(B) Correct. Resistivity depends on the nature of the material and its temperature.
(C) Incorrect. Resistivity does not depend on dimensions.
(D) Incorrect. While it depends on temperature, it also fundamentally depends on the material itself.
Step 3: Final Answer:
The resistivity of a conductor is an intrinsic property that depends on the nature of the material and its temperature.
Quick Tip: Distinguish clearly between Resistance (\(R\), in Ohms, \(\Omega\)) and Resistivity (\(\rho\), in Ohm-meters, \(\Omega\cdot m\)). Resistance is a property of an object (like a specific wire), while Resistivity is a property of a material (like copper in general).
In the (i) absence of electric field, and in the (ii) presence of electric field, the paths of electrons between successive collisions with the positive ions of the metal, are
View Solution
Step 1: Understanding the Concept:
This question describes the motion of free electrons within a metallic conductor under two different conditions: with no external electric field and with an external electric field. We need to determine the nature of the electron's path between two consecutive collisions with the lattice ions.
Step 2: Detailed Explanation:
(i) In the absence of an electric field:
The free electrons in a metal are in constant random motion due to thermal energy. Between two successive collisions with the positive ions of the metal lattice, there is no net force acting on an electron (ignoring gravitational forces, which are negligible). According to Newton's first law, an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force. Therefore, the electron travels in a straight line at a constant velocity between collisions.
(ii) In the presence of an electric field:
When an external electric field (\(\vec{E}\)) is applied, each electron experiences a constant electrostatic force \(\vec{F} = -e\vec{E}\). This constant force causes the electron to have a constant acceleration (\(\vec{a} = \vec{F}/m_e = -e\vec{E}/m_e\)) in the direction opposite to the field. An object moving with an initial velocity and subject to a constant acceleration follows a parabolic path. Thus, the path of the electron between successive collisions becomes curved. The overall motion is a combination of random thermal velocity and a directed drift caused by the field.
Step 3: Final Answer:
In the absence of an electric field, the path is a straight line. In the presence of an electric field, the path is curved due to the constant electrostatic force.
Quick Tip: Think of the electron's motion in the presence of an electric field as analogous to a projectile's motion in a uniform gravitational field. Both experience a constant force, leading to a parabolic (curved) trajectory between "collisions" (or from launch to landing).
A resistor develops 800 J of thermal energy in 20 s on applying a potential difference of 20 V. Its resistance is
View Solution
Step 1: Understanding the Concept:
This problem involves the heating effect of electric current, also known as Joule heating. When a potential difference is applied across a resistor, electrical energy is converted into thermal energy. We are given the energy, time, and voltage, and we need to find the resistance.
Step 2: Key Formula or Approach:
The electrical power \(P\) dissipated in a resistor is the rate at which energy is converted. \[ P = \frac{E}{t} \]
where \(E\) is the energy and \(t\) is the time.
The power dissipated in a resistor can also be expressed in terms of voltage \(V\) and resistance \(R\): \[ P = \frac{V^2}{R} \]
By combining these two formulas, we can solve for the resistance \(R\).
Step 3: Detailed Explanation:
Given data:
Thermal energy, \(E = 800 \, J\).
Time, \(t = 20 \, s\).
Potential difference, \(V = 20 \, V\).
Calculation:
First, calculate the power \(P\) dissipated by the resistor: \[ P = \frac{E}{t} = \frac{800 \, J}{20 \, s} = 40 \, W \]
Now, use the power formula involving voltage and resistance to find \(R\): \[ P = \frac{V^2}{R} \]
Rearranging for \(R\): \[ R = \frac{V^2}{P} \]
Substitute the given values: \[ R = \frac{(20 \, V)^2}{40 \, W} = \frac{400 \, V^2}{40 \, W} = 10 \, \Omega \]
Step 4: Final Answer:
The resistance of the resistor is 10 \(\Omega\).
Quick Tip: Remember the three main formulas for electrical power: \(P = VI\), \(P = I^2R\), and \(P = V^2/R\). Choose the formula that directly uses the quantities given in the problem (here, V and E/t) to avoid unnecessary intermediate calculations (like finding the current I).
A wire of resistance 4 \(\Omega\) is used to make a coil of radius 7 cm. The wire has a diameter of 1.4 mm and the resistivity of its material is 2 x 10\(^{-7}\) \(\Omega\) m. The number of turns in the coil will be
View Solution
Step 1: Understanding the Concept:
This is a multi-step problem that connects the electrical properties of a wire (resistance, resistivity) with its geometrical properties (length, area) and how it's shaped into a coil (number of turns, radius). We first need to find the total length of the wire using the resistance formula and then use that length to find the number of turns in the coil.
Step 2: Key Formula or Approach:
1. Resistance of a wire: \(R = \rho \frac{L}{A}\), where \(R\) is resistance, \(\rho\) is resistivity, \(L\) is length, and \(A\) is the cross-sectional area.
2. Cross-sectional area of the wire: \(A = \pi r_{wire}^2\), where \(r_{wire}\) is the radius of the wire.
3. Total length of the wire in the coil: \(L = n \times (circumference of one turn)\), where \(n\) is the number of turns and the circumference is \(2\pi r_{coil}\).
Step 3: Detailed Explanation:
Given data:
Total resistance, \(R = 4 \, \Omega\).
Coil radius, \(r_{coil} = 7 \, cm = 0.07 \, m\).
Wire diameter, \(d_{wire} = 1.4 \, mm\), so wire radius, \(r_{wire} = 0.7 \, mm = 0.7 \times 10^{-3} \, m\).
Resistivity, \(\rho = 2 \times 10^{-7} \, \Omega \cdot m\).
Calculation:
Part 1: Find the total length (L) of the wire.
First, calculate the cross-sectional area (\(A\)) of the wire: \[ A = \pi r_{wire}^2 = \pi (0.7 \times 10^{-3} \, m)^2 = \pi (0.49 \times 10^{-6} \, m^2) \]
Now, use the resistance formula to find the length \(L\): \[ R = \rho \frac{L}{A} \implies L = \frac{R A}{\rho} \] \[ L = \frac{(4 \, \Omega) \times (\pi \times 0.49 \times 10^{-6} \, m^2)}{2 \times 10^{-7} \, \Omega \cdot m} \] \[ L = \frac{4 \pi \times 0.49 \times 10^{-6}}{2 \times 10^{-7}} = 2 \pi \times 0.49 \times 10 = 9.8\pi \, m \]
Part 2: Find the number of turns (n).
The length of the wire required for one turn is the circumference of the coil: \[ Circumference = 2 \pi r_{coil} = 2 \pi (0.07 \, m) = 0.14\pi \, m \]
The total number of turns \(n\) is the total length of the wire divided by the length of one turn: \[ n = \frac{Total Length}{Length of one turn} = \frac{L}{2 \pi r_{coil}} \] \[ n = \frac{9.8\pi \, m}{0.14\pi \, m} = \frac{9.8}{0.14} = \frac{980}{14} = 70 \]
Step 4: Final Answer:
The number of turns in the coil will be 70.
Quick Tip: In such problems, break down the question into smaller parts. First, deal with the wire's intrinsic properties (resistance, resistivity, dimensions) to find the total length. Then, use that length in the context of the coil's geometry to find the required quantity (number of turns).
A battery of emf 12 V and internal resistance 3 \(\Omega\) is connected to an external resistor. If the current in the circuit is 0.6 A, the voltage across the external resistor will be
View Solution
Step 1: Understanding the Concept:
This problem deals with a simple DC circuit containing a real battery (which has both an electromotive force, EMF, and an internal resistance) and an external resistor. The voltage available to the external circuit (the terminal voltage) is the EMF minus the voltage drop across the internal resistance.
Step 2: Key Formula or Approach:
The terminal voltage \(V_T\) of a battery supplying a current \(I\) is given by: \[ V_T = \mathcal{E} - Ir \]
where \(\mathcal{E}\) is the EMF of the battery and \(r\) is its internal resistance.
The voltage across the external resistor is equal to the terminal voltage of the battery.
Step 3: Detailed Explanation:
Given data:
EMF, \(\mathcal{E} = 12 \, V\).
Internal resistance, \(r = 3 \, \Omega\).
Current in the circuit, \(I = 0.6 \, A\).
Calculation:
The voltage across the external resistor is the terminal voltage \(V_T\). We can calculate this using the formula: \[ V_T = \mathcal{E} - Ir \]
Substitute the given values: \[ V_T = 12 \, V - (0.6 \, A \times 3 \, \Omega) \] \[ V_T = 12 \, V - 1.8 \, V \] \[ V_T = 10.2 \, V \]
Step 4: Final Answer:
The voltage across the external resistor will be 10.2 V.
Quick Tip: Remember that the EMF (\(\mathcal{E}\)) is the total voltage the battery can provide, while the terminal voltage (\(V_T\)) is the actual voltage delivered to the external circuit. The difference, \(Ir\), is the 'lost volts' due to the battery's own internal resistance. The terminal voltage will always be less than the EMF when the battery is discharging (supplying current).
A uniform wire of resistance 12 \(\Omega\) is cut into three pieces in the ratio of length 1: 2: 3. Now the three pieces are connected to form a triangle. A cell of emf 8 V and internal resistance 5 \(\Omega\) is connected across the highest of the three resistors. The current through the circuit is:
View Solution
Step 1: Understanding the Concept:
This is a circuit analysis problem. First, we need to determine the resistance of each piece of wire. Then, we analyze the circuit formed by the triangle of resistors to find the equivalent external resistance. Finally, we use Ohm's law for the entire circuit, including the internal resistance of the cell, to find the total current.
Step 2: Key Formula or Approach:
1. For a uniform wire, resistance is proportional to length (\(R \propto L\)).
2. Resistors in series: \(R_{series} = R_1 + R_2 + \dots\)
3. Resistors in parallel: \(\frac{1}{R_{parallel}} = \frac{1}{R_1} + \frac{1}{R_2} + \dots\)
4. Ohm's law for a complete circuit: \(I = \frac{\mathcal{E}}{R_{ext} + r}\), where \(R_{ext}\) is the equivalent external resistance and \(r\) is the internal resistance.
Step 3: Detailed Explanation:
Part 1: Find the resistances of the three pieces.
Total resistance \(R_{total} = 12 \, \Omega\).
The lengths are in the ratio 1:2:3. Since \(R \propto L\), the resistances will also be in the ratio 1:2:3.
Let the resistances be \(R_1, R_2, R_3\). \[ R_1 = \left(\frac{1}{1+2+3}\right) \times 12 \, \Omega = \frac{1}{6} \times 12 = 2 \, \Omega \] \[ R_2 = \left(\frac{2}{1+2+3}\right) \times 12 \, \Omega = \frac{2}{6} \times 12 = 4 \, \Omega \] \[ R_3 = \left(\frac{3}{1+2+3}\right) \times 12 \, \Omega = \frac{3}{6} \times 12 = 6 \, \Omega \]
The highest resistance is \(R_3 = 6 \, \Omega\).
Part 2: Find the equivalent external resistance (\(R_{ext}\)).
The three resistors form a triangle. The cell is connected across the highest resistor, \(R_3\).
This means that resistors \(R_1\) and \(R_2\) are in series with each other, and this series combination is in parallel with \(R_3\).
Resistance of the series combination: \(R_{12} = R_1 + R_2 = 2 \, \Omega + 4 \, \Omega = 6 \, \Omega\).
Now, \(R_{12}\) is in parallel with \(R_3\). The equivalent external resistance \(R_{ext}\) is: \[ \frac{1}{R_{ext}} = \frac{1}{R_{12}} + \frac{1}{R_3} = \frac{1}{6 \, \Omega} + \frac{1}{6 \, \Omega} = \frac{2}{6 \, \Omega} = \frac{1}{3 \, \Omega} \] \[ R_{ext} = 3 \, \Omega \]
Part 3: Calculate the total current.
Given data for the cell:
EMF, \(\mathcal{E} = 8 \, V\).
Internal resistance, \(r = 5 \, \Omega\).
Using Ohm's law for the complete circuit: \[ I = \frac{\mathcal{E}}{R_{ext} + r} = \frac{8 \, V}{3 \, \Omega + 5 \, \Omega} = \frac{8 \, V}{8 \, \Omega} = 1 \, A \]
Step 4: Final Answer:
The current through the circuit (drawn from the cell) is 1 A.
Quick Tip: When a source is connected across one side of a triangle of resistors, the other two sides are always in series with each other, and that combination is in parallel with the first side. Visualizing or redrawing the circuit can make this clearer.
A bar magnet of magnetic moment 5.0 A m² has poles 20 cm apart. The pole strength would be
View Solution
Step 1: Understanding the Concept:
This problem relates the magnetic moment of a bar magnet to its pole strength and magnetic length. The magnetic moment is a vector quantity that represents the overall magnetic strength and orientation of a magnet.
Step 2: Key Formula or Approach:
The magnetic moment (\(M\)) of a bar magnet is defined as the product of its pole strength (\(m\)) and its magnetic length (\(2l\)). \[ M = m \times (2l) \]
The magnetic length (\(2l\)) is the distance between the two poles of the magnet.
Step 3: Detailed Explanation:
Given data:
Magnetic moment, \(M = 5.0 \, A m^2\).
Distance between poles (magnetic length), \(2l = 20 \, cm = 0.20 \, m\).
Calculation:
We need to find the pole strength \(m\). Rearranging the formula: \[ m = \frac{M}{2l} \]
Substitute the given values: \[ m = \frac{5.0 \, A m^2}{0.20 \, m} \] \[ m = \frac{5}{0.2} = \frac{50}{2} = 25 \, A m \]
Step 4: Final Answer:
The pole strength of the bar magnet would be 25 A m.
Quick Tip: Pay close attention to units. The magnetic moment is in Ampere-meter squared (A m²), while pole strength is in Ampere-meter (A m). The distance must be in meters to ensure consistency. Always convert cm to m before calculating.
Match List-I with List-II
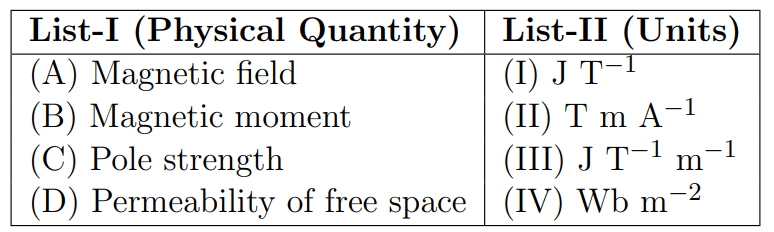
View Solution
Step 1: Understanding the Concept:
This question requires matching physical quantities related to magnetism with their corresponding SI units. This involves recalling the definitions and key formulas for each quantity to derive or identify their units.
Step 2: Detailed Explanation:
Let's analyze each physical quantity and find its unit.
(A) Magnetic field (B):
The magnetic field is also known as magnetic flux density. The unit of magnetic flux is the Weber (Wb) and the unit of area is m².
Therefore, Magnetic Field \(B = \frac{Magnetic Flux}{Area}\). Its unit is Wb/m² or Wb m\(^{-2}\). The unit Wb/m² is also called the Tesla (T).
So, (A) matches with (IV).
(B) Magnetic moment (M):
The potential energy \(U\) of a magnetic dipole in a magnetic field \(B\) is given by \(U = -M B \cos\theta\).
From this, the magnitude of the magnetic moment can be expressed as \(M = U/B\).
The unit of energy \(U\) is Joule (J) and the unit of magnetic field \(B\) is Tesla (T).
So, the unit of magnetic moment is J/T or J T\(^{-1}\).
So, (B) matches with (I).
(C) Pole strength (m):
The magnetic moment \(M\) is defined as the product of pole strength \(m\) and magnetic length \(l\), i.e., \(M = m \times l\).
Therefore, pole strength \(m = M/l\).
Using the unit for M from the previous step (J T\(^{-1}\)) and the unit for length \(l\) (m), we get the unit for pole strength as (J T\(^{-1}\)) / m or J T\(^{-1}\) m\(^{-1}\).
So, (C) matches with (III).
(D) Permeability of free space (\(\mu_0\)):
From the Biot-Savart law or Ampere's law, we can find the units. For a long solenoid, the magnetic field inside is \(B = \mu_0 n I\), where \(n\) is the number of turns per unit length (unit: m\(^{-1}\)) and \(I\) is the current (unit: A).
So, \(\mu_0 = \frac{B}{nI}\).
The unit for \(\mu_0\) would be \(\frac{T}{m^{-1} \cdot A} = T m A^{-1}\).
So, (D) matches with (II).
Step 3: Final Answer:
Based on the analysis:
(A) \(\rightarrow\) (IV)
(B) \(\rightarrow\) (I)
(C) \(\rightarrow\) (III)
(D) \(\rightarrow\) (II)
This corresponds to option (B).
Quick Tip: For matching questions involving units, try to recall a defining formula for each physical quantity. For example, for magnetic field, \(B = F/(qv)\) or \(B = \Phi/A\). For magnetic moment, \(U = -MB\). These fundamental relationships are the key to deriving the units if you don't remember them directly.
A long wire with a small current element of length 1 cm is placed at the origin and carries a current of 10 A along the x-axis. The magnitude of the magnetic field, due to the element, on the y-axis at a distance 0.5 m from it, would be
View Solution
Step 1: Understanding the Concept:
This problem requires the application of the Biot-Savart Law to find the magnetic field produced by a small current-carrying element. The Biot-Savart Law gives the magnetic field at a point in space due to a current element.
Step 2: Key Formula or Approach:
The magnitude of the magnetic field \(dB\) due to a current element \(Id\vec{l}\) at a distance \(r\) is given by the Biot-Savart Law: \[ dB = \frac{\mu_0}{4\pi} \frac{I dl \sin\theta}{r^2} \]
where \(\mu_0\) is the permeability of free space (\(4\pi \times 10^{-7} \, T\cdot m/A\)), \(I\) is the current, \(dl\) is the length of the element, \(r\) is the distance from the element to the point, and \(\theta\) is the angle between the direction of the current element and the position vector to the point.
Step 3: Detailed Explanation:
Given data:
Current, \(I = 10 \, A\).
Length of the element, \(dl = 1 \, cm = 0.01 \, m\).
Distance to the point on the y-axis, \(r = 0.5 \, m\).
The current element is along the x-axis, and the point is on the y-axis. Therefore, the angle \(\theta\) between the current element \(d\vec{l}\) and the position vector \(\vec{r}\) is \(90^\circ\). Thus, \(\sin\theta = \sin(90^\circ) = 1\).
The constant \(\frac{\mu_0}{4\pi} = 10^{-7} \, T\cdot m/A\).
Calculation:
Substitute the values into the Biot-Savart Law formula: \[ dB = (10^{-7}) \frac{(10 \, A) \times (0.01 \, m) \times 1}{(0.5 \, m)^2} \] \[ dB = 10^{-7} \frac{0.1}{0.25} \] \[ dB = 10^{-7} \times 0.4 \] \[ dB = 4 \times 10^{-8} \, T \]
Step 4: Final Answer:
The magnitude of the magnetic field due to the element at the given point is \(4 \times 10^{-8}\) T.
Quick Tip: In problems involving Biot-Savart Law, first identify the given parameters: \(I, dl, r\), and the angle \(\theta\). Pay close attention to the geometry to correctly determine \(\theta\). For perpendicular axes (like x and y), \(\theta\) is \(90^\circ\). Also, remember the value of the constant \(\frac{\mu_0}{4\pi} = 10^{-7}\) T·m/A for easy calculation.
A conductor is placed along z-axis carrying current in z direction in uniform magnetic field directed along y-axis. The magnetic force acting on the conductor is directed along:
View Solution
Step 1: Understanding the Concept:
This problem involves finding the direction of the magnetic force on a current-carrying conductor placed in a uniform magnetic field. The direction of this force is determined by the vector cross product of the current direction and the magnetic field direction, often visualized using the right-hand rule.
Step 2: Key Formula or Approach:
The magnetic force \(\vec{F}\) on a straight conductor of length \(\vec{L}\) carrying current \(I\) in a uniform magnetic field \(\vec{B}\) is given by: \[ \vec{F} = I (\vec{L} \times \vec{B}) \]
The direction of the force is given by the direction of the cross product \(\vec{L} \times \vec{B}\). We can use the Cartesian unit vectors (\(\hat{i}, \hat{j}, \hat{k}\) for x, y, z axes respectively) to determine this direction.
Step 3: Detailed Explanation:
Given directions:
The current is in the z-direction. So, the direction of the length vector \(\vec{L}\) is along the z-axis, which can be represented by the unit vector \(\hat{k}\).
The magnetic field is in the y-direction. So, the direction of \(\vec{B}\) is along the y-axis, represented by the unit vector \(\hat{j}\).
Calculation of Direction:
The direction of the force \(\vec{F}\) is determined by the cross product \(\hat{k} \times \hat{j}\).
Using the cyclic property of the cross product of unit vectors: \(\hat{i} \times \hat{j} = \hat{k}\)
\(\hat{j} \times \hat{k} = \hat{i}\)
\(\hat{k} \times \hat{i} = \hat{j}\)
And the anti-cyclic property: \(\hat{j} \times \hat{i} = -\hat{k}\)
\(\hat{k} \times \hat{j} = -\hat{i}\)
\(\hat{i} \times \hat{k} = -\hat{j}\)
From this, we find that \(\hat{k} \times \hat{j} = -\hat{i}\).
The vector \(-\hat{i}\) represents the direction along the negative x-axis.
Step 4: Final Answer:
The magnetic force acting on the conductor is directed along the negative x-axis.
Quick Tip: Use Fleming's Left-Hand Rule as a quick check. Point your Forefinger in the direction of the Magnetic Field (y-axis). Point your Middle finger in the direction of the Current (z-axis). Your Thumb will point in the direction of the Force, which will be the negative x-axis.
A galvanometer of resistance 520 \(\Omega\) is shunted with 20 \(\Omega\) resistance to convert it into an ammeter. The resistance of the ammeter will be
View Solution
Step 1: Understanding the Concept:
To convert a galvanometer into an ammeter, a low-resistance wire called a "shunt" is connected in parallel with the galvanometer. The resulting device, the ammeter, has an overall resistance that is the equivalent resistance of the galvanometer and the shunt connected in parallel. An ideal ammeter should have zero resistance.
Step 2: Key Formula or Approach:
When two resistors, \(R_G\) (galvanometer resistance) and \(R_S\) (shunt resistance), are connected in parallel, their equivalent resistance \(R_A\) (resistance of the ammeter) is given by: \[ \frac{1}{R_A} = \frac{1}{R_G} + \frac{1}{R_S} \]
or, more conveniently for two resistors: \[ R_A = \frac{R_G \times R_S}{R_G + R_S} \]
Step 3: Detailed Explanation:
Given data:
Galvanometer resistance, \(R_G = 520 \, \Omega\).
Shunt resistance, \(R_S = 20 \, \Omega\).
Calculation:
Substitute the values into the formula for parallel equivalent resistance: \[ R_A = \frac{520 \times 20}{520 + 20} \] \[ R_A = \frac{10400}{540} \] \[ R_A = \frac{1040}{54} = \frac{520}{27} \] \[ R_A \approx 19.259 \, \Omega \]
Rounding to one decimal place, we get 19.3 \(\Omega\).
Step 4: Final Answer:
The resistance of the ammeter will be approximately 19.3 \(\Omega\).
Quick Tip: Remember that the equivalent resistance of a parallel combination is always less than the smallest individual resistance in the combination. Here, the smallest resistance is the shunt (20 \(\Omega\)), so the answer must be less than 20 \(\Omega\). This can help you eliminate incorrect options like 540 \(\Omega\).
The magnitude of magnetic field inside a solenoid of length 0.3 m having 800 turns carrying a current of 6 A is
View Solution
Step 1: Understanding the Concept:
A solenoid is a coil of wire that produces a nearly uniform magnetic field in its interior when a current is passed through it. The strength of this magnetic field depends on the number of turns per unit length, the current, and the permeability of the medium inside.
Step 2: Key Formula or Approach:
The magnitude of the magnetic field \(B\) inside a long solenoid is given by the formula: \[ B = \mu_0 n I \]
where \(\mu_0\) is the permeability of free space (\(4\pi \times 10^{-7} \, T\cdot m/A\)), \(I\) is the current, and \(n\) is the number of turns per unit length.
The number of turns per unit length \(n\) is calculated as \(n = \frac{N}{L}\), where \(N\) is the total number of turns and \(L\) is the length of the solenoid.
Step 3: Detailed Explanation:
Given data:
Length of the solenoid, \(L = 0.3 \, m\).
Total number of turns, \(N = 800\).
Current, \(I = 6 \, A\).
Calculation:
First, calculate the number of turns per unit length, \(n\): \[ n = \frac{N}{L} = \frac{800}{0.3} = \frac{8000}{3} \, turns/m \]
Now, substitute the values into the magnetic field formula: \[ B = \mu_0 n I = (4\pi \times 10^{-7}) \times \left(\frac{8000}{3}\right) \times 6 \] \[ B = (4\pi \times 10^{-7}) \times (8000 \times 2) \] \[ B = 4\pi \times 10^{-7} \times 16000 \] \[ B = 64000 \pi \times 10^{-7} = 6.4\pi \times 10^{-3} \, T \]
Now, we calculate the numerical value using \(\pi \approx 3.14159\): \[ B \approx 6.4 \times 3.14159 \times 10^{-3} \, T \] \[ B \approx 20.106 \times 10^{-3} \, T \]
This is equal to 20.106 mT. The closest option is 20 mT.
Step 4: Final Answer:
The magnitude of the magnetic field inside the solenoid is approximately 20 mT.
Quick Tip: The formula \(B = \mu_0 n I\) is for an ideal, infinitely long solenoid. However, it provides a very good approximation for the field near the center of a real solenoid as long as its length is much greater than its diameter. In exams, unless specified otherwise, use this ideal formula.
A charged particle accelerated through a potential difference of V volts acquires a speed u. The particle is then made to enter perpendicularly in a uniform magnetic field B. The radius of the circular path followed by the charged particle will be proportional to
View Solution
Step 1: Understanding the Concept:
This problem combines two key concepts: the work-energy theorem for a charged particle in an electric field, and the dynamics of a charged particle in uniform circular motion in a magnetic field. We need to find a relationship between the radius of the circular path and the initial accelerating voltage and final speed.
Step 2: Key Formula or Approach:
1. When a particle of charge \(q\) is accelerated by a potential difference \(V\), the kinetic energy gained is equal to the work done: \(KE = qV\). Also, \(KE = \frac{1}{2}mu^2\). Therefore, \(qV = \frac{1}{2}mu^2\).
2. When this particle enters a magnetic field \(B\) perpendicularly, the magnetic force provides the centripetal force for circular motion: \(quB = \frac{mu^2}{r}\).
3. From this second equation, the radius of the circular path is: \(r = \frac{mu}{qB}\).
Step 3: Detailed Explanation:
We have two main equations:
(i) \(V = \frac{mu^2}{2q}\)
(ii) \(r = \frac{mu}{qB}\)
The question asks for the proportionality of \(r\) in terms of \(V\) and \(u\). We need to combine the equations to find this relationship. Let's look at the expression in option (A), which is \(V/u\).
From equation (i), we can write: \[ \frac{V}{u} = \frac{mu^2/2q}{u} = \frac{mu}{2q} \]
Now let's compare this with our expression for the radius \(r\) from equation (ii): \[ r = \frac{mu}{qB} \]
We can see that both \(r\) and \(V/u\) are directly proportional to the term \(mu/q\). We can write \(r\) in terms of \(V/u\): \[ r = \frac{mu}{qB} = \frac{2}{B} \left( \frac{mu}{2q} \right) = \frac{2}{B} \left( \frac{V}{u} \right) \]
Since the magnetic field \(B\) is uniform and constant, we have the proportionality: \[ r \propto \frac{V}{u} \]
Step 4: Final Answer:
The radius of the circular path is proportional to \(V/u\).
Quick Tip: In questions asking for proportionality, write down the main equations for the physical quantities involved. Then, manipulate these equations to express one quantity in terms of the others. Here, expressing both \(r\) and the options in terms of fundamental quantities like \(m, u, q\) helps to find the correct relationship.
Figure shows a coil C connected to a galvanometer G. When the North-pole of a bar magnet is pushed towards the coil, the pointer in the galvanometer deflects. Regarding this set up, the following statements are given:
(A) It indicates the presence of electric current in the coil.
(B) The deflection is found to be smaller when the magnet is pushed towards the coil faster.
(C) There is repulsion in the moving magnet and the magnetic pole induced in the coil facing towards the N pole of the magnet.
(D) If the bar magnet does not move, there is no induced current in the coil.
Choose the correct answer from the options given below:

View Solution
Step 1: Understanding the Concept:
This question tests the understanding of electromagnetic induction, specifically Faraday's Law of Induction and Lenz's Law. Faraday's Law relates the change in magnetic flux to the induced electromotive force (EMF), and Lenz's Law gives the direction of the induced current.
Step 2: Detailed Explanation:
Let's analyze each statement:
(A) It indicates the presence of electric current in the coil.
A galvanometer is a device that detects electric current. The deflection of its pointer is a direct indication that a current is flowing through the coil. This statement is correct.
(B) The deflection is found to be smaller when the magnet is pushed towards the coil faster.
According to Faraday's Law of Induction, the magnitude of the induced EMF (and hence the induced current and galvanometer deflection) is directly proportional to the rate of change of magnetic flux (\(|\mathcal{E}| \propto |d\Phi_B/dt|\)). Pushing the magnet faster increases the rate of change of flux, which results in a larger induced current and a larger deflection. This statement is incorrect.
(C) There is repulsion in the moving magnet and the magnetic pole induced in the coil facing towards the N pole of the magnet.
According to Lenz's Law, the induced current flows in a direction that opposes the change that produced it. As the North pole of the magnet approaches the coil, the magnetic flux through the coil increases. To oppose this increase, the coil must generate a magnetic field pointing away from the magnet. This means the face of the coil nearer to the magnet becomes a North pole. Since like poles repel, there will be a repulsive force between the coil and the magnet. This statement is correct.
(D) If the bar magnet does not move, there is no induced current in the coil.
For an EMF to be induced, there must be a change in the magnetic flux through the coil. If the magnet is stationary relative to the coil, the magnetic flux is constant (\(d\Phi_B/dt = 0\)). Therefore, no EMF is induced, and no current flows. This statement is correct.
Step 3: Final Answer:
Statements (A), (C), and (D) are correct, while (B) is incorrect. Therefore, the correct option includes only (A), (C), and (D).
Quick Tip: Remember the core principles:
1. \(\textbf{Faraday's Law}\): Changing magnetic flux induces an EMF. Faster change = larger EMF.
2. \(\textbf{Lenz's Law:}\) The induced current opposes the change in flux. (Nature abhors a change in flux!) This determines the direction of the current and the nature of the force (attraction or repulsion).
Figure shows a rectangular conductor PQRS in which the conductor PQ is free to move. The conductor PQ is moved towards the left with a constant velocity V as shown in the figure. Assume that there is no loss of energy due to friction. What will be the magnetic flux linked with the loop PQRS and the motional emf?

View Solution
Step 1: Understanding the Concept:
This problem involves calculating the magnetic flux through a changing area and the motional electromotive force (EMF) induced in a conductor moving through a magnetic field.
Step 2: Key Formula or Approach:
1. Magnetic Flux (\(\Phi_B\)): The magnetic flux through a surface is defined as \(\Phi_B = B A \cos\theta\), where \(B\) is the magnetic field strength, \(A\) is the area of the surface, and \(\theta\) is the angle between the magnetic field and the normal to the surface.
2. Motional EMF (\(\mathcal{E}\)): When a conductor of length \(l\) moves with velocity \(v\) perpendicular to a uniform magnetic field \(B\), an EMF is induced across its ends, given by \(\mathcal{E} = Blv\). Alternatively, using Faraday's Law, \(\mathcal{E} = -d\Phi_B/dt\).
Step 3: Detailed Explanation:
Magnetic Flux Calculation:
Let the length of the conductor PQ be \(l\) and its distance from the side RS be \(x\) at any instant.
The area of the rectangular loop PQRS is \(A = l \times x\).
The magnetic field \(\vec{B}\) is uniform and directed perpendicularly into the plane of the loop. So, the angle \(\theta\) between \(\vec{B}\) and the area vector is \(0^\circ\), and \(\cos(0^\circ) = 1\).
The magnetic flux linked with the loop is: \[ \Phi_B = B \cdot A = B (lx) = Blx \]
Motional EMF Calculation:
Method 1: Using the motional EMF formula
The conductor PQ of length \(l\) is moving with a constant velocity \(V\) perpendicular to the magnetic field \(B\).
The motional EMF induced across PQ is directly given by: \[ \mathcal{E} = BlV \]
Method 2: Using Faraday's Law of Induction
The EMF is the rate of change of magnetic flux. \[ \mathcal{E} = -\frac{d\Phi_B}{dt} = -\frac{d}{dt}(Blx) \]
Since \(B\) and \(l\) are constant, we have: \[ \mathcal{E} = -Bl \frac{dx}{dt} \]
The conductor is moved towards the left, so the distance \(x\) is decreasing. The rate of change of position, \(dx/dt\), is the velocity. Since \(x\) decreases, \(dx/dt = -V\). \[ \mathcal{E} = -Bl(-V) = BlV \]
Both methods give the same result for the motional EMF.
Step 4: Final Answer:
The magnetic flux is \(Blx\) and the motional EMF is \(BlV\). This matches option (C).
Quick Tip: For motional EMF problems, you can often use either \(\mathcal{E} = Blv\) (if B, l, v are mutually perpendicular) or Faraday's Law \(\mathcal{E} = -d\Phi/dt\). The formula \(\mathcal{E} = Blv\) is usually quicker if applicable. Remember that the \(x\) in the flux expression represents an instantaneous position, while \(V\) in the EMF expression represents the constant velocity.
The average emf induced in a coil is 2 V when current is changed in 0.4 s
(A) from 5 A to 2 A and the self-inductance of the coil is 0.266 mH
(B) from 4 A to 4 A in the opposite direction, the self-inductance of the coil is 0.10 mH
View Solution
Step 1: Understanding the Concept:
This question deals with self-inductance, which is the property of a coil to induce an EMF in itself when the current flowing through it changes. The magnitude of this induced EMF is proportional to the rate of change of the current.
Step 2: Key Formula or Approach:
The average EMF (\(\mathcal{E}\)) induced in a coil due to self-inductance (\(L\)) is given by: \[ \mathcal{E} = -L \frac{\Delta I}{\Delta t} \]
where \(\Delta I\) is the change in current and \(\Delta t\) is the time interval over which the change occurs.
We are interested in the magnitude, so we use: \[ |\mathcal{E}| = L \left| \frac{\Delta I}{\Delta t} \right| \implies L = \frac{|\mathcal{E}| \cdot \Delta t}{|\Delta I|} \]
Step 3: Detailed Explanation:
Given common data:
Average induced EMF, \(|\mathcal{E}| = 2 \, V\).
Time interval, \(\Delta t = 0.4 \, s\).
Analysis of Statement (A):
The current changes from \(I_{initial} = 5 \, A\) to \(I_{final} = 2 \, A\).
The change in current is \(\Delta I = I_{final} - I_{initial} = 2 - 5 = -3 \, A\).
The magnitude of the change is \(|\Delta I| = 3 \, A\).
Now, let's calculate the self-inductance \(L\): \[ L = \frac{2 \, V \times 0.4 \, s}{3 \, A} = \frac{0.8}{3} \, H \approx 0.267 \, H \]
Converting to millihenries (mH): \(0.267 \, H = 267 \, mH\).
Statement (A) says the self-inductance is 0.266 mH. Our calculated value is approximately 267 mH. There is a factor of 1000 difference. Thus, statement (A) is incorrect.
Analysis of Statement (B):
The current changes from \(I_{initial} = 4 \, A\) to \(I_{final} = -4 \, A\) (4 A in the opposite direction).
The change in current is \(\Delta I = I_{final} - I_{initial} = -4 - 4 = -8 \, A\).
The magnitude of the change is \(|\Delta I| = 8 \, A\).
Now, let's calculate the self-inductance \(L\): \[ L = \frac{2 \, V \times 0.4 \, s}{8 \, A} = \frac{0.8}{8} \, H = 0.1 \, H \]
Converting to millihenries (mH): \(0.1 \, H = 100 \, mH\).
Statement (B) says the self-inductance is 0.10 mH. Our calculated value is 100 mH. Again, there is a factor of 1000 difference. Thus, statement (B) is incorrect.
Step 4: Final Answer:
Since both statements (A) and (B) are incorrect, the correct option is (D).
Quick Tip: Be extremely careful with SI prefixes like 'milli' (m, \(10^{-3}\)). A common mistake in exams is to misread or miscalculate units. Always perform calculations in base SI units (Volts, Amperes, Seconds, Henries) and then convert to the required prefix at the end to avoid errors.
An inductor of 500 mH is in series with a resistance and a variable capacitor connected to a source of frequency 0.4 kHz. The value of capacitance of the capacitor to get a maximum current will be
View Solution
Step 1: Understanding the Concept:
This question describes a series RLC circuit. The current in such a circuit is maximum when the circuit is in a state of resonance. Resonance occurs when the inductive reactance (\(X_L\)) becomes equal to the capacitive reactance (\(X_C\)), causing the total impedance of the circuit to be at its minimum value (equal to the resistance \(R\)).
Step 2: Key Formula or Approach:
The condition for resonance in a series RLC circuit is: \[ X_L = X_C \]
where \(X_L = 2\pi f L\) is the inductive reactance and \(X_C = \frac{1}{2\pi f C}\) is the capacitive reactance.
By equating these, we get the formula for the resonant frequency, or we can solve for the capacitance \(C\) needed for resonance at a given frequency \(f\). \[ 2\pi f L = \frac{1}{2\pi f C} \implies C = \frac{1}{(2\pi f)^2 L} = \frac{1}{4\pi^2 f^2 L} \]
Step 3: Detailed Explanation:
Given data:
Inductance, \(L = 500 \, mH = 500 \times 10^{-3} \, H = 0.5 \, H\).
Frequency, \(f = 0.4 \, kHz = 0.4 \times 10^3 \, Hz = 400 \, Hz\).
Calculation:
Substitute the values into the formula for capacitance at resonance: \[ C = \frac{1}{4\pi^2 f^2 L} \] \[ C = \frac{1}{4\pi^2 (400)^2 (0.5)} \] \[ C = \frac{1}{4\pi^2 (160000) (0.5)} \] \[ C = \frac{1}{2\pi^2 (160000)} = \frac{1}{320000 \pi^2} \, F \]
Using the approximation \(\pi^2 \approx 9.87\): \[ C \approx \frac{1}{320000 \times 9.87} = \frac{1}{3158400} \, F \] \[ C \approx 3.166 \times 10^{-7} \, F \]
To express this value in microfarads (µF), we multiply by \(10^6\): \[ C \approx 3.166 \times 10^{-7} \times 10^6 \, \mu F = 0.3166 \, \mu F \]
This value is approximately 0.32 µF.
Step 4: Final Answer:
The required capacitance to achieve maximum current (resonance) is approximately 0.32 µF.
Quick Tip: The condition for maximum current in a series RLC circuit is resonance. The key formula to remember is \(X_L = X_C\), which leads to the resonant frequency \(f_0 = \frac{1}{2\pi\sqrt{LC}}\). You can rearrange this formula to solve for L or C if the frequency is given.
A 12 V battery connected to a 6 \(\Omega\), 10 mH coil through a switch drives a constant current in the circuit. The switch is suddenly opened. Assuming that it took 1 ms to open the switch, the average emf induced across the coil would be
View Solution
Step 1: Understanding the Concept:
This problem involves the concept of self-induction in an inductor (coil). When the current through an inductor changes, it induces an electromotive force (EMF) that opposes this change. The magnitude of this induced EMF is proportional to the rate of change of the current.
Step 2: Key Formula or Approach:
The average EMF (\(\mathcal{E}\)) induced in a coil with self-inductance \(L\) is given by Faraday's law of induction: \[ \mathcal{E}_{avg} = -L \frac{\Delta I}{\Delta t} \]
where \(\Delta I\) is the change in current (\(I_{final} - I_{initial}\)) and \(\Delta t\) is the time taken for this change. We are interested in the magnitude of the EMF.
Step 3: Detailed Explanation:
Part 1: Calculate the initial steady current.
When the switch is closed for a long time, a constant (steady) current flows. In this DC steady state, the inductor behaves like a simple wire, and the current is determined by the battery voltage \(V\) and the resistance \(R\). \[ I_{initial} = \frac{V}{R} = \frac{12 \, V}{6 \, \Omega} = 2 \, A \]
Part 2: Determine the change in current.
When the switch is opened, the circuit is broken, and the current drops to zero. \[ I_{final} = 0 \, A \]
The change in current is: \[ \Delta I = I_{final} - I_{initial} = 0 \, A - 2 \, A = -2 \, A \]
Part 3: Calculate the average induced EMF.
Given data:
Inductance, \(L = 10 \, mH = 10 \times 10^{-3} \, H\).
Time interval, \(\Delta t = 1 \, ms = 1 \times 10^{-3} \, s\).
Using the formula for the magnitude of the average induced EMF: \[ |\mathcal{E}_{avg}| = \left| -L \frac{\Delta I}{\Delta t} \right| = L \left| \frac{\Delta I}{\Delta t} \right| \] \[ |\mathcal{E}_{avg}| = (10 \times 10^{-3} \, H) \times \left| \frac{-2 \, A}{1 \times 10^{-3} \, s} \right| \]
The \(10^{-3}\) terms in the numerator and denominator cancel out. \[ |\mathcal{E}_{avg}| = 10 \times 2 = 20 \, V \]
Step 4: Final Answer:
The average EMF induced across the coil would be 20 V.
Quick Tip: In a steady DC circuit, an inductor acts as a short circuit (its resistance is zero unless specified, here the coil itself has resistance). The current is simply given by \(I = V/R\). The induced EMF is only generated when the current is changing, such as when a switch is opened or closed.
For an ac source rated at 220 V, 50 Hz, which of the following statements is correct?
View Solution
Step 1: Understanding the Concept:
The rated voltage of an AC source (like household mains) is its Root Mean Square (RMS) value. We need to analyze the properties of this sinusoidal AC voltage, such as its peak and average values over a full cycle.
Step 2: Key Formula or Approach:
For a sinusoidal AC voltage:
- The RMS voltage is related to the peak voltage (\(V_0\)) by \(V_{rms} = \frac{V_0}{\sqrt{2}}\).
- The frequency \(f\) is the reciprocal of the time period \(T\), i.e., \(T = 1/f\).
- The average value of a sinusoidal function over a complete cycle is zero.
Step 3: Detailed Explanation:
Given data:
RMS voltage, \(V_{rms} = 220 \, V\).
Frequency, \(f = 50 \, Hz\).
The time period of the AC source is \(T = 1/f = 1/50 \, s\). The question asks for properties over this period, which is one full cycle.
Analysis of the options:
1. The peak value over a period of (1/50) s is 220 V.
The peak value is \(V_0 = V_{rms} \times \sqrt{2} = 220\sqrt{2}\) V. The given statement is incorrect.
2. The average value over a period of (1/50) s is 220 V.
The period of (1/50) s is one full cycle. The average value of a sine wave over a full cycle is zero. 220 V is the RMS value, not the average value. The statement is incorrect.
3. The average value over a period of (1/50) s is 0 V.
For any sinusoidal AC quantity (voltage or current), the waveform is symmetric about the time axis. The positive half-cycle has an area equal to the negative half-cycle. Therefore, the average value over one complete cycle is always zero. This statement is correct.
4. The average value over a period of (1/50) s is 220\(\sqrt{2}\) V.
This is the peak value, not the average value. The statement is incorrect.
Step 4: Final Answer:
The only correct statement is that the average value over a full period is 0 V.
Quick Tip: Always remember that the standard voltage rating for AC circuits is the RMS value. For a sine wave, the average value over a full cycle is 0, and the average value over a half cycle is \(\frac{2V_0}{\pi}\). Don't confuse RMS, peak, and average values.
Which of the following statements is not correct for electromagnetic induction?
View Solution
Step 1: Understanding the Concept:
This question tests the fundamental laws of electromagnetic induction: Faraday's Law and Lenz's Law. We need to identify the statement that incorrectly describes these principles.
Step 2: Detailed Explanation:
1. The magnitude of induced emf in a circuit is equal to the time rate of change of magnetic flux through the circuit.
This is a direct statement of Faraday's Law of Induction, \(|\mathcal{E}| = \left|\frac{d\Phi_B}{dt}\right|\). The EMF is proportional to the rate of change of flux. This statement is correct.
2. The magnitude of induced emf in a circuit is equal to the total change of magnetic flux through the circuit.
This statement claims \(|\mathcal{E}| = \left|\Delta\Phi_B \right|\). This is incorrect. The induced EMF depends on how quickly the flux changes (the rate, \(\Delta\Phi_B / \Delta t\)), not just the total change in flux. A large change in flux that happens very slowly will induce a very small EMF. This statement is not correct.
3. The induced emf can be increased by increasing the number of turns N of a closed coil.
For a coil with N turns, Faraday's Law is written as \(|\mathcal{E}| = N \left|\frac{d\Phi_B}{dt}\right|\). The total EMF is the sum of the EMFs induced in each turn. Therefore, increasing the number of turns \(N\) directly increases the total induced EMF. This statement is correct.
4. The polarity of induced emf is such that it tends to produce a current which opposes the change in magnetic flux that produced it.
This is a precise statement of Lenz's Law, which determines the direction of the induced current and the polarity of the induced EMF. This statement is correct.
Step 3: Final Answer:
The question asks for the statement that is not correct. Statement (2) is a factually incorrect description of electromagnetic induction.
Quick Tip: The key term in Faraday's Law is "rate of change." Many incorrect statements will omit the "rate" part and just mention the "change" in flux. Always look for the dependence on time (\(d/dt\) or \(\Delta/\Delta t\)).
Maxwell's displacement current is
View Solution
Step 1: Understanding the Concept:
Maxwell introduced the concept of displacement current to generalize Ampere's circuital law. He postulated that a changing electric field in a region of space produces a magnetic field, just as a conduction current does. This "effective" current arising from a time-varying electric field is called displacement current.
Step 2: Key Formula or Approach:
The displacement current \(I_D\) is defined as: \[ I_D = \varepsilon_0 \frac{d\Phi_E}{dt} \]
where \(\varepsilon_0\) is the permittivity of free space and \(\Phi_E\) is the electric flux. The term \(\frac{d\Phi_E}{dt}\) represents the rate of change of electric flux, which is caused by a changing electric field.
Step 3: Detailed Explanation:
Let's analyze the options:
1. due to flow of charges
The current due to the actual flow of charges (like electrons in a wire) is called conduction current. This is not displacement current. So, this is incorrect.
2. due to changing gravitational field
Gravitational fields are not related to electric or magnetic fields in the context of Maxwell's equations. This is incorrect.
3. due to changing electric field
As per the definition \(I_D = \varepsilon_0 \frac{d\Phi_E}{dt}\), a changing electric flux (which implies a changing electric field) is the source of the displacement current. This is the correct definition. A classic example is the space between the plates of a charging capacitor where the electric field changes with time, creating a displacement current.
4. \(\varepsilon_0\) times the rate of change of magnetic flux
The rate of change of magnetic flux, \(\frac{d\Phi_B}{dt}\), is related to the induced electric field (Faraday's Law of Induction), not the displacement current. This is incorrect.
Step 4: Final Answer:
Maxwell's displacement current is fundamentally due to a time-varying electric field.
Quick Tip: Remember the symmetry proposed by Maxwell: a changing magnetic field creates an electric field (Faraday's Law), and a changing electric field creates a magnetic field (Displacement Current in Ampere-Maxwell Law).
Match List-I with List-II

View Solution
Step 1: Understanding the Concept:
This question requires knowledge of the electromagnetic spectrum, which arranges different types of electromagnetic waves in order of their wavelength (or frequency). We need to match each type of wave with its approximate wavelength range.
Step 2: Detailed Explanation:
Let's recall the order of the EM spectrum from shortest to longest wavelength: Gamma rays, X-rays, Ultraviolet, Visible, Infrared, Microwaves, Radio waves.
(A) X-rays: These have very short wavelengths, shorter than ultraviolet light. The given range (III) 1 nm to \(10^{-3}\) nm (or 1 picometer) is the characteristic range for X-rays. So, (A) matches (III).
(B) Radio waves: These have the longest wavelengths in the electromagnetic spectrum. The range (IV) \(>\) 0.1 m correctly describes radio waves. So, (B) matches (IV).
(C) Infrared waves: These waves have wavelengths longer than visible red light (which is around 700 nm). The range given in (I) 1 mm to 700 nm is the accepted range for infrared radiation. So, (C) matches (I).
(D) Microwaves: These are located between infrared waves and radio waves. The range (II) 0.1 m to 1 mm fits the microwave region. So, (D) matches (II).
Step 3: Final Answer:
The correct matching is:
- (A) \(\rightarrow\) (III)
- (B) \(\rightarrow\) (IV)
- (C) \(\rightarrow\) (I)
- (D) \(\rightarrow\) (II)
This combination corresponds to option (D).
Quick Tip: Memorize the electromagnetic spectrum sequence using a mnemonic, for example: "Rich Men In Vegas Use X-ray Guns" (Radio, Microwaves, Infrared, Visible, Ultraviolet, X-rays, Gamma rays). This gives the order of decreasing wavelength and increasing frequency/energy.
The electric field E associated with a progressive electromagnetic wave is given by E = E\(_0\)sin(kx - \(\omega\)t). If B\(_0\) is the amplitude of the magnetic field associated with the wave, then
View Solution
Step 1: Understanding the Concept:
In an electromagnetic (EM) wave, the electric field (E) and magnetic field (B) are mutually perpendicular and also perpendicular to the direction of wave propagation. Their magnitudes are related by the speed of the wave.
Step 2: Key Formula or Approach:
1. For an EM wave propagating in vacuum, the ratio of the magnitudes of the electric field and magnetic field at any instant is equal to the speed of light, \(c\).
\[ \frac{E}{B} = c \]
This relationship also holds for their amplitudes:
\[ \frac{E_0}{B_0} = c \]
2. For any wave described by an equation of the form \(\sin(kx - \omega t)\), the speed of the wave (\(v\)) is given by the ratio of the angular frequency (\(\omega\)) to the wave number (\(k\)):
\[ v = \frac{\omega}{k} \]
For an electromagnetic wave in vacuum, this speed is \(c\).
Step 3: Detailed Explanation:
From the first principle, we have: \[ \frac{E_0}{B_0} = c \]
From the second principle, the speed of this EM wave is: \[ c = \frac{\omega}{k} \]
By substituting the expression for \(c\) into the first equation, we get the relationship between the amplitudes and the wave parameters: \[ \frac{E_0}{B_0} = \frac{\omega}{k} \]
Step 4: Final Answer:
The correct relationship is \(\frac{E_0}{B_0} = \frac{\omega}{k}\).
Quick Tip: A simple way to remember the core relationships for EM waves is \(E = cB\) and \(c = f\lambda\). Remembering that \(\omega = 2\pi f\) and \(k = 2\pi/\lambda\) allows you to quickly derive \(c = \omega/k\). Combining these gives the answer.
Which of the following statements are correct?
(A) All mirrors follow the laws of reflection.
(B) The angle between the ray of incidence and the plane surface of the mirror is equal to the angle between the plane surface of mirror and the ray of reflection for plane mirror
(C) the rays coming parallel to the principal axis will go after reflection through the focus of the curved mirror
(D) the rays coming to the pole of a curved mirror making an angle with axis will be reflected making the equal angle with the axis on the other side of the axis.
Choose the correct answer from the options given below:
View Solution
Step 1: Understanding the Concept:
This question assesses the understanding of the fundamental laws and principles of reflection as applied to plane and curved mirrors. We need to evaluate the correctness of each statement.
Step 2: Detailed Explanation:
(A) All mirrors follow the laws of reflection.
This is the fundamental principle of geometric optics for mirrors. The laws of reflection (angle of incidence equals angle of reflection; incident ray, reflected ray, and normal lie in the same plane) apply to any reflection, whether from a plane or a curved surface. This statement is correct.
(B) The angle between the ray of incidence and the plane surface of the mirror is equal to the angle between the plane surface of mirror and the ray of reflection for plane mirror.
(C) the rays coming parallel to the principal axis will go after reflection through the focus of the curved mirror.
This is a standard rule used in ray tracing. It is the definition of the principal focus for a concave mirror. For a convex mirror, parallel rays appear to diverge from the principal focus located behind the mirror. The wording "will go after reflection through the focus" is strictly true only for concave mirrors. However, it is often stated as a general property in introductory texts. This is a key principle for image formation. This statement is generally considered correct in the context of ray diagram rules.
(D) the rays coming to the pole of a curved mirror making an angle with axis will be reflected making the equal angle with the axis on the other side of the axis.
For any spherical mirror, the principal axis is normal to the mirror at the pole. Therefore, a ray incident at the pole will reflect such that the angle of incidence equals the angle of reflection, with the principal axis acting as the normal. This statement is correct.
Step 3: Final Answer:
Assuming the question prioritizes the formal rules and definitions used in ray optics, statements (A), (B), (C), and (D) represent these fundamental principles.
Quick Tip: Be careful with the precise wording of laws and definitions in physics. The laws of reflection are formally defined using the angle to the normal. While the grazing angles (to the surface) are also equal as a consequence, a question might test your knowledge of the formal definition.
Which of the following statement(s) is/are correct?
(A) The power of a lens is the ability of the lens to converge or diverge the incident rays.
(B) S.I unit of the power of a lens is dioptre while focal length is in centimetres
(C) For a lens of larger focal length, power is smaller
(D) In any combination of lenses, the power of combination is not algebraic addition of power of combined lenses
Choose the correct answer from the options given below:
View Solution
Step 1: Understanding the Concept:
This question tests the definition and properties of the power of a lens. Power is a measure of how much a lens bends light.
Step 2: Detailed Explanation:
(A) The power of a lens is the ability of the lens to converge or diverge the incident rays.
This is the correct qualitative definition of lens power. A lens with high power bends light rays more strongly than a lens with low power. This statement is correct.
(B) S.I unit of the power of a lens is dioptre while focal length is in centimetres.
The SI unit of power is indeed the dioptre (D). However, power is defined as the reciprocal of the focal length expressed in meters (\(P (in D) = 1 / f (in m)\)). The statement that the focal length is in centimetres for this definition is incorrect. This statement is incorrect.
(C) For a lens of larger focal length, power is smaller.
Since power \(P\) is inversely proportional to the focal length \(f\) (\(P = 1/f\)), a lens with a larger focal length will have a smaller power. This statement is correct.
(D) In any combination of lenses, the power of combination is not algebraic addition of power of combined lenses.
For thin lenses placed in contact, the power of the combination is the algebraic sum of the individual powers (\(P_{eq} = P_1 + P_2 + \dots\)). The statement claims it is *not* an algebraic addition, which is false for this common configuration. This statement is incorrect.
Step 3: Final Answer:
Only statements (A) and (C) are correct.
Quick Tip: The most common mistake related to lens power is the unit of focal length. Always remember that for the power to be in dioptres (the SI unit), the focal length MUST be in meters.
In an experiment with a convex lens, the length of an image is 1 cm, and the object length is 5 cm. If the object is placed at a distance of 40 cm from the lens, then the focal length of the lens is
View Solution
Step 1: Understanding the Concept:
This problem requires using the lens formula and the magnification formula for a convex lens. We can find the image distance using the magnification and then use the lens formula to calculate the focal length.
Step 2: Key Formula or Approach:
1. Magnification, \(m = \frac{height of image (h_i)}{height of object (h_o)} = \frac{image distance (v)}{object distance (u)}\).
2. Lens Formula: \(\frac{1}{f} = \frac{1}{v} - \frac{1}{u}\).
3. New Cartesian Sign Convention: Light travels from left to right. Distances measured against the incident light are negative. Distances in the direction of light are positive. Object distance \(u\) is negative.
Step 3: Detailed Explanation:
Given data:
Height of object, \(h_o = 5 \, cm\).
Height of image, \(h_i = 1 \, cm\).
Object distance, \(u = -40 \, cm\) (by sign convention).
Since the image is smaller than the object (\(h_i < h_o\)), the image formed by the convex lens must be real and inverted. Therefore, the image height should be taken as negative. \(h_i = -1 \, cm\).
Part 1: Calculate the image distance (v).
Using the magnification formula: \[ m = \frac{h_i}{h_o} = \frac{-1 \, cm}{5 \, cm} = -\frac{1}{5} \]
Also, \(m = \frac{v}{u}\). \[ -\frac{1}{5} = \frac{v}{-40 \, cm} \] \[ v = (-40 \, cm) \times \left(-\frac{1}{5}\right) = +8 \, cm \]
The positive sign for \(v\) confirms that a real image is formed on the opposite side of the lens.
Part 2: Calculate the focal length (f).
Using the lens formula: \[ \frac{1}{f} = \frac{1}{v} - \frac{1}{u} \] \[ \frac{1}{f} = \frac{1}{8} - \frac{1}{-40} = \frac{1}{8} + \frac{1}{40} \]
To add the fractions, find a common denominator, which is 40. \[ \frac{1}{f} = \frac{5}{40} + \frac{1}{40} = \frac{6}{40} = \frac{3}{20} \] \[ f = \frac{20}{3} \, cm \approx 6.67 \, cm \]
Step 4: Final Answer:
The focal length of the lens is 6.67 cm.
Quick Tip: Applying the sign convention correctly is crucial. For real images formed by a single convex lens, the image is inverted, so \(h_i\) is negative. This leads to a negative magnification \(m\), and the image distance \(v\) will be positive.
In a Young's double-slit experiment, two slits are 1.5 mm apart while the screen is 1.2 m away. When a light of wavelength 600 nm is incident on slits, the fringe width will be
View Solution
Step 1: Understanding the Concept:
This problem requires the direct application of the formula for fringe width in a Young's double-slit experiment (YDSE). The fringe width is the separation between consecutive bright fringes or consecutive dark fringes.
Step 2: Key Formula or Approach:
The fringe width (\(\beta\)) in a YDSE is given by the formula: \[ \beta = \frac{\lambda D}{d} \]
where \(\lambda\) is the wavelength of the light, \(D\) is the distance from the slits to the screen, and \(d\) is the distance between the two slits.
Step 3: Detailed Explanation:
Given data:
Slit separation, \(d = 1.5 \, mm = 1.5 \times 10^{-3} \, m\).
Screen distance, \(D = 1.2 \, m\).
Wavelength, \(\lambda = 600 \, nm = 600 \times 10^{-9} \, m = 6 \times 10^{-7} \, m\).
Calculation:
It is essential to use consistent units (SI units are recommended).
Substitute the values into the formula: \[ \beta = \frac{(6 \times 10^{-7} \, m) \times (1.2 \, m)}{1.5 \times 10^{-3} \, m} \] \[ \beta = \frac{7.2 \times 10^{-7}}{1.5 \times 10^{-3}} \, m \] \[ \beta = 4.8 \times 10^{-4} \, m \]
The options are in millimeters (mm). To convert from meters to millimeters, multiply by \(10^3\). \[ \beta = (4.8 \times 10^{-4}) \times 10^3 \, mm = 4.8 \times 10^{-1} \, mm = 0.48 \, mm \]
Step 4: Final Answer:
The fringe width will be 0.48 mm.
Quick Tip: In YDSE calculations, always convert all lengths (\(d, D, \lambda\)) to the same unit, preferably the base SI unit (meters), before plugging them into the formula. This minimizes the chance of unit conversion errors. Convert the final answer to the unit required by the options.
The critical angle of incidence \(i_c\) for a ray incident from a denser to rarer medium, is that angle for which
View Solution
Step 1: Understanding the Concept:
The critical angle is a specific angle of incidence that occurs only when light travels from a denser medium to a rarer medium. It is the boundary condition for the phenomenon of total internal reflection.
Step 2: Key Formula or Approach:
According to Snell's Law of refraction: \[ n_1 \sin \theta_1 = n_2 \sin \theta_2 \]
where \(n_1\) and \(n_2\) are the refractive indices of the first (denser) and second (rarer) media, and \(\theta_1\) and \(\theta_2\) are the angles of incidence and refraction, respectively. The critical angle (\(i_c\)) is the angle of incidence (\(\theta_1\)) for which the angle of refraction (\(\theta_2\)) is exactly 90°. At this point, the refracted ray grazes the boundary between the two media.
Step 3: Detailed Explanation:
When light travels from a denser medium (\(n_1\)) to a rarer medium (\(n_2\)), where \(n_1 > n_2\), as the angle of incidence \(\theta_1\) increases, the angle of refraction \(\theta_2\) also increases.
There exists a particular angle of incidence, called the critical angle \(i_c\), for which the angle of refraction becomes 90°.
Setting \(\theta_1 = i_c\) and \(\theta_2 = 90^\circ\) in Snell's Law: \[ n_1 \sin i_c = n_2 \sin 90^\circ \]
Since \(\sin 90^\circ = 1\), we get: \[ \sin i_c = \frac{n_2}{n_1} \]
If the angle of incidence is greater than the critical angle (\(\theta_1 > i_c\)), the light ray does not refract into the rarer medium at all; instead, it is completely reflected back into the denser medium. This phenomenon is called total internal reflection.
Therefore, the critical angle is defined as the angle of incidence that results in an angle of refraction of 90°. The other options are incorrect: the angle of reflection is always equal to the angle of incidence, so it would be \(i_c\), not 0° or 90°. An angle of refraction of 0° corresponds to normal incidence (\(\theta_1=0^\circ\)).
Step 4: Final Answer:
The critical angle is the angle of incidence for which the angle of refraction is 90°.
Quick Tip: Remember the two conditions for total internal reflection (TIR): 1. Light must travel from a denser medium to a rarer medium. 2. The angle of incidence in the denser medium must be greater than the critical angle. The critical angle itself is the "tipping point" where the refracted ray just skims the surface.
A polaroid sheet is rotated between two crossed polarizers. The intensity of transmitted light would be maximum, when the angle between the axes of the first polarizer and the polaroid sheet is
View Solution
Step 1: Understanding the Concept:
This problem involves Malus's Law, which describes the intensity of light transmitted through a series of polarizers. We have three polarizers: a first polarizer (P1), a middle polaroid sheet (P2), and a third polarizer (P3) which is crossed with the first.
Step 2: Key Formula or Approach:
Malus's Law states that if the angle between the transmission axes of two polarizers is \(\theta\), the intensity of the transmitted light \(I\) is related to the incident polarized light intensity \(I_{inc}\) by: \[ I = I_{inc} \cos^2\theta \]
Let's denote the angles of the transmission axes of P1, P2, and P3 with respect to some reference (e.g., the vertical) as \(\theta_1, \theta_2, \theta_3\).
Step 3: Detailed Explanation:
Let the initial unpolarized light have intensity \(I_0\).
The first polarizer (P1) polarizes the light, and its transmitted intensity is \(I_1 = I_0/2\). Let's set the axis of P1 to be at \(\theta_1 = 0\).
The third polarizer (P3) is "crossed" with the first one. This means their axes are perpendicular. So, \(\theta_3 = \pi/2\) (or 90°).
The middle polaroid sheet (P2) is rotated. Let its axis be at an angle \(\theta\) with respect to the first polarizer's axis. So, \(\theta_2 = \theta\).
Now, let's trace the intensity:
1. Intensity after P1: \(I_1 = I_0/2\).
2. Intensity after P2: The light incident on P2 has intensity \(I_1\) and is polarized at angle 0. The angle between P1 and P2 is \(\theta\). Using Malus's Law:
\[ I_2 = I_1 \cos^2(\theta) = \left(\frac{I_0}{2}\right) \cos^2(\theta) \]
3. Intensity after P3: The light incident on P3 has intensity \(I_2\) and is polarized at angle \(\theta\). The axis of P3 is at \(\pi/2\). The angle between P2 and P3 is \((\pi/2 - \theta)\). Using Malus's Law again:
\[ I_3 = I_2 \cos^2(\pi/2 - \theta) = I_2 \sin^2(\theta) \]
Substituting the expression for \(I_2\):
\[ I_3 = \left(\frac{I_0}{2}\right) \cos^2(\theta) \sin^2(\theta) \]
We want to find the angle \(\theta\) that maximizes this final intensity \(I_3\). We can use the trigonometric identity \(\sin(2\theta) = 2\sin\theta\cos\theta\). \[ I_3 = \frac{I_0}{2} (\sin\theta\cos\theta)^2 = \frac{I_0}{2} \left(\frac{\sin(2\theta)}{2}\right)^2 = \frac{I_0}{8} \sin^2(2\theta) \]
The intensity \(I_3\) will be maximum when \(\sin^2(2\theta)\) is maximum. The maximum value of \(\sin^2(2\theta)\) is 1. This occurs when: \[ \sin(2\theta) = \pm 1 \] \[ 2\theta = \frac{\pi}{2}, \frac{3\pi}{2}, \dots \] \[ \theta = \frac{\pi}{4}, \frac{3\pi}{4}, \dots \]
The angle given in the options is \(\pi/4\).
Step 4: Final Answer:
The transmitted intensity is maximum when the angle between the first polarizer and the middle polaroid is \(\pi/4\).
Quick Tip: For a system of three polarizers where the first and last are crossed, the maximum transmission always occurs when the middle polarizer is placed at 45° (\(\pi/4\) radians) to both of them. This is a standard result worth remembering.
Which of the following statements are correct?
(A) Total internal reflection occurs when a ray of light travels from a rarer transparent medium to a denser medium.
(B) In total internal reflection, the incident ray of light remains in the same medium after reflection.
(C) In total internal reflection, the angle of incidence inside the denser transparent medium is equal to the angle of reflection in the same medium.
(D) In total internal reflection inside a denser medium there is no angle of refraction
Choose the correct answer from the options given below:
View Solution
Step 1: Understanding the Concept:
This question tests the conditions and phenomena associated with Total Internal Reflection (TIR). We need to evaluate each statement for its correctness.
Step 2: Detailed Explanation:
(A) Total internal reflection occurs when a ray of light travels from a rarer transparent medium to a denser medium.
This is incorrect. A necessary condition for TIR is that the light must travel from a denser medium to a rarer medium. So, this statement is false.
(B) In total internal reflection, the incident ray of light remains in the same medium after reflection.
The term "reflection" itself implies that the ray bounces back into the original medium. In total internal reflection, the entire ray is reflected, so it certainly remains in the same (denser) medium. This statement is true.
(C) In total internal reflection, the angle of incidence inside the denser transparent medium is equal to the angle of reflection in the same medium.
Total internal reflection is still a reflection phenomenon. Therefore, it must obey the laws of reflection. The first law of reflection states that the angle of incidence is equal to the angle of reflection (\(i=r\)). This statement is true.
(D) In total internal reflection inside a denser medium there is no angle of refraction.
TIR occurs when the angle of incidence exceeds the critical angle. Under this condition, no light passes into the rarer medium, meaning there is no refracted ray. Consequently, there is no angle of refraction to be measured. This statement is true.
Step 3: Final Answer:
Statements (B), (C), and (D) are correct, while statement (A) is incorrect. The correct option is the one that includes (B), (C), and (D).
Quick Tip: Remember the two key conditions for TIR: 1) Denser to rarer medium. 2) Angle of incidence must be greater than the critical angle. Once TIR occurs, it's a reflection event, so all the standard laws of reflection apply.
If focal length of a concave lens is 50 cm, then the power of the lens would be
View Solution
Step 1: Understanding the Concept:
The power of a lens is a measure of its ability to converge or diverge light rays. It is defined as the reciprocal of the focal length of the lens. The sign convention for focal length is crucial.
Step 2: Key Formula or Approach:
The power \(P\) of a lens is given by: \[ P = \frac{1}{f} \]
where the focal length \(f\) must be expressed in meters for the power \(P\) to be in dioptres (D).
By sign convention, a concave lens (diverging lens) has a negative focal length.
Step 3: Detailed Explanation:
Given data:
Lens type: Concave lens.
Focal length magnitude = 50 cm.
Step 1: Apply sign convention.
For a concave lens, the focal length is negative.
So, \(f = -50 \, cm\).
Step 2: Convert focal length to meters.
\[ f = -50 \, cm = -0.5 \, m \]
Step 3: Calculate the power.
\[ P = \frac{1}{f} = \frac{1}{-0.5 \, m} = -2 \, D \]
Step 4: Final Answer:
The power of the concave lens is -2 D.
Quick Tip: Remember the sign conventions for lenses: - Concave (diverging) lens: Focal length is negative, Power is negative. - Convex (converging) lens: Focal length is positive, Power is positive. And always convert the focal length to meters before calculating power in dioptres.
The photoelectric current is directly proportional to the number of photo electrons emitted per second. This implies that
View Solution
Step 1: Understanding the Concept:
This question relates to the laws of the photoelectric effect. The intensity of light is related to the number of photons incident on a surface per unit area per unit time. The photoelectric current is due to the flow of emitted photoelectrons.
Step 2: Detailed Explanation:
In the quantum picture of light, the intensity of radiation is proportional to the number of photons incident per second. The photoelectric effect is a one-to-one interaction: one incident photon ejects one electron (provided the photon has enough energy, i.e., its frequency is above the threshold frequency).
Therefore:
- A higher intensity means more photons are hitting the surface per second.
- More incident photons will lead to more photoelectrons being ejected per second.
- More photoelectrons ejected per second means a larger flow of charge, which constitutes a larger photoelectric current.
This establishes a direct proportionality:
Intensity of incident radiation \(\propto\) Number of photons per second \(\propto\) Number of photoelectrons emitted per second \(\propto\) Photoelectric current.
Let's evaluate the options based on this understanding:
1. Incorrect. The number of photoelectrons depends on the number of photons (intensity), not the energy of each photon (frequency).
2. Incorrect. It's a direct proportionality, not inverse.
3. Correct. As explained above, the number of photoelectrons emitted per second is directly proportional to the intensity of the incident radiation.
4. Incorrect. There is a direct and fundamental relationship.
Step 3: Final Answer:
The photoelectric current being proportional to the number of photoelectrons emitted per second implies that this number is directly proportional to the intensity of the incident radiation.
Quick Tip: Remember the two key aspects of the photoelectric effect:
1. \(\textbf{Intensity}\) determines the \(\textbf{number}\) of photoelectrons (and thus the current).
2. \(\textbf{Frequency}\) determines the \(\textbf{maximum kinetic energy}\) of the photoelectrons.
This separation of roles is a cornerstone of the quantum explanation of the effect.
The de-Broglie wavelength associated with a ball of mass 150 g traveling at 30.0 m/s would be
View Solution
Step 1: Understanding the Concept:
This problem requires the calculation of the de-Broglie wavelength of a macroscopic object. The de-Broglie hypothesis states that all matter has wave-like properties, and the wavelength (\(\lambda\)) is inversely proportional to the momentum (\(p\)) of the object.
Step 2: Key Formula or Approach:
The de-Broglie wavelength (\(\lambda\)) is given by the formula: \[ \lambda = \frac{h}{p} = \frac{h}{mv} \]
where \(h\) is Planck's constant (\(6.626 \times 10^{-34} \, J\cdots\)), \(m\) is the mass of the object, and \(v\) is its velocity.
Step 3: Detailed Explanation:
Given data:
Mass, \(m = 150 \, g = 0.150 \, kg\) (It's crucial to convert to SI units).
Velocity, \(v = 30.0 \, m/s\).
Planck's constant, \(h = 6.626 \times 10^{-34} \, J\cdots\).
Calculation:
First, calculate the momentum \(p\): \[ p = mv = (0.150 \, kg) \times (30.0 \, m/s) = 4.5 \, kg\cdot m/s \]
Now, calculate the de-Broglie wavelength: \[ \lambda = \frac{h}{p} = \frac{6.626 \times 10^{-34} \, J\cdots}{4.5 \, kg\cdot m/s} \] \[ \lambda \approx 1.4724 \times 10^{-34} \, m \]
Rounding the result, we get \(1.47 \times 10^{-34} \, m\).
Step 4: Final Answer:
The de-Broglie wavelength of the ball is \(1.47 \times 10^{-34}\) m.
Quick Tip: For macroscopic objects (like a ball), the de-Broglie wavelength is extremely small, typically on the order of \(10^{-34}\) m. This is far too small to be measured, which is why we don't observe wave-like properties for everyday objects. Always convert mass to kilograms before calculation.
Which of the following statements are correct?
(A) A nucleus of mass number A has a radius R given by the expression R = R\(_0\)A\(^{1/3}\)
(B) Volume of nucleus is proportional to mass number A
(C) The density of nucleus increases with the radius of nucleus.
(D) Density of nuclear matter does not depend on its mass number A
Choose the correct answer from the options given below:
View Solution
Step 1: Understanding the Concept:
This question assesses the understanding of the basic properties of the atomic nucleus, specifically its size (radius), volume, and density, and how they relate to the mass number A.
Step 2: Detailed Explanation:
(A) A nucleus of mass number A has a radius R given by the expression R = R\(_0\)A\(^{1/3}\)
This is the standard empirical formula for the nuclear radius, where \(R_0\) is a constant approximately equal to 1.2 fm. This relationship is derived from experimental data and is a fundamental concept in nuclear physics. This statement is correct.
(B) Volume of nucleus is proportional to mass number A
Assuming the nucleus is spherical, its volume \(V\) is given by \(V = \frac{4}{3}\pi R^3\). Substituting the expression for radius from statement (A): \[ V = \frac{4}{3}\pi (R_0 A^{1/3})^3 = \frac{4}{3}\pi R_0^3 (A^{1/3})^3 = \left(\frac{4}{3}\pi R_0^3\right) A \]
Since \(\frac{4}{3}\pi R_0^3\) is a constant, the volume \(V\) is directly proportional to the mass number A (\(V \propto A\)). This statement is correct.
(C) The density of nucleus increases with the radius of nucleus.
Nuclear density (\(\rho\)) is defined as mass divided by volume (\(\rho = Mass/Volume\)).
The mass of the nucleus is approximately \(A \times m_p\), where \(m_p\) is the mass of a nucleon (proton/neutron).
The volume of the nucleus is \(V = \left(\frac{4}{3}\pi R_0^3\right) A\).
So, the density is: \[ \rho = \frac{A \cdot m_p}{\left(\frac{4}{3}\pi R_0^3\right) A} = \frac{m_p}{\frac{4}{3}\pi R_0^3} \]
As we can see, the mass number \(A\) cancels out. The density \(\rho\) is approximately constant for all nuclei, independent of their radius or mass number. Therefore, the statement that density increases with radius is incorrect.
(D) Density of nuclear matter does not depend on its mass number A
As derived above, the expression for nuclear density is independent of the mass number A. This remarkable property means that all atomic nuclei have roughly the same extremely high density. This statement is correct.
Step 3: Final Answer:
Statements (A), (B), and (D) are correct, while statement (C) is incorrect. The correct option is (C).
Quick Tip: A key takeaway from nuclear physics is the near-constant density of nuclear matter. This implies that nucleons are packed together like incompressible spheres. This concept directly leads to \(R \propto A^{1/3}\) and \(V \propto A\).
An electron in the ground state of a hydrogen atom absorbs 12.09 eV energy. The angular momentum of the electron increases by
View Solution
Step 1: Understanding the Concept:
This problem connects the energy level transitions in a hydrogen atom with the quantization of angular momentum as described by the Bohr model. We first need to identify the final energy level of the electron after absorbing the given energy, and then calculate the change in its angular momentum.
Step 2: Key Formula or Approach:
1. Energy of an electron in the \(n\)-th orbit of a hydrogen atom: \(E_n = -\frac{13.6}{n^2}\) eV.
2. Angular momentum of an electron in the \(n\)-th orbit: \(L_n = n \frac{h}{2\pi} = n\hbar\).
3. The change in energy is \(\Delta E = E_{final} - E_{initial}\).
4. The change in angular momentum is \(\Delta L = L_{final} - L_{initial}\).
Step 3: Detailed Explanation:
Part 1: Find the final energy level (n\(_f\)).
The electron is initially in the ground state, so its initial principal quantum number is \(n_i = 1\).
The initial energy is \(E_1 = -\frac{13.6}{1^2} = -13.6\) eV.
The electron absorbs 12.09 eV of energy.
The final energy of the electron is \(E_f = E_i + \Delta E = -13.6 \, eV + 12.09 \, eV = -1.51 \, eV\).
Now, we find the final quantum number \(n_f\) using the energy formula: \[ E_f = -\frac{13.6}{n_f^2} \] \[ -1.51 = -\frac{13.6}{n_f^2} \] \[ n_f^2 = \frac{13.6}{1.51} \approx 9 \] \[ n_f = 3 \]
So, the electron jumps from the n=1 state to the n=3 state.
Part 2: Calculate the change in angular momentum (\(\Delta L\)).
Initial angular momentum (\(n_i = 1\)): \[ L_i = n_i \frac{h}{2\pi} = 1 \cdot \frac{h}{2\pi} \]
Final angular momentum (\(n_f = 3\)): \[ L_f = n_f \frac{h}{2\pi} = 3 \cdot \frac{h}{2\pi} \]
The increase in angular momentum is: \[ \Delta L = L_f - L_i = 3\frac{h}{2\pi} - 1\frac{h}{2\pi} = 2\frac{h}{2\pi} \]
Step 4: Final Answer:
The angular momentum of the electron increases by 2(h/2\(\pi\)).
Quick Tip: It is helpful to memorize the energies of the first few levels of the hydrogen atom: E1 = -13.6 eV, E2 = -3.4 eV, E3 = -1.51 eV, E4 = -0.85 eV. This can save time in calculating the final state.
Which of the following statements are correct?
(A) The electrostatic repulsive force between the protons can be greater than the nuclear force to bind the nucleons together inside a nucleus.
(B) The repulsive electrostatic force between protons in smaller nuclei is much smaller than the nuclear force between nucleons inside a nucleus.
(C) The gravitational force between nucleons is much smaller than the nuclear force between the nucleons inside a nucleus.
(D) The binding energy per nucleon between nucleons is almost constant because the nuclear force is a long range force.
Choose the correct answer from the options given below:
View Solution
Step 1: Understanding the Concept:
This question probes the properties of the nuclear force (strong force) that holds the nucleus together, comparing it with other fundamental forces and relating it to nuclear stability and binding energy.
Step 2: Detailed Explanation:
(A) The electrostatic repulsive force between the protons can be greater than the nuclear force to bind the nucleons together inside a nucleus.
If the electrostatic repulsion were greater than the attractive nuclear force, the nucleus would fly apart. This statement describes the condition for instability in very large, proton-rich nuclei, leading to fission or decay. It is not a general condition for all nuclei. However, the statement implies this can happen, which is true for unstable heavy nuclei. Let's hold this. For a stable nucleus, the nuclear force must be stronger. The statement is ambiguously worded. Let's re-evaluate. The question asks for correct statements in general. For stable nuclei, this is false. For unstable ones, it is true. Let's see other options.
(B) The repulsive electrostatic force between protons in smaller nuclei is much smaller than the nuclear force between nucleons inside a nucleus.
The strong nuclear force is the strongest force in nature over short distances (within the nucleus). In small, stable nuclei (like Helium or Carbon), the attractive nuclear force overwhelmingly dominates the electrostatic repulsion between the few protons present. This is why these nuclei are very stable. This statement is correct.
(C) The gravitational force between nucleons is much smaller than the nuclear force between the nucleons inside a nucleus.
The gravitational force is by far the weakest of the four fundamental forces. At the nuclear scale, the gravitational attraction between nucleons is completely negligible compared to both the strong nuclear force and the electrostatic force. For instance, the strong force is about \(10^{38}\) times stronger than gravity. This statement is correct.
(D) The binding energy per nucleon between nucleons is almost constant because the nuclear force is a long range force.
The binding energy per nucleon is almost constant for most nuclei (saturation property), but this is precisely because the nuclear force is a short-range force. A nucleon only interacts with its immediate neighbours. If the force were long-range, every nucleon would interact with every other nucleon, and the binding energy per nucleon would keep increasing with the mass number A. Thus, the reason given is incorrect. This statement is incorrect.
Re-evaluating (A): Given that (B) and (C) are definitively correct and (D) is definitively incorrect, let's look at the options. Option (2) contains (B) and (C). This suggests that statement (A) should be considered incorrect in the general context. For a nucleus to exist, even transiently, the nuclear force must be dominant. The electrostatic repulsion becoming greater is the cause of its disintegration. So, in the context of a bound system, (A) is false.
Step 3: Final Answer:
Statements (B) and (C) are correct descriptions of the forces within a nucleus. Statement (D) provides an incorrect reason for a correct observation. Statement (A) describes a condition for nuclear instability, not a general property of bound nuclei. Thus, (B) and (C) are the correct statements.
Quick Tip: Key properties of the nuclear force to remember:
1. \(\textbf{Strongest force at short distances.}\)
2. \(\textbf{Short-range}\) (acts only over a few femtometers).
3. \(\textbf{Charge-independent}\) (acts equally between p-p, n-n, and p-n).
4. \(\textbf{Saturation property}\) (a nucleon interacts only with its nearest neighbors), which leads to nearly constant binding energy per nucleon.
Below given are some statements about electronic devices:
(A) Diodes can be used for rectifying an ac voltage.
(B) For semiconductors, band gap energy E\(_g\) > 3 eV.
(C) By changing the external applied voltage, junction barriers can be changed.
(D) p-n junction is the 'key' to all semiconductor devices.
Choose the correct answer from the options given below:
View Solution
Step 1: Understanding the Concept:
This question tests fundamental knowledge about semiconductors and p-n junction diodes. We need to evaluate each statement's validity.
Step 2: Detailed Explanation:
(A) Diodes can be used for rectifying an ac voltage.
A diode allows current to flow easily in one direction (forward bias) and offers very high resistance in the opposite direction (reverse bias). This unidirectional property is exactly what is needed to convert alternating current (AC) into direct current (DC), a process called rectification. This statement is correct.
(B) For semiconductors, band gap energy E\(_g\) > 3 eV.
Materials are classified based on their band gap energy (\(E_g\)). For semiconductors, the band gap is relatively small, typically in the range of 0.2 eV to 3 eV (e.g., Silicon \(E_g \approx 1.1\) eV, Germanium \(E_g \approx 0.7\) eV). Materials with a band gap \(E_g > 3\) eV are generally classified as insulators (e.g., Diamond \(E_g \approx 5.5\) eV). Therefore, this statement is incorrect.
(C) By changing the external applied voltage, junction barriers can be changed.
A p-n junction has a potential barrier (or depletion region). Applying an external voltage (biasing) alters this barrier. A forward bias voltage reduces the barrier height, allowing current to flow. A reverse bias voltage increases the barrier height, blocking current flow. Thus, the junction barrier can be controlled by an external voltage. This statement is correct.
(D) p-n junction is the 'key' to all semiconductor devices.
The p-n junction is the fundamental building block for a vast majority of semiconductor devices, including diodes, transistors (which can be seen as two back-to-back p-n junctions), solar cells, LEDs, etc. Its ability to control current flow is central to modern electronics. This statement is generally considered correct in the context of introductory electronics.
Step 3: Final Answer:
Statements (A), (C), and (D) are correct, while (B) is incorrect. The correct option is (D).
Quick Tip: Memorize the approximate band gap energies for conductors, semiconductors, and insulators.
- \(\textbf{Conductors:}\) Overlapping bands (\(E_g \approx 0\)).
- \(\textbf{Semiconductors:}\) Small band gap (\(E_g < 3\) eV).
- \(\textbf{Insulators:}\) Large band gap (\(E_g > 3\) eV).
This is a common point of confusion tested in exams.
On connecting a device X in a series circuit with a battery and a resistor, a current passes through the circuit. On reversing the polarity of the battery, the current in the circuit drops to almost zero. The device X may be a
View Solution
Step 1: Understanding the Concept:
The question describes a device that exhibits unidirectional current flow. It allows current to pass when connected to a battery in one polarity but blocks the current when the polarity is reversed. This is the defining characteristic of a rectifying device.
Step 2: Detailed Explanation:
Let's analyze the behavior of each device listed:
1. p-type semiconductor / 2. n-type semiconductor:
Both p-type and n-type semiconductors are simply resistive materials. They obey Ohm's law and conduct current regardless of the direction of the applied voltage. Reversing the battery polarity would simply reverse the direction of the current, but its magnitude would remain the same. They do not exhibit the described behavior.
3. p-n junction diode:
A p-n junction diode is specifically designed to allow current to flow in only one direction. When it is forward-biased (p-side connected to the positive terminal of the battery), it has very low resistance and a significant current flows. When it is reverse-biased (p-side connected to the negative terminal), it has very high resistance and the current drops to almost zero. This perfectly matches the description in the problem.
4. capacitor:
When a capacitor is connected to a DC battery, a transient charging current flows for a short time until the capacitor is fully charged. After that, the current stops (becomes zero). If the polarity is reversed, a transient discharging and then recharging current will flow in the opposite direction, eventually stopping again. It does not allow a steady current in one direction and block it in the other.
Step 3: Final Answer:
The device X, which allows current in one direction but blocks it in the reverse direction, is a p-n junction diode.
Quick Tip: The key property described is "rectification" or "unidirectional conduction." Whenever a question mentions that a device's behavior depends on the polarity of the connection (allowing current one way but not the other), a diode should be the first thing that comes to mind.
Which of the following statement(s) is/are true for p-type semiconductors?
(A) Holes are minority carriers and pentavalent atoms are the dopants.
(B) Electrons are majority carriers and trivalent atoms are the dopants.
(C) Holes are majority carriers and trivalent atoms are the dopants.
(D) Electrons are minority carriers and pentavalent atoms are the dopants.
Choose the correct answer from the options given below:
View Solution
Step 1: Understanding the Concept:
This question tests the definitions of p-type semiconductors, including the type of dopant atom used and the nature of the majority and minority charge carriers.
Step 2: Detailed Explanation:
A p-type semiconductor is created by doping an intrinsic semiconductor (like silicon or germanium, which are Group 14 elements) with trivalent impurity atoms (Group 13, e.g., Boron, Aluminium, Gallium).
- A trivalent atom has three valence electrons. When it replaces a silicon atom (which has four), it forms covalent bonds with three neighboring silicon atoms, leaving one bond incomplete. This creates a vacancy for an electron, which is known as a hole.
- This process introduces a large number of holes into the crystal lattice. These holes act as positive charge carriers.
- Therefore, in a p-type semiconductor, holes are the majority charge carriers.
- Thermally generated electrons still exist, but they are far fewer in number than the holes. Thus, electrons are the minority charge carriers.
Let's evaluate the statements:
(A) Holes are minority carriers (Incorrect) and pentavalent atoms are the dopants (Incorrect).
(B) Electrons are majority carriers (Incorrect) and trivalent atoms are the dopants (Correct). The first part is wrong.
(C) Holes are majority carriers (Correct) and trivalent atoms are the dopants (Correct). This statement is entirely true.
(D) Electrons are minority carriers (Correct) and pentavalent atoms are the dopants (Incorrect). Pentavalent dopants create n-type semiconductors.
Step 3: Final Answer:
The options are: 1. (B) only, 2. (C) only, 3. (C) and (D) only, 4. (A) and (C) only.
The best fit is option 2.
Let's re-examine statement (D) one more time in case it is intended to be paired with something else. Pentavalent dopants are for n-type semiconductors, where electrons are majority carriers and holes are minority. Statement D mixes these up. It is definitively incorrect. So only (C) is correct.
Quick Tip: Use mnemonics to remember dopant types:
- \(\textbf{P}\)-type is for \(\textbf{P}\)ositive holes as majority carriers. It is doped with trivalent impurities (e.g. B, Al, Ga from Group 13).
- \(\textbf{N}\)-type is for \(\textbf{N}\)egative electrons as majority carriers. It is doped with pe\(\textbf{N}\)tavalent impurities (e.g. P, As, Sb from Group 15).
In the following nuclear reaction, \(^1_0n + ^{235}_{92}U \rightarrow ^{140}_{54}Xe + ^b_aSr + 2(^1_0n)\) we have
View Solution
Step 1: Understanding the Concept:
This problem involves balancing a nuclear reaction. In any nuclear reaction, two quantities must be conserved:
1. The total mass number (A), which is the superscript.
2. The total atomic number (Z), which is the subscript (representing charge).
Step 2: Detailed Explanation:
The given nuclear reaction is: \[ ^1_0n + ^{235}_{92}U \rightarrow ^{140}_{54}Xe + ^b_aSr + 2(^1_0n) \]
Conservation of Mass Number (Superscript):
The sum of the mass numbers on the left side must equal the sum on the right side.
Left side: \(1 + 235 = 236\)
Right side: \(140 + b + 2(1) = 142 + b\)
Equating the two sides: \[ 236 = 142 + b \] \[ b = 236 - 142 = 94 \]
Conservation of Atomic Number (Subscript):
The sum of the atomic numbers on the left side must equal the sum on the right side.
Left side: \(0 + 92 = 92\)
Right side: \(54 + a + 2(0) = 54 + a\)
Equating the two sides: \[ 92 = 54 + a \] \[ a = 92 - 54 = 38 \]
Step 3: Final Answer:
We have found that the atomic number \(a = 38\) and the mass number \(b = 94\). This corresponds to option (A).
Quick Tip: When balancing nuclear equations, always balance the superscripts (mass numbers) and subscripts (atomic numbers) separately. It's a simple bookkeeping process. Be careful with coefficients, like the "2" in front of the neutron on the product side.
A proton accelerated through a potential difference of V volts has a de-Broglie wavelength \(\lambda\) associated with it. In order to get the same wavelength associated with an \(\alpha\)-particle, the required accelerating potential is
View Solution
Step 1: Understanding the Concept:
This problem connects the de-Broglie wavelength of a charged particle with the kinetic energy it gains when accelerated through a potential difference. We need to find the potential required for an alpha particle to have the same wavelength as a proton accelerated through potential V.
Step 2: Key Formula or Approach:
1. The kinetic energy (KE) gained by a particle with charge \(q\) accelerated through a potential difference \(V_{acc}\) is \(KE = qV_{acc}\).
2. The de-Broglie wavelength (\(\lambda\)) is related to momentum (\(p\)) by \(\lambda = h/p\).
3. Momentum is related to kinetic energy by \(p = \sqrt{2m(KE)}\).
Combining these, we get an expression for the de-Broglie wavelength in terms of the accelerating potential: \[ \lambda = \frac{h}{\sqrt{2m(KE)}} = \frac{h}{\sqrt{2mqV_{acc}}} \]
Step 3: Detailed Explanation:
Let's denote the properties of the proton with subscript 'p' and the alpha particle with subscript '\(\alpha\)'.
- Proton: mass \(m_p\), charge \(q_p = e\).
- Alpha particle (\(^{4}_{2}He\)): mass \(m_\alpha \approx 4m_p\), charge \(q_\alpha = 2e\).
For the proton:
It is accelerated through potential \(V\). Its wavelength is: \[ \lambda_p = \frac{h}{\sqrt{2m_p q_p V}} = \frac{h}{\sqrt{2m_p e V}} \]
For the alpha particle:
Let it be accelerated through a potential \(V_\alpha\). Its wavelength is: \[ \lambda_\alpha = \frac{h}{\sqrt{2m_\alpha q_\alpha V_\alpha}} = \frac{h}{\sqrt{2(4m_p)(2e)V_\alpha}} = \frac{h}{\sqrt{16m_p e V_\alpha}} \]
Equating the wavelengths:
We are given that we want the same wavelength, so \(\lambda_\alpha = \lambda_p\). \[ \frac{h}{\sqrt{16m_p e V_\alpha}} = \frac{h}{\sqrt{2m_p e V}} \]
Squaring both sides (and canceling \(h\)): \[ \frac{1}{16m_p e V_\alpha} = \frac{1}{2m_p e V} \]
The terms \(m_p\) and \(e\) cancel out. \[ \frac{1}{16V_\alpha} = \frac{1}{2V} \]
Rearranging to solve for \(V_\alpha\): \[ 16V_\alpha = 2V \] \[ V_\alpha = \frac{2V}{16} = \frac{V}{8} \]
Step 4: Final Answer:
The required accelerating potential for the alpha particle is V/8.
Quick Tip: From the formula \(\lambda = \frac{h}{\sqrt{2mqV_{acc}}}\), we can see that for a constant wavelength \(\lambda\), the product \(mqV_{acc}\) must be constant. So, \(m_p q_p V_p = m_\alpha q_\alpha V_\alpha\). Plugging in \(m_\alpha = 4m_p\) and \(q_\alpha = 2q_p\), we get \(m_p q_p V = (4m_p)(2q_p)V_\alpha\), which simplifies to \(V = 8V_\alpha\) or \(V_\alpha = V/8\). This ratio method is very fast for comparison problems.



Comments