Jasmine Grover Content Strategy Manager
Content Strategy Manager
Calculus is the branch of mathematics that does the study of a function’s rate of change. It’s also known as infinitesimal calculus or "the calculus of infinitesimals". It has an important role in various fields such as Engineering, Science, Navigation, and so on. Generally, we use calculus to get a proper solution by developing a Mathematical model. Calculus can be of two different kinds, like integral calculus and differential calculus. Sir Isaac Newton from England and Gottfried Wilhelm Leibniz from Germany were the first ones to independently develop Calculus in the 17th century. However, vector calculus is a topic that we are usually not aware of. Vector Calculus, which is also known as vector analysis, basically deals with the differentiation and integration of vector field, especially in the three-dimensional Euclidean space.
| Table of Content |
Key Terms: Vector, Calculus, Integral, Differential, Function, Vector Analysis, Fundamental Theorem, Circulation-Curl Form, Flux – Divergence Form, Line Integral, Divergence Function, Gradient Function
What is Vector Calculus?
[Click Here for Sample Questions]
Vector calculus can also be called vector analysis. It deals with the integration and the differentiation of the vector field in the Euclidean Space of three dimensions. Vector fields show the distribution of a particular vector to each point in the space’s subset. In the Euclidean space, a domain’s vector field is shown as a vector-valued function that does the comparison of the real number’s n-tuple to each point on the domain.
Vector analysis is the kind of analysis where we deal with quantities having both the magnitude and the direction. Vector calculus is also shown to work in two different forms of integrals known as the line integrals and the surface integrals.

Vector Calculus
Line Integral
[Click Here for Sample Questions]
A line integral of a vector field is some function’s integral along a curve. In other words, it can be defined as an integral in which the function is calculated along with a curve when it is about to be integrated. The integration can be done with some specific type of functions with vector value along with a curve. For example, one can also integrate a scalar-valued function along a curve. Sometimes, a line integral can also be called a curve integral, curvilinear integral or path integral.
Read More: Differentiation and Integration Formula
Surface Integral
[Click Here for Sample Questions]
A surface integral is an abstraction of various integrals to the integrations over surfaces. It means that the double integral is related to the line integral. For a particular surface, a scalar field or a vector field can be integrated over a surface.
Vector Calculus Formulas
[Click Here for Sample Questions]
Various important formulas for vector calculus are given below:
We use the fundamental theorems to get the following
F(x, y, z) = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k
- Fundamental Theorem of Line Integral
If F = ∇f and curve C has endpoints A and B, so
∫c F. dr= f(B) − f(A)
- Circulation – Curl Form
Green’s Theorem: ∫∫D (∂Q /∂x) – (∂P/ ∂y)dA = C F· dr
Stokes’ Theorem: ∫∫D ∇ × F · n dσ = ![]() C F· dr, where C is the edge curve of S
C F· dr, where C is the edge curve of S
- Flux – Divergence Form
Green’s Theorem: ∫∫D ∇· F dA = ![]() C F · n ds
C F · n ds
Divergence Theorem: ∫∫∫D ∇· F dV =![]() S F · n dσ
S F · n dσ
Read More: Fundamental Theorem of Calculus
Vector Calculus Identities
The list of identities of Vector Calculus are given below for different functions such as Divergence function, Gradient function, Curl function, Degree Two functions and Laplacian function.
- Gradient Function
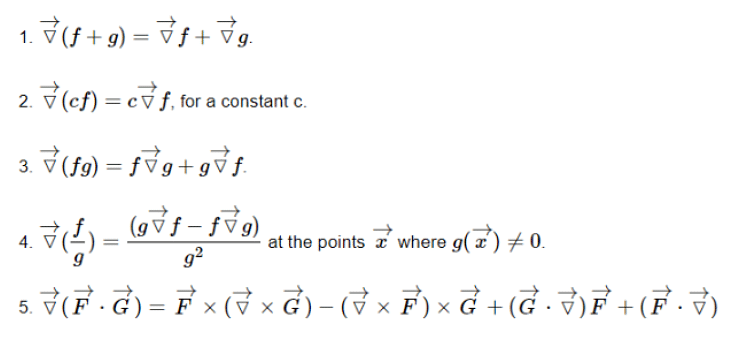
- Divergence Function

- Curl Function

- Laplacian Function

- Degree Two Function

Applications of Vector Calculus
[Click Here for Sample Questions]
Vector Calculus has an important role in various fields such as
- It is used for heat transfer
- It is used for Navigation
- It is used in Sports
- Useful in Three-dimensional Geometry
- It is used in Partial differential equation
Read More: Differential Equations
Things to Remember
- Vector Calculus can also be called vector analysis.
- It deals with the integration and the differentiation of the vector field in the Euclidean Space of three dimensions.
- Vector fields show the distribution of a particular vector to each point in the space’s subset.
- In the Euclidean space, a domain’s vector field is shown as a vector-valued function that does the comparison of the real number’s n-tuple to each point on the domain.
- A line integral of a vector field is some function’s integral along a curve.
- A surface integral is an abstraction of various integrals to the integrations over surfaces.
- The Fundamental Theorem of Line Integral states that If F = ∇f and curve C has endpoints A and B, then ∫c F. dr = f(B) − f(A).
Sample Questions
Ques. What is the difference between Differential Calculus and Vector Calculus? (3 Marks)
Ans. Differential calculus is the part of the calculus that's related to the derivations of the functions. Calculus is commonly supposed to be differential calculus and integral calculus. The differential is just a part of the derivations, whereas the integral is a part of the integrals and the integration.
The variables that are involved in both the differential and the integral calculation are generally taken as the real or the complex figures, although the distinct notions of vector, vector spaces, etc. don't actually enter in. The vector calculus, on the other hand, is related to the aspects of the vector spaces which you treat by using differential and/ or integral calculus. In particular, there are three types of vector quantities that you can make by using the derivations that are gradient, divergence, and curl. There are theorems too which relate some unique integrals of these quantities to the other integrals.
Ques. What is the difference between surface integral and double integral? (3 Marks)
Ans. A Surface integral is an integral where the function is integrated or estimated along a surface that lies on advanced-dimensional space. We can just take it over a field of 2D shape as a surface integral is taken on a shape bedded in an advanced terminational region and a double integral can be only taken on a two-dimensional space. That means like a circle or a square or any other shape with an inside, we can just take it over a region of 2D space.
Ques. What is the difference between volume integral and triple integral? (3 Marks)
Ans. A Volume integral is an integral where the function is integrated or estimated along a volume that lies on an advanced-dimensional region. However, in triple integral, it can only integrate a function that's bounded by the 3D area with respect to infinitesimal volume. Triple integral is a distinct kind of volume integral.
Ques. Find the normal to the curve x2 + y2 = 2x + 2y that is parallel to the line y + x = 0. (5 Marks)
Ans. The Given Data is
The equation of the curve is x2 + y2 = 2x + 2y
And The equation of a line is y + x = 0
Now, we have to differentiate the curve equation with respect to x.
d/dx(x2+y2) = d/dx(2x+2y)
2x + 2ydy/dx = 2 + 2dy/dx
(x+y)dy/dx = 1+ dy/dx
ydy/dx − dy/dx = 1−x
dy/dx = (1−x)/(y−1)
The slope of the curve here is m = (1−x)/(y−1)
let the slope of normal line be m1 = −1/m = −1/(1−x)/(y−1) = (1−y)/(1−x)
Rewrite the given equation of line as:
y + x = 0
y = −x
Now, We have the slope of line:
m2 = −1
As We know that two parallel lines have equal slopes.
m1 = m2
(1−y)/(1−x) = −1
1−y = −1 + x
y = 2−x
Putting this value in the curve equation. We have,
x2 + (2−x)2 = 2x + 2(2−x)
x2 + 4 + x2 − 4x = 2x + 4 − 2x
2x2 − 4x = 0
2x (x−2) = 0
x = 0,2
Therefore, the point is:
(0,2) and (2,0)
At a point (0,2) the slope of normal is,
m1 = (1 − y)/(1 − x)
= 1 − 2/1 − 0
= −1
Therefore, the slope of normal to the given curve is
m1 = −1
Ques. What will the slope of the tangent line at the point (1, -1) for the curve xy3 – yx3 = 6? (3 Marks)
Ans. Let us consider that y = f(x) as the equation of the curve, so the slope of the tangent at any point (x1, y1) will be
m = \([\frac{dy}{dx}]_{(x_1,y_1)}\)
The curve is given as xy3 – yx3 = 6
By partial differentiating the equation of the curve with respect to x, we get that
3xy2\(\frac{dy}{dx}\) + y3 – 3x2y – x3 \(\frac{dy}{dx}\) = 0
\(\frac{dy}{dx}\)(3xy2 – x3) = 3x2y – y3
\(\frac{dy}{dx}\) = \(\frac{3x^2y - y^2}{3xy^2 - x^3}\)
\(\frac{dy}{dx}\) = \(\frac{y(3x^2 - y^2)}{x(3y^2 - x^3)}\)
Therefore, the slope (m), i.e, dx/dy of the tangent at (1, -1) will be as m = -1
Ques. How are vectors used in real life? (3 Marks)
Ans. Vectors have numerous real-life uses, including situations involving force or haste. For instance, look at the forces acting on a watercraft crossing a stream. The watercraft's engine generates a force in one direction, and the drift of the stream generates a force in another direction. Both forces are vectors.
Ques. What is the major difference between line integral and single integral? (3 Marks)
Ans. A line integral can be described as an integral where the function is integrated or estimated along a curve that lies on advanced-dimensional space therefore it's also called path integral. We all know about simple integral, in geometric outlook, we find the area under a curve in the 2D region also in the line integral we will find an area under the curve which in advanced dimension ( higher than 2), in physical view, we find total work done by both lines and normal integral but the difference is work will be estimated along the path or curve given.
Read More:



Comments