Namrata Das Exams Prep Master
Exams Prep Master
The angle between two vectors (i.e., a and b) is found by using the formula θ = cos-1 [ (a · b) / (|a| |b|) ]. If the two vectors are equal, then b = a is substituted in this formula to get θ = cos-1 [ (a · a) / (|a| |a|) ] = cos-1 (|a|2/|a|2) = cos-11 = 0°. A vector is essentially a specific item with a defined length. The Magnitude is the name of this length. Additionally, vectors have a direction. There are two formulas for calculating the angle between two vectors: one in terms of dot product and the other in terms of the cross product.
NCERT Solutions for: Class 12 Mathematics Chapter 10 Vector Algebra
| Table of Content |
Key Terms: Vector, Angle, Two vectors, Dot Product, Cross Product, Magnitude, Angles between two Vectors, vector erection
What is Vector?
[Click Here for Sample Questions]
A vector is a physical quantity that has both magnitude and direction, that is, a number and a direction. Vectors can be oriented in different directions and form different angles. This angle exists between two vectors and is what defines vector erection.
Vectors are used to simulate the flow of air around an aircraft wing, fluid through a pipe, and a variety of other situations.
Read more:
What is the Angle formed by Two Vectors?
[Click Here for Previous year Questions]
The angle formed by the intersection of two vectors' tails is defined as the angle between them. If the vectors are not merged tail-to-tail, we must join them from tail to tail by parallel shifting one of the vectors. Here are a few examples of how to calculate the angle between two vectors.
The angle between Two Vectors:
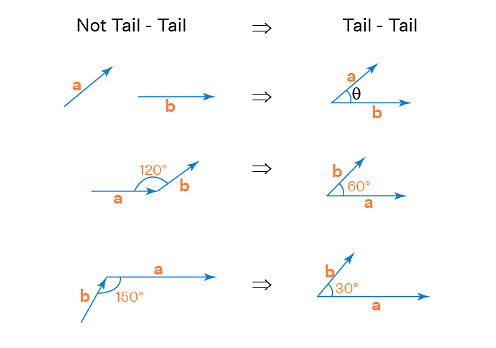
The angle formed when the head of a vector is joined to the tail of another vector is NOT the angle between vectors. Instead, one of them should be shifted in the same direction or parallel to itself, so that the tails of vectors are joined to measure the angle.
Read more: Real-Valued Functions
Angle Formula
[Click Here for Sample Questions]
This is the formula for calculating the angle between two vectors, a and b.
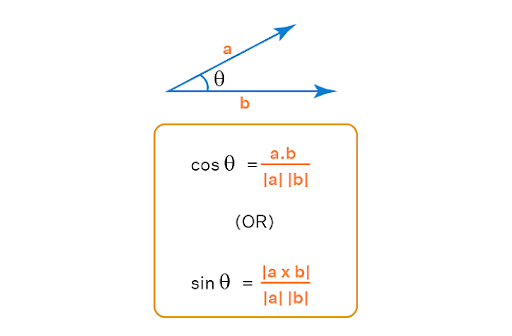
Angle Formula
- The examples below will demonstrate how to use the equation to find theta (θ), or the angle between two vectors.
- If the two vectors are supposed to be a and b, the resulting dot is defined as a.b. Suppose these two vectors are separated by an angle. To determine the angle measurement, we will use the following formula:
- We are familiar with the dot product:
\(\overrightarrow{a}. \overrightarrow{b}\) = |\(\overrightarrow{a}\)| |\(\overrightarrow{b}\)| cosθ
Now, the formula for the angle between two vectors is:
θ = cos -1 \(\frac{\overrightarrow{a}. \overrightarrow{b}}{|\overrightarrow{a}|| \overrightarrow{b}|}\)
Where theta is the angle formed by the a and b vectors.
Read more: Addition of Vectors
Solved Examples of Angle Between Two Vectors Formula
[Click Here for Previous year Questions]
Q.1: Find the angle formed by the vectors 3i + 4j - k and 2i - j + k.
Solution: To let,
a = 3i + 4j – k and
b = 2i – j + k
The dot product is defined as follows:
a .b = (3i + 4j – k).(2i – j + k)
= (3)(2) + (4)(-1) + (-1)(1)
= 6-4-1
= 1
Thus, a .b = 1
Vectors have the following magnitude:
\(\overrightarrow{a}\)| = \(\sqrt{(3^2 + 4^2 + (-1)^2)}\) = \(\sqrt{26}\) = 5.09
And,
|\(\overrightarrow{b}\)| = \(\sqrt{(2^2 +(-1)^2 + 1^2)}\) = \(\sqrt{6}\) = 2.45
The angle formed by the two vectors is
θ = cos -1 \(\frac{\overrightarrow{a}. \overrightarrow{b}}{|\overrightarrow{a}|| \overrightarrow{b}|}\)
θ = cos -1 \(\frac{1}{(5.09)(2.45)}\)
θ = cos -1 \(\frac{1}{12.47}\)
θ = cos -1 (0.0802)
= 85.39o
Read more: Negative of a vector
Dot Product Angle Between Two Vectors
[Click Here for Sample Questions]
A b = |a| |b| cos θ, according to the definition of the dot product. Let's solve it for cos θ.
Both sides are divided by |a| |b|.
cos θ = (a · b) / (|a| |b|)
θ = cos-1 [ (a · b) / (|a| |b|) ]
This is the formula for calculating the angle between two vectors using the dot product (scalar product).
Using the Cross Product to Determine the Angle Between Two Vectors
[Click Here for Previous year Questions]
a × b = |a| |b| sin θ according to the definition of the cross product. To solve this, consider the magnitude on both sides. Then we have
|a × b| = |a| |b| sin θ |^n|.
We know that n is a unit vector, so its magnitude is 1. So
|a × b| = |a| |b| sin θ
Both sides are divided by |a| |b|.
sin θ = |a × b| / (|a| |b|)
θ = sin-1 [ |a × b| / (|a| |b|) ]
This is the cross product formula for calculating the angle between two vectors (vector product).
Read more:
Things to Remember
- The angle created at the intersection of two vectors' tails is the angle between the two vectors
- The product of a vector and its magnitude is a unit vector.
- The zero vector has the coordinates (0,0,0) and is typically represented by 0 with an arrow (→)at the top or simply 0.
- According to Commutative Law, the sequence of addition is irrelevant, so a + b = b + a.
- A unit vector is a vector with a magnitude of one (i.e., one unit).
- It should be noted that the angle formed by two vectors will always be between 0° and 180°.
Previous Year Questions
- If i^+j^,j^+k^,i^+k^ are the position vectors of the vertices of a triangle…?
- If a→,b→,c→ are mutually perpendicular vectors having magnitudes 1, 2, 3 respectively…?
- The edges of a parallelopiped are of unit length and are parallel to non-coplanar unit vector a^,b^,c^ such that…? [JEE Advanced 2008]
- If the volume of a parallelepiped whose coterminous edges are…? [JEE Main 2020]
- The position of a particle is given by r=i^+2j^−k^ and its linear momentum… [KEAM]
- From a point A with position vector p(i^+j^+k^), AB and AC are drawn perpendicular to the lines… [JEE Main 2018]
- A constant power is supplied to a rotating disc. The relationship between the angular velocity… [CBSE Class 12]
- Two vectors are given by A→=3i^+j^+3k^ and… [JKCET 2007]
- Let a→,b→, c→ be non-coplanar unit vectors equally inclined to one another at an acute angle… [BITSAT 2017]
- If a is a unit vector, then… [TS EAMCET 2017]
- Two vectors A=3 and B=4 are perpendiculars… [UPSEE 2016]
Sample Questions
Ques 1: Find the angle between two vectors 5i – j + k and i + j – k. (3 marks)
Ans: Let,
\(\overrightarrow{a}\)= 5i – j + k and \(\overrightarrow{b}\)= i + j – k
The dot product is defined as
\(\overrightarrow{a}. \overrightarrow{b}\)= (5i – j + k)(i + j – k)
\(\overrightarrow{a}. \overrightarrow{b}\)= (5)(1) + (-1)(1) + (1)(-1)
\(\overrightarrow{a}. \overrightarrow{b}\)= 5-1-1
\(\overrightarrow{a}. \overrightarrow{b}\)= 3
Ques 2: Find the angle between the two vectors 5i + 5j - k and 3i - 2j + k. (3 marks)
Ans: Let, a = 5i + 5j – k and b = 3i – 2j + k
So, the dot product is,
a.b = (5i + 5j – k).(3i – 2j + k)
= (5)(3) + (5)(2) + (-1)(1)
= 15 + 10 - 1
= 24
Ques 3: In what way does the Triangle Law of Vector Addition work? (2 marks)
Ans: The magnitude and direction of the resultant vector are represented by the third side of the triangle when two vectors are represented as two sides of a triangle with the same order of magnitude and direction.
To obtain, R, which is the sum of vectors\(\overrightarrow{A}\) and \(\overrightarrow{B}\)with the same order of magnitude and direction.
As a result, the Resultant vector is given by,
\(\overrightarrow{R} = \overrightarrow{A} + \overrightarrow{B}\)
Ques 4: What are the Properties of Dot Product? (2 marks)
Ans: If u, v, and w are vectors and c is a scalar then:
u · v = v · u
u · (v + w) = u · v + u · w
0 · v = 0
v · v = || v || 2
(cu) · v = c(u · v) = u · (cv)
Ques 5: If u = –i + 3j, v = 7i – 4j and w = 2i + j then find (3u) · (v + w). (3 marks)
Ans:
| Find 3u 3u = 3(–i + 3j) 3u = –3i + 9j | Find v + w v + w = (7i – 4j) + (2i + j) v + w = (7 + 2) i + (–4 + 1) j v + w = 9i – 3j |
Ques 6: Compute the angle between two vectors p and q, where p x q = 1 / 3i + 1 / 4j. (3 marks)
Ans: |a| = |b| = 1
Where,
| a x b | = √ ( (1 / 3)^2 + ( 1 / 4)^2) = 1 / 5
Put the given values in the above formula, we get
| a x b | = |a| |b| sin θ
1 / 5 = (1) (1) sin θ
θ = sin-1 (1/ 5)
θ = 30º
Ques 7: Find the Angle between the Given Two Vectors 4i + 5j – k and 2i – j + k. (3 marks)
Ans: Let, a = 4i + 5j – k and b = 2i – j + k
So, the dot product is,
a.b = (4i + 5j – k).(2i – j + k)
= (4)(2) + (5)(-1) + (-1)(1)
= 8 - 5 - 1
= 2
Ques 8: What is the angle formed by two vectors, a and b, such that |a b| = |a b|? (3 marks)
Ans: It is assumed that |a b| = |axb|.
According to the definitions of dot product and cross product,x
Since is a unit vector with a magnitude of one.
|a| |b| sin θ = |a| |b| cos θ
sin θ = cos θ
This occurs only when θ = 45°.
Therefore, When the dot product and cross product are equal, the angle between the two vectors is = 45°
Ques 9: What is the angle between two vectors a and b if |a| = 3, |b| = 2/3, and their cross product is a unit vector? (3 marks)
Ans: Given that the cross product of a and b is a unit vector, |axb| = 1.
Using the cross product formula, calculate the angle between two vectors:
θ = sin-1 [ |a × b| / (|a| |b|) ]
= sin-1 (1/ (3 × √2/3))
= sin-1 (1/√2)
= 45°
Hence, The required angle is 45°.
Ques 10: In 2D, how do I compute the angle between two vectors? (2 marks)
Ans: To compute the angle between two vectors in 2D space, use the following formula:
- Determine the vectors' dot product.
- Divide the dot product by the magnitude of the first vector
- Divide the result from the magnitude of the second vector.
For Latest Updates on Upcoming Board Exams, Click Here:https://t.me/class_10_12_board_updates
Do Check Out:



Comments