Symmetric Matrix: Transpose of a Matrix, Skew Symmetric Matrix

In simple words “a square matrix which is equal to its transpose is called a symmetric matrix”. Generally we can say , if A = A^T  then A is a symmetric matrix. Here A is the matrix and A^T is the transpose of the matrix A.

Note: A square matrix is a matrix having an equal number of rows and columns.

Keyterms: Transpose of a Matrix, Skew Symmetric Matrix, Row matrix, Column Matrix, Diagonal Matrix, Identity Matrix, Scalar Matrix, Communicative Law

---

Symmetric Matrix

[Click Here for Sample Questions]

Here we can clearly see that the given matrix is a square matrix of order 2. On transposing the given matrix the resultant matrix on the right has its rows and columns interchanged. Clearly these two matrices are not equal, and hence not symmetric. Now let us take another example and find if the transposed matrix is the same as the given matrix.

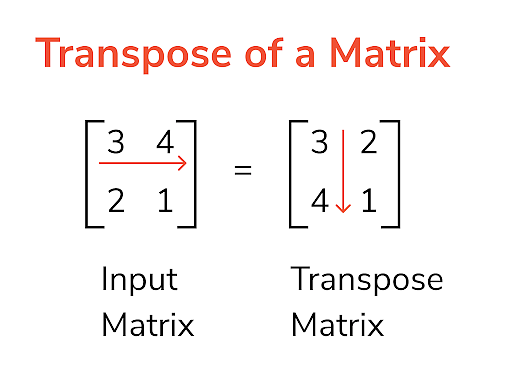
So here it is clear that both the matrix and its transpose are equal. Hence these matrices are symmetric.

Read Also: Matrix Addition

---

Properties of Symmetric Matrix

[Click Here for Previou Year Questions]

• A symmetric matrix is always a square matrix.
• If A and B are symmetric matrices then (A+B) and (A-B) are also symmetric.
• Inverse of a symmetric matrix is also symmetric.
• Scalar multiple of a symmetric matrix is also symmetric.
• If two matrices A and B follow the commutative property i.e. AB=BA, then AB and BA are also symmetric.
• If A is a symmetric matrix, then for any integer n, the matrix An will always be symmetric.

If  \(A = \begin{bmatrix} 3 & 2 & 5 \\ 2 & 5 & 4 \\ 5 & 4 & 7 \end{bmatrix}\) , then  \(A^T = \begin{bmatrix} 3 & 2 & 5 \\ 2 & 5 & 4 \\ 5 & 4 & 7 \end{bmatrix}\)

There are two basic theorems related to symmetric matrices

Theorem 1: For any square matrix A+A^T is symmetric and A-A^T is skew symmetric.

Let B= A+AT , So B^T=(A+A^T)^T = A^T+(A^T)^T =A^T+A = B.

This implies that A+A^T is a symmetric matrix.

Similarly let C=A-A^T,

So C^T=(A-A^T)^T=A^T-A=-(C).

This implies that A-A^T is a skew symmetric matrix.

Note: A is a skew symmetric matrix if A^T= – (A).

Theorem 2: Any square matrix can be expressed as the sum of a skew symmetric matrix and a symmetric matrix. To find the sum of a symmetric and skew symmetric matrix, we use this formula:

Let B be a square matrix. Then,

B = (1/2) × (B + B^T) + (1/2 ) × (B - B^T). Here, B^T is the transpose of the square matrix B.

If B + B^T is a symmetric matrix, then (1/2) × (B + B^T) is also a symmetric matrix.

If B - B^T is a skew symmetric matrix, then (1/2 ) × (B - B^T) is also a skew symmetric matrix.

Thus, any square matrix can be expressed as the sum of a skew symmetric matrix and a symmetric matrix.

Now let us understand the application of these concepts through this example from NCERT.

Example: Express the matrix B = \(\begin{bmatrix} 2 & -1 & -4 \\[0.3em] -1 & 3 & 4 \\[0.3em] 1 & -2 & -3 \end{bmatrix}\) as the sum of a symmetric and a skew symmetric matrix.

Solution: Here

\(B' = \begin{bmatrix} 2 & -1 & 1 \\[0.3em] -2 & 3 & -2 \\[0.3em] -4 & 4 & -3 \end{bmatrix}\)

Let  \(P = \frac{1}{2}(B + B') =\frac{1}{2} \begin{bmatrix} 4 & -3 & -3 \\ -3 & 6 & 2 \\ -3 & 2 & -6 \end{bmatrix} = \begin{bmatrix} 2 & \frac{-3}{2} & \frac{-3}{2} \\ \frac{-3}{2} & 3 & 1 \\ \frac {-3}{2} & 1 & -3 \end{bmatrix}\)               

Now \(P' = \begin{bmatrix} 2 & \frac{-3}{2} & \frac{-3}{2} \\ \frac{-3}{2} & 3 & 1 \\ \frac {-3}{2} & 1 & -3 \end{bmatrix} = P\)

Thus \(P =\frac{1}{2} (B + B') \) is a symmetric matrix.

Also, let

\(Q = \frac{1}{2}(B - B') = \frac{1}{2} \begin{bmatrix} 0 & -1 & -5 \\ 1 & 0 & 6 \\ 5 & -6 & 0 \end{bmatrix} = \begin{bmatrix} 0 & \frac{-1}{2} & \frac{-5}{2} \\ \frac{1}{2} & 0 & 3 \\ \frac{5}{2} & -3 & 0 \end{bmatrix}\)

Then, Q’ = \(\begin{bmatrix} 0 & \frac{1}{2} & \frac{5}{2} \\ \frac{-1}{2} & 0 & -3 \\ \frac{-5}{2} & 3 & 0 \end{bmatrix}\) = – Q

Thus,  \(Q = \frac{1}{2}(B - B') \) is a skew symmetric matrix.

Now,  \(P + Q = \begin{bmatrix} 2 & \frac{-3}{2} & \frac{-3}{2} \\ \frac{-3}{2} & 3 & 1 \\ \frac {-3}{2} & 1 & -3 \end{bmatrix} + \begin{bmatrix} 0 & \frac{-1}{2} & \frac{-5}{2} \\ \frac{1}{2} & 0 & 3 \\ \frac{5}{2} & -3 & 0 \end{bmatrix} = \begin{bmatrix} 2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3 \end{bmatrix} = B\)

Thus, B is represented as the sum of a symmetric and a skew symmetric matrix.

The video below explains this:

Matrices Detailed Video Explanation:

Also Read:

---

Things to Remember

• A matrix is an ordered rectangular array of numbers or functions which are called as the entries of a matrix.
• A matrix having m rows and n columns is said to be a ‘m by n’ matrix.
• A square matrix is a matrix whose rows and columns are equal,i.e. m=n.
• Different types of matrices are row matrix, Column Matrix, Diagonal Matrix, Identity Matrix and Scalar Matrix.
• Two matrices are said to be equal if the number of rows and columns in both matrices are the same and each element of one matrix is equal to the corresponding element of the other matrix.
• Addition of matrices follows the commutative law,associative law,existence of additive identity and existence of additive inverse.
• Multiplication of matrices follows all the above rules except the Commutative Law.
• A rectangular matrix does not have an inverse matrix .
• Inverse of a matrix,if it exists,is unique.

---

Previous Year Questions

1. If O(A) = 2 \times 3, O (B) = 3 \times 2O(A)=2×3,O(B)=3×2, and O(C) = 3 \times 3O(C)=3×3, which one of the following is not defined….[KCET 2006]
2. If A=​1−11​212​324​​ then =(A2−5A)A−1=..[BCECE 2018]
3. If P and Q are symmetric matrices of the same order then PQ - QP is..[KCET 2019]
4. If A and B are square matrices of the same order such that..[KCET 2009]
5. If 3A + 4B' =[70​−106​1731​] and 2B - 3A−14−5​180−7​​ then B =...[KCET 2019]
6. A−B is equal to...[KCET 2016]
7. If A = [cosα−sinα​sinαcosα​] , then AA' =…..[KCET 2018]
8. If A is 3×4 matrix and B is a matrix such that A'B and BA' are both defined. Then B is of the type...[KCET 2014]
9. If x[−34​]+y[43​]=[10−5​], then...[JKCET 2007]
10. If A=[31​−4−1​], then (A-A') is equal to (where, A' is transpose of matrix A)...[JKCET 2013]
11. Let A be a square matrix and AT is its transpose, then A+AT is….​[JKCET 2007]
12. Let M and N be two 3×3 matrices such that MN=NM. Further, if M=N2 and M2=N4, then...[JEE ADVANCED 2014]
13. If A is a square matrix such that A2 = A , then (I−A)3+A is equal to….[AMUEEE 2010]
14. If [αγ​β−α​] is to be square root of the two rowed unit matrix, then α , β and γ should statisfy the relation...[AMUEEE 2016]
15. If A and B are two square matrices such that AB= A and BA = B , then..[AMUEEE 2016]
16. Let ω be a complex cube root of unity with 0ω=0 and P = [Pii​] be an n×n matrix with pij​=ωi+j Then, P2=0 when n =[JEE ADVANCED 2013]
17. If A and B are square matrices of order 3 such that det A = 1 andB=−1, then det(−10AB)=?..[JKCET 2010]