Content Writer | Journalism Graduate | Updated 3+ months ago

CUET PG B.Ed. Mathematics Question Paper 2024 is available here for download. NTA conducted CUET PG B.Ed. Mathematics paper 2024 on from March 27 in Shift 3. CUET PG Question Paper 2024 is based on objective-type questions (MCQs). According to latest exam pattern, candidates get 105 minutes to solve 75 MCQs in CUET PG 2024 B.Ed. Mathematics question paper.

CUET PG B.Ed. Mathematics Question Paper 2024 PDF Download

CUET PG B.Ed Mathematics Question Paper 2024 with Answer Key	Download	Check Solutions

B.Ed. Mathematics 2024 Questions with Solutions

Question 1:

Which of the following is a singleton set?

{x: |x| = 5, x is a natural number}
{x: |x| = 7, x is an integer}
{x: x^2 + 5x + 1 = 0, x is a natural number}
{x: x^2 = 5, x is a natural number}

Correct Answer: 1. {x: |x| = 5, x is a natural number}

View Solution

Option 1: |x| = 5 is satisfied by x = 5, which belongs to natural numbers. The set contains exactly one element: {5}, making it a singleton set.
Option 2: |x| = 7 is satisfied by x = 7 and x = -7. The set contains two elements, so it is not a singleton.
Option 3: Solving x^2 + 5x + 1 = 0 gives irrational roots, which are not natural numbers. The set is empty.
Option 4: Solving x^2 = 5 gives x = ±sqrt(5), which are not natural numbers. The set is empty.

Conclusion: The only singleton set is {x: |x| = 5, x is a natural number}, containing exactly one element: {5}.

Question 2:

Let R be a relation defined by R = {(a, b): a >= b, a, b are real numbers}. Then R is:

an equivalence relation
reflexive, transitive but not symmetric
symmetric, transitive but not reflexive
only reflexive

Correct Answer: 2. Reflexive, transitive but not symmetric

View Solution

Reflexive: For any a, a >= a is true. Hence, (a, a) is in R, making R reflexive.
Symmetric: If (a, b) is in R, it implies a >= b. However, b >= a is not guaranteed unless a = b. Hence, R is not symmetric.
Transitive: If (a, b) is in R and (b, c) is in R, then a >= b and b >= c. From this, a >= c, so R is transitive.
Equivalence Relation: Since R is not symmetric, it is not an equivalence relation.

Conclusion: The relation R is reflexive, transitive but not symmetric.

Question 3:

The function f(x) = cos(x), x is a real number, is:

an even function
an odd function
neither even nor odd
a power function

Correct Answer: 1. An even function

View Solution

Even Function: For f(x) = cos(x), f(-x) = cos(-x). Since cos(-x) = cos(x), the function is even.
Odd Function: For f(x) = cos(x), f(-x) = cos(-x) is not equal to -cos(x). Hence, it is not odd.
Neither Even Nor Odd: Since the function satisfies the condition of being even, it cannot be classified as neither.
Power Function: A power function has the form f(x) = x^n. The function f(x) = cos(x) does not fit this form.

Conclusion: The function f(x) = cos(x) is an even function.

Question 4:

The number ((1 + i)^n) / ((1 - i)^(n - 2)) is equal to:

2i^(n + 3)
2i^(n - 3)
4i^(n + 2)
4i^(n + 4)

Correct Answer: 1. 2i^(n + 3)

View Solution

Step 1: Express 1 + i and 1 - i in polar form. The modulus of 1 + i is sqrt(2) and its argument is π/4. Thus, 1 + i = sqrt(2) * e^(iπ/4). Similarly, 1 - i = sqrt(2) * e^(-iπ/4).
Step 2: Substitute the polar forms into the given expression: ((1 + i)^n) / ((1 - i)^(n - 2)) = ((sqrt(2) * e^(iπ/4))^n) / ((sqrt(2) * e^(-iπ/4))^(n - 2)).
Step 3: Simplify the modulus: ((sqrt(2))^n) / ((sqrt(2))^(n - 2)) = 2.
Step 4: Simplify the argument: e^(i * n * π/4) * e^(i * (n - 2) * π/4) = e^(i * (2n - 2) * π/4).
Step 5: Combine the results: The expression becomes 2 * e^(i * (2n - 2) * π/4), which simplifies to 2i^(n + 3).

Conclusion: The given expression simplifies to 2i^(n + 3).

Question 5:

Solution of |x^2 - 10| <= 6 is:

(2, 4)
(-4, -2)
(-4, -2) U (2, 4)
[-4, -2] U [2, 4]

Correct Answer: 4. [-4, -2] U [2, 4]

View Solution

Step 1: Rewrite the inequality: |x^2 - 10| <= 6 becomes -6 <= x^2 - 10 <= 6.
Step 2: Solve for x^2: Adding 10 throughout, 4 <= x^2 <= 16.
Step 3: Solve for x: Taking square roots, -4 <= x <= -2 or 2 <= x <= 4.
Step 4: Write the solution in interval notation: The solution is [-4, -2] U [2, 4].

Conclusion: The solution of the inequality is [-4, -2] U [2, 4].

Question 6:

If A is an orthogonal matrix, then:

|A| = 0
|A| = ±1
|A| = ±2
|A| = ±3

Correct Answer: 2. |A| = ±1

View Solution

An orthogonal matrix \( A \) satisfies \( A^T A = I \), where \( A^T \) is the transpose of \( A \), and \( I \) is the identity matrix.
Taking the determinant: det(\( A^T A \)) = det(\( I \)).
Using determinant properties: det(\( A^T A \)) = det(\( A^T \)) * det(\( A \)). Since det(\( A^T \)) = det(\( A \)), det(\( A \))² = 1.
Solving gives det(\( A \)) = ±1.

Conclusion: If \( A \) is an orthogonal matrix, its determinant is ±1.

Question 7:

If α, β are roots of the equation ax^2 + bx + c = 0, then the equation whose roots are 2α + 3β and 3α + 2β is:

a²x² + 5acx + 6c² + bc = 0
a²x² + 5bcx + 6b² + bc = 0
a²x² + 6abx + 5b² + ac = 0
a²x² + 5abx + 6b² + ac = 0

Correct Answer: 4. a²x² + 5abx + 6b² + ac = 0

View Solution

Sum of roots: S = 5(α + β). Using α + β = -b/a, S = -5b/a.
Product of roots: P = (2α + 3β)(3α + 2β) = 6α² + 15αβ + 6β². Substitute α² + β² and simplify to get P = 6b²/a² + 3c/a.
Quadratic equation: The equation is a²x² - S * ax + P = 0. Substitute values to get a²x² + 5abx + 6b² + ac = 0.

Conclusion: The required equation is a²x² + 5abx + 6b² + ac = 0.

Question 8:

12 persons are to be arranged on a round table. If two particular persons among them are not to sit side by side, the number of arrangements is:

9 × (10!)
2 × (10!)
8 × (45!)
10!

Correct Answer: 1. 9 × (10!)

View Solution

Total arrangements without restrictions: For 12 people seated at a round table, the total arrangements are (12-1)! = 11!.
Restricted arrangement: If two specific persons must sit together, treat them as one unit. This gives (11-1)! × 2! = 10! × 2.
Valid arrangements: Subtract restricted arrangements from total arrangements: 11! - 10! × 2 = 10! × (11 - 2) = 10! × 9.

Conclusion: The number of arrangements where the two persons do not sit side by side is 9 × (10!).

Question 9:

The coefficient of \(x^2\) in the expansion of \((1 + 4x + x^2)^{1/2}\) is:

-3
-2
-3/2
2

Correct Answer: 3. -3/2

View Solution

Step 1: Use the binomial theorem to expand \( (1 + 4x + x^2)^{1/2} \).
Step 2: Identify terms contributing to \(x^2\) for \(k = 1\) and \(k = 2\).
Step 3: Combine contributions: The total coefficient of \(x^2\) is \(-3/2\).

Conclusion: The coefficient of \(x^2\) in the expansion is \(-3/2\).

Question 10:

If \((a^(n+1) + b^(n+1)) / (a^n + b^n)\) is the Arithmetic Mean between \(a\) and \(b\), then \(n\) is equal to:

0
-1
1
2

Correct Answer: 1. 0

View Solution

Step 1: Use the given formula and simplify: Multiply both sides by \(2(a^n + b^n)\).
Step 2: Expand and simplify terms to isolate \(n\).
Step 3: Solve for \(n\): The solution is \(n = 0\).

Conclusion: The value of \(n\) is 0.

Question 11:

Domain of the function \(f(x) = \sqrt{\log_3(\sin x)}\) is:

2nπ + π/2, n ∈ ℕ
nπ + π/2, n ∈ ℕ
2nπ - π/2, n ∈ ℕ
nπ - π/2, n ∈ ℕ

Correct Answer: 1. 2nπ + π/2, n ∈ ℕ

View Solution

The function \(f(x) = \sqrt{\log_3(\sin x)}\) is defined when \(\log_3(\sin x) ≥ 0\) and \(\sin x > 0\).
For \(\log_3(\sin x) ≥ 0\), \(\sin x = 1\), which occurs at \(x = 2nπ + π/2, n ∈ ℕ\).

Conclusion: The domain of the function is \(x = 2nπ + π/2, n ∈ ℕ\).

Question 12:

Evaluate \(\lim_{x \to \frac{\pi}{4}} \frac{\sqrt{2} \cos x - 1}{\cot x - 1}\):

1
1/2
1/√2
1/(2√2)

Correct Answer: 2. 1/2

View Solution

The limit is given by \(\lim_{x \to \frac{\pi}{4}} \frac{\sqrt{2} \cos x - 1}{\cot x - 1}\).
Expand the numerator and denominator near \(x = \frac{\pi}{4}\), using small angle approximations.
Simplify and evaluate the limit: The value is \(1/2\).

Conclusion: The value of the limit is \(1/2\).

Question 13:

Which of the following are true?

(A) \(d/dx (\sin x) = \cos x, ∀ x ∈ ℝ\)

(B) \(d/dx (\cos x) = -\sin x, ∀ x ∈ ℝ\)

(D) \(d/dx (\sec x) = \sec x \tan x, x ∈ ℝ - {(2n+1)π / 2, n ∈ ℤ}\)

Choose the correct answer from the options given below:

(A), (B), (C) only
(A), (B), (C), (D)
(A), (D), (C) only
(C), (B), (D) only

Correct Answer: 2. (A), (B), (C), (D)

View Solution

(A): The derivative of \(\sin x\) is \(\cos x\), valid for all \(x ∈ ℝ\).
(B): The derivative of \(\cos x\) is \(-\sin x\), valid for all \(x ∈ ℝ\).
(C): The derivative of \(\tan x\) is \(\sec^2 x\), valid except where \(\tan x\) is undefined at \(x = (2n+1)π / 2, n ∈ ℤ\).
(D): The derivative of \(\sec x\) is \(\sec x \tan x\), valid except at \(x = (2n+1)π / 2, n ∈ ℤ\).

Conclusion: All statements (A), (B), (C), and (D) are correct.

Question 14:

Which of the following are true?

(A) \(\int \csc x \cot x \, dx = -\csc x + C\)

(B) \(\int dx / \sqrt{x^2 - a^2} = \log |x + \sqrt{x^2 - a^2}| + C\)

(D) \(\int dx / \sqrt{a^2 - x^2} = \sin^{-1} (x/a) + C \, \text{(equivalent form: -\cos^{-1} (x/a) + C)}\)

Choose the correct answer from the options given below:

(A), (C), (D) only
(A), (B), (C) only
(B), (A), (D) only
(C), (B), (D) only

Correct Answer: 1. (A), (C), (D) only

View Solution

(A): \(\int \csc x \cot x \, dx = -\csc x + C\). Correct.
(B): \(\int dx / \sqrt{x^2 - a^2}\) differs from the given form. Incorrect.
(C): \(\int \tan x \, dx = \log |\sec x| + C \, \text{(equivalently, } -\log |\cos x| + C\text{)}.\) Correct.
(D): \(\int dx / \sqrt{a^2 - x^2} = \sin^{-1} (x/a) + C \, \text{(equivalently, } -\cos^{-1} (x/a) + C\text{)}.\) Correct.

Conclusion: The correct statements are (A), (C), and (D).

Question 15:

Which of the following are true?

(A) The equation of a circle with center (h, k) and radius r is \((x - h)^2 + (y - k)^2 = r^2\).

(B) The equation of a parabola with focus at (a, 0), a > 0, and directrix \(x = -a\) is \(y^2 = 4ax\).

(D) The length of the latus rectum of the ellipse \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) is \(\frac{2b^2}{a}\).

Choose the correct answer from the options given below:

(A), (B), (C) only
(A), (B), (D) only
(A), (D), (C) only
(C), (B), (D), (A)

Correct Answer: 2. (A), (B), (D) only

View Solution

(A): The equation of a circle with center (h, k) and radius r is \((x - h)^2 + (y - k)^2 = r^2\). Correct.
(B): The standard equation of a parabola with focus at (a, 0) and directrix \(x = -a\) is \(y^2 = 4ax\). Correct.
(C): The equation of an ellipse \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) is valid for \(a > b\), but this condition is not explicitly mentioned. Incorrect.
(D): The length of the latus rectum of the ellipse \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) is \(\frac{2b^2}{a}\). Correct.

Conclusion: The correct statements are (A), (B), and (D).

Question 16:

If \(f(x)\) is periodic with period \(T\), then which of the following are true?

(A) \(\int_{a+nT}^{b+nT} f(x) dx = \int_a^b f(x) dx\), where \(n\) is an integer.

(B) \(\int_a^{a+T} f(x) dx = \int_0^T f(x) dx\), where \(n\) is an integer.

(D) \(\int_a^{a+nT} f(x) dx = n \int_0^T f(x) dx\), where \(n\) is an integer.

Choose the correct answer from the options given below:

(A), (B), (C) only
(B), (C), (D) only
(B), (A), (D) only
(A), (B), (C), (D)

Correct Answer: 4. (A), (B), (C), (D)

View Solution

(A): \(\int_{a+nT}^{b+nT} f(x) dx = \int_a^b f(x) dx\), valid for periodic \(f(x)\).
(B): \(\int_a^{a+T} f(x) dx = \int_0^T f(x) dx\), valid over one period.
(C): \(\int_0^{nT} f(x) dx = n \int_0^T f(x) dx\), valid over multiple periods.
(D): \(\int_a^{a+nT} f(x) dx = n \int_0^T f(x) dx\), valid over \(n\) periods.

Conclusion: All statements are true.

Question 17:

Choose the correct statements.

(A) Equation of the line passing through \((x_1, y_1)\) and parallel to \(ax + by + c = 0\) is:

\(a(y - y_1) + b(x - x_1) = 0.\)

(B) Equation of the line passing through \((x_1, y_1)\) and perpendicular to \(ax + by + c = 0\) is:

\(b(x - x_1) - a(y - y_1) = 0.\)

(C) Equation of the line passing through \((x_1, y_1)\) and making an angle \(\theta\) with \(y = x \tan \alpha + c\) is:

\(y - y_1 = \tan(\alpha \pm \theta)(x - x_1).\)

(D) Equation of the line if its intercepts on the axes are \(a, b\) is:

\(\frac{x}{a} + \frac{y}{b} = 1.\)

Choose the correct answer from the options given below:

(B), (C), (D) only
(A), (B), (C) only
(A), (D), (C) only
(A), (B), (C), (D)

Correct Answer: 1. (B), (C), (D) only

View Solution

(A): Incorrect, as it does not guarantee the line passes through \((x_1, y_1)\).
(B): Correct. The equation of the line perpendicular to \(ax + by + c = 0\) is \(b(x - x_1) - a(y - y_1) = 0.\)
(C): Correct. The equation making an angle \(\theta\) is \(y - y_1 = \tan(\alpha \pm \theta)(x - x_1).\)
(D): Correct. The intercept form is \(\frac{x}{a} + \frac{y}{b} = 1.\)

Conclusion: Only (B), (C), and (D) are correct.

Question 18:

Which of the following are true?

(A) Line \(lx + my + n = 0\) will touch the circle \(x^2 + y^2 + 2gx + 2fy + c = 0\) if:

\((lg + mf - n)^2 = (l^2 + m^2)(g^2 + f^2 - c).\)

(B) If the center is \((h, k)\) and the radius is \(r\), then the equation of the circle is:

\((x - h)^2 + (y - k)^2 = r^2.\)

(C) If coordinates of the endpoints of the diameter of a circle are \((x_1, y_1)\) and \((x_2, y_2)\), then the equation of the circle is:

\((x - x_1)(x - x_2) + (y - y_1)(y - y_2) = 0.\)

(D) The general point on a circle \(x^2 + y^2 = a^2\) is:

\((a \sin \theta, a \cos \theta).\)

Choose the correct answer from the options given below:

(A), (B), and (D) only
(A), (B), and (C) only
(A), (B), (C), and (D)
(B), (C), and (D) only

Correct Answer: 3. (A), (B), (C), and (D)

View Solution

(A): Correct. The condition satisfies the requirement for a line to touch a circle.
(B): Correct. The equation of a circle with center \((h, k)\) and radius \(r\) is \((x - h)^2 + (y - k)^2 = r^2\).
(C): Correct. The equation with endpoints of the diameter matches the given condition.
(D): Correct. The parametric form of a circle's general point is \((a \sin \theta, a \cos \theta).\)

Conclusion: All statements (A), (B), (C), and (D) are correct.

Question 19:

\(\tan \theta =\)

\(\frac{1 - \cos 2\theta}{\sin 2\theta}\)
\(\frac{\sin 2\theta}{1 + \cos 2\theta}\)
\(\frac{\sqrt{1 - \cos 2\theta}}{\sqrt{1 + \cos 2\theta}}\)
\(\frac{\cos 2\theta}{1 + \cos 2\theta}\)

Choose the correct answer from the options given below:

(A), (B), and (D) only
(A), (B), and (C) only
(A), (B), (C), and (D)
(B), (C), and (D) only

Correct Answer: 2. (A), (B), and (C) only

View Solution

(A): Correct. \(\frac{1 - \cos 2\theta}{\sin 2\theta} = \tan \theta.\)
(B): Correct. \(\frac{\sin 2\theta}{1 + \cos 2\theta} = \tan \theta.\)
(C): Correct. \(\frac{\sqrt{1 - \cos 2\theta}}{\sqrt{1 + \cos 2\theta}} = \tan \theta.\)
(D): Incorrect. \(\frac{\cos 2\theta}{1 + \cos 2\theta} \neq \tan \theta.\)

Conclusion: The correct statements are (A), (B), and (C).

Question 20:

If \(a, b, c\) are the lengths of \(BC, CA,\) and \(AB\) of a triangle \(ABC\) respectively, then:

\(\tan \left[\frac{B - C}{2}\right] = \frac{(a - b)(a + b)}{c} \cot \left(\frac{A}{2}\right)\)
\(\tan \left[\frac{C - A}{2}\right] = \frac{(c - a)}{(c + a)} \cot \left(\frac{B}{2}\right)\)
\(\tan \left[\frac{B - C}{2}\right] = \frac{(b - c)}{(b + c)} \cot \left(\frac{A}{2}\right)\)
\(\tan \left[\frac{A - B}{2}\right] = \frac{(a - b)}{(a + b)} \cot \left(\frac{C}{2}\right)\)

Choose the correct answer from the options given below:

(A), (B), and (D) only
(A), (B), and (C) only
(A), (B), (C), and (D)
(B), (C), and (D) only

Correct Answer: 4. (B), (C), and (D) only

View Solution

(A): Incorrect. The formula is not consistent with the relationship.
(B): Correct. \(\tan \left[\frac{C - A}{2}\right] = \frac{(c - a)}{(c + a)} \cot \left(\frac{B}{2}\right).\)
(C): Correct. \(\tan \left[\frac{B - C}{2}\right] = \frac{(b - c)}{(b + c)} \cot \left(\frac{A}{2}\right).\)
(D): Correct. \(\tan \left[\frac{A - B}{2}\right] = \frac{(a - b)}{(a + b)} \cot \left(\frac{C}{2}\right).\)

Conclusion: The correct statements are (B), (C), and (D).

Question 21:

A student was asked to prove a statement by induction. The student proved:

\(P(5)\) is true.
Truth of \(P(n) \implies\) truth of \(P(n+1)\), \(n \in \mathbb{N}\).

On the basis of this, the student could conclude that:

(A) \(P(n)\) is true for no value of \(n\).
(B) \(P(n)\) is true for all \(n \leq 5\).
(C) \(P(n)\) is true for all \(n\).
(D) \(P(n)\) is true for all \(n \geq 5\).

Choose the correct answer from the options given below:

(D) only
(C) only
(A) and (B) only
(C) and (D) only

Correct Answer: 1. (D) only

View Solution

The base case shows that \(P(5)\) is true, establishing its validity for \(n = 5\).
The induction step proves that \(P(n)\) implies \(P(n+1)\), making \(P(n)\) true for \(n \geq 5\).
\(P(n)\) is not guaranteed for \(n < 5\).

Conclusion: The correct answer is Option 1: (D) only.

Question 22:

Which of the following are true?

\(\sum_{n=0}^{\infty} \frac{1}{(n-1)!} = e\)
\(\sum_{n=1}^{\infty} \frac{1}{n!} = e - 1\)
\(\sum_{n=0}^{\infty} \frac{1}{(n+2)!} = e - 2\)
\(\sum_{n=0}^{\infty} \frac{1}{(n+3)!} = e - 3\)

Choose the correct answer:

(A), (B), and (D) only
(A), (B), and (C) only
(B) and (D) only
(A), (B), (C), and (D)

Correct Answer: 2. (A), (B), and (C) only

View Solution

(A): True. Substituting \(k = n-1\), this summation equals \(e\).
(B): True. The series omits the first term \(\frac{1}{0!}\), resulting in \(e - 1\).
(C): True. The series omits the first two terms, resulting in \(e - 2\).
(D): False. The value does not equal \(e - 3\).

Conclusion: The correct answer is Option 2: (A), (B), and (C) only.

Question 23:

Match List I with List II

List I	List II
A. \(\lim_{x \to 0} \frac{\sin x}{x}\)	IV. \(\frac{\pi}{180^\circ}\)
B. \(\lim_{x \to 0} \frac{\sin^{-1}x}{x}\)	III. \(1\)
C. \(\lim_{x \to 0} \left(1 + \frac{1}{x}\right)^x\)	II. \(e\)
D. \(\lim_{x \to 0} \tan x\)	I. \(0\)

Choose the correct answer from the options given below:

(A) - (I), (B) - (III), (C) - (III), (D) - (IV)
(A) - (I), (B) - (III), (C) - (II), (D) - (IV)
(A) - (IV), (B) - (III), (C) - (II), (D) - (I)
(A) - (III), (B) - (IV), (C) - (I), (D) - (II)

Correct Answer: 3. (A) - (IV), (B) - (III), (C) - (II), (D) - (I)

View Solution

(A): Matches IV. Relates to radian-degree conversion.
(B): Matches III. At \(x = 0\), evaluates to 1.
(C): Matches II. Exponential limit evaluates to \(e\).
(D): Matches I. \(\tan x \to 0\) as \(x \to 0\).

Conclusion: The correct answer is Option 3.

Question 24:

Match List I with List II

List I	List II
A. \(\int \left[\sin(\log x) + \cos(\log x)\right] dx\)	III. \(x \sin (\log x) + C\)
B. \(\int \frac{dx}{1 + \sin x + \cos x}\)	II. \(\log\left\|1 + \tan \frac{x}{2}\right\| + C\)
C. \(\int \frac{\cos x + \sin x}{x + \cos x} dx\)	IV. \(\log \left(\frac{x}{x + \cos x}\right) + C\)
D. \(\int \frac{\cos x}{\sin x + \cos x} dx\)	I. \(\frac{1}{2} \left(x + \log(\sin x + \cos x)\right) + C\)

Choose the correct answer from the options given below:

(A) - (IV), (B) - (III), (C) - (II), (D) - (I)
(A) - (I), (B) - (IV), (C) - (III), (D) - (II)
(A) - (III), (B) - (IV), (C) - (II), (D) - (I)
(A) - (III), (B) - (II), (C) - (IV), (D) - (I)

Correct Answer: 4. (A) - (III), (B) - (II), (C) - (IV), (D) - (I)

View Solution

(A): Matches III. Integration gives \(x \sin(\log x) + C\).
(B): Matches II. Simplifies to \(\log\left|1 + \tan \frac{x}{2}\right| + C\).
(C): Matches IV. Simplifies to \(\log\left(\frac{x}{x + \cos x}\right) + C\).
(D): Matches I. Simplifies to \(\frac{1}{2} \left(x + \log(\sin x + \cos x)\right) + C\).

Conclusion: The correct answer is Option 4.

Question 25:

Match List I with List II

List I	List II
A. Circle with origin as centre and radius \(a\)	III. \(x^2 + y^2 = a^2\)
B. Sphere with centre at origin and radius \(a\)	I. \(x^2 + y^2 + z^2 = a^2\)
C. Hyperbola	II. \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\)
D. Ellipse	IV. \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\)

Choose the correct answer from the options given below:

(A) - (I), (B) - (III), (C) - (II), (D) - (IV)
(A) - (III), (B) - (I), (C) - (IV), (D) - (II)
(A) - (III), (B) - (I), (C) - (II), (D) - (IV)
(A) - (III), (B) - (IV), (C) - (I), (D) - (II)

Correct Answer: 3. (A) - (III), (B) - (I), (C) - (II), (D) - (IV)

View Solution

(A): Matches III. The equation of a circle with centre at origin and radius \(a\) is \(x^2 + y^2 = a^2\).
(B): Matches I. The equation of a sphere with centre at origin and radius \(a\) is \(x^2 + y^2 + z^2 = a^2\).
(C): Matches II. A hyperbola is represented as \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\).
(D): Matches IV. An ellipse is represented as \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\).

Conclusion: The correct answer is Option 3.

Question 26:

Which of the following is the value of the variable which divides the total observations into two equal halves?

Arithmetic Mean
Median
Mode
Standard Deviation

Correct Answer: 2. Median

View Solution

The Median is the value of a variable that separates the dataset into two equal halves. It is the middle value in an ordered dataset such that 50% of the observations lie below it and 50% lie above it.

Arithmetic Mean: It is the average of the dataset but does not divide it into equal halves.
Mode: It is the most frequent value in the dataset.
Standard Deviation: It measures the spread of the data around the mean and is not related to dividing the data.

Conclusion: The median is the correct choice as it divides the dataset into two equal parts.

Question 27:

The arithmetic mean of squares of first n natural numbers is:

n * (n + 1) / 2
(n + 1) / 6
((n + 1) * (2n + 1)) / 6
((n^2) - 1) / 6

Correct Answer: 3. ((n + 1) * (2n + 1)) / 6

View Solution

The sum of squares of the first n natural numbers is given by:

S = (n * (n + 1) * (2n + 1)) / 6

The arithmetic mean (AM) is the sum divided by n:

AM = S / n = ((n * (n + 1) * (2n + 1)) / 6) / n = ((n + 1) * (2n + 1)) / 6

Conclusion: The arithmetic mean formula for the squares of natural numbers is derived as ((n + 1) * (2n + 1)) / 6.

Question 28:

Coefficient of correlation is independent of:

Shift of origin and change of scale
Shift of origin but not change of scale
Change of scale but not shift of origin
Neither shift of origin nor change of scale

Correct Answer: 1. Shift of origin and change of scale

View Solution

The coefficient of correlation (r) is computed as:

r = Cov(X, Y) / (σ_X * σ_Y)

Shift of Origin: Adding/subtracting constants to variables does not affect r.
Change of Scale: Multiplying/dividing variables by constants also does not affect r because standard deviations adjust proportionally.

Conclusion: The coefficient of correlation remains unaffected by both the shift of origin and the change of scale.

Question 29:

Which of the following measures of dispersion is easiest to understand and easiest to calculate?

Mean Deviation
Mode
Range
Standard Deviation

Correct Answer: 3. Range

View Solution

Mean Deviation: Involves calculating the average of absolute deviations from the mean/median, requiring more computation.
Mode: A measure of central tendency, not dispersion.
Range: The difference between maximum and minimum values, simple to calculate.
Standard Deviation: Measures data spread around the mean, more complex to compute.

Conclusion: The Range is the simplest and easiest measure of dispersion.

Question 30:

Let x_1, x_2, ..., x_n be n observations with x̄ as the mean, the variance is given by:

n * Σ(x_i - x̄)^2
(1 / n) * Σ(x_i - x̄)^2
(n / 2) * Σ(x_i - x̄)^2
sqrt((1 / n) * Σ(x_i - x̄)^2)

Correct Answer: 2. (1 / n) * Σ(x_i - x̄)^2

View Solution

Variance is a measure of the spread of data points around the mean. It is defined as:

Variance = Σ(x_i - x̄)^2 / n

x_i: Each individual observation.
x̄: The mean of the observations.
n: Total number of observations.

Conclusion: Option 2 correctly represents the formula for variance, which is the average of squared deviations.

Question 31:

Marks obtained by four students are 25, 35, 45, 55. The mean deviation from the mean is:

Correct Answer: 1. 10

View Solution

The formula for mean deviation from the mean is:

Mean Deviation = Sum of |x_i - x̄| / n

Calculate the Mean (x̄):
x̄ = (25 + 35 + 45 + 55) / 4 = 40
Calculate Absolute Deviations:
|25 - 40| = 15, |35 - 40| = 5, |45 - 40| = 5, |55 - 40| = 15
Sum of Absolute Deviations:
15 + 5 + 5 + 15 = 40
Calculate Mean Deviation:
Mean Deviation = 40 / 4 = 10

Conclusion: The mean deviation from the mean is 10.

Question 32:

The Quartile deviation of daily wages (in Rs.) of 7 persons is given as 12, 7, 15, 10, 17, 25, 5. Find the Quartile Deviation:

Correct Answer: 3. 5.5

View Solution

The formula for quartile deviation is:

Q.D. = (Q3 - Q1) / 2

Arrange data in ascending order:
5, 7, 10, 12, 15, 17, 25
Calculate Q1 (lower quartile):
Q1 = Median of 5, 7, 10 → Q1 = 7
Calculate Q3 (upper quartile):
Q3 = Median of 15, 17, 25 → Q3 = 17
Compute Quartile Deviation:
Q.D. = (17 - 7) / 2 = 5.5

Conclusion: The Quartile Deviation of the given data is 5.5.

Question 33:

Spearman's formula for correlation, if d is the difference between the ranks and n is the number of pairs in the data, is:

1 + (6 Σd²) / n(n² - 1)
1 - Σd² / n(n² - 1)
1 - (6 Σd²) / n(n² - 1)
1 + Σd² / n(n² - 1)

Correct Answer: 3. 1 - (6 Σd²) / n(n² - 1)

View Solution

Spearman's rank correlation formula is given as:

r_s = 1 - (6 Σd²) / n(n² - 1)

where:

d = difference between ranks of paired observations
n = number of pairs
Σd² = sum of squared rank differences

Conclusion: This formula computes the Spearman rank correlation.

Question 34:

The line of regression of x on y estimates:

x for a given value of y
y for a given value of x
Covariance of x and y
Intercept of x

Correct Answer: 1. x for a given value of y

View Solution

The regression line of x on y estimates x as:

x = a + by

where:

a = intercept
b = slope = Cov(x, y) / Var(y)

Conclusion: The regression of x on y predicts the value of x for a given value of y.

Question 35:

If x, y are two independent variables, then:

cov(x, y) = 1
cov(x, y) = -1
cov(x, y) = 0
cov(x, y) = ±1

Correct Answer: 3. cov(x, y) = 0

View Solution

For two independent variables:

cov(x, y) = E(xy) - E(x)E(y) = 0

Key Points:

Independence implies zero covariance.
Zero covariance does not imply independence.

Conclusion: The covariance of two independent variables is always 0.

Question 36:

For a binomial distribution B(n, p):

Mean = Variance
Mean > Variance
Mean < Variance
No relation exists between Mean and Variance

Correct Answer: 2. Mean > Variance

View Solution

For a binomial distribution B(n, p):

Mean: n × p
Variance: n × p × (1 - p)

Since the variance includes the factor (1 - p) and p lies between 0 and 1, the variance is always less than the mean.

Conclusion: The mean is always greater than the variance for a binomial distribution.

Question 37:

For any given set of observations, which of the following relationships is correct?

Arithmetic mean ≥ Geometric mean ≥ Harmonic mean
Arithmetic mean ≤ Geometric mean ≤ Harmonic mean
Arithmetic mean ≤ Geometric mean ≥ Harmonic mean
Arithmetic mean ≥ Geometric mean ≤ Harmonic mean

Correct Answer: 1. Arithmetic mean ≥ Geometric mean ≥ Harmonic mean

View Solution

The inequality for any positive dataset is:

Arithmetic Mean (AM) ≥ Geometric Mean (GM) ≥ Harmonic Mean (HM).

This equality holds if and only if all observations are identical.

Conclusion: Arithmetic Mean is always greater than or equal to Geometric Mean, which in turn is greater than or equal to Harmonic Mean.

Question 38:

Objectives of measures of dispersion are:

(A) To judge the reliability of measures of central tendency
(B) To make the comparative study of variability of two series
(C) To get a single value which is representative of mass data
(D) To obtain other statistical measures for further analysis of data

Options:

(A), (B), (D) only
(B), (C), (D) only
(A), (D), (C) only
(B), (D), (A), (C)

Correct Answer: 1. (A), (B), (D) only

View Solution

The primary objectives of measures of dispersion are:

(A) To judge the reliability of measures of central tendency.
(B) To make a comparative study of variability of two series.
(D) To obtain other statistical measures like variance and standard deviation.

Explanation: Option (C) is incorrect because dispersion focuses on spread, not a single representative value.

Conclusion: The correct objectives are (A), (B), and (D) only.

Question 39:

Which of the following are true?

(A) Standard Deviation is independent of the change of origin
(B) Standard Deviation is the minimum root mean square deviation
(C) Coefficient of standard deviation is obtained by dividing the standard deviation by the arithmetic mean
(D) Probability error is equal to 0.67 times the standard deviation

Options:

(A), (B), (C) only
(B), (C), (D) only
(B), (A), (D) only
(A), (B), (C), (D)

Correct Answer: 4. (A), (B), (C), (D)

View Solution

(A) Standard deviation is independent of the change of origin.
(B) It represents the minimum root mean square deviation.
(C) Coefficient of standard deviation is obtained by dividing standard deviation by the arithmetic mean.
(D) Probability error is 0.67 times the standard deviation.

Conclusion: All statements are true.

Question 40:

In case of normal distribution, the relationship between mean and deviations are:

(A) Mean ± Quartile Deviation covers 50% of the observations of the distribution
(B) Mean ± Mean Deviation covers 57.5% of the observations of the distribution
(C) Mean ± Standard Deviation covers 68.27% of the observations of the distribution
(D) Mean ± 2 Standard Deviation covers 99.73% of the observations of the distribution

Options:

(A), (B), (C) only
(A), (B), (C), (D)
(A), (D), (C) only
(B), (D), (A) only

Correct Answer: 1. (A), (B), (C) only

View Solution

(A) Mean ± Quartile Deviation includes 50% of the data.
(B) Mean ± Mean Deviation includes 57.5% of the data.
(C) Mean ± Standard Deviation includes 68.27% of the data.

Conclusion: The correct relationships are (A), (B), and (C).

Question 41:

Which of the following are true?

(A) Coefficient of Quartile Deviation is (Q3 - Q1) / (Q3 + Q1)
(B) Coefficient of Quartile Deviation is (Q3 + Q1) / (Q3 - Q1)
(C) The relationship between mean, median, and mode is Mode = 3Median - 2Mean
(D) The relationship between mean, median, and mode is Mode = 2Median - 3Mean

Choose the correct answer from the options given below:

(A), (D) only
(A), (C) only
(B), (D) only
(B), (C) only

Correct Answer: 2. (A), (C) only

View Solution

(A): Correct. The formula for Coefficient of Quartile Deviation is (Q3 - Q1) / (Q3 + Q1).
(B): Incorrect. This reverses the numerator and denominator.
(C): Correct. The relationship Mode = 3Median - 2Mean is valid for moderately skewed distributions.
(D): Incorrect. This formula does not represent the relationship.

Conclusion: Statements (A) and (C) are correct.

Question 42:

Which of the following are true?

(A) Median can be graphically determined from Ogive
(B) Range is a measure of Dispersion
(C) Mean deviation from the median is greater than that measured from any other value
(D) Mean is the most suitable measure of central location when the distribution is normal

Choose the correct answer from the options given below:

(A), (B), and (D) only
(A), (B), and (C) only
(A), (B), (C), and (D)
(B), (C), and (D) only

Correct Answer: 1. (A), (B), and (D) only

View Solution

(A): Correct. Median can be graphically determined from an ogive by identifying the value at the 50th percentile.
(B): Correct. Range is a measure of dispersion that shows the difference between the maximum and minimum values.
(C): Incorrect. Mean deviation from the mean is smaller than that from the median.
(D): Correct. The mean is the most suitable measure of central location for normally distributed data.

Conclusion: Statements (A), (B), and (D) are correct.

Question 43:

Which of the following are true?

(A) A group of objects or observations is referred to as a population
(B) A population includes limited elements from a set of data
(C) A portion of a population selected to represent the population is referred to as a sample
(D) An observed set of the population that has been selected for analysis is referred to as a sample

Choose the correct answer from the options given below:

(A), (B), and (D) only
(A), (B), and (C) only
(A), (B), (C), and (D)
(A), (C), and (D) only

Correct Answer: 4. (A), (C), and (D) only

View Solution

(A): Correct. A group of objects or observations is called a population.
(B): Incorrect. A population includes all elements, not limited elements, from a dataset.
(C): Correct. A sample is a portion of a population selected to represent the entire population.
(D): Correct. A sample is an observed set of data derived from the population for analysis.

Conclusion: Statements (A), (C), and (D) are correct.

Question 44:

Which of the following are true?

(A) A measurable characteristic of a population is called a statistic
(B) A measurable characteristic of a sample is called a statistic
(C) A parameter is used to describe the population
(D) A parameter is used to describe the sample

Choose the correct option from the below:

(A) and (D) only
(B) and (D) only
(A) and (C) only
(B) and (C) only

Correct Answer: 4. (B) and (C) only

View Solution

(A): Incorrect. A measurable characteristic of a population is called a parameter, not a statistic.
(B): Correct. A measurable characteristic of a sample is referred to as a statistic.
(C): Correct. A parameter is used to describe the population.
(D): Incorrect. A parameter is not used to describe the sample; instead, it describes the population.

Conclusion: Statements (B) and (C) are correct.

Question 45:

Which of the following are true?

(A) Cluster sampling is a type of probability sampling
(B) Systematic sampling is a type of probability sampling
(C) Snowball sampling is a type of non-probability sampling
(D) Stratified sampling is a type of non-probability sampling

Choose the correct option from below:

(A), (B), and (D) only
(A), (B), and (C) only
(A), (B), (C), and (D)
(B), (C), and (D) only

Correct Answer: 2. (A), (B), and (C) only

View Solution

(A): Correct. Cluster sampling is a probability sampling method where groups, not individuals, are randomly selected.
(B): Correct. Systematic sampling is a type of probability sampling where every kth individual is selected.
(C): Correct. Snowball sampling is a non-probability sampling method, often used for hard-to-reach populations.
(D): Incorrect. Stratified sampling is a type of probability sampling where the population is divided into strata.

Conclusion: Statements (A), (B), and (C) are correct.

Question 46:

Match List I with List II

List I:

(A) Mean deviation about the mean for the data 6, 7, 10, 12, 13, 4, 8, 12
(B) Mean deviation about the median for the data 3, 9, 5, 3, 12, 10, 18, 4, 7, 19, 21
(C) Variance of the data 6, 8, 10, 12, 14, 16, 18, 20, 22, 24
(D) Mean of first 10 multiples of 3

List II:

I. 5.27
II. 16.50
III. 2.75
IV. 5.74

Choose the correct answer from the options given below:

(A) - (I), (B) - (II), (C) - (III), (D) - (IV)
(A) - (I), (B) - (III), (C) - (IV), (D) - (II)
(A) - (III), (B) - (II), (C) - (IV), (D) - (I)
(A) - (III), (B) - (IV), (C) - (I), (D) - (II)

Correct Answer: 3. (A) - (III), (B) - (II), (C) - (IV), (D) - (I)

View Solution

(A) - (III): The mean deviation about the mean for the data 6, 7, 10, 12, 13, 4, 8, 12 is 2.75.
(B) - (II): The mean deviation about the median for the data 3, 9, 5, 3, 12, 10, 18, 4, 7, 19, 21 is 16.50.
(C) - (IV): The variance of the data 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 is 5.74.
(D) - (I): The mean of the first 10 multiples of 3 is 5.27.

Conclusion: Based on the calculations, Option 3 correctly matches the items in List I and List II.

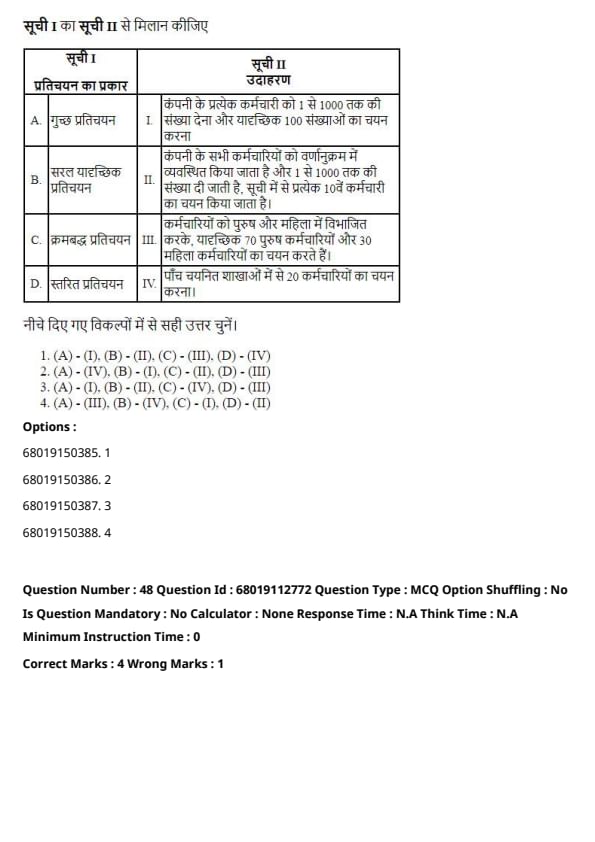
Question 47:

Match List I with List II

Match the sampling techniques in List I with their respective descriptions in List II:

List I:

(A) Cluster sampling
(B) Simple random sampling
(C) Systematic sampling
(D) Stratified sampling

List II:

(I) Assigning a number to every employee in the company from 1 to 1000 and selecting randomly 100 numbers
(II) All employees of the company arranged in alphabetical order and assigned a number 1 to 1000, every 10th employee on the list is selected
(III) Dividing the employees into male and female, select 70 male employees and 30 female employees randomly
(IV) Selecting 20 employees from five selected branches

Choose the correct answer from the options given below:

(A) - (I), (B) - (II), (C) - (III), (D) - (IV)
(A) - (IV), (B) - (I), (C) - (II), (D) - (III)
(A) - (III), (B) - (IV), (C) - (I), (D) - (II)
(A) - (III), (B) - (IV), (C) - (II), (D) - (I)

Correct Answer: 2. (A) - (IV), (B) - (I), (C) - (II), (D) - (III)

View Solution

(A) - (IV): Cluster sampling involves selecting 20 employees from five selected branches.
(B) - (I): Simple random sampling assigns a number to each employee and selects 100 randomly.
(C) - (II): Systematic sampling selects every 10th employee from an ordered list.
(D) - (III): Stratified sampling divides employees into male and female groups and selects randomly from each group.

Conclusion: The correct mapping of List I to List II is as given in Option 2.

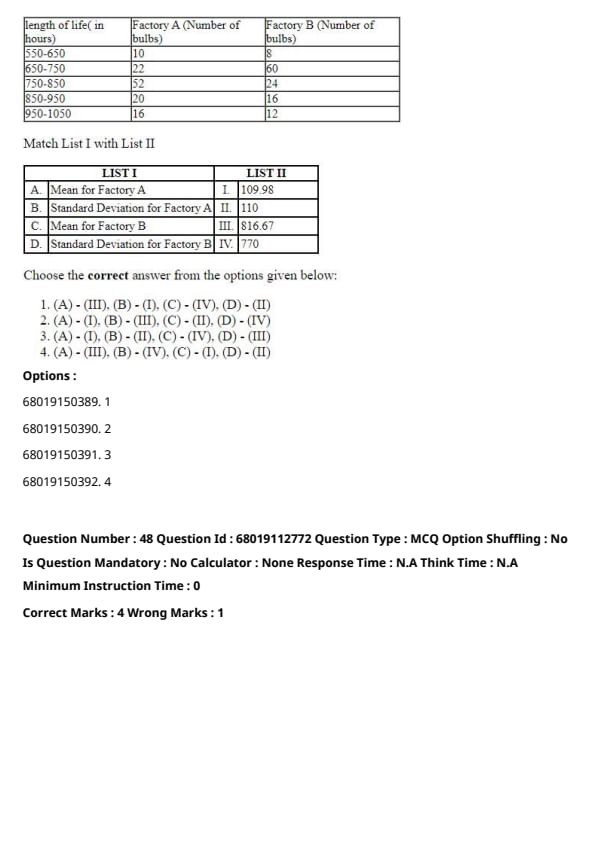
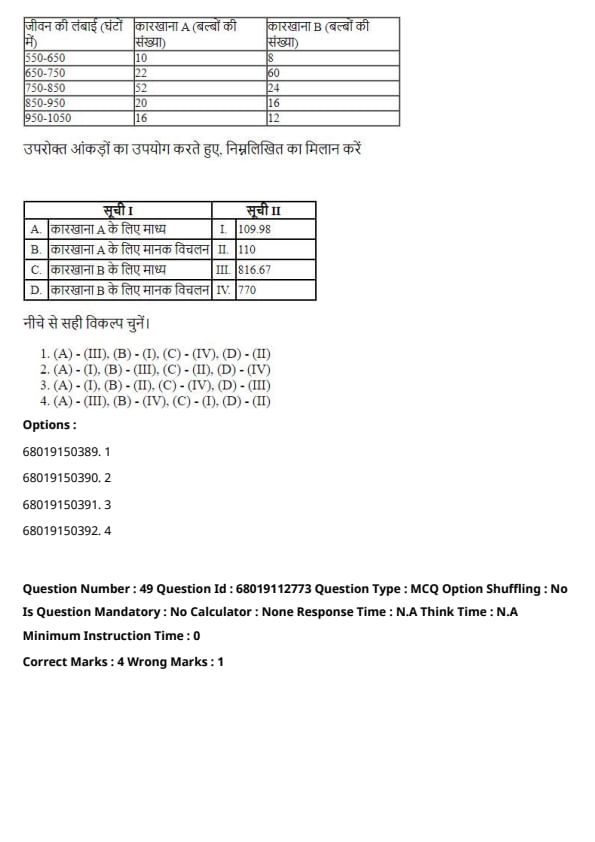
Question 48:

Match List I with List II

The following table provides the length of life (in hours) and the number of bulbs produced by two factories (Factory A and Factory B):

Length of Life (in hours)	Factory A (Number of Bulbs)	Factory B (Number of Bulbs)
550-650	10	8
650-750	22	60
750-850	52	24
850-950	20	16
950-1050	16	12

List I:

(A) Mean for Factory A
(B) Standard Deviation for Factory A
(C) Mean for Factory B
(D) Standard Deviation for Factory B

List II:

(I) 109.98
(II) 110
(III) 816.67
(IV) 770

Choose the correct answer from the options given below:

(A) - (III), (B) - (I), (C) - (IV), (D) - (II)
(A) - (I), (B) - (III), (C) - (II), (D) - (IV)
(A) - (III), (B) - (II), (C) - (I), (D) - (IV)
(A) - (I), (B) - (IV), (C) - (III), (D) - (II)

Correct Answer: 1. (A) - (III), (B) - (I), (C) - (IV), (D) - (II)

View Solution

(A) - (III): The mean for Factory A is calculated as 816.67, aligning it with List II (III).
(B) - (I): The standard deviation for Factory A is 109.98, matching List II (I).
(C) - (IV): The mean for Factory B is 770, which corresponds to List II (IV).
(D) - (II): The standard deviation for Factory B is 110, linking it to List II (II).

Conclusion: The correct mapping of List I to List II is as given in Option 1.

Question 49:

Match List I with List II

List I:

(A) Mean of First n natural numbers
(B) Mean deviation about mean of the set of first n natural numbers when n is an odd number
(C) Mean deviation about mean of the set of first n natural numbers when n is an even number
(D) Variance of first n natural numbers

List II:

(I) (n²−1)/12
(II) n/4
(III) (n+1)/2
(IV) (n²−1)/4n

Choose the correct answer from the options given below:

(A) - (III), (B) - (II), (C) - (I), (D) - (IV)
(A) - (II), (B) - (III), (C) - (IV), (D) - (I)
(A) - (I), (B) - (III), (C) - (IV), (D) - (II)
(A) - (III), (B) - (IV), (C) - (II), (D) - (I)

Correct Answer: 4. (A) - (III), (B) - (IV), (C) - (II), (D) - (I)

View Solution

(A) - (III): The mean of the first n natural numbers is calculated as (n+1)/2.
(B) - (IV): The mean deviation about the mean when n is odd is (n²−1)/4n.
(C) - (II): The mean deviation about the mean when n is even is n/4.
(D) - (I): The variance of the first n natural numbers is (n²−1)/12.

Conclusion: The correct mapping of List I to List II is as given in Option 4.

Question 50:

Match List I with List II

List I:

(A) Point of estimate of the population mean from the data 5, 8, 10, 7, 10, 14
(B) Point of estimate of the population standard deviation from the data 5, 8, 10, 7, 10, 14
(C) Point estimate of the proportion in the population who respond YES, i.e., 80 out of 200 sample of individuals in a survey
(D) Point estimate of the proportion in the population who respond NO, i.e., 100 out of 200 sample of individuals in a survey

List II:

(I) 9
(II) 3.1
(III) 0.5
(IV) 0.4

Choose the correct answer from the options given below:

(A) - (I), (B) - (II), (C) - (III), (D) - (IV)
(A) - (III), (B) - (I), (C) - (II), (D) - (IV)
(A) - (I), (B) - (II), (C) - (IV), (D) - (III)
(A) - (III), (B) - (IV), (C) - (I), (D) - (II)

Correct Answer: 3. (A) - (I), (B) - (II), (C) - (IV), (D) - (III)

View Solution

(A) - (I): The mean of the data 5, 8, 10, 7, 10, 14 is calculated as (ΣX) / n = 54 / 6 = 9.
(B) - (II): The standard deviation is calculated as 3.1 for the given data.
(C) - (IV): The proportion of individuals who respond YES is calculated as 80 / 200 = 0.4.
(D) - (III): The proportion of individuals who respond NO is calculated as 100 / 200 = 0.5.

Conclusion: The correct mapping of List I to List II is as given in Option 3.

Question 51:

Which unit of the CPU performs the mathematical and logical operations?

Arithmetic Logic Unit
Control Unit
Memory Unit
Input and Output Unit

Correct Answer: 1. Arithmetic Logic Unit

View Solution

The Arithmetic Logic Unit (ALU) is a critical component of the CPU responsible for performing all arithmetic and logical operations. It processes data by executing mathematical computations (like addition, subtraction) and logical comparisons (like AND, OR, NOT).

Control Unit: Directs operations within the computer but does not perform calculations.
Memory Unit: Stores data and instructions for processing.
Input and Output Unit: Manages data transfer between the computer and peripherals.

Conclusion: The ALU handles all mathematical and logical tasks.

Question 52:

’DBMS’ stands for?

Database Memory System
Database Management System
Display Base Memory System
Data Browsing Management System

Correct Answer: 2. Database Management System

View Solution

The Database Management System (DBMS) is software used for creating, managing, and accessing databases. It allows users to efficiently store, retrieve, and manipulate data while ensuring security and integrity.

Database Memory System: Incorrect, as it does not describe the full functionality of a DBMS.
Display Base Memory System: Irrelevant to databases.
Data Browsing Management System: Does not describe the core purpose of a DBMS.

Conclusion: A DBMS is essential for database operations in applications across various domains.

Question 53:

Short form of binary digit is...

Byte
Hertz
Bit
Watt

Correct Answer: 3. Bit

View Solution

The short form of a binary digit is Bit. It represents the smallest unit of data in a computer, which can have a value of either 0 or 1. The term “byte” represents a group of bits, typically 8.

Question 54:

Decimal number 147 is equivalent to binary number...

10010011
11010010
10001011
10010101

Correct Answer: 1. 10010011

View Solution

To convert the decimal number 147 to binary:

Divide 147 by 2 repeatedly and record the remainders.
Write the remainders in reverse order to get the binary equivalent.
Calculation:
- 147 ÷ 2 = 73 remainder 1
- 73 ÷ 2 = 36 remainder 1
- 36 ÷ 2 = 18 remainder 0
- 18 ÷ 2 = 9 remainder 0
- 9 ÷ 2 = 4 remainder 1
- 4 ÷ 2 = 2 remainder 0
- 2 ÷ 2 = 1 remainder 0
- 1 ÷ 2 = 0 remainder 1
Result: 10010011

Question 55:

1 TB is equal to...

1024 KB
1024 Bytes
1024 MB
1024 GB

Correct Answer: 4. 1024 GB

View Solution

1 Terabyte (TB) equals 1024 Gigabytes (GB). This is based on the binary system used in computing, where:

1 TB = 1024 GB

Question 56:

Which protocol is used in this address “http://www.computerstudy.co.in/ict_books.html”?

www.computerstudy.co.in
ict_books.html
http
.co.in

Correct Answer: 3. http

View Solution

The protocol used in the given address is HTTP (HyperText Transfer Protocol). It is the protocol for transmitting hypermedia documents such as HTML and is the foundation of communication on the World Wide Web.

www.computerstudy.co.in: This is the domain name, not the protocol.
ict_books.html: This refers to the file or resource on the server.
http: This is the protocol used to access the resource.
.co.in: This is the top-level domain and subdomain.

Conclusion: HTTP is the protocol used for communication in the given address.

Question 57:

Which of the following is NOT the name of a networking topology?

Mesh topology
Bus topology
Plant topology
Tree topology

Correct Answer: 3. Plant topology

View Solution

Networking topologies define the arrangement of different elements in a computer network. Common topologies include:

Mesh topology: Every node is interconnected, offering high redundancy.
Bus topology: A single cable connects all nodes in a linear arrangement.
Tree topology: A hierarchical structure combining characteristics of star and bus topologies.
Plant topology: This is not a recognized networking topology; it is an incorrect option.

Question 58:

High-speed storage areas within the computer are:

Interrupts
Registers
Buses
RAM

Correct Answer: 2. Registers

View Solution

Registers are high-speed storage areas within the CPU that store data temporarily during processing. They are faster than RAM and are used for quick access to instructions and intermediate data.

Interrupts: Signals sent to the processor to indicate an event that needs immediate attention.
Buses: Communication systems that transfer data between components.
RAM: A form of memory for temporarily storing data and instructions but slower than registers.

Conclusion: Registers are specialized, high-speed storage locations within the CPU, making them the correct answer.

Question 59:

’Buffer’ means:

Temporary area of memory.
Software running in the background.
Signals from device to the processor.
Controlling unit in the system.

Correct Answer: 1. Temporary area of memory.

View Solution

A buffer is a temporary storage area in memory that holds data while it is being transferred from one place to another. Buffers are commonly used to manage differences in data transfer rates between devices or processes.

Software running in the background: This refers to processes that run without user intervention but are unrelated to buffering.
Signals from device to the processor: These are typically referred to as interrupts, not buffers.
Controlling unit in the system: This refers to the control unit in a CPU, which is different from a buffer.

Conclusion: The correct definition of a buffer is a temporary area of memory used for managing data transfer.

Question 60:

Function of the Control Unit in the computer system is:

Carries out arithmetic operations.
Carries out logical operations.
Send signals to coordinate all components.
Hold memory locations.

Correct Answer: 3. Send signals to coordinate all components.

View Solution

The Control Unit (CU) in a computer system is responsible for managing and coordinating all components of the system. It sends signals to direct the flow of data between the processor, memory, and peripherals. It ensures that operations are carried out in a sequential and efficient manner.

Carries out arithmetic operations: This is the responsibility of the Arithmetic Logic Unit (ALU), not the Control Unit.
Carries out logical operations: This is also a function of the ALU.
Hold memory locations: This is handled by the Memory Unit.

Conclusion: The Control Unit’s primary role is to send signals to coordinate all components of the computer system, ensuring synchronized operations.

Question 61:

is an example of an Output Device.

Projector
Scanner
QR Reader
Joystick

Correct Answer: 1. Projector

View Solution

An Output Device is a hardware component that conveys information from a computer to the user or another device. Among the options:

Projector: Displays visual output on a screen and is an output device.
Scanner: Used to input images or documents into a computer, making it an input device.
QR Reader: Reads QR codes and is also an input device.
Joystick: A device used to provide input for games or simulations.

Conclusion: The projector is the correct example of an output device as it projects visual data from the computer.

Question 62:

A set of possible data values for a database is called:

Degree
Attribute
Domain
Field

Correct Answer: 3. Domain

View Solution

In the context of databases:

Domain: Refers to the set of possible values that a database attribute can have. For example, a "Gender" attribute might have a domain of "Male," "Female."
Degree: Refers to the number of attributes in a relation (not the set of values).
Attribute: Refers to a column or field in a table, not a set of values.
Field: Refers to a single piece of data within a record.

Conclusion: The domain is the correct term for the set of possible data values for an attribute in a database.

Question 63:

Arrange the following steps of Pseudocode for counting even numbers between 50 and 500 including both values:

(A) num = 50, count = 0
(B) PRINT count
(C) num = num + 2, count = count + 1
(D) WHILE num ≤ 500 THEN

Options:

(A), (C), (D), (B)
(B), (A), (C), (D)
(A), (B), (D), (C)
(A), (D), (C), (B)

Correct Answer: 4. (A), (D), (C), (B)

View Solution

The correct sequence is as follows:

Initialize the variables: num = 50 and count = 0 (Step A).
Create a loop: WHILE num ≤ 500 THEN (Step D).
Inside the loop:
- Increment num by 2 and increment count by 1 (Step C).
After exiting the loop, print the count of even numbers (Step B).

Conclusion: The logical order of the pseudocode steps is (A), (D), (C), (B).

Question 64:

ATM stands for:

Any Time Money
Automated Teller Machine
Automated Transfer Money
Automatic Transfer Machine

Correct Answer: 2. Automated Teller Machine

View Solution

The term ATM (Automated Teller Machine) refers to an electronic banking outlet that allows customers to perform financial transactions, such as withdrawing cash, checking account balances, or transferring money, without the need for direct human assistance.

Option 1: "Any Time Money" is an informal phrase, not the correct expansion.
Option 3: "Automated Transfer Money" refers to money transfers but is not the correct acronym.
Option 4: "Automatic Transfer Machine" is not the correct term.

Conclusion: Option 2 is the correct answer as ATM officially stands for Automated Teller Machine.

Question 65:

Arrange the following steps of an algorithm to calculate the factorial of a given number:

(A) Keep multiplying the Result with num until the num decreases to 1.
(B) After each multiplication, subtract 1 from num.
(C) Accept a number, num, from the user and set the value of Result as 1.
(D) Display the Result.

Options:

(C), (A), (B), (D)
(A), (B), (D), (C)
(C), (D), (A), (B)
(C), (B), (D), (A)

Correct Answer: 1. (C), (A), (B), (D)

View Solution

The correct sequence for calculating the factorial of a number is as follows:

Step 1 (C): Accept the input number and initialize Result to 1.
Step 2 (A): Multiply Result by the current value of num.
Step 3 (B): Decrease the value of num by 1 after each multiplication.
Step 4 (D): Finally, display the value of Result.

Conclusion: The logical order of the algorithm steps is (C), (A), (B), (D).

Question 66:

Arrange the following according to the given sequence: (Input Device – Output Device – Storage Device – Operating System)

(A) Ubuntu
(B) Printer
(C) Blue Ray Disk
(D) Scanner

Options:

(A), (B), (C), (D)
(D), (B), (C), (A)
(B), (A), (D), (C)
(C), (B), (D), (A)

Correct Answer: 2. (D), (B), (C), (A)

View Solution

The correct order based on the given sequence is:

Input Device: (D) Scanner is used to input data into the system.
Output Device: (B) Printer is used to provide output from the system.
Storage Device: (C) Blue Ray Disk is a storage medium for saving data.
Operating System: (A) Ubuntu is an operating system that manages hardware and software.

Conclusion: The arrangement (D), (B), (C), (A) matches the sequence Input Device – Output Device – Storage Device – Operating System.

Question 67:

Which of the following statement(s) are TRUE?

(A) Digital Communication includes E-mail, texting, and instant messaging.
(B) Trojan is an example of Social media platform.
(C) Credit card details of a person is an example of sensitive data.
(D) Digital citizen is anyone who uses digital technology along with the internet.

Options:

(A), (B) and (D) only.
(A), (B) and (C) only.
(A), (B), (C) and (D).
(A), (C) and (D) only.

Correct Answer: 4. (A), (C) and (D) only.

View Solution

(A): Digital communication includes E-mail, texting, and instant messaging. This is correct.
(B): Trojan is a type of malware, not a social media platform. Hence, this statement is incorrect.
(C): Credit card details are sensitive data as they require protection to prevent fraud. This is correct.
(D): A digital citizen refers to anyone who uses digital technology along with the internet responsibly. This statement is correct.

Conclusion: Statements (A), (C), and (D) are true, while (B) is incorrect.

Question 68:

Arrange the following data elements in order from smallest to largest:

(A) Field
(B) File
(C) Database
(D) Record

Options:

(A), (B), (D), (C).
(B), (A), (C), (D).
(A), (D), (B), (C).
(B), (A), (D), (C).

Correct Answer: 3. (A), (D), (B), (C).

View Solution

Field: The smallest unit in a data structure that holds a single value.
Record: A collection of related fields representing a single data entity.
File: A collection of records stored together.
Database: The largest data structure, consisting of multiple related files.

Conclusion: The correct order from smallest to largest is Field, Record, File, Database.

Question 69:

Which of the following statements are clear examples of Computer Ethics followed?

(A) An engineer works for a software company during the day but also does freelancing without informing his parent company.
(B) A company employs people in different countries to write software modules, and these modules are put together to produce software packages.
(C) A software engineer develops software for a security company. He used the same features for developing software for his friend’s organization.
(D) A software engineer undergoes training by a different company to improve his software development skills.

Options:

(B), (D) only.
(A), (B) and (C) only.
(C), (D) only.
(B), (C) and (D) only.

Correct Answer: 1. (B), (D) only.

View Solution

(B): Employing people globally to work on software modules and combining them ethically follows computer ethics.
(D): Improving skills through training provided by another company is a professional and ethical practice.
(A): Freelancing without informing the parent company is a violation of computer ethics.
(C): Using the same features for a friend’s organization without consent violates intellectual property ethics.

Conclusion: Statements (B) and (D) are clear examples of computer ethics being followed.

Question 70:

is an extension of Batch file.

.exe
.doc
.wav
.bat

Correct Answer: 4. .bat

View Solution

A batch file is a script file in Windows, containing a series of commands to be executed by the command-line interpreter. The extension .bat is used to indicate batch files.

Option 1 (.exe): This is an executable file format for Windows programs.
Option 2 (.doc): This is a file format for Microsoft Word documents.
Option 3 (.wav): This is a file format for audio files.

Conclusion: The correct extension for a batch file is .bat.

Question 71:

Which of the following statement(s) is/are TRUE?

(A) Virus is a program code that causes the computer to malfunction.
(B) Phishing means sending legitimate-looking emails to encourage users to give out sensitive data.
(C) Firewall examines traffic between a user's computer and the public network.
(D) Freeware is software that a user can download free of charge.

Options:

(A), (B) and (D) only.
(A), (B) and (C) only.
(A), (B), (C) and (D).
(B), (C) and (D) only.

Correct Answer: 3. (A), (B), (C) and (D).

View Solution

(A): A virus is a malicious program designed to damage or disrupt computers. This is correct.
(B): Phishing is a cyber-attack that deceives users into revealing sensitive information. This is correct.
(C): A firewall acts as a barrier that monitors and controls traffic. This is correct.
(D): Freeware is software provided at no cost. This is correct.

Conclusion: Since all the statements are true, the correct option is 3. (A), (B), (C), and (D).

Question 72:

Arrange the following types of printers in the increasing order of their printing speed:

(A) Inkjet Printer
(B) Laser Printer
(C) Dot Matrix Printer
(D) Daisy Wheel Printer

Options:

(B), (A), (D), (C)
(A), (B), (D), (C)
(B), (A), (C), (D)
(D), (C), (A), (B)

Correct Answer: 4. (D), (C), (A), (B).

View Solution

The printing speeds of the printers in increasing order are:

Daisy Wheel Printer (D): Slowest due to mechanical operation.
Dot Matrix Printer (C): Slightly faster than Daisy Wheel but still uses impact technology.
Inkjet Printer (A): Faster than impact printers with better resolution.
Laser Printer (B): The fastest among these, using advanced laser technology.

Conclusion: The correct order is (D), (C), (A), (B).

Question 73:

Match List I with List II:

List I:

(A) UMANG
(B) DIGILOCKER
(C) C-DAC
(D) PRAGATI

List II:

(I) Single mobile platform to deliver e-Gov various services across India.
(II) R & D organization of Ministry of Electronics & IT for carrying out R & D in IT, electronics, and other associated areas.
(III) Allows individuals to store, share, and verify documents and certificates.
(IV) ICT platform of Prime Minister's Office to review and monitor various Central Government projects.

Options:

(A) - (IV), (B) - (III), (C) - (II), (D) - (I)
(A) - (I), (B) - (III), (C) - (II), (D) - (IV)
(A) - (II), (B) - (III), (C) - (I), (D) - (IV)
(A) - (I), (B) - (III), (C) - (IV), (D) - (II)

Correct Answer: 2. (A) - (I), (B) - (III), (C) - (II), (D) - (IV).

View Solution

UMANG: A unified mobile platform providing access to various government services across India (I).
DIGILOCKER: A platform enabling individuals to securely store, share, and verify digital documents (III).
C-DAC: A research and development organization under the Ministry of Electronics and IT (II).
PRAGATI: An ICT-based platform for real-time governance and project monitoring by the Prime Minister’s Office (IV).

Conclusion: The associations match option 2 as the correct answer.

Question 74:

Verification of a login name and password is known as:

Configuration
Encryption
Authentication
Automation

Correct Answer: 3. Authentication

View Solution

Authentication: The process of verifying the identity of a user or system by validating login credentials like usernames and passwords. It ensures that access is restricted to authorized users.
Configuration: Involves setting up hardware or software but is unrelated to login verification.
Encryption: Protects data by converting it into a secure format but does not verify credentials.
Automation: Refers to tasks being performed automatically, unrelated to user verification.

Conclusion: Authentication is the correct term for the process of verifying login credentials.

Question 75:

Match List I with List II:

List I:

(A) CD
(B) Magnetic Tape
(C) Cache Memory
(D) DRAM

List II:

(I) It is made up of capacitors and transistors.
(II) It is a faster memory used to reduce the average time to access data from main memory.
(III) It is a long and narrow strip of plastic having thin magnetic material coated on.
(IV) It stores and retrieves data with the help of an optical mechanism.

Options:

(A) - (IV), (B) - (III), (C) - (II), (D) - (I)
(A) - (III), (B) - (IV), (C) - (II), (D) - (I)
(A) - (IV), (B) - (III), (C) - (I), (D) - (II)
(A) - (III), (B) - (IV), (C) - (I), (D) - (II)

Correct Answer: 1. (A) - (IV), (B) - (III), (C) - (II), (D) - (I).

View Solution

CD: Stores and retrieves data using an optical mechanism (IV).
Magnetic Tape: A long and narrow strip of plastic coated with magnetic material (III).
Cache Memory: A faster memory designed to reduce data access time (II).
DRAM: Made up of capacitors and transistors (I).

Conclusion: The correct matching is as per option 1.