KCET 2023 Mathematics Question Paper Set B1 is available here for download. KCET 2023 Question Paper May 20 Shift 2 2:30 PM to 3:50 PM was conducted for Mathematics Paper. KCET 2023 Question Paper included 60 MCQ-based questions in total. Each candidate will be awarded +1 for correct answers, however, there will be no negative marking for incorrect responses. Students got 80 minutes to attempt KCET 2023 Mathematics Question Paper.
KCET 2023 Mathematics Question Paper with Answer Key PDF Set B1
| KCET 2024 Mathematics Question Paper with Answer Key | Check Solutions |
KCET 2023 Mathematics Questions with Solutions
Question 1:
If y = a sin x + b cos x, then y² + (dy/dx)² is a:
If f(x) = 1 + nx + [n(n-1)x²]/2! + [n(n-1)(n-2)x³]/3! + ... + xⁿ, then f"(1) is:
If A = [[1, tan(x/2)], [tan(x/2), 1]] and AB = I, then B =:
If u = sin⁻¹[2x/(1+x²)] and v = tan⁻¹[2x/(1-x²)], then du/dv is:
The function f(x) = cot x is discontinuous on every point of the set:
An enemy fighter jet is flying along the curve given by y = -x² + 2. A soldier is placed at (3,2) and wants to shoot down the jet when it is nearest to him. Then the nearest distance is:
Evaluate ∫[2 to 5] (√(10-x)) / (5√x + 5√(10-x)) dx:
Evaluate the integral: ∫ √(cosec x – sin x) dx
If f(x) and g(x) are two functions with g(x) = x - (1/x) and f(g(x)) = x³ - (1/x³), then f'(x) is:
A circular plate of radius 5 cm is heated. Due to expansion, its radius increases at the rate of 0.05 cm/sec. The rate at which its area is increasing when the radius is 5.2 cm is:
The distance s in meters travelled by a particle in t seconds is given by s = (2t³)/3 - 18t + (5/3). The acceleration when the particle comes to rest is:
A particle moves along the curve x²/4 + y²/16 = 1. When the rate of change of abscissa is 4 times that of its ordinate, then the quadrant in which the particle lies is:
Evaluate ∫ dx/(1+3sin²x+8cos²x):
Evaluate ∫[-2 to 2] (x³ + 3x² + 3x + 3 + (x + 1)) cos x dx:
View Solution
Evaluate ∫[0 to π] (x tan x) / (sec x * csc x) dx:
In the interval (0, π/2), the area lying between the curves y = tan x and y = cot x and the x-axis is:
The area of the region bounded by the line y = x - x + 1, and the lines x = 3 and x = 5 is:
If a curve passes through the point (1, 1) and at any point (x, y) on the curve, the product of the slope of its tangent and the x-coordinate of the point is equal to the y-coordinate of the point, then the curve also passes through the point:
If (2, 3, -1) is the foot of the perpendicular from (4, 2, 1) to a plane, then the equation of the plane is:
If |a × b|² + |a · b|² = 144 and |a| = 4, then |b| is equal to:
If a + 2b + 3c = 0 and (a × b) + (b × c) + (c × a) = λ(b × c), then the value of λ is equal to:
If a line makes an angle of π/3 with each X and Y axis, then the acute angle made by the Z-axis is:
The length of perpendicular drawn from the point (3, -1, 11) to the line x/2 = (y-2)/3 = (z-3)/4 is:
If A and B are events such that P(A) = 1/4, P(A | B) = 1/2 and P(B|A) = 2/3, then P(B) is:
A bag contains 2n + 1 coins. It is known that n of these coins have heads on both sides, whereas the other n+1 coins are fair. One coin is selected at random and tossed. If the probability that the toss results in heads is 31/42, then the value of n is:
Let A = {x, y, z, u} and B = {a, b}. A function f : A → B is selected randomly. The probability that the function is an onto function is:
The modulus of the complex number (1+i)²(1+3i) ÷ (2−6i)(2−2i) is:
Given that a,b and x are real numbers and a < b, x < 0, then:
Ten chairs are numbered as 1 to 10. Three women and two men wish to occupy one chair each. First, the women choose the chairs marked 1 to 6, and then the men choose the chairs from the remaining. The number of possible ways is:
Which of the following is an empty set?
If f(x) = ax+b, where a and b are integers, f(-1) = −5 and f(3) = 3, then a and b are respectively:
The value of elog₁₀(tan 1°) + log₁₀(tan 2°) + log₁₀(tan 3°) + … + log₁₀(tan 89°) is:
The value of (sin² 14°/sin² 66°) + (sin² 66°/sin² 14°) + (tan 135°/tan 135°) is:
If n is even and the middle term in the expansion of (x² + 1/x)ⁿ is 924x⁶, then n is equal to:
The n-th term of the series 1 + 3/7 + 5/7² + 7/7³ + ... is:
If p(1/p + 1/r), q(1/r + 1/p), r(1/p + 1/q) are in A.P., then p, q, r are:
A line passes through (2, 2) and is perpendicular to the line 3x + y = 3. Its y-intercept is:
The contrapositive of the statement "If two lines do not intersect in the same plane then they are parallel." is:
The mean of 100 observations is 50 and the standard deviation is 5. Then the sum of squares of all observations is:
Let f: R → R and g : [0,∞) → R be defined by f(x) = x² and g(x) = √x. Which one of the following is not true?
Let f : R → R be defined by f(x) = 3x² - 5 and g : R → R by g(x) = x/(x²+1). Then g ο f is:




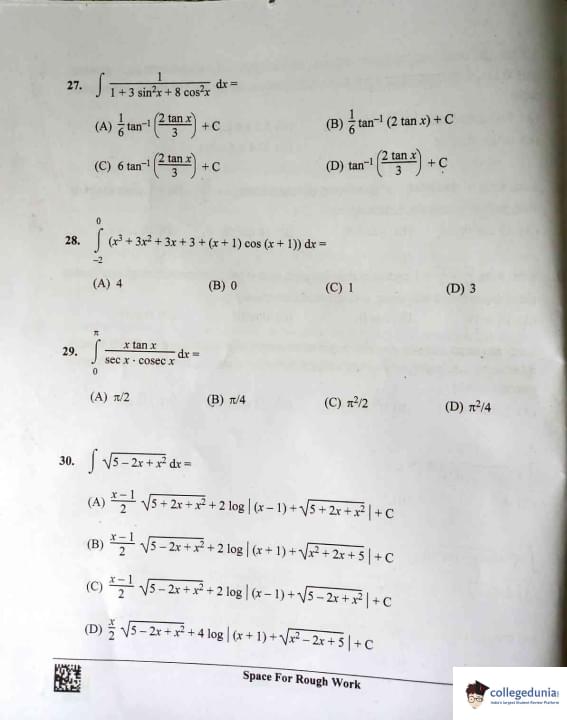






KCET 2023 Paper Analysis May 20
KCET 2023 paper analysis May 20 is available here. Candidates can check KCET 2023 paper analysis by clicking on the link provided below.
Also Check:
KCET Previous Year Question Paper
| KCET 2022 Question Paper | KCET 2021 Question Paper | KCET 2020 Question Paper |
| KCET 2019 Question Paper | KCET 2018 Question Paper | KCET 2017 Question Paper |






Comments